Simulation Study on Attosecond Inverse Compton Scattering Source from Laser Wakefield Acceleration with Near-Threshold Ionization Injection
Abstract
:1. Introduction
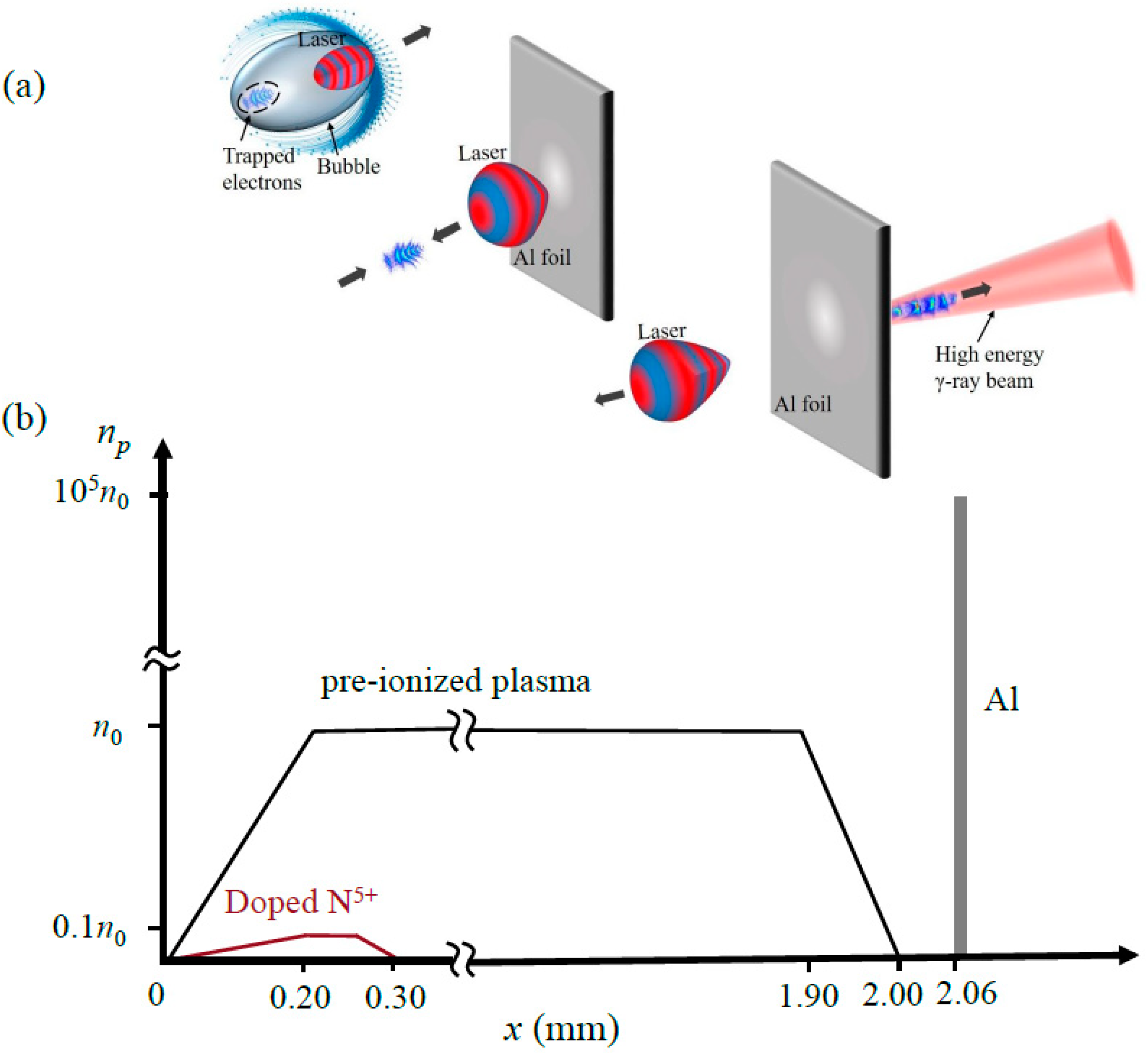
2. Simulation Setup
3. Results and Discussion
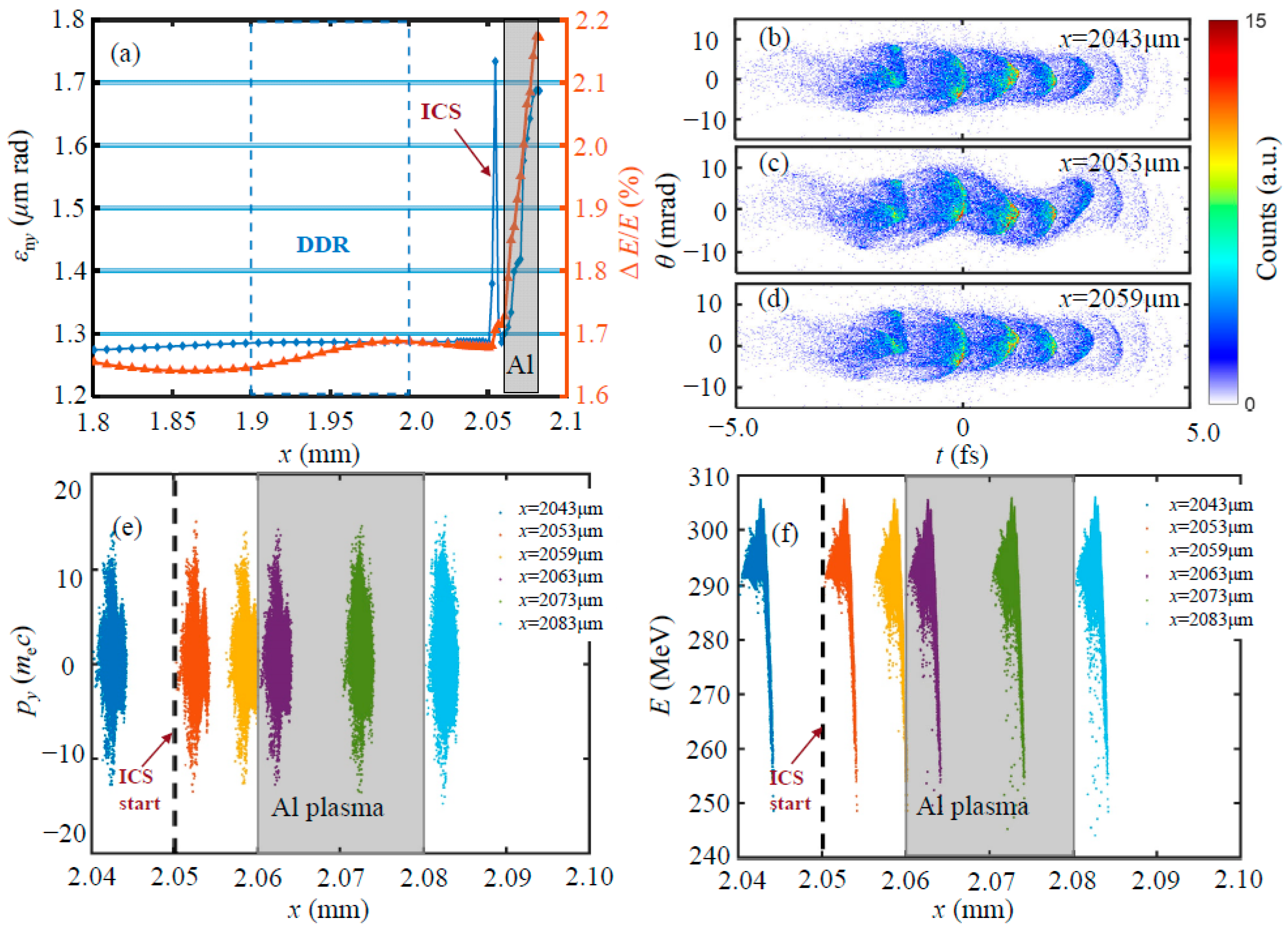
3.1. Generation of Attosecond Micro-Bunched Electron Beams from LWFA
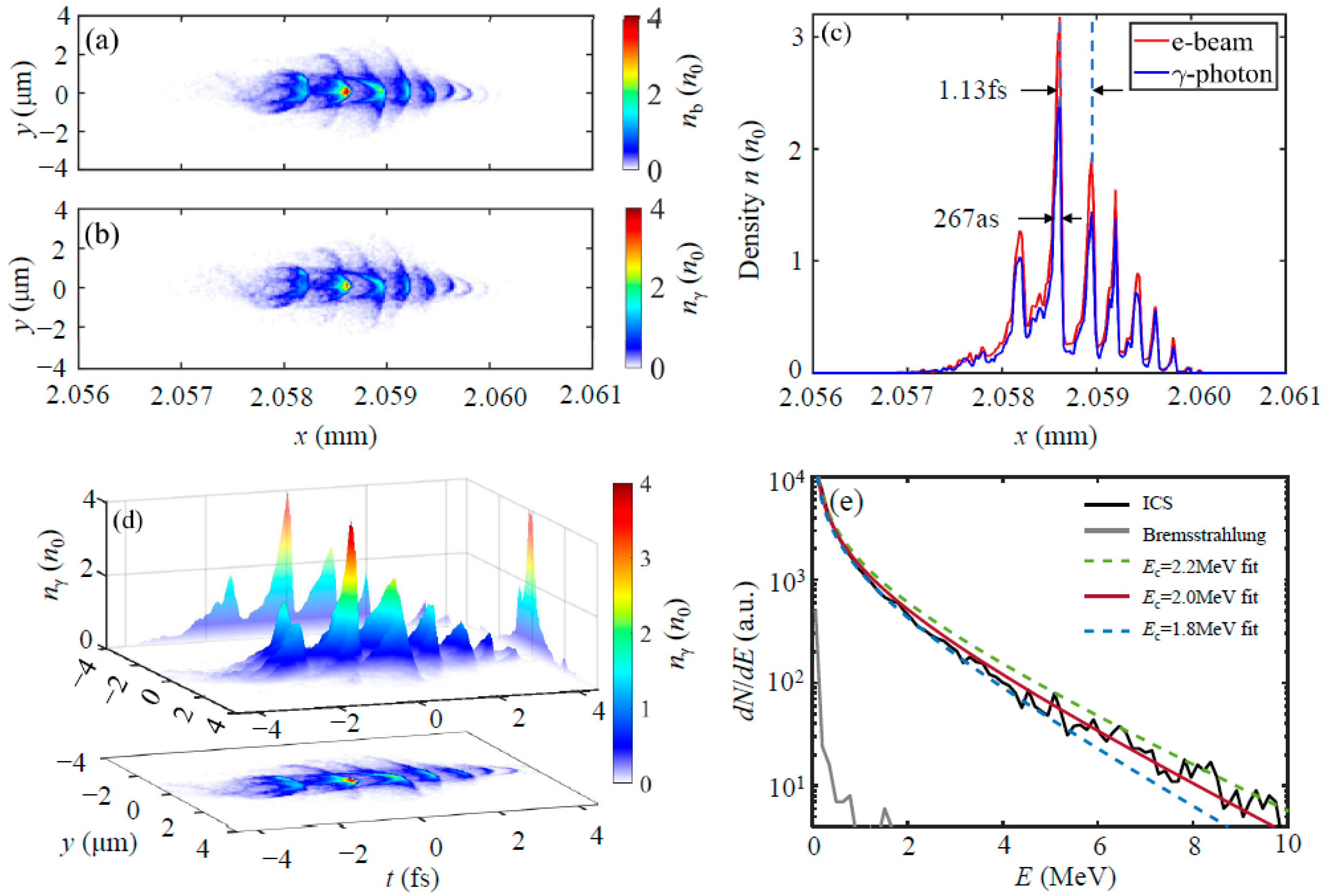
3.2. Attosecond Gamma-Ray Source from ICS
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Geddes, C.G.R.; Toth, C.S.; van Tilborg, J.; Esarey, E.; Schroeder, C.B.; Bruhwiler, D.; Nieter, C.; Cary, J.; Leemans, W.P. High-quality electron beams from a laser wakefield accelerator using plasma-channel guiding. Nature. High-quality electron beams from a laser wakefield accelerator using plasma-channel guiding. Nature 2004, 431, 538–541. [Google Scholar] [CrossRef]
- Faure, J.; Gaines, Y.; Pukhov, A.; Kiselev, S.; Gordienko, S.; Lefebvre, E.; Rousseau, J.-P.; Burgy, F.; Malka, V. A laser-plasma accelerator producing monoenergetic electron beams. Nature 2004, 431, 541–544. [Google Scholar] [CrossRef]
- Mangles, S.P.D.; Murphy, C.D.; Najmudin, Z.; Thomas, A.G.R.; Collier, J.L.; Dangor, A.E.; Divall, E.J.; Foster, P.S.; Gallacher, J.G.; Hooker, C.J.; et al. Monoenergetic beams of relativistic electrons from intense laser-plasma interactions. Nature 2004, 431, 535–538. [Google Scholar] [CrossRef]
- Kim, H.T.; Pathak, V.B.; Hojbota, C.I.; Mirzaie, M.; Pae, K.H.; Kim, C.M.; Yoon, J.W.; Sung, J.H.; Lee, S.K. Multi-GeV Laser Wakefield Electron Acceleration with PW Lasers. Appl. Sci. 2021, 11, 5831. [Google Scholar] [CrossRef]
- Aniculaesei, C.; Ha, T.; Yoffe, S.; Labun, L.; Milton, S.; McCary, E.; Spinks, M.M.; Quevedo, H.J.; Labun, O.Z.; Sain, R.; et al. The acceleration of a high-charge electron bunch to 10 GeV in a 10-cm nanoparticle-assisted wakefield accelerator. Matter Radiat. Extrem. 2024, 9, 014001. [Google Scholar] [CrossRef]
- Couperus, J.P.; Pausch, R.; Köhler, A.; Zarini, O.; Krämer, J.M.; Garten, M.; Huebl, A.; Gebhardt, R.; Helbig, U.; Bock, S.; et al. Demonstration of a beam loaded nanocoulomb-class laser wakefield accelerator. Nat. Commun. 2017, 8, 487. [Google Scholar] [CrossRef]
- Buck, A.; Nicolai, M.; Schmid, K.; Sears, C.M.; Sävert, A.; Mikhailova, J.M.; Krausz, F.; Kaluza, M.C.; Veisz, L. Real-time observation of laser-driven electron acceleration. Nat. Phys. 2011, 7, 543–548. [Google Scholar]
- Lundh, O.; Lim, J.; Rechatin, C.; Ammoura, L.; Ben-Ismaïl, A.; Davoine, X.; Gallot, G.; Goddet, J.P.; Lefebvre, E.; Malka, V.; et al. Few femtosecond, few kiloampere electron bunch produced by a laser–plasma accelerator. Few femtosecond, few kiloampere electron bunch produced by a laser–plasma accelerator. Nat. Phys. 2011, 7, 219–222. [Google Scholar] [CrossRef]
- Ke, L.T.; Feng, K.; Wang, W.T.; Qin, Z.Y.; Yu, C.H.; Wu, Y.; Chen, Y.; Qi, R.; Zhang, Z.J.; Xu, Y.; et al. Near-GeV Electron Beams at a Few Per-Mille Level from a Laser Wakefield Accelerator via Density-Tailored Plasma. Phys. Rev. Lett. 2021, 126, 214801. [Google Scholar] [CrossRef]
- Maier, A.R.; Delbos, N.M.; Eichner, T.; Hübner, L.; Jalas, S.; Jeppe, L.; Jolly, S.W.; Weingartner, M.R.; Raith, S.; Popp, A.; et al. Ultralow emittance electron beams from a laser-wakefield accelerator. Phys. Rev. Spec. Top. Accel. Beams 2012, 15, 111302. [Google Scholar]
- Plateau, G.R.; Geddes, C.G.R.; Thorn, D.B.; Chen, M.; Benedetti, C.; Esarey, E.; Gonsalves, A.J.; Matlis, N.H.; Nakamura, K.; Schroeder, C.B.; et al. Low-emittance electron bunches from a laser-plasma accelerator measured using single-shot X-ray spectroscopy. Phys. Rev. Lett. 2012, 109, 064802. [Google Scholar] [CrossRef]
- Corde, S.; Ta Phuoc, K.; Lambert, G.; Fitour, R.; Malka, V.; Rousse, A.; Beck, A.; Lefebvre, E. Femtosecond X-rays from laser-plasma accelerators. Rev. Mod. Phys. 2013, 85, 1–48. [Google Scholar] [CrossRef]
- Hartmann, F.V.; Gibson, D.J.; Brown, W.J.; Rousse, A.; Phuoc, K.T.; Mallka, V.; Faure, J.; Pukhov, A.A. Compton scattering X-ray sources driven by laser wakefield acceleration. Phys. Rev. Spec. Top. Accel. Beams 2007, 10, 011310. [Google Scholar] [CrossRef]
- Martin, M.; Hynes, J.T. Femtochemistry and Femtobiology: Ultrafast Events in Molecular Science; Elsevier: Oxford, UK, 2004. [Google Scholar]
- Albert, F.; Thomas, A.G.R. Applications of laser wakefield accelerator-based light sources. Plasma Phys. Control. Fusion 2016, 58, 103001. [Google Scholar] [CrossRef]
- Sarri, G.; Corvan, D.J.; Schumaker, W.; Cole, J.M.; Di Piazza, A.; Ahmed, H.; Harvey, C.; Keitel, C.H.; Krushelnick, K.; Mangles, S.P.D.; et al. Ultrahigh Brilliance Multi-MeV γ-Ray Beams from Nonlinear Relativistic Thomson Scattering. Phys. Rev. Lett. 2014, 113, 224801. [Google Scholar] [CrossRef]
- Phuoc, K.T.; Corde, S.; Thaury, C.; Malka, V.; Tafzi, A.; Goddet, J.P.; Shah, R.C.; Sebban, S.; Rousse, A. All-optical Compton gamma-ray source. Nat. Photon. 2012, 6, 308. [Google Scholar] [CrossRef]
- Powers, N.D.; Ghebregziabher, I.; Golovin, G.; Liu, C.; Chen, S.; Banerjee, S.; Umstadter, D.P. Quasi-monoenergetic and tunable X-rays from a laser-driven Compton light source. Nat. Photonics 2013, 8, 28–31. [Google Scholar] [CrossRef]
- Chen, S.; Powers, N.D.; Ghebregziabher, I.; Maharjan, C.M.; Liu, C.; Golovin, G.; Banerjee, S.; Zhang, J.; Cunningham, N.; Moorti, A.; et al. MeV-energy X rays from inverse compton scattering with laser-wakefield accelerated electrons. Phys. Rev. Lett. 2013, 110, 155003. [Google Scholar] [CrossRef]
- Khrennikov, K.; Wenz, J.; Buck, V.; Xu, J.; Heigoldt, M.; Veisz, L.; Karsch, S. Tunable all optical quasimonochromatic Thomson X-ray source in the nonlinear regime. Phys. Rev. Lett. 2015, 114, 195003. [Google Scholar] [CrossRef]
- Tsai, H.-E.; Wang, X.; Shaw, J.M.; Li, Z.; Arefiev, A.V.; Zhang, X.; Zgadzaj, R.; Henderson, W.; Khudik, V.; Shvets, G.; et al. Compact tunable Compton X-ray source from laser-plasma accelerator and plasma mirror. Phys. Plasmas 2015, 22, 023106. [Google Scholar] [CrossRef]
- Döpp, A.; Guillaume, E.; Thaury, C.; Gautier, J.; Andriyash, I.; Lifschitz, A.; Malka, V.; Rousse, A.; Phuoc, K.T. An all-optical Compton source for single-exposure X-ray imaging. Plasma Phys. Control. Fusion 2016, 58, 034005. [Google Scholar] [CrossRef]
- Yu, C.; Qi, R.; Wang, W.; Liu, J.; Li, W.; Wang, C.; Zhang, Z.; Liu, J.; Qin, Z.; Fang, M.; et al. Ultrahigh brilliance quasi-monochromatic MeV gamma-rays based on self-synchronized all-optical Compton scattering. Sci. Rep. 2016, 6, 29518. [Google Scholar]
- Hannasch, A.; Garcia, A.L.; LaBerge, M.; Zgadzaj, R.; Köhler, A.; Couperus Cabadağ, J.P.; Zarini, O.; Kurz, T.; Ferrari, A.; Molodtsova, M.; et al. Compact spectroscopy of keV to MeV X-rays from a laser wakefield accelerator. Sci. Rep. 2021, 11, 14368. [Google Scholar] [CrossRef]
- Krämer, J.M.; Jochmann, A.; Budde, M.; Bussmann, M.; Couperus, J.P.; Cowan, T.E.; Debus, A.; Köhler, A.; Kuntzsch, M.; García, A.L.; et al. Making spectral shape measurements in in-verse Compton scattering a tool for advanced diagnostic applications. Sci. Rep. 2018, 8, 1398. [Google Scholar] [CrossRef]
- Brümmer, T.; Bohlen, S.; Grüner, F.; Osterhoff, J.; Põder, K. Compact all-optical precision-tunable narrowband hard Compton X-ray source. Sci. Rep. 2022, 12, 16017. [Google Scholar] [CrossRef]
- Maroju, P.K.; Grazioli, C.; Fraia, M.; Moioli, M.; Ertel, D.; Ahmadi, H.; Plekan, O.; Finetti, P.; Allaria, E.; Giannessi, L.; et al. Attosecond pulse shaping using a seeded free-electron laser. Nature 2020, 578, 386–391. [Google Scholar] [CrossRef]
- Duris, J.P.; MacArthur, J.P.; Glownia, J.M.; Li, S.; Vetter, S.; Miahnahri, A.; Coffee, R.; Hering, P.; Fry, A.; Welch, M.E.; et al. Controllable X-ray pulse trains from enhanced self-amplified spontaneous emission. Phys. Rev. Lett. 2021, 126, 104802. [Google Scholar] [CrossRef] [PubMed]
- Arber, T.D.; Bennett, K.; Brady, C.S.; Lawrence-Douglas, A.; Ramsay, M.G.; Sircombe, N.J.; Gillies, P.; Evans, R.G.; Schmitz, H.; Bell, A.R.; et al. Contemporary particle-in-cell approach to laser-plasma modeling. Plasma Phys. Control. Fusion 2015, 57, 113001. [Google Scholar] [CrossRef]
- Mirzaie, M.; Li, S.; Zeng, M.; Hafz, N.A.M.; Chen, M.; Li, G.Y.; Zhu, Q.J.; Liao, H.; Sokollik, T.; Liu, F.; et al. Demonstration of self-truncated ionization injection for GeV electron beams. Sci. Rep. 2015, 5, 14659. [Google Scholar] [CrossRef]
- Ridgers, C.; Kirk, J.; Duclous, R.; Blackburn, T.; Brady, C.; Bennett, K.; Arber, T.; Bell, A. Modelling gamma-ray photon emission and pair production in high-intensity laser–matter interactions. J. Comput. Phys. 2014, 260, 273–285. [Google Scholar] [CrossRef]
- Morris, S.; Robinson, A.; Ridgers, C.P. Highly efficient conversion of laser energy to hard X-rays in high-intensity laser–solid simulations. Phys. Plasmas 2021, 28, 103304. [Google Scholar] [CrossRef]
- Qiao, B.; Chang, H.X.; Xie, Y.; Xu, Z.; He, X.T. Gamma-ray generation from laser-driven electron resonant acceleration: In the non-QED and the QED regimes. Phys. Plasmas 2017, 24, 123101. [Google Scholar] [CrossRef]
- Pak, A.; Marsh, K.A.; Martins, S.F.; Lu, W.; Mori, W.B.; Joshi, C. Injection and trapping of tunnel-ionized electrons into laser-produced wakes. Phys. Rev. Lett. 2010, 104, 025003. [Google Scholar] [CrossRef] [PubMed]
- Xu, X.L.; Pai, C.H.; Zhang, C.J.; Li, F.; Wan, Y.; Wu, Y.P.; Hua, J.F.; Lu, W.; An, W.; Yu, P.; et al. Nanoscale electron bunching in laser-triggered ionization injection in plasma accelerators. Phys. Rev. Lett. 2016, 117, 034801. [Google Scholar] [CrossRef] [PubMed]
- Deng, A.; Li, X.; Luo, L.; Li, Y.; Zeng, J. Generation of attosecond micro bunched beam using ionization injection in laser wakefield acceleration. Opt. Express 2023, 31, 19958–19967. [Google Scholar] [CrossRef]
- Li, M.; Chen, L.; Li, D.; Huang, K.; Li, Y.; Ma, Y.; Yan, W.; Tao, M.; Tan, J.; Sheng, Z.; et al. Collimated gamma rays from laser wakefield accelerated electrons. Matter Radiat. Extrem. 2018, 3, 188–196. [Google Scholar] [CrossRef]
- Hidding, B.; Pretzler, G.; Rosenzweig, J.B.; Königstein, T.; Schiller, D.; Bruhwiler, D.L. Ultracold Electron Bunch Generation via Plasma Photocathode Emission and Acceleration in a Beam-Driven Plasma Blowout. Phys. Rev. Lett. 2012, 108, 035001. [Google Scholar] [CrossRef]
- Deng, A.; Karger, O.S.; Heinemann, T.; Knetsch, A.; Scherkl, P.; Manahan, G.G.; Beaton, A.; Ullmann, D.; Wittig, G.; Habib, A.F.; et al. Generation and acceleration of electron bunches from a plasma photocathode. Nat. Phys. 2019, 15, 1156–1160. [Google Scholar] [CrossRef]
- LaBerge, M.; Bowers, B.; Chang, Y.Y.; Cabadağ, J.C.; Debus, A.; Hannasch, A.; Pausch, R.; Schöbel, S.; Tiebel, J.; Ufer, P.; et al. Revealing the three-dimensional structure of microbunched plasma-wakefield-accelerated electron beams. Nat. Photonics 2024. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, A.; Li, Y.; Weng, Y.; Luo, Z.; Yu, X.; Zeng, J. Simulation Study on Attosecond Inverse Compton Scattering Source from Laser Wakefield Acceleration with Near-Threshold Ionization Injection. Appl. Sci. 2024, 14, 7749. https://doi.org/10.3390/app14177749
Deng A, Li Y, Weng Y, Luo Z, Yu X, Zeng J. Simulation Study on Attosecond Inverse Compton Scattering Source from Laser Wakefield Acceleration with Near-Threshold Ionization Injection. Applied Sciences. 2024; 14(17):7749. https://doi.org/10.3390/app14177749
Chicago/Turabian StyleDeng, Aihua, Yan Li, Yugan Weng, Zhiling Luo, Xitao Yu, and Jiaolong Zeng. 2024. "Simulation Study on Attosecond Inverse Compton Scattering Source from Laser Wakefield Acceleration with Near-Threshold Ionization Injection" Applied Sciences 14, no. 17: 7749. https://doi.org/10.3390/app14177749
APA StyleDeng, A., Li, Y., Weng, Y., Luo, Z., Yu, X., & Zeng, J. (2024). Simulation Study on Attosecond Inverse Compton Scattering Source from Laser Wakefield Acceleration with Near-Threshold Ionization Injection. Applied Sciences, 14(17), 7749. https://doi.org/10.3390/app14177749





