Green Scalar Function Method for Analyzing Dielectric Media
Abstract
:1. Introduction
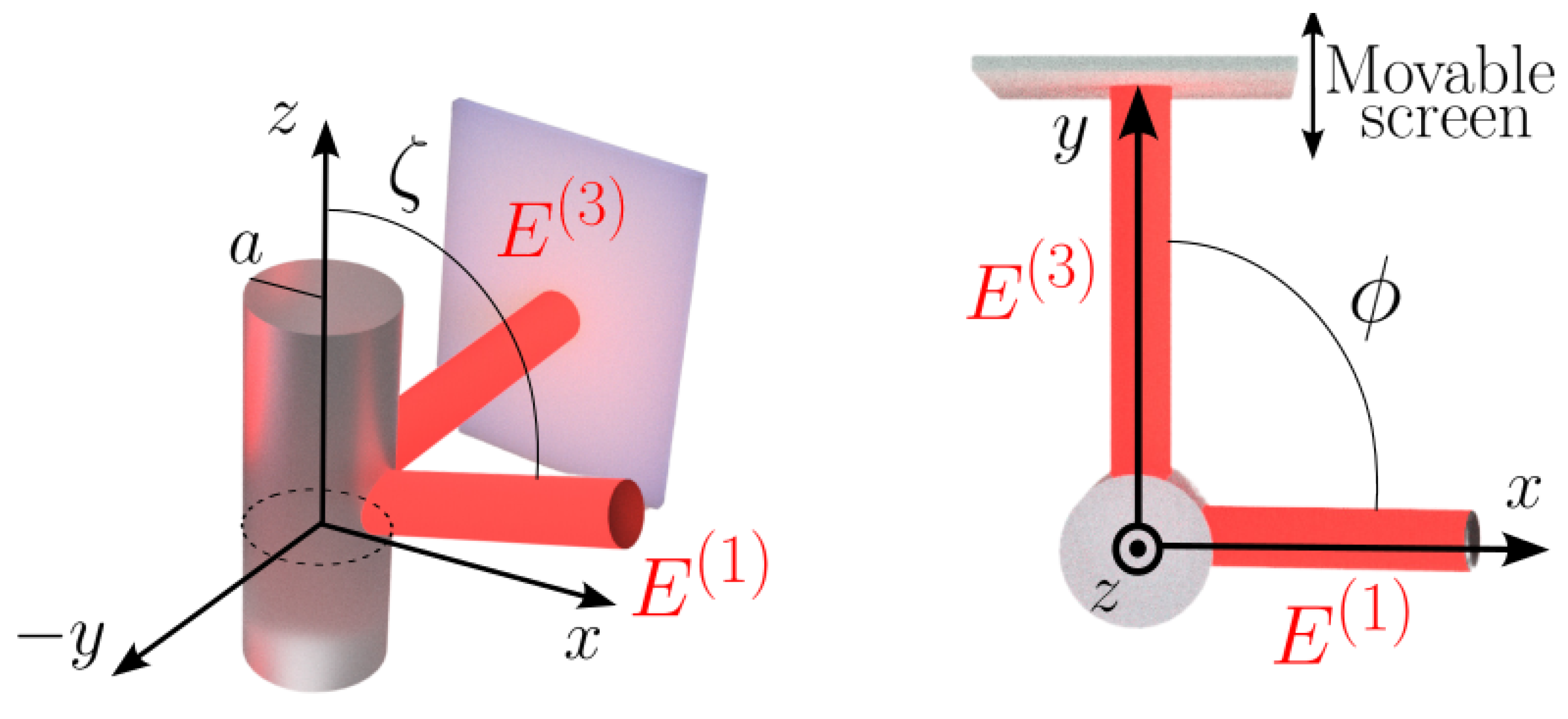
2. Theoretical Background
2.1. 2D Green Function
2.2. Discretization of the Equations
2.3. Scalar Analytical Solution
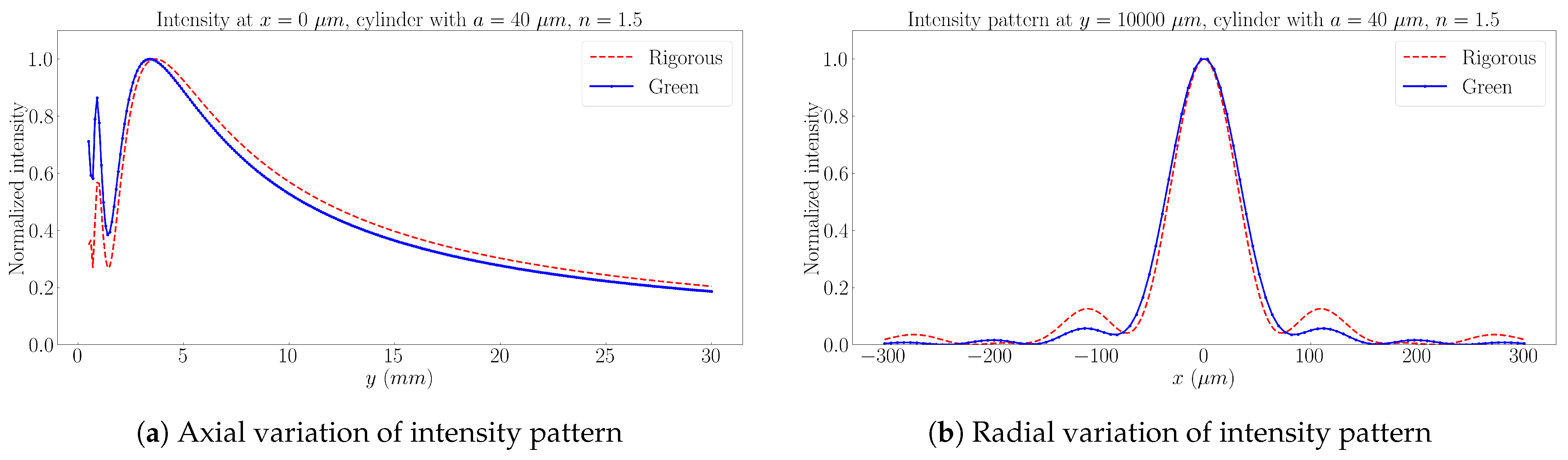
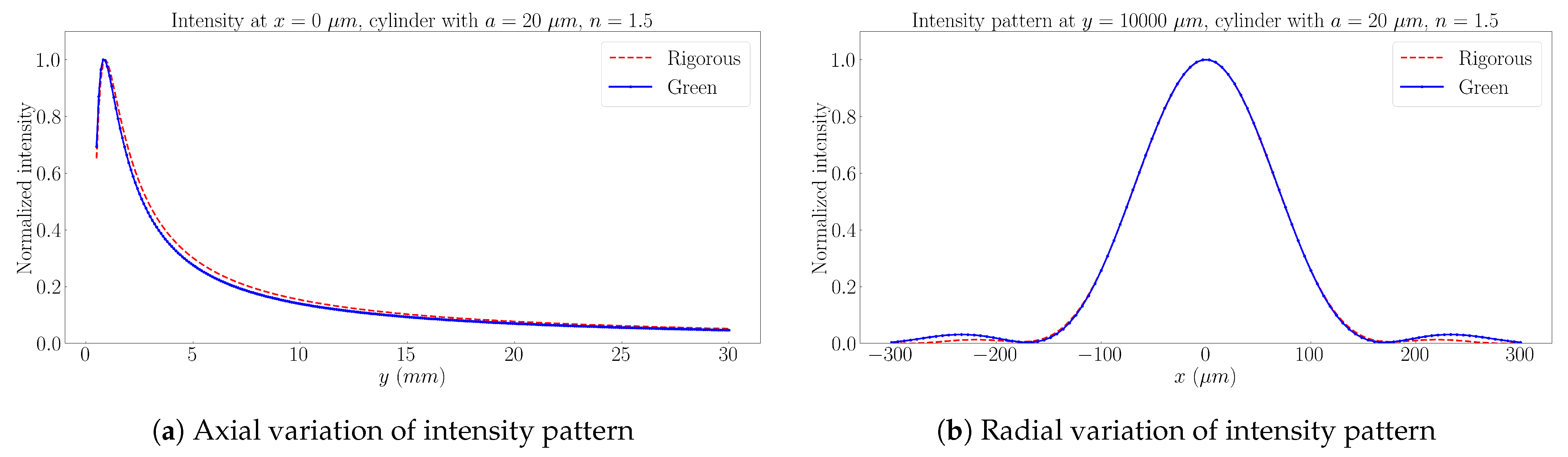
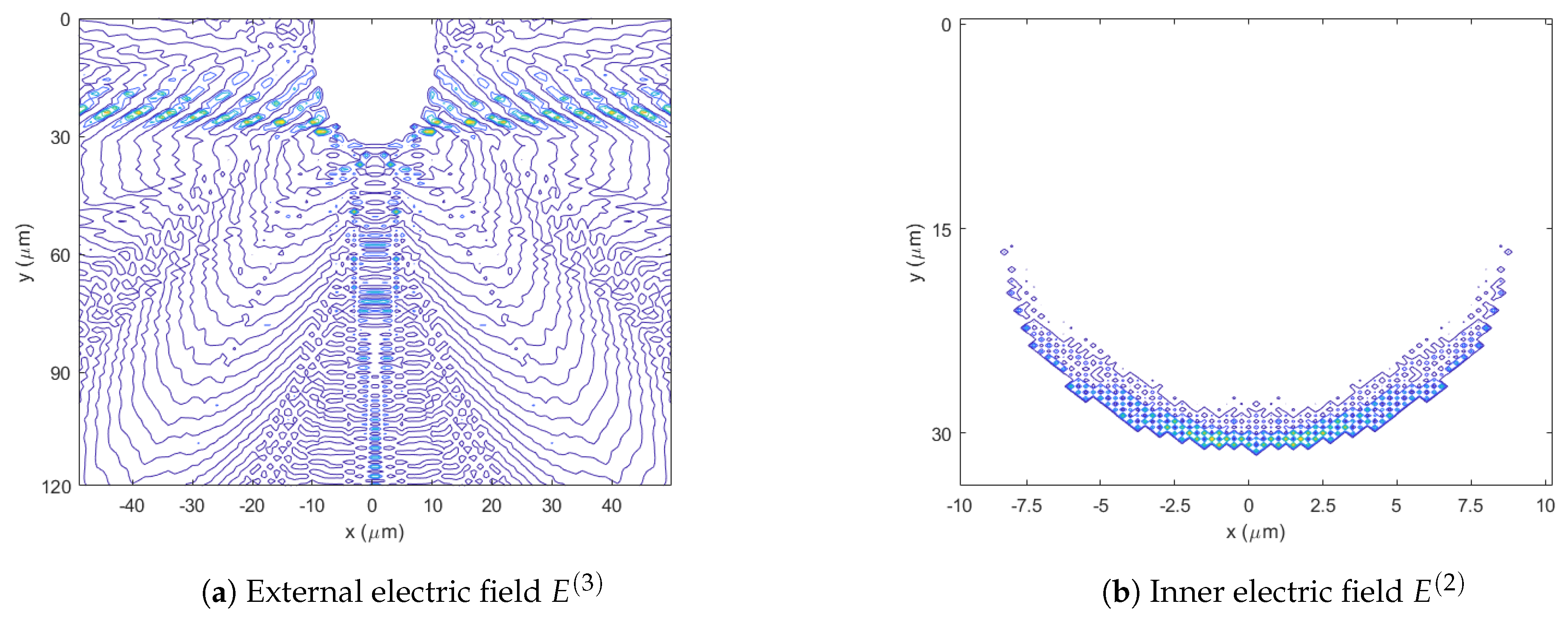
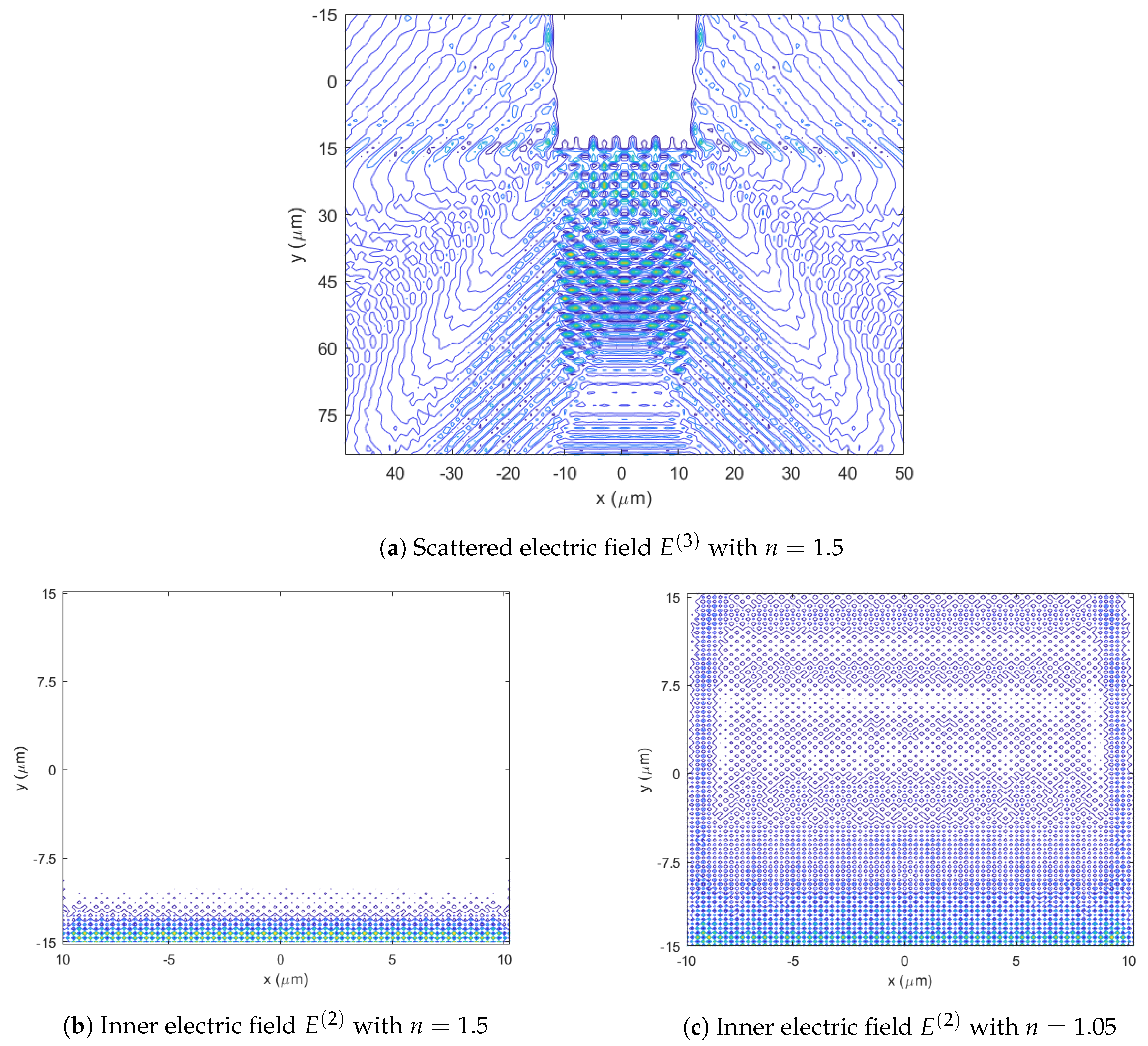
3. Numerical Results
4. Discussions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Stefanou, N.; Karathanos, V.; Modinos, A. Scattering of electromagnetic waves by periodic structures. J. Phys. Condens. Matter 1992, 4, 7389. [Google Scholar] [CrossRef]
- Rekanos, I.T. Neural-network-based inverse-scattering technique for online microwave medical imaging. IEEE Trans. Magn. 2002, 38, 1061–1064. [Google Scholar] [CrossRef]
- Doicu, A.; Wriedt, T.; Eremin, Y.A. Light Scattering by Systems of Particles: Null-Field Method with Discrete Sources: Theory and Programs; Springer: Berlin/Heidelberg, Germany, 2006; Volume 124. [Google Scholar]
- Bohren, C.F.; Huffman, D.R. Absorption and Scattering of Light by Small Particles; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Nieto-Vesperinas, M. Fundamentals of Mie scattering. In Dielectric Metamaterials; Elsevier: Amsterdam, The Netherlands, 2020; pp. 39–72. [Google Scholar]
- Zhang, S.; Zhang, W.; Liu, L. Light scattering by a charged infinite cylinder in a transparent medium. J. Quant. Spectrosc. Radiat. Transf. 2020, 253, 107167. [Google Scholar] [CrossRef]
- Habashy, T.M.; Groom, R.W.; Spies, B.R. Beyond the Born and Rytov approximations: A nonlinear approach to electromagnetic scattering. J. Geophys. Res. Solid Earth 1993, 98, 1759–1775. [Google Scholar] [CrossRef]
- Rao, S.; Wilton, D.; Glisson, A. Electromagnetic scattering by surfaces of arbitrary shape. IEEE Trans. Antennas Propag. 1982, 30, 409–418. [Google Scholar] [CrossRef]
- Rother, T. Self-consistent Green’s function formalism for acoustic and light scattering, Part 1: Scalar notation. Opt. Commun. 2005, 251, 254–269. [Google Scholar] [CrossRef]
- Ishimaru, A. Electromagnetic Wave Propagation, Radiation, and Scattering: From Fundamentals to Applications; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Kahnert, F.M. Numerical methods in electromagnetic scattering theory. J. Quant. Spectrosc. Radiat. Transf. 2003, 79, 775–824. [Google Scholar] [CrossRef]
- Taflove, A.; Brodwin, M.E. Numerical solution of steady-state electromagnetic scattering problems using the time-dependent Maxwell’s equations. IEEE Trans. Microw. Theory Tech. 1975, 23, 623–630. [Google Scholar] [CrossRef]
- Nick, J.; Kovács, B.; Lubich, C. Time-dependent electromagnetic scattering from thin layers. Numer. Math. 2022, 150, 1123–1164. [Google Scholar] [CrossRef]
- Shah, G.A. Numerical methods for Mie theory of scattering by a sphere. Kodalkenel Obs. Bull. Ser. A 1977, 2, 42–63. [Google Scholar]
- Alyones, S.; Bruce, C.W.; Buin, A.K. Numerical methods for solving the problem of electromagnetic scattering by a thin finite conducting wire. IEEE Trans. Antennas Propag. 2007, 55, 1856–1861. [Google Scholar] [CrossRef]
- Liu, R.Q.; Huang, X.W.; Du, Y.L.; Yang, M.L.; Sheng, X.Q. Massively parallel discontinuous Galerkin surface integral equation method for solving large-scale electromagnetic scattering problems. IEEE Trans. Antennas Propag. 2021, 69, 6122–6127. [Google Scholar] [CrossRef]
- Glisson, A.; Wilton, D. Simple and efficient numerical methods for problems of electromagnetic radiation and scattering from surfaces. IEEE Trans. Antennas Propag. 1980, 28, 593–603. [Google Scholar] [CrossRef]
- Sevgi, L. Complex Electromagnetic Problems and Numerical Simulation Approaches; John Wiley & Sons: Hoboken, NJ, USA, 2003. [Google Scholar]
- Paknys, R. Applied Frequency-Domain Electromagnetics; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Wubs, M.; Suttorp, L.; Lagendijk, A. Multiple-scattering approach to interatomic interactions and superradiance in inhomogeneous dielectrics. Phys. Rev. A-At. Mol. Opt. Phys. 2004, 70, 053823. [Google Scholar] [CrossRef]
- Huang, J.; Yao, J.; Xu, D.; Li, R. Green function method for the time domain simulation of pulse propagation. Appl. Opt. 2014, 53, 3533–3539. [Google Scholar] [CrossRef] [PubMed]
- Huang, J. Green Function. In Perturbation Theory; Uzunov, D.I., Ed.; IntechOpen: Rijeka, Croatia, 2017; Chapter 3. [Google Scholar] [CrossRef]
- Bevacqua, M.T.; Isernia, T. An effective rewriting of the inverse scattering equations via Green’s function decomposition. IEEE Trans. Antennas Propag. 2021, 69, 4883–4893. [Google Scholar] [CrossRef]
- Born, M.; Wolf, E. Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Martin, O.J.; Piller, N.B. Electromagnetic scattering in polarizable backgrounds. Phys. Rev. E 1998, 58, 3909–3915. [Google Scholar] [CrossRef]
- Taleb, S.I.; Neipp, C.; Francés, J.; Márquez, A.; Alvarez, M.L.; Hernández, A.; Gallego, S.; Beléndez, A. Validation of Fresnel–Kirchhoff Integral Method for the Study of Volume Dielectric Bodies. Appl. Sci. 2021, 11, 3800. [Google Scholar] [CrossRef]
- Petropoulos, P.G. Reflectionless sponge layers as absorbing boundary conditions for the numerical solution of Maxwell equations in rectangular, cylindrical, and spherical coordinates. SIAM J. Appl. Math. 2000, 60, 1037–1058. [Google Scholar] [CrossRef]
- Frezza, F.; Mangini, F.; Tedeschi, N. Introduction to electromagnetic scattering: Tutorial. JOSA A 2018, 35, 163–173. [Google Scholar] [CrossRef]
- Levine, H.; Schwinger, J. On the theory of electromagnetic wave diffraction by an aperture in an infinite plane conducting screen. Commun. Pure Appl. Math. 1950, 3, 355–391. [Google Scholar] [CrossRef]
- Taleb, S.I.; Neipp, C.; Francés, J.; Martínez Guardiola, F.J.; Alvarez, M.L.; Márquez, A.; Gallego, S.; Beléndez, A. 2D Green’s tensor for the analysis of dielectric structures with translational geometries. In Optics, Photonics and Lasers: Proceedings of the 4th International Conference on Optics, Photonics and Lasers (OPAL’ 2021), 13-15 October 2021, Curfu, Greece; International Frequency Sensor Association (IFSA) Publishing: Barcelona, Spain, 2021. [Google Scholar]
- Yaghjian, A.D. Electric dyadic Green’s functions in the source region. Proc. IEEE 1980, 68, 248–263. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bravo, J.C.; Colomina-Martínez, J.; Sirvent-Verdú, J.J.; Mena, E.J.; Álvarez, M.L.; Francés, J.; Neipp, C.; Gallego, S. Green Scalar Function Method for Analyzing Dielectric Media. Appl. Sci. 2024, 14, 8045. https://doi.org/10.3390/app14178045
Bravo JC, Colomina-Martínez J, Sirvent-Verdú JJ, Mena EJ, Álvarez ML, Francés J, Neipp C, Gallego S. Green Scalar Function Method for Analyzing Dielectric Media. Applied Sciences. 2024; 14(17):8045. https://doi.org/10.3390/app14178045
Chicago/Turabian StyleBravo, J. C., J. Colomina-Martínez, J. J. Sirvent-Verdú, E. J. Mena, M. L. Álvarez, J. Francés, C. Neipp, and Sergi Gallego. 2024. "Green Scalar Function Method for Analyzing Dielectric Media" Applied Sciences 14, no. 17: 8045. https://doi.org/10.3390/app14178045
APA StyleBravo, J. C., Colomina-Martínez, J., Sirvent-Verdú, J. J., Mena, E. J., Álvarez, M. L., Francés, J., Neipp, C., & Gallego, S. (2024). Green Scalar Function Method for Analyzing Dielectric Media. Applied Sciences, 14(17), 8045. https://doi.org/10.3390/app14178045







