Fundamental Challenges and Complexities of Damage Identification from Dynamic Response in Plate Structures
Abstract
1. Introduction
2. Fundamentals of Plate Structural Vibration
2.1. Plate Theories
2.2. Nonlinear Deflection Theory
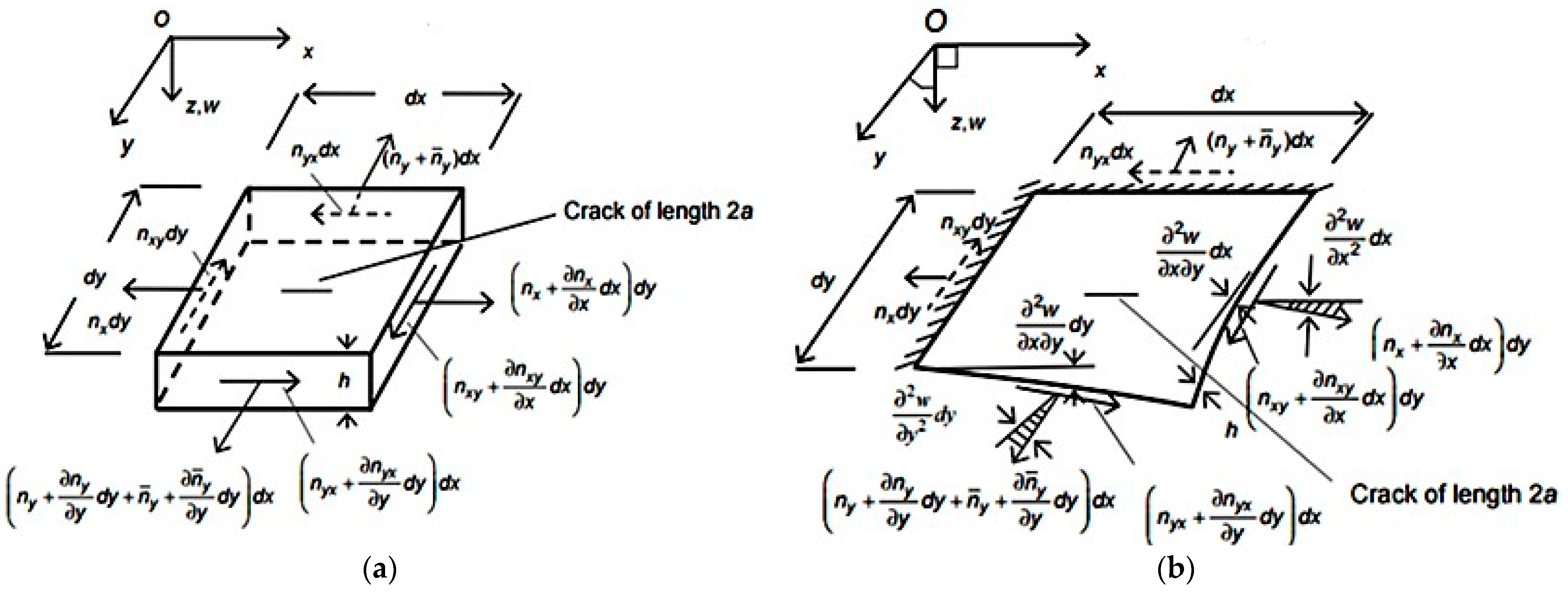
2.3. Equation of Motion of Cracked Plates
3. Crack Detection in Plates Using Dynamic Response (DR)
3.1. Forward Problem for the DR of the Cracked Plate
3.1.1. Plate of the Uniform Thickness (UT)
3.1.2. Plate of Thickness (VT)
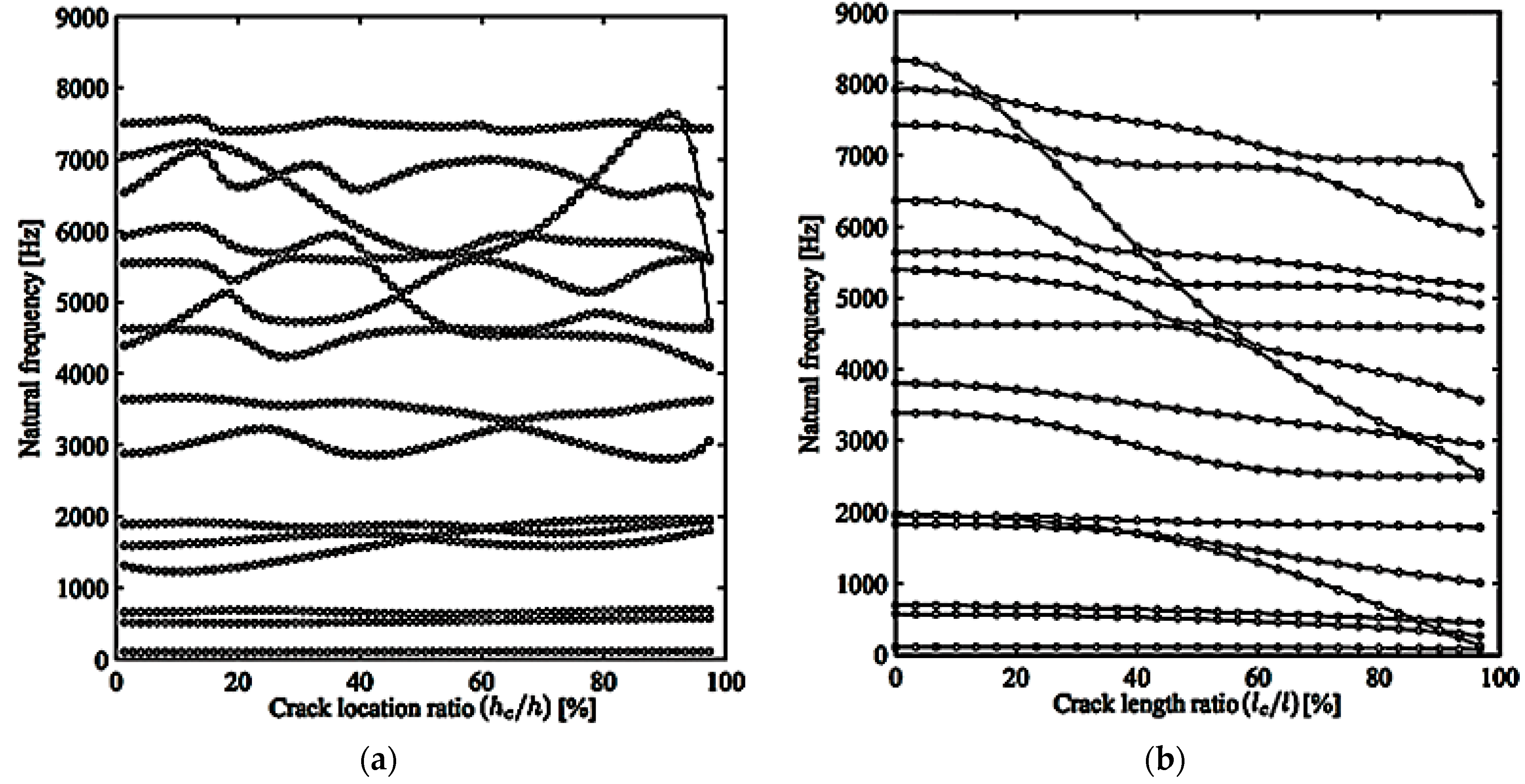
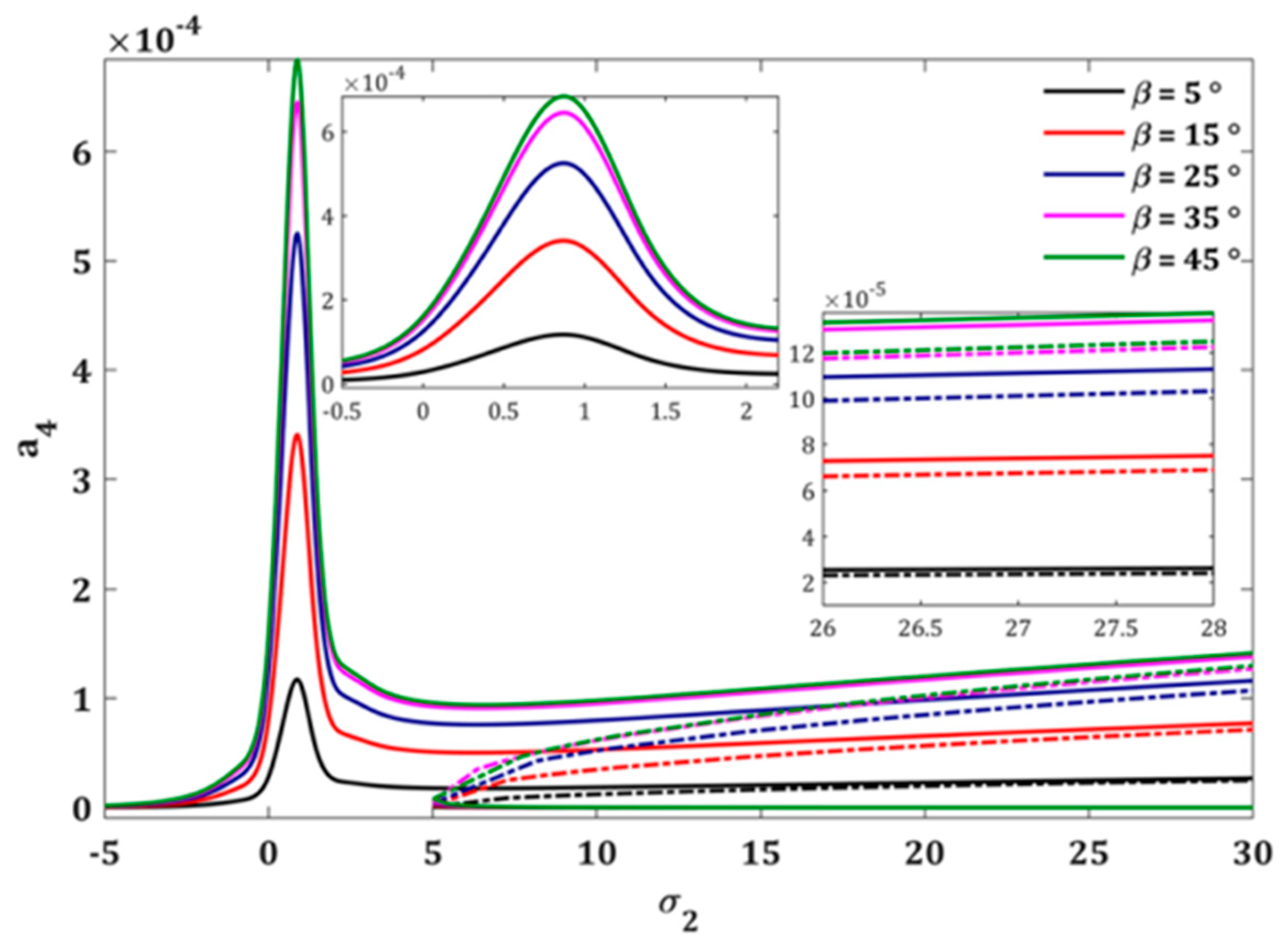
3.2. Inverse Problem for the DR of the Cracked Plate
4. Discussion
5. Conclusions
- Most research on damage detection in plates has focused on the forward problem, which is to study how crack damage affects the DR of plates. This work has provided valuable insights and developed various models for different structures. However, there is a need to apply these models to the inverse problem, which is to detect damage from vibration measurements.
- Additionally, most research on the inverse problem has focused on plates with the UT, even though plates with VT are important in many applications. This oversight needs to be addressed to comprehensively address the challenges of damage detection in the VT plates.
- Moreover, many studies on the inverse problem have not been able to accurately identify crack parameters such as size, length, and propagation rate. They often only pinpoint the damage location in plates with UT based on changes in vibration responses. Future research should focus on improving the accuracy of these parameters.
- Finally, crack path identification, a critical area of research for beam structures, has yet to be studied in plate structures. This important gap in the literature needs to be addressed.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| A and B | A and B are constants |
| SSSS | All edges simply supported |
| ∇4 | Biharmonic operator |
| CP | Circular plates |
| CS | clamped supported |
| Coefficients at the center of crack | |
| Compliance of stretching-bending | |
| DLV | Damage location vector |
| ρ | Density |
| q | Distributed transverse loading |
| DR | Dynamic response |
| B(x,y) | Effective torsional rigidity |
| FE | Finite element |
| D | Flexural rigidity |
| DRSBFEMU | Dynamic response sensitivity-based finite element model updating |
| FD | Fractal dimension |
| FRF | Frequency response function |
| FGM | Functionally graded material |
| FSDT | First-order shear deformation theory |
| a | Half-crack length |
| HSDT | higher-order shear deformation theory |
| nx | In-plane or membrane force per unit length |
| LSM | Line spring model |
| LVT | Linear varying thickness |
| Pz | Load acting at the surface per unit area |
| MR | Mindlin–Reissner |
| E | Modulus of elasticity |
| Moment | |
| NDT | Non-destructive testing |
| Nondimensional bending compliance | |
| PVT | Parabolically varying thickness |
| υ | Poisson’s ratio |
| RP | Rectangular plates |
| RRM | Rayleigh–Ritz method |
| SPT | Signal processing technique |
| SS | Simply supported |
| SP | Squire plate |
| Stretching compliance | |
| SHM | Structural health monitoring |
| h | Thickness |
| 3D | Three dimensions |
| Dt | Torsional rigidity |
| w | Transverse deflection |
| CCFF | Two edges clamped and two free supported |
| CCSS | Two edges clamped and two simply supported |
| 2D | Two dimensions |
| ULS | Uniform load surface |
| UT | Uniform thickness |
| VT | Varying thickness |
| WT | Wavelet transformation |
References
- Dai, H.H.; Song, Z. On a Consistent Finite-Strain Plate Theory Based on Three-Dimensional Energy Principle. Proc. R. Soc. A Math. Phys. Eng. Sci. 2014, 470, 20140494. [Google Scholar] [CrossRef]
- Sanders Robert, E.; Marshall, G.J. Chapter 14. Aluminum in Marine Transportation. In Aluminium-Technology, Industry, and Applications; ASM International: Materials Park, OH, USA, 2023. [Google Scholar]
- Sanders Robert, E.; Marshall, G.J. Chapter 13. Aluminum in Ground Transportation. In Aluminium-Technology, Industry, and Applications; ASM International: Materials Park, OH, USA, 2023. [Google Scholar]
- Sanders Robert, E.; Marshall, G.J. Chapter 11. Aluminum in Aircraft and Space Applications. In Aluminium-Technology, Industry, and Applications; ASM International: Materials Park, OH, USA, 2023. [Google Scholar]
- Zhang, Y.; Du, J. Dynamic Analysis of Two Parallel Rectangular Plates Coupled with Mechanical Links. Int. J. Struct. Stab. Dyn. 2021, 21, 2150157. [Google Scholar] [CrossRef]
- Lu, C. 7.2.1 Damaged Plate. In Damage and Repair of Aerospace Composite Materials; SAE International: Warrendale, PA, USA, 2020. [Google Scholar]
- Israr, A.; Cartmell, M.P.; Manoach, E.; Trendafilova, I.; Ostachowicz, W.; Krawczuk, M.; Zak, A. Analytical Modeling and Vibration Analysis of Partially Cracked Rectangular Plates with Different Boundary Conditions and Loading. J. Appl. Mech. Trans. ASME 2009, 76, 011005. [Google Scholar] [CrossRef]
- Obenchain, M.B.; Nadella, K.S.; Cesnik, C.E.S. Hybrid Global Matrix/Local Interaction Simulation Approach for Wave Propagation Simulation in Composite Laminates. In Proceedings of the 54th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Boston, MA, USA, 8–11 April 2013; American Institute of Aeronautics and Astronautics (AIAA): Reston, VA, USA, 2013. [Google Scholar]
- Goetz, J.; Tan, H.; Tovvar, A.; Renaud, J. Multi-Material Structural Topology Optimization for Blast Mitigation Using Hybrid Cellular Automata. In Proceedings of the 51st AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Orlando, FL, USA, 12–15 April 2010; American Institute of Aeronautics and Astronautics (AIAA): Reston, VA, USA, 2010. [Google Scholar]
- Israr, A. Vibration Analysis of Cracked Aluminium Plates; University of Glasgow: Glasgow, UK, 2008. [Google Scholar]
- Dimarogonas, A.D. Vibration of Cracked Structures: A State of the Art Review. Eng. Fract. Mech. 1996, 55, 831–857. [Google Scholar] [CrossRef]
- Qiu, Z.; Wu, H.; Ye, C. Acceleration Sensors Based Modal Identification and Active Vibration Control of Flexible Smart Cantilever Plate. Aerosp. Sci. Technol. 2009, 13, 277–290. [Google Scholar] [CrossRef]
- Khan, S.Z.; Khan, T.M.; Joya, Y.F.; Khan, M.A.; Ahmed, S.; Shah, A. Assessment of Material Properties of AISI 316L Stainless Steel Using Non-Destructive Testing. Nondestruct. Test. Eval. 2016, 31, 360–370. [Google Scholar] [CrossRef]
- Chen, Z.; Gui, H.; Liao, X.; Du, M. Dynamic Response Analysis of a Bulk Carrier by Nonlinear Hydroelastic Method. J. Mar. Sci. Eng. 2021, 9, 877. [Google Scholar] [CrossRef]
- Hairer, M.; Majda, A.J. A Simple Framework to Justify Linear Response Theory. Nonlinearity 2010, 23, 909–922. [Google Scholar] [CrossRef]
- Spann, F. A Procedure for Comparing Dynamic Test Severities Based on Equipment Response Characteristics. J. IEST 1988, 31, 62–66. [Google Scholar] [CrossRef]
- Ma, Y.; Chen, X.; Geng, Y.; Zhang, X. Effect of Clogging on the Permeability of Porous Asphalt Pavement. Adv. Mater. Sci. Eng. 2020, 2020, 4851291. [Google Scholar] [CrossRef]
- He, X.; Fulton, R.E. Nonlinear Dynamics Analysis of a Laminated Printed Wiring Board. J. Electron. Packag. 2002, 124, 77–84. [Google Scholar] [CrossRef]
- Zai, B.A.; Khan, M.; Khan, K.A.; Mansoor, A.; Shah, A.; Shahzad, M. The Role of Dynamic Response Parameters in Damage Prediction. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2019, 233, 4620–4636. [Google Scholar] [CrossRef]
- Limongelli, M.P.; Manoach, E.; Quqa, S.; Giordano, P.F.; Bhowmik, B.; Pakrashi, V.; Cigada, A. Vibration Response-Based Damage Detection. In Structural Health Monitoring Damage Detection Systems for Aerospace; Springer: Cham, Switzerland, 2021; pp. 133–173. [Google Scholar]
- Fan, W.; Qiao, P. Vibration-Based Damage Identification Methods: A Review and Comparative Study. Struct. Health Monit. 2011, 10, 83–111. [Google Scholar] [CrossRef]
- Avci, O.; Abdeljaber, O.; Kiranyaz, S.; Hussein, M.; Gabbouj, M.; Inman, D.J. A Review of Vibration-Based Damage Detection in Civil Structures: From Traditional Methods to Machine Learning and Deep Learning Applications. Mech. Syst. Signal Process. 2021, 147, 107077. [Google Scholar] [CrossRef]
- Zai, B.A.; Khan, M.A.; Khan, S.Z.; Asif, M.; Khan, K.A.; Saquib, A.N.; Mansoor, A.; Shahzad, M.; Mujtaba, A. Prediction of Crack Depth and Fatigue Life of an Acrylonitrile Butadiene Styrene Cantilever Beam Using Dynamic Response. J. Test. Eval. 2020, 48, 20180674. [Google Scholar] [CrossRef]
- Alotaibi, M.; Honarvar Shakibaei Asli, B.; Khan, M. Non-Invasive Inspections: A Review on Methods and Tools. Sensors 2021, 21, 8474. [Google Scholar] [CrossRef]
- Zai, B.A.; Khan, M.A.; Khan, K.A.; Mansoor, A. A Novel Approach for Damage Quantification Using the Dynamic Response of a Metallic Beam under Thermo-Mechanical Loads. J. Sound Vib. 2020, 469, 115134. [Google Scholar] [CrossRef]
- Alshammari, Y.L.A.; He, F.; Khan, M.A. Modelling and Investigation of Crack Growth for 3D-Printed Acrylonitrile Butadiene Styrene (ABS) with Various Printing Parameters and Ambient Temperatures. Polymers 2021, 13, 3737. [Google Scholar] [CrossRef]
- Gupta, A.; Jain, N.K.; Salhotra, R.; Joshi, P.V. Effect of Crack Location on Vibration Analysis of Partially Cracked Isotropic and FGM Micro-Plate with Non-Uniform Thickness: An Analytical Approach. Int. J. Mech. Sci. 2018, 145, 410–429. [Google Scholar] [CrossRef]
- Francese, A.; Khan, M.; He, F. Role of Dynamic Response in Inclined Transverse Crack Inspection for 3D-Printed Polymeric Beam with Metal Stiffener. Materials 2023, 16, 3095. [Google Scholar] [CrossRef]
- Yang, Z.; He, F.; Khan, M. An Empirical Torsional Spring Model for the Inclined Crack in a 3D-Printed Acrylonitrile Butadiene Styrene (ABS) Cantilever Beam. Polymers 2023, 15, 496. [Google Scholar] [CrossRef] [PubMed]
- Aravanis, T.-C.I.; Sakellariou, J.S.; Fassois, S.D. Damage Precise Localization under Varying Operating Conditions via the Vibration-Data-Based Functional Model Method: Formulation and Experimental Validation. J. Sound Vib. 2022, 535, 117078. [Google Scholar] [CrossRef]
- Zhang, Y.; Bernal, D. Damage Localization from Projections of Free Vibration Signals. J. Sound Vib. 2017, 394, 146–154. [Google Scholar] [CrossRef]
- Xu, W.; Zhu, W.; Cao, M.; Wu, H.; Zhu, R. A Novel Damage Index for Damage Detection and Localization of Plate-Type Structures Using Twist Derivatives of Laser-Measured Mode Shapes. J. Sound Vib. 2020, 481, 115448. [Google Scholar] [CrossRef]
- Tondreau, G.; Deraemaeker, A. Automated Data-Based Damage Localization under Ambient Vibration Using Local Modal Filters and Dynamic Strain Measurements: Experimental Applications. J. Sound Vib. 2014, 333, 7364–7385. [Google Scholar] [CrossRef][Green Version]
- Haywood-Alexander, M.; Dervilis, N.; Worden, K.; Dobie, G.; Rogers, T.J. Informative Bayesian Tools for Damage Localisation by Decomposition of Lamb Wave Signals. J. Sound Vib. 2022, 535, 117063. [Google Scholar] [CrossRef]
- Manoach, E.; Trendafilova, I. Large Amplitude Vibrations and Damage Detection of Rectangular Plates. J. Sound Vib. 2008, 315, 591–606. [Google Scholar] [CrossRef]
- Timoshenko, S. History of Strength of Materials: With a Brief Account of the History of Theory of Elasticity and Theory of Structures; Dover Publications: Mineola, NY, USA, 1983; ISBN 0486611876. [Google Scholar]
- Szilard, R. Theories and Applications of Plate Analysis: Classical, Numerical and Engineering Methods; John Wiley and Sons Ltd.: Hoboken, NJ, USA, 2004. [Google Scholar]
- Rayleigh, J.W.S.B. The Theory of Sound; Cambridge University Press: Cambridge, UK, 1877; ISBN 9781108032209. Available online: https://books.google.co.uk/books/about/The_Theory_of_Sound.html?id=v4NSAlsTwnQC&redir_esc=y (accessed on 1 September 2024).
- Rayleigh, J.W.S.B. The Theory of Sound; Dover Publications, Inc.: New York, NY, USA, 1945; Volume 2, Available online: https://books.google.co.uk/books/about/The_Theory_of_Sound.html?id=Frvgu1wSFfUC&redir_esc=y (accessed on 1 September 2024).
- Timoshenko, S.P. On the Correction for Shear of the Differential Equation for Transverse Vibrations of Prismatic Bars. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1921, 41, 744–746. [Google Scholar] [CrossRef]
- Tomotika, S. The Transverse Vibration of a Square Plate Clamped at Four Edges. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1936, 21, 745–760. [Google Scholar] [CrossRef]
- Young, D. Vibration of Rectangular Plates by the Ritz Method. J. Appl. Mech. 1950, 17, 448–453. [Google Scholar] [CrossRef]
- Warburton, G.B. The Vibration of Rectangular Plates. Proc. Inst. Mech. Eng. 1954, 168, 371–384. [Google Scholar] [CrossRef]
- Reissner, E. The Effect of Transverse Shear Deformation on the Bending of Elastic Plates. J. Appl. Mech. 1945, 12, A69–A77. [Google Scholar] [CrossRef]
- Mindlin, R.D. Influence of Rotatory Inertia and Shear on Flexural Motions of Isotropic, Elastic Plates. J. Appl. Mech. 1951, 18, 31–38. [Google Scholar] [CrossRef]
- Chen, H.; Kumar, A.V. Implicit Boundary Approach for Reissner-Mindlin Plates. In Proceedings of the Volume 2A: 33rd Computers and Information in Engineering Conference, Portland, OR, USA, 4–7 August 2013; American Society of Mechanical Engineers: New York, NY, USA, 2013. [Google Scholar]
- Lo, K.H.; Christensen, R.M.; Wu, E.M. A High-Order Theory of Plate Deformation—Part 1: Homogeneous Plates. J. Appl. Mech. 1977, 44, 663–668. [Google Scholar] [CrossRef]
- Lo, K.H.; Christensen, R.M.; Wu, E.M. A High-Order Theory of Plate Deformation—Part 2: Laminated Plates. J. Appl. Mech. 1977, 44, 669–676. [Google Scholar] [CrossRef]
- Challamel Noël, K.J.T.I. 2.3.2 Reduction of the Governing Equations by Mathematical Techniques. In Modern Trends in Structural and Solid Mechanics 2: Vibrations; John Wiley & Sons: Hoboken, NJ, USA, 2021. [Google Scholar]
- Reddy, J.N. A Simple Higher-Order Theory for Laminated Composite Plates. J. Appl. Mech. 1984, 51, 745–752. [Google Scholar] [CrossRef]
- Neves, A.M.A.; Ferreira, A.J.M.; Carrera, E.; Roque, C.M.C.; Cinefra, M.; Jorge, R.M.N.; Soares, C.M.M. A Quasi-3D Sinusoidal Shear Deformation Theory for the Static and Free Vibration Analysis of Functionally Graded Plates. Compos. B Eng. 2012, 43, 711–725. [Google Scholar] [CrossRef]
- Ghazwani, M.H.; Alnujaie, A.; Van Vinh, P.; Sedighi, H.M. Effects of Porosity and Nonlocality on the Low- and High-Frequency Vibration Characteristics of Al/Si3N4 Functionally Graded Nanoplates Using Quasi-3D Theory. Arch. Civ. Mech. Eng. 2024, 24, 49. [Google Scholar] [CrossRef]
- Li, R.; Yang, Z.; Chen, G.; Wu, B. Analytical Solutions for Nonlinear Deflections of Corner-Fillet Leaf-Springs. Mech. Mach. Theory 2021, 157, 104182. [Google Scholar] [CrossRef]
- Akhavan, H.; Ribeiro, P.; de Moura, M.F.S.F. Large Deflection and Stresses in Variable Stiffness Composite Laminates with Curvilinear Fibres. Int. J. Mech. Sci. 2013, 73, 14–26. [Google Scholar] [CrossRef]
- Karagiozova, D.; Yu, T.X.; Shi, S.Y.; Zhu, L. On the Influence of Elasticity on the Large Deflections Response of Circular Plates to Uniform Quasi-Static Pressure. Int. J. Mech. Sci. 2017, 131–132, 894–907. [Google Scholar] [CrossRef]
- Yamaki, N. Influence of Large Amplitudes on Flexural Vibrations of Elastic Plates. ZAMM Z. Angew. Math. Mech. 1961, 41, 501–510. [Google Scholar] [CrossRef]
- Wah, T. Large Amplitude Flexural Vibration of Rectangular Plates. Int. J. Mech. Sci. 1963, 5, 425–438. [Google Scholar] [CrossRef]
- SRINIVASAN, A.V. Large Amplitude-Free Oscillations of Beams and Plates. AIAA J. 1965, 3, 1951–1953. [Google Scholar] [CrossRef]
- Stanišić, M.M.; Payne, J.G. A Rapidly Converging Technique for Vibration Analysis of Plates with a Discrete Mass Distribution. Ing. Arch. 1968, 37, 189–195. [Google Scholar] [CrossRef]
- Rehfield, L.W. Nonlinear Free Vibrations of Elastic Structures. Int. J. Solids Struct. 1973, 9, 581–590. [Google Scholar] [CrossRef]
- Mei, C. Finite Element Displacement Method for Large Amplitude Free Flexural Vibrations of Beams and Plates. Comput. Struct. 1973, 3, 163–174. [Google Scholar] [CrossRef]
- Mazumdar, J.; Jones, R. A Simplified Approach to the Large Amplitude Vibration of Plates and Membranes. J. Sound Vib. 1977, 50, 389–397. [Google Scholar] [CrossRef]
- Karmakar, B.M. Amplitude-Frequency Characteristics of Non-Linear Vibrations of Clamped Elliptic Plates Carrying a Concentrated Mass. Int. J. Non-Linear Mech. 1978, 13, 351–359. [Google Scholar] [CrossRef]
- Benamar, R.; Bennouna, M.M.K.; White, R.G. The Effects of Large Vibration Amplitudes on the Fundamental Mode Shape of a Fully Clamped, Symmetrically Laminated Rectangular Plate. In Proceedings of the 4th International Conference on Recent Advances in Structural Dynamics, Southampton, UK, 15–18 July 1991; pp. 749–760. Available online: https://ui.adsabs.harvard.edu/abs/1991sdra.proc..749B/abstract (accessed on 1 September 2024).
- Benamar, R.; Bennouna, M.M.K.; White, R.G. The Effects of Large Vibration Amplitudes on the Mode Shapes and Natural Frequencies of Thin Elastic Structures, Part II: Fully Clamped Rectangular Isotropic Plates. J. Sound Vib. 1993, 164, 295–316. [Google Scholar] [CrossRef]
- Benamar, R.; Bennouna, M.M.K.; White, R.G. The Effects of Large Vibration Amplitudes on the Mode Shapes and Natural Frequencies of Thin Elastic Structures Part I: Simply Supported and Clamped-Clamped Beams. J. Sound Vib. 1991, 149, 179–195. [Google Scholar] [CrossRef]
- Abdelali, H.M.; Bikri, K.E.; Benamar, R. The Effects of Large Vibration Amplitudes on the Mode Shapes and Natural Frequencies of Thin Isotropic Skew Plates; EDP Sciences: Ulis, France, 2012. [Google Scholar]
- Lacarbonara, W. Nonlinear Structural Mechanics; Springer: Boston, MA, USA, 2013; ISBN 978-1-4419-1275-6. [Google Scholar]
- Tang, D.; Zhao, M.; Dowell, E.H. Inextensible Beam and Plate Theory: Computational Analysis and Comparison with Experiment. J. Appl. Mech. 2014, 81, 061009. [Google Scholar] [CrossRef]
- Liu, X.; Cai, G.; Peng, F.; Zhang, H.; Lv, L. Nonlinear Vibration Analysis of a Membrane Based on Large Deflection Theory. J. Vib. Control 2018, 24, 2418–2429. [Google Scholar] [CrossRef]
- Lu, Y.; Shao, Q.; Amabili, M.; Yue, H.; Guo, H. Nonlinear Vibration Control Effects of Membrane Structures with In-Plane PVDF Actuators: A Parametric Study. Int. J. Non-Linear Mech. 2020, 122, 103466. [Google Scholar] [CrossRef]
- Alhaifi, K.; Arshid, E.; Khorshidvand, A.R. Large Deflection Analysis of Functionally Graded Saturated Porous Rectangular Plates on Nonlinear Elastic Foundation via GDQM. Steel Compos. Struct. 2021, 39, 795. [Google Scholar]
- Love, A.E.H. On the Small Free Vibrations and Deformations of Elastic Shells. Philos. Trans. R. Soc. Lond. 1888, 179, 491–546. [Google Scholar]
- Von Karman, T. Festigkeitsprobleme in Maschinenbau, Encykl. D. Math. Wiss. 1910, 4, 311–385. [Google Scholar]
- Bromberg, E.; Stoker, J.J. Non-Linear Theory of Curved Elastic Sheets. Q. Appl. Math. 1945, 3, 246–265. [Google Scholar] [CrossRef]
- Berger, H.M. A New Approach to the Analysis of Large Deflections of Plates. J. Appl. Mech. 1955, 22, 465–472. [Google Scholar] [CrossRef]
- Chu, H.-N.; Herrmann, G. Influence of Large Amplitudes on Free Flexural Vibrations of Rectangular Elastic Plates. J. Appl. Mech. 1956, 23, 532–540. [Google Scholar] [CrossRef]
- Casado-Pascual, J.; Gómez-Ordóñez, J.; Morillo, M.; Hänggi, P. Two-State Theory of Nonlinear Stochastic Resonance. Phys. Rev. Lett. 2003, 91, 210601. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Zhou, F.; Mao, Q. Analytical Theory for the Nonlinear Optical Response of a Kerr-Type Standing-Wave Cavity Side-Coupling to a MIM Waveguide. Opt. Express 2013, 21, 23687. [Google Scholar] [CrossRef]
- Liu, R.; Xue, J. Development of Nonlinear Mechanics for Laminated Composite Plates and Shells. Lixue Xuebao/Chin. J. Theor. Appl. Mech. 2017, 49, 487–506. [Google Scholar] [CrossRef]
- Yang, Z.; Xiong, W. Molecular Vibrational Polaritons towards Quantum Technologies. Adv. Quantum Technol. 2022, 5, 2100163. [Google Scholar] [CrossRef]
- Leissa, A.W. Vibration of Plates; NASA: Washington, DC, USA, 1969. [Google Scholar]
- Israr, A. Model for Vibration of Cracked Plates for Use with Damage Detection Methodologies. J. Space Technol. 2011, 1, 1. [Google Scholar]
- Ismail, R.; Cartmell, M.P. An Investigation into the Vibration Analysis of a Plate with a Surface Crack of Variable Angular Orientation. J. Sound Vib. 2012, 331, 2929–2948. [Google Scholar] [CrossRef]
- Rice, J.R.; Levy, N. The Part-through Surface Crack in an Elastic Plate. J. Appl. Mech. Trans. ASME 1972, 39, 185–194. [Google Scholar] [CrossRef]
- Joseph, P.F.; Erdogan, F. Surface Crack in a Plate under Antisymmetric Loading Conditions. Int. J. Solids Struct. 1991, 27, 725–750. [Google Scholar] [CrossRef]
- Chandrakar, B.K.; Jain, N.K.; Gupta, A. Non-Linear Vibration Analysis of Specially Orthotropic Tapered Micro-Plates with Arbitrary Located Crack: A Non-Classical Analytical Approach. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2022, 236, 1406–1429. [Google Scholar] [CrossRef]
- Tao, N.; Ma, Y.; Jiang, H.; Dai, M.; Yang, F. Investigation on Non-Linear Vibration Response of Cantilevered Thin Plates with Crack Using Electronic Speckle Pattern Interferometry. Proceedings 2018, 2, 539. [Google Scholar] [CrossRef]
- Lynn, P.P.; Kumbasar, N. Free Vibration of Thin Rectangular Plates Having Narrow Cracks with Simply Supported Edges. In Proceedings of the 10th Midwestern Mechanics Conference, Fort Collins, CO, USA, 21–23 August 1967; pp. 911–928. [Google Scholar]
- Stahq, B.; Keer, L.M. Vibration and Stability of Cracked Rectangular Plates. Int. J. Solids Struct. 1972, 8, 69–91. [Google Scholar]
- Joseph, P.F.; Erdogan, F. A Surface Crack in Shells under Mixed-Mode Loading Conditions. J. Appl. Mech. 1988, 55, 795–804. [Google Scholar] [CrossRef]
- Mauyama, K.; Ichnomiya, O. Experimental Study of Free Vibration of Clamped Rectangular Plates with Straight Narrow Slits. JSME Int. J. 1989, 32, 187–193. [Google Scholar]
- Liew, K.M.; Hung, K.C.; Lim, M.K. A Solution Method for Analysis of Cracked Plates under Vibration. Eng. Fract. Mech. 1994, 48, 393–404. [Google Scholar] [CrossRef]
- Khadem, S.E.; Rezaee, M. Introduction of Modified Comparison Functions for Vibration Analysis of a Rectangular Cracked Plate. J. Sound Vib. 2000, 236, 245–258. [Google Scholar] [CrossRef]
- Pai, P.F.; Oh, Y.; Kim, B.-S. Detection and Estimation of Defects in a Circular Plate Using Operational Deflection Shapes. Proc. SPIE 2002, 4702, 376–388. [Google Scholar]
- Wu, G.Y.; Shih, Y.S. Dynamic Instability of Rectangular Plate with an Edge Crack. Comput. Struct. 2005, 84, 1–10. [Google Scholar] [CrossRef]
- Salehi-Khojin, A.; Zhamu, A.; Zhong, W.H.; Gan, Y. Effects of Patch Layer and Loading Frequency on Fatigue Fracture Behavior of Aluminum Plate Repaired with a Boron/Epoxy Composite Patch. J. Adhes. Sci. Technol. 2006, 20, 107–123. [Google Scholar] [CrossRef]
- Israr, A.; Cartmell, M.P.; Krawczuk, M.; Ostachowicz, W.M.; Manoach, E.; Trendafilova, I.; Shishkina, E.V.; Palacz, M. On Approximate Analytical Solutions for Vibrations in Cracked Plates. Appl. Mech. Mater. 2006, 5–6, 315–322. [Google Scholar] [CrossRef]
- Saito, A.; Castanier, M.P.; Pierre, C. Vibration Response of Cracked Cantilevered Plates near Natural Frequency Veerings. In Proceedings of the 49th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Schaumburg, IL, USA, 7–10 April 2008. [Google Scholar]
- Natarajan, S.; Baiz, P.M.; Ganapathi, M.; Kerfriden, P.; Bordas, S. Linear Free Flexural Vibration of Cracked Functionally Graded Plates in Thermal Environment. Comput. Struct. 2011, 89, 1535–1546. [Google Scholar] [CrossRef]
- Huang, C.S.; Leissa, A.W.; Chan, C.W. Vibrations of Rectangular Plates with Internal Cracks or Slits. Int. J. Mech. Sci. 2011, 53, 436–445. [Google Scholar] [CrossRef]
- Huang, T.; Lu, H.; McFarland, D.M.; Li, W.L.; Tan, C.A.; Bergman, L.A.; Gong, J. Natural Frequency Veering and Mode Localization Caused by Straight through–Cracks in Rectangular Plates with Elastic Boundary Conditions. Acta Mech. 2018, 229, 4017–4031. [Google Scholar] [CrossRef]
- Bose, T.; Mohanty, A.R. Vibration Analysis of a Rectangular Thin Isotropic Plate with a Part-through Surface Crack of Arbitrary Orientation and Position. J. Sound Vib. 2013, 332, 7123–7141. [Google Scholar] [CrossRef]
- Bose, T.; Mohanty, A.R. Detection and Monitoring of Side Crack in a Rectangular Plate Using Mobility. JVC/J. Vib. Control 2016, 22, 585–594. [Google Scholar] [CrossRef]
- Jung, W.Y.; Park, W.T.; Han, S.C. Bending and Vibration Analysis of S-FGM Microplates Embedded in Pasternak Elastic Medium Using the Modified Couple Stress Theory. Int. J. Mech. Sci. 2014, 87, 150–162. [Google Scholar] [CrossRef]
- Khalili, S.M.R.; Shariyat, M.; Mokhtari, M. Static Tensile and Transient Dynamic Response of Cracked Aluminum Plate Repaired with Composite Patch—Numerical Study. Appl. Compos. Mater. 2014, 21, 441–455. [Google Scholar] [CrossRef]
- Beigi, A.; Edalat, P.; Khedmati, M.R.; Fadavi, M. A Numerical Investigation into the Crack Effects on the Natural Frequencies of Plates. Int. J. Marit. Technol. 2014, 2, 29–41. [Google Scholar]
- Joshi, P.V.; Jain, N.K.; Ramtekkar, G.D. Analytical Modeling and Vibration Analysis of Internally Cracked Rectangular Plates. J. Sound Vib. 2014, 333, 5851–5864. [Google Scholar] [CrossRef]
- Joshi, P.V.; Jain, N.K.; Ramtekkar, G.D. Analytical Modeling for Vibration Analysis of Thin Rectangular Orthotropic/Functionally Graded Plates with an Internal Crack. J. Sound Vib. 2015, 344, 377–398. [Google Scholar] [CrossRef]
- Joshi, P.V.; Jain, N.K.; Ramtekkar, G.D. Analytical Modelling for Vibration Analysis of Partially Cracked Orthotropic Rectangular Plates. Eur. J. Mech. A/Solids 2015, 50, 100–111. [Google Scholar] [CrossRef]
- Joshi, P.V.; Jain, N.K.; Ramtekkar, G.D. Effect of Thermal Environment on Free Vibration of Cracked Rectangular Plate: An Analytical Approach. Thin-Walled Struct. 2015, 91, 38–49. [Google Scholar] [CrossRef]
- Joshi, P.V.; Jain, N.K.; Ramtekkar, G.D.; Singh Virdi, G. Vibration and Buckling Analysis of Partially Cracked Thin Orthotropic Rectangular Plates in Thermal Environment. Thin-Walled Struct. 2016, 109, 143–158. [Google Scholar] [CrossRef]
- Joshi, P.V.; Gupta, A.; Jain, N.K.; Salhotra, R.; Rawani, A.M.; Ramtekkar, G.D. Effect of Thermal Environment on Free Vibration and Buckling of Partially Cracked Isotropic and FGM Micro Plates Based on a Non Classical Kirchhoff’s Plate Theory: An Analytical Approach. Int. J. Mech. Sci. 2017, 131–132, 155–170. [Google Scholar] [CrossRef]
- Akgöz, B.; Civalek, Ö. A Microstructure-Dependent Sinusoidal Plate Model Based on the Strain Gradient Elasticity Theory. Acta Mech. 2015, 226, 2277–2294. [Google Scholar] [CrossRef]
- Gupta, A.; Jain, N.K.; Salhotra, R.; Joshi, P.V. Effect of Microstructure on Vibration Characteristics of Partially Cracked Rectangular Plates Based on a Modified Couple Stress Theory. Int. J. Mech. Sci. 2015, 100, 269–282. [Google Scholar] [CrossRef]
- Gupta, A.; Jain, N.K.; Salhotra, R.; Rawani, A.M.; Joshi, P.V. Effect of Fibre Orientation on Non-Linear Vibration of Partially Cracked Thin Rectangular Orthotropic Micro Plate: An Analytical Approach. Int. J. Mech. Sci. 2016, 105, 378–397. [Google Scholar] [CrossRef]
- Gao, K.; Gao, W.; Wu, D.; Song, C. Nonlinear Dynamic Characteristics and Stability of Composite Orthotropic Plate on Elastic Foundation under Thermal Environment. Compos. Struct. 2017, 168, 619–632. [Google Scholar] [CrossRef]
- Ghadiri, M.; Mahinzare, M.; Shafiei, N.; Ghorbani, K. On Size-Dependent Thermal Buckling and Free Vibration of Circular FG Microplates in Thermal Environments. Microsyst. Technol. 2017, 23, 4989–5001. [Google Scholar] [CrossRef]
- Shojaeefard, M.H.; Saeidi Googarchin, H.; Ghadiri, M.; Mahinzare, M. Micro Temperature-Dependent FG Porous Plate: Free Vibration and Thermal Buckling Analysis Using Modified Couple Stress Theory with CPT and FSDT. Appl. Math. Model. 2017, 50, 633–655. [Google Scholar] [CrossRef]
- Shojaeefard, M.H.; Saeidi Googarchin, H.; Mahinzare, M.; Eftekhari, S.A. Magnetic Field Effect on Free Vibration of Smart Rotary Functionally Graded Nano/Microplates: A Comparative Study on Modified Couple Stress Theory and Nonlocal Elasticity Theory. J. Intell. Mater. Syst. Struct. 2018, 29, 2492–2507. [Google Scholar] [CrossRef]
- Mahinzare, M.; Ranjbarpur, H.; Ghadiri, M. Free Vibration Analysis of a Rotary Smart Two Directional Functionally Graded Piezoelectric Material in Axial Symmetry Circular Nanoplate. Mech. Syst. Signal Process. 2018, 100, 188–207. [Google Scholar] [CrossRef]
- Mahinzare, M.; Barooti, M.M.; Ghadiri, M. Vibrational Investigation of the Spinning Bi-Dimensional Functionally Graded (2-FGM) Micro Plate Subjected to Thermal Load in Thermal Environment. Microsyst. Technol. 2018, 24, 1695–1711. [Google Scholar] [CrossRef]
- Chouiyakh, H.; Azrar, L.; Alnefaie, K.; Akourri, O. Crack Identification Based on the Nonlinear Response of Plates with Variably Oriented Surface Crack. MATEC Web Conf. 2018, 149, 02061. [Google Scholar] [CrossRef][Green Version]
- Moradi, S.; Makvandi, H.; Poorveis, D.; Shirazi, K.H. Free Vibration Analysis of Cracked Postbuckled Plate. Appl. Math. Model. 2019, 66, 611–627. [Google Scholar] [CrossRef]
- Gupta, A.; Jain, N.K.; Salhotra, R.; Joshi, P.V.; Soni, S. Effect of Crack Location on Vibration Analysis of Cracked FGM Plate under Thermal Environment. Mater. Today Proc. 2018, 5, 28043–28050. [Google Scholar] [CrossRef]
- Soni, S.; Jain, N.K.; Joshi, P.V. Vibration Analysis of Partially Cracked Plate Submerged in Fluid. J. Sound Vib. 2018, 412, 28–57. [Google Scholar] [CrossRef]
- Soni, S.; Jain, N.K.; Joshi, P.V.; Gupta, A.; Soni, S. Effect of Thermal Environment on Vibration Response of Partially Cracked Functionally Graded Plate Coupled with Fluid. Mater. Today Proc. 2018, 5, 27810–27819. [Google Scholar] [CrossRef]
- Soni, S.; Jain, N.K.; Joshi, P.V. Effect of Thermal Environment on Vibration Analysis of Partially Cracked Thin Isotropic Plate Submerged in Fluid. J. Solid Mech. 2019, 11, 120–143. [Google Scholar] [CrossRef]
- Soni, S.; Jain, N.K.; Joshi, P.V. Effect of Microstructure on Vibration Analysis of Partially Cracked Thin Orthotropic Plate Based on Strain Gradient Theory. In AIP Conference Proceedings, Proceedings of the 1st International Conference on Advances in Mechanical Engineering and Nanotechnology (ICAMEN 2019), Jaipur, India, 8–9 March 2019; American Institute of Physics Inc.: College Park, MD, USA, 2019; Volume 2148. [Google Scholar]
- Soni, S.; Jain, N.K.; Joshi, P.V. Vibration and Deflection Analysis of Thin Cracked and Submerged Orthotropic Plate under Thermal Environment Using Strain Gradient Theory. Nonlinear Dyn. 2019, 96, 1575–1604. [Google Scholar] [CrossRef]
- Soni, S.; Jain, N.K.; Joshi, P.V. Stability and Dynamic Analysis of Partially Cracked Thin Orthotropic Microplates under Thermal Environment: An Analytical Approach. Mech. Based Des. Struct. Mach. 2020, 48, 299–325. [Google Scholar] [CrossRef]
- Mashrouteh, S.; Younesian, D.; Esmailzadeh, E. Multi-Resonance Analysis of a Viscoelastically Supported Orthotropic Plate with an Inclined Crack. Nonlinear Dyn. 2019, 96, 1717–1734. [Google Scholar] [CrossRef]
- Ranjbaran, M.; Seifi, R. Analysis of Free Vibration of an Isotropic Plate with Surface or Internal Long Crack Using Generalized Differential Quadrature Method. J. Strain. Anal. Eng. Des. 2020, 55, 42–52. [Google Scholar] [CrossRef]
- Dean, A.; Asur Vijaya Kumar, P.K.; Reinoso, J.; Gerendt, C.; Paggi, M.; Mahdi, E.; Rolfes, R. A Multi Phase-Field Fracture Model for Long Fiber Reinforced Composites Based on the Puck Theory of Failure. Compos. Struct. 2020, 251, 112446. [Google Scholar] [CrossRef]
- Doan, D.H.; Van Do, T.; Nguyen, N.X.; Van Vinh, P.; Trung, N.T. Multi-Phase-Field Modelling of the Elastic and Buckling Behaviour of Laminates with Ply Cracks. Appl. Math. Model. 2021, 94, 68–86. [Google Scholar] [CrossRef]
- Gonenli, C.; Das, O. Effect of Crack Location on Buckling and Dynamic Stability in Plate Frame Structures. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 311. [Google Scholar] [CrossRef]
- Aftab, H.; Baneen, U.; Israr, A. Identification and Severity Estimation of a Breathing Crack in a Plate via Nonlinear Dynamics. Nonlinear Dyn. 2021, 104, 1973–1989. [Google Scholar] [CrossRef]
- Nikkhoo, A.; Banihashemi, S.; Kiani, K. Parametric Investigations on Dynamics of Cracked Thin Rectangular Plates, Excited by a Moving Mass. Sci. Iran. 2022, 30, 860–876. [Google Scholar] [CrossRef]
- Song, Y.; Xue, K.; Li, Q. A Solution Method for Free Vibration of Intact and Cracked Polygonal Thin Plates Using the Ritz Method and Jacobi Polynomials. J. Sound Vib. 2022, 519, 116578. [Google Scholar] [CrossRef]
- Al-Shammari, M.A.; Husain, M.A.; Al-Waily, M. Free Vibration Analysis of Rectangular Plates with Cracked Holes. In AIP Conference Proceedings, Proceedings of the 3rd International Scientific Conference of Alkafeel University (ISCKU 2021), Najaf, Iraq, 22–23 March 2021; American Institute of Physics Inc.: College Park, MD, USA, 2022; Volume 2386. [Google Scholar]
- Migot, A.; Naser, H.N.H.; Ugla, A.A.; Giurgiutiu, V. Investigations of Fatigue Crack Detection Using Local Vibration Techniques: Numerical and Experimental Studies. J. Nondestruct. Eval. 2023, 42, 12. [Google Scholar] [CrossRef]
- Wang, Y.-S.; Shih, Y.-S. Analysis of the Vibration of a Cracked Ferromagnetic Rectangular Plate in a Transverse Magnetic Field. J. Vib. Control. 2023, 29, 2501–2514. [Google Scholar] [CrossRef]
- Kou, S.; Zhang, X.; Li, W.; Song, C. Dynamic Response Parameter Analysis of Steel Frame Joints under Blast Loading. Buildings 2022, 12, 433. [Google Scholar] [CrossRef]
- Cannon, L.; Clubley, S.K. Structural Response of Simple Partially-Clad Steel Frames to Long-Duration Blast Loading. Structures 2021, 32, 1260–1270. [Google Scholar] [CrossRef]
- Yussof, M.M.; Silalahi, J.H.; Kamarudin, M.K.; Chen, P.-S.; Parke, G.A.R. Numerical Evaluation of Dynamic Responses of Steel Frame Structures with Different Types of Haunch Connection Under Blast Load. Appl. Sci. 2020, 10, 1815. [Google Scholar] [CrossRef]
- Curry, R.J.; Langdon, G.S. Transient Response of Steel Plates Subjected to Close Proximity Explosive Detonations in Air. Int. J. Impact Eng. 2017, 102, 102–116. [Google Scholar] [CrossRef]
- Wang, Z.; Gao, Y.; Zhang, Y.; Duan, Y.; Huang, C.; Wu, H. Analysis of Damage Characteristics of the Rectangular Steel Container under Near-Earth Explosion Loading. Case Stud. Constr. Mater. 2024, 21, e03518. [Google Scholar] [CrossRef]
- Hu, Z.; Yang, Y.; Zhou, C.; Zheng, X.; Li, R. On the Symplectic Superposition Method for New Analytic Free Vibration Solutions of Side-Cracked Rectangular Thin Plates. J. Sound Vib. 2020, 489, 115695. [Google Scholar] [CrossRef]
- Xue, J.; Wang, Y.; Chen, L. Nonlinear Vibration of Cracked Rectangular Mindlin Plate with In-Plane Preload. J. Sound Vib. 2020, 481, 115437. [Google Scholar] [CrossRef]
- Das, O.; Gonenli, C.; Das, D.B. Crack Detection in Folded Plates with Back-Propagated Artificial Neural Network. Steel Compos. Struct. 2023, 46, 319–334. [Google Scholar] [CrossRef]
- Bachene, M.; Tiberkak, R.; Rechak, S. Vibration Analysis of Cracked Plates Using the Extended Finite Element Method. Arch. Appl. Mech. 2009, 79, 249–262. [Google Scholar] [CrossRef]
- Tran, L.V.; Ly, H.A.; Lee, J.; Wahab, M.A.; Nguyen-Xuan, H. Vibration Analysis of Cracked FGM Plates Using Higher-Order Shear Deformation Theory and Extended Isogeometric Approach. Int. J. Mech. Sci. 2015, 96–97, 65–78. [Google Scholar] [CrossRef]
- Hu, Z.; Ni, Z.; An, D.; Chen, Y.; Li, R. Hamiltonian System-Based Analytical Solutions for the Free Vibration of Edge-Cracked Thick Rectangular Plates. Appl. Math. Model. 2023, 117, 451–478. [Google Scholar] [CrossRef]
- Milazzo, A. Free Vibrations Analysis of Cracked Variable Stiffness Composite Plates by the EXtended Ritz Method. Mech. Adv. Mater. Struct. 2023, 30, 1675–1691. [Google Scholar] [CrossRef]
- Li, T.Y.; Liu, J.X.; Zhang, T. Vibrational Power Flow Characteristics of Circular Plate Structures with Peripheral Surface Crack. J. Sound Vib. 2004, 276, 1081–1091. [Google Scholar] [CrossRef]
- Rucka, M.; Wilde, K. Application of Continuous Wavelet Transform in Vibration Based Damage Detection Method for Beams and Plates. J. Sound Vib. 2006, 297, 536–550. [Google Scholar] [CrossRef]
- Dwivedi, K.; Raza, A.; Pathak, H.; Talha, M.; Upadhyaya, R. Free Flexural Vibration of Cracked Composite Laminated Plate Using Higher-Order XFEM. Eng. Fract. Mech. 2023, 289, 109420. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, Z. Transverse Vibration of Viscoelastic Rectangular Plate with Linearly Varying Thickness and Multiple Cracks. J. Sound Vib. 2008, 318, 1005–1023. [Google Scholar] [CrossRef]
- Phạm Minh, P. Analysis Free Vibration of the Functionally Grade Material Cracked Plates with Varying Thickness Using the Phase-Field Theory. Transp. Commun. Sci. J. 2019, 70, 122–131. [Google Scholar] [CrossRef][Green Version]
- Minh, P.P.; Duc, N.D. The Effect of Cracks on the Stability of the Functionally Graded Plates with Variable-Thickness Using HSDT and Phase-Field Theory. Compos. B Eng. 2019, 175, 107086. [Google Scholar] [CrossRef]
- Pham Minh, P. Using Phase Field and Third-Order Shear Deformation Theory to Study the Effect of Cracks on Free Vibration of Rectangular Plates with Varying Thickness. Transp. Commun. Sci. J. 2020, 71, 853–867. [Google Scholar] [CrossRef]
- Minh, P.P.; Duc, N.D. The Effect of Cracks and Thermal Environment on Free Vibration of FGM Plates. Thin-Walled Struct. 2021, 159, 107291. [Google Scholar] [CrossRef]
- Minh, P.P.; Manh, D.T.; Duc, N.D. Free Vibration of Cracked FGM Plates with Variable Thickness Resting on Elastic Foundations. Thin-Walled Struct. 2021, 161, 107425. [Google Scholar] [CrossRef]
- Le, M.; Lee, J. Ultrasonic Testing of Corrosion in Aircraft Rivet Using Spiking Neural Network. J. Nondestruct. Eval. 2023, 42, 78. [Google Scholar] [CrossRef]
- Heo, J.; Yang, Z.; Xia, W.; Oterkus, S.; Oterkus, E. Free Vibration Analysis of Cracked Plates Using Peridynamics. Ships Offshore Struct. 2020, 15, S220–S229. [Google Scholar] [CrossRef]
- Chandrakar, B.K.; Jain, N.K.; Gupta, A. Crack Orientation Effects on Vibration Characteristics of Bi-Directional Linearly Varying Thickness Partially Cracked Isotropic Micro-Plate: An Analytical Approach. Springer Proc. Mater. 2021, 13, 315–323. [Google Scholar] [CrossRef]
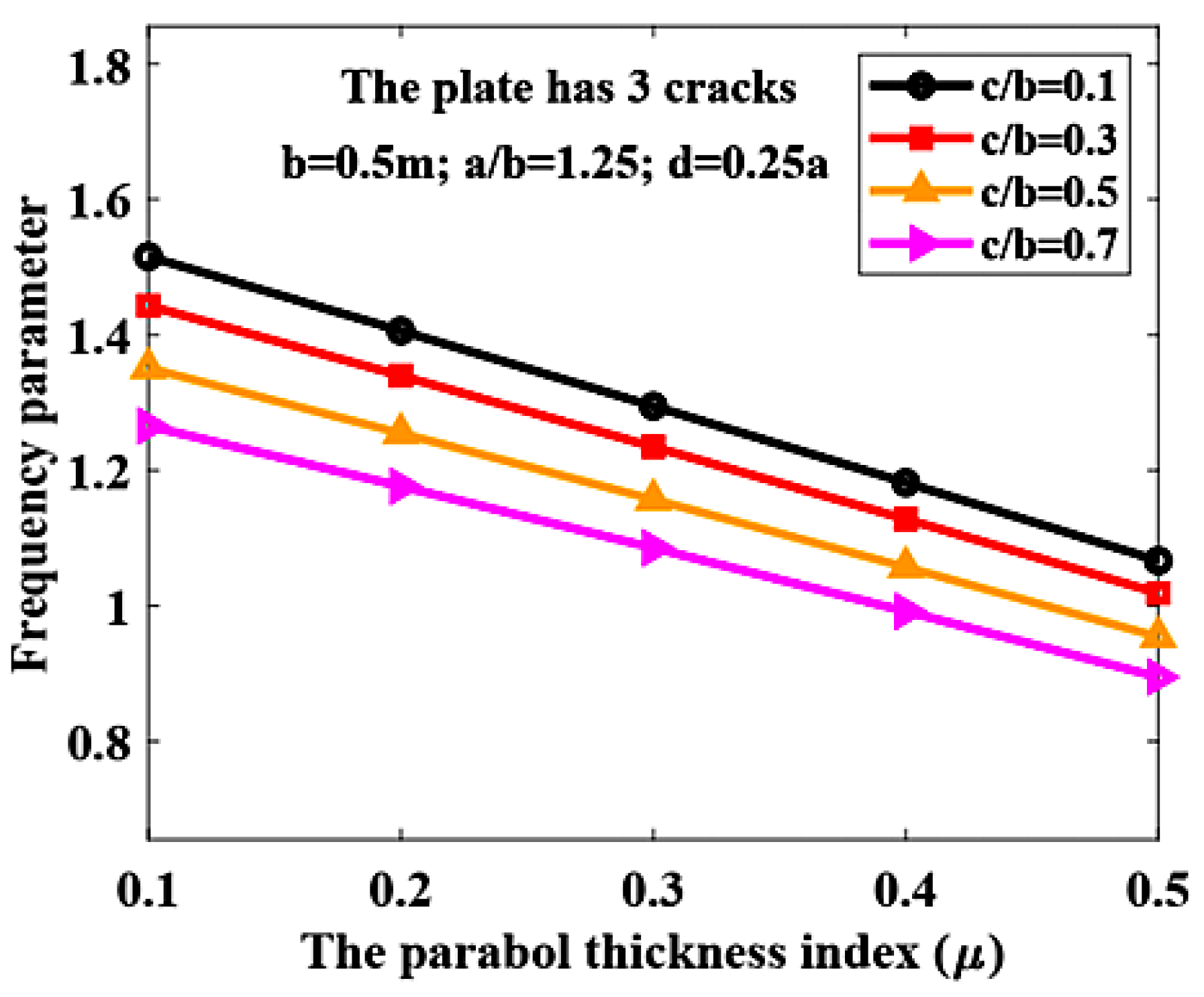
- Le, V.A.; Nguyen, X.T. The Effect of Cracks on the Free Vibration of a Plate with Parabolic Thickness. Eng. Technol. Appl. Sci. Res. 2023, 13, 11100–11105. [Google Scholar] [CrossRef]
- Adams, R.D.; Cawley, P.; Pye, C.J.; Stone, B.J. A Vibration Technique for Non-Destructively Assessing the Integrity of Structures. J. Mech. Eng. Sci. 1978, 20, 93–100. [Google Scholar] [CrossRef]
- Lee, U.; Lesieutre, G.A.; Fang, L. Anisotropic Damage Mechanics Based on Strain Energy Equivalence and Equivalent Elliptical Microcracks. Int. J. Solids Strucfures 1997, 34, 4377–4397. [Google Scholar] [CrossRef]
- Lee, U.; Kim, N.; Shin, J. Identification of Damages within a Plate Structure. In Proceedings of the 19th AIAA Applied Aerodynamics Conference, Anaheim, CA, USA, 1–14 June 2001; American Institute of Aeronautics and Astronautics Inc.: Reston, VA, USA, 2001. [Google Scholar]
- Lee, U.; Cho, K.; Shin, J. Identification of Orthotropic Damages within a Thin Uniform Plate. Int. J. Solids Struct. 2003, 40, 2195–2213. [Google Scholar] [CrossRef]
- Cornwell, P.; Doebling, S.W.; Farrar, C.R. Application of the Strain Energy Damage Detection Method to Plate-like Structures. J. Sound Vib. 1999, 224, 359–374. [Google Scholar] [CrossRef]
- Li, Y.Y.; Cheng, L.; Yam, L.H.; Wong, W.O. Identification of Damage Locations for Plate-like Structures Using Damage Sensitive Indices: Strain Modal Approach. Comput. Struct. 2002, 80, 1881–1894. [Google Scholar] [CrossRef]
- Wu, D.; Law, S.S. Damage Localization in Plate Structures from Flexibility and Its Derivatives. In Proceedings of the Smart Structures and Materials 2004: Sensors and Smart Structures Technologies for Civil, Mechanical, and Aerospace Systems, San Diego, CA, USA, 14–18 March 2004; SPIE: Bellingham, WA, USA, 2004; Volume 5391, p. 449. [Google Scholar]
- Wu, D.; Law, S.S. Damage-Detection-Oriented Model for a Cracked Rectangular Plate. In Proceedings of the Smart Structures and Materials 2004: Sensors and Smart Structures Technologies for Civil, Mechanical, and Aerospace Systems, San Diego, CA, USA, 14–18 March 2004; SPIE: Bellingham, WA, USA, 2004; Volume 5391, p. 470. [Google Scholar]
- Wu, D.; Law, S.S. Anisotropic Damage Model for an Inclined Crack in Thick Plate and Sensitivity Study for Its Detection. Int. J. Solids Struct. 2004, 41, 4321–4336. [Google Scholar] [CrossRef]
- Wu, D.; Law, S.S. Damage Localization in Plate Structures from Uniform Load Surface Curvature. J. Sound Vib. 2004, 276, 227–244. [Google Scholar] [CrossRef]
- Wu, D.; Law, S.S. Sensitivity of Uniform Load Surface Curvature for Damage Identification in Plate Structures. J. Vib. Acoust. Trans. ASME 2005, 127, 84–92. [Google Scholar] [CrossRef]
- Wu, D.; Law, S.S. Crack Identification in Thin Plates with Anisotropic Damage Model and Vibration Measurements. J. Appl. Mech. Trans. ASME 2005, 72, 852–861. [Google Scholar] [CrossRef]
- Yam, L.H.; Yan, Y.J.; Wei, Z. Vibration-Based Non Destructive Structural Damage Detection. Key Eng. Mater. 2004, 270–273, 1446–1453. [Google Scholar] [CrossRef]
- Yam, L.H.; Cheng, L.; Wei, Z.; Yan, Y.J. Damage Detection of Composite Structures Using Dynamic Analysis. Key Eng. Mater. 2005, 295–296, 33–38. [Google Scholar] [CrossRef]
- Huynh, D.; Tran, D. A Non-Destructive Crack Detection Technique Using Vibration Tests. In Proceedings of the Structural Integrity and Fracture International Conference (SIF’04), Brisbane, Australia, 26–29 September 2004; Atrens, A., Boland, J.N., Clegg, R., Griffiths, J.R., Eds.; The University of Queensland: Brisbane, Australia, 2004; pp. 155–162. [Google Scholar]
- Huynh, D.; He, J.; Tran, D. Damage Location Vector: A Non-Destructive Structural Damage Detection Technique. Comput. Struct. 2005, 83, 2353–2367. [Google Scholar] [CrossRef]
- Qiao, P.Z.; Lu, K.; Lestari, W. A Combined Static/Dynamic Technique for Damage Detection of Laminated Composite Plates. Exp. Mech. 2008, 48, 17–35. [Google Scholar] [CrossRef]
- Ramos, L.F.; De Roeck, G.; Lourenço, P.B.; Campos-Costa, A. Damage Identification on Arched Masonry Structures Using Ambient and Random Impact Vibrations. Eng. Struct. 2010, 32, 146–162. [Google Scholar] [CrossRef]
- Trana, D. Crack Detection in Structures Using Frequency Response Functions. In AIP Conference Proceedings, Proceedings of the 2nd International Symposium on Computational Mechanics and the 12th International Conference on the Enhancement and Promotion of Computational Methods in Engineering and Science, Hong Kong, Macau, China, 30 November–3 December 2009; American Institute of Physics Inc.: College Park, MD, USA, 2010; Volume 1233, pp. 1273–1278. [Google Scholar]
- Xu, W.; Radzieński, M.; Ostachowicz, W.; Cao, M. Damage Detection in Plates Using Two-Dimensional Directional Gaussian Wavelets and Laser Scanned Operating Deflection Shapes. Struct. Health Monit. 2013, 12, 457–468. [Google Scholar] [CrossRef]
- Fu, Y.Z.; Lu, Z.R.; Liu, J.K. Damage Identification in Plates Using Finite Element Model Updating in Time Domain. J. Sound Vib. 2013, 332, 7018–7032. [Google Scholar] [CrossRef]
- Fu, Y.; Liu, J.; Wei, Z.; Lu, Z. A Two-Step Approach for Damage Identification in Plates. J. Vib. Control. 2016, 22, 3018–3031. [Google Scholar] [CrossRef]
- Al-Agamy, M.; Abo-Elkhier, M.; Hamada, A.A.; Student, P.G. Damage Detection in Composite Plates Using Dynamic Response. Int. J. Innov. Res. Sci. 2019, 8, 1–15. [Google Scholar]
- Huang, Y.-H.; Chen, J.-E.; Ge, W.-M.; Bian, X.-L.; Hu, W.-H. Research on Geometric Features of Phase Diagram and Crack Identification of Cantilever Beam with Breathing Crack. Results Phys. 2019, 15, 102561. [Google Scholar] [CrossRef]
- Duvnjak, I.; Damjanović, D.; Bartolac, M.; Skender, A. Mode Shape-Based Damage Detection Method (MSDI): Experimental Validation. Appl. Sci. 2021, 11, 4589. [Google Scholar] [CrossRef]
- Wei, Z.; Yam, L.H.; Cheng, L. NARMAX Model Representation and Its Application to Damage Detection for Multi-Layer Composites. Compos. Struct. 2005, 68, 109–117. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, L.; Xiang, Z. Damage Detection by Mode Shape Squares Extracted from a Passing Vehicle. J. Sound Vib. 2012, 331, 291–307. [Google Scholar] [CrossRef]
- Wei, Z.T.; Liu, J.K.; Lu, Z.R. Damage Identification in Plates Based on the Ratio of Modal Strain Energy Change and Sensitivity Analysis. Inverse Probl. Sci. Eng. 2016, 24, 265–283. [Google Scholar] [CrossRef]
- De Castro, B.A.; Baptista, F.G.; Ciampa, F. Impedance-Based Structural Health Monitoring under Low Signal-to-Noise Ratio Conditions. In Proceedings of the 9 th European Workshop on Structural Health Monitoring, Manchester, UK, 10–13 July 2018. [Google Scholar]
- Yam, L.H.; Li, Y.Y.; Wong, W.O. Sensitivity Studies of Parameters for Damage Detection of Plate-like Structures Using Static and Dynamic Approaches. Eng. Struct. 2002, 24, 1465–1475. [Google Scholar] [CrossRef]
- Zhang, Y.; Lie, S.T.; Xiang, Z. Damage Detection Method Based on Operating Deflection Shape Curvature Extracted from Dynamic Response of a Passing Vehicle. Mech. Syst. Signal Process. 2013, 35, 238–254. [Google Scholar] [CrossRef]
- Alsaadi, A.; Shi, Y.; Jia, Y. Delamination Detection via Reconstructed Frequency Response Function of Composite Structures. In Proceedings of the 13th International Conference on Damage Assessment of Structures, Porto, Portugal, 9–10 July 2019; pp. 837–843. [Google Scholar]
- Zhong, Y.; Yuan, S.; Qiu, L. Multiple Damage Detection on Aircraft Composite Structures Using Near-Field MUSIC Algorithm. Sens. Actuators A Phys. 2014, 214, 234–244. [Google Scholar] [CrossRef]
- He, J.; Yuan, F.-G. Lamb Wave-Based Subwavelength Damage Imaging Using the DORT-MUSIC Technique in Metallic Plates. Struct. Health Monit. 2016, 15, 65–80. [Google Scholar] [CrossRef]
- Katunin, A. Damage Identification in Composite Plates Using Two-Dimensional B-Spline Wavelets. Mech. Syst. Signal Process. 2011, 25, 3153–3167. [Google Scholar] [CrossRef]
- Cao, M.S.; Ostachowicz, W.; Bai, R.B.; Radzieński, M. Fractal Mechanism for Characterizing Singularity of Mode Shape for Damage Detection. Appl. Phys. Lett. 2013, 103, 221906. [Google Scholar] [CrossRef]
- Huang, T.; Schröder, K.-U. A Bayesian Probabilistic Approach for Damage Identification in Plate Structures Using Responses at Vibration Nodes. Mech. Syst. Signal. Process. 2021, 146, 106998. [Google Scholar] [CrossRef]
- Zuo, H.; Yang, Z.; Xu, C.; Tian, S.; Chen, X. Damage Identification for Plate-like Structures Using Ultrasonic Guided Wave Based on Improved MUSIC Method. Compos. Struct. 2018, 203, 164–171. [Google Scholar] [CrossRef]
- Reddy, D.M.; Swarnamani, S. Application of the FRF Curvature Energy Damage Detection Method to Plate like Structures. World J. Model. Simul. 2012, 8, 147–153. [Google Scholar]
- Rouquand, A.; Pontiroli, C.; Canton, E. An Explicit Damage Model for Dynamic Concrete Behaviour. In Numerical Simulations and Comparisons with Experimental Results on Reinforced Concrete Plates under Blast Loading; WIT Press: Cambridge, MA, USA, 1996; Volume 22. [Google Scholar]
- Ivančević, D.; Smojver, I. Explicit Multiscale Modelling of Impact Damage on Laminated Composites–Part II: Multiscale Analyses. Compos. Struct. 2016, 145, 259–268. [Google Scholar] [CrossRef]
- Kim, E.-H.; Rim, M.-S.; Lee, I.; Hwang, T.-K. Composite Damage Model Based on Continuum Damage Mechanics and Low Velocity Impact Analysis of Composite Plates. Compos. Struct. 2013, 95, 123–134. [Google Scholar] [CrossRef]
- Maire, J.-F.; Lesne, P.-M. An Explicit Damage Model for the Design of Composites Structures. Compos. Sci. Technol. 1998, 58, 773–778. [Google Scholar] [CrossRef]
- Moreau, K.; Moës, N.; Picart, D.; Stainier, L. Explicit Dynamics with a Non-Local Damage Model Using the Thick Level Set Approach. Int. J. Numer. Methods Eng. 2015, 102, 808–838. [Google Scholar] [CrossRef]
- Zhou, Y.; Yazdani Nezhad, H.; Hou, C.; Wan, X.; McCarthy, C.T.; McCarthy, M.A. A Three Dimensional Implicit Finite Element Damage Model and Its Application to Single-Lap Multi-Bolt Composite Joints with Variable Clearance. Compos. Struct. 2015, 131, 1060–1072. [Google Scholar] [CrossRef]
- César de Sá, J.M.A.; Areias, P.M.A.; Zheng, C. Damage Modelling in Metal Forming Problems Using an Implicit Non-Local Gradient Model. Comput. Methods Appl. Mech. Eng. 2006, 195, 6646–6660. [Google Scholar] [CrossRef]
- Seupel, A.; Hütter, G.; Kuna, M. An Efficient FE-Implementation of Implicit Gradient-Enhanced Damage Models to Simulate Ductile Failure. Eng. Fract. Mech. 2018, 199, 41–60. [Google Scholar] [CrossRef]
- Tran, H.T.; Bui, T.Q.; Chijiwa, N.; Hirose, S. A New Implicit Gradient Damage Model Based on Energy Limiter for Brittle Fracture: Theory and Numerical Investigation. Comput. Methods Appl. Mech. Eng. 2023, 413, 116123. [Google Scholar] [CrossRef]
- Kurtaran, H. Shape Effect on Free Vibration of Functionally Graded Plates. Int. J. Eng. Appl. Sci. 2014, 6, 52. [Google Scholar] [CrossRef][Green Version]
- Wang, F.; Chan, T. Review of Vibration-Based Damage Detection and Condition Assessment of Bridge Structures Using Structural Health Monitoring. In Proceedings of The Second Infrastructure Theme Postgraduate Conference: Rethinking Sustainable Development-Planning, Infrastructure Engineering, Design and Managing Urban Infrastructure; Queensland University of Technology: Brisbane, Australia, 2009; pp. 35–47. [Google Scholar]
- Yang, Z.; Chen, X.; Yu, J.; Liu, R.; Liu, Z.; He, Z. A Damage Identification Approach for Plate Structures Based on Frequency Measurements. Nondestruct. Test. Eval. 2013, 28, 321–341. [Google Scholar] [CrossRef]
- Xu, Y.; Zhu, W. Non-Model-Based Damage Identification of Plates Using Measured Mode Shapes. Struct. Health Monit. 2017, 16, 3–23. [Google Scholar] [CrossRef]
- Beskhyroun, S.; Wegner, L.D.; Sparling, B.F. New Methodology for the Application of Vibration-Based Damage Detection Techniques. Struct. Control. Health Monit. 2012, 19, 632–649. [Google Scholar] [CrossRef]
- Catbas, F.N.; Brown, D.L.; Aktan, A.E. Use of Modal Flexibility for Damage Detection and Condition Assessment: Case Studies and Demonstrations on Large Structures. J. Struct. Eng. 2006, 132, 1699–1712. [Google Scholar] [CrossRef]
- Pandey, A.K.; Biswas, M. Experimental Verification of Flexibility Difference Method for Locating Damage in Structures. J. Sound Vib. 1995, 184, 311–328. [Google Scholar] [CrossRef]
- Abdel wahab, M.M.; De roeck, G. Damage Detection in Bridges Using Modal Curvatures: Application to a Real Damage Scenario. J. Sound Vib. 1999, 226, 217–235. [Google Scholar] [CrossRef]
- Shi, Z.Y.; Law, S.S.; Zhang, L.M. Structural Damage Detection from Modal Strain Energy Change. J. Eng. Mech. 2000, 126, 1216–1223. [Google Scholar] [CrossRef]
- Hu, H.; Wang, B.-T.; Lee, C.-H.; Su, J.-S. Damage Detection of Surface Cracks in Composite Laminates Using Modal Analysis and Strain Energy Method. Compos. Struct. 2006, 74, 399–405. [Google Scholar] [CrossRef]
- Meruane, V.; Lasen, M.; López Droguett, E.; Ortiz-Bernardin, A. Modal Strain Energy-Based Debonding Assessment of Sandwich Panels Using a Linear Approximation with Maximum Entropy. Entropy 2017, 19, 619. [Google Scholar] [CrossRef]
- Siow, P.Y.; Ong, Z.C.; Khoo, S.Y.; Lim, K.-S. Damage Sensitive PCA-FRF Feature in Unsupervised Machine Learning for Damage Detection of Plate-like Structures. Int. J. Struct. Stab. Dyn. 2021, 21, 2150028. [Google Scholar] [CrossRef]
- Zhao, M.; Zhou, W.; Huang, Y.; Li, H. Sparse Bayesian Learning Approach for Propagation Distance Recognition and Damage Localization in Plate-like Structures Using Guided Waves. Struct. Health Monit. 2021, 20, 3–24. [Google Scholar] [CrossRef]
- Lu, Z.R.; Law, S.S. Identification of System Parameters and Input Force from Output Only. Mech. Syst. Signal Process. 2007, 21, 2099–2111. [Google Scholar] [CrossRef]
- Zimmerman, D.C.; Kaouk, M. Structural Damage Detection Using a Minimum Rank Update Theory. J. Vib. Acoust. 1994, 116, 222–231. [Google Scholar] [CrossRef]
- Messina, A.; Williams, E.J.; Contursi, T. Structural Damage Detection by a Sensitivity and Statistical-Based Method. J. Sound Vib. 1998, 216, 791–808. [Google Scholar] [CrossRef]
- Wang, Q.P.; Guo, X.; Wang, H.X. Application of Damage Location Vector Method in Structural Damage Identification. In Proceedings of the Road Materials and New Innovations in Pavement Engineering, American Society of Civil Engineers, Reston, VA, USA, 23 May 2011; pp. 136–143. [Google Scholar]
- Nguyen-Thoi, T.; Tran-Viet, A.; Nguyen-Minh, N.; Vo-Duy, T.; Ho-Huu, V. A Combination of Damage Locating Vector Method (DLV) and Differential Evolution Algorithm (DE) for Structural Damage Assessment. Front. Struct. Civ. Eng. 2018, 12, 92–108. [Google Scholar] [CrossRef]
- Jepsen, M.; Ulriksen, M.D.; Bernal, D. Closed-Loop Damage-Locating Vectors. In European Workshop on Structural Health Monitoring; Springer: Cham, Switzerland, 2023; pp. 697–707. [Google Scholar]
- Gao, Y.; Spencer, B.F.; Bernal, D. Experimental Verification of the Damage Locating Vector Method. J. Eng. Mech. 2004, 133. [Google Scholar]
- Bernal, D.; Gunes, B. Flexibility Based Approach for Damage Characterization: Benchmark Application. J. Eng. Mech. 2004, 130, 61–70. [Google Scholar] [CrossRef]
- Bernal, D. Load Vectors for Damage Localization. J. Eng. Mech. 2002, 128, 7–14. [Google Scholar] [CrossRef]
- Cheng, C.; Nie, Z.H.; Ma, H.W. Structural Damage Detection of the Simple Beam Based on Responses Phase Space. Adv. Mat. Res. 2012, 605–607, 989–995. [Google Scholar] [CrossRef]
- Zhang, W.; Ma, H.; Zeng, J.; Wu, S.; Wen, B. Vibration Responses Analysis of an Elastic-Support Cantilever Beam with Crack and Offset Boundary. Mech. Syst. Signal Process. 2017, 95, 205–218. [Google Scholar] [CrossRef]
- Rezaee, M.; Shaterian-Alghalandis, V. A New Crack Detection Method in a Beam under Geometrically Nonlinear Vibration. Arch. Appl. Mech. 2018, 88, 1491–1506. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, J.; Yao, Z.; Yang, X.; Sun, R.; Zhao, Y. Nonlinear Characteristics of a Multi-Degree-of-Freedom Spur Gear System with Bending-Torsional Coupling Vibration. Mech. Syst. Signal Process. 2019, 121, 810–827. [Google Scholar] [CrossRef]
- Andreaus, U.; Baragatti, P. Cracked Beam Identification by Numerically Analysing the Nonlinear Behaviour of the Harmonically Forced Response. J. Sound Vib. 2011, 330, 721–742. [Google Scholar] [CrossRef]
- Andreaus, U.; Baragatti, P. Experimental Damage Detection of Cracked Beams by Using Nonlinear Characteristics of Forced Response. Mech. Syst. Signal Process. 2012, 31, 382–404. [Google Scholar] [CrossRef]
- Bovsunovsky, A.P.; Surace, C. Considerations Regarding Superharmonic Vibrations of a Cracked Beam and the Variation in Damping Caused by the Presence of the Crack. J. Sound Vib. 2005, 288, 865–886. [Google Scholar] [CrossRef]
- Bovsunovsky, A.P.; Bovsunovsky, O. Crack Detection in Beams by Means of the Driving Force Parameters Variation at Non-Linear Resonance Vibrations. Key Eng. Mater. 2007, 347, 413–420. [Google Scholar] [CrossRef]
- Douka, E.; Hadjileontiadis, L.J. Time–Frequency Analysis of the Free Vibration Response of a Beam with a Breathing Crack. NDT E Int. 2005, 38, 3–10. [Google Scholar] [CrossRef]
- Alexandrino, P.D.S.L.; Gomes, G.F.; Cunha, S.S. A Robust Optimization for Damage Detection Using Multiobjective Genetic Algorithm, Neural Network and Fuzzy Decision Making. Inverse Probl. Sci. Eng. 2020, 28, 21–46. [Google Scholar] [CrossRef]
- Tan, Z.X.; Thambiratnam, D.P.; Chan, T.H.T.; Gordan, M.; Abdul Razak, H. Damage Detection in Steel-Concrete Composite Bridge Using Vibration Characteristics and Artificial Neural Network. Struct. Infrastruct. Eng. 2020, 16, 1247–1261. [Google Scholar] [CrossRef]
- Padil, K.H.; Bakhary, N.; Abdulkareem, M.; Li, J.; Hao, H. Non-Probabilistic Method to Consider Uncertainties in Frequency Response Function for Vibration-Based Damage Detection Using Artificial Neural Network. J. Sound Vib. 2020, 467, 115069. [Google Scholar] [CrossRef]
- Nasiri, M.R.; Mahjoob, M.J.; Aghakasiri, A. Damage Detection in a Composite Plate Using Modal Analysis and Artificial Intelligence. Appl. Compos. Mater. 2011, 18, 513–520. [Google Scholar] [CrossRef]
- Yam, L.H.; Yan, Y.J.; Jiang, J.S. Vibration-Based Damage Detection for Composite Structures Using Wavelet Transform and Neural Network Identification. Compos. Struct. 2003, 60, 403–412. [Google Scholar] [CrossRef]

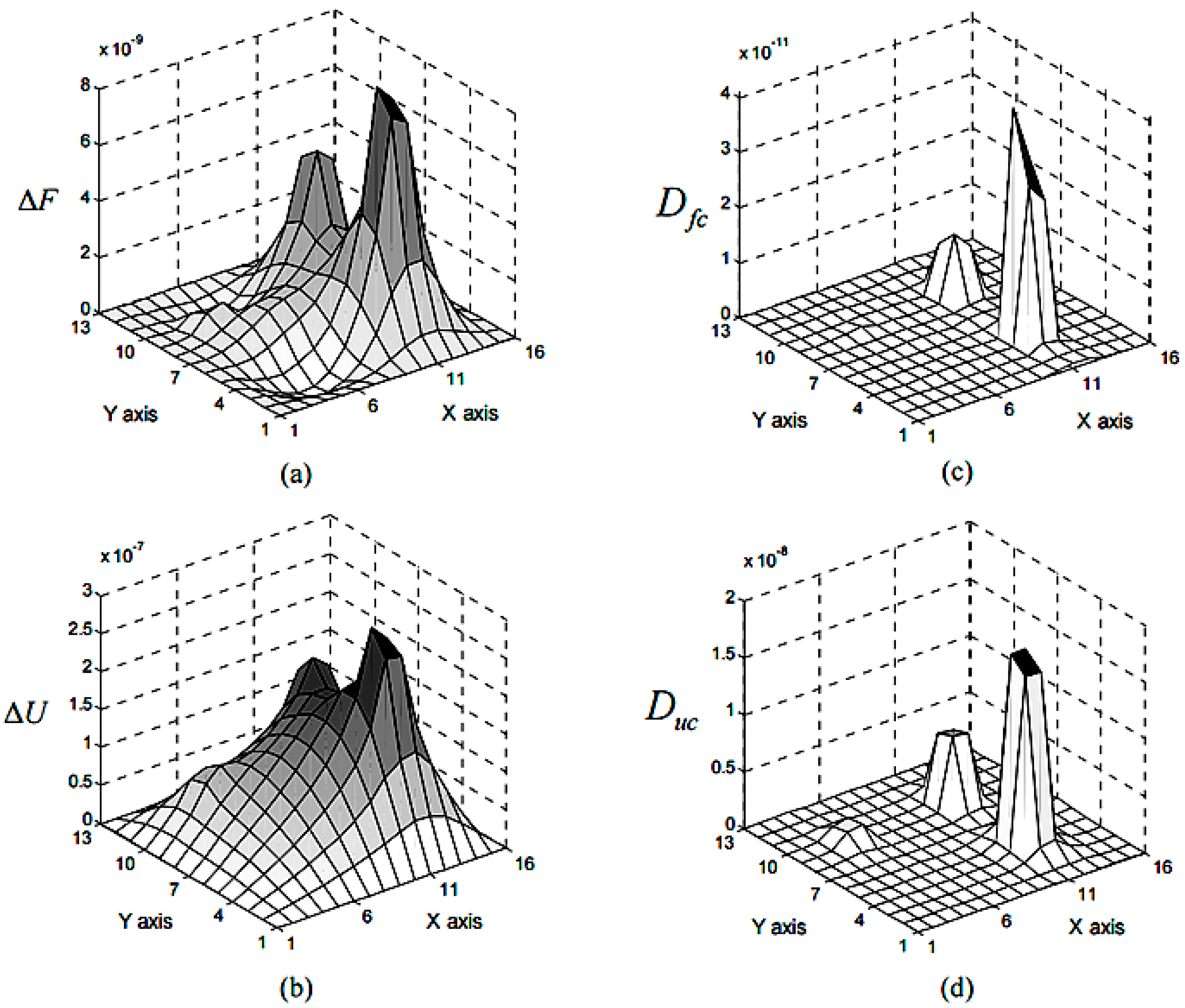
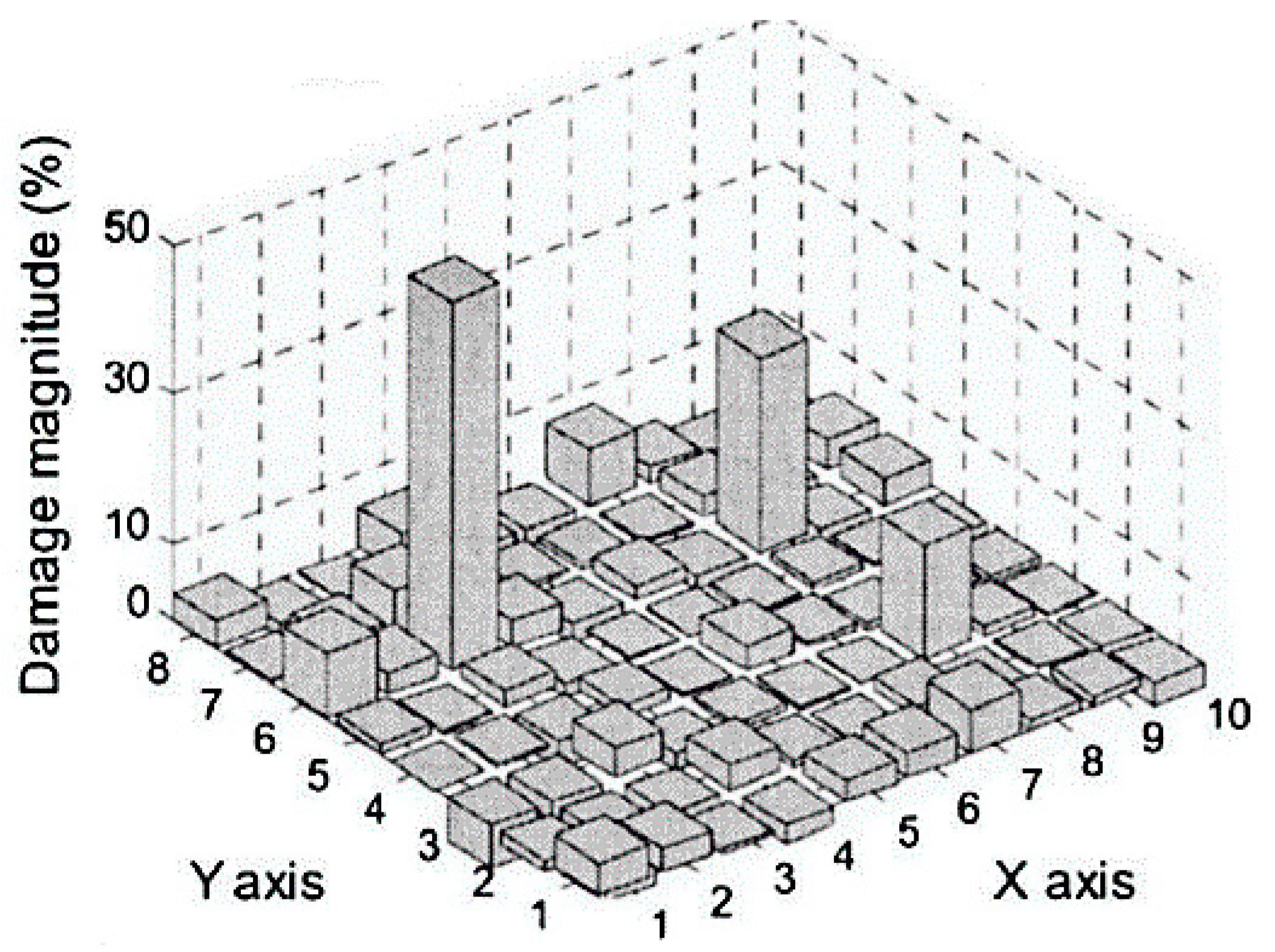
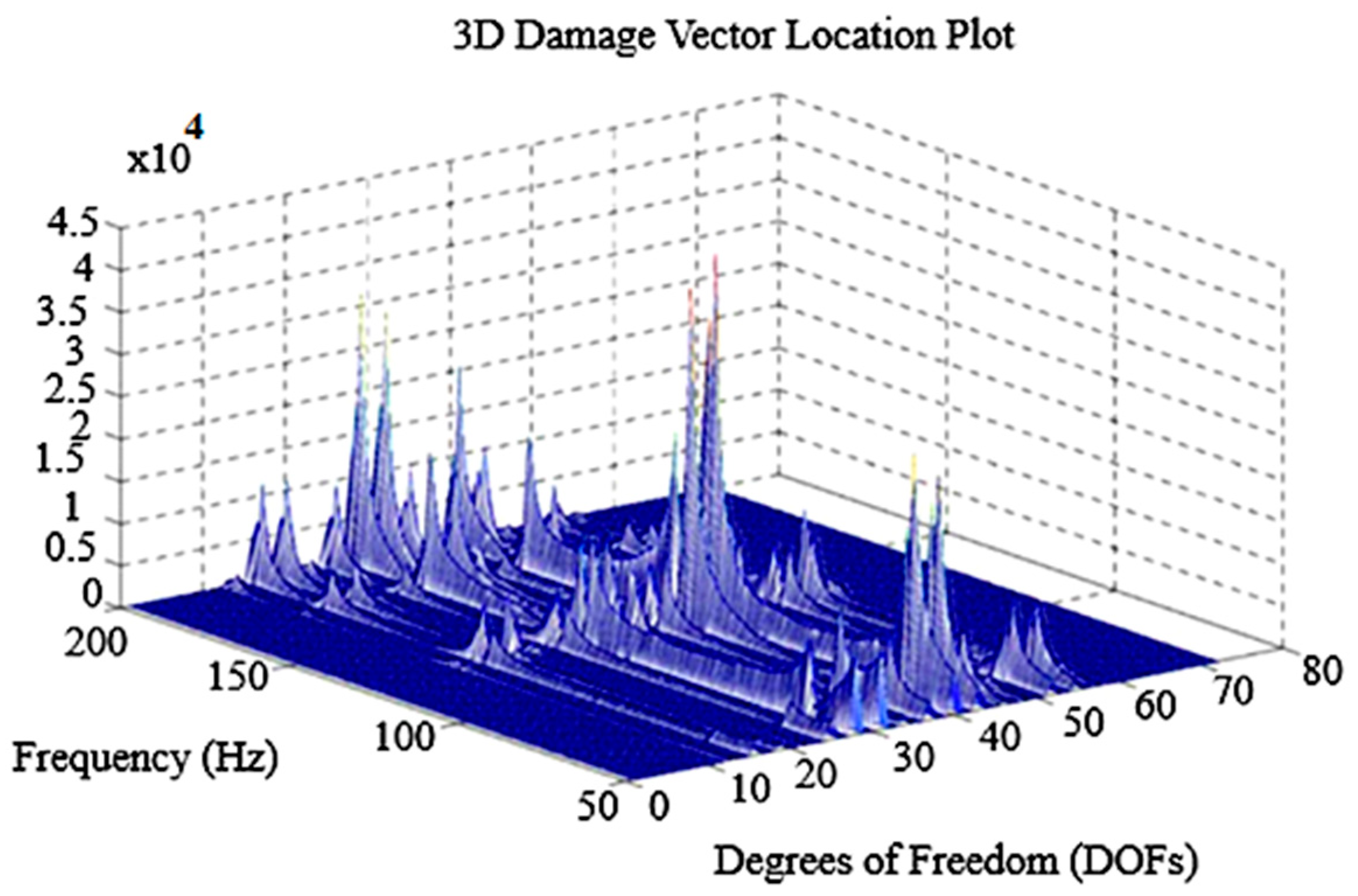

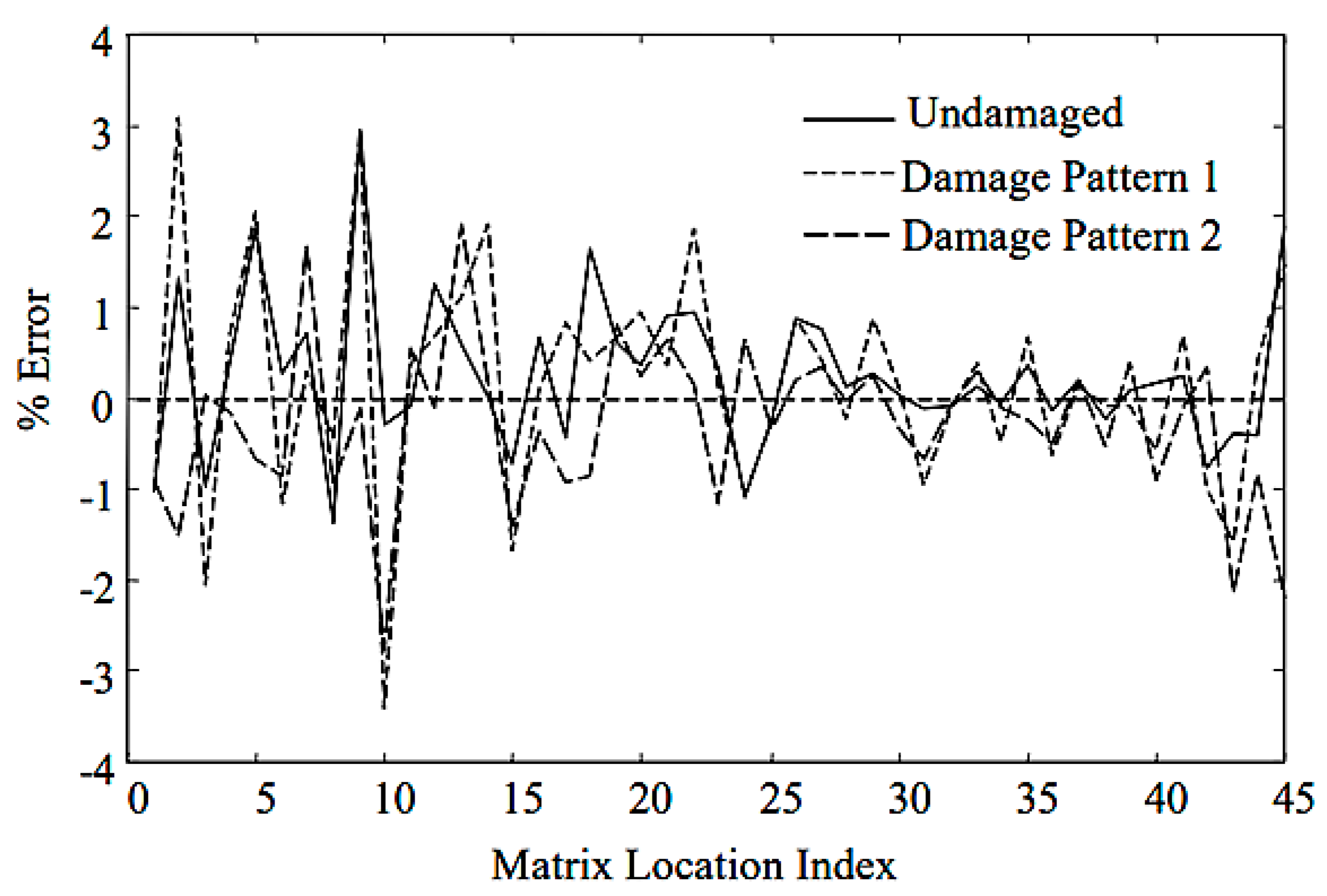
| Lengths of the Sides of the Plate | CCFF | CCSS | SSSS | ||||
|---|---|---|---|---|---|---|---|
| 1-Mode Natural Frequency, ωmn (rad/s) for a ½-Crack Length, a = 0.05 (m) | |||||||
| I1 (m) | I2 (m) | Intact | Damaged | Intact | Damaged | Intact | Damaged |
| 1 | 1 | 80.46 | 70.56 | 445.67 | 403.78 | 77.58 | 71.12 |
| 0.5 | 1 | 231.06 | 227.61 | 1161.77 | 1138.53 | 193.95 | 189.58 |
| 0.5 | 0.5 | 321.85 | 282.24 | 1782.66 | 1615.12 | 310.32 | 284.48 |
| Author | Method | Type of Damage | Plate Shape |
|---|---|---|---|
| Hu et al. 2020 [148] | Symplectic superposition method | Side crack | RP |
| Xue et al. 2020 [149] | RRM | Side crack | |
| Das et al. 2023 [150] | Back-propagated artificial neural networks (ANN) | Central crack | |
| Bachene et al. 2009 [151] | Extended FEM | Central crack | |
| Tran et al. 2015 [152] | Extended iso geometric approach (XIGA) and HSDT | Central and edge crack | |
| Hu et al. 2023 [153] | Symplicit superposition method (SSM) | Edge crack | |
| Milazzo 2022 [154] | RRM | Central and edge crack | |
| Li et al. 2004 [155] | Strain energy method | Surface crack | CP |
| Rucka et al. 2006 [156] | Wavelet-based | Central defect | SP |
| Dwivedi et al. 2023 [157] | Higher-order XFEM | Edge and internal crack |
| Thickness Variation | Gradient Index ‘n’ | Crack Length ‘a’ | Fundamental Frequency ω (rad/s) | ||||
|---|---|---|---|---|---|---|---|
| Taper Parameter | |||||||
| α = β = 0 | α (1 D) | α = β (2 D) | |||||
| 0.5 | 1 | 0.5 | 1 | ||||
| LVT | 0 | 0 | 719.70 | 731.55 | 752.15 | 736.10 | 756.10 |
| 0.01 | 700.11 | 711.98 | 732.60 | 716.54 | 736.56 | ||
| 0.02 | 685.82 | 697.70 | 718.35 | 702.27 | 722.31 | ||
| 0.05 | 674.91 | 671.31 | 692.02 | 675.89 | 696.00 | ||
| 0.5 | 0 | 505.66 | 513.98 | 528.45 | 517.18 | 531.23 | |
| 0.01 | 491.90 | 500.23 | 514.72 | 503.44 | 517.50 | ||
| 0.02 | 481.85 | 490.20 | 504.71 | 493.41 | 507.49 | ||
| 0.05 | 463.27 | 471.66 | 486.21 | 474.88 | 489.00 | ||
| PVT | 0 | 0 | 719.70 | 736.19 | 769.07 | 746.37 | 786.59 |
| 0.01 | 700.11 | 716.94 | 750.04 | 727.37 | 767.90 | ||
| 0.02 | 685.82 | 703.04 | 736.45 | 713.78 | 754.72 | ||
| 0.05 | 659.37 | 677.70 | 711.94 | 689.26 | 731.32 | ||
| 0.5 | 0 | 505.66 | 517.25 | 540.34 | 524.40 | 552.66 | |
| 0.01 | 491.90 | 503.72 | 526.98 | 511.05 | 539.52 | ||
| 0.02 | 481.85 | 493.96 | 517.42 | 501.50 | 530.26 | ||
| 0.05 | 463.27 | 476.15 | 500.21 | 484.27 | 513.83 | ||
| Author | Method | Type of Damage | Material | Plate Shape |
|---|---|---|---|---|
| Wei et al. 2005 [193] | Nonlinear autoregressive moving average with exogenous excitation (ARMAX) | Delamination | Composite | RP |
| Zhang et al. 2012 [194] | Mode shape curvature (MSC) | Single impact damages | Plywood | |
| Wei et al. 2016 [195] | MSECR | Single and multi-damage | Isotropic | |
| Castro et al. 2018 [196] | Electro-mechanical impedance (EMI) and FRF | Central crack | Aluminum | |
| Yam et al. 2002 [197] | MSC and strain FRF | 2-Out-of-plane deflection | Steel | |
| Zhang et al. 2013 [198] | Operating deflection shape curvature (ODSC) | Delamination | Plywood | |
| Alsaadi et al. 2020 [199] | FRF | Delamination | Glass fiber composite laminate | Squire Plate (SP) |
| Zhong et al. 2014 [200] | 2D-Multiple signal classification (MUSIC) | 2-Delamination | Carbon fiber composite | |
| He and Yuan, 2016 [201] | SPT | 3-damage location | T6061 aluminum | |
| Katunin, 2011 [202] | Two-dimensional B-spline wavelets | Crack, notch and spatial damage | polymeric composite | |
| Cao et al. 2013 [203] | FD | Small cross-shaped crack | Aluminum | |
| Huang et al. 2021 [204] | NODIS-based | Delamination | Isotropic plate | |
| Zuo et al. 2018 [205] | 2D-MUSIC | 2-damage location | Laminate composite | |
| Reddy et al. 2012 [206] | FRF | 4-Different damage cases | Aluminum |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alshammari, Y.L.A.; He, F.; Alrwili, A.A.; Khan, M. Fundamental Challenges and Complexities of Damage Identification from Dynamic Response in Plate Structures. Appl. Sci. 2024, 14, 8230. https://doi.org/10.3390/app14188230
Alshammari YLA, He F, Alrwili AA, Khan M. Fundamental Challenges and Complexities of Damage Identification from Dynamic Response in Plate Structures. Applied Sciences. 2024; 14(18):8230. https://doi.org/10.3390/app14188230
Chicago/Turabian StyleAlshammari, Yousef Lafi A., Feiyang He, Abdullah Ayed Alrwili, and Muhammad Khan. 2024. "Fundamental Challenges and Complexities of Damage Identification from Dynamic Response in Plate Structures" Applied Sciences 14, no. 18: 8230. https://doi.org/10.3390/app14188230
APA StyleAlshammari, Y. L. A., He, F., Alrwili, A. A., & Khan, M. (2024). Fundamental Challenges and Complexities of Damage Identification from Dynamic Response in Plate Structures. Applied Sciences, 14(18), 8230. https://doi.org/10.3390/app14188230









