Numerical Study on Heat Transfer and Thermal–Mechanical Performance of Actively Cooled Channel of All-Movable Rudder under Supercritical Pressure
Abstract
:1. Introduction
2. Numerical Modeling
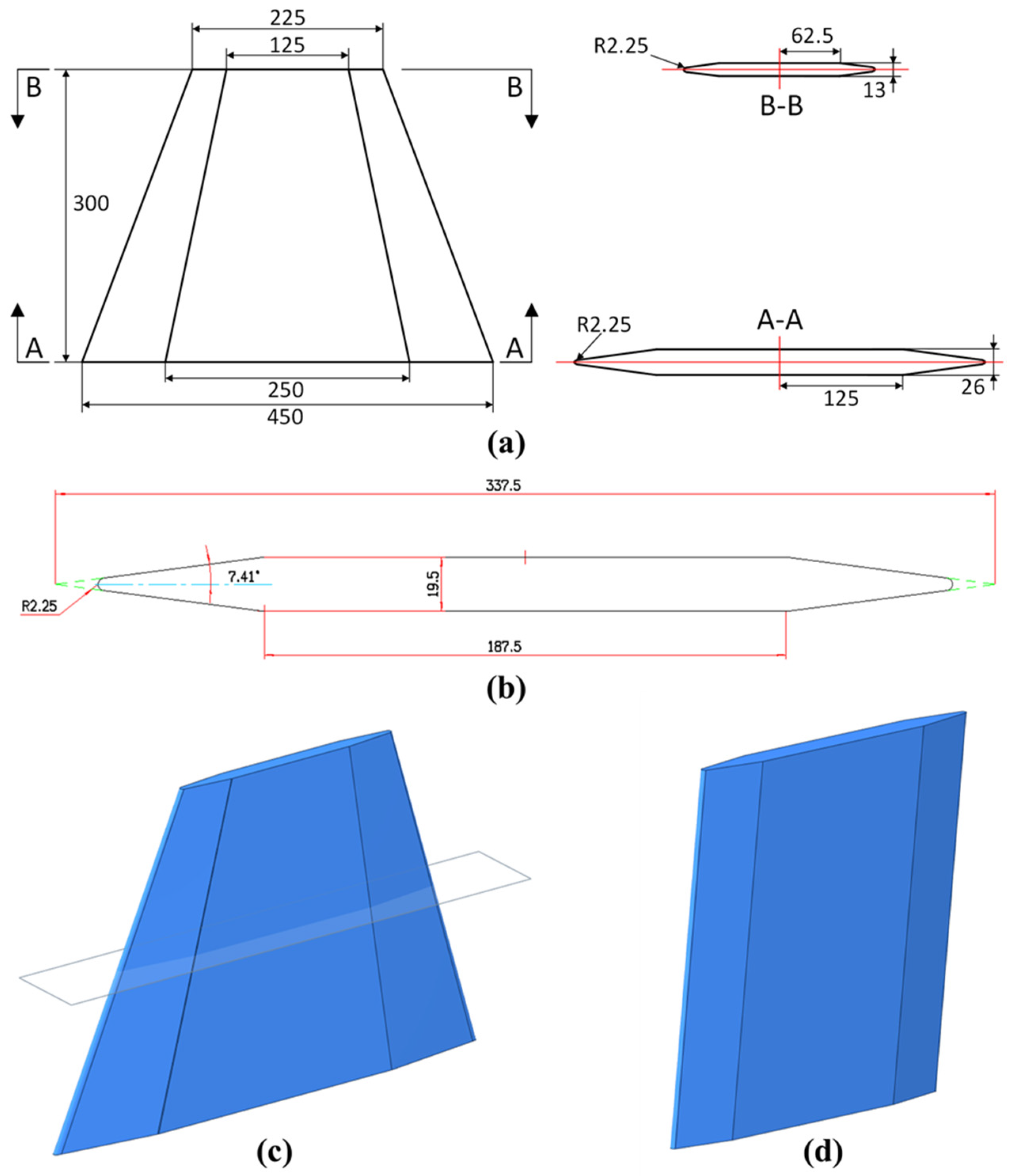
2.1. Physical Model Details
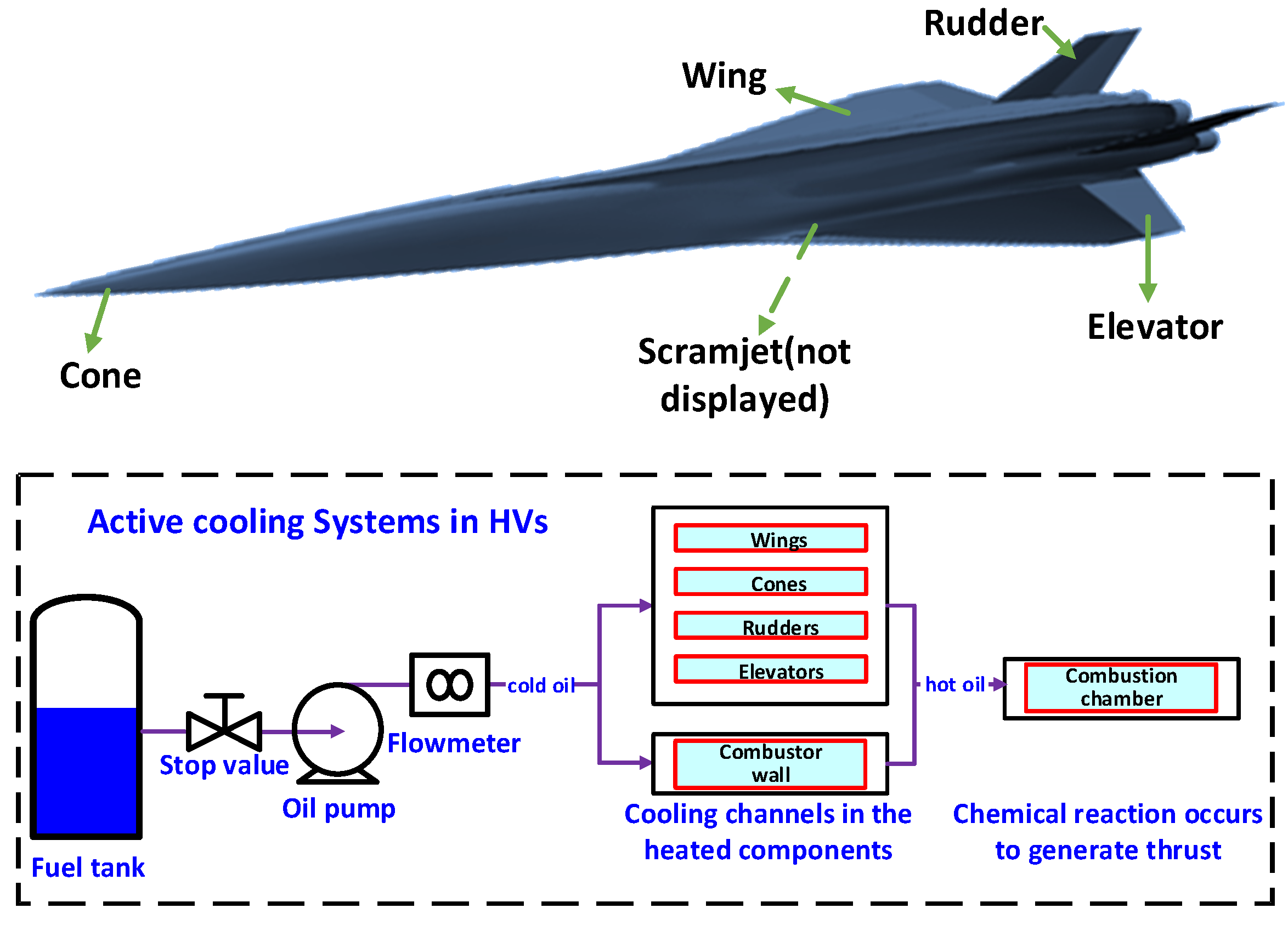
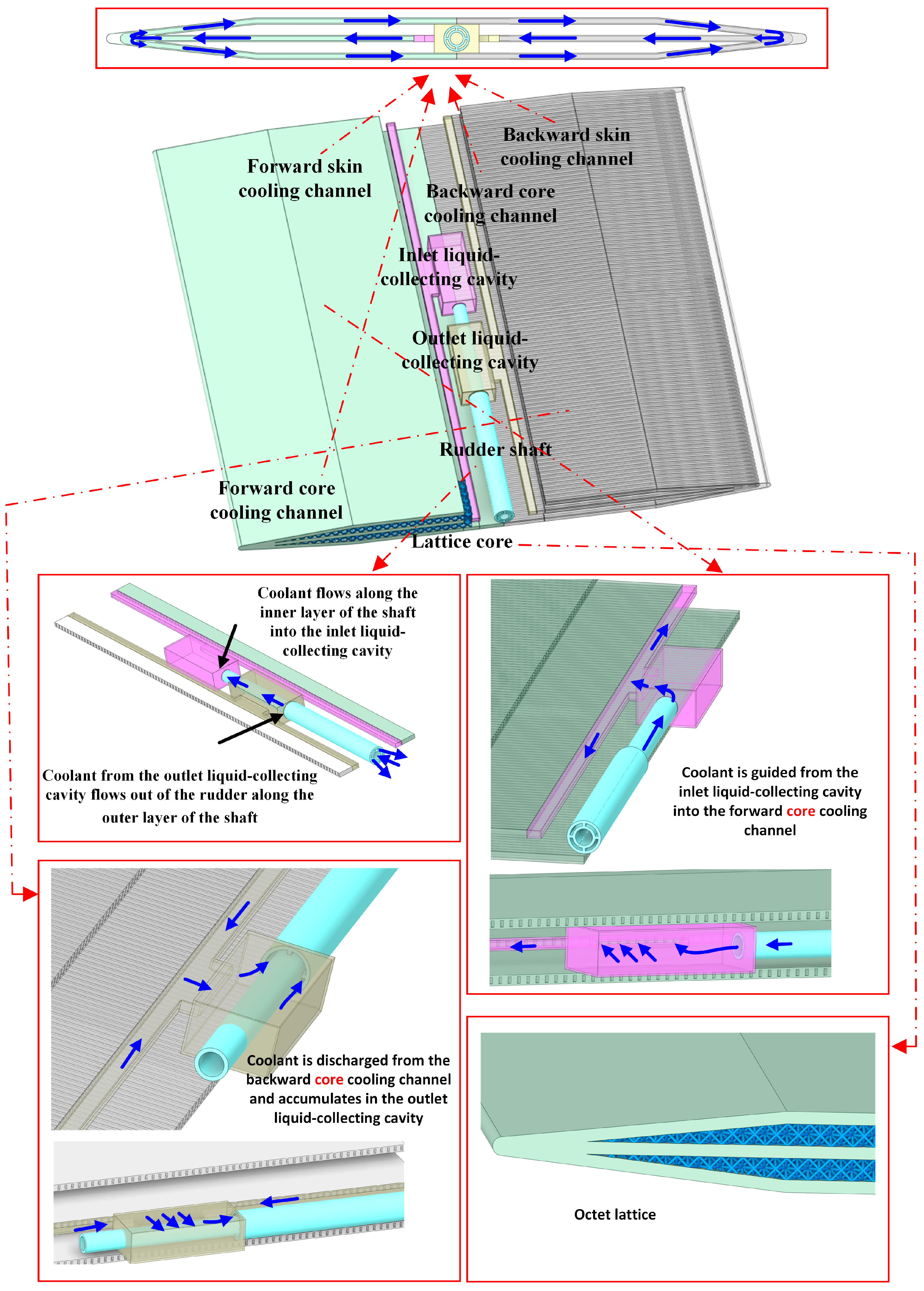
2.1.1. Description of Active Cooling System and Simplified All-Movable Rudder
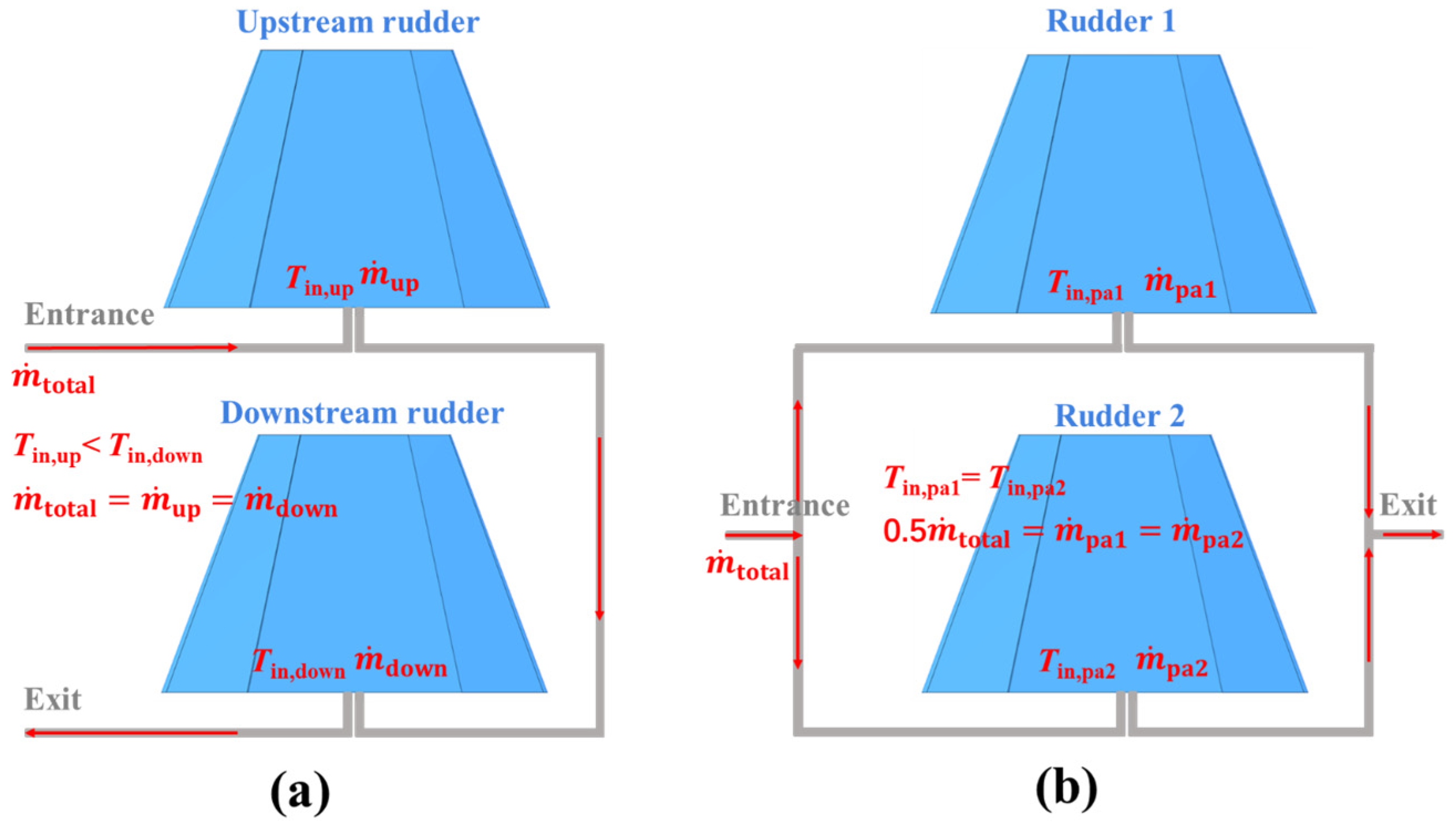
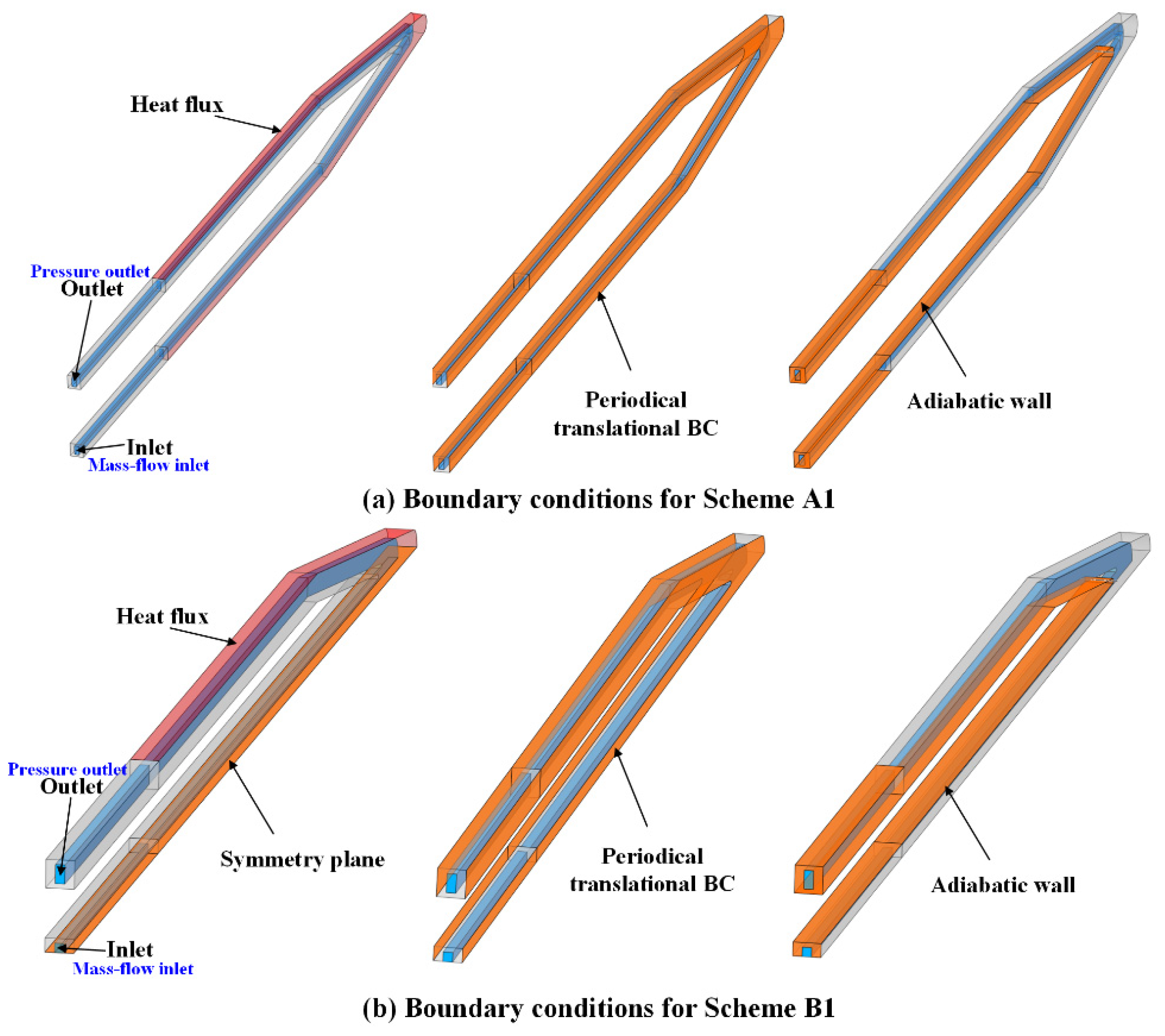
2.1.2. Two Actively Cooled Options for the Simplified All-Movable Rudder
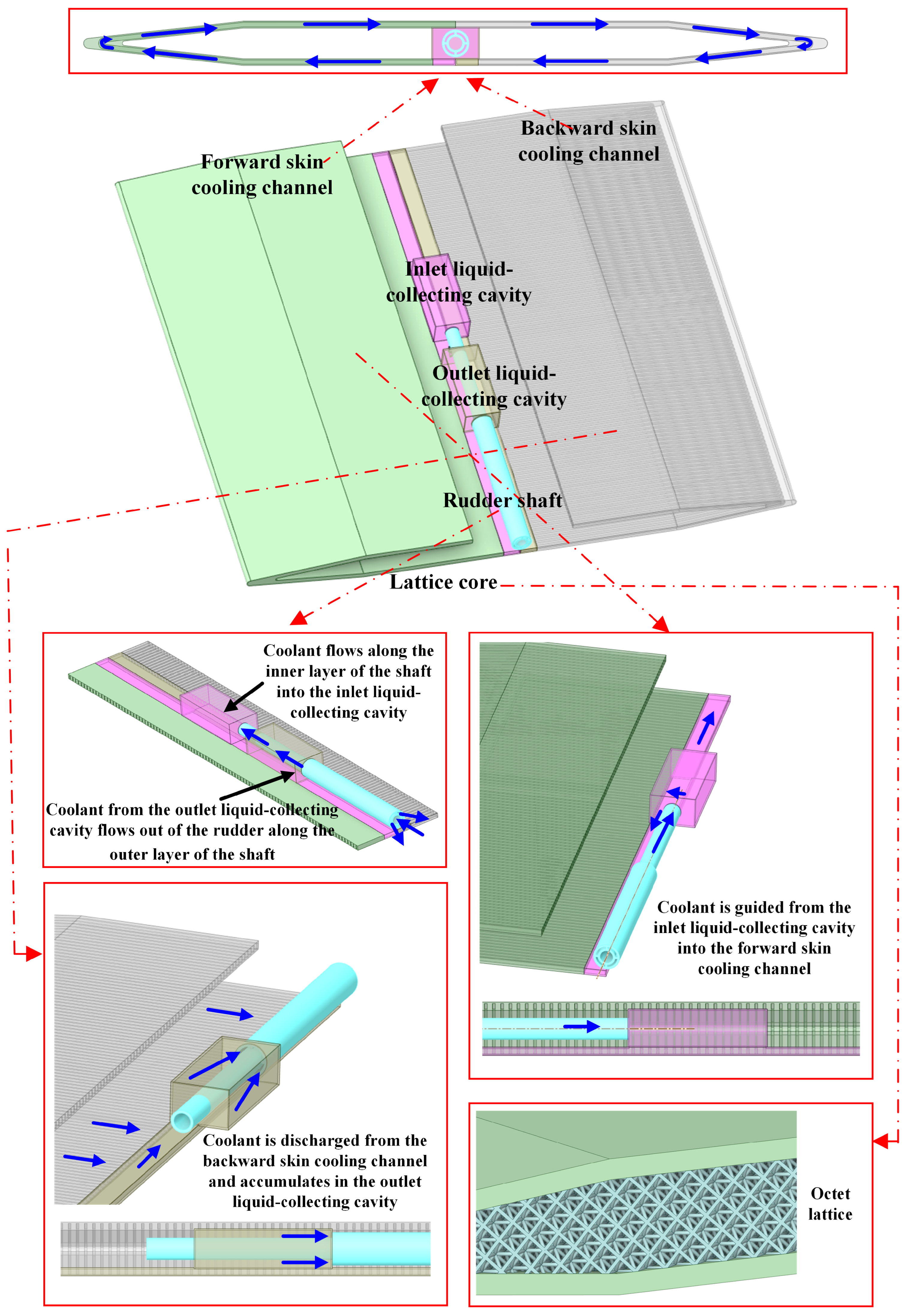
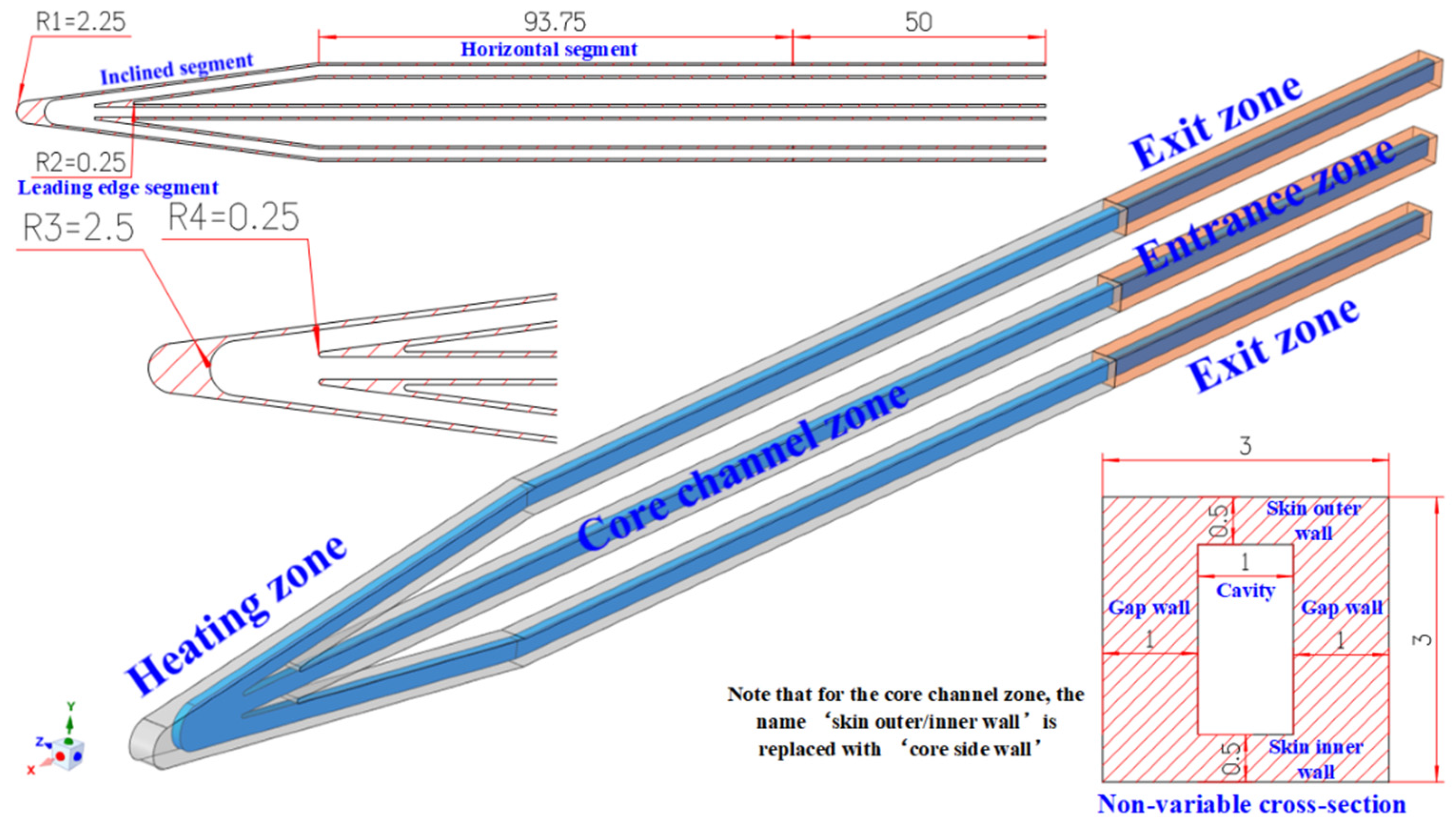
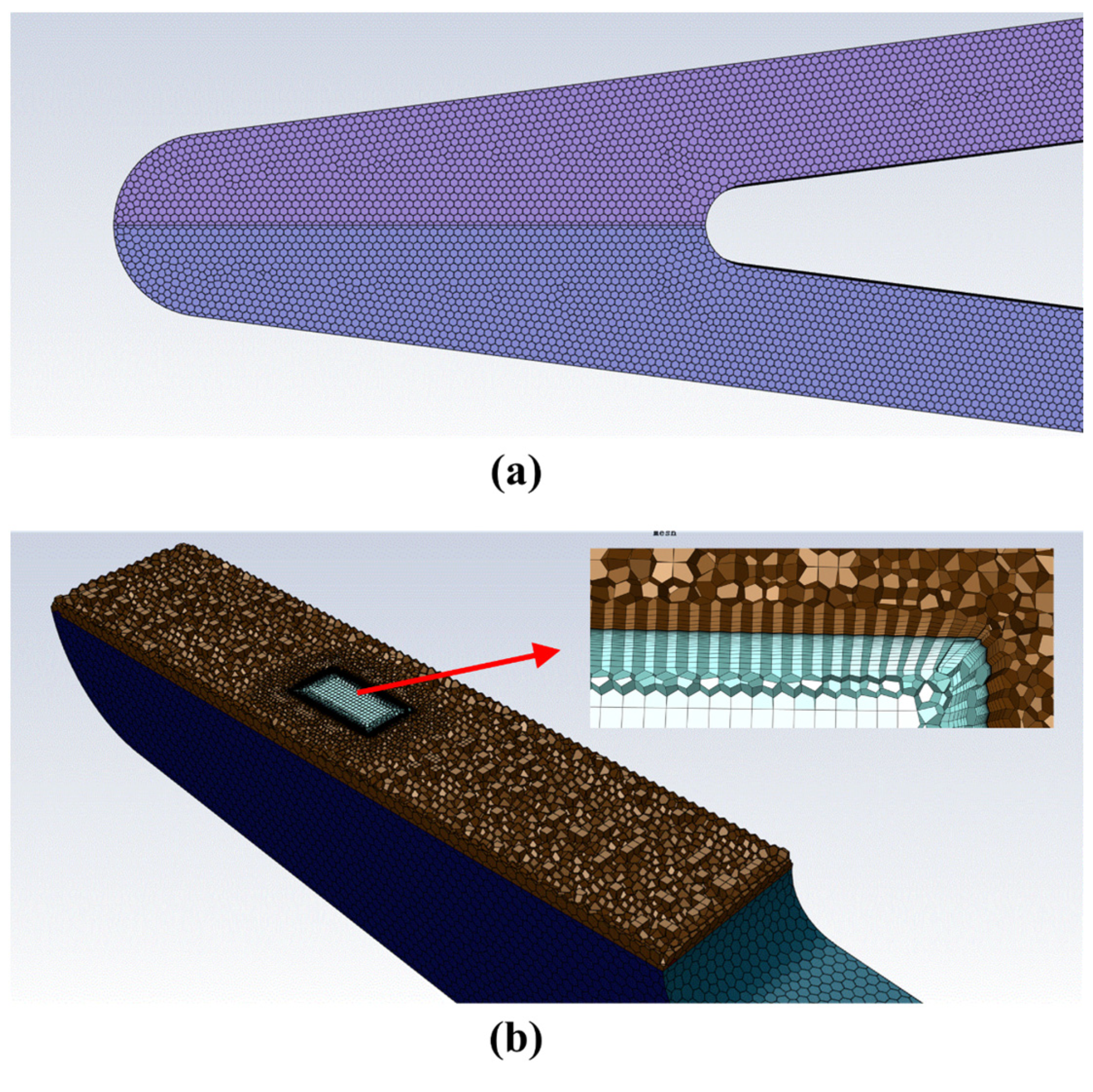
2.1.3. Periodic Modeling of Cooling Channels
2.1.4. Material Properties of Coolants and Channel Structures
2.2. Governing Equations and Solution Strategy
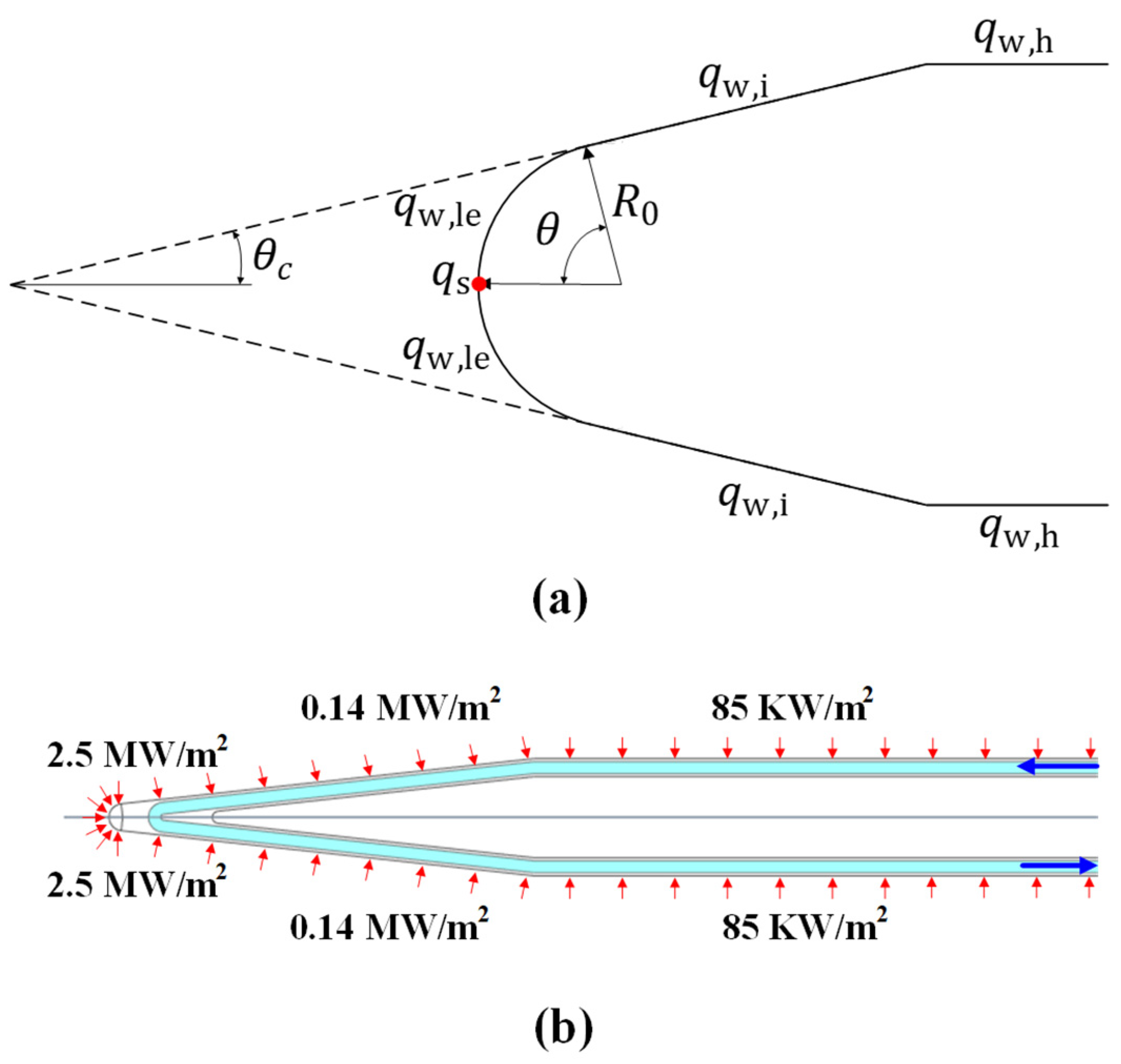
2.3. Analysis Cases and Mesh Sensitivity
3. Results and Discussion
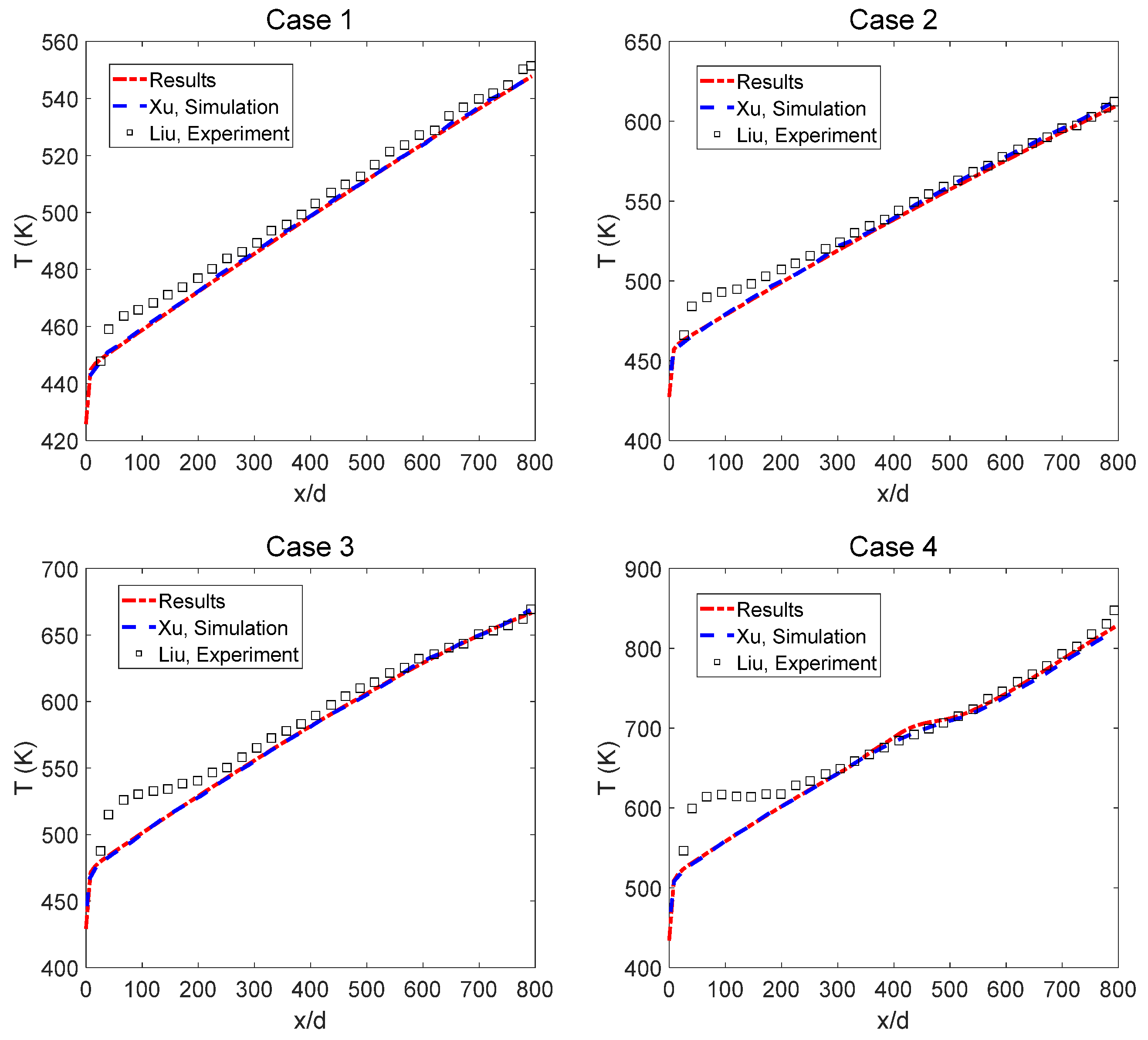
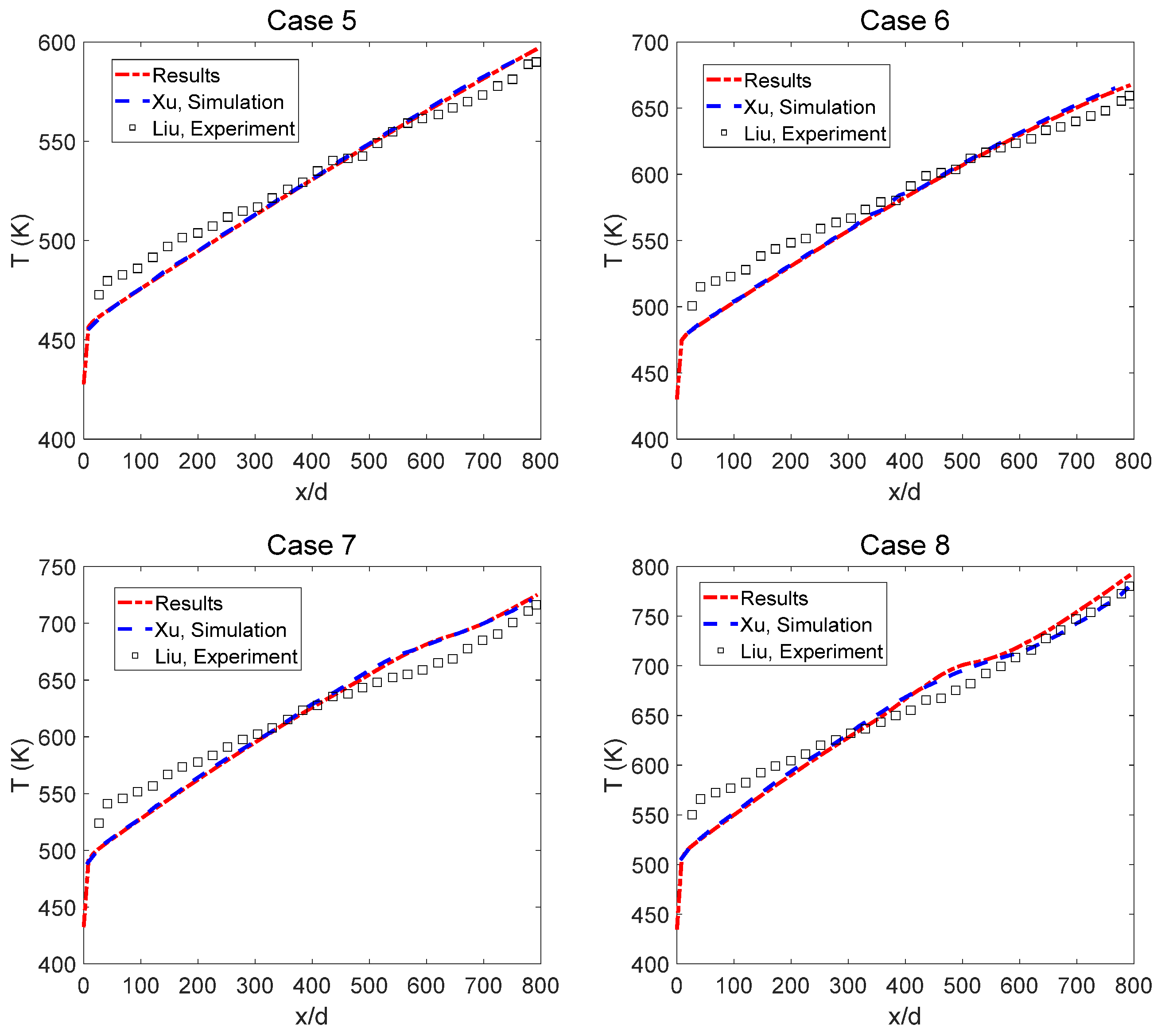
3.1. Model Validation
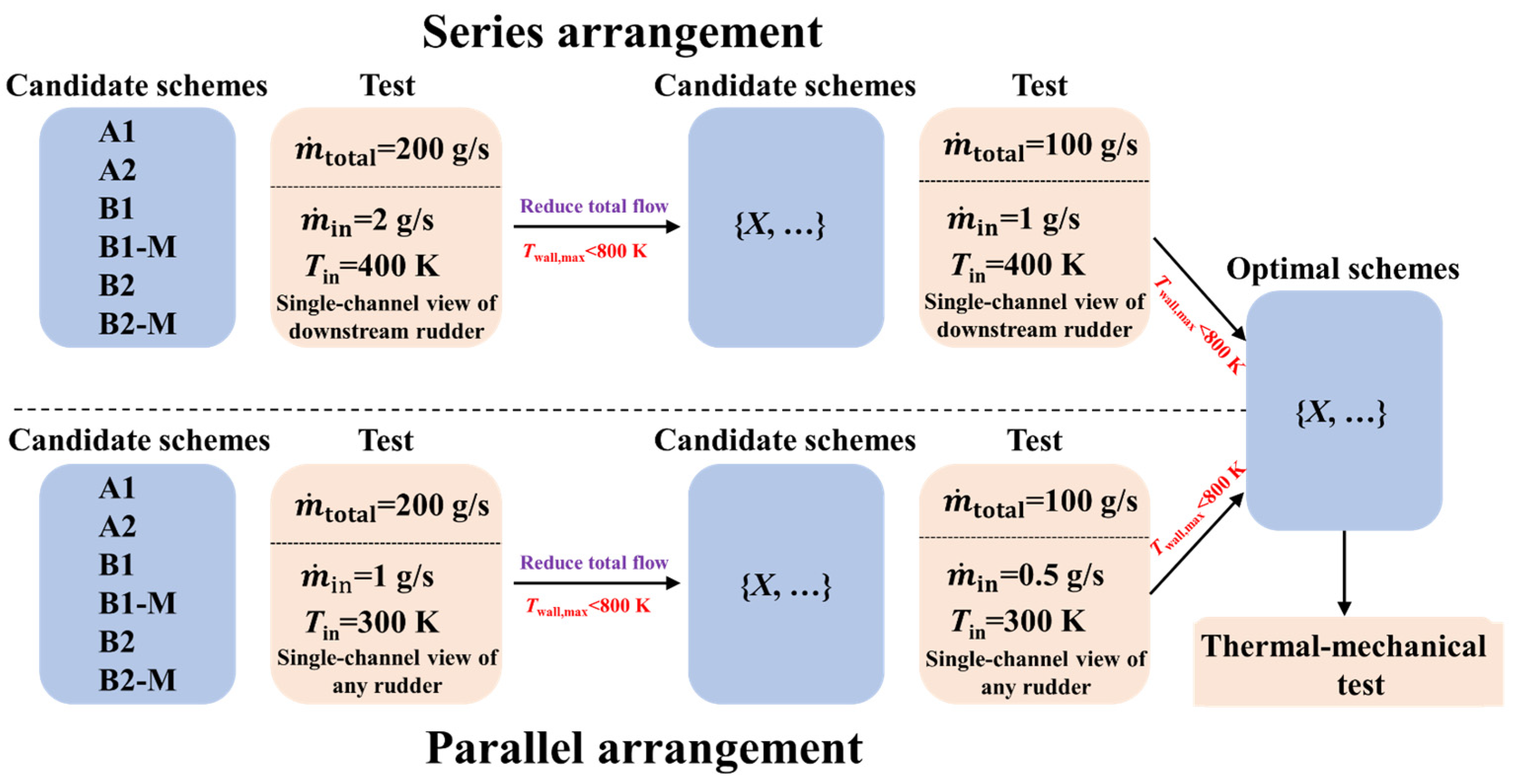
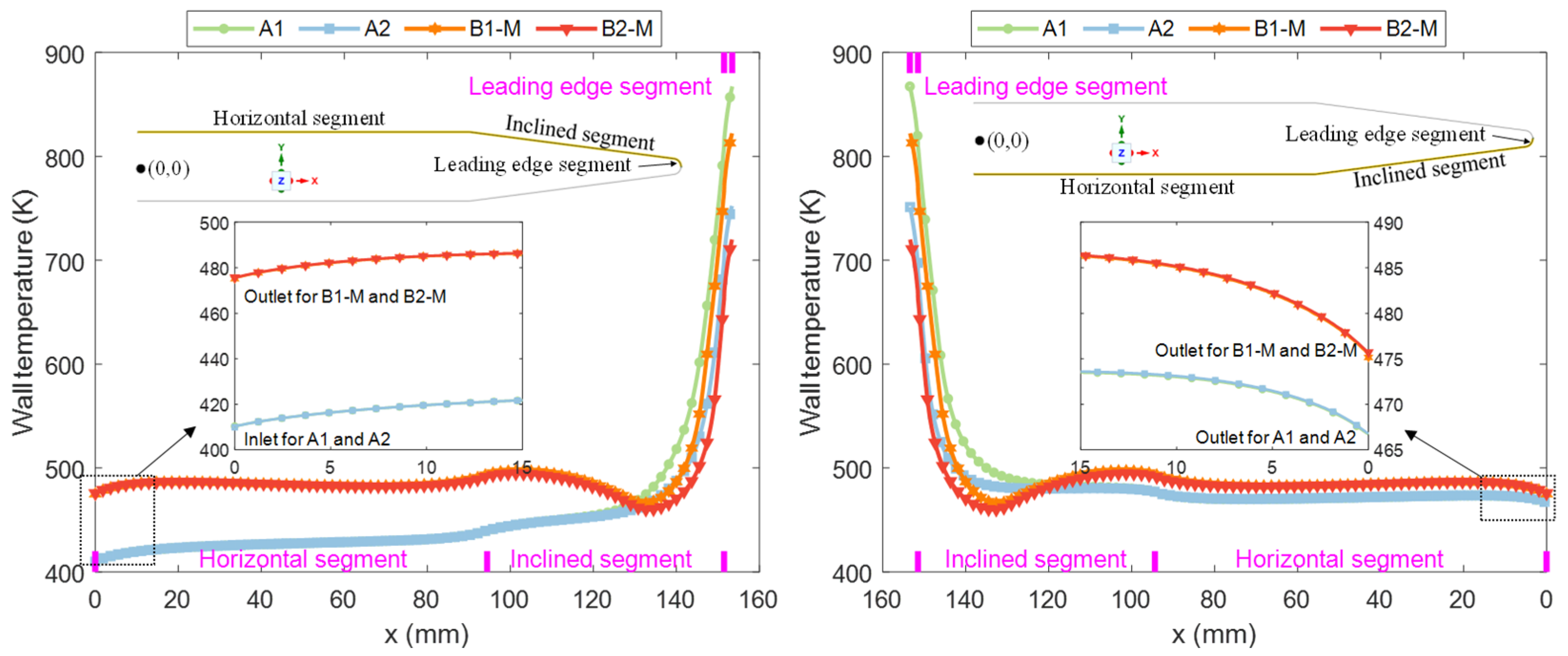
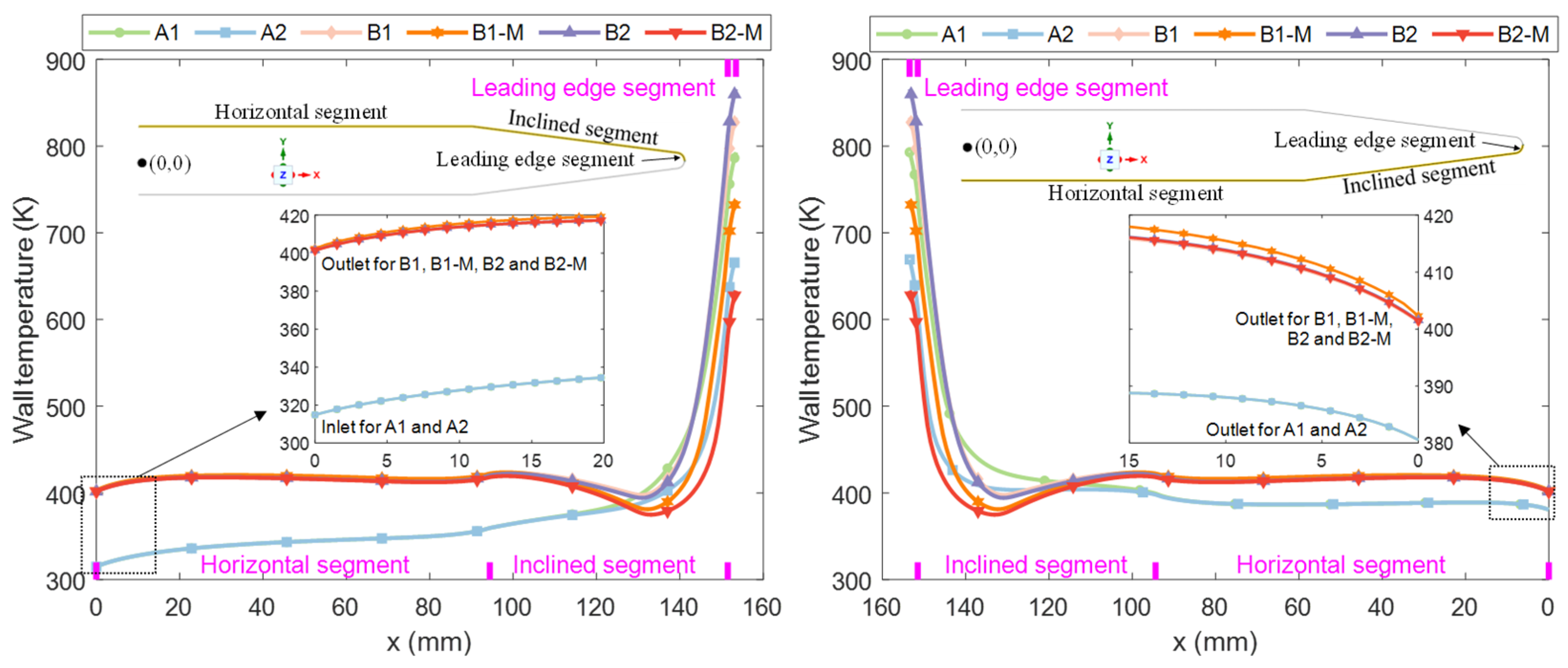
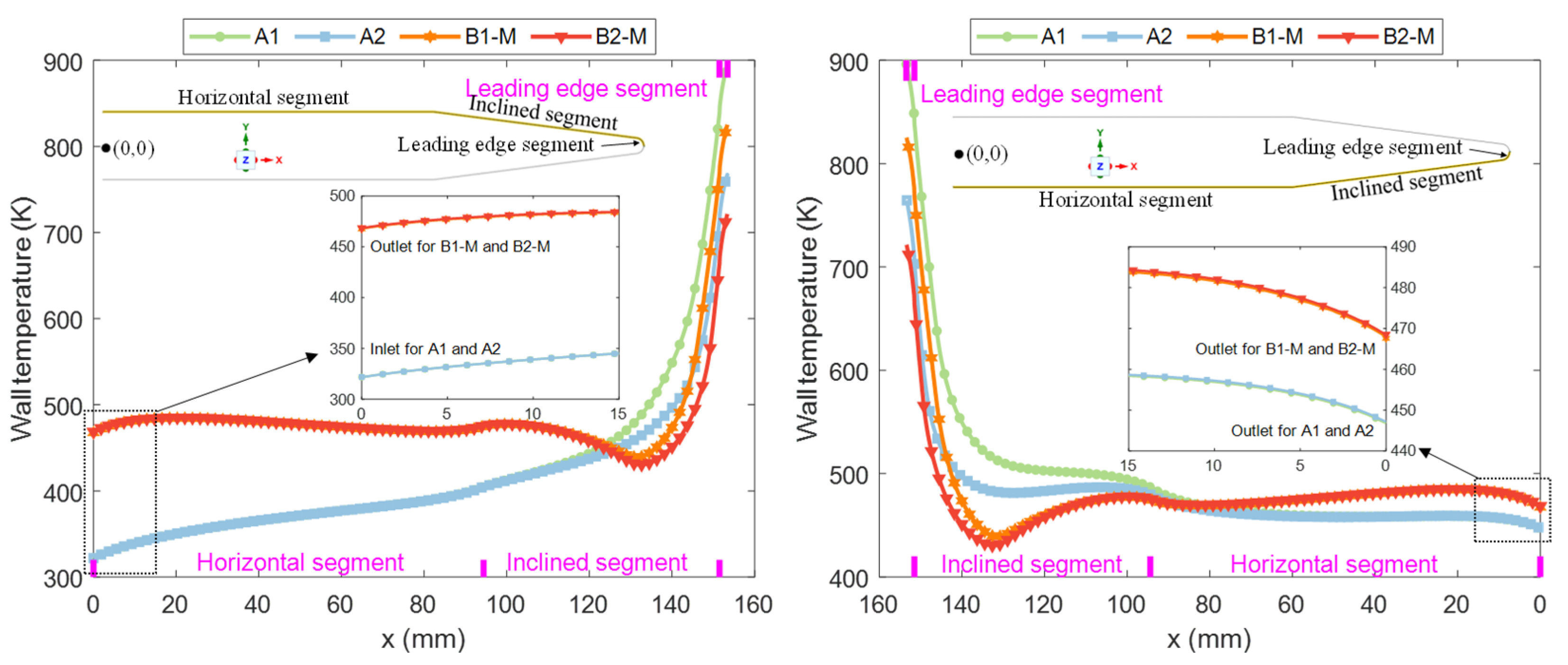
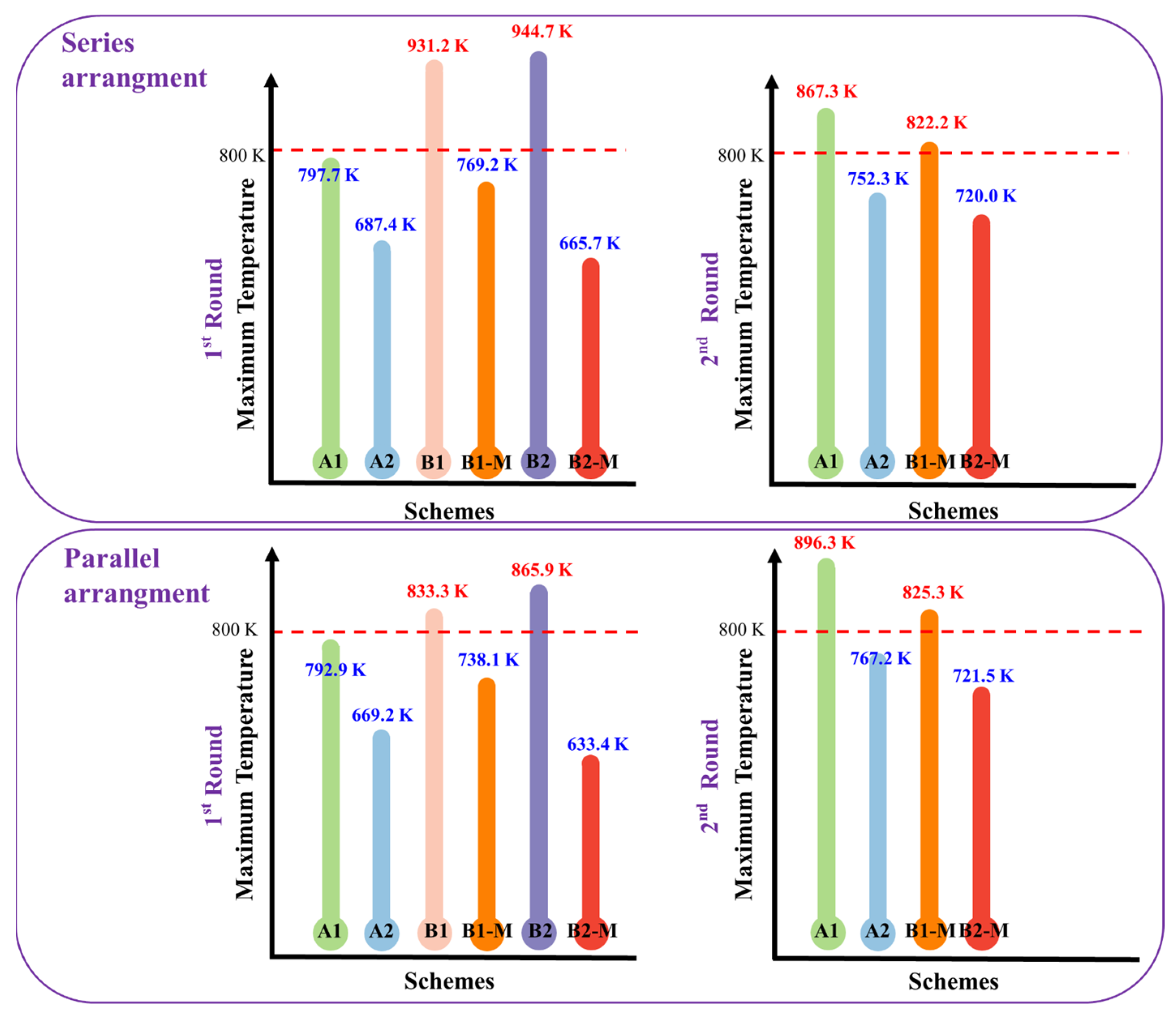
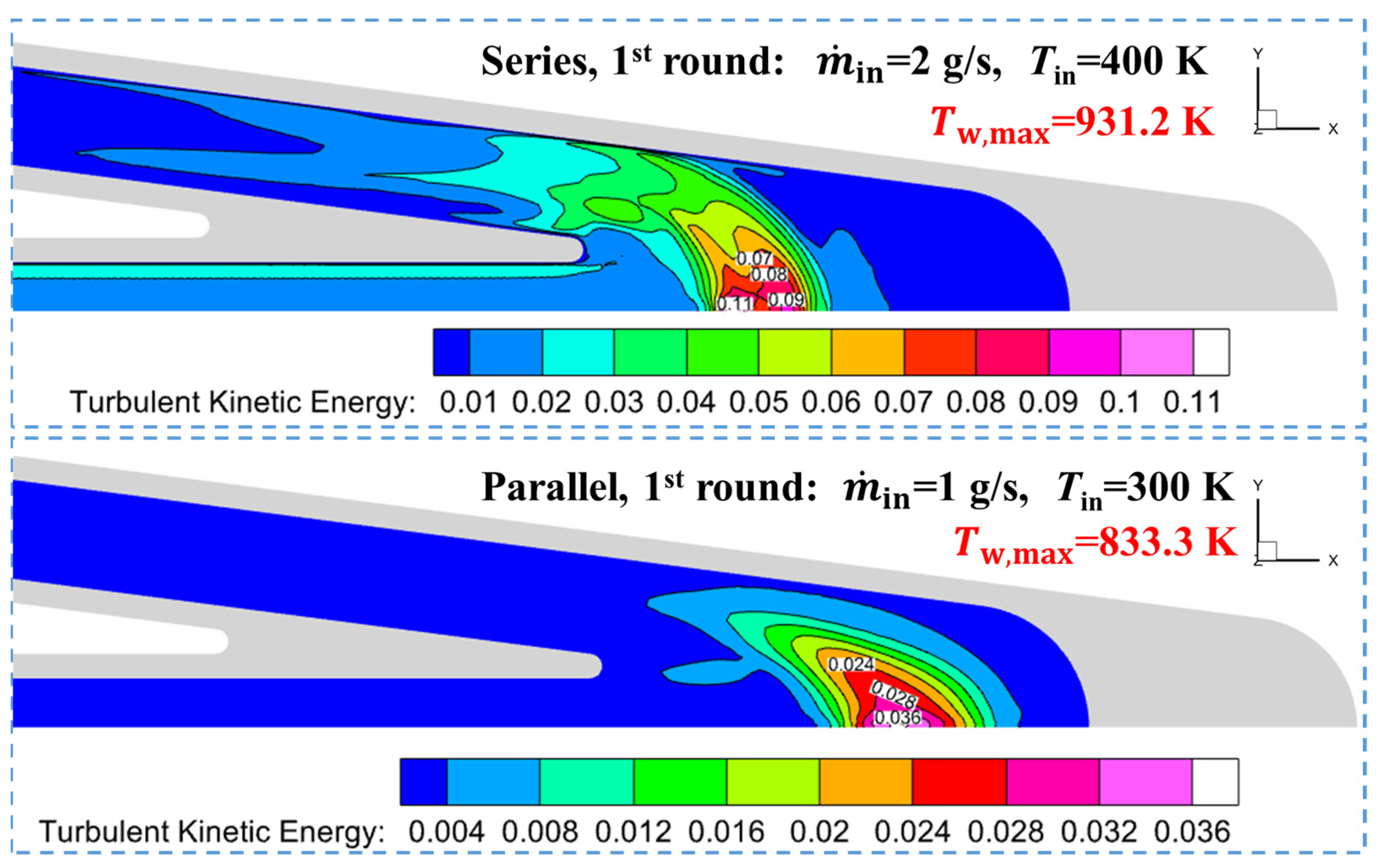
3.2. Temperature Test for Competitive Selection of Optimal Channel Scheme
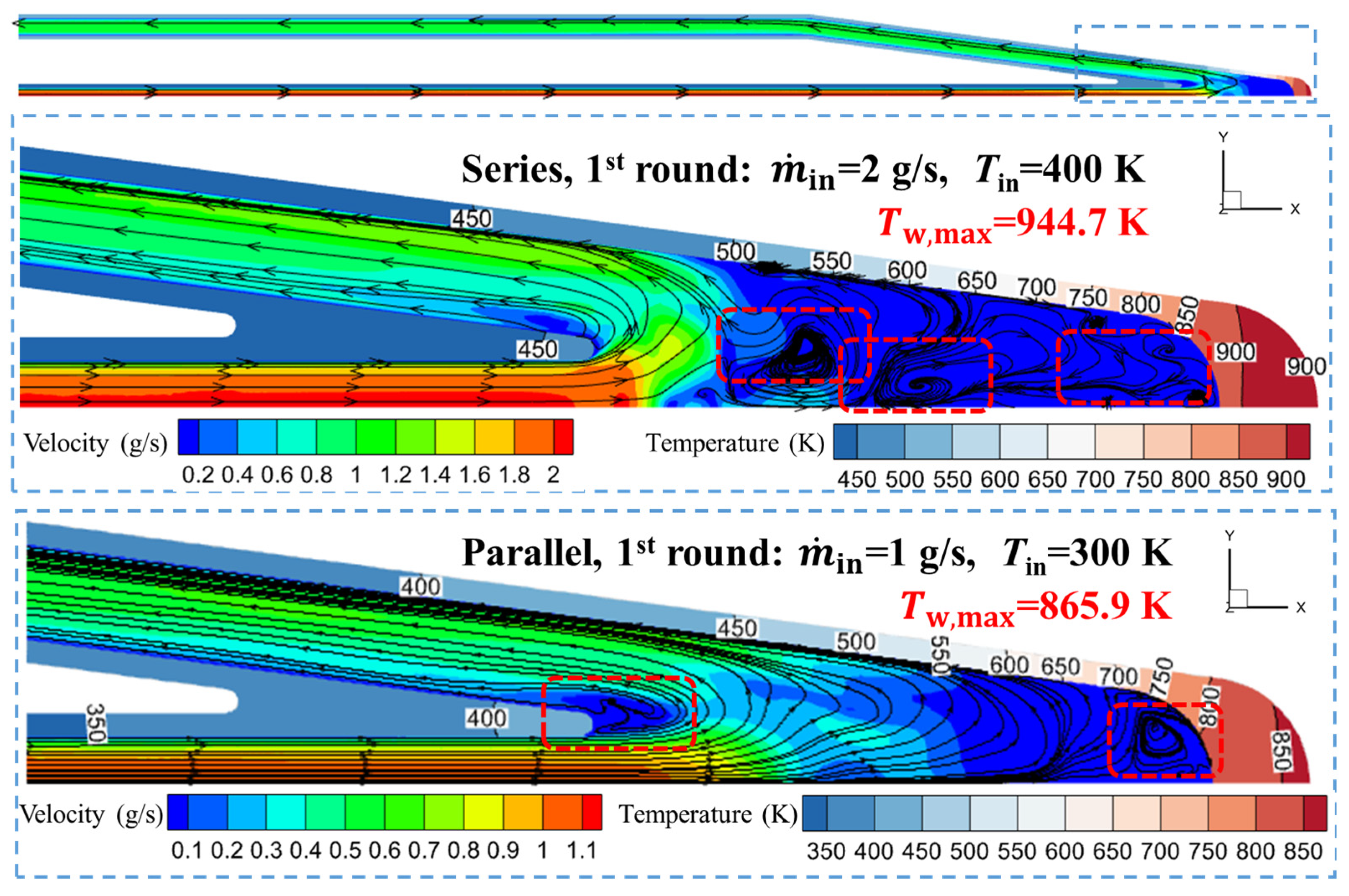
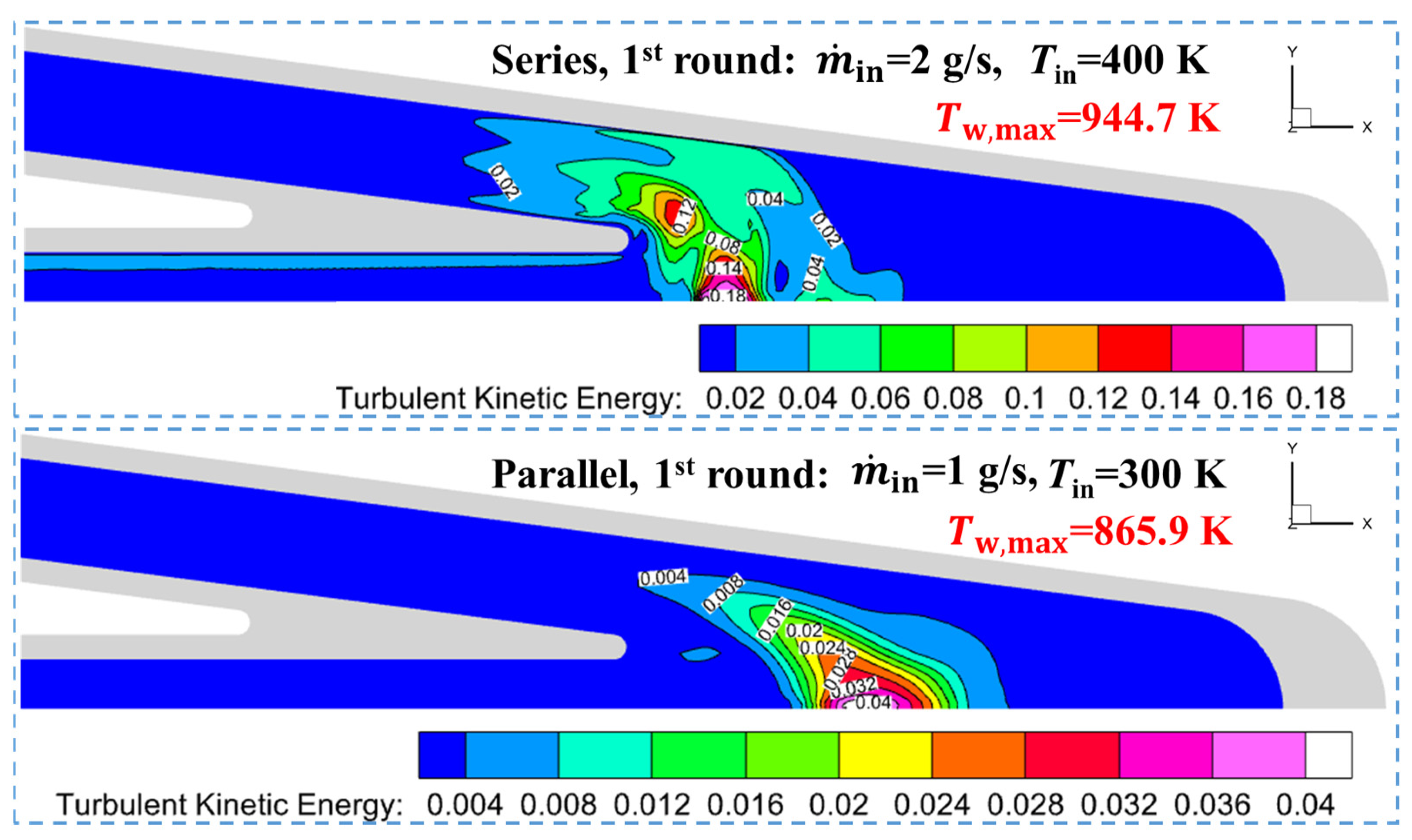
3.3. Flow Characteristics
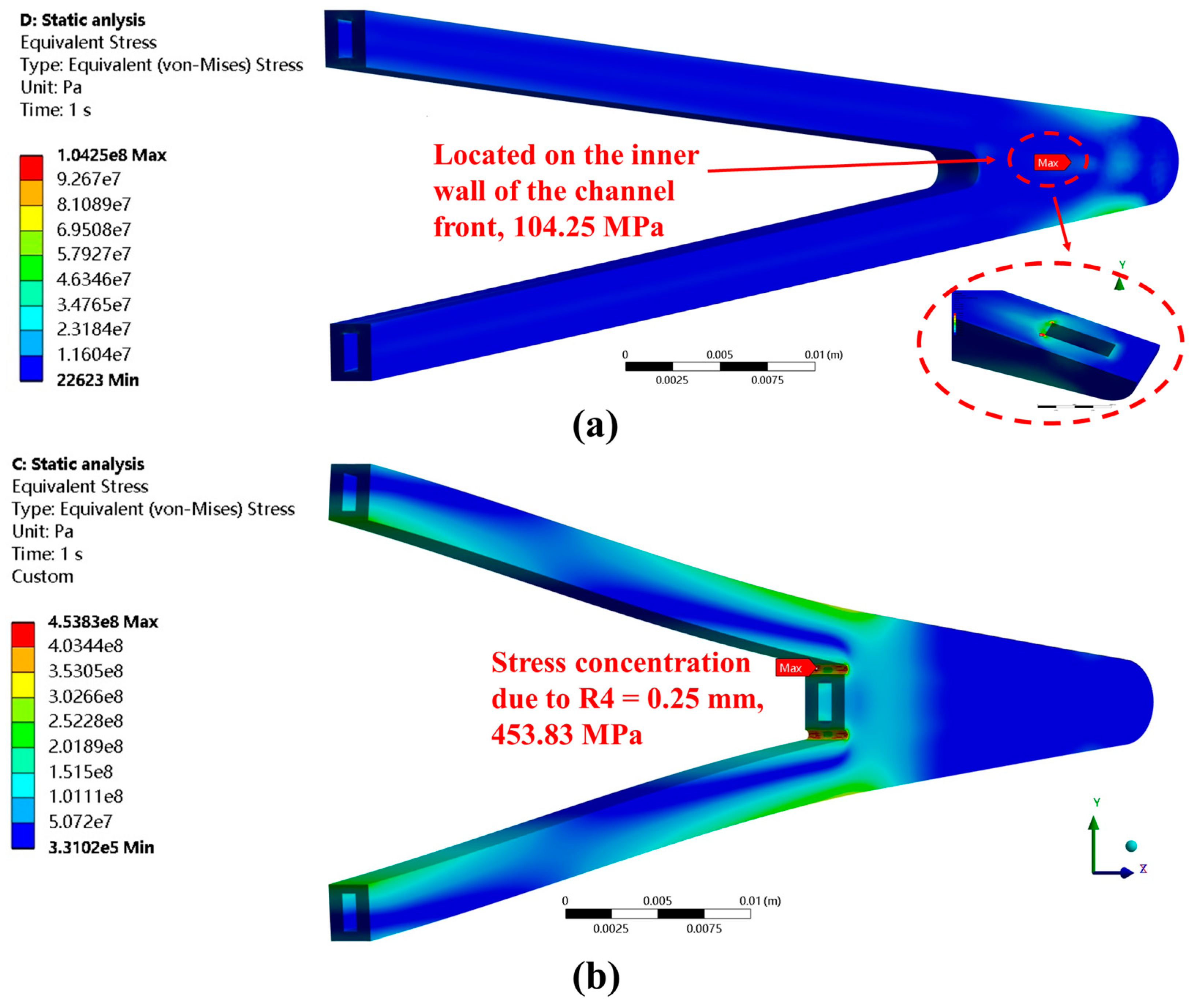
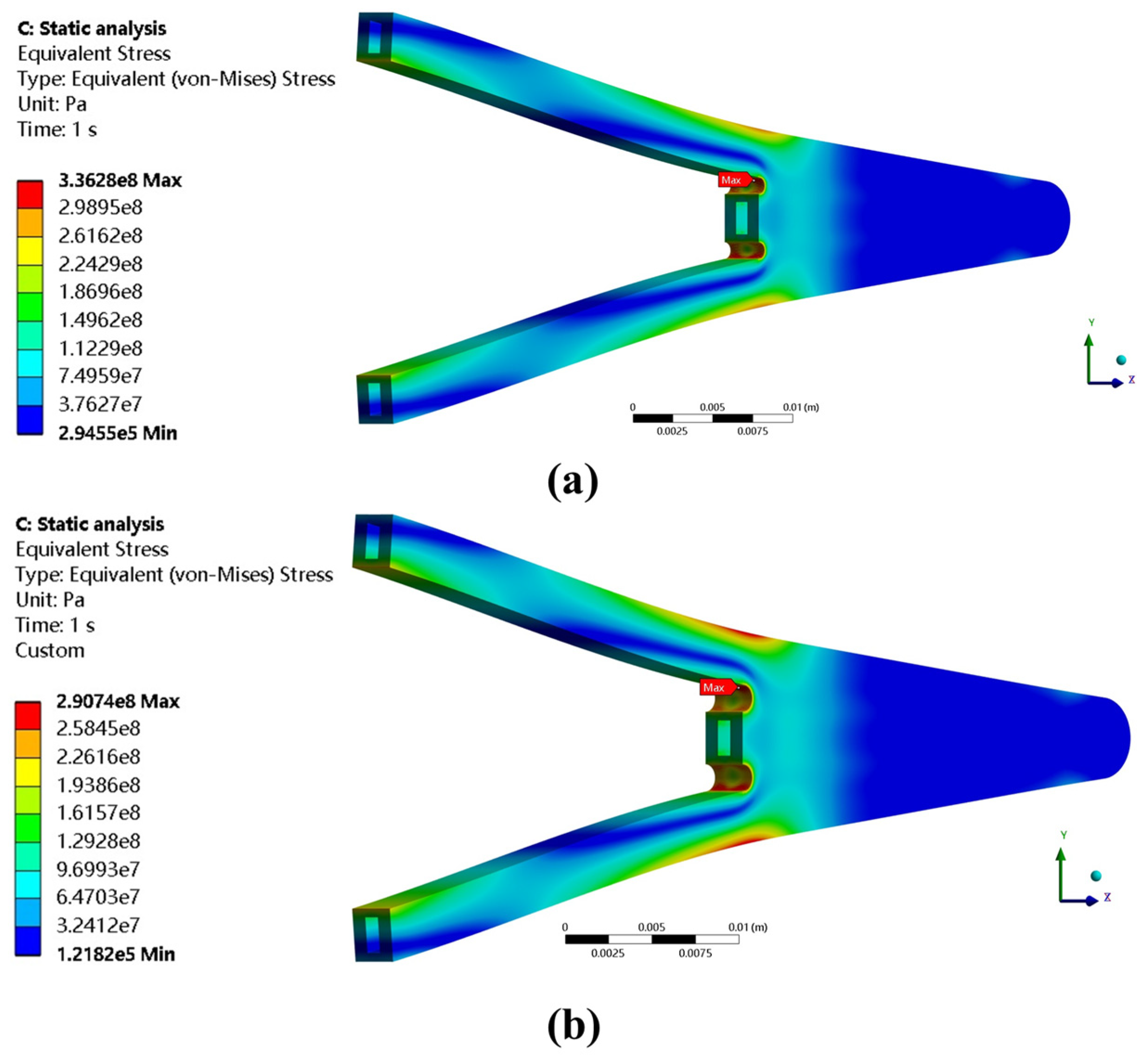
3.4. Thermal–Mechanical Test
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sziroczak, D.; Smith, H. A Review of Design Issues Specific to Hypersonic Flight Vehicles. Prog. Aerosp. Sci. 2016, 84, 1–28. [Google Scholar] [CrossRef]
- Gaitonde, D.V. Progress in Shock Wave/boundary Layer Interactions. Prog. Aerosp. Sci. 2015, 72, 80–99. [Google Scholar] [CrossRef]
- Song, L.; Gao, T.; Tang, L.; Du, X.; Zhu, J.; Lin, Y.; Shi, G.; Liu, H.; Zhou, G.; Zhang, W. An All-movable Rudder Designed by Thermo-elastic Topology Optimization and Manufactured by Additive Manufacturing. Comput. Struct. 2021, 243, 106405. [Google Scholar] [CrossRef]
- Shi, G.; Jia, Y.; Hao, W.; Wu, W.; Li, Q.; Lin, Y.; Du, Z. Optimal Design of Rudder Structures Based on Data-driven Method. Chin. J. Theor. Appl. Mech. 2023, 55, 2577–2587. (In Chinese) [Google Scholar]
- Uyanna, O.; Najafi, H. Thermal Protection Systems for Space Vehicles: A Review on Technology Development, Current Challenges and Future Prospects. Acta Astronaut. 2020, 176, 341–356. [Google Scholar] [CrossRef]
- Le, V.T.; Ha, N.S.; Goo, N.S. Advanced Sandwich Structures for Thermal Protection Systems in Hypersonic Vehicles: A Review. Compos. Part B-Eng. 2021, 226, 109301. [Google Scholar] [CrossRef]
- Glass, D.E. Ceramic Matrix Composite (CMC) Thermal Protection Systems (TPS) and Hot Structures for Hypersonic Vehicles. In Proceedings of the 15th AIAA Space Planes and Hypersonic Systems and Technologies Conference, Dayton, OH, USA, 28 April–1 May 2008; p. 2682. [Google Scholar]
- Behrens, B.; Müller, M. Technologies for Thermal Protection Systems Applied on Re-useable Launcher. Acta Astronaut. 2004, 55, 529–536. [Google Scholar] [CrossRef]
- Letchworth, G. X-33 Reusable Launch Vehicle Demonstrator, Spaceport and Range. In Proceedings of the AIAA Space 2011 Conference & Exposition, Long Beach, CA, USA, 27–29 September 2011; p. 7314. [Google Scholar]
- Leonard, C.P.; Amundsen, R.M.; Bruce, W.E. Hyper-X Hot Structures Design and Comparison with Flight Data. In Proceedings of the AIAA/CIRA 13th International Space Planes and Hypersonics Systems and Technologies Conference, Capua, Italy, 16–20 May 2005; p. 3438. [Google Scholar]
- Blet, N.; Lips, S.; Sartre, V. Heats Pipes for Temperature Homogenization: A Literature Review. Appl. Therm. Eng. 2017, 118, 490–509. [Google Scholar] [CrossRef]
- Steeves, C.A.; He, M.Y.; Kasen, S.D.; Valdevit, L.; Wadley, H.N.G.; Evans, A.G. Feasibility of Metallic Structural Heat Pipes as Sharp Leading Edges for Hypersonic Vehicles. ASME J. Appl. Mech. 2009, 76, 031014. [Google Scholar] [CrossRef]
- Xiao, G.; Du, Y.; Gui, Y.; Liu, L.; Yang, X.; Wei, D. Heat Transfer Characteristics and Limitations Analysis of Heat-pipe-cooled Thermal Protection Structure. Appl. Thermal Eng. 2014, 70, 655–664. [Google Scholar]
- Liu, H.; Liu, W. A Numerical Model for the Platelet Heat-pipe-cooled Leading Edge of Hypersonic Vehicle. Acta Astronaut. 2016, 118, 210–217. [Google Scholar] [CrossRef]
- Liu, H.; Liu, W. Thermal–structural Analysis of the Platelet Heat-pipe-cooled Leading Edge of Hypersonic Vehicle. Acta Astronaut. 2016, 127, 13–19. [Google Scholar]
- Zhu, Y.; Peng, W.; Jiang, P.; Xu, R. Review on Active Thermal Protection and its Heat Transfer for Airbreathing Hypersonic Vehicles. Chin. J. Aeronaut. 2018, 31, 1929–1953. [Google Scholar] [CrossRef]
- Zhang, S.; Li, X.; Zuo, J.; Qin, J.; Cheng, K.; Feng, Y.; Bao, W. Research Progress on Active Thermal Protection for Hypersonic Vehicles. Prog. Aerosp. Sci. 2020, 119, 100646. [Google Scholar] [CrossRef]
- Helenbrook, R.G.; Anthony, F.M. Design of a Convective Cooling System for a Mach 6 Hypersonic Transport Airframe; NASA Technical Report; NASA-CR-1918; NASA: Washington, DC, USA, 1971. [Google Scholar]
- Anthony, F.M.; Dukes, W.H.; Helenbrook, R.G. Internal Convective Cooling Systems for Hypersonic Aircraft; NASA Technical Report; NASA-CR-2480; NASA: Washington, DC, USA, 1975. [Google Scholar]
- Youn, B.; Mills, A.F. Cooling Panel Optimization for the Active Cooling System of a Hypersonic Aircraft. AIAA J. Thermophys. Heat Tran. 1995, 9, 136–143. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, S.; Wang, C.; Tan, X. Recent Advances in Film Cooling Enhancement: A Review. Chin. J. Aeronaut. 2020, 33, 1119–1136. [Google Scholar] [CrossRef]
- Naved, I.; Hermann, T.; McGilvray, M. Numerical Simulation of Transpiration Cooling for a High-speed Vehicle with Substructure. AIAA J. 2021, 59, 3043–3053. [Google Scholar] [CrossRef]
- Dechaumphai, P.; Thornton, E.A.; Wieting, A.R. Flow-thermal-structural Study of Aerodynamically Heated Leading Edges. J. Spacecr. Rockets 1989, 26, 201–209. [Google Scholar] [CrossRef]
- Maruyama, S.; Viskanta, R.; Aihara, T. Active Thermal Protection System Against Intense Irradiation. AIAA J. Thermophys. Heat Tran. 1989, 3, 389–394. [Google Scholar] [CrossRef]
- Calmidi, V.V.; Mahajan, R.L. Forced Convection in High Porosity Metal Foams. ASME J. Heat Transf. 2000, 122, 557–565. [Google Scholar] [CrossRef]
- Rakow, J.F.; Waas, A.M. Response of Actively Cooled Metal Foam Sandwich Panels Exposed to Thermal Loading. AIAA J. 2007, 45, 329–336. [Google Scholar] [CrossRef]
- Liu, S.; Zhang, B. Effects of Active Cooling on the Metal Thermal Protection Systems. Aerosp. Sci. Technol. 2011, 15, 526–533. [Google Scholar] [CrossRef]
- Ferrari, L.; Barbato, M.; Esser, B.; Petkov, I.; Kuhn, M.; Gianella, S.; Barcena, J.; Jimenez, C.; Francesconi, D.; Liedtke, V.; et al. Sandwich Structured Ceramic Matrix Composites with Periodic Cellular Ceramic Cores: An Active Cooled Thermal Protection for Space Vehicles. Compos. Struct. 2016, 154, 61–68. [Google Scholar] [CrossRef]
- Xie, G.; Wang, C.; Ji, T.; Sunden, B. Investigation on Thermal and Thermomechanical Performances of Actively Cooled Corrugated Sandwich Structures. Appl. Therm. Eng. 2016, 103, 660–669. [Google Scholar] [CrossRef]
- Xie, J.; Zhang, R.; Xie, G.; Manca, O. Thermal and Thermomechanical Performance of Actively Cooled Pyramidal Sandwich Panels. Int. J. Therm. Sci. 2019, 139, 118–128. [Google Scholar] [CrossRef]
- Qiao, Y.; Liu, P.; Liu, W.; Liu, Z. Analysis and Optimization of Flow and Heat Transfer Performance of Active Thermal Protection Channel for Hypersonic Aircraft. Case Stud. Therm. Eng. 2022, 39, 102476. [Google Scholar] [CrossRef]
- Qiao, Y.; Liu, W.; Liu, Z. Design and Optimization Study of Discrete Inclined Ribs Enhanced Bend Tube Based on “Diamond” Active Cooling Thermal Protection Systems of Hypersonic Aircraft. Appl. Therm. Eng. 2023, 228, 120526. [Google Scholar] [CrossRef]
- Hu, G.; Zhong, F.; Chen, K. An Analytical Model for Maximum Temperature and Temperature Distribution of Plate Structure with Active Cooling. Acta Mech. Sin. 2023, 39, 322290. [Google Scholar] [CrossRef]
- Gou, J.; Chang, Y.; Yan, Z.; Chen, B.; Gong, C. The Design of Thermal Management System for Hypersonic Launch Vehicles Based on Active Cooling Networks. Appl. Therm. Eng. 2019, 159, 113938. [Google Scholar] [CrossRef]
- Gou, J.; Yan, Z.; Hu, J.; Gao, G.; Gong, C. The Heat Dissipation, Transport and Reuse Management for Hypersonic Vehicles Based on Regenerative Cooling and Thermoelectric Conversion. Aerosp. Sci. Technol. 2021, 108, 106373. [Google Scholar] [CrossRef]
- Chen, W.; Men, Z.; Liu, S. Fast Parameterized Fractal Modeling of Active Heat Transfer Channel. Appl. Therm. Eng. 2022, 209, 118297. [Google Scholar] [CrossRef]
- Lees, L. Laminar Heat Transfer over Blunt-nosed Bodies at Hypersonic Flight Speeds. Jet Propuls. 1956, 26, 259–269. [Google Scholar] [CrossRef]
- Rubesin, M.W.; Johnson, H.A. A Critical Review of Skin-friction and Heat Transfer Solutions of the Laminar Boundary Layer of a Flat Plate. ASME Trans. 1949, 71, 383–388. [Google Scholar] [CrossRef]
- Li, Y.; Xie, G.; Sunden, B. Flow and Thermal Performance of Supercritical n-decane in Double-layer Channels for Regenerative Cooling of a Scramjet Combustor. Appl. Therm. Eng. 2020, 180, 115695. [Google Scholar] [CrossRef]
- Tao, Z.; Cheng, Z.; Zhu, J.; Li, H. Effect of Turbulence Models on Predicting Convective Heat Transfer to Hydrocarbon Fuel at Supercritical Pressure. Chin. J. Aeronaut. 2016, 29, 1247–1261. [Google Scholar] [CrossRef]
- Liu, B.; Zhu, Y.; Yan, J.; Lei, Y.; Zhang, B.; Jiang, P. Experimental Investigation of Convection Heat Transfer of n-decane at Supercritical Pressures in Small Vertical Tubes. Int. J. Heat Mass Tran. 2015, 91, 734–746. [Google Scholar] [CrossRef]
- Fu, Y.; Wen, J.; Tao, Z.; Xu, G.; Huang, H. Experimental Research on Convective Heat Transfer of Supercritical Hydrocarbon Fuel Flowing Through U-turn Tubes. Appl. Therm. Eng. 2017, 116, 43–55. [Google Scholar] [CrossRef]
- Xu, K.; Ruan, B.; Meng, H. Validation and Analyses of RANS CFD Models for Turbulent Heat Transfer of Hydrocarbon Fuels at Supercritical Pressures. Int. J. Therm. Sci. 2018, 124, 212–226. [Google Scholar] [CrossRef]
- Zhong, F.; Fan, X.; Yu, G.; Li, J. Heat Transfer of Aviation Kerosene at Supercritical Conditions. AIAA J. Thermophys. Heat Tran. 2009, 23, 543–550. [Google Scholar] [CrossRef]








| Thermal Properties | Thermal Conductivity (W/m·K) | Specific Heat (J/kg·K) | Expansion Coefficient (1/K) |
|---|---|---|---|
| Value | 91.74 | 460.6 | 1.2 × 10−5 |
| Mechanical Properties | Density (kg/m3) | Young’s Modulus (Gpa) | Poisson’s Ratio |
| Value | 8900 | 190 | 0.31 |
| Test Type | Branch Configuration | Test Round | Branch Total Flow Rate | Single-Channel BC Conditions | Candidate Schemes | |
|---|---|---|---|---|---|---|
| Temperature test | Series arrangement | First | 200 g/s | , | Schemes A1, A2, B1, B1-M, B2, B2-M | |
| Second | 100 g/s | , | Schemes that met in the first test round | |||
| Parallel arrangement | First | 200 g/s | , | Schemes A1, A2, B1, B1-M, B2, B2-M | ||
| Second | 100 g/s | , | Schemes that met in the first test round | |||
| Thermal–mechanical test | - | - | - | Temperature field, fixed BC, channel pressure | Optimal schemes | |
| Mesh Resolution | Number | , K | , % | , kPa | , % |
|---|---|---|---|---|---|
| Coarse | 3.26 million | 799.43 | 1.00 | 2.60 | 6.47 |
| Medium | 5.33 million | 792.92 | 0.18 | 2.77 | 0.36 |
| Fine | 11.18 million | 791.51 | - | 2.78 | - |
| Cases | (K) | (MPa) | (m/s) | Rein | (kW/m2) |
|---|---|---|---|---|---|
| 423.15 | 3 | 1.1474 | 2700 | 72 | |
| 2 | 114 | ||||
| 3 | 163 | ||||
| 4 | 294 | ||||
| 5 | 423.15 | 3 | 1.7 | 4000 | 154 |
| 6 | 240 | ||||
| 7 | 319 | ||||
| 8 | 393 |
| Scheme | A1 | A2 | B1 | B1-M | B2 | B2-M |
|---|---|---|---|---|---|---|
| , mm | 0.449 | 0.420 | 0.415 | 0.416 | 0.414 | 0.410 |
| , MPa | 98.83 | 104.25 | 463.04 | 467.65 | 463.21 | 453.83 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, T.; Li, T.; Li, S.; Sha, J. Numerical Study on Heat Transfer and Thermal–Mechanical Performance of Actively Cooled Channel of All-Movable Rudder under Supercritical Pressure. Appl. Sci. 2024, 14, 8434. https://doi.org/10.3390/app14188434
Wang T, Li T, Li S, Sha J. Numerical Study on Heat Transfer and Thermal–Mechanical Performance of Actively Cooled Channel of All-Movable Rudder under Supercritical Pressure. Applied Sciences. 2024; 14(18):8434. https://doi.org/10.3390/app14188434
Chicago/Turabian StyleWang, Tianyu, Teng Li, Shangzhong Li, and Jianke Sha. 2024. "Numerical Study on Heat Transfer and Thermal–Mechanical Performance of Actively Cooled Channel of All-Movable Rudder under Supercritical Pressure" Applied Sciences 14, no. 18: 8434. https://doi.org/10.3390/app14188434
APA StyleWang, T., Li, T., Li, S., & Sha, J. (2024). Numerical Study on Heat Transfer and Thermal–Mechanical Performance of Actively Cooled Channel of All-Movable Rudder under Supercritical Pressure. Applied Sciences, 14(18), 8434. https://doi.org/10.3390/app14188434






