Prediction of Flotation Deinking Performance: A Comparative Analysis of Machine Learning Techniques
Abstract
:1. Introduction
2. Materials and Methods
2.1. Machine Learning Techniques for Prediction of Flotation Deinking Performance
2.1.1. Support Vector Regression
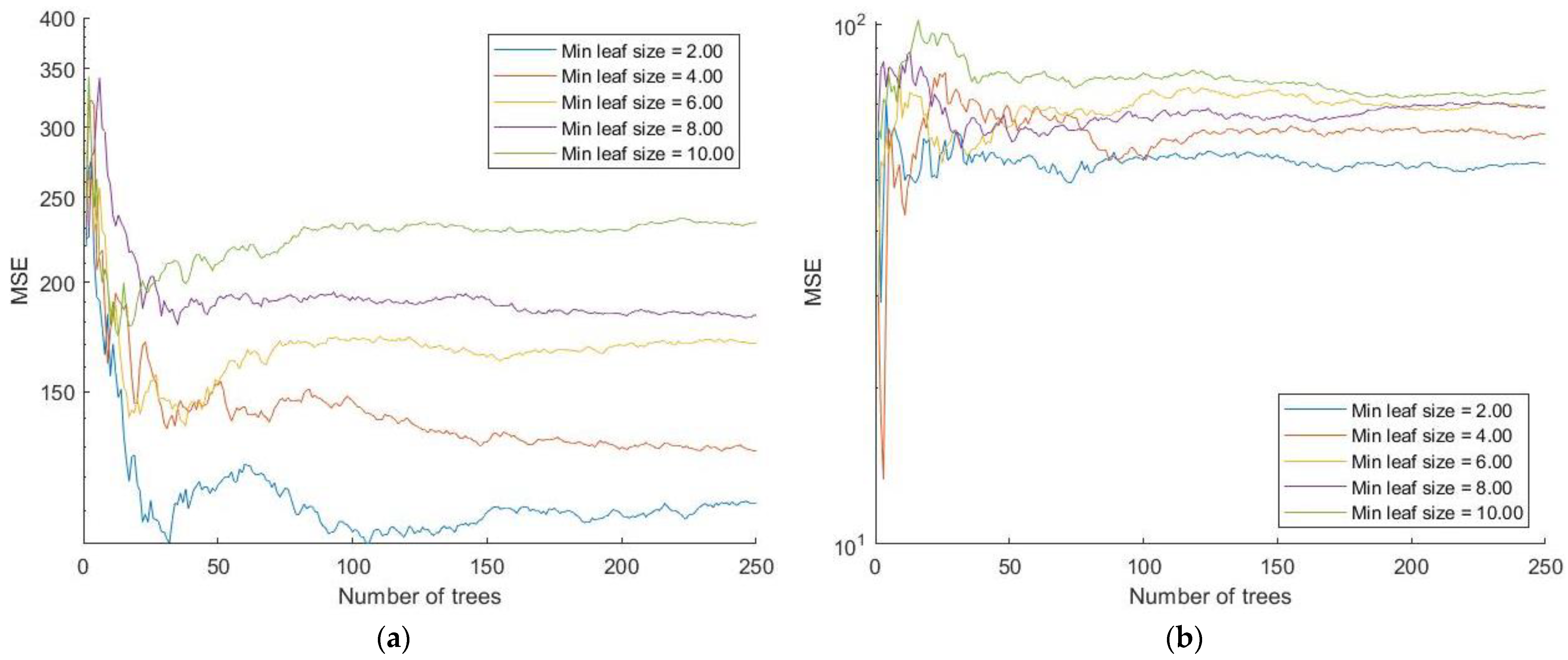
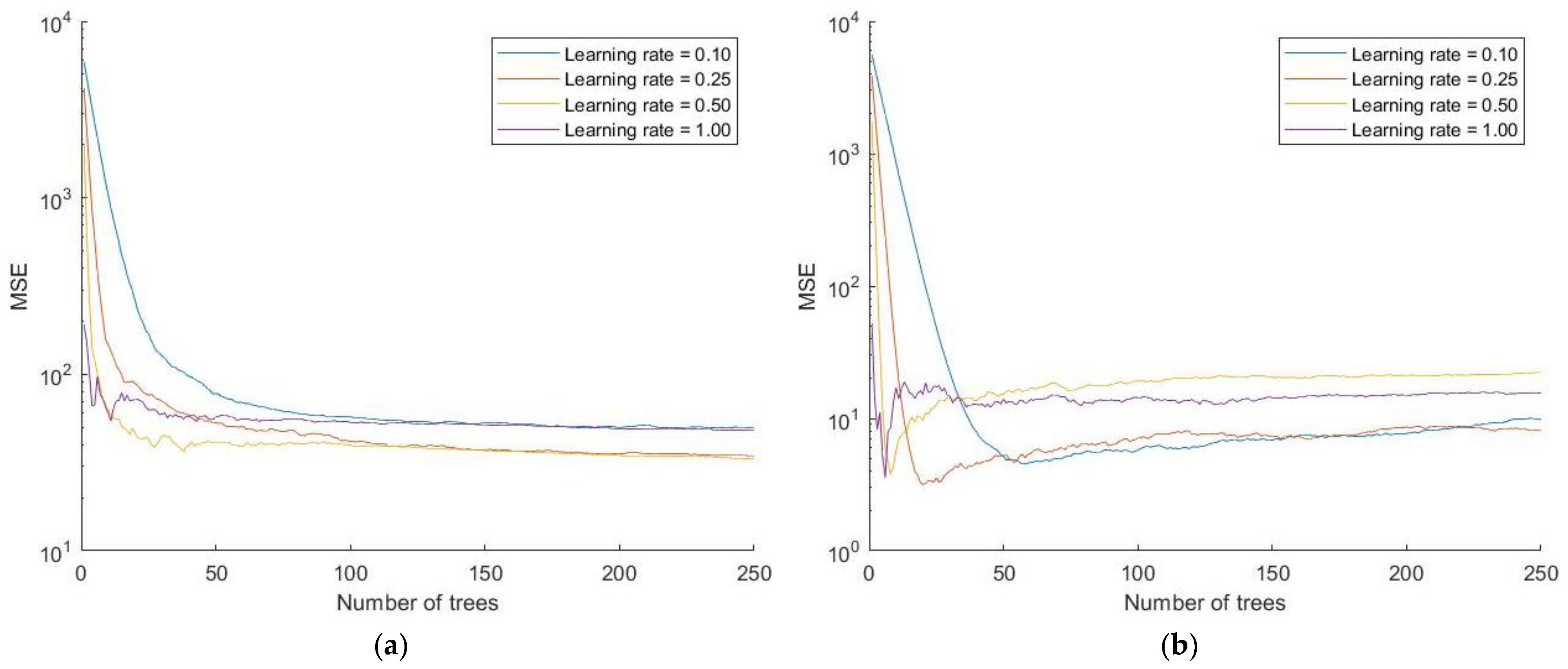
2.1.2. Regression Tree Ensembles
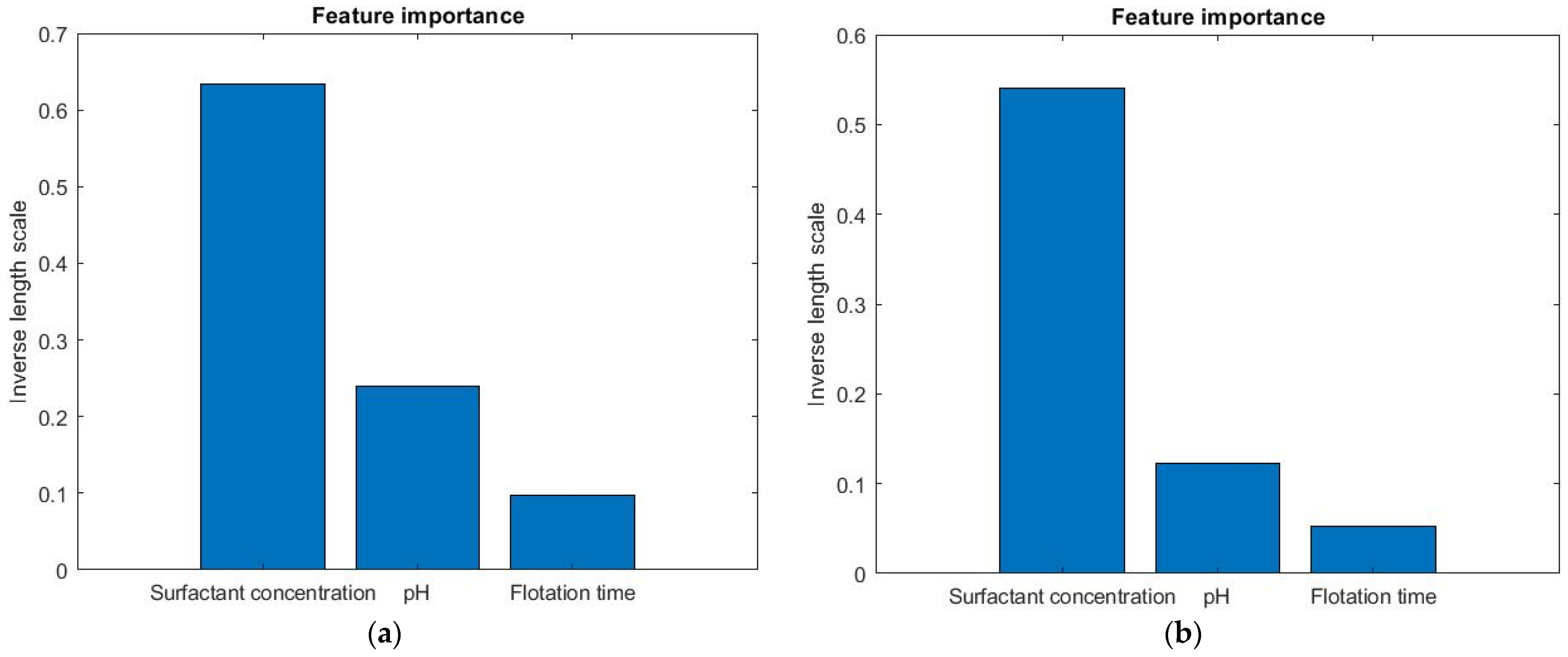
2.1.3. Gaussian Process Regression
2.2. Dataset
2.3. Performance Measure
3. Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jovanovic, I.; Miljanović, I.; Jovanović, T. Soft computing-based modeling of flotation processes—A review. Miner. Eng. 2015, 84, 34–63. [Google Scholar] [CrossRef]
- Mohammed, A.S.; Qarani, A.S. Dissolved Air Flotation (DAF): Operational Parameters and Limitations for Wastewaters Treatment with Cost Study. Recycl. Sustain. Dev. 2023, 16, 91–97. [Google Scholar] [CrossRef]
- Mehari, A. Deinking of Black Toner Ink from Laser Printed Paper by Using Anionic Surfactant. Master’s Thesis, Addis Ababa University, Addis Ababa, Ethiopia, 2017. [Google Scholar]
- Pauck, W.J.; Venditti, R.; Pocock, J.; Andrew, J. Neural network modelling and prediction of the flotation deinking behaviour of industrial paper recycling processes. Recycl. Nord. Pulp Pap. Res. J. 2014, 29, 521–532. [Google Scholar] [CrossRef]
- Costa, C.A.; Rubio, J. Deinking flotation: Influence of calcium soap and surface-active substance. Miner. Eng. 2005, 18, 59–64. [Google Scholar] [CrossRef]
- Pauck, W.J.; Venditti, R.; Pocock, J.; Andrew, J. Using statistical experimental design techniques to determine the most effective variables for the control of the flotation deinking of mixed recycled paper grades. Tappsa J. 2012, 2, 28–41. [Google Scholar]
- Husovska, V. Investigation of Recycled Paper Deinking Mechanisms. Ph.D. Thesis, Western Michigan University, Kalamazoo, MI, USA, 2013. [Google Scholar]
- Abraha, M.; Kifle, Z. Deinking of Black Toner Ink from Laser Printed Paper by Using Anionic Surfactant. Chem. Biomol. Eng. 2019, 4, 23–30. [Google Scholar] [CrossRef]
- Kumar, A.; Dutt, D. A comparative study of conventional chemical deinking and environment-friendly bio-deinking of mixed office wastepaper. Sci. Afr. 2021, 12, e00793. [Google Scholar] [CrossRef]
- Gomez-Flores, A.; Heyes, G.W.; Ilyas, S.; Kim, H. Prediction of grade and recovery in flotation from physicochemical and operational aspects using machine learning models. Miner. Eng. 2022, 183, 107627. [Google Scholar] [CrossRef]
- Labidi, J.; Pelach, M.A.; Turon, X.; Mutje, P. Predicting flotation efficiency using neural networks. Intensification 2007, 46, 314–322. [Google Scholar] [CrossRef]
- Verikas, A.; Malmqvist, K.; Bacauskiene, M. Monitoring the De-Inking Process through Neural Network-Based Colour Image Analysis. Neural Comput. Appl. 2000, 9, 142–151. [Google Scholar] [CrossRef]
- Laperrière, L.; Wasik, L. Modeling and simulation of pulp and paper quality characteristics using neural networks. Tappi J. 2001, 84, 59. [Google Scholar]
- Lü, Q.; Liu, S.; Mao, W.; Yu, Y.; Long, X. A numerical simulation-based ANN method to determine the shear strength parameters of rock minerals in nanoscale. Comput. Geotech. 2024, 169, 106175. [Google Scholar] [CrossRef]
- Nakhaei, F.; Irannajad, M. Application and comparison of RNN, RBFNN and MNLR approaches on prediction of flotation column performance. Int. J. Min. Sci. Technol. 2015, 25, 983–990. [Google Scholar] [CrossRef]
- Chehreh Chelgania, S.; Shahbazib, B.; Hadavandi, E. Support vector regression modeling of coal flotation based on variable importance measurements by mutual information method. Measurement 2018, 114, 102–108. [Google Scholar] [CrossRef]
- Szmigiel, A.; Apel, D.B.; Skrzypkowski, K.; Wojtecki, L.; Pu, Y. Advancements in Machine Learning for Optimal Performance in Flotation Processes: A Review. Minerals 2024, 14, 331. [Google Scholar] [CrossRef]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer: New York, NY, USA, 1995. [Google Scholar] [CrossRef]
- Vapnik, V.; Golowich, S.; Smola, A. Support vector method for function approximation, regression estimation, and signal processing. In Advances in Neural Information Processing Systems; Mozer, M.C., Jordan, M.I., Petsche, T., Eds.; MIT Press: Cambridge, MA, USA, 1997; Volume 9, pp. 281–287. [Google Scholar]
- Smola, A.J.; Schölkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef]
- Kovačević, M.; Ivanišević, N.; Petronijević, P.; Despotović, V. Construction cost estimation of reinforced and prestressed concrete bridges using machine learning. Građevinar 2021, 73, 1–13. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. Boosting and Additive Trees. In The Elements of Statistical Learning; Springer Series in Statistics; Springer: New York, NY, USA, 2009. [Google Scholar] [CrossRef]
- Cormen, T.H.; Leiserson, C.E.; Rivest, R.L.; Stein, C. Introduction to Algorithms, 3rd ed.; The MIT Press: Cambridge, MA, USA, 2009. [Google Scholar]
- Despotovic, V.; Skovranek, T.; Schommer, C. Speech Based Estimation of Parkinson’s Disease Using Gaussian Processes and Automatic Relevance Determination. Neurocomputing 2020, 401, 173–181. [Google Scholar] [CrossRef]
- Rasmussen, C.E.; Williams, C.K.I. Gaussian Processes for Machine Learning; The MIT Press: Cambridge, MA, USA, 2006. [Google Scholar]
- Lin, D.; Kuang, Y.; Chen, G.; Kuang, Q.; Wang, C.; Zhu, P.; Peng, C.; Fang, Z. Enhancing moisture resistance of starch-coated paper by improving the film forming capability of starch film. Ind. Crops Prod. 2017, 100, 12–18. [Google Scholar] [CrossRef]
- Dorris, G.M.; Sayegh, N.N. The role of print layer thickness and cohesiveness on deinking of toner printed papers. Tappi J. 1997, 80, 181–191. [Google Scholar]
- Azevedo, M.A.D.; Drelich, J.; Miller, J.D. The Effect of pH On Pulping and Flotation of Mixed Office Wastepaper. J. Pulp Pap. Sci. 1999, 25, 317–320. [Google Scholar]
- Dorris, G.; Ben, Y.; Richard, M. Overview of flotation Deinking, Progress in paper recycling. Tappi J. 2011, 20, 3–43. [Google Scholar]
- Gong, R. New Approaches on Deinking Evaluations. Ph.D. Thesis, Western Michigan University, Kalamazoo, MI, USA, 2013. [Google Scholar]
- Yilmaz, U.; Tutus, A.; Sönmez, S. Effects of using recycled paper in inkjet printing system on colour difference. Pigment. Resin Technol. 2022, 51, 336–343. [Google Scholar] [CrossRef]
- Muangnamsuk, R.; Chuetor, S.; Kirdponpattara, S. Development and Optimization of Chemical Deinking of Laser-Printed Paper. Mater. Sci. Forum 2023, 1098, 151–155. [Google Scholar] [CrossRef]
- Behin, J.; Vahed, S. Effect of alkyl chain in alcohol deinking of recycled fibers by flotation process. Colloids Surf. A Physicochem. Eng. Asp. 2007, 297, 131–141. [Google Scholar] [CrossRef]
- Jiang, C.; Ma, J. Deinking of waste paper: Flotation. In Encyclopedia of Separation Science; Academic Press: London, UK, 2000; pp. 2537–2544. [Google Scholar]
- Tsatsis, D.E.; Valta, K.A.; Vlyssides, A.G.; Economides, D.G. Assessment of the impact of toner composition, printing processes and pulping conditions on the deinking of office waste paper. J. Environ. Chem. Eng. 2019, 7, 103258. [Google Scholar] [CrossRef]
- Ghanbarzadeh, B.; Ataeefard, M.; Etezad, S.M.; Mahdavi, S. Optical and Printing Properties of Deinked Office Waste Printed Paper. Prog. Color Color. Coat. 2024, 17, 75–84. [Google Scholar]
- Yilmaz, U. Investigation of deinking efficiencies of trigromi laserjet printed papers depending on the number of recycling. Pigment. Resin Technol. 2024, 53, 475–483. [Google Scholar] [CrossRef]
- Ali, T.; McLellan, F.; Adiwinata, J.; May, M.; Evants, T. Functional and perfomance characteristics of solube silicate in deinking. Part I: Alkaline deinking of newsprint/magazine. J. Pulp Pap. Sci. 1994, 20, J3–J8. [Google Scholar]
- Liphard, M.; Schereck, B.; Hornfeck, K. Surface chemical aspects of filler flotation in waste paper recycling. Pulp Pap. Can. 1993, 94, 218–222. [Google Scholar]
- Luo, Q.; Deng, Y.; Zhu, J.; Shin, W.T. Foam control using a foaming agent spray: A novel concept for flotation deinking of waste paper. Ind. Eng. Chem. Res. 2003, 15, 3578–3583. [Google Scholar] [CrossRef]
- Pathak, P.; Bhardwaj, N.K.; Singh, A.K. Optimization of Chemical and Enzymatic Deinking of Photocopier Waste Paper. BioResources 2011, 6, 447–463. [Google Scholar] [CrossRef]
- Chandranupap, P.; Chandranupap, P. Enzymatic Deinking of Xerographic Waste Paper with Non-ionic Surfactant. Appl. Sci. Eng. Prog. 2020, 13, 136–145. [Google Scholar] [CrossRef]
- Yilmaz, U.; Tutuş, A.; Sönmez, S. Fiber Classification, Physical and Optical Properties of Recycled Paper. Cellul. Chem. Technol. 2021, 55, 689–696. [Google Scholar] [CrossRef]
- Despotović, V.; Trumić, M.S.; Trumić, M.Ž. Modeling and prediction of flotation performance using support vector regression. Recycl. Sustain. Dev. 2017, 10, 31–36. [Google Scholar] [CrossRef]
- Khadka, K.; Chandrasekaran, J.; Lei, Y.; Kacker, R.N.; Kuhn, D.R. A Combinatorial Approach to Hyperparameter Optimization. In Proceedings of the 2024 IEEE/ACM 3rd International Conference on AI Engineering—Software Engineering for AI (CAIN), Lisbon, Portugal, 14–15 April 2024; pp. 140–149. [Google Scholar]
- Chang, C.C.; Lin, C.J. LIBSVM: A Library for Support Vector Machines. ACM Trans. Intell. Syst. Technol. 2011, 2, 1–27. [Google Scholar] [CrossRef]

| Process Control Variables | Range of Process Control Variables |
|---|---|
| Flotation pH | 3–12 |
| Surfactant in flotation cell: | |
| Oleic acid | 0.1–7 kg/t |
| Oleic acid + CaCl2 | 0.125–1.5 kg/t + 30 kg/t |
| Flotation time | 1–20 min |
| Optimization Variables | Range of Optimization Variables | Adopted Value |
|---|---|---|
| Pulping pH | 7–10 [5,27,28,29,30,31,32] | 8 |
| Pulping time | 4–60 min [6,31,33,34,35,36,37] | 35 min |
| Pulping temperature | 35–60 °C [4,9,27,33,35,38] | 45 °C |
| Pulping consistency | 8–18 wt % [9,33,34,35,36,37,39] | 10 wt % |
| Flotation temperature | 20–45 °C [4,27,35,40,41,42,43] | 22 °C |
| Flotation consistency | 0.5–1.5% [6,11,28,29,31,35,36,37,41,42] | 1 wt % |
| Agitation speed | 1000–1400 rpm [11,27,28,31,41,44] | 1000 rpm |
| Airflow rate | 225–775 L/h [9,11,35,43] | 260 L/h |
| Models | Oleic Acid | Oleic Acid + CaCl2 | |||
|---|---|---|---|---|---|
| MSE | R2 [%] | MSE | R2 [%] | ||
| SVR | Linear | 101.33 | 63.72 | 104.24 | 71.02 |
| RBF | 20.31 | 93.56 | 30.97 | 93.37 | |
| Regression trees | Random forests | 51.31 | 88.19 | 44.47 | 92.06 |
| Boosting | 21.16 | 94.05 | 24.27 | 93.87 | |
| GPR | Exponential | 24.06 | 94.87 | 27.67 | 93.34 |
| Squared exponential | 11.85 | 97.32 | 19.72 | 95.43 | |
| Matérn 3/2 | 14.03 | 97.66 | 19.73 | 95.95 | |
| Matérn 5/2 | 12.64 | 97.77 | 20.21 | 95.73 | |
| Rational quadratic | 12.48 | 97.66 | 21.44 | 95.24 | |
| Models | Oleic Acid | Oleic Acid + CaCl2 | |||
|---|---|---|---|---|---|
| MSE | R2 [%] | MSE | R2 [%] | ||
| SVR | Linear | 82.20 | 49.22 | 56.24 | 43.91 |
| RBF | 12.52 | 90.95 | 19.71 | 73.96 | |
| Regression trees | Random forests | 31.80 | 84.01 | 29.12 | 63.96 |
| Boosting | 7.33 | 93.90 | 7.95 | 88.33 | |
| GPR | Exponential | 24.37 | 84.50 | 32.13 | 64.83 |
| Squared exponential | 45.43 | 69.07 | 40.45 | 55.48 | |
| Matérn 3/2 | 20.27 | 86.31 | 30.87 | 65.80 | |
| Matérn 5/2 | 21.62 | 84.51 | 38.05 | 55.83 | |
| Rational quadratic | 21.57 | 84.94 | 35.98 | 60.88 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gavrilović, T.; Despotović, V.; Zot, M.-I.; Trumić, M.S. Prediction of Flotation Deinking Performance: A Comparative Analysis of Machine Learning Techniques. Appl. Sci. 2024, 14, 8990. https://doi.org/10.3390/app14198990
Gavrilović T, Despotović V, Zot M-I, Trumić MS. Prediction of Flotation Deinking Performance: A Comparative Analysis of Machine Learning Techniques. Applied Sciences. 2024; 14(19):8990. https://doi.org/10.3390/app14198990
Chicago/Turabian StyleGavrilović, Tamara, Vladimir Despotović, Madalina-Ileana Zot, and Maja S. Trumić. 2024. "Prediction of Flotation Deinking Performance: A Comparative Analysis of Machine Learning Techniques" Applied Sciences 14, no. 19: 8990. https://doi.org/10.3390/app14198990









