A Study on the Coarse-to-Fine Error Decomposition and Compensation Method of Free-Form Surface Machining
Abstract
1. Introduction
1.1. Problem Statement of Motivation and Methodology
1.2. Literature Review
2. The Coarse-to-Fine Free-Form Surface Machining Error Decomposition and Compensation Process
2.1. Calculation of the Machining Error for the Free-Form Surface Part
2.2. Correlation Coefficient Principle
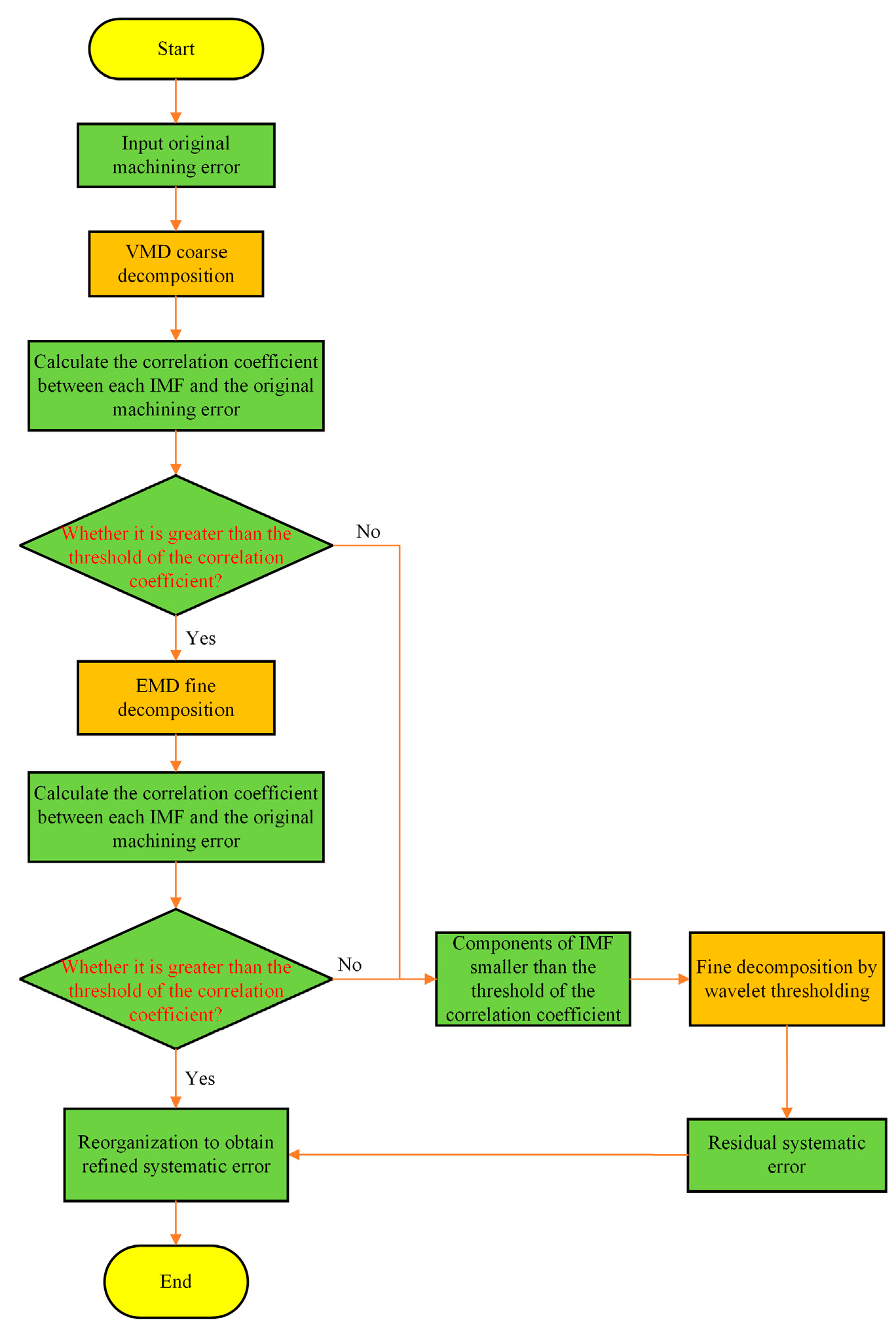
2.3. Principle of Machining Error Decomposition from Coarse to Fine
2.3.1. Principle of the VMD Algorithm
- 1.
- Construction of constrained variational models
- 2.
- Solution of the constrained variational model
2.3.2. Principle of the EMD Algorithm
- (1)
- Within the entire signal, the number of extremum and zero crossing points must be the same, and the number of both must not differ by more than one at most;
- (2)
- At any point within the signal, the upper envelope consisting of local maximum values and the lower envelope consisting of local minimum values both have an average value of 0, which is the local mean value.
- (1)
- Assuming that is the average of the upper and lower envelopes of the original signal and that is the difference between and , it can be expressed by
- (2)
- Treating as the signal to be decomposed and repeating step (1), it can be expressed by
- (3)
- Separate from in the original signal to obtain a new data sequence :
- (4)
- After decomposition, the original signal can be expressed as
2.3.3. Principle of the Wavelet Thresholding Method
2.3.4. Principle of the Coarse-to-Fine Machining Error Decomposition Method
- (1)
- Let the original machining error be , and use VMD to coarsely decompose the machining error to obtain K components of IMFs of length n, which can be expressed by
- (2)
- EMD is utilized to perform a fine decomposition of the coarse systematic error X1 after VMD into M IMF components and a trend term, which can be expressed by
- (3)
- The IMF components with correlation coefficients of less than 0.3 in the VMD coarse decomposition and EMD fine decomposition processes may also contain a small systematic error. To ensure that the decomposed systematic error is as complete and accurate as possible, the weakly correlated IMF components with correlation coefficients of less than 0.3 in the first two decomposition processes are decomposed using the wavelet thresholding method. The random errors are removed, and the systematic errors are retained.
- (4)
- The systematic error X2 decomposed by EMD is reconstructed with the systematic error X3 decomposed by the wavelet thresholding method to obtain the refined systematic error X4, which can be expressed by
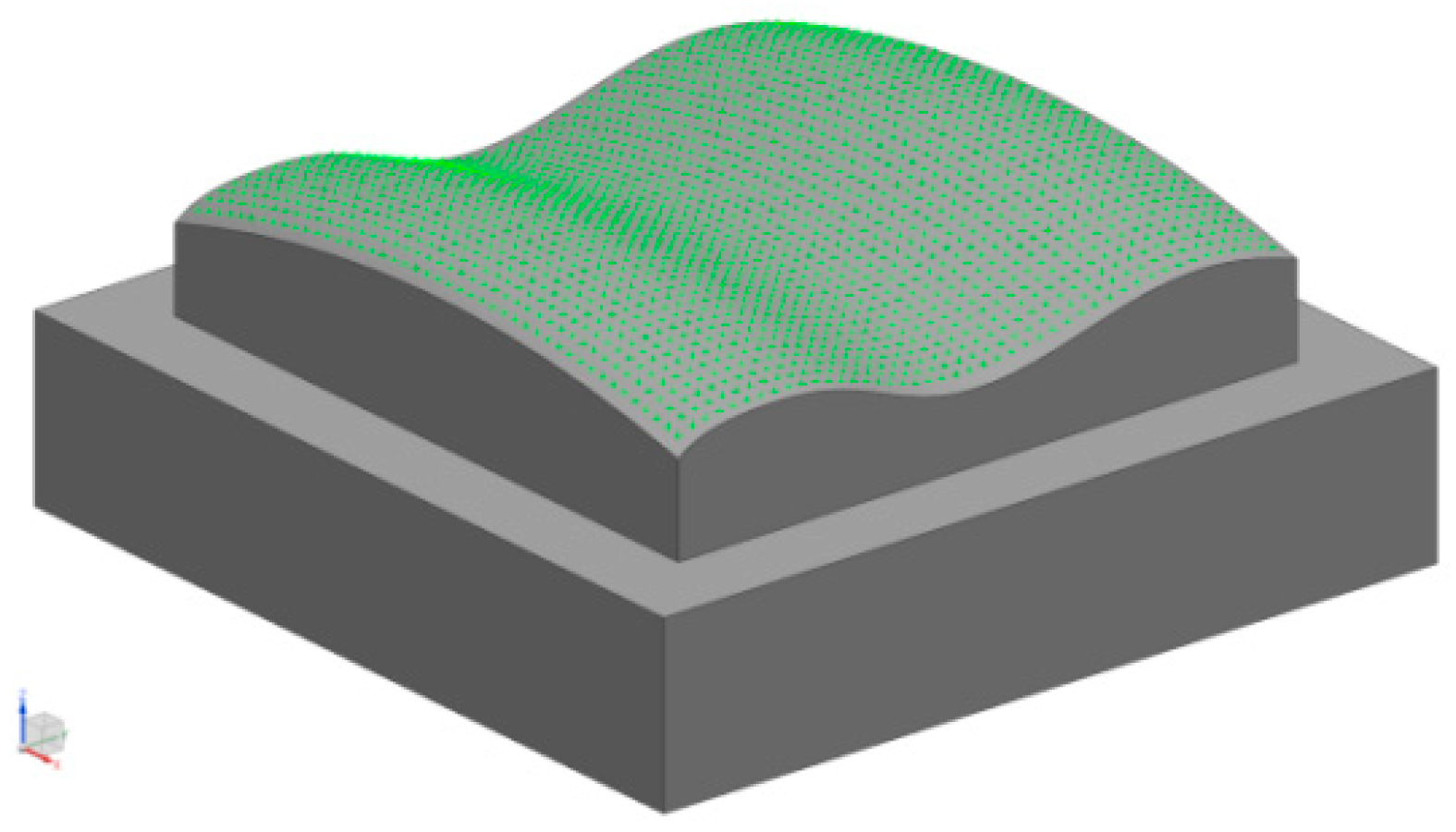
3. Simulation Experiment of Machining Error Decomposition from Coarse to Fine
3.1. VMD Algorithm Coarse Decomposition of the Simulation Machining Error
3.2. EMD Algorithm Fine Decomposition of the Simulation Machining Error
3.3. Residual Systematic Error Decomposition by the Wavelet Thresholding Method
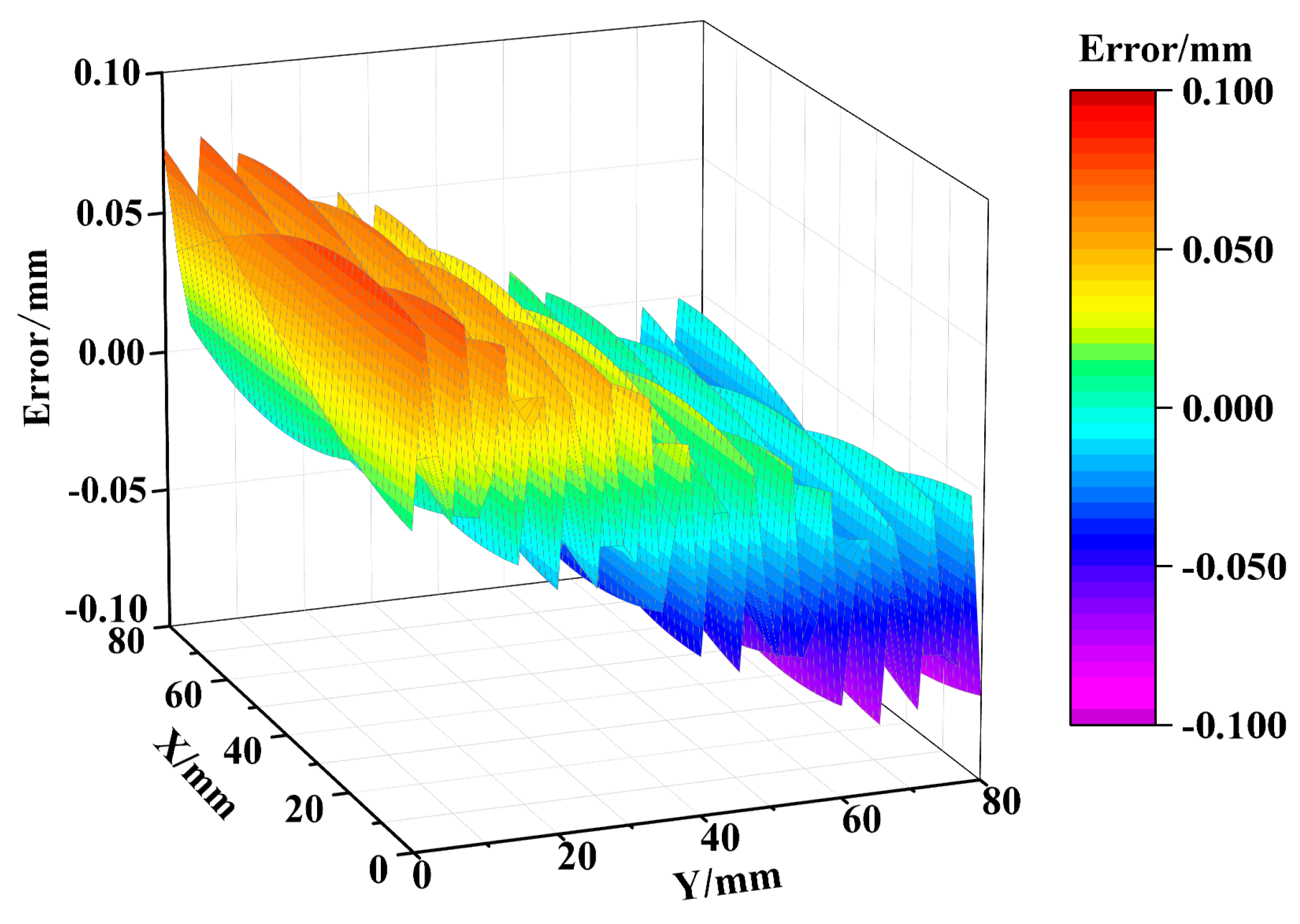
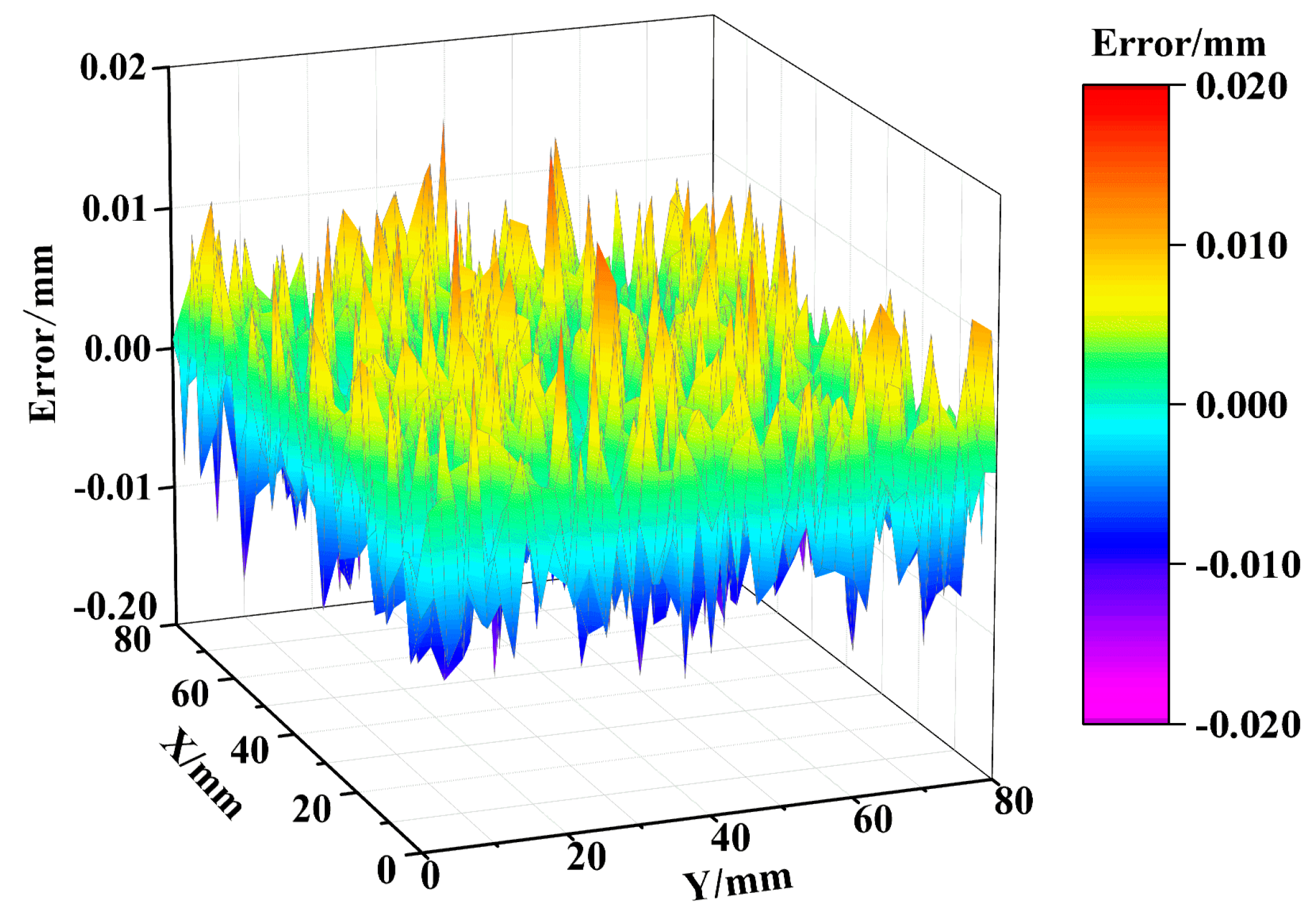
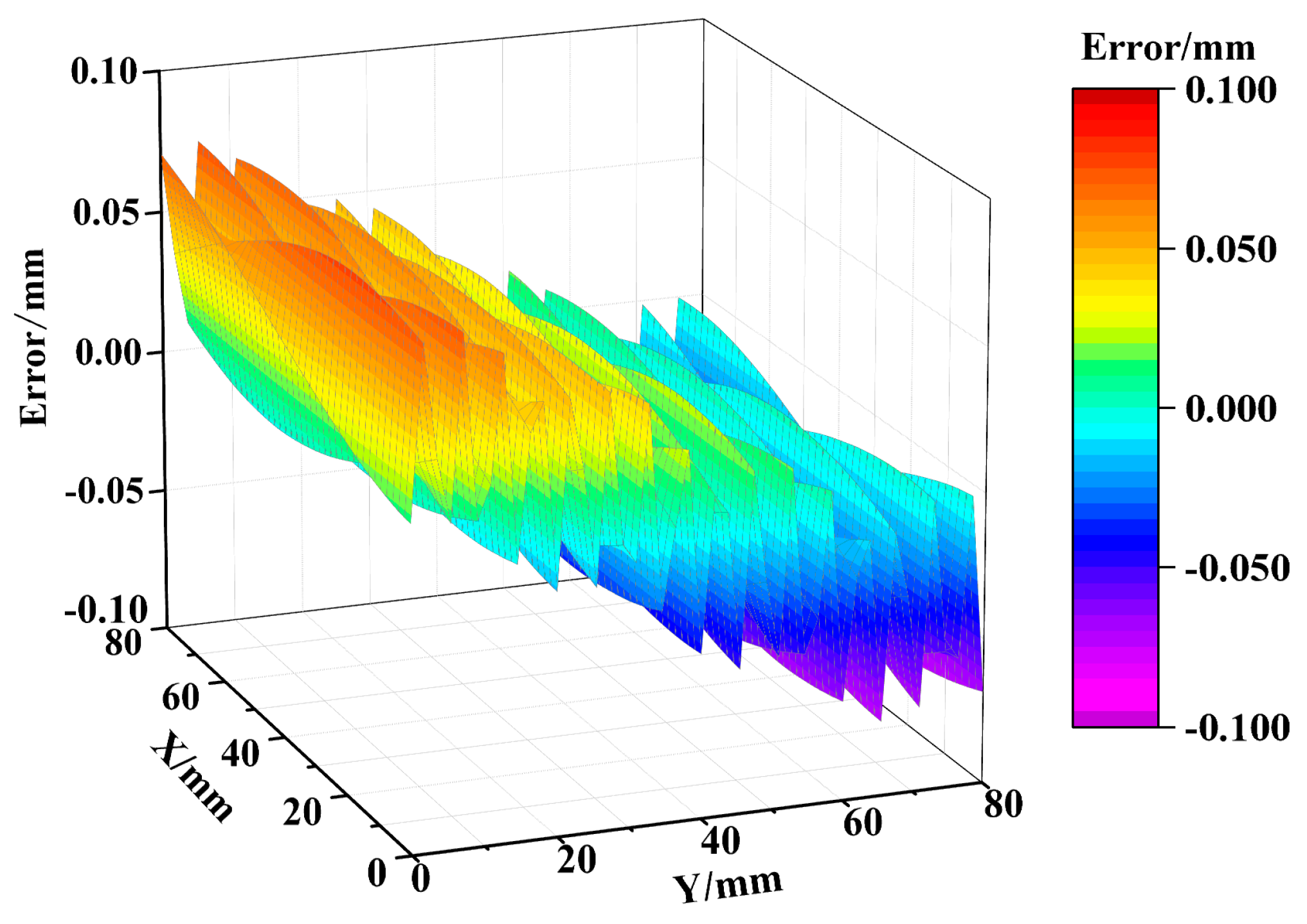
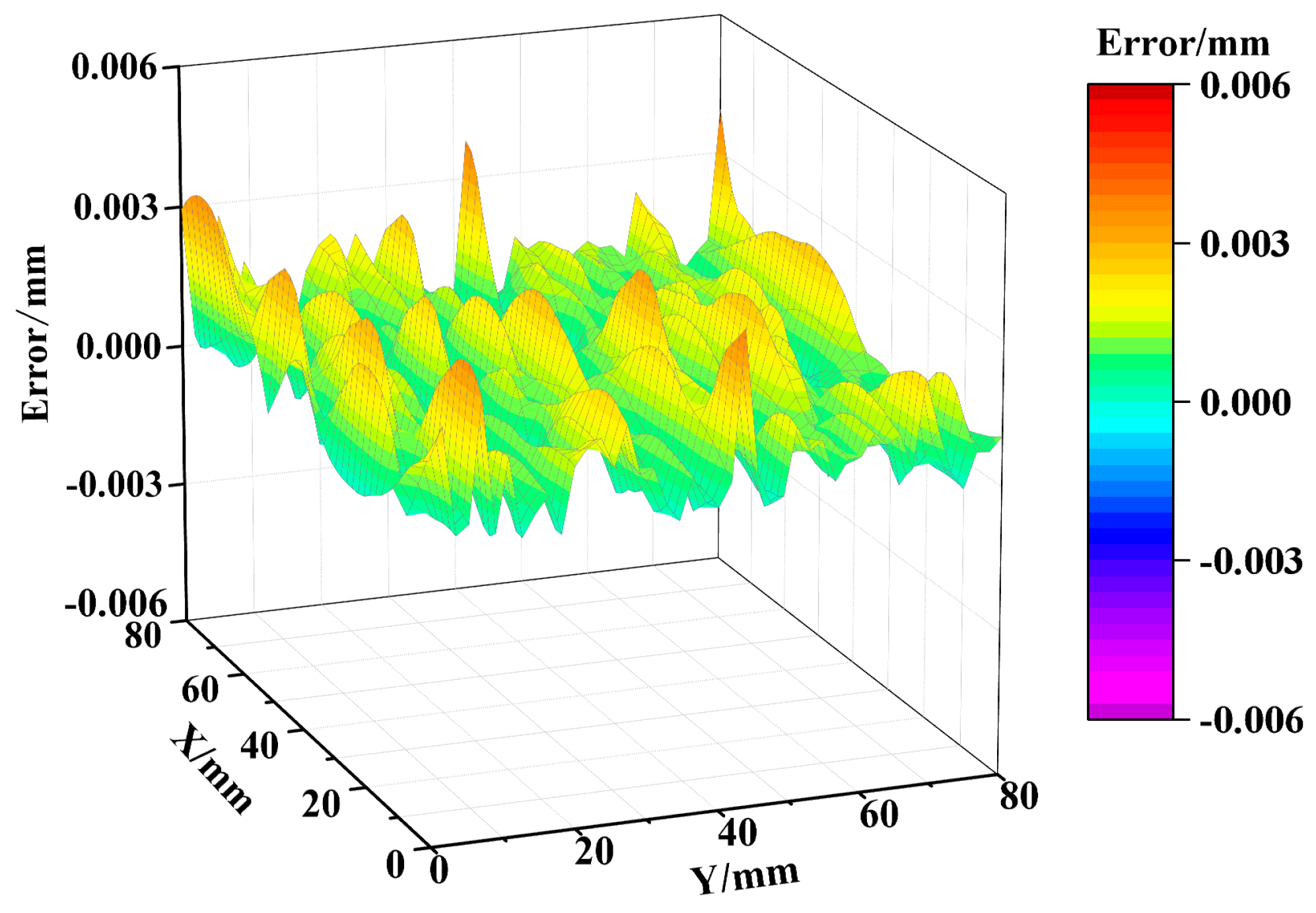
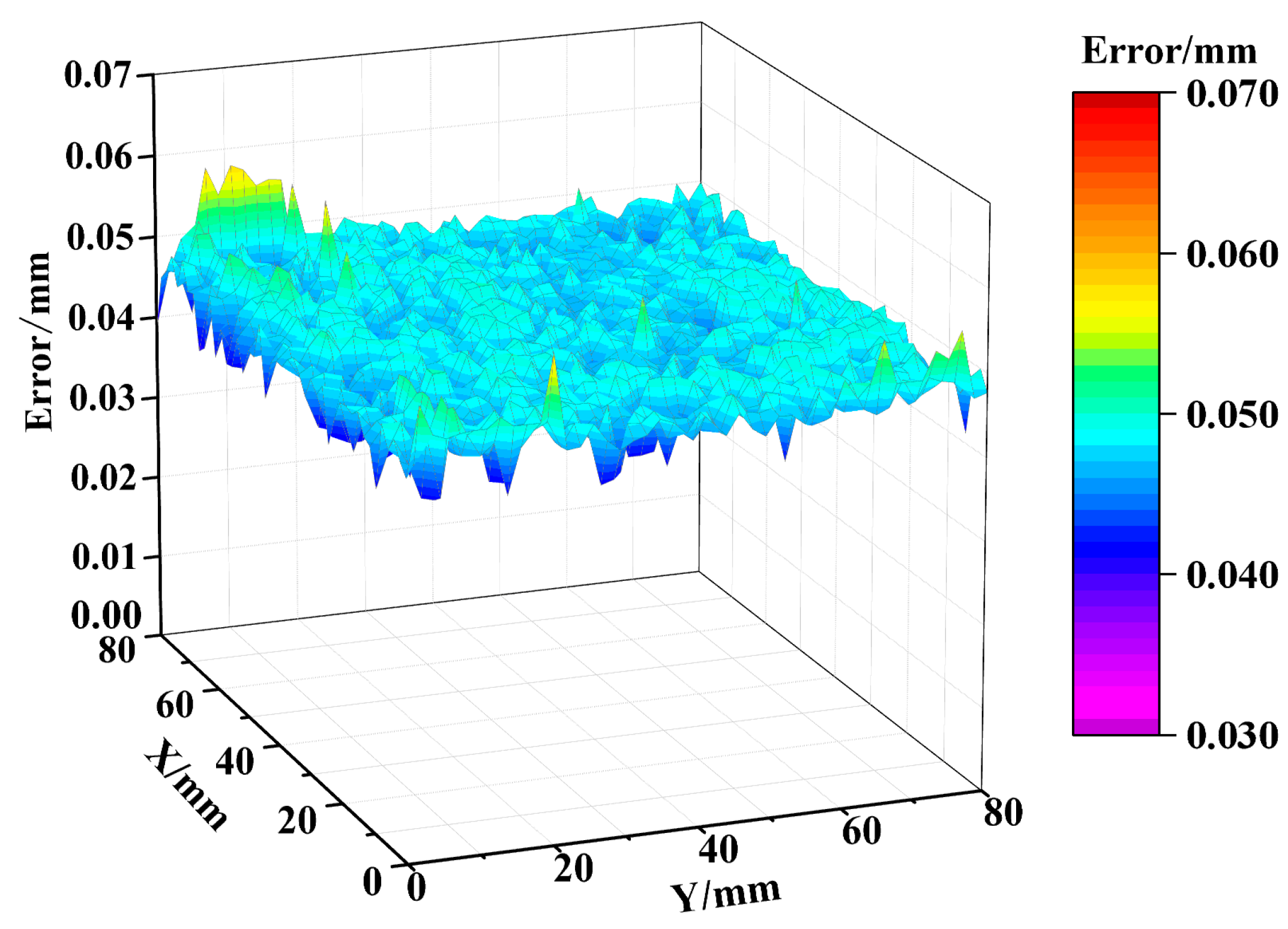
3.4. Simulation Results Analysis
4. Coarse-to-Fine Free-Form Surface Machining Error Decomposition and Compensation Experiments
4.1. CNC Machining and On-Machine Measurement Processes
4.2. Coarse-to-Fine Decomposition of the Original Machining Error Processes
4.3. Compensation for the Fine System Error
4.4. Measurement Experiment Using CMM
4.5. Data Analysis
- All three methods compensate for the error of each measurement point sequentially, and use the surface reconstruction method to make the tool trajectory in the compensated machining smoother, and thereby improve the machining accuracy of the part.
- Because the random error was more random, it was not easy to compensate for, and, because the processing error was relatively small, direct processing error compensation rather than only the system error compensation effect was good.
- According to the experimental data in Table 3 and Table 7, the more complete and accurate the decomposed system error was, the better the compensation effect. Compared with the VMD algorithm, the coarse-to-fine machining error decomposition method proposed in this paper was superior in its ability to decompose and compensate for machining errors.
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Poniatowska, M. Free-form surface machining error compensation applying 3D CAD machining pattern model. Comput. Aided Des. 2015, 62, 227–235. [Google Scholar] [CrossRef]
- He, J.M.; Luo, J.X.; Zhong, W.J.; Liu, Z.L.; Ding, K. Error source analysis and compensation method of CNC machine tools. Mod. Manuf. Technol. Equip. 2020, 2, 131–132. [Google Scholar] [CrossRef]
- Zhang, Z.; Jiang, F.; Luo, M.; Wu, B.; Zhang, D.; Tang, K. Geometric error measuring, modeling, and compensation for CNC machine tools: A review. Chin. J. Aeronaut. 2024, 37, 163–198. [Google Scholar] [CrossRef]
- Ge, G.Y.; Du, Z.C.; Feng, X.B.; Yang, J. An integrated error compensation method based on on-machine measurement for thin web part machining. Precis. Eng. 2020, 63, 206–213. [Google Scholar] [CrossRef]
- Liu, Y.; Wan, M.; Xing, W.J.; Xiao, Q.B.; Zhang, W.H. Generalized actual inverse kinematic model for compensating geometric error in five-axis machine tools. Int. J. Mech. Sci. 2018, 145, 299–317. [Google Scholar] [CrossRef]
- Li, Z.H.; Feng, W.L.; Yang, J.G.; Huang, Y. An investigation on modeling and compensation of synthetic geometric error on large machine tools based on moving least squares method. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2018, 232, 412–427. [Google Scholar] [CrossRef]
- Msaddek, E.B.; Baili, M.; Bouaziz, Z.; Dessein, G. Compensation of machining error of B spline and C spline. Int. J. Adv. Manuf. Technol. 2018, 97, 4055–4064. [Google Scholar] [CrossRef]
- Fu, G.Q.; Zhang, L.; Fu, J.Z.; Gao, H.; Jin, Y. F test-based automatic modeling of single geometric error component for error compensation of five-axis machine tools. Int. J. Adv. Manuf. Technol. 2018, 94, 4493–4505. [Google Scholar] [CrossRef]
- Wu, B.H.; Yin, Y.J.; Zhang, Y.; Luo, M. A new approach to geometric error modeling and compensation for a three-axis machine tool. Int. J. Adv. Manuf. Technol. 2019, 102, 1249–1256. [Google Scholar] [CrossRef]
- Chen, Y.P.; Tang, H.; Tang, Q.C.; Zhang, A.; Chen, D.; Li, K. Machining error decomposition and compensation of complicated surfaces by EMD method. Measurement 2018, 116, 341–349. [Google Scholar] [CrossRef]
- Lin, Z.X.; Tian, W.J.; Zhang, D.J.; Gao, W.; Wang, L. A method of geometric error identification and compensation of CNC machine tools based on volumetric diagonal error measurements. Int. J. Adv. Manuf. Technol. 2023, 124, 51–68. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, D.H.; Wu, B.H. An approach for machining allowance optimization of complex part with integrated structure. J. Comput. Des. Eng. 2015, 2, 248–252. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, J.; Ji, S.J. Thermal positioning error modeling of machine tools using a bat algorithm-based back propagation neural network. Int. J. Adv. Manuf. Technol. 2018, 97, 2575–2586. [Google Scholar] [CrossRef]
- Reddy, T.N.; Shanmugaraj, V.; Vinod, P.; Krishna, S.G. Real-time thermal error compensation strategy for precision machine tools. Mater. Today Proc. 2020, 22, 2386–2396. [Google Scholar] [CrossRef]
- Wei, J.; Jiang, L.; Liang, B. Geometric error compensation method of five-axis CNC machine tool based on improved genetic algorithm. J. Phys. Conf. Ser. 2024, 2825, 012029. [Google Scholar] [CrossRef]
- Zha, J.; Villarrazo, N.; de Pisson, G.M.; Li, Y.; Zhang, H.; de Lacalle, L.N.L. An accuracy evolution method applied to five-axis machining of curved surfaces. Int. J. Adv. Manuf. Technol. 2023, 125, 3475–3487. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, Z.S.; Zhou, Y.F.; Dai, M.; Shi, J.F. Stream of variation modeling and analysis for manufacturing processes based on a semi-parametric regression model. J. Mech. Eng. 2013, 49, 180–185. [Google Scholar] [CrossRef]
- Wang, G.; Li, W.L.; Tong, G.; Pang, C.-T. Improving the machining accuracy of thin-walled part by online measuring and allowance compensation. Int. J. Adv. Manuf. Technol. 2017, 92, 2755–2763. [Google Scholar] [CrossRef]
- Lee, W.; Lee, Y.; Wei, C.C. Automatic error compensation for free-form surfaces by using on-machine measurement data. Appl. Sci. 2019, 9, 3073. [Google Scholar] [CrossRef]
- Chen, Y.P.; Jin, L.; Lu, H.Y.; Feng, Z.J.; Chen, Y.H. Application of spatial statistical analysis in decomposition of machining errors for free-form surfaces. J. Beijing Inst. Technol. 2017, 37, 260–266. [Google Scholar] [CrossRef]
- Liu, R.N.; Xin, Y.Z.; Li, Y. Dynamic signature verification method based on Pearson correlation coefficient. Chin. J. Sci. Instrum. 2022, 43, 279–287. [Google Scholar] [CrossRef]
- Asuero, A.G.; Sayago, A.; González, A.G. The correlation coefficient: An overview. Crit. Rev. Anal. Chem. 2006, 36, 41–59. [Google Scholar] [CrossRef]
- Cohen, J. Statistical Power Analysis for the Behavioral Sciences; Routledge: New York, NY, USA, 1988. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational mode decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Zhang, X.; Miao, Q.; Zhang, H.; Wang, L. A parameter-adaptive VMD method based on grasshopper optimization algorithm to analyze vibration signals from rotating machinery. Mech. Syst. Signal Process. 2018, 108, 58–72. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.-C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Song, X.J.; Sun, H.W.; Zhan, L.W. Novel complete ensemble EMD with adaptive noise-based hybrid filtering for rolling bearing fault diagnosis. J. Vibroeng. 2019, 21, 1845–1858. [Google Scholar] [CrossRef]
- Lu, Q.; Pang, L.X.; Huang, H.Q.; Shen, C.; Cao, H.; Shi, Y.; Liu, J. High-G calibration denoising method for high-G MEMS accelerometer based on EMD and wavelet thresholding. Micromachines 2019, 10, 134. [Google Scholar] [CrossRef] [PubMed]
- Xie, B.; Xiong, Z.Q.; Wang, Z.J.; Zhang, L.; Zhang, D.; Li, F. Gamma spectrum denoising method based on improved wavelet thresholding. Nucl. Eng. Technol. 2020, 52, 1771–1776. [Google Scholar] [CrossRef]
- Chang, Y.; Bao, G.Q.; Cheng, S.K.; He, T.; Yang, Q. Improved VMD-KFCM algorithm for the fault diagnosis of rolling bearing vibration signals. IET Signal Process. 2021, 15, 238–250. [Google Scholar] [CrossRef]
- Li, S.L.; Zeng, L.; Feng, P.F.; Li, Y.; Xu, C.; Ma, Y. Accurate compensation method for probe pre-travel error in on-machine inspections. Int. J. Adv. Manuf. Technol. 2019, 103, 2401–2410. [Google Scholar] [CrossRef]
- Cheng, X.; Liu, X.P.; Feng, P.F.; Zeng, L.; Jiang, H.; Sun, Z.; Zhang, S. Efficient adaptive sampling methods based on deviation analysis for on-machine inspection. Measurement 2022, 188, 110497. [Google Scholar] [CrossRef]

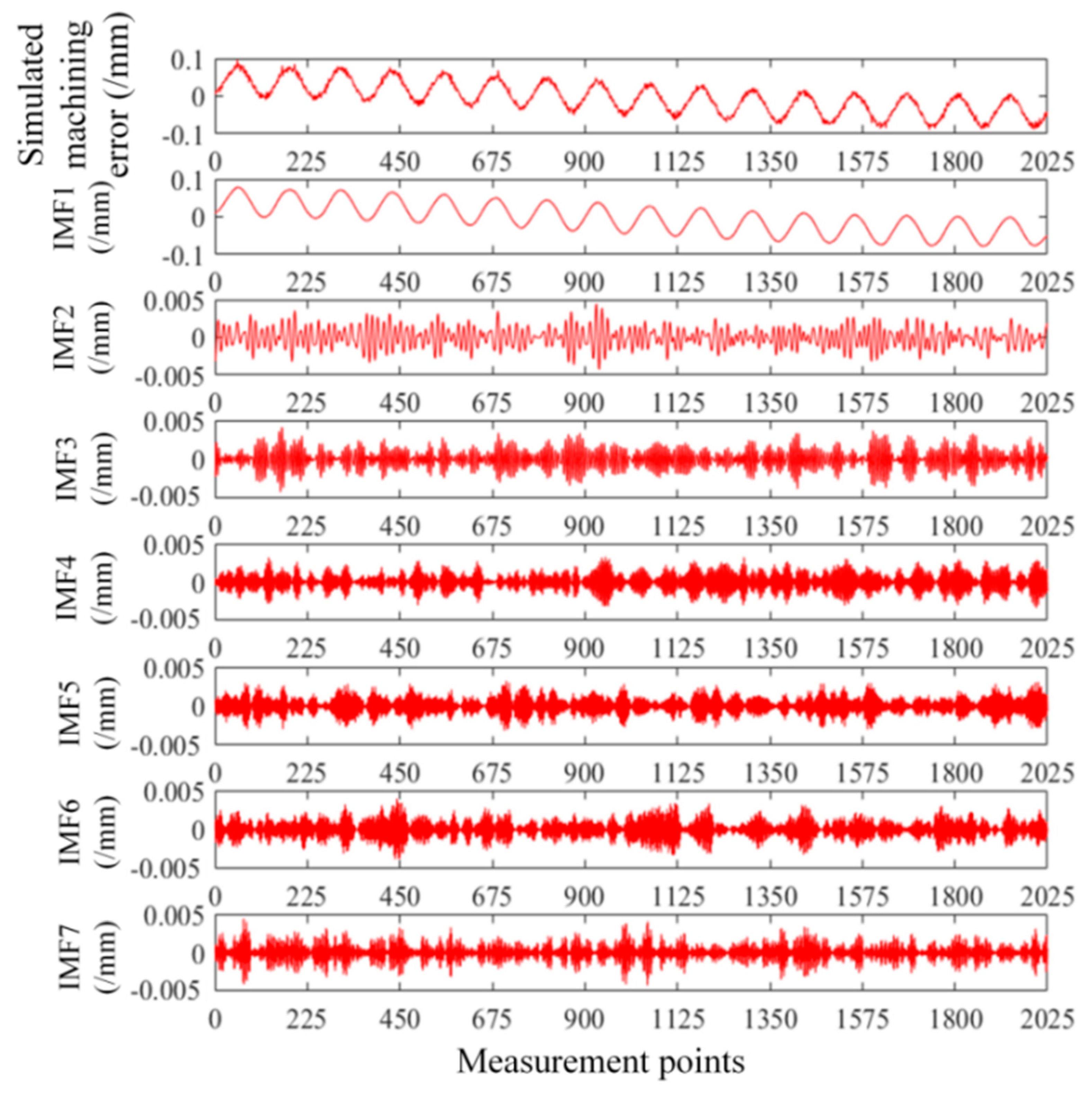




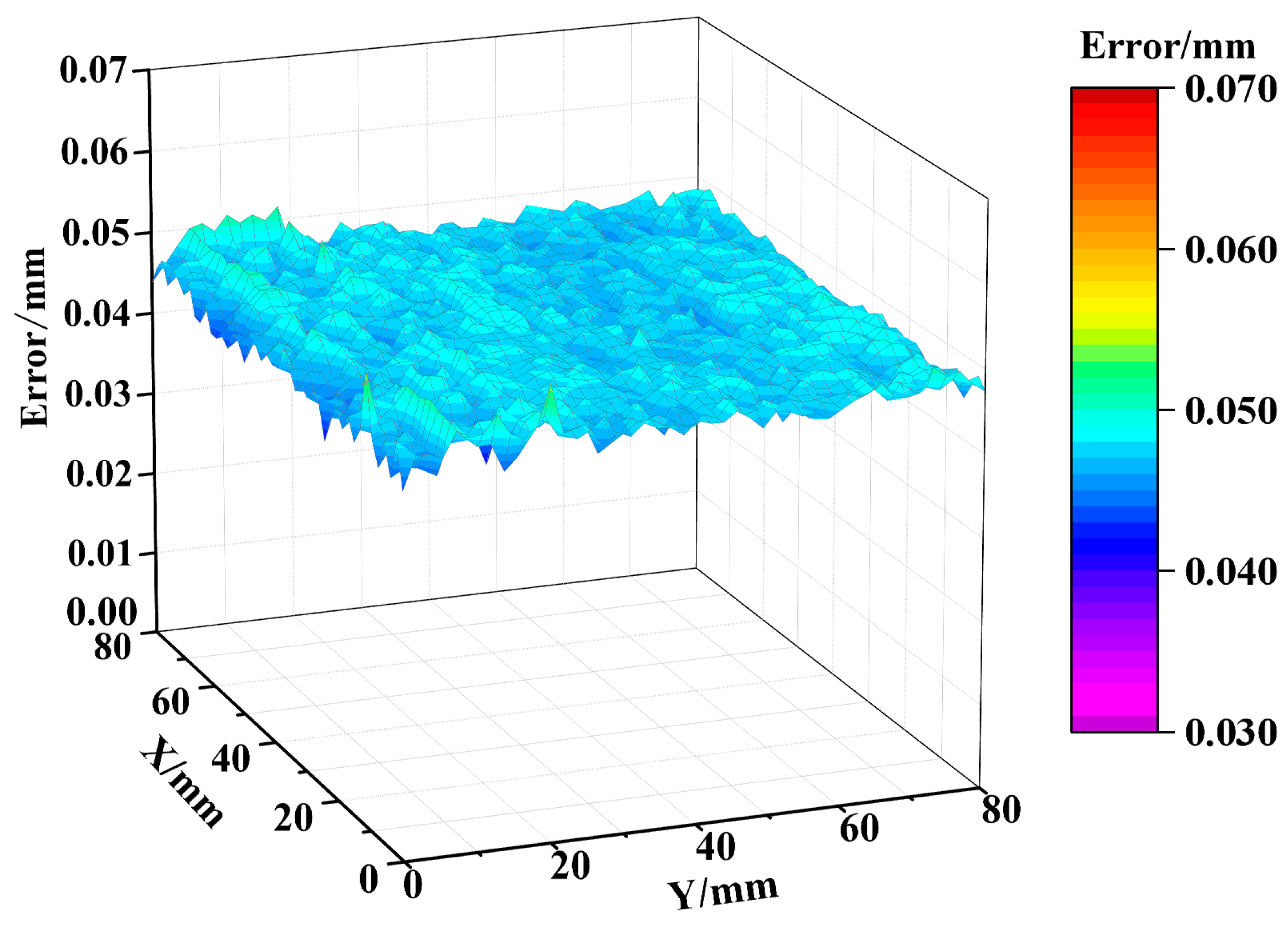
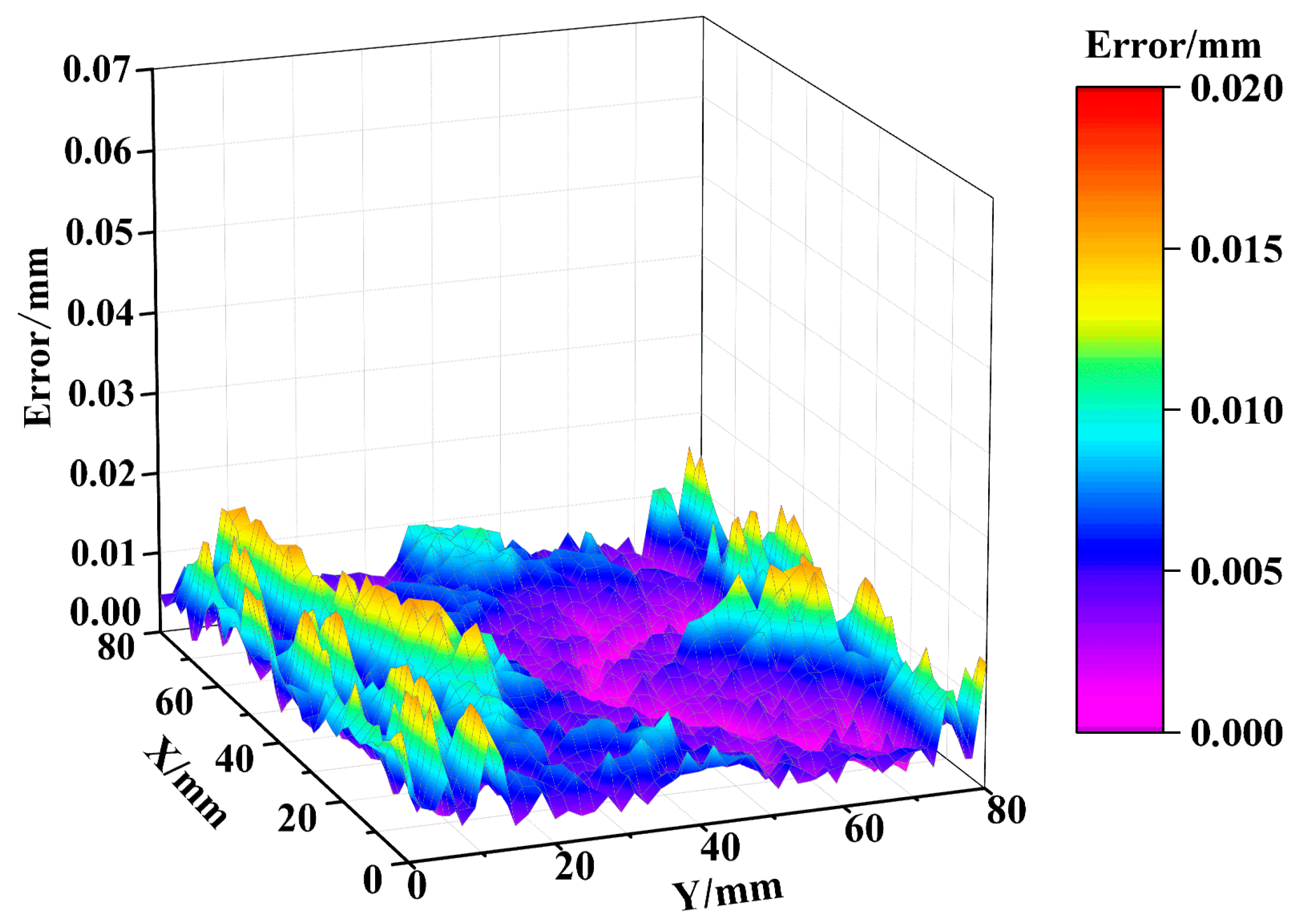


| IMF Component | IMF1 | IMF2 | IMF3 | IMF4 | IMF5 | IMF6 | IMF7 |
| correlation coefficient | 0.9931 | 0.1604 | 0.0743 | 0.0606 | 0.0546 | 0.0534 | 0.0537 |
| IMF Component | IMF1 | IMF2 | IMF3 |
| correlation coefficient | 0.7134 | 0.0342 | 0.7125 |
| Decomposition Methods | Correlation Coefficient | Maximum Absolute Error (mm) | Mean Absolute Error (mm) |
|---|---|---|---|
| VMD | 0.9991 | 0.0106 | 0.0015 |
| EMD | 0.9993 | 0.0088 | 0.0013 |
| Wavelet thresholding method | 0.9994 | 0.0083 | 0.0012 |
| Machining error decomposition method based on coarse-to-fine machining | 0.9998 | 0.0039 | 0.0008 |
| IMF Component | IMF1 | IMF2 | IMF3 | IMF4 | IMF5 | IMF6 | IMF7 |
| correlation coefficient | 0.4113 | 0.3893 | 0.2431 | 0.3775 | 0.2406 | 0.1158 | 0.3662 |
| IMF Component | IMF1 | IMF2 | IMF3 | IMF4 | IMF5 | IMF6 | IMF7 | IMF8 | IMF9 |
| correlation coefficient | 0.4688 | 0.3410 | 0.3160 | 0.3500 | 0.3369 | 0.1652 | 0.1511 | 0.1236 | 0.3650 |
| Detection Method | Before Machining Error Compensation | After Compensation for Machining Error | ||
|---|---|---|---|---|
| Maximum absolute machining error | Mean absolute machining error | Maximum absolute machining error | Mean absolute machining error | |
| On-machine measurement | 0.0580 | 0.0472 | 0.0159 | 0.0059 |
| CMM measurement | / | / | 0.0148 | 0.0055 |
| Mode of Compensation | Before Machining Error Compensation | After Machining Error Compensation | ||
|---|---|---|---|---|
| Maximum absolute machining error | Mean absolute machining error | Maximum absolute machining error | Mean absolute machining error | |
| Machining error direct compensation method | 0.0575 | 0.0435 | 0.0201 | 0.0124 |
| Machining error decomposition and compensation method based on VMD algorithm | 0.0594 | 0.0449 | 0.0186 | 0.0082 |
| Coarse-to-fine machining error decomposition and compensation method | 0.0580 | 0.0472 | 0.0159 | 0.0059 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Wang, J.; Tang, Q.; Li, J. A Study on the Coarse-to-Fine Error Decomposition and Compensation Method of Free-Form Surface Machining. Appl. Sci. 2024, 14, 9044. https://doi.org/10.3390/app14199044
Chen Y, Wang J, Tang Q, Li J. A Study on the Coarse-to-Fine Error Decomposition and Compensation Method of Free-Form Surface Machining. Applied Sciences. 2024; 14(19):9044. https://doi.org/10.3390/app14199044
Chicago/Turabian StyleChen, Yueping, Junchao Wang, Qingchun Tang, and Jie Li. 2024. "A Study on the Coarse-to-Fine Error Decomposition and Compensation Method of Free-Form Surface Machining" Applied Sciences 14, no. 19: 9044. https://doi.org/10.3390/app14199044
APA StyleChen, Y., Wang, J., Tang, Q., & Li, J. (2024). A Study on the Coarse-to-Fine Error Decomposition and Compensation Method of Free-Form Surface Machining. Applied Sciences, 14(19), 9044. https://doi.org/10.3390/app14199044






