Abstract
The fundamental period is one of the most important parameters for the design of new structures as well as for estimating the capacity of existing ones. Thus, to estimate it, various design codes and researchers have adopted several approximate analytical equations based on a number of key structural parameters. To this end, the present study introduces a novel methodology for deriving the analytical equations for the fundamental period of reinforced concrete structures. The methodology is based on machine learning explainability techniques, specifically the so-called SHapley Additive exPlanations values. These values are commonly employed as an explainability tool. However, in the proposed novel approach they are employed as a basis to fit analytical curves, which allows the resulting equations to be constructed sequentially and in an informed manner while controlling the balance between accuracy and complexity. An extended dataset consisting of 4026 data points is employed, on which a Gradient Boosting Machine model is fitted. The model achieves excellent accuracy, with a coefficient of determination , while the equations derived from the proposed formulation achieve an and Mean Absolute Error . This demonstrates the potential applicability of the proposed methodology in a wide array of similar engineering challenges.
1. Introduction
The Fundamental Period (FUP) of buildings is a very important parameter in the context of new structures’ seismic design. Moreover, it is a crucial feature that can be used to determine existing buildings’ seismic capacity [1,2]. The design spectrum of available seismic codes in combination with the estimated FUP can lead to the determination of the forces introduced by a seismic excitation in a building, i.e., the calculation of the seismic base shear. Furthermore, the FUP is a crucial feature that can be employed under the corresponding acceleration spectrum for near-real-time estimation of the seismic forces introduced on buildings by a strong seismic excitation. In this way, the level of seismic damage can be macroscopically estimated and documented [3,4].
However, as is well known, calculation of the fundamental period requires the solution of an eigenvalue problem. The formulation and solution of this problem under the finite elements’ framework requires knowledge of the values of numerous parameters to be used in estimating the stiffness and mass matrix of the building [5,6]. Furthermore, in the design of new buildings, the values of the above parameters cannot be known before the final design. Therefore, it is particularly useful to develop approximation methods for estimating FUP. This can be achieved by considering only some of the problem’s parameters that can be easily calculated at the design stage of new buildings, or by directly estimating them by working on already existing buildings, e.g., buildings for which a rapid assessment of their seismic capacity has been performed before or after a strong seismic excitation.
In particular, for the case of new reinforced concrete (RC) buildings, in recent decades the respective design codes [7,8,9,10,11,12,13,14,15,16,17,18] have globally incorporated approximate equations for the estimation of FUP, recognizing its usefulness in the design process. However, in addition to these codes, the formulation of approximate equations for the calculation of the fundamental period has been the subject of a significant number of research papers [19,20,21,22,23,24,25,26,27,28,29,30,31,32,33]. These research studies have utilized instrumental measurements of buildings during strong seismic excitations as well as measurements of ambient vibrations. In addition, numerical finite element models have been used to increase the number of buildings from which the FUP equations have been developed. The obtained results have been used both to document the existing approximate equations of the codes and to improve them.
One of the parameters that can significantly affect the value of the fundamental period is the masonry infill. Through a series of numerical and experimental researches, it has been shown that masonry infills can significantly increase the horizontal stiffness of RC buildings, resulting in a significant change in the seismic forces that they receive. Thus, specific study to assess the influence of masonry infills on the FUP approximation equations has been the subject of a significant number of research papers [34,35,36,37,38,39,40,41,42,43,44].
Statistical processing of instrumental measurements or results obtained from computational analyses is a basic research approach aiming at the formulation of approximate equations for the estimation of FUP in RC buildings. This can be done with or without masonry infills. In this approach, the problem is reduced to the processing of available databases containing values of the fundamental periods of buildings with different structural characteristics. In this regard, the recent rapid increase in the use of machine learning (ML) algorithms for solving civil engineering problems [45,46,47,48,49] has provided a new perspective on the investigation of equations for estimating the fundamental periods of RC buildings with masonry infills (RCB_MI). The inherent ability of ML algorithms to handle large volumes of data and their potential in modeling multiparametric cases [50,51,52,53,54] have led to their engagement as the main modeling tools for the estimation of FUP in infilled RC buildings. This has led to different research efforts over the last several years, a brief review of which is presented below.
Kose [55] developed relationships for calculating the fundamental period of masonry infilled buildings using a multiple Linear Regression model. To investigate the structural parameters that most influence the value of the fundamental period, he performed sensitivity analyses using a feed-forward artificial neural network (ANN) with one hidden layer. In this way, he derived models that correlate the FUP with the height, the percentage of RC walls, and the percentage of masonry infills of the buildings. The employed dataset consisted of 189 data points generated using a 3D finite element approach.
On the other hand, Asteris developed a much more extended dataset [56] consisting of 4026 data points, which was suitable for training ML algorithms to develop simplified equations for estimating the fundamental period of RCB_MI. This dataset has been used by other researchers, and is briefly described in Section 2.1 of the present paper. Asteris et al. [57] used the above dataset [56] to train feed-forward ANNs with one or two hidden layers. The developed model offered values for the fundamental period of infilled RC buildings. These values have been compared with the ones derived from the equations suggested by the codes with the comparisons showing that the correlation between the FUP and the structural parameters (e.g., the buildings’ height, the number and the length of their openings, and the strength and percentage of masonry infills) leads to more realistic results than correlation of the fundamental period with the height of the building, as proposed by most available codes. In a later study, Asteris and Nikoo [58] used the aforementioned dataset [56] to train feed-forward ANNs which were optimized via an artificial bee colony optimization algorithm. Using this methodology, they obtained high correlation coefficients between the considered structural parameters (building height, number and length of openings, strength and percentage of masonry infills) and the fundamental period.
Similar to Asteris et al. [56,58], Charalampakis et al. [59] employed the same dataset [56] to train feed-forward ANNs with a different architecture consisting of two or three hidden layers, which can be considered too complicated for a general model. They extended their work by applying the M5Rules algorithm, which belongs to the group of decision tree learners. They finally arrived at a set of simplified equations for computing the fundamental period as a function of the number of stories, the stiffness of the infill walls, and the frames’ span length. They derived separate equations for different masonry infill ratios (opening ratio from 0% for bare frames to 100% for fully infilled RC frames) and a single equation for all masonry infill rates (opening ratios).
Deviating from the work of Asteris et al. [56,58] and Charalampakis et al. [59], in which ANNs were employed, Somala et al. [60] applied a series of ML algorithms (linear regression, ridge regression, k-nearest neighbors, support vector regression, random forest, decision tree, extreme gradient boosting, and adaptive boosting) using the same training dataset created by Asteris [56]. In their study, they reached the main conclusion that the XGBoost algorithm is the most effective algorithm for predicting the value of the FUP. Moreover, they concluded that the number of stories is the most important structural parameter. This conclusion is consistent with the choice of most codes to relate the FUP to the height of RC buildings.
Based on the same Asteris dataset [56], Mirrashid and Naderpour [61] experimented with the use of Fuzzy Logic, which combines rigorous mathematical modeling with the experience of experts. They compared a feed forward neural network model with one hidden layer and a Neuro Fuzzy (ANFIS) model [62] and they tried to derive equations for computing the FUP values. One of their most remarkable conclusions was that the most effective parameter for calculating the fundamental period was the masonry infill ratios of the frames (opening ratios).
Yahiaoui et al. [63], also working on the Asteris training dataset [56], focused on the so-called boosting ensemble technique and employed three ML models, namely, LightGBM, Gradient Boosting Decision Trees, and CatBoost. Moreover, by applying the “Multivariate Adaptive Regression Spline” technique, they arrived at an approximate equation for computing the FUP values. From the comparisons they made with similar relations from the literature, they concluded that the combined use of the LightGBM model and the Multivariate Adaptive Regression Spline technique leads to the most efficient relation both in terms of the level of accuracy and avoidance of overfitting effects.
Thisovithan et al. [64] compared the outcome of four ML algorithms (artificial neural network, k-nearest Neighbors, support vector regression, and random forest). Emphasizing interpretability, they employed three different explainability techniques, namely, SHAP, Local Interpretable Model-Agnostic Explanations (LIME), and Partial Dependence Plots (PDPs), to analyze the predictions of their models. It should be clarified that such post hoc explainability methods analyze and interpret the decision-making process of a trained model after it has made predictions, providing insights into how the model arrived at its outputs. In addition, the authors developed an (explainability) XAI-based user interface [65] through which it is possible to input the appropriate structural data/parameters and automatically extract the estimated fundamental period. Using this application, it is possible to achieve the selection of structural parameters in real time in order to optimize the design of the infilled RC frames and interpret how each structural parameter influences the final result.
This research has strong elements of novelty, as it introduces an explainable modeling approach using the SHapley Additive exPlanations (SHAP values) technique. The SHAP machine learning explainability methodology is used to provide interpretable analytical equations that approximate the behavior of the underlying ML model. They quantify each feature’s importance based on the predictive power that it contributes, thereby accounting for complex feature interactions. They employ game theory to assign credit to each feature or feature value, resulting in good prediction capacity on the part of the developed model. The way SHAP works is to decompose the output of a model by summing the impacts of each feature. As shown in Section 2.4, SHAP values are feature attribution methods, i.e., they analyze the predictions of ML models into components pertaining to each individual feature. However, in the currently established literature this methodology is employed as an explainability tool, i.e., to quantify the effect of each input parameter on the model’s prediction [60,64]. In our proposed formulation, SHAP values are not only used in this regard; in addition, departing from the currently established literature, they are also employed as a basis for the creation of interpretable and simplified analytical equations that approximate the behavior of the underlying ML model.
Thus, the benefit of the proposed formulation is threefold: first, the analytical equations are derived independently and sequentially; second, again by utilizing the SHAP values, features are inserted into the simplified model in an informed manner starting from the most important; lastly, as determined by the specific application at hand, this allows for the determination of a controlled tradeoff between accuracy and model complexity.
2. Materials and Methods
2.1. Dataset Description
The dataset employed in the present study is the so-called “FP4026 Research Database” introduced by Asteris in 2016 [56]. The dataset consists of 4026 data points, corresponding to infilled reinforced concrete plane frames. For each frame, five structural parameters were recorded: (1) the number of stories, (2) the number of spans, (3) the length of the spans, (4) the stiffness of the masonry walls, and (5) the opening percentage, i.e., the percentage of the panel area covered by the infill walls. The corresponding fundamental period was estimated using the Seismostruct Finite Element Package [66]. The modeling of the infill walls followed the equivalent strut nonlinear cyclic formulation introduced by Crisafulli [67].
The material properties and dimensions of the frames affect the overall stiffness, and consequently the fundamental period. In this dataset, the concrete corresponded to C25/30 (25 MPa compressive strength and 31 GPa modulus of elasticity), while the steel in the reinforcement bars had a strength of 500 MPa, corresponding to B500c. The dimensions of the structural members were designed based on EN1998-1 [7]. The beams and slabs had constant dimensions (250/600 and 150 mm, respectively) for all frames. The dimensions of the columns varied with the number of stories, although this variation was not one of the parameters considered in this study.
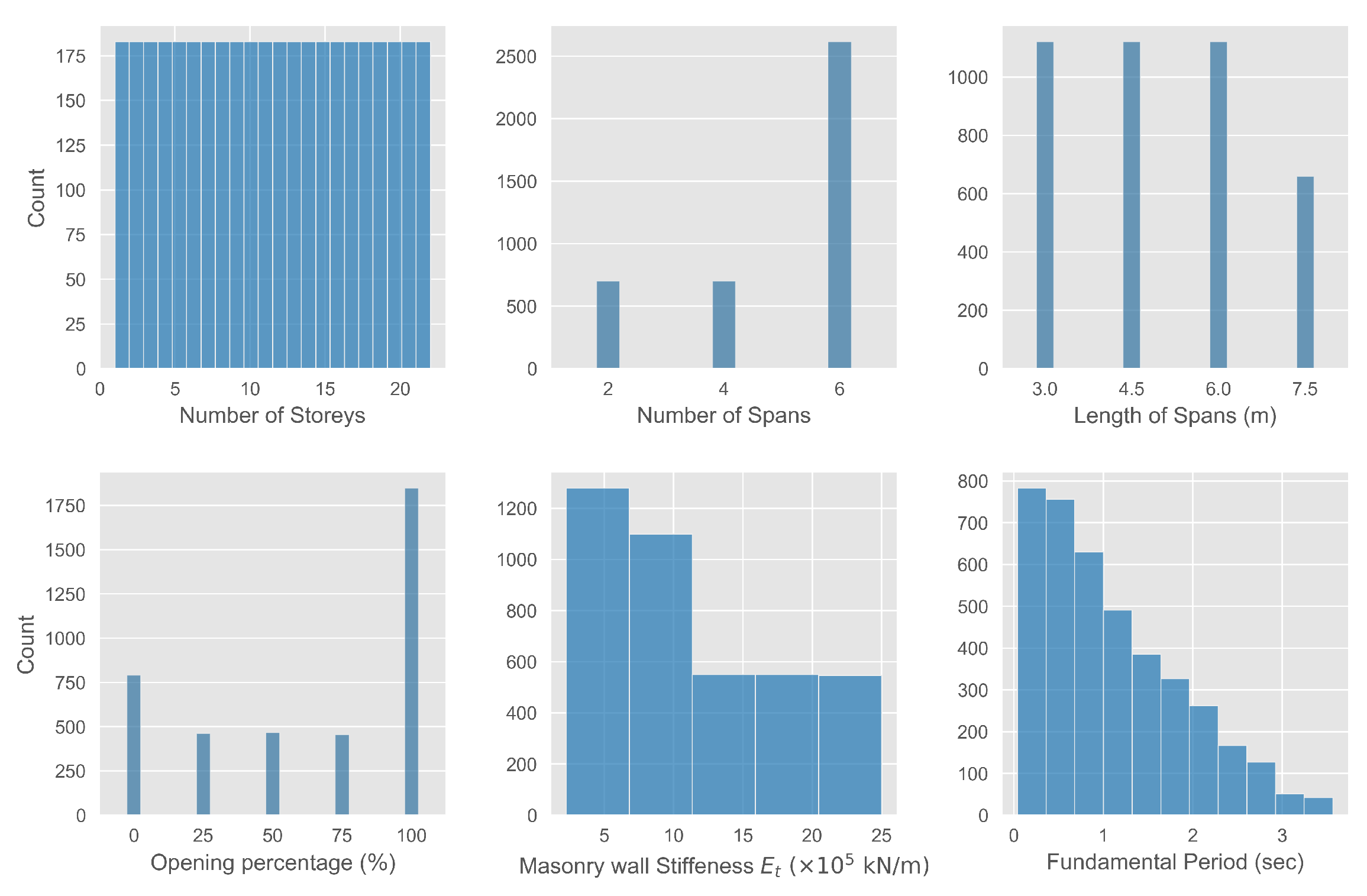
Figure 1 shows the distributions of the five measured structural parameters along with the estimated fundamental period. The number of stories ranged uniformly between 1 and 22, while the number of spans was either 2, 4, or 6, with the majority of the frames (65%) having six spans. The corresponding length of the spans was uniformly distributed between 3, 4.5, and 6 meters, with a smaller number of structures having 7.5 m span length. The masonry wall stiffness ranged from 2.25 to 25 × kN/m, while the corresponding opening percentage ranged from 0 to 100%, with approximately 46% of the cases corresponding to bare frames.
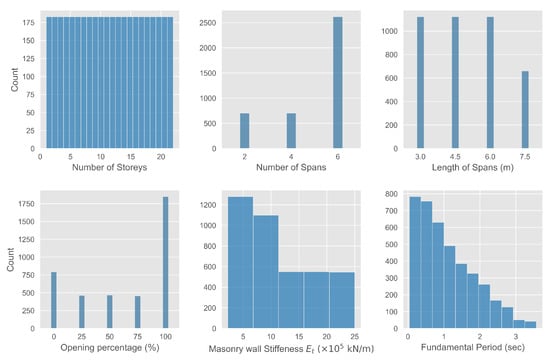
Figure 1.
Distributions of the considered structural parameters and estimated fundamental period.
2.2. Data Preprocessing
Following the above observations, we preprocessed the available dataset as follows. First, we scaled the opening percentage to the [0, 1] range to ensure that its values were not much larger than the rest of the features. Subsequently, we transformed the given fundamental period using the natural logarithm to ensure that the regression models output strictly positive values when using the inverse exponential transformation. Finally, even though 46% of the cases were bare frames, the corresponding data points had values for the masonry wall stiffness that covered the entire range of that feature, resulting in data points that do not make physical sense. From a mathematical point of view, any regression model trained using these data points would be trained on non-physical data points. Thus, we removed the corresponding stiffness values, treating them as NaNs (“not a number”, i.e., missing values). As examined in the sequel, this modeling decision affects the choice of regression models as well as the computation of SHAP values.
2.3. Machine Learning Modeling
While it is possible to try to compare all available algorithms with the potential to offer high accuracy, the most important aim of our research team is not to find the “one and only optimal model” for a specific dataset and another “optimal” model for another dataset; a more realistic target is to develop an easily adjustable model with low complexity that can effectively generalize with high accuracy while avoiding overfitting. This can be ensured by employing explainability techniques, which we do in this study by estimating the respective SHAP values. This approach can lead to the development of simplified analytical equations. Thus, our trained ML model must exhibit a sufficiently high accuracy level to ensure the obtained SHAP values are reliable without overfitting to the available dataset. There are many available regression models in the literature that can help in achieving this goal.
In this study, we employ a Gradient Boosting Machine [68], which offers several advantages. First, it is a powerful algorithm that combines a group of “weak models” to produce an ensemble model through an iterative procedure known as boosting [68]. In boosting, the errors from each iteration are used as input in the next. Specifically, the algorithm employs the learning function in Equation (1) [68]:
where are “weak models” (usually decision trees, although other models have been employed as well [69]), are the learned parameters of each individual model, are the learned weights used for ensembling, and N is the user-defined maximum number of base models. In the present study, we use a maximum number of trees, each with a maximum depth of 5.
The models’ hyperparameters are typically determined through a trial-and-error approach. As already mentioned, the aim of this study is not to identify the “best” model, but rather a model with a sufficient balance between high accuracy and low complexity to avoid overfitting to a particular dataset.
One of the advantages of the employed algorithm compared to other widely employed models, e.g., ANNs, is that it natively supports Not a Number (NaN) values, which, as mentioned previously, we introduced into the dataset as part of the preprocessing. These NaN values are somewhat restrictive as regards the choice of regression model, as not all algorithms support them; however, they have two distinct advantages. On the one hand, they are conceptually correct; on the other, SHAP values, which are central to our formulation, are able to model NaN values exactly, as we discuss in the sequel. A second benefit is that tree-based algorithms are not susceptible to features with different scales; thus, it is not necessary to scale the features. Finally, an additional computational advantage of the employed ML model is that its tree-based structure allows for efficient computation of the SHAP values, which can be a time-consuming process in general [70].
2.4. Shapley Additive Explanations (SHAP)
SHapley Additive exPlanations (SHAP) is a machine learning explainability technique recently developed by Scott Lundberg [71]. Intuitively, SHAP values decompose the ML model’s predictions into a summation of terms corresponding to each individual feature by extending the so-called Shapley values [72], first proposed by Lloyd Shapley in 1951 in the context of cooperative game theory. Formally, given a trained ML model f, a local approximation g is defined as follows (Equation (2) [71]):
where m is the number of features, is the mean model prediction, are the SHAP values, and is the so-called “simplified input” [71], i.e., a binary vector for which the value shows whether or not the corresponding feature is missing. Thus, for each data point, the model’s predictions are decomposed into terms pertaining to each individual term along with a constant term, i.e., the average prediction. Importantly, SHAP values satisfy a property called missingness [71], which states that features with missing values have no contribution to the model, i.e., (Equation (3) [71]):
Following the notation of Lundberg and Su-In Lee [71], let be the complete feature set that was employed by the model and let be a subset; then, the coefficients are provided by the following Equation (4) [71]:
The intuitive interpretation of the above equation is that the SHAP values are a weighted average over all possible feature combinations of the gain in the model’s prediction when feature i is included. From the above, it is apparent that if the underlying ML model has high enough accuracy, then the sum of the corresponding SHAP values will be close to the true target values.
3. Results
As previously stated, the aim of this study is to employ explainability techniques, in particular SHAP values, to derive simple, analytical, and additive formulas for estimating the fundamental period. To ensure that these SHAP values are reliable, they must be derived from an ML model that has not overfitted to the available dataset. Similarly, the trained ML model must have high enough accuracy that its predictions closely resemble the truth.
Thus, in the first part of this section, Section 3.1, we present the results of our fitted ML regression model that was presented in Section 2.3. We use well-known regression metrics to measure its performance and assess its reliability. Subsequently, in Section 3.2 we present the main results of this study, demonstrating how SHAP values can be employed to provide simplified analytical equations that can be used in lieu of complex ML models. We also demonstrate how these equations can be obtained in an incremental manner, which is important in allowing complexity to be added or removed according to the desired level of accuracy.
3.1. Machine Learning Regression
As mentioned in Section 2.3, we employed a Gradient Boosting machine learning model for the regression task, using a maximum number of trees, each with a maximum depth of 5. We arrived at this configuration using a trial-and-error approach, in which these hyperparameters achieved excellent accuracy without an enormous amount of complexity. The computations were carried out on a PC with an AMD Ryzen 12-Core Processor utilizing 16 GB of RAM. The model required approximately 0.11 seconds of training time. We trained the model using a so-called 75–25 split, i.e., 75% of the dataset was randomly selected for training and the remaining 25% was used to gauge the model’s performance on truly unseen data. We used the well-known regression metrics of Mean Absolute Error (MAE), Root Mean Squared Error (RMSE), and Coefficient of Determination . Their corresponding formulae are shown in Table 1. Table 2 summarizes their computed values on both the training and testing datasets in the log-transformed space as well as the original space by using the inverse exponential transformation.

Table 1.
Formulae of the employed regression metrics; the true and predicted values are denoted by and , respectively, while N denotes the total number of data points.

Table 2.
Regression metrics of the fully trained ML model on the training and test datasets.
It can be readily observed that the trained ML model achieved excellent performance in both the log-transformed and original spaces, with values of equal to and , respectively. In addition, the performance was similar between the training and test dataset in both cases, indicating that the model did not overfit. Finally, the values of MAE and RMSE were low and relatively close to each other, indicating that the trained model did not have very many large values in its errors. Such errors are accentuated when squared in the calculation of RMSE; thus, this effect manifests in a large discrepancy between RMSE and MAE, which is not present in our case.
3.2. Regression Using SHAP
In this section we present the main results of our proposed methodology, which focus on employing SHAP values to obtain analytical equations that approximate the predictions of the trained ML model. Furthermore, these equations can be constructed in an incremental manner, allowing accuracy to be increased at the cost of adding more terms that increase the complexity of the equations.
To this end, we first obtained the SHAP values for each feature and for each data point in the training set. We opted to compute these values on the training and test set separately because we wanted to utilize them to “train” our simplified equations and subsequently test them on the unseen test dataset. The execution time for the computation of SHAP main effects was low, requiring approximately 0.29 s on the aforementioned hardware. Subsequently, we aggregated them using the mean absolute value and normalized the results to obtain the percentages, i.e., we computed the following Equation (5):
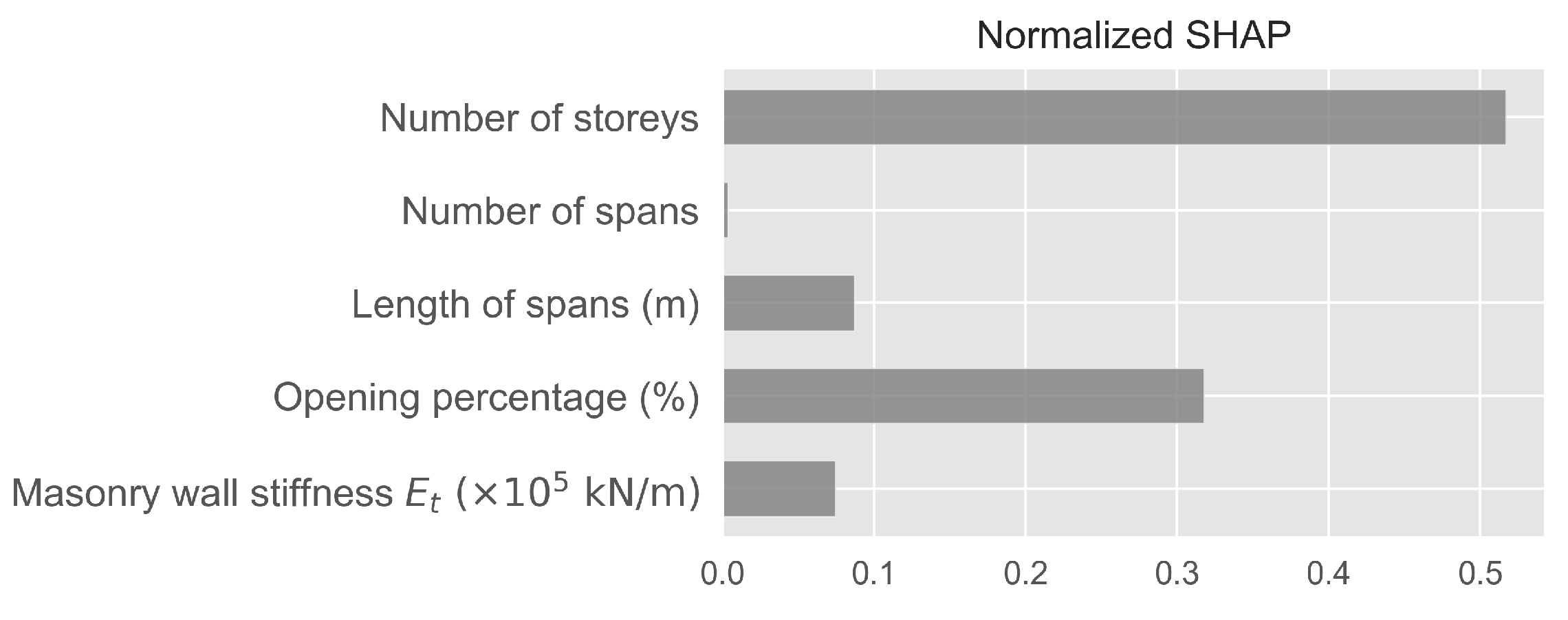
where are the SHAP values of the feature for the data point, N is the total number of data points and M is the total number of features. The results are shown in Figure 2. As can be readily observed, the most important features by far were the number of stories and the opening percentage of the panels, with an overall importance of approximately 50% and 30%, respectively. The stiffness of the masonry walls and the length of the spans had an overall effect of approximately 7–8%, respectively, while the influence of the number of spans was negligible.
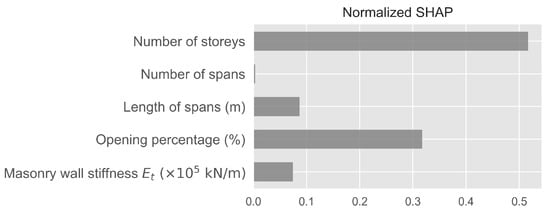
Figure 2.
Normalized SHAP values as in Equation (5).
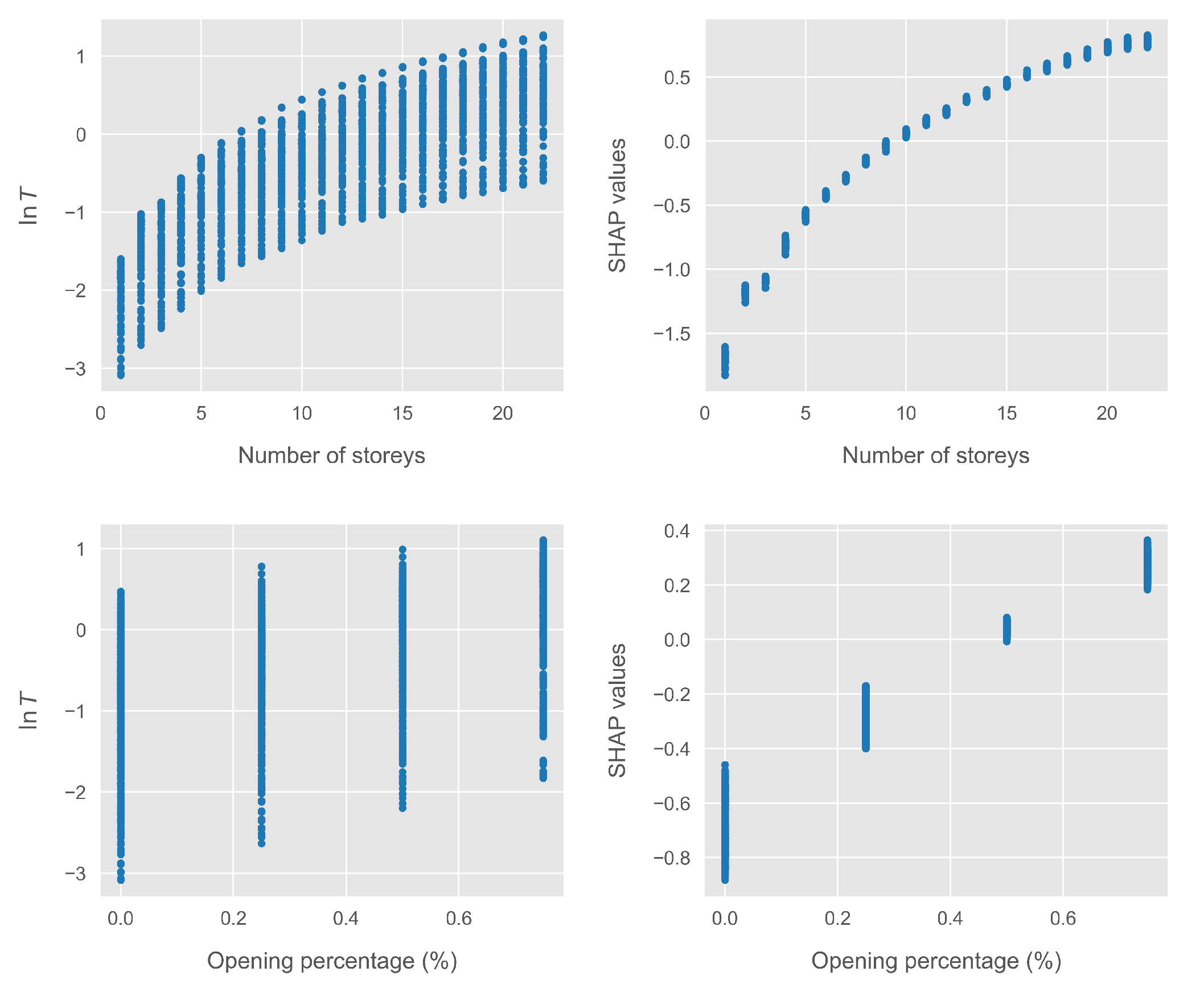
The core of the proposed formulation lies in providing analytical approximations to the obtained SHAP values. As discussed in Section 2.4, the SHAP values are additive and sum to the predictions of the ML model. Thus, the advantage of our proposed formulation becomes apparent, as it is possible to approximate the SHAP values of each individual feature and add as many terms as required to obtain the desired level of accuracy, guided by the feature importance hierarchy shown in Figure 2. The form of each individual analytical approximation is determined by the corresponding plot of the SHAP values. To demonstrate this, Figure 3 presents the scatter plots of the top two features, namely, the number of stories and the opening percentage, compared with the corresponding plots of the log-transformed fundamental period. For the opening percentage, we present the SHAP values corresponding to 0, 25, 50, and 75% opening percentage, as the bare frame case is treated separately.
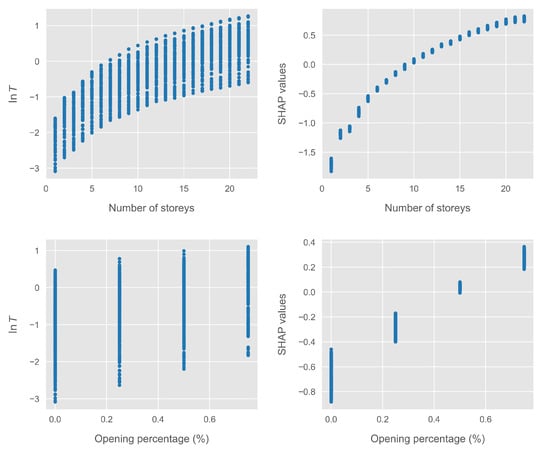
Figure 3.
Scatterplots of the SHAP values of the top two features compared with the corresponding plots of the log-transformed fundamental period.
First, it can be readily observed that while the log-transformed period has a significant variance for a fixed value of number of stories, the corresponding SHAP values exhibit a much smaller variance. Thus, an analytical curve fitted to the SHAP values instead of the raw data provides a much more accurate representation of the contribution of this feature to the output. The corresponding SHAP values for the opening percentage exhibit a somewhat larger variance. This is attributed to feature interaction, i.e., variation of the contribution of one feature in dependence on the value of a different feature [73]. Such interaction effects can be more accurately captured using SHAP interaction values [70]. However, this adds significant complexity to the derived equations. As shown below, in our case the derived equations achieved excellent accuracy; thus, as our aim was to derive simple analytical equations, this additional complexity was not justified.
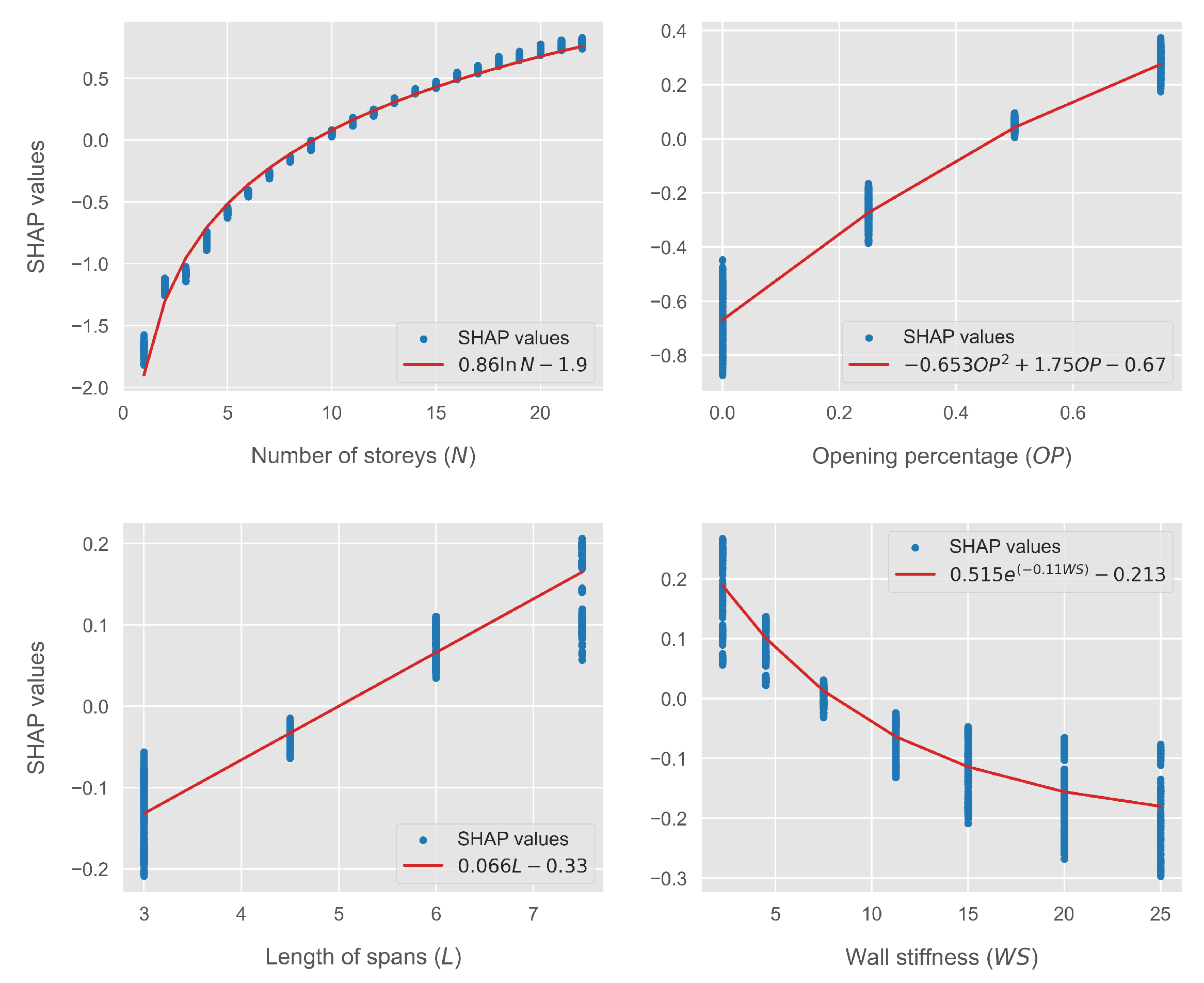
Given the shape of each individual curve, we experimented with a variety of analytical curves for each one, including quadratic polynomials, square roots, logarithms, and exponentials. The results are shown in Table 3. Note that the contribution of the “number of spans” feature was negligible and was ignored; similarly, the curves with the best fits for each feature are presented in Figure 4.

Table 3.
Fitted curves of the SHAP values of each feature. The provided equations for opening percentage and wall stiffness are valid for non-bare frames.
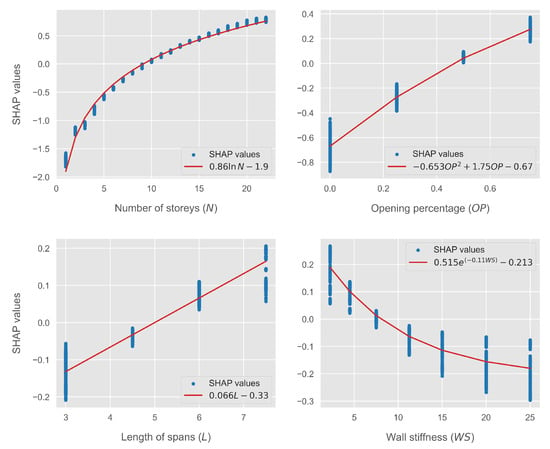
Figure 4.
Analytical curves with the best fit for each feature.
The equations in Table 3 are valid for non-bare frames, i.e., cases where the opening percentage is <100%. For bare frames, the contribution of the wall stiffness is set to 0 due to the missingness property (Equation (3)). Similarly, when the “opening percentage” is equal to 1, as in the bare frame case, the SHAP values of this feature range from 0.27 to 0.325. Thus, the contribution of this feature for bare frames can be obtained using a single value. As is well known, the median minimizes MAE, while the mean minimizes RMSE. In our case, both the mean and median were very close, approximately equal to 0.33. From the above equations, we selected those with the overall best performance. Finally, it should be noted that the above equations only approximate the SHAP values in Equation (4). In order for the local approximation (Equation (2)) to be accurate, it is necessary to include the constant , i.e., the average model prediction. In our case, this was approximately equal to −0.21.
Combining the above, we obtain two analytical equations for the prediction of the fundamental period; specifically, for bare frames we obtain Equation (6)
while for non-bare frames we obtain Equation (7)
In the above equations, N is an integer representing the number of stories, L is the length of the spans measured in meters, is the opening percentage, which is dimensionless and normalized in the [0, 1] range, and is the stiffness of the masonry walls measured in units of kN/m.
As previously discussed, the benefit of the above formulation is that both the number of terms and their complexity can be individually adjusted to achieve the desired balance between accuracy and simplicity of the derived formulas.
Using the above equations, we computed the regression metrics shown in Table 1. We computed them in both the log-transformed space, where the regression was fitted, and in the original space, allowing us to examine how the inverse exponential transform affects the results. As can be readily observed (Table 4), the regression results using these simplified analytical equations are excellent, achieving low MSE and MAE values and an of approximately 0.97 and 0.95 in the log-transformed and original spaces, respectively. Thus, the proposed relationships can be confidently employed in lieu of the fully trained ML model without a significant loss in accuracy. Finally, due to the excellent regression results, the complexity of adding terms pertaining to SHAP interaction values is not deemed justifiable. However, these terms can be examined in cases where the interactions are significant and high accuracy cannot be achieved using SHAP values alone.

Table 4.
Regression metrics of the simplified analytical equations.
4. Summary and Conclusions
In the framework of the present study, a novel regression approach is presented based on ML explainability methodologies, in particular, the so-called SHapley Additive exPlanations (SHAP values). SHAP values are commonly employed in the literature as an explainability tool. However, in the present study, they are used as a basis to provide interpretable analytical equations that approximate the behavior of the underlying machine learning model. We have implemented our proposed methodology on the problem of estimating the fundamental period of buildings, which is a very important parameter in the context of seismic design of new buildings and evaluating the seismic capacity of existing buildings.
Similar problems of great importance in the engineering community have been addressed in various design codes by providing simplified analytical equations that approximate the target variable. On the other hand, ML models have demonstrated the ability to tackle such problems and produce state-of-the-art results with excellent accuracy. This is demonstrated in the present paper, where our fully trained ML model achieved a coefficient of determination . In addition, our model obtained MAE in both the log-transformed and original spaces, while the corresponding RMSE ranged from ≈0.065–0.085. However, ML models often lack interpretability, which hinders their full adoption by the engineering community.
Our proposed novel methodology can help to bridge this gap. On the one hand, we employ fully trained ML models to achieve state-of-the-art results; on the other, we utilize an explainability technique based on SHAP values as a basis for providing interpretable analytical equations, which offers distinct advantages compared to the previously established literature.
First, due to the additive nature of SHAP values, our proposed methodology allows for the incremental addition of terms in simplified analytical equations. This in turn allows for a controlled tradeoff between model complexity and the desired level of accuracy according to the application at hand. Second, as Figure 2 demonstrates, SHAP values allow the percentage of influence of each individual parameter to be quantified. Specifically, we found that approximately 50% on average of the total model predictions were based on the “Number of Stories” feature, while an additional 30% were attributed to the “Opening Percentage” feature. Approximately 10% of predictions were attributed to each of the “Length of Spans” and “Masonry Wall Stiffness” features, while the effect of the “Number of Spans” feature was found to be negligible.
Thus, the controlled tradeoff between accuracy and model complexity in our proposed methodology is not carried out blindly, but rather in an informed manner guided by the feature importance ranking provided by the SHAP values. Due to the fact that SHAP values approximate the behavior of the underlying ML model, the proposed methodology can provide simplified equations with comparable accuracy to that of the fully trained ML model, as demonstrated in Table 2 and Table 4. Indeed, the fully trained model achieved , while the simplified equations achieved and in the log-transformed and original spaces, respectively.
Finally, due to the attractive missingness property of SHAP values, the missing values which can potentially be found in many real datasets pertaining to engineering applications are handled seamlessly and effectively, avoiding the need to impute potentially misleading values.
Although the model presented in this study achieved excellent accuracy, it should be reiterated that the proposed methodology provides an approximation of the behavior of the underlying fully trained ML model; thus, in the event that the underlying model’s performance is unsatisfactory, the resulting analytical equations will not be satisfactory either. In addition, it should be noted that the scope of applicability of the presented models is bounded by the ranges of the features employed for training. It is well known that while ML models perform well when interpolating, i.e., when making predictions on inputs within their training range, their performance can deteriorate when extrapolating.
Finally, even though the proposed methodology was implemented in the framework of estimating the fundamental period of buildings, a future research direction could include its application to various similar engineering challenges. The utilization of SHAP interaction values could also be explored for cases where sufficient accuracy cannot be achieved via SHAP main effects. This would help to bridge the gap between the demonstrated power of ML models in producing state-of-the-art results and the need for simplified analytical equations for their implementation that instill confidence in the engineering community.
Author Contributions
Conceptualization, I.K., K.M. and L.I.; methodology, I.K., K.M. and L.I.; software, I.K., K.M. and L.I.; validation, I.K., K.M. and L.I.; formal analysis, I.K. and K.M.; investigation, I.K., K.M. and L.I.; resources, K.M. and L.I.; data curation, I.K., K.M. and L.I.; writing—original draft preparation, I.K. and K.M.; writing—review and editing, L.I.; visualization, I.K. and K.M.; supervision L.I. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data that support the findings of this study are available upon reasonable request.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| RC | Reinforced Concrete |
| ML | Machine Learning |
| SHAP | Shapley Additive Explanations |
| FUP | Fundamental Period |
| RCB_MI | Reinforced Concrete Building with Masonry Infills |
| ANN | Artificial Neural Network |
| LIME | Local Interpretable Model-Agnostic Explanations |
| PDP | Partial Dependence Plot |
References
- Penelis, G.; Kappos, A. Earthquake-Rresistant Concrete Structures; E and FN Spon: London, UK, 1997. [Google Scholar]
- Elnashai, A.S.; Di Sarno, L. Fundamentals of Earthquake Engineering: From Source to Fragility; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Theodoulidis, N.; Karakostas, C.; Lekidis, V.; Makra, K.; Margaris, B.; Morfidis, K.; Papaioannou, C.; Rovithis, E.; Salonikios, T.; Savvaidis, A. The Cephalonia, Greece, January 26 (M6. 1) and February 3, 2014 (M6. 0) earthquakes: Near-fault ground motion and effects on soil and structures. Bull. Earthq. Eng. 2016, 14, 1–38. [Google Scholar] [CrossRef]
- Eleftheriadou, A.; Karabinis, A.; Baltzopoulou, A. Fundamental Period versus Seismic Damage for Reinforced Concrete Buildings. In Proceedings of the 15th World Conference on Earthquake Engineering 2012 (15WCEE), Lisbon, Portugal, 24–28 September 2012. [Google Scholar]
- Bathe, K.J. Finite Element Procedures; Prentice Hall: Hoboken, NJ, USA, 2006. [Google Scholar]
- Bhatt, P. Programming the Dynamic Analysis of Structures; Spon Press: London, UK, 2002. [Google Scholar]
- EN 1998-1:2005; Eurocode 8: Design of Structures for Earthquake Resistance-Part 1: General Rules, Seismic Actions and Rules for Buildings. European Committee for Standardization: Brussels, Belgium, 2005.
- NZS3101; The Design of Concrete Structures. Technical Report; Standards New Zealand: Wellington, New Zealand, 2006.
- IS 1893-1; Criteria for Earthquake Resistant Design of Structures-Part 1: General Provisions and Buildings. Technical Report; Bureau of Indian Standards: New Delhi, India, 2002.
- ECP-201; Egyptian Code for Computation of Loads and Forces in Structural and Building Works. Technical Report; Housing and Building Research Center: Cairo, Egypt, 2012.
- AFPS. Recommendations for the Redaction of Rules Relative to the Structures and Installation Built in Regions Prone to Earthquakes; Technical Report; France Association of Earthquake Engineering: Paris, France, 1990. [Google Scholar]
- National Research Council. The National Building Code (NBC); Technical Report; National Research Council: Ottawa, ON, Canada, 1995.
- NEHRP Recommended Provisions for the Development of Seismic Regulations for New Buildings; Technical Report; Building Seismic Safety Council: Washington, DC, USA, 1994.
- Uniform Building Code; Technical Report; International Conference of Building Officials: Whittier, CA, USA, 1997.
- Tentative Provisions for the Development of Seismic Regulations for Buildings; Technical Report; Applied Technology Council: Palo Alto, CA, USA, 1978.
- Minimum Design Loads for Buildings and Other Structures; Technical Report; American Society of Civil Engineers: Reston, VA, USA, 2010.
- Building Standard Law of Japan; Technical Report; Building Center of Japan: Tokyo, Japan, 2016.
- Recommended Lateral Force Requirements and Commentary; Technical Report; Structural Engineers Association of California: Sacramento, CA, USA, 1999.
- Crawford, R.; Ward, H.S. Determination of the natural periods of buildings. Bull. Seismol. Soc. Am. 1964, 54, 1743–1756. [Google Scholar] [CrossRef]
- Bertero, V.V. Fundamental Period of Reinforced Concrete Moment-Resisting Frame Structures; Number 87; John A. Blume Earthquake Engineering Center: Stanford, CA, USA, 1988. [Google Scholar]
- Goel, R.K.; Chopra, A.K. Period formulas for moment-resisting frame buildings. J. Struct. Eng. 1997, 123, 1454–1461. [Google Scholar] [CrossRef]
- Goel, R.K.; Chopra, A.K. Period formulas for concrete shear wall buildings. J. Struct. Eng. 1998, 124, 426–433. [Google Scholar] [CrossRef]
- Balkaya, C.; Kalkan, E. Estimation of fundamental periods of shear-wall dominant building structures. Earthq. Eng. Struct. Dyn. 2003, 32, 985–998. [Google Scholar] [CrossRef]
- Hong, L.L.; Hwang, W.L. Empirical formula for fundamental vibration periods of reinforced concrete buildings in Taiwan. Earthq. Eng. Struct. Dyn. 2000, 29, 327–337. [Google Scholar] [CrossRef]
- Verderame, G.M.; Iervolino, I.; Manfredi, G. Elastic period of sub-standard reinforced concrete moment resisting frame buildings. Bull. Earthq. Eng. 2010, 8, 955–972. [Google Scholar] [CrossRef]
- Chiauzzi, L.; Masi, A.; Mucciarelli, M.; Cassidy, J.; Kutyn, K.; Traber, J.; Ventura, C.; Yao, F. Estimate of fundamental period of reinforced concrete buildings: Code provisions vs. experimental measures in Victoria and Vancouver (BC, Canada). In Proceedings of the 15th World Conference on Earthquake Engineering, Lisbon, Portugal, 24–28 September 2012; Volume 3033. [Google Scholar]
- Salama, M.I. Estimation of period of vibration for concrete moment-resisting frame buildings. HBRC J. 2015, 11, 16–21. [Google Scholar] [CrossRef][Green Version]
- Hadzima-Nyarko, M.; Morić, D.; Draganić, H.; Štefić, T. Comparison of fundamental periods of reinforced shear wall dominant building models with empirical expressions. Teh. Vjesn. 2015, 22, 685–694. [Google Scholar] [CrossRef]
- El-saad, M.N.A.; Salama, M.I. Estimation of period of vibration for concrete shear wall buildings. HBRC J. 2017, 13, 286–290. [Google Scholar] [CrossRef]
- Badkoubeh, A.; Massumi, A. Fundamental period of vibration for seismic design of concrete shear wall buildings. Sci. Iran. 2017, 24, 1010–1016. [Google Scholar] [CrossRef][Green Version]
- Mohamed, A.N.; El Kashif, K.F.; Salem, H.M. An investigation of the fundamental period of vibration for moment resisting concrete frames. Civ. Eng. J. 2019, 5, 2626–2642. [Google Scholar] [CrossRef]
- Shatnawi, A.S.; Al-Beddawe, E.H.; Musmar, M.A. Estimation of fundamental natural period of vibration for reinforced concrete shear walls systems. Earthq. Struct. 2019, 16, 295–310. [Google Scholar]
- Alrudaini, T. Estimating vibration period of reinforced concrete moment resisting frame buildings. Res. Eng. Struct. Mater. 2023, 9, 1417–1432. [Google Scholar] [CrossRef]
- Dominguez Morales, M. Fundamental Period of Vibration for Reinforced Concrete Buildings; University of Ottawa: Ottawa, ON, Canada, 2000. [Google Scholar]
- Amanat, K.M.; Hoque, E. A rationale for determining the natural period of RC building frames having infill. Eng. Struct. 2006, 28, 495–502. [Google Scholar] [CrossRef]
- Kwon, O.S.; Kim, E.S. Evaluation of building period formulas for seismic design. Earthq. Eng. Struct. Dyn. 2010, 39, 1569–1583. [Google Scholar] [CrossRef]
- Crowley, H.; Pinho, R. Revisiting Eurocode 8 formulae for periods of vibration and their employment in linear seismic analysis. Earthq. Eng. Struct. Dyn. 2010, 39, 223–235. [Google Scholar] [CrossRef]
- Ricci, P.; Verderame, G.M.; Manfredi, G. Analytical investigation of elastic period of infilled RC MRF buildings. Eng. Struct. 2011, 33, 308–319. [Google Scholar] [CrossRef]
- Asteris, P.G.; Repapis, C.C.; Cavaleri, L.; Sarhosis, V.; Athanasopoulou, A. On the fundamental period of infilled RC frame buildings. Struct. Eng. Mech. 2015, 54, 1175–1200. [Google Scholar] [CrossRef]
- Asteris, P.G.; Repapis, C.C.; Tsaris, A.K.; Di Trapani, F.; Cavaleri, L. Parameters affecting the fundamental period of infilled RC frame structures. Earthq. Struct. 2015, 9, 999–1028. [Google Scholar] [CrossRef]
- Perrone, D.; Leone, M.; Aiello, M.A. Evaluation of the infill influence on the elastic period of existing RC frames. Eng. Struct. 2016, 123, 419–433. [Google Scholar] [CrossRef]
- Asteris, P.G.; Repapis, C.C.; Repapi, E.V.; Cavaleri, L. Fundamental period of infilled reinforced concrete frame structures. Struct. Infrastruct. Eng. 2017, 13, 929–941. [Google Scholar] [CrossRef]
- Al-Balhawi, A.; Zhang, B. Investigations of elastic vibration periods of reinforced concrete moment-resisting frame systems with various infill walls. Eng. Struct. 2017, 151, 173–187. [Google Scholar] [CrossRef][Green Version]
- Ruggieri, S.; Fiore, A.; Uva, G. A new approach to predict the fundamental period of vibration for newly-designed reinforced concrete buildings. J. Earthq. Eng. 2022, 26, 6943–6968. [Google Scholar] [CrossRef]
- Harirchian, E.; Hosseini, S.E.A.; Jadhav, K.; Kumari, V.; Rasulzade, S.; Işık, E.; Wasif, M.; Lahmer, T. A review on application of soft computing techniques for the rapid visual safety evaluation and damage classification of existing buildings. J. Build. Eng. 2021, 43, 102536. [Google Scholar] [CrossRef]
- Xie, Y.; Ebad Sichani, M.; Padgett, J.E.; DesRoches, R. The promise of implementing machine learning in earthquake engineering: A state-of-the-art review. Earthq. Spectra 2020, 36, 1769–1801. [Google Scholar] [CrossRef]
- Sun, H.; Burton, H.V.; Huang, H. Machine learning applications for building structural design and performance assessment: State-of-the-art review. J. Build. Eng. 2021, 33, 101816. [Google Scholar] [CrossRef]
- Flah, M.; Nunez, I.; Ben Chaabene, W.; Nehdi, M.L. Machine learning algorithms in civil structural health monitoring: A systematic review. Arch. Comput. Methods Eng. 2021, 28, 2621–2643. [Google Scholar] [CrossRef]
- Avci, O.; Abdeljaber, O.; Kiranyaz, S. Structural Damage Detection in Civil Engineering with Machine Learning: Current State of the Art. In Proceedings of the Sensors and Instrumentation, Aircraft/Aerospace, Energy Harvesting & Dynamic Environments Testing, Volume 7: Proceedings of the 39th IMAC, A Conference and Exposition on Structural Dynamics 2021; Springer: Berlin/Heidelberg, Germany, 2022; pp. 223–229. [Google Scholar]
- Haykin, S. Neural Networks and Learning Machines, 3rd ed.; Prentice Hall: Hoboken, NJ, USA, 2009. [Google Scholar]
- Deka, P.C. A Primer on Machine Learning Applications in Civil Engineering; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar]
- Chatterjee, P.; Yazdani, M.; Fernández-Navarro, F.; Pérez-Rodríguez, J. Machine Learning Algorithms and Applications in Engineering; CRC Press: Boca Raton, FL, USA, 2023. [Google Scholar]
- Bishop, C. Pattern Recognition and Machine Learning; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Koutroumbas, K.; Theodoridis, S. Pattern Recognition, 4th ed.; Elsevier: Amsterdam, The Netherlands, 2008. [Google Scholar]
- Kose, M.M. Parameters affecting the fundamental period of RC buildings with infill walls. Eng. Struct. 2009, 31, 93–102. [Google Scholar] [CrossRef]
- Asteris, P.G. The FP4026 Research Database on the fundamental period of RC infilled frame structures. Data Brief 2016, 9, 704–709. [Google Scholar] [CrossRef]
- Asteris, P.G.; Tsaris, A.K.; Cavaleri, L.; Repapis, C.C.; Papalou, A.; Di Trapani, F.; Karypidis, D.F. Prediction of the fundamental period of infilled RC frame structures using artificial neural networks. Comput. Intell. Neurosci. 2016, 2016, 5104907. [Google Scholar] [CrossRef] [PubMed]
- Asteris, P.G.; Nikoo, M. Artificial bee colony-based neural network for the prediction of the fundamental period of infilled frame structures. Neural Comput. Appl. 2019, 31, 4837–4847. [Google Scholar] [CrossRef]
- Charalampakis, A.E.; Tsiatas, G.C.; Kotsiantis, S.B. Machine learning and nonlinear models for the estimation of fundamental period of vibration of masonry infilled RC frame structures. Eng. Struct. 2020, 216, 110765. [Google Scholar] [CrossRef]
- Somala, S.N.; Karthikeyan, K.; Mangalathu, S. Time period estimation of masonry infilled RC frames using machine learning techniques. Structures 2021, 34, 1560–1566. [Google Scholar] [CrossRef]
- Mirrashid, M.; Naderpour, H. Computational intelligence-based models for estimating the fundamental period of infilled reinforced concrete frames. J. Build. Eng. 2022, 46, 103456. [Google Scholar] [CrossRef]
- Jang, J.S. ANFIS: Adaptive-network-based fuzzy inference system. IEEE Trans. Syst. Man Cybern. 1993, 23, 665–685. [Google Scholar] [CrossRef]
- Yahiaoui, A.; Dorbani, S.; Yahiaoui, L. Machine learning techniques to predict the fundamental period of infilled reinforced concrete frame buildings. Structures 2023, 54, 918–927. [Google Scholar] [CrossRef]
- Thisovithan, P.; Aththanayake, H.; Meddage, D.; Ekanayake, I.; Rathnayake, U. A novel explainable AI-based approach to estimate the natural period of vibration of masonry infill reinforced concrete frame structures using different machine learning techniques. Results Eng. 2023, 19, 101388. [Google Scholar] [CrossRef]
- Adadi, A.; Berrada, M. Peeking inside the black-box: A survey on explainable artificial intelligence (XAI). IEEE Access 2018, 6, 52138–52160. [Google Scholar] [CrossRef]
- Seismosoft. SeismoStruct—A Computer Program for Static and Dynamic Nonlinear Analysis of Framed Structures; Seismosoft: Lombardia, Italy, 2013. [Google Scholar]
- Crisafulli, F.J.; Carr, A.J. Proposed macro-model for the analysis of infilled frame structures. Bull. N. Z. Soc. Earthq. Eng. 2007, 40, 69–77. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Natekin, A.; Knoll, A. Gradient boosting machines, a tutorial. Front. Neurorobot. 2013, 7, 21. [Google Scholar] [CrossRef] [PubMed]
- Lundberg, S.M.; Erion, G.G.; Lee, S.I. Consistent individualized feature attribution for tree ensembles. arXiv 2018, arXiv:1802.03888. [Google Scholar]
- Lundberg, S.M.; Lee, S.I. A unified approach to interpreting model predictions. Adv. Neural Inf. Process. Syst. 2017, 30, 4765–4774. [Google Scholar]
- Shapley, L.S. Notes on the n-Person Game-II: The Value of an n-Person Game; RAND Corporation: Santa Monica, CA, USA, 1951. [Google Scholar]
- Goldstein, A.; Kapelner, A.; Bleich, J.; Pitkin, E. Peeking inside the black box: Visualizing statistical learning with plots of individual conditional expectation. J. Comput. Graph. Stat. 2015, 24, 44–65. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).