Integrating Root Morphology Based on Whole-Pullout Test of Model Roots: A Case Study
Abstract
1. Introduction
2. Materials and Methods
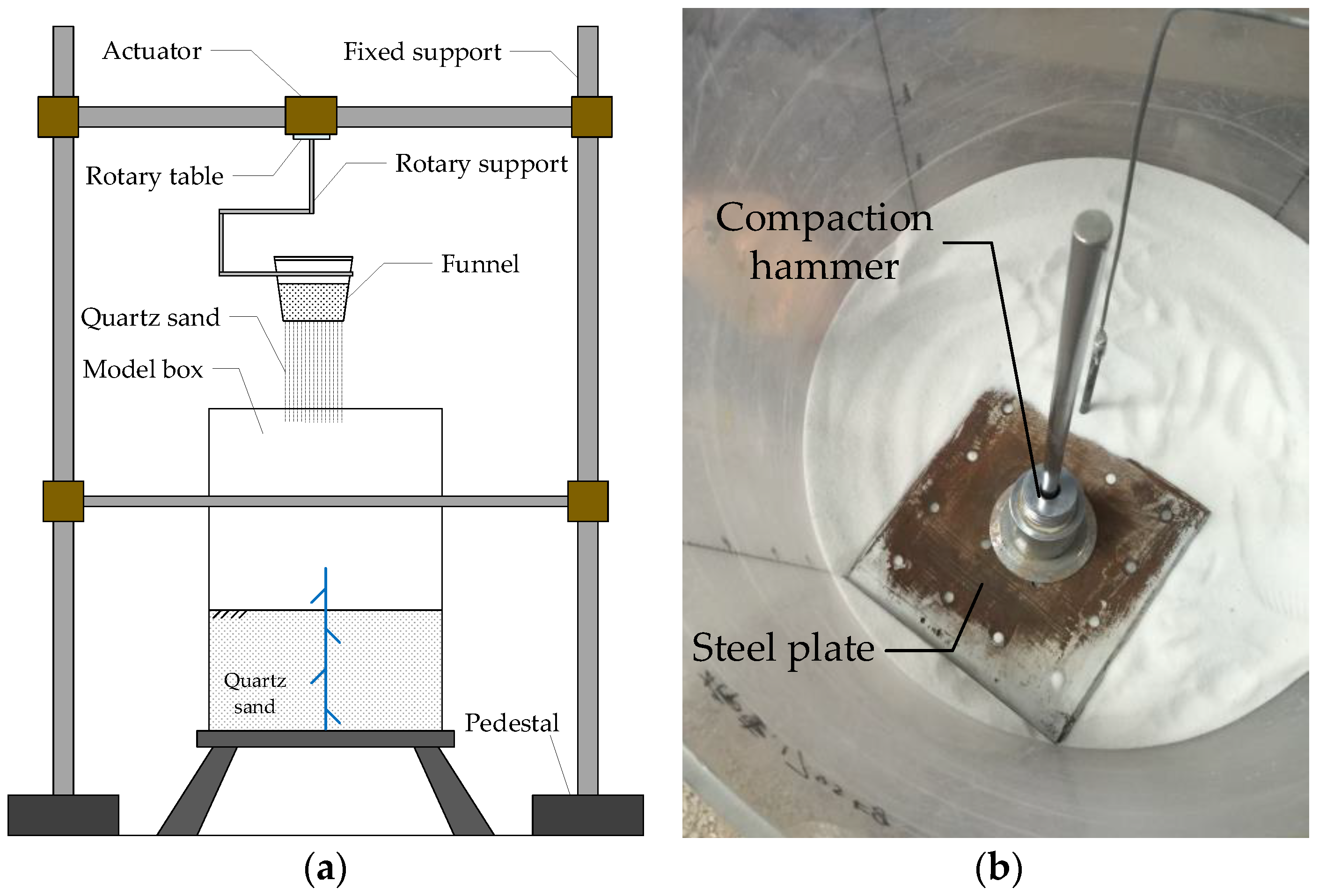
2.1. Experimental Materials and Apparatus
2.2. Experimental Design
2.2.1. Levels of Experimental Factors
2.2.2. Orthogonal Experimental Design
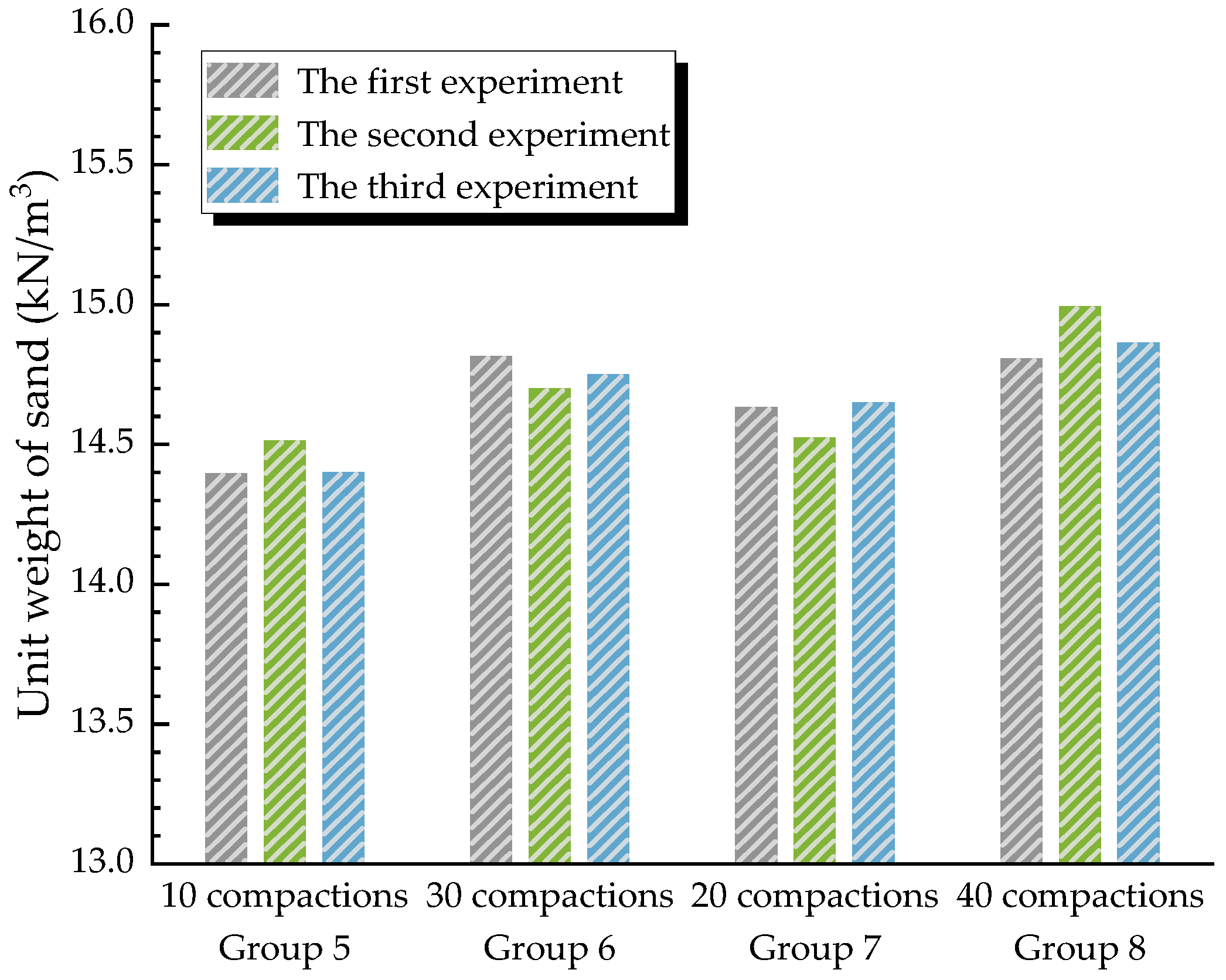
2.2.3. Experimental Procedure
3. Results
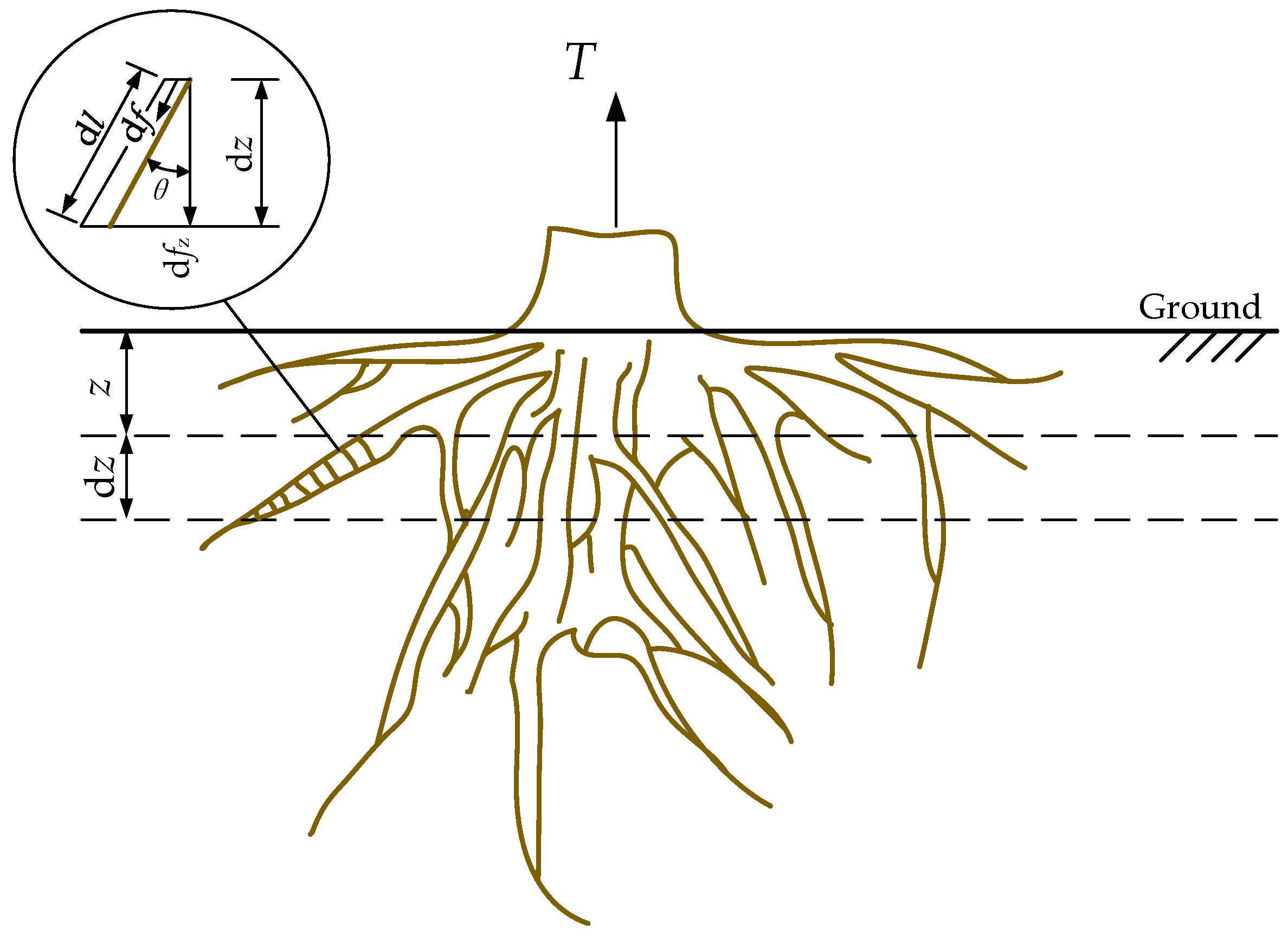
3.1. Experimental Data Processing
3.2. Range Analysis
3.3. Analysis of Variance
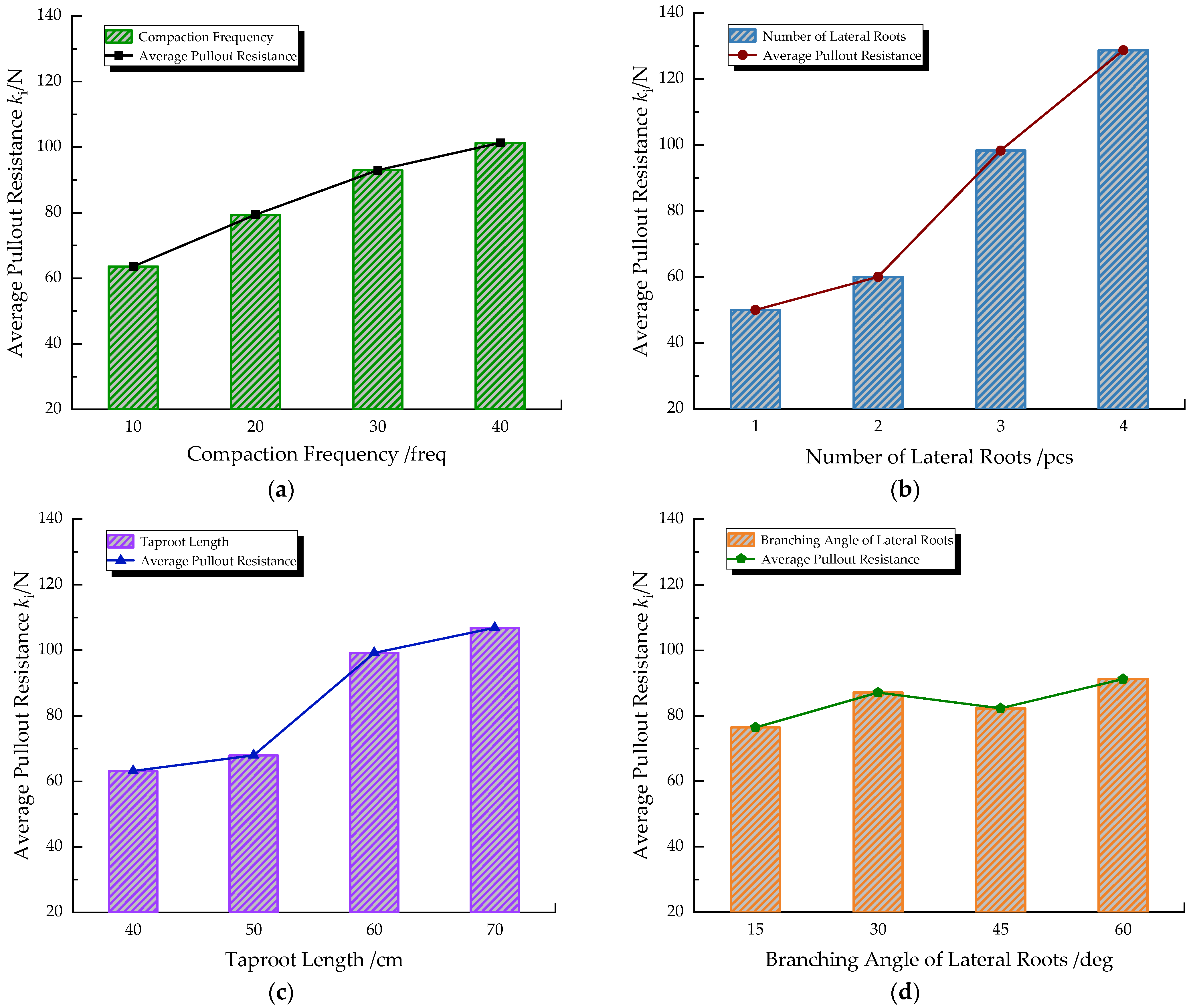
3.4. Trend Analysis of Various Factors in Resistance to Pulling
4. Discussion
5. Conclusions
- (1)
- The results of the range analysis indicate that the factors influencing the vertical pullout resistance of a plant root system can be ordered in terms of sensitivity, from highest to lowest, as follows: number of lateral roots, taproot length, unit weight of soil around the root, and branching angle of the lateral root. A variance analysis further confirmed that the number of lateral roots and taproot length were the primary factors affecting the magnitude of the root system’s vertical pullout resistance.
- (2)
- An analysis of the trend for the vertical pullout resistance of a root system with changes in various factors showed that an increase in the number of lateral roots from two to three leads to a 64% increase in the average vertical pullout resistance. An increase in the taproot length from 50 cm to 60 cm results in a 46% increase in average vertical pullout resistance. Additionally, for every 10 additional compaction hits, the average vertical pullout resistance increases by 25%. The average vertical pullout resistance is positively correlated with the number of lateral roots, taproot length, and the unit weight of soil around the root, reaching its maximum at the highest levels for these factors. Therefore, further enhancing these factors’ levels can lead to greater vertical pullout resistance and better combinations of these factors.
- (3)
- Incorporating the sensitivity index () into the calculations further confirmed the order of sensitivity for the four factors—lateral root number, main root length, soil weight around the root periphery, and lateral root branching angle—on the vertical pullout resistance of plant root systems. The obtained results were consistent with Conclusion (1).
- (4)
- Through the results of the vertical pullout orthogonal experiments on model roots and a comprehensive theoretical analysis method, it was concluded that the branching angle of the lateral roots had no significant effect on the vertical pullout resistance of the root system. In vegetative slope protection projects, preference should be given to plants with well-developed lateral roots, longer taproot lengths, and stronger root systems for slope reinforcement.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhao, H.; Tian, W.P.; Li, J.C.; Ma, B.C. Hazard zoning of trunk highway slope disasters: A case study in northern Shaanxi, China. Bull. Eng. Geol. Environ. 2018, 77, 1355–1364. [Google Scholar] [CrossRef]
- Ashfaq, M.; Moghal, A.A.B. Cost and carbon footprint analysis of flyash utilization in earthworks. Int. J. Geosynth. Ground Eng. 2022, 8, 21. [Google Scholar] [CrossRef]
- Varsha, B.; Moghal, A.A.B.; Rehman, A.U.; Chittoori, B.C.S. Shear, consolidation characteristics and carbon footprint analysis of clayey soil blended with calcium lignosulphonate and granite sand for earthen dam application. Sustainability 2023, 15, 6117. [Google Scholar] [CrossRef]
- Wu, X.P.; Yi, C.; Cui, W.W.; Zhang, Z.; Yan, C.; Xie, X.C. Analysis of Human Disturbance Features in Natural Reserves and Empirical Research on Their Restoration: A Case Study of the Huangchulin Nature Reserve in Fujian Province. Sustainability 2023, 15, 2017. [Google Scholar] [CrossRef]
- Ahlström, J.; Tidblad, J.; Sederholm, B.; Wadsö, L. Influence of chloride and moisture content on steel rebar corrosion in concrete. Mater. Corros. 2016, 67, 1049–1058. [Google Scholar] [CrossRef]
- Shen, Y.F.; Li, Q.; Pei, X.J.; Wei, R.J.; Yang, B.M.; Lei, N.F.; Zhang, X.C.; Yin, D.Q.; Wang, S.J.; Tao, Q.Z. Ecological Restoration of Engineering Slopes in China—A Review. Sustainability 2023, 15, 5354. [Google Scholar] [CrossRef]
- Masi, E.B.; Segoni, S.; Tofani, V. Root Reinforcement in Slope Stability Models: A Review. Geosciences 2021, 11, 212. [Google Scholar] [CrossRef]
- Capilleri, P.P.; Cuomo, M.; Motta, E.; Todaro, M. Experimental Investigation of Root Tensile Strength for Slope Stabilization. Indian Geotech. J. 2019, 49, 687–697. [Google Scholar] [CrossRef]
- Reubens, B.; Poesen, J.; Danjon, F.; Geudens, G.; Muys, B. The role of fine and coarse roots in shallow slope stability and soil erosion control with a focus on root system architecture: A review. Trees 2007, 21, 385–402. [Google Scholar] [CrossRef]
- Wang, B.Y.; Wang, S.J. Shear Strength Analysis and Slope Stability Study of Straight Root Herbaceous Root Soil Composite. Appl. Sci. 2023, 13, 12632. [Google Scholar] [CrossRef]
- Kong, G.Q.; Wen, L.; Liu, H.L.; Wang, C.Q. Strength properties of root compound soil and morphological observation of plant root. Rock Soil Mech. 2019, 40, 3717–3723. [Google Scholar]
- Lian, B.Q.; Peng, J.B.; Zhan, H.B.; Wang, X.G. Mechanical response of root-reinforced loess with various water contents. Soil Tillage Res. 2019, 193, 85–94. [Google Scholar] [CrossRef]
- Zhou, X.L.; Fu, D.S.; Wan, J.; Xiao, H.L.; He, X.Y.; Li, Z.X.; Deng, Q.X. The Shear Strength of Root–Soil Composites in Different Growth Periods and Their Effects on Slope Stability. Appl. Sci. 2023, 13, 11116. [Google Scholar] [CrossRef]
- Xu, H.; Yuan, H.L.; Wang, X.Y.; Wang, D.; Chen, J.X.; Rong, C.Q. Study on influence of morphology and hierarchy of root on mechanical characteristics of root soil comp. Chin. J. Geotech. Eng. 2022, 44, 926–935. [Google Scholar]
- Ajedegba, J.O.; Choi, J.W.; Jones, K.D. Analytical modeling of coastal dune erosion at South Padre Island: A consideration of the effects of vegetation roots and shear strength. Ecol. Eng. 2019, 127, 187–194. [Google Scholar] [CrossRef]
- Wang, Y.B.; Wu, M.S.; Zhou, C. Direct shear tests and numerical simulation on slope soils reinforced by composite roots. Chin. J. Geotech. Eng. 2020, 42, 177–182. [Google Scholar]
- Cardoza, R.; Oka, L. Measuring the effect of grass roots on shear strength parameters of sandy soils. In Proceedings of the Geo-Congress 2020, Minneapolis, MN, USA, 25–28 February 2020; American Society of Civil Engineers: Reston, VA, USA, 2020; pp. 214–223. [Google Scholar]
- Mao, Z.J.; Bi, Y.L.; Geng, M.M.; An, N. Pull-out characteristics of herbaceous roots of alfalfa on the loess in different growth stages and their impacts on slope stability. Soil Tillage Res. 2023, 225, 105542. [Google Scholar] [CrossRef]
- Bransby, F.; Davies, M.C.R.; Mickovski, S.; Sonnenberg, R.; Bengough, A.; Hallett, P. Stabilisation of slopes by vegetation reinforcement. In Physical Modelling in Geotechnics, Two Volume Set, Proceedings of the Sixth International Conference on Physical Modelling in Geotechnics, 6th ICPMG’06, Hong Kong, China, 4–6 August 2006; Taylor and Francis: London, UK, 2006; p. 317. [Google Scholar]
- Ali, F.; Osman, R.; Kamil, S.S.S.M. The influences of root branching patterns on pullout resistance. Electron. J. Geotech. Eng. 2013, 18, 3967–3977. [Google Scholar]
- Yang, Y.J.; Chen, L.H.; Li, N.; Zhang, Q.F. Effect of Root Moisture Content and Diameter on Root Tensile Properties. PLoS ONE 2016, 11, e0151791. [Google Scholar] [CrossRef]
- Capilleri, P.P.; Motta, E.; Raciti, E. Experimental Study on Native Plant Root Tensile Strength for Slope Stabilization. Procedia Eng. 2016, 158, 116–121. [Google Scholar] [CrossRef]
- Yang, Q.H.; Zhang, C.B.; Liu, P.C.; Jiang, J. The Role of Root Morphology and Pulling Direction in Pullout Resistance of Alfalfa Roots. Front. Plant Sci. 2021, 12, 580825. [Google Scholar] [CrossRef]
- Zhou, L.H.; Hu, X.S.; Liu, C.Y.; Xu, Z.W.; Xu, T.; Shen, Z.Y. In-Situ Pull-out Test of Four Shrub Plants in Xining Basin of the Loess Plateau. Res. Soil Water Conserv. 2019, 26, 236–242. [Google Scholar]
- Ennos, A.R. The Anchorage of Leek Seedlings: The Effect of Root Length and Soil Strength. Ann. Bot. 1990, 65, 409–416. [Google Scholar] [CrossRef]
- Mickovski, S.B.; Bransby, F.; Bengough, A.G.; Davies, M.C.R.; Hallett, P.D. Resistance of simple plant root systems to uplift loads. Can. Geotech. J. 2010, 47, 78–95. [Google Scholar] [CrossRef]
- Khalid, U.; ur Rehman, Z.; Mujtaba, H.; Farooq, K. 3D response surface modeling based in-situ assessment of physico-mechanical characteristics of alluvial soils using dynamic cone penetrometer. Transp. Geotech. 2022, 36, 100781. [Google Scholar] [CrossRef]
- Farooq, K.; ur Rehman, Z.; Shahzadi, M.; Mujtaba, H.; Khalid, U. Optimization of Sand-Bentonite mixture for the stable engineered barriers using desirability optimization methodology: A Macro-Micro-Evaluation. KSCE J. Civ. Eng. 2023, 27, 40–52. [Google Scholar] [CrossRef]
- Mujtaba, H.; Shimobe, S.; Farooq, K.; ur Rehman, Z.; Khalid, U. Relating gradational parameters with hydraulic conductivity of sandy soils: A renewed attempt. Arab. J. Geosci. 2021, 14, 1–17. [Google Scholar] [CrossRef]
- ur Rehman, Z.; Khalid, U.; Ijaz, N.; Mujtaba, H.; Haider, A.; Farooq, K.; Ijaz, Z. Machine learning-based intelligent modeling of hydraulic conductivity of sandy soils considering a wide range of grain sizes. Eng. Geol. 2022, 311, 106899. [Google Scholar] [CrossRef]
- Pan, T.H.; Du, F.; Wang, Y. Analysis of Root Distributions and Shear Strengths of Slope Protection Plants in the Loess Region of Northern Shaanxi. Res. Soil Water Conserv. 2020, 27, 357–363+371. [Google Scholar]
- Ji, X.L.; Yang, P. The effects of roots angles of nerium indicum on the stability of slopes. Ecol. Environ. Sci. 2012, 21, 1966–1970. [Google Scholar]
- Bai, X.; Zhao, C.Z.; Kang, M.P. Relationship between root forks and branch angle of Tamarix ramosissima at different stand ages in oasis of Jinta County. Acta Ecol. Sin. 2021, 41, 1878–1884. [Google Scholar]
- GB 50007-2011; Code for Design of Building Foundation. China Architecture & Building Press: Beijing, China, 2011; pp. 124–125.
- GB 50330-2013; Technical Code for Building Slope Engineering. China Architecture & Building Press: Beijing, China, 2013; pp. 110–113.
- Khari, M.; Kassim, K.A.; Adnan, A. Sand samples’ preparation using mobile pluviator. Arab. J. Sci. Eng. 2014, 39, 6825–6834. [Google Scholar] [CrossRef]
- Hakhamaneshi, M.; Black, J.A.; Cargill, A.; Cox, C.M.; Elmrom, T. Development and calibration of a sand pluviation device for preparation of model sand bed for centrifuge tests. In Proceedings of the 3rd Conference on Physical Modelling in Geotechnics, IFSTTAR Nantes Centre, France, 1–3 June 2016. [Google Scholar]
- Ma, X.F.; Kong, L.G.; Fang, W.; Gong, B.W.; Li, H.; Xu, G.M.; Zhao, W.; Zhang, X.D.; Chen, Y.M. Parallel tests on preparation of samples with sand pourer. Chin. J. Geotech. Eng. 2014, 36, 1791–1801. [Google Scholar] [CrossRef]
- Fang, H.; Duan, X.F.; Wang, Y.Z.; Wang, H.; Yuan, X.M.; Wang, T.Q. Research and prospect of preparation technique for centrifugal pluviation model. World Earthq. Eng. 2018, 34, 60–66. [Google Scholar]
- Bauer, L.R.; Hamby, D.M. Relative Sensitivities of Existing and Novel Model Parameters in Atmospheric Tritium Dose Estimates. Radiat. Prot. Dosim. 1991, 37, 253–260. [Google Scholar]
- Luo, C.Y.; Wu, C.; Lu, G.X.; De, K.J.; Zhang, M.; Wang, J.B. Tensile resistance characteristics of root-soil composite system and influence factor analysis in Sanjiangyuan regions of Qinghai-Tibet plateau. Res. Soil Water Conserv. 2014, 21, 260–266+271. [Google Scholar]
- Li, H.; Huang, Y.H.; Jiang, F.S.; Lin, J.S.; Li, S.S.; Li, F.; Zheng, Z. Effects of two herbal plants’ roots on soil shear strength in a collapsing gully alluvial fan. J. Soil Water Conserv. 2017, 31, 96–101. [Google Scholar] [CrossRef]
- Xie, M.S. A study on the soil mechanical role of tree roots in the stability of slopes. J. Soil Water Conserv. 1990, 7–14+50. [Google Scholar] [CrossRef]


| Factor Levels | A (Compaction Frequency/freq) | B (Number of Lateral Roots/pcs) | C (Taproot Length/cm) | D (Branching Angle of the Lateral Roots/deg) |
|---|---|---|---|---|
| 1 | 10 | 1 | 40 | 15 |
| 2 | 20 | 2 | 50 | 30 |
| 3 | 30 | 3 | 60 | 45 |
| 4 | 40 | 4 | 70 | 60 |
| Group Number | Column Number | Experimental Design | ||||
|---|---|---|---|---|---|---|
| A (Compaction Frequency/freq) | B (Number of Lateral Roots/pcs) | C (Taproot Length/cm) | D (Branching Angle of the Lateral Roots/deg) | Blank Column | ||
| 1 | 1 | 2 | 3 | 2 | 3 | A1B2C3D2 |
| 2 | 3 | 4 | 1 | 2 | 2 | A3B4C1D2 |
| 3 | 2 | 4 | 3 | 3 | 4 | A2B4C3D3 |
| 4 | 4 | 2 | 1 | 3 | 1 | A4B2C1D3 |
| 5 | 1 | 3 | 1 | 4 | 4 | A1B3C1D4 |
| 6 | 3 | 1 | 3 | 4 | 1 | A3B1C3D4 |
| 7 | 2 | 1 | 1 | 1 | 3 | A2B1C1D1 |
| 8 | 4 | 3 | 3 | 1 | 2 | A4B3C3D1 |
| 9 | 1 | 1 | 4 | 3 | 2 | A1B1C4D3 |
| 10 | 3 | 3 | 2 | 3 | 3 | A3B3C2D3 |
| 11 | 2 | 3 | 4 | 2 | 1 | A2B3C4D2 |
| 12 | 4 | 1 | 2 | 2 | 4 | A4B1C2D2 |
| 13 | 1 | 4 | 2 | 1 | 1 | A1B4C2D1 |
| 14 | 3 | 2 | 4 | 1 | 4 | A3B2C4D1 |
| 15 | 2 | 2 | 2 | 4 | 2 | A2B2C2D4 |
| 16 | 4 | 4 | 4 | 4 | 3 | A4B4C4D4 |
| Group Number | Measured Value/N | Mean Value/N | 30% of the Mean Value/N | Range/N | Pullout Resistance Characteristic Value/N | ||
|---|---|---|---|---|---|---|---|
| 1 | 60 | 60 | 65 | 61.7 | 18.5 | 5 | 61.7 |
| 2 | 120 | 120 | 140 | 126.7 | 38 | 20 | 126.7 |
| 3 | 140 | 140 | 140 | 140 | 42 | 0 | 140 |
| 4 | 40 | 35 | 40 | 38.3 | 11.5 | 5 | 38.3 |
| 5 | 65 | 65 | 70 | 66.7 | 20 | 5 | 66.7 |
| 6 | 55 | 70 | 70 | 65 | 19.5 | 15 | 65 |
| 7 | 20 | 20 | 22.5 | 20.8 | 6.2 | 2.5 | 20.8 |
| 8 | 70 | 130 | 130 | 110 | 33 | 60 | 130 |
| 9 | 60 | 55 | 75 | 63.3 | 19 | 20 | 57.5 |
| 10 | 90 | 90 | 100 | 93.3 | 28 | 10 | 93.3 |
| 11 | 100 | 110 | 100 | 103.3 | 31 | 10 | 103.3 |
| 12 | 50 | 60 | 60 | 56.7 | 17 | 10 | 56.7 |
| 13 | 65 | 70 | 70 | 68.3 | 20.5 | 5 | 68.3 |
| 14 | 90 | 90 | 80 | 86.7 | 26 | 10 | 86.7 |
| 15 | 50 | 55 | 55 | 53.3 | 16 | 5 | 53.3 |
| 16 | 180 | 180 | 180 | 180 | 54 | 0 | 180 |
| Factors | A (Compaction Frequency/freq) | B (Number of Lateral Roots/pcs) | C (Taproot Length/cm) | D (Branching Angle of the Lateral Roots/deg) | Error Column | |
|---|---|---|---|---|---|---|
| Ki | K1 | 254.2 | 200.0 | 252.5 | 305.8 | 274.9 |
| K2 | 317.4 | 240.0 | 271.6 | 348.4 | 367.5 | |
| K3 | 371.7 | 393.3 | 396.7 | 329.1 | 355.8 | |
| K4 | 405.0 | 515.0 | 427.5 | 365.0 | 350.1 | |
| ki | k1 | 63.6 | 50.0 | 63.1 | 76.5 | 68.7 |
| k2 | 79.4 | 60.0 | 67.9 | 87.1 | 91.9 | |
| k3 | 92.9 | 98.3 | 99.2 | 82.3 | 89.0 | |
| k4 | 101.3 | 128.8 | 106.9 | 91.3 | 87.5 | |
| 150.8 | 315.0 | 175.0 | 59.2 | 92.6 | ||
| Factor Priority | B → C → A → D | |||||
| Optimal Solution | B4C4A4D4 | |||||
| Sources of Variance | Sum of Squared Deviations | Degrees of Freedom | Mean Square | F-Value | Critical Value | Significance |
|---|---|---|---|---|---|---|
| A | 3267.02 | 3 | 1089.01 | 3.60 | F0.1(3,6) = 3.29 | o |
| B | 15,757.92 | 3 | 5252.64 | 17.36 | F0.01(3,6) = 9.78 | ** |
| C | 5792.93 | 3 | 1930.98 | 6.38 | F0.05(3,6) = 4.76 | * |
| D | 487.45 | 3 | 162.48 | — | Compare the F-values of each factor with their critical values. | — |
| Error Column | 1327.92 | 3 | 442.64 | — | — | |
| The mean square value of factor D, 162.48, is lower than the mean square value of the error term, 442.64. Consequently, factor D is incorporated into a new error term, and a recalibration of the sums of squares, degrees of freedom, and mean squares is performed. | — | |||||
| New Error Term | 1815.37 | 6 | 302.56 | — | — | — |
| Factors | |||
|---|---|---|---|
| A (Compaction Frequency/freq) | 101.3 | 63.6 | 0.372 |
| B (Number of Lateral Roots/pcs) | 128.8 | 50.0 | 0.612 |
| C (Taproot Length/cm) | 106.9 | 63.1 | 0.410 |
| D (Branching Angle of the Lateral Roots/deg) | 91.3 | 76.5 | 0.162 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhai, K.; Zhang, J.; Zhang, L.; Luo, X.; Wang, K. Integrating Root Morphology Based on Whole-Pullout Test of Model Roots: A Case Study. Appl. Sci. 2024, 14, 764. https://doi.org/10.3390/app14020764
Zhai K, Zhang J, Zhang L, Luo X, Wang K. Integrating Root Morphology Based on Whole-Pullout Test of Model Roots: A Case Study. Applied Sciences. 2024; 14(2):764. https://doi.org/10.3390/app14020764
Chicago/Turabian StyleZhai, Kexiang, Junyun Zhang, Le Zhang, Xiaolong Luo, and Kai Wang. 2024. "Integrating Root Morphology Based on Whole-Pullout Test of Model Roots: A Case Study" Applied Sciences 14, no. 2: 764. https://doi.org/10.3390/app14020764
APA StyleZhai, K., Zhang, J., Zhang, L., Luo, X., & Wang, K. (2024). Integrating Root Morphology Based on Whole-Pullout Test of Model Roots: A Case Study. Applied Sciences, 14(2), 764. https://doi.org/10.3390/app14020764






