Analysis of the Effects of Parameters on the Performance of Resonators Based on a ZnO/SiO2/Diamond Structure
Abstract
:1. Introduction
2. Simulation Principle and Model Structure
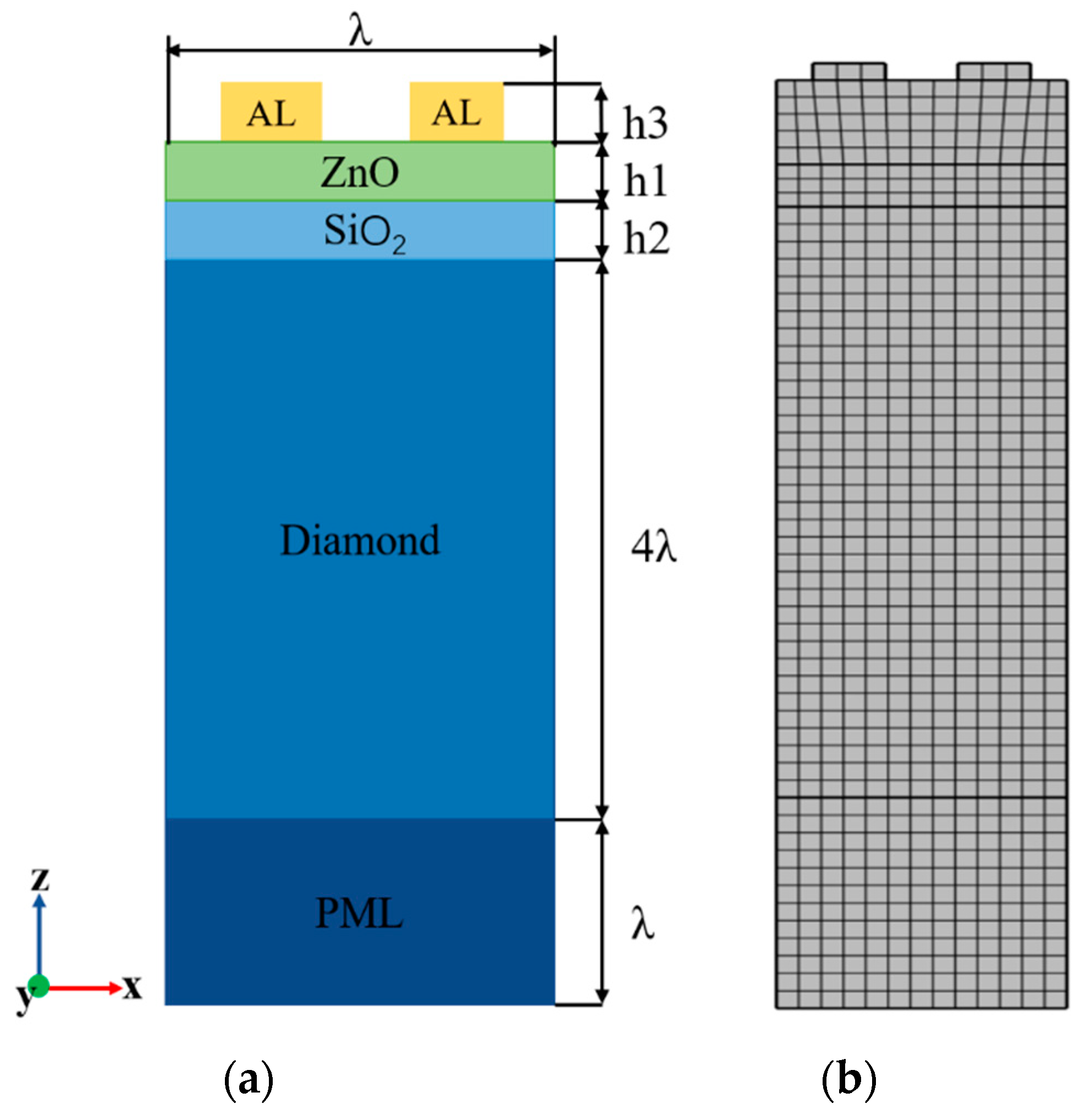
2.1. Model Structure
2.2. Model’s Material Parameters
3. Simulation Performance Analysis
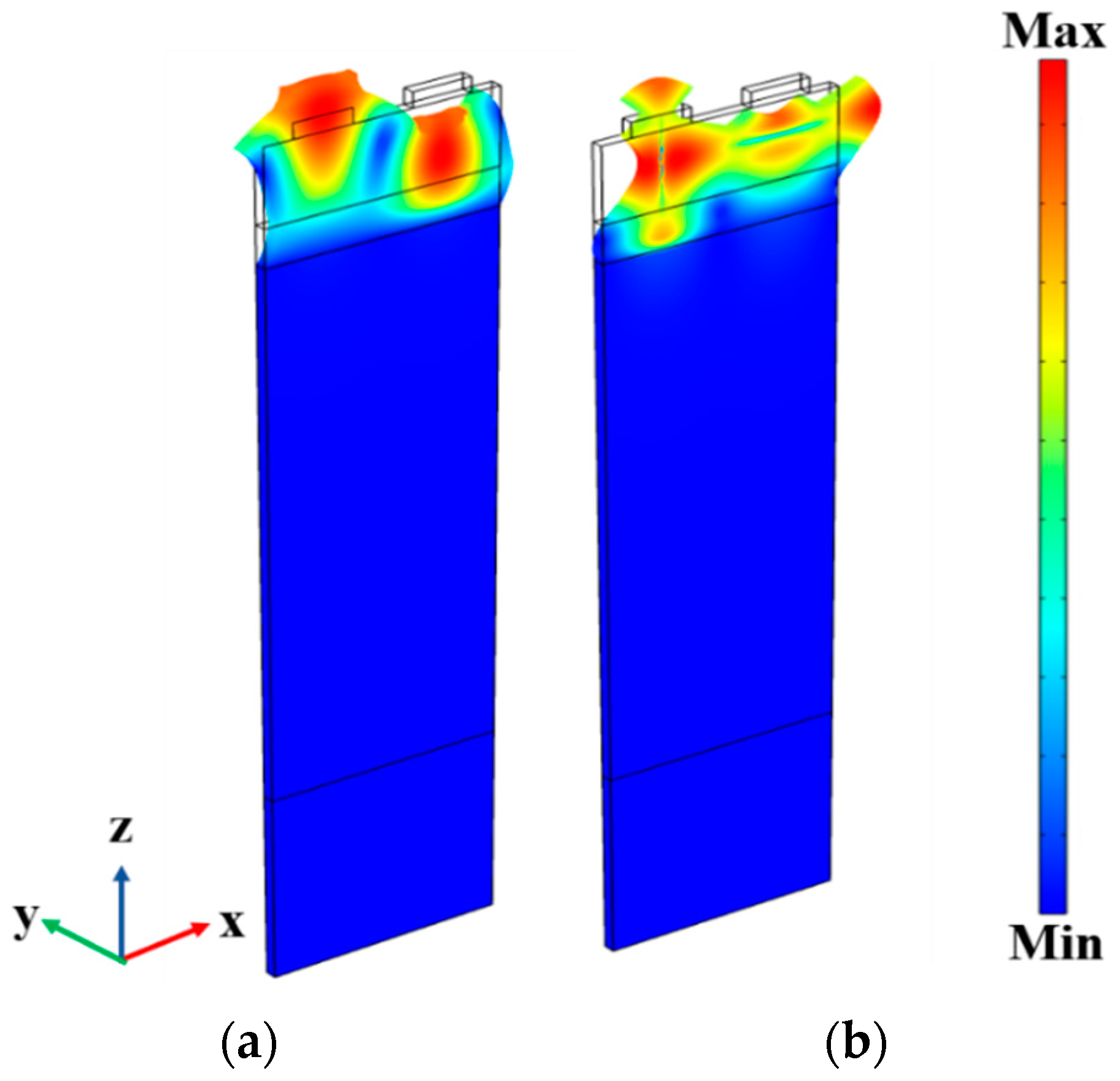
3.1. Modal Analysis
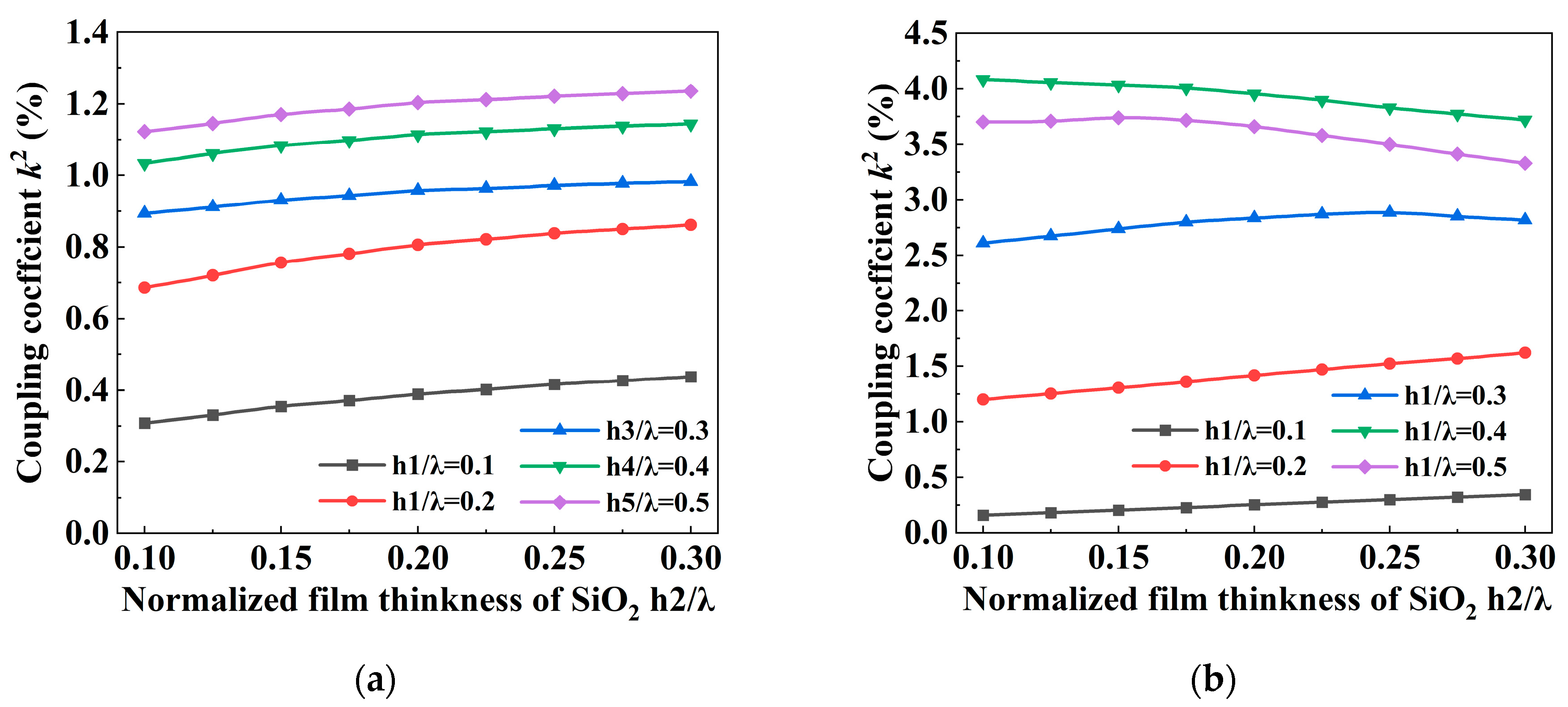
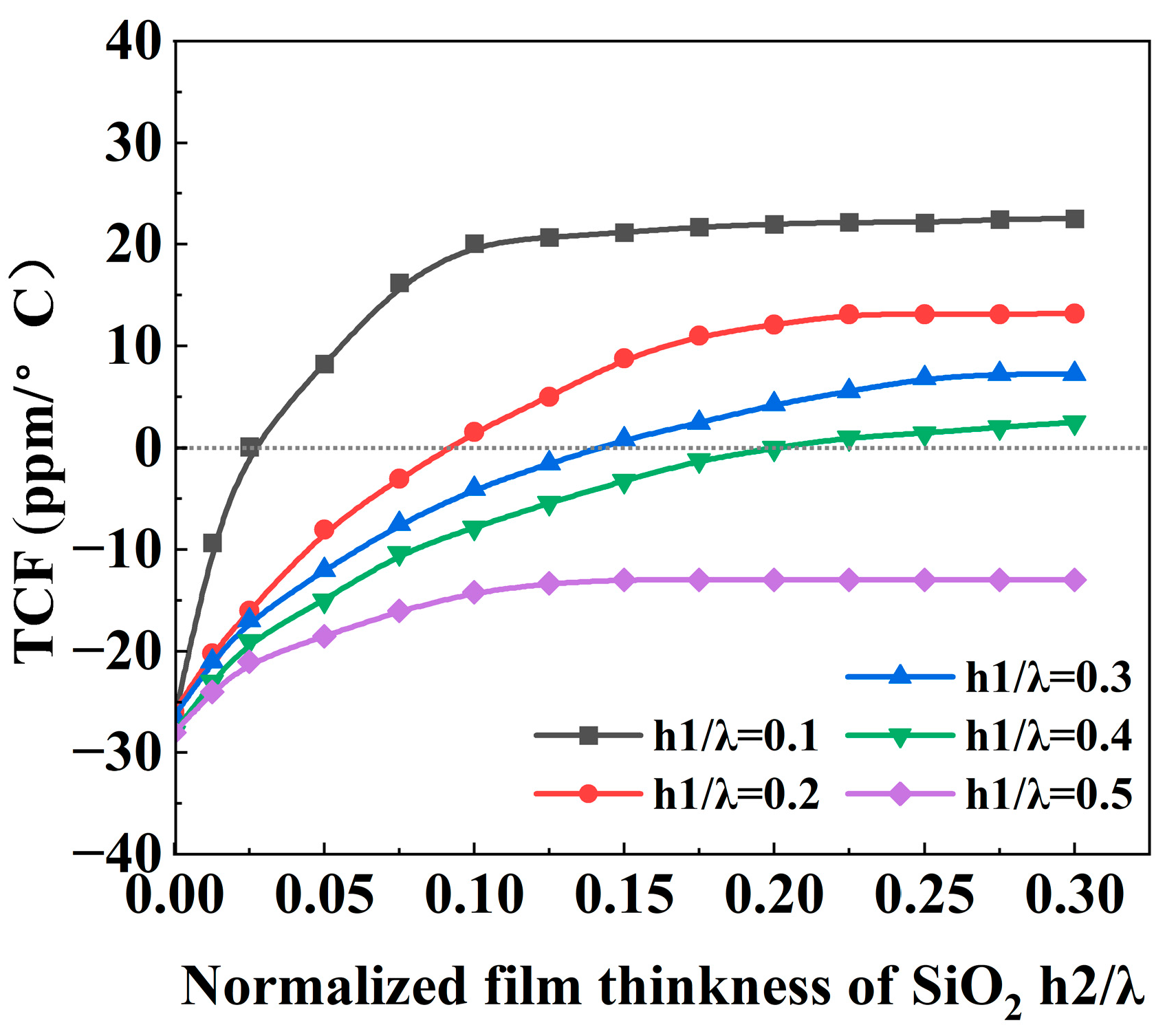
3.2. Piezoelectric and SiO2 Film Effects on the Properties of SAW Propagation
3.3. Impact of Electrode Thickness on SAW Propagation Properties
3.4. Modal Analysis of Rayleigh and Sezawa Modes
3.5. Resonator Design and Simulation
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hashimoto, K. RF Bulk Acoustic Wave Filters for Communications; ARTECH House: Norwood, MA, USA, 2009. [Google Scholar]
- Ruby, R. A Snapshot in Time: The Future in Filters for Cell Phones. IEEE Microw. Mag. 2015, 16, 46–59. [Google Scholar] [CrossRef]
- Park, M.; Hao, Z.; Dargis, R.; Clark, A.; Ansari, A. Epitaxial Aluminum Scandium Nitride Super High Frequency Acoustic Resonators. J. Microelectromech. Syst. 2020, 29, 490–498. [Google Scholar] [CrossRef]
- Zou, J.; Yantchev, V.; Iliev, F.; Plessky, V.; Samadian, S.; Hammond, R.B.; Turner, P.J. Ultra-Large-Coupling and Spurious-Free SH 0 Plate Acoustic Wave Resonators Based on Thin LiNbO3. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2020, 67, 374–386. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.; Kadota, M.; Tanaka, S. Investigation on the Temperature Coefficient of Frequency Performance of LiNbO3 on Quartz and Glass Surface Acoustic Wave Resonators. Jpn. J. Appl. Phys. 2023, 62, SJ1024. [Google Scholar] [CrossRef]
- Zhu, J.; Wang, H.; Zhang, F.; Ding, Q. High-Performance SAW Low Temperature Sensors with Double Electrode Transducers Based on 128° YX LiNbO3. Micromachines 2022, 13, 1912. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Fu, S.-L.; Song, C.; Wang, G.-Y.; Zeng, F.; Pan, F. Improved Resistance to Electromigration and Acoustomigration of Al Interdigital Transducers by Ni Underlayer. Rare Met. 2018, 37, 823–830. [Google Scholar] [CrossRef]
- Qian, J.; Li, C.; Qian, L.; Li, M.; Li, H.; Yang, B. Three-Dimensional Finite Element Simulation of Love Mode Surface Acoustic Wave in Layered Structures Including ZnO Piezoelectric Film and Diamond Substrate. Diam. Relat. Mater. 2018, 88, 123–128. [Google Scholar] [CrossRef]
- Assouar, M.B.; Elmazria, O.; Jiménez Riobóo, R.; Sarry, F.; Alnot, P. Modelling of SAW Filter Based on ZnO/Diamond/Si Layered Structure Including Velocity Dispersion. Appl. Surf. Sci. 2000, 164, 200–204. [Google Scholar] [CrossRef]
- Su, R.; Shen, J.; Lu, Z.; Xu, H.; Niu, Q.; Xu, Z.; Zeng, F.; Song, C.; Wang, W.; Fu, S.; et al. Wideband and Low-Loss Surface Acoustic Wave Filter Based on 15° YX-LiNbO₃/SiO₂/Si Structure. IEEE Electron Device Lett. 2021, 42, 438–441. [Google Scholar] [CrossRef]
- Ishihara, M.; Nakamura, T.; Kokai, F.; Koga, Y. Preparation of AlN and LiNbO3 Thin Films on Diamond Substrates by Sputtering Method. Diam. Relat. Mater. 2002, 11, 408–412. [Google Scholar] [CrossRef]
- Lamanna, L.; Rizzi, F.; Guido, F.; Algieri, L.; Marras, S.; Mastronardi, V.M.; Qualtieri, A.; De Vittorio, M. Flexible and Transparent Aluminum-Nitride-Based Surface-Acoustic-Wave Device on Polymeric Polyethylene Naphthalate. Adv. Electron. Mater. 2019, 5, 1900095. [Google Scholar] [CrossRef]
- Fu, S.; Wang, W.; Qian, L.; Li, Q.; Lu, Z.; Shen, J.; Song, C.; Zeng, F.; Pan, F. High-Frequency Surface Acoustic Wave Devices Based on ZnO/SiC Layered Structure. IEEE Electron Device Lett. 2019, 40, 103–106. [Google Scholar] [CrossRef]
- Li, Q.; Qian, L.; Fu, S.; Song, C.; Zeng, F.; Pan, F. Characteristics of One-Port Surface Acoustic Wave Resonator Fabricated on ZnO/6H-SiC Layered Structure. J. Phys. D Appl. Phys. 2018, 51, 145305. [Google Scholar] [CrossRef]
- Luo, J.; Quan, A.; Fu, C.; Li, H. Shear-Horizontal Surface Acoustic Wave Characteristics of a (110) ZnO/SiO2/Si Multilayer Structure. J. Alloys Compd. 2017, 693, 558–564. [Google Scholar] [CrossRef]
- Fu, S.; Li, Q.; Gao, S.; Wang, G.; Zeng, F.; Pan, F. Quality-Enhanced AlN Epitaxial Films Grown on c-Sapphire Using ZnO Buffer Layer for SAW Applications. Appl. Surf. Sci. 2017, 402, 392–399. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, H. Investigation of Surface Acoustic Wave Propagation Characteristics in New Multilayer Structure: SiO2/IDT/LiNbO3/Diamond/Si. Micromachines 2021, 12, 1286. [Google Scholar] [CrossRef] [PubMed]
- Maouhoub, S.; Aoura, Y.; Mir, A. FEM Simulation of Rayleigh Waves for SAW Devices Based on ZnO/AlN/Si. Microelectron. Eng. 2015, 136, 22–25. [Google Scholar] [CrossRef]
- Su, R.; Fu, S.; Shen, J.; Chen, Z.; Lu, Z.; Yang, M.; Wang, R.; Zeng, F.; Wang, W.; Song, C.; et al. Enhanced Performance of ZnO/SiO2/Al2O3 Surface Acoustic Wave Devices with Embedded Electrodes. ACS Appl. Mater. Amp. Interfaces 2020, 12, 42378–42385. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, S.-Y.; Fan, L.; Shui, X.-J.; Zhang, Z.-N.; Wasa, K. Characteristics of Surface Acoustic Waves Excited by (1120) Zno Films Deposited on R-Sapphire Substrates. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2013, 60, 1213–1218. [Google Scholar] [CrossRef]
- Fang, J.; Wu, Z. Generalized Perfectly Matched Layer-an Extension of Berenger’s Perfectly Matched Layer Boundary Condition. IEEE Microw. Guid. Wave Lett. 1995, 5, 451–453. [Google Scholar] [CrossRef]
- Kannan, T. Finite Element Analysis of Surface Acoustic Wave Resonators. Master’s Thesis, University of Saskatchewan, Saskatoon, Canada, 2006. [Google Scholar]
- Tomar, M.; Gupta, V.; Sreenivas, K.; Mansingh, A. Temperature Stability of ZnO Thin Film SAW Device on Fused Quartz. IEEE Trans. Device Mater. Reliab. 2005, 5, 494–500. [Google Scholar] [CrossRef]
- Maouhoub, S.; Aoura, Y.; Mir, A. FEM Simulation of AlN Thin Layers on Diamond Substrates for High Frequency SAW Devices. Diam. Relat. Mater. 2016, 62, 7–13. [Google Scholar] [CrossRef]
- Aslam, M.; Jeoti, V.; Karuppanan, S.; Malik, A.; Iqbal, A. FEM Analysis of Sezawa Mode SAW Sensor for VOC Based on CMOS Compatible AlN/SiO₂/Si Multilayer Structure. Sensors 2018, 18, 1687. [Google Scholar] [CrossRef] [PubMed]
- Benetti, M.; Cannata, D.; Di Pictrantonio, F.; Verona, E. Growth of AlN Piezoelectric Film on Diamond for High-Frequency Surface Acoustic Wave Devices. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2005, 52, 1806–1811. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Shao, M.; Jiang, B.; Cao, L. Surface Acoustic Wave Pressure Sensor and Its Matched Antenna Design. Meas. Control. 2019, 52, 947–954. [Google Scholar] [CrossRef]
- Qianliang, X. Simulation of Surface Acoustic Wave Tag Based on COMSOL. Yadian Shengguang 2012, 34, 494–497. [Google Scholar]
- Kaletta, U.C.; Santos, P.V.; Wolansky, D.; Scheit, A.; Fraschke, M.; Wipf, C.; Zaumseil, P.; Wenger, C. Monolithic Integrated SAW Filter Based on AlN for High-Frequency Applications. Semicond. Sci. Technol. 2013, 28, 065013. [Google Scholar] [CrossRef]
- Zhou, C.; Yang, Y.; Cai, H.; Ren, T.-L.; Chan, M.; Yang, C.Y. Temperature-Compensated High-Frequency Surface Acoustic Wave Device. IEEE Electron Device Lett. 2013, 34, 1572–1574. [Google Scholar] [CrossRef]
- Li, L.; Wang, F.; Li, K.; Han, Y.; Hu, K.; Sun, Z.; Xie, Y.; Kong, D.; Song, D.; Qian, L.; et al. Effect of Interdigital Transducers Structure on Insertion Loss of High-Frequency Surface Acoustic Wave Devices. J. Mater. Sci. Mater. Electron. 2022, 33, 22017–22026. [Google Scholar] [CrossRef]
- Feld, D.A.; Parker, R.; Ruby, R.; Bradley, P.; Dong, S. After 60 Years: A New Formula for Computing Quality Factor Is Warranted. In Proceedings of the 2008 IEEE Ultrasonics Symposium, Beijing, China, 2–5 November 2008. [Google Scholar]




| Item | Symbol | Al | ZnO | SiO2 | Diamond |
|---|---|---|---|---|---|
| Elastic constant (1011 N/m2) | C11 | 1.11 | 2.096 | 0.785 | 11.531 |
| C12 | 0.59 | 1.205 | 0.161 | 0.864 | |
| C13 | 0.59 | 1.046 | 0.161 | 0.864 | |
| C33 | 1.11 | 2.106 | 0.785 | 11.531 | |
| C44 | 0.26 | 0.423 | 0.311 | 5.333 | |
| Temperature coefficients of elastic constants (10−4/°C) | TC11 | −5.9 | −1.12 | 2.39 | −0.14 |
| TC13 | −0.8 | −1.61 | 5.84 | −0.57 | |
| TC33 | −5.9 | −1.23 | 2.39 | −0.14 | |
| TC44 | −5.2 | −0.70 | 1.51 | −0.125 | |
| Piezoelectric constants (C/m2) | e15 | - | −0.48 | - | - |
| e31 | - | −0.573 | - | - | |
| e33 | - | 1.321 | - | - | |
| Relative dielectric constants | ε11/ ε0 | 1 | 8.55 | 3.32 | 5.67 |
| ε33/ε0 | 1 | 10.2 | 3.32 | 5.67 | |
| Mass density (103 kg/m3) | p | 2.7 | 5.665 | 2.2 | 3.512 |
| Temperature coefficients of mass density (10−6/°C) | TP | −1.65 | −10.1 | −54 | −3.6 |
| Item | Symbol | Value |
|---|---|---|
| Wavelength (um) | λ | 2 |
| ZnO thickness (um) | h1 | 0.4 λ |
| SiO2 thickness (um) | h2 | 0.2 λ |
| Al electrode thickness | h3 | 0.08 λ |
| Metallization rate | MR | 50% |
| IDT pairs | Nt | 130 |
| Aperture width (um) | W | 40 λ |
| Reflecting grating pairs | Ng | 25 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, G.; Wang, H.; Zhang, P. Analysis of the Effects of Parameters on the Performance of Resonators Based on a ZnO/SiO2/Diamond Structure. Appl. Sci. 2024, 14, 874. https://doi.org/10.3390/app14020874
Cao G, Wang H, Zhang P. Analysis of the Effects of Parameters on the Performance of Resonators Based on a ZnO/SiO2/Diamond Structure. Applied Sciences. 2024; 14(2):874. https://doi.org/10.3390/app14020874
Chicago/Turabian StyleCao, Gang, Hongliang Wang, and Peng Zhang. 2024. "Analysis of the Effects of Parameters on the Performance of Resonators Based on a ZnO/SiO2/Diamond Structure" Applied Sciences 14, no. 2: 874. https://doi.org/10.3390/app14020874
APA StyleCao, G., Wang, H., & Zhang, P. (2024). Analysis of the Effects of Parameters on the Performance of Resonators Based on a ZnO/SiO2/Diamond Structure. Applied Sciences, 14(2), 874. https://doi.org/10.3390/app14020874






