Experimental and Numerical Research on the Splitting Capacity of European Beech Beams Loaded Perpendicular to the Grain by Connections: Influence of Different Geometrical Parameters
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Test
2.2. Numerical Analysis
2.3. Design Models
3. Results and Discussion
3.1. Experimental Results
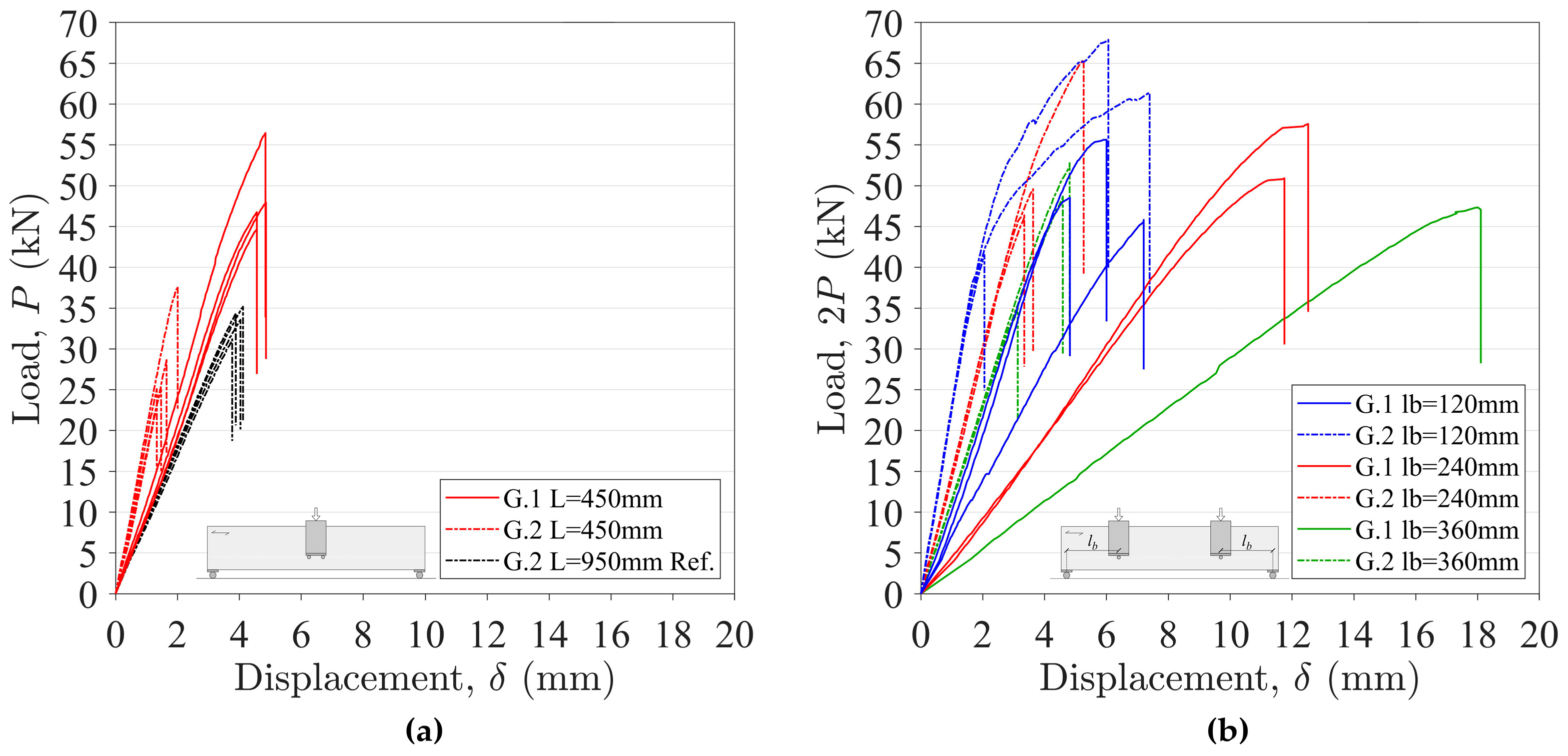
3.1.1. Splitting Loads and Failure Modes
3.1.2. Influence of the Number of Dowels at the Connection
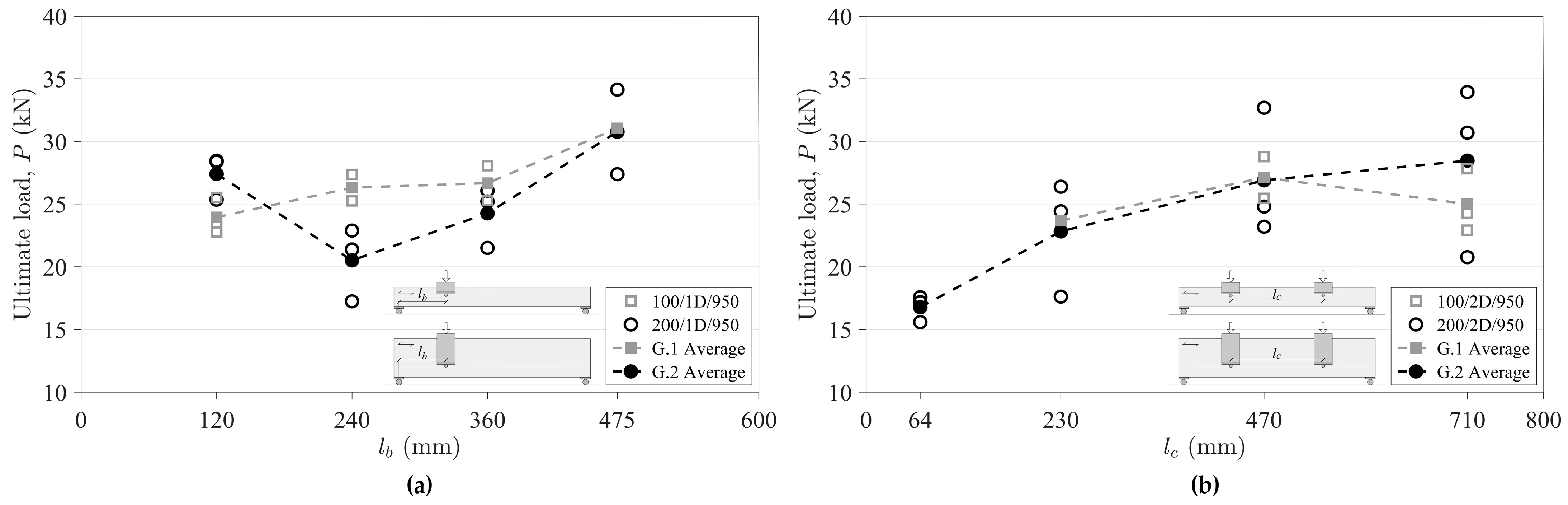
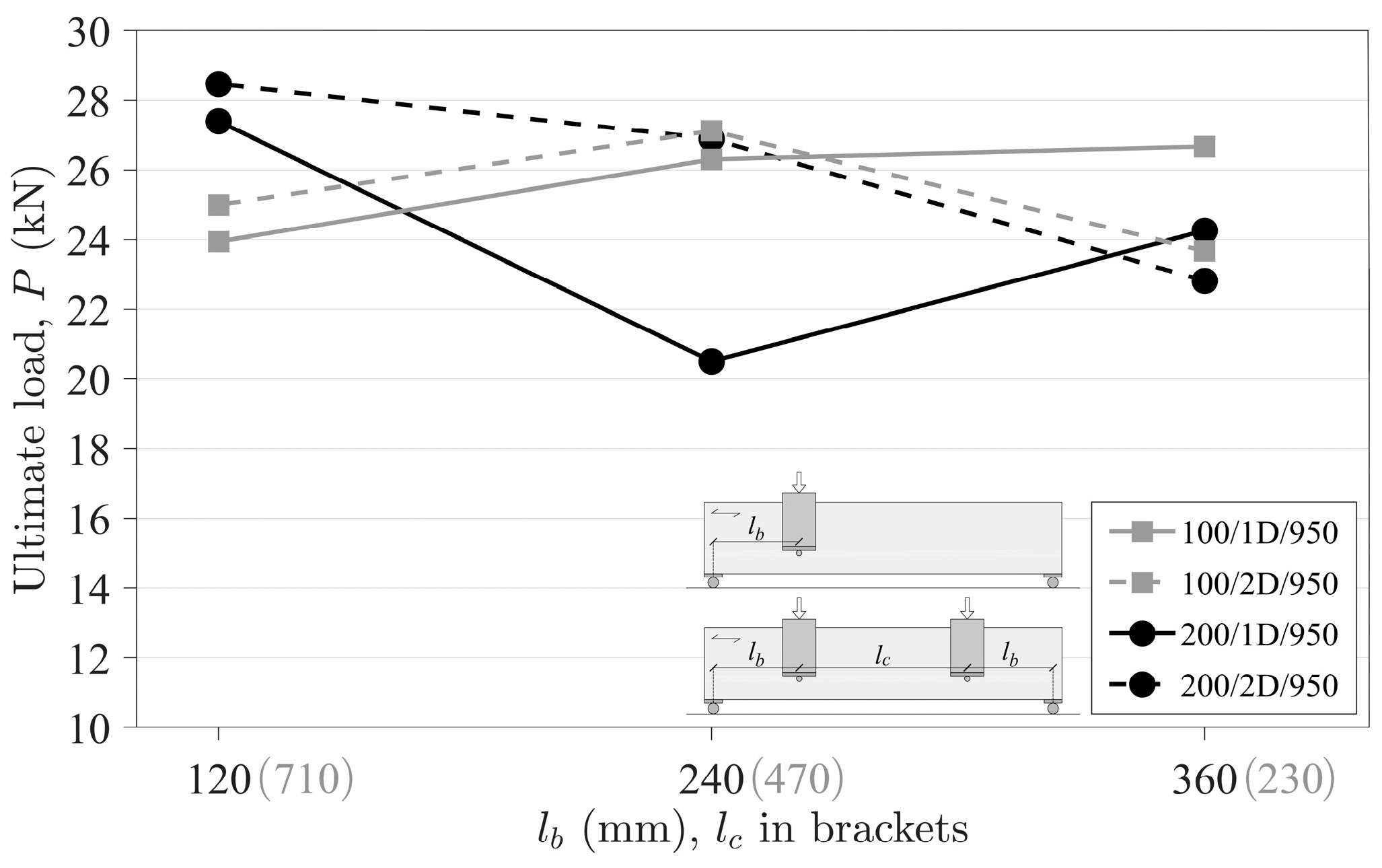
3.1.3. Influence of Distances lb and lc
3.1.4. Influence of the Number of Connections
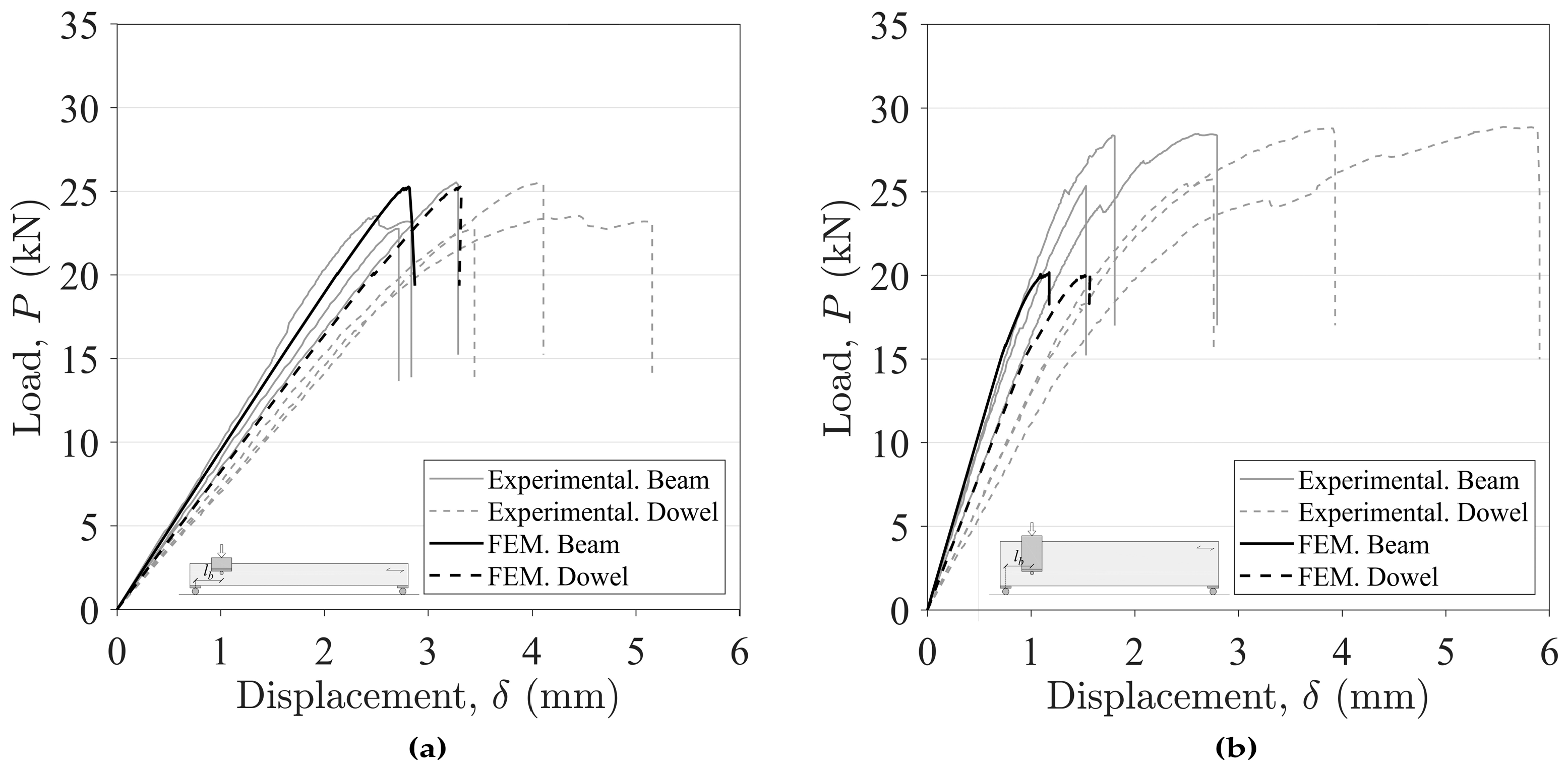
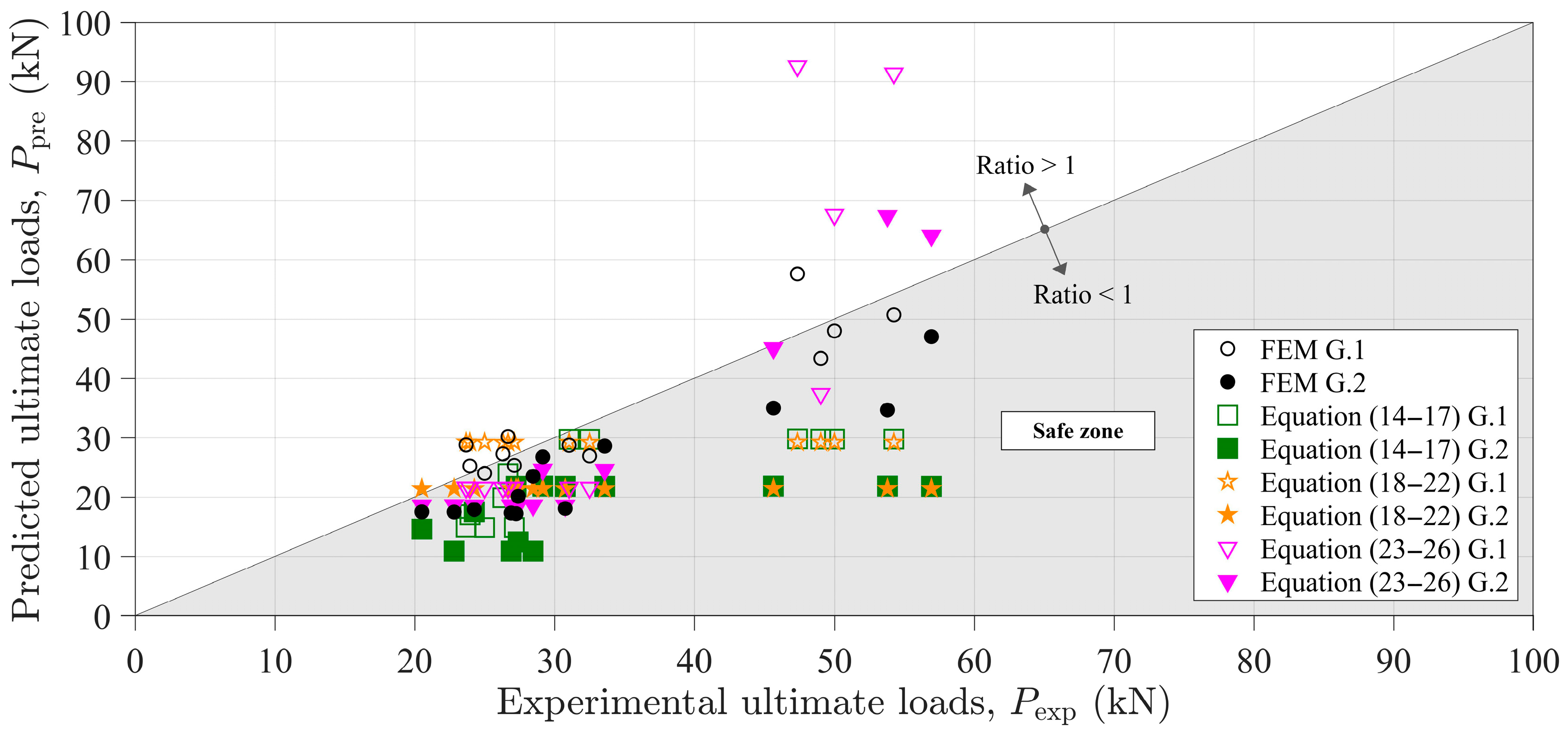
3.2. Comparison between Experimental, Numerical, and Theoretical Failure Loads
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gustavsson, L.; Sathre, R. Variability in Energy and Carbon Dioxide Balances of Wood and Concrete Building Materials. Build. Environ. 2006, 41, 940–951. [Google Scholar] [CrossRef]
- UNEP. Buildings and Climate Change: Summary for Decision-Makers; UNEP DTIE, Sustainable Consumption & Production Branch: Paris, France, 2009; ISBN 987-9-28073-064-7. [Google Scholar]
- Buchanan, A.H.; Honey, B.G. Energy and Carbon Dioxide Implications of Building Construction. Energy Build. 1994, 20, 205–217. [Google Scholar] [CrossRef]
- Sathre, R.; Gustavsson, L. Using Wood Products to Mitigate Climate Change: External Costs and Structural Change. Appl. Energy 2009, 86, 251–257. [Google Scholar] [CrossRef]
- UNECE; FAO. Circularity Concepts in Wood Construction; United Nations Publication: Geneva, Switzerland, 2023; ISBN 978-9-21117-328-4. [Google Scholar]
- Aicher, S.; Christian, Z.; Dill-Langer, G. Hardwood Glulams—Emerging Timber Products of Superior Mechanical Properties. In Proceedings of the World Conference on Timber Engineering (WCTE), Quebec City, QC, Canada, 10–14 August 2014. [Google Scholar]
- Camú, C.T.; Aicher, S. A Stochastic Finite Element Model for Glulam Beams of Hardwoods. In Proceedings of the World Conference on Timber Engineering, Seoul, Republic of Korea, 20–23 August 2018. [Google Scholar]
- De Rigo, D.; Caudullo, G. Fagus Sylvatica in Europe: Distribution, Habitat, Usage and Threats. In European Atlas of Forest Tree Species; Publication Office of the European Union: Luxembourg, 2016; pp. 94–95. ISBN 978-9-27617-291-8. [Google Scholar]
- Antonucci, S.; Santopuoli, G.; Marchetti, M.; Tognetti, R.; Chiavetta, U.; Garfì, V. What Is Known About the Management of European Beech Forests Facing Climate Change? A Review. Curr. For. Rep. 2021, 7, 321–333. [Google Scholar] [CrossRef]
- Gómez-Royuela, J.L.; Majano-Majano, A.; Lara-Bocanegra, A.J.; Reynolds, T.P.S. Determination of the Elastic Constants of Thermally Modified Beech by Ultrasound and Static Tests Coupled with 3D Digital Image Correlation. Constr. Build. Mater. 2021, 302, 124270. [Google Scholar] [CrossRef]
- Ozyhar, T.; Hering, S.; Niemz, P. Viscoelastic Characterization of Wood: Time Dependence of the Orthotropic Compliance in Tension and Compression. J. Rheol. 2013, 57, 699–717. [Google Scholar] [CrossRef]
- Ozyhar, T.; Hering, S.; Sanabria, S.J.; Niemz, P. Determining Moisture-Dependent Elastic Characteristics of Beech Wood by Means of Ultrasonic Waves. Wood Sci. Technol. 2013, 47, 329–341. [Google Scholar] [CrossRef]
- Ozyhar, T.; Hering, S.; Niemz, P. Moisture-Dependent Orthotropic Tension-Compression Asymmetry of Wood. Holzforschung 2013, 67, 395–404. [Google Scholar] [CrossRef]
- Ozyhar, T.; Hering, S.; Niemz, P. Moisture-Dependent Elastic and Strength Anisotropy of European Beech Wood in Tension. J. Mater. Sci. 2012, 47, 6141–6150. [Google Scholar] [CrossRef]
- Widmann, R.; Fernandez-Cabo, J.L.; Steiger, R. Mechanical Properties of Thermally Modified Beech Timber for Structural Purposes. Eur. J. Wood Wood Prod. 2012, 70, 775–784. [Google Scholar] [CrossRef]
- Franke, S.; Magnière, N. The Embedment Failure of European Beech Compared to Spruce Wood and Standards. In Materials and Joints in Timber Structures; Aicher, S., Reinhardt, H.-W., Garrecht, H., Eds.; RILEM Bookseries; Springer: Dordrecht, The Netherlands, 2014; pp. 221–229. ISBN 978-9-40077-810-8. [Google Scholar]
- Gómez-Royuela, J.L.; Majano-Majano, A.; Lara-Bocanegra, A.J.; Xavier, J.; de Moura, M.F.S.F. Evaluation of R-Curves and Cohesive Law in Mode I of European Beech. Theor. Appl. Fract. Mech. 2022, 118, 103220. [Google Scholar] [CrossRef]
- Gómez-Royuela, J.L.; Majano-Majano, A.; Lara-Bocanegra, A.J.; Xavier, J.; de Moura, M.F.S.F. Shear Traction-separation Laws of European Beech under Mode II Loading by 3D Digital Image Correlation. Wood Sci. Technol. 2022, 56, 1631–1655. [Google Scholar] [CrossRef]
- Ehrhart, T.; Steiger, R.; Frangi, A. European Beech Glued Laminated Timber. Bautechnik 2021, 98, 104–114. [Google Scholar] [CrossRef]
- Blass, H.; Frese, M.; Enders-Comberg, M. Beech LVL—High Strength Material for Engineered Timber Structures. In Structures and Architecture: Beyond Their Limits, 1st ed.; Cruz, P.J., Ed.; CRC Press: Boca Raton, FL, USA, 2016; pp. 102–109. ISBN 978-1-31573-076-9. [Google Scholar]
- Lara-Bocanegra, A.J. Láminas Reticulares de Madera Deformadas Elásticamente. Del Material a La Construcción (In English: Elastic Timber Gridshells. From Material to Construction). Ph.D. Thesis, Universidad Politécnica de Madrid, Madrid, Spain, 2022. [Google Scholar] [CrossRef]
- Caldeira, T. Caracterização Experimental e Numérica Do Comportamento Frágil de Ligações Com Cavilhas Em Estruturas de Madeira (In English: Experimental and Numerical Characterisation of the Brittle Behaviour of Dowel Connections in Timber Structures). Ph.D. Thesis, Universidade de Trás-os-Montes e Alto Douro, Vila Real, Portugal, 2011. [Google Scholar]
- Franke, S.; Franke, B.; Heubuch, S.; Frangi, A.; Jockwer, R. Anschlüsse in Buchenholz. Ermittlung von Grundlagen Zur Bemessung von Anschlüssen Für Die Marktimplementierung in Der Schweiz; Berner Fachhochschule: Bern, Switzerland, 2019; ISBN 978-3-90687-806-5. [Google Scholar]
- EN 1995-1-1; Eurocode 5: Design of Timber Structures. Part 1-1: General. Common Rules and Rules for Buildings. European Committee for Standardization: Brussels, Belgium, 2016.
- Johansen, K.W. Theory of Timber Connections. Int. Assoc. Bridge Struct. Eng. 1949, 9, 249–262. [Google Scholar]
- Van der Put, T.A.C.M. Tension Perpendicular to the Grain at Notches and Joints. In Proceedings of the International Council for Research and Innovation in Building and Construction (CIB-W18), Lisbon, Portugal, 10–14 September 1990. [Google Scholar]
- Van der Put, T.A.C.M.; Leitjen, A.J.M. Evaluation of Perpendicular to Grain Failure of Beams Caused by Concentrated Loads of Joints. In Proceedings of the International Council for Research and Innovation in Building and Construction (CIB-W18), Delft, The Netherlands, 28–30 August 2000. [Google Scholar]
- Jensen, J.L.; Quenneville, P. Splitting of Beams Loaded Perpendicular to Grain by Connections. Some Issues with EC5. In Proceedings of the International Council for Research and Innovation in Building and Construction (CIB-W18), Alghero, Italy, 29 August–1 September 2011. [Google Scholar]
- Ballerini, M. A New Set of Experimental Tests on Beams Loaded Perpendicular to Grain by Dowel Type Joints. In Proceedings of the International Council for Research and Innovation in Building and Construction (CIB-W18), Graz, Austria, 23–25 August 1999. [Google Scholar]
- Möhler, K.; Lautenschläger, R. Groβflächige Queranschlüsse Bei Brettschichtholz; Forschungsbericht des Lehrstuhls für Ingenieurholzbau und Baukonstruktionen, Univ. Karlsruhe: Karlsruhe, Germany, 1978. [Google Scholar]
- Möhler, K.; Siebert, W. Ausbildung von Queranschlüssen Bei Angehängten Lasten an Brettschichtholzträger; Forschungsbericht des Lehrstuhls für Ingenieurholzbau und Baukonstruktionen, Univ. Karlsruhe: Karlsruhe, Germany, 1980. [Google Scholar]
- Ehlbeck, J.; Görlacher, R. Tragverhalten von Queranschlüssen Mittels Stahlblechformteilen, Insbesondere Balkenschuhen, Im Holzbau; Forschungsbericht der Versuchsanstalt für Stahl, Holz und Steine, Abt. Ingenieurholzbau, Univ. Karlsruhe: Karlsruhe, Germany, 1983. [Google Scholar]
- Ballerini, M. Beams Transversally Loaded by Dowel-Type Joints: Influence on Splitting Strength of Beam Thickness and Dowel Size. In Proceedings of the International Council for Research and Innovation in Building and Construction (CIB-W18), CO, USA, 11–14 August 2003. [Google Scholar]
- Schoenmakers, J.C.M. Fracture and Failure Mechanisms in Timber Loaded Perpendicular to the Grain by Mechanical Connections. Ph.D. Thesis, Technische Universiteit Eindhoven, Eindhoven, The Netherlands, 18 May 2010. [Google Scholar]
- Jensen, J.L.; Girhammar, U.A.; Quenneville, P.; Källsner, B. Splitting of Beams Loaded Perpendicular to Grain by Connections: Simple Fracture Mechanics Models. In Proceedings of the World Conference on Timber Engineering (WCTE), Auckland, New Zealand, 15–19 July 2012. [Google Scholar]
- Leijten, A.J.M. Splitting of Timber Beams Caused by Perpendicular to Grain Forces of Multiple Connections. Eng. Struct. 2018, 171, 10–14. [Google Scholar] [CrossRef]
- Franke, S.; Franke, B.; Quenneville, P. Analysis of the Failure Behaviour of Multiple Dowel-Type Connections Loaded Perpendicular to the Grain in LVL. In Proceedings of the World Conference on Timber Engineering (WCTE), Auckland, New Zealand, 16–19 July 2012. [Google Scholar]
- Hindman, D.P.; Finkenbinder, D.E.; Loferski, J.R.; Line, P. Strength of Sawn Lumber and Wood Composite Dowel Connections Loaded Perpendicular to Grain. I: NDS Design Equations. J. Mater. Civ. Eng. 2010, 22, 1217–1225. [Google Scholar] [CrossRef]
- Patel, M.C.; Hindman, D.P. Comparison of Single- and Two-Bolted LVL Perpendicular-to-Grain Connections. I: National Design Specification for Wood Construction Equations. J. Mater. Civ. Eng. 2012, 24, 339–346. [Google Scholar] [CrossRef]
- Majano-Majano, A.; Lara-Bocanegra, A.J.; Xavier, J.; Guaita, M. Splitting Capacity of Eucalyptus Globulus Beams Loaded Perpendicular to the Grain by Connections. Mater. Struct. 2022, 55, 147. [Google Scholar] [CrossRef]
- Franke, B.; Quenneville, P. Analyses of the Failure Behaviour of Transversely Loaded Dowel Type Connections in Wood. In Proceedings of the World Conference on Timber Engineering (WCTE), Trentino, Italy, 20–24 June 2010. [Google Scholar]
- Dourado, N.; Silva, F.G.A.; de Moura, M.F.S.F. Fracture Behavior of Wood-Steel Dowel Joints under Quasi-Static Loading. Constr. Build. Mater. 2018, 176, 14–23. [Google Scholar] [CrossRef]
- Shi, D.; Huang, H.; Li, N.; Liu, Y.; Demartino, C. Bolted Steel to Laminated Timber and Glubam Connections: Axial Behavior and Finite-Element Modeling. Int. J. Mech. Sci. 2023, 252, 108364. [Google Scholar] [CrossRef]
- Boström, L. Method of Determination of the Softening Behaviour of Wood and the Applicability of a Nonlinear Fracture Mechanics Model. Ph.D. Thesis, Lund University, Lund, Sweden, 1992. [Google Scholar]
- Franke, S.; Franke, B.; Magnière, N. Load Carrying Capacity of Cracked Beams. In Proceedings of the World Conference on Timber Engineering (WCTE), Vienna, Austria, 22–25 August 2016. [Google Scholar]
- Jensen, J.L.; Gustafsson, P.J.; Larsen, H.J. A Tensile Fracture Model for Joints with Rods or Dowels Loaded Perpendicular to Grain. In Proceedings of the International Council for Research and Innovation in Building and Construction (CIB-W18), Colorado, CO, USA, 11–14 August 2003. [Google Scholar]
- Franke, B.; Quenneville, P. Design Approach for the Splitting Failure of Dowel-Type Connections Loaded Perpendicular to Grain. In Proceedings of the International Council for Research and Innovation in Building and Construction (CIB-W18), Vancouver, BC, Canada, 26–29 August 2013. [Google Scholar]
- DIN 4074-5:2008; Strength Grading of Wood-Part 5: Sawn Hard Wood. DIN: Berlin, Germany, 2008. (In German)
- EN 1912:2012; Structural Timber. Strength Classes. Assignment of Visual Grades and Species. European Committee for Standardization: Brussels, Belgium, 2012.
- EN 13183-1:2002; Moisture Content of a Piece of Sawn Timber. Part 1: Determination by Oven Dry Method. European Committee for Standardization: Brussels, Belgium, 2002.
- EN 408:2010+A1:2012; Timber Structures. Structural Timber and Gluedlaminated Timber. Determination of Some Physical and Mechanical Properties. European Committee for Standardization: Brussels, Belgium, 2012.
- EN 384:2016+A1; Structural Timber. Determination of Characteristic Values of Mechanical Properties and Density. European Committee for Standardization: Brussels, Belgium, 2019.
- ABAQUS 2021 Documentation; Dassault Systèmes Simulia Corp.: Johnston, RI, USA, 2021.
- Gonçalves, J.P.M.; de Moura, M.F.S.F.; de Castro, P.M.S.T.; Marques, A.T. Interface Element Including Point-to-surface Constraints for Three-dimensional Problems with Damage Propagation. Eng. Comput. 2000, 17, 28–47. [Google Scholar] [CrossRef]
- Franke, B.; Quenneville, P. Numerical Modeling of the Failure Behavior of Dowel Connections in Wood. J. Eng. Mech. 2011, 137, 186–195. [Google Scholar] [CrossRef]
- McKenzie, W.M.; Karpovich, H. The Frictional Behaviour of Wood. Wood Sci. Technol. 1968, 2, 139–152. [Google Scholar] [CrossRef]
- Durão, L.M.P.; de Moura, M.F.S.F.; Marques, A.T. Numerical Simulation of the Drilling Process on Carbon/Epoxy Composite Laminates. Compos. Part A Appl. Sci. Manuf. 2006, 37, 1325–1333. [Google Scholar] [CrossRef]
- Silva, F.G.A.; de Moura, M.F.S.F.; Dourado, N.; Xavier, J.; Pereira, F.A.M.; Morais, J.J.L.; Dias, M.I.R. Mixed-Mode I+II Fracture Characterization of Human Cortical Bone Using the Single Leg Bending Test. J. Mech. Behav. Biomed. Mater. 2016, 54, 72–81. [Google Scholar] [CrossRef]
- Davila, C.; Camanho, P.; de Moura, M.F. Mixed-Mode Decohesion Elements for Analyses of Progressive Delamination. In Proceedings of the 19th AIAA Applied Aerodynamics Conference, Reston, VA, USA, 16–19 April 2001. [Google Scholar]
- Jockwer, R.; Dietsch, P. Review of Design Approaches and Test Results on Brittle Failure Modes of Connections Loaded at an Angle to the Grain. Eng. Struct. 2018, 171, 362–372. [Google Scholar] [CrossRef]
- Jensen, J.L.; Quenneville, P.; Girhammar, U.A.; Källsner, B. Brittle Failures in Timber Beams Loaded Perpendicular to Grain by Connections. J. Mater. Civ. Eng. 2015, 27, 4015026. [Google Scholar] [CrossRef]
- Leijten, A.J.M.; Jorissen, A.J.M. Splitting Strength of Beams Loaded by Connections Perpendicular to Grain, Model Validation. In Proceedings of the International Council for Research and Innovation in Building and Construction (CIB-W18), Venice, Italy, 22–24 August 2001. [Google Scholar]
- Jensen, J.L. Splitting Strength of Beams Loaded by Connections. In Proceedings of the International Council for Research and Innovation in Building and Construction (CIB-W18), CO, USA, 11–14 August 2003. [Google Scholar]
- Jensen, J.L. Splitting Strength of Beams Loaded Perpendicular to Grain by Dowel Joints. J. Wood Sci. 2005, 51, 480–485. [Google Scholar] [CrossRef]
- Ballerini, M. A New Prediction Formula for the Splitting Strength of Beams Loaded by Dowel-Type Connections. In Proceedings of the International Council for Research and Innovation in Building and Construction (CIB-W18), Edinburgh, Scotland, 31 August–3 September 2004. [Google Scholar]
- Habkirk, R.; Quenneville, J.H.P. Bolted Wood Connections Loaded Perpendicular-to-Grain: Effect on Wood Species. In Proceedings of the World Conference on Timber Engineering (WCTE), Portland, OR, USA, 6–10 August 2006. [Google Scholar]
- Reshke, R.G. Bolted Timber Connections Loaded Perpendicular-to-Grain. Influence of Joint Configuration Parameters on Strength. Ph.D. Thesis, Royal Military College of Canada, Kingston, ON, Canada, 11 May 1999. [Google Scholar]
- Yasumura, M. Criteria for Damage and Failure of Dowel-Type Joints Subjected To Force Perpendicular To the Grain. In Proceedings of the International Council for Research and Innovation in Building and Construction (CIB-W18), Venice, Italy, 22–24 August 2001. [Google Scholar]
- Jensen, J.L.; Quenneville, P.; Girhammar, U.A.; Källsner, B. Beams Loaded Perpendicular to Grain by Connections—Combined Effect of Edge and End Distance. In Proceedings of the International Council for Research and Innovation in Building and Construction (CIB-W18): Meeting Forty-Five, Växjö, Sweden, 27–30 August 2012. CIB-W18/45-7-2. [Google Scholar]
- Kasim, M.; Quenneville, P. Effect of Row Spacing on the Capacity of Bolted Timber Connections Loaded Perpendicular-to-Grain. In Proceedings of the International Council for Research and Innovation in Building and Construction (CIB-W18), Kyoto, Japan, 16–19 September 2002. [Google Scholar]

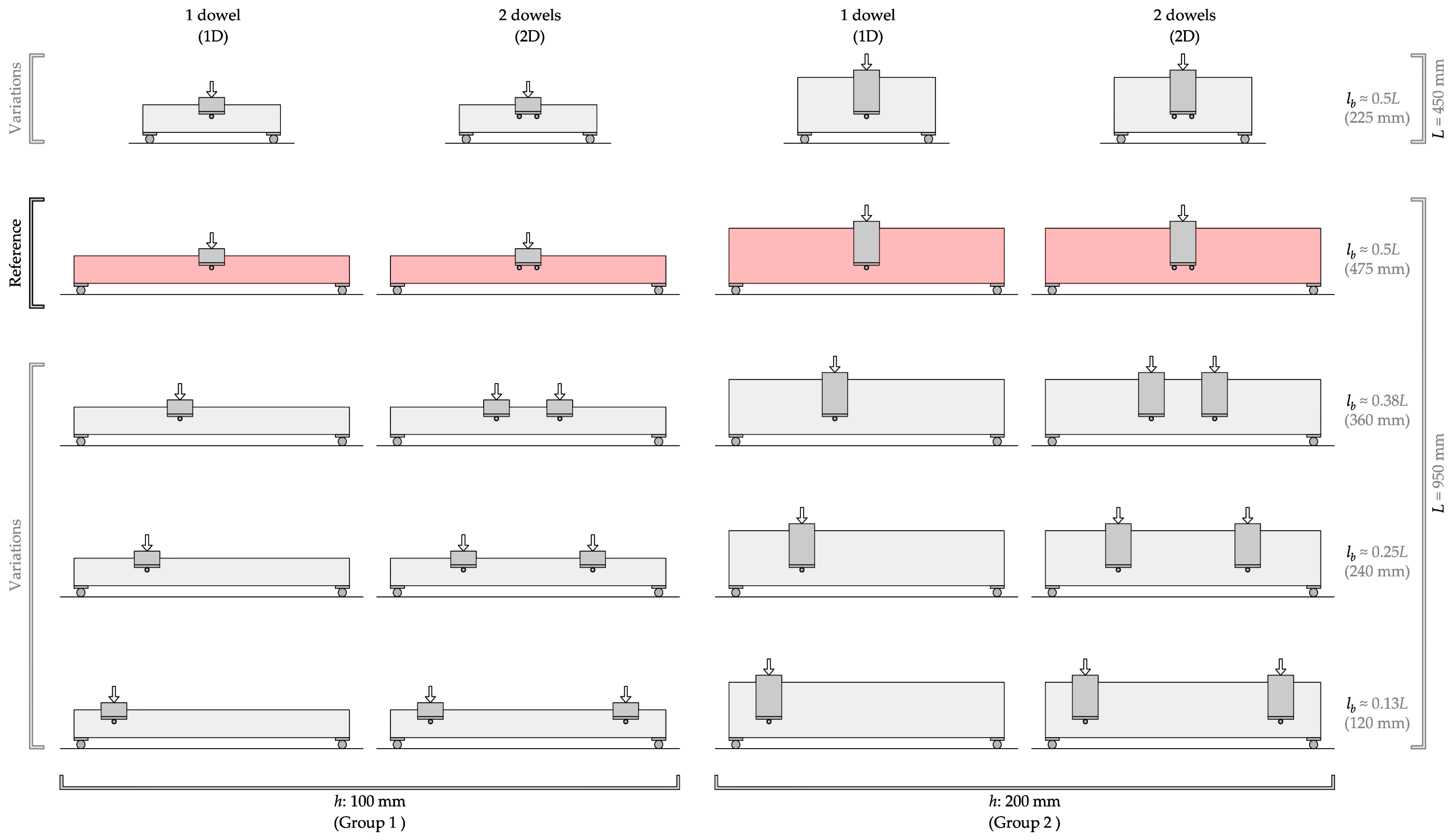
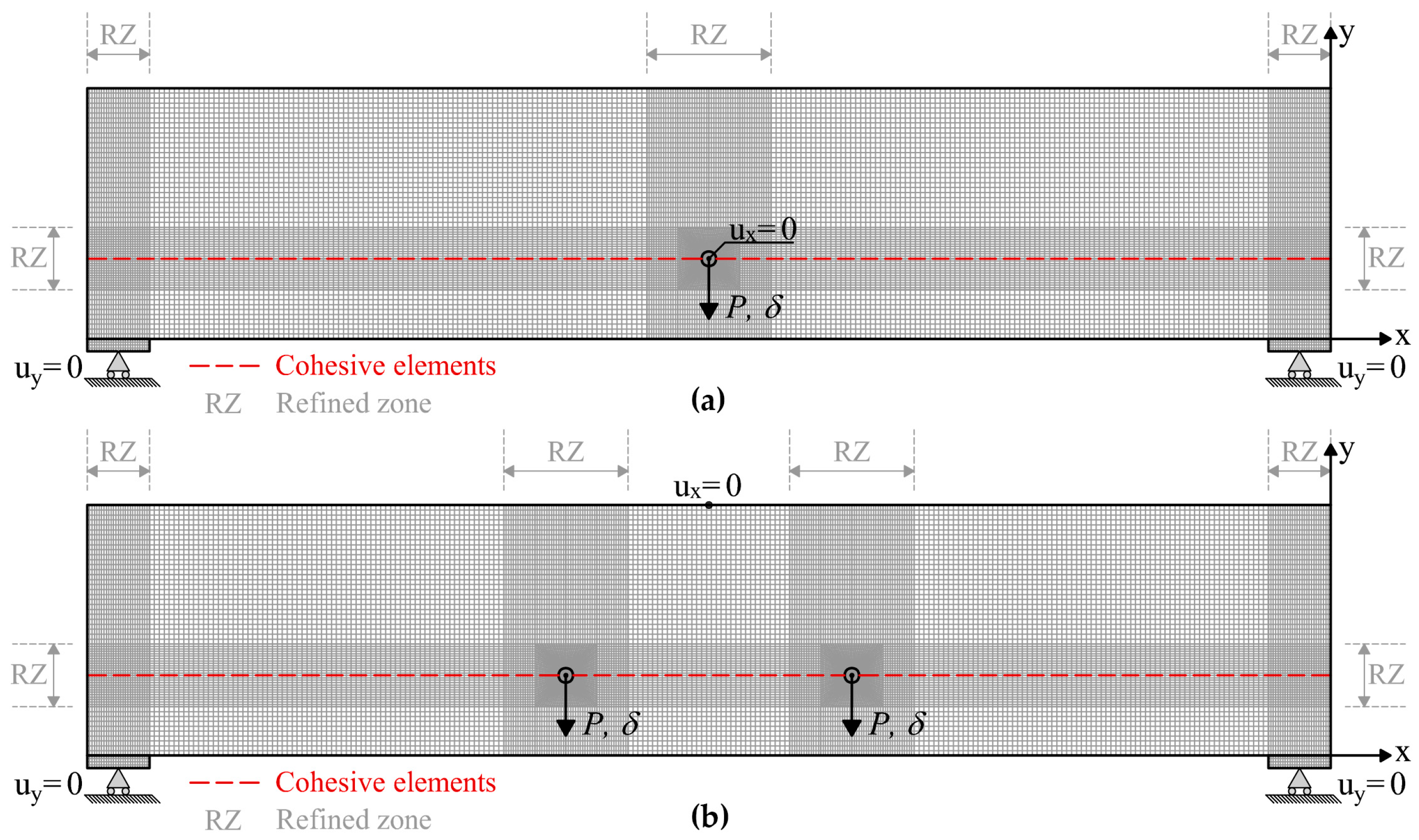
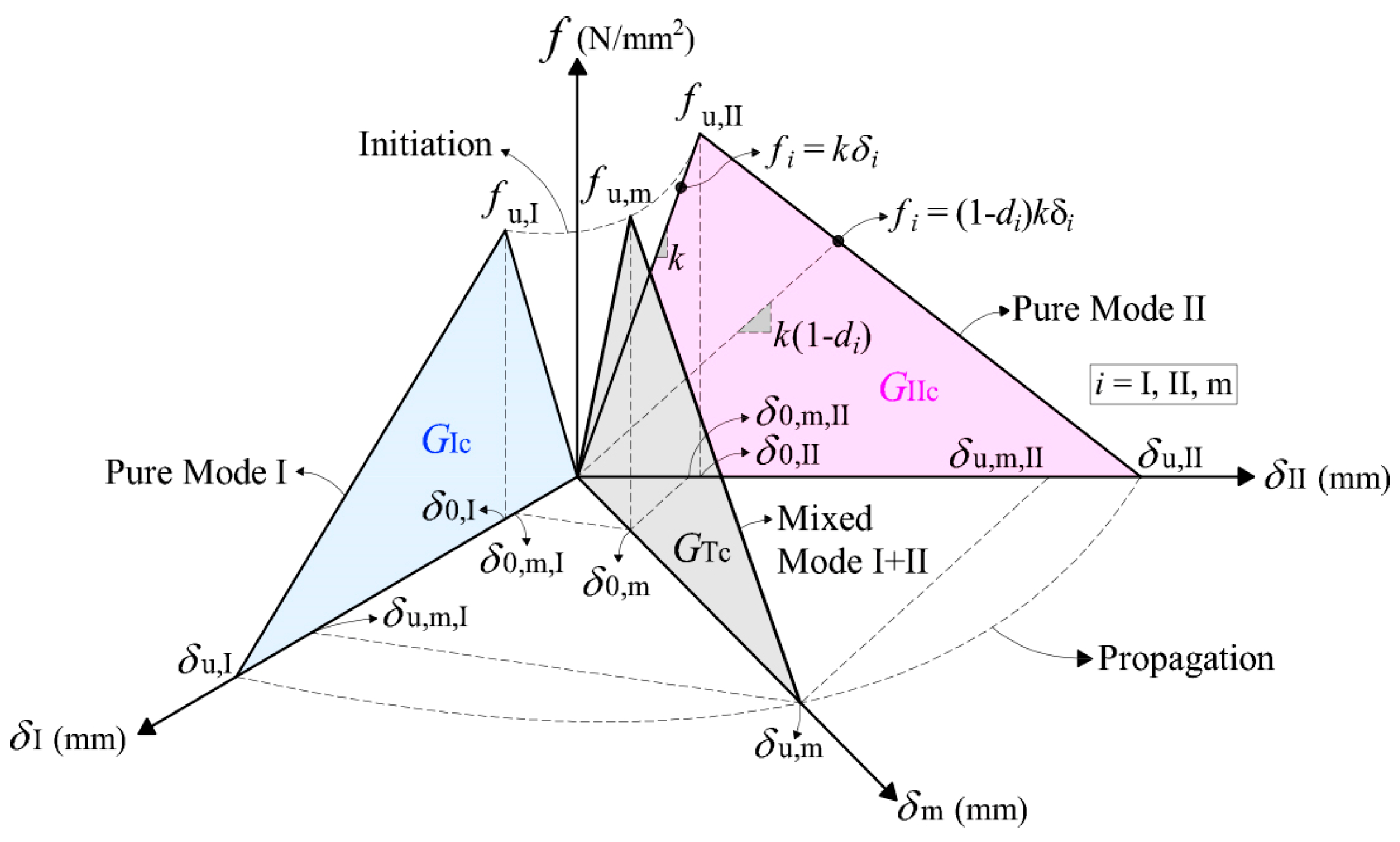
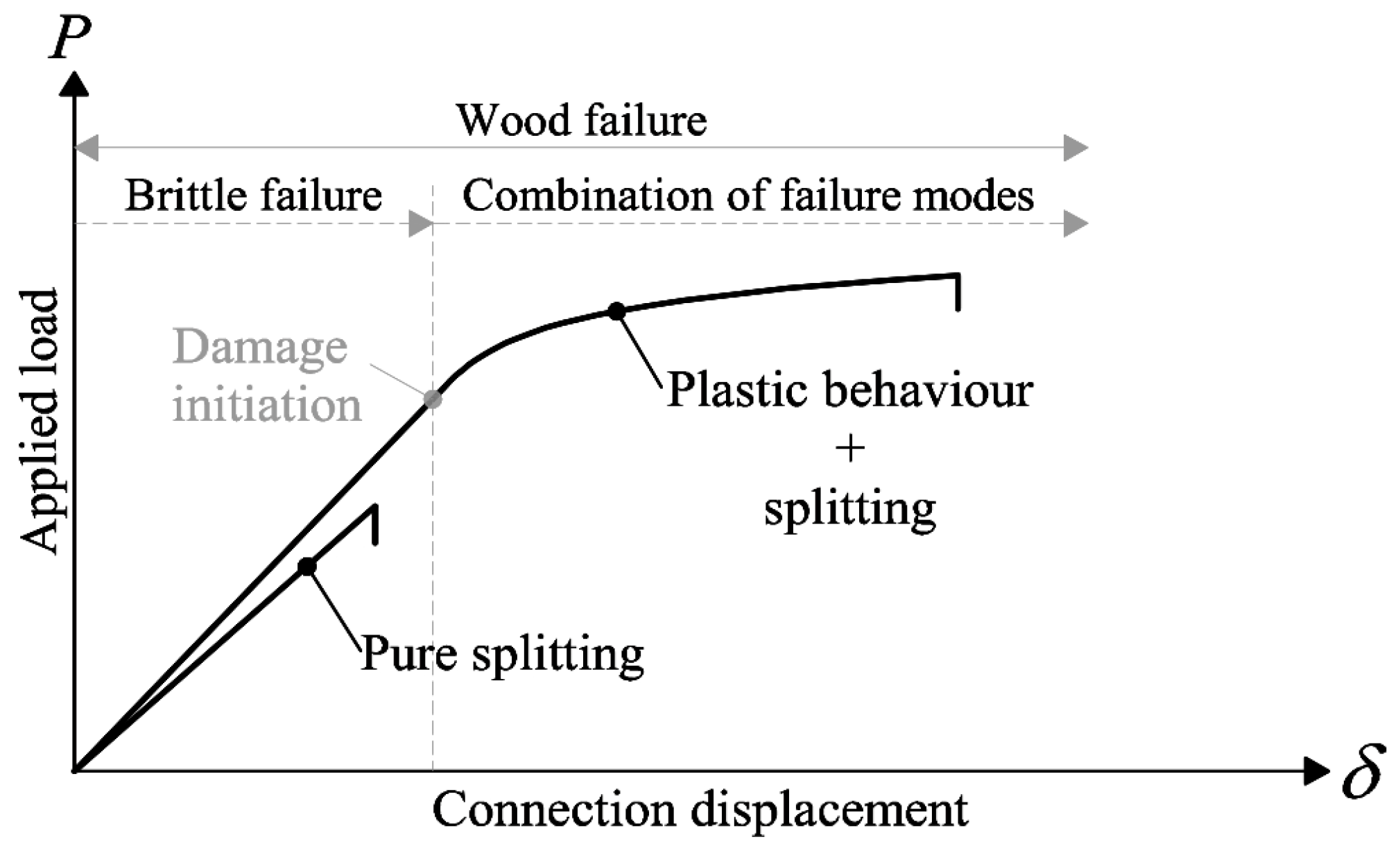





| Number of Dowels | Span L | Connection–Support Distance | Series | Number of Specimens | Density ρ | Moisture Content | Connection Spacing | α | |
|---|---|---|---|---|---|---|---|---|---|
| (no.dowels) | (mm) | lb (mm) | h/no.dowels/L/lb | (kg/m3) | (%) | lc (mm) | he/h | ||
| Group 1 (h: 100 mm) | 1D | 450 | 225 | 100/1D/450/0.5L | 4 | 747 | 9.7 | - | 0.64 |
| 950 | 475 | 100/1D/950/0.5L | 4 | 734 | 11.1 | ||||
| 360 | 100/1D/950/0.38L | 3 | 708 | 10.4 | |||||
| 240 | 100/1D/950/0.25L | 3 | 727 | 10.4 | |||||
| 120 | 100/1D/950/0.13L | 3 | 730 | 10.1 | |||||
| 2D | 450 | 225 | 100/2D/450/0.5L | 4 | 727 | 10.2 | - | 0.64 | |
| 950 | 475 | 100/2D/950/0.5L | 4 | 710 | 10.7 | ||||
| 360 | 100/2D/950/0.38L | 3 | 748 | 10.7 | 230 | ||||
| 240 | 100/2D/950/0.25L | 3 | 738 | 11.5 | 470 | ||||
| 120 | 100/2D/950/0.13L | 3 | 717 | 10.9 | 710 | ||||
| Group 2 (h: 200 mm) | 1D | 450 | 225 | 200/1D/450/0.5L | 4 | 756 | 9.7 | - | 0.32 |
| 950 | 475 | 200/1D/950/0.5L | 3 | 744 | 10.0 | ||||
| 360 | 200/1D/950/0.38L | 3 | 716 | 9.7 | |||||
| 240 | 200/1D/950/0.25L | 3 | 730 | 10.1 | |||||
| 120 | 200/1D/950/0.13L | 3 | 758 | 9.9 | |||||
| 2D | 450 | 225 | 200/2D/450/0.5L | 4 | 730 | 9.6 | - | 0.32 | |
| 950 | 475 | 200/2D/950/0.5L | 4 | 713 | 10.0 | ||||
| 360 | 200/2D/950/0.38L | 3 | 741 | 10.0 | 230 | ||||
| 240 | 200/2D/950/0.25L | 3 | 742 | 10.9 | 470 | ||||
| 120 | 200/2D/950/0.13L | 3 | 716 | 10.3 | 710 |
| EL (N/mm2) | ER (N/mm2) | ET (N/mm2) | νRL (-) | νTL (-) | νRT (-) | GLR (N/mm2) | GLT (N/mm2) | GRT (N/mm2) | |
|---|---|---|---|---|---|---|---|---|---|
| Average | 13,811 | 1590 | 832 | 0.51 | 0.44 | 0.32 | 1108 | 706 | 349 |
| St. Dev. | 1323 | 541 | 115 | 0.030 | 0.015 | 0.041 | 202 | 139 | 53 |
| fI,u (N/mm2) | fII,u (N/mm2) | GIc (N/mm) | GIIc (N/mm) | |
|---|---|---|---|---|
| Average | 8.74 | 18.88 | 0.46 | 1.17 |
| St. Dev. | 1.97 | 3.34 | 0.10 | 0.26 |
| Failure Mode | ||||||
|---|---|---|---|---|---|---|
| Series | Splitting/Bending | |||||
| h/no.dowels/L/lb | % | Pexp (kN) | Vshear.max (kN) | COV (%) | lb/h | |
| Group 1 (h: 100 mm) | 100/1D/450/0.5L | 100/- | 32.5/- | 16.3/- | 5.1/- | 2.25 |
| 100/1D/950/0.5L | 25/75 | 31.0/30.3 | 15.5/15.2 | -/4.1 | 4.75 | |
| 100/1D/950/0.38L | 67/33 | 26.7/33.3 | 16.6/20.7 | 7.4/0 | 3.60 | |
| 100/1D/950/0.25L | 67/33 | 26.3/28.3 | 19.7/21.1 | 5.7/0 | 2.40 | |
| 100/1D/950/0.13L | 100/- | 23.9/- | 20.9/- | 6.0/- | 1.20 | |
| 100/2D/450/0.5L | 100/- | 49.0/- | 24.5/- | 10.5/- | 1.93 | |
| 100/2D/950/0.5L | -/100 | -/37.6 | -/18.8 | -/8 | 4.43 | |
| 100/2D/950/0.38L | 33/67 | 23.7/23.9 | 23.7/23.9 | 0/0.4 | 3.60 | |
| 100/2D/950/0.25L | 67/33 | 27.1/21.5 | 27.1/21.5 | 8.7/0 | 2.40 | |
| 100/2D/950/0.13L | 100/- | 25.0/- | 25.0/- | 10.1/- | 1.20 | |
| Group 2 (h: 200 mm) | 200/1D/450/0.5L | 100/- | 27.2/- | 13.6/- | 7.8/- | 1.13 |
| 200/1D/950/0.5L | 100/- | 30.8/- | 15.4/- | 11/- | 2.38 | |
| 200/1D/950/0.38L | 100/- | 24.3/- | 15.1/- | 10.0/- | 1.80 | |
| 200/1D/950/0.25L | 100/- | 20.5/- | 15.3/- | 14.2/- | 1.20 | |
| 200/1D/950/0.13L | 100/- | 27.4/- | 23.9/- | 6.5/- | 0.60 | |
| 200/2D/450/0.5L | 100/- | 29.2/- | 14.6/- | 20.5/- | 0.97 | |
| 200/2D/950/0.5L | 100/- | 33.6/- | 16.8/- | 5.1/- | 2.22 | |
| 200/2D/950/0.38L | 100/- | 22.8/- | 22.8/- | 20.1/- | 1.80 | |
| 200/2D/950/0.25L | 100/- | 26.9/- | 26.9/- | 18.9/- | 1.20 | |
| 200/2D/950/0.13L | 100/- | 28.5/- | 28.5/- | 24.1/- | 0.60 | |
| Number of Dowels (no.dowels) | Series h/no.dowels/L/lb | L (mm) | Slenderness (L/h) | he (mm) | α he/h | Pexp (kN) | Load Increase (%) |
|---|---|---|---|---|---|---|---|
| 1D | 100/1D/450/0.5L | 450 | 4.50 | 64 | 0.64 | 32.5 | 51% |
| 2D | 100/2D/450/0.5L | 49.0 | |||||
| 1D | 200/1D/450/0.5L | 450 | 2.25 | 64 | 0.32 | 27.2 | 7% |
| 2D | 200/2D/450/0.5L | 29.2 | |||||
| 1D | 200/1D/950/0.5L | 950 | 4.75 | 64 | 0.32 | 30.8 | 9% |
| 2D | 200/2D/950/0.5L | 33.6 |
| Series | Exp. Test | Numerical Analysis | Design Models | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Eurocode 5 [24] Equations (14)–(17) | Jensen [46] Equations (18)–(22) | Franke and Quenneville [47] Equations (23)–(26) | ||||||||
| h/no.dowels/L/lb | Pexp (kN) | Ppre (kN) | Ppre/Pexp | Ppre (kN) | Ppre/Pexp | Ppre (kN) | Ppre/Pexp | Ppre (kN) | Ppre/Pexp | |
| G.1 | 100/1D/450/0.5L | 32.5 | 27.0 | 0.83 | 29.8 | 0.92 | 29.2 | 0.90 | 21.6 | 0.66 |
| 100/1D/950/0.5L | 31.0 | 28.8 | 0.93 | 29.8 | 0.96 | 29.2 | 0.94 | 21.6 | 0.70 | |
| 100/1D/950/0.38L | 26.7 | 30.2 | 1.13 | 24.0 | 0.90 | 29.2 | 1.10 | 21.6 | 0.81 | |
| 100/1D/950/0.25L | 26.3 | 27.3 | 1.04 | 19.9 | 0.76 | 29.2 | 1.11 | 21.6 | 0.82 | |
| 100/1D/950/0.13L | 23.9 | 25.3 | 1.06 | 17.0 | 0.71 | 29.2 | 1.22 | 21.6 | 0.90 | |
| 100/2D/450/0.5L | 49.0 | 43.4 | 0.89 | 29.8 | 0.61 | 29.3 | 0.60 | 37.4 | 0.76 | |
| 100/2D/950/0.5L | - | - | - | - | - | - | - | - | - | |
| 100/2D/950/0.38L | 23.7 | 28.8 | 1.22 | 14.9 | 0.63 | 29.3 | 1.24 | 21.6 | 0.91 | |
| 100/2D/950/0.25L | 27.1 | 25.4 | 0.94 | 14.9 | 0.55 | 29.2 | 1.08 | 21.6 | 0.80 | |
| 100/2D/950/0.13L | 25.0 | 24.0 | 0.96 | 14.9 | 0.60 | 29.2 | 1.17 | 21.6 | 0.86 | |
| G.1 * (P = 2P) | 100/2D/950/0.38L | 47.3 | 57.6 | 1.22 | 29.8 | 0.63 | 29.3 | 0.62 | 92.6 | 1.96 |
| 100/2D/950/0.25L | 54.2 | 50.7 | 0.94 | 29.8 | 0.55 | 29.2 | 0.54 | 91.4 | 1.69 | |
| 100/2D/950/0.13L | 50.0 | 48.0 | 0.96 | 29.8 | 0.60 | 29.2 | 0.58 | 67.6 | 1.35 | |
| G.2 | 200/1D/450/0.5L | 27.2 | 17.2 | 0.63 | 21.8 | 0.80 | 21.4 | 0.79 | 18.6 | 0.68 |
| 200/1D/950/0.5L | 30.8 | 18.1 | 0.59 | 21.8 | 0.71 | 21.4 | 0.70 | 18.6 | 0.60 | |
| 200/1D/950/0.38L | 24.3 | 17.9 | 0.74 | 17.6 | 0.72 | 21.4 | 0.88 | 18.6 | 0.77 | |
| 200/1D/950/0.25L | 20.5 | 17.5 | 0.85 | 14.6 | 0.71 | 21.4 | 1.05 | 18.6 | 0.91 | |
| 200/1D/950/0.13L | 27.4 | 20.2 | 0.74 | 12.5 | 0.46 | 21.4 | 0.78 | 18.6 | 0.68 | |
| 200/2D/450/0.5L | 29.2 | 26.8 | 0.92 | 21.8 | 0.75 | 21.5 | 0.74 | 24.7 | 0.85 | |
| 200/2D/950/0.5L | 33.6 | 28.6 | 0.85 | 21.8 | 0.65 | 21.4 | 0.64 | 24.6 | 0.73 | |
| 200/2D/950/0.38L | 22.8 | 17.5 | 0.77 | 10.9 | 0.48 | 21.5 | 0.94 | 18.6 | 0.82 | |
| 200/2D/950/0.25L | 26.9 | 17.3 | 0.64 | 10.9 | 0.41 | 21.5 | 0.80 | 18.6 | 0.69 | |
| 200/2D/950/0.13L | 28.5 | 23.5 | 0.83 | 10.9 | 0.38 | 21.4 | 0.75 | 18.6 | 0.65 | |
| G.2 * (P = 2P) | 200/2D/950/0.38L | 45.6 | 35.0 | 0.77 | 21.8 | 0.48 | 21.5 | 0.47 | 45.1 | 0.99 |
| 200/2D/950/0.25L | 53.8 | 34.7 | 0.64 | 21.8 | 0.41 | 21.5 | 0.40 | 67.4 | 1.25 | |
| 200/2D/950/0.13L | 56.9 | 47.1 | 0.83 | 21.8 | 0.38 | 21.4 | 0.38 | 64.1 | 1.13 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gómez-Royuela, J.L.; Majano-Majano, A.; Lara-Bocanegra, A.J.; Xavier, J.; de Moura, M.F.S.F. Experimental and Numerical Research on the Splitting Capacity of European Beech Beams Loaded Perpendicular to the Grain by Connections: Influence of Different Geometrical Parameters. Appl. Sci. 2024, 14, 900. https://doi.org/10.3390/app14020900
Gómez-Royuela JL, Majano-Majano A, Lara-Bocanegra AJ, Xavier J, de Moura MFSF. Experimental and Numerical Research on the Splitting Capacity of European Beech Beams Loaded Perpendicular to the Grain by Connections: Influence of Different Geometrical Parameters. Applied Sciences. 2024; 14(2):900. https://doi.org/10.3390/app14020900
Chicago/Turabian StyleGómez-Royuela, José Luis, Almudena Majano-Majano, Antonio José Lara-Bocanegra, José Xavier, and Marcelo F. S. F. de Moura. 2024. "Experimental and Numerical Research on the Splitting Capacity of European Beech Beams Loaded Perpendicular to the Grain by Connections: Influence of Different Geometrical Parameters" Applied Sciences 14, no. 2: 900. https://doi.org/10.3390/app14020900
APA StyleGómez-Royuela, J. L., Majano-Majano, A., Lara-Bocanegra, A. J., Xavier, J., & de Moura, M. F. S. F. (2024). Experimental and Numerical Research on the Splitting Capacity of European Beech Beams Loaded Perpendicular to the Grain by Connections: Influence of Different Geometrical Parameters. Applied Sciences, 14(2), 900. https://doi.org/10.3390/app14020900









