Calculation of Maximum Permissible Load of Underground Power Cables–Numerical Approach for Systems with Stabilized Backfill

Abstract

The maximum permissible load of underground power cables (known in U.S. engineering as “ampacity”) is a function of many parameters, in particular, the thermal resistivity of the native soil. If this resistivity is relatively high, thermal/stabilized backfill is applied, i.e., another material is placed around the cables, providing favourable conditions for heat transfer to the environment. It has a positive impact on the reliability of the power supply and favours the operational durability of the cables. In design practice, however, there is a difficult task—correct determination of the ampacity of the cable line depending on the thermal parameters and the geometry of the backfill. Therefore, this article presents the results of a numerical analysis to determine the ampacity of cable lines in which stabilized backfill is used. A new mathematical relationship is proposed that allows the correction of the ampacity of cable lines depending on their cross-section as well as the thermal and geometric parameters of the cable surroundings.

1. Introduction

1.1. General Description of the Topic

The vast majority of cable systems and the associated modelling relate to underground cable installations. The widespread increase in demand for electricity (especially in developing countries) and the constant desire to develop the distribution network, also in unfavourable soil conditions, require cable line designers to use both standard and case-specific design methods. There are a number of aspects of power cable installation design that must be considered to improve the modelling of underground cable systems while maintaining power network flexibility and reliability [1]. In the indicated context, issues related to the operational reliability of power systems are important, as widely described by the author of the publication [2]. The operational reliability of power systems relates, among other factors, to the transmission capacity of cable lines (current-carrying capacity/ampacity), resistance to damage, and economic efficiency [3]. The authors of the paper [4] emphasize the importance of optimizing reliability in cable system design, which also relates to the topic of this research. The indicated factors apply to the entire assumed operational period of underground cable systems (usually a minimum of 30 years). In order to ensure the required parameters, the frequently used design solution is thermal/stabilized backfill in underground power cable systems. The use of this type of solution is widely described, for instance, in [5,6,7]. The most frequently raised issue in studies is how to maintain appropriate and predictable mechanical and thermal properties of the stabilized backfill so as to ensure proper operating conditions of underground power cable lines [8,9]. The thermal resistivity of the soil undoubtedly influences the ampacity of power cable lines laid in the ground. In order to improve the conditions of heat exchange between the cable and the ground (increasing the ampacity), the surrounding soil is most often replaced by stabilized backfill with a lower thermal resistivity. Because the resistivity of the native soil depends on several factors, including grain composition, grain size and moisture content [10,11], the use of stabilized backfill allows for uniform heat exchange conditions between the power cables and the surroundings. Uniform and good heat exchange conditions help to avoid local thermal exposure of cables in places where the thermal resistivity of the native soil is high [3,12]. Local overheating of cables leads to the rapid aging of their insulation, and it reduces the operational durability of cables [12,13,14]. Stabilized backfill is also beneficial to avoid mechanical stress on the cables. The native soil may contain stones and other sharp elements, whereas the backfill is homogeneous and free from damaging fractions [10]. The use of stabilized backfill also makes it possible to avoid the occurrence of so-called dry zones in underground installations. Dry zones occur as a result of local moisture migration due to the heating of power cables’ surroundings by Joule heat. As a consequence, the thermal resistance of the surrounding soil increases and the long-term permissible temperature for a power cable’s insulation may be exceeded [15]. Therefore, both designers and power system operators are concerned about maintaining stable and optimal thermal conditions around the installed power cable lines [11,16,17]. In addition to the technical arguments indicated, economic issues are also important for the use of stabilized backfill [8,18]. Taking into account the above information, the main issue when designing a cable line is determining its long-term ampacity correctly in order to avoid thermal damage to the cables. If no stabilized backfill is used, this is not a major problem. In this respect, the use of common standards [19,20,21,22] is sufficient, and their provisions can be used to verify numerical calculations [3,23,24,25,26]. As noted by the authors of article [26], the ampacity determined based on standards [20,21,22] is overestimated when compared to numerical models.

1.2. The Issue of Cable Placement in Stabilized Backfill

Determining the ampacity of power cables laid in the ground with the use of stabilized backfill is not obvious and the recommended method using the aforementioned standards is inadequate. This is primarily due to the fact that the cited standards are based on the Neher–McGrath approach [27], which provides analytical solutions for simple computational models. In this case, the only accurate solution is to use numerical calculations of the thermal states of power cables, which allows us to obtain the values of the ampacity of power cable lines in the assumed conditions. Therefore, there is a real need to develop computational methods based on numerical calculations of thermal states for power cables laid in the ground with the use of stabilized backfill. This article is dedicated to this issue. It should be emphasized that similar issues have been studied by other scientists, but there are some gaps. The authors of article [1] presented the problem related to the drying out of the surroundings of power cable installations and the possible consequences of this in the form of the aging of the cables’ insulation and indicated the possibility of using stabilized backfill with no indication of the load of the power cables in the new configuration/geometry with stabilized backfill. In paper [12], the authors pointed out important factors affecting the ampacity of power cables laid in the ground; however, the influence of stabilized backfill on ampacity was only briefly mentioned. Article [28] included an analysis of various types of stabilized backfill and their impact on ampacity; however, the relationship between the ampacity and the thermal parameters of the soil/stabilized backfill was not developed. Paper [14] contains a description of the work carried out using the system of dynamic line rating (DLR) for underground installations, while also considering various types of stabilized backfill. Nevertheless, such an application is appropriate for smart grids and presents a challenge for the future. Similar conclusions regarding the usefulness of numerical calculations and their comparison with standards are included in article [29], but the authors of the publication did not summarize their calculations with a general relationship. The authors of article [30] presented a computational model of the ampacity of power cables buried in the ground with stabilized backfill, which is based on the thermal circuit model. The article does not provide an assessment of the accuracy of the computational model used. The authors of article [31] undertook research related to the grounding system covered with stabilized backfill and claim that the modern simulation approach, especially in complicated computational cases, gives accurate results which are often impossible to determine analytically. Article [16] addresses the issue of developing analytical methods for determining the ampacity of power cable lines laid in the ground using stabilized backfill (in particular, improving the accuracy of determining the ampacity by using standards). The obtained research results were summarized in analytical relationships (with some limitations). The authors of paper [16] emphasized the importance of using bentonite as a stabilized backfill to improve the ampacity of power cables; however, they did not refer the results of their research to the numerical determination of the increase in the ampacity. Paper [11] contains information on the influence of stabilized backfill material type, particle density and particle dimensions on the thermal properties of the backfill. However, the authors of the article did not consider the direct impact of these parameters on the ampacity of power cables laid in the discussed stabilized backfill. The authors of study [32] examined the influence of soil moisture on the permissible long-term temperature of certain types of power cables. They estimated the possible reduction in the service life of the power cable line at nominal load but did not take this phenomenon into account when calculating the ampacity of the power cable line.

The research results presented in this article constitute a significant extension of the content included in the authors’ article [3], commenting on the problem and indicating possible solutions for cables laid in thermal/stabilized backfill. Based on further, extensive analyses, the authors have introduced a method to calculate ampacity, taking into account the cross-sectional area of the cables and the dimensions of the stabilized backfill. Thanks to the implementation of advanced numerical models and calculations, a mathematical relationship for a correction factor is proposed that allows for the determination of the ampacity of cables. As a result of the authors’ approach, it is possible to maximize the transmission potential of cables for their given cross-sectional area and stabilized backfill dimensions. The authors’ proposal will have a positive impact on the reliability of cable systems. The authors’ approach is an alternative to other solutions and a contribution to the current state of knowledge. This is very important for design practice, because proper modelling of ground properties has a significant impact on the thermal parameters of cable lines and, therefore, their ampacity [33].

The rest of the article is organized as follows: Section 2 applies to the power cable system without stabilized backfill and presents the computer model of the analyzed system, assumptions for simulation calculations, and visualization of the temperature fields for the cable system for various parameters. Section 3 contains the results of relevant computer tests on the ampacity of power cables placed in the ground with stabilized backfill. This section also includes a discussion of the results as well as a mathematical relationship summarizing the obtained results. Section 4 provides an overall summary of the article and related conclusions.

2. Materials and Methods

The numerical analysis used in the authors’ research is based mainly on the quantitative examination of the thermal states of power cables (cable lines) placed in the ground with and without the use of stabilized backfill. The power cable lines consisting of three single-core copper conductors were analyzed (three-phase system—three cables in a flat, touching formation). The cross-sectional area of the cables was taken into account in the model tests. The tested power cable lines consisted of cables with a cross-sectional area of 3 × 35 mm², 3 × 120 mm², and 3 × 240 mm², respectively. The cross-sectional view of the analyzed cable type is shown in Figure 1.

The characteristic dimensions of a given type of power cable are included in

Table 1. List of dimensions of the analyzed power cables.

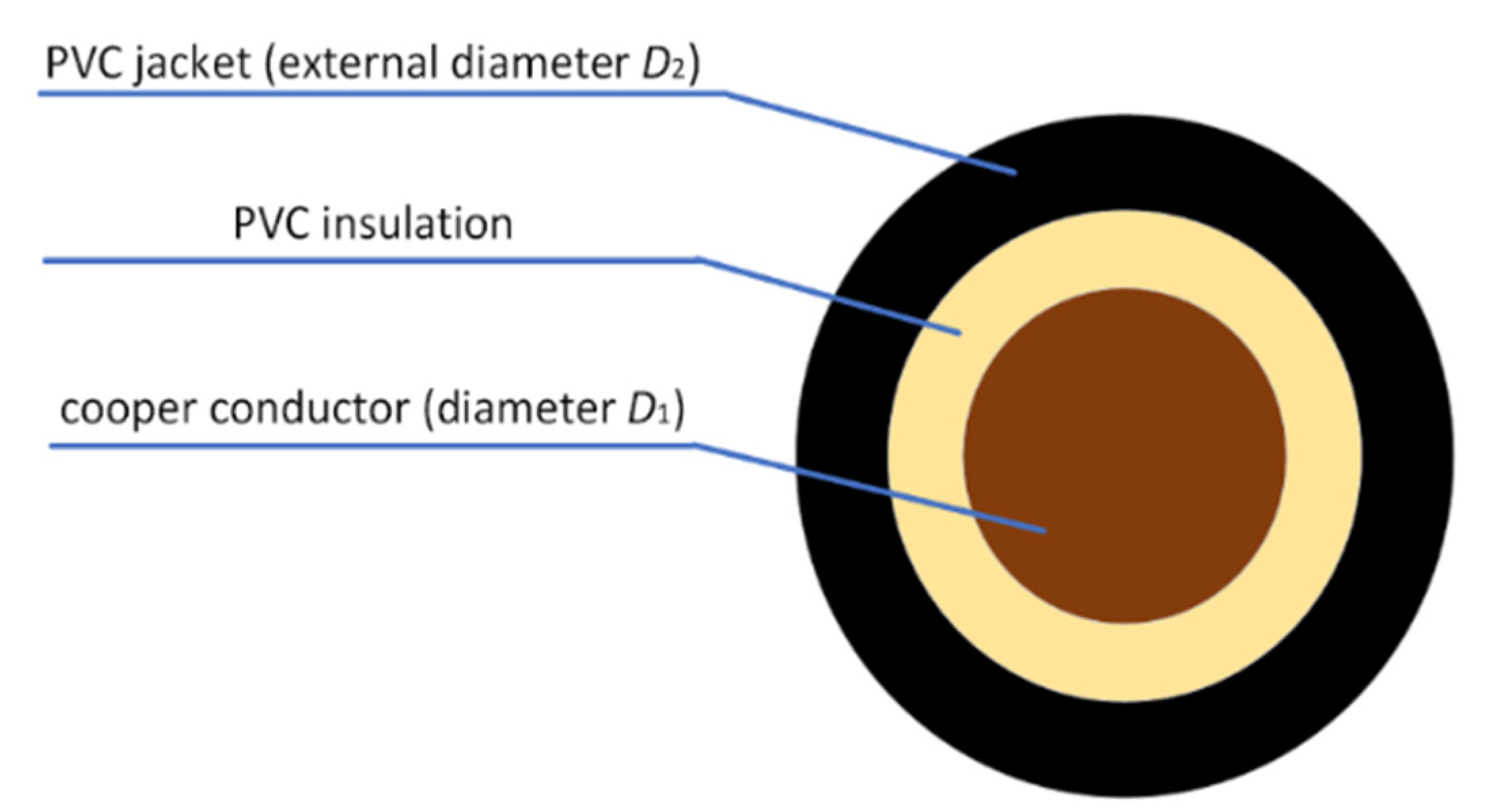
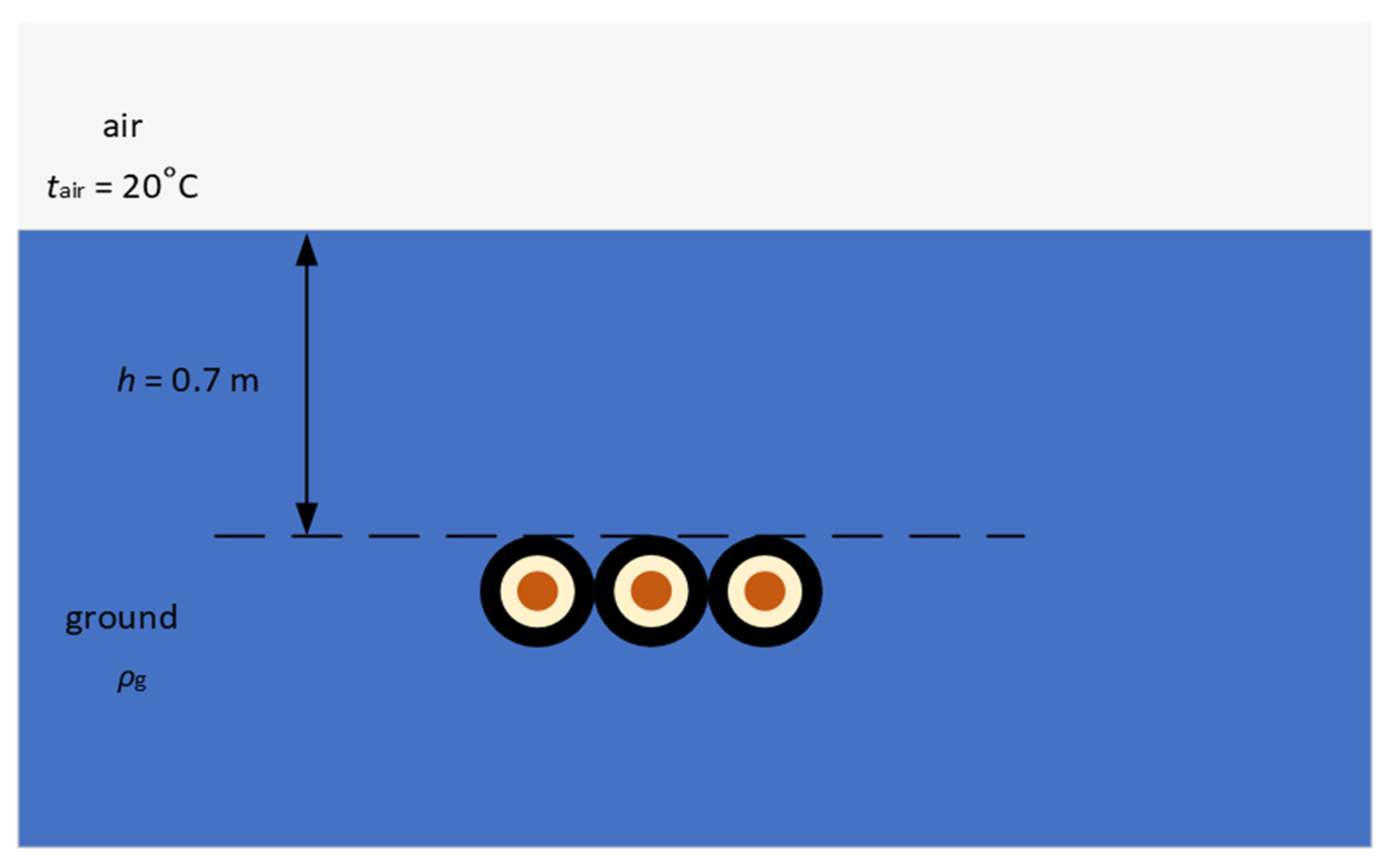
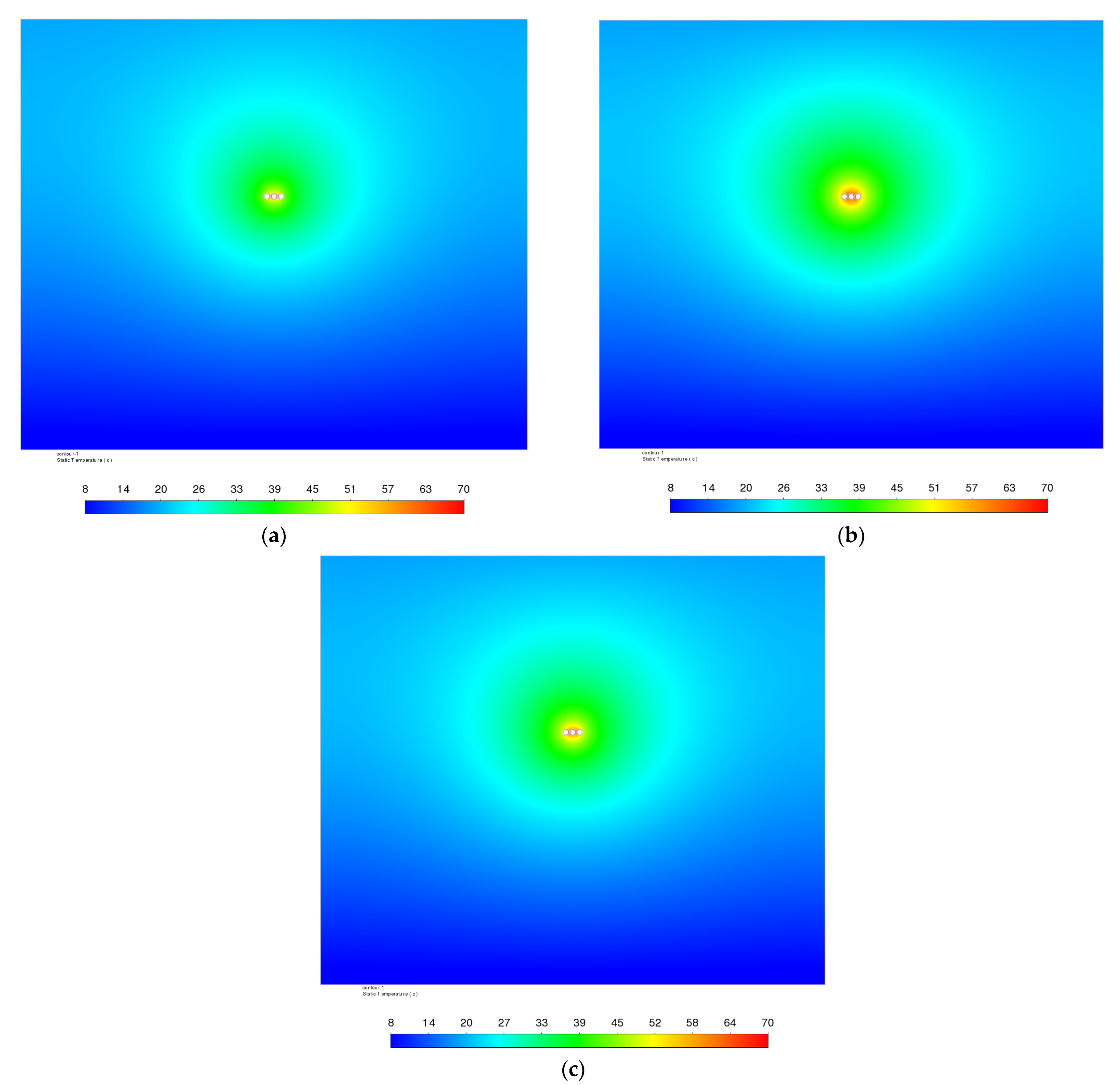
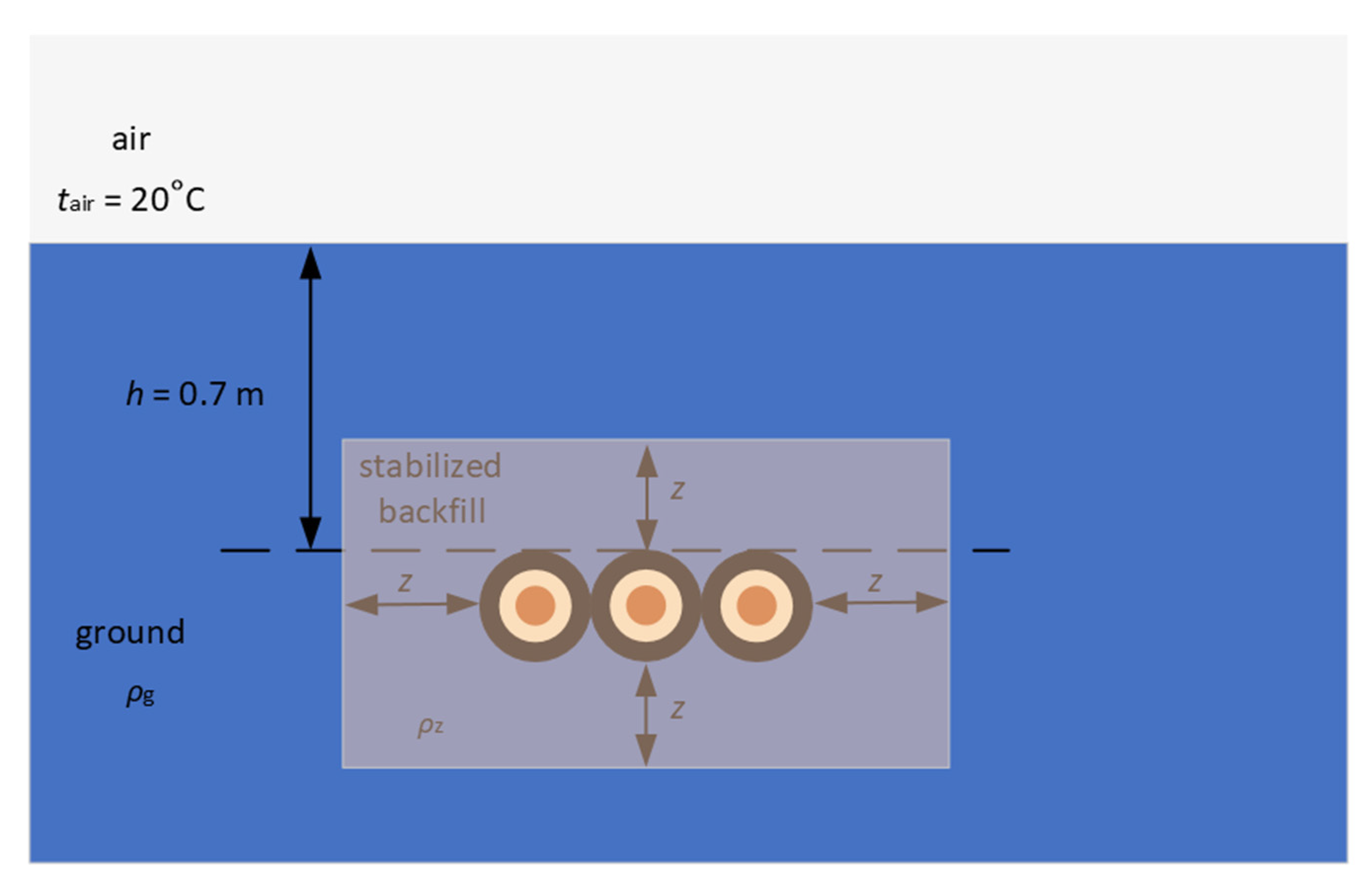
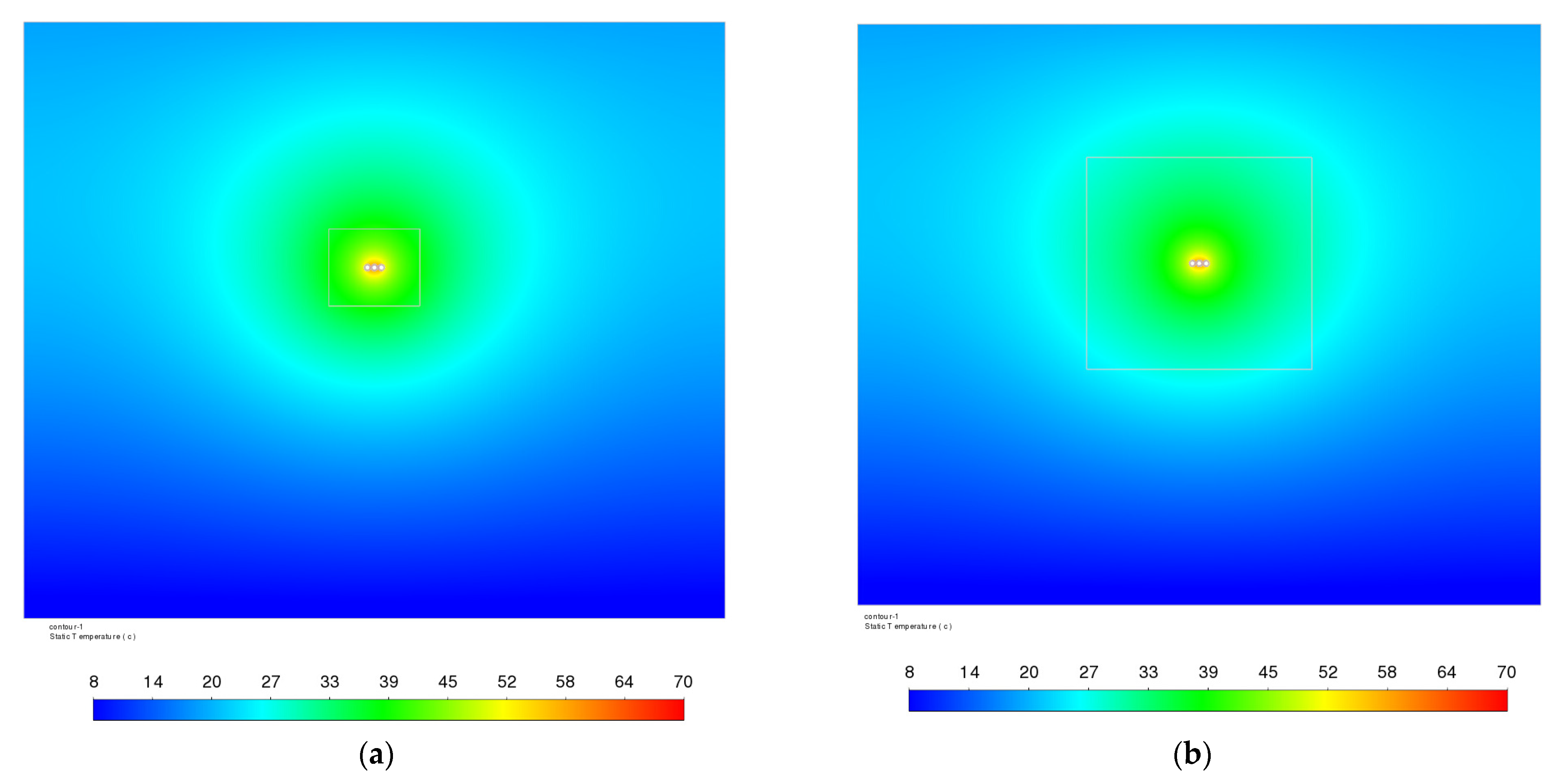
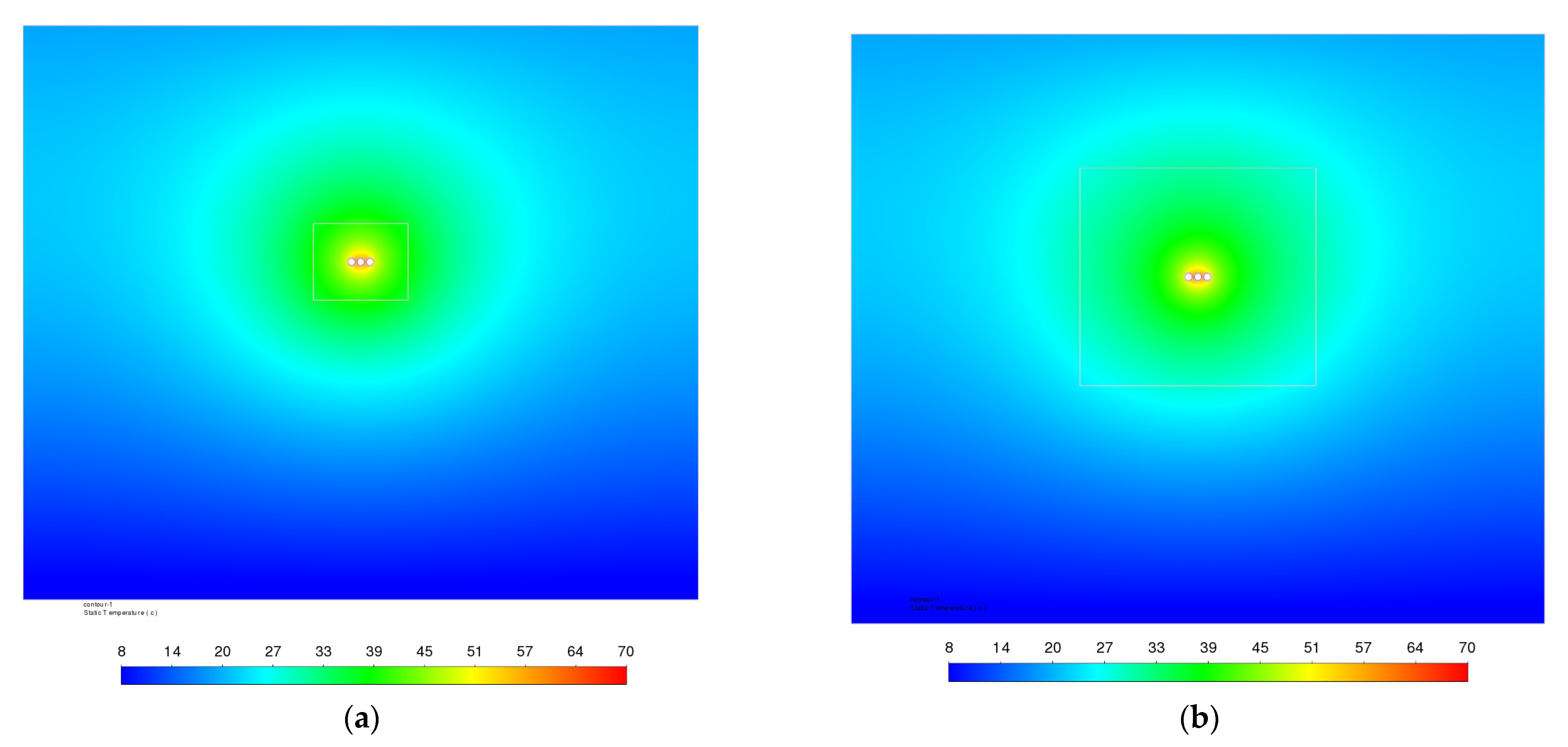
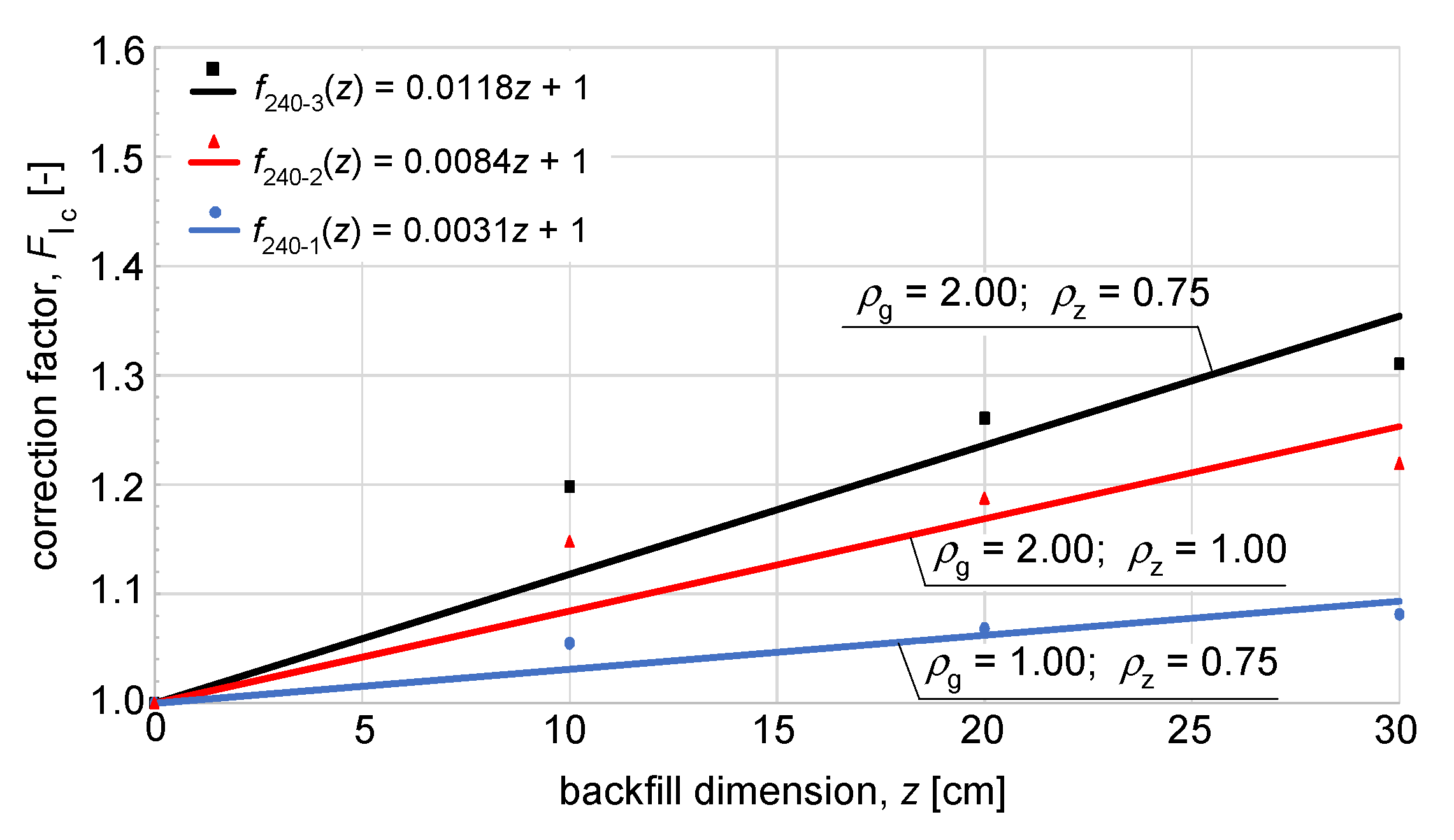
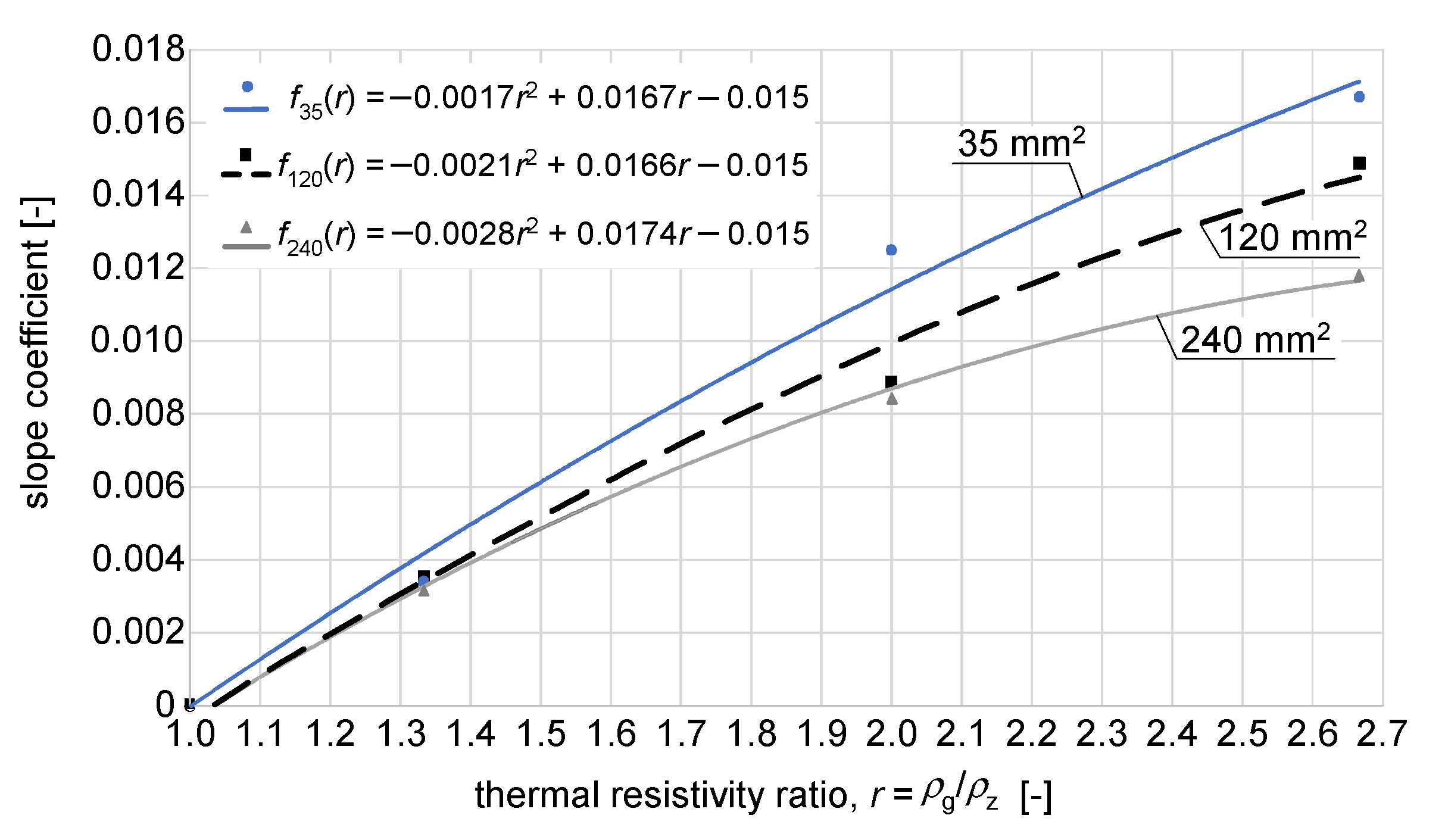
Cross-Sectional Area, mm2	Copper Conductor Diameter D1, mm	External Diameter D2, mm
35	7.2	12.4
120	13.2	19.4
240	18.8	26.8

.

The introduction to detailed analyses related to the influence of stabilized backfill parameters on the ampacity of power cable lines is conditional to the verification of the numerical model. Verification of the numerical model can be performed on a relatively simple model—in this case, it will concern a power cable line buried directly in the ground without the use of stabilized backfill. The illustrative model is presented in Figure 2. The results of numerical calculations for the simple model (without stabilized backfill) will be compared with the known values contained in the standard [19].

The simplified model shown in Figure 2 was implemented in the ANSYS Fluent software(version 2020 R2 and 19.1). According to the presented model, the power cable line is arranged in a flat, touching arrangement and is embedded in the ground to a depth of h = 0.7 m. The assumption made, as well as a certain simplification, is the homogeneity of materials in the analyzed geometric system. A steady-state simulation was conducted to analyze the heat transfer between power cables and their surrounding material. During the simulation, the energy equation was enabled and the physical properties of various materials, such as density and thermal characteristics (including thermal conductivity and specific heat), were implemented into the model. The energy equation in ANSYS Fluent is complex; however, for the specified computational case, thermal conduction in the solid body is the only heat transfer mechanism that needs to be resolved. The temperature boundary condition in the lower part of the model was set to 20 °C, which aligns with Polish geological and thermal conditions. The design air temperature t_air is 20 °C and the convective heat coefficient of 15 W/(m²K) is set on the upper boundary of the domain. These parameters are consistent with the assumptions of the standard [22] and possible unfavourable conditions of heat exchange in the environment.

Figure 3 shows an example of the distribution of computational mesh elements for a selected part of the model. The computational domain encompasses approximately 400,000 computational cells in total. Within this domain, calculations were conducted to determine the ampacity (I_A) of the power cable line under investigation, which was modelled using varying values of soil thermal resistivity ρ_g: 0.5, 1.0, and 2.0 (K·m)/W. The determination of the ampacities results from the thermal balance, or more precisely, from the Joule’s heat portion supplied to the working conductor of the power cable so as to achieve the maximum permissible temperature. The critical temperature threshold for PVC material was determined to be 70 °C. By incrementally augmenting the heat flux applied to the internal surface of the insulation, the system’s maximum temperature was elevated to meet this limit, which represents the maximum permissible temperature for cable insulation.

To enhance calculation accuracy, a second-order discretization scheme was implemented for energy residue. In general, for the second order spatial discretization, quantities at cell faces are computed using a multidimensional linear reconstruction approach, whereas for the first order discretization, a cell is represented by its cell-center value. Only the energy equation was solved within the solver framework, with the flow and turbulence equations disabled. Convergence criteria were set to “none”, and iterative computations were monitored via the energy equation residual chart until the residual exhibited negligible further changes, signalling computational stability.

Table 2. Summary of the results of numerical model verification (I_A—ampacity).

Cross-Section of All Three Cables, mm2	Soil Thermal Resistivity, ρg, (K∙m)/W	Numerical Simulations, IA, A	Standard IEC 60364-5-52 [19], IA, A	Difference between Simulation Results and the Standard [19] Data, %
35 based on [3]	0.5	219.4	207.0	6.0
	1.0	169.8	165.0	2.9
	2.0	127.4	124.0	2.7
120	0.5	431.3	414.0	4.2
	1.0	330.0	330.0	0.0
	2.0	245.2	246.4	0.5
240	0.5	627.1	602.0	4.2
	1.0	482.4	480.0	0.5
	2.0	357.5	358.4	0.3

shows the results of numerical simulations and a comparison of their results with data from the standard [19]. Examples of temperature distributions/fields around the cables can be found in Figure 4.

Summarizing the results obtained in Table 2, it is possible to prove the high convergence of the numerical model with the values given in the standard [19]. Differences in ampacity I_A amount to a maximum of 6% (for a thermal resistivity of soil equal to ρ_g = 0.5 (K$·$m)/W). It should be mentioned here that the authors of the standard [19] assume that the overall accuracy of the values included in the standards is around 5%. Based on the verification of the numerical model, it can be concluded that the presented model is correct and accurate enough. These results justify the development of a model of a system containing stabilized backfill.

3. Results and Discussion

A computational model was developed to determine the ampacity of power cable lines using stabilized backfill, according to Figure 5.

The model presented in Figure 5 assumes, similarly to the verification of the previous model in Figure 2, a flat formation of the power cable line with a cross-sectional area of 35 mm², 120 mm² and 240 mm². Unlike the original model (see Figure 2), a stabilized backfill was used. Stabilized backfill is contained in the area limited by dimension “z”. The value of this parameter varied accordingly: z = 10 cm, 20 cm, and 30 cm. The thermal resistivity of stabilized backfill ρ_z varied (two values): 0.75 and 1.0 (K∙m)/W. The stabilized backfill parameters presented above are often used in practice.

Table 3. Ampacity (I_A−sb) for the cable system with stabilized backfill (z = 10 cm, 20 cm, 30 cm)—summary of the results of numerical calculation.

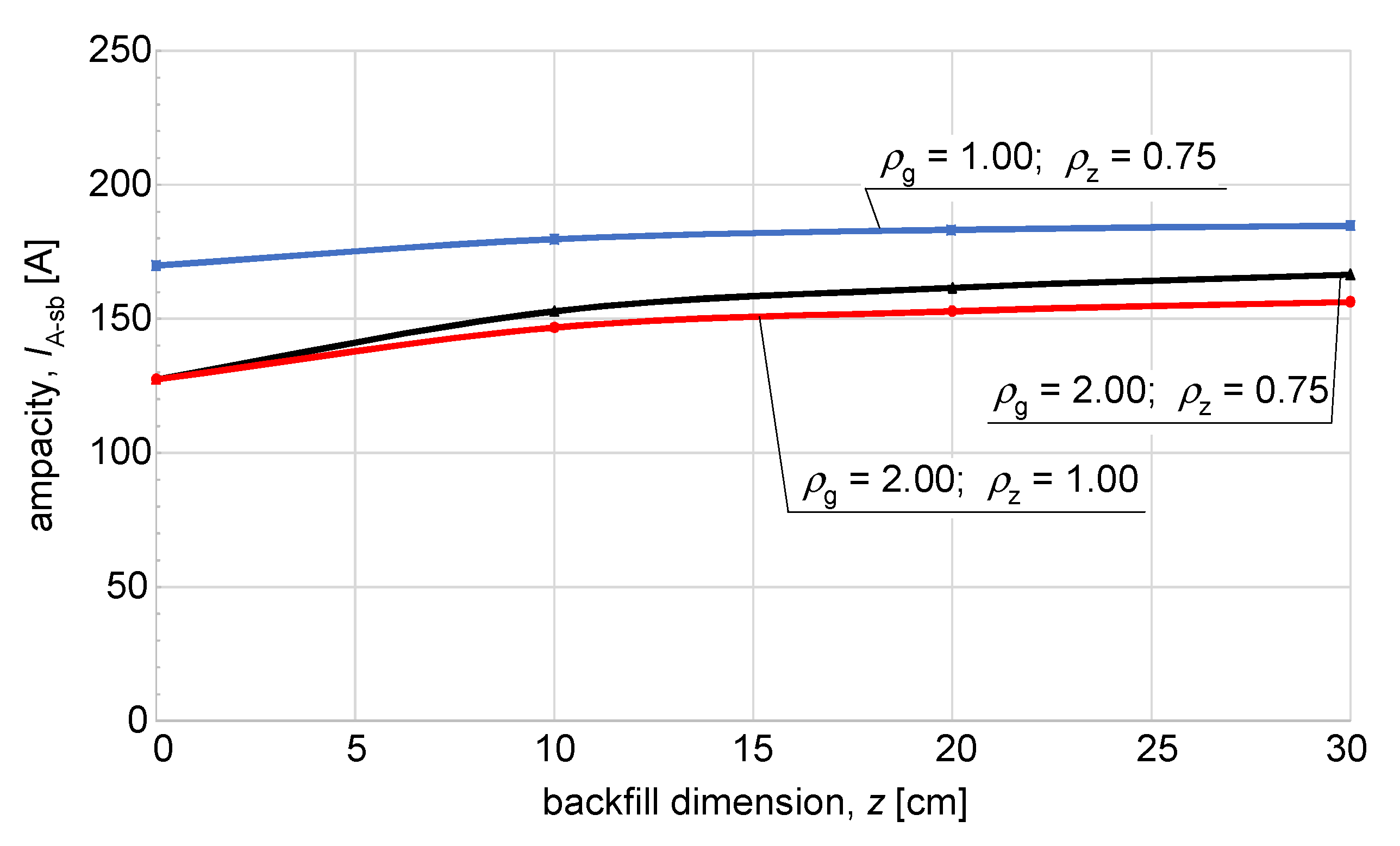
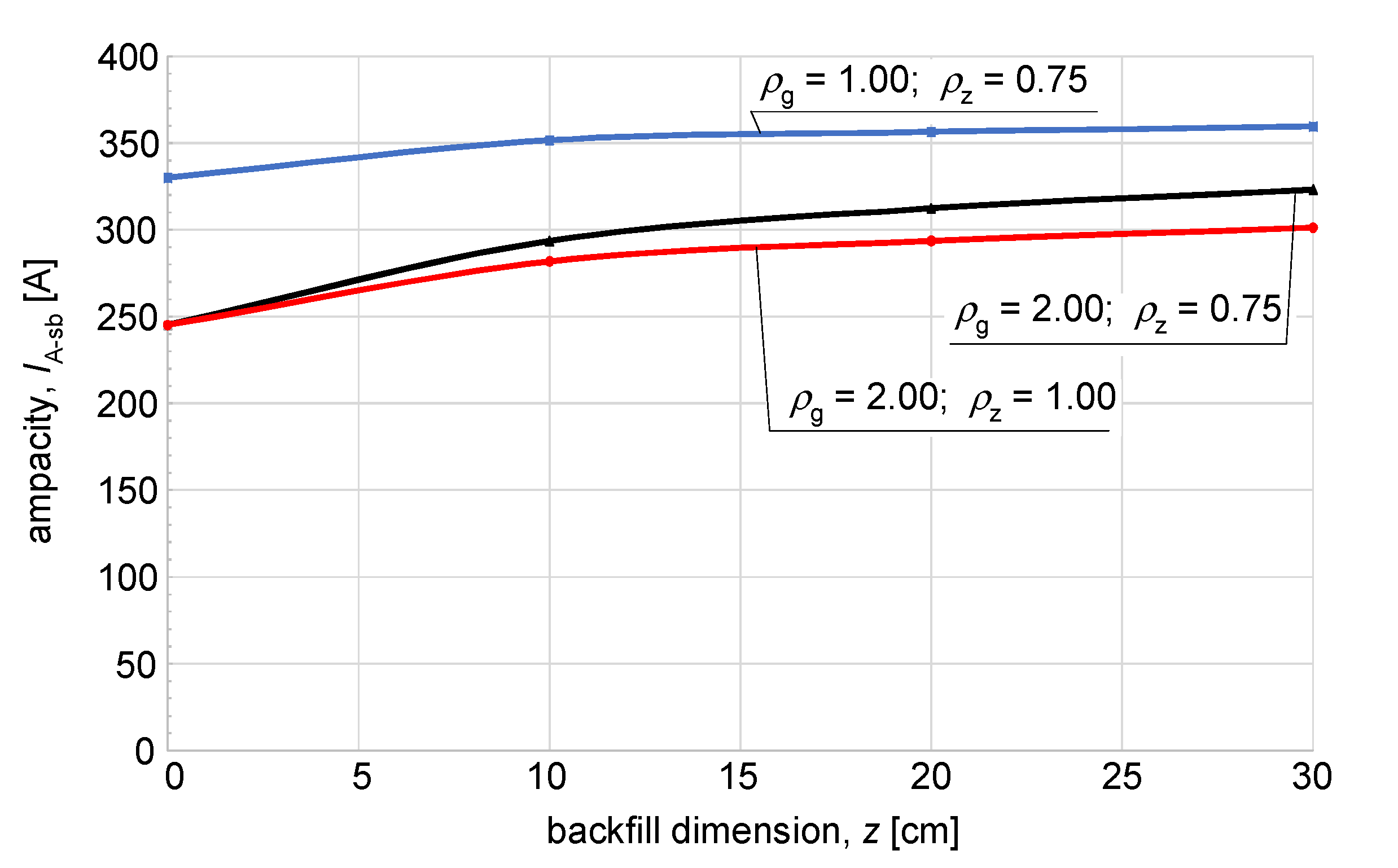
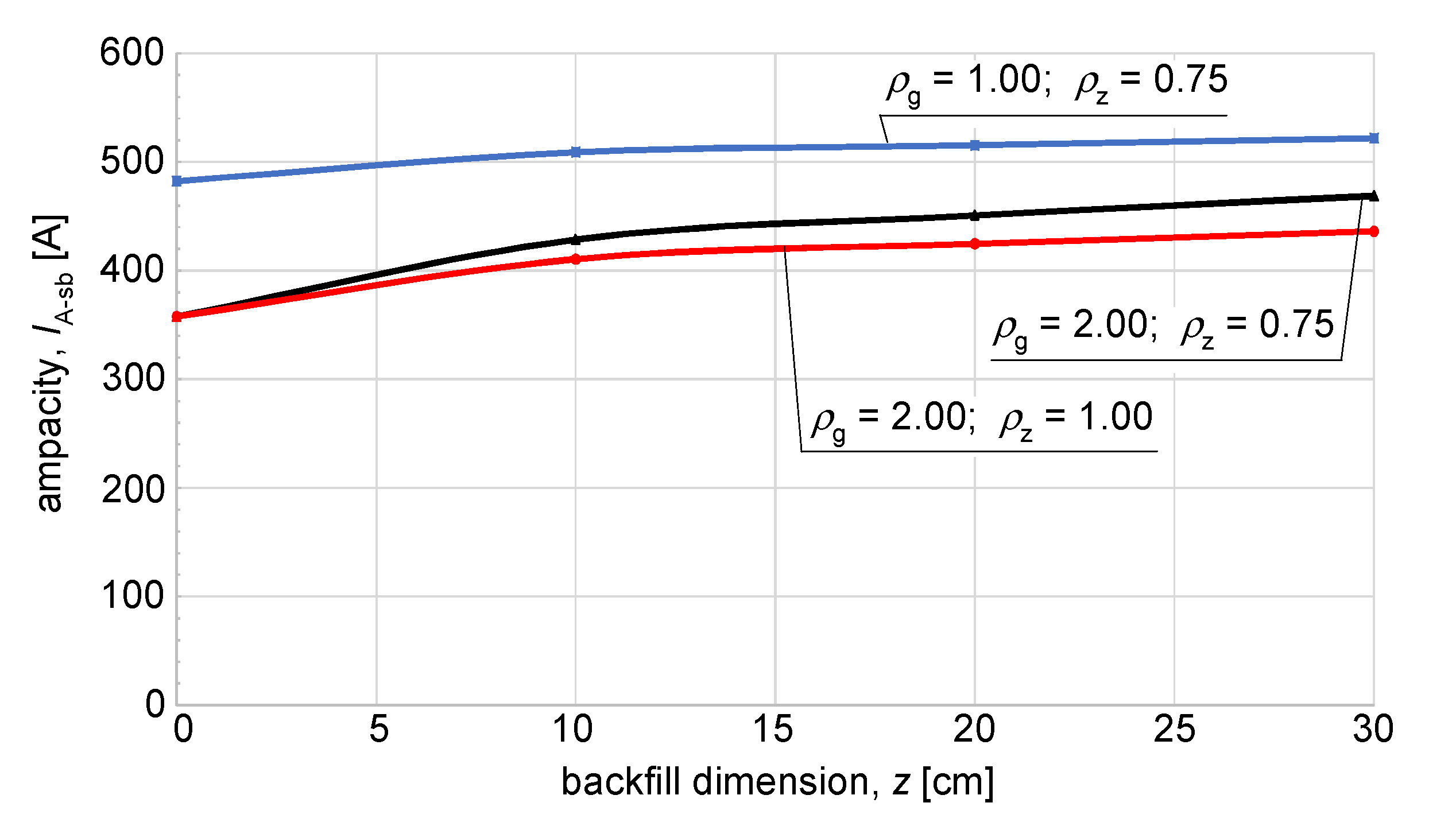
z, cm	ρg, (K∙m)/W	ρz, (K∙m)/W	IA−sb, A (for 35 mm2 Based on [3])	IA−sb, A (for 120 mm2)	IA−sb, A (for 240 mm2)
10	0.5	0.75	200.3	395.6	575.3
10	1.0	0.75	179.7	351.6	508.8
10	2.0	0.75	152.8	293.6	428.4
10	0.5	1.0	187.6	365.8	537.0
10	2.0	1.0	146.7	281.8	410.4
20	0.5	0.75	197.6	386.9	566.7
20	1.0	0.75	183.2	356.4	515.2
20	2.0	0.75	161.5	312.3	450.8
20	0.5	1.0	181.2	354.8	518.4
20	2.0	1.0	152.8	293.6	424.6
30	0.5	0.75	195.7	384.0	560.9
30	1.0	0.75	184.7	359.6	521.6
30	2.0	0.75	166.5	323.0	468.6
30	0.5	1.0	178.2	348.3	508.8
30	2.0	1.0	156.3	301.2	436.0

contains the results of calculations of the ampacity for the analyzed power cable lines and the parameters of stabilized backfill.

Graphical interpretations of the results obtained in Table 3 are presented in Figure 6, Figure 7 and Figure 8. In order to better present the obtained results, further considerations cover calculation cases for which the thermal resistivity of the ground (native soil) is equal to ρ_g = 1.0 and 2.0 (K∙m)/W. For practical reasons, further analyses do not present results for native soil resistivity ρ_g = 0.5 (K∙m)/W (soil would be better than stabilized backfill).

The contents of Figure 6, Figure 7 and Figure 8 present approximate characteristics of the variability ampacity depending on the characteristic dimension (z) of stabilized backfill and the thermal resistivity parameters of the ground and stabilized backfill, respectively, for cable lines of 35 mm² (see Figure 6), 120 mm² (see Figure 7), 240 mm² (see Figure 8). According to the presented relationships, which show the same trends for each of the three lines laid in the ground (native soil) with the following thermal resistivities: ρ_g = 1.0 and 2.0 (K∙m)/W, the use of stabilized backfill is justified—as the stabilized backfill volume increases, the permissible load/ampacity of the line increases. Figure 9 and Figure 10 show (as an example) selected temperature distributions for the analyzed calculation cases of a power cable line with a conductor cross-section equal to 120 mm².

Based on the presented temperature field drawings, it can be concluded that in cases where there is a relatively high value of native soil thermal resistivity (here ρ_g = 2.0), the heating area around power cable lines is much wider compared to soil with low thermal resistivity (here ρ_g = 1.0)—Figure 9 vs. Figure 10, and Figure 11 vs. Figure 12. Comparing cases (a) and (b) for Figure 9, Figure 10, Figure 11 and Figure 12, it can be seen that with the increase in stabilized backfill volume, the area of increased ground temperature also increases.

Later in the article, the authors will make an algebraic generalization of the given relationships regarding the determination of the ampacity of power cable lines depending on the thermal and geometric parameters of stabilized backfill and the cross-sectional area of the power cables. For this purpose, a correction factor for the ampacity is introduced:

$$F_{\mathrm{I}\mathrm{c}}={\displaystyle \frac{I_{\mathrm{A}-\mathrm{s}\mathrm{b}}}{I_{\mathrm{A}}}}$$

(1)

where:

F_Ic—correction factor, [-];

I_A−sb—ampacity with stabilized backfill, [A];

I_A—ampacity without stabilized backfill, [A].

The value of ampacity I_A−sb for power cable lines with stabilized backfill is included in Table 3. For comparison, the value of ampacity I_A for power cable lines without stabilized backfill is included in Table 2.

Figure 13, Figure 14 and Figure 15 show graphical relationships between correction factor values and stabilized backfill dimensions. The given dependencies have been linearized to a family of straight lines intersecting on the coordinate system at point (0; 1.0)—this point physically means a calculation case for an arrangement without stabilized backfill.

In a further stage, the description of the family of straight lines was generalized. Figure 16 shows the relationship between the slope coefficients of the family of lines defined in Figure 13, Figure 14 and Figure 15 and the ratio (r) of the thermal resistivity of the ground to the thermal resistivity of stabilized backfill.

As can be seen, the relationship for all three types of power cable lines considered is a second-degree polynomial (in general: ax² + bx + c). Coefficient “c” is constant for all cases and coefficient “b” changes from 0.0166 to 0.0174, so the relative difference is below 5%. The changes in coefficient “a”, for various cross-sections, are definitely more significant, so the strongest dependency is between coefficient “a” and the cross-sectional area. To generalize the first term of the polynomial, the function in Figure 17 has been presented.

It can be seen that the relationship presented in Figure 17 is approximated by a straight line, which facilitates further considerations.

As a result of further analyses, the obtained results and transformations, a generalized notation of the correction factor was obtained according to the following relationship proposed in (2):

$$F_{\mathrm{I}\mathrm{c}}=\left(\left(-5·{10}^{-6}·s-0.0015\right)·{\left({\displaystyle \frac{{\rho }_{\mathrm{g}}}{{\rho }_{\mathrm{z}}}}\right)}^2+0.0169·\left({\displaystyle \frac{{\rho }_{\mathrm{g}}}{{\rho }_{\mathrm{z}}}}\right)-0.015\right)·z+1$$

(2)

Taking into account the scope of the simulations performed by the authors and the related limitations, the application of Formula (2) is possible for the following values of the considered parameters:

• cross-section of cable cores: $s\in 〈35;240〉$, [mm²];
• native soil thermal resistivity: ${\rho }_{\mathrm{g}}\in 〈1.0;2.0〉$, [(K∙m)/W];
• stabilized backfill thermal resistivity: ${\rho }_{\mathrm{z}}\in 〈0.75;1.0〉$, [(K∙m)/W];
• thermal resistivity ratio: ${\rho }_{\mathrm{g}}/{\rho }_{\mathrm{z}}\in 〈1.0;2.7〉$, [-];
• stabilized backfill dimension: $z\in 〈0;30〉$, [cm].

By employing (1) and (2) provided herein, one can ascertain the ampacity of a power cable line situated within a stabilized backfill medium. This is achieved by multiplying the correction factor F_Ic by the ampacity I_A of a power cable line placed directly in the ground, devoid of stabilized backfill (e.g., as delineated by line 4 in Table 2).

Table 4. Summary of the comparison results of the calculated ampacity values for a power cable line with a cross-sectional area of 240 mm².

z, cm	ρg, (K∙m)/W	ρz, (K∙m)/W	IA−sb, A (from Table 3, ANSYS Simulations)	IA−sb = (F1c·IA), A (Correction Factor FIc–Rel. (2))	Relative Error, %
10	1.0	0.75	508.8	493.1	3.1
10	2.0	0.75	428.4	397.3	7.3
10	2.0	1.0	410.4	387.1	5.7
20	1.0	0.75	515.2	506.2	1.7
20	2.0	0.75	450.8	436.3	3.2
20	2.0	1.0	424.6	415.7	2.1
30	1.0	0.75	521.6	519.4	0.4
30	2.0	0.75	468.6	475.2	1.4
30	2.0	1.0	436.0	444.4	1.9

offers a comparative analysis, demonstrating the calculated ampacity for a power cable line featuring a cross-sectional area of 240 mm² and positioned within a thermally stabilized medium, and the parameters of stabilized backfill.

The fourth column of Table 4 (I_A) contains a repetition of the results of the numerical calculations for the analyzed cases involving stabilized backfill, which are included in Table 3. Column 5 of Table 4 contains results for the same cases, but multiplying the ampacity included in Table 2 (for the same values of thermal resistivity of the native soil) by the value of the correction factor F_Ic from (2). As we can observe, the accuracy of determining ampacity by using the correction factor F_Ic is high, and the average error of the obtained comparison is 2.4% (arithmetic mean of the results contained in the last column of Table 4).

4. Conclusions

Evaluation of the ampacity of power cable lines placed in the ground without stabilized backfill is not a major problem. The situation changes when stabilized backfill materials with different thermal resistivity values to that of the native soil are used. In such cases, numerical calculations of the thermal states of power cable installations in these conditions are necessary. Installation users and designers are not always equipped with tools to determine precise calculations. The mathematical relationship proposed by the authors allows for the determination of the load/ampacity based on industry standards, supplemented by the known thermal and geometric parameters of materials involved in the heat exchange between cables and the environment. No specialized computer software is required to implement the correction factor. The presented results of these innovative calculations are characterized by good accuracy. The results related to the proposed calculation method can be used for other voltage levels/cable types, but under certain conditions—the cables must be of similar construction and must be laid in the same way (touching each other in a flat formation).