High-Sensitivity Displacement Sensor Using Few-Mode Optical Fibers and the Optical Vernier Effect
Abstract
:Featured Application
Abstract
1. Introduction
2. Principle of the OVE and Harmonics in Cascading SFS Sections
3. Experimental Setup
4. Results and Discussion
4.1. Fast Fourier Transform Analysis
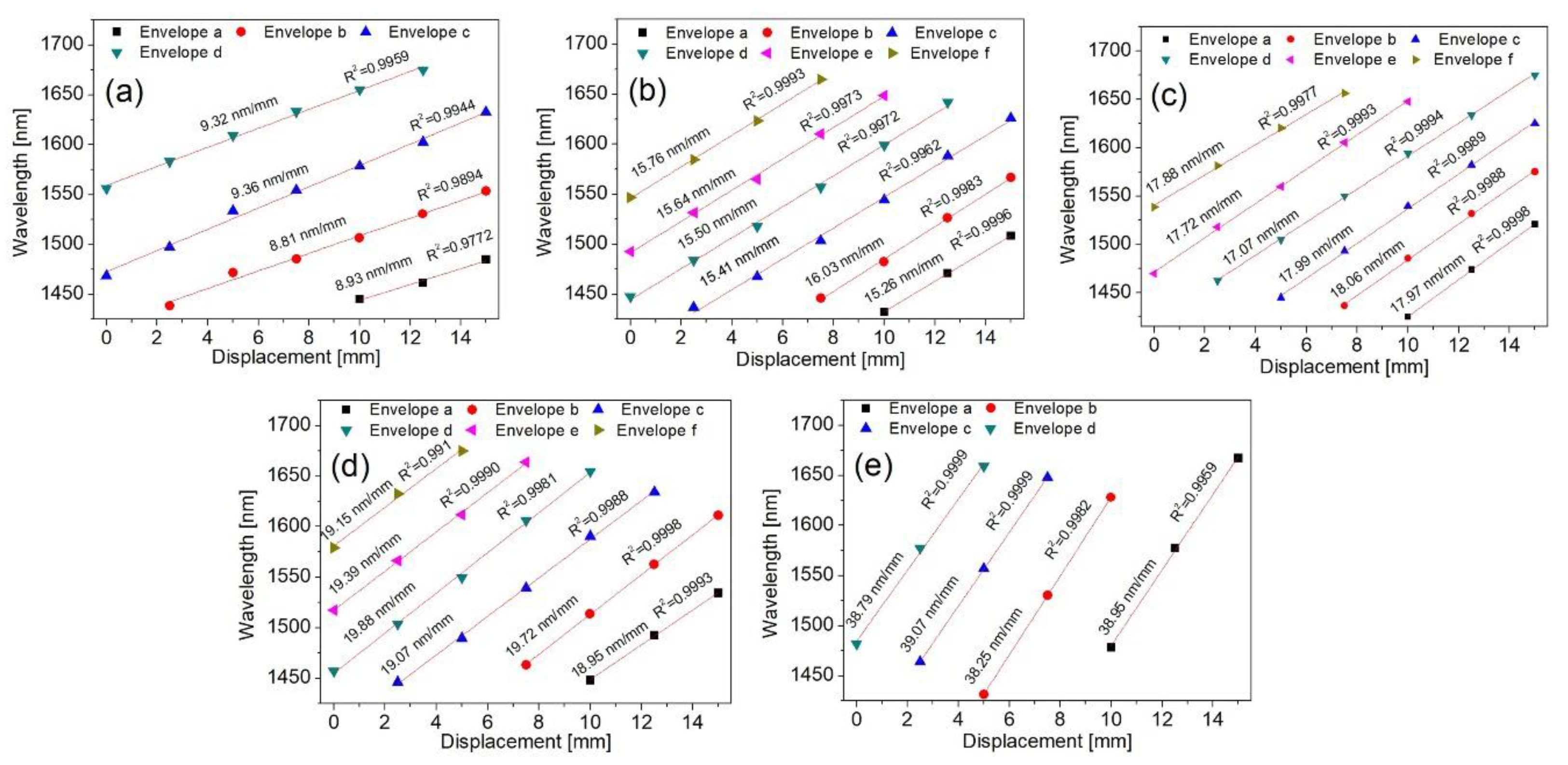
4.2. OVE Analysis (Spectral Shift and Slope)
4.3. Harmonic OVE Analysis
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, Y.; Li, X.; Zhang, Y.-N.; Zhao, Y. Fiber-optic sensors based on Vernier effect. Measurement 2020, 167, 108451. [Google Scholar] [CrossRef]
- Gomes, A.D.; Bartelt, H.; Frazão, O. Optical Vernier Effect: Recent Advances and Developments. Laser Photonics Rev. 2021, 15, 2000588. [Google Scholar] [CrossRef]
- Lashari, G.A.; Mumtaz, F.; Ai, Z.; Dai, Y. Recent advancements and future challenges in hybrid optical fiber interferometers. Optik 2023, 282, 170860. [Google Scholar] [CrossRef]
- Liu, L.; Ning, T.; Zheng, J.; Pei, L.; Li, J.; Cao, J.; Gao, X.; Zhang, C. High-sensitivity strain sensor implemented by hybrid cascaded interferometers and the Vernier-effect. Opt. Laser Technol. 2019, 119, 105591. [Google Scholar] [CrossRef]
- Lu, C.; Dong, X.; Lu, L.; Guan, Y.; Ding, S. Label Free All-Fiber Static Pressure Sensor Based on Vernier Effect with Temperature Compensation. IEEE Sens. J. 2020, 20, 4726–4731. [Google Scholar] [CrossRef]
- Xie, L.; Sun, B.; Chen, M.; Zhang, Z. Sensitivity enhanced temperature sensor with serial tapered two-mode fibers based on the Vernier effect. Opt. Express 2020, 28, 32447–32455. [Google Scholar] [CrossRef]
- Gomes, A.D.; Kobelke, J.; Bierlich, J.; Dellith, J.; Rothhardt, M.; Bartelt, H.; Frazão, O. Giant refractometric sensitivity by combining extreme optical Vernier effect and modal interference. Sci. Rep. 2020, 10, 19313. [Google Scholar] [CrossRef]
- Fu, X.; Ran, R.; Li, Q.; Zhang, R.; Li, D.; Fu, G.; Jin, W.; Bi, W.; Qi, Y.; Hu, Q. A sensitivity-enhanced temperature sensor with end-coated PDMS in few mode fiber based on vernier effect. Opt. Commun. 2021, 497, 127173. [Google Scholar] [CrossRef]
- Fu, X.; Ran, R.; Li, Q.; Huang, Z.; Li, D.; Zhang, R.; Fu, G.; Jin, W.; Qi, Y.; Bi, W. A Few Mode Fiber Temperature Sensor Filled with PDMS Based on Vernier Effect. IEEE Photonics J. 2021, 13, 6800205. [Google Scholar] [CrossRef]
- Yang, P.; Jiang, S.; Wang, Z.; Peng, X.; Peng, B. Enhancing Sensor Strain Sensitivity via Simulated Reference Arm for Optical Harmonic Vernier Effect. IEEE Sens. J. 2023, 23, 27375–27381. [Google Scholar] [CrossRef]
- Deng, L.; Jiang, C.; Guo, X.; Sun, S.; Jiang, G.; Cao, T.; Shu, Y.; Liu, C.; Huang, H. Ultra-sensitive strain sensor composed of tapered two-mode fiber micro-cantilever inserted into quartz capillary. Opt. Fiber Technol. 2024, 84, 103738. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, P.; Wei, W.; Jiang, S.; Bao, W.; Zhu, X.; Wu, G.; Chen, D. Highly Sensitive Salinity Sensor Based on Virtual Vernier Effect of Micro-Nano Fiber Mode Interferometer. IEEE Sens. J. 2024, 24, 16121–16129. [Google Scholar] [CrossRef]
- Guillen-Ruiz, L.; Anzueto-Sánchez, G.; Torres-Gómez, I.; Camas-Anzueto, J.; Martínez-Rios, A.; Salceda-Delgado, G. Experimental demonstration of optical Vernier effect by cascading tapered single-mode optical fibres. Opt. Fiber Technol. 2022, 70, 102869. [Google Scholar] [CrossRef]
- Guillen-Ruiz, L.; Anzueto-Sanchez, G.; Martínez-Rios, A.; Camas-Anzueto, J.; Nuñez-Gomez, R.E.; Martin-Vela, J.A. Demonstration of Improving the Performance of a Fibre Optic Displacement Sensor Using the Optical Harmonic Vernier Effect by Cascading Tapered Optical Single-Mode Fibres. IEEE Photonics J. 2023, 15, 7101309. [Google Scholar] [CrossRef]
- Su, J.; Dong, X.; Lu, C. Characteristics of few mode fiber under bending. IEEE J. Sel. Top. Quantum Electron. 2016, 22, 139–145. [Google Scholar] [CrossRef]
- Su, J.; Dong, X.; Lu, C. Property of Bent Few-Mode Fiber and Its Application in Displacement Sensor. IEEE Photonics Technol. Lett. 2016, 28, 1387–1390. [Google Scholar] [CrossRef]
- Wang, S.; Yang, Y.; Wu, L.; Mohanty, L.; Jin, R.-B.; Zhang, L.; Lu, P. In-situ adjustable fiber-optic piezometer based on parallelly structured external Fabry-Perot interferometers with Vernier effect and its harmonics. Opt. Express 2021, 29, 42800–42812. [Google Scholar] [CrossRef]
- Gomes, A.D.; Ferreira, M.S.; Bierlich, J.; Kobelke, J.; Rothhardt, M.; Bartelt, H.; Frazão, O. Optical harmonic vernier effect: A new tool for high performance interferometric fibre sensors. Sensors 2019, 19, 5431. [Google Scholar] [CrossRef]
- Yang, X.; Yang, G.; Chen, M.; Bing, P.; Li, Z.; Yang, X.; Liu, Y.; Yao, J. Ultrasensitive RI and temperature sensor based on cascaded microfiber MZIs with Vernier effect. Opt. Laser Technol. 2024, 177, 111082. [Google Scholar] [CrossRef]
- Presti, D.L.; Massaroni, C.; Leitao, C.S.J.; Domingues, M.D.F.; Sypabekova, M.; Barrera, D.; Floris, I.; Massari, L.; Oddo, C.M.; Sales, S.; et al. Fiber Bragg Gratings for Medical Applications and Future Challenges: A Review. IEEE Access 2020, 8, 156863–156888. [Google Scholar] [CrossRef]
- Vaiano, P.; Carotenuto, B.; Pisco, M.; Ricciardi, A.; Quero, G.; Consales, M.; Crescitelli, A.; Esposito, E.; Cusano, A. Lab on Fiber Technology for biological sensing applications (Laser Photonics Rev. 10(6)/2016). Laser Photonics Rev. 2016, 10, 858. [Google Scholar] [CrossRef]
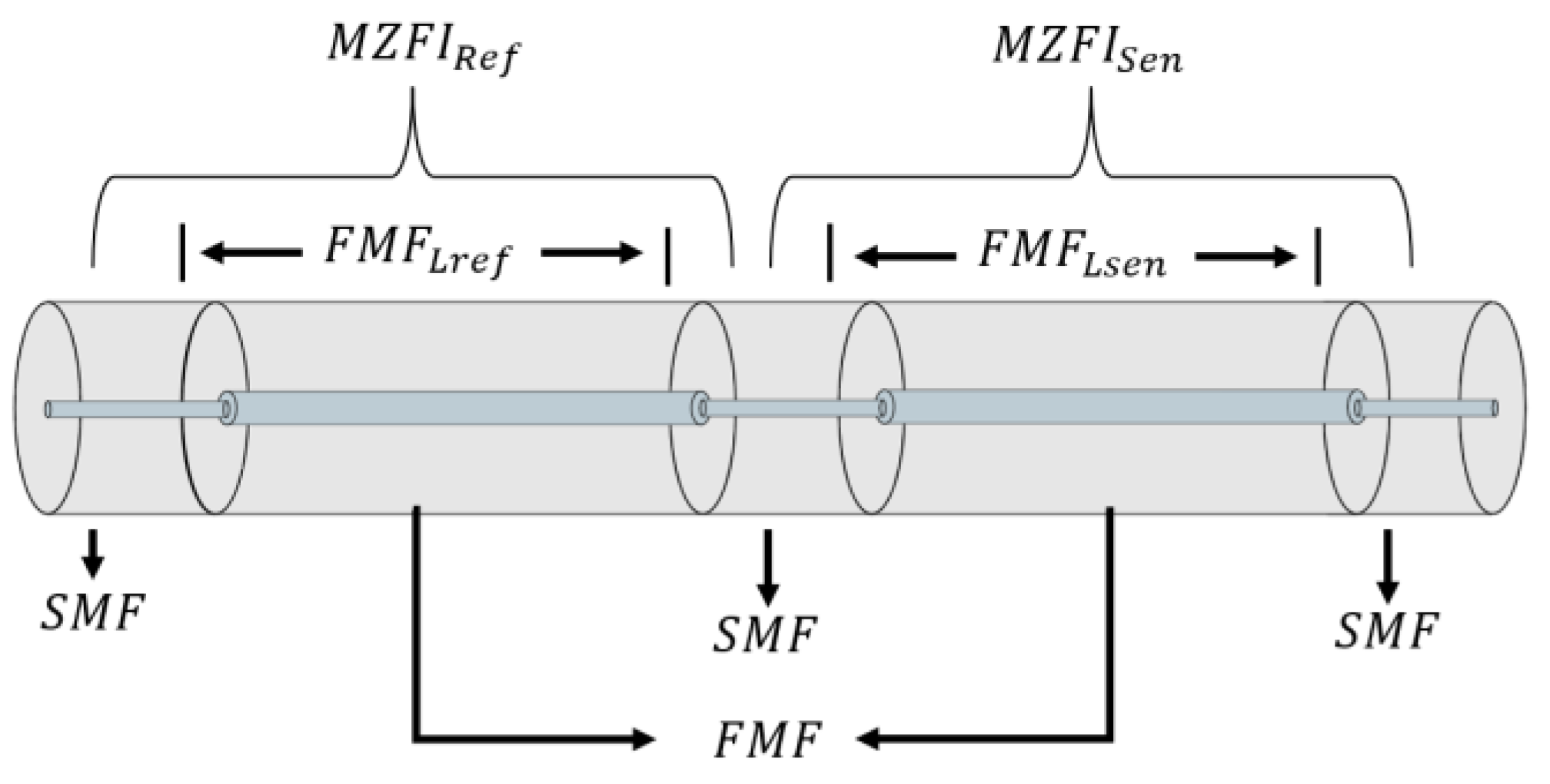


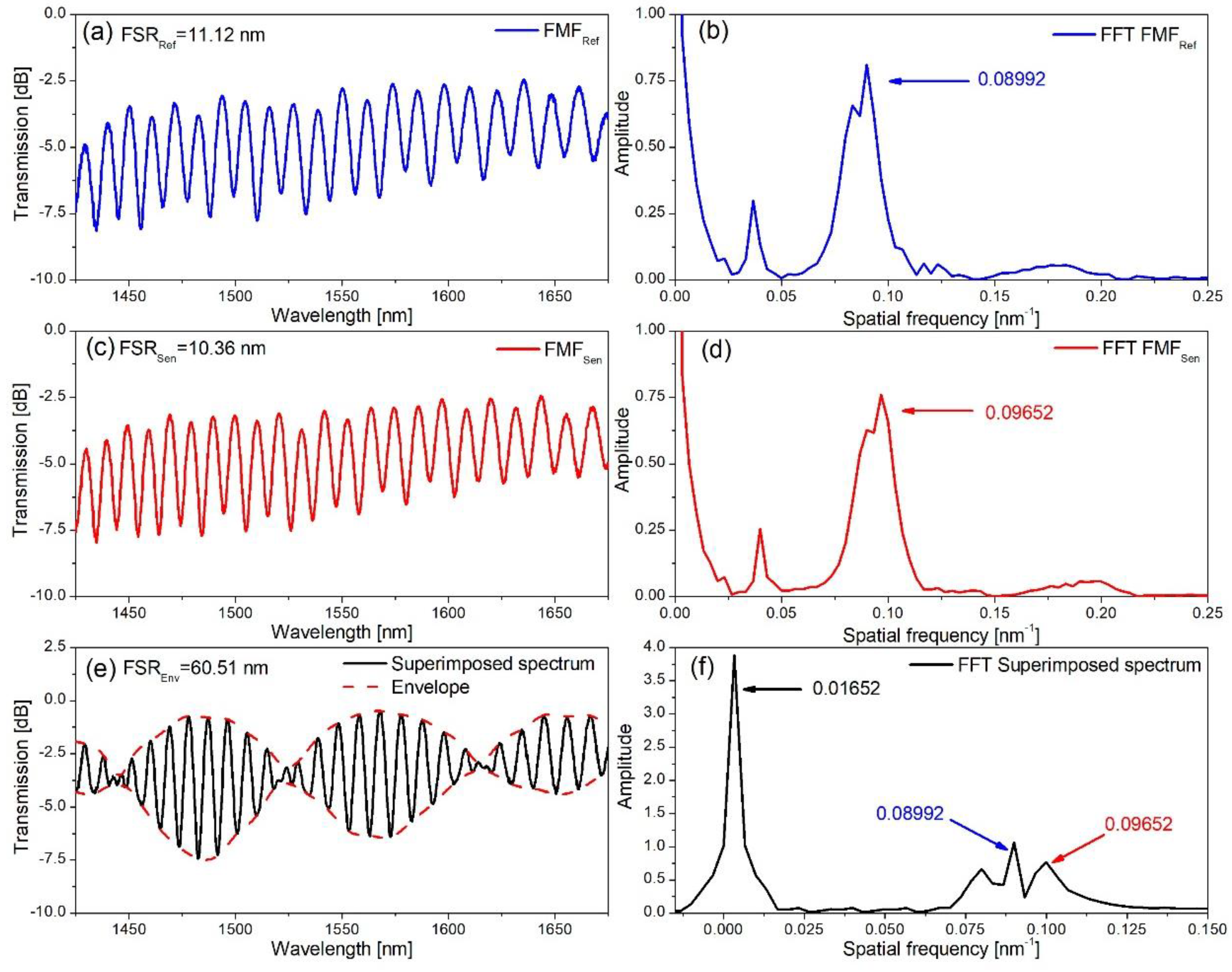






| Number of Experiment | (cm) | (cm) | (cm) | (nm) | (nm) | M Factor |
|---|---|---|---|---|---|---|
| 1 | 10 | 10.5 | 11.12 | 10.36 | 60.51 | 5.84 |
| 2 | 20 | 20.5 | 5.96 | 5.84 | 63.53 | 10.87 |
| 3 | 30 | 30.5 | 4.2 | 3.96 | 67.93 | 17.15 |
| 4 | 40 | 40.5 | 3.1 | 2.94 | 70.08 | 25.19 |
| 5 | 50 | 50.5 | 2.45 | 2.31 | 115.72 | 50.09 |
| Order | (cm) | Detuning Factor Δ (cm) | (cm) | (nm) | (nm) | (nm) | (nm) | Factor | |
|---|---|---|---|---|---|---|---|---|---|
| Experimental setup 1 | First Harmonic | 10.5 | +0.5 | 21.5 | 10.36 | 5.83 | 46.46 | 92.92 | 15.93 |
| Second Harmonic | 32 | 3.78 | 39.96 | 119.88 | 31.71 | ||||
| Third Harmonic Fourth Harmonic | 42.5 53 | 2.79 2.34 | 36.13 18.09 | 144.52 90.45 | 51.8 36.65 | ||||
| Experimental setup 2 | First Harmonic | 12.5 | +1 | 26 | 9.24 | 4.55 | 300.3 | 600.6 | 132 |
| Second Harmonic | 38.5 | 3.19 | 89.32 | 267.96 | 84 | ||||
| Third Harmonic | 51 | 2.4 | 61.6 | 246.4 | 102.66 | ||||
| Fourth Harmonic | 63.5 | 1.98 | 27.72 | 138.6 | 70 | ||||
| Experimental setup 3 | First Harmonic | 16.5 | −1 | 32 | 7.54 | 3.78 | 1425.06 | 2850.12 | 754 |
| Second Harmonic | 48.5 | 2.54 | 239.39 | 718.185 | 282.75 | ||||
| Third Harmonic | 65 | 1.81 | 45.49 | 181.96 | 100.53 | ||||
| Fourth Harmonic | 81.5 | 1.45 | 37.7 | 188.5 | 130 |
| Number of Experiment | (cm) | (cm) | (nm) | (nm) | (nm) | (nm−1) | (nm−1) | (nm−1) |
|---|---|---|---|---|---|---|---|---|
| 1 (Figure 4) | 10 | 10.5 | 11.12 | 10.36 | 60.51 | 0.08992 | 0.09652 | 0.01652 |
| 2 (Figure 5) | 20 | 20.5 | 5.96 | 5.84 | 63.53 | 0.1677 | 0.1712 | 0.01574 |
| 3 (Figure 6) | 30 | 30.5 | 4.2 | 3.96 | 67.93 | 0.2380 | 0.2525 | 0.01472 |
| 4 (Figure 7) | 40 | 40.5 | 3.1 | 2.94 | 74.08 | 0.3225 | 0.3401 | 0.01349 |
| 5 (Figure 8) | 50 | 50.5 | 2.45 | 2.31 | 115.72 | 0.4081 | 0.4329 | 0.008864 |
| Number of Experiment | Label in Figure 14 | (cm) | (cm) |
|---|---|---|---|
| 1 | (a) | 17.5 | 18.5 |
| (b) | 18.5 | 17.5 | |
| 2 | (c) | 26.5 | 27.5 |
| (d) | 27.5 | 26.5 | |
| 3 | (e) | 34.5 | 35 |
| (f) | 35 | 34.5 | |
| 4 | (g) | 41.5 | 42.5 |
| (h) | 42.5 | 41.5 | |
| 5 | (i) | 50.5 | 51.5 |
| (j) | 51.5 | 50.5 |
| Year | Configuration | Application | Measurement Range | Sensitivity | M Factor | Ref. | |
|---|---|---|---|---|---|---|---|
| 2019 | Cascading an SI and an FMF | Strain | 0–300 µε | 65.71 pm/µε | 20 | [4] | |
| 2020 | Structure SMF-TTFMF-SMF | Temperature | 25–60 °C | −3.348 nm/°C | 11.3 | [5] | |
| 2020 | Structure SMF-TTFMF-SMF | Temperature | 25–60 °C | −3.348 nm/°C | 11.3 | [5] | |
| 2020 | Structure SMF-FMF-SMF | Gas Pressure Temperature | 0–10 MPa 25–40 °C | 4.072 nm/MPa 1.753 nm/°C | 21 40.4 | [6] | |
| 2020 | Fabry–Perot in parallel with two access holes milled in the sensing FPI | RIU | 0–8 × 10−5 RIU | −568 nm/RIU −28,496 nm/RIU −418,387 nm/RIU | 1 50.2 865 | [7] | |
| 2021 | FMF with cascaded microcavities using a PDMS coating | Temperature | 35–45 °C | 4.7 nm/°C | 4.9 | [8] | |
| 2021 | FMF and PDMS to form the SMF-air microcavity-FMF-PDMS-FMF structure. | Temperature | 40–56 °C | 3.98 nm/°C | 4.76 | [9] | |
| 2023 | Multimode interferometer (MMI) with FMF and a simulated reference arm technique SRA | Strain | 0–1356.5 µε | −5.18 pm/µε −20.38 pm/µε | 10.36 40.76 | [10] | |
| 2024 | Micro-nano tapered TTMF | Salinity Temperature | 0–39.22% 30–50 °C | 6.138 nm/% −3.672 nm/°C | 13.64 14.81 | [11] | |
| 2024 | Two parallel FP formed between tapered two-mode fiber cantilever beam inserted into quartz capillary and SMF | Strain | 0–150 µε | −2.30 nm/µε −2.98 nm/µε | 13.7 35.9 | [12] | |
| Temperature | 20–40 °C | −79.6 pm/°C −69.3 pm/°C | 4.76 | ||||
| 2024 | SFS | Displacement | Proposed | Achieved | (1) 9.36 nm/mm (2) 16.03 nm/mm (3) 18.06 nm/mm (4) 19.88 nm/mm (5) 39.07 nm/mm | (1) 5.84 (2) 10.87 (3) 17.15 (4) 25.19 (5) 50.09 | This Work |
| 0–15 mm | (1) 0–15 mm (2) 0–12.5 mm (3) 0–10 mm (4) 0–10 mm (5) 0–5 mm | ||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guillen-Ruiz, L.E.; Anzueto-Sánchez, G.; Martínez-Rios, A.; Jiménez-Mares, M.C.; Martin-Vela, J.A. High-Sensitivity Displacement Sensor Using Few-Mode Optical Fibers and the Optical Vernier Effect. Appl. Sci. 2024, 14, 9300. https://doi.org/10.3390/app14209300
Guillen-Ruiz LE, Anzueto-Sánchez G, Martínez-Rios A, Jiménez-Mares MC, Martin-Vela JA. High-Sensitivity Displacement Sensor Using Few-Mode Optical Fibers and the Optical Vernier Effect. Applied Sciences. 2024; 14(20):9300. https://doi.org/10.3390/app14209300
Chicago/Turabian StyleGuillen-Ruiz, Luis E., Gilberto Anzueto-Sánchez, Alejandro Martínez-Rios, Myriam C. Jiménez-Mares, and Javier A. Martin-Vela. 2024. "High-Sensitivity Displacement Sensor Using Few-Mode Optical Fibers and the Optical Vernier Effect" Applied Sciences 14, no. 20: 9300. https://doi.org/10.3390/app14209300
APA StyleGuillen-Ruiz, L. E., Anzueto-Sánchez, G., Martínez-Rios, A., Jiménez-Mares, M. C., & Martin-Vela, J. A. (2024). High-Sensitivity Displacement Sensor Using Few-Mode Optical Fibers and the Optical Vernier Effect. Applied Sciences, 14(20), 9300. https://doi.org/10.3390/app14209300







