A Bi-Objective Optimization Strategy of a Distribution Network Including a Distributed Energy System Using Stepper Search
Abstract
:1. Introduction
1.1. Literature Review
1.2. Contributions and Paper Organization
- (1)
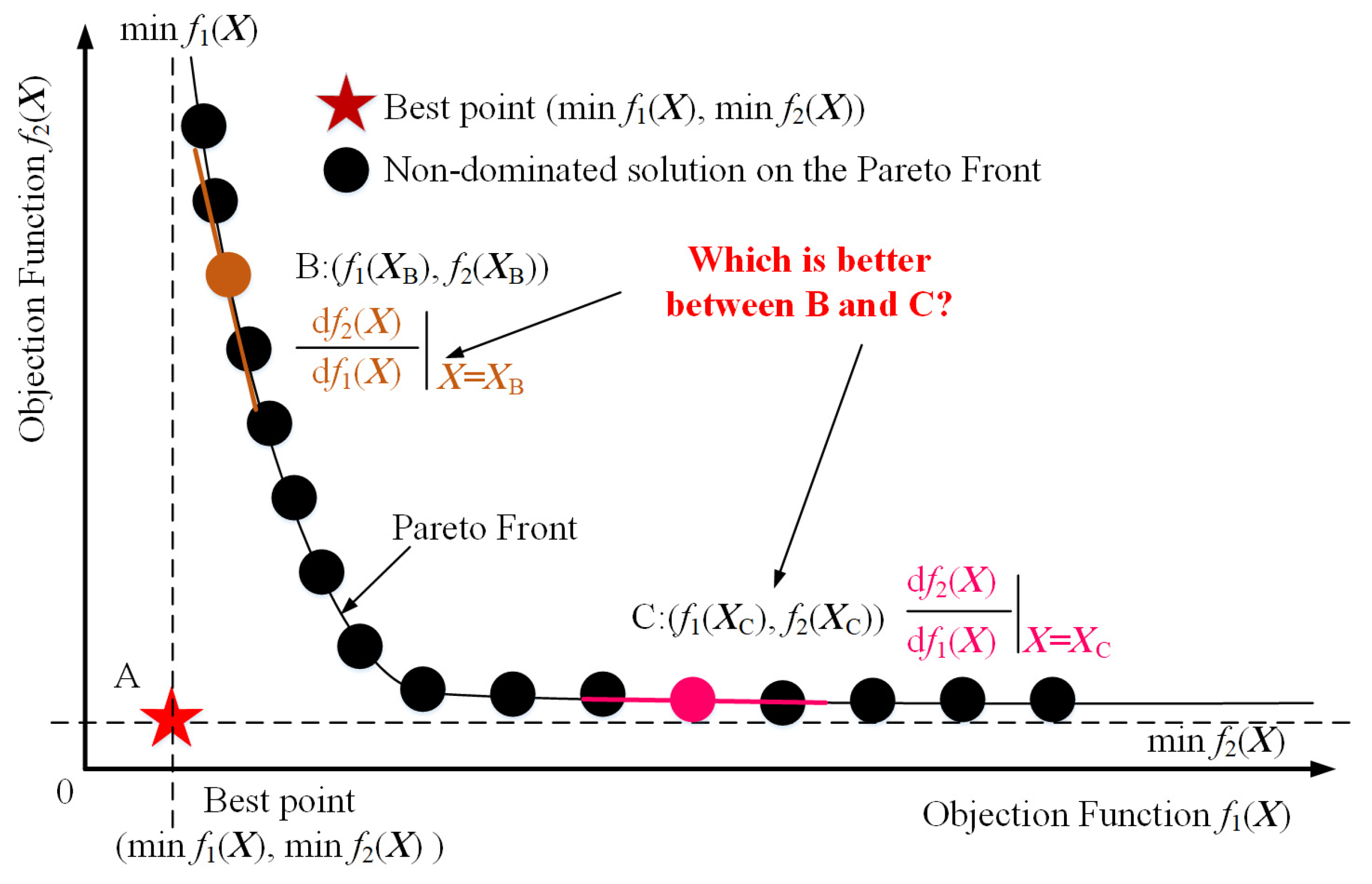
- The SSO method has transformed a BiOP into a CSiOP by changing the boundary conditions. It can effectively describe the pareto front of the BiOP, which helps to solve the problem of how to choose the recommended solution on the pareto front.
- (2)
- For the first time, the SSO method adopts stepper search on the pareto front to form the best-recommended solution of a BiOP based on the change rate of each non-dominated solution, with a novel approach being provided for selecting the recommended solution of a BiOP.
2. Mathematical Model of Distribution Network
2.1. The Operation Constraints of Distribution Network
2.2. The Objective Function of Distribution Network
- (1)
- To reduce the power line loss of the DES, the first optimization objective function J1 is established, as shown in Expression (12), and is a key index that effects the transmission efficiency of the power grid.
- (2)
- To reduce the operating costs of the DES, the second optimization objective function J2 is established including the cost of DG, ESS and the new energy generation station, as shown in Expression (13), where SDG,i, and respectively represent the electricity consumption of the i-th DG, ESS and new energy during time period Δt. = × Δt, = × Δt and = × Δt. In this paper, Δt = 1 h. Then, where k1,I, k2,I and k3,i respectively represent the cost coefficient of DG [30,31], ¥/kWh2, ¥/kWh, ¥. Significantly, k1,i represents the cost coefficient of the square of the active power of DG. Therefore, the unit of coefficient k1,i is ¥/kWh2. The levelized cost coefficient of the ESS and the new energy generation station have been defined as k4,i and k5,i, ¥/kWh.
3. The Problem and Solution of the BiOP
3.1. The Problem of the BiOP
3.2. A Bi-Objective Optimization Method Based on SSO
| Algorithm 1 Pseudo code of the SSO method. |
Input: In the DES described in this article, the BiOP has been shown in mathematical relation (1)~(13), and the mathematical model for transforming the BiOP of the DES is shown in Expression (16). The initial step parameter Δc and the deadline of stepper search are defined. The deadline of the stepper search is the maximum number of iterations Nmax and stop threshold λ. Assuming that the iteration N is 0,
|
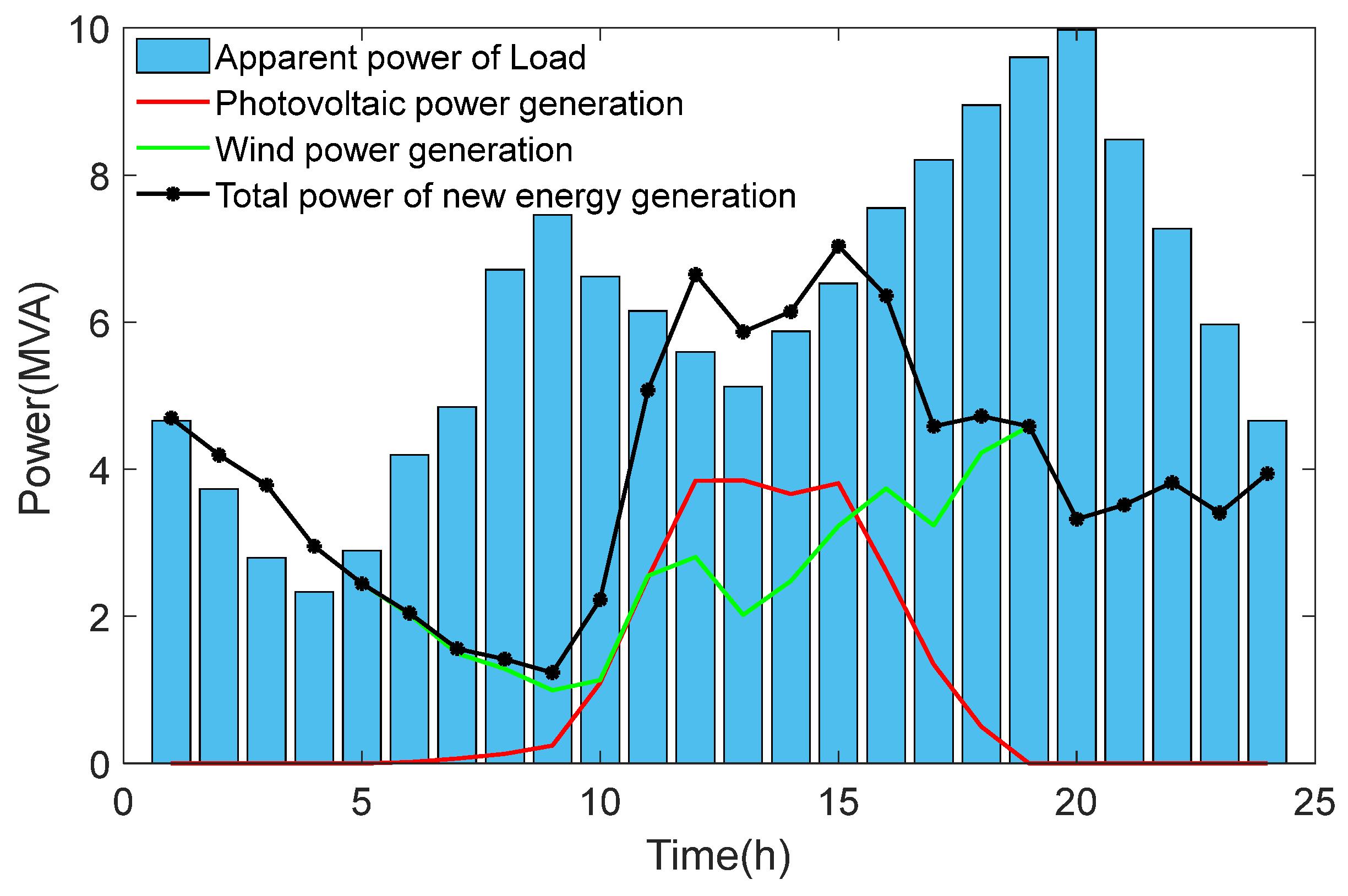
4. Case and Discussion
4.1. Case Condition
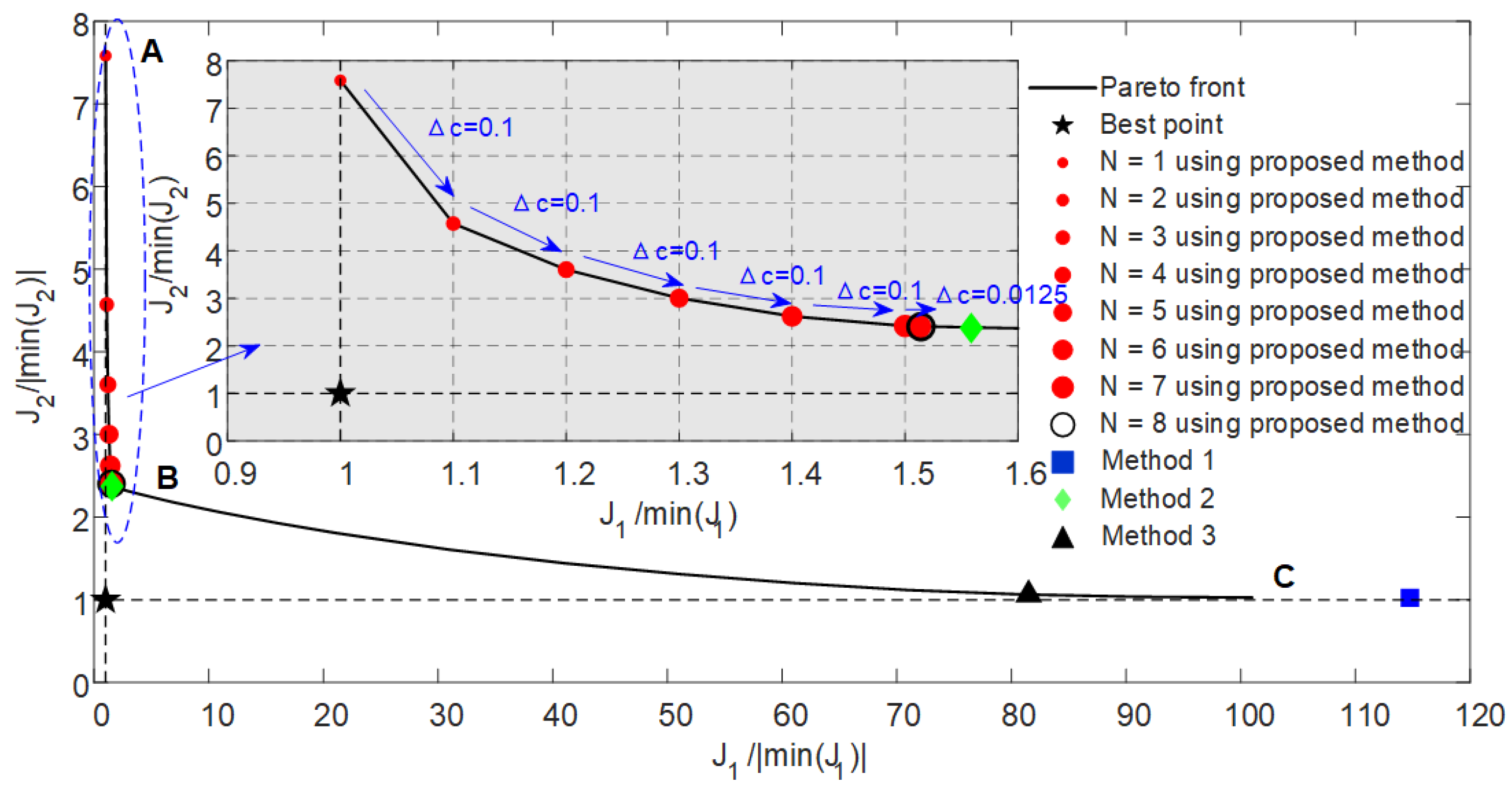
4.2. Result Analysis
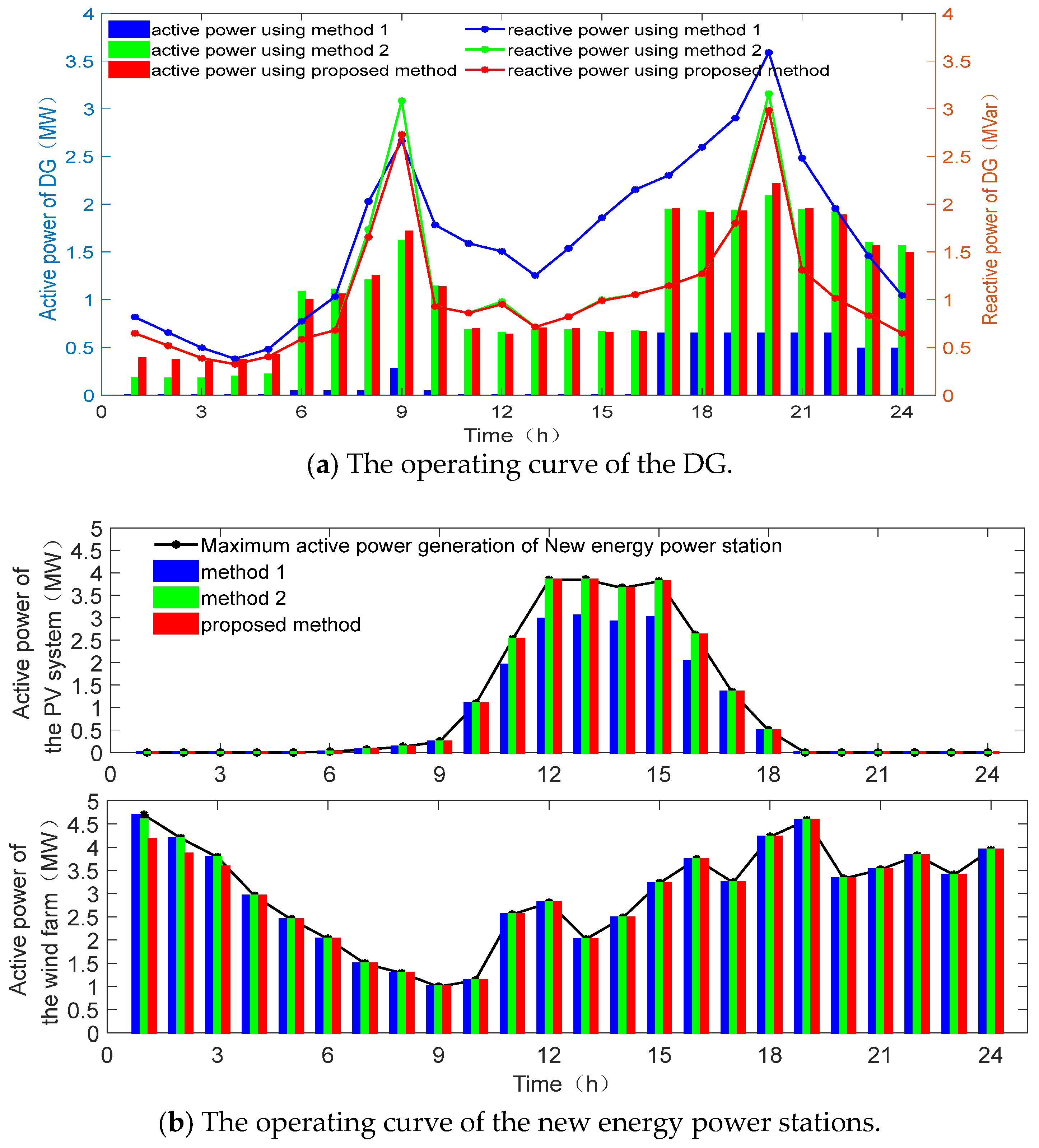
4.3. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, Q.; Wang, J.; Chen, J.; Ding, T.; Gu, C. A hierarchical multi-area capacity planning model considering configuration ratios of renewable energy and energy storage systems with multi-area coordination. IET Gener. Transm. Distrib. 2023, 17, 3658–3677. [Google Scholar] [CrossRef]
- Zeng, L.; Xu, J.; Wang, Y.; Liu, Y.; Tang, J.; Wen, M.; Chen, Z. Day-ahead interval scheduling strategy of power systems based on improved adaptive diffusion kernel density estimation. Electr. Power Energy Syst. 2023, 147, 108850. [Google Scholar] [CrossRef]
- Zuo, H.; Teng, Y.; Cheng, S.; Sun, P.; Chen, Z. Distributed multi-energy storage cooperative optimization control method for power grid voltage stability enhancement. Electr. Power Syst. Res. 2023, 216, 109012. [Google Scholar] [CrossRef]
- Ahmadi, B.; Ceylan, O.; Ozdemir, A.; Fotuhi-Firuzabad, M. A multi-objective framework for distributed energy resources planning and storage management. Appl. Energy 2022, 314, 118887. [Google Scholar] [CrossRef]
- Cheng, T.; Chen, M.; Wang, Y.; Li, B.; Hassan, M.A.; Chen, T.; Xu, R. Adaptive Robust Method for Dynamic Economic Emission Dispatch Incorporating Renewable Energy and Energy Storage. Complexity 2018, 2018, 2517987. [Google Scholar] [CrossRef]
- Di, H.; Xin, Y.; Lin, G.; Zhang, C.; Chen, H. Interval economic dispatch of multi-objective cooperative game considering wind power and energy storage connected to power grid. Control Theory Appl. 2021, 38, 1061–1070. [Google Scholar]
- Sandgani, M.R.; Sirouspour, S. Coordinated Optimal Dispatch of Energy Storage in a Network of Grid-connected Microgrids. IEEE Trans. Sustain. Energy 2017, 8, 1166–1176. [Google Scholar] [CrossRef]
- Wu, X.; Liao, B.; Su, Y.; Li, S. Multi-objective and multi-algorithm operation optimization of integrated energy system considering ground source energy and solar energy. Int. J. Electr. Power Energy Syst. 2023, 144, 108529. [Google Scholar] [CrossRef]
- Liu, Z.; Xiao, Z.; Wu, Y.; Hou, H.; Xu, T.; Zhang, Q.; Xie, C. Integrated optimal dispatching strategy considering power generation and consumption interaction. IEEE Access 2021, 9, 1338–1349. [Google Scholar] [CrossRef]
- Ma, S.; Wu, Y.; Li, J.; Hou, X.; Li, D. Optimal economic planning method of energy storage system to improve grid reliability. Acta Energiae Solaris Sin. 2024, 45, 251–262. [Google Scholar]
- Jiang, W.; Chen, Z. Optimization of microgrid energy storage system capacity based on improved artifical bee colony algorithm. J. Shanghai Univ. Electr. Power 2021, 37, 415–421+427. [Google Scholar]
- Mishra, A.; Arora, B.B.; Arora, A. Multi-Objective Optimization of an Inlet Air-Cooled Combined Cycle Power Plant. J. Therm. Sci. Eng. Appl. Trans. ASME 2023, 15, 071005. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, Q.; Guan, H.; Li, X.; Bi, D.; Guo, Y.; Sun, H. Optimization Strategy of Configuration and Scheduling for User-Side Energy Storage. Electronics 2021, 11, 120. [Google Scholar] [CrossRef]
- Sun, J.; Li, Z.; Li, J.; Wu, G.; Xia, Y. Hybrid power system with adaptive adjustment of weight coefficients multi-objective model predictive control. Int. J. Electr. Power Energy Syst. 2023, 153, 109296. [Google Scholar] [CrossRef]
- Li, L.; Liu, P.; Li, Z.; Wang, X. A multi-objective optimization approach for selection of energy storage systems. Comput. Chem. Eng. 2018, 115, 213–225. [Google Scholar] [CrossRef]
- Terlouw, T.; Gabrielli, P.; AlSkaif, T.; Bauer, C.; McKenna, R.; Mazzotti, M. Optimal economic and environmental design of multi-energy systems. Appl. Energy 2023, 347, 121374. [Google Scholar] [CrossRef]
- Fan, W.; Tan, Q.; Zhang, A.; Ju, L.; Wang, Y.; Yin, Z.; Li, X. A Bi-level optimization model of integrated energy system considering wind power uncertainty. Renew. Energy 2023, 202, 973–991. [Google Scholar] [CrossRef]
- Pourghaderi, N.; Fotuhi-Firuzabad, M.; Moeini-Aghtaie, M.; Kabirifar, M.; Lehtonen, M. Optimal energy and flexibility self-scheduling of a technical virtual power plant under uncertainty: A two-stage adaptive robust approach. IET Gener. Transm. Distrib. 2023, 17, 3828–3847. [Google Scholar] [CrossRef]
- Qiu, Y.; Li, Q.; Ai, Y.; Chen, W.; Benbouzid, M.; Liu, S.; Gao, F. Two-stage distributionally robust optimization-based coordinated scheduling of integrated energy system with electricity-hydrogen hybrid energy storage. Prot. Control Mod. Power Syst. 2023, 8, 33. [Google Scholar] [CrossRef]
- Luo, Y.; Gao, Y.; Fan, D. Real-time demand response strategy base on price and incentive considering multi-energy in smart grid: A bi-level optimization method. Int. J. Electr. Power Energy Syst. 2023, 153, 109354. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhong, K.; Deng, W.; Cheng, R.; Chen, M.; An, Y.; Tang, Y. An optimal scheduling of renewable energy in flexible interconnected distribution networks considering extreme scenarios. IET Renew. Power Gener. 2023, 17, 2531–2541. [Google Scholar] [CrossRef]
- Yang, H.; Wu, J.; Du, X. Thermo-economic analysis and multi-objective optimization of solar aided pumped thermal electricity storage system. J. Energy Storage 2023, 70, 107994. [Google Scholar] [CrossRef]
- Zhao, J.; Ju, L.; Luo, W.; Zhao, J. Reactive voltage control model and method considering partitioned dynamic reactive power reserve. Electr. Power Autom. Equip. 2015, 35, 100–105. [Google Scholar]
- Sagawa, D.; Tanaka, K. Machine Learning-Based Estimation of COP and Multi-Objective Optimization of Operation Strategy for Heat Source Considering Electricity Cost and On-Site Consumption of Renewable Energy. Energies 2023, 16, 4893. [Google Scholar] [CrossRef]
- Zhong, Y.; Huang, M.; Ye, C. Multi-objective optimization of microgrid operation based on dynamic dispatch of battery energy storage system. Electr. Power Autom. Equip. 2014, 34, 114–121. [Google Scholar]
- Liao, X.; Qian, B.; Jiang, Z.; Fu, B.; He, H. Integrated Energy Station Optimal Dispatching Using a Novel Many-Objective Optimization Algorithm Based on Multiple Update Strategies. Energies 2023, 16, 5216. [Google Scholar] [CrossRef]
- Ma, S.; Wu, Y.; Li, J.; Xiong, J.; Zeng, W. Research on optimal configuration of centralized battery energy storage for multiple service objectives. High Volt. Appar. 2023, 59, 75–86. [Google Scholar]
- Ma, G.; Li, J.; Zhang, X.P. Energy Storage Capacity Optimization for Improving the Autonomy of Grid-Connected Microgrid. IEEE Trans. Smart Grid 2023, 14, 2921–2933. [Google Scholar] [CrossRef]
- Chen, Y.; Feng, L.; Li, X.; Zoghi, M.; Javaherdeh, K. Exergy-economic analysis and multi-objective optimization of a multi-generation system based on efficient waste heat recovery of combined wind turbine and compressed CO2 energy storage system. Sustain. Cities Soc. 2023, 96, 104714. [Google Scholar] [CrossRef]
- Ma, S.; Wu, Y.; Jiang, Y.; Li, Y.; Sha, G. Research on two-stage optimization control method for energy storage systems based on multi service attribute utility evaluation. J. Energy Storage 2024, 46, 3041–3060. [Google Scholar] [CrossRef]
- Lu, M.; Guan, J.; Wu, H.; Chen, H.; Gu, W.; Wu, Y.; Ling, C.; Zhang, L. Day-ahead optimal dispatching of multi-source power system. Renew. Energy 2022, 183, 435–446. [Google Scholar] [CrossRef]
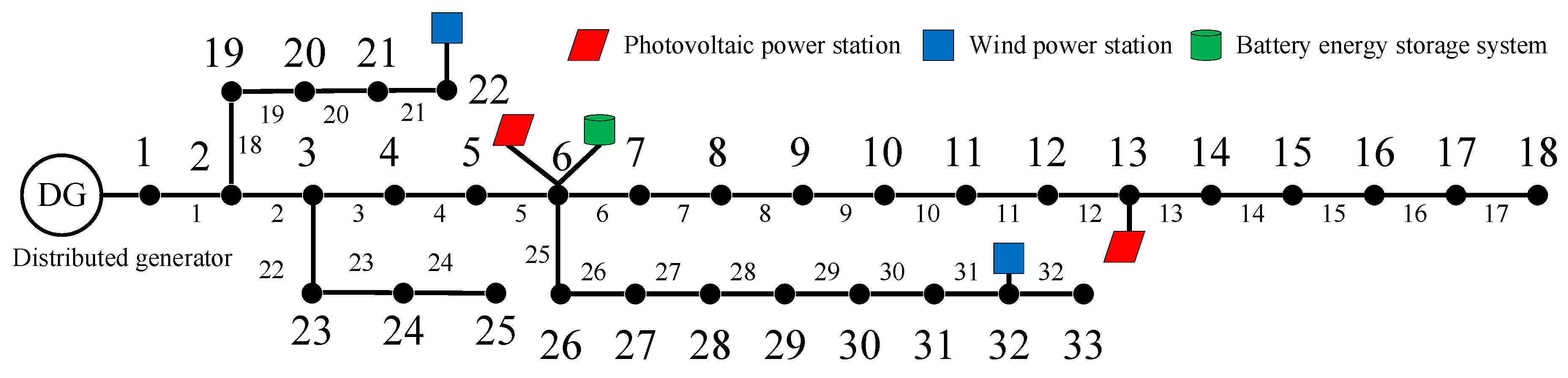



| Reference | System Components | Grid | Number of Objective Functions | Methodology | ||||
|---|---|---|---|---|---|---|---|---|
| DG | WF | PV | BESS | Other | ||||
| [5] | ✓ | ✓ | ✓ | 2 | PSO-TLBO | |||
| [6] | ✓ | ✓ | ✓ | ✓ | 2 | ECA + TOPSIS | ||
| [8] | ✓ | ✓ | ✓ | 3 | MO-NSGA-II | |||
| [10] | ✓ | ✓ | ✓ | 3 | MC + TOPSIS | |||
| [11] | ✓ | ✓ | ✓ | ✓ | ✓ | 3 | EW + ABC | |
| [13] | ✓ | ✓ | ✓ | 11 | Weighted summation | |||
| [14] | ✓ | ✓ | 3 | MPC + adaptive weight | ||||
| [16] | ✓ | ✓ | ✓ | ✓ | ✓ | 2 | Weighted summation | |
| [17] | ✓ | ✓ | ✓ | ✓ | 2 | B-L optimization model | ||
| [19] | ✓ | ✓ | ✓ | ✓ | ✓ | 3 | TSDRO | |
| [21] | ✓ | ✓ | ✓ | 3 | Multi-OPF model | |||
| [26] | ✓ | ✓ | ✓ | 3 | MOMUS | |||
| Case Parameter | Numerical Value | Case Parameter | Numerical Value |
|---|---|---|---|
| Capacity of power grid | 10 MVA | Rated power of DG | 10 MVA |
| Nominal voltage | 12.66 kV | Cost coefficient k1 of DG | 40,000 ¥/kWh2 |
| The voltage range | ±10% | Cost coefficient k2 of DG | 650 ¥/kWh |
| The maximum branch current | 456 A | Cost coefficient k3 of DG | 8 ¥ |
| Charge/discharge efficiency of BESS | 95%, 92% | Rated power of photovoltaic at #6 node | 4 MW |
| SOE range of BESS | 90%, 10% | Rated power of photovoltaic at #13 node | 2 MW |
| Initial SOE of BESS | 50% | Levelized cost of photovoltaic | 0.293 ¥/kWh |
| Rated power of BESS | 3.3 MW | Rated power of wind farm at #22 node | 3 MW |
| Rated capacity of BESS | 13.2 MWh | Rated power of wind farm at #22 node | 2 MW |
| Levelized cost of BESS | 0.574 ¥/kWh | Levelized cost of wind farm | 0.3 ¥/kWh |
| Initial stepper parameter Δc | 0.1 | The stop threshold λ | 1 × 10−4 |
| min J1 | min J2 | Method 1 | Method 2 | Method 3 | SSO Method | |
|---|---|---|---|---|---|---|
| J1/|min(J1)| | 1 | 140.7114 | 114.7497 | 1.5586 | 81.4999 | 1.5141 |
| J2/|min(J2)| | 7.7836 | 1 | 1.0248 | 2.3756 | 1.0637 | 2.4047 |
| Computing time | 18.44 s | 18.67 s | 21.94 s | 26.22 s | 3907.16 s | 280.44 s |
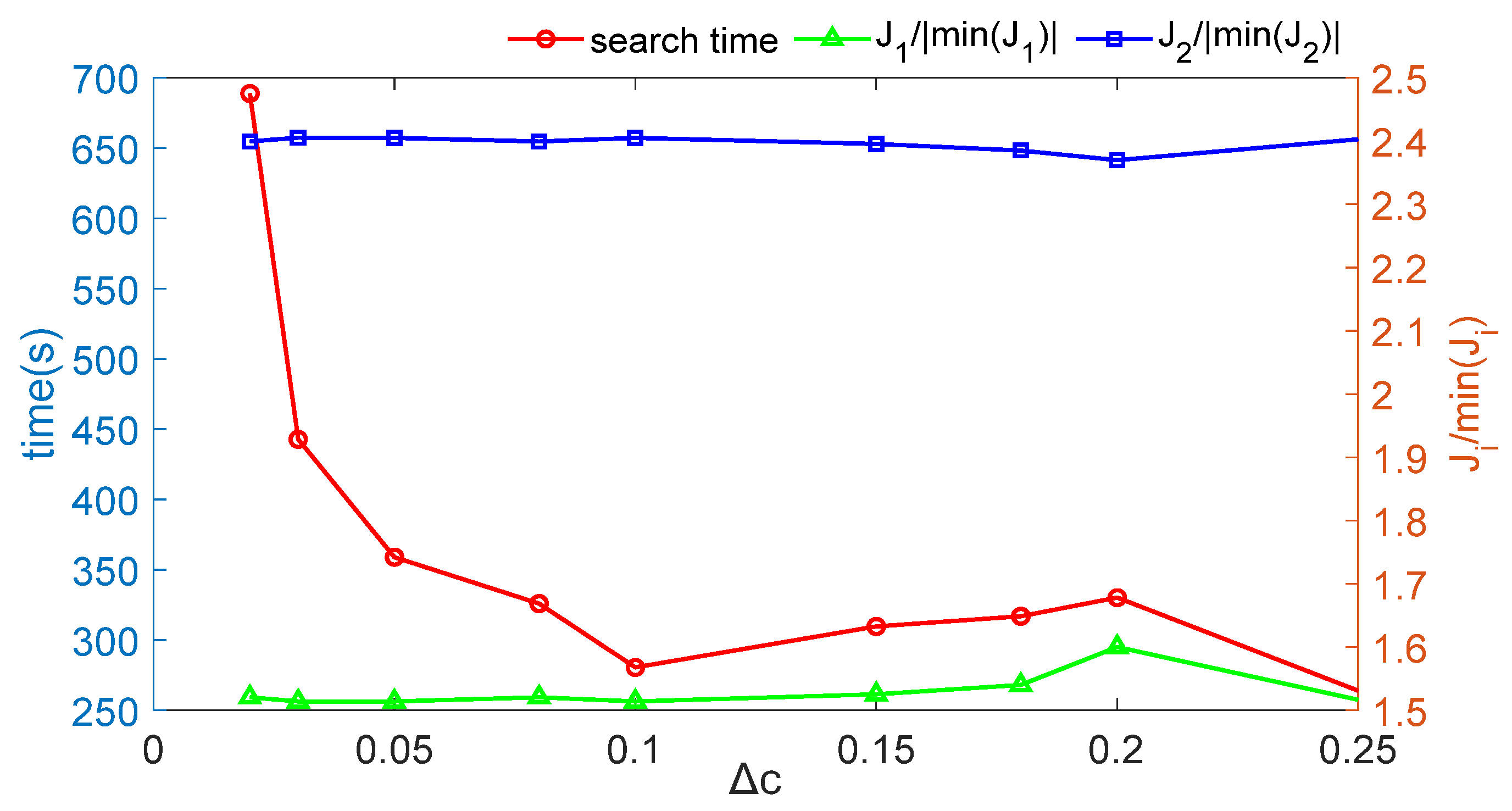
| Δc | 0.02 | 0.03 | 0.05 | 0.08 | 0.1 | 0.15 | 0.18 | 0.2 | 0.25 |
|---|---|---|---|---|---|---|---|---|---|
| Search time | 688.67 | 442.67 | 358.85 | 325.88 | 280.44 | 309.58 | 316.85 | 330.09 | 263.99 |
| J1/|min(J1)| | 1.52 | 1.51 | 1.51 | 1.52 | 1.51 | 1.53 | 1.54 | 1.60 | 1.52 |
| J2/|min(J2)| | 2.40 | 2.40 | 2.40 | 2.40 | 2.40 | 2.40 | 2.38 | 2.37 | 2.40 |
| min J1 | min J3 | Method 1 | Method 2 | Method 3 | SSO Method | |
|---|---|---|---|---|---|---|
| J1/|(min(J1)| | 1 | 65.9354 | 1.4879 | 1.5170 | 1.0161 | 1.5031 |
| J3/|min(J3)| | 78.7690 | 1 | 1.5731 | 1.5448 | 71.4381 | 1.5581 |
| Computing time | 18.44 s | 18.61 s | 17.34 s | 21.42 s | 7715.89 s | 263.52 s |
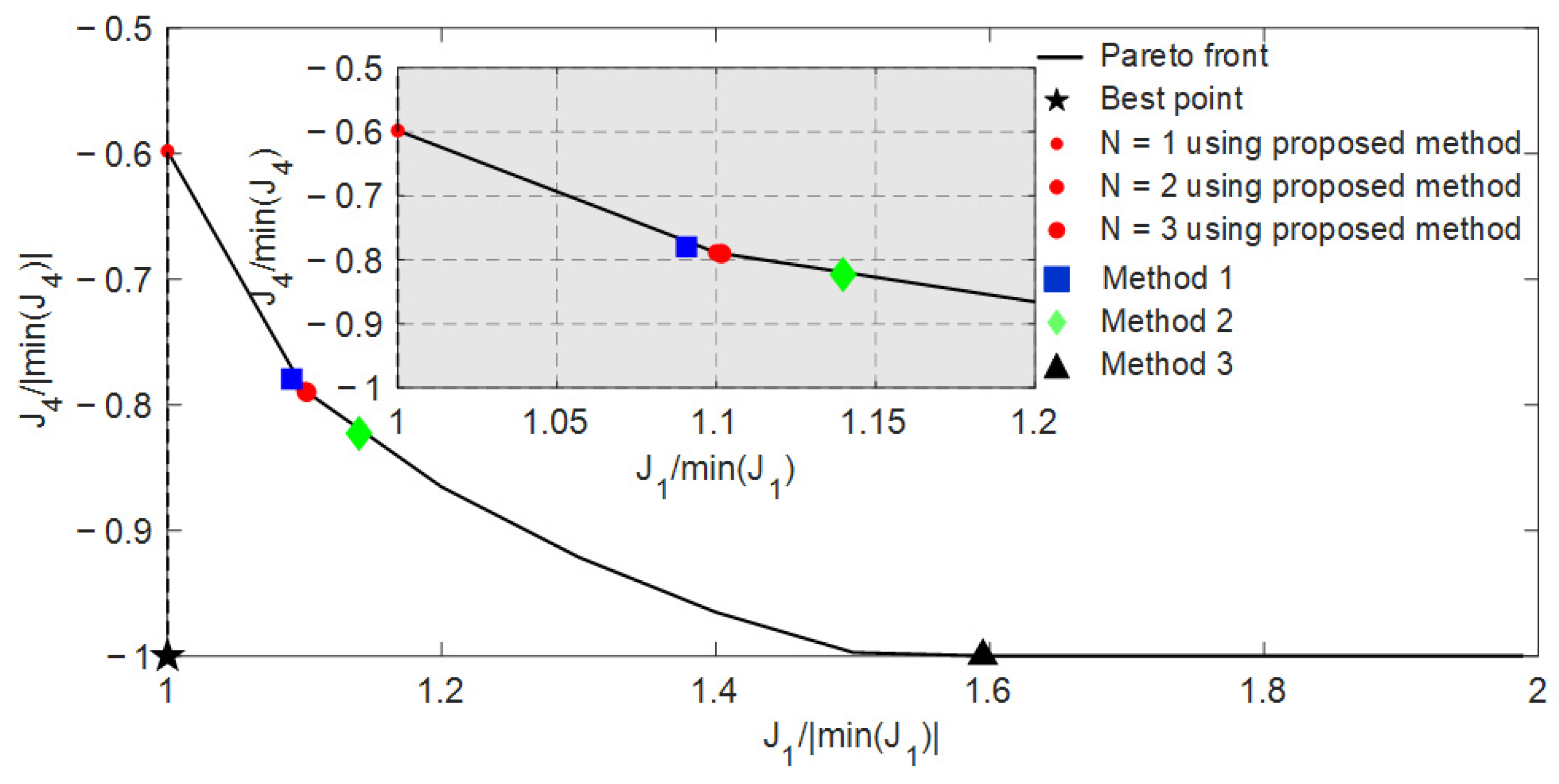
| min J1 | min J4 | Method 1 | Method 2 | Method 3 | SSO Method | |
|---|---|---|---|---|---|---|
| J1/|(min(J1)| | 1 | 49.5009 | 1.0906 | 1.1398 | 1.5947 | 1.1016 |
| J4/|min(J4))| | −0.5872 | −1 | −0.7795 | −0.8228 | −1.0000 | −0.7900 |
| Computing time | 18.44 s | 14.03 s | 11.96 s | 13.15 s | 2251.62 s | 109.45 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, S.; Meng, Z.; Cui, Y.; Sha, G. A Bi-Objective Optimization Strategy of a Distribution Network Including a Distributed Energy System Using Stepper Search. Appl. Sci. 2024, 14, 9480. https://doi.org/10.3390/app14209480
Ma S, Meng Z, Cui Y, Sha G. A Bi-Objective Optimization Strategy of a Distribution Network Including a Distributed Energy System Using Stepper Search. Applied Sciences. 2024; 14(20):9480. https://doi.org/10.3390/app14209480
Chicago/Turabian StyleMa, Suliang, Zeqing Meng, Yilin Cui, and Guanglin Sha. 2024. "A Bi-Objective Optimization Strategy of a Distribution Network Including a Distributed Energy System Using Stepper Search" Applied Sciences 14, no. 20: 9480. https://doi.org/10.3390/app14209480
APA StyleMa, S., Meng, Z., Cui, Y., & Sha, G. (2024). A Bi-Objective Optimization Strategy of a Distribution Network Including a Distributed Energy System Using Stepper Search. Applied Sciences, 14(20), 9480. https://doi.org/10.3390/app14209480






