The Value of Fractal Analysis in Ultrasound Imaging: Exploring Intricate Patterns
Abstract
1. Introduction
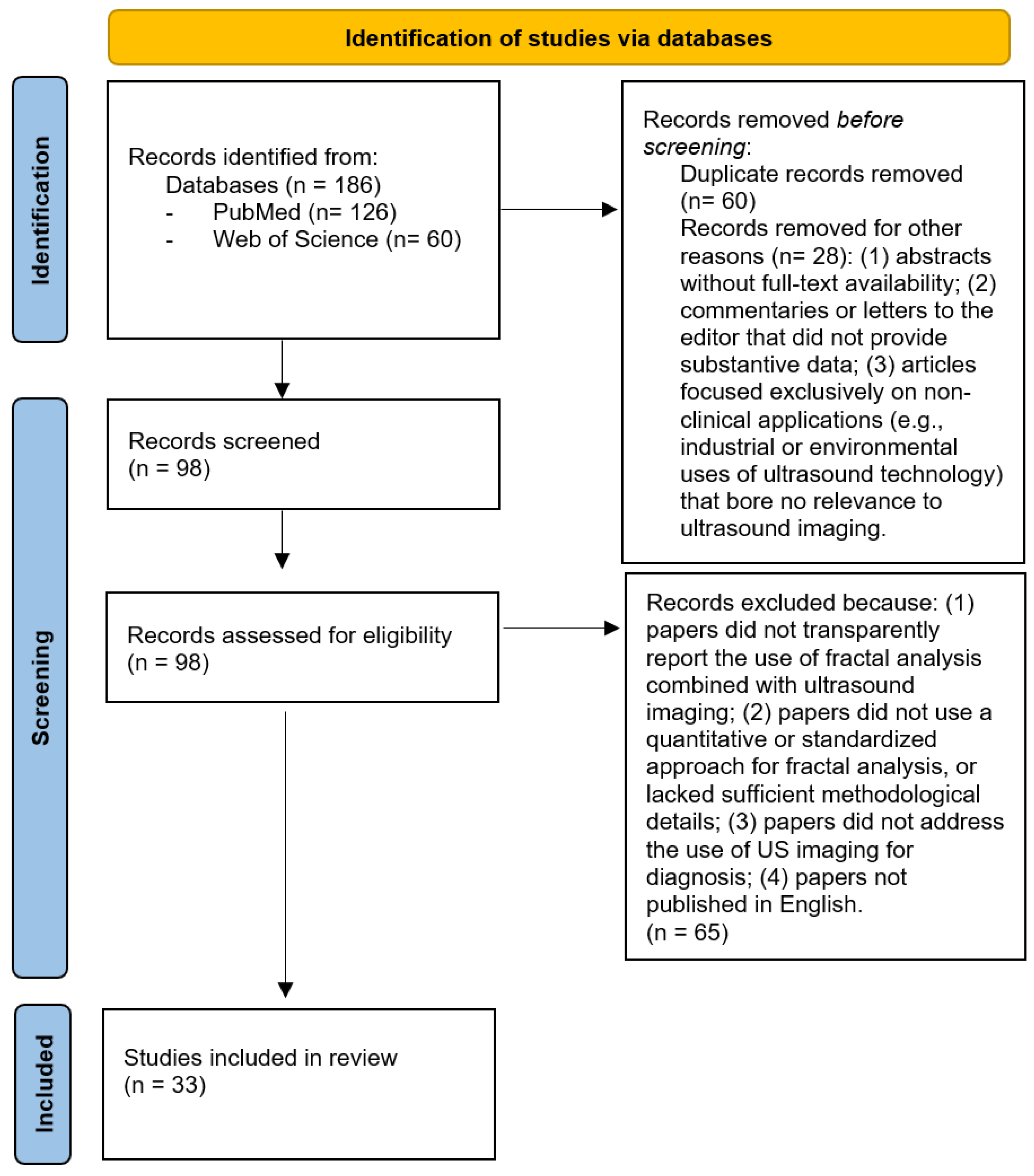
2. Materials and Methods
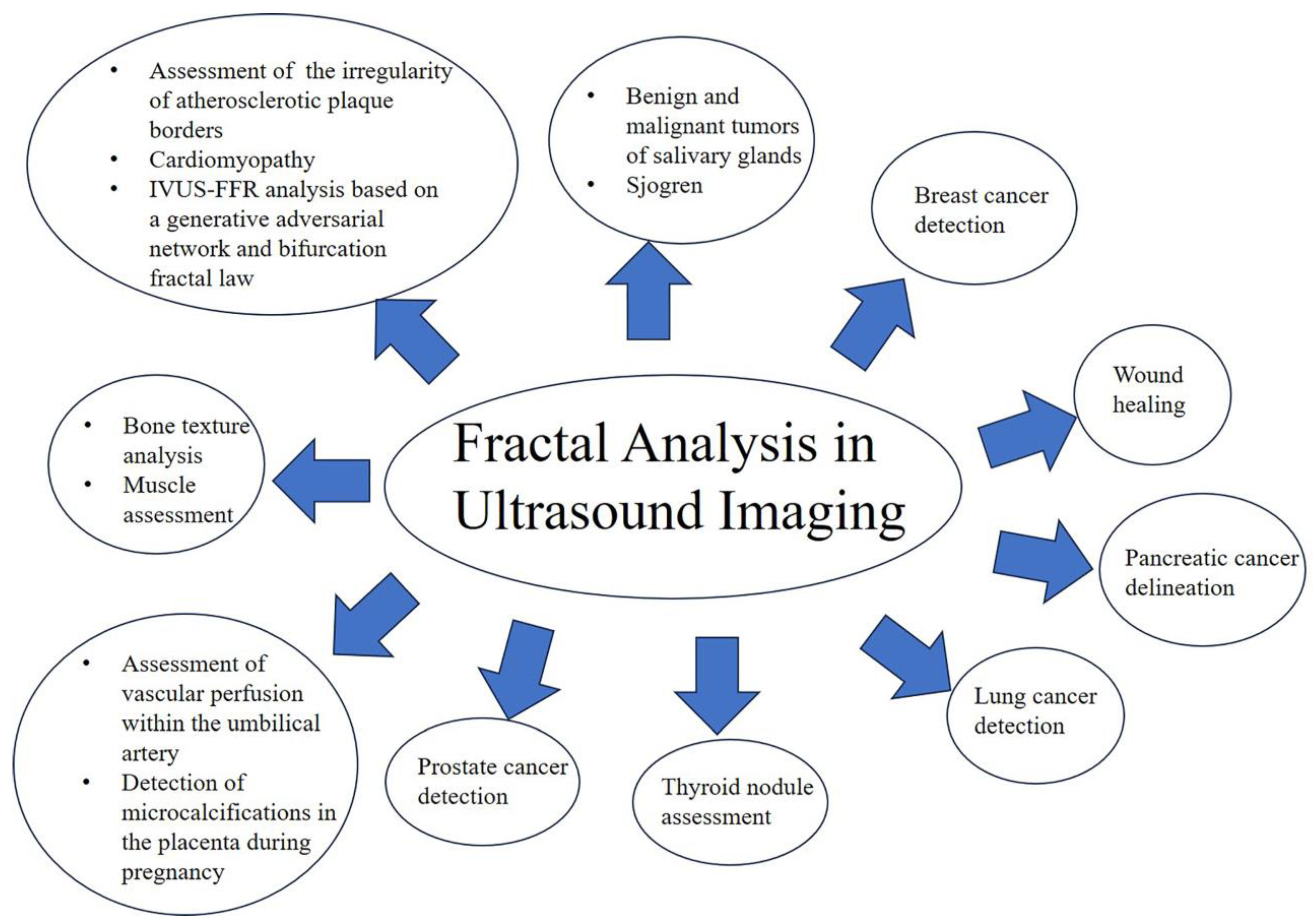
3. Results
3.1. Bone Texture Analysis
3.2. Breast Cancer Detection
3.3. Lung Cancer Detection
3.4. Salivary Glands
3.5. Pancreatic Cancer Delineation
3.6. Prostate Cancer Detection
3.7. Skin and Wound Healing
3.8. Pregnancy
3.9. Heart and Blood Vessels
3.10. Thyroid
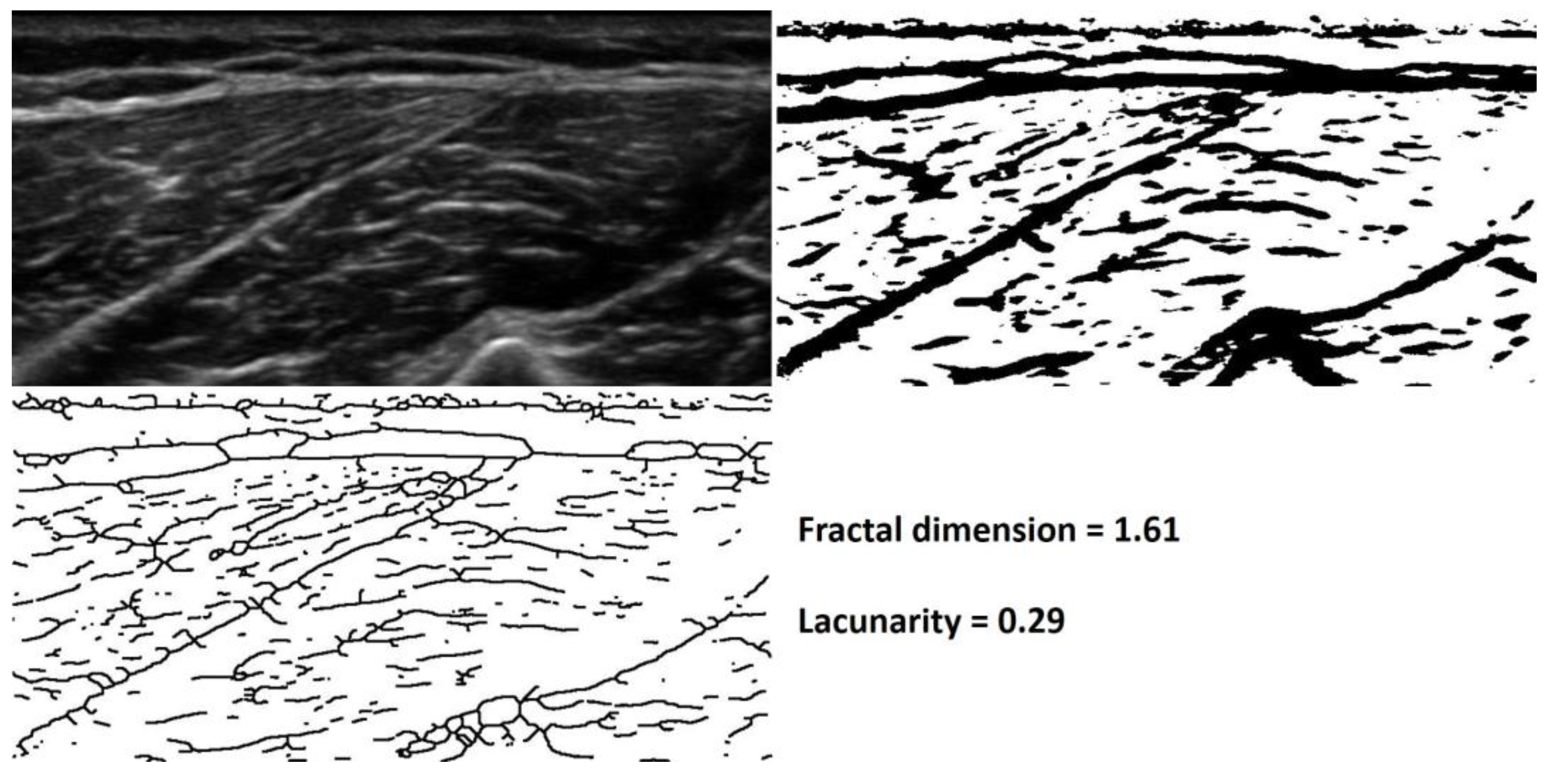
3.11. Muscle
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mandelbrot, B.B. The Fractal Geometry of Nature; W.H. Freeman and Company: New York, NY, USA, 1982. [Google Scholar]
- Peitgen, H.O.; Jürgens, H.; Saupe, D. Chaos and Fractals: New Frontiers of Science; Springer: Berlin/Heidelberg, Germany, 1992. [Google Scholar]
- Falcone, K. Fractal Geometry: Mathematical Foundations and Applications; John Wiley and Sons: Hoboken, NJ, USA, 2003. [Google Scholar]
- Lopes, R.; Betrouni, N. Fractal and multifractal analysis: A review. Med. Image Anal. 2009, 13, 634–649. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Hu, W.Y.; Liu, L.Z.; Pang, Y.C.; Shao, Y.Z. Evaluation of breast cancer chemotherapy efficacy with multifractal spectrum analysis of magnetic resonance image. Biomed. Mater. Eng. 2014, 24, 163–171. [Google Scholar] [CrossRef] [PubMed]
- Acharya, U.R.; Sree, S.V.; Muthu Rama Krishnan, M.; Krishnananda, N.; Ranjan, S.; Umesh, P.; Suri, J.S. Automated classification of patients with coronary artery disease using grayscale features from left ventricle echocardiographic images. Comput. Methods Programs Biomed. 2013, 112, 624–632. [Google Scholar] [CrossRef] [PubMed]
- Biswas, A.K.; Karmakar, S.; Sharma, S. Performance analysis of a new fractal compression method for medical images based on fixed partition. Int. J. Inf. Technol. 2021, 14, 411–419. [Google Scholar] [CrossRef]
- Sree, S.V.; Ng, E.Y.; Acharya, R.U.; Faust, O. Breast imaging: A survey. World J. Clin. Oncol. 2011, 2, 171–178. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Bianciardi, G.; Bisogno, S.; Bertoldi, I.; Laurini, L.; Coviello, G.; Frediani, B. Fractal dimension of bone texture in radiographs correlates to ultrasound broadband attenuation T-score. Clin. Exp. Rheumatol. 2013, 31, 389–393. [Google Scholar] [PubMed]
- Franciotti, R.; Moharrami, M.; Quaranta, A.; Bizzoca, M.E.; Piattelli, A.; Aprile, G.; Perrotti, V. Use of fractal analysis in dental images for osteoporosis detection: A systematic review and meta-analysis. Osteoporos. Int. 2021, 32, 1041–1052. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Alman, A.C.; Johnson, L.R.; Calverley, D.C.; Grunwald, G.K.; Lezotte, D.C.; Hokanson, J.E. Diagnostic capabilities of fractal dimension and mandibular cortical width to identify men and women with decreased bone mineral density. Osteoporos. Int. 2012, 23, 1631–1636. [Google Scholar] [CrossRef]
- Jurczyszyn, K.; Kubasiewicz-Ross, P.; Nawrot-Hadzik, I.; Gedrange, T.; Dominiak, M.; Hadzik, J. Fractal dimension analysis a supplementary mathematical method for bone defect regeneration measurement. Ann. Anat. 2018, 219, 83–88. [Google Scholar] [CrossRef]
- Mu, T.J.; Lee, D.W.; Park, K.H.; Moon, I.S. Changes in the fractal dimension of peri-implant trabecular bone after loading: A retrospective study. J. Periodontal Implant. Sci. 2013, 43, 209–214. [Google Scholar] [CrossRef]
- Chen, D.R.; Chang, R.F.; Chen, C.J.; Ho, M.F.; Kuo, S.J.; Chen, S.T.; Hung, S.J.; Moon, W.K. Classification of breast ultrasound images using fractal feature. Clin. Imaging 2005, 29, 235–245. [Google Scholar] [CrossRef] [PubMed]
- Yap, M.H.; Edirisinghe, E.A.; Bez, H.E. A novel algorithm for initial lesion detection in ultrasound breast images. J. Appl. Clin. Med. Phys. 2008, 9, 181–199. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Alam, S.K.; Feleppa, E.J.; Rondeau, M.; Kalisz, A.; Garra, B.S. Ultrasonic multi-feature analysis procedure for computer-aided diagnosis of solid breast lesions. Ultrason. Imaging 2011, 33, 17–38. [Google Scholar] [CrossRef] [PubMed]
- Moraru, L.; Moldovanu, S.; Biswas, A. Optimization of breast lesion segmentation in texture feature space approach. Med. Eng. Phys. 2014, 36, 129–135. [Google Scholar] [CrossRef] [PubMed]
- Casti, P.; Mencattini, A.; Salmeri, M.; Ancona, A.; Lorusso, M.; Pepe, M.L.; Natale, C.D.; Martinelli, E. Towards localization of malignant sites of asymmetry across bilateral mammograms. Comput. Methods Programs Biomed. 2017, 140, 11–18. [Google Scholar] [CrossRef] [PubMed]
- Bennji, S.M.; Sagar, D.; Jarnagin, L.; Dairi, M.S.; Sagar, A.E.S. Endobronchial Ultrasound Staging for Lung Cancer: What We Know Now and What We Need to Know. Curr. Pulmonol. Rep. 2023, 12, 198–209. [Google Scholar] [CrossRef]
- Fiz, J.A.; Monte-Moreno, E.; Andreo, F.; Auteri, S.J.; Sanz-Santos, J.; Serra, P.; Bonet, G.; Castellà, E.; Manzano, J.R. Fractal dimension analysis of malignant and benign endobronchial ultrasound nodes. BMC Med. Imaging 2014, 14, 22. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Fujiwara, T.; Yasufuku, K.; Nakajima, T.; Chiyo, M.; Yoshida, S.; Suzuki, M.; Shibuya, K.; Hiroshima, K.; Nakatani, Y.; Yoshiro, I. The utility of sonographic features during endobronchial ultrasoubd-guided transbronchial needle aspiration for lymph node staging in patients with lung cancer: A Standard endobronchial ultrasound image classification system. Chest 2010, 138, 641–647. [Google Scholar] [CrossRef]
- Bhatia, K.S.; Rasalkar, D.D.; Lee, Y.P.; Wong, K.T.; King, A.D.; Yuen, H.Y.; Ahuja, A.T. Evaluation of real-time qualitative sonoelastography of focal lesions in the parotid and submandibular glands: Applications and limitations. Eur. Radiol. 2010, 20, 1958–1964. [Google Scholar] [CrossRef] [PubMed]
- Chikui, T.; Shimizu, M.; Kawazu, T.; Okamura, K.; Shiraishi, T.; Yoshiura, K. A quantitative analysis of sonographic images of the salivary gland: A comparison between sonographic and sialographic findings. Ultrasound Med. Biol. 2009, 35, 1257–1264. [Google Scholar] [CrossRef] [PubMed]
- Ariji, Y.; Ohki, M.; Eguchi, K.; Izumi, M.; Ariji, E.; Mizokami, K.; Nagataki, S.; Nakamura, T. Texture analysis of sonographic features of the parotid gland in Sjögren's syndrome. Am. J. Roentgenol. 1996, 166, 935–941. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Kitano, M.; Yoshida, T.; Itonaga, M.; Tamura, T.; Hatamaru, K.; Yamashita, Y. Impact of endoscopic ultrasonography on diagnosis of pancreatic cancer. J. Gastroenterol. 2019, 54, 19–32. [Google Scholar] [CrossRef] [PubMed]
- Spadaccini, M.; Koleth, G.; Emmanuel, J.; Khalaf, K.; Facciorusso, A.; Grizzi, F.; Hassan, C.; Colombo, M.; Mangiavillano, B.; Fugazza, A.; et al. Enhanced endoscopic ultrasound imaging for pancreatic lesions: The road to artificial intelligence. World J. Gastroenterol. 2022, 28, 3814–3824. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Carrara, S.; Di Leo, M.; Grizzi, F.; Correale, L.; Rahal, D.; Anderloni, A.; Auriemma, F.; Fugazza, A.; Preatoni, P.; Maselli, R.; et al. EUS elastography (strain ratio) and fractal-based quantitative analysis for the diagnosis of solid pancreatic lesions. Gastrointest. Endosc. 2018, 87, 1464–1473. [Google Scholar] [CrossRef] [PubMed]
- Moradi, M.; Mousavi, P.; Siemens, D.R.; Sauerbrei, E.E.; Isotalo, P.; Boag, A.; Abolmaesumi, P. Discrete Fourier analysis of ultrasound RF time series for detection of prostate cancer. Annu. Int. Conf. IEEE Eng. Med. Biol. Soc. 2007, 2007, 1339–1342. [Google Scholar] [CrossRef] [PubMed]
- Saidov, T.; Heneweer, C.; Kuenen, M.; von Broich-Oppert, J.; Wijkstra, H.; Rosette, J.; Mischi, M. Fractal Dimension of Tumor Microvasculature by DCE-US: Preliminary Study in Mice. Ultrasound Med. Biol. 2016, 42, 2852–2863. [Google Scholar] [CrossRef] [PubMed]
- Imani, F.; Ramezani, M.; Nouranian, S.; Gibson, E.; Khojaste, A.; Gaed, M.; Moussa, M.; Gomez, J.A.; Romagnoli, C.; Leveridge, M.; et al. Ultrasound-Based Characterization of Prostate Cancer Using Joint Independent Component Analysis. IEEE Trans. Biomed. Eng. 2015, 62, 1796–1804. [Google Scholar] [CrossRef] [PubMed]
- Mirpuri, N.G.; Dyson, M.; Rymer, J.; Bolton, P.A.; Young, S.R. High-frequency ultrasound imaging of the skin during normal and hypertensive pregnancies. Ski. Res. Technol. 2001, 7, 65–69. [Google Scholar] [CrossRef] [PubMed]
- Rahman, A.; Zhou, Y.Q.; Yee, Y.; Dazai, J.; Cahill, L.S.; Kingdom, J.; Macgowan, C.K.; Sled, J.G. Ultrasound detection of altered placental vascular morphology based on hemodynamic pulse wave reflection. Am. J. Physiol. Heart Circ. Physiol. 2017, 312, H1021–H1029. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Latifoğlu, F.; Kara, S.; Güney, M. Determining fractal dimension of umbilical artery Doppler signals using Hurst exponent. J. Med. Syst. 2007, 31, 529–536. [Google Scholar] [CrossRef] [PubMed]
- Miron, M.; Moldovanu, S.; Ștefănescu, B.I.; Culea, M.; Pavel, S.M.; Culea-Florescu, A.L. A New Approach in Detectability of Microcalcifications in the Placenta during Pregnancy Using Textural Features and K-Nearest Neighbors Algorithm. J. Imaging 2022, 8, 81. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Mahon, N.G.; Hedman, A.E.; Padula, M.; Gang, Y.; Savelieva, I.; Waktare, J.E.; Malik, M.M.; Huikuri, H.V.; McKenna, W.J. Fractal correlation properties of R-R interval dynamics in asymptomatic relatives of patients with dilated cardiomyopathy. Eur. J. Heart Fail. 2002, 4, 151–158. [Google Scholar] [CrossRef] [PubMed]
- Moroni, F.; Magnoni, M.; Vergani, V.; Ammirati, E.; Camici, P.G. Fractal analysis of plaque border, a novel method for the quantification of atherosclerotic plaque contour irregularity, is associated with pro-atherogenic plasma lipid profile in subjects with non-obstructive carotid stenoses. PLoS ONE 2018, 13, e0192600. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Dong, Y.; Chen, M.; Zhao, Y.; Wang, J.; Liu, Z.; Li, P.; Lai, X.; Liu, X.; Del Ser, J. Diagnostic performance of IVUS-FFR analysis based on generative adversarial network and bifurcation fractal law for assessing myocardial ischemia. Front. Cardiovasc. Med. 2023, 10, 1155969. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Acharya, U.R.; Vinitha Sree, S.; Krishnan, M.M.; Molinari, F.; Garberoglio, R.; Suri, J.S. Non-invasive automated 3D thyroid lesion classification in ultrasound: A class of ThyroScan™ systems. Ultrasonics 2012, 52, 508–520. [Google Scholar] [CrossRef] [PubMed]
- Prochazka, A.; Gulati, S.; Holinka, S.; Smutek, D. Classification of Thyroid Nodules in Ultrasound Images Using Direction-Independent Features Extracted by Two-Threshold Binary Decomposition. Technol. Cancer Res. Treat. 2019, 18, 1533033819830748. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Raghavendra, U.; Rajendra Acharya, U.; Gudigar, A.; Hong Tan, J.; Fujita, H.; Hagiwara, Y.; Molinari, F.; Kongmebhol, P.; Hoong, N.K. Fusion of spatial gray level dependency and fractal texture features for the characterization of thyroid lesions. Ultrasonics 2017, 77, 110–120. [Google Scholar] [CrossRef] [PubMed]
- Moradi, M.; Mousavi, P.; Abolmaesumi, P. Tissue characterization using fractal dimension of high frequency ultrasound RF time series. Med. Image Comput. Comput. Assist. Interv. 2007, 10 Pt 2, 900–908. [Google Scholar] [CrossRef] [PubMed]
- Mirón Mombiela, R.; Vucetic, J.; Monllor, P.; Cárdenas-Herrán, J.S.; Taltavull de La Paz, P.; Borrás, C. Diagnostic Performance of Muscle Echo Intensity and Fractal Dimension for the Detection of Frailty Phenotype. Ultrason. Imaging 2021, 43, 337–352. [Google Scholar] [CrossRef] [PubMed]
- Gonzato, G.; Mulargia, F.; Marzocchi, W. Practical application of fractal analysis: Problems and solutions. Geophys. J. Int. 1998, 132, 275–282. [Google Scholar] [CrossRef]
- Michallek, F.; Dewey, M. Fractal analysis in radiological and nuclear medicine perfusion imaging: A systematic review. Eur. Radiol. 2014, 24, 60–69. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pirri, C.; Pirri, N.; Macchi, V.; Guidolin, D.; Porzionato, A.; De Caro, R.; Stecco, C. The Value of Fractal Analysis in Ultrasound Imaging: Exploring Intricate Patterns. Appl. Sci. 2024, 14, 9750. https://doi.org/10.3390/app14219750
Pirri C, Pirri N, Macchi V, Guidolin D, Porzionato A, De Caro R, Stecco C. The Value of Fractal Analysis in Ultrasound Imaging: Exploring Intricate Patterns. Applied Sciences. 2024; 14(21):9750. https://doi.org/10.3390/app14219750
Chicago/Turabian StylePirri, Carmelo, Nina Pirri, Veronica Macchi, Diego Guidolin, Andrea Porzionato, Raffaele De Caro, and Carla Stecco. 2024. "The Value of Fractal Analysis in Ultrasound Imaging: Exploring Intricate Patterns" Applied Sciences 14, no. 21: 9750. https://doi.org/10.3390/app14219750
APA StylePirri, C., Pirri, N., Macchi, V., Guidolin, D., Porzionato, A., De Caro, R., & Stecco, C. (2024). The Value of Fractal Analysis in Ultrasound Imaging: Exploring Intricate Patterns. Applied Sciences, 14(21), 9750. https://doi.org/10.3390/app14219750












