Predicting Lightweight Powders with Useful Sound Absorption Characteristics from Their Specifications
Abstract
1. Introduction
2. Materials and Methods
Samples Used for Measurements
3. Results
3.1. Powder Classification
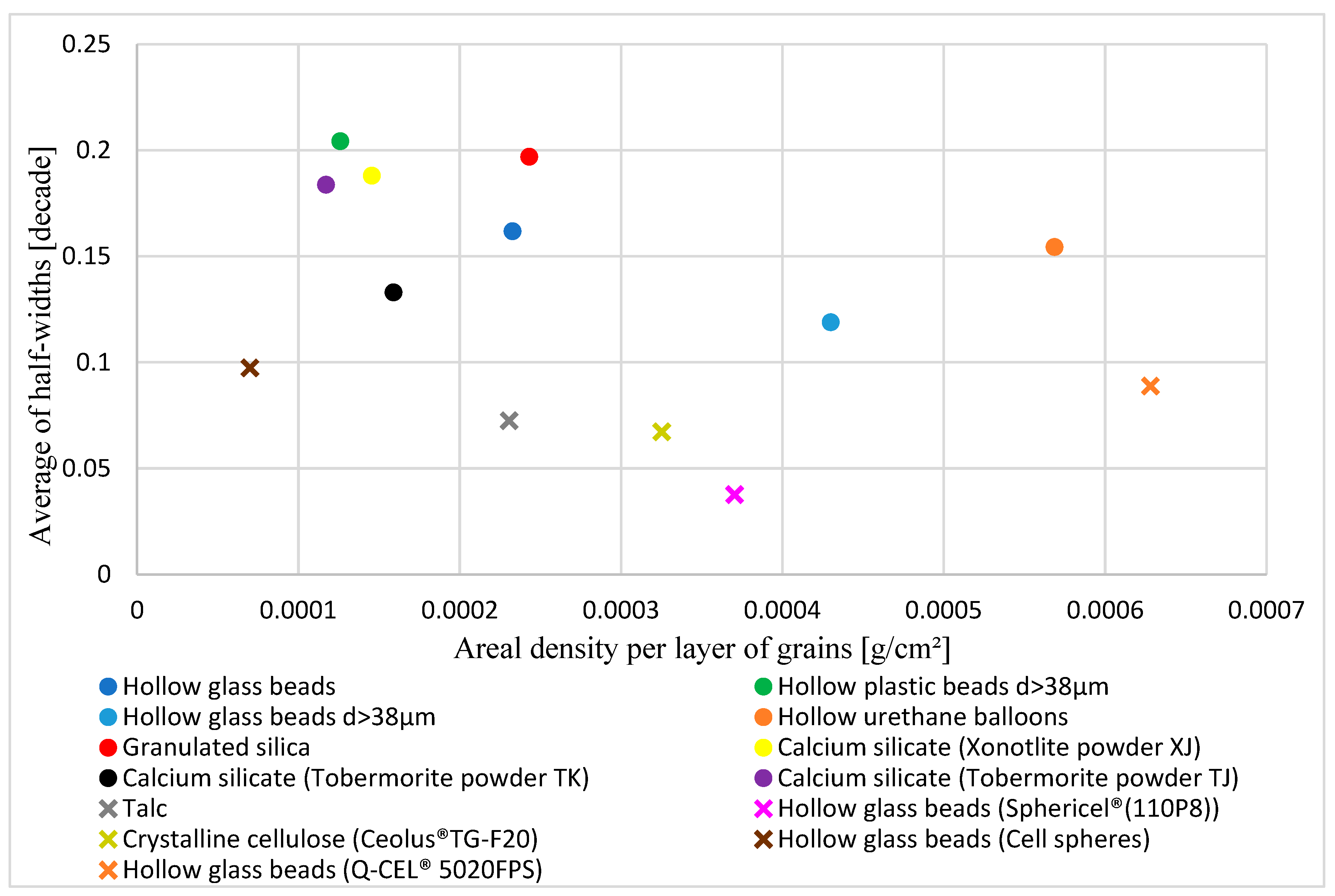
3.1.1. Relationship Between the Areal Density per Grain Layer and Sound Absorption Coefficient
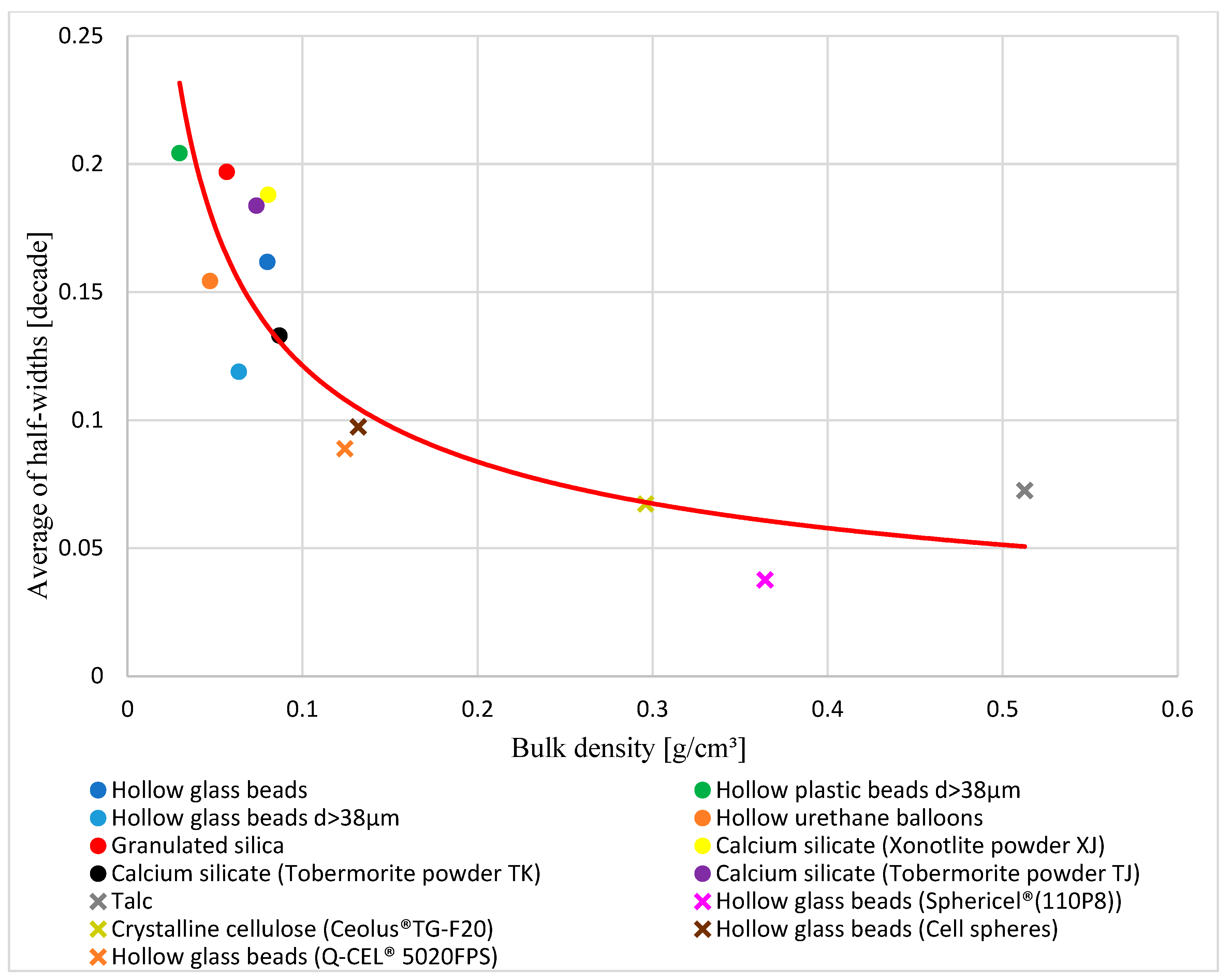
3.1.2. Correlation Between the Half-Width and Powder Specifications
3.1.3. Classification by Powder Specifications
3.2. Regression Analysis
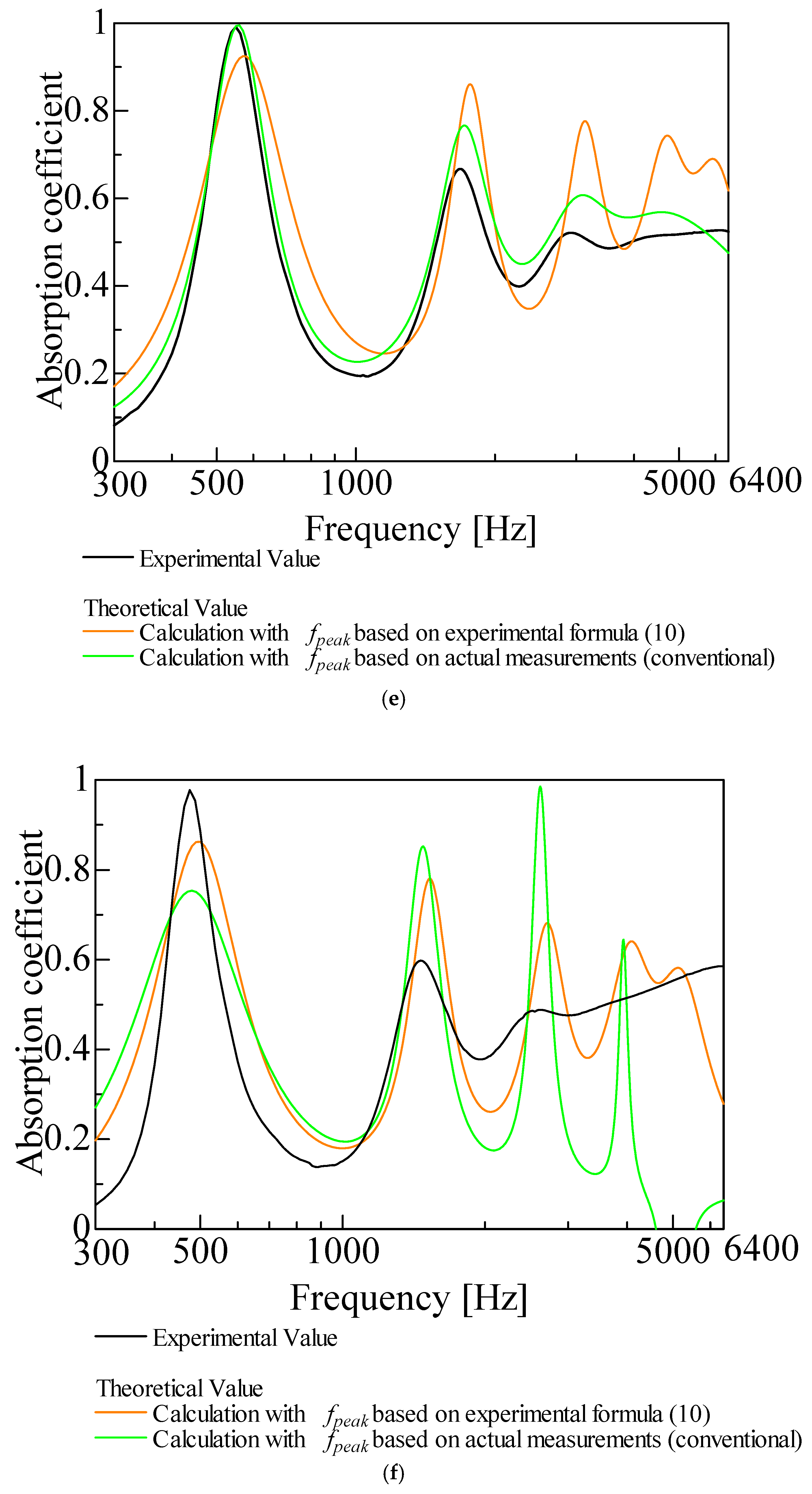
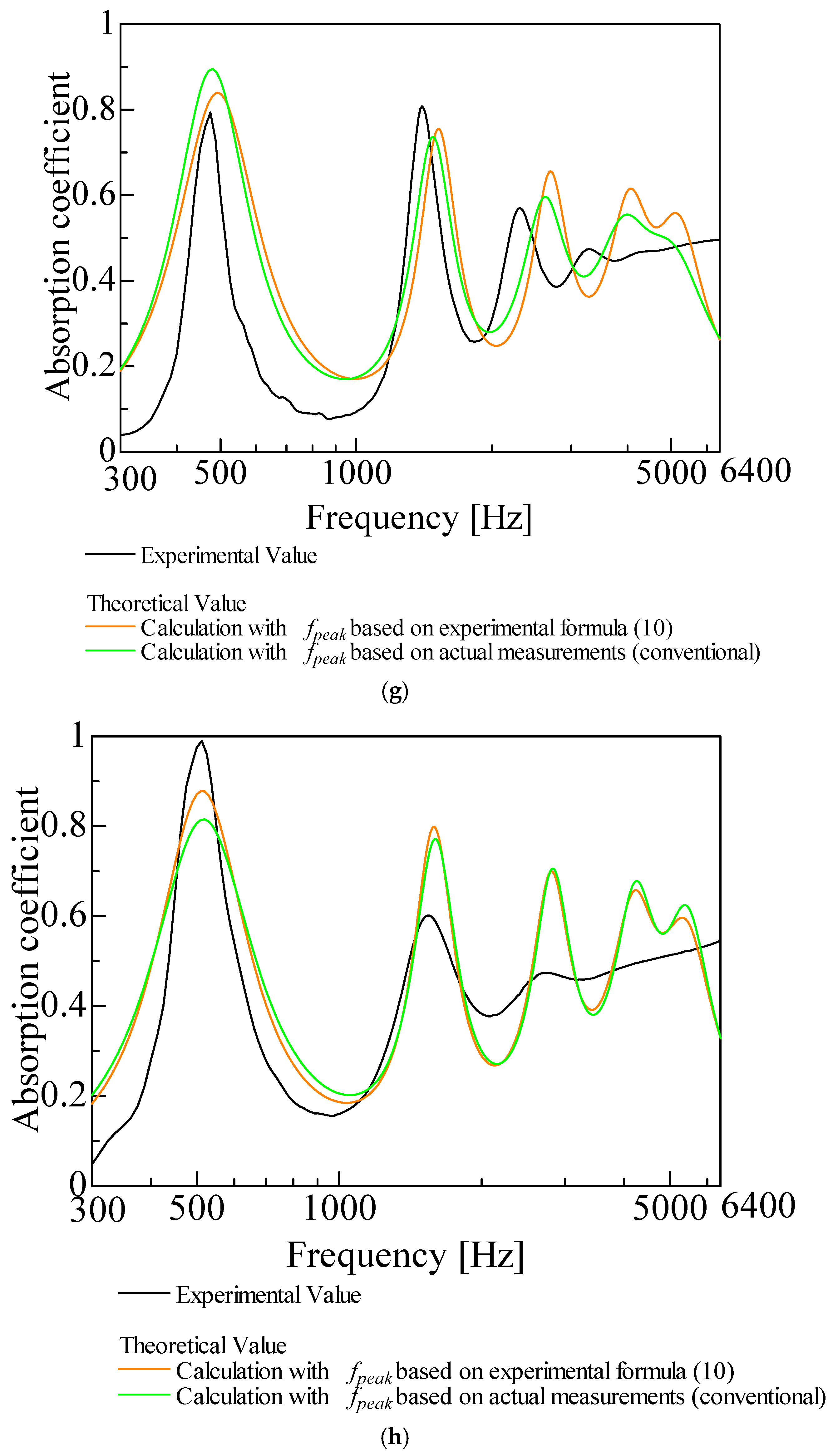
3.2.1. Peak Sound Absorption Frequency
3.2.2. Damping Ratio
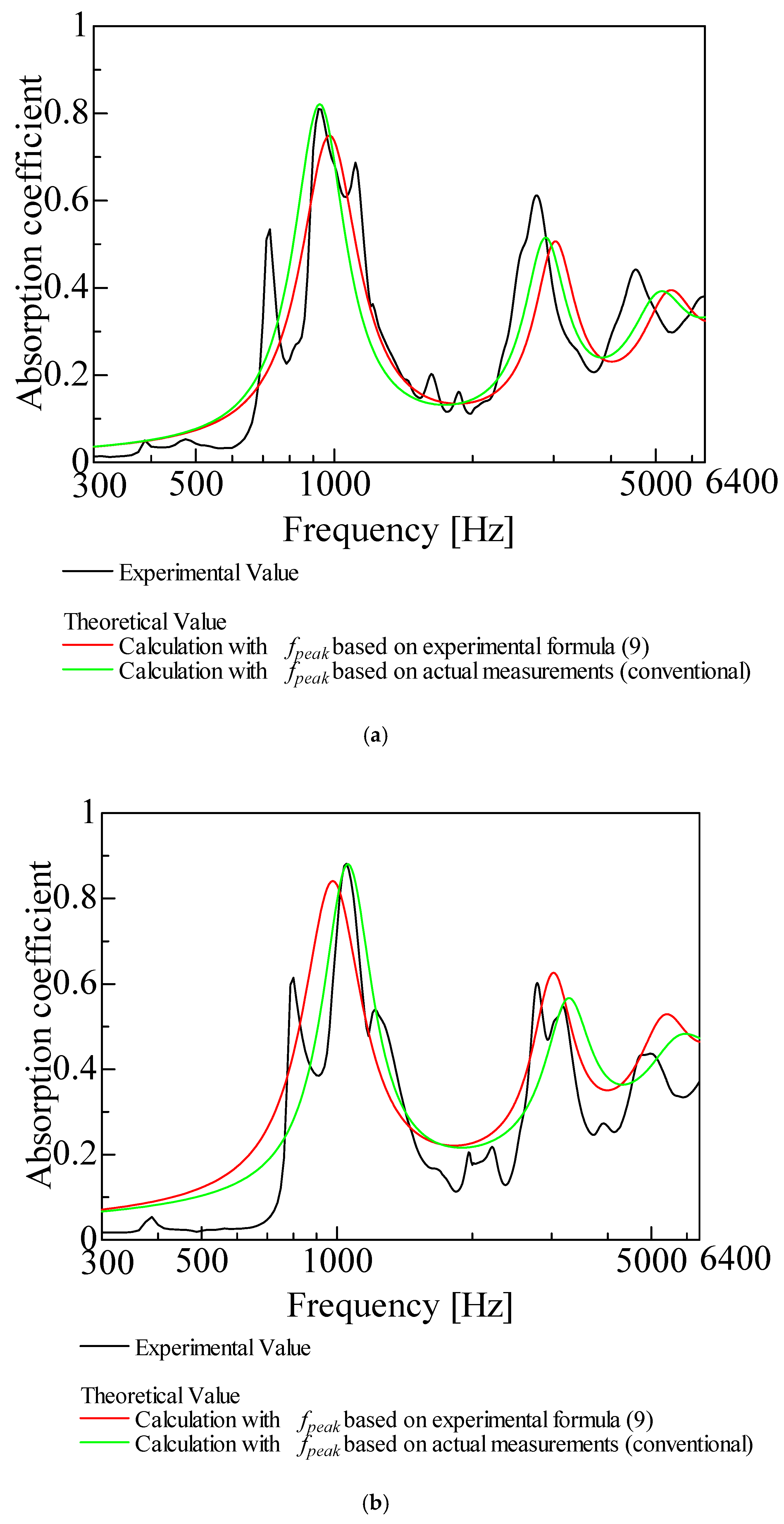
3.2.3. Sound Absorption Coefficient
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Arenas, J.P.; Crocker, M.J. Recent trends in porous sound-absorbing materials. Sound Vib. 2010, 44, 12–17. [Google Scholar]
- Sakamoto, S.; Ii, K.; Katayama, I.; Suzuki, K. Measurement and Theoretical Analysis of Sound Absorption of Simple Cubic and Hexagonal Lattice Granules. Noise Control Eng. J. 2021, 69, 401–410. [Google Scholar] [CrossRef]
- Sakamoto, S.; Suzuki, K.; Toda, K.; Seino, S. Estimation of the Acoustic Properties of the Random Packing Structures of Granular Materials: Estimation of the Sound Absorption Coefficient Based on Micro-CT Scan Data. Materials 2023, 16, 337. [Google Scholar] [CrossRef] [PubMed]
- Satti, F.; Hoppe, K.A.; Marburg, S.; Horoshenkov, K.V. The accuracy of some models to predict the acoustical properties of granular media. Appl. Acoust. 2022, 185, 108358. [Google Scholar] [CrossRef]
- Zhu, Y.; Muhammed, H. The exploration and recent updates on the relation between sound speed in mixtures of granular materials and the composition of the mixtures. Appl. Acoust. 2021, 178, 107992. [Google Scholar] [CrossRef]
- Cobo, P.; Simón, F.A. comparison of impedance models for the inverse estimation of the non-acoustical parameters of granular absorbers. Appl. Acoust. 2016, 104, 119–126. [Google Scholar] [CrossRef]
- Voronina, N.N.; Horoshenkov, K.V. A new empirical model for the acoustic properties of loose granular media. Appl. Acoust. 2003, 64, 415–432. [Google Scholar] [CrossRef]
- Arenas, J.P.; Marin, V.; Venegas, R. Membrane sound absorber with a granular activated carbon infill. Appl. Acoust. 2023, 202, 109180. [Google Scholar] [CrossRef]
- Samaei, S.E.; Berardi, U.; Taban, E.; Soltani, P.; Mousavi, S.M. Natural fibro-granular composite as a novel sustainable sound-absorbing material. Appl. Acoust. 2021, 181, 108157. [Google Scholar] [CrossRef]
- Železnik, A.; Murovec, J.; Čurović, L.; Cerkovnik, N.; Prezelj, J. Transmission loss measurement of recycled granular material using wave decomposition by impulse response extraction based on deconvolution. Appl. Acoust. 2023, 211, 109498. [Google Scholar] [CrossRef]
- Dragonetti, R.; Iannace, G.; Ianniello, C. Insertion loss of a heap of gravel outdoors. Acta Acust. 2003, 89, S56–S57. [Google Scholar]
- Okudaira, Y.; Kurihara, Y.; Ando, H.; Satoh, M.; Miyanami, K. Sound absorption measurements for evaluating dynamic physical properties of a powder bed. Powder Technol. 1993, 77, 39–48. [Google Scholar] [CrossRef]
- Okudaira, Y.; Ando, H.; Satoh, M.; Miyanami, K. The effect of grain diameter on the acoustic properties of a powder bed sound absorption characteristic and sound velocity. J. Soc. Powder Technol. 1995, 32, 311–318. (In Japanese) [Google Scholar] [CrossRef]
- Okudaira, Y.; Kurihara, Y.; Ando, H.; Satoh, M.; Miyanami, K. Sound Absorption Characteristics of Powder Beds Comprised of Binary Powder Mixtures. J. Jpn. Soc. Powder Powder Metall. 1995, 42, 239–244. [Google Scholar] [CrossRef]
- Zhou, H.; Bo, L.; Guangsu, H. Sound absorption characteristics of polymer microparticles. J. Appl. Polym. Sci. 2006, 101, 2675–2679. [Google Scholar] [CrossRef]
- Begum, H.; Xue, Y.; Bolton, J.S.; Horoshenkov, K.V. The acoustical absorption by air-saturated aerogel powders. J. Acoust. Soc. Am. 2022, 151, 1502–1515. [Google Scholar] [CrossRef]
- Biot, M.A. Theory of Propagation of Elastic Waves in a Fluid-Saturated Porous Solid. I. Low-Frequency Range. J. Acoust. Soc. Am 1956, 28, 168–178. [Google Scholar] [CrossRef]
- Tsuruha, T.; Yamada, Y.; Otani, M.; Takano, Y. Effect of casing on sound absorption characteristics of fine spherical granular material. J. Acoust. Soc. Am. 2020, 147, 3418–3428. [Google Scholar] [CrossRef]
- Sakamoto, S.; Yamaguchi, K.; Ii, K.; Takakura, R.; Nakamura, Y.; Suzuki, R. Theoretical and experiment analysis on the sound absorption characteristics of a layer of fine lightweight powder. J. Acoust. Soc. Am. 2019, 146, 2253–2262. [Google Scholar] [CrossRef]
- Sakamoto, S.; Takakura, R.; Suzuki, R.; Katayama, I.; Saito, R.; Suzuki, K. Theoretical and experimental analyses of acoustic characteristics of fine-grain powder considering longitudinal vibration and boundary layer viscosity. J. Acoust. Soc. Am. 2021, 149, 1030–1040. [Google Scholar] [CrossRef]
- Sakamoto, S.; Saito, R.; Jindai, K.; Ikeda, K. Conditions for Sound Absorption Caused by Longitudinal Vibration of Lightweight Powder. Noise Control. Eng. J. 2024, 72, NCEJ-D-23-00043. [Google Scholar]
- Merkus, H.G. Particle Size Measurements: Fundamentals, Practice, Quality; Springer Science and Business Media: New York, NY, USA, 2019; p. 15. [Google Scholar]
- Saiki, S.; Matsumura, T.; Fujise, A. Speaker System. European Patent EP 2003924A1, 25 April 2012. [Google Scholar]
- ISO 10534-2; Acoustics—Determination of Sound Absorption Coefficient and Impedance in Impedance Tubes—Part 2: Transfer-function Method. International Organization for Standardization: Geneva, Switzerland, 2002.
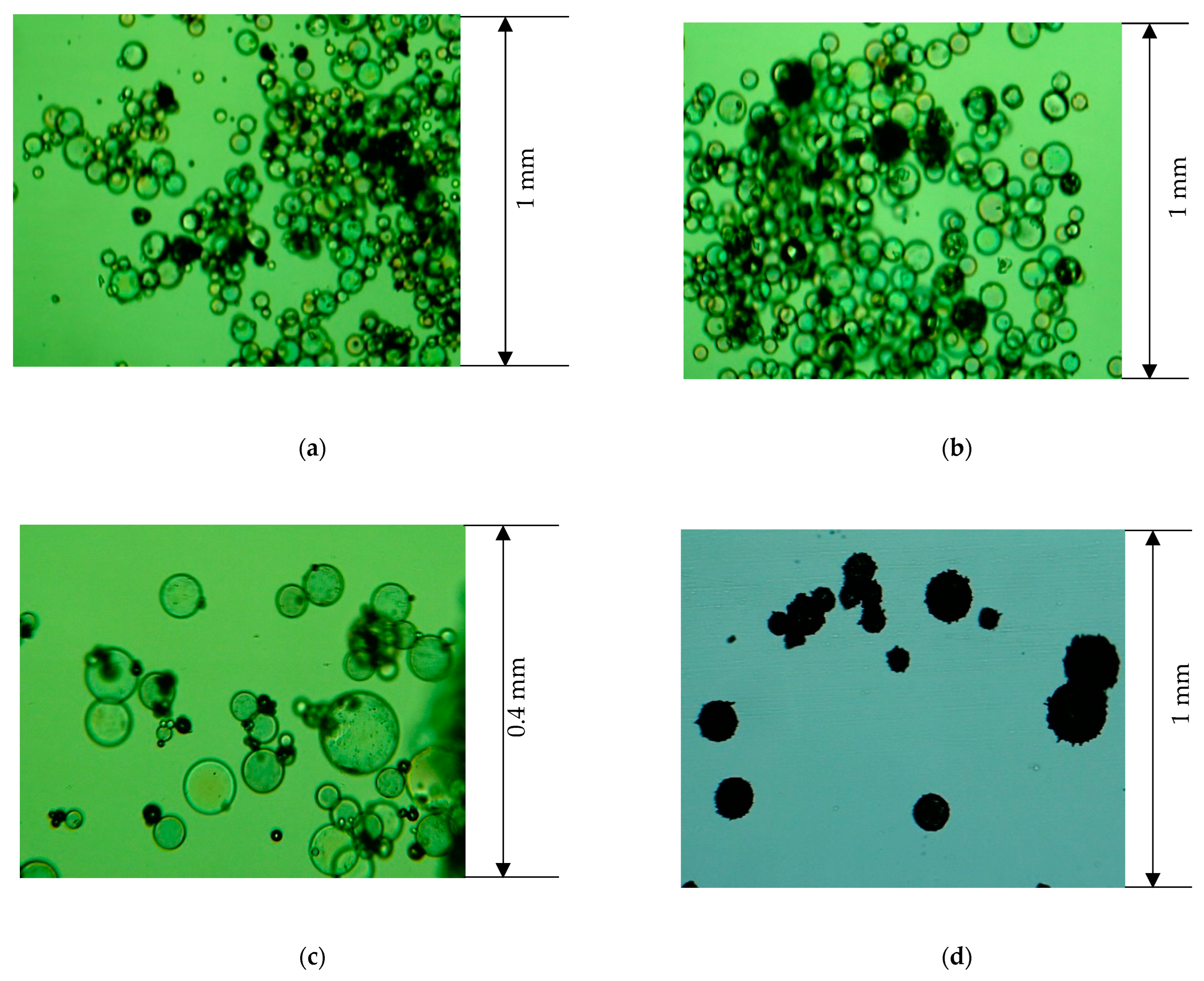


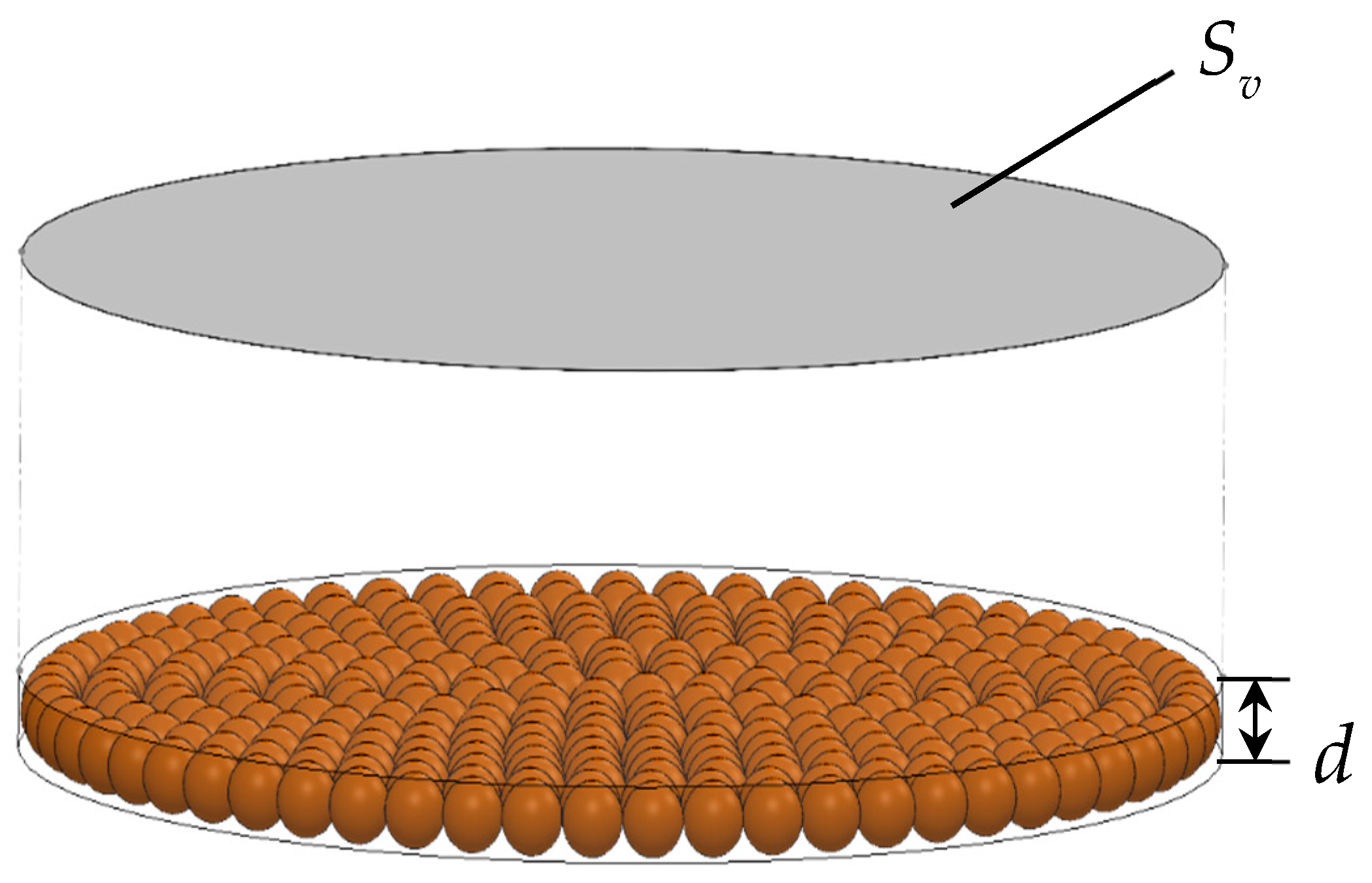




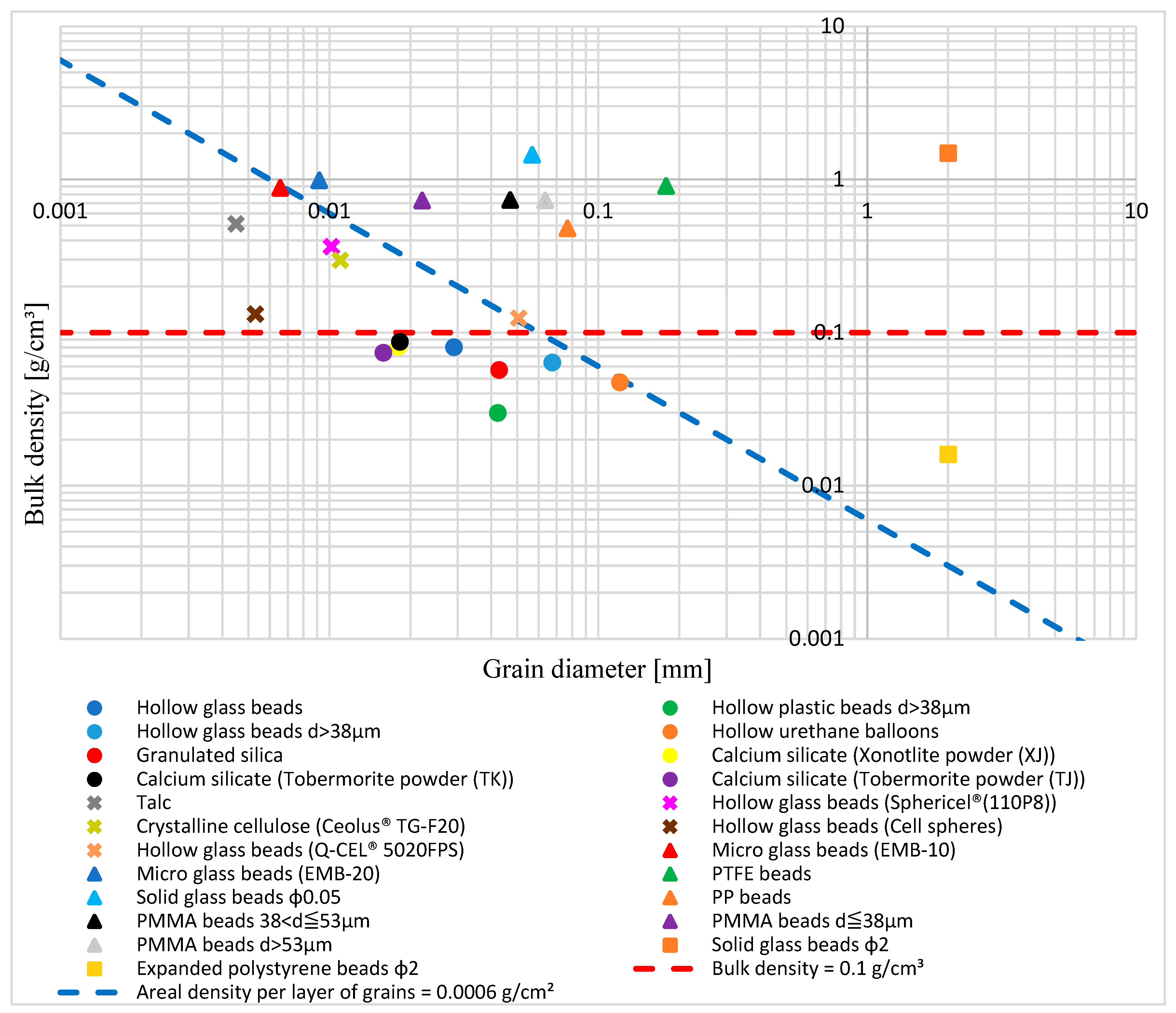
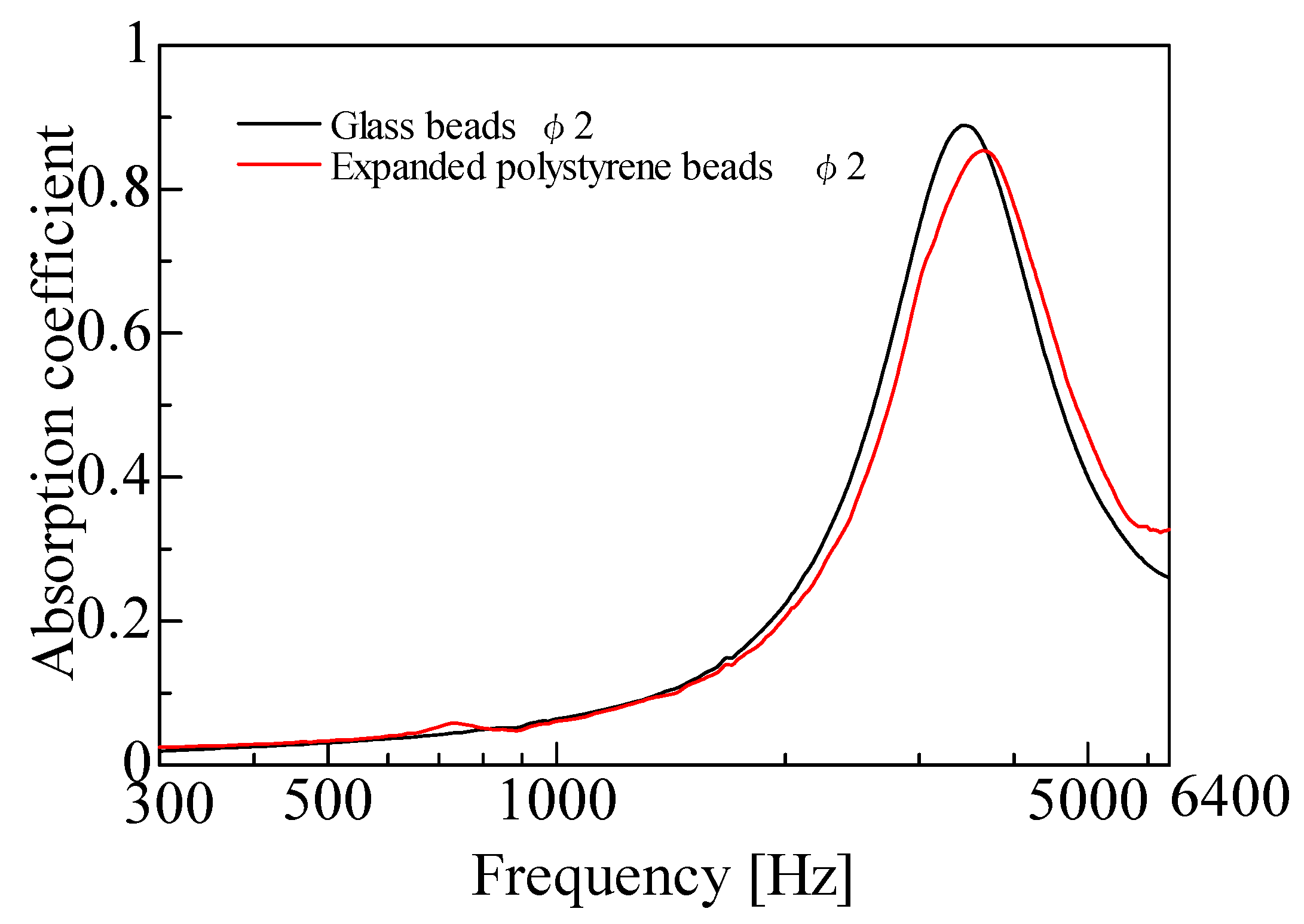



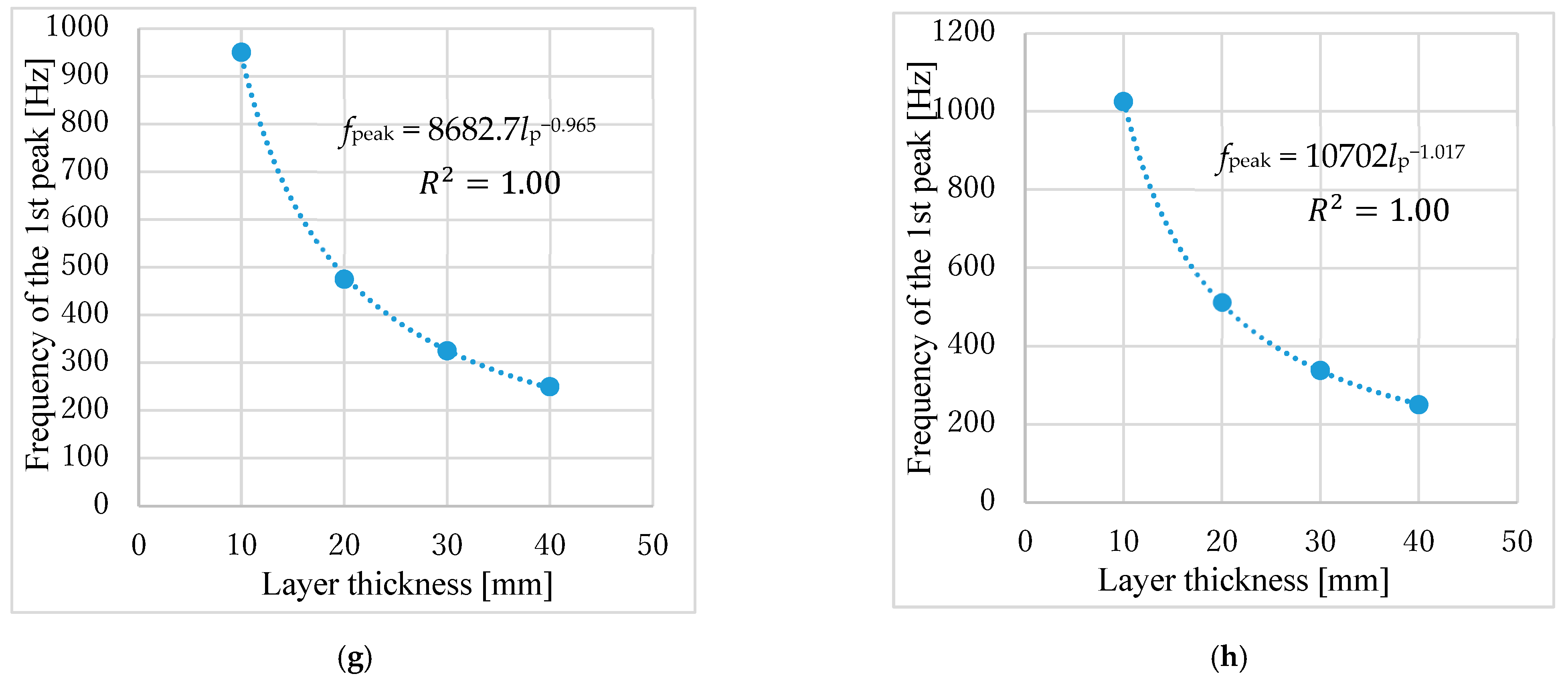
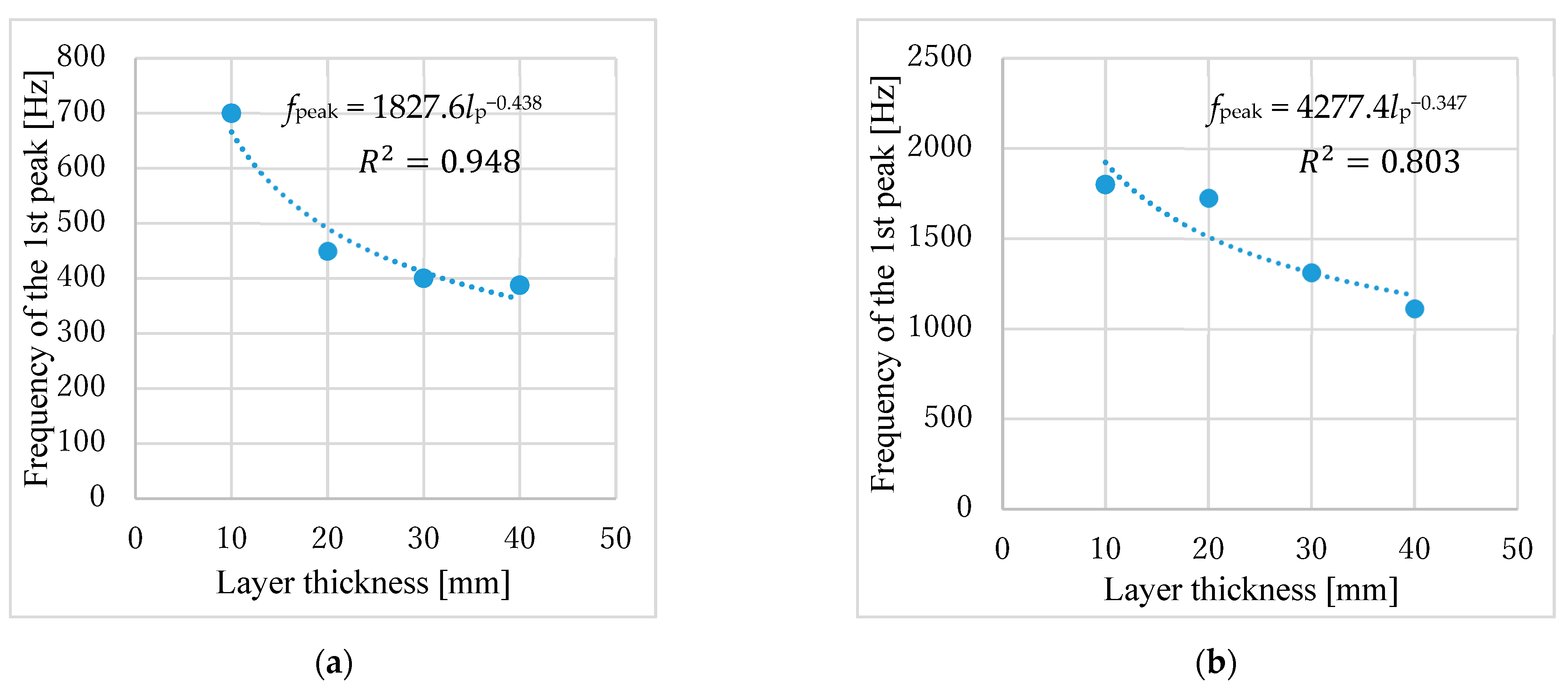
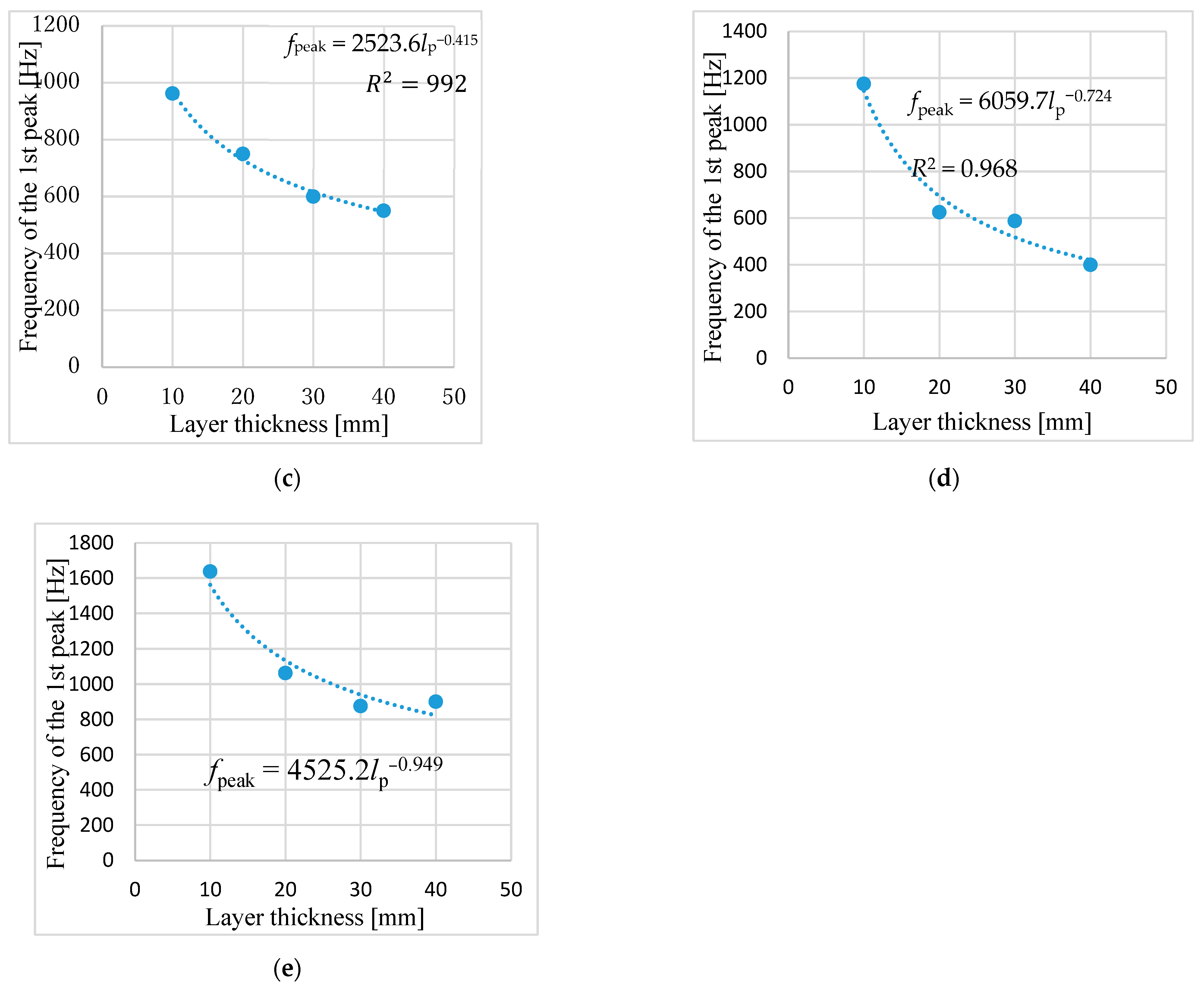
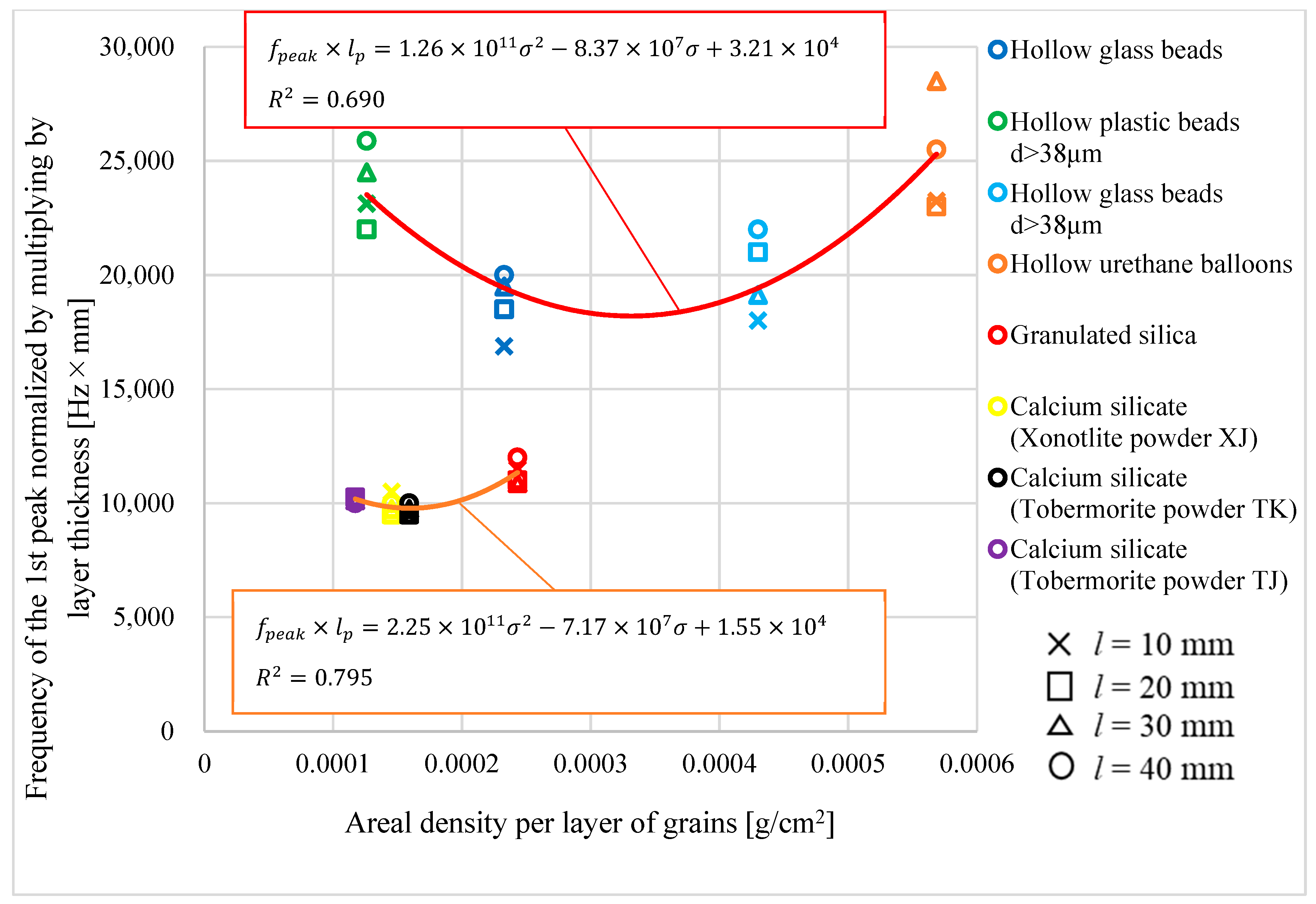
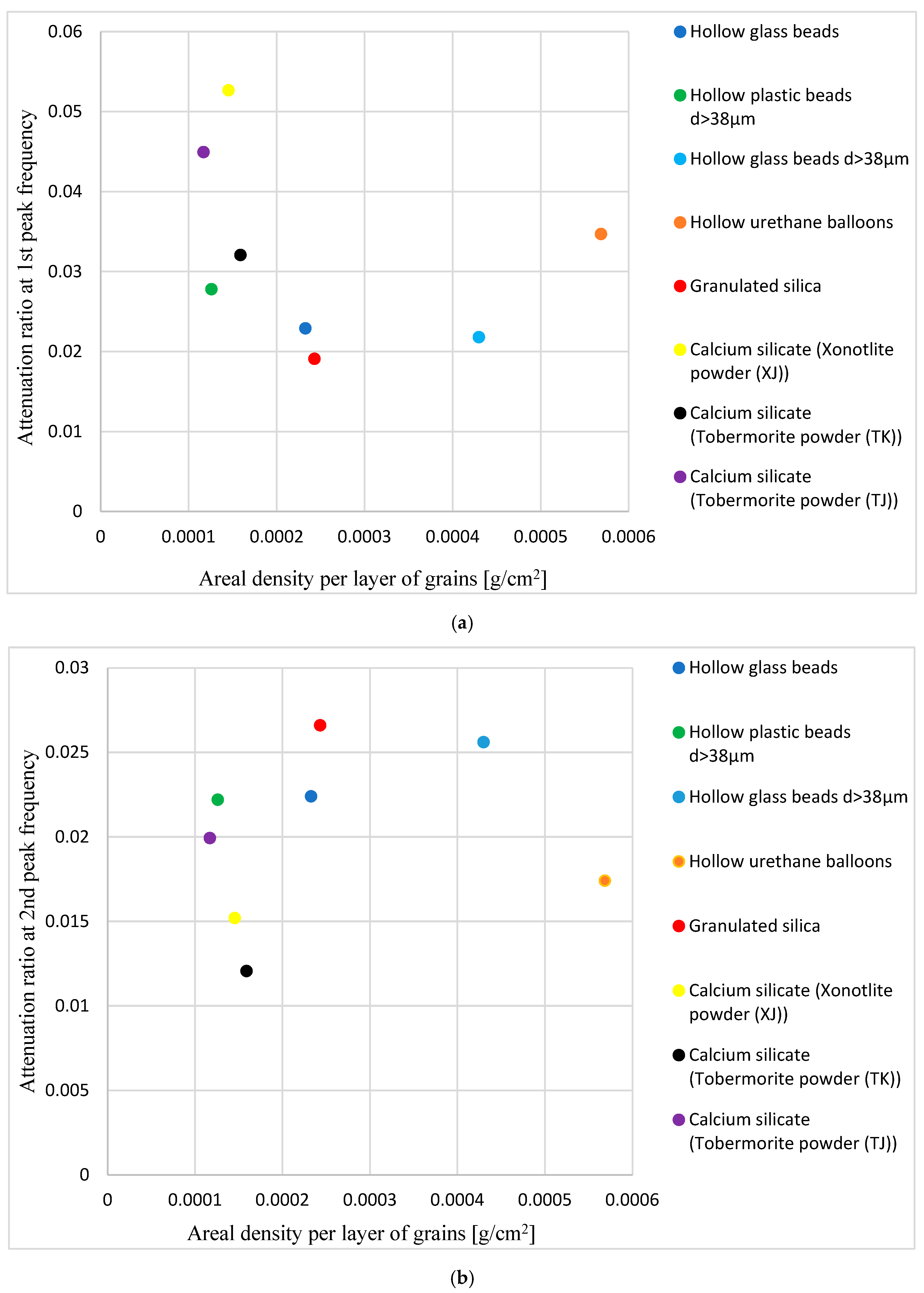

| Powder Code | Powder Name | Grain Size [mm] | Bulk Density [g/cm3] | Areal Density per Grain Layer [g/cm2] | Standard Deviation of Grain Size [mm] | Porosity | Plot on Figures |
|---|---|---|---|---|---|---|---|
| A1-1 | Hollow glass beads (Hobbico, Inc., Champaign, IL, USA) | 0.0291 | 0.080 | 2.33 × 10−4 | 1.49 × 10−3 | N/A * | ● |
| A1-2 | Hollow glass beads d > 38 μm (Hobbico, Inc., Champaign, IL, USA) | 0.0675 | 0.064 | 4.30 × 10−4 | 1.71 × 10−3 | N/A * | ● |
| A1-3 | Hollow plastic beads d > 38 μm (Japan Fillite Co., Ltd., Osaka, Japan) | 0.0423 | 0.030 | 1.26 × 10−4 | 1.41 × 10−2 | N/A * | ● |
| A1-4 | Hollow urethane balloons (OK Model Co., Ltd., Osaka, Japan) | 0.1205 | 0.0472 | 5.69 × 10−4 | 3.77 × 10−2 | N/A * | ● |
| A2-1 | Granulated silica (Featherfield Co., Ltd., Hiroshima, Japan) | 0.0428 | 0.057 | 2.43 × 10−4 | 2.23 × 10−2 | 0.974 | ● |
| A2-2 | Calcium silicate (Xonotlite powder (XJ)) (Japan Insulation Co., Ltd., Osaka, Japan) | 0.0181 | 0.0805 | 1.46 × 10−4 | 8.29 × 10−3 | N/A * | ● |
| A2-3 | Calcium silicate (Tobermorite powder (TK)) (Japan Insulation Co., Ltd., Osaka, Japan) | 0.0183 | 0.0868 | 1.59 × 10−4 | 7.09 × 10−3 | N/A * | ● |
| A2-4 | Calcium silicate (Tobermorite powder (TJ)) (Japan Insulation Co., Ltd., Osaka, Japan) | 0.0159 | 0.0737 | 1.17 × 10−4 | 4.24 × 10−3 | N/A * | ● |
| B-1 | Talc (Featherfield Co., Ltd., Hiroshima, Japan) | 0.00450 | 0.5126 | 2.31 × 10−4 | 3.67 × 10−3 | 0.810 | ✕ |
| B-2 | Hollow glass beads (Sphericel® (110P8)) (Potters-Ballotini Co., Ltd., Ibaraki, Japan) | 0.0102 | 0.3642 | 3.70 × 10−4 | 4.30 × 10−3 | N/A * | × |
| B-3 | Crystalline cellulose (Ceolus® TG-F20) (Asahi Kasei Corporation. Tokyo, Japan) | 0.0110 | 0.2961 | 3.25 × 10−4 | 8.94 × 10−3 | N/A * | × |
| B-4 | Hollow glass beads (Cell spheres) (Taiheiyo Cement Corporation. Tokyo, Japan) | 0.0053 | 0.1319 | 6.99 × 10−5 | 2.33 × 10−3 | N/A * | × |
| B-5 | Hollow glass beads (Q-CEL® 5020FPS) (Potters-Ballotini Co., Ltd., Ibaraki, Japan) | 0.0506 | 0.1242 | 6.28 × 10−4 | 1.70 × 10−2 | N/A * | × |
| C-1 | Micro glass beads (EMB-10) (Potters-Ballotini Co., Ltd., Ibaraki, Japan) | 0.0066 | 0.8820 | 5.78 × 10−4 | 2.79 × 10−3 | 0.661 | ▲ |
| C-2 | Micro glass beads (EMB-20) (Potters-Ballotini Co., Ltd., Ibaraki, Japan) | 0.009158 | 0.9885 | 9.05 × 10−4 | 4.08 × 10−3 | 0.620 | ▲ |
| C-3 | PTFE beads (3M Japan Limited. Tokyo, Japan) | 0.1786 | 0.907 | 1.62 × 10−2 | 7.16 × 10−2 | 0.578 | ▲ |
| C-4 | Solid glass beads φ0.05 (Toshin Riko Co., Ltd., Tokyo, Japan) | 0.0567 | 1.450 | 8.22 × 10−3 | 5.37 × 10−3 | 0.42 | ▲ |
| C-5 | PP beads (Sumitomo Seika Chemicals Company, Limited. Tokyo, Japan) | 0.0767 | 0.480 | 3.68 × 10−3 | 3.81 × 10−2 | N/A * | ▲ |
| C-6 | PMMA beads 38 < d ≤ 53 μm (Sekisui Kasei Co., Ltd., Tokyo, Japan) | 0.0470 | 0.735 | 3.45 × 10−3 | 8.02 × 10−3 | 0.388 | ▲ |
| C-7 | PMMA beads d ≤ 38 μm (Sekisui Kasei Co., Ltd., Tokyo, Japan) | 0.0221 | 0.730 | 1.61 × 10−3 | 9.13 × 10−3 | 0.392 | ▲ |
| C-8 | PMMA beads d > 53 μm (Sekisui Kasei Co., Ltd., Tokyo, Japan) | 0.0634 | 0.730 | 4.63 × 10−3 | 1.13 × 10−2 | 0.392 | ▲ |
| Powder Code | Balloon Powders (Powders with Gentle Curves) | First Peak Frequency (Measurement Value) [Hz] | First Peak Frequency Calculated from Experimental Equation (9) [Hz] |
|---|---|---|---|
| A1-1 | Hollow glass beads | 925 | 971 |
| A1-2 | Hollow glass beads d > 38 μm | 1050 | 1176 |
| A1-3 | Hollow plastic beads d > 38 μm | 1100 | 971 |
| A1-4 | Hollow urethane balloons | 1150 | 1265 |
| Powder Code | Non-Balloon Powders (Powders with Gentle Waveform) | First Peak Frequency (Measurement Value) [Hz] | First Peak Frequency Calculated from Experimental Equation (10) [Hz] |
|---|---|---|---|
| A2-1 | Granulated silica | 550 | 567 |
| A2-2 | Calcium silicate (Xonotlite powder (XJ)) | 475 | 491 |
| A2-3 | Calcium silicate (Tobermorite powder (TK)) | 475 | 489 |
| A2-4 | Calcium silicate (Tobermorite powder (TJ)) | 512.5 | 509 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sakamoto, S.; Jindai, K.; Ikeda, K.; Kawakami, Y.; Soeta, H. Predicting Lightweight Powders with Useful Sound Absorption Characteristics from Their Specifications. Appl. Sci. 2024, 14, 9765. https://doi.org/10.3390/app14219765
Sakamoto S, Jindai K, Ikeda K, Kawakami Y, Soeta H. Predicting Lightweight Powders with Useful Sound Absorption Characteristics from Their Specifications. Applied Sciences. 2024; 14(21):9765. https://doi.org/10.3390/app14219765
Chicago/Turabian StyleSakamoto, Shuichi, Keisuke Jindai, Koki Ikeda, Yuya Kawakami, and Hiroaki Soeta. 2024. "Predicting Lightweight Powders with Useful Sound Absorption Characteristics from Their Specifications" Applied Sciences 14, no. 21: 9765. https://doi.org/10.3390/app14219765
APA StyleSakamoto, S., Jindai, K., Ikeda, K., Kawakami, Y., & Soeta, H. (2024). Predicting Lightweight Powders with Useful Sound Absorption Characteristics from Their Specifications. Applied Sciences, 14(21), 9765. https://doi.org/10.3390/app14219765






