Design and Stability Analysis of Six-Degree-of-Freedom Hydro-Pneumatic Spring Wheel-Leg
Abstract
:1. Introduction
2. Dual In-Wheel Motor Wheel-Leg
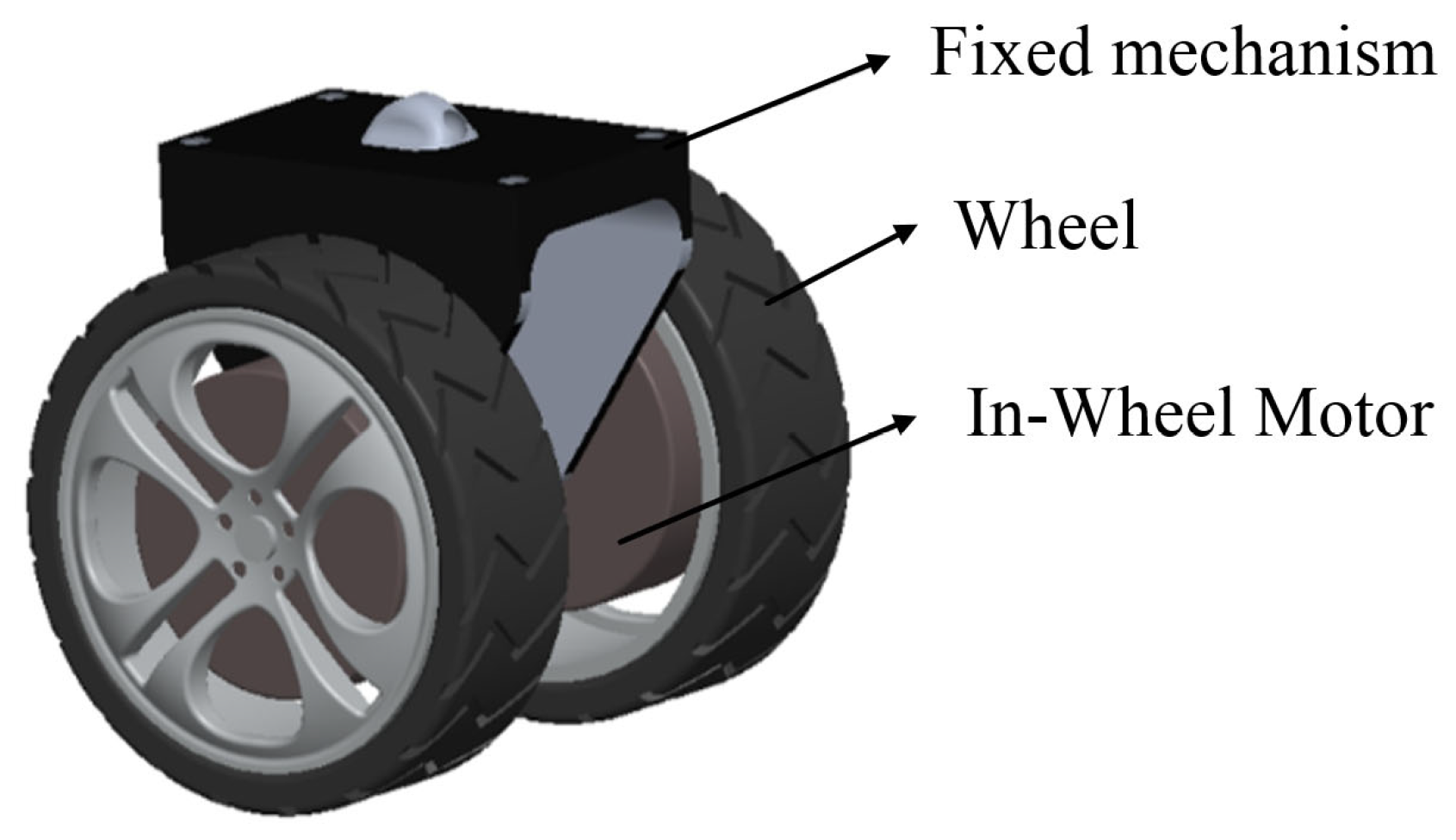
2.1. Dual In-Wheel Motor Wheelset Unit
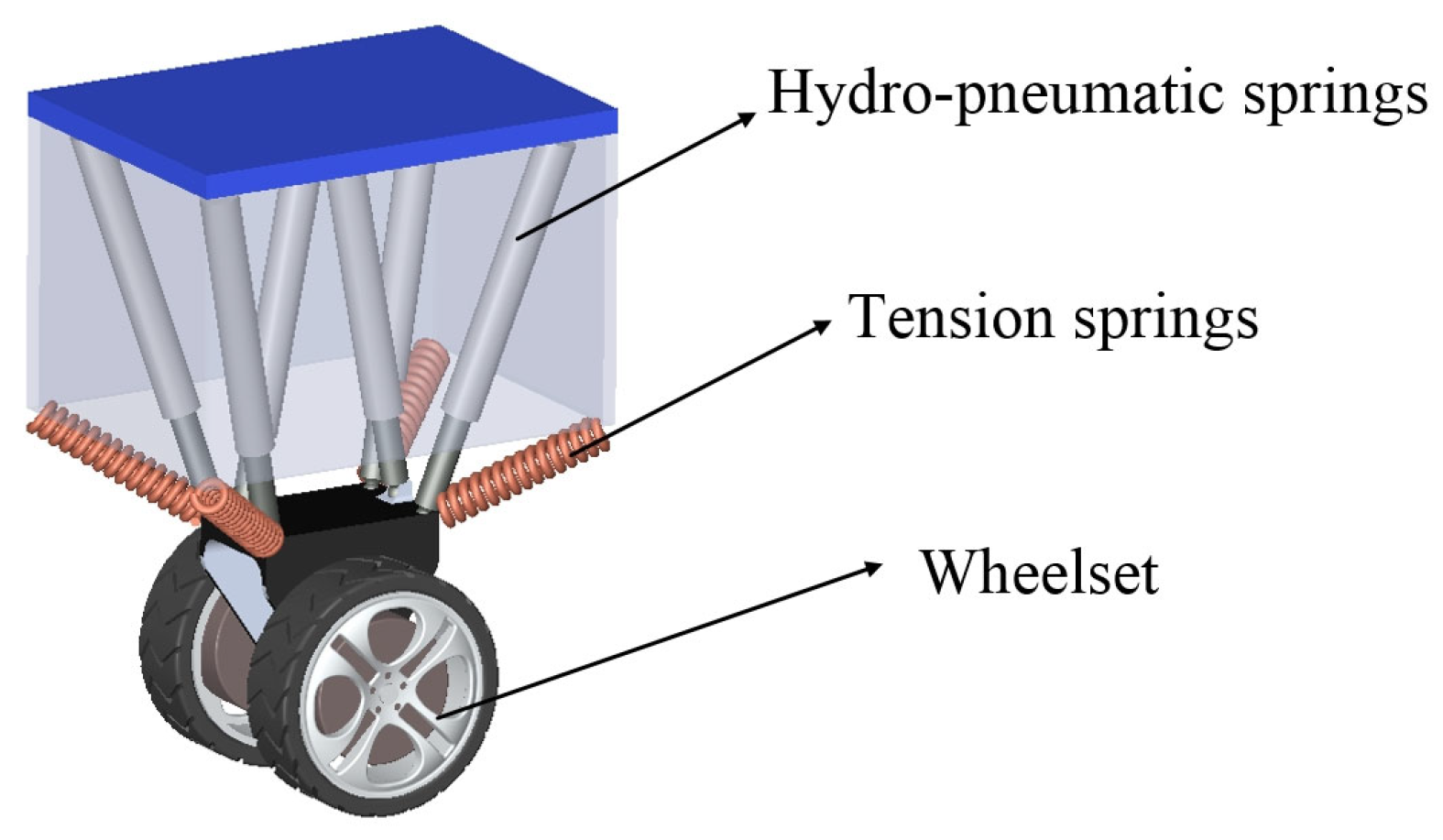
2.2. Design of Six-Arm Hydro-Pneumatic Spring Suspension
2.3. Functional Characteristics
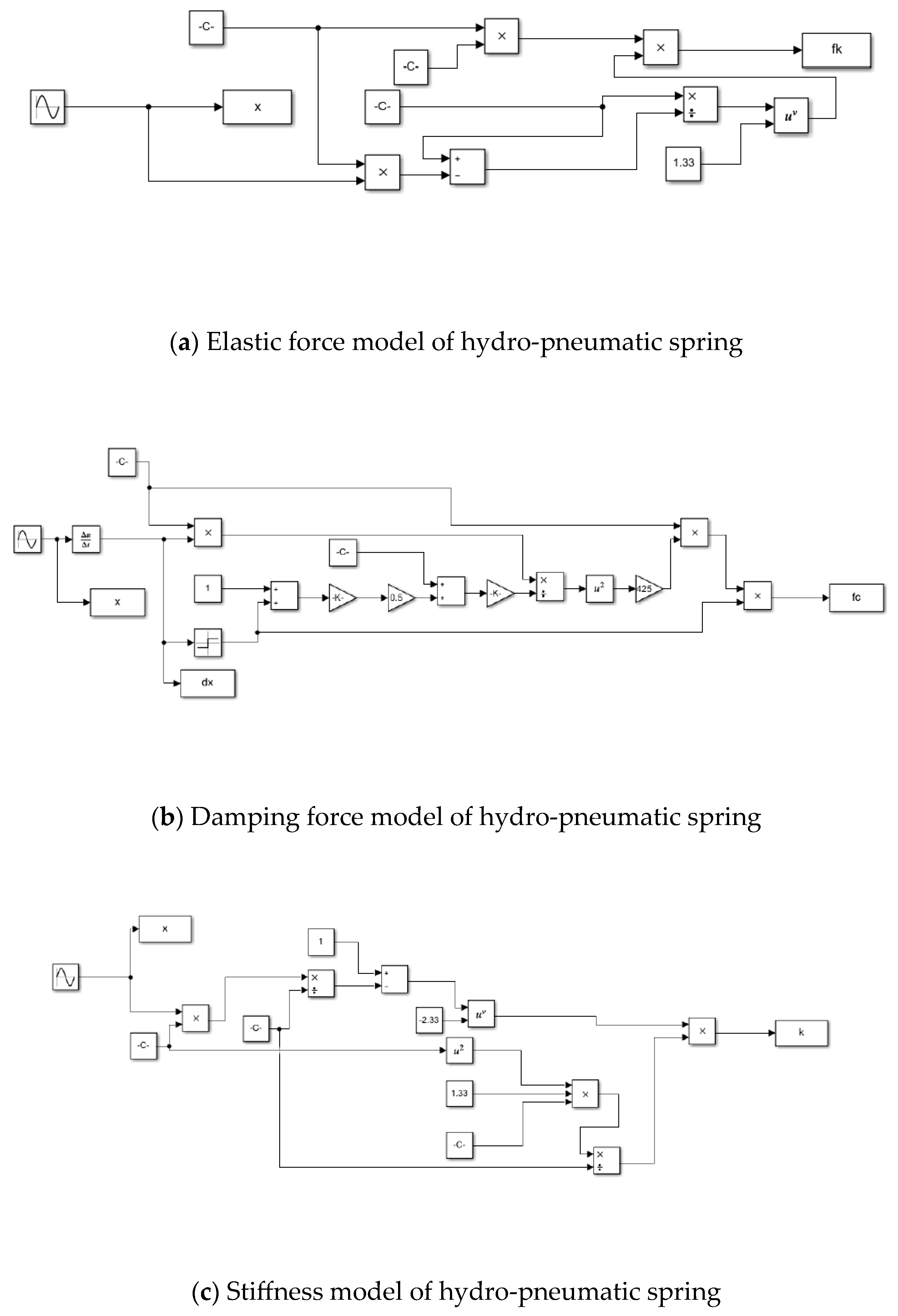
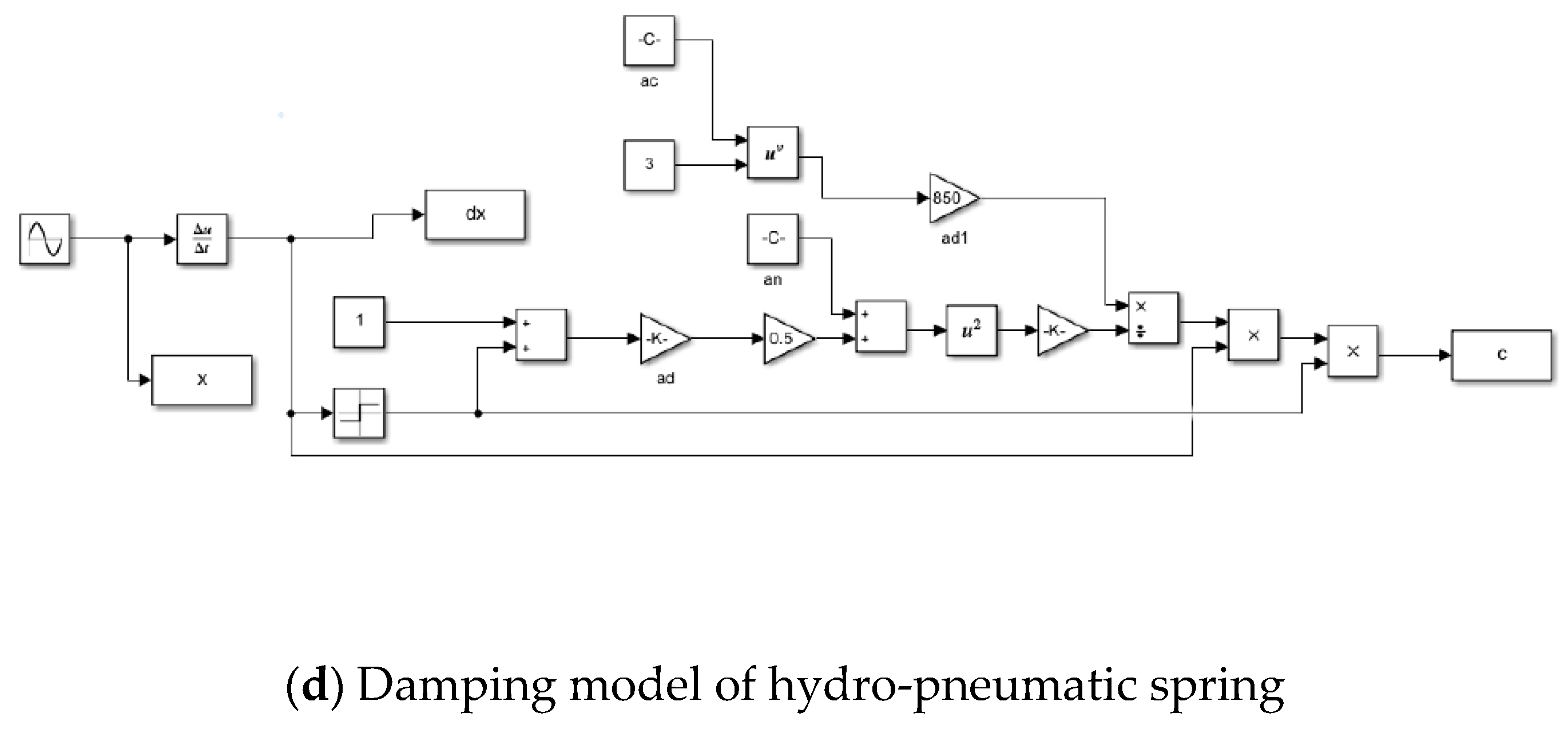
3. Theoretical Analysis of Hydro-Pneumatic Spring
3.1. External Single-Chamber Hydro-Pneumatic Springs
3.2. Mathematical Derivation of Hydro-Pneumatic Spring
3.2.1. Force of Hydro-Pneumatic Spring
3.2.2. Mathematical Model of Damping Valve
3.2.3. Mathematical Model of Pipeline
3.2.4. Mathematical Model of Accumulator
3.2.5. Mathematical Model of Hydro-Pneumatic Spring
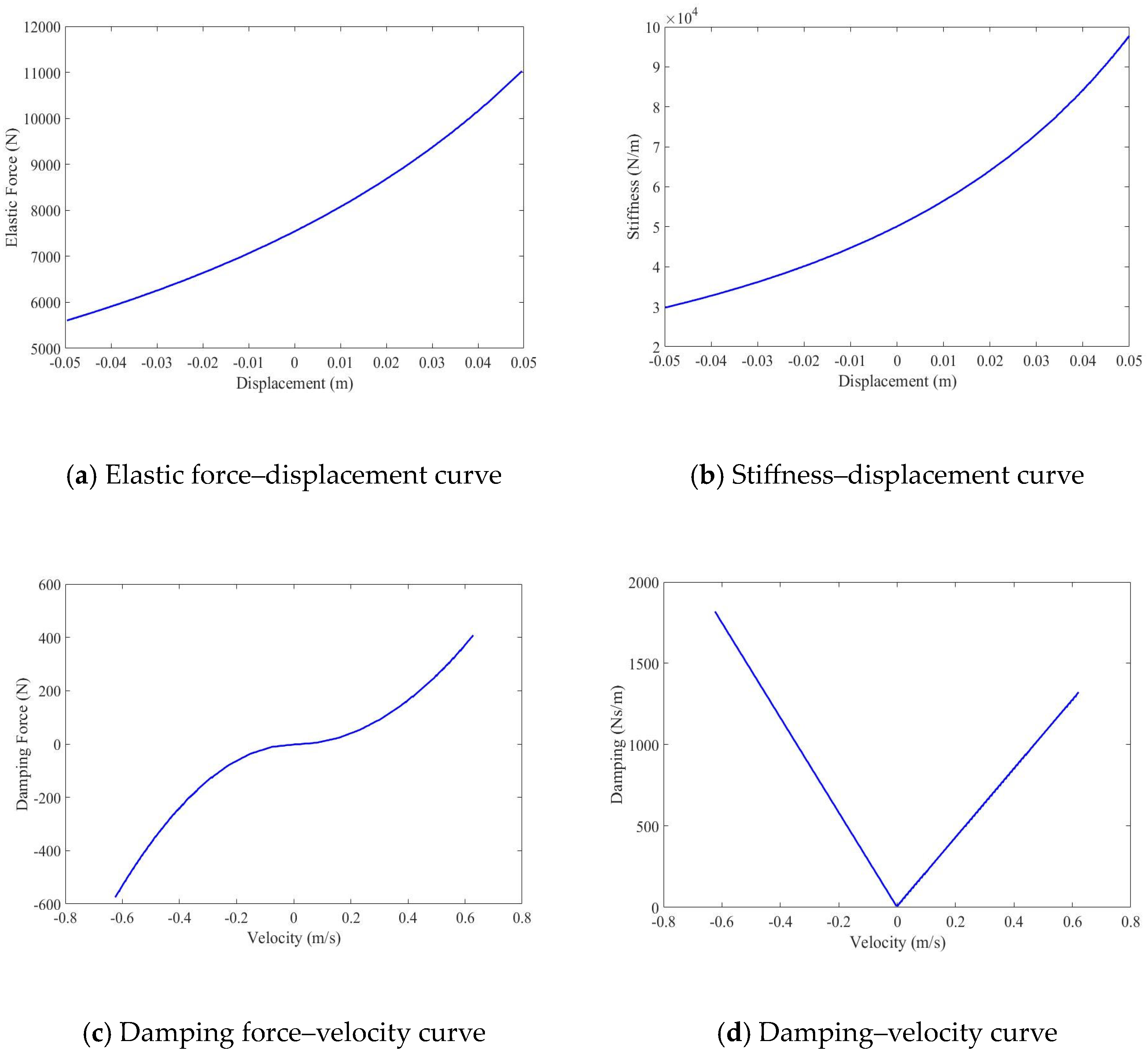
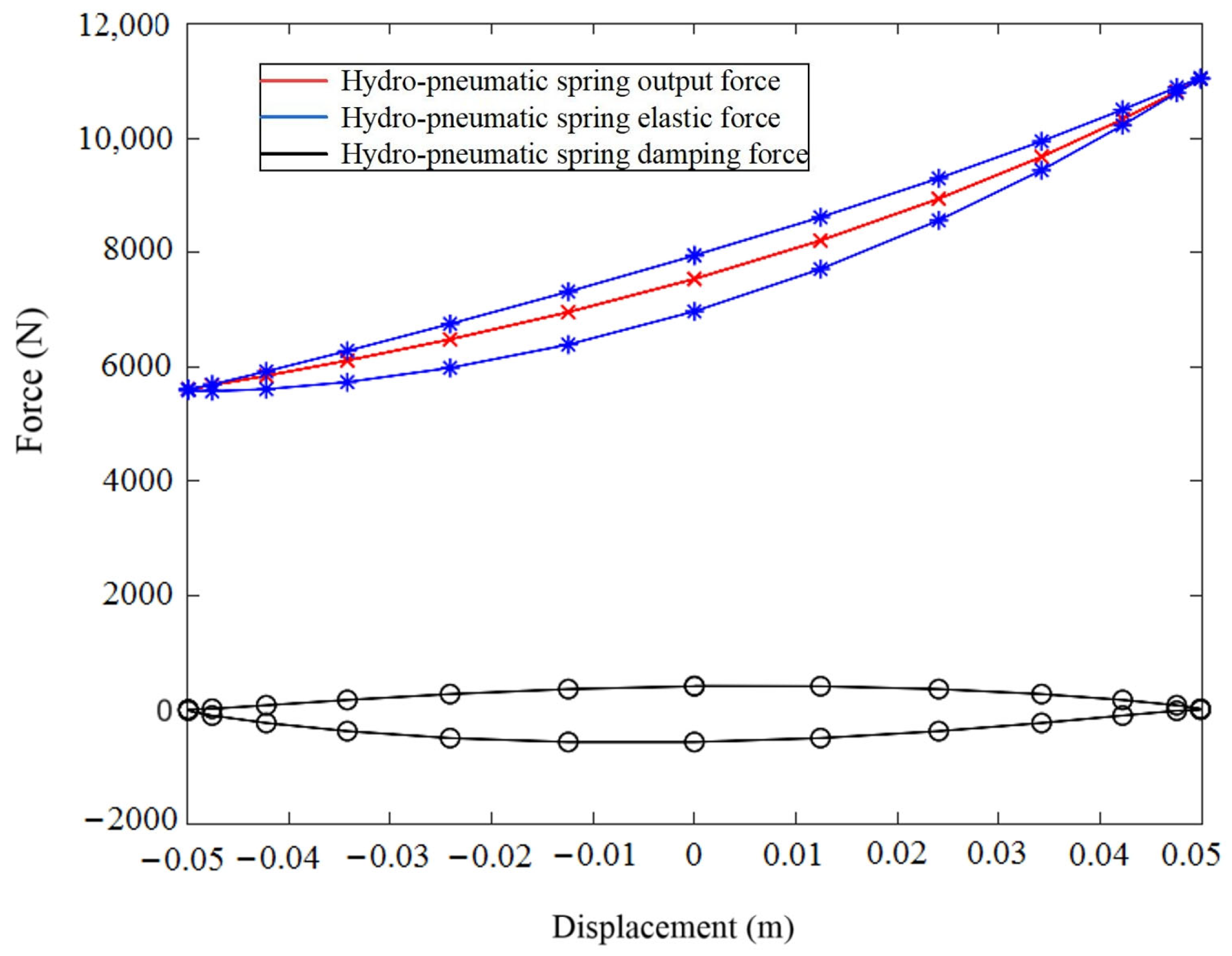
3.3. Simulation and Analysis of Hydro-Pneumatic Springs
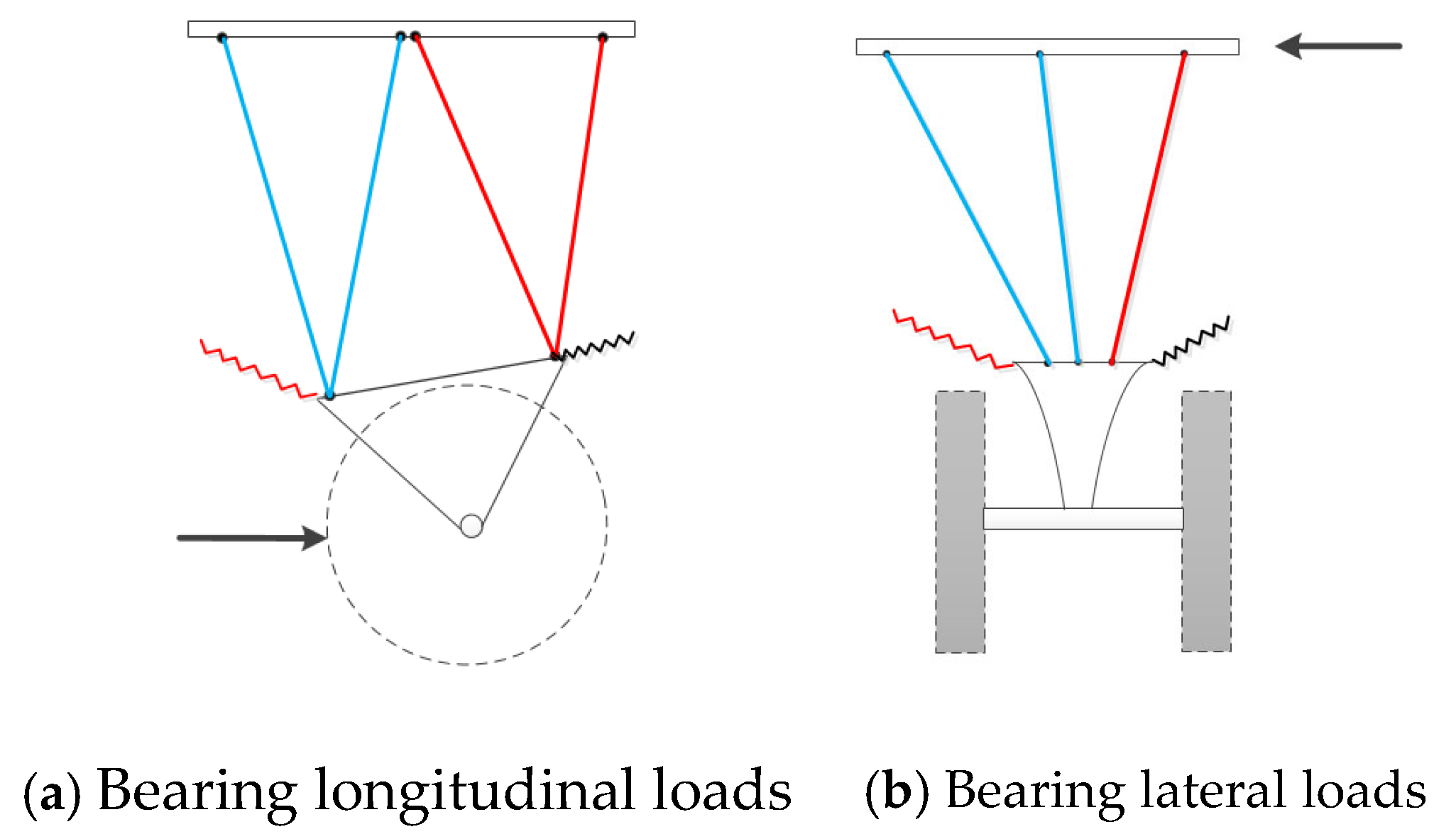
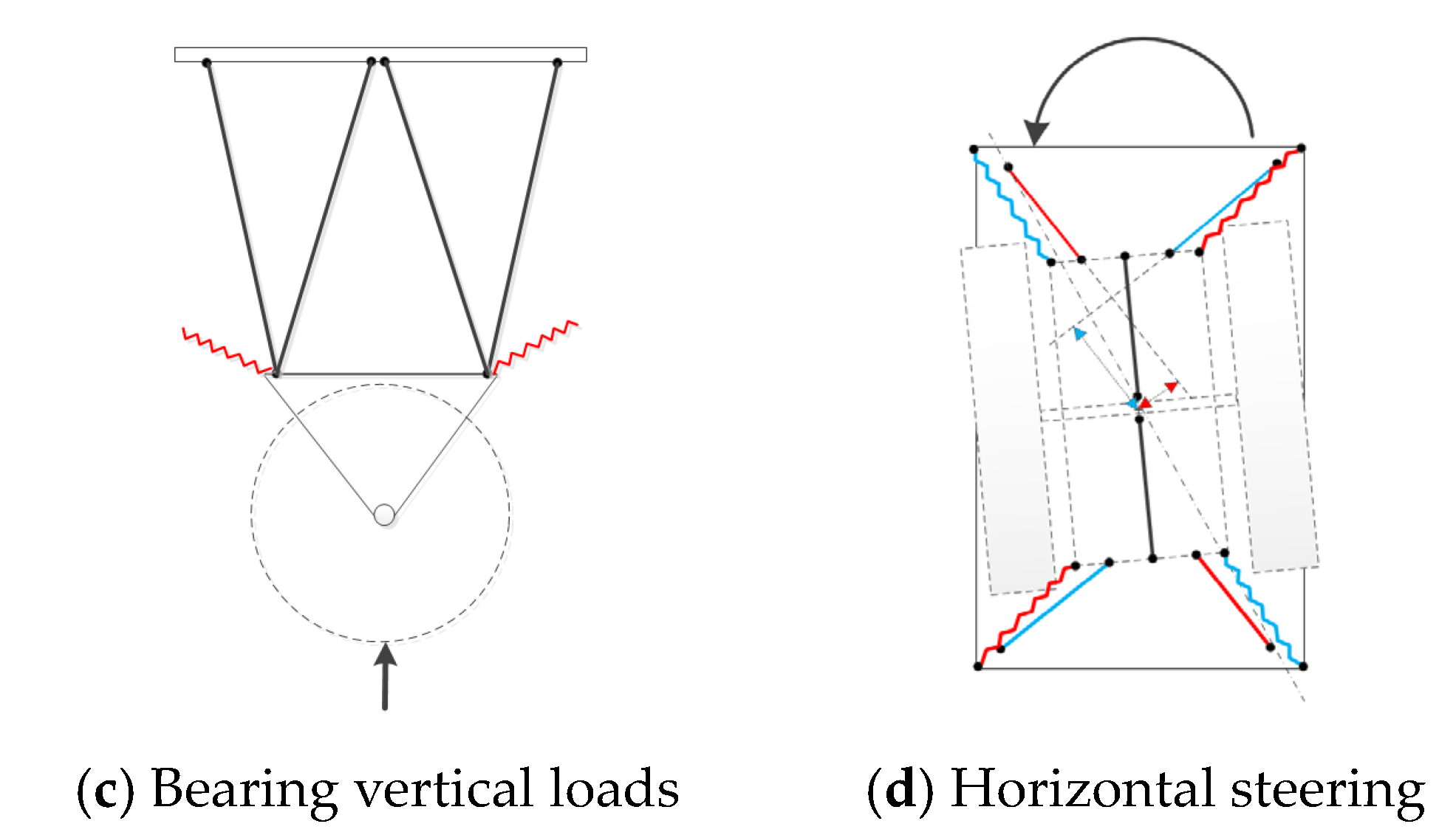
4. Analysis of Horizontal Rotational Stability
4.1. Displacement Load Variation of Hydro-Pneumatic Springs
4.1.1. Displacement Load Variation of Left Hydro-Pneumatic Spring
4.1.2. Displacement Load Variation of Right Hydro-Pneumatic Spring
4.2. Analysis of Spring Correction Force
4.2.1. Displacement and Tensile Force Variations of Left Tension Spring
4.2.2. Displacement and Tensile Force Variations of Right Tension Spring
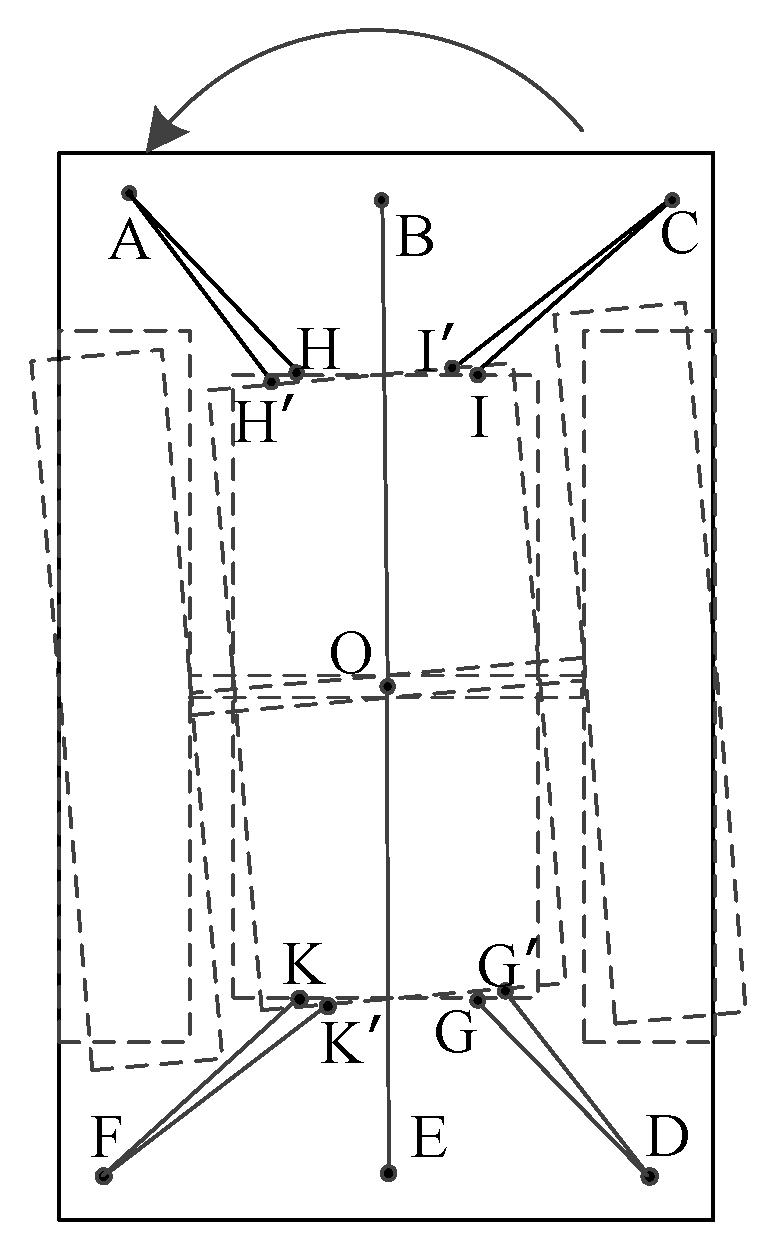
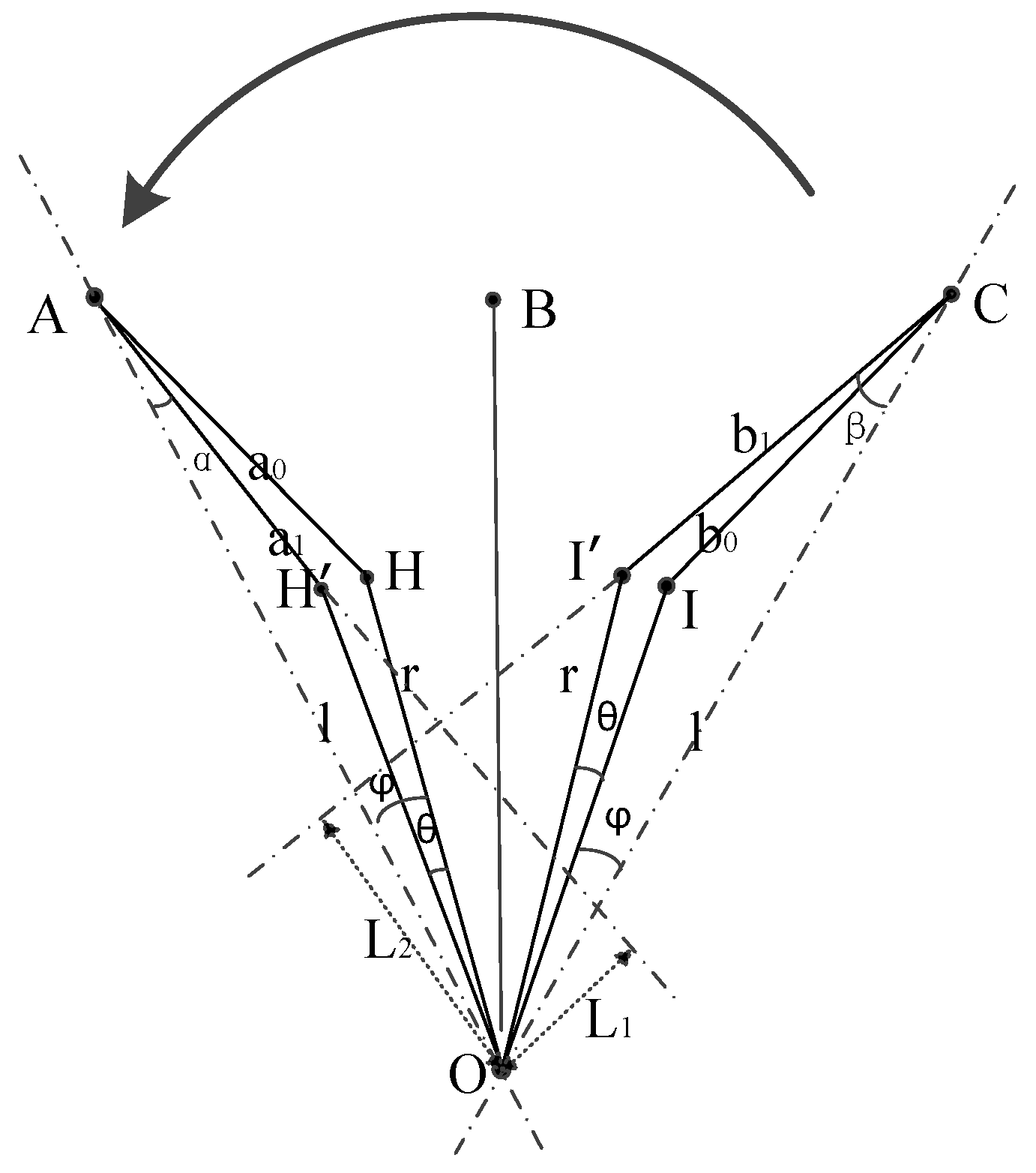
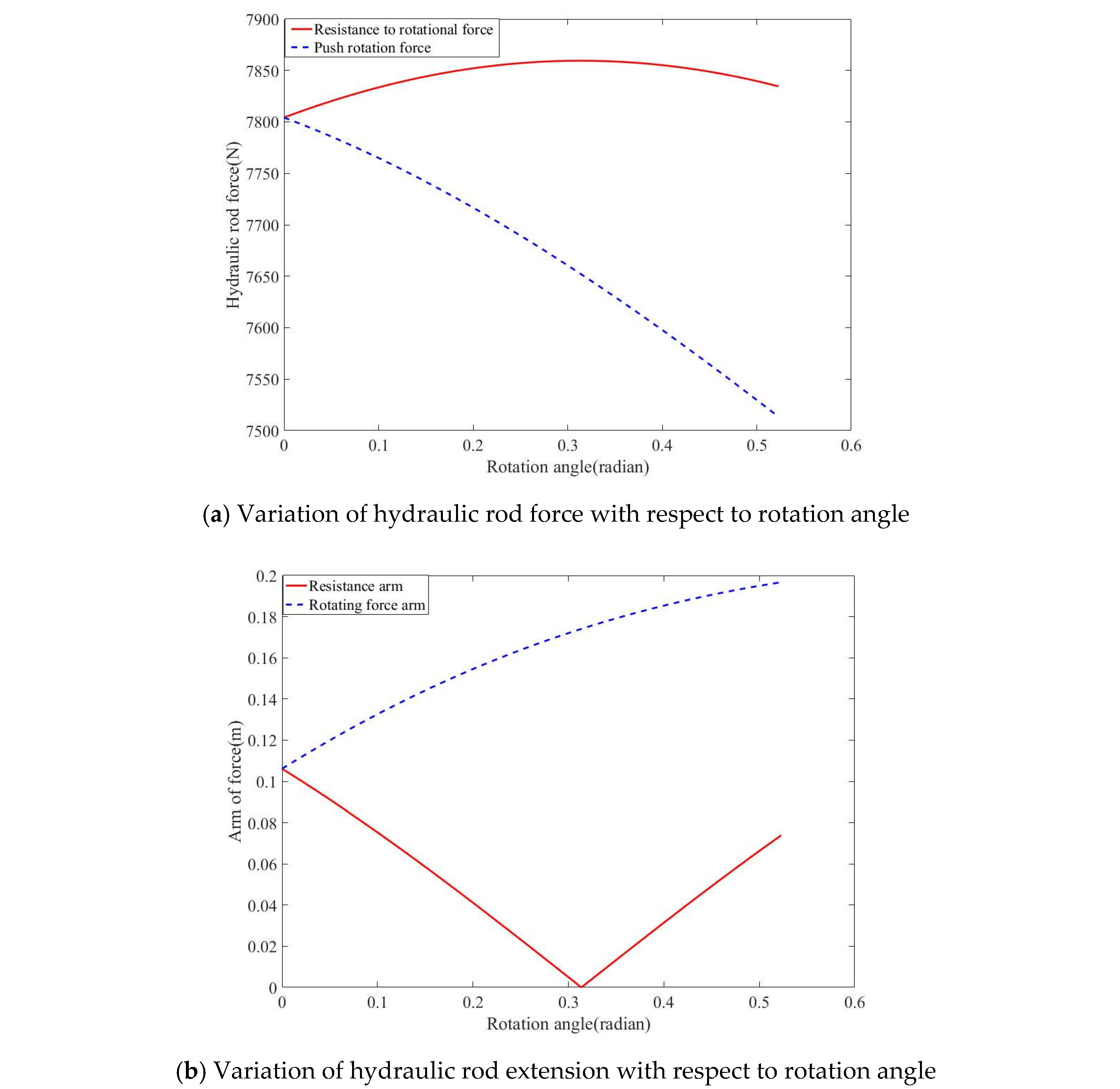
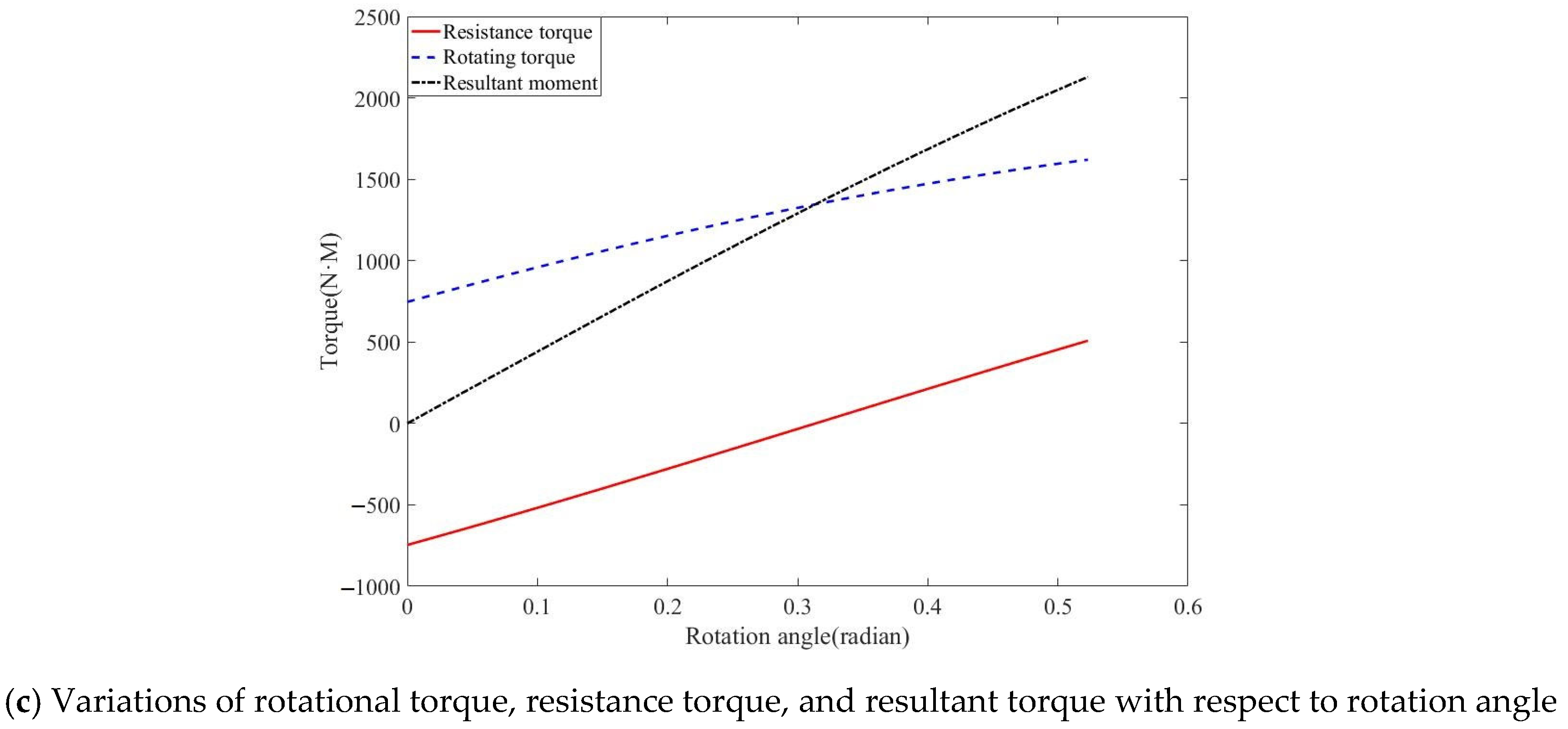
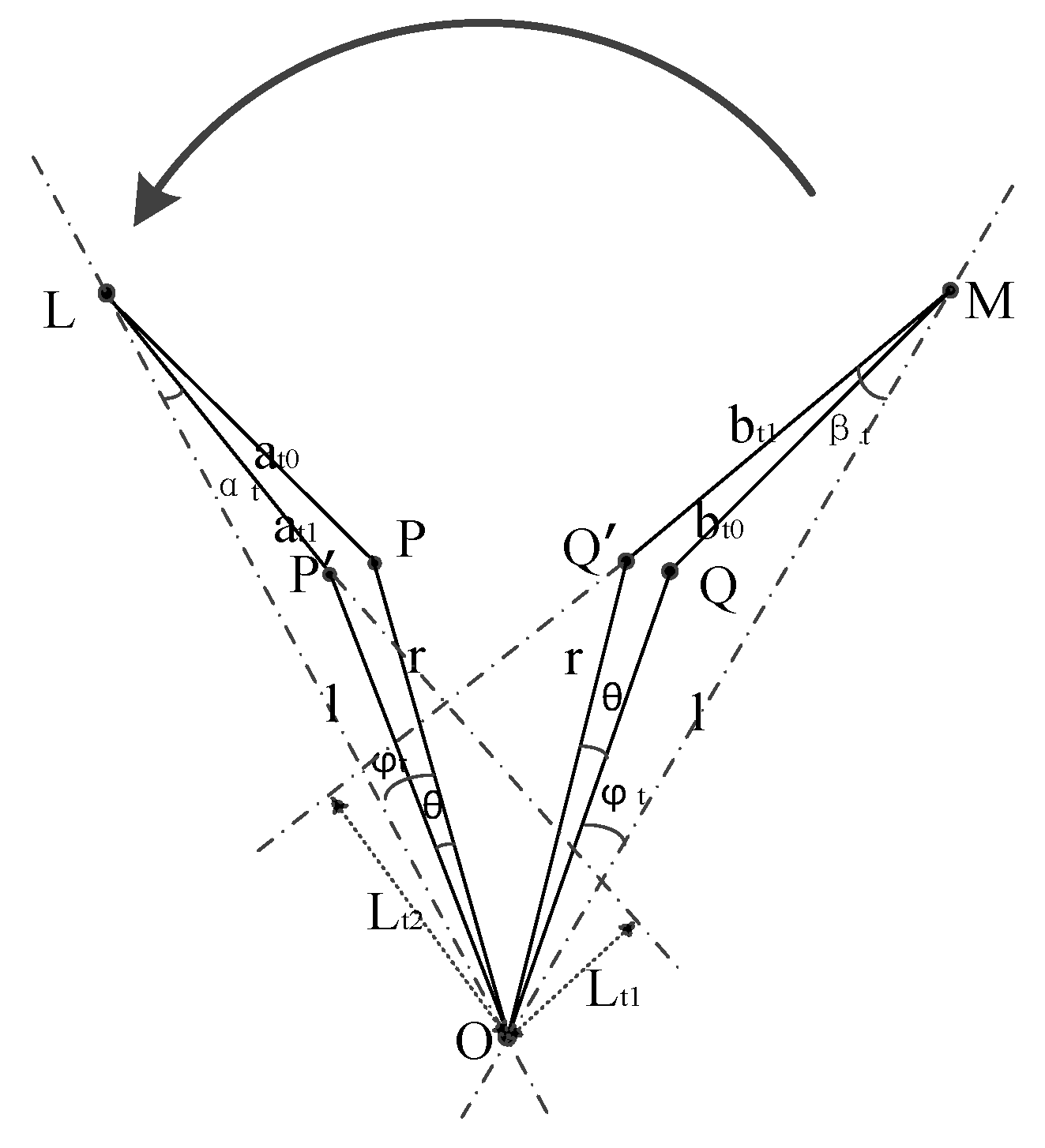
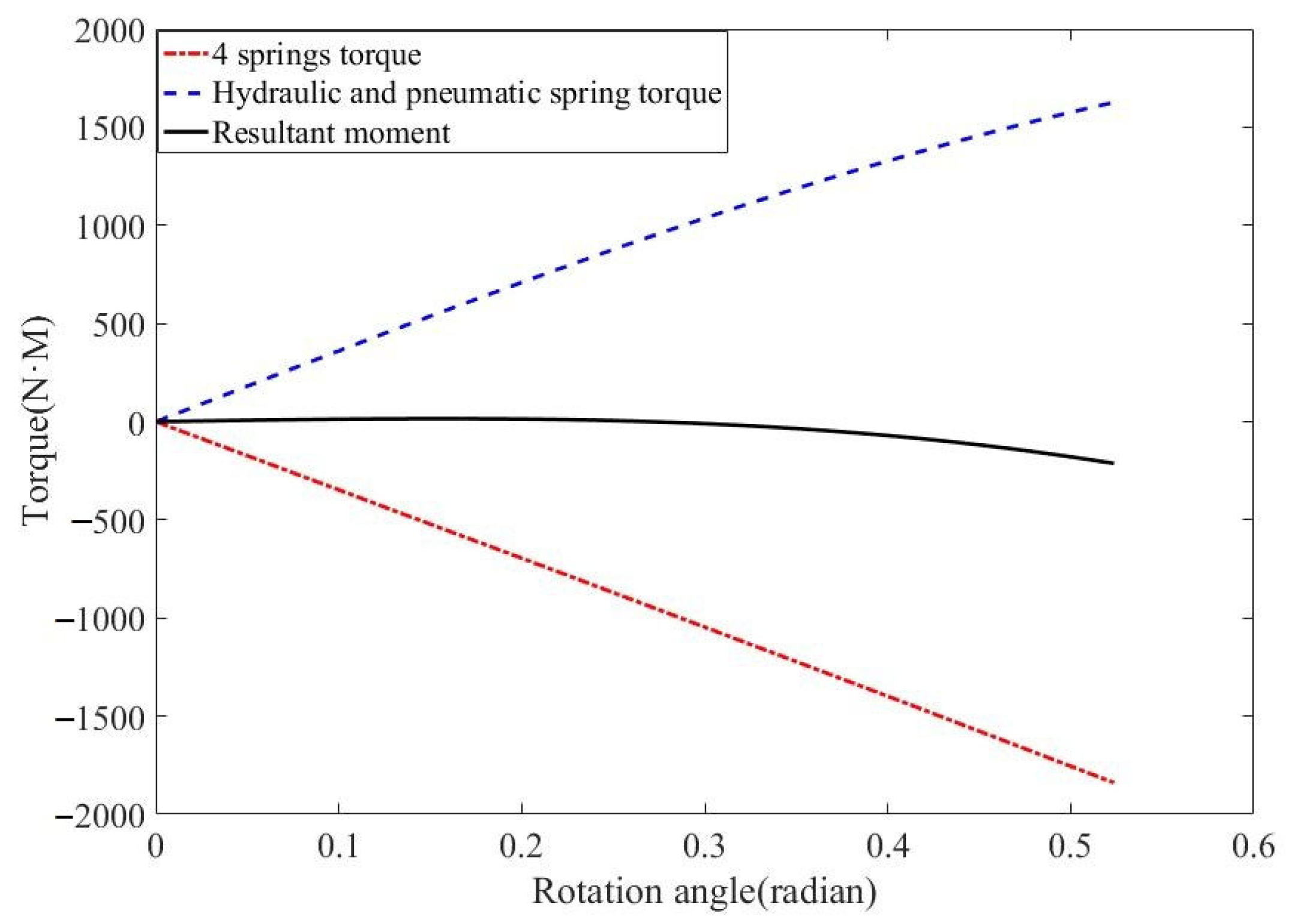
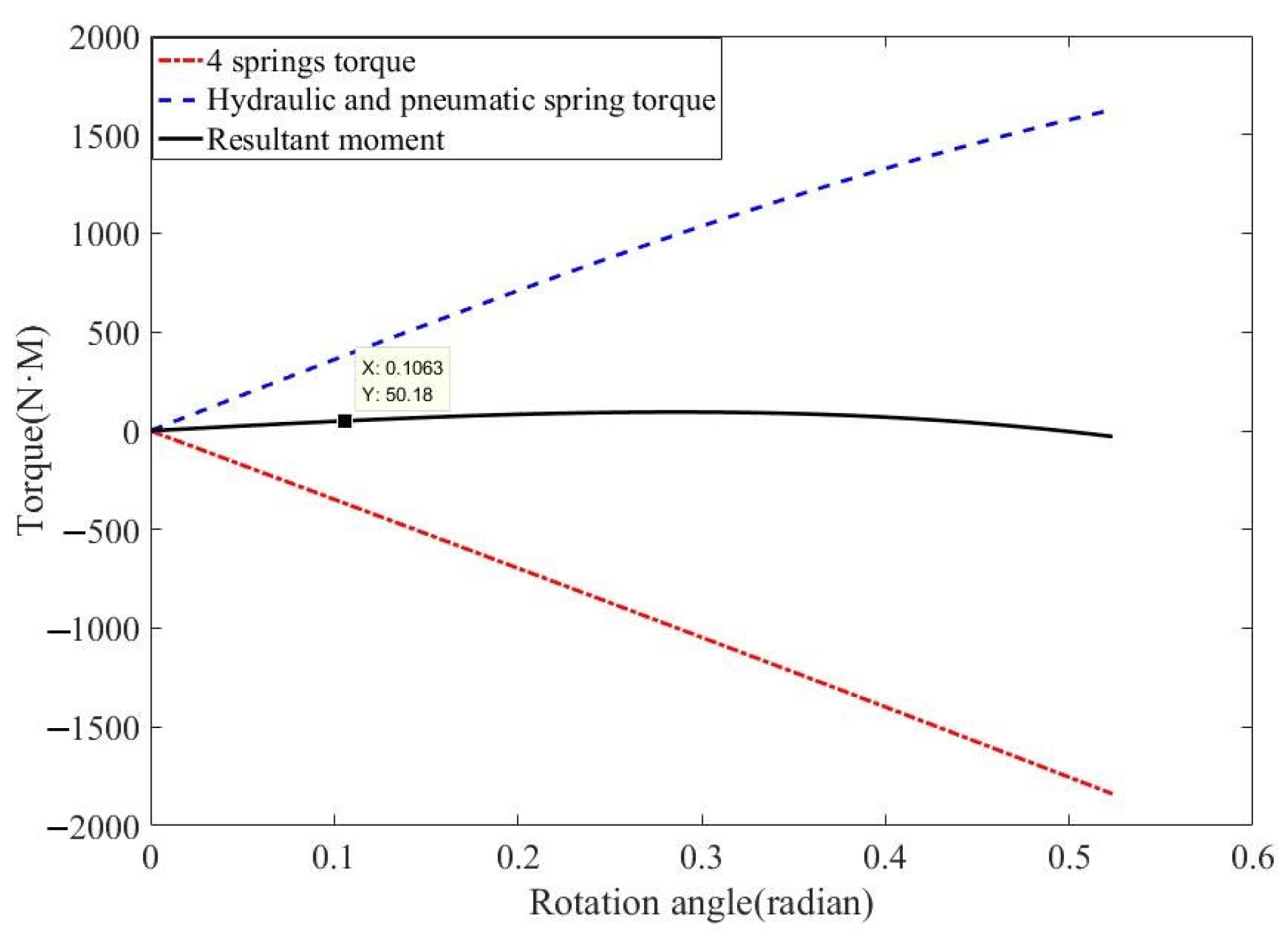
4.3. Analysis of Horizontal Rotational Torque of Wheelset
4.4. Analysis of Spring Consistency and Stiffness Calibration
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, J. Automobile Construction; China Machine Press: Beijing, China, 2011. [Google Scholar]
- Wolfgang, B. Hydropneumatic Suspension Systems; Springer: Berlin/Heidelberg, Germany, 2022. [Google Scholar]
- Wu, Z.; Jiao, B.; Sun, C.; Zhang, Y.; Zhao, H. Design and Optimization of Hydropneumatic Suspension Simulation Test Bench with Electro-Hydraulic Proportional Control. Machines 2023, 11, 907. [Google Scholar] [CrossRef]
- Sohail, A.; Liu, C. Study on the vibration isolation characteristics of an anti-resonant hydropneumatic suspension. J. Eng. 2019, 13, 208–210. [Google Scholar] [CrossRef]
- Solomon, U.; Padmanabhan, C. Hydro-gas suspension system for a tracked vehicle: Modeling and analysis. J. Terramech. 2011, 48, 125–137. [Google Scholar] [CrossRef]
- Qin, B.; Zeng, R.; Li, X.; Yang, J. Design and performance analysis of the hydropneumatic suspension system for a novel road-rail vehicle. Appl. Sci. 2021, 11, 2221. [Google Scholar] [CrossRef]
- Zhang, Z.; Cao, S.; Ruan, C. Statistical linearization analysis of a hydropneumatic suspension system with nonlinearity. IEEE Access 2018, 6, 73760–73773. [Google Scholar] [CrossRef]
- Zhao, Z.; Gu, L.; Wu, J.; Zhang, X.; Yang, H. An Integrated Vibration Elimination System with Mechanical-Electrical-Magnetic Coupling Effects for In-Wheel-Motor-Driven Electric Vehicles. Electronics 2023, 12, 1117. [Google Scholar] [CrossRef]
- Shi, T. Suspension and Steering System Design and Performance Matching for In-wheel Motor Electric Vehicle. PhD Thesis, Jilin University, Jilin, China, 2015. [Google Scholar]
- Chen, L.; Dong, H.; Li, L. A new type suspension design suitable for an in-wheel motor driving syetem. J. Vib. Shock. 2015, 34, 174–180. [Google Scholar]
- Zhang, D.; Cao, Q.; Xu, L. Comparative Study on the Configuration of Two Wheel Motor Suspension Systems. Mach. Tool Hydraul. 2022, 50, 29–35. [Google Scholar]
- Cao, Q.; Xu, L.; Yi, X. Research on a Kind of Suspension Structure for In-wheel Motor and its performance of Vibration Suppression. Comput. Simul. 2021, 38, 94–98. [Google Scholar]
- Ma, Y.; Deng, Z.; Xie, D. Analysis and optimization of in-wheel motor suspension configuration. J. Cent. South Univ. (Sci. Technol.) 2014, 45, 3008–3014. [Google Scholar]
- Tan, D.; Lu, C. The Influence of the Magnetic Force Generated by the In-Wheel Motor on the Vertical and Lateral Coupling Dynamics of Electric Vehicles. IEEE Trans. Veh. Technol. 2015, 65, 4655–4668. [Google Scholar] [CrossRef]
- Yao, J.; Ding, S.; Li, Z.; Taheri, S.; Zhang, Z. Composite Control and Co-Simulation in In-Wheel Motor Electric Vehicle Suspension. Open Autom. Control. Syst. J. 2015, 7, 996–1001. [Google Scholar] [CrossRef]
- Li, Z.; Zheng, L.; Hu, Y.; Li, Y. Negative vibration effects of in-wheel motor electric vehicles and the method for suppressing them. J. Chongqing Univ. 2019, 42, 20–29. [Google Scholar]
- Wang, R.; Jing, H.; Yan, F.; Karimi, H.R.; Chen, N. Optimization and finite-frequency H∞ control of active suspensions in in-wheelmotor driven electric ground vehicles. J. Frankl. Inst. 2015, 352, 468–484. [Google Scholar] [CrossRef]
- Li, Z.; Zheng, L.; Ren, Y.; Li, Y.; Xiong, Z. Multi-objective optimization of active suspension system in electric vehicle with in-wheel-motor against the negative electromechanical coupling effects. Mech. Syst. Signal Process. 2019, 116, 545–565. [Google Scholar] [CrossRef]
- Liang, R.; Yu, Z.; Ning, G. Restraint of negative effection vertical vibration of wheel rim driven motor vehicle based on shake absorption principle. J. Mach. Des. 2008, 25, 28–30. [Google Scholar]
- Wang, R.; Yu, F.; Shao, K.; Meng, X.; Ding, R.; Chen, L. Design and performance analysis of electromagnetic suspension based on in-wheel motor car. Trans. Chin. Soc. Agri-Cult. Mach. 2018, 49, 382–389. [Google Scholar]
- Han, Y.; Li, G.; Wang, Q.; Chen, T. Ride comfort of a new in-wheel motor driving electric vehicle based on the negative effect of vertical vibration. Sci. Technol. Eng. 2019, 19, 363–369. [Google Scholar]
- Zhao, Y.; Zhang, J.; Han, X. Design and study on the dynamic-damper mechanism for an in-wheel motor individual drive electric vehicle. Mech. Sci. Technol. Aerosp. Eng. 2008, 27, 395–398. [Google Scholar]
- Yang, D.; Jia, S.; Liang, D.; Feng, S. Coordinated Control Strategy Under Synchronous Condition of Permanent Magnet Brushless Hub Motor Wheelset System. Proc. CSEE 2024, 44, 2418–2428. [Google Scholar]
- Feng, W.; Wu, Z.; Jiao, B.; Ma, T. Analysis of six arm wheelset suspension based on hydro pneumatic spring. J. Ordnance Equip. Eng. 2022, 43, 260–267. [Google Scholar]
- Wang, H.; Jiang, C.; Liu, Q. Modeling and simulation analysis of working characteristics of single chamber hydro pneumatic spring. Comput. Simul. 2016, 33, 197–200+227. [Google Scholar]
- Zhang, D. A Study on Ride Comfort of Dump Truck’s Hydro-Pneumatic Suspension. Master’s Thesis, Jiangsu University, Zhenjiang, China, 2016. [Google Scholar]
- Cai, X.; Gu, Z.; Li, W.; Liang, X.; Peng, G. Hydro-pneumatic suspension parameters dynamical optimization design based on ride comfort. Mod. Manuf. Eng. 2011, 6, 53–57. [Google Scholar]
- Fan, B.; Mao, M.; Cai, W.; Chen, Y.; Du, F. Damping Characteristics Analysis of Hydro-Pneumatic Spring Damping Valve for Armored Vehicle. J. Ordnance Equip. Eng. 2021, 42, 1–7. [Google Scholar] [CrossRef]
- Wang, Y.; Wei, B.; Yang, Y. Establishment and verification of real gas polytropic index model for hydropneumatic suspension bladder accumulator. J. Agric. Eng. 2019, 35, 10–16. [Google Scholar]
- Wang, Y. Design, Simulation and Analysis of a Vehicle Hydro-Pneumatic Spring. Master’s Thesis, Changchun University of Science and Technology, Changchun, China, 2014. [Google Scholar]
- Wang, D. Determination of the Gas Polytropic Exponent in the Charge Proscess of the Energy Accumulator. Chin. Hydraul. Pneum. 2007, 9, 77–79. [Google Scholar]
- Feng, W. Design and Analysis of Wheel Set Suspension with Six-Arm Structure Based on Hydro Pneumatic Spring. Master’s Thesis, North University of China, Taiyuan, China, 2022. [Google Scholar]

| Name | Value | Name | Value |
|---|---|---|---|
| Hydraulic fluid density ρ/(kg/m3) | 850 | Diameter of check valve hole dd/(m) | 0.003 |
| Initial pressure of gas in accumulator Pgc/(MPa) | 6 | Cross-sectional diameter of pipeline Dp/(m) | 0.012 |
| Initial height of gas in accumulator ha/(m) | 0.2 | Pipeline length l/(m) | 0.2 |
| Inner diameter of accumulator d/(m) | 0.04 | Flow coefficient Cd | 0.61 |
| Inner diameter of piston D/(kg/m3) | 40 | Gas polytropic index γ [31] | 1.33 |
| Diameter of damping hole dc/(m) | 0.005 |
| Name | Value |
|---|---|
| Initial length of hydro-pneumatic spring s0/mm | 800 |
| Vertical distance between upper and lower ball joints of hydro-pneumatic spring hc/mm | 560 |
| Distance from lower ball joint to rotation center rc/mm | 290 |
| Horizontal projection distance from upper ball joint to rotation center lc/mm | 470 |
| Name | Value |
|---|---|
| Shear modulus of materials G/GPa | 79 |
| Wire diameter d1/mm | 10 |
| Mean diameter of the spring D2/mm | 54 |
| Number of active coils | 30 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Z.; Jiao, B.; Sun, C.; Xin, Z.; Jia, Y.; Zhao, H. Design and Stability Analysis of Six-Degree-of-Freedom Hydro-Pneumatic Spring Wheel-Leg. Appl. Sci. 2024, 14, 9815. https://doi.org/10.3390/app14219815
Wu Z, Jiao B, Sun C, Xin Z, Jia Y, Zhao H. Design and Stability Analysis of Six-Degree-of-Freedom Hydro-Pneumatic Spring Wheel-Leg. Applied Sciences. 2024; 14(21):9815. https://doi.org/10.3390/app14219815
Chicago/Turabian StyleWu, Zhibo, Bin Jiao, Chuanmeng Sun, Zezhou Xin, Yinzhi Jia, and Heming Zhao. 2024. "Design and Stability Analysis of Six-Degree-of-Freedom Hydro-Pneumatic Spring Wheel-Leg" Applied Sciences 14, no. 21: 9815. https://doi.org/10.3390/app14219815
APA StyleWu, Z., Jiao, B., Sun, C., Xin, Z., Jia, Y., & Zhao, H. (2024). Design and Stability Analysis of Six-Degree-of-Freedom Hydro-Pneumatic Spring Wheel-Leg. Applied Sciences, 14(21), 9815. https://doi.org/10.3390/app14219815






