Compression Law and Settlement Calculation Method of Over-Wet Soil Based on Large Samples

Abstract

Previous studies have shown that over-wet soil is challenging to compact and exhibits large creep deformation. The consolidation test of small specimens cannot accurately reflect the compression law, and creep is underestimated owing to size effects, which affects the engineering quality. In order to accurately analyze the compression process of over-wet soil and establish its settlement calculation method, this study focuses on over-wet soil in Anhui Province, China, and uses a large-sized tester to load and analyze its compression law. The thermogravimetric analysis method was employed to investigate the changes in water with different binding forces during the compression process, and the settlement calculation method for over-wet soil was explored. The results show that the creep of over-wet soil is large and long-lasting, and the three-stage consolidation division method based on the $d-t$ curve is more effective in analyzing its regularity. The creep of over-wet soil is directly proportional to its water content. When the load exceeds the pre-consolidation pressure, the creep deformation becomes more significant, accounting for about 60% of the deformation under a single level load. It is recommended to use the creep coefficient ($\lambda$) for calculation. The results of the thermogravimetric analysis indicate that during the primary consolidation stage, free water is discharged, and weakly bound water is mainly discharged during the third consolidation stage, which is the main cause of creep. Finally, based on the relationship between the creep strain and water content of large samples, a calculation method for the settlement of over-wet soil foundations based on the layered summation method was established, which had a higher prediction accuracy than the conventional layered summation method. The results of this study will help clarify the deformation process and principle of over-wet soil and improve the quality of engineering.

1. Introduction

Over-wet soil is soft soil with a water content higher than the optimal moisture content, which is challenging to dry. However, no clear definition exists. Sha [1] proposed that over-wet soil cannot be compacted to its maximum degree when its water content exceeds a particular value. Wang et al. [2] proposed that soil is overmoist when the water content of soft soil exceeds the optimal water content by approximately 2%. Du et al. [3] proposed a definition for over-wet soil based on its consistency (Equation (1)), which does not reflect the compaction characteristics. Sha’s definitions suggest that over-wet soil can be defined based on optimal moisture content, as shown in Equation (2). When the humidity was below 1, the water content exceeded the optimal moisture content, indicating over-wet soil.

$$w_c=(w_L-w)/(w_L-w_P),$$

(1)

where $w_c$ = consistence;

$w_L$ = liquid limit (%);

$w$ = water content (%);

$w_P$ = plastic limit (%).

$$w_h=\left[\right(w_L-w)/(w_L-w_{\mathrm{omc}}\left)\right]\times 100\%,$$

(2)

where $w_h$ = humidity, (%);

$w_{omc}$ = optimal water content (%).

Over-wet soil has a high water content and a low permeability coefficient. During compaction, it behaves similarly to a “spring” and is not easily compacted, resulting in low foundation-bearing capacity. After loading, it produces significant creep owing to the slow water discharge that affects project quality [4,5]. Currently, most studies on over-wet soil focus on disposal methods. Improvement schemes using fly ash [6], carbide slag [7], cement [8], etc., have been proposed, but research results on the deformation law of over-wet soil are still limited. Lai et al. [9] analyzed the stress distribution characteristics in an over-wet soil layer through model tests. Guo [10] proposed the Tseng–Lytton model to estimate permanent deformation through elastic deformation, but it cannot reflect the nonlinear characteristics. Therefore, the Chai–Muria model is more suitable for predicting the deformation of over-wet soil. Deng [11] developed a discrete element model for over-wet soil using the Edinburgh elasto-plastic adhesion (EEPA) contact model and suggested that the contact plasticity ratio and surface energy played a significant role in characterizing the mechanical behavior of clay-moist soil.

Research on disposal methods for over-wet soil has achieved some results. However, meaningful conclusions on compression laws and settlement calculation methods remain unreached, resulting in significant problems. If the deformation process of over-wet soil is independent of the sample size, the test results of samples of different sizes should be consistent. However, due to the high water content and low permeability of over-wet soil, employing standard compression test methods underestimates creep deformation owing to size effects [12,13], resulting in higher post-construction settlement than expected. In this study, one-way compression tests were performed on large samples of over-wet soils with different compaction degrees to investigate the compression laws and analyze the effects of water content and compaction degree. Second, based on the compression data, the compression process of over-wet soil was divided into three stages, and the deformation law was analyzed. Thermogravimetric analysis was employed to analyze the changes in free water, weakly bound water, and strongly bound water during compression [14]. Finally, based on the layer-wise summation method, a calculation method for the settlement of an over-wet soil foundation considering the creep process was proposed and verified. The results of this study will provide a theoretical basis for the disposal of over-wet soil, which will help to accurately select foundation disposal measures and reduce potential resource waste.

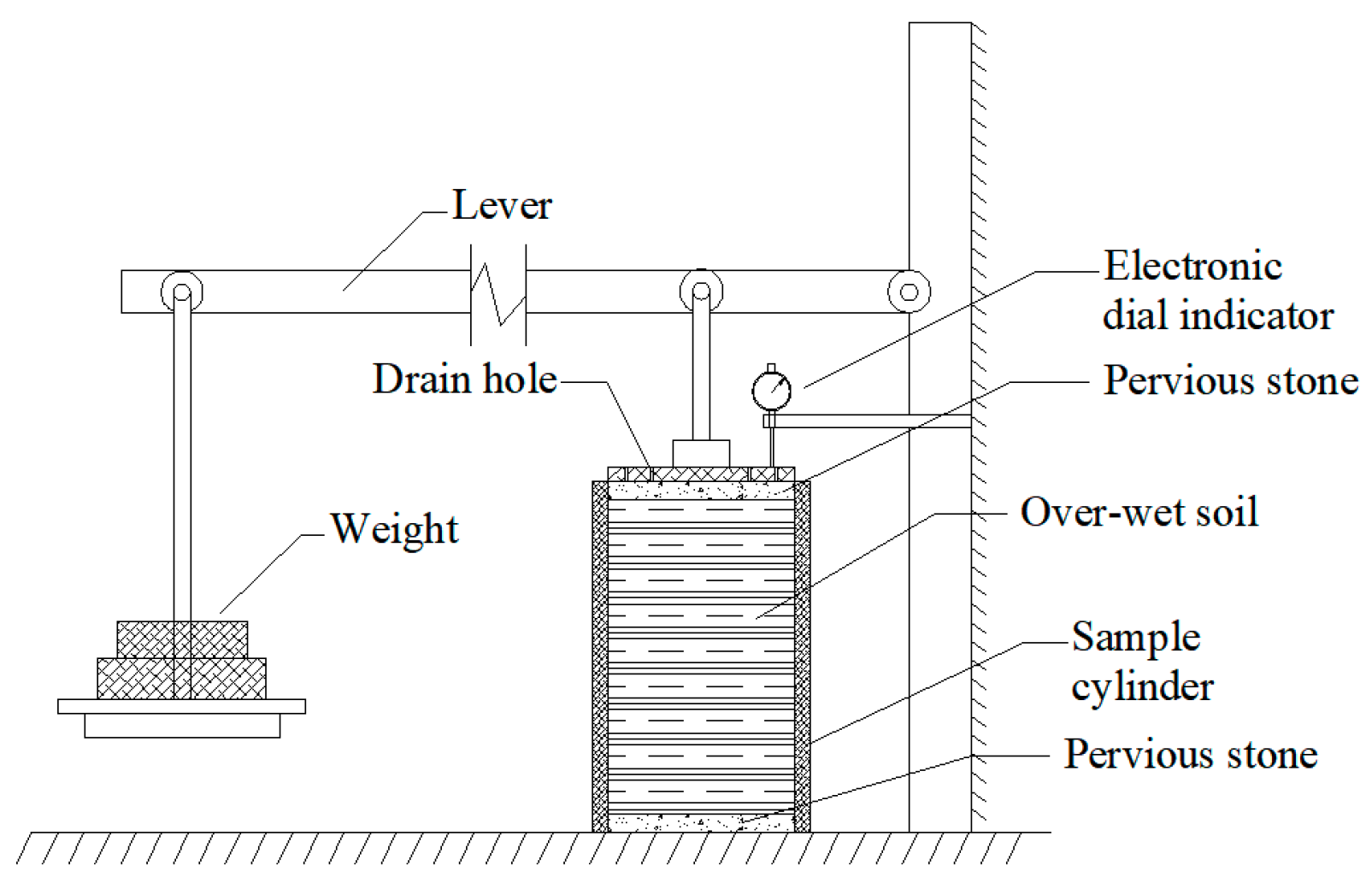
2. Materials and Methods

The soil samples were obtained from Hefei, Anhui Province, East China, which has a subtropical humid climate with an average annual precipitation of 900–1000 mm. The soil sample was approximately 0.5 m below ground level and was brownish-yellow, ranging from plastic to soft plastic. The sampling locations are shown in Figure 1. Figure 2 shows the sampling site.

The water content, liquid limit, and plastic limit of the soil samples were measured in accordance with the guidelines given by ASTM [15]. The compaction curve of the sample is shown in Figure 3, with a maximum dry density of 1.765 g/cm³ and an optimal moisture content of 12.62%. The humidity of each group of samples was calculated using Equation (2), and the results are presented in

Table 1. Natural water content as well as liquid and plastic limits of soil samples.

Water Content w/%	Liquid Limit wL/%	Plastic Limit wP/%	Plasticity Index IP/%	Optimum Water Content/%	Maximum Dry Density/g·cm−3	Humidity (%)
16.80	58.0	24.2	33.8	13.3	1.765	92

. Soil samples with a humidity of less than 100% were considered over-wet soil. The liquid limit exceeded 50%, which indicates a high-liquid-limit soil. The particle screening results are listed in

Table 2. Particle size distribution.

Gradation/%					Classification
5 mm–20 mm	2 mm–5 mm	0.25 mm–2 mm	0.075 mm–0.25 mm	<0.075 mm
0	0.17	1.88	1.03	96.92	High liquid limit clay

, with approximately 80% of the particles being less than 0.075 mm; therefore, the soil is classified as clay.

Compacting over-wet soil is challenging owing to the high water content and difficulty in draining water. The phenomenon of “springing” may occur during compaction, where the compressed area sinks in, and the surrounding area springs back. Conventional one-way compression tests or triaxial tests have small sample sizes ($\phi$ = 61.8 mm, $h$ = 20 mm, and $\phi$ = 50 mm, $h$ = 100 mm) and short drainage paths, which cannot reflect the true conditions of over-wet soils in the stratum. In this study, a large-scale compression test apparatus was used. Figure 4 shows a schematic of the loading device. The sample size is $\phi$ = 200 mm, and $h$ = 320 mm, with filter paper and permeable stone placed on the top and bottom of the sample, and with Vaseline applied on the inner wall. The lever loading method was employed, and electronic dial indicators and data collectors (SYNTEK, Hangzhou, China) were used to collect the deformation data continuously. The loading device was fixed to a steel frame, enabling the performance of multiple simultaneous sets of tests. Figure 5 shows the loading process.

Using the water content and compaction as control parameters, samples were prepared with target water contents of 8%, 13%, 18%, 21%, and 26%. To prepare the samples, the soil was divided into three layers and placed in a sample cylinder. After leveling, the samples were compacted. The actual parameters measured after sample preparation are listed in

Table 3. Soil sample parameters.

Number	Target Water Content/%	Actual Water Content, w/%	Dry Density/g·cm−3	Compaction Degree, K/%	Humidity/%
1	8	7.80	1.702	96.4	112
2	13	13.09	1.728	97.9	100
3	18	17.65	1.687	95.6	90
4	21	21.13	1.675	94.9	82
5	26	26.06	1.578	89.4	71

. Based on the humidity data in the table, all samples except 1 and 2 were over-wet soil. A large compression apparatus was employed to apply loads corresponding to 50, 100, 200, 300, and 400 kPa. The deformation stability standard is that after 24 h of loading, the deformation in the last hour must be approximately 0.01 mm.

To analyze the changes in free and bound water during the compression process of over-wet soil, a thermogravimetric (TG) analysis was conducted on sample 5 before loading and after different compression stages of 200 kPa (below the pre-consolidation pressure) and 400 kPa (above the pre-consolidation pressure). Figure 6 shows the ZRT thermogravimetric analysis system (Beijing Jingyi Hi-Tech Technology Co., Ltd., Beijing, China). The initial temperature was set to room temperature (about 23 °C), and the heating rate was set to 10 °C/min. Because only a few milligrams of soil samples are required for thermogravimetric analysis, the impact of sampling on large samples can be neglected.

3. Results and Discussion

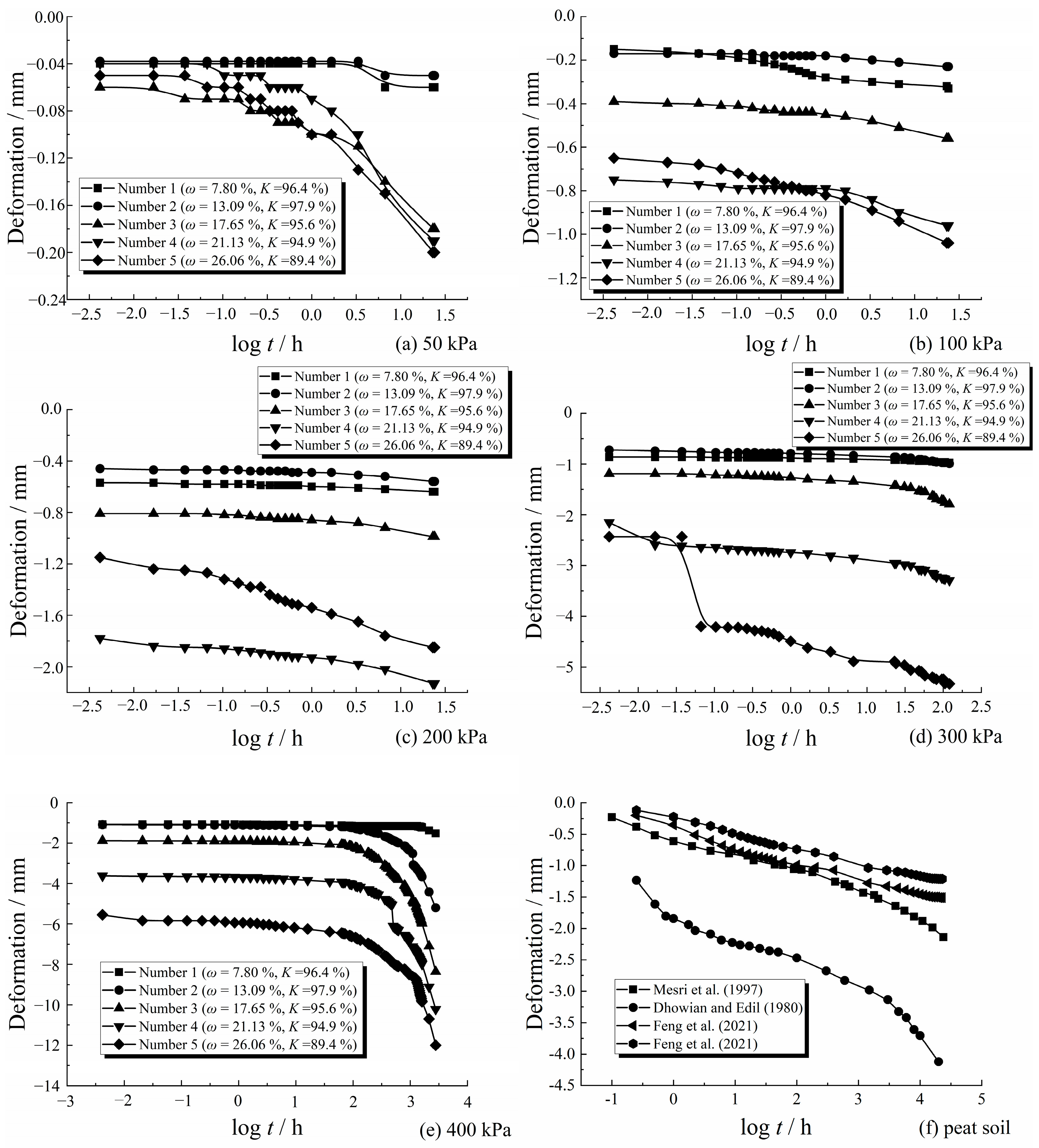
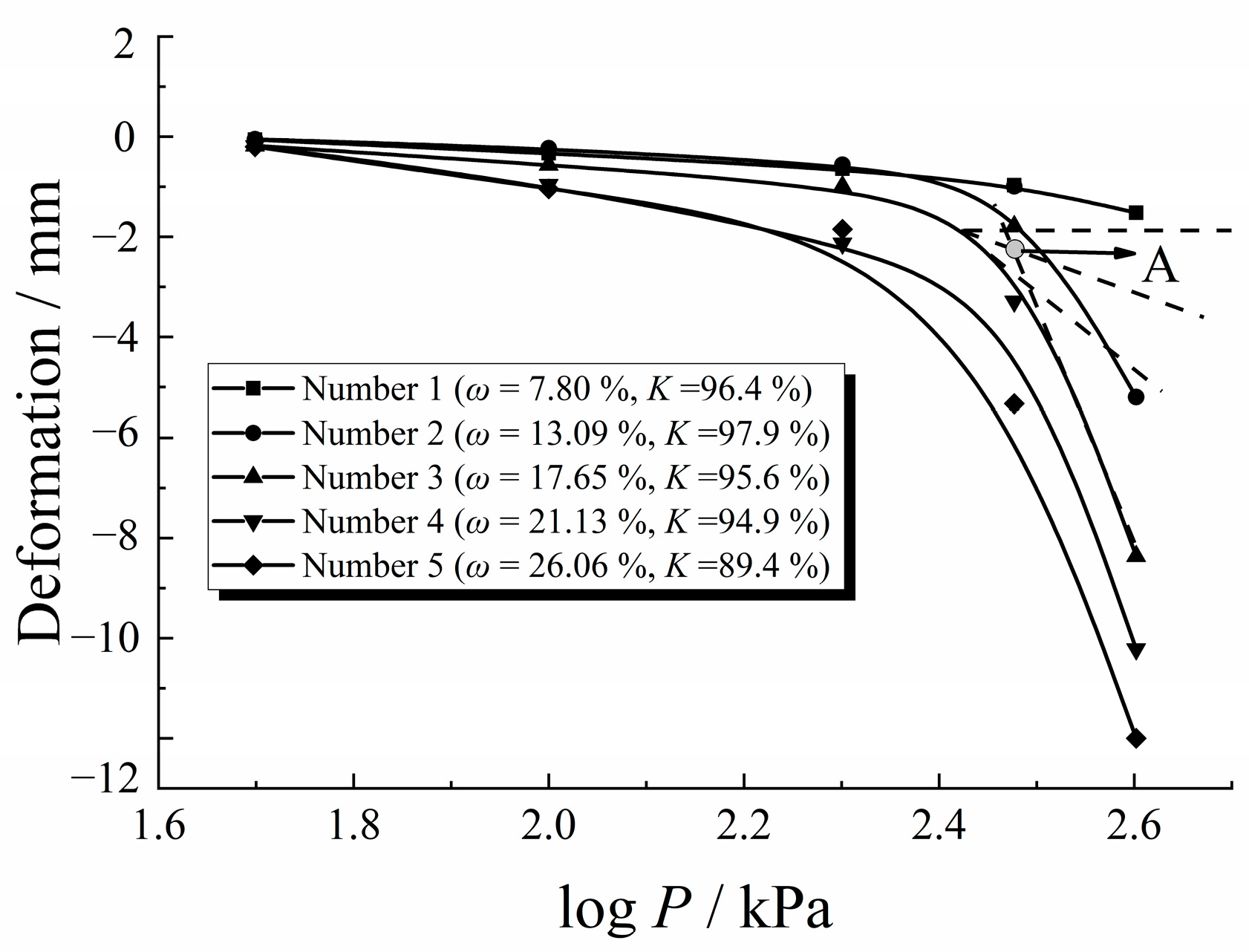
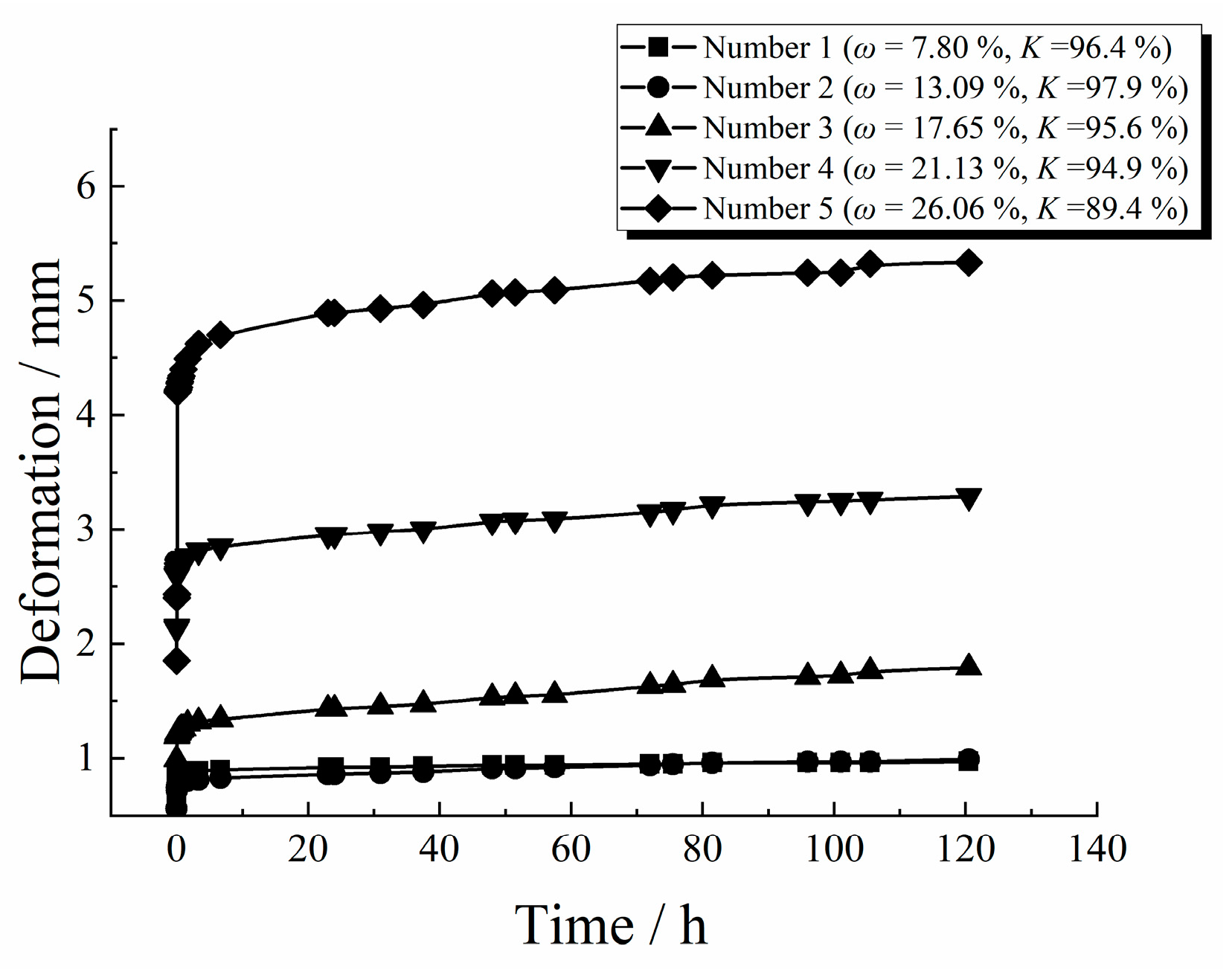
3.1. Analysis of Compression Deformation of Over-Wet Soil

The graphical method proposed by Casagrande was employed to calculate the samples’ pre-consolidation pressures [16]. Figure 7 shows the $d-\mathrm{l}\mathrm{o}\mathrm{g}P$ curves for five samples, and sample 3 is used as an example for the calculation. The abscissa of point A, determined using the graphical method, represents the maximum stress experienced historically.

Table 4. Pre-consolidation stress of the samples.

Number	Pre-Consolidation Pressure/kPa
1	304
2	316
3	297
4	281
5	257

lists the results for the five samples, indicating that the pre-consolidation pressure increases with increasing compaction.

Figure 8 shows the $d-\mathrm{l}\mathrm{o}\mathrm{g}t$ curves of the standard compression test ($h$ = 20 mm) with sample number 3. It can be seen from the figure that the $d-\mathrm{l}\mathrm{o}\mathrm{g}t$ curve of the standard compression specimen is not significantly different from that of general soft soil, which conforms to the anti-“$S$” deformation law.

Figure 9 shows the $d-\mathrm{l}\mathrm{o}\mathrm{g}t$ curves of large samples. The deformation curves of samples 1 and 2 conform to the anti-“$S$” deformation law when the load is less than the pre-consolidation pressure. The anti-“$S$” shape of sample 2 disappears when the load exceeds the pre-consolidation pressure. Samples 3, 4, and 5 do not exhibit an inverse “$S$” deformation law at any loads. As the deformation increases, the $d-\mathrm{l}\mathrm{o}\mathrm{g}t$ curves gradually approach a stable secondary consolidation stage because samples 1 and 2 are non-over-wet soils with high compaction. Thus, the long-term deformation is insignificant. However, when the load was low, the deformation of the over-wet soil gradually increased as the compaction degree decreased. When the load exceeded the pre-consolidation pressure, the deformation of the sample was no longer positively correlated with the compaction degree but increased as the water content increased.

Because the x-axis of the $d-\mathrm{l}\mathrm{o}\mathrm{g}t$ curve is a logarithmic function of time, analyzing the compression law of over-wet soil based on this curve results in the compression of the x-axis, weakening the characteristics of long-term deformation. Therefore, the conventional analysis methods for the primary and secondary consolidation stages have limitations with excessively wet soil.

A significant difference between the compression process of over-wet soil and general soft soil exists, as shown in Figure 9, which is similar to that of peat soil with a similarly high water content (Figure 9f). Feng et al. [19] proposed a three-stage compression method based on the long-term creep process of peat soil, as shown in Figure 10, in which the third consolidation stage is a uniformly slow creep stage.

To analyze the creep process of over-wet soils, the division method of the three stages of compression was employed to draw the $d-t$ curve, similar to that in Figure 10, using 300 kPa as an example (Figure 11). The deformation of samples 1 and 2 tended to stabilize quickly, as shown in Figure 11. However, samples 3, 4, and 5 of over-wet soil exhibited a slow and long-lasting tertiary consolidation stage with time, meeting the criteria for dividing the three stages of compression. Figure 12a–c shows the relationship between the deformation and load in the three stages of compression of the over-wet soil. According to Equation (3), the proportion of creep deformation under a single-level load was calculated (Figure 12d).

$$C_i={\displaystyle \frac{d_{t,i}}{d_i}}\times 100\mathrm{\%},$$

(3)

where $C_i$ = proportion of creep at the ith load (%).

$d_{t,i}$ = deformation during the tertiary consolidation stage (i.e., creep) at the ith load (mm).

$d_i$ = total deformation at the ith load (mm).

As shown in Figure 12, the deformations of the three samples during the primary consolidation stage differs slightly at 50 kPa. As the load increases, the deformation during the primary consolidation stage gradually increases and stabilizes, slightly decreasing at 400 kPa. The deformation during the secondary consolidation stage gradually increases as the load increases, and the increase rate is proportional to the water content. When the load exceeds the pre-consolidation pressure, the deformation increases rapidly.

For the creep generated in the tertiary consolidation stage, when the load was below the pre-consolidation pressure, the creep of the over-wet soil was insignificant (<0.5 mm). When the load exceeded the pre-consolidation pressure, the creep variable rapidly increased by >3 mm, and the creep of specimen 5 reached 4.3 mm. As shown in Figure 12 (d), the proportion of creep deformation in the over-wet soil first decreased and then increased as the load increased. When the load was 400 kPa, the creep proportion exceeded 60% and increased as the water content increased.

The total creep amount of the wet soil was calculated from 50 to 400 kPa (

Table 5. Creep of three specimens.

Number	3	4	5
Water content/%	17.65	21.13	26.06
Creep deformation/mm	4.58	4.51	5.09
Creep strain	0.014	0.034	0.016

). Table 5 indicates a strong correlation between the creep deformation, creep strain, and water content of the over-wet soil.

Figure 13 shows the creep curve of the over-wet soil with increasing water content. As the water content increases, the creep of over-wet soil increases linearly, with linear correlation coefficients exceeding 0.94 and an average value of 0.966, as shown in Figure 13. When the load is low, the creep rate decreases. As the load increases, the creep rate significantly increases when the load exceeds the pre-consolidation pressure.

The creep coefficient of over-wet soil was proposed based on the data in Figure 13 and Table 6 as the ratio of creep strain to water content, as shown in the following Equation (4):

$${\epsilon }_c=\lambda w,$$

(4)

where ${\epsilon }_c$ = creep strain of over-wet soil.

$\lambda$ = creep coefficient of over-wet soil.

$w$ = water content (%).

The compression data of large-sized specimens indicate that the data of small-sized specimens [10,11] underestimated the creep deformation of over-wet soil, which can mislead the disposal measures and affect the progress and quality of the project. On the other hand, during the experimental process, the water content of the sample needs to be given special attention.

Table 6. Fitting curve for the creep strain of over-wet soil.

Load	${\mathit{\epsilon }}_{\mathit{c}}$	${\mathit{R}}^2$
50	${\epsilon }_c=6.0\times {10}^{-6}w$	$0.961$
100	${\epsilon }_c=7.1\times {10}^{-6}w$	$0.943$
200	${\epsilon }_c=1.9\times {10}^{-5}w$	$0.944$
300	${\epsilon }_c=4.8\times {10}^{-5}w$	$0.981$
400	${\epsilon }_c=6.5\times {10}^{-4}w$	$0.999$

Table 6. Fitting curve for the creep strain of over-wet soil.

Load	${\mathit{\epsilon }}_{\mathit{c}}$	${\mathit{R}}^2$
50	${\epsilon }_c=6.0\times {10}^{-6}w$	$0.961$
100	${\epsilon }_c=7.1\times {10}^{-6}w$	$0.943$
200	${\epsilon }_c=1.9\times {10}^{-5}w$	$0.944$
300	${\epsilon }_c=4.8\times {10}^{-5}w$	$0.981$
400	${\epsilon }_c=6.5\times {10}^{-4}w$	$0.999$

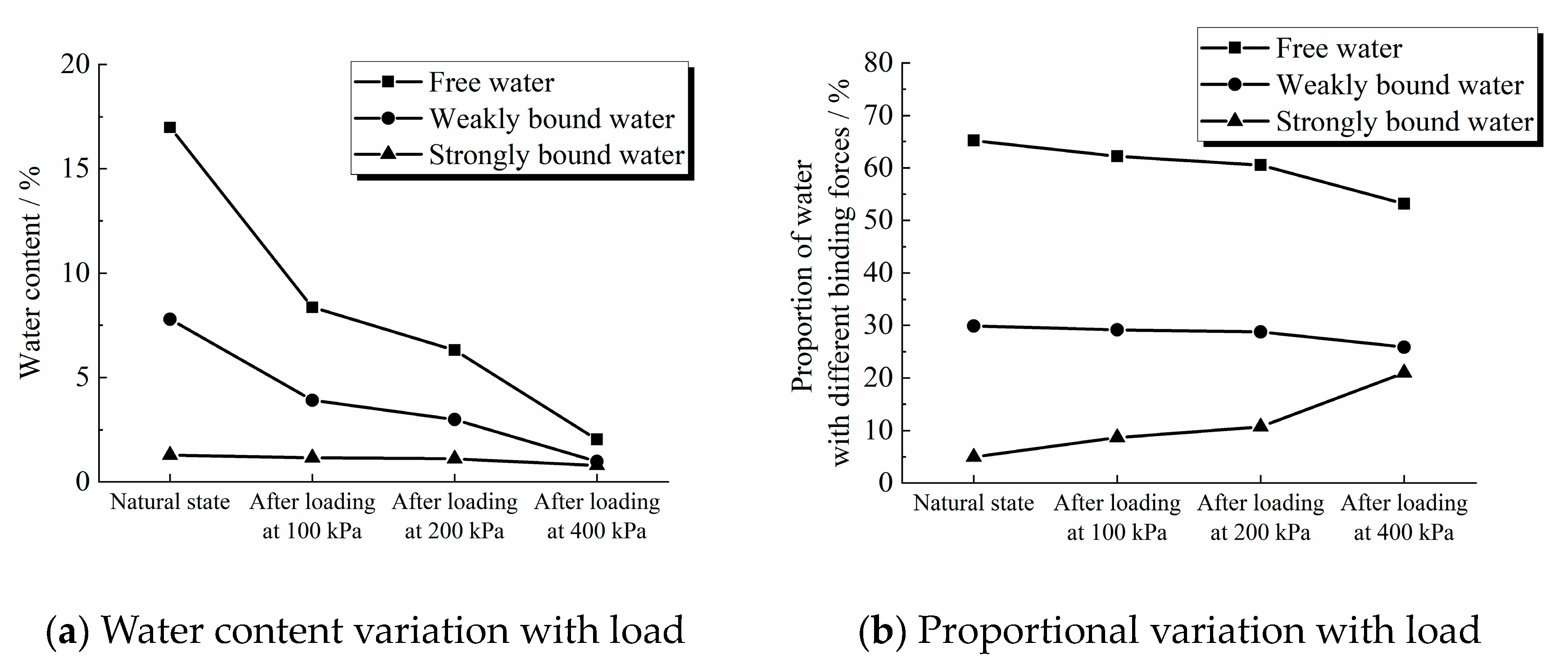
3.2. Analysis of Water Changes in Different Compression Stages of Over-Wet Soil

The strain of soil was significantly affected by water [20]. To further analyze the water variation law with different binding forces during the compression process of excessively wet soil, the durations of the primary and secondary consolidation stages under loads of 200 kPa (below the pre-consolidation pressure) and 400 kPa (above the pre-consolidation pressure) were calculated using compression curve 5. The results are summarized in

Table 7. End time of the three compression stages.

Load/kPa	Primary Consolidation Stage/h	Secondary Consolidation Stage/h	Tertiary Consolidation Stage
200	1.54	10.3	Until deformation stabilizes
400	6.08	359.1

.

A small amount of soil was collected from the consolidated sample at the end of the different stages of thermogravimetric analysis based on the data in Table 7. The test data at 200 kPa are used as an example for the analysis because the variation patterns of all curves are similar, as shown in Figure 14. The Y-axis in Figure 14a represents the percentage of remaining sample mass (TG), while the Y-axis in Figure 14b represents the derivative of the percentage of remaining sample mass (DTG).

As the temperature increases, the mass percentage of over-wet soil rapidly decreases in the early stage of heating (Figure 14a). When the temperature exceeds approximately 60 °C (point A), the weight loss rate of the over-wet soil reduces and remains stable. When the temperature exceeds approximately 110 °C (point B), the rate gradually reduces and stabilizes.

In thermogravimetric analysis, the mass changes during the heating process of a sample are measured, distinguishing different components based on the trough position of the differential curve (DTG). Because the weight loss temperatures of free and bound water in the soil samples were relatively continuous, the DTG curve shows a continuous trough (Figure 14b). Conventional methods cannot accurately distinguish between free and weakly bound water. Therefore, researchers have proposed distinguishing between different types of water in soil using critical temperatures [21,22,23,24]. Li et al. [25] proposed through the analysis of the thermogravimetric curve that free water loses weight before approximately 60 °C, while weakly bound water loses weight between 60 °C and 108 °C. At this point, the TG curve is a straight line, and when the temperature exceeds 108 °C, the main loss is owing to strongly bound water. This conclusion is consistent with the results of wet soil tests. Based on the data presented in Figure 14a, the temperature range for weight loss of free water in over-wet soil is from room temperature to 60 °C, the weight loss temperature range for weakly bound water is from 60 °C to 110 °C, and the weight loss temperature range for strongly bound water is above 110 °C. The variation in water with different binding forces in over-wet soil is calculated as shown in Figure 15.

Figure 15 shows that the changes in free water, weakly bound water, and strongly bound water exhibit strong regularity. Free water decreases significantly in the primary consolidation stage, with an average decrease of approximately 81% (200 kPa) and 64% (400 kPa) for the two sets of data (Figure 15a). However, the decrease in the secondary and tertiary consolidation stages is insignificant. Weakly bound water minimally decreases during the primary consolidation stage (Figure 15b). However, it significantly decreases in the tertiary consolidation stage at approximately 77.9% (200 kPa) and 57.6% (400 kPa) for the two sets of data. Figure 15c shows that the content of strongly bound water is lower than that of free and weakly bound water. However, except for a decrease in the third consolidation stage at 400 kPa, there is almost no change (Figure 15d). Studies have indicated that bound water affects the creep deformation of soil [26,27]. Based on the data in Figure 10 and Figure 13, the discharge of weakly bound water during creep is approximately 15 times that of strongly bound water, indicating that the discharge of weakly bound water is the main cause of creep.

Figure 16a shows the relationship curve between the water content and load for water with different binding forces. According to Equation (5), the proportion of water with different binding forces to the total water content was calculated, and a curve was drawn, as shown in Figure 16b. Equation (5) is as follows:

$$Z={\displaystyle \frac{w_{i,j}}{w_t}}\times 100\mathrm{\%},$$

(5)

where $Z$ = proportion of water with different binding forces (%).

$w_{i,j}$ = water content of the jth type of binding force at the ith load (%).

$w_{i,t}$ = total water content at ith load (%).

Figure 16. Relationship between water and load with different binding forces.

Figure 16. Relationship between water and load with different binding forces.

Figure 16a shows that the free and weakly bound water contents continuously decrease during loading. The decrease at 200 kPa is below that at 400 kPa, and the ratios of the two load levels are 1:2.08 (free water) and 1:2.18 (weakly bound water). The content of strongly bound water minimally changes as the load increases.

Figure 16b shows that despite the content of free and weakly bound water decreasing significantly, their ratio to the total moisture content slightly changed by 9.97% and 4.04%, respectively. However, owing to the insignificant change in the content of strongly bound water, its proportion increased from 4.97% to 20.98%.

Thermogravimetric data indicate that the creep of over-wet soil is related to the discharge of bound water, but researchers have not yet obtained similar research results. In the process of foundation treatment, the effect of reducing post-construction settlement of excessively wet soil can be achieved by accelerating the discharge of weakly bound water.

3.3. Calculation Method for Settlement of Over-Wet Soil

The sample size in conventional one-way compression tests is small. Owing to the size effects, the creep process differs from the actual situation, leading to errors in predicting foundation settlement and causing engineering problems. Therefore, if the creep law of a large sample can be used to correct foundation creep based on the water content, the accuracy of the calculation results can be improved.

Equations (6) and (7) are the layered summation method calculation equations for general foundations [28,29,30], where the compressive modulus $E_s$ is obtained from one-way compression tests, as follows:

$$S={\sum }_{i=1}^n{S}_i,$$

(6)

$$S_i={\displaystyle \frac{1}{E_{si}}}{P}_i{H}_i,$$

(7)

where $S$ = settlement of foundation (m).

$S_i$ = settlement of ith soil layer (m).

$E_{si}$ = compression modulus of the ith soil layer (kPa).

$P_i$ = average stress of the ith soil layer (kPa).

$H_i$ = thickness of the ith soil layer (m).

According to Equations (4), (6) and (7), the settlement calculation equation for an over-wet soil foundation is expressed in the following Equation (8):

$$S_{io}={\sum }_{n=1}^i{(\lambda }_i{w}_i+{\displaystyle \frac{P_i}{{\mathrm{E}}_i}}){·H}_i,$$

(8)

where $S_{io}$ = settlement of the over-wet soil layer (m).

${\lambda }_i$ = creep coefficient of the ith soil layer.

$w_i$ = water content of ith soil layer.

To verify Equation (8), conventional one-way compression tests were conducted using the soil samples listed in Table 3, and the compression data are shown in Figure 17. The compressive moduli of the specimens were calculated using the data in Figure 17 and according to the guidelines given by ASTM [31], as listed in

Table 8. Compressive modulus of over-wet soil.

Number	1	2	3	4	5
$\mathrm{Compression}\mathrm{modulus},E_i$/Mpa	110.5	88.2	62.1	27.0	18.6

.

To simplify the calculation of the creep coefficient $\lambda$ in Equation (8), based on the data in Table 6, the variation law of $\lambda$ with load was analyzed, as shown in Figure 18. Figure 18 shows that as the load increases, $\lambda$ exhibits a typical exponential increase. Equation (9) shows the fitting curve with a correlation coefficient of 0.989, as follows:

$$\lambda =5.0\times {10}^{-21}{P}^{6.57},$$

(9)

where $P$ = load (kPa).

By combining Equations (8) and (9), the calculation equation for the creep strain of over-wet soil can be obtained, as shown in Equation (10).

$$S_{io}=\sum _{n=1}^i(5.0\times {10}^{-21}{P}_i^{6.57}{w}_i+{\displaystyle \frac{P_i}{{\mathrm{E}}_i}}){·H}_i.$$

(10)

Based on Equation (10), the deformations of the large specimens were calculated according to the compression moduli in Table 8. The height of the sample was 320 mm, which meets the requirement of a soil layer thickness of between 0.3 m and 1 m. Figure 19a compares the calculated and measured results. Figure 19b shows the calculation results obtained using the conventional layered summation method (Equations (7) and (8)).

Figure 19a shows that the settlement of the over-wet soil calculated using Equation (10) is consistent with the measured values, with errors within 1 mm and an average error of 0.4 mm, indicating high accuracy. The calculation results of the conventional layered summation method, shown in Figure 19b, differed significantly from the measured values, with a maximum error of 6.3 mm and an average value of 2.3 mm. However, the conventional layered summation method does not calculate creep deformation. Figure 19b shows that the conventional layered summation method is more accurate in predicting non-over-wet soil (number 1). However, for sample 2 with a humidity of 1, its accuracy decreases when the load exceeds the pre-consolidation pressure (400 kPa) because of the significant creep.

Therefore, when evaluating the settlement of over-wet soil foundations, using the conventional layered summation method will seriously underestimate the post-construction settlement of the foundation, mislead the selection of disposal plans, and bring hidden dangers to the construction of the project.

4. Conclusions

This study analyzed the compression process of over-wet soil through compression and thermogravimetric tests of large specimens, clarified the differences in compression laws between large-sized and small-sized specimens, and proposed a calculation method that conforms to the in-situ settlement law. The main conclusions are as follows:

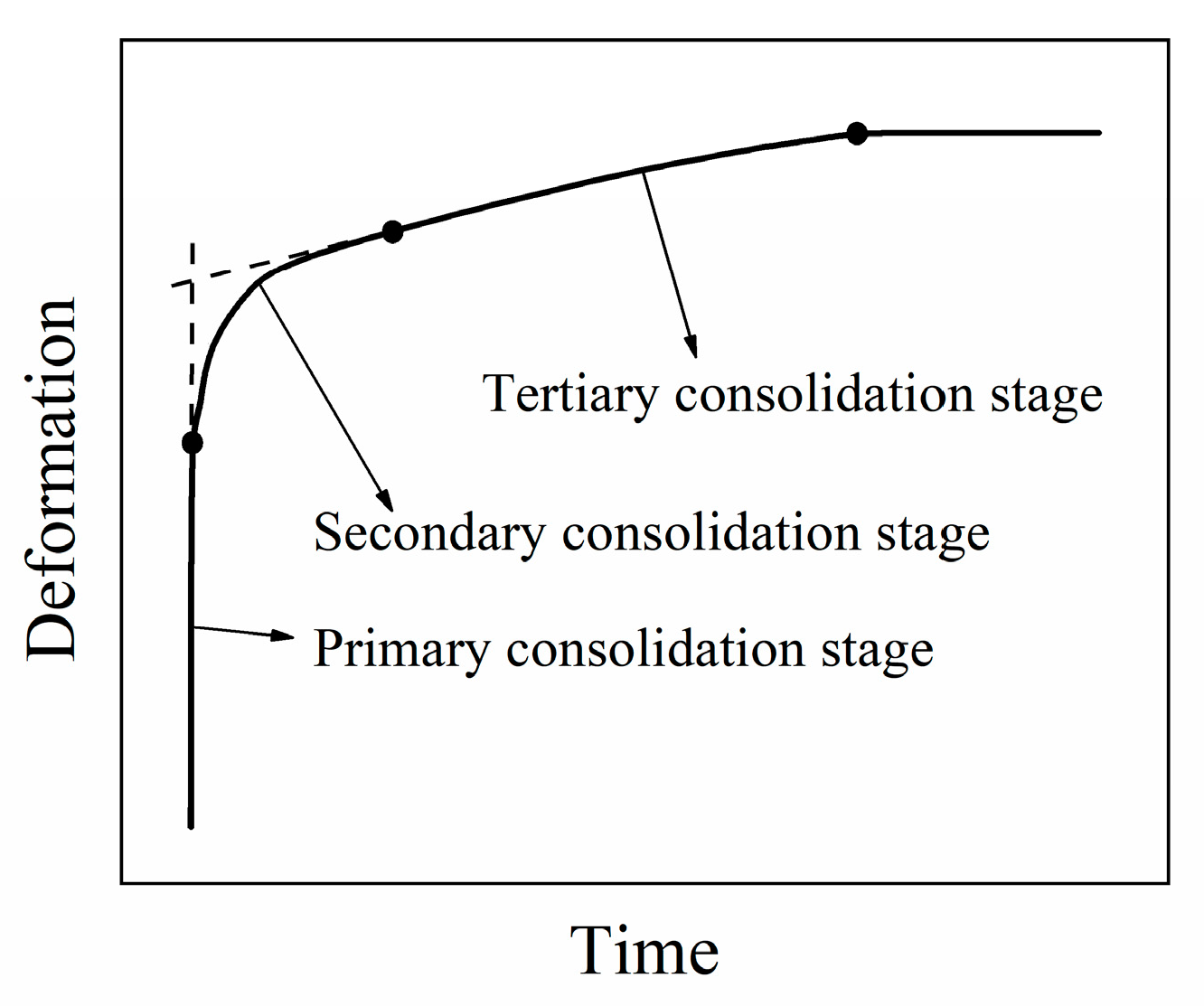
• The $d-\mathrm{l}\mathrm{o}\mathrm{g}t$ curve of the over-wet soil differed significantly from that of general soft soil. The deformation could not be stabilized within a short period. Employing a three-stage compression division method based on the $d-t$ curves is recommended.
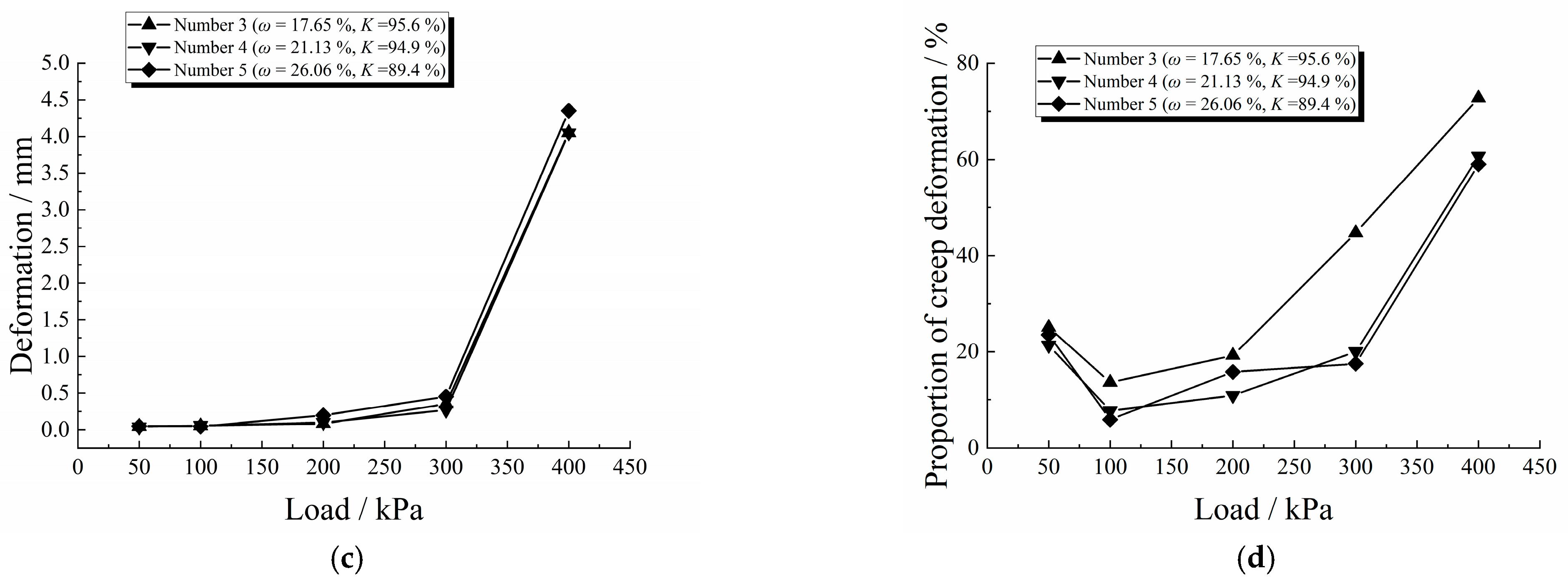
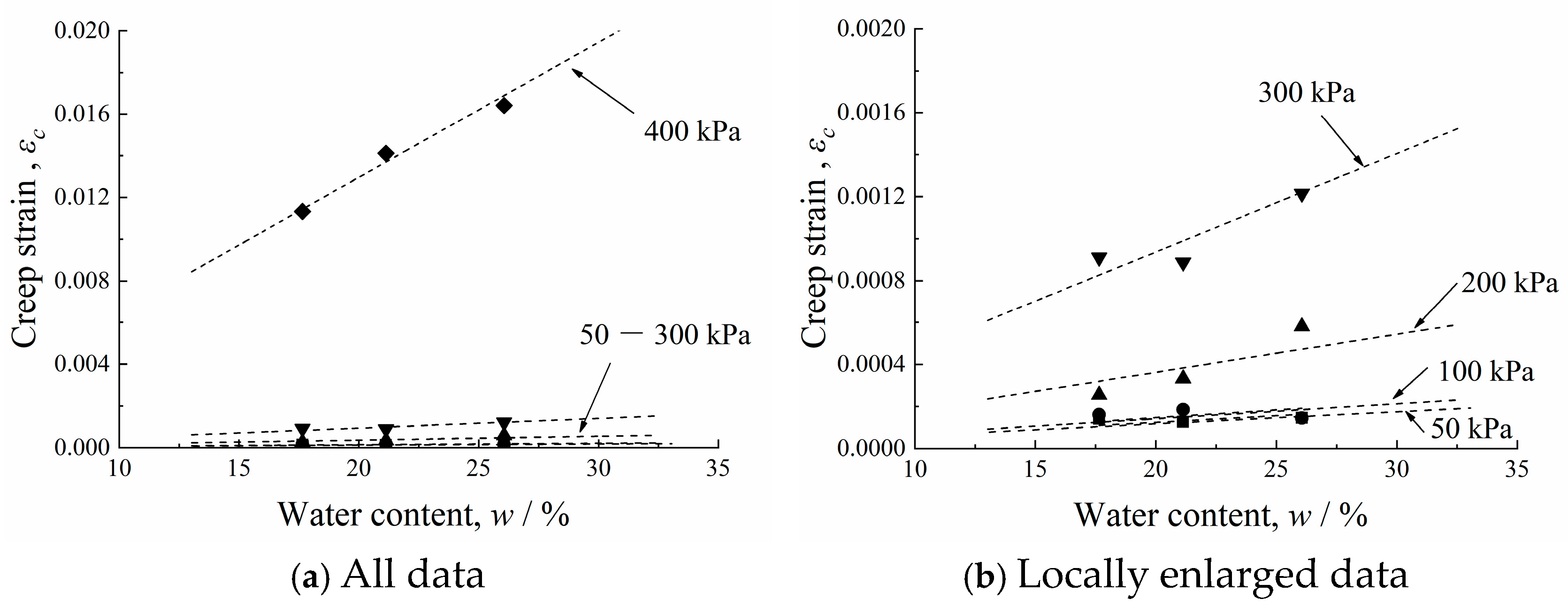
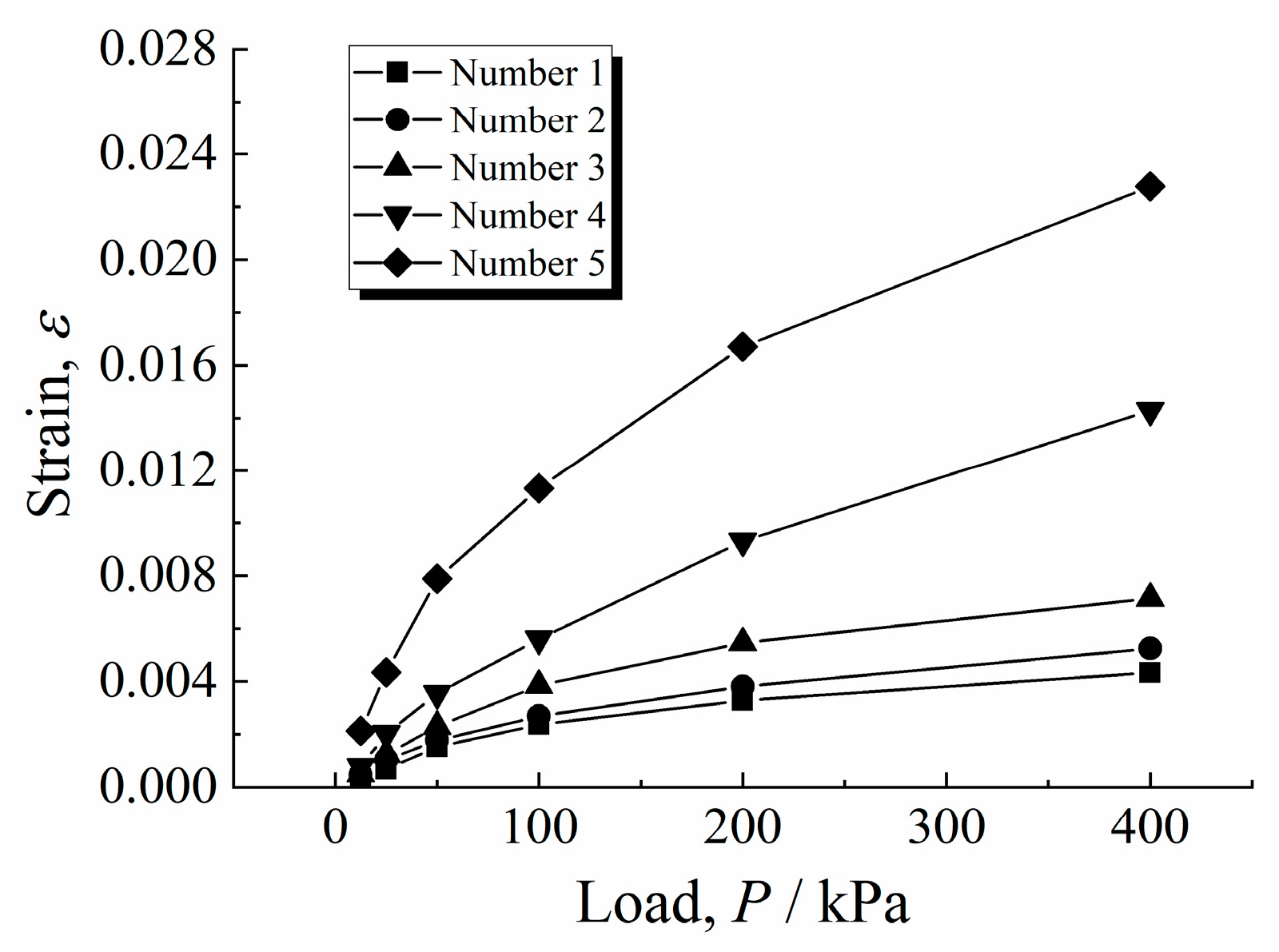
• When the load was below the pre-consolidation pressure, the deformation of the over-wet soil increased as the compaction degree decreased, and the creep deformation was insignificant. When the load exceeded the pre-consolidation pressure, the deformation of the over-wet soil increased as the water content increased. The proportion of creep deformation exceeded 60%.
• Free water in over-wet soil was mainly discharged during the primary consolidation stage. Weakly bound water was mainly discharged during the tertiary consolidation stage, and strongly bound water remained almost unchanged. The large creep deformation of over-wet soil was caused by the discharge of weakly bound water, which was determined by comparing the drainage amounts of weakly bound water and strongly bound water.
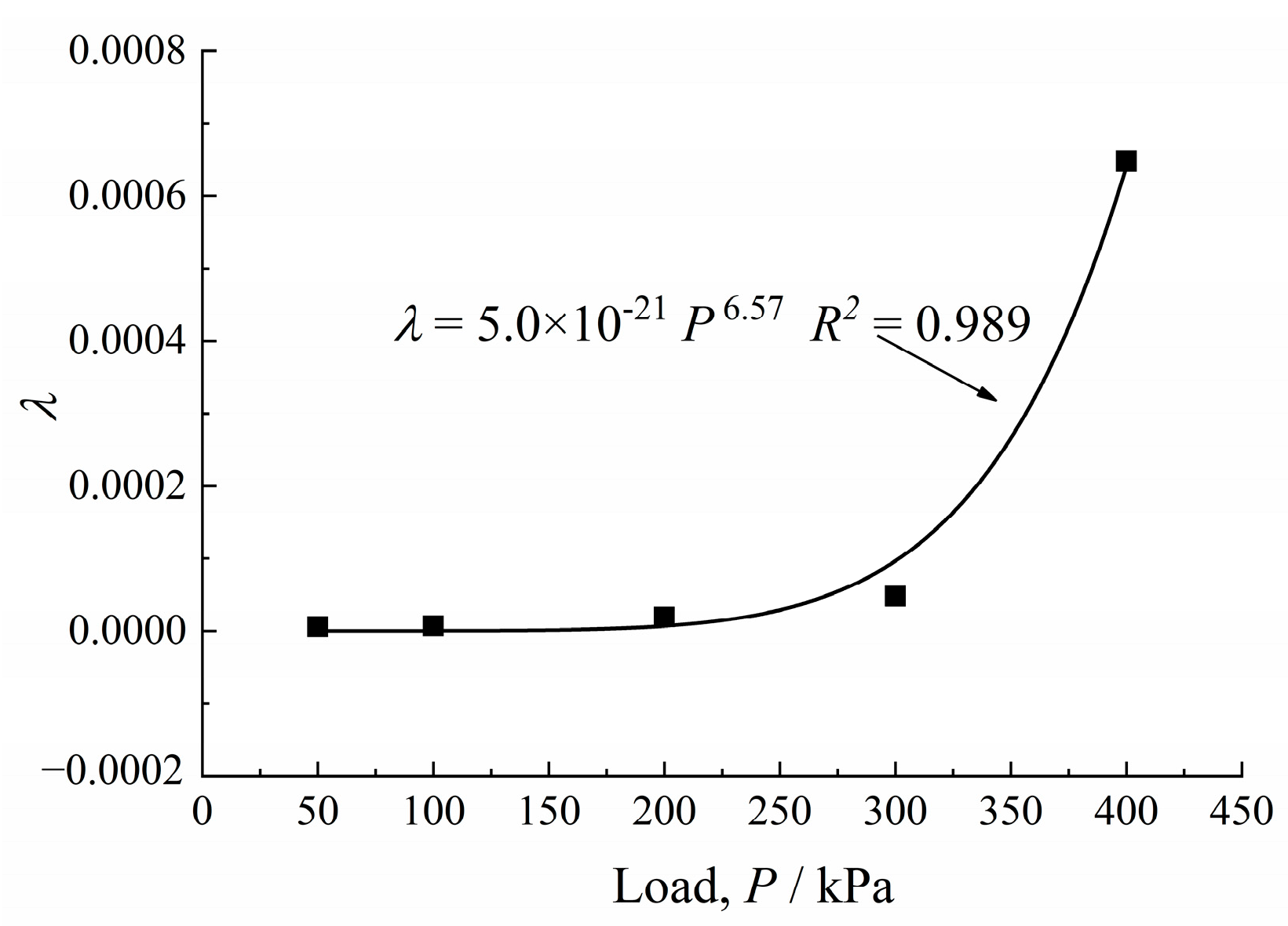
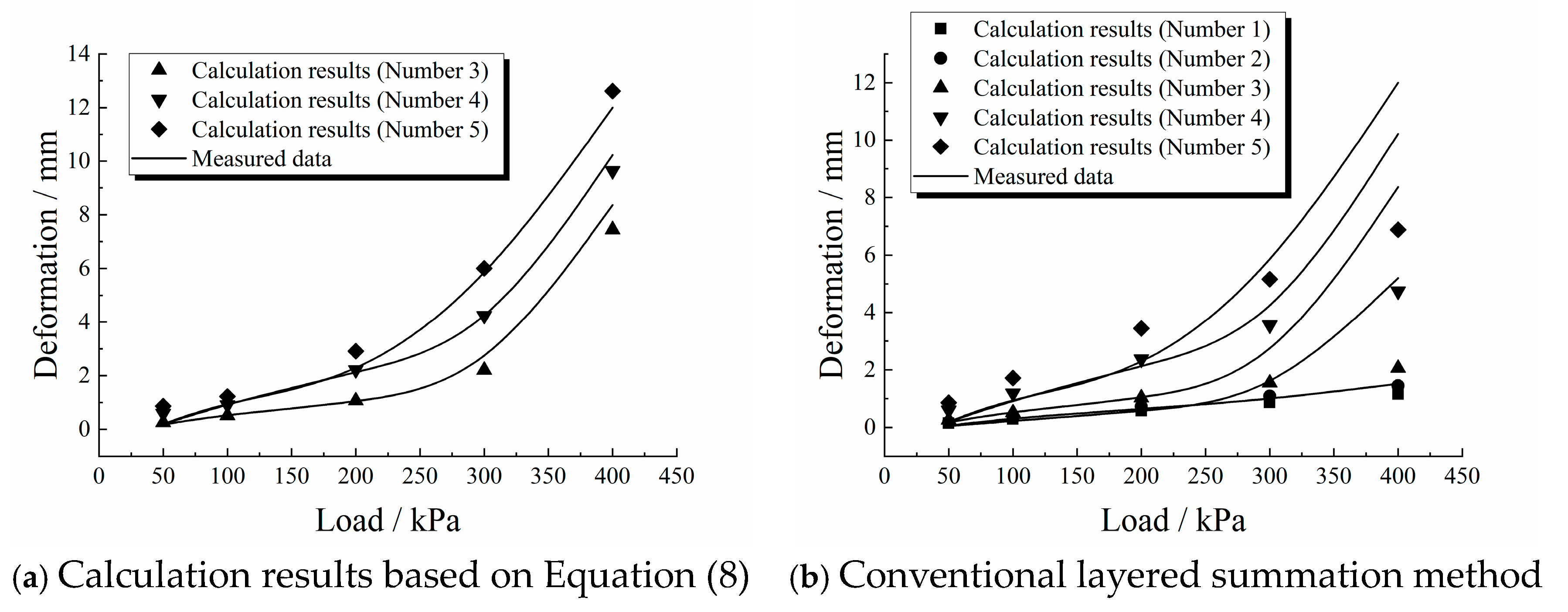
• The creep of the over-wet soil increased linearly with the water content, and its linear correlation coefficient exceeded 0.94. This law was the first to define the creep coefficient. Based on the conventional layered summation method, an exponential relationship between the creep coefficient and load was proposed. Furthermore, a calculation method for the foundation settlement of over-wet soil was established with a higher prediction accuracy than the conventional method.

In this study, in-depth research was conducted on the compression law and settlement of over-wet soil. However, owing to the single source of soil samples, potential deviations may have been present, and further research is needed to determine the applicability of the findings to different types of soils; thus, the study’s universality still needs to be further expanded. In the future, research can be conducted on over-wet soil in different regions to verify the conclusions of this study.