Vehicle Collision Analysis of the Reinforced Concrete Barriers Installed on Bridges Using Node-Independent Model
Abstract
:1. Introduction
2. Materials and Methods
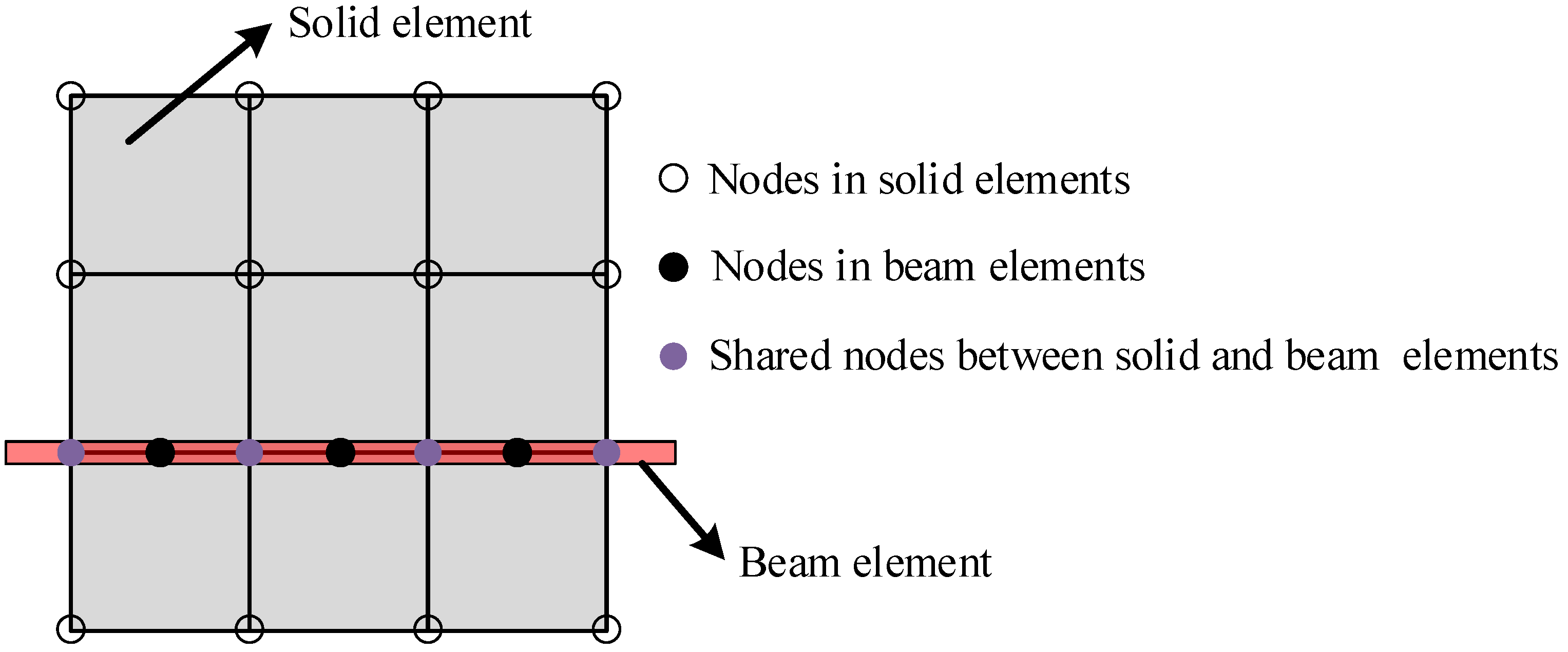
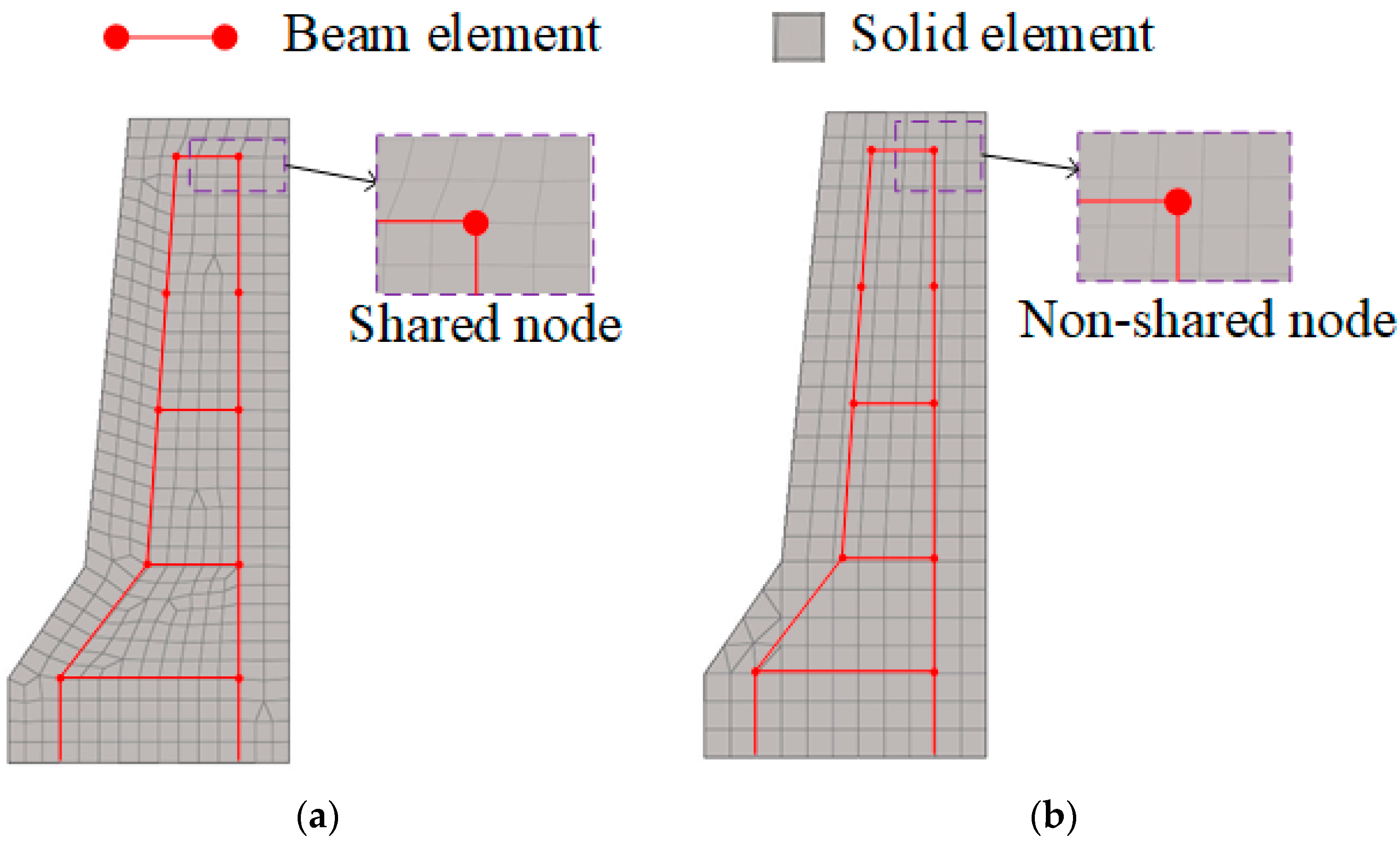
2.1. Node-Independent Model for Reinforced Concrete
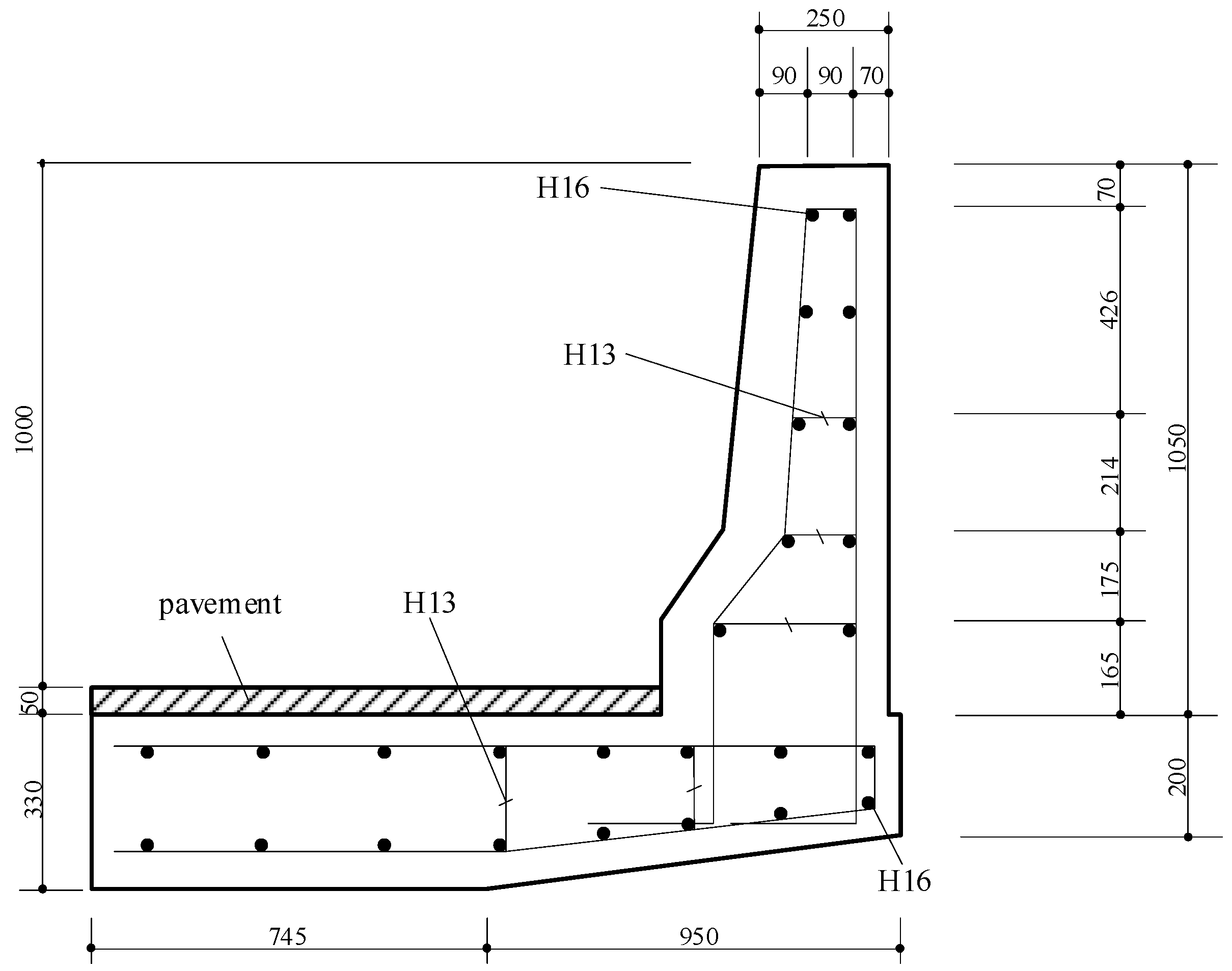
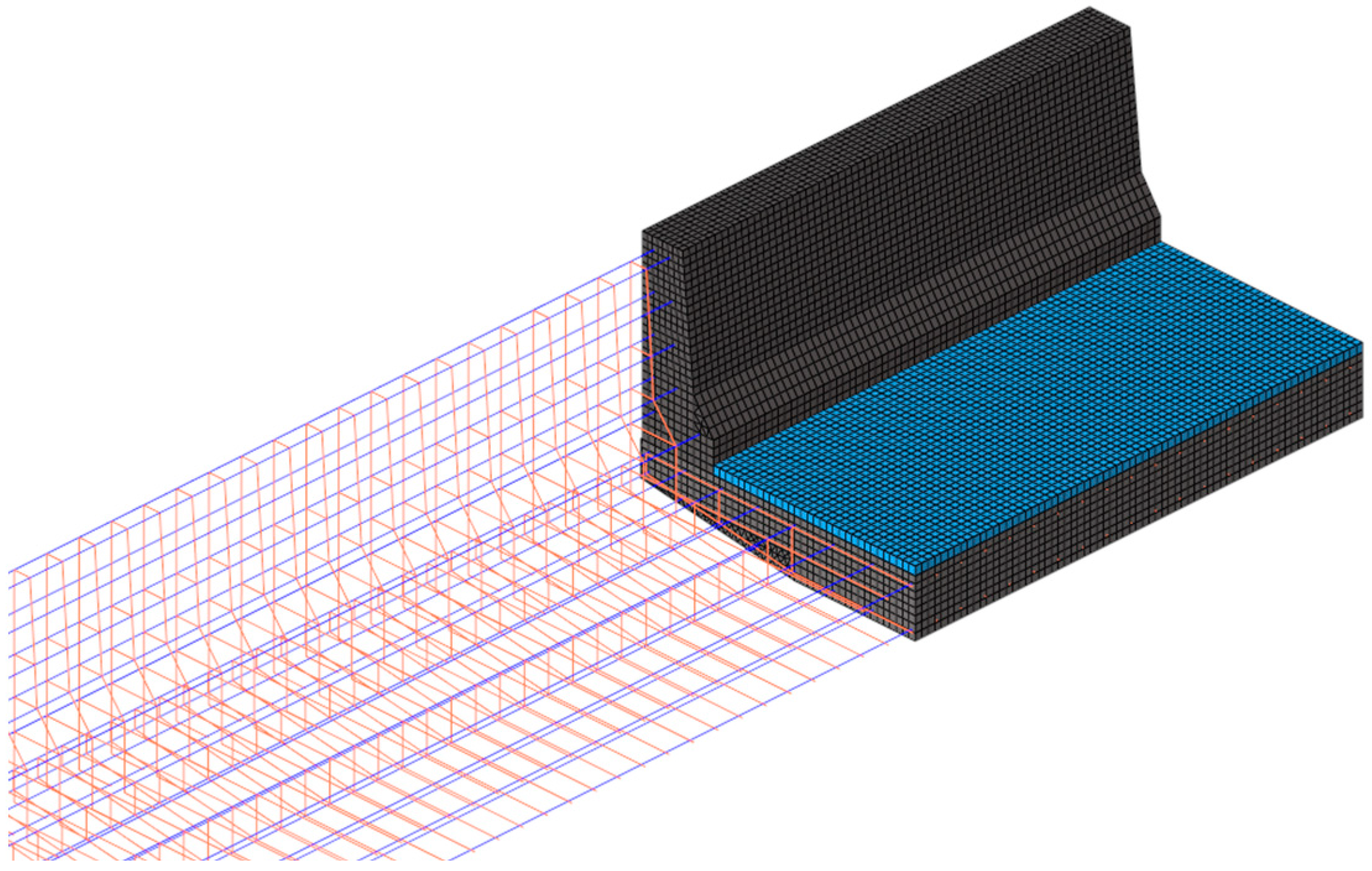
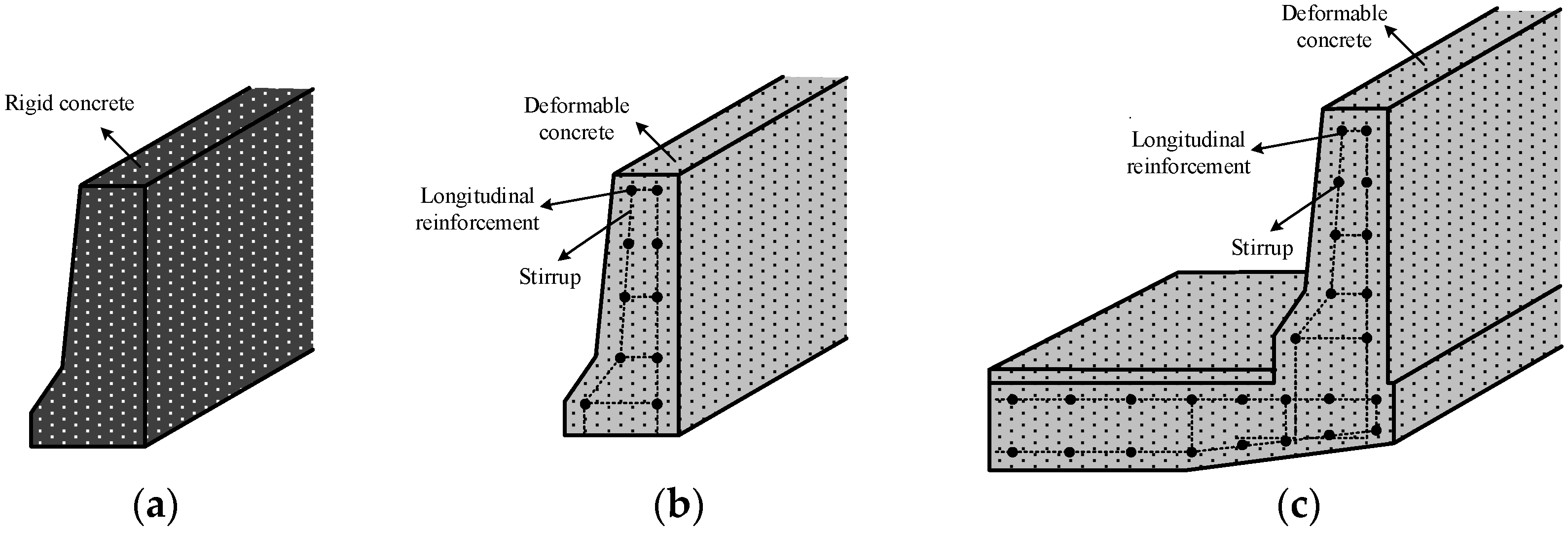
2.2. Modeling of Reinforced Concrete Barriers
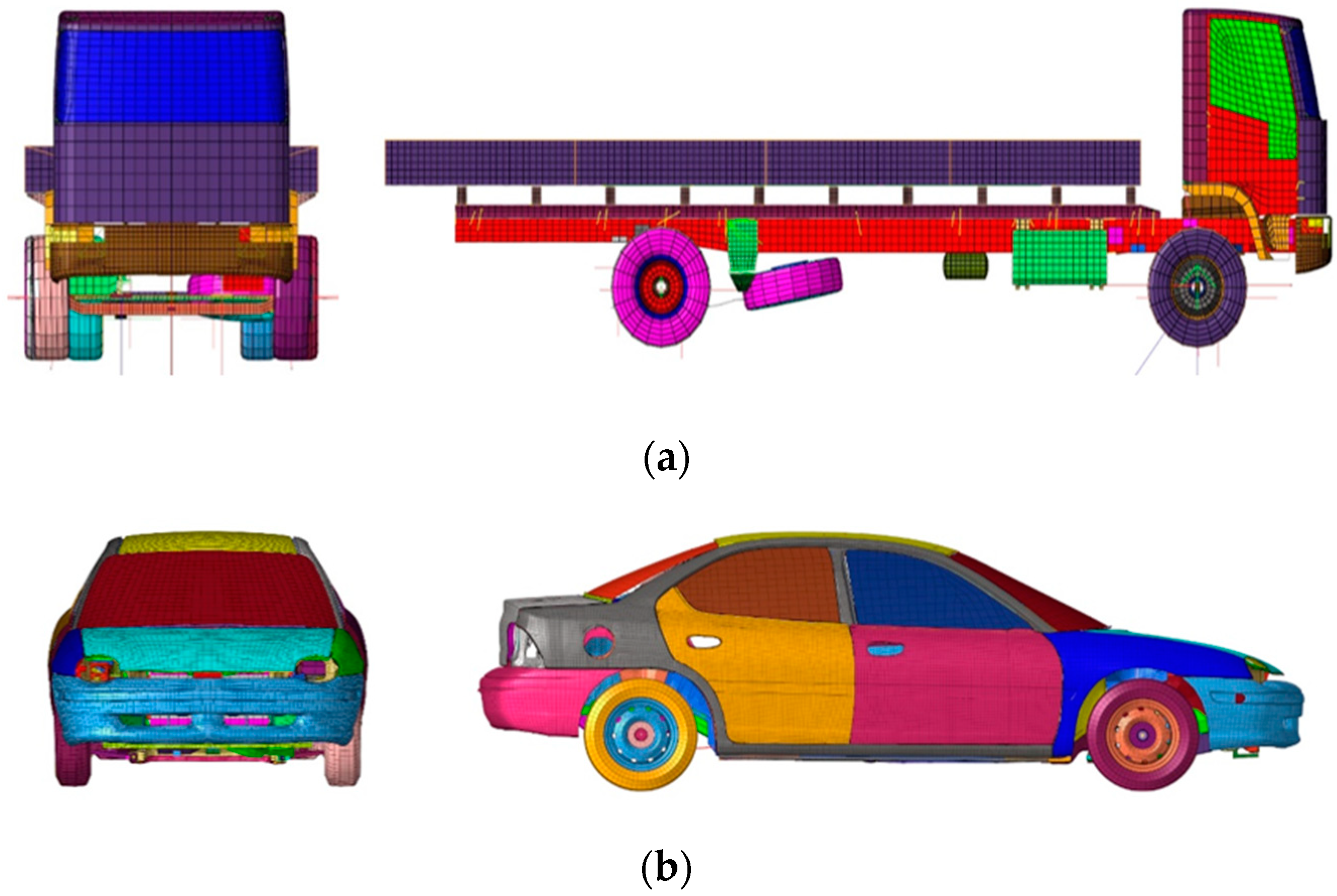
2.3. Vehicle Model
2.4. Material Models for Concrete and Reinforced Steel
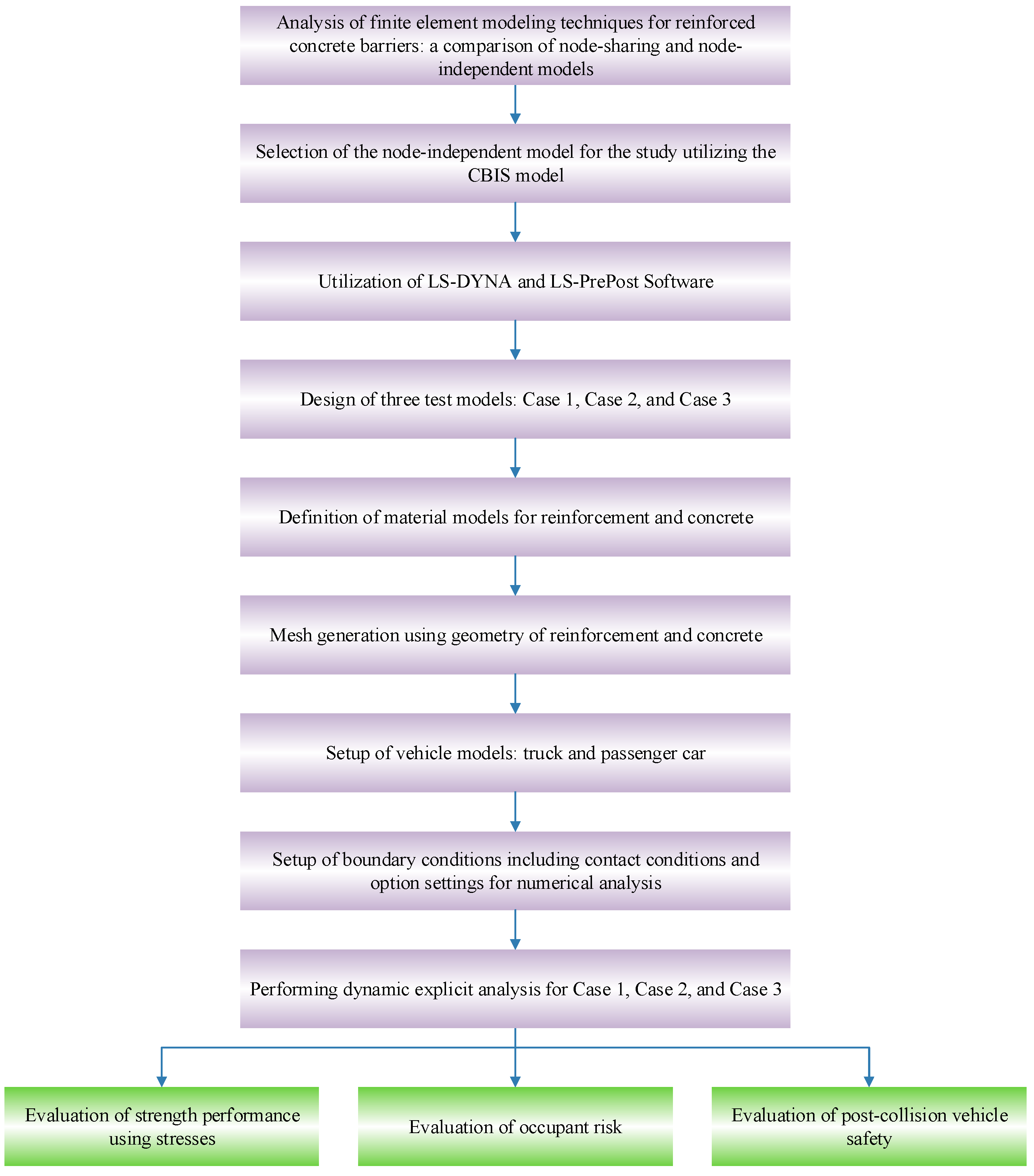
2.5. Overview of the Research Methodology
3. Results
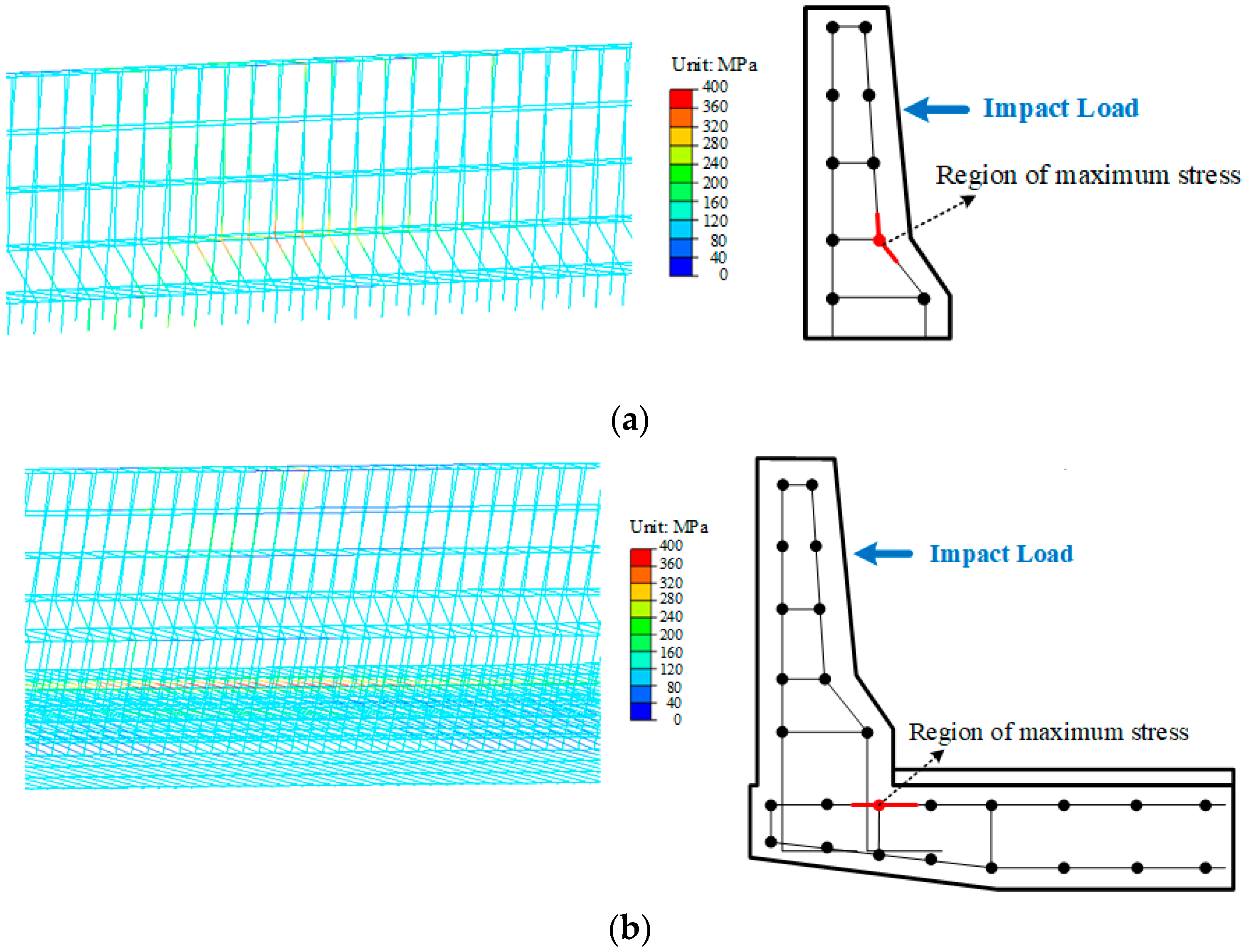
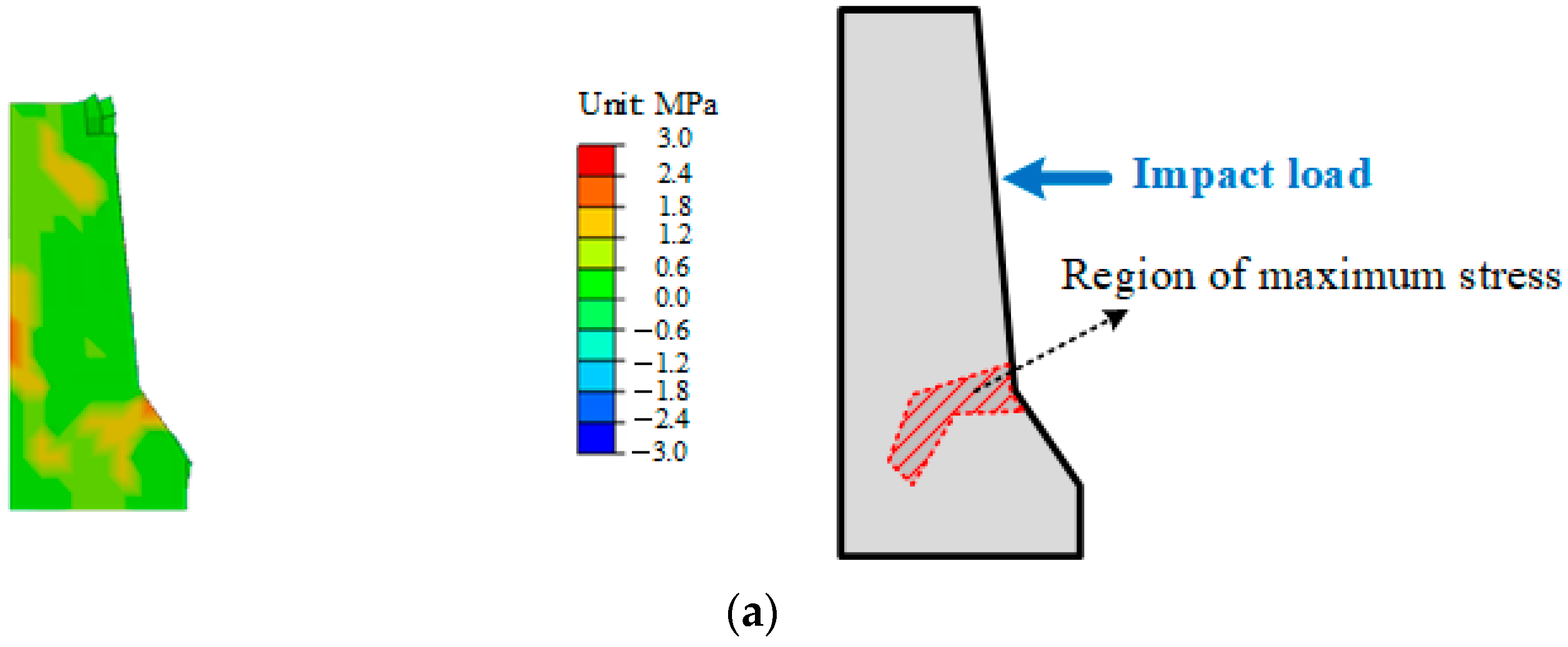
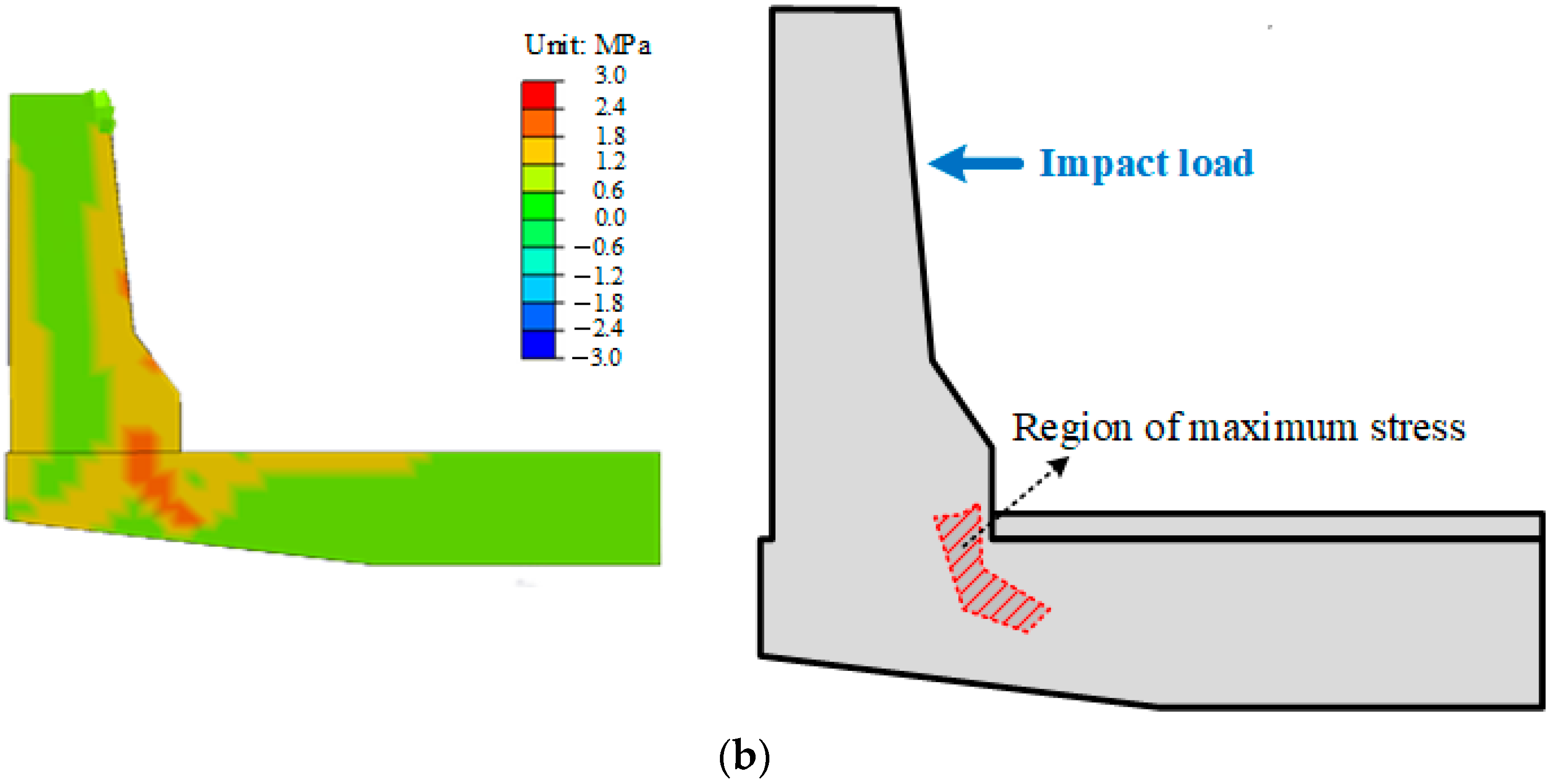
3.1. Evaluation of Strength Performance
3.2. Evaluation of Occupant Risk
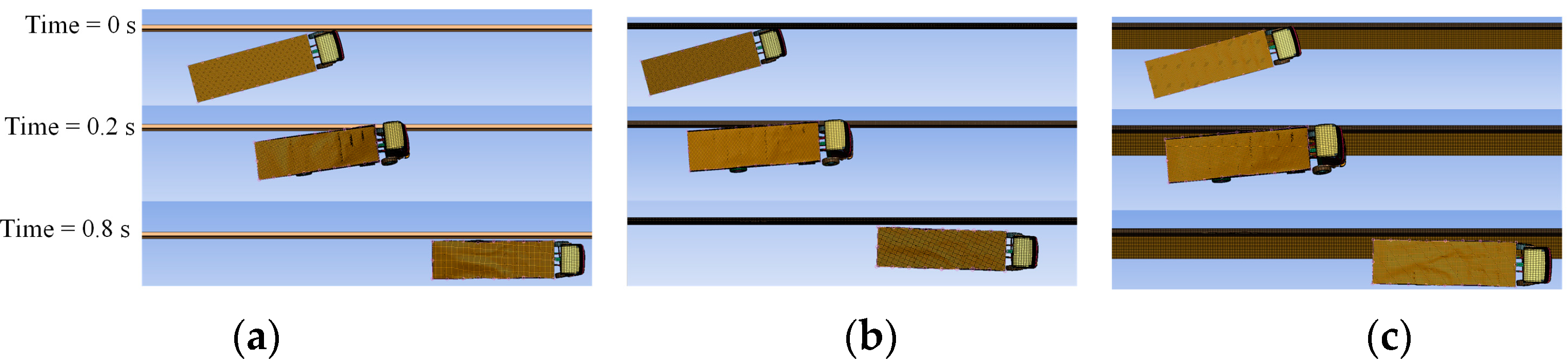
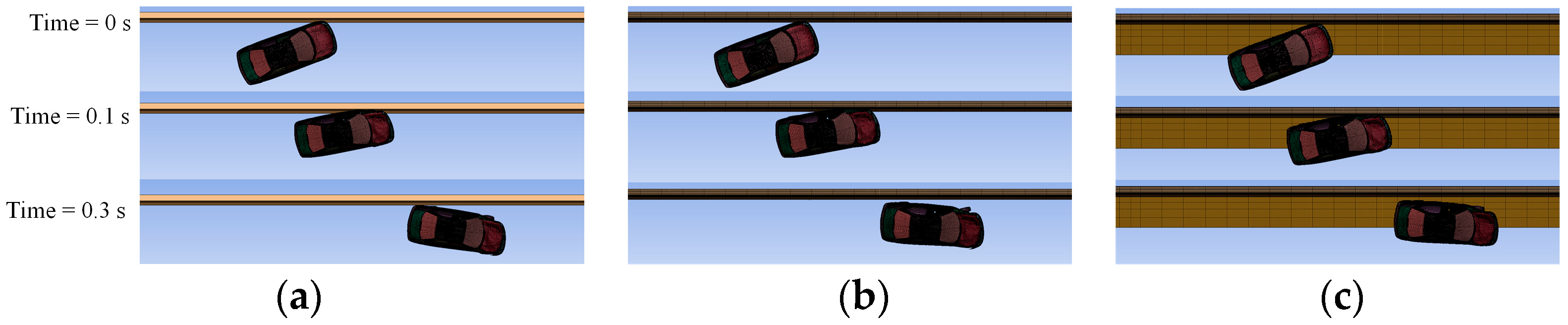
3.3. Evaluation of Post-Collision Vehicle Safety
4. Discussion
5. Conclusions
- This study demonstrates that utilizing a node-independent model for collision analysis of reinforced concrete barriers effectively eliminates the need for node sharing, reducing the time and complexity involved in the modeling process.
- The strength performance comparison between steel reinforcement and concrete revealed differences based on the presence of the bridge deck. Higher stress occurs over a larger area when the bridge deck is included, which is crucial for considering economic efficiency in the design process.
- The assessment of passenger impact severity using THIV and PHD indicators showed that the deformable model with the bridge deck provides more favorable results in terms of passenger safety. This suggests that including the bridge deck in the design may be more advantageous, particularly from an economic standpoint.
- In terms of vehicle stability post-collision, all three models produced similar results. This indicates that an approach assuming the barrier as a rigid body without considering the bridge deck and treating the barrier foundation as a fixed point may be practical. It suggests the potential to efficiently verify vehicle stability without complex modeling analyses.
- These findings provide important guidelines for the design and evaluation of reinforced concrete barriers. Future research should include additional experiments and analyses under various conditions to further validate these results.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xu, X.; Zhang, H.; Du, X.; Liu, Q. Vehicle Collision with RC Structures: A State-of-the-Art Review. Structures 2022, 44, 1617–1635. [Google Scholar] [CrossRef]
- Cao, R.; Agrawal, A.K.; El-Tawil, S.; Wong, W. Numerical Studies on Concrete Barriers Subject to MASH Truck Impact. J. Bridge Eng. 2020, 25, 04020035. [Google Scholar] [CrossRef]
- Cao, R.; Agrawal, A.K.; El-Tawil, S.; Wong, W. Performance-based design framework for concrete barriers subjected to truck collision. J. Bridge Eng. 2021, 26, 04021047. [Google Scholar] [CrossRef]
- Zhao, L.; Karbhari, V.M.; Hegemier, G.A.; Seible, F. Connection of Concrete Barrier Rails to FRP Bridge Decks. Compos. Part B Eng. 2004, 35, 269–278. [Google Scholar] [CrossRef]
- Namy, M.; Charron, J.P.; Massicotte, B. Structural Behavior of Bridge Decks with Cast-in-Place and Precast Concrete Barriers: Numerical Modeling. J. Bridge Eng. 2015, 20, 04015014. [Google Scholar] [CrossRef]
- Sennah, K.; Khederzadeh, H.R. Development of Cost-Effective PL-3 Concrete Bridge Barrier Reinforced with Sand-Coated Glass Fibre Reinforced Polymer (GFRP) Bars: Vehicle Crash Test. Can. J. Civ. Eng. 2014, 41, 357–367. [Google Scholar] [CrossRef]
- Neves, R.R.; Fransplass, H.; Langseth, M.; Driemeier, L.; Alves, M. Performance of Some Basic Types of Road Barriers Subjected to the Collision of a Light Vehicle. J. Braz. Soc. Mech. Sci. Eng. 2018, 40, 274. [Google Scholar] [CrossRef]
- Raj, A.; Nagarajan, P.; Aikot Pallikkara, S. Application of Fiber-Reinforced Rubcrete for Crash Barriers. J. Mater. Civ. Eng. 2020, 32, 04020358. [Google Scholar] [CrossRef]
- Wang, S.; Lei, Z.; Zhao, J.; Li, Y.; Lei, M.; Liu, Y. A Research of Similarity Design of Collision Guardrails under the Overpass. In Proceedings of the 2011 Second International Conference on Mechanic Automation and Control Engineering, Hohhot, China, 15–17 July 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 1903–1906. [Google Scholar] [CrossRef]
- Trajkovski, J.; Ambrož, M.; Kunc, R. The Importance of Friction Coefficient between Vehicle Tyres and Concrete Safety Barrier to Vehicle Rollover: FE Analysis Study. Stroj. Vestn. 2018, 64, 753–762. [Google Scholar] [CrossRef]
- Yang, J.; Xu, G.; Cai, C.S.; Kareem, A. Crash Performance Evaluation of a New Movable Median Guardrail on Highways. Eng. Struct. 2019, 182, 459–472. [Google Scholar] [CrossRef]
- Heng, K.; Li, R.; Li, Z.; Wu, H. Dynamic Responses of Highway Bridge Subjected to Heavy Truck Impact. Eng. Struct. 2021, 232, 111828. [Google Scholar] [CrossRef]
- Karunarathna, S.; Linforth, S.; Kashani, A.; Liu, X.; Ngo, T. Numerical Investigation on the Behaviour of Concrete Barriers Subjected to Vehicle Impacts Using Modified K&C Material Model. Eng. Struct. 2024, 308, 117943. [Google Scholar] [CrossRef]
- Pan, L.; Hao, H.; Cui, J.; Pham, T.M. Numerical Study on Impact Resistance of Rubberised Concrete Roadside Barrier. Adv. Struct. Eng. 2023, 26, 17–35. [Google Scholar] [CrossRef]
- Kotsovos, M.D. Finite-Element Modelling of Structural Concrete: Short-Term Static and Dynamic Loading Conditions; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Mergos, P.E.; Kappos, A.J. A Distributed Shear and Flexural Flexibility Model with Shear-Flexure Interaction for R/C Members Subjected to Seismic Loading. Earthq. Eng. Struct. Dyn. 2008, 37, 1349–1370. [Google Scholar] [CrossRef]
- Saritas, A.; Filippou, F.C. Numerical Integration of a Class of 3D Plastic-Damage Concrete Models and Condensation of 3D Stress–Strain Relations for Use in Beam Finite Elements. Eng. Struct. 2009, 31, 2327–2336. [Google Scholar] [CrossRef]
- Kwak, H.G.; Kim, D.Y. Cracking Behavior of RC Panels Subject to Biaxial Tensile Stresses. Comput. Struct. 2006, 84, 305–317. [Google Scholar] [CrossRef]
- Ahn, J.S.; Woo, K.S.; Basu, P.K.; Park, J.H. p-Version Nonlinear Analysis of RC Beams and Slabs Strengthened with Externally Bonded Plates. Finite Elem. Anal. Des. 2006, 42, 726–739. [Google Scholar] [CrossRef]
- Papanikolaou, V.K.; Kappos, A.J. Numerical Study of Confinement Effectiveness in Solid and Hollow Reinforced Concrete Bridge Piers: Analysis Results and Discussion. Comput. Struct. 2009, 87, 1440–1450. [Google Scholar] [CrossRef]
- Mourlas, C.; Markou, G.; Papadrakakis, M. Accurate and Computationally Efficient Nonlinear Static and Dynamic Analysis of Reinforced Concrete Structures Considering Damage Factors. Eng. Struct. 2019, 178, 258–285. [Google Scholar] [CrossRef]
- Jawdhari, A.; Harik, I. Finite Element Analysis of RC Beams Strengthened in Flexure with CFRP Rod Panels. Constr. Build. Mater. 2018, 163, 751–766. [Google Scholar] [CrossRef]
- Cusson, D.; Repette, W.L. Early-Age Cracking in Reconstructed Concrete Bridge Barrier Walls. ACI Mater. J. 2000, 97, 438–446. [Google Scholar] [CrossRef]
- Chen, H. An Introduction to CONSTRAINED_BEAM_IN_SOLID. FEA Inf. 2016, 5, 79–83. Available online: https://ftp.lstc.com/anonymous/outgoing/hao/cbis/tutorials/CBIS1.pdf (accessed on 1 September 2024).
- Pena, O.; Faller, R.K.; Rasmussen, J.D.; Steelman, J.S.; Rosenbaugh, S.K.; Bielenberg, R.W.; Duren, J.T. Development of a MASH Test Level 4 Steel, Side-Mounted, Beam-and-Post, Bridge Rail; Report No. TRP-03-410-20; Nebraska Transportation Center: Lincoln, NE, USA, 2020. Available online: https://rosap.ntl.bts.gov/view/dot/58330 (accessed on 1 September 2024).
- Ministry of Land, Infrastructure and Transport of the Republic of Korea. Guidelines for Installation and Management of Road Safety Facilities—Vehicle Protection Safety Facilities Section. 2022. Available online: https://www.law.go.kr (accessed on 15 August 2024). (In Korean)
- Hayashi, S.; Chen, H.; Hu, W. Compression Molding Analysis of Long Fiber Reinforced Plastics Using Coupled Method of Beam and 3D Adaptive EFG in LS-DYNA. In Proceedings of the 11th European LS-DYNA Conference, Salzburg, Austria, 9–11 May 2017; Available online: https://ftp.lstc.com/anonymous/outgoing/hao/cbis/tutorials/01_Hayashi_JSOL.pdf (accessed on 15 August 2024).
- Korea Expressway Corporation. Standard Drawings for Highway Construction; Publication No. AN01145-000132-10; Korea Expressway Corporation: Gimcheon-si, Republic of Korea, 2019. (In Korean) [Google Scholar]
- LSTC. LS-PrePost User’s Manual; Version 4.8; Livermore Software Technology Corporation: Livermore, CA, USA, 2023. [Google Scholar]
- Yang, S.H.; Woo, K.S.; Kim, J.J.; Ahn, J.S. Finite Element Analysis of RC Beams by the Discrete Model and CBIS Model Using LS-DYNA. Adv. Civ. Eng. 2021, 2021, 8857491. [Google Scholar] [CrossRef]
- Li, N.; Fang, H.; Zhang, C.; Gutowski, M.; Palta, E.; Wang, Q. A Numerical Study of Occupant Responses and Injuries in Vehicular Crashes into Roadside Barriers Based on Finite Element Simulations. Adv. Eng. Softw. 2015, 90, 22–40. [Google Scholar] [CrossRef]
- Esfahani, E.S.; Marzougui, D.; Opiela, K.S. Safety Performance of Concrete Median Barriers Under Updated Crashworthiness Criteria; No. NCAC 2008-W-002; The National Crash Analysis Center: Ashburn, VA, USA, 2008; Available online: https://citeseerx.ist.psu.edu/document?repid=rep1&type=pdf&doi=d420a3b55f0ae4e4b9463dfd463f4265797d0ac1 (accessed on 15 August 2024).
- LSTC. LS-DYNA Keyword User’s Manual, Volume II; Version 11 R11.0.0; Livermore Software Technology Corporation: Livermore, CA, USA, 2019. [Google Scholar]
- Murray, Y.D.; Abu-Odeh, A.Y.; Bligh, R.P. Evaluation of LS-DYNA Concrete Material Model 159; No. FHWA-HRT-05-063; U.S. Department of Transportation, Federal Highway Administration, Research, Development, and Technology Turner-Fairbank Highway Research Center: McLean, VA, USA, 2007. Available online: https://rosap.ntl.bts.gov/view/dot/38728/dot_38728_DS1.pdf (accessed on 15 August 2024).
- Mohammed, T.A.; Parvin, A. Vehicle bridge pier collision validation analysis and parametric study using multiple impact data. In Proceedings of the 2010 FHWA Bridge Engineering Conference: Highways for LIFE and Accelerated Bridge Construction, Orlando, FL, USA, 8–9 April 2010; Volume 89, pp. 287–294. [Google Scholar]



| Vehicle Type | Impact Speed (km/h) | Impact Angle (°) |
|---|---|---|
| Truck | 80 | 15 |
| Passenger car | 100 | 20 |
| Property | Concrete | Reinforced Steel |
|---|---|---|
| Density (t/mm3) | 2.35 × 10−9 | 7.8 × 10−9 |
| Elastic modulus (MPa) | 28,800 | 200 × 103 |
| Poisson’s ratio | 0.25 | 0.3 |
| Yield strength (MPa) | - | 400 |
| Compressive strength (MPa) | 35 | - |
| Maximum aggregate (mm) | 19 | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, J.J.; Ahn, J.S. Vehicle Collision Analysis of the Reinforced Concrete Barriers Installed on Bridges Using Node-Independent Model. Appl. Sci. 2024, 14, 10518. https://doi.org/10.3390/app142210518
Kim JJ, Ahn JS. Vehicle Collision Analysis of the Reinforced Concrete Barriers Installed on Bridges Using Node-Independent Model. Applied Sciences. 2024; 14(22):10518. https://doi.org/10.3390/app142210518
Chicago/Turabian StyleKim, Jeong J., and Jae S. Ahn. 2024. "Vehicle Collision Analysis of the Reinforced Concrete Barriers Installed on Bridges Using Node-Independent Model" Applied Sciences 14, no. 22: 10518. https://doi.org/10.3390/app142210518
APA StyleKim, J. J., & Ahn, J. S. (2024). Vehicle Collision Analysis of the Reinforced Concrete Barriers Installed on Bridges Using Node-Independent Model. Applied Sciences, 14(22), 10518. https://doi.org/10.3390/app142210518






