Machine Learning Models for Traffic Prediction on Arterial Roads Using Traffic Features and Weather Information
Abstract
:1. Introduction
2. Literature Review
2.1. Parametric Approaches
2.2. Non-Parametric Approaches
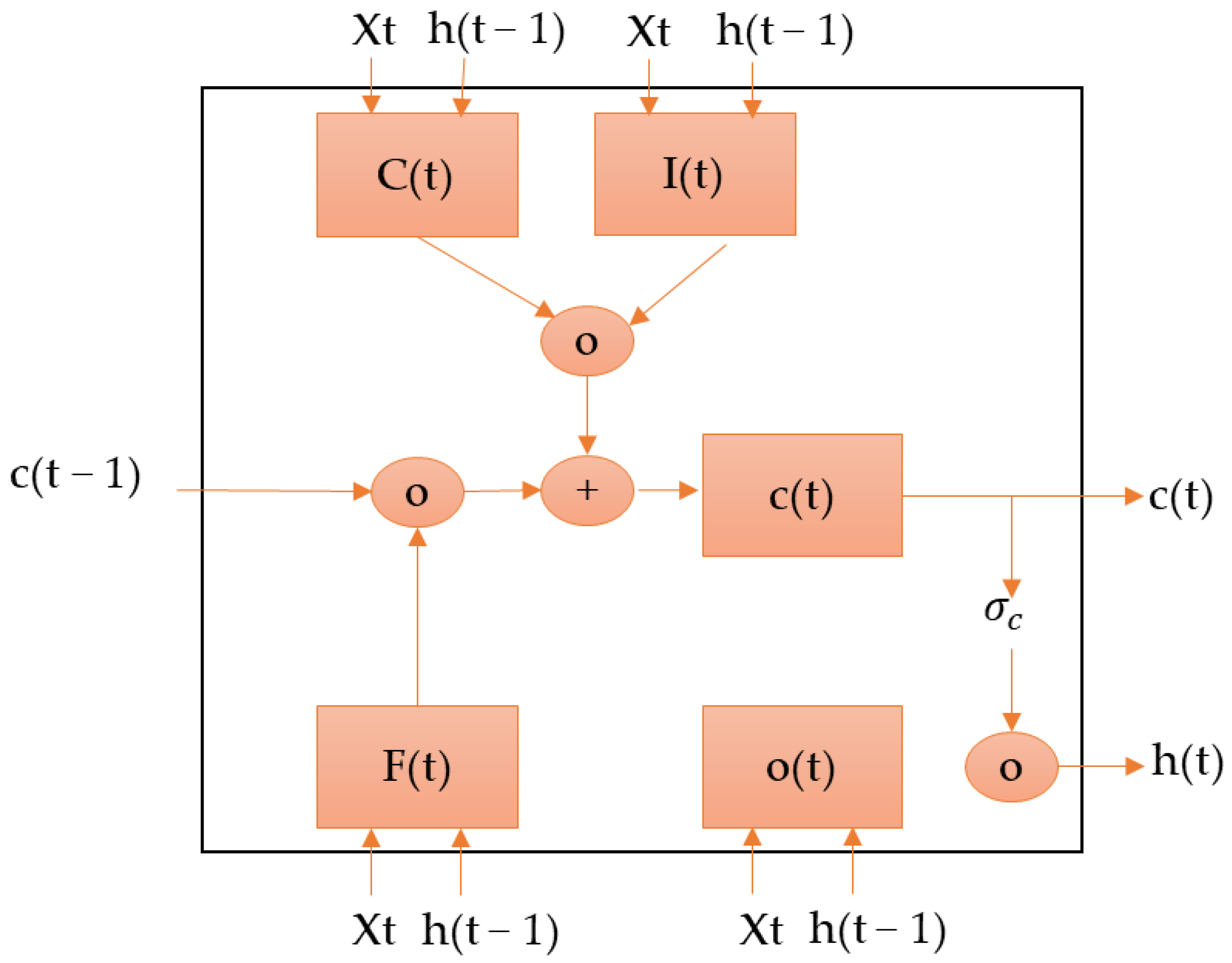
2.3. LSTM Models for Traffic Prediction
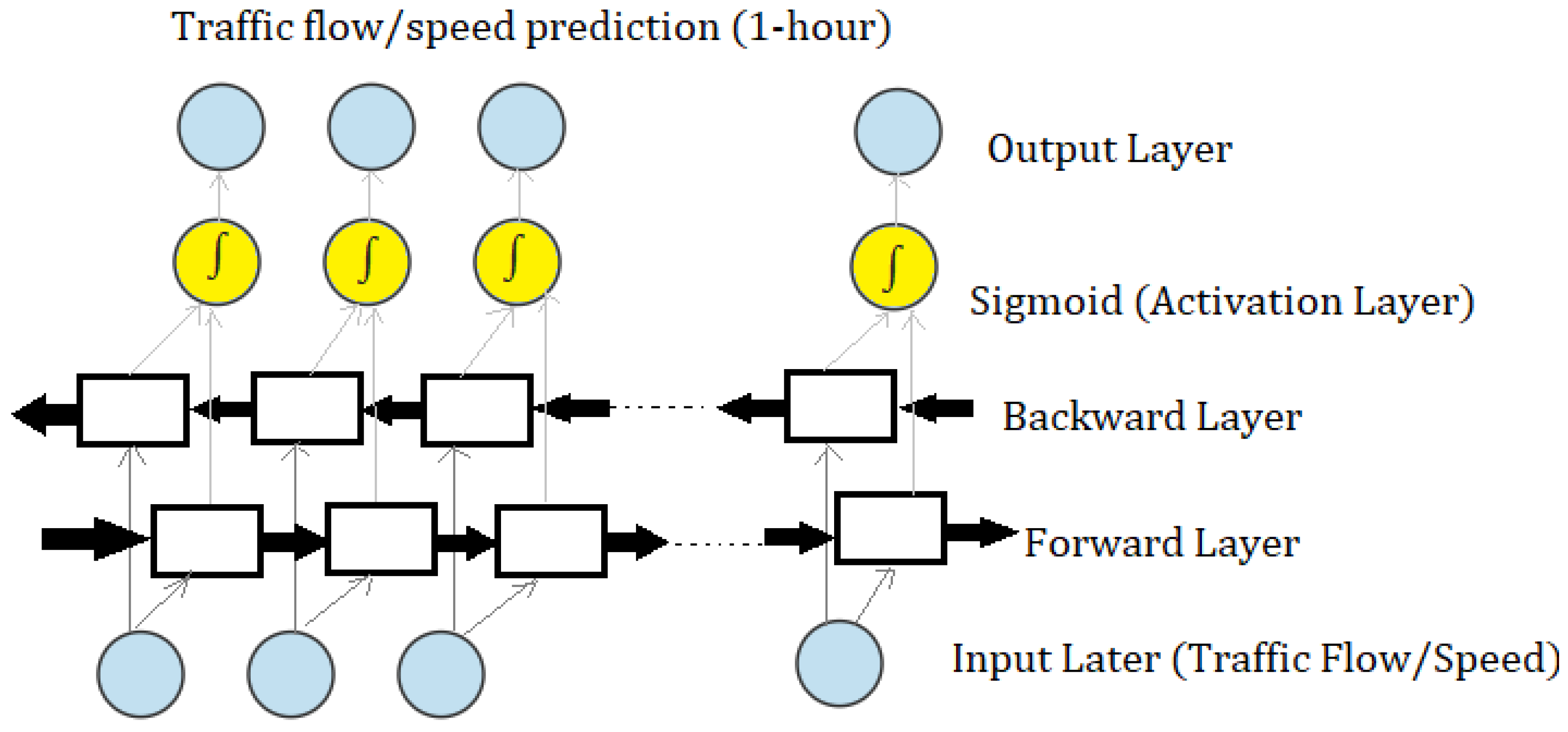
2.4. BiLSTM Models
2.5. Impact of Weather and Incidents
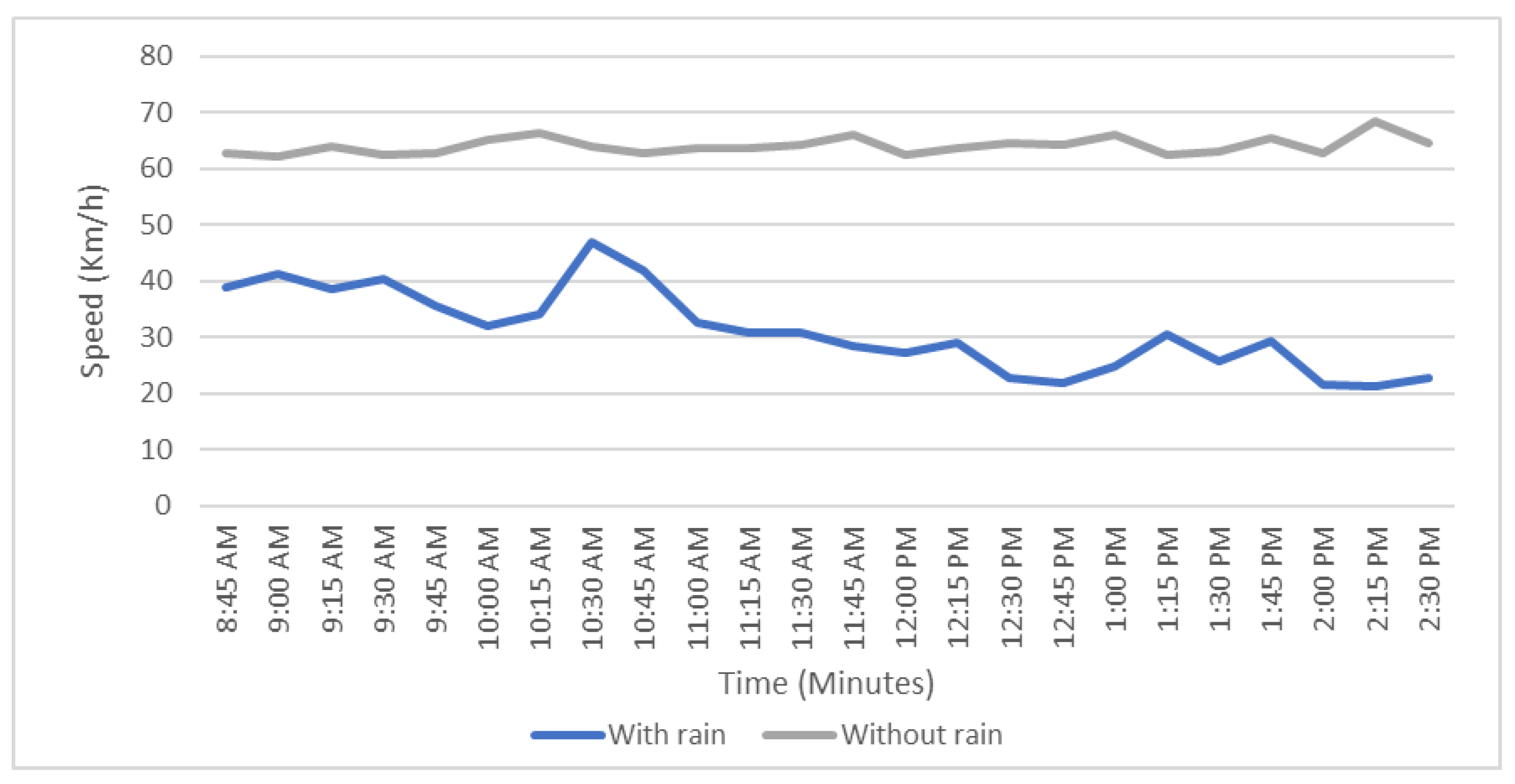
3. Data Collection
3.1. Field Speed and Flow Data
3.2. Weather Data
- Rainfall observation in mm.
- Air temperature in degrees Celsius.
- Relative humidity in percentage %.
- Wind (1 min) speed in km/h.
4. Model Development
- LSTM and BiLSTM were chosen due to their strong ability to capture temporal dependencies and non-linear relationships in traffic data. While LSTM can model long-range dependencies in time-series data, BiLSTM enhances this by learning from past and future time steps, which is particularly beneficial for capturing the bidirectional nature of traffic patterns.
- RNN was used as a baseline model, offering a simple yet effective architecture for time-series forecasting. It was included to benchmark the performance of more complex models like LSTM and BiLSTM.
- Elman networks, a type of simple recurrent neural network, were also evaluated to investigate the performance of less complex models in traffic prediction, providing a reference for comparison with the more advanced models.
- DLBP was included to explore the potential of deep learning-based approaches in handling traffic flow prediction complexities and assess the added value of deeper architectures in this context.
Long Short-Term Memory (LSTM) and Bidirectional Long-Short Term Memory (BiLSTM)
5. Model Evaluation
- Traffic Flow: Measured as the number of vehicles passing a specific point per unit of time.
- Traffic Speed: The average speed of vehicles at each measurement point.
- Time of Day: Categorised as peak or off-peak hours.
5.1. Model Experiment 1: Speed Prediction
5.2. Model Experiment 2: Flow Prediction
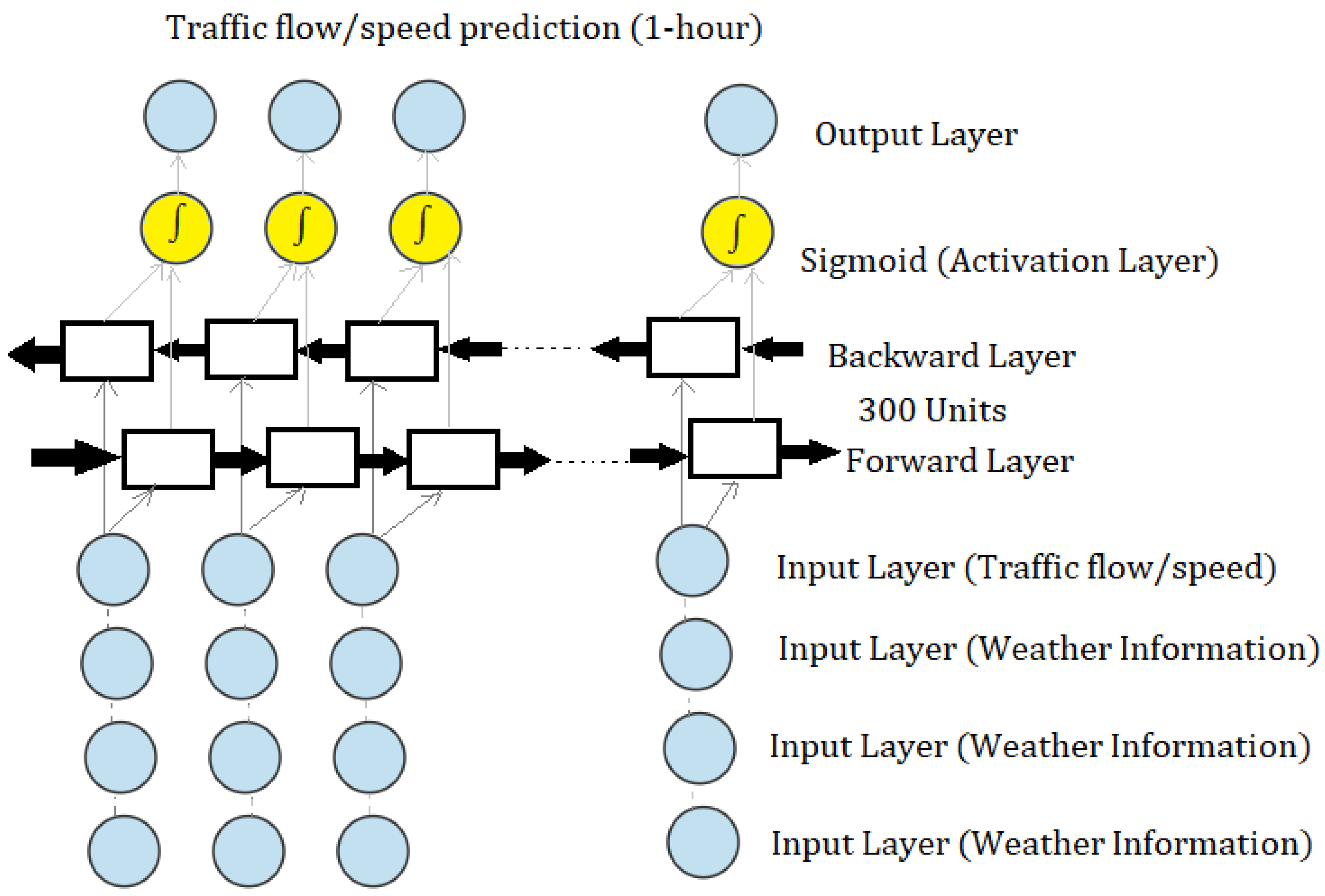
5.3. Model Experiment 3: Weather Integrated Speed Prediction
5.4. Model Experiment 4: Weather Integrated Volume Prediction
6. Analysis of Results
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bartlett, Z.; Han, L.; Nguyen, T.T.; Johnson, P. A machine learning based approach for the prediction of road traffic flow on urbanised arterial roads. In Proceedings of the 2018 IEEE 20th International Conference on High Performance Computing and Communications; IEEE 16th International Conference on Smart City; IEEE 4th International Conference on Data Science and Systems (HPCC/SmartCity/DSS), Exeter, UK, 28–30 June 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1285–1292. [Google Scholar]
- Mackenzie, J.; Roddick, J.F.; Zito, R. An evaluation of HTM and LSTM for short-term arterial traffic flow prediction. IEEE Trans. Intell. Transp. Syst. 2018, 20, 1847–1857. [Google Scholar] [CrossRef]
- Cui, Z.; Ke, R.; Pu, Z.; Wang, Y. Deep bidirectional and unidirectional LSTM recurrent neural network for network-wide traffic speed prediction. arXiv 2018, arXiv:1801.02143. [Google Scholar]
- Cui, Z.; Ke, R.; Pu, Z.; Wang, Y. Stacked bidirectional and unidirectional LSTM recurrent neural network for forecasting network-wide traffic state with missing values. Transp. Res. Part C Emerg. Technol. 2020, 118, 102674. [Google Scholar] [CrossRef]
- Kouziokas, G.N. Deep bidirectional and unidirectional LSTM neural networks in traffic flow forecasting from environmental factors. In Advances in Mobility-as-a-Service Systems, Proceedings of 5th Conference on Sustainable Urban Mobility, Virtual CSUM2020, Volos, Greece, 17–19 June 2020; Springer: Berlin/Heidelberg, Germany, 2021; pp. 171–180. [Google Scholar]
- Lippi, M.; Bertini, M.; Frasconi, P. Short-term traffic flow forecasting: An experimental comparison of time-series analysis and supervised learning. IEEE Trans. Intell. Transp. Syst. 2013, 14, 871–882. [Google Scholar] [CrossRef]
- Lund, R. Time Series Analysis and Its Applications: With R Examples; Taylor & Francis: Abingdon, UK, 2007. [Google Scholar]
- Papageorgiou, M.; Diakaki, C.; Dinopoulou, V.; Kotsialos, A.; Wang, Y. Review of road traffic control strategies. Proc. IEEE 2003, 91, 2043–2067. [Google Scholar] [CrossRef]
- Vlahogianni, E.I.; Karlaftis, M.G.; Golias, J.C. Short-term traffic forecasting: Where we are and where we’re going. Transp. Res. Part C Emerg. Technol. 2014, 43, 3–19. [Google Scholar] [CrossRef]
- Jiang, B.; Fei, Y. Vehicle speed prediction by two-level data driven models in vehicular networks. IEEE Trans. Intell. Transp. Syst. 2016, 18, 1793–1801. [Google Scholar] [CrossRef]
- Song, Z.; Guo, Y.; Wu, Y.; Ma, J. Short-term traffic speed prediction under different data collection time intervals using a SARIMA-SDGM hybrid prediction model. PLoS ONE 2019, 14, e0218626. [Google Scholar] [CrossRef]
- Yang, F.; Yin, Z.; Liu, H.; Ran, B. Online recursive algorithm for short-term traffic prediction. Transp. Res. Rec. 2004, 1879, 1–8. [Google Scholar] [CrossRef]
- Kalman, R.E. A New Approach to Linear Filtering and Prediction Problems. J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef]
- Lv, Y.; Duan, Y.; Kang, W.; Li, Z.; Wang, F.-Y. Traffic flow prediction with big data: A deep learning approach. IEEE Trans. Intell. Transp. Syst. 2014, 16, 865–873. [Google Scholar] [CrossRef]
- Lee, W.H.; Tseng, S.S.; Shieh, J.L.; Chen, H.H. Discovering Traffic Bottlenecks in an Urban Network by Spatiotemporal Data Mining on Location-Based Services. IEEE Trans. Intell. Transp. Syst. 2011, 12, 1047–1056. [Google Scholar] [CrossRef]
- Stathopoulos, A.; Karlaftis, M.G. A multivariate state space approach for urban traffic flow modeling and prediction. Transp. Res. Part C Emerg. Technol. 2003, 11, 121–135. [Google Scholar] [CrossRef]
- Abduljabbar, R.; Dia, H. A deep learning approach for freeway vehicle speed and flow prediction. In Proceedings of the Australasian Transport Research Forum, Canberra, Australia, 30 September–2 October 2019. [Google Scholar]
- Ding, Q.Y.; Wang, X.F.; Zhang, X.Y.; Sun, Z.Q. Forecasting traffic volume with space-time ARIMA model. Adv. Mater. Res. 2011, 156, 979–983. [Google Scholar] [CrossRef]
- Williams, B.M.; Hoel, L.A. Modeling and forecasting vehicular traffic flow as a seasonal ARIMA process: Theoretical basis and empirical results. J. Transp. Eng. 2003, 129, 664–672. [Google Scholar] [CrossRef]
- Karlaftis, M.G.; Vlahogianni, E.I. Statistical methods versus neural networks in transportation research: Differences, similarities and some insights. Transp. Res. Part C Emerg. Technol. 2011, 19, 387–399. [Google Scholar] [CrossRef]
- Dia, H.; Rose, G. Development and evaluation of neural network freeway incident detection models using field data. Transp. Res. Part C Emerg. Technol. 1997, 5, 313–331. [Google Scholar] [CrossRef]
- Thomas, K.; Dia, H. Comparative Evaluation of Freeway Incident Detection Models Using Field Data. In IEE Proceedings-Intelligent Transport Systems; IET: Stevenage, UK, 2006; Volume 153, pp. 230–241. [Google Scholar]
- Thomas, K.; Dia, H. Neural network incident detection on arterials using fusion of simulated probe vehicle and loop detector data. In Proceedings of the 12th ITS World Congress, San Francisco, CA, USA, 6–10 November 2005; pp. 1–12. [Google Scholar]
- Thomas, K.; Dia, H.; Cottman, N. Simulation of arterial incident detection using neural networks. In Proceedings of the 8th World Congress on Intelligent Transport Systems, Sydney, Australia, 30 September–4 October 2001. [Google Scholar]
- CVan Hinsbergen, I.; Van Lint, J.; Van Zuylen, H. Bayesian committee of neural networks to predict travel times with confidence intervals. Transp. Res. Part C Emerg. Technol. 2009, 17, 498–509. [Google Scholar] [CrossRef]
- Ahmed, M.S.; Cook, A.R. Analysis of Freeway Traffic Time-Series Data by Using Box-Jenkins Techniques; Transportation Research Board: Washington, DC, USA, 1979. [Google Scholar]
- Guo, J.; Huang, W.; Williams, B.M. Adaptive Kalman filter approach for stochastic short-term traffic flow rate prediction and uncertainty quantification. Transp. Res. Part C Emerg. Technol. 2014, 43, 50–64. [Google Scholar] [CrossRef]
- Davis, G.A.; Nihan, N.L. Nonparametric regression and short-term freeway traffic forecasting J. Transp. Eng. 1991, 117, 178–188. [Google Scholar] [CrossRef]
- Chan, K.Y.; Dillon, T.S.; Singh, J.; Chang, E. Neural-network-based models for short-term traffic flow forecasting using a hybrid exponential smoothing and Levenberg–Marquardt algorithm. IEEE Trans. Intell. Transp. Syst. 2011, 13, 644–654. [Google Scholar] [CrossRef]
- Zahid, M.; Chen, Y.; Jamal, A.; Mamadou, C.Z. Freeway short-term travel speed prediction based on data collection time-horizons: A fast forest quantile regression approach. Sustainability 2020, 12, 646. [Google Scholar] [CrossRef]
- Fusco, G.; Colombaroni, C.; Isaenko, N. Short-term speed predictions exploiting big data on large urban road networks. Transp. Res. Part C Emerg. Technol. 2016, 73, 183–201. [Google Scholar] [CrossRef]
- Karlaftis, M.G.; Vlahogianni, E.I. Memory properties and fractional integration in transportation time-series. Transp. Res. Part C Emerg. Technol. 2009, 17, 444–453. [Google Scholar] [CrossRef]
- Kashinath, S.A.; Mostafa, S.A.; Mustapha, A.; Mahdin, H.; Lim, D.; Mahmoud, M.A.; Mohammed, M.A.; Al-Rimy, B.A.S.; Fudzee, M.F.M.; Yang, T.J. Review of Data Fusion Methods for Real-Time and Multi-Sensor Traffic Flow Analysis. IEEE Access 2021, 9, 51258–51276. [Google Scholar] [CrossRef]
- Ross, P. Exponential Filtering of Traffic Data; Transportation Research Board: Washington, DC, USA, 1982. [Google Scholar]
- Dougherty, M. A review of neural networks applied to transport. Transp. Res. Part C Emerg. Technol. 1995, 3, 247–260. [Google Scholar] [CrossRef]
- Sivaraman, S.; Trivedi, M.M. Real-time vehicle detection using parts at intersections. In Proceedings of the 2012 15th International IEEE Conference on Intelligent Transportation Systems, Anchorage, AK, USA, 16–19 September 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 1519–1524. [Google Scholar]
- Gu, Y.; Lu, W.; Qin, L.; Li, M.; Shao, Z. Short-term prediction of lane-level traffic speeds: A fusion deep learning model. Transp. Res. Part C Emerg. Technol. 2019, 106, 1–16. [Google Scholar] [CrossRef]
- Castro-Neto, M.; Jeong, Y.-S.; Jeong, M.-K.; Han, L.D. Online-SVR for short-term traffic flow prediction under typical and atypical traffic conditions. Expert Syst. Appl. 2009, 36, 6164–6173. [Google Scholar] [CrossRef]
- Smith, B.L.; Demetsky, M.J. Short-term traffic flow prediction models-a comparison of neural network and nonparametric regression approaches. In Proceedings of the IEEE International Conference on Systems, Man and Cybernetics, San Antonio, TX, USA, 2–5 October 1994; IEEE: Piscataway, NJ, USA, 1994; Volume 2, pp. 1706–1709. [Google Scholar]
- Sun, C.; Hu, X.; Moura, S.J.; Sun, F. Velocity predictors for predictive energy management in hybrid electric vehicles. IEEE Trans. Control. Syst. Technol. 2014, 23, 1197–1204. [Google Scholar]
- Chen, C.; Hu, J.; Meng, Q.; Zhang, Y. Short-time traffic flow prediction with ARIMA-GARCH model. In Proceedings of the 2011 IEEE Intelligent Vehicles Symposium (IV), Baden-Baden, Germany, 5–9 June 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 607–612. [Google Scholar]
- Vanajakshi, L.; Rilett, L.R. Support vector machine technique for the short term prediction of travel time. In Proceedings of the 2007 IEEE Intelligent Vehicles Symposium, Istanbul, Turkey, 13–15 June 2007; IEEE: Piscataway, NJ, USA, 2007; pp. 600–605. [Google Scholar]
- Wang, J.; Shi, Q. Short-term traffic speed forecasting hybrid model based on chaos–wavelet analysis-support vector machine theory. Transp. Res. Part C Emerg. Technol. 2013, 27, 219–232. [Google Scholar] [CrossRef]
- Laña, I.; Lobo, J.L.; Capecci, E.; Del Ser, J.; Kasabov, N. Adaptive long-term traffic state estimation with evolving spiking neural networks. Transp. Res. Part C Emerg. Technol. 2019, 101, 126–144. [Google Scholar] [CrossRef]
- Li, L.; Qin, L.; Qu, X.; Zhang, J.; Wang, Y.; Ran, B. Day-ahead traffic flow forecasting based on a deep belief network optimized by the multi-objective particle swarm algorithm. Knowl.-Based Syst. 2019, 172, 1–14. [Google Scholar] [CrossRef]
- Kuang, X.; Xu, L.; Huang, Y.; Liu, F. Real-time forecasting for short-term traffic flow based on general regression neural network. In Proceedings of the 2010 8th World Congress on Intelligent Control and Automation, Jinan, China, 7–9 July 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 2776–2780. [Google Scholar]
- Lefèvre, S.; Sun, C.; Bajcsy, R.; Laugier, C. Comparison of parametric and non-parametric approaches for vehicle speed prediction. In Proceedings of the 2014 American Control Conference, Portland, OR, USA, 4–6 June 2014; IEEE: Piscataway, NJ, USA, 2010; pp. 3494–3499. [Google Scholar]
- Ma, X.; Dai, Z.; He, Z.; Ma, J.; Wang, Y.; Wang, Y. Learning traffic as images: A deep convolutional neural network for large-scale transportation network speed prediction. Sensors 2017, 17, 818. [Google Scholar] [CrossRef]
- Manibardo, E.L.; Laña, I.; Del Ser, J. Deep learning for road traffic forecasting: Does it make a difference? IEEE Trans. Intell. Transp. Syst. 2021, 23, 6164–6188. [Google Scholar] [CrossRef]
- Gers, F.A.; Schmidhuber, J.; Cummins, F. Learning to forget: Continual prediction with LSTM. Neural Comput. 2000, 12, 2451–2471. [Google Scholar] [CrossRef]
- Guo, J.; Luo, Y.; Li, K. Adaptive neural-network sliding mode cascade architecture of longitudinal tracking control for unmanned vehicles. Nonlinear Dyn. 2017, 87, 2497–2510. [Google Scholar] [CrossRef]
- Yeon, K.; Min, K.; Shin, J.; Sunwoo, M.; Han, M. Ego-vehicle speed prediction using a long short-term memory based recurrent neural network. Int. J. Automot. Technol. 2019, 20, 713–722. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Li, Y.; Yu, R.; Shahabi, C.; Liu, Y. Diffusion convolutional recurrent neural network: Data-driven traffic forecasting. arXiv 2017, arXiv:1707.01926. [Google Scholar]
- Morton, J.; Wheeler, T.A.; Kochenderfer, M.J. Analysis of recurrent neural networks for probabilistic modeling of driver behavior. IEEE Trans. Intell. Transp. Syst. 2016, 18, 1289–1298. [Google Scholar] [CrossRef]
- Abduljabbar, R.L.; Dia, H.; Tsai, P.-W.; Liyanage, S. Short-Term Traffic Forecasting: An LSTM Network for Spatial-Temporal Speed Prediction. Future Transp. 2021, 1, 21–37. [Google Scholar] [CrossRef]
- Yu, H.; Wu, Z.; Wang, S.; Wang, Y.; Ma, X. Spatiotemporal recurrent convolutional networks for traffic prediction in transportation networks. Sensors 2017, 17, 1501. [Google Scholar] [CrossRef] [PubMed]
- Vlahogianni, E.I.; Golias, J.C.; Karlaftis, M.G. Short-term traffic forecasting: Overview of objectives and methods. Transp. Rev. 2004, 24, 533–557. [Google Scholar] [CrossRef]
- Vlahogianni, E.I.; Karlaftis, M.G.; Golias, J.C. Spatio-temporal short-term urban traffic volume forecasting using genetically optimized modular networks. Comput.-Aided Civ. Infrastruct. Eng. 2007, 22, 317–325. [Google Scholar] [CrossRef]
- Ma, X.; Tao, Z.; Wang, Y.; Yu, H.; Wang, Y. Long short-term memory neural network for traffic speed prediction using remote microwave sensor data. Transp. Res. Part C Emerg. Technol. 2015, 54, 187–197. [Google Scholar] [CrossRef]
- Cai, D.; Chen, K.; Lin, Z.; Li, D.; Zhou, T.; Ling, Y.; Leung, M.F. JointSTNet: Joint Pre-Training for Spatial-Temporal Traffic Forecasting. IEEE Trans. Consum. Electron. 2024. [Google Scholar] [CrossRef]
- Intelematics. Case Study: Predicting Traffic Speeds and Volumes 60 Minutes in Advance. Available online: https://www.intelematics.com/case-studies/predicting-60-minutes-ahead-a-case-study-in-predicting-traffic-speeds-and-volumes/ (accessed on 5 September 2023).
- Google Earth. Available online: https://earth.google.com/web/@0,-1.9336001,0a,22251752.77375655d,35y,0h,0t,0r/data=CgRCAggBOgMKATBKDQj___________8BEAA (accessed on 31 August 2024).
- Yasanthi, R.G.; Mehran, B. Modeling free-flow speed variations under adverse road-weather conditions: Case of cold region highways. Case Stud. Transp. Policy 2020, 8, 22–30. [Google Scholar] [CrossRef]
- Bi, H.; Ye, Z.; Zhu, H. Data-driven analysis of weather impacts on urban traffic conditions at the city level. Urban Clim. 2022, 41, 101065. [Google Scholar] [CrossRef]
- Abdelaziz, N.; El-Hakim, R.T.A.; El-Badawy, S.M.; Afify, H.A. International Roughness Index prediction model for flexible pavements. Int. J. Pavement Eng. 2020, 21, 88–99. [Google Scholar] [CrossRef]
- Alonso-Solorzano, Á.; Pérez-Acebo, H.; Findley, D.J.; Gonzalo-Orden, H. Transition probability matrices for pavement deterioration modelling with variable duty cycle times. Int. J. Pavement Eng. 2023, 24, 2278694. [Google Scholar] [CrossRef]
- Neuralware. Neural Ware. Available online: https://www.neuralware.com/ (accessed on 5 September 2024).
- Matlab. Long Short-Term Memory (LSTM) Networks—MATLAB & Simulink. Available online: https://www.mathworks.com/help/deeplearning/ug/long-short-term-memory-networks.html (accessed on 9 February 2024).
- Matlab. Recurrent Neural Network (RNN)—MATLAB & Simulink. Available online: https://www.mathworks.com/discovery/rnn.html (accessed on 9 February 2024).






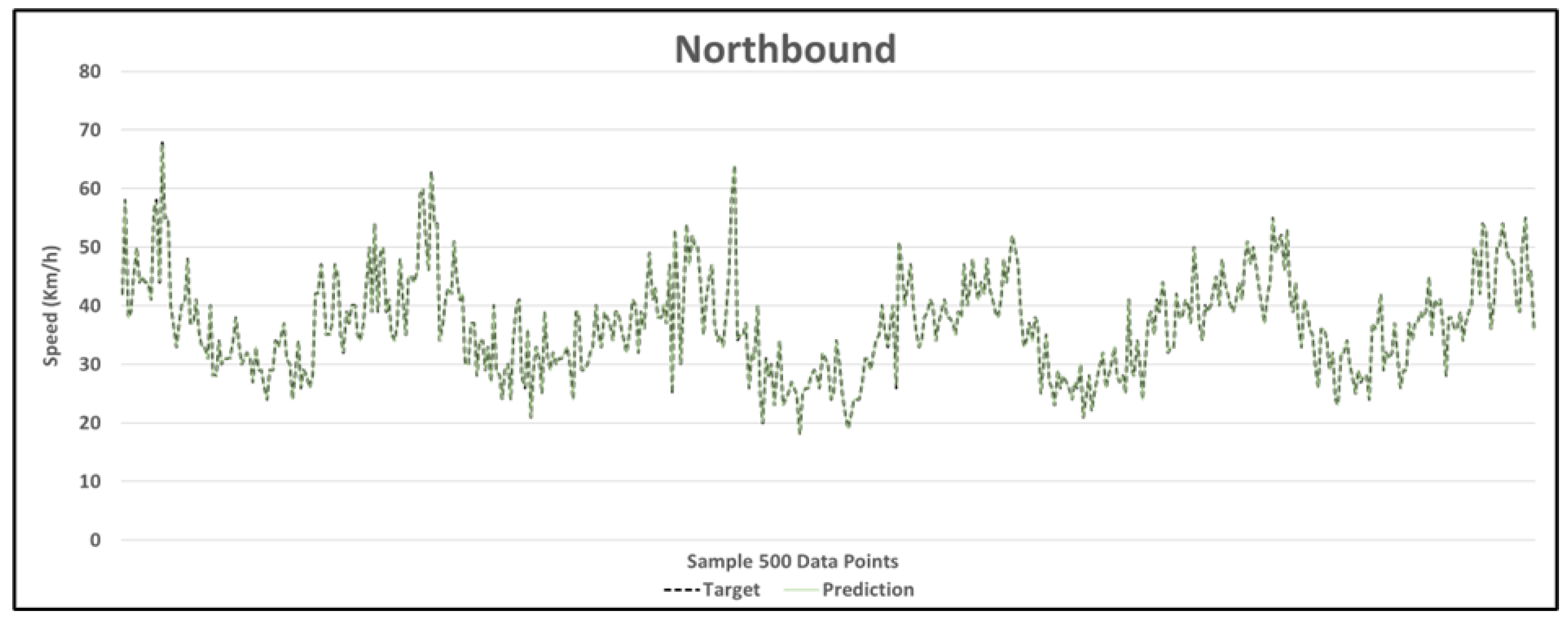

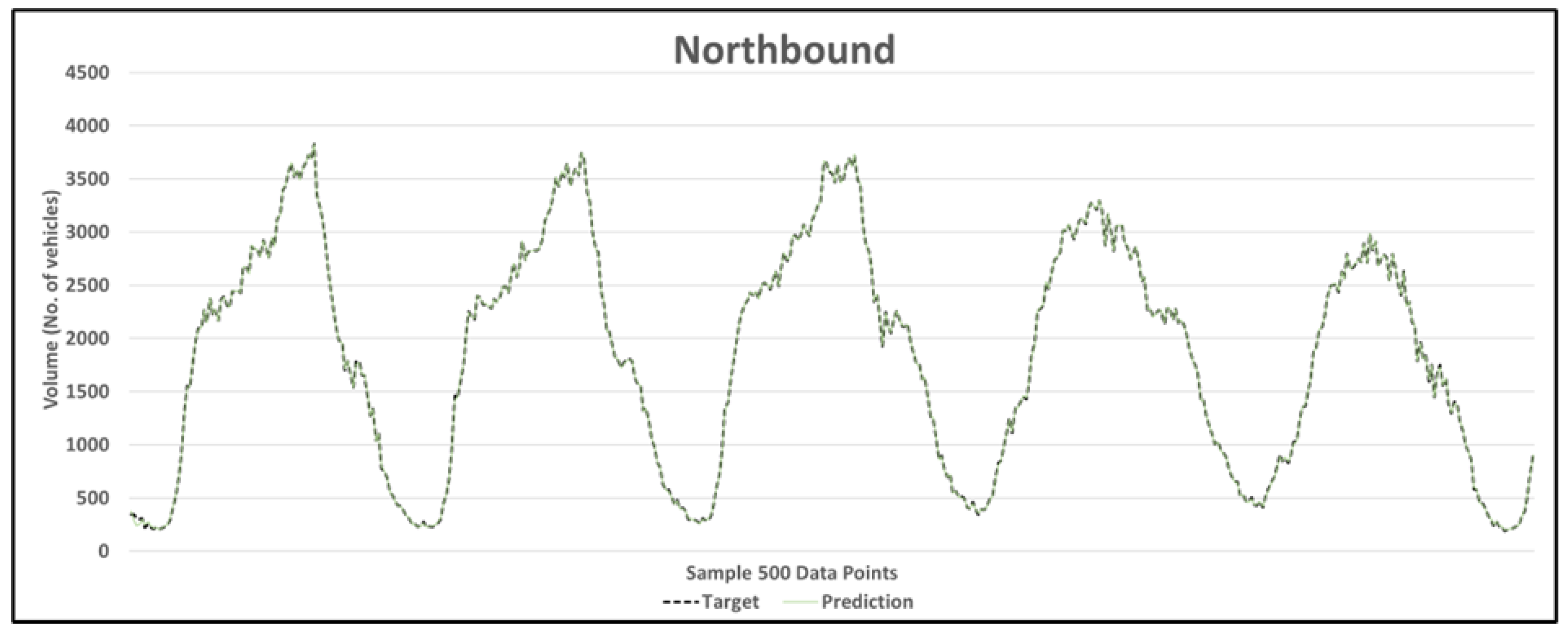
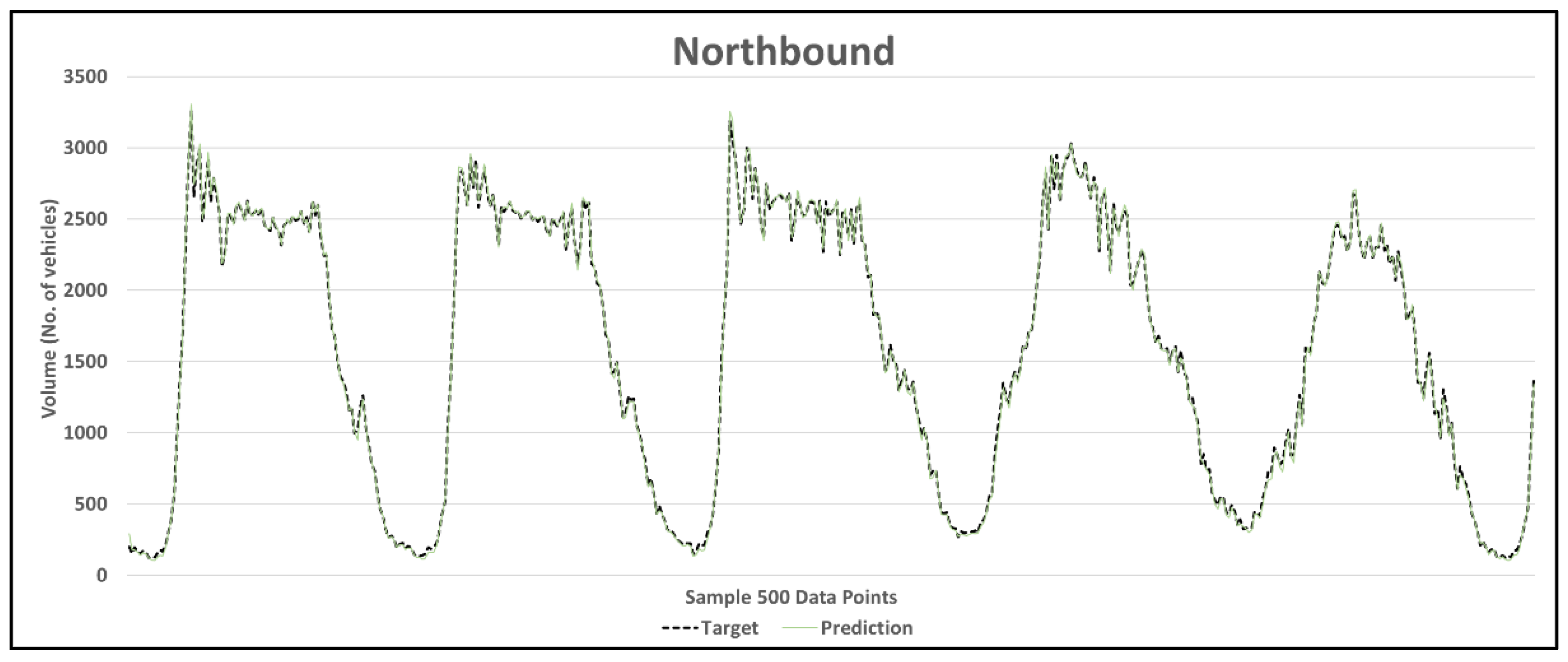
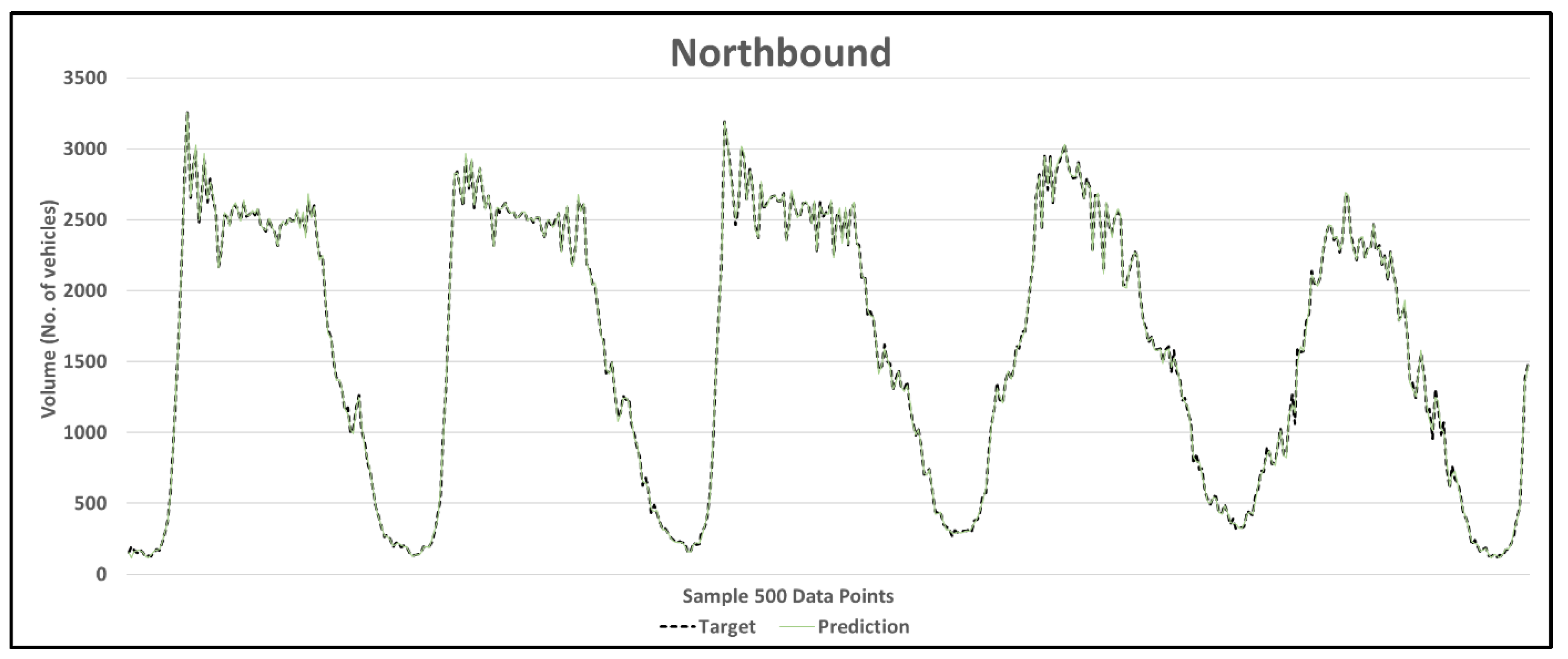
| Location | Total Data Set | Training Data Set (60%) | Test and Validation Data Set (40%) |
|---|---|---|---|
| Hoddle Street, Southbound | 35,036 observations | 21,022 observations | 14,014 observations |
| Hoddle Street, Northbound | 35,036 observations | 21,022 observations | 14,014 observations |
| Total | 70,072 observations | 42,044 observations | 28,028 observations |
| Parameters | Values |
|---|---|
| Gradient decay factor | 0.9 |
| Initial learning rate | 0.005 |
| Minimum batch size | 128 |
| Maximum epochs | 300 |
| Training optimiser | Adaptive moment estimation optimiser |
| Dropping learning rate during training | Piecewise |
| Learning rate drop period | 125 |
| The factor for the learning rate dropping | 0.2 |
| Prediction Horizons | Speed (km/h) Northbound | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| BiLSTM | Uni-LSTM | RNN | Elman | DLBP | ||||||
| MAPE (%) | Accuracy (%) | MAPE (%) | Accuracy (%) | MAPE (%) | Accuracy (%) | MAPE (%) | Accuracy (%) | MAPE (%) | Accuracy (%) | |
| 15 min | 0.07% | 99.93% | 8.63% | 91.37% | 10.77% | 89.23% | 10.88% | 89.12% | 11.16% | 88.84% |
| 30 min | 0.14% | 99.86% | 9.24% | 90.76% | 12.74% | 87.26% | 12.72% | 87.28% | 12.85% | 87.15% |
| 45 min | 0.11% | 99.89% | 9.21% | 90.79% | 12.78% | 87.22% | 12.67% | 87.33% | 16.17% | 83.83% |
| 60 min | 0.16% | 99.84% | 9.42% | 90.58% | 13.74% | 86.26% | 13.62% | 86.38% | 12.89% | 87.11% |
| Prediction Horizons | Speed (km/h) Southbound | |||||||||
| BiLSTM | LSTM | RNN | Elman | DLBP | ||||||
| MAPE (%) | Accuracy (%) | MAPE (%) | Accuracy (%) | MAPE (%) | Accuracy (%) | MAPE (%) | Accuracy (%) | MAPE (%) | Accuracy (%) | |
| 15 min | 0.13% | 99.87% | 11.24% | 88.76% | 13.94% | 86.06% | 14.06% | 85.94% | 16.06% | 83.94% |
| 30 min | 0.14% | 99.86% | 12.35% | 87.65% | 17.05% | 82.95% | 17.33% | 82.67% | 17.86% | 82.14% |
| 45 min | 0.16% | 99.84% | 12.46% | 87.54% | 17.67% | 82.33% | 18.07% | 81.93% | 18.37% | 81.63% |
| 60 min | 0.20% | 99.80% | 12.59% | 87.41% | 18.41% | 81.59% | 18.77% | 81.23% | 17.11% | 82.89% |
| Prediction Horizons | Volume (No. of Vehicles) Northbound | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| BiLSTM | Uni-LSTM | RNN | Elman | DLBP | ||||||
| MAPE (%) | Accuracy (%) | MAPE (%) | Accuracy (%) | MAPE (%) | Accuracy (%) | MAPE (%) | Accuracy (%) | MAPE (%) | Accuracy (%) | |
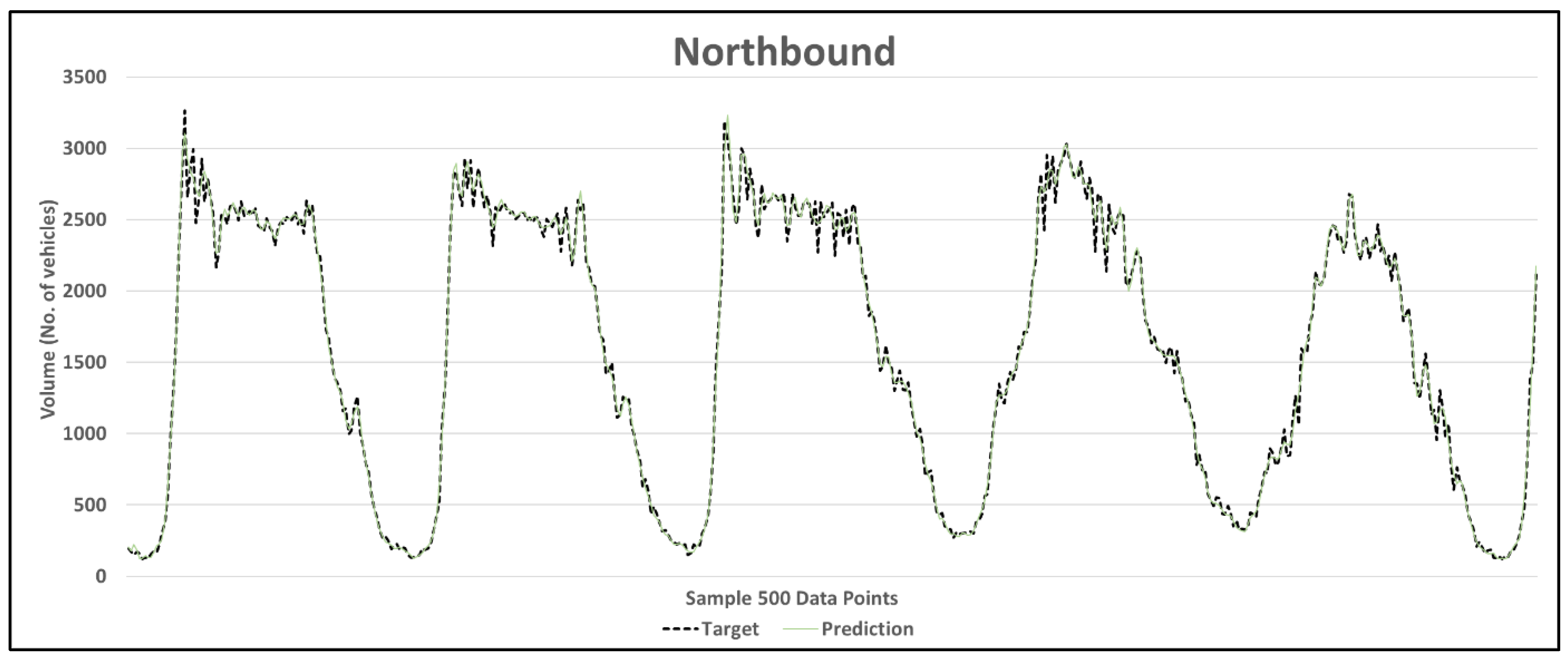
| 15 min | 0.54% | 99.46% | 4.77% | 95.23% | 7.32% | 92.68% | 7.30% | 92.70% | 8.38% | 91.62% |
| 30 min | 2.37% | 97.63% | 5.12% | 94.88% | 12.41% | 87.59% | 12.34% | 87.66% | 11.68% | 88.32% |
| 45 min | 3.20% | 96.80% | 5.13% | 94.87% | 18.17% | 81.83% | 17.86% | 82.14% | 17.58% | 82.42% |
| 60 min | 3.18% | 96.82% | 5.92% | 94.08% | 24.46% | 75.54% | 24.03% | 75.97% | 21.45% | 78.55% |
| Prediction Horizons | Volume (No. of Vehicles) Southbound | |||||||||
| BiLSTM | LSTM | RNN | Elman | DLBP | ||||||
| MAPE (%) | Accuracy (%) | MAPE (%) | Accuracy (%) | MAPE (%) | Accuracy (%) | MAPE (%) | Accuracy (%) | MAPE (%) | Accuracy (%) | |
| 15 min | 1.07% | 98.93% | 6.80% | 93.20% | 9.43% | 90.57% | 9.38% | 90.62% | 9.86% | 90.14% |
| 30 min | 1.24% | 98.76% | 7.67% | 92.33% | 15.23% | 84.77% | 14.90% | 85.10% | 13.94% | 86.06% |
| 45 min | 2.15% | 97.85% | 8.67% | 91.33% | 22.18% | 77.82% | 21.32% | 78.68% | 23.58% | 76.42% |
| 60 min | 3.87% | 96.13% | 9.87% | 90.13% | 28.67% | 71.33% | 29.05% | 70.95% | 26.96% | 73.04% |
| Prediction Horizons | Speed (km/h) | |||||||
|---|---|---|---|---|---|---|---|---|
| 15 min | 30 min | 45 min | 60 min | |||||
| MAPE (%) | Accuracy (%) | MAPE (%) | Accuracy (%) | MAPE (%) | Accuracy (%) | MAPE (%) | Accuracy (%) | |
| BiLSTM_No weather | 0.12 | 99.88 | 0.15 | 99.85 | 0.17 | 99.83 | 0.25 | 99.75 |
| BiLSTM_Rain | 0.40 | 99.60 | 0.28 | 99.72 | 0.41 | 99.59 | 2.02 | 97.98 |
| BiLSTM_Rain and Wind | 0.30 | 99.70 | 0.23 | 99.77 | 0.55 | 99.45 | 1.91 | 98.09 |
| BiLSTM_Weather | 0.21 | 99.79 | 0.32 | 99.68 | 0.32 | 99.68 | 0.23 | 99.77 |
| LSTM_No weather | 7.08 | 92.92 | 7.76 | 92.24 | 7.87 | 92.13 | 8.09 | 91.91 |
| LSTM_Rain | 7.40 | 92.60 | 8.07 | 91.93 | 8.32 | 91.68 | 8.47 | 91.53 |
| LSTM_Rain and Wind | 7.40 | 92.60 | 8.18 | 91.82 | 8.22 | 91.78 | 8.38 | 91.62 |
| LSTM_All Weather | 7.34 | 92.66 | 8.04 | 91.96 | 8.18 | 91.82 | 8.35 | 91.65 |
| Prediction Horizons | Volume (No. of Vehicles) | |||||||
|---|---|---|---|---|---|---|---|---|
| 15 min | 30 min | 45 min | 60 min | |||||
| MAPE (%) | Accuracy (%) | MAPE (%) | Accuracy (%) | MAPE (%) | Accuracy (%) | MAPE (%) | Accuracy (%) | |
| BiLSTM_No weather | 1.16 | 98.84 | 2.46 | 97.54 | 2.38 | 97.62 | 3.14 | 96.86 |
| BiLSTM_Rain | 0.87 | 99.13 | 2.47 | 97.53 | 2.62 | 97.38 | 2.87 | 97.13 |
| BiLSTM_Rain and Wind | 2.34 | 97.66 | 2.60 | 97.40 | 2.75 | 97.25 | 2.87 | 97.13 |
| BiLSTM_Weather | 2.13 | 97.87 | 2.40 | 97.60 | 3.42 | 96.58 | 2.94 | 97.06 |
| LSTM_No weather | 4.37 | 95.63 | 4.60 | 95.40 | 4.89 | 95.11 | 5.97 | 94.03 |
| LSTM_Rain | 5.02 | 94.98 | 5.03 | 94.97 | 5.39 | 94.61 | 6.00 | 94.00 |
| LSTM_Rain and Wind | 4.73 | 95.27 | 5.52 | 94.48 | 5.37 | 94.63 | 6.19 | 93.81 |
| LSTM_All Weather | 4.93 | 95.07 | 5.50 | 94.50 | 5.86 | 94.14 | 6.61 | 93.39 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abduljabbar, R.; Dia, H.; Liyanage, S. Machine Learning Models for Traffic Prediction on Arterial Roads Using Traffic Features and Weather Information. Appl. Sci. 2024, 14, 11047. https://doi.org/10.3390/app142311047
Abduljabbar R, Dia H, Liyanage S. Machine Learning Models for Traffic Prediction on Arterial Roads Using Traffic Features and Weather Information. Applied Sciences. 2024; 14(23):11047. https://doi.org/10.3390/app142311047
Chicago/Turabian StyleAbduljabbar, Rusul, Hussein Dia, and Sohani Liyanage. 2024. "Machine Learning Models for Traffic Prediction on Arterial Roads Using Traffic Features and Weather Information" Applied Sciences 14, no. 23: 11047. https://doi.org/10.3390/app142311047
APA StyleAbduljabbar, R., Dia, H., & Liyanage, S. (2024). Machine Learning Models for Traffic Prediction on Arterial Roads Using Traffic Features and Weather Information. Applied Sciences, 14(23), 11047. https://doi.org/10.3390/app142311047






