Abstract
This study proposes a multi-objective optimization framework for peer-to-peer (P2P) energy trading in South Korea’s tiered electricity pricing system. The framework employs the Multi-Objective Evolutionary Algorithm based on Decomposition (MOEA/D) to optimize three conflicting objectives: minimizing consumer costs, maximizing prosumer benefits, and enhancing energy utilization. Using real microgrid data from a South Korean community, the framework’s performance is validated through simulations. The results highlight that MOEA/D achieved an optimal cost of KRW 32,205.0, a benefit of KRW 32,205.0, and an energy utilization rate of 57.46%, outperforming the widely used NSGA-II algorithm. Pareto front analysis demonstrates MOEA/D’s ability to generate diverse and balanced solutions, making it well suited for regulated energy markets. These findings underline the framework’s potential to improve energy efficiency, lower costs, and foster sustainable energy trading practices. This research offers valuable insights for advancing decentralized energy systems in South Korea and similar environments.
1. Introduction
In recent years, peer-to-peer (P2P) energy trading has emerged as a game-changing option in the energy industry, which provides prosumers (producers + consumers) with a dynamic way to actively engage in the market. Previously, prosumers, who are not only consuming but also producing energy, used to be limited to buying energy from utilities or conducting transactions within microgrid networks. However, the development of P2P trading has changed this environment by giving power to prosumers to trade their surplus energy directly with fellow participants, therefore increasing their benefits and simultaneously improving consumer advantages [1,2]. These paradigm modifications are supported by technological innovations like blockchain and smart metering, which enable safe and transparent energy transactions between parties. By using these technologies, P2P trading goes beyond traditional centralized energy distribution methods and allows a decentralized energy ecosystem with improved efficiency, resilience, and sustainability.
In microgrid systems, prosumers can choose to connect with a utility company and buy power or transact energy from other prosumers as shown in Figure 1. This model assumes that the prosumers know the required information through the broadcasting of signaling messages, which is possible due to the cooperative approaches of community-based controllers. The problem solved is really single medium access control in disguise. For instance, when prosumers are unable to meet their own energy needs with their small-scale production capacities, they can purchase or loan energy from other producers. Additionally, prosumers have the option of selling or lending any excess electricity to other prosumers [3]. This leads to the establishment of a dynamic environment, where not only centralized entities but also actions undertaken by individuals determine how energy flows through the grid, leading to its resilience and sustainability.
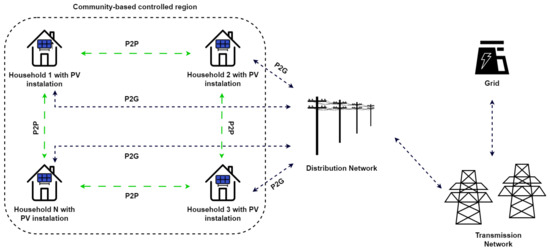
Figure 1.
P2P energy trading model.
Piclo in the United Kingdom, Sonnen Community in Germany, and Yeloha (in Boston) in the USA are examples of global P2P energy trading platforms. By showing several business models, as well as innovative solutions for P2P electricity exchange, these platforms reveal how much change this technology can bring to the existing world’s energy balance, illustrate the potential for P2P trading to reduce grid congestion, enhance energy security, and create new revenue streams for participants by adjusting energy prices dynamically in response to local supply and demand conditions [4]. In South Korea, on the other hand, there was no progress toward the diversification of business models among P2P businesses since the Korea Electric Power Corporation (KEPCO) monopolizes all P2P electricity transactions. But since second half of 2024, KEPCO has started to consider the recent trend of allowing P2P energy trading in specific regions. In addition, taxation in Korea is based on a tiered pricing system, unlike the United States, which implements a Time Of Use (TOU)-type residential electricity cost system that takes peak load times into account.
In order to overcome these issues, this work suggests a framework for P2P energy trading within South Korea’s tiered pricing system. The system model is designed to develop a plan for the reactivation of P2P electricity trading in Korea through the development of a tiered pricing model. This paper also presents the average prosumer benefit as a time series, identifies factors affecting the transaction utility for the exact price model, and indicates the level of customer bill reduction before and after P2P energy trading in South Korea. However, while this study is applied specifically to South Korea’s tiered electricity pricing system, the framework has potential adaptability to and relevance in other global markets.
This study aims to obtain the Pareto curve through a multi-objective optimization technique using a Multi-Objective Evolutionary Algorithm based on Decomposition (MOEA/D) [5,6]. Henceforth, this analysis will provide direction for designing an action plan for increasing P2P transactions within South Korea, which has no infrastructure for P2P trading yet. In conclusion, the objective is to suggest how prosumer benefits can be maximized alongside those of prosumers to enhance a more efficient energy system in South Korea that is sustainable as well.
Contributions
The paper makes a contribution by proposing a comprehensive framework for implementing P2P energy trading within South Korea’s existing tiered pricing model. Addressing the current monopoly by KEPCO, this work proposes a system that facilitates direct energy exchange between prosumers and consumers, encouraging a decentralized and resilient energy market. A key strength of the study is the use of real data from a Korean microgrid within the Grida Energy c2x project, which validates the practicality of the model by testing its performance under the actual energy generation and demand patterns. The framework utilizes an MOEA/D to optimize several goals, such as minimizing consumer costs, maximizing prosumer revenues, and enhancing the utilization of locally generated energy. Additionally, the model motivates participation through a discounted grid price, ensuring affordability even during energy deficits. The simulation results indicate that the proposed approach can lead to substantial cost savings, increase prosumer revenues, and improve energy efficiency while highlighting the feasibility and benefits of implementing P2P energy trading in South Korea.
2. Literature Survey
Recent technological advancements have created enormous opportunities for P2P energy trading, so it is considered as one of the most promising solutions to address many issues in the energy sector such as integrating renewable energy, mitigating grid congestion, and reducing energy-related costs [1,7]. In P2P trading, prosumers can directly exchange energy with each other. This results in a decentralized and dynamic market, where energy can be exchanged based on the real-time supply and demand conditions of participants [3]. This business model promotes market efficiency and motivates producers and consumers to participate more actively in order to develop sustainable energy consumption practices [3]. However, integrating P2P trading in markets such as South Korea requires a comprehensive framework that considers local economic, technical, and regulatory constraints, as an appropriate regulatory and pricing structure already exists in South Korea, which is a tiered pricing system [4]. This paper intends to contribute to the formulation of a theoretical P2P structure that can enhance prosumer efficiency, adapt to tiered pricing structures, and ensure a fit for operation with the grid.
Numerous studies have been conducted with the aim of providing insights into P2P energy trading. The authors of [8] propose a new pricing model for P2P trading in a microgrid environment. According to the authors, they have suggested an evaluation mechanism in an attempt to enhance market efficiency with regard to the microgrid and the earnings proportion for households in the microgrid. The study is situated against the background of advanced distributed energy resources (DERs) and changing consumer functions from simply customers to producers of energy, known as prosumers. The value-based pricing model is further supported by an evaluation-based framework that provides feedback on household energy service usage. This optimal quotation point of energy bidding involves an evaluation coefficient for each household obtained from the results of previous evaluations. Households that secure and maintain higher levels of services have higher evaluation coefficients, which makes them more favorable for ranking in the auction. This pricing scheme is supposed to rely on performance-based forms of evaluation, thus keeping an impact on the general efficiency and reliability within the markets at heart. This approach helps to favor those households that have a good performance in comparison with others, thus stimulating the increase in the level of service, as well as contributing to the leaps and bounds in the development of competitive energy market within the microgrid.
Additional research has evaluated different types of electricity trading such as Net Metering, Feed-in Tariff (FIT), and P2P [9]. Researchers also estimate the Levelized Cost of Electricity (LCOE) for each type of trading, uncovering that P2P-Tier 1 is the least costly trading method. It also analyses the evaluation of monthly electricity tariffs on the basis of progressive tariffs and verifies that there are considerable amounts of savings because of improved energy intensity and effective trading outlets. In [10], insights are gained based on the analysis of the maximum electrical trading prices, which show the interdependence between monthly electricity consumption, electricity purchase rates, and the profitability of the electric trading process for both buyers and sellers. Furthermore, the paper illustrates that higher committee consumption increases maximum trades for consumers when monthly consumption is also higher, while the minimum number of maximum trades occurs when the committee’s purchase rate is higher. Otherwise, fluctuations in trading performance are observed depending on the seasons of the year, and the summer period accommodates progressive tariffs at relatively lower premiums. In terms of both breadth and depth, the study provides an adequate picture of prospective trading mechanisms, which provides the necessary information to distinguish profitable and worthwhile trading strategies for players within the energy trading market. Reference [11] reveals the integration of distributed photovoltaic (PV) systems and battery storage to optimize P2P energy trading, demonstrating significant cost savings and enhancing market participation through the effective use of locally generated energy. The model is beneficial for making households spend less on electricity and earn money for prosumers. In the social context, it recognizes the de-centralized nature of energy delivery, the possibility of a reduction in state finances in power infrastructure, and the promotion of distributed renewable energy. The authors of [12] utilize a multi-objective optimization approach to determine the optimal sizing of a hybrid microgrid that includes PV systems, wind turbines, diesel generators, and batteries. The study incorporates the probability of power supply loss, electricity cost, and the renewable energy factors as the primary objective functions for the optimization process. In [13], the authors proposed Genetic Algorithm (GA) and Wind-Driven Optimization (WDO) methods, comparing their outcomes. The results indicated a reduction of 29% in bill cost and 36.2% in peak-to-average ratio. Reference [14] develops a modified MOEA/D to address the multi-objective optimal power flow (OPF) problem. It aims to minimize multiple conflicting objectives, including fuel costs, emissions, power losses, and voltage magnitude deviations. Studies by [15] used the MOEA/D algorithm to address objectives such as minimizing completion time, machine load, energy consumption, and the number of tools required. Moreover, to optimize multiple conflicting objectives like energy consumption, cost, and user comfort, a multi-agent-assisted MOEA/D framework is developed to address multi-objective optimization problems [16].
Further contributions to the literature have applied advanced computational techniques, such as game theory and machine learning, to P2P energy trading [17]. The researchers of [18] discuss solutions, built on game theory, including how to guarantee the equal shares of gains for all prosumers, how to minimize the data exchange and enhance convergence through the decentralized platforms, and how to raise the profitability of self-organized markets with the help of deep Q-Learning (DQL). Peer-to-grid (P2G) regimes are integrated in a coordinated fashion with P2P protocols to deal with them, and intelligent battery participation and demand response proposals stand out for the value they create. Studies also analyze the key issues associated with external retailer-based energy trading and ancillary services and have increased the community revenue as well as operation efficiency demonstrative. These techniques are used in agent-based methods to optimize energy sharing and dispatch control, and this substantially minimizes costs and enhances dependability.
Moreover, ref. [19] discusses two main types of pricing mechanisms: energy pricing and network service pricing (NSP). This reveals that although great effort has been made in the research with regard to energy pricing, NSP receives little attention. Inasmuch as there is a growing body of research on these two forms of pricing, there is a lack of research that compares both the financial conflicts and the financial relationship between these two pricing types. The authors [19] suggest that integrating both pricing mechanisms can provide valuable insights for the development of a comprehensive P2P energy market, ultimately contributing to a more sustainable and economically viable energy sector.
Consequently, for P2P energy trading, the authors [20] seek to enhance energy efficiency and cost savings by enabling direct energy transactions between households owning PV systems and those without them. They investigate three primary methods: pricing techniques such as as bill sharing, mid-market rate pricing, and auction-based pricing also come under the second category of pricing strategies. The goal of the study is to build a more robust and resource-optimal power system by utilizing local production and consumption, which means that there is less focus on possibly high losses of energy, which are usually present when energy is transported through longer distances. Another innovative approach is presented in [21], which is the Alternating-Direction Method of Multipliers (ADMM), a distributed optimization approach. The paper’s methodology involves modeling the utility functions of prosumers and consumers, establishing a P2P market operator (P2PMO) to balance supply and demand, and solving the pricing problem in a decentralized manner. The ADMM approach is used to handle the optimization problem, ensuring that each prosumer or consumer optimizes its objectives independently, leading to an equilibrium state in the market.
Another ADMM approach is proposed in [22]. A decentralized framework for P2P energy trading accounts for distribution network constraints while preserving the independence of participants. The authors apply the ADMM to address the coordination between agents, ensuring minimal information exchange while maintaining network security. By using a sensitivity-based approach, the study incorporates voltage and current constraints into the agents’ local optimization problems, which effectively maintains network integrity during P2P transactions. The framework reduces the role of the Distribution System Operator (DSO) while empowering prosumers to participate autonomously, ensuring secure and independent energy exchanges. The results demonstrate the model’s efficiency in handling network voltage and current constraints in practical applications, offering a solution for integrating decentralized renewable energy resources into existing grids. The framework is particularly notable for its computational efficiency, allowing fast convergence even under complex network constraints.
The authors of [23] introduce a decentralized energy management system for P2P community microgrids, focusing on maximizing social welfare while ensuring privacy and communication efficiency. The system integrates demand response (DR) programs and P2P energy trading, where prosumers and consumers exchange surplus energy in a decentralized framework. By employing a novel Segmentation-Based Distributed Alternating-Direction Method of Multipliers (SBD-ADMM), the authors optimize energy scheduling and reduce the overall electricity costs for consumers and prosumers. The decentralized nature of the system preserves participants’ privacy and reduces the number of communications required for optimal energy trading, offering a scalable solution for modern community microgrids. Through simulations, the approach proves its efficiency in achieving lower electricity bills, better integration of renewable energy, and enhanced community-wide energy sustainability.
As mentioned above, there are a number of research papers in which the authors employ one or more of the above-discussed methodologies for managing the former problem and exploiting the latter opportunity associated with P2P energy trading. Thus, this work seeks to achieve the above noble goals by developing an appropriate framework geared towards the enforcement of P2P energy trading in South Korea. Unlike other studies, this study introduces a novel multi-objective optimization framework for P2P energy trading within a regulated, tiered pricing system, addressing key deficiencies in previous studies. While most P2P frameworks optimize for cost savings or prosumer benefits individually, they often overlook the complex trade-offs required in a tiered pricing structure. By employing the MOEA/D algorithm, this study achieves a comprehensive optimization of multiple objectives: cost minimization, revenue maximization, and energy utilization, demonstrating adaptability for regulated markets. Additionally, this study validates the framework using real microgrid data from South Korea, showcasing its practical application in a monopolized energy market. Unlike prior models based primarily on theoretical or unrestricted market scenarios, this approach provides quantifiable improvements, such as cost savings and increased local energy use, which are based on real consumption and generation patterns.
3. Proposed Approach
This study proposes a comprehensive methodology to facilitate P2P energy trading among households with PV installations within a microgrid in South Korea. The primary objective of this approach is to integrate a progressive rate system to minimize costs for consumers, maximize revenue for prosumers, and optimize the overall usage of locally generated energy. The monthly energy generation and demand for three households for a 12-month period are considered. The energy cost calculation follows a progressive rate system, as shown in Table 1, where the unit price increases with higher consumption levels.

Table 1.
Electricity charges for different seasons.
The proposed approach involves employing MOEA/D to optimize the P2P energy trading framework. MOEA/D is a powerful approach used to solve multi-objective optimization problems. Unlike traditional evolutionary algorithms, MOEA/D decomposes a multi-objective problem into a set of single-objective sub-problems, each associated with a specific weight vector that represents a trade-off among objectives. This allows for a more efficient search process as it focuses on optimizing multiple objectives.
The selection of MOEA/D for this study is based on its strengths in handling multi-objective optimization in complex environments, unlike traditional multi-objective algorithms such as NSGA-II, which focus on Pareto-front optimization without decomposition. MOEA/D comprises structured neighborhood sharing and crossover mutation processes that enable efficient exploration of trade-offs, making it ideal for optimizing multiple conflicting objectives in a regulated, multi-level pricing context.
In MOEA/D, each individual in the population is represented by a decision vector. The algorithm maintains a population of individuals and evolves them through selection, crossover, and mutation operators. Each individual is evaluated based on its performance across multiple objectives, and a neighborhood structure is used to share information among individuals, which enhances convergence toward the Pareto front.
The weight vectors can be generated to ensure a diverse representation of the objectives. A common approach is to distribute the weights uniformly in the objective space. If represents the weight vector for sub-problem i, it can be defined as follows:
The fitness of each individual can be evaluated based on its objectives. For an individual x and its associated weight vector , the fitness can be computed as
The neighborhood structure can be defined based on the distance between weight vectors. Two weight vectors and are considered neighbors if they are the closest in terms of Euclidean distance, and they are considered as
Crossover can be performed using techniques like blend crossover:
where and are parent solutions and is a parameter controlling the spread of the offspring. Mutation can be defined as
where represents Gaussian noise added to the individual x.
The algorithm proceeds through several generations, where in each generation, individuals are evaluated, offspring are generated, and non-dominated solutions are updated. The weight vectors are typically distributed uniformly to ensure a diverse representation of the Pareto front. This process is expressed in Algorithm 1.
| Algorithm 1 Multi-Objective Evolutionary Algorithm based on Decomposition (MOEA/D) |
 |
3.1. Progressive Rate System
The energy cost calculation follows a tiered pricing model, where the unit price increases with higher consumption levels. The model is divided into three tiers:
- : Price per kWh for consumption up to 200 kWh,
- : Price per kWh for consumption between 201 and 400 kWh,
- : Price per kWh for consumption above 400 kWh.
The cost for a given demand D is calculated as follows:
where is the total cost of energy consumption for the household, D represents the total energy demand (kWh) consumed by the household, is the price per kWh for consumption up to 200 kWh, is the price per kWh for consumption between 201 and 400 kWh, and is the price per kWh for consumption exceeding 400 kWh.
This tiered system reflects the actual pricing model used in South Korea and considers both summer and non-summer seasons, with distinct rates for each.
3.2. Incentivizing P2P Participation Through Discounted Grid Prices
To encourage active participation in the P2P trading system, a discounted grid price is offered to households during periods of energy deficit. This ensures that even when a household’s energy demand exceeds the available P2P supply, they can purchase energy from the grid at a lower rate than the standard grid price. The fixed discounted price reduces the risk for the participants because it provides a financial safety net.
In this system, the fixed discounted grid price is set at 150 won/kWh, compared to the standard grid price. This discount encourages the participants to remain engaged in the P2P market. This incentive is particularly important for fostering trust in the system, as it guarantees that households will not face excessively high energy prices during deficits, making the P2P market a more attractive alternative to traditional grid reliance.
3.3. Cost Calculation After P2P Trading
If a household generates more energy than it consumes, it can sell this surplus to peers in the P2P market. The surplus energy can be defined as follows:
where , and is the energy generated by the household i. The cost after P2P trading in the surplus case is calculated as
- Surplus Energy: Ifwhere represents the total monthly energy cost after engaging in P2P trading, D represents the total energy demand (kWh) of the household, S represents the surplus energy generated by the household (kWh), and is the price per kWh of energy traded between peers.
- Deficit Energy: IfThe benefit from trading surplus energy is given byThe benefit from trading in a deficit is zero:
3.4. Cost Difference
The difference in cost before and after P2P trading is expressed by
4. Objective Functions for P2P Energy Trading
4.1. Cost Minimization for Consumers
The first objective is to minimize the electricity cost for each household. This involves reducing the total amount spent on both grid and peer-supplied energy as shown below:
subject to
where is the cost for household i, is the grid price, is the peer trading price, is the energy bought from the grid, and is the energy bought from peers by household i.
4.2. Benefit Maximization for Prosumers
The second objective in this case is to maximize the benefit for households generating surplus energy. This is achieved by maximizing the income from selling surplus energy to peers and can be formulated as
subject to
where is the benefit for household i selling energy, is the peer trading price, and is the energy sold to peers by household i.
4.3. Maximization for Energy Utilization
The third goal is to maximize the utilization of locally generated energy, which encourages the efficient use of renewable energy sources within the community as can be represented as
subject to
where is the utilization rate for household i, is the energy traded with peers, and is the energy generated by the household.
5. Evaluation and Simulation Results
The data for this study were obtained within Shinhyeocheon village from Grida Energy for the c2x project, an area situated in South Korea. This work involves analysis of the data collected over twelve months, as shownin Table 2, with the recorded data involving specific information on energy generation and consumption for three houses.

Table 2.
Monthly energy generation and demand for three households from April to March.
The data also provide an assessment of how P2P affects household electricity cost and value. Figure 2 displays the energy generation and consumption for three households for a twelve-month period. Further, we can see that there exists variation in energy generation and consumption every year in different months. For instance, household 2 shows a high energy generation profile in summer, from the months of June to August, with a small drop in July. However, when it comes to the energy demand, it more or less stays almost constantly the same, with a slight surge in the winter season, that is, from December to February. To assess the economic benefits of P2P energy trading, we compared the costs before and after implementing P2P trading for each household.
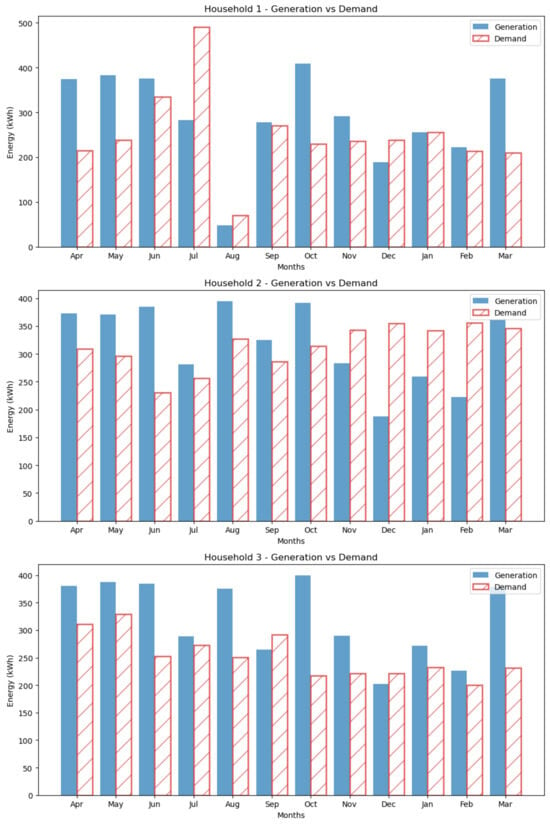
Figure 2.
Demand and generation for three households.
In order to evaluate the economic incentive of P2P energy trading, the differential costs for each household before and after the P2P implementation are calculated. These comparisons are captured in Figure 3. Each column represents a different household.
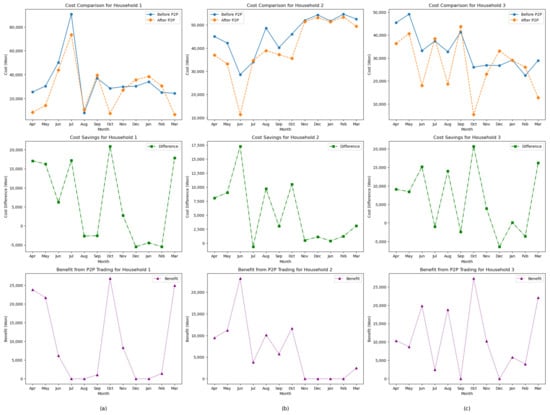
Figure 3.
(a) cost comparison and savings for household 1, (b) cost comparison and savings for household 2, (c) cost comparison and savings for household 3, highlighting the impact of P2P trading in reducing costs, achieving savings, and generating benefits from surplus energy trading.
The first row of graphs shows the monthly cost comparison before and after P2P trading. The solid lines represent the costs before P2P trading, where households only buy electricity from the grid. The dashed lines represent the costs after P2P trading, which incorporates trading surplus energy with peers and obtaining discounted grid electricity. For most months, the cost after P2P trading is lower than before, which indicates that P2P trading reduces the energy expenses for households, particularly during high-surplus months. The middle row highlights the cost savings achieved through P2P trading. These graphs highlight the monthly cost savings resulting from P2P trading. The difference between before and after P2P trading costs is plotted, indicating how much each household saves each month due to energy trading. Some households have more consistent savings, while others experience peak savings during months when they generate more surplus energy. The bottom row shows the monthly benefits gained from trading surplus energy with peers. The benefit is the income households earn by selling their excess energy to other households. This benefit fluctuates depending on the surplus generation in each month. For example, during months of high energy generation, households tend to earn more from P2P trading.
- Household 1: The cost savings are substantial, particularly during the summer months, when P2P trading significantly reduces costs;
- Household 2: Consistent cost savings are shown throughout the year, with notable reductions during the autumn months;
- Household 3: Variable cost savings are demonstrated, with the highest benefits observed in October and March.
The Pareto front analysis was conducted using MOEA/D, which evaluated a total of 100 points across 50 generations. Figure 4 presents the 3D Pareto front, highlighting the optimal trade-off points.
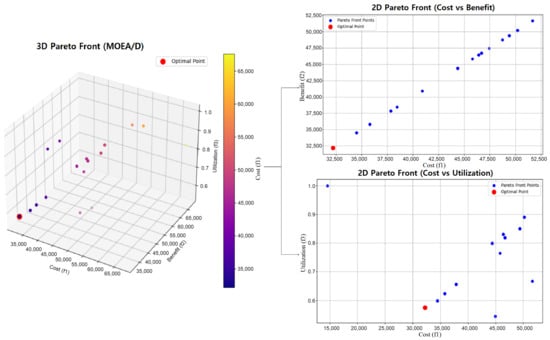
Figure 4.
Pareto Front for three objectives (MOEA/D).
In this 3D representation, the algorithm aims to find the optimal balance between cost, benefit, and utilization for P2P energy trading. Each point on the Pareto front indicates a possible solution, where the axes represent the cost (f1), benefit (f2), and utilization (f3). The points on this front are non-dominated solutions, meaning no other solutions in the space perform better in all three objectives simultaneously. The algorithm evaluates solutions iteratively, improving them via crossover, mutation, and neighborhood search. The weight vectors and the decomposition approach of MOEA/D allow for exploring various trade-offs between the objectives.
The evaluation history shows that each generation consistently evaluated 100 points, reflecting a stable and systematic approach to the optimization process. The resulting Pareto front coordinates indicate a range of solutions, each representing different trade-offs between the three objectives. Most points on the Pareto front maintain a high benefit-to-cost ratio with near-perfect utilization values. For example, several points, with a cost of KRW 102,339.649, a benefit of KRW 77,584.546, and a utilization rate of 100%, consistently appeared across different generations, indicating stable and reliable solutions. However, the optimal solutions derived from the Pareto front provide clear insights into the most balanced outcomes for households. One solution, with a cost of KRW 32,205.0, a benefit of KRW 32,205.0, and a utilization rate of approximately 57.5%, highlights a scenario where cost minimization, benefit maximization, and utilization are balanced. Other optimal solutions, such as those balancing cost and benefit or cost and utilization, underscore the flexibility of the P2P trading model. These solutions reflect the potential for substantial economic benefits while maintaining efficient energy use, allowing decision-makers to explore and select the most suitable balance for their energy strategy.
To validate the effectiveness of the proposed MOEA/D-based multi-objective optimization framework, a comparative analysis with the Non-dominated Sorting Genetic Algorithm II (NSGA-II), a widely recognized evolutionary algorithm in multi-objective optimization, is conducted Figure 5. The performance is evaluated based on three objectives: cost minimization, benefit maximization, and energy utilization. NSGA-II results in a cost of KRW 51,754.5, a benefit of KRW 44,853.9, and an energy utilization rate of 49.86%. While NSGA-II produced higher benefit values, MOEA/D demonstrated better performance in cost minimization and energy utilization, highlighting its suitability for applications emphasizing these objectives.
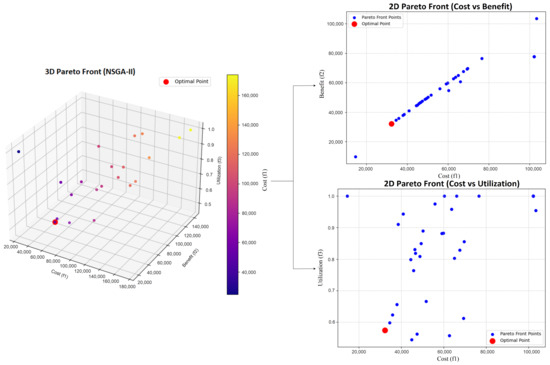
Figure 5.
Pareto Front for 3 objectives (NSGA-II).
6. Conclusions
This paper brought into focus the feasibility and possibilities associated with P2P energy trading, especially given the current conditions in South Korea, where the energy market is dominated by KEPCO. Nevertheless, some hurdles confine the development of the South Korean market, including the current system of tiered prices and a limited set of business models in the P2P trading arena. In order to mitigate these challenges, we presented a detailed framework of a tiered cost model to help fix the cost issues, increase the revenue, and promote the major use of locally available energy. To address these challenges, we proposed a comprehensive study involving a tiered rate system to optimize costs, maximize revenue, and enhance the utilization of locally generated energy. Through multi-objective optimization using the MOEA/D algorithm, we aimed to achieve a Pareto front solution that balanced these objectives. To ensure the results of the analysis were accurate, the graphical outputs of energy production and use over 12 months for three households were incorporated. These graphs depict fluctuation in energy production and consumption, particularly in seasons. Furthermore, using the Pareto approach derived from the optimization process, the distribution of cost-saving and revenue-maximization values defined the Pareto front, which showed the possibility of the best trade-offs between cost-saving and revenue maximization. The simulation results demonstrated that MOEA/D achieved an optimal solution with a cost of KRW 32,205.0, a benefit of KRW 32,205.0, and an energy utilization rate of 57.46%, outperforming the traditional NSGA-II algorithm, which resulted in a cost of KRW 51,754.5, a benefit of KRW 44,853.9, and a utilization rate of 49.86%. These findings underscore the framework’s potential to enhance energy efficiency, reduce costs, and promote sustainability in decentralized energy systems Subsequently, for future research, the focus will delve deeper into P2P energy trading.
Author Contributions
The research was carried out successfully with contributions from all authors. The main research idea and manuscript preparation were contributed by L.K., R.G., Z.M. and Y.C. contributed to the manuscript preparation and gave several suggestions from industrial perspectives. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Ministry of Education of the Republic of Korea and the National Research Foundation of Korea (NRF-2023S1A5C2A07096111).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in the study are included in the article, and further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Soto, E.A.; Bosman, L.B.; Wollega, E.; Leon-Salas, W.D. Peer-to-peer energy trading: A review of the literature. Appl. Energy 2021, 283, 116268. [Google Scholar] [CrossRef]
- Gantassi, R.; Gouissem, B.B.; Othman, J.B. Combination of MDC and K-means to improve LEACH. In Proceedings of the ICC 2021—IEEE International Conference on Communications, Montreal, QC, Canada, 14–23 June 2021; pp. 1–5. [Google Scholar] [CrossRef]
- Luo, Y.; Itaya, S.; Nakamura, S.; Davis, P. Autonomous cooperative energy trading between prosumers for microgrid systems. In Proceedings of the 39th Annual IEEE Conference on Local Computer Networks Workshops, Edmonton, AB, Canada, 8–11 September 2014; pp. 693–696. [Google Scholar] [CrossRef]
- Park, C.; Yong, T. Comparative review and discussion on P2P electricity trading. Energy Procedia 2017, 128, 3–9. [Google Scholar] [CrossRef]
- Ho-Huu, V.; Hartjes, S.; Visser, H.G.; Curran, R. An improved MOEA/D algorithm for bi-objective optimization problems with complex Pareto fronts and its application to structural optimization. Expert Syst. Appl. 2018, 92, 430–446. [Google Scholar] [CrossRef]
- Ishibuchi, H.; Doi, K.; Nojima, Y. On the effect of normalization in MOEA/D for multi-objective and many-objective optimization. Complex Intell. Syst. 2017, 3, 279–294. [Google Scholar] [CrossRef]
- Gantassi, R.; Gouissem, B.B.; Othman, J.B. The use of Grid-sizes Clustering and K-means Algorithms to enhance the QoS in LEACH protocol. In Proceedings of the ICC 2021—IEEE International Conference on Communications, Montreal, QC, Canada, 14–23 June 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Wang, D.; Su, P.; Yang, Q. A novel pricing scheme for peer-to-peer energy trading based on evaluation mechanism in microgrid. In Proceedings of the 2019 IEEE Innovative Smart Grid Technologies—Asia (ISGT Asia), Chengdu, China, 21–24 May 2019; pp. 4318–4322. [Google Scholar] [CrossRef]
- Chung, M.H. Comparison of economic feasibility for efficient peer-to-peer electricity trading of PV-equipped residential house in Korea. Energies 2020, 13, 3568. [Google Scholar] [CrossRef]
- An, J.; Lee, M.; Yeom, S.; Hong, T. Determining the Peer-to-Peer electricity trading price and strategy for energy prosumers and consumers within a microgrid. Appl. Energy 2020, 261, 114335. [Google Scholar] [CrossRef]
- Huang, H.; Nie, S.; Lin, J.; Wang, Y.; Dong, J. Optimization of peer-to-peer power trading in a microgrid with distributed PV and battery energy storage systems. Sustainability 2020, 12, 923. [Google Scholar] [CrossRef]
- Ramli, M.A.M.; Bouchekara, H.R.E.H.; Alghamdi, A.S. Optimal sizing of PV/wind/diesel hybrid microgrid system using multi-objective self-adaptive differential evolution algorithm. Renew. Energy 2018, 121, 400–411. [Google Scholar] [CrossRef]
- Jiang, X.; Xiao, C. Household energy demand management strategy based on operating power by Genetic Algorithm. IEEE Access 2019, 7, 96414–96423. [Google Scholar] [CrossRef]
- Zhang, J.; Tang, Q.; Li, P.; Deng, D.; Chen, Y. A modified MOEA/D approach to the solution of multi-objective optimal power flow problem. Appl. Soft Comput. 2016, 47, 494–514. [Google Scholar] [CrossRef]
- Xiao, B.; Zhao, Z.; Wu, Y.; Zhu, X.; Peng, S.; Su, H. An improved MOEA/D for multi-objective flexible job shop scheduling by considering efficiency and cost. Comput. Oper. Res. 2024, 167, 106674. [Google Scholar] [CrossRef]
- Guo, W.; Dong, Y. Enhancing energy-efficient building design: A multi-agent-assisted MOEA/D approach for multi-objective optimization. Energy Inform. 2024, 7, 102. [Google Scholar] [CrossRef]
- Shafique, T.; Gantassi, R.; Soliman, A.H.; Amjad, A.; Hui, Z.Q.; Choi, Y. A review of energy hole mitigating techniques in multi-hop many to one communication and its significance in IoT-oriented smart city infrastructure. IEEE Access 2023, 11, 121340–121367. [Google Scholar] [CrossRef]
- Zhou, Y.; Lund, P.D. Peer-to-peer energy sharing and trading of renewable energy in smart communities trading pricing models, decision-making and agent-based collaboration. Renew. Energy 2023, 207, 177–193. [Google Scholar] [CrossRef]
- Das, A.; Peu, S.D.; Akanda, M.A.M.; Islam, A.R.M.T. Peer-to-peer energy trading pricing mechanisms: Towards a comprehensive analysis of energy and network service pricing (NSP) mechanisms to get sustainable enviro-economical energy sector. Energies 2023, 16, 2198. [Google Scholar] [CrossRef]
- Long, C.; Wu, J.; Zhang, C.; Thomas, L.; Cheng, M.; Jenkins, N. Peer-to-peer energy trading in a community microgrid. In Proceedings of the 2017 IEEE Power & Energy Society General Meeting, Chicago, IL, USA, 16–20 July 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Paudel, A.; Gooi, H.B. Pricing in peer-to-peer energy trading using distributed optimization approach. In Proceedings of the 2019 IEEE Power & Energy Society General Meeting (PESGM), Atlanta, GA, USA, 4–8 August 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Tarashandeh, N.; Karimi, A. Peer-to-peer energy trading under distribution network constraints with preserving independent nature of agents. Appl. Energy 2024, 355, 122240. [Google Scholar] [CrossRef]
- Hussain, J.; Huang, Q.; Li, J.; Zhang, Z.; Hussain, F.; Ahmed, S.A.; Manzoor, K. Optimization of social welfare in P2P community microgrid with efficient decentralized energy management and communication-efficient power trading. J. Energy Storage 2024, 81, 110458. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).