Modeling and Characterization of Complex Dynamical Properties of Railway Ballast
Abstract
1. Introduction
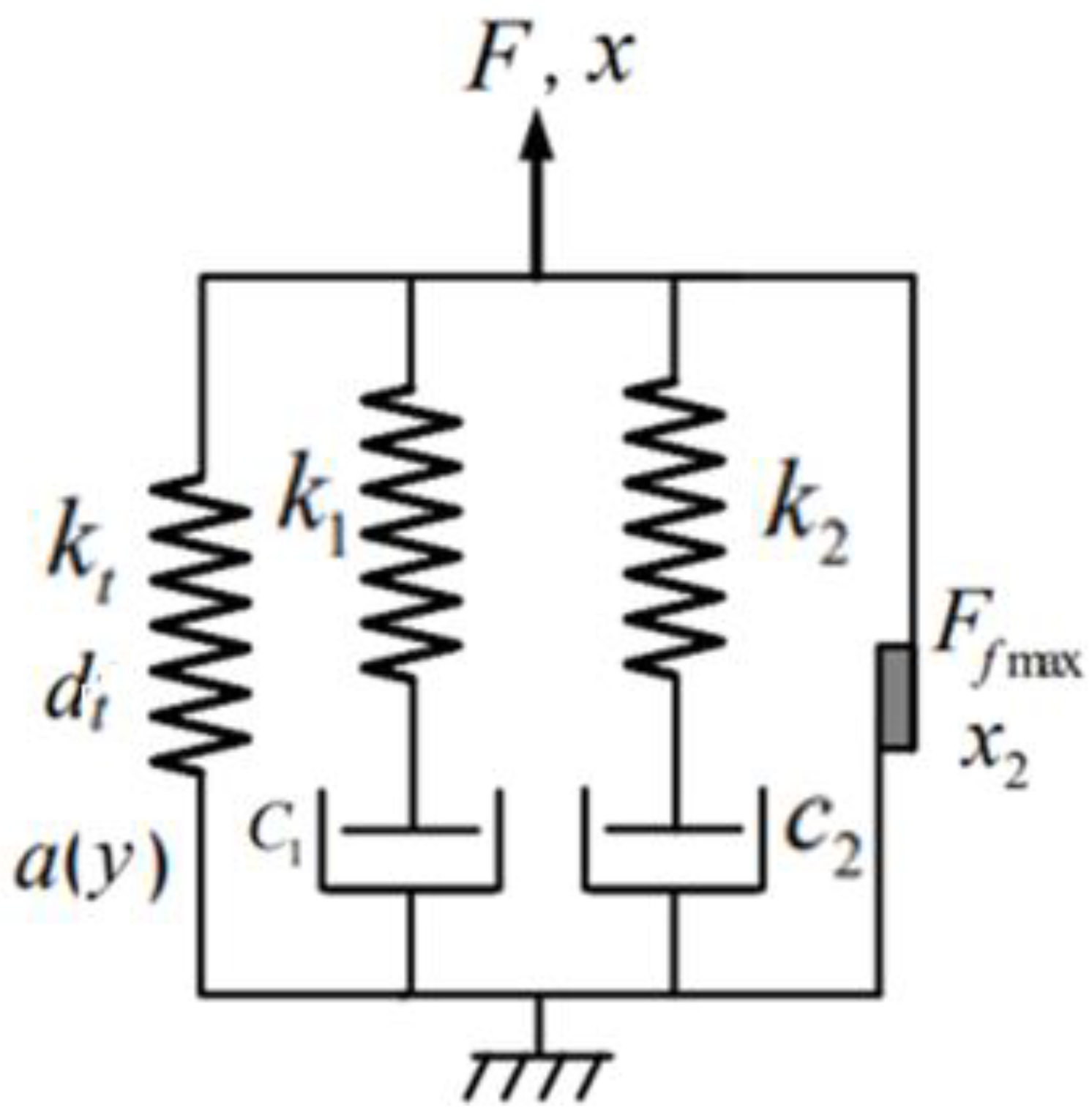
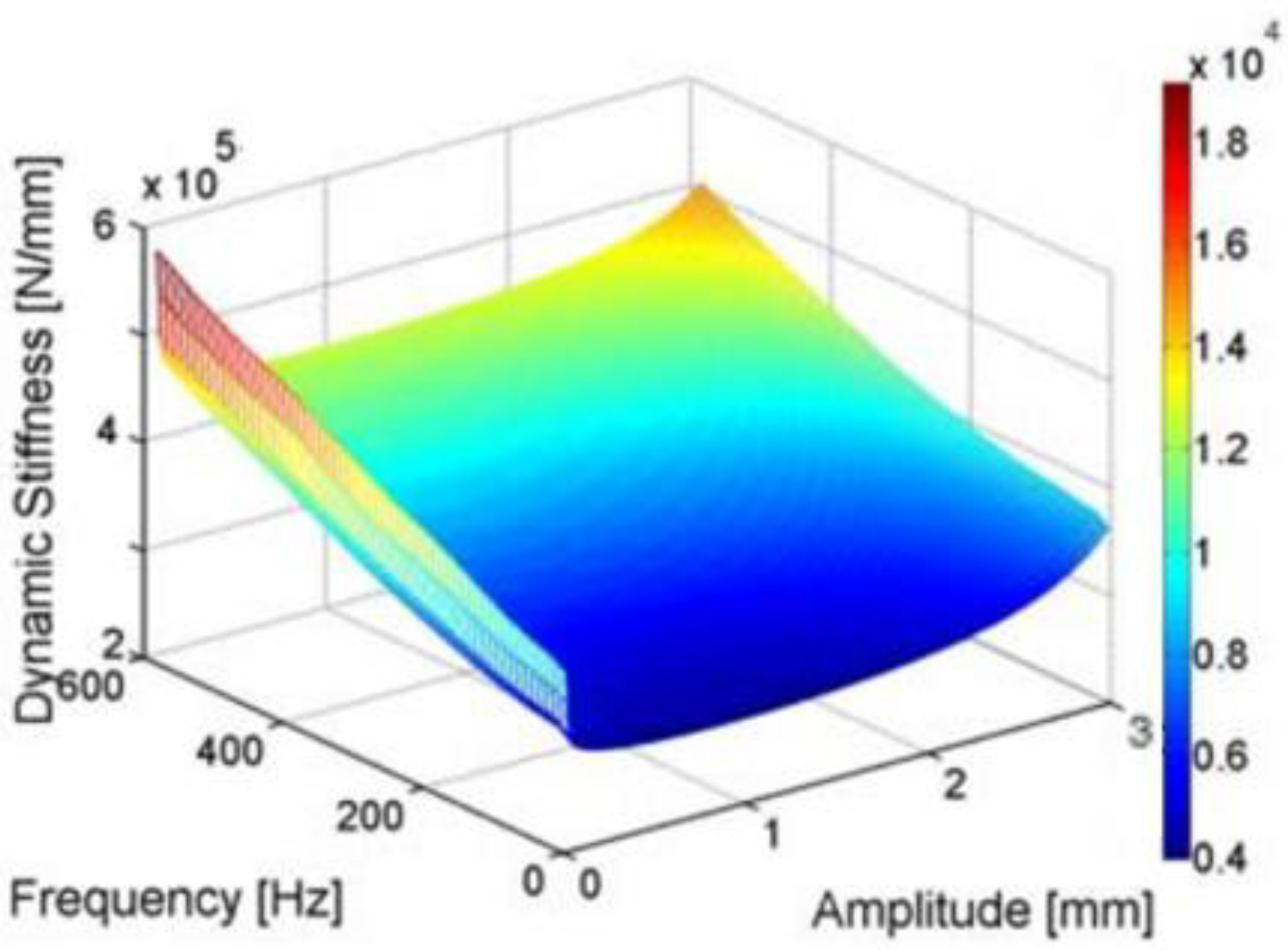
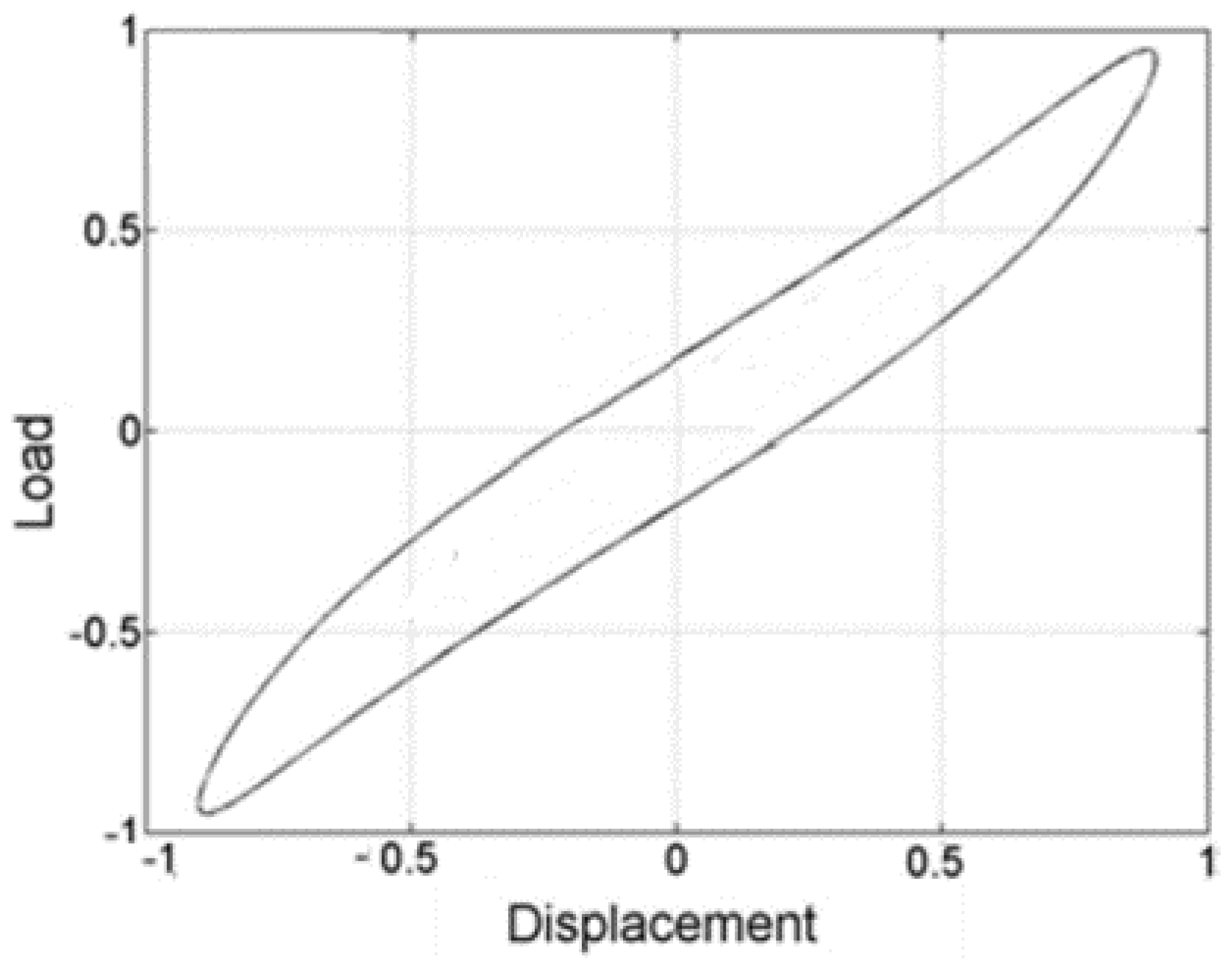
2. Modeling of Complex Dynamical Properties of the Railway Track and Ballast
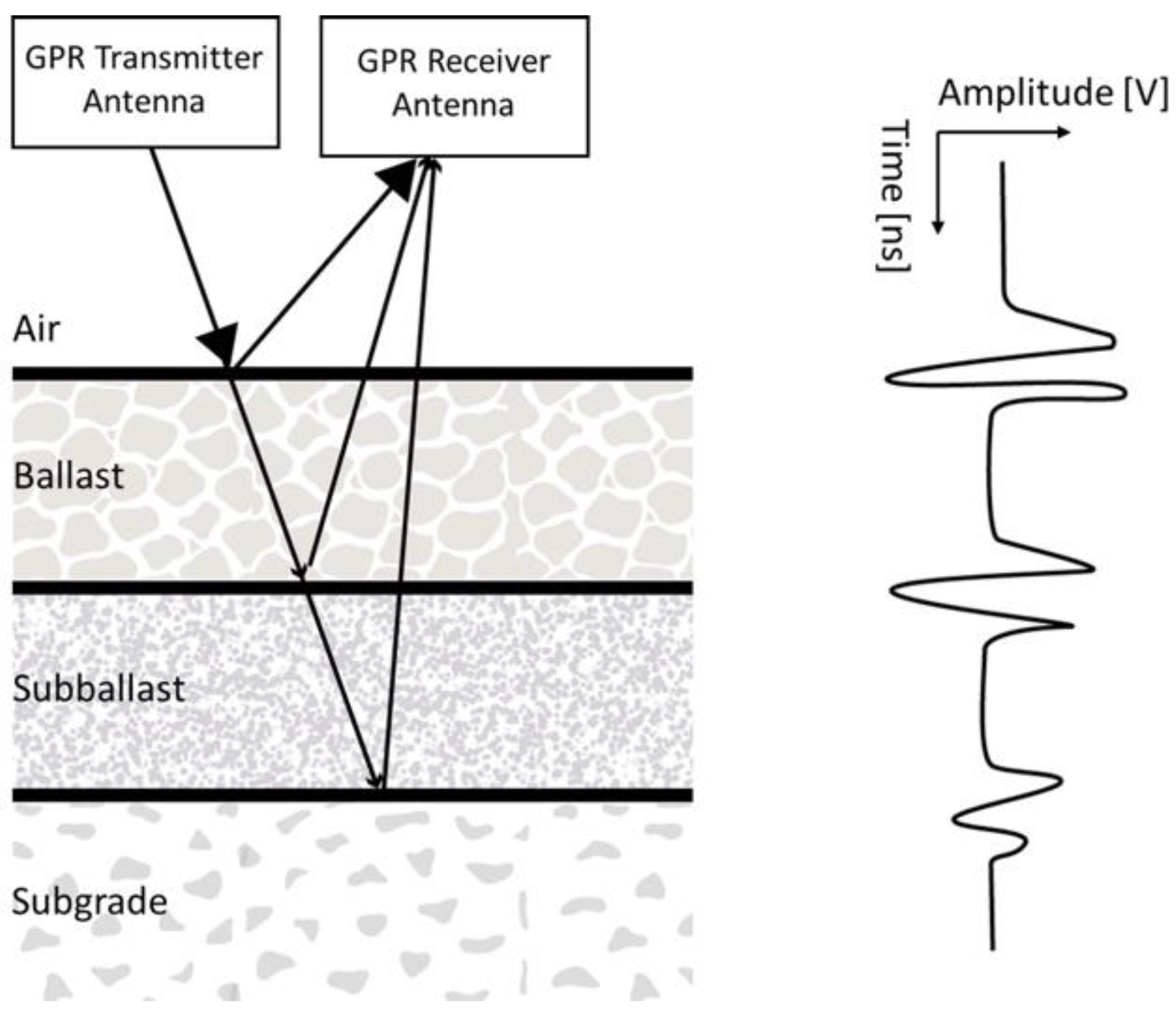
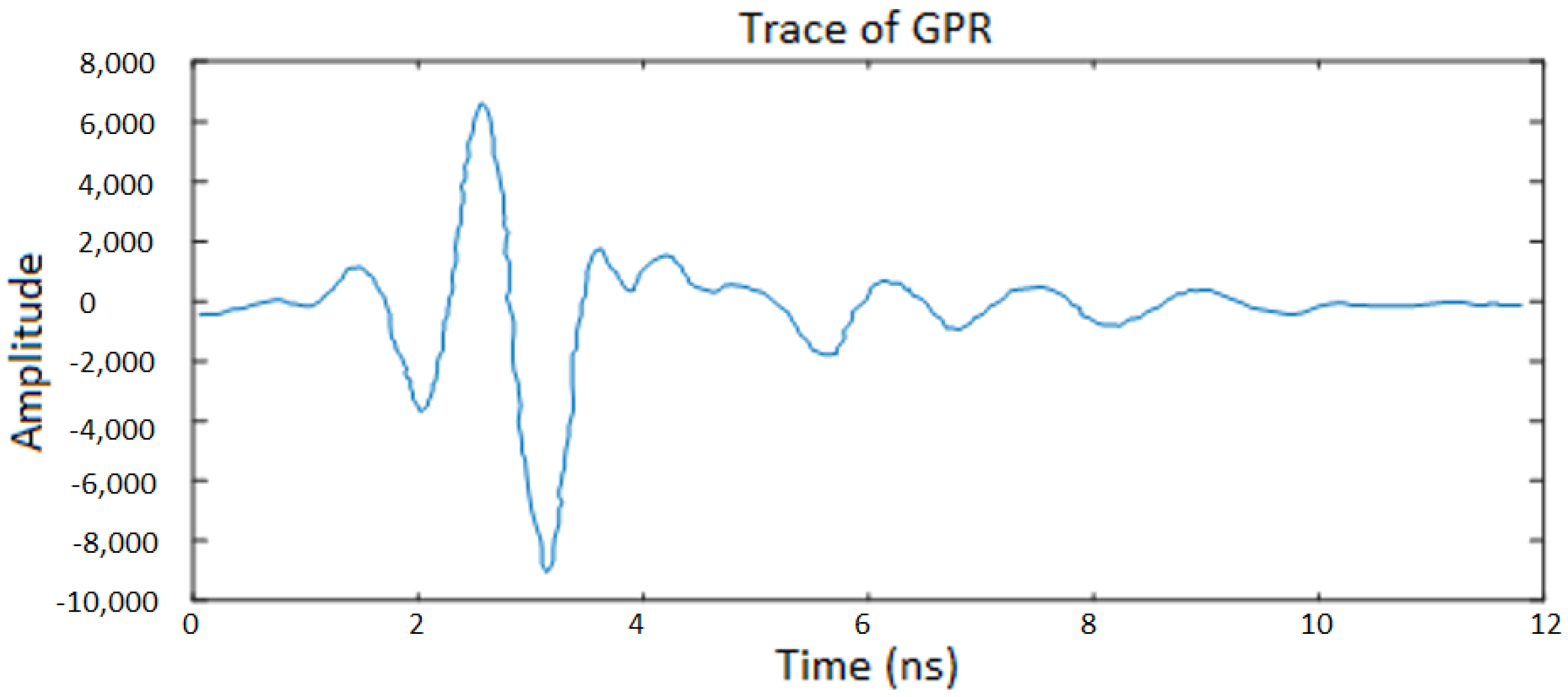
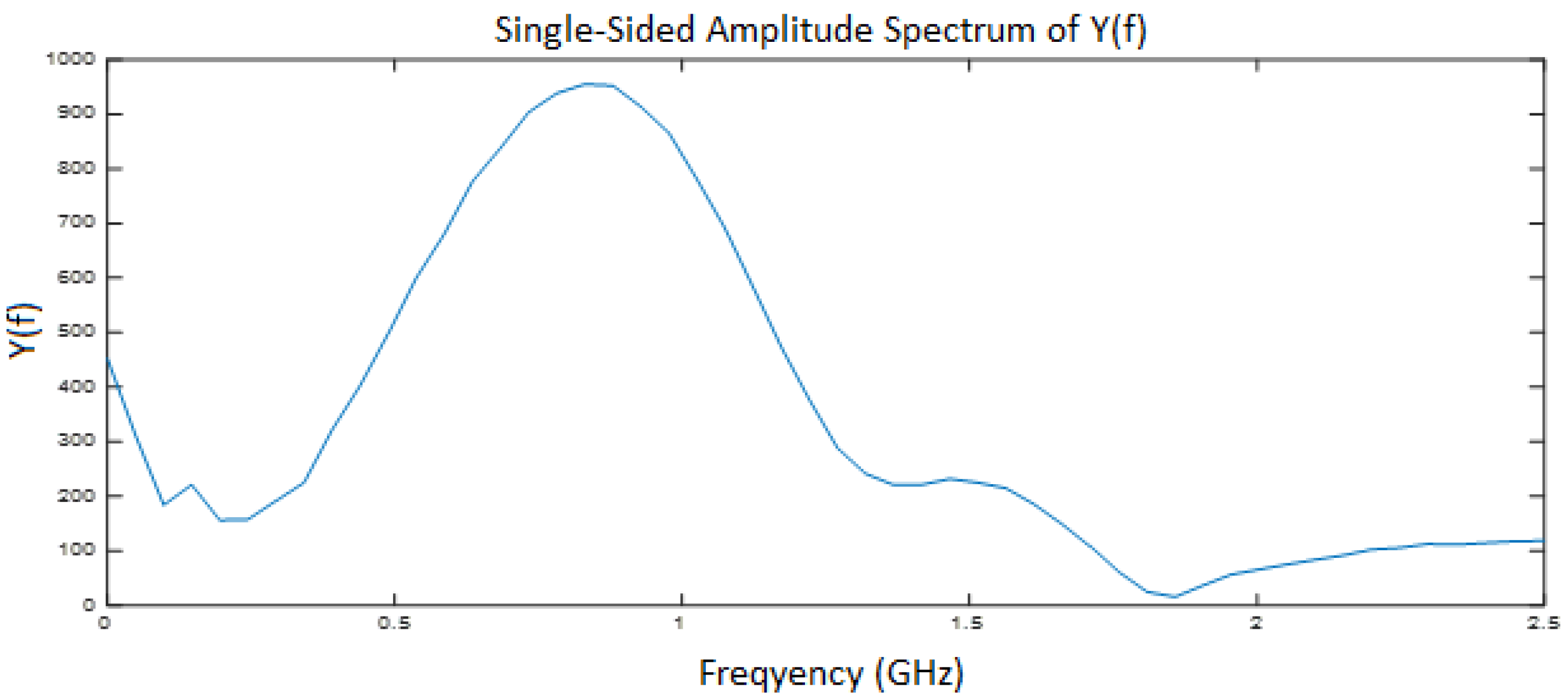
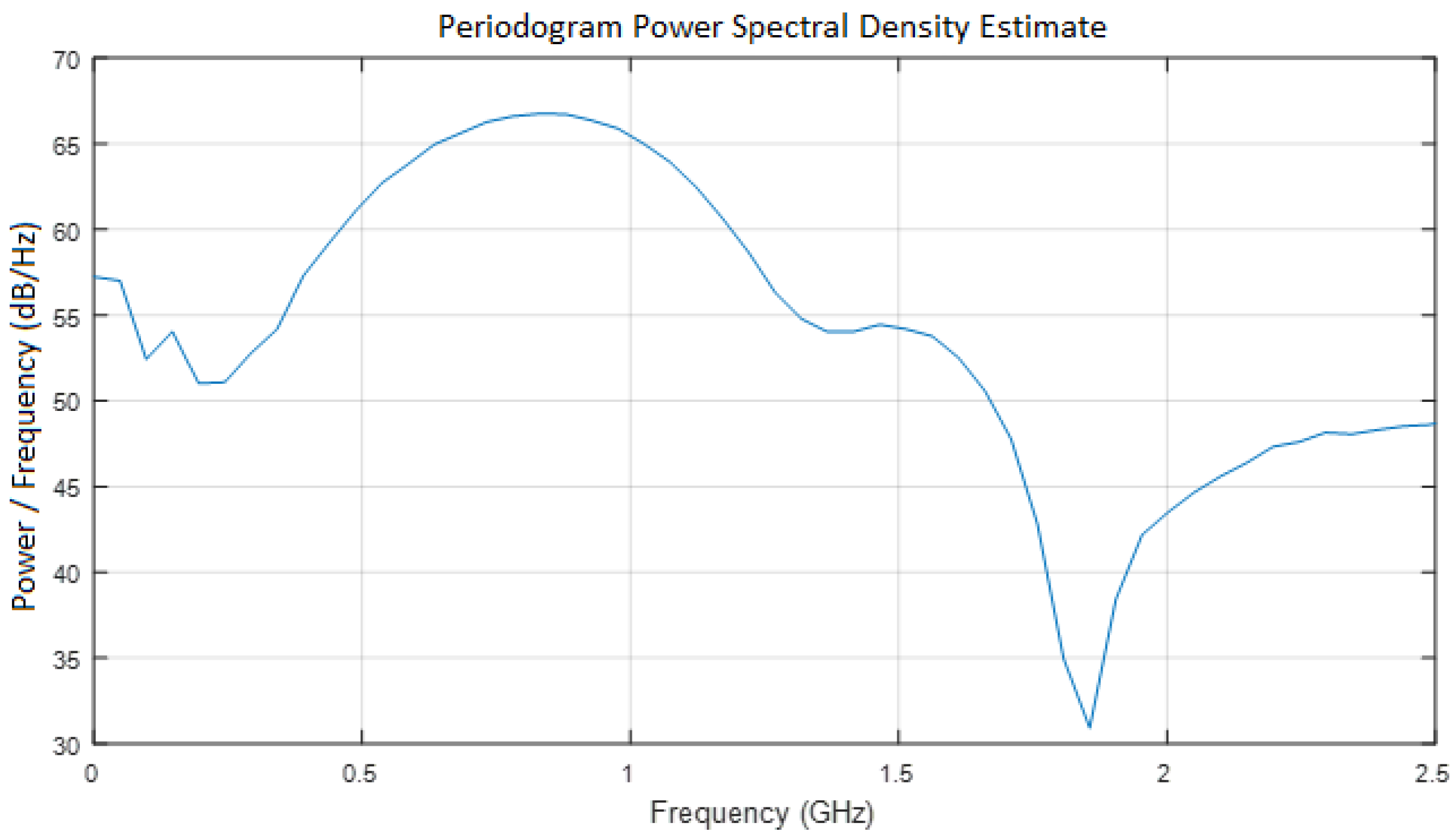
3. Detecting Time-Varying Dynamic Properties of Ballast Using GPR
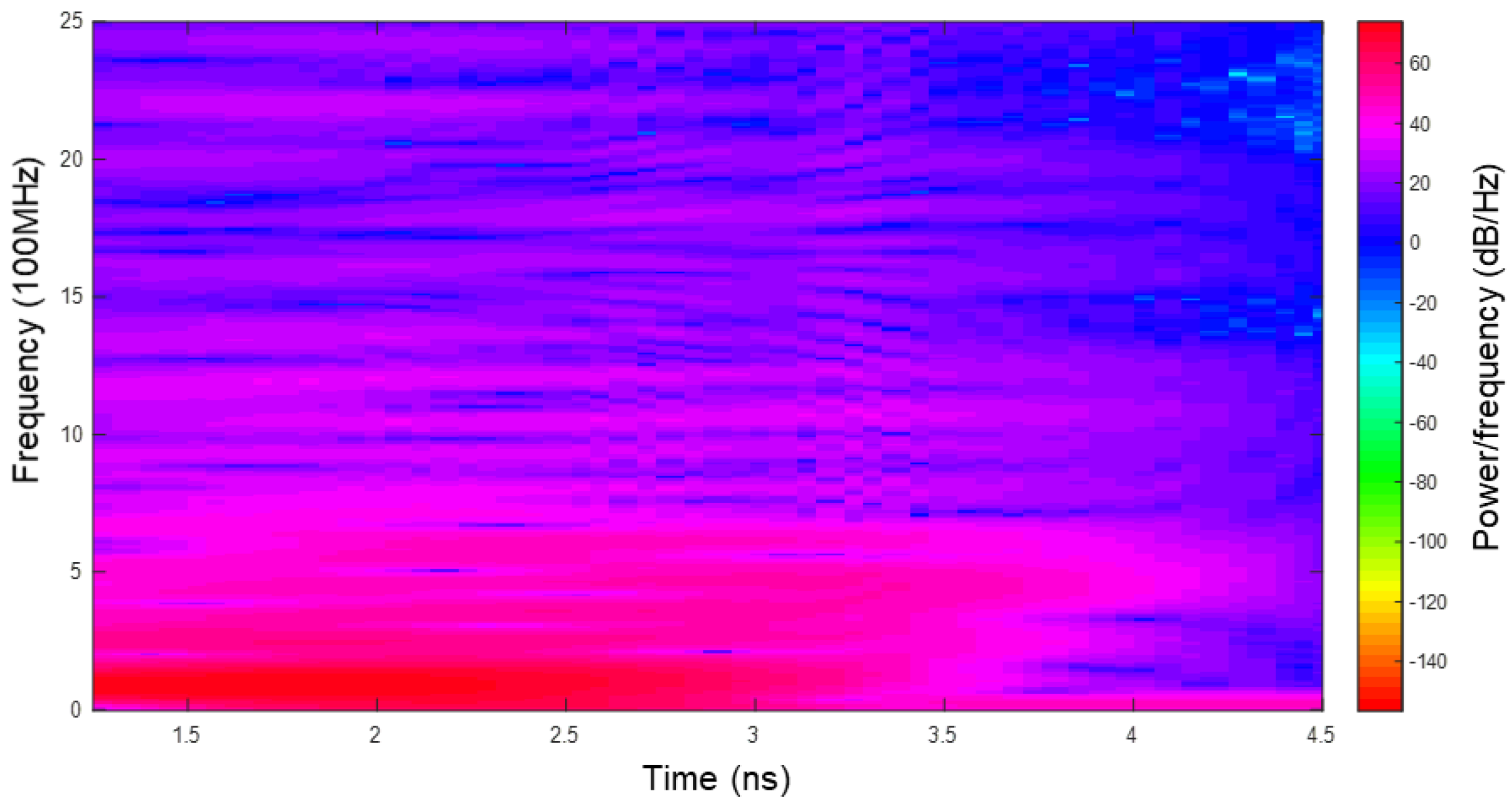
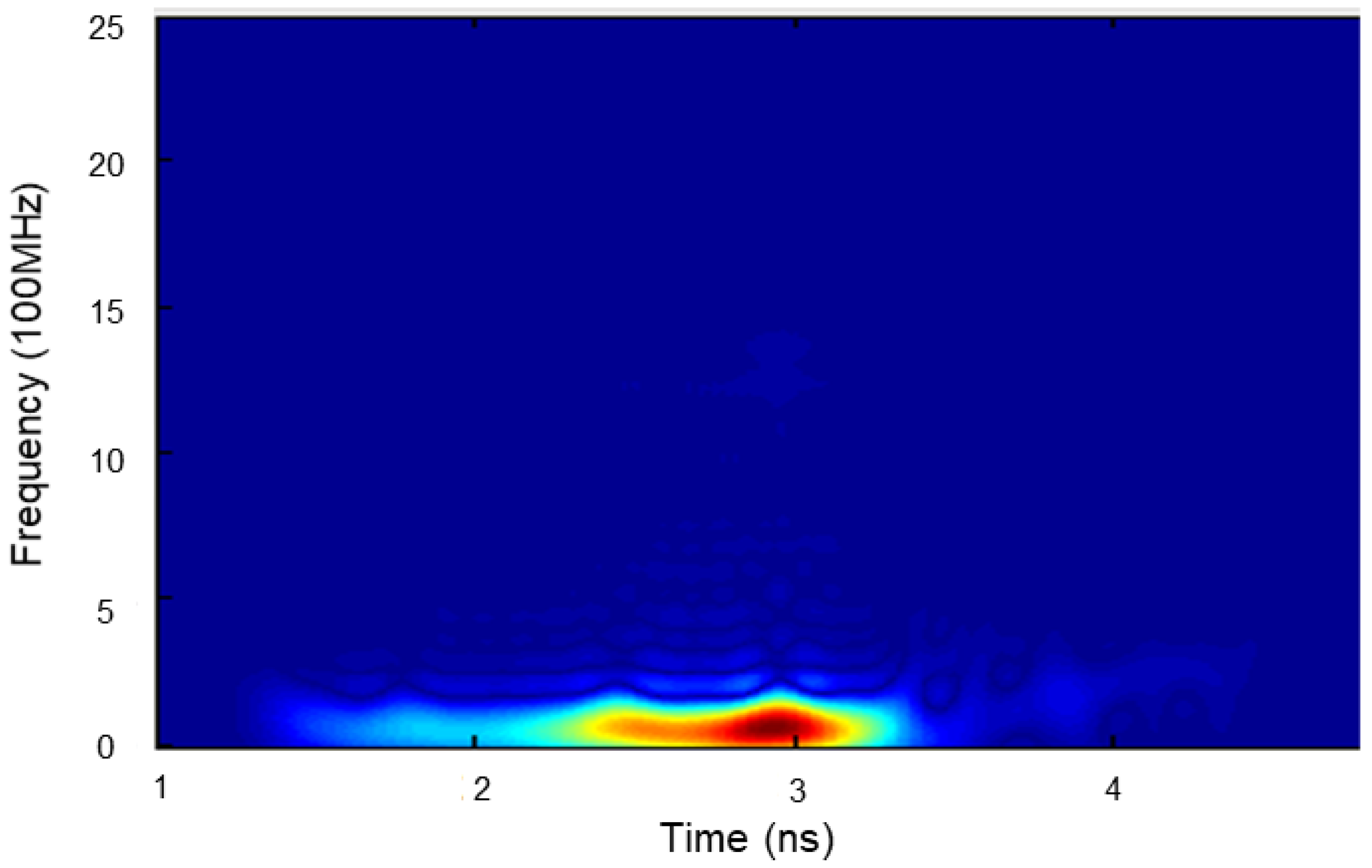
4. Characterization of Dynamic Properties of Ballast GPR Signal Using AOKTFR
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Knothe, K.; Stichel, S. Rail Vehicle Dynamics; Springer: Cham, Switzerland, 2003. [Google Scholar]
- Zhai, W. Vehicle-Track Coupled Dynamics: Theory and Applications; Springer: Cham, Switzerland, 2019. [Google Scholar]
- Shih, J.Y.; Kostovasilis, D.; Bezin, Y.; Thompson, D.J. Modelling options for ballast track dynamics. In Proceedings of the 24th International Congress on Sound and Vibration, London, UK, 23–27 July 2017. [Google Scholar]
- Chen, G.; Zheng, H. Railway wear monitoring. In Encyclopedia of Tribology; Springer: Cham, Switzerland, 2013; pp. 2740–2743. [Google Scholar]
- Mosayebi, S.-A.; Zakeri, J.-A.; Esmaeili, M. Vehicle/track dynamic interaction considering developed railway substructure models. Struct. Eng. Mech. 2017, 61, 775–784. [Google Scholar] [CrossRef]
- Milne, D.; Harkness, J.; Le Pen, L.; Powrie, W. The influence of variation in track level and support system stiffness over longer lengths of track for track performance and vehicle track interaction. Veh. Syst. Dyn. 2021, 59, 245–268. [Google Scholar] [CrossRef]
- Burrow, P.F.T.; Dahlberg, T.; Berggren, E. Track stiffness considerations for high speed railway lines. In Railway Transportation; Scott, N.P., Ed.; Nova Science Publishers: New York, NY, USA, 2017; pp. 1–55. [Google Scholar]
- Wang, P.; Wang, L.; Chen, R.; Xu, J.; Gao, M. Overview and outlook on railway track stiffness measurement. J. Mod. Transp. 2016, 24, 89–102. [Google Scholar] [CrossRef]
- Grossoni, I.; Andrade, A.R.; Bezin, Y.; Thompson, D. The role of track stiffness and its spatial variability on long-term track quality deterioration. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2019, 233, 16–32. [Google Scholar] [CrossRef]
- Hua, X.; Zatar, W.; Gadedesi, A.; Liao, Z. Assessment technologies of rail systems’ structural adequacy—A review from mechanical engineering perspectives. Sci. Prog. 2022, 105, 00368504221099877. [Google Scholar] [CrossRef]
- Tong, Y.; Liu, G.; Yousefian, K.; Jing, G. Track vertical stiffness—Value, measurement methods, effective parameters and challenges: A review. Transp. Geotech. 2022, 37, 100833. [Google Scholar] [CrossRef]
- Lee, J.-I.; Oh, K.-H.; Park, Y.-G. Separate track impact factor application depending on track types through correlative analysis with track support stiffness. Infrastructures 2020, 5, 17. [Google Scholar] [CrossRef]
- Shen, C.; Dollevoet, R.; Li, Z. Fast and robust identification of railway track stiffness from simple field measurement. Mech. Syst. Signal Process. 2021, 152, 107431. [Google Scholar] [CrossRef]
- Rodrigues, A.F.S.; Dimitrovová, Z. Applicability of a three-layer model for the dynamic analysis of ballasted railway tracks. Vibration 2021, 4, 151–174. [Google Scholar] [CrossRef]
- Huang, J.; Yin, X.; Kaewunruen, S. Quantification of dynamic track stiffness using machine learning. IEEE Access 2024, 10, 78747–78753. [Google Scholar] [CrossRef]
- Dimitrovová, Z. On the critical velocity of moving force and instability of moving mass in layered railway track models by semianalytical approaches. Vibration 2023, 6, 113–146. [Google Scholar] [CrossRef]
- Kurhan, D.; Kurhan, M.; Horváth, B.; Fischer, S. Determining the deformation characteristics of railway ballast by mathematical modeling of elastic wave propagation. Appl. Mech. 2023, 4, 803–815. [Google Scholar] [CrossRef]
- Liu, D.; Su, C.; Zhang, D.; Lan, C. The influence of an unsupported sleeper on the vertical bearing characteristics of heavy-haul railway ballast. Materials 2024, 17, 1434. [Google Scholar] [CrossRef] [PubMed]
- Eroğlu, M.; Koç, M.A.; Esen, İ. Realistic modelling for analysis of train-structure and ballasted-track interaction for high-speed trains. J. Vib. Eng. Technol. 2024, 12, 7065–7097. [Google Scholar] [CrossRef]
- Coop, M.R.; Altuhafi, F.N.; Wong, C.P.Y. The discrete and continuum behavior of railway ballast. Transp. Geotech. 2024, 46, 101251. [Google Scholar] [CrossRef]
- Uyulan, C.; Gokasan, M. Nonlinear dynamic characteristics of the railway. Nonlin. Eng. 2017, 6, 123–137. [Google Scholar] [CrossRef]
- Qi, F.; Lei, Y.; Deng, P.; Huang, Q. Car body vertical vibration analysis under track medium wave irregularity and the influence factors of ballast bed. J. Low Freq. Noise Vib. Act. Control 2019, 38, 1160–1177. [Google Scholar] [CrossRef]
- Uzzal, R.U.A.; Ahmed, A.K.W.; Bhat, R.B. Modelling, validation, and analysis of a three-dimensional railway vehicle-track system model with linear and nonlinear track properties in the presence of wheel flats. Veh. Syst. Dyn. 2013, 51, 1695–1721. [Google Scholar] [CrossRef]
- Thompson, D. Railway Noise and Vibration: Mechanisms, Modelling and Means of Control; Elsevier: Amsterdam, The Netherlands, 2008. [Google Scholar]
- Zhang, X.; Thompson, D.; Jeong, H.; Toward, M.; Herron, D.; Jones, C.; Vincent, N. Measurements of the high frequency dynamic stiffness of railway ballast and subgrade. J. Sound Vib. 2020, 468, 115081. [Google Scholar] [CrossRef]
- Alabbasi, Y.; Hussein, M. Geomechanical modelling of railroad ballast: A review. Arch. Comput. Methods Eng. 2021, 28, 815–839. [Google Scholar] [CrossRef]
- Punetha, P.; Nimbalkar, S.; Khabbaz, H. Simplified geotechnical rheological model for simulating viscoelasto-plastic response of ballasted railway substructure. Int. J. Numer. Anal. Methods Geomech. 2021, 45, 2019–2047. [Google Scholar] [CrossRef]
- Punetha, P.; Nimbalkar, S. Geotechnical rheological modelling of ballasted railway tracks considering the effect of principal stress rotation. Can. Geotech. J. 2022, 59, 10. [Google Scholar] [CrossRef]
- Kaewunruen, S.; Tang, T. Idealisations of dynamic modelling for railway ballast in flood conditions. Appl. Sci. 2019, 9, 1785. [Google Scholar] [CrossRef]
- Bai, W.; Xu, L. Theoretical studies on the longitudinal inhomogeneity of track stiffness and a track status estimation method. Adv. Civ. Eng. 2021, 15, 8847633. [Google Scholar] [CrossRef]
- Adeagbo, M.O.; Lam, H.-F.; Ni, Y.Q. A Bayesian methodology for detection of railway ballast damage using the modified Ludwik nonlinear model. Eng. Struct. 2021, 236, 112047. [Google Scholar] [CrossRef]
- Lam, H.-F.; Adeagbo, M.O.; Yang, Y.-B. Time-domain Markov chain Monte Carlo-based Bayesian damage detection of ballasted tracks using nonlinear ballast stiffness model. Struct. Health Monit. 2021, 20, 2653–2677. [Google Scholar] [CrossRef]
- Adeagbo, M.O.; Lam, H.-F.; Hu, Q. On the selection of the most plausible non-linear axial stress–strain model for railway ballast under different impulse magnitudes. Struct. Health Monit. 2022, 21, 1447–1473. [Google Scholar] [CrossRef]
- Tahiri, M.; Khamlichi, A.; Bezzazi, M. Nonlinear analysis of the ballast influence on the train-bridge resonance of a simply supported railway bridge. Structures 2022, 35, 303–313. [Google Scholar] [CrossRef]
- Liu, J.; Liu, Z.; Wang, P.; Kou, L.; Sysyn, M. Dynamic characteristics of the railway ballast bed under water-rich and low-temperature environments. Eng. Struct. 2022, 252, 113605. [Google Scholar] [CrossRef]
- Altuhafi, F.N.; Coop, M.R. The Small-Strain Stiffness of a Railway Ballast. Géotechnique 2023, ahead of print. [Google Scholar] [CrossRef]
- Shi, C.; Zhou, Y.; Xu, L.; Zhang, X.; Guo, Y. A critical review on the vertical stiffness irregularity of railway ballasted track. Constr. Build. Mater. 2023, 400, 132715. [Google Scholar] [CrossRef]
- Robles, R.; Correa, N.; Vadillo, E.G.; Blanco-Lorenzo, J. Comprehensive efficient vertical and lateral track dynamic model to study the evolution of rail corrugation in sharp curves. J. Sound Vib. 2023, 545, 117448. [Google Scholar] [CrossRef]
- Farooq, H.; Nimbalkar, S.; Punetha, P.; Sheng, D. Viscoelastic rheological modelling of the lateral dynamic response of ballasted railway tracks. Transp. Infrastruct. Geotech. 2024, 11, 3667–3693. [Google Scholar] [CrossRef]
- Lamprea-Pineda, A.C.; Connolly, D.P.; Castanheira-Pinto, A.; Alves-Costa, P.; Hussein, M.F.M.; Woodward, P.K. On railway track receptance. Soil Dyn. Earthq. Eng. 2024, 177, 108331. [Google Scholar] [CrossRef]
- Jain, A.; Marykovskiy, Y.; Metrikine, A.V.; van Dalen, K.N. Quantifying the impact of stiffness distributions on the dynamic behaviour of railway transition zones. Transp. Geotech. 2024, 45, 101211. [Google Scholar] [CrossRef]
- Powrie, W. Railway track substructure: Recent research and future directions. Transp. Geotech. 2024, 46, 101234. [Google Scholar] [CrossRef]
- Dafert, M.; Pistrol, J.; Kopf, F.; Adam, D. Ballast stiffness estimation based on measurements during dynamic track stabilization. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2024, ahead of print. [Google Scholar] [CrossRef]
- Germonpré, M.; Nielsen, J.C.O.; Degrande, G.; Lombaert, G. Contributions of longitudinal track unevenness and track stiffness variation to railway induced vibration. J. Sound Vib. 2018, 437, 292–307. [Google Scholar] [CrossRef]
- Nasrollahi, K.; Ramos, A.; Nielsen, J.C.O.; Dijkstra, J.; Ekh, M. Benchmark of calibrated 2D and 3D track models for simulation of differential settlement in a transition zone using field measurement data. Eng. Struct. 2024, 316, 118555. [Google Scholar] [CrossRef]
- Vampire Dynamics. VAMPIRE® User Manual; Resonate Group Ltd.: Derby, UK, 2016. [Google Scholar]
- Wilson, N.; Shu, X.; Gonzales, K. TTCI’s Scientific Software Suite and NUCARS® Overview; Transportation Technology Centre Inc.: Pueblo, CO, USA, 2015. [Google Scholar]
- VI-Grade GmbH. VI-Rail 16.0 Documentation; 2020 VI-Grade Engineering Software & Services: Marburg, Germany, 2014. [Google Scholar]
- Fu, H.; Yang, Y.; Kaewunruen, S. Multi-hazard effects of crosswinds on cascading failures of conventional and interspersed railway tracks exposed to ballast washaway and moving train loads. Sensors 2023, 23, 1786. [Google Scholar] [CrossRef]
- Giner, I.G.; Alvarez, A.R.; García-Moreno, S.S.; Camacho, J.L. Dynamic modelling of high-speed ballasted railway tracks: Analysis of the behavior. Transp. Res. Proc. 2016, 18, 357–365. [Google Scholar] [CrossRef]
- Sayeed, M.A.; Shahin, M.A. Dynamic Response Analysis of Ballasted Railway Track–Ground System under Train Moving Loads using 3D Finite Element Numerical Modelling. Transp. Infrastruct. Geotech. 2023, 10, 639–659. [Google Scholar] [CrossRef]
- Balamonica, K.; Bergamini, A.; Van Damme, B. Estimation of the dynamic stiffness of railway ballast over a wide frequency range using the discrete element method. J. Sound Vib. 2023, 547, 117533. [Google Scholar] [CrossRef]
- Shi, C.; Zhao, C.; Yang, Y.; Guo, Y. Analysis of railway ballasted track stiffness and behavior with a hybrid discrete–continuum approach. Int. J. Geomech. 2021, 21, 3. [Google Scholar] [CrossRef]
- de Oliveira Barbosa, J.M.; Fărăgău, A.B.; van Dalen, K.N.; Steenbergen, M.J.M.M. Modelling ballast via a non-linear lattice to assess its compaction behaviour at railway transition zones. J. Sound Vib. 2022, 530, 116942. [Google Scholar] [CrossRef]
- Kumar, N.; Suhr, B.; Marschnig, S.; Dietmaier, P.; Marte, C.; Six, K. Micro-mechanical investigation of railway ballast behavior under cyclic loading in a box test using DEM: Effects of elastic layers and ballast types. Granul. Matter 2019, 21, 106. [Google Scholar] [CrossRef]
- Guo, Y.; Jia, W.; Markine, V.; Jing, G. Rheology study of ballast-sleeper interaction with particle image velocimetry (PIV) and discrete element modelling (DEM). Constr. Build. Mater. 2021, 282, 122710. [Google Scholar] [CrossRef]
- Narayanan, R.M.; Jakub, J.W.; Li, D.; Elias, S.E. Railroad track modulus estimation using ground penetrating radar measurements. NDT E Int. 2004, 37, 141–151. [Google Scholar] [CrossRef]
- Bold, R. Evaluation of Railway Trackbed Ballast. Ph.D. Thesis, University of Edinburgh, Edinburgh, UK, 2011. [Google Scholar]
- Berggren, E.; Kaynia, A.; Dehlbom, B. Identification of substructure properties of railway tracks by dynamic stiffness measurements and simulations. J. Sound Vib. 2010, 329, 3999–4016. [Google Scholar] [CrossRef]
- Leng, Z.; Al-Qadi, I.L. Railroad ballast evaluation using ground-penetrating radar. Transp. Res. Rec. 2010, 2159, 110–117. [Google Scholar] [CrossRef]
- Shao, W.; Bouzerdoum, A.; Phung, S.L.; Su, L.; Indraratna, B.; Rujikiatkamjorn, C. Automatic classification of ground-penetrating-radar signals for railway-ballast assessment. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3961–3972. [Google Scholar] [CrossRef]
- Tosti, F.; Bianchini Ciampoli, L.B.; Calvi, A.; Alani, A.M.; Benedetto, A. An investigation into the railway ballast dielectric properties using different GPR antennas and frequency systems. NDT E Int. 2013, 93, 131–140. [Google Scholar] [CrossRef]
- Walton-Macaulay, C.; Bryson, L.S.; Guenther, K.J. Experimental study on the stiffness degradation of railroad ballast subjected to clay fouling. In Proceedings of the ASME/IEEE 2014 Joint Rail Conference, Colorado Springs, CO, USA, 2–4 April 2014. [Google Scholar]
- Kelsey, C. Permanent deformation and stiffness of fouled ballast. NDT E Int. 2017, 90, 39–47. [Google Scholar]
- Bianchini Ciampoli, L.; Tosti, F.; Brancadoro, M.G.; D’Amico, F.; Alani, A.M.; Benedetto, A. A spectral analysis of ground-penetrating radar data for the assessment of the railway ballast geometric properties. NDT E Int. 2017, 90, 39–47. [Google Scholar] [CrossRef]
- Fontul, S.; Paixão, A.; Solla, M.; Pajewski, L. Railway track condition assessment at network level by frequency domain analysis of GPR data. Remote Sens. 2018, 10, 559. [Google Scholar] [CrossRef]
- Al-Qadi, I.L.; Zhao, S.; Shangguan, P. Railway ballast fouling detection using GPR data: Introducing a combined time-frequency and discrete wavelet techniques. Near Surf. Geophys. 2016, 14, 145–153. [Google Scholar] [CrossRef]
- Scanlan, K.M.; Hendry, M.T.; Martin, C.S.; Schmitt, D. A review of methods for estimating ballast degradation using ground-penetrating radar. In Railroad Ballast Testing and Properties; Stark, T., Swan, R., Szecsy, R., Eds.; ASTM International: West Conshohocken, PA, USA, 2018; pp. 54–76. [Google Scholar]
- Tamrakar, P.; Nazarian, S. Permanent deformation and stiffness of fouled ballast based on static and impact load tests. In Proceedings of the GAP 2019, Colorado Springs, CO, USA, 4–7 November 2019; Minerva TRI: Austin, TX, USA, 2019. [Google Scholar]
- Ciampoli, L.B.; Calvi, A.; D’Amico, F. Railway ballast monitoring by GPR: A test site investigation. Remote Sens. 2019, 11, 2381. [Google Scholar] [CrossRef]
- Ciampoli, L.B.; Calvi, A.; Oliva, E. Test-site operations for the health monitoring of railway ballast using ground-penetrating radar. Transp. Res. Proc. 2020, 45, 763–770. [Google Scholar]
- Birhane, F.N.; Choi, Y.T.; Lee, S.J. Development of condition assessment index of ballast track using ground-penetrating radar. Sensors 2021, 21, 6875. [Google Scholar] [CrossRef]
- Wang, S.; Liu, G.; Jing, G.; Feng, Q.; Liu, H.; Guo, Y. Review state-of-the-art review of ground penetrating radar (GPR) applications for railway ballast inspection. Sensors 2022, 22, 2450. [Google Scholar] [CrossRef]
- Guo, Y.; Liu, G.; Jing, G.; Qu, J.; Wang, S.; Qiang, W. Ballast fouling inspection and quantification with ground-penetrating radar (GPR). Int. J. Rail Transp. 2023, 11, 151–168. [Google Scholar] [CrossRef]
- Hou, Z.; Zhao, W.; Yang, Y. Identification of railway subgrade defects based on ground-penetrating radar. Sci. Rep. 2023, 13, 6030. [Google Scholar] [CrossRef]
- Shi, C.; Fan, Z.; Connolly, D.P.; Jing, G.; Markine, V.; Guo, Y. Railway ballast performance: Recent advances in the understanding of geometry, distribution, and degradation. Transp. Geotech. 2023, 41, 101042. [Google Scholar] [CrossRef]
- Alzarrad, A.; Wise, C.; Chattopadhyay, A.; Chowdhury, S.; Cisko, A.; Beasley, J. Railroad infrastructure management: A novel tool for automatic interpretation of GPR imaging to minimize human intervention in railroad inspection. Civ. Eng. 2024, 5, 378–394. [Google Scholar]
- Kim, Y.; Wiggins, R.; Byun, Y.-H.; Qamhia, I.I.A.; Tutumluer, E.; Beasley, J.; Cisko, A.; Kashani, H.; Langlois, R.; Harrell, M.J. Characterization of Degraded Ballast Strength: A Field Application of Ground Penetrating Radar and Dynamic Cone Penetration. Transp. Res. Rec. 2024, ahead of print. [Google Scholar] [CrossRef]
- Rahman, M.H.; Bhuyan, M.H.; Hayano, K. Fouling conditions and associated deformation characteristics of railway ballast. Int. J. Rail Transp. 2024, ahead of print. [Google Scholar] [CrossRef]
- Jones, D.L.; Baraniuk, R.G. An adaptive optimal-kernel time-frequency representation. IEEE Trans. Signal Process. 1995, 43, 2361–2371. [Google Scholar] [CrossRef]
- Wang, X.; Gao, J.; Chen, W.; Zhao, W.; Jiang, X.; Zhu, Z. Seismic attenuation qualitative characterizing method based on adaptive optimal-kernel time-frequency representation. J. Appl. Geophys. 2013, 89, 125–133. [Google Scholar] [CrossRef]
- Liao, R.; Guo, C.; Wang, K.; Zuo, Z.; Zhuang, A. Adaptive optimal kernel time–frequency representation technique for partial discharge ultra-high-frequency signals classification. Electr. Power Compon. Syst. 2015, 43, 449–460. [Google Scholar] [CrossRef]
- Chen, H.; Wang, J.; Li, J.; Tang, B. A texture-based rolling bearing fault diagnosis scheme using adaptive optimal kernel time frequency representation and uniform local binary patterns. Meas. Sci. Technol. 2017, 28, 035903. [Google Scholar] [CrossRef]
- Gao, Z.K.; Cai, Q.; Yang, Y.X.; Dong, N.; Zhang, S.S. Visibility graph from adaptive optimal kernel time-frequency representation for classification of epileptiform EEG. Int. J. Neural Syst. 2017, 27, 1750005. [Google Scholar] [CrossRef]
- Gao, Z.; Zhang, K.; Dang, W.; Yang, Y.; Wang, Z.; Duan, H.; Chen, G. An adaptive optimal-kernel time-frequency representation-based complex network method for characterizing fatigued behavior using the SSVEP-based BCI system. Knowl. Based Syst. 2018, 152, 163–171. [Google Scholar] [CrossRef]
- Tsugawa, J.K.; Romano, R.C.; Pileggi, R.G.; Boscov, M.E.G. Review: Rheology concepts applied to geotechnical engineering. Appl. Rheol. 2019, 29, 202–221. [Google Scholar] [CrossRef]
- Austrell, P.E. Modeling of Elasticity and Damping for Filled Elastomers. Ph.D. Dissertation, Lund University, Lund Institute of Technology, Lund, Sweden, 1997. [Google Scholar]
- Irazábal, J.; Salazar, F.; Oñate, E. Numerical modelling of granular materials with spherical discrete particles and the bounded rolling friction model: Application to railway ballast. Comput. Geotech. 2017, 85, 220–229. [Google Scholar] [CrossRef]
- Macosko, C.W. Rheology Principles, Measurements, and Applications; Wiley-VCH: New York, NY, USA, 1994. [Google Scholar]
- Zhang, L.; Meng, D.; Chen, G. Noise, Vibration and Harshness of Electric and Hybrid Vehicles; SAE International: Warrendale, PA, USA, 2020; ISBN 978-0-7680-9964-5. [Google Scholar]
- Zhang, L.; Yu, Z.; Yu, Z. Novel model of rubber bushing in automotive suspension. In Proceedings of the ISMA2010-USD2010 Conference, Leuven, Belgium, 20–22 September 2010. [Google Scholar]
- Yang, Y.; Peng, Z.; Zhang, W.; Meng, G. Parameterised time-frequency analysis methods and their engineering applications: A review of recent advances. Mech. Syst. Signal Process. 2019, 119, 182–221. [Google Scholar] [CrossRef]
- Cui, X.; Ke, B.; Yu, S.; Li, P.; Zhao, M. Energy characteristics of seismic waves on Cardox blasting. Geofluids 2021, 2021, 9919764. [Google Scholar] [CrossRef]
- Wang, Y.; Zhou, P.; Zhou, C.; Zhou, W.; Li, J. Analysis of cavitation-induced vibration characteristics of a vortex pump based on adaptive optimal kernel time-frequency representation. J. Appl. Fluid Mech. 2024, 17, 591–603. [Google Scholar]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hua, X.; Zatar, W.; Cheng, X.; Chen, G.S.; She, Y.; Xu, X.; Liao, Z. Modeling and Characterization of Complex Dynamical Properties of Railway Ballast. Appl. Sci. 2024, 14, 11224. https://doi.org/10.3390/app142311224
Hua X, Zatar W, Cheng X, Chen GS, She Y, Xu X, Liao Z. Modeling and Characterization of Complex Dynamical Properties of Railway Ballast. Applied Sciences. 2024; 14(23):11224. https://doi.org/10.3390/app142311224
Chicago/Turabian StyleHua, Xia, Wael Zatar, Xiangle Cheng, Gang S. Chen, Yini She, Xiaotian Xu, and Zhicheng Liao. 2024. "Modeling and Characterization of Complex Dynamical Properties of Railway Ballast" Applied Sciences 14, no. 23: 11224. https://doi.org/10.3390/app142311224
APA StyleHua, X., Zatar, W., Cheng, X., Chen, G. S., She, Y., Xu, X., & Liao, Z. (2024). Modeling and Characterization of Complex Dynamical Properties of Railway Ballast. Applied Sciences, 14(23), 11224. https://doi.org/10.3390/app142311224







