Airfoil Design and Flow Analysis of a Multi-Blade Centrifugal Fan: An Experimental and Simulation Study
Abstract
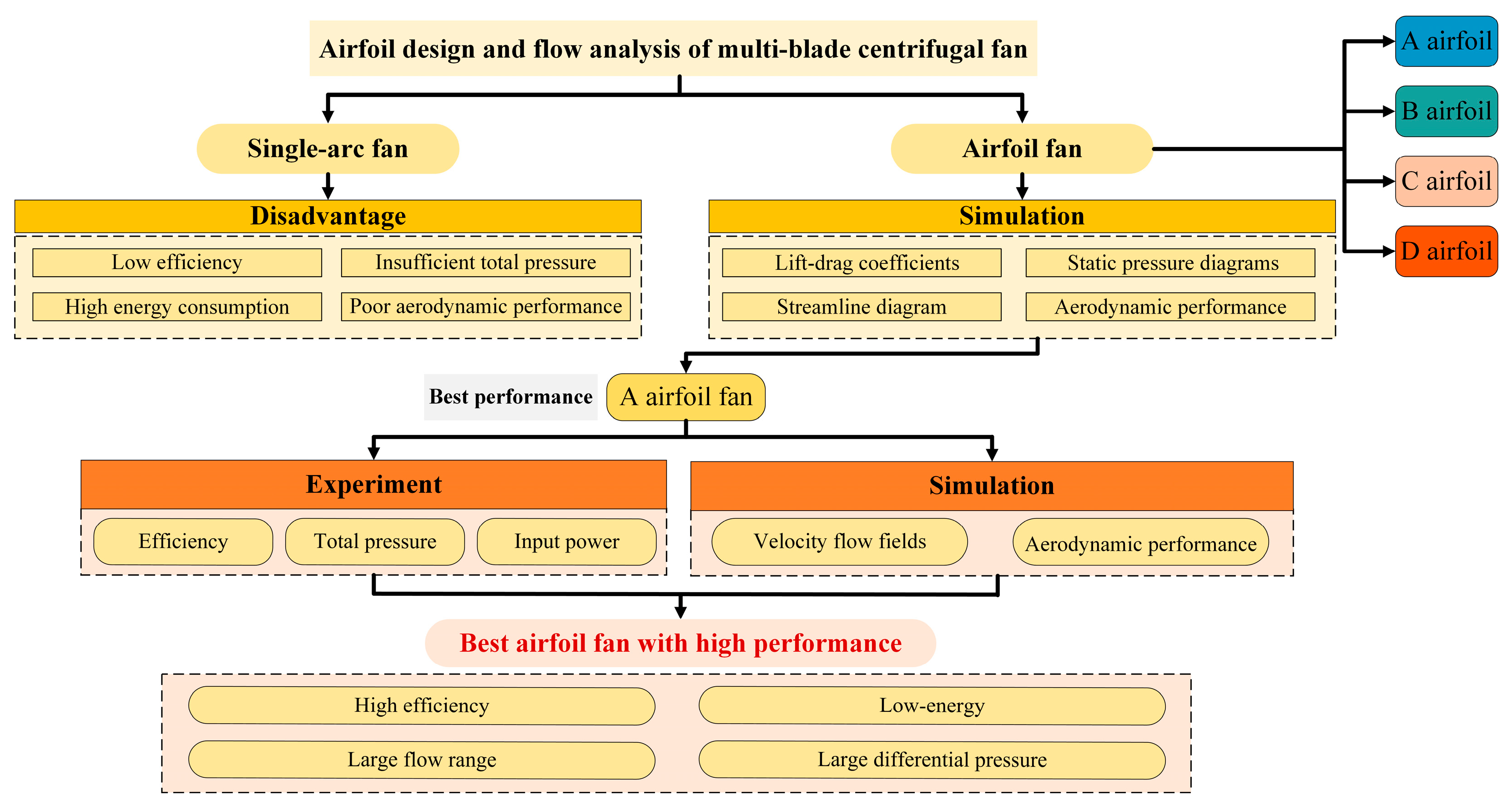
:1. Introduction
2. Methodology
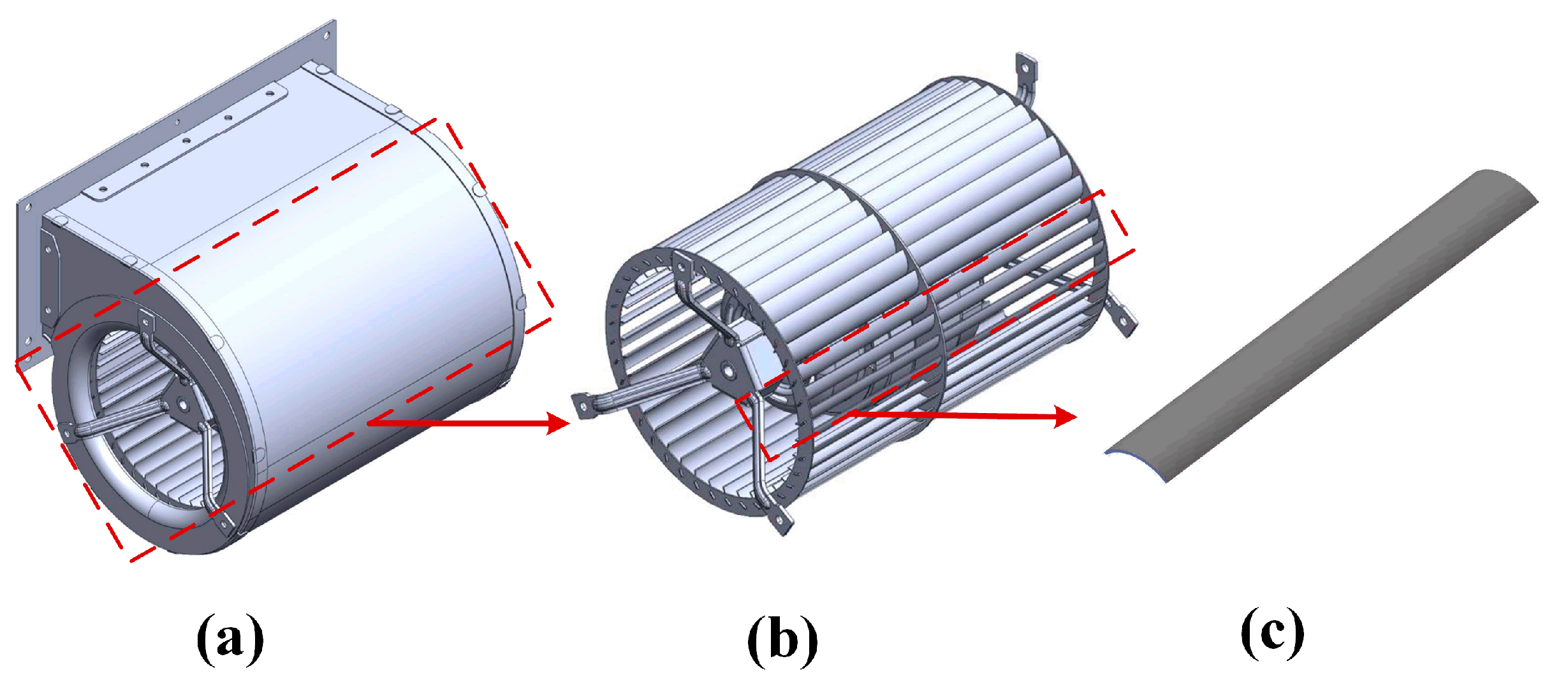
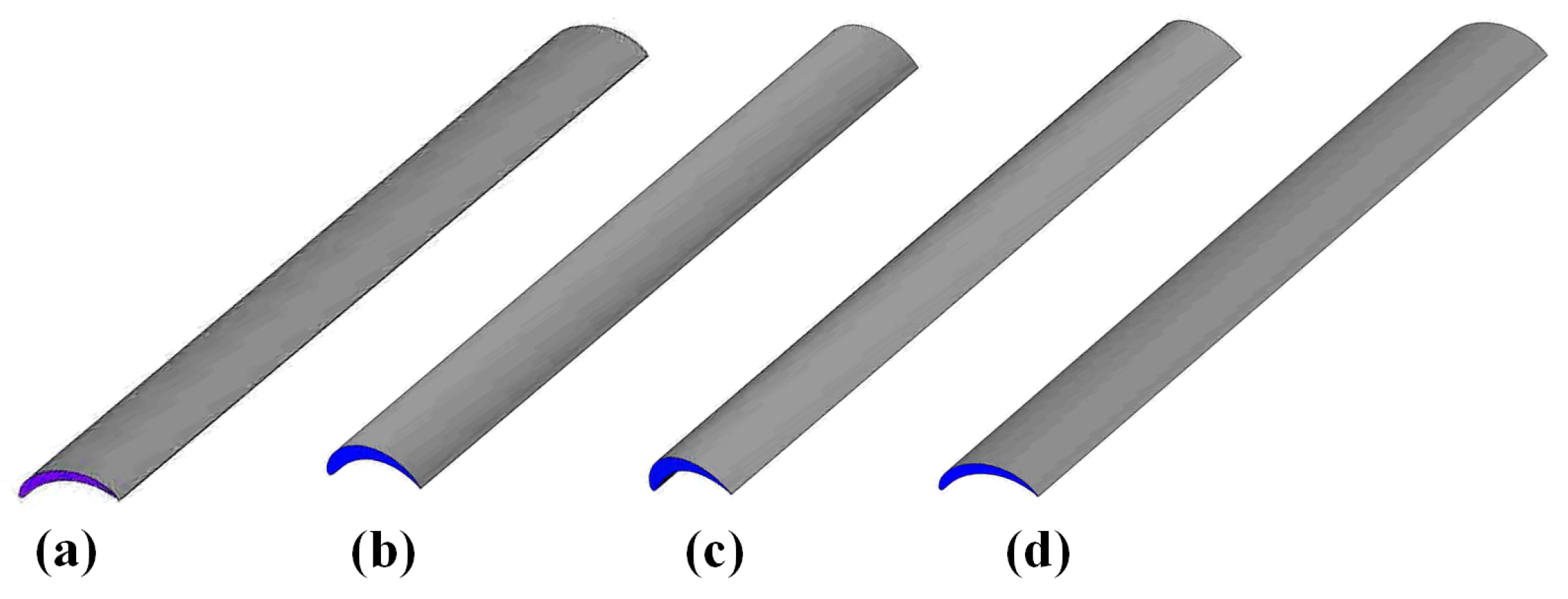
2.1. Geometric and Mathematical Models
2.2. Airfoil Theory
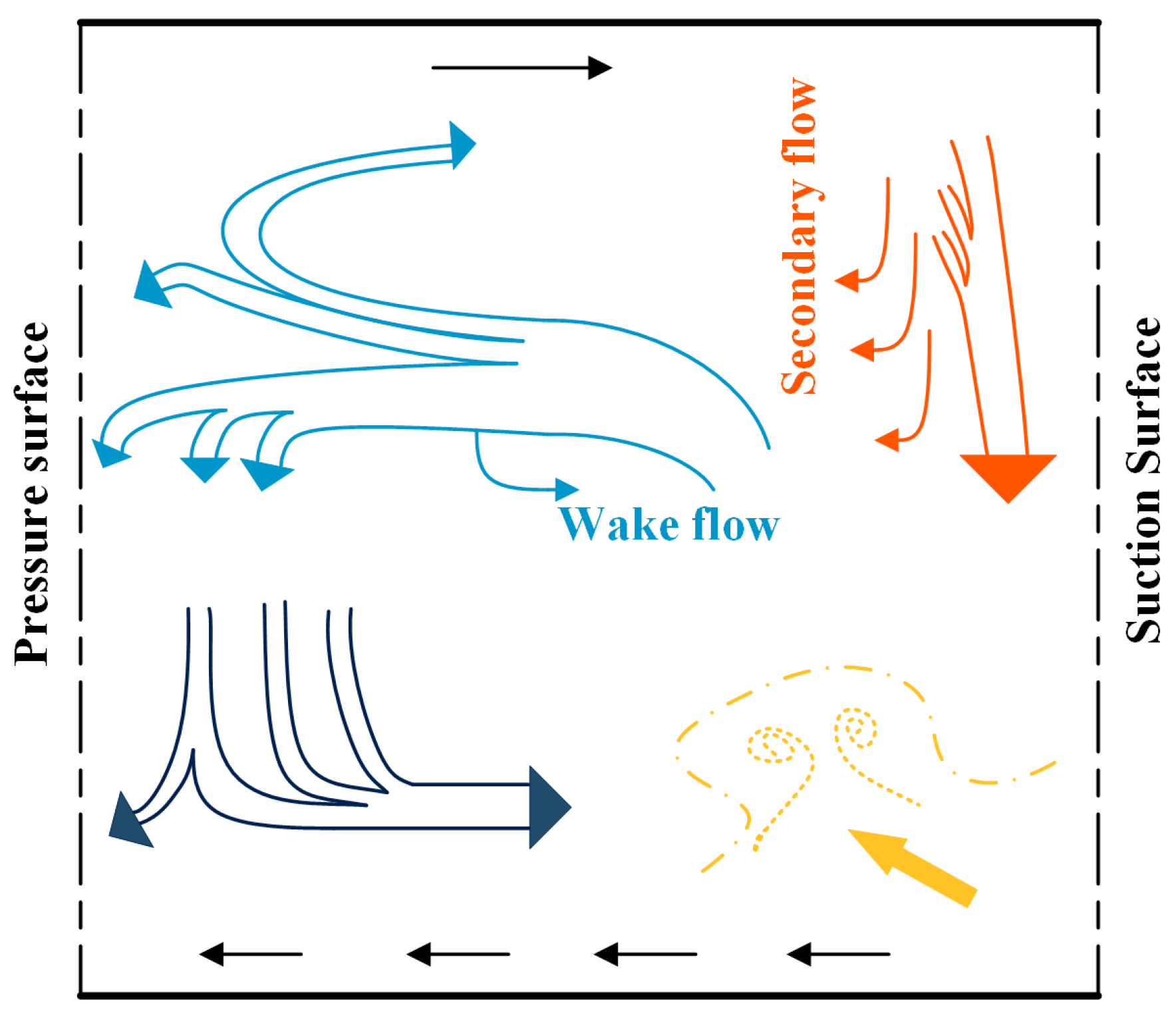
2.3. Flow Effect in Impeller
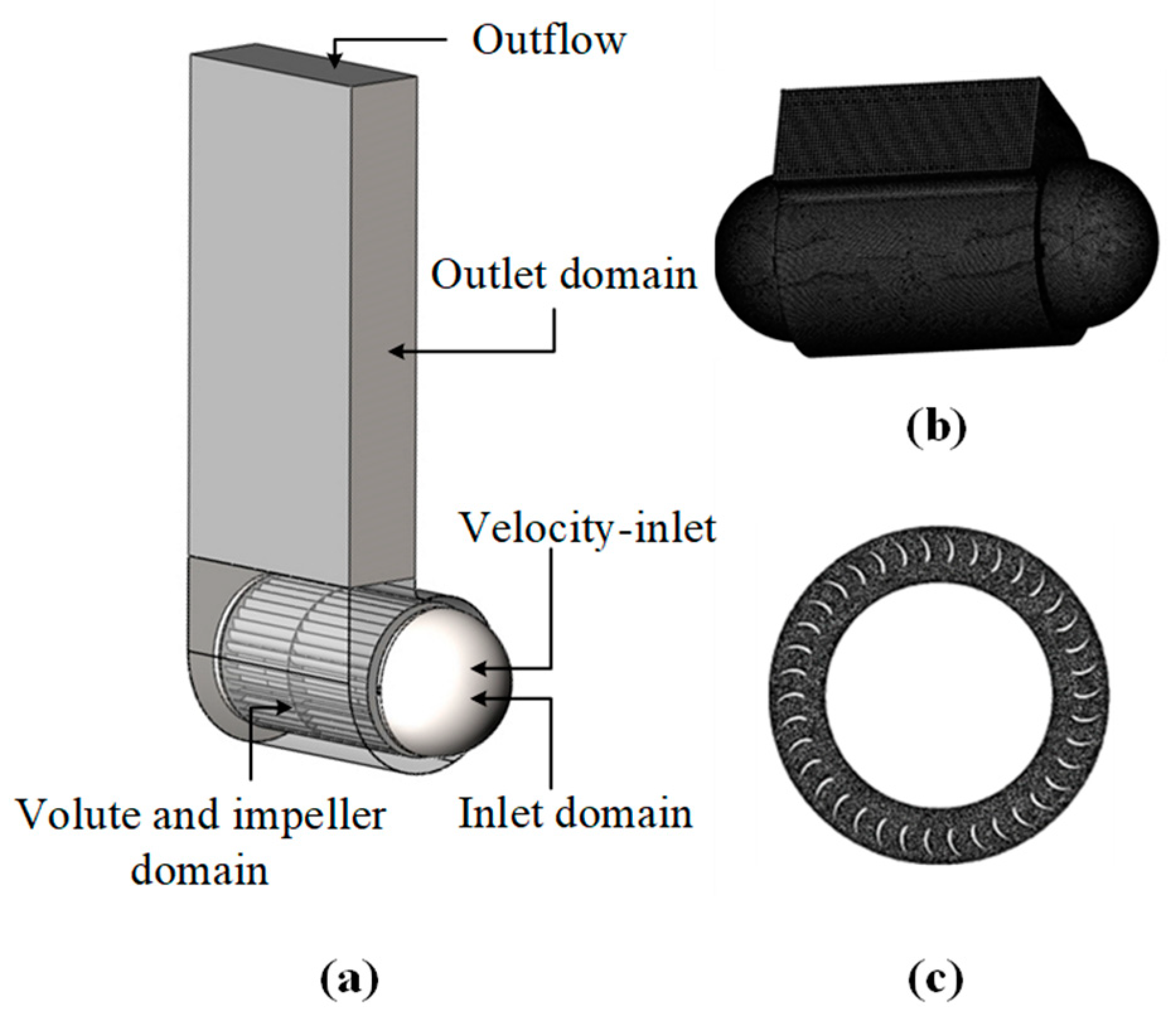
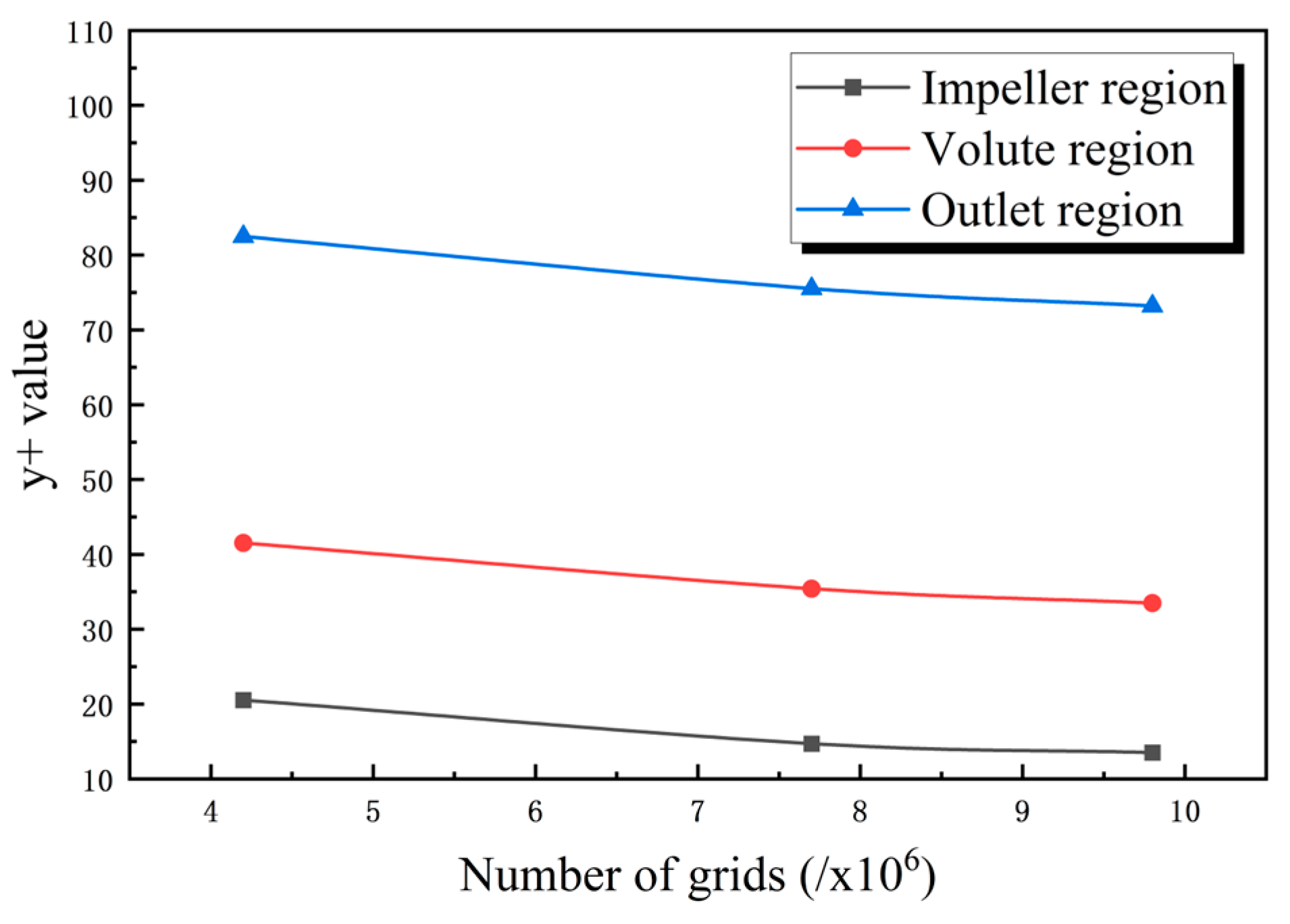
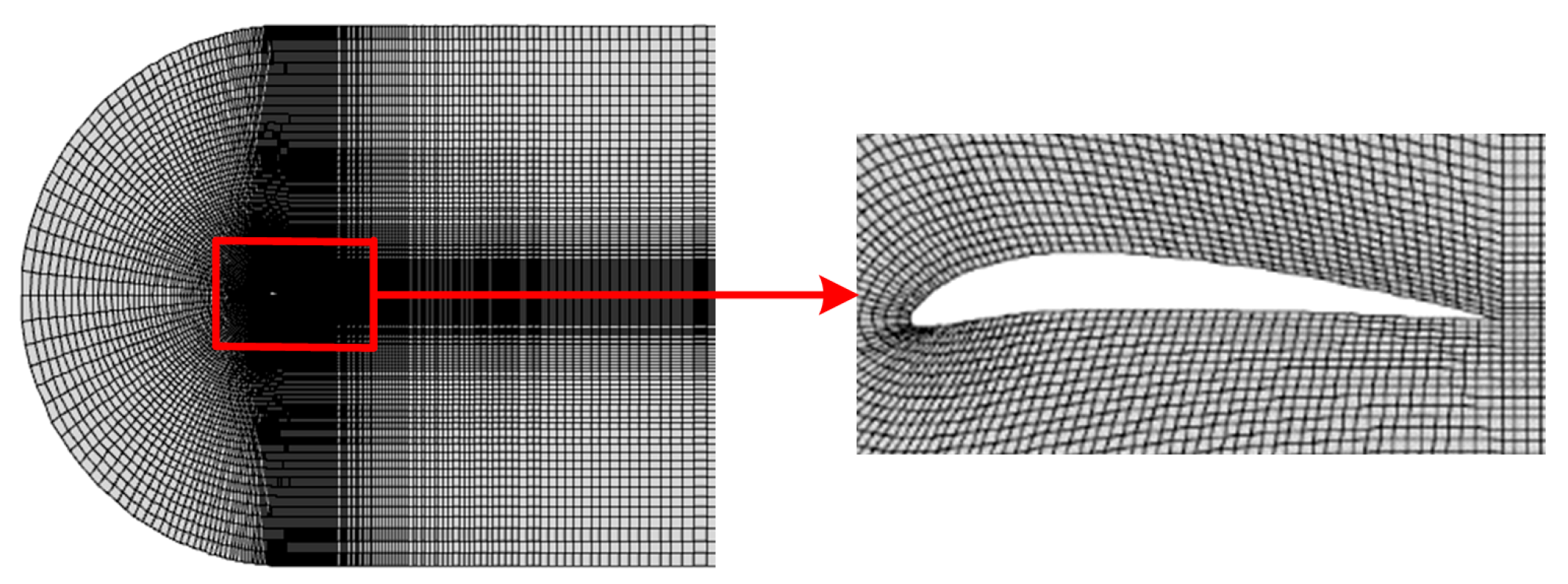
2.4. Model Simulation and Experimental Verification
3. Results and Discussion
3.1. Effects of Airfoil on Fan Performance
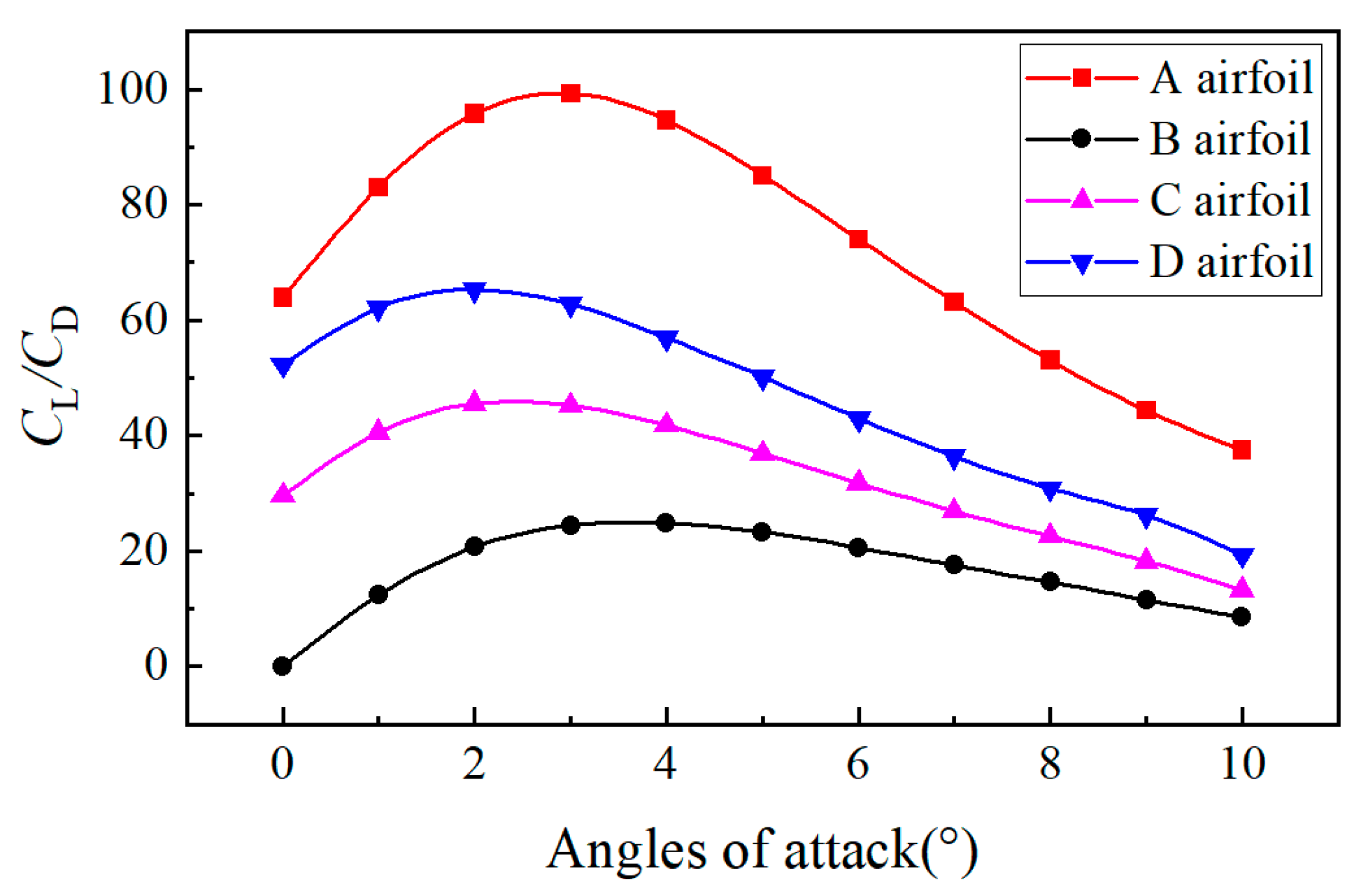
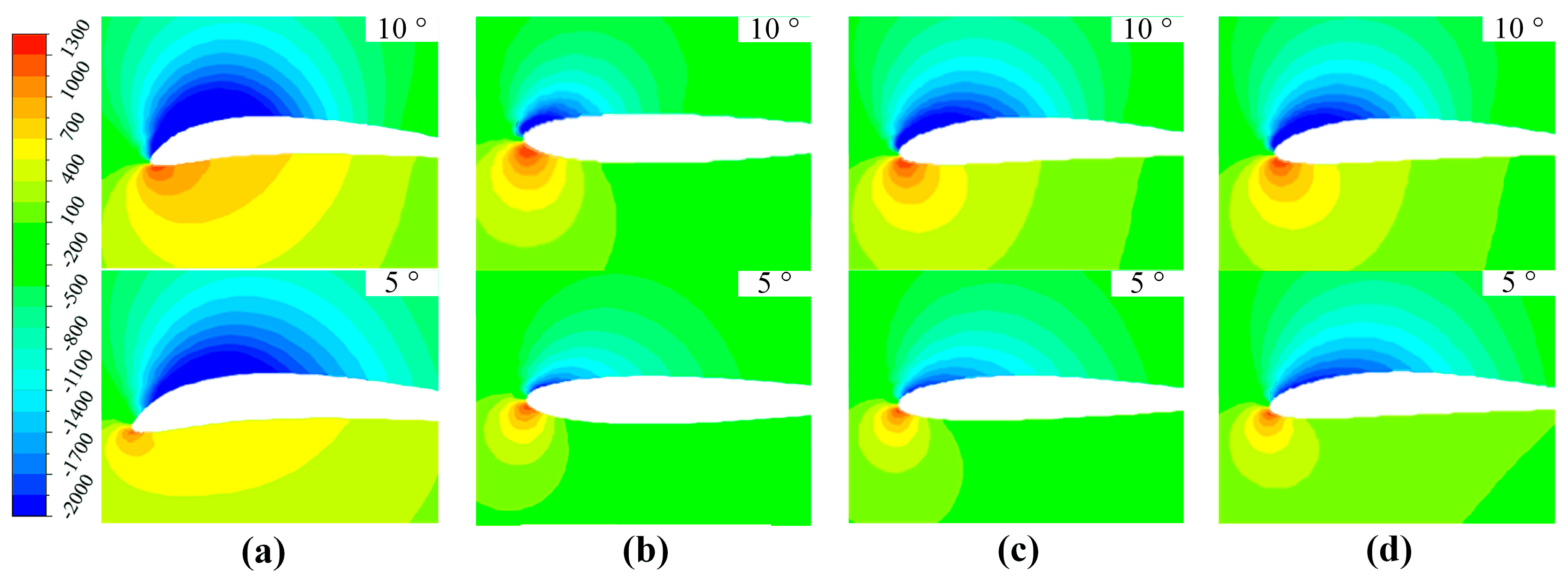
3.1.1. Lift-to-Drag Ratios of Different Airfoils
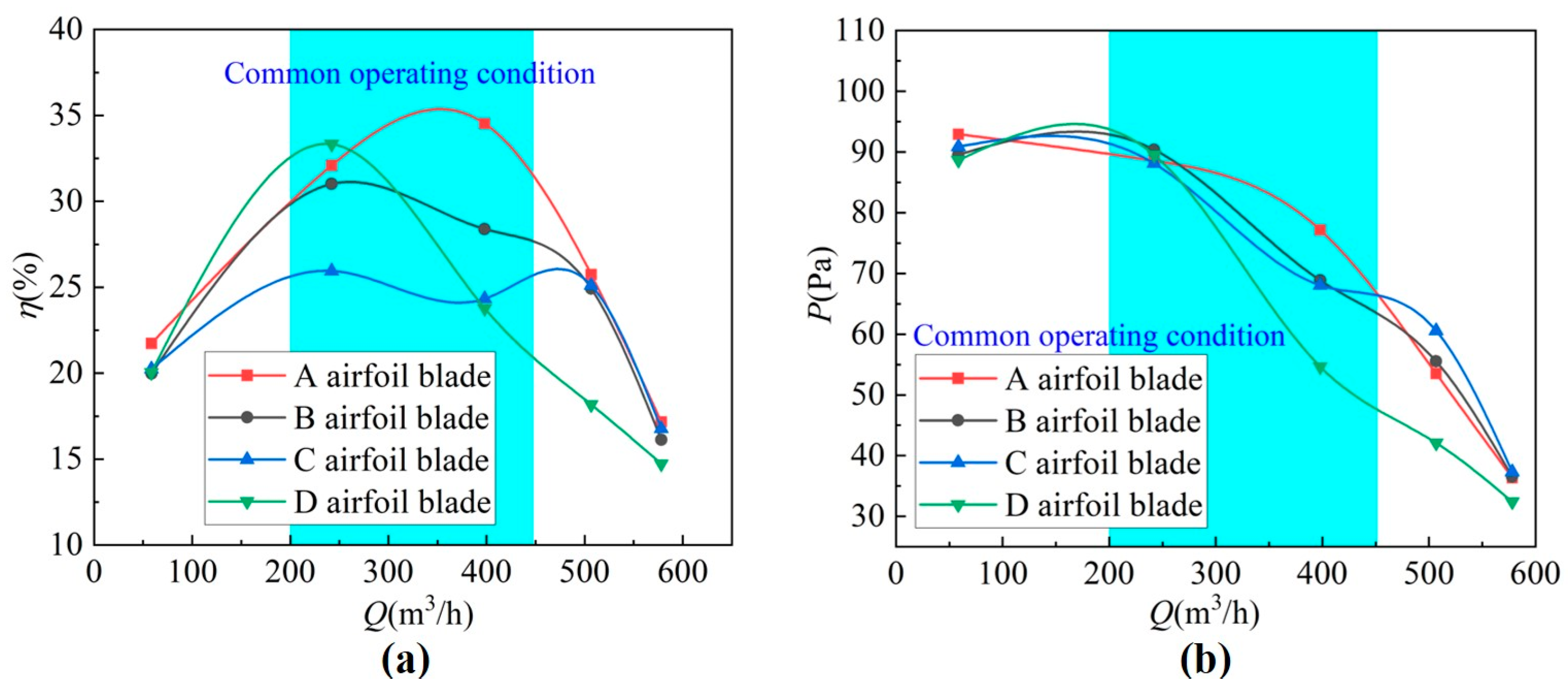
3.1.2. Aerodynamic Performance of Different Airfoil Fans
3.2. Performance Comparison of Airfoil Fan and Single-Arc Fan
3.2.1. Velocity Flow Fields
3.2.2. Aerodynamic Performance
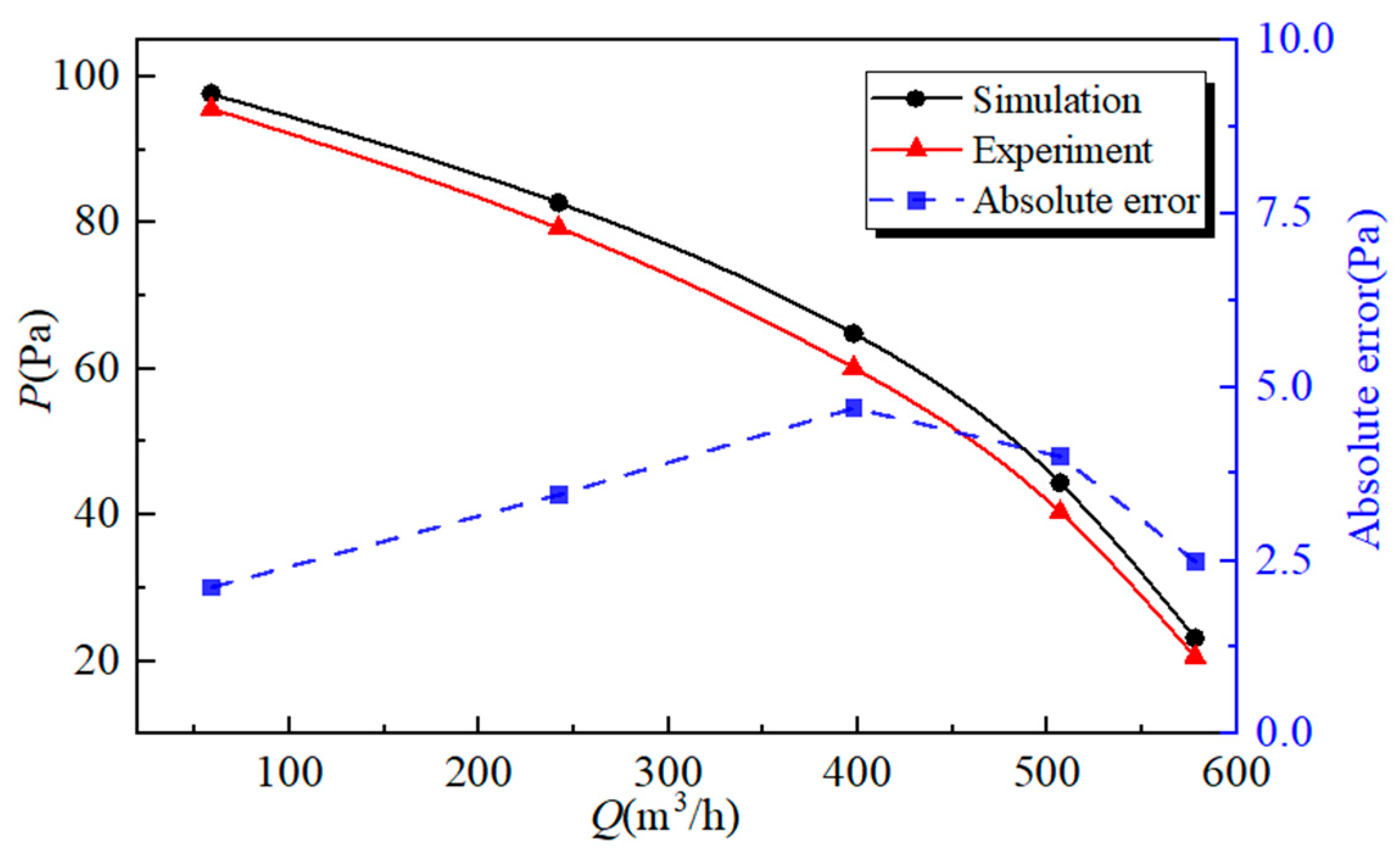
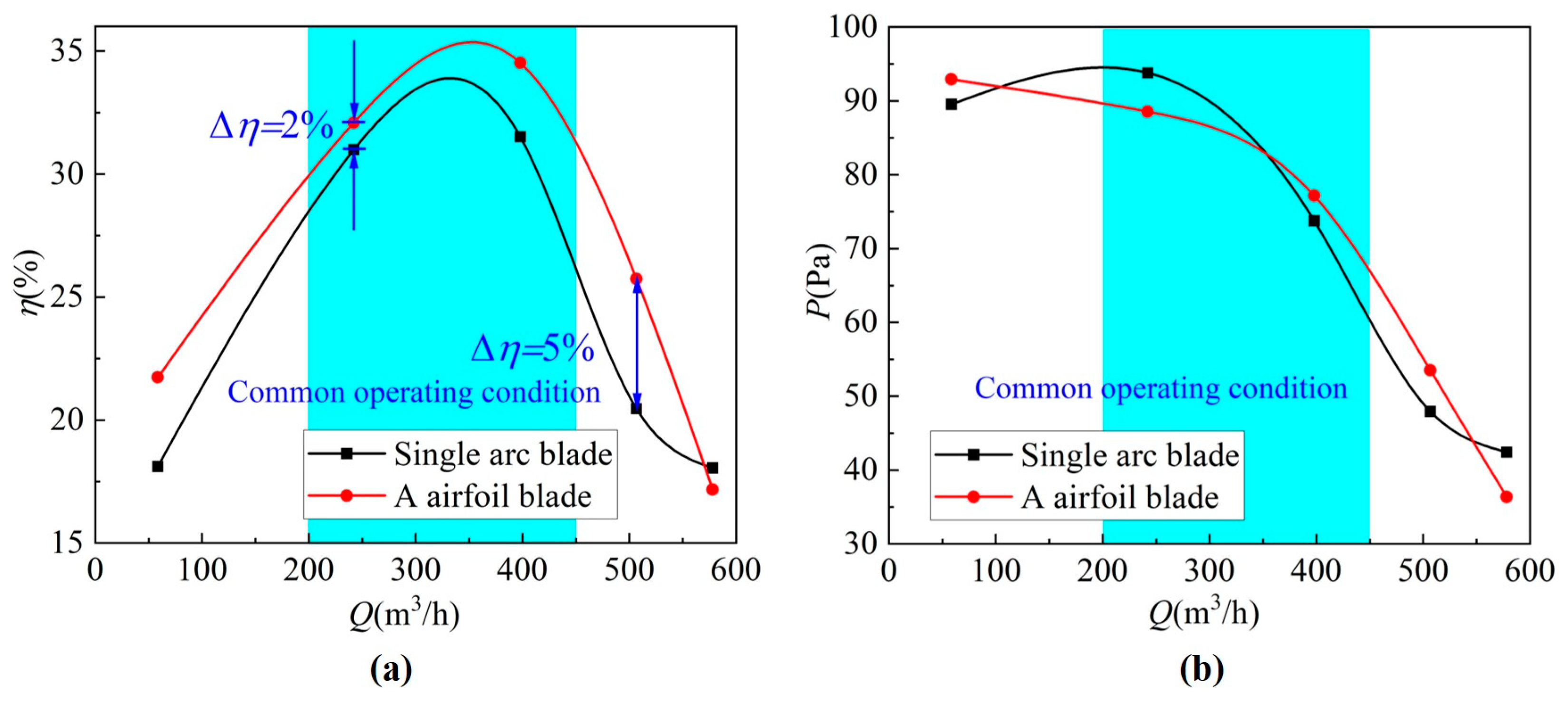
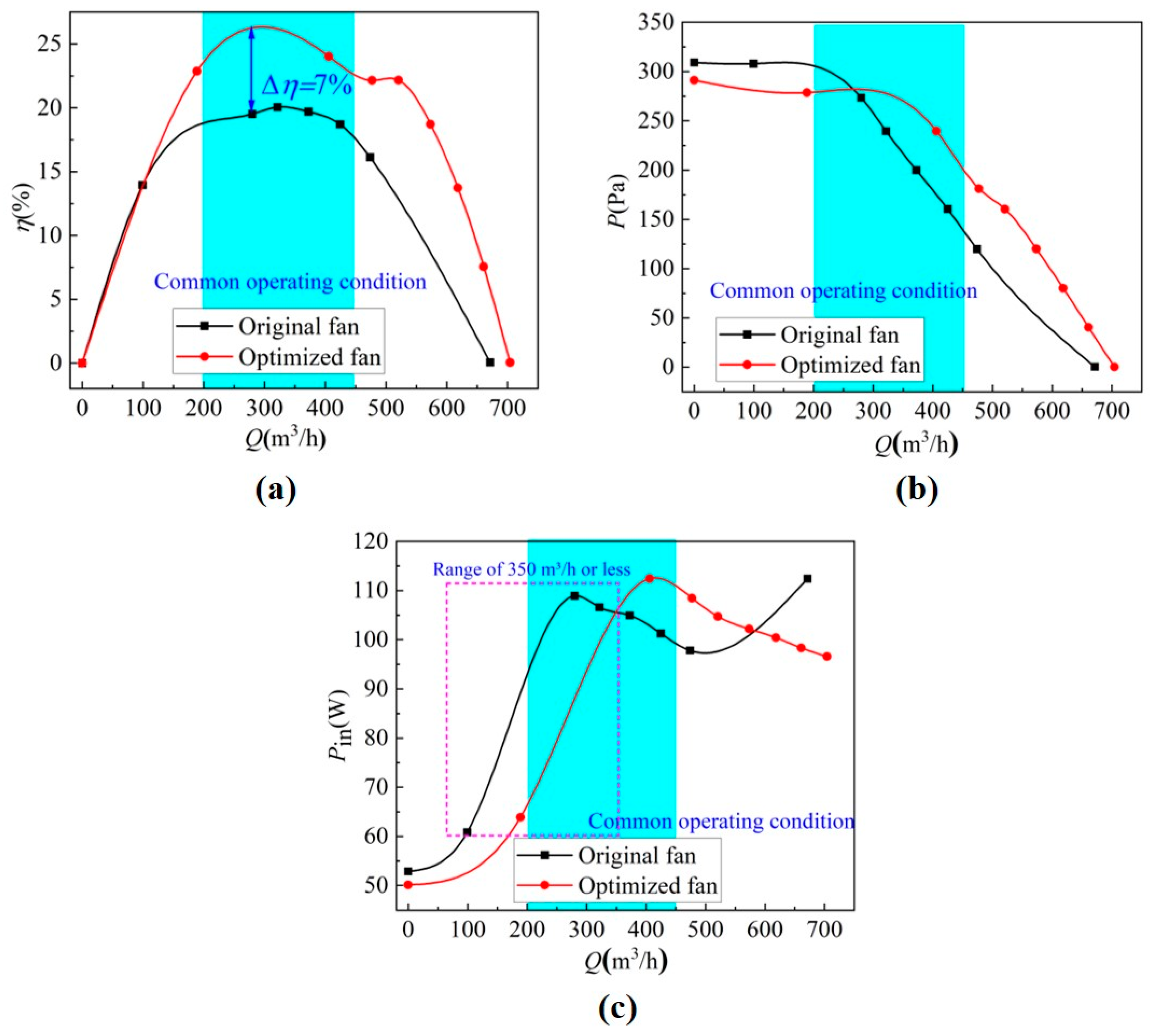
3.3. Experimental Verification of the Effects of Airfoil on Fan Performance
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Turbulent dissipation rate, representing the rate at which turbulent energy is dissipated. | |
| Turbulent viscosity, calculated by the turbulence model. | |
| Turbulent kinetic energy, representing the energy caused by turbulent fluctuations. | |
| Empirical constant. | |
| Empirical constants that control the relative strength of turbulent kinetic energy generation and dissipation. | |
| Prandtl number for turbulent dissipation rate. | |
| Reynolds number. | |
| Relaxation factor. | |
| Lift coefficient. | |
| Drag coefficient. | |
| Lift force. | |
| Drag force. | |
| Flow rate. | |
| Efficiency. | |
| Turbulent production rate factor. | |
| Attenuation factor in the dissipation equation. | |
| Turbulent prandtl number for k equation. | |
| Turbulent prandtl number for ω equation. | |
| Limiting factor for shear stress transport term. | |
| Turbulent prandtl number for k in wall region. | |
| Turbulent prandtl number for k in free-stream region. | |
| Turbulent prandtl number for ω in wall region. | |
| Turbulent prandtl number for ω in the free-stream region. |
References
- Mansy, R.E.; Bergadà, J.M.; Sarwar, W.; Mellibovsky, F. Aerodynamic performances and wake topology past a square cylinder in the interface of two different-velocity streams. Phys. Fluids 2022, 34, 064106. [Google Scholar] [CrossRef]
- He, Y.; Li, R.; Fan, Y.; Zheng, Y.; Chen, G. Study on the performance of a solid-state thermoelectric refrigeration system equipped with ionic wind fans for ultra-quiet operation. Int. J. Refrig. 2021, 130, 441–451. [Google Scholar] [CrossRef]
- Ye, X.; Zhang, J.; Li, C. Effect of blade tip pattern on performance of a twin-stage variable-pitch axial fan. Energy 2017, 126, 535–563. [Google Scholar] [CrossRef]
- Amirat, Y.; Benbouzid, M.E.H.; Al-Ahmar, E.; Bensaker, B.; Turri, S. A brief status on condition monitoring and fault diagnosis in wind energy conversion systems. Renew. Sustain. Energy Rev. 2009, 13, 2629–2636. [Google Scholar] [CrossRef]
- Xiao, M.; Xiao, Q.; Dou, H.S.; Ma, X.; Chen, Y.; He, H.; Ye, X. Study of flow instability in a centrifugal fan based on energy gradient theory. J. Mech. Sci. Technol. 2016, 30, 507–517. [Google Scholar] [CrossRef]
- Horcas, S.G.; Sørensen, N.N.; Zahle, F.; Pirrung, G.R.; Barlas, T. Vibrations of wind turbine blades in standstill: Mapping the influence of the inflow angles. Phys. Fluids 2022, 34, 054105. [Google Scholar] [CrossRef]
- Corsini, A.; Delibra, G.; Rispoli, F.; Sheard, A.G.; Venturini, P. Aerodynamic Simulation of a High-Pressure Centrifugal Fan for Process Industries. In Proceedings of the ASME Turbo Expo 2013: Turbine Technical Conference and Exposition, San Antonio, TX, USA, 3–7 June 2013. [Google Scholar] [CrossRef]
- Wang, K.; Ju, Y.; Zhang, C. Experimental and numerical investigations on effect of blade trimming on aerodynamic performance of squirrel cage fan. Int. J. Mech. Sci. 2020, 177, 105579. [Google Scholar] [CrossRef]
- Son, P.; Kim, J.; Ahn, E. Effects of bell mouth geometries on the flow rate of centrifugal blowers. J. Mech. Sci. Technol. 2011, 25, 2267–2276. [Google Scholar] [CrossRef]
- Huang, Q.; Qin, D.; Pan, G. Numerical simulation of the wake dynamics of the pumpjet propulsor in oblique inflow. Phys. Fluids 2022, 34, 065103. [Google Scholar] [CrossRef]
- Ottersten, M.; Yao, H.-D.; Davidson, L. Tonal noise of voluteless centrifugal fan generated by turbulence stemming from upstream inlet gap. Phys. Fluids 2021, 33, 075110. [Google Scholar] [CrossRef]
- Hofer, D.; Krieger, M.; Kirchhofer, M. Particle image velocimetry and constant temperature anemometer measurements of the jet produced by a centrifugal fan. Phys. Fluids 2021, 33, 065126. [Google Scholar] [CrossRef]
- Li, D.Y.; Gong, R.Z.; Wang, H.J.; Zhang, J.; Wei, X.Z.; Shu, L.F. Numerical Investigation in the Vaned Distributor under Different Guide Vanes Openings of a Pump Turbine in Pump Mode. J. Appl. Fluid Mech. 2016, 9, 253–266. [Google Scholar] [CrossRef]
- Song, H.; Zhang, J.; Huang, P.; Cai, H.; Cao, P.; Hu, B. Analysis of Rotor-Stator Interaction of a Pump-Turbine with Splitter Blades in a Pump Mode. Mathematics 2020, 8, 1465. [Google Scholar] [CrossRef]
- Li, K.; Chen, X.; Dou, H.S.; Zhu, Z.; Zheng, L.; Luo, X. Study of Flow Instability in a Miniature Centrifugal Pump Based on Energy Gradient Method. J. Appl. Fluid Mech. 2019, 12, 701–713. [Google Scholar] [CrossRef]
- Yang, H.; Yu, P.; Xu, J.; Ying, C.; Cao, W.; Wang, Y.; Zhu, Z.; Wei, Y. Experimental investigations on the performance and noise characteristics of a forward-curved fan with the stepped tongue. Meas. Control. 2019, 52, 002029401987748. [Google Scholar] [CrossRef]
- Tantakitti, P.; Pattana, S.; Wiratkasem, K. The performance of backward curved centrifugal fan with various impeller inlet and outlet angles. In Proceedings of the International Conference on Engineering Science and Innovative Technology, North Bangkok, Thailand, 19–22 April 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–3. [Google Scholar] [CrossRef]
- Xue, Y.-J.; Cai, X.-F.; Liu, H. Effects of wing–body interaction on hawk moth aerodynamics and energetics at various flight velocities. Phys. Fluids 2022, 34, 051915. [Google Scholar] [CrossRef]
- Yu, H.; Sheng, K.; Lan, B.; Hsu, K.L.; Yang, J.T. Optimal thrust efficiency for a tandem wing in forward flight using varied hindwing kinematics of a damselfly. Phys. Fluids 2022, 34, 061909. [Google Scholar] [CrossRef]
- Abreu, L.I.; Tanarro, A.; Cavalieri, A.V.; Schlatter, P.; Vinuesa, R.; Hanifi, A.; Henningson, D.S. Spanwise-coherent hydrodynamic waves around flat plates and airfoils. J. Fluid Mech. 2021, 927, A1. [Google Scholar] [CrossRef]
- Liu, T.; Zhang, Y.; Li, K.; Wang, Y.; Li, J. Aerodynamic Optimization of a Centrifugal Fan Using Response Surface Methodology. Open J. Fluid Dyn. 2019, 9, 92. [Google Scholar] [CrossRef]
- Clemen, C. Aero-mechanical optimisation of a structural fan outlet guide vane. Struct. Multidiscip. Optim. 2011, 44, 125–136. [Google Scholar] [CrossRef]
- Huang, C.-H.; Hung, M.-H. An optimal design algorithm for centrifugal fans: Theoretical and experimental studies. J. Mech. Sci. Technol. 2013, 27, 761–773. [Google Scholar] [CrossRef]
- Zhou, S.; Zhou, H.; Yang, K.; Dong, H.; Gao, Z. Research on blade design method of multi-blade centrifugal fan for building efficient ventilation based on Hicks-Henne function. Sustain. Energy Technol. Assess. 2021, 43, 100971. [Google Scholar] [CrossRef]
- Zuo, K.-C.; Wang, Y.; Zheng, X. Simulation study on the time-invariant air-flow characterization of centrifugal fan. In Proceedings of the INTER-NOISE and NOISE-CON Congress and Conference Proceedings, Seoul, Republic of Korea, 23 August 2020. [Google Scholar]
- Shen, Y.; Li, Y.; Wang, H.; Shen, W.; Chen, Y.; Si, H. Numerical simulation and performance optimization of the centrifugal fan in a vacuum cleaner. Mod. Phys. Lett. B 2019, 33, 1950440. [Google Scholar] [CrossRef]
- Park, K.; Chang, H. Application of Airfoil Impeller for Enhancement of Aerodynamic Performance of High Speed Centrifugal Fan. Trans. Korean Soc. Mech. Eng. B 2016, 40, 321–327. [Google Scholar] [CrossRef]
- Suresh, M.; Sitaram, N. Effect of Gurney Flap Configuration on the Performance of a Centrifugal Fan. J. Appl. Fluid Mech. 2019, 12, 565–571. [Google Scholar] [CrossRef]
- Lin, S.-C.; Huang, C.-L. An integrated experimental and numerical study of forward–curved centrifugal fan. Exp. Therm. Fluid Sci. 2002, 26, 421–434. [Google Scholar] [CrossRef]
- Zhuang, M. The effects of curvature on wake-dominated incompressible free shear layers. Phys. Fluids 1999, 11, 3106–3115. [Google Scholar] [CrossRef]
- Prabu, T.; Viswanathan, P.; Gokul Kannan, N.; Rudramoorthy, R.; Firthouse, A. Optimization of Wrap Angle in the Mixed Flow Impeller for Reducing Flow Losses. J. Appl. Fluid Mech. 2020, 13, 1949–1957. [Google Scholar] [CrossRef]
- Acarer, S. Peak lift-to-drag ratio enhancement of the DU12W262 airfoil by passive flow control and its impact on horizontal and vertical axis wind turbines. Energy 2020, 201, 117659. [Google Scholar] [CrossRef]
- Jeong, J.-H.; Kim, S.-H. Optimization of thick wind turbine airfoils using a genetic algorithm. J. Mech. Sci. Technol. 2018, 32, 3191–3199. [Google Scholar] [CrossRef]
- Oukassou, K.; El Mouhsine, S.; El Hajjaji, A.; Kharbouch, B. Comparison of the power, lift and drag coefficients of wind turbine blade from aerodynamics characteristics of Naca0012 and Naca2412. Procedia Manuf. 2019, 32, 983–990. [Google Scholar] [CrossRef]
- 210-16/ASHRAE; Ansi/Amca. Laboratory Methods of Testing Fans for Certified Aerodynamic Performance Rating. Air Movement and Control Association International Inc.: Arlington Heights, IL, USA, 2016.
- ANSYS, Inc. ANSYS Fluent 2021R2 [Computer Software]. 2021. Available online: https://www.ansys.com/products/fluids/ansys-fluent (accessed on 7 August 2022).





| Parameter | Value |
|---|---|
| Inner diameter of impeller D1 (mm) | 108 |
| Outer diameter of impeller D2 (mm) | 133 |
| Installation angle of blade inlet β1 (°) | 81 |
| Installation angle of blade outlet β2 (°) | 173 |
| Number of blades Z | 38 |
| Volute width B (mm) | 215 |
| Number of Grids | Impeller Region | Volute Region | Outlet Region | |
|---|---|---|---|---|
| Grid 1 | 4.2 × 106 | 20.52 | 41.51 | 82.47 |
| Grid 2 | 7.7 × 106 | 14.7 | 35.4 | 75.5 |
| Grid 3 | 9.8 × 106 | 13.5 | 33.5 | 73.2 |
| Total Elements | CL | CD | |
|---|---|---|---|
| Grid 1 | 2.9 × 106 | 7.51 × 10−1 | 3.23 × 10−2 |
| Grid 2 | 4.7 × 106 | 7.52 × 10−1 | 3.25 × 10−2 |
| Grid 3 | 6.8 × 106 | 7.50 × 10−1 | 3.23 × 10−2 |
| Flow (m3/h) | Rotating Speed (rpm) | Inlet Speed (m/s) | |
|---|---|---|---|
| Case 1 | 58.60 | 1466 | 0.29 |
| Case 2 | 242.10 | 1449 | 1.19 |
| Case 3 | 398.00 | 1429 | 1.95 |
| Case 4 | 506.70 | 1410 | 2.49 |
| Case 5 | 578.10 | 1389 | 2.84 |
| Fan Parameter | Single-Arc Fan | A Airfoil Fan |
|---|---|---|
| Volume flow (m3/h) | 0–700 | 0–701 |
| Total pressure (Pa) | 0–310 | 0–310 |
| Rotating speed (r/min) | 1500–2700 | 1500–2700 |
| Axle power (W) | 50–110 | 50–111 |
| Temperature (°C) | 25 | 25 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, H.; Zhao, H.; Li, Y.; Zhao, J.; Zhang, K. Airfoil Design and Flow Analysis of a Multi-Blade Centrifugal Fan: An Experimental and Simulation Study. Appl. Sci. 2024, 14, 11229. https://doi.org/10.3390/app142311229
Yin H, Zhao H, Li Y, Zhao J, Zhang K. Airfoil Design and Flow Analysis of a Multi-Blade Centrifugal Fan: An Experimental and Simulation Study. Applied Sciences. 2024; 14(23):11229. https://doi.org/10.3390/app142311229
Chicago/Turabian StyleYin, Haonan, Hanqing Zhao, Yiping Li, Jie Zhao, and Kai Zhang. 2024. "Airfoil Design and Flow Analysis of a Multi-Blade Centrifugal Fan: An Experimental and Simulation Study" Applied Sciences 14, no. 23: 11229. https://doi.org/10.3390/app142311229
APA StyleYin, H., Zhao, H., Li, Y., Zhao, J., & Zhang, K. (2024). Airfoil Design and Flow Analysis of a Multi-Blade Centrifugal Fan: An Experimental and Simulation Study. Applied Sciences, 14(23), 11229. https://doi.org/10.3390/app142311229






