Experimental Investigation of Free-Motion Task Implementation on a Serial Metamorphic Manipulator

Featured Application

The findings of this study contribute to the development of more versatile robotic systems capable of efficiently performing complex dynamic tasks in variable environments. This work enhances the potential for integration of such systems into flexible manufacturing processes, enabling greater adaptability and responsiveness in dynamic operational scenarios.

Abstract

This paper presents an experimental investigation into the implementation of free-motion tasks on a serial metamorphic manipulator (SMM). Utilizing a previously established task-based optimization methodology, the dynamic performance of the SMM is evaluated through a combination of theoretical performance metrics and experimental data. The study aims to validate the SMM’s ability to achieve optimized performance through structural reconfiguration. Theoretical models are compared against real-world free-motion task data, demonstrating strong correlations between analytical calculations and experimental outcomes. The discussion focuses on three key areas: the efficiency of joint controllers, end-effector acceleration capabilities, and joint controller performance. Results indicate that an optimized anatomy can achieve more than 40% reduction in produced torques during task execution and a 35% improvement in the torque-to-velocity ratio. While the simple controller implemented in the robot prototype exhibits adequate performance, notable limitations are observed in task segments with lower dynamic performance, particularly in terms of positional accuracy and energy efficiency. During XY-plane task execution, the Z-axis position error deviates by 1 to 2 cm in areas of lower dynamic performance. These findings provide key insights and establish a robust foundation for advancing SMM capabilities in practical applications, with future work focusing on addressing the identified limitations.

1. Introduction

1.1. Recent Advances in Reconfigurable Robots and Challenges

Unlike fixed-structure serial manipulators, which have a predetermined and unchangeable architecture, modular reconfigurable robots (MRRs) consist of modular components that can be rearranged or replaced to modify the robot’s structure. This modularity is achieved through special connectors, joints, and modules that can be manually adjusted and assembled in various configurations, providing adaptability and versatility. Additionally, modularity enables the faster replacement of broken hardware parts, on-the-fly adjustments to accommodate changing requirements, and enhanced scalability and reduces the need for multiple specialized robots, making them ideal for dynamic environments. MRRs provide significant cost savings and improved operational efficiency, making them highly advantageous for the rapidly evolving technological landscape. The design of MRRs has thus become significant in a wide range of applications, from autonomous extraterrestrial missions [1] to wireless robotic arms for networked flexible manufacturing systems [2].

Recent years have seen substantial research efforts dedicated to both the mechanical design and software integration of MRRs. Recent advancements in the mechanical design of MRRs have primarily focused on enhancing the modularity and robustness of these systems, leading to significantly enhanced reconfiguration efficiency, upgraded interconnection capabilities, and improved mechanical and electrical capacities of the modules [3,4,5,6,7,8,9]. On the software front, computational performance has been enhanced by aggregating the free computing resources of unused modules [10], and automated modeling procedures have been introduced to handle advanced genderless and multi-output connection ports, thereby reducing the time and effort required for reprogramming after reconfiguration, ensuring greater flexibility [11,12]. The flexibility and adaptability of MRRs to varying task requirements have led to the development and implementation of numerous optimal task-based design methodologies. These approaches focus on tailoring the robot’s configuration to specific operational objectives, enhancing performance while maintaining structural integrity [13,14,15].

SMMs as a subclass of MRRs [16], employ a modular heterogeneous structure comprising active and passive modules. Active modules facilitate the robot’s operations, while passive modules enable reconfiguration through manual offline operation. These modules adhere to strict interconnection rules within the serial chain and are developed to achieve a finite number of configurations. The topology changes induced by metamorphic structure synthesis and anatomy metamorphosis lead to a robotic system with modified kinematic and dynamic properties.

Despite the significant advantages introduced by reconfiguration, numerous challenges emerge in the design, development, and operation of this category of robots. Reconfiguration introduces additional variables, that have a significant effect on the kinematic and dynamic characteristics and must be taken into account for accurate modeling, simulation, and control processes. Several methods have been proposed to address these challenges, including unified kinematics and dynamics models [17,18,19] and robust [20,21] and adaptive control strategies [22,23,24]. Despite these advancements, it remains essential from an engineering point-of-view to be able to realize the effect of reconfiguration on overall performance and proceed to the validation of theoretical models and methods with actual experimental data to ensure accuracy and effectiveness.

1.2. Dynamic Performance Evaluation

Numerous metrics for dynamic performance evaluation have been proposed to address the identification of performance capabilities and limitations of robotic systems [25,26,27]. These metrics rely on a comprehensive understanding of the robot’s kinematics and dynamics, allowing for the identification of areas with improved or diminished performance. Understanding the dynamic performance of a robot manipulator enables the precise prediction of behavior across diverse operational scenarios, facilitating the design of optimized control strategies for specific tasks. By comparing simulated performance data with actual task implementation results, a more comprehensive insight can be gained, validating theoretical models and identifying the need for more advanced control software. While complex control algorithms may offer higher precision and adaptability, their implementation often necessitates advanced, costlier hardware, which may not always be feasible. Adopting a simpler control method based on an accurate dynamic model fundamentally reduces computational overhead and ensures reliable performance within the required specifications.

1.3. Motivation and Contribution

While previous research of the authors [28,29,30] focused on structural and kinematic optimization, this paper extends the optimization framework by incorporating simple SMM dynamics formulation and dynamic performance evaluation based on experimental data, which is essential for understanding the robot’s behavior under real operational conditions. The primary scientific claims of this study are articulated as follows:

• Assessing system modeling accuracy: This study provides insights into the accuracy of the proposed system model for SMMs. In order to test modeling accuracy, experimental validation is conducted to bridge the gap between theoretical predictions and real-world performance. Robot performance varies along the task path, necessitating the use of theoretical foundations and an accurate dynamic model to identify regions of higher and lower performance. This understanding is critical for the optimal configuration of task execution strategies and the precise tuning of controller parameters.
• Dynamic performance evaluation: Reconfiguration introduces additional variables that significantly affect kinematic and dynamic characteristics. The primary focus is to study the achieved performance along the free-motion task path execution for the optimized robot configurations. Optimized robot configurations should achieve higher efficiency in robot joints’ motions and achieve higher acceleration capabilities with reduced joint effort.

By integrating established performance evaluation tools, the analytical dynamic modeling of SMMs, and experimental validation, this research makes a key contribution to advancing the understanding of SMM dynamics and establishing a foundation for the development of more sophisticated control algorithms for SMMs. The insights gained from the dynamic performance evaluation, along with the recognition of the limitations in task execution performance, serve as a basis for designing control algorithms aimed at enhancing system performance under conditions of higher dynamic demands and load uncertainties, addressing critical challenges in optimizing task execution capabilities of SMMs.

The remainder of this paper is arranged as follows. Section 2 outlines the fundamentals of dynamic modeling for SMMs, the performance measures employed and the methodology applied for experimental analysis. Section 3 provides a theoretical validation of the proposed dynamic model, while Section 4 presents the experimental case study with a detailed discussion of the results. Section 5 summarizes the main conclusions and outlines the direction for future scientific work.

2. Preliminaries and Methodology

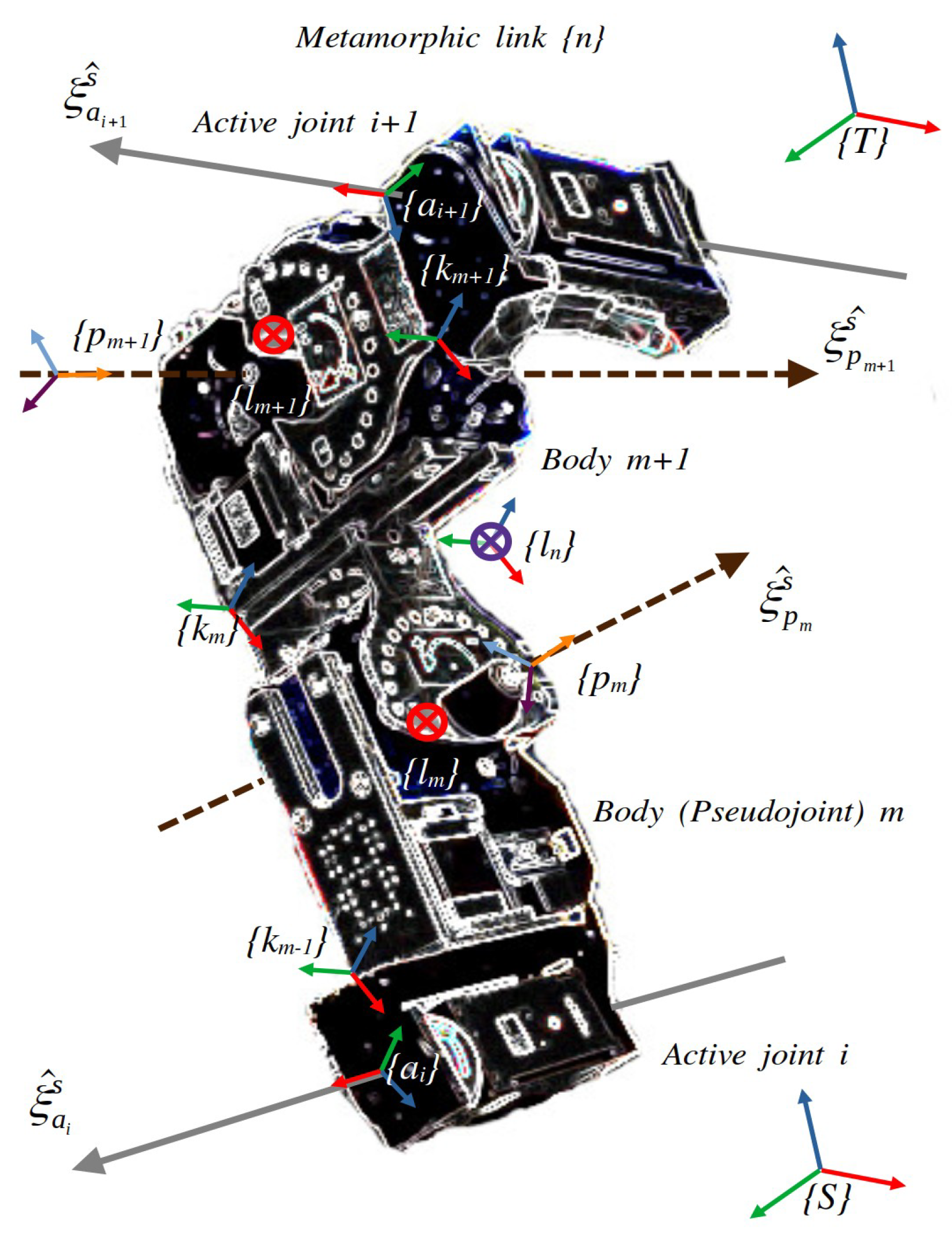
2.1. Dynamic Modeling of SMMs

In this work, the terminology established in previous studies was utilized [28,29]. The robot assembly, comprising both active and passive modules interconnected according to specific interconnection rules, is referred to as the metamorphic structure. Passive modules employed for reconfiguration are designated as pseudojoints, and the process of altering the pseudojoints’ configuration is termed metamorphosis. The resultant robot configuration following metamorphosis is known as anatomy. A metamorphic structure can encompass a large number of anatomies, contingent on the number of pseudojoints used to form the serial chain.

The formulation of the dynamic model was implemented through screw theory tools. A simplified model was extracted, since it helped isolate core dynamics, making it easier to understand the fundamental behavior of the system before more detailed models were introduced for fine-tuning and precision. Dynamic equations were defined in a compact analytical form that was aligned with the physical structure assembly, allowing the mechanics of reconfiguration to be parameterized and incorporated into the dynamic matrices’ expressions without additional complexity [30].

A brief presentation of the derivation of the analytical dynamic model for SMMs is provided, mainly focused on the Generalized Inertia Matrix (GIM). For a robot with $n_a$ active joints, the GIM is an $n_a\times n_a$ symmetric, positive definite matrix that relates to the current active joint configuration, ${\mathbf{q}}_{\mathbf{a}}$, anatomy, ${\mathbf{q}}_{\mathbf{p}}$, and metamorphic structure, $\mathbf{s}$. The detailed presentation of the structural parameters for the SMM prototype under study, are thoroughly discussed in [30]. The GIM of an SMM has the form

$$\mathcal{M}({\mathbf{q}}_{\mathbf{a}},{\mathbf{q}}_{\mathbf{p}},\mathbf{s})=\sum _{n=1}^{n_a}{{\mathbf{J}}_{\mathbf{n}}^{\mathbf{b}}}^{\top }·{\mathbf{M}}_{\mathrm{n}}^b·{\mathbf{J}}_{\mathbf{n}}^{\mathbf{b}}$$

(1)

where ${\mathbf{J}}_{\mathbf{n}}^{\mathbf{b}}$ are the Link Body Jacobians (LBJs) and ${\mathbf{M}}_{\mathrm{n}}^b$ are the Link Inertia Matrices (LIMs) with respect to each link’s center of mass (CM). Both LBJs and LIMs should be constructed for the current SMM metamorphic structure and anatomy. In Figure 1, a metamorphic link n is illustrated along with the main geometric components used for analytical calculations. The link consists of the intermediate bodies (pseudojoints) between two active modules. The inertia matrix ${\mathrm{M}}_m^b$ of the m intermediate bodies expressed in the local reference frame is predetermined from Computer-Aided Design (CAD) software FreeCAD 1.0. In order to extract the LIM of a metamorphic link, the body inertia matrices are expressed in the base frame $\left\{S\right\}$.

$${\mathrm{M}}_m^s=A{d}_{g_{s{l}_m}^{-1}}^{\top }·{\mathrm{M}}_m^b·A{d}_{g_{s{l}_m}^{-1}}$$

(2)

Then, the LIM of a metamorphic link n with $\left\{N_m\right\}$ intermediate bodies, expressed in the base frame $\left\{S\right\}$, can be extracted

$${\mathbf{M}}_{\mathrm{n}}^s=\sum _{m=1}^{{\mathrm{N}}_m}{\mathrm{M}}_m^s$$

(3)

and is expressed in the CM frame of each link $\left\{l_n\right\}$ given its spatial transformation $g_{s{l}_n}$

$${\mathbf{M}}_{\mathrm{n}}^b=A{d}_{g_{s_{l_n}}}^{\top }·{\mathbf{M}}_{\mathrm{n}}^s·A{d}_{g_{s_{l_n}}}$$

(4)

The LBJ of the nth link is given by

$$\begin{array}{cc}\hfill {\mathbf{J}}_{\mathbf{n}}^{\mathbf{b}}& =\left[{{\mathcal{J}}_1}^{\left(n\right)}\dots {{\mathcal{J}}_{n-1}}^{\left(n\right)}0\dots 0\right]\hfill \\ & =A{d}_{g_{s_{l_n}}^{-1}}·\left[{\mathcal{A}}_{n1}{\widehat{\xi }}_{a_1}^s\dots {\mathcal{A}}_{nn}{\widehat{\xi }}_{a_n}^{s}0\dots 0\right]\hfill \end{array}$$

(5)

where the adjoint transformation ${\mathcal{A}}_{nc}\in {\mathbb{R}}^{6\times 6}$ is utilized to form the cth Jacobian column of the nth link.

$${\mathcal{A}}_{nc}=\left\{\begin{array}{cc}A{d}_{e^{{\widehat{\xi }}_{a_{c+1}}^s·q_{a_{c+1}}}·e^{{\widehat{\xi }}_{a_{c+2}}^s·q_{a_{c+2}}}\dots e^{{\widehat{\xi }}_{a_n}^s·q_{a_n}}}^{-1}\hfill & n>c\hfill \\ I\hfill & n=c\hfill \\ 0\hfill & n<c\hfill \end{array}\right.$$

(6)

The anatomy metamorphosis is integrated through the reference pseudojoint twists, ${\widehat{\xi }}_{p_m}^s$, and the desired pseudojoint angles $q_{p_m}$. When the $(m+1)$th pseudojoint module is assembled, its reference passive twist is transformed due to the rotation induced by the change in preceding pseudojoints’ angles,

$${\widehat{\xi }}_{p_{m+1}}^{s^{\prime }}=A{d}_{e^{{\widehat{\xi }}_{p_1}·q_{p_1}}\cdots e^{{\widehat{\xi }}_{p_m}·q_{p_m}}}·{\widehat{\xi }}_{p_{m+1}}^s$$

(7)

and the reference spatial transformation, $g_{s{k}_{m+1}}\left(0\right)$, of the assembled pseudojoint is transformed

$$g_{s{k}_{m+1}}^{\prime }=e^{{\widehat{\xi }}_{p_{m+1}}^{s^{\prime }}·q_{p_{m+1}}}·g_{s{k}_{m+1}}\left(0\right)$$

(8)

The spatial transformation of the preceding active joint frame $g_{s{a}_{i+1}}$ can be defined as

$$g_{s{a}_{i+1}}=g_{s{k}_{m+1}}^{\prime }·g_{k_{m+1}{a}_{i+1}}$$

(9)

Given the current spatial transformation of the active joint frame $g_{s{a}_{i+1}}$ and the definition of the active joint twists ${\widehat{\xi }}_{a_i^b}$ based on the local body frame, the calculation of the spatial active joint twists ${\widehat{\xi }}_{a_i}^s$ is straightforward.

$${\widehat{\xi }}_{a_{i+1}}^s=g_{s{a}_{i+1}}·{\widehat{\xi }}_{a_{i+1}}^b·g_{s{a}_{i+1}}^{-1}=A{d}_{g_{s{a}_{i+1}}}·{\widehat{\xi }}_{a_{i+1}}^b$$

(10)

Finally, screw algebra is utilized to extract the analytical expression of the manipulator Jacobian expressed in TCP body frame $\left\{T\right\}$.

$${\mathcal{J}}_{\mathbf{t}}^{\mathbf{b}}=\left[{\mathcal{J}}_{t,1}^b{\mathcal{J}}_{t,2}^b{\mathcal{J}}_{t,3}^b\right]$$

(11)

The $6\times 3$ Jacobian ${\mathcal{J}}_{\mathbf{t}}^{\mathbf{b}}$ is extracted through the adjoint transformation of the reference anatomy joint frames, $g_{s{a}_i}\left(0\right)$, the current joint frames, $g_{s{a}_i}$, and the robot’s TCP frame’s spatial transformation, $g_{st}$, where each $6\times 1$ column vector has the form

$${\mathcal{J}}_{t,i}^b=A{d}_{g_{st}^{-1}·g_{s{a}_i}·g_{s{a}_i}^{-1}\left(0\right)}·{\widehat{\xi }}_{a_i}^s$$

(12)

The Jacobian is expressed in task space by applying the corresponding rotation matrix of the TCP spatial orientation, ${\mathcal{R}}_{st}$, to the $3\times 3$ position sub-matrix counterpart of the Jacobian ${\mathcal{J}}_{\mathbf{t}}^{\mathbf{b}}$.

$$\mathcal{J}={\mathcal{R}}_{st}·{\mathcal{J}}_{\mathbf{t}}^{\mathbf{b}}{|}_{pos}$$

(13)

2.2. Performance Evaluation

For each task implemented, the corresponding simulation was executed, the kinematic and dynamic matrices were calculated, and robot performance was evaluated using established quantitative measures. Four well-known DPMs, which relate to the GIM, were used to evaluate the performance of the anatomies during each task path execution. The Dynamic Manipulability Ellipsoid (DME) index proposed in [25] is an established measure of the ability of the manipulator to generate TCP acceleration ${\underline{a}}_{\mathrm{t}cp}$ based on a joint driving force $\underline{\tau }$.

$${\underline{a}}_{\mathrm{t}cp}^{\top }·{\mathbf{A}}_{\mathbf{d}}^{-1}·{\underline{a}}_{\mathrm{t}cp}={\underline{\tau }}^{\top }·\underline{\tau }\le 1$$

(14)

where ${\mathbf{A}}_{\mathbf{d}}$ is a symmetric and positive definite matrix that determines the volume and orientation of the DME.

$${\mathbf{A}}_{\mathbf{d}}=[\mathcal{J}·{\mathcal{M}}^{-1}]·{[\mathcal{J}·{\mathcal{M}}^{-1}]}^{\top }$$

(15)

Given the DME’s core matrix ${\mathbf{A}}_{\mathbf{d}}$ and for a non-redundant manipulator, the Dynamic Manipulability Index (DMI) is defined as

$$DMI=\sqrt{det\left({\mathbf{A}}_{\mathbf{d}}\right)}=\left|{\displaystyle \frac{det\left(\mathcal{J}\right)}{det\left(\mathcal{M}\right)}}\right|$$

(16)

Furthermore, the two indices discussed in [26] that stem from the analysis of the following operational point kinetic energy matrix ${\mathrm{\Lambda }}_v$ were used.

$${\mathrm{\Lambda }}_v={\left[\mathcal{J}·\mathcal{M}·{\mathcal{J}}^{\top }\right]}^{-1}$$

(17)

The first was the the condition number of the eigenvalues of ${\mathrm{\Lambda }}_v$ which in this work was stated as the Lambda Conditioning Index (LCI),

$$LCI={\displaystyle \frac{min\left({\sigma }_{{\mathrm{\Lambda }}_v}\right)}{max\left({\sigma }_{{\mathrm{\Lambda }}_v}\right)}}$$

(18)

and the second was the Effective Mass Index (EMI):

$$EMI={\widehat{\underline{v}}}_{tcp}^{\top }·{\mathrm{\Lambda }}_v^{-1}·{\widehat{\underline{v}}}_{tcp}$$

(19)

where ${\widehat{\underline{v}}}_{tcp}$ is the unit vector describing the direction of the TCP velocity. Both measures provide an insight on the inertial properties of the robot at the operational point. The eigenvalues of ${\mathrm{\Lambda }}_v$ provide a useful characterization of the bounds on the magnitude of the inertial properties, making the LCI an accurate measure of the dynamic limitations at a given task point. The EMI is perceived at the operational point but also considers the direction of motion. Its magnitude can provide a measure of the acceleration along the direction of motion.

Finally, the dimensionless definition of the Dynamic Conditioning Index (DCI) [27] was used since it provides a measure of the degree of isotropy of the GIM and can be used as a general performance index for comparing the GIM of different robots.

$$DCI={\displaystyle \frac{1}{2}}·{\mathbf{e}}^{\top }·W·\mathbf{e}$$

(20)

The GIM diagonal elements’ deviation $6\times 1$ column vector is arranged as

$$\mathbf{e}={\displaystyle \frac{1}{{\sigma }_{\mathcal{M}}}}·{\left[{\mathcal{M}}_{11}-{\sigma }_{\mathcal{M}},{\mathcal{M}}_{22}-{\sigma }_{\mathcal{M}},{\mathcal{M}}_{33}-{\sigma }_{\mathcal{M}},{\mathcal{M}}_{12},{\mathcal{M}}_{13},{\mathcal{M}}_{23}\right]}^{\top }$$

(21)

Furthermore, the $6\times 6$ positive definite weighting matrix W is defined by the user, to regulate the effect of each of the elements of $\mathbf{e}$ vector, while ${\sigma }_{\mathcal{M}}$ is a scalar defined as

$${\sigma }_{\mathcal{M}}={\displaystyle \frac{trace\left({\mathcal{M}}^2\right)}{trace\left(\mathcal{M}\right)}}$$

(22)

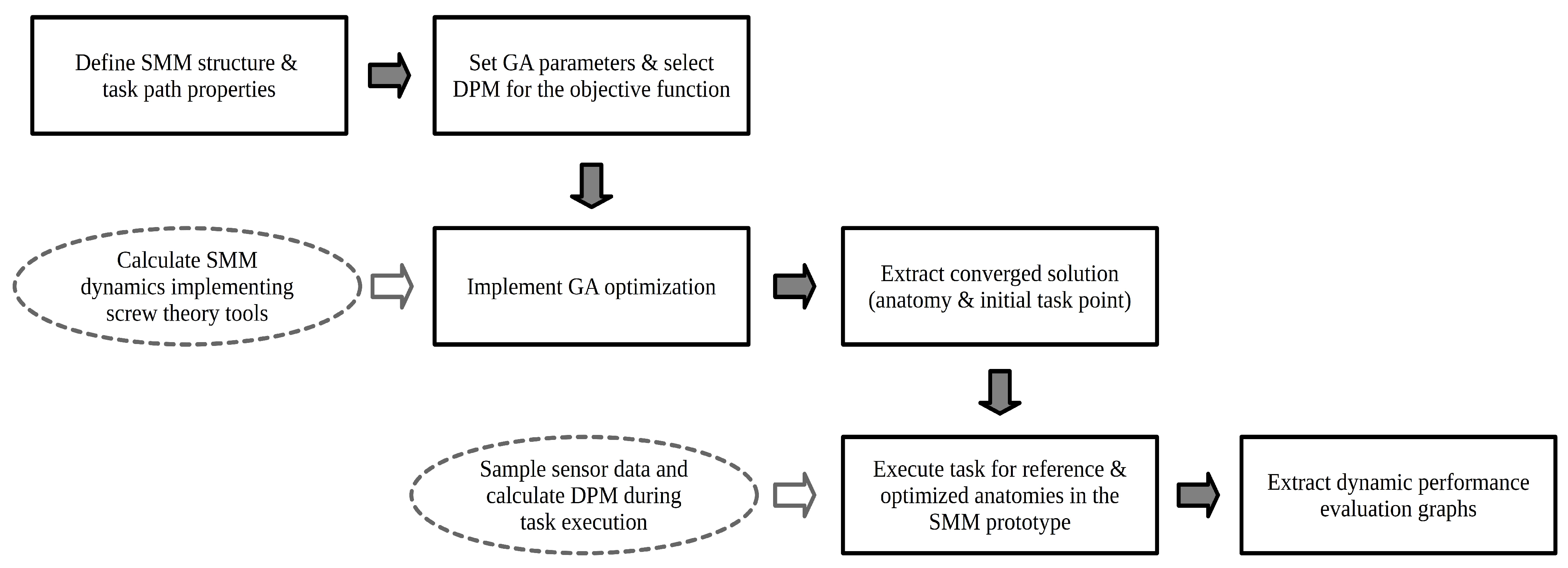
2.3. Methodology

In this work, the offline optimization methodology presented in [28] was implemented. An overview of the methodology is illustrated in Figure 2. The proposed framework comprised four major steps. The definition of the SMM and the desired task path, the optimization algorithm implementation, the real-life task execution, and the performance evaluation.

A fixed metamorphic structure was assembled, and multiple circular and rectangular paths defined in task space with varying specifications and constraints were selected. Genetic algorithm (GA) optimization was selected for its ability to effectively navigate complex, high-dimensional solution spaces, making it suitable for nonlinear problems such as optimized anatomy determination for an SMM.

The optimization employed a $max\left(min\right(·\left)\right)$ objective function, where established dynamic performance measures (DPMs) were evaluated across a set of task points along each predefined path. The objective function aimed to maximize the minimum performance index along a task path, ensuring robust performance across all task points.

$$f^{★}=max\left(min\left(\widehat{\mathbf{F}}\right)\right),\widehat{\mathbf{F}}=\{DPM\left(p_1\right),\dots ,DPM\left(p_N\right)\}$$

(23)

The chromosome structure was composed of two sets of variables. The first consisted of 3 integers in the range of $c_j\in \left[1,15\right],j=1,2,3$ representing the predetermined number of available passive module angles (PMA). The latter was formed with 3 float numbers, representing the Cartesian coordinates ($x_0\in \left[-0.6,0.6\right],y_0\in \left[-0.1,0.4\right],z_0\in \left[0,0.7\right]$) of the initial point (IP) of the task path. User-defined parameters such as population size ($PopulationSize$), tolerance ($FunctionTolerance$), and the maximum number of generations ($MaxGenerations$) were tailored to control the convergence of the algorithm. The GA optimization problem was solved using MATLAB (2021a) Global Optimization Toolbox built-in functions for mixed-integer problems. In Figure 3, the variables that formed the chromosome are depicted, and the utilized MATLAB functions are provided along with the selected parameters. The GA optimization was executed multiple times to assess solution convergence.

Each task was executed for both the reference and the optimized anatomies. The actual data accumulated from the robot’s sensors, alongside the performance measures calculated during offline simulations, were plotted for each task under study. To gain a comprehensive understanding of the robot’s performance, various charts were generated and the correlation between theoretical assumptions and actual performance was analyzed.

3. Main Theoretical Results

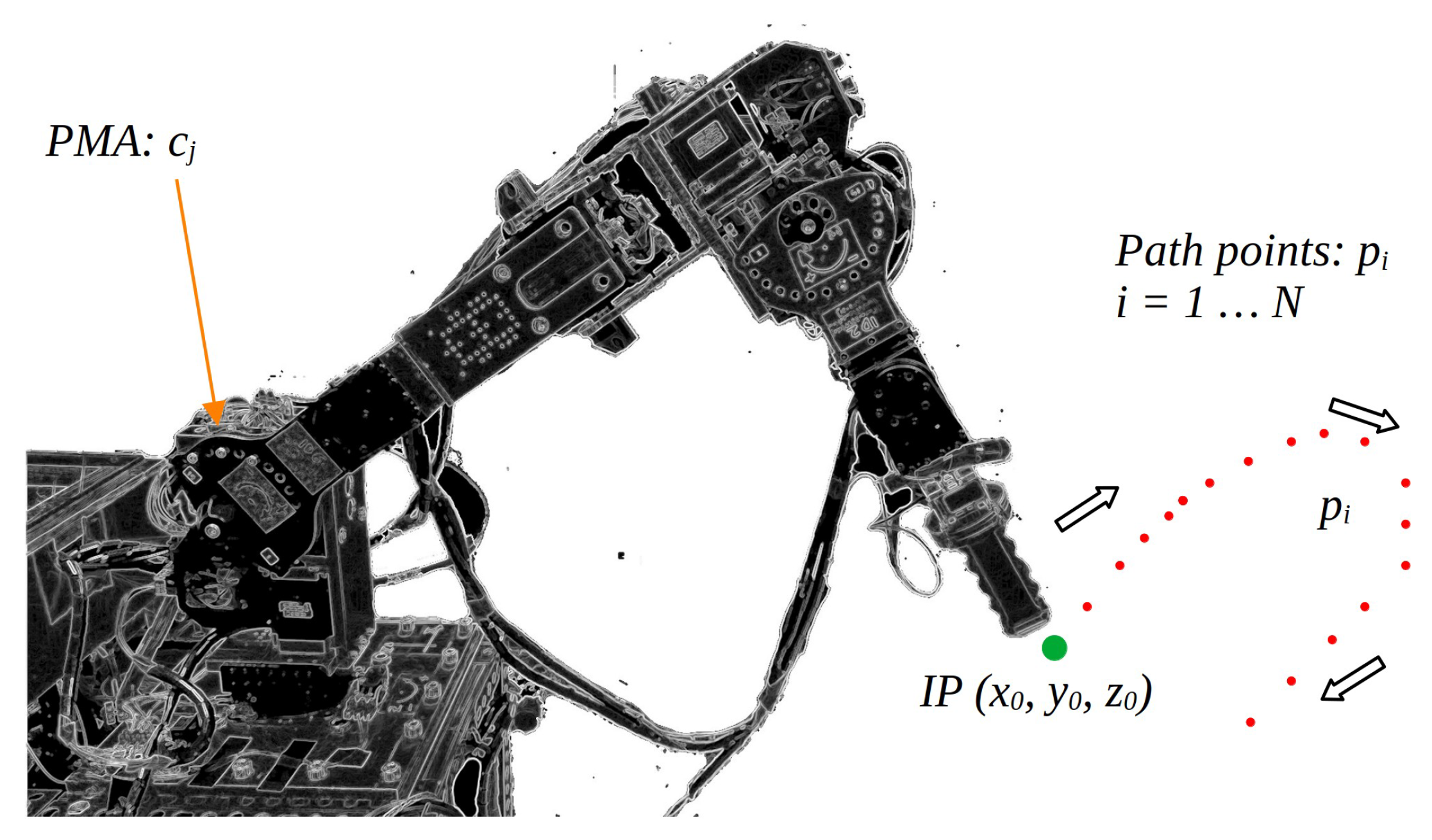
3.1. Task Paths

For theoretical and experimental validation, circular and rectangle paths (CP/RP) were selected in different areas of the manipulator workspace, as shown in Figure 4a. Rectangle paths were selected in order to study the effect of rapid direction changes and the effect of a variable TCP velocity when direction was constant.

Circular paths were selected to study the effects of circular motion, which inherently involves variable acceleration and velocity profiles. These varying loads required the control system to adeptly manage the torque and velocity outputs to maintain precise trajectory tracking. For both tasks selected, the necessity to handle the imposing dynamic variations without compromising accuracy and stability was investigated in order to obtain a deeper understanding of the effect of SMM mechanical design and consider the areas to improve by implementing a more sophisticated control architecture.

3.2. GA Optimization Results

Following the methodology outlined in Section 2.3, a GA was employed for the task-based optimization to determine optimized anatomies for each task execution. The anatomies presented in

Table 1. Extracted SMM anatomies.

Anatomies	ID	IP Cartesian Coordinates [m]	Pseudojoints’ Angles [rad]
Reference	0	-	$\left[0,0,0\right]$
Optimized EMI CP	1	$\left[0.16,-0.29,0.57\right]$	$\left[0.4488,0,0.6732\right]$
Optimized LCI CP	2	$\left[0.11,-0.34,0.59\right]$	$\left[0.8976,-0.4488,-0.2244\right]$
Optimized LCI RP	3	$\left[-0.07,-0.18,0.50\right]$	$\left[0.8976,0,0\right]$

were extracted for performance evaluation. In Figure 5a, the SMM prototype was assembled and reconfigured for the LCI RP anatomy (ID: 3) with the TCP located at the extracted IP-RP.

In order to acquire a more detailed view of the optimization effect, a 3D scatter of the manipulator workspace is demonstrated in Figure 5b. The optimized LCI RP anatomy (ID:3) is visualized, at the same configuration, along with the LCI values calculated within its workspace. It is evident that the IP-RP was located in a workspace region with the highest LCI values, providing an initial indication that the proposed dynamic model aligned with theoretical performance evaluation.

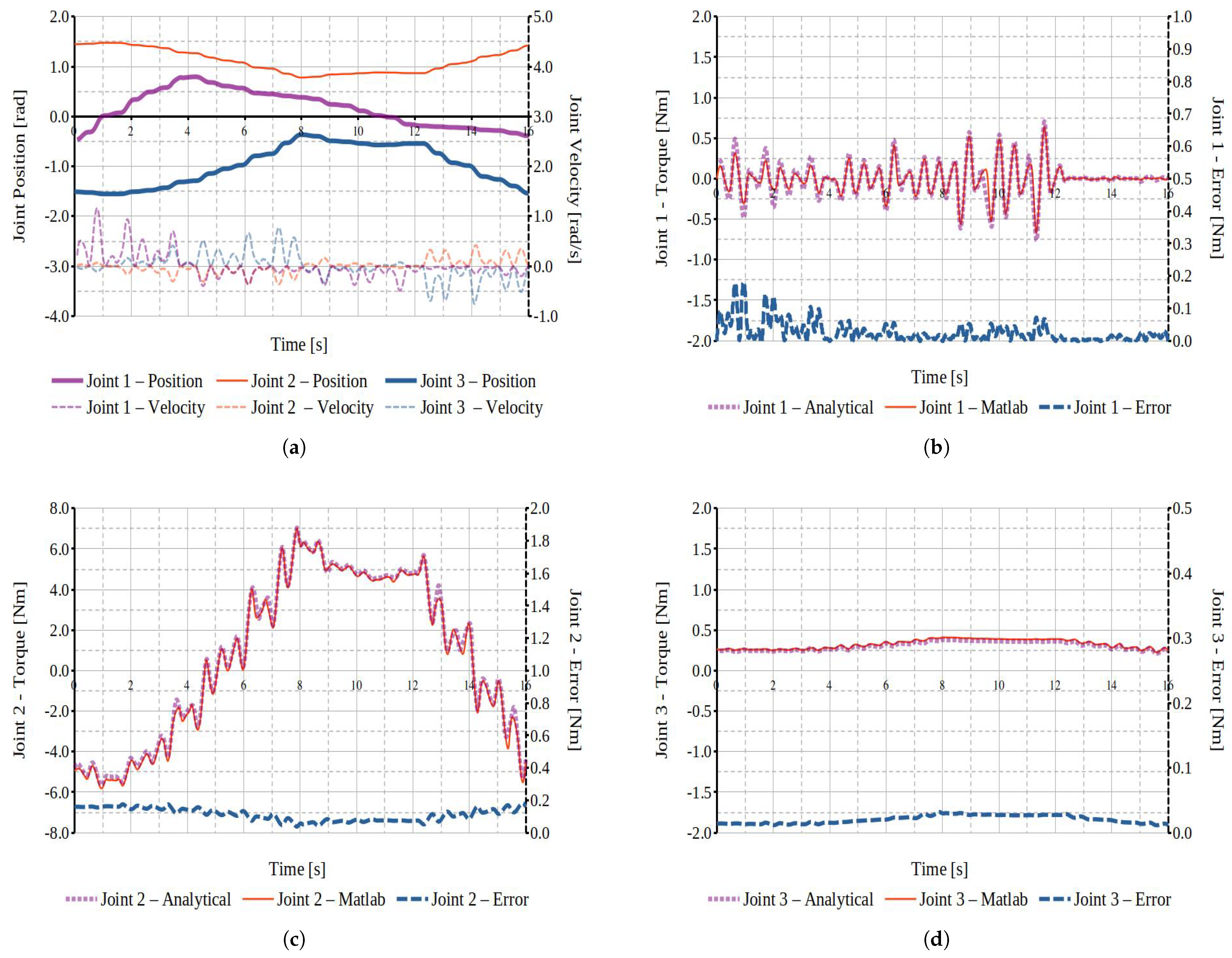
3.3. Theoretical Validation of Dynamic Modeling

A detailed theoretical validation was conducted using the optimized LCI RP anatomy (ID: 3, task path: 28) illustrated in Figure 5b. The rectangular task path from the optimized IP was simulated in MATLAB. Joint torques were calculated using the analytical simplified-dynamics model and compared with torques obtained from the built-in dynamics solver of MATLAB’s Robotics Toolbox.

Figure 6a presents the joint positions and velocities for the simulated trajectory, while Figure 6b–d show the simulated torques and the corresponding absolute errors. The simplified dynamic model closely approximated the MATLAB dynamics solver, with torque deviations consistently below 0.2 Nm at all joints. Joint 2, which carried the main load, exhibited the largest torque values and deviations. Joint 1 also exhibited greater torque deviations during dynamic transitions. The error graphs confirmed the model’s consistency in capturing general trends but highlighted limitations in precision under high-load conditions.

4. Experimental Case Study

4.1. The SMM Prototype

The experimental investigation utilized the SMM prototype developed in our laboratory, executing the predefined task paths and analyzing the acquired sensor data using the established theoretical model and performance evaluation metrics. The three-degree-of-freedom (DoF) SMM prototype used for this work is presented in Figure 4b at a reference anatomy along with the main components used for the structuring and operation. The metamorphic structure comprised three pseudojoints, assembled to achieve a robot with orthogonal axes configured in a Z–X–X arrangement when set to its reference anatomy. The properties of the metamorphic structure, system architecture, and control software along with the hardware setup are presented in detail in [29].

The joints of the SMM prototype used fixed-gain Proportional–Integral–Derivative (PID) position controllers to generate the required efforts. The fixed controller gains were manually tuned to mitigate potential instability under high dynamic loads or external disturbances. Although limitations were observable, the overall performance of the system provided a stable foundation for studying the performance of the SMM. Despite the challenges, the implementation of the PID controller ensured a reliable basis for further analysis and optimization. This implementation ensured precise control over each joint’s movements, allowing for the accurate execution of the planned trajectories. However, the inherent limitations of the PID controller, such as sensitivity to parameter tuning and difficulty in handling nonlinear dynamics, could not be completely avoided.

4.2. Executed Task Paths

Figure 7 and Figure 8 depict the implemented trajectories in 3D space alongside the TCP position error. Both anatomies exhibited variable dynamic performance along the task path, with a clear correlation between lower performance index scores and reduced position tracking accuracy. In both tasks, the most pronounced deviations were observed along the Z-axis, highlighting challenges in maintaining vertical trajectory precision during task execution confined to the XY-plane. In segments with lower performance index scores, the X- and Y-axis position errors did not converge to zero, maintaining an accuracy of approximately 5 mm. In both tasks, in these segments, the Z-axis error was not adequately managed by the position controller and ranged between 1.5 cm and 2 cm. These results underline the interconnection between dynamic manipulability and position tracking, emphasizing the significance of optimizing performance indices to enhance accuracy.

The achieved performance demonstrates the validity of the proposed metrics in evaluating dynamic performance across various task anatomies. Moreover, these results indicate that the simple PID joint position controller utilized in the SMM prototype software (available at https://github.com/StravopodisNikos/MetamorphicManipulator_devel.git, accessed on 30 November 2024), encounters challenges in mitigating vertical deviations, particularly in regions of low performance indices. Addressing these issues in future work could involve refining control algorithms to adapt dynamically to performance variations along the task path. Furthermore, incorporating higher-fidelity dynamic models and accounting for unmodeled factors, such as joint compliance and coupling effects, could enhance the robot’s ability to maintain precise trajectory tracking and improve overall dynamic performance.

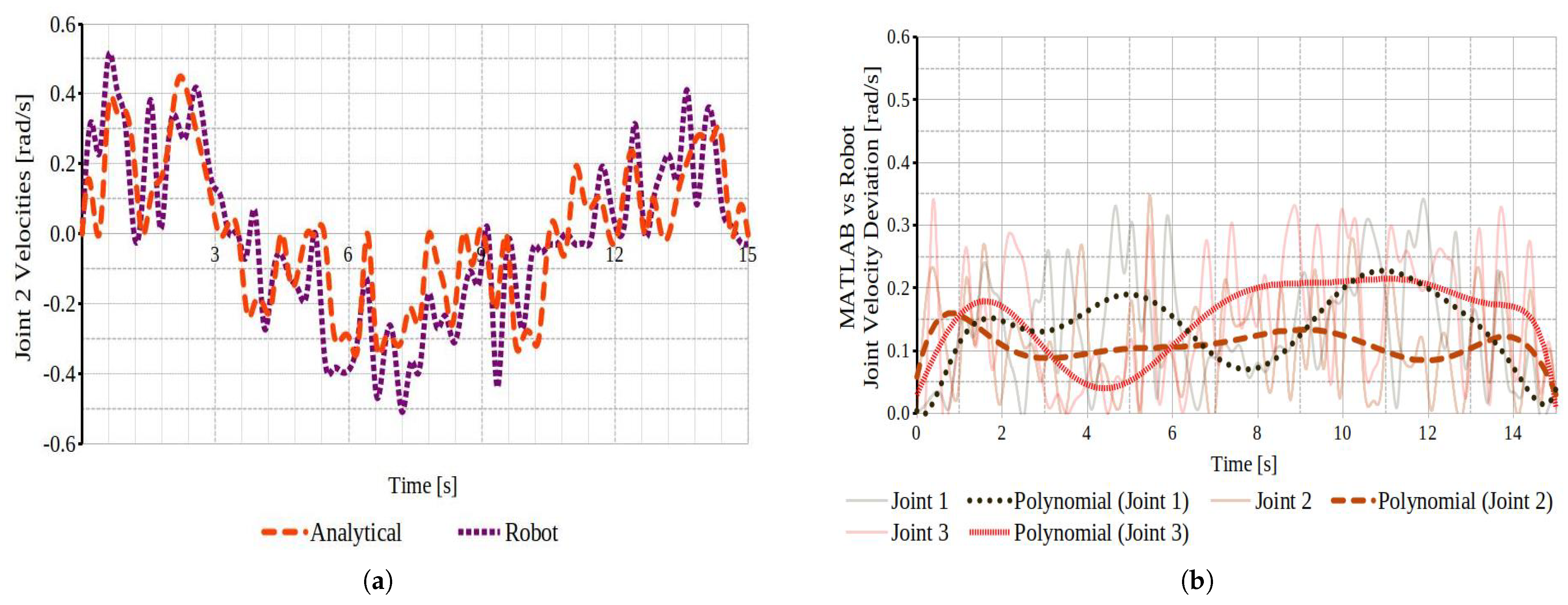
4.3. Experimental Validation of Dynamic Modeling

The next phase of the validation process evaluated the accuracy of the simplified dynamic model by comparing analytical calculations with experimental data. That phase focused on assessing the model’s ability to capture the system’s fundamental behavior under basic task conditions, including low end-effector speed and the absence of external forces or loads. Analytical calculations executed in MATLAB for a specific anatomy (ID: 1) and the Cartesian path were compared with experimental data, particularly focusing on joint 2, the main contributor to the joint effort. Graphs of joint torques and velocities, as well as torque and velocity deviation for all joints, were used for the investigation. This comparison enabled a detailed assessment of how effectively the theoretical model reflected the core system dynamics. Additionally, the comparison highlighted the limitations of the simplified model by quantifying discrepancies and offering insights into the effects of unmodeled factors such as joint friction, stiffness, parameter uncertainties, and external disturbances.

In Figure 9 and Figure 10, the torques and velocities calculated by the dynamic model and the ones produced by robot joints are compared. In Figure 9a and Figure 10a the ability of the established dynamic model to effectively capture the general trend in torque and velocity is illustrated. The torque comparison, shown in Figure 9a, reveals that the theoretical calculations were noticeably smoother, largely due to the simplified model used in MATLAB. The experimental data from the robot presented fluctuations, primarily attributed to the PID controller’s influence and unmodeled dynamics such as friction, joint compliance, and external disturbances. To extract a more detailed view of the observed discrepancies, the deviation between theoretical and experimental data is illustrated in Figure 9b and Figure 10b. In both graphs, polynomial regression trend lines were employed to analyze the deviation patterns. Joints 1 and 2 produced lower effort values, with their discrepancies exhibiting smaller variations (approximately 0.5 Nm), primarily due to evenly distributed sensor noise over the task’s duration. The fluctuations in torque deviations observed for joint 2 correlated with the overall effort trend, suggesting that joint friction had a more significant impact. Additionally, transient effects and controller response contributed to the observed variations. The observed torque peak deviations reached approximately 3.5 Nm, with a median deviation value of 1.5 Nm. Velocity discrepancies displayed similar sensitivity to unmodeled system uncertainties, with trend lines remaining below 0.2 rad/s, which was considered adequate for this analysis.

These results, although not optimal, offered a reliable base reference for evaluating the experimental data obtained from the corresponding task paths executed by the robot prototype. This evaluation, presented in the remainder of this section, focused on the following three main areas: optimizing joint torque to velocity output, optimizing end-effector translation response, and the joint torque controller output.

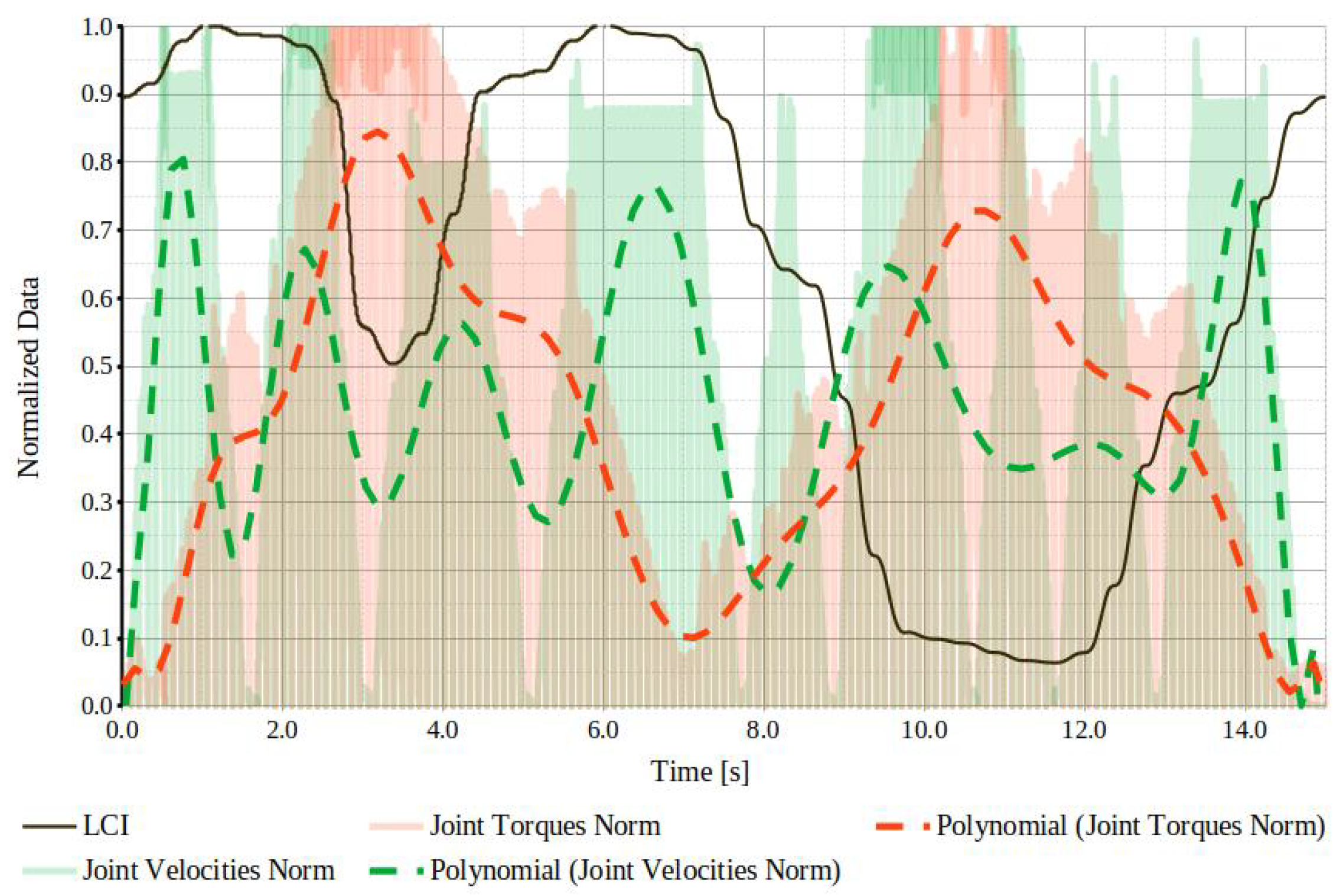
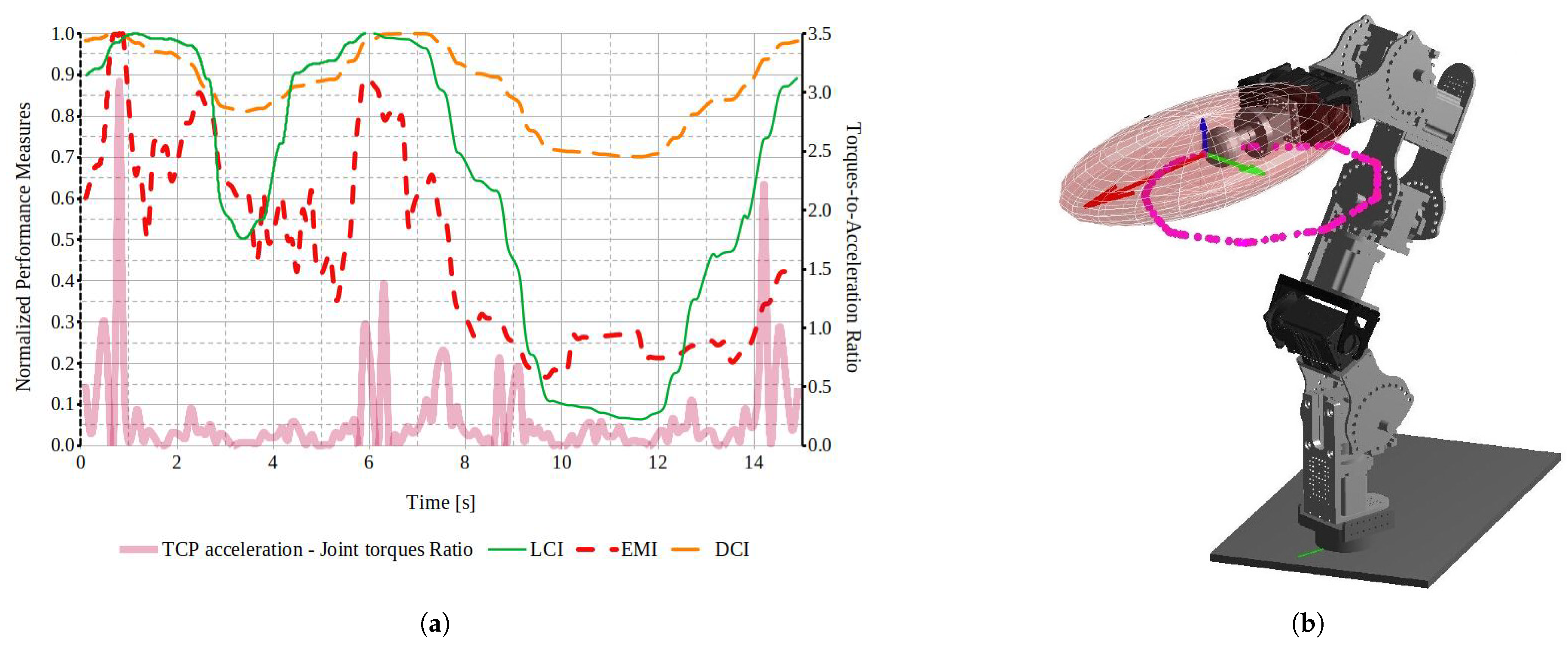
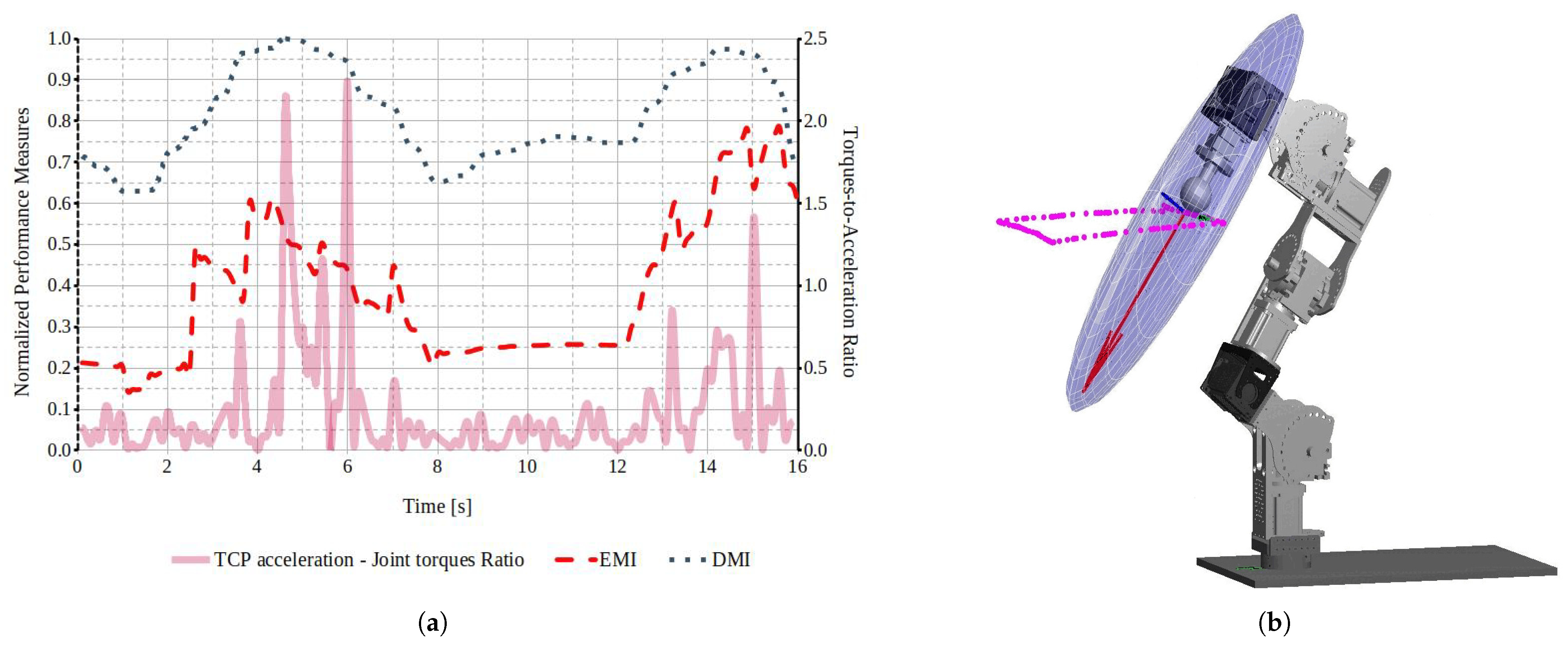
4.4. Dynamic Performance Evaluation

4.4.1. Optimizing Joint Torque to Velocity Output

The initial segment of the performance analysis was focused on comprehending the overall dynamic performance and efficiency. This involved comparing the supplied joint torques with the resultant joint velocities. The norms of the joint torques and velocities were normalized given the maximum value achieved along the path waypoints and were plotted in the same chart for each of the executed tasks. Figure 11 presents the notable correlation between joint velocities and joint torques. It is observed that larger joint velocities were achieved with smaller joint torques in these optimal performance segments, where the LCI achieved its higher values. Larger values of the LCI reflect higher joint velocities with lower effort. Moreover, the variation in the LCI accurately tracked the changing relation, providing a valuable tool for the offline identification of efficient operating conditions.

In Figure 12, the normalized DCI values are presented to compare the index’s capability in providing accurate information about the task implementation on the real robot. The DCI only considered the conditioning of the GIM, with no further investigation on robot configuration and task space characteristics. During the time span of $[1.75,6]\left[\mathrm{s}\right]$, the DCI presented its peak values, suggesting that the robot was closer to an isotropic configuration. However, this information did not offer any useful insights into the overall robot effort and its maximum torque. In contrast, the LCI within the same time span clearly indicated a higher robot effort to achieve the desired joint velocities. For a comprehensive performance analysis during task execution, it is crucial to consider not only the inertia properties of the robot in joint space but also their relationship to the operational space. This approach yields more accurate and relevant information.

In Figure 13, two distinct anatomies were compared during the execution of the same circular path, with key numerical results presented in

Table 2. Optimized anatomy scores.

Performance Area	Optimized (ID:2)	Reference (ID:0)
Best LCI score along the task path	66%	34%
Lower torques norm along the task path	74%	26%
Maximum torque norm [Nm]	7.4	16.0
Median torque norm [Nm]	2.86	4.86
Median velocity norm [rad/s]	0.27	0.29
Median torque-norm-to-velocity-norm ratio	10.81	16.84

. Task path 19 corresponded to the LCI-optimized anatomy (ID: 2), while task path 25 was executed with the robot configured in its reference anatomy (ID: 0). Both anatomies exhibited the previously identified behavior, where higher torque peaks were associated with lower LCI values. The LCI-optimized anatomy (ID: 2) demonstrated relatively consistent index values with minor fluctuations, highlighting the effectiveness of the optimization process. The optimized anatomy achieved a substantial reduction in maximum torques produced, maintaining lower torque values for 74% of the task execution time compared to the reference anatomy. Both anatomies demonstrated comparable median velocity norms (0.27 [rad/s] for the optimized anatomy and 0.29 [rad/s] for the reference anatomy). However, the optimized anatomy performed the task with a median torque norm of 2.86 Nm, representing a 41% reduction relative to the 4.86 Nm observed for the reference anatomy. Furthermore, the joint’s torque-to-velocity ratio improved by 35%, decreasing from 16.84 to 10.81. This improvement signified a marked enhancement in task execution efficiency through the reduction in the torque-to-velocity ratio.

In Figure 13, the most significant difference in the LCI score was observed between the two anatomies during the time interval of approximately $[8,14]\left[\mathrm{s}\right]$. Within that period, the optimized anatomy demonstrated a substantial reduction in joint effort. Conversely, during the time interval $[1,5.8]\left[\mathrm{s}\right]$, the reference anatomy exhibited a slightly higher LCI score, with a correspondingly higher torque-to-velocity ratio. This observation indicates that anatomy optimization may result in task segments where suboptimal performance is observed. Consequently, analyzing LCI scores along the task path provides a more comprehensive understanding of task execution performance, highlighting areas of improvement and potential trade-offs in trajectory implementation and control algorithms.

Overall, the analysis revealed a clear correlation between LCI and dynamic performance. These insights are crucial for task-based optimization and highlight the importance of considering both joint space and operational space dynamics in the performance evaluation. The LCI can also be used to quantify the relative behavior of two anatomies of the same SMM structure, providing a useful metric for a comparative analysis.

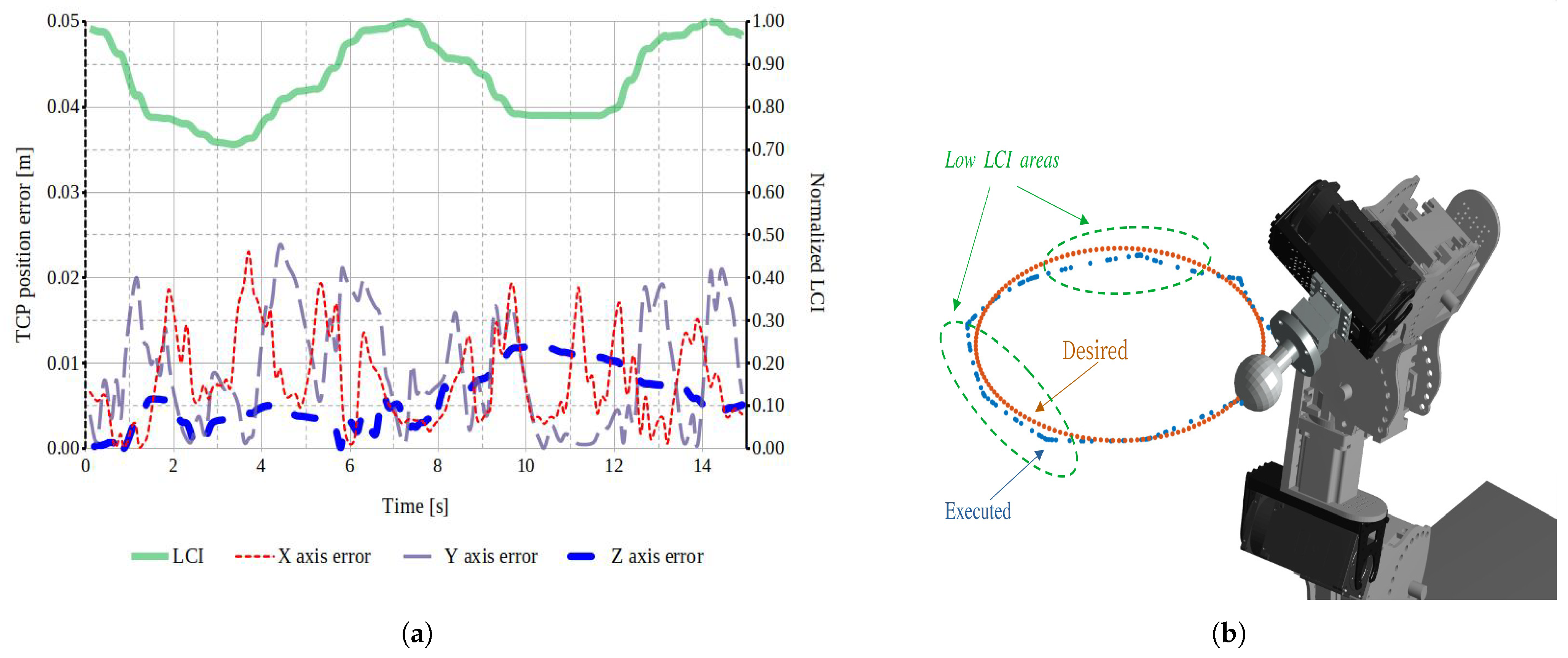
4.4.2. Optimizing End-Effector Translation Response

In this section, the evolution of the ratio between the achieved TCP acceleration and the produced joint torques is investigated. Circular motion inherently involves variable acceleration and velocity profiles. As the TCP traverses the circular path, the centripetal and tangential accelerations continuously change, imposing varying dynamic loads on the manipulator’s joints. This study aimed to determine which of the utilized performance measures provided the most accurate representation of the achieved ratio. The introduced EMI proved to be the most effective in capturing the evolution of the ratio with higher resolution, as it also considered the direction of motion.

In Figure 14a and Figure 15a, the ratio extracted from robot data and the performance measures extracted from task simulation are plotted for a CP executed by the optimized EMI CP (ID: 1) and the optimized LCI RP (ID: 3) anatomies, respectively. The utilized performance measures are plotted in order to discuss the achieved accuracy in tracking the efficiency of producing TCP acceleration from the joints’ torques. As expected, the DCI did not provide adequate detail on the evolution of the ratio. Furthermore, the LCI presented the three main path segments where an optimal ratio could be found but adequate fidelity was still not achieved. The EMI demonstrated high sensitivity to dynamic changes, closely reflecting performance variations, thus providing detailed performance insights, but demanded a higher computational cost. In summary, the EMI presents a behavior that should become a useful tool for identifying maximum load scenarios during path execution, while metrics such as the DME and DCI can be useful for broader performance assessments where stability and less noise are advantageous. As previously discussed, the DCI should not be considered for a task-based dynamic performance analysis.

To obtain a more detailed view of the dynamic performance of the robot during task execution, the DME index is plotted in Figure 14b and Figure 15b for the best- and worst-case path waypoints. For the highest scoring waypoint, it is observed that the largest axis of the ellipsoid, which corresponds to the highest eigenvalue, is aligned with the direction of motion. Conversely, in the case of the lowest scoring waypoint, one of the smaller axes, corresponding to a lower eigenvalue, is aligned with the TCP velocity direction.

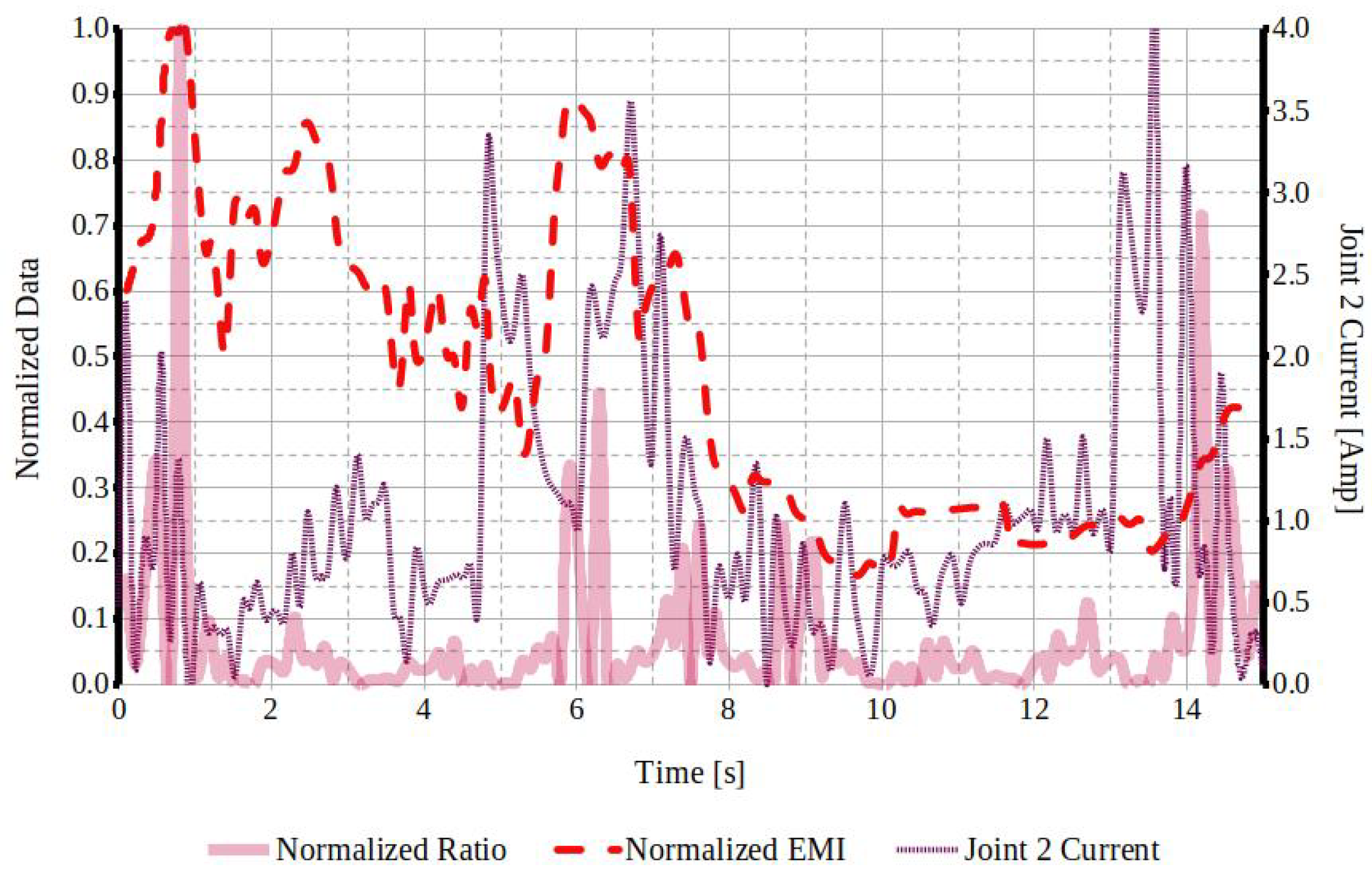
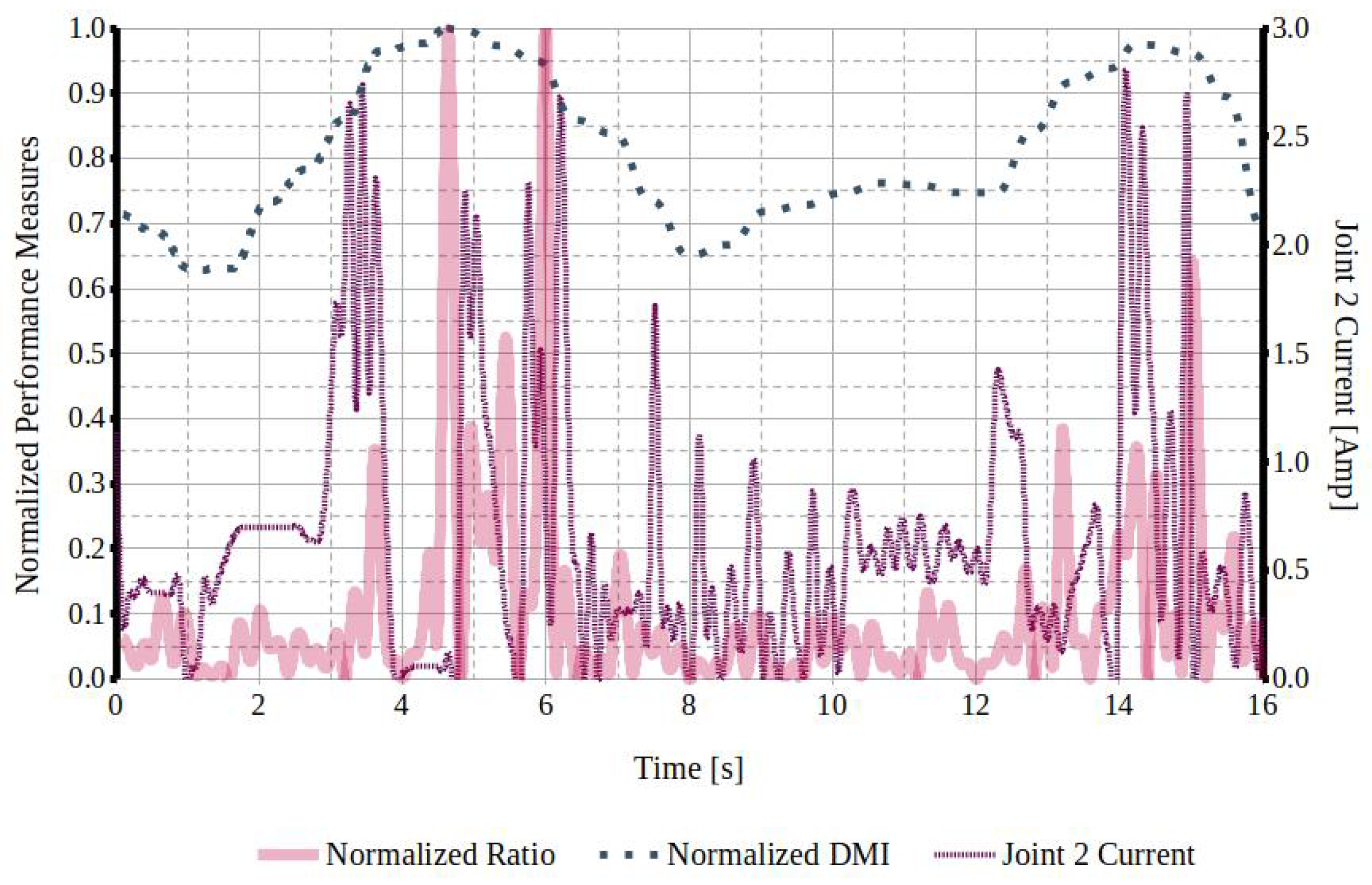
4.4.3. Joint Torque Controller Output

Building on previous findings, the performance measures identified task segments with higher torque-to-acceleration ratios, which exhibited larger TCP accelerations and increased joint currents. To examine these effects on joint controller efficiency, only current data from the second active joint were analyzed, as it bore the primary load for achieving the desired task path.

In Figure 16, data from the execution of a circular path are presented. The controller output was not smooth, exhibiting larger current spikes in segments where a higher torque-to-acceleration ratio was achieved. This indicated significant dynamic load changes. The EMI could track the current output behavior, but accuracy was reduced, reflecting the complexity of dynamic interactions during circular motion. In Figure 17, data from rectangular path execution are shown alongside the simulated DME. A similar non-smooth behavior was observed, with current spikes occurring during motion along the Y-axis. This movement was primarily facilitated by joints 2 and 3. The DME index, despite being less sensitive to rapid dynamic changes, could effectively capture the controller behavior with greater fidelity, pinpointing the possible high-stress segments more accurately. This suggests that DME should be a reliable indicator for predicting current spikes and dynamic stresses during linear motion.

The significant current spikes observed in both task paths indicated areas of highest energy consumption, likely due to poorly tuned PID controllers or suboptimal trajectory planning. These spikes highlight the necessity of utilizing advanced trajectory optimization tools and refining the control system architecture to enhance dynamic performance.

5. Conclusions and Future Work

This study successfully verified the ability of an SMM prototype to achieve task execution efficiency through structural reconfiguration. The validation of theoretical models, based on data from real-world free-motion tasks and simulated performance metrics, was a critical aspect of this research. Based on the scientific claims stated, the main conclusions of this work are the following:

• Modeling accuracy: Given the simplified dynamic model employed for this initial evaluation, the focus was on analyzing the system’s fundamental behavior under basic task conditions, including low end-effector speed and the absence of external forces or loads. Both theoretical and experimental validation results confirmed the adequacy of the proposed dynamic model, providing a reliable baseline for comparing simulation data with experimental findings. The theoretical analysis confirmed the model’s accuracy, while the experimental validation highlighted that unmodeled dynamics contributed to deviations in joint torques, though overall trends remained consistent. Additionally, systematic errors arising from the inherent inaccuracies and imperfections of the physical robot prototype were evident but did not alter the general representation of the system’s dynamic behavior. These findings underscore the utility of the simplified model as a foundational tool for understanding system dynamics and guiding future refinements in modeling and experimental validation.
• Dynamic performance evaluation: Various metrics were analyzed to assess their effectiveness in extracting accurate information about the robot’s actual behavior. The results of this study successfully identified robot structures that led to enhanced performance and optimized task execution, consistent with findings in the literature [13,15,18]. The results demonstrated the value of performance measures in identifying task segments with optimized performance and areas requiring improvement. Despite using a simplified dynamic model, the framework effectively correlated performance indices with trajectory accuracy, highlighting its utility for evaluating and refining control strategies in reconfigurable robotic systems. The results demonstrated that task-based optimization, which incorporated the robot’s dynamic properties, brought performance evaluations closer to real-world conditions. This approach provided a more accurate reflection of how modular reconfigurable robots performed in practice, offering significant improvements in task adaptability and precision.
• Controller performance: The implementation of simple PID joint position controllers with fixed gains to execute motion commands on the SMM prototype resulted in reduced positional accuracy, particularly in task segments with lower dynamic performance. While task optimization increased the torque-to-acceleration ratio, it also introduced counterproductive effects that must be addressed to enhance controller efficiency and overall performance. Elevated joint currents and current spikes observed in regions with high torque-to-acceleration ratios indicated significant dynamic load variations. These findings underscore the necessity for advanced trajectory optimization techniques and refined control system architectures to achieve improved dynamic performance and energy efficiency.

This work provided insights in the fundamental dynamics and interactions within the SMM during simple task execution scenarios. However, the findings also underscore the need for more advanced control and trajectory implementation tools. Future work should focus on developing and integrating these sophisticated tools, which can build upon the foundational results of this study to further enhance the dynamic performance and operational efficiency of SMMs. The insights gained from this research pave the way for more advanced control strategies, ultimately contributing to advancement in the scientific field of MRRs and their introduction into real-life applications.