Response Characteristics of Anchored Surrounding Rock in Roadways Under the Influence of Vibrational Waves
Abstract
:1. Introduction
2. Engineering Background
2.1. Engineering Geology
2.2. Failure Characteristics of Roadway Failures
3. Vibration Wave Splitting and Loading
3.1. Measured Waveform Calibration
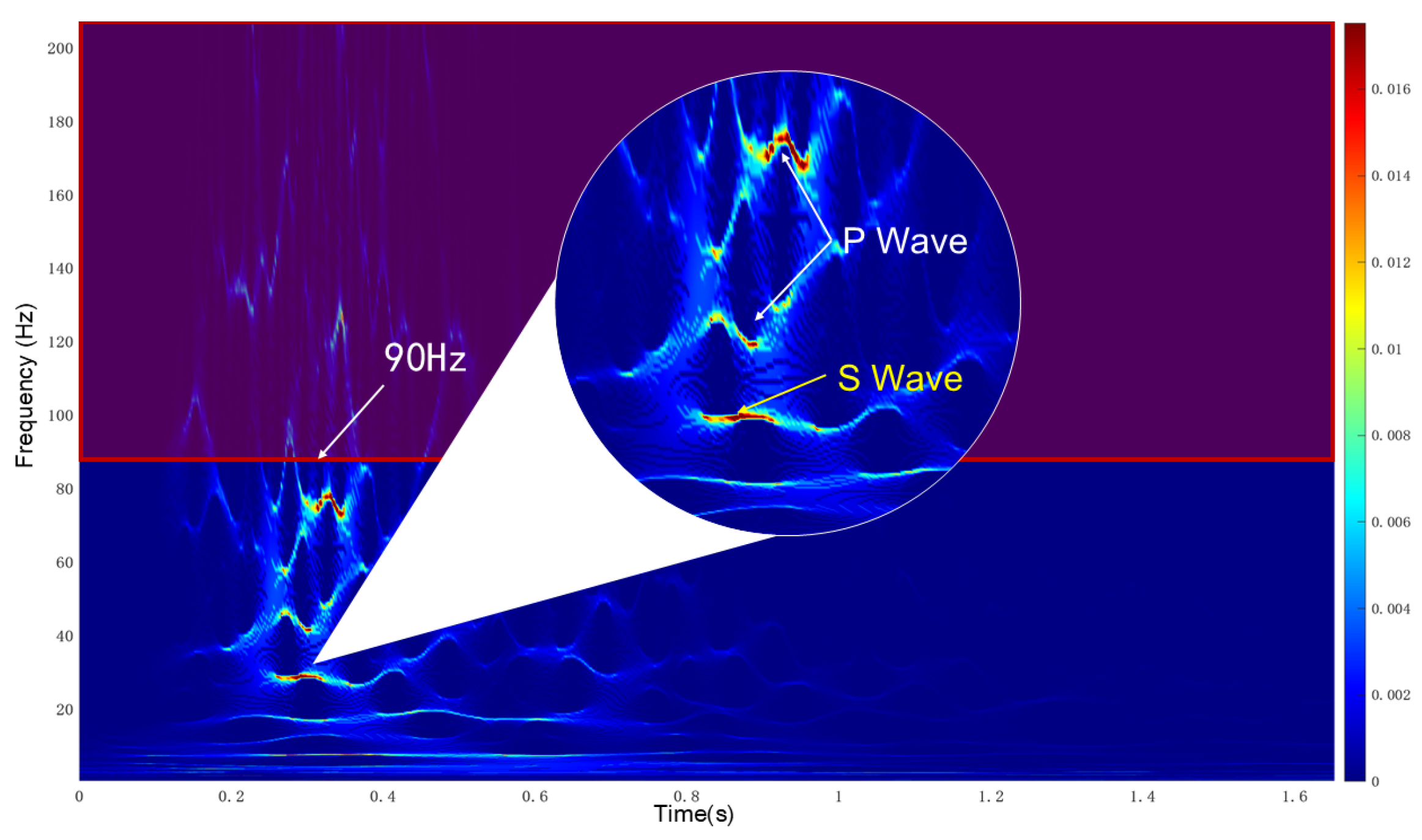
3.2. Separation and Filtering of Vibration Waveforms
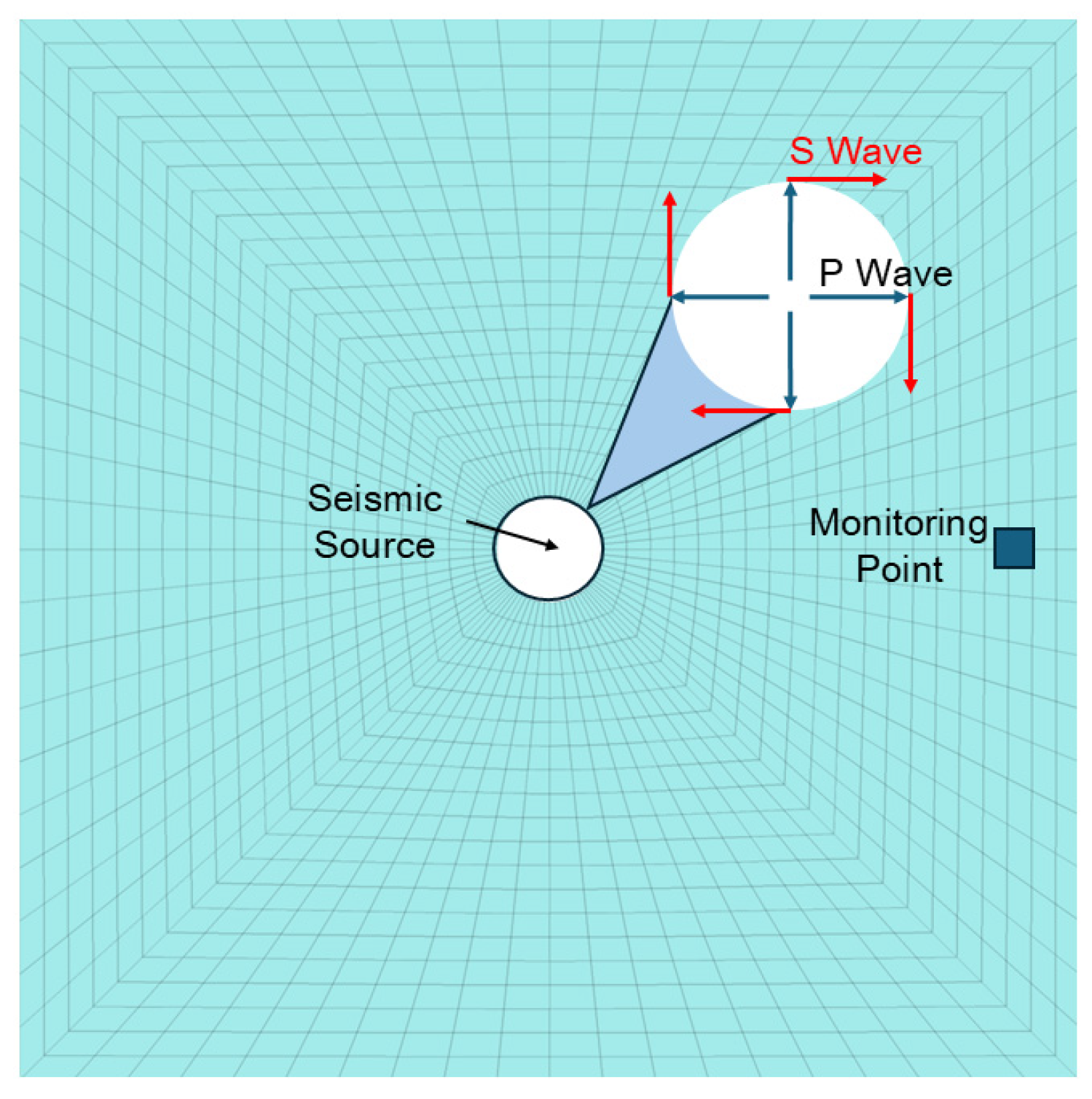
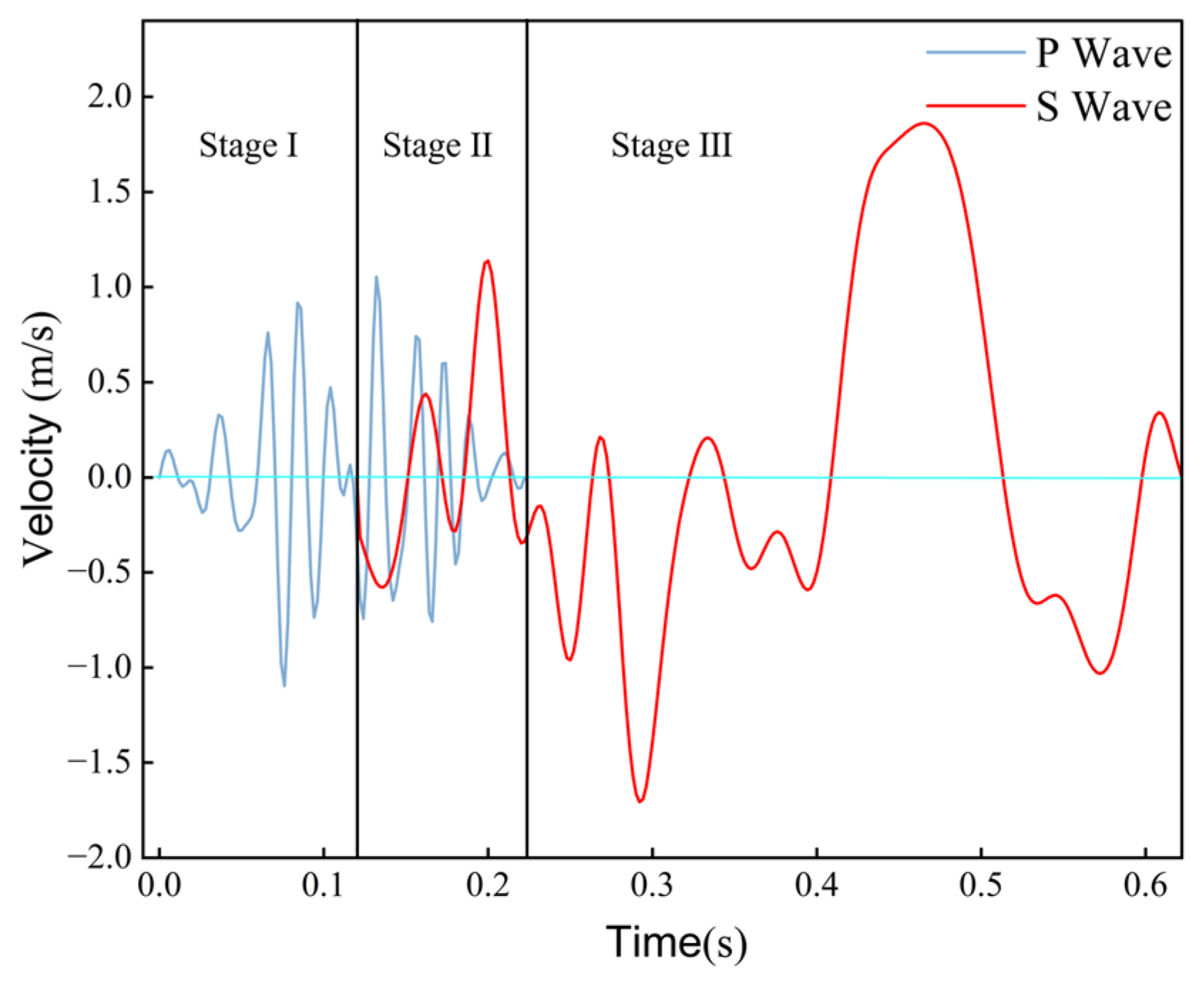
3.3. Longitudinal and Transverse Wave Propagation and Loading Modes
4. Model Establishment and Instability Evaluation Method
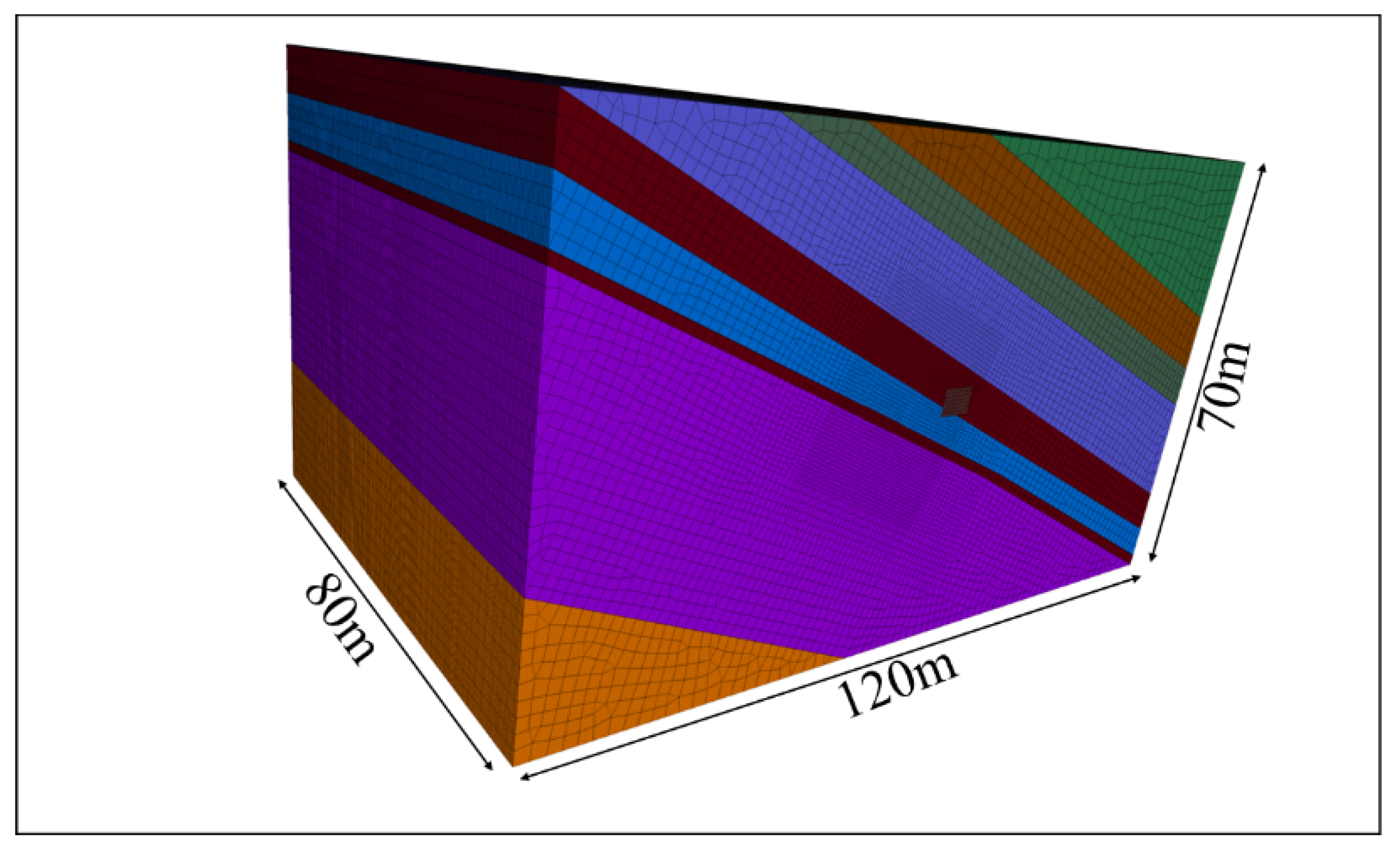
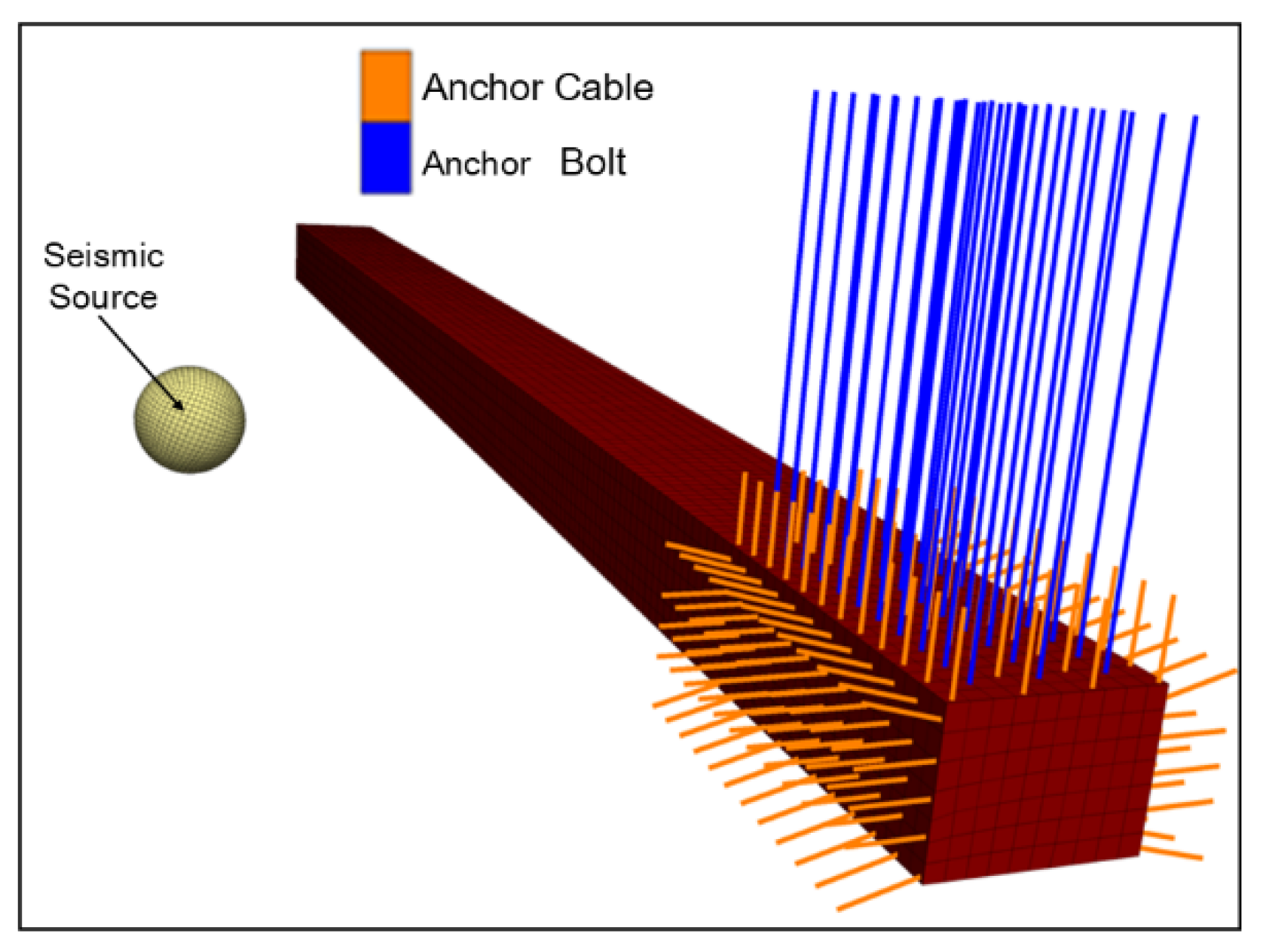
4.1. Development of a Numerical Model
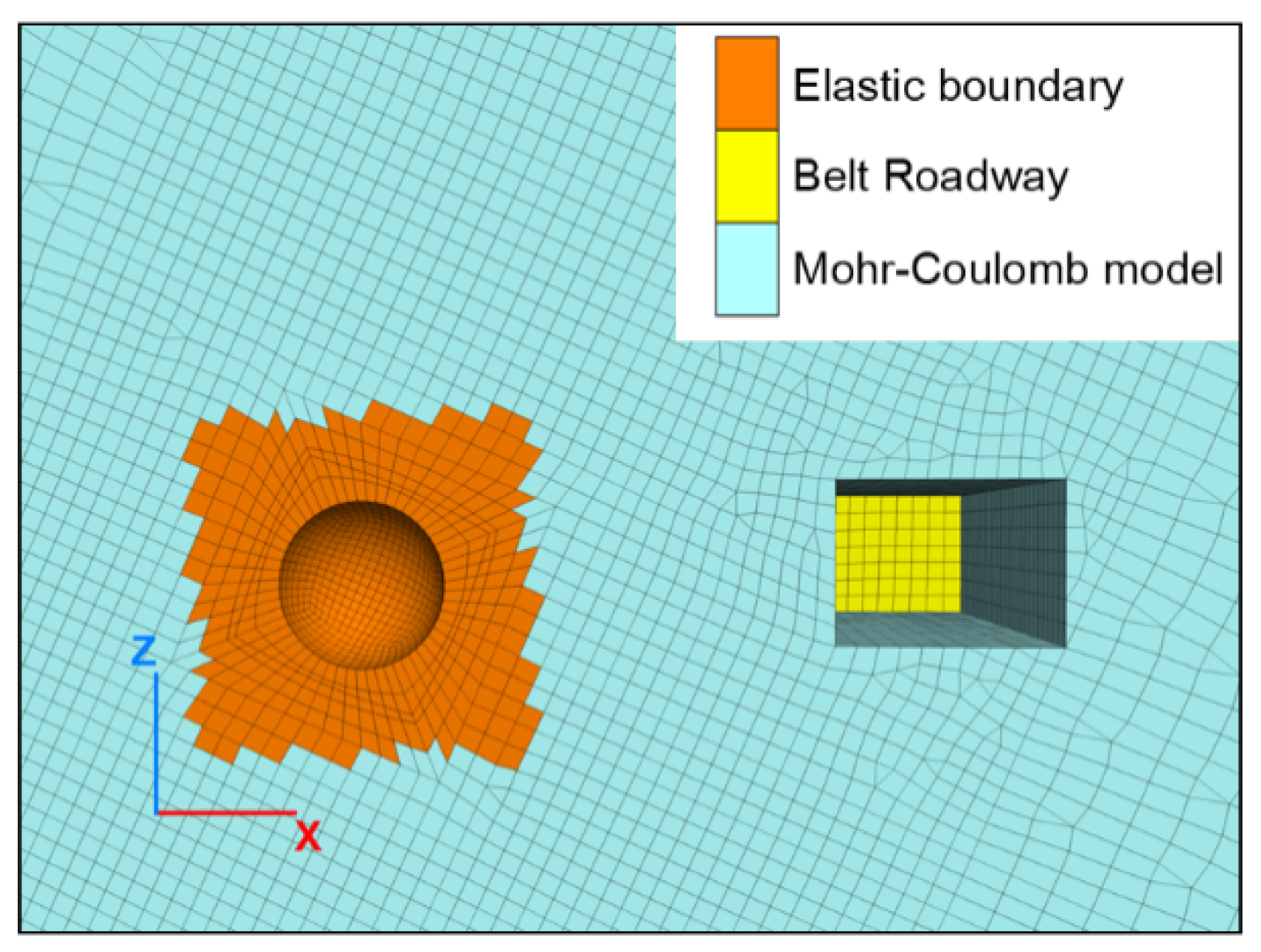
4.2. Boundary Condition Setting
4.3. Impact Instability Energy Evaluation Method
5. Numerical Simulation Results Analysis
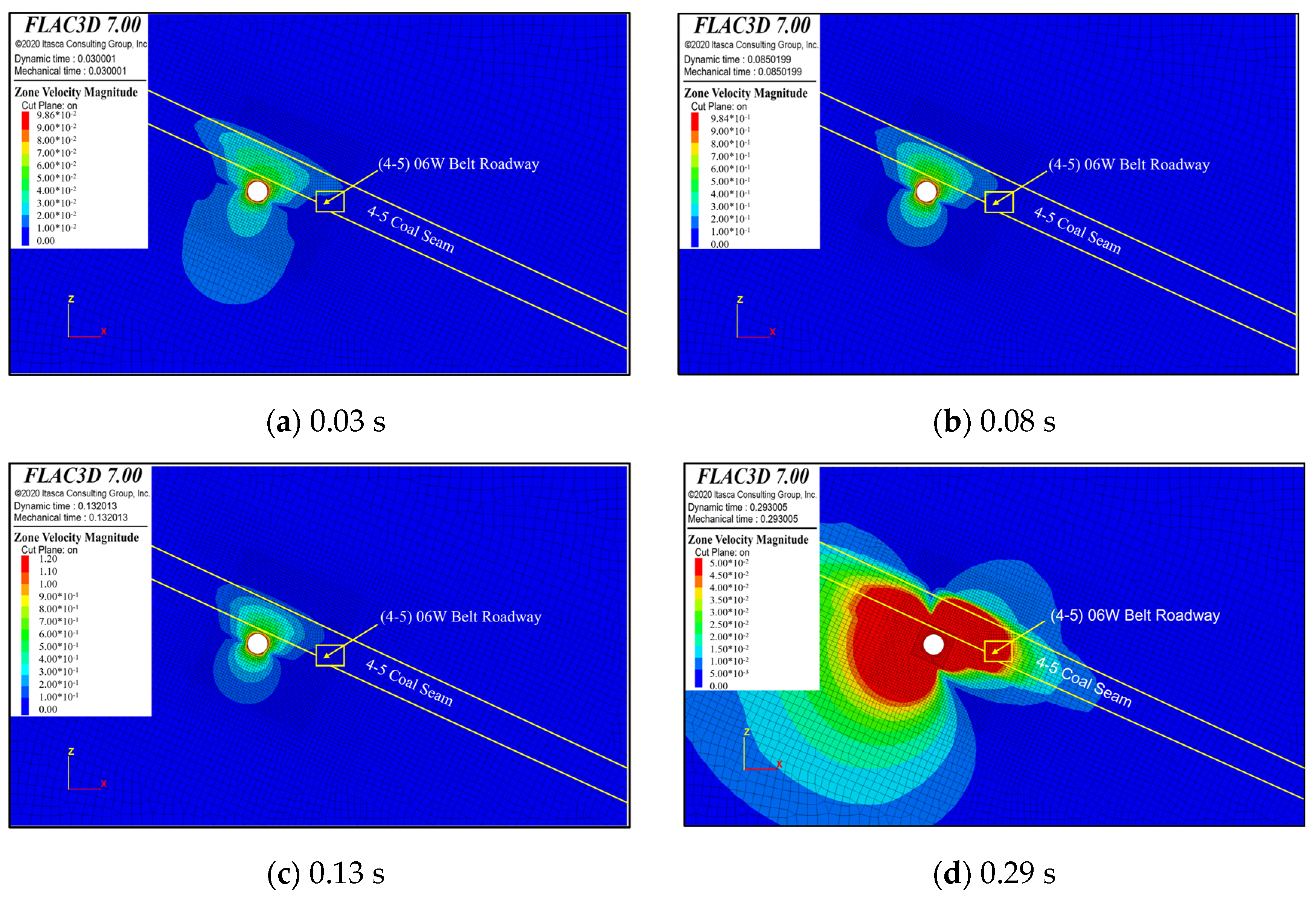
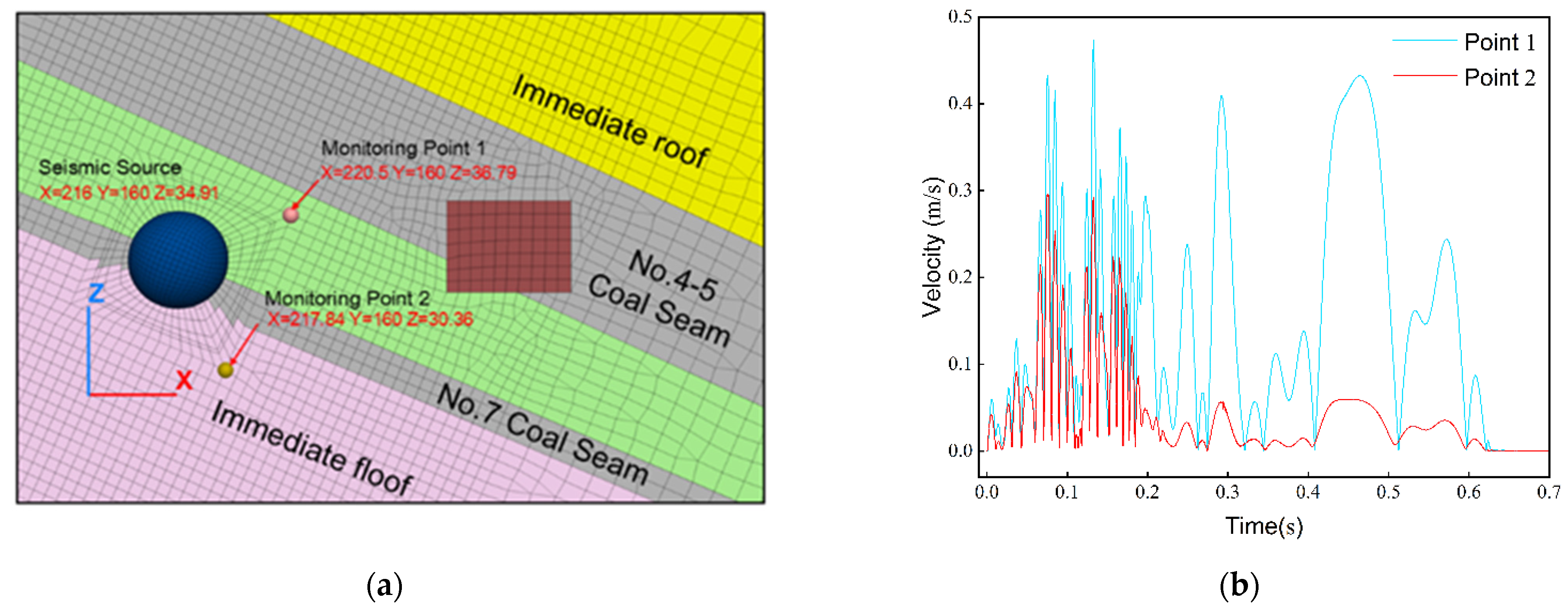
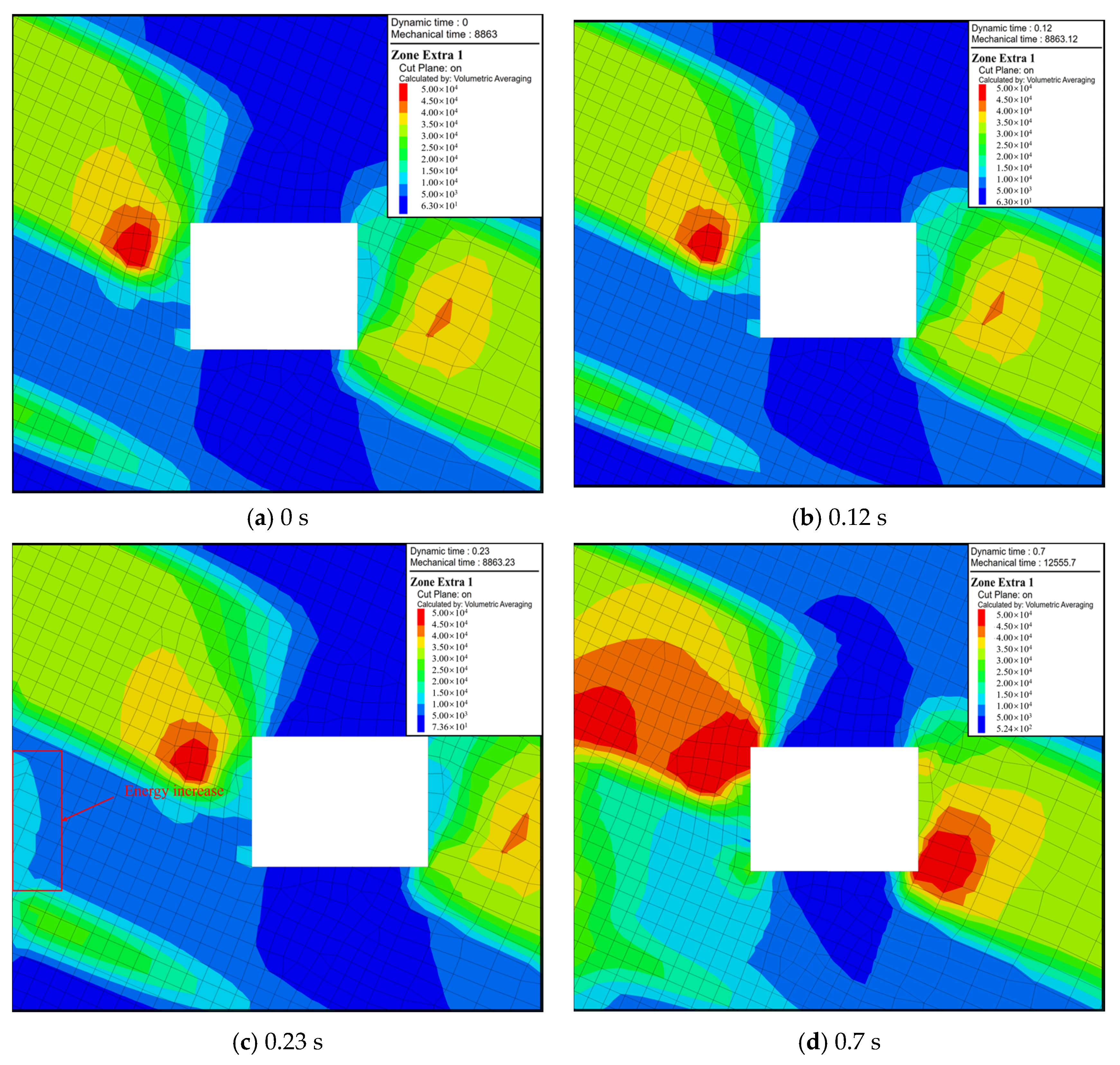
5.1. Seismic Wave Propagation Characteristics
5.2. Response Characteristics of Roadway-Anchored Surrounding Rock
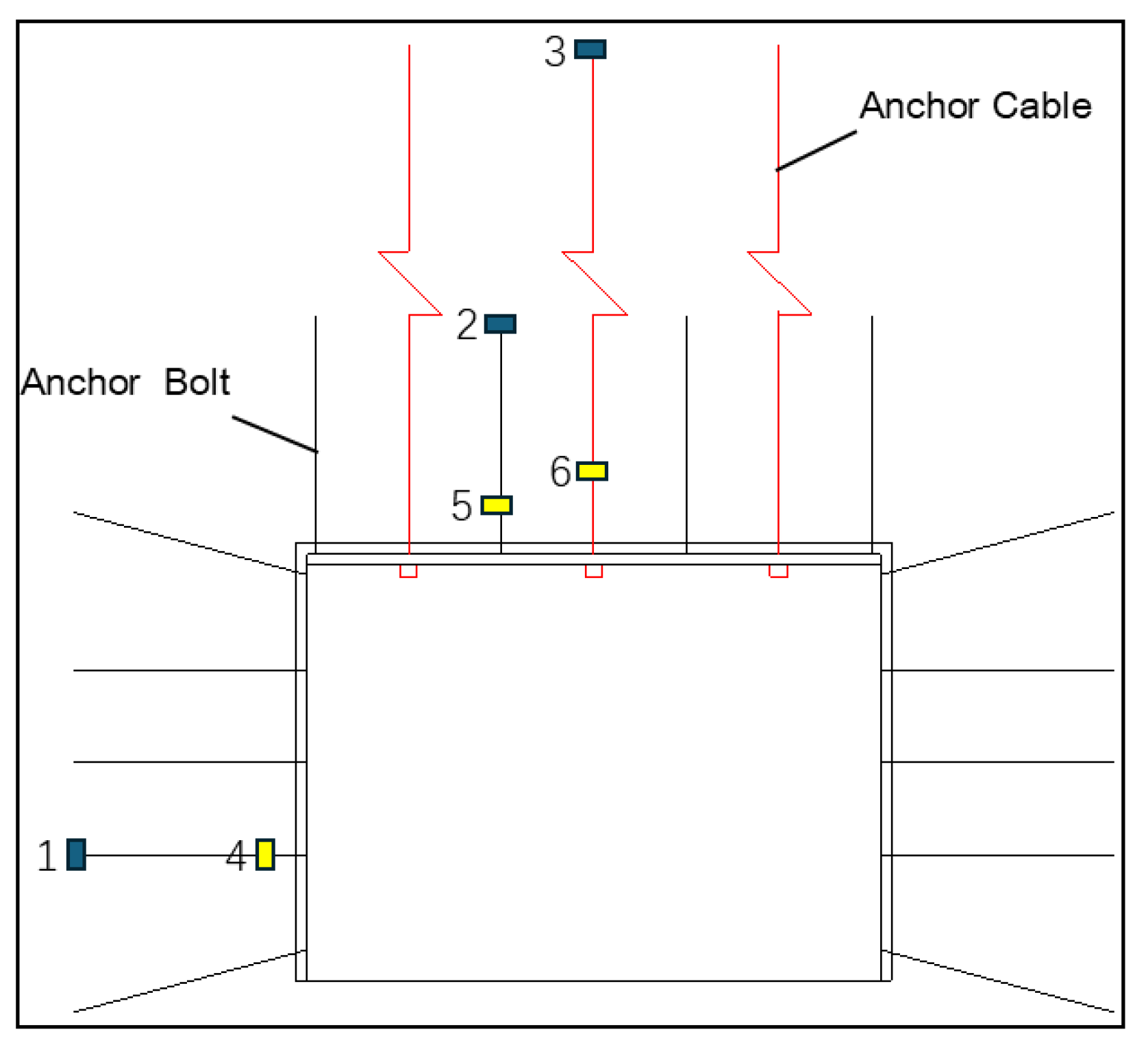
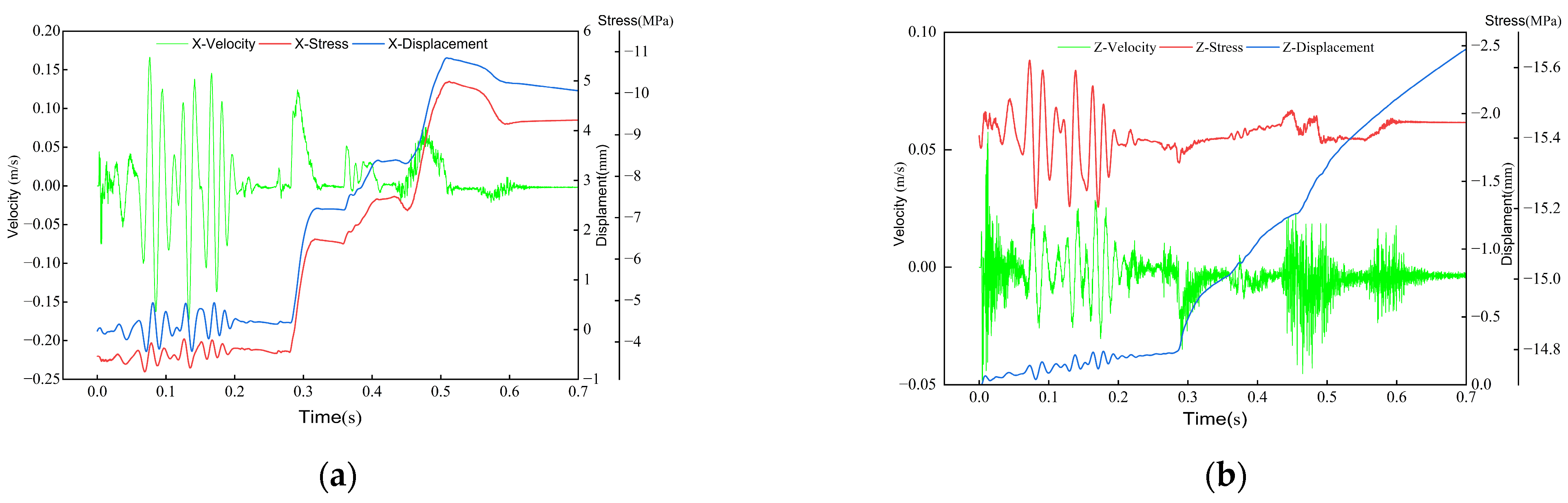
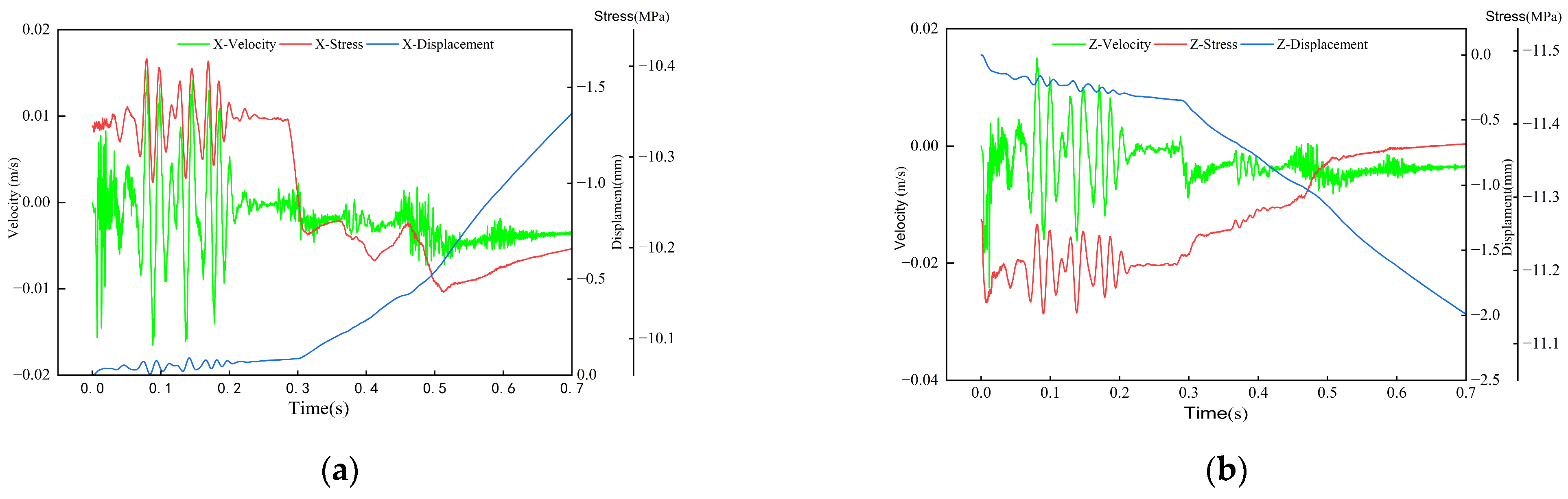
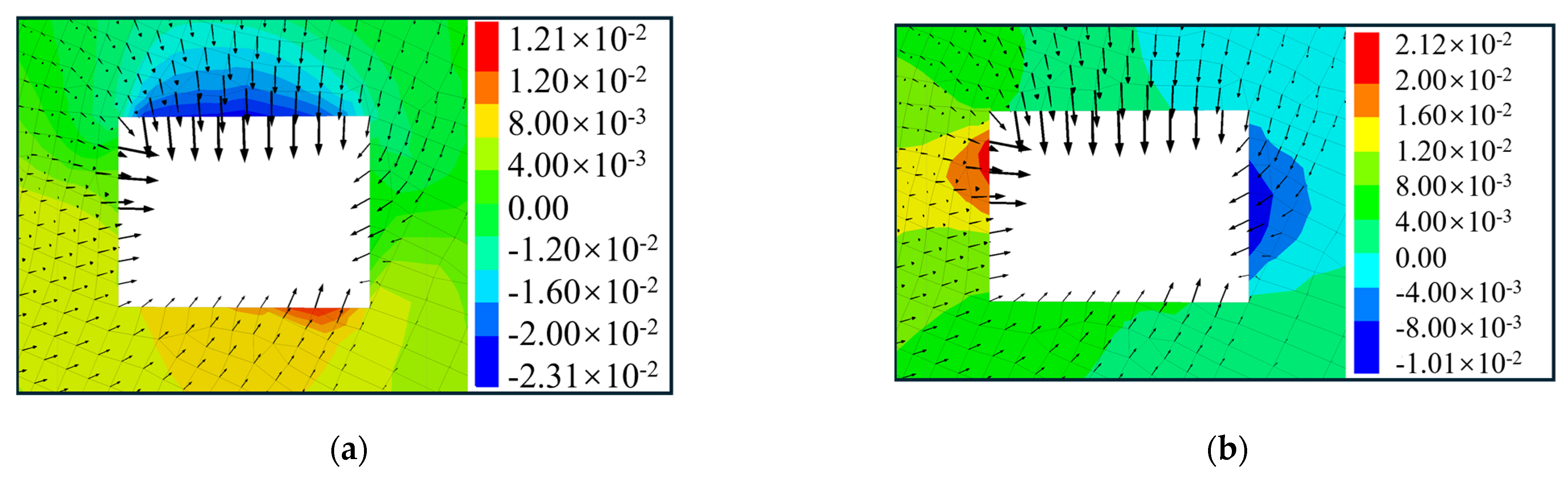
5.2.1. Response Characteristics of Rock at the Anchorage End
- (1)
- Anchorage end of left-side anchor bolt
- (2)
- Roof anchor bolt anchorage end
- (3)
- Roof anchor cable anchorage end
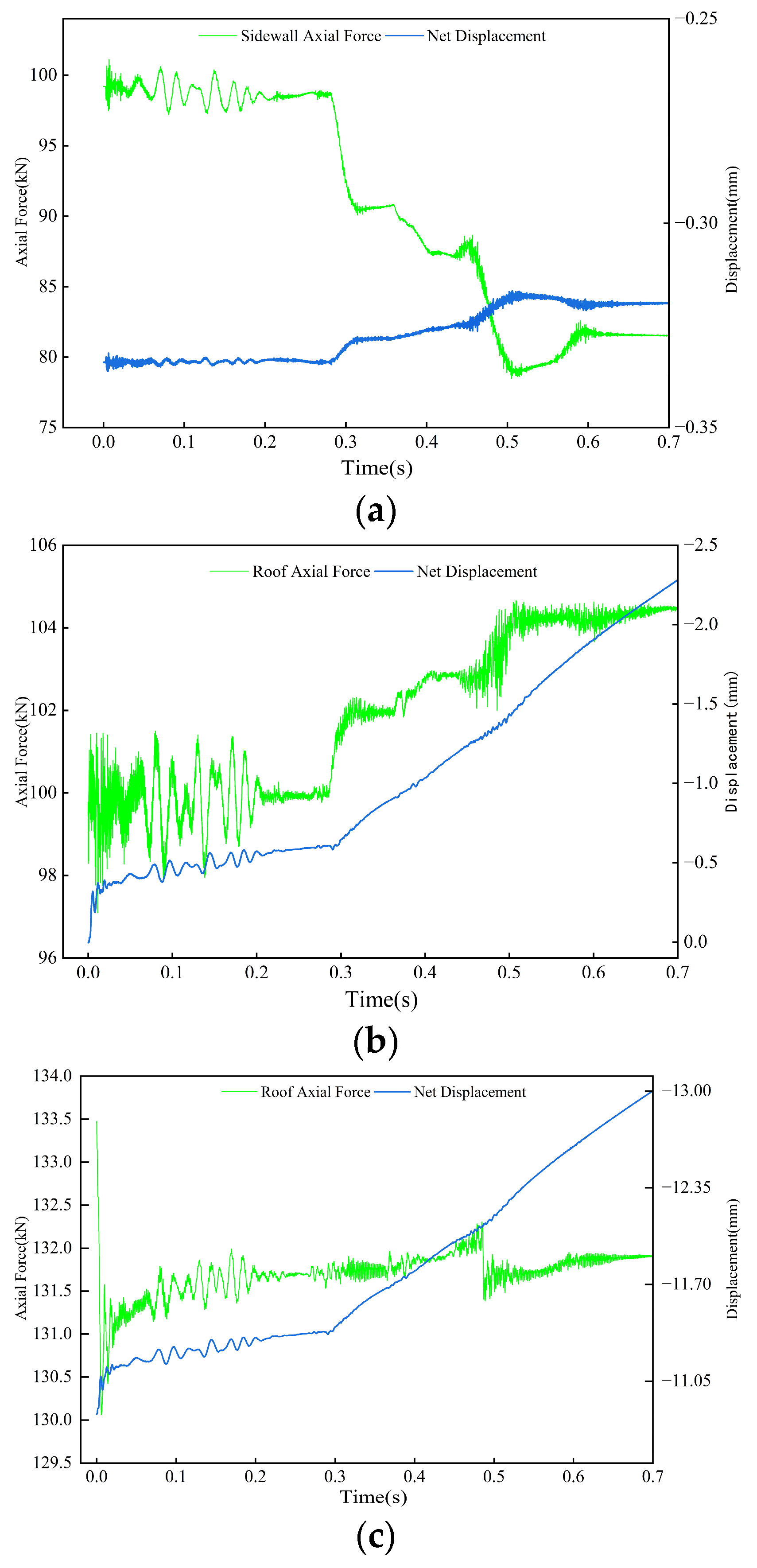
5.2.2. Axial Force Response Characteristics of Anchor Bolt and Anchor Cable
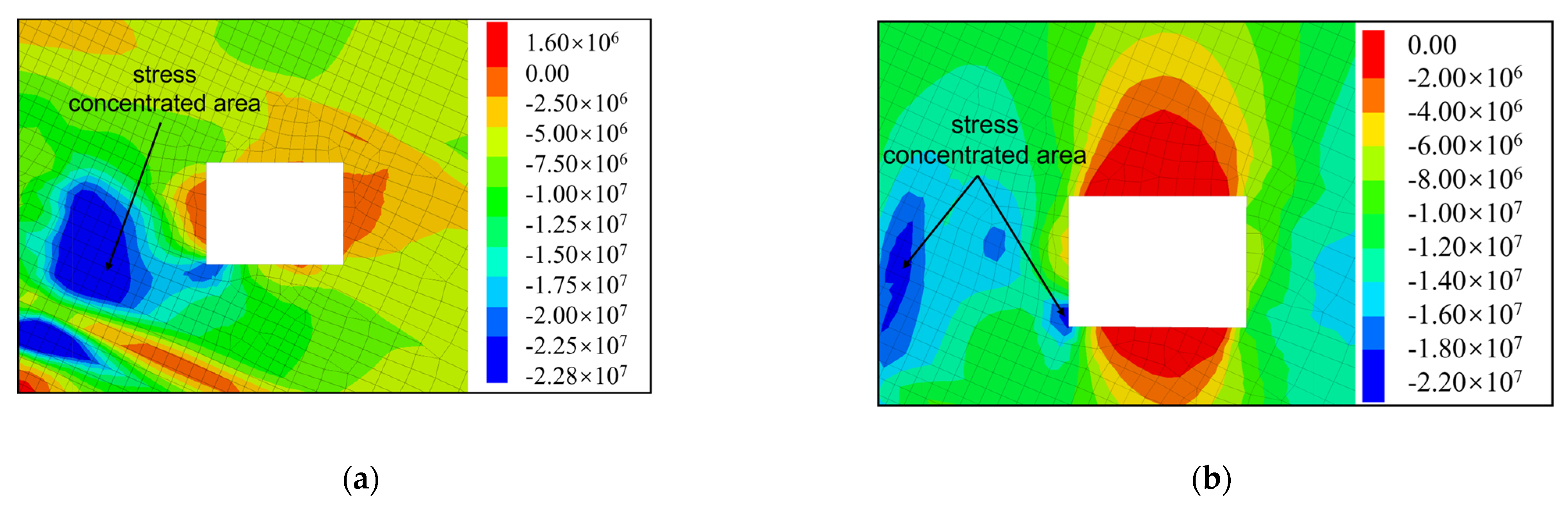
5.3. Response Characteristics of Roadway Surrounding Rock
6. Conclusions
- (1)
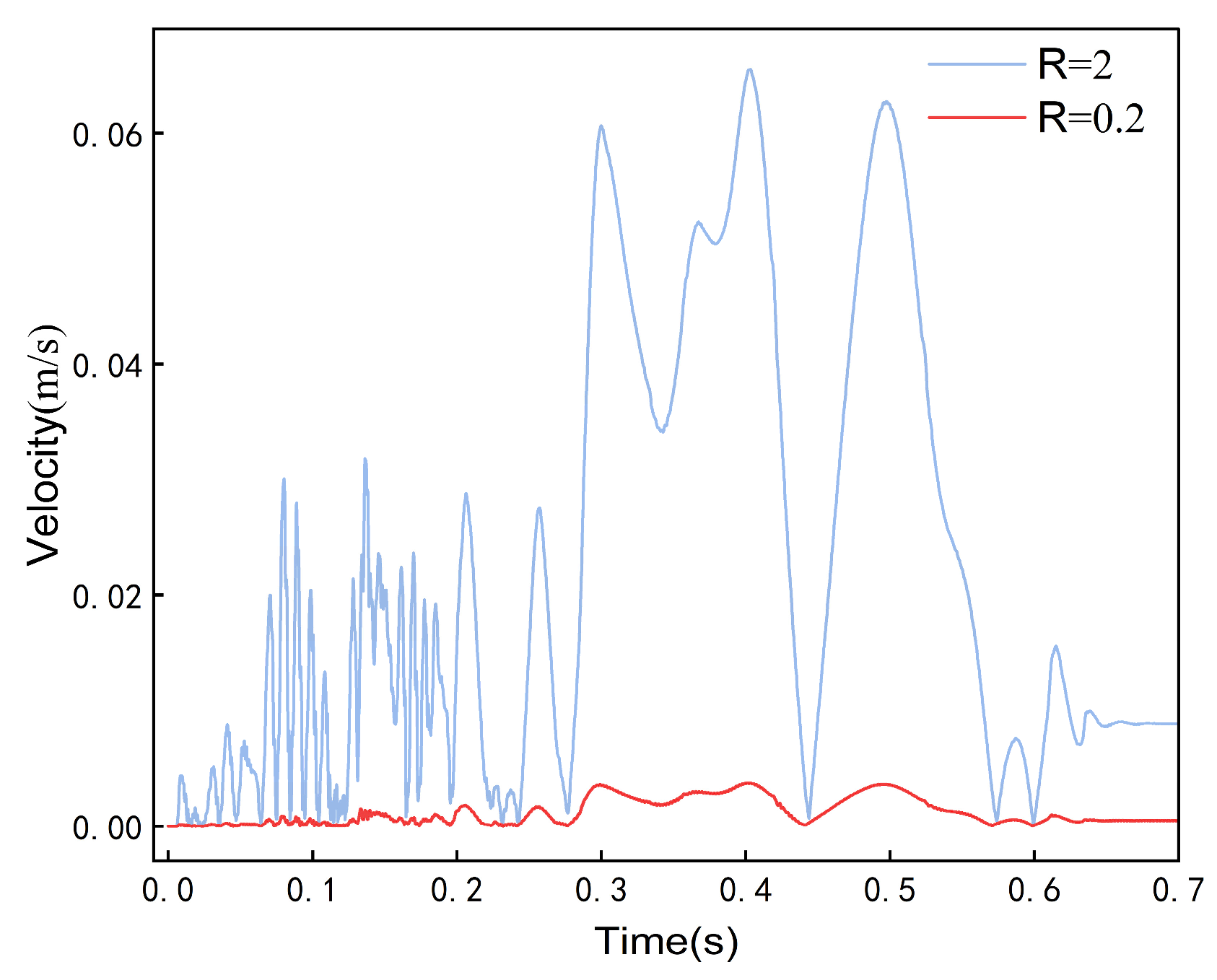
- The weak rock layer demonstrates a significant capacity for energy absorption and attenuation of vibrational waves, particularly affecting the energy absorption and propagation velocity of the S-wave. This interaction results in a notable decrease in the energy of the S-wave during propagation, as well as a reduction in its propagation speed.
- (2)
- The response phase of anchorage within the surrounding rock of a roadway can be categorized into three distinct stages: the P-wave action stage, the mixed wave action stage, and the S-wave action stage. During the P-wave action stage, the surrounding rock experiences vibrations at a uniform frequency. The stress and displacement recorded at each measurement point exhibit synchronous variations in relation to the vibration velocity, indicating that the overall stability of the surrounding rock is preserved. During the mixed wave action phase, the vibration velocity at the measurement point is predominantly influenced by P-waves, resulting in a tendency for the measurement point to exhibit periodic vibrations at a consistent frequency. The elastic energy within the surrounding rock on the source side of the roadway undergoes significant accumulation due to the influence of the S-wave. This phenomenon results in the creation and subsequent expansion of a stress concentration zone, which is particularly pronounced in the upper region of the left side of the roadway. The low-frequency, high-energy S-waves generate significant horizontal and vertical stress concentration zones on the left side of the roadway, leading to considerable displacement of both sides and the roof structure. The maximum recorded displacement on the left side is 21.2 mm, whereas the maximum vertical displacement of the roof attains a value of 23.1 mm.
- (3)
- Under the influence of P-waves, the stress, velocity, and displacement of the surrounding rock in the anchorage section demonstrate oscillatory vibration characteristics at a consistent frequency, with no structural failure detected in the anchorage system. Under the influence of low-frequency, high-energy S-waves, the axial force exerted on the bolts surrounding the roadway exhibits rapid fluctuations. Notably, the axial force of the bolt positioned on the side facing the wave experienced a reduction of 23 kN, whereas the axial force of the bolt located at the top demonstrated a significant increase. The significant attenuation of the S-wave during its propagation to the top anchor cable results in negligible variation in the axial force experienced by the top anchor cable. The fluctuations in high-frequency reciprocating vibrations of axial force suggest that the predominant factor contributing to the localized failure of the support system and the instability of the roadway is the influence of low-frequency, high-energy S-waves. The accumulation of high energy, along with the localized stress concentration associated with these low-frequency, high-energy S-waves, significantly intensifies the instability of the surrounding rock.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Qi, Q.; Dou, L. Theory and Technology of Rockburst; China University of Mining and Technology Press: Xuzhou, China, 2008; pp. 32–38. [Google Scholar]
- Jiang, Y.D.; Pan, Y.S.; Jiang, F.X.; Dou, L.M.; Ju, Y. State of the art review on mechanism and prevention of coal bumps in China. J. China Coal Soc. 2014, 39, 205–213. [Google Scholar]
- Xie, H.; Gao, F.; Ju, Y. Research and development of rock mechanics in deep ground engineering. Chin. J. Rock Mech. Eng. 2015, 34, 2161–2178. [Google Scholar]
- Pan, Y.S.; Xiao, Y.H.; Li, Z.H.; Wang, K.X. Study of tunnel support theory of rockburst in coal mine and its application. J. China Coal Soc. 2014, 39, 222–228. [Google Scholar]
- Wang, G.; Gong, S.; Dou, L.; Wang, H.; Cai, W.; Cao, A. Rockburst characteristics in syncline regions and microseismic precursors based on energy density clouds. Tunn. Undergr. Space Technol. 2018, 81, 83–93. [Google Scholar] [CrossRef]
- Cai, W.; Dou, L.; Zhang, M.; Cao, W.; Shi, J.Q.; Feng, L. A fuzzy comprehensive evaluation methodology for rock burst forecasting using microseismic monitoring. Tunn. Undergr. Space Technol. 2018, 80, 232–245. [Google Scholar] [CrossRef]
- Qi, Q.; Pan, Y.; Shu, L.; Li, H.; Jiang, D.; Zhao, S.; Li, H. Theory and technical framework of prevention and control with different sources in multiscales for coal and rock dynamic disasters in deep mining of coal mines. J. China Coal Soc. 2018, 43, 1801–1810. [Google Scholar]
- Wang, Z.; Dou, L.; Wang, G. Failuer mechanism of anchored bolts supporting structure of circular roadway under dynamic load. Chin. J. Geotech. Eng. 2015, 37, 1901–1909. [Google Scholar]
- Wang, Z.; Dou, L.; Wang, G.; He, J.; Hu, J. Failure mechanism of anchored roadway surrounding rocks under near-field dynamic disturbance. KSCE J. Civ. Eng. 2024, 28, 2454–2468. [Google Scholar] [CrossRef]
- Jing, H.; Yin, Q.; Zhu, D. Experimental study on the whole process of instability and failure of anchorage structure in surrounding rock of deep-buried roadway. J. China Coal Soc. 2020, 45, 889–901. [Google Scholar]
- Liu, Y.; Zhu, S.; Zhang, X.; Wang, X.; Li, Z.; Zhou, J.; Zhang, B.; Wang, G. Study on mechanism of pressure relief failure of bottom coal induced by strong vibration in driving face of thick coal seam. J. Min. Strata Control Eng. 2024, 6, 053021. [Google Scholar]
- Chang, J.; Qi, C.; Yin, Z. Propagation and failure characteristics of stress wave of full anchor solid under dynamic load. J. China Coal Soc. 2023, 48, 1996–2007. [Google Scholar]
- Wu, Y.Z.; Chen, J.Y.; Jiao, J.K.; Zheng, Y.; He, J. Damage and failure mechanism of anchored surrounding rock with impact loading. J. China Coal Soc. 2018, 43, 2389–2397. [Google Scholar]
- Wu, Y.; Fu, Y.; He, S.; Li, J.; Jiao, J. Characteristics of deformation and failure of surrounding rock in roadway under strong impact load and control technology. Coal Sci. Tech. 2024, 52, 76–87. [Google Scholar]
- Jiao, J.; Ju, W. Burst failure mechanism of roadway anchorage bearing structure under dynamic load disturbance. J. China Coal Soc. 2021, 46, 94–105. [Google Scholar]
- Gao, M.; Xu, D.; Wang, H.; Yu, X.; Liu, R. Shock failure mechanism of roadway in extra thick coal seam and full anchor cable support technology. J. China Coal Soc. 2023, 48, 1943–1956. [Google Scholar]
- Durrheim, R.J. Functional specifications for in-stope support based on seismic and rockburst observations in South African mines. In Proceedings of the Sixth International Seminar on Deep and High Stress Mining, Australian Centre for Geomechanics, Perth, Australia, 28–30 March 2012. [Google Scholar]
- Mcgarr, A. Scaling of ground motion parameters, state of stress, and focal depth. J. Geophys. Res. 1984, 89, 6969–6979. [Google Scholar] [CrossRef]
- Zhao, C.; Dawson, E. Applications of Maxwell Damping for Time Domain Seismic Analyses. In Geo-Congress 2022: Geophysical and Earthquake Engineering and Soil Dynamics; ASCE: Reston, VA, USA, 2022. [Google Scholar] [CrossRef]
- Flandrin, P.; Rilling, G.; Goncalves, P. Empirical mode decomposition as a filter bank. IEEE Signal Process Lett. 2004, 11, 112–114. [Google Scholar] [CrossRef]
- Daubechies, I.; Lu, J.; Wu, H. Synchro squeezed wavelet transforms: An empirical mode decomposition-like tool. Appl. Comput. Harmon. Anal. 2011, 30, 243–261. [Google Scholar] [CrossRef]
- Li, Z. The design of Butterworth Lowpass filter based on MATLAB. Inf. Technol. 2003, 27, 49–50+52. [Google Scholar]
- Kaiser, P.K.; Maloney, S.M. Scaling laws for the design of rock support. Pure Appl. Geophys. 1997, 150, 415–434. [Google Scholar] [CrossRef]
- Kuhlemeyer, R.L.; Lysmer, J. Finite element method accuracy for wave propagation problems. J. Soil Mech. Found. Div. 1973, 99, 421–427. [Google Scholar] [CrossRef]
- Aki, K.; Richards, P.G. Quantitative Seismology; University Science Books: Sausalito, CA, USA, 2002. [Google Scholar]
- Cao, A. Research on seismic effort of burst and failure of coal-rock mass associated with mining and its application. J. China Coal Soc. 2011, 36, 177–178. [Google Scholar]
- Li, Z.; Dai, R.; Jiang, Y. Improvement of the generation of the initial stress field by using FLAC3D and application in a huge underground cavern group. Chin. J. Rock Mech. Eng. 2002, 21, 2387–2392. [Google Scholar]
- Raffaldi, M.J.; Loken, M.C. Rock mass modeling approach for simulating wave propagation, rock fracture, and rock ejection. In Proceedings of the 50th US Rock Mechanics Symposium, American Rock Mechanics Association, Alexandria, WV, USA, 26–29 June 2016. [Google Scholar]
- Xie, H.P.; Ju, Y.; Li, L.Y.; Peng, R.D. Energy mechanism of deformation and failure of rock masses. Chin. J. Rock Mech. Eng. 2008, 27, 1729–1740. [Google Scholar]
- Wang, M.; Song, Z.; Zheng, D.; Shen, W.; Gou, P.; Wei, S. Development and application of rock energy dissipation model in FLAC3D. J. China Coal Soc. 2021, 46, 2565–2573. [Google Scholar]
- Pan, J.F.; Ning, Y.; Mao, D.B.; Lan, H.; Du, T.T.; Peng, Y.W. Theory of rockburst start-up during coal mining. Chin. J. Rock Mech. Eng. 2012, 31, 586–596. [Google Scholar]
- Zhao, Y.; Wan, Z.; Feng, Z. Least energy priciple of dynamical failure of rock mass. Chin. J. Rock Mech. Eng. 2003, 22, 1781–1783. [Google Scholar]
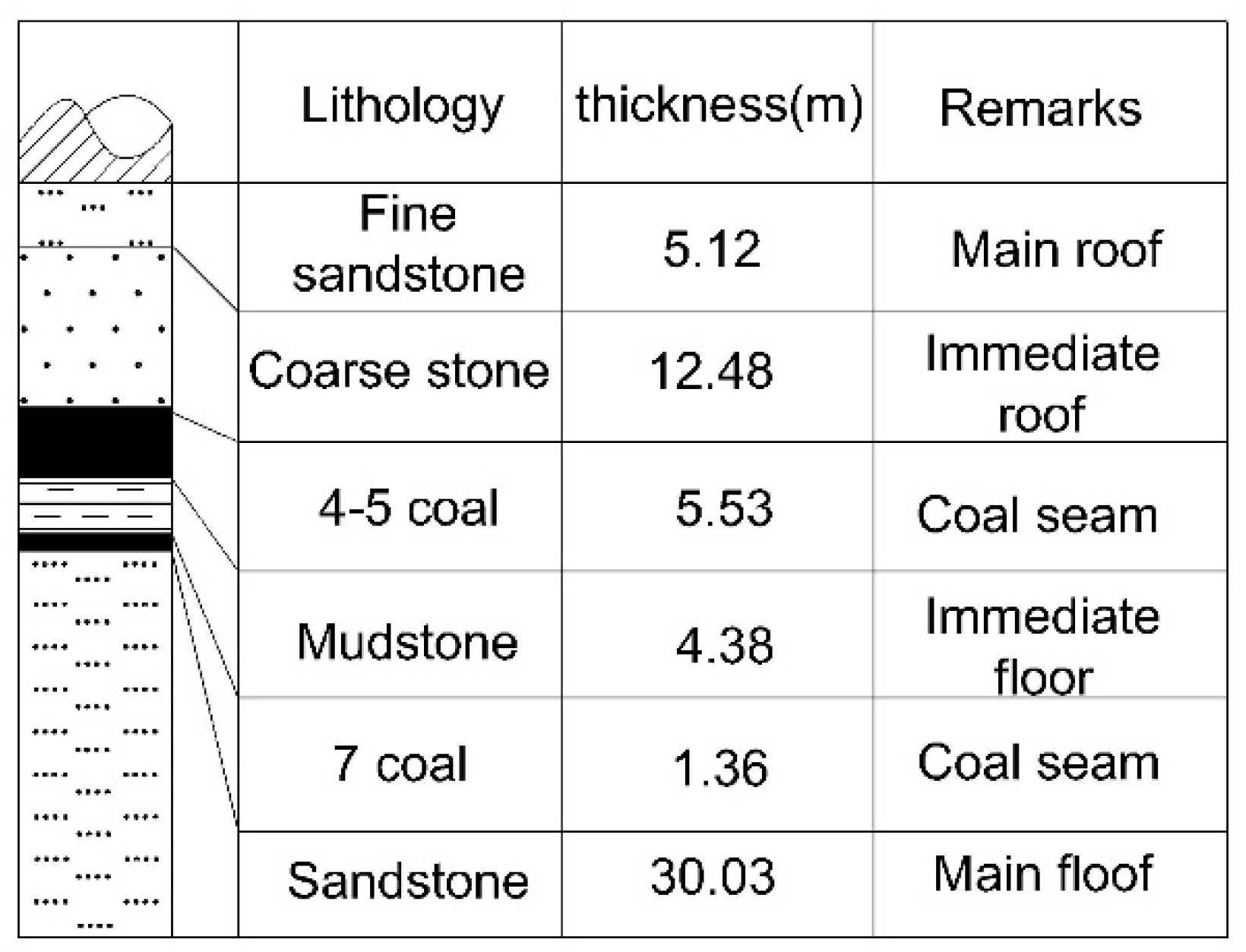







| Lithology | Elastic Modulus (GPa) | Poisson Ratio | Internal Friction Angle (°) | Cohesion (MPa) | Tensile Strength (MPa) |
|---|---|---|---|---|---|
| Sandstone | 14.0 | 0.36 | 38.06 | 12.60 | 3.28 |
| Mudstone | 12.36 | 0.24 | 38.36 | 19.69 | 5.24 |
| Fine sandstone | 15.55 | 0.29 | 46.82 | 11.83 | 7.95 |
| Coarse sandstone | 20.55 | 0.21 | 35.94 | 12.6 | 6.3 |
| NO. 4-5 coal seam | 2.56 | 0.24 | 24.00 | 2.4 | 1.34 |
| Mudstone | 11.70 | 0.24 | 36.61 | 8.76 | 3.56 |
| NO. 7 coal seam | 2.56 | 0.24 | 24.00 | 2.4 | 1.34 |
| Sandstone | 30.73 | 0.28 | 41.21 | 12.6 | 6.84 |
| Coarse sandstone | 16.21 | 0.41 | 46.82 | 11.83 | 7.95 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Wei, S.; Zhu, G.; Yuan, Y.; Guo, W. Response Characteristics of Anchored Surrounding Rock in Roadways Under the Influence of Vibrational Waves. Appl. Sci. 2024, 14, 11266. https://doi.org/10.3390/app142311266
Wang H, Wei S, Zhu G, Yuan Y, Guo W. Response Characteristics of Anchored Surrounding Rock in Roadways Under the Influence of Vibrational Waves. Applied Sciences. 2024; 14(23):11266. https://doi.org/10.3390/app142311266
Chicago/Turabian StyleWang, Hongsheng, Siyuan Wei, Guang’an Zhu, Yuxin Yuan, and Weibin Guo. 2024. "Response Characteristics of Anchored Surrounding Rock in Roadways Under the Influence of Vibrational Waves" Applied Sciences 14, no. 23: 11266. https://doi.org/10.3390/app142311266
APA StyleWang, H., Wei, S., Zhu, G., Yuan, Y., & Guo, W. (2024). Response Characteristics of Anchored Surrounding Rock in Roadways Under the Influence of Vibrational Waves. Applied Sciences, 14(23), 11266. https://doi.org/10.3390/app142311266






