Computational and Mathematical Methods for Neuroscience

1. Introduction

As our understanding of the brain continues to advance, so too does the demand for sophisticated tools that can model, simulate, and interpret the intricate data generated by contemporary neuroimaging and electrophysiological techniques. The interdisciplinary field of theoretical and computational neuroscience, drawing on biology, mathematics, computer science, and physics, seeks to capture the complexities of the nervous system through rigorous quantitative models and simulations. In recent years, this field has grown rapidly, with computational and mathematical methodologies becoming essential for probing the nuances of neural circuitry and cognitive function.

Computational approaches in neuroscience encompass diverse techniques, from advanced statistical methods to machine learning algorithms, each designed to identify meaningful patterns in high-dimensional data. Complementing these are mathematical models that provide a robust framework for understanding neural dynamics, connectivity, and information processing across various scales, from single neurons to vast networks. Together, these computational and mathematical strategies empower researchers to generate precise hypotheses, make quantitative predictions, and gain deeper insights into the fundamental principles that drive brain function, neural plasticity, and the mechanisms behind neurological disorders.

This Special Issue brings together the latest advancements in computational and mathematical methods in neuroscience, showcasing articles that address foundational concepts, established models, and emerging technologies at the forefront of the field. By bridging theoretical frameworks with empirical data, these approaches not only expand our knowledge of neural systems but also open new pathways for therapeutic innovation and applications in clinical neuroscience.

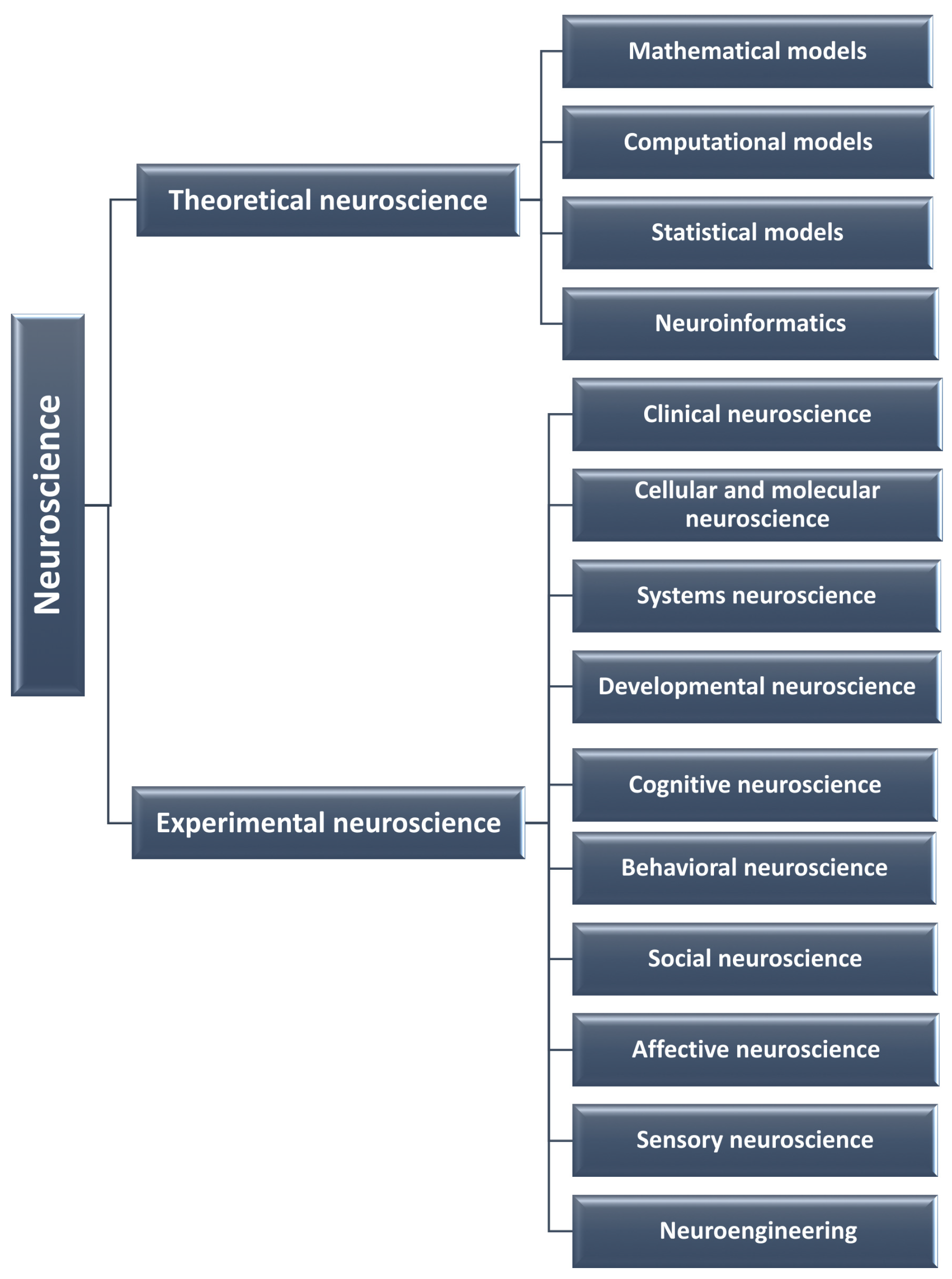
2. Fields of Neuroscience

Neuroscience is a vast and inherently interdisciplinary field dedicated to understanding the complexities of the nervous system. It encompasses a diverse array of subfields, each focusing on different levels of neural organization and function, as illustrated in Figure 1. At its core, neuroscience integrates both theoretical and experimental approaches, each bringing distinct methodologies and perspectives that, together, drive a more comprehensive understanding of brain mechanisms and behavior. The synergy between these approaches allows researchers to bridge molecular-, cellular-, and systems-level insights, advancing our knowledge of how neural processes underpin cognition, perception, and action.

2.1. Theoretical Neuroscience

Theoretical neuroscience focuses on developing mathematical, computational, and statistical models to represent neural processes across multiple scales, from an individual neuron to the brain.

Mathematical neuroscience applies mathematical theories, models, and equations to describe and analyze the mechanisms of the nervous system at various levels, from single neurons to whole-brain dynamics. This branch of neuroscience aims to build theoretical frameworks for neural activity, capturing phenomena such as neuronal electrical properties, network dynamics, and brain connectivity patterns. Some of the most widely used neural models include the Hodgkin–Huxley (HH) [1], FitzHugh–Nagumo (FHN) [2,3], Hindmarsh–Rose (HR) [4], Wilson–Cowan (WC) [5], and Izhikevich [6] models.

The HH model provides a detailed description of neuronal electrical behavior based on ion channel dynamics, offering a foundation for understanding neuron excitability. The FHN and HR models, simplified versions of the HH model, are commonly used to simulate excitable systems due to their computational efficiency. The WC model, on the other hand, captures the collective dynamics of populations of excitatory and inhibitory neurons, making it useful for studying large-scale neural networks. The Izhikevich model combines biological realism with computational efficiency, enabling the simulation of a wide range of spiking and bursting patterns observed in neurons.

In addition to these continuous-time models, various discrete-time models are employed in theoretical neuroscience, such as the Leaky Integrate-and-Fire (LIF) model [7] and the Rulkov map [8]. The LIF model approximates biological neurons by simulating membrane potential decay in the absence of input spikes, while the Rulkov map generates spike patterns through the interplay of membrane potential dynamics and recovery variables. The Rulkov model also incorporates a reset mechanism, allowing neurons to recover after firing.

These mathematical models play a crucial role in predicting and explaining phenomena such as neural oscillations, wave propagation in the brain, and the synchronization of neuronal activity, processes essential for neural communication and understanding neurological conditions like epilepsy [9]. These models enable theoretical neuroscience to uncover fundamental principles of neural behavior, enhancing our capacity to analyze and interpret the intricate dynamics of neural systems.

Computational neuroscience aims to develop quantitative tools to analyze neural data and predict neural system dynamics, helping to uncover the principles that govern brain function. Computational neuroscience involves developing and using computer simulations, algorithms, and artificial neural network (ANN) models to investigate the functioning of the nervous system. It bridges theoretical models with experimental data, often serving as a testing ground for hypotheses. Computational neuroscience focuses on simulating neural circuits, analyzing large datasets from neural recordings, and predicting brain activity and behavior. Popular examples of computational techniques are neural network simulations, machine learning (ML), and data-driven models. Former methods simulate networks of neurons to study how they encode, process, and retrieve information. ML models are used to classify patterns in brain data, such as electroencephalography (EEG), magnetoencephalography (MEG), Magnetic Resonance Imaging (MRI), functional Magnetic Resonance Imaging (fMRI), and Positron Emission Tomography (PET), to model learning and adaptation in neural systems. Finally, data-driven models use real experimental data to create models of complex phenomena like sensory processing, decision-making, or motor control. Computational neuroscience helps us understand brain function (e.g., sensory processing, memory, and emotions), design brain–machine interfaces (BMIs), and develop treatments for neurological diseases through predictive modeling.

Statistical neuroscience applies advanced statistical techniques to analyze and interpret the complex data generated by neuroscience experiments, addressing challenges such as high dimensionality, noise, and the temporal structure of neural activity. By providing robust tools for managing the variability inherent in neural data, statistical neuroscience helps researchers identify patterns, relationships, and statistical dependencies, which are essential for testing hypotheses and making inferences about neural function.

Key methods in statistical neuroscience include Spike Train Analysis (STA), Dimensionality Reduction (DR), Bayesian inference, and information theory. STA encompasses statistical techniques for analyzing the timing and patterns of neuronal spikes, which carry critical information about neural signaling. DR techniques, such as Principal Component Analysis (PCA) and t-distributed Stochastic Neighbor Embedding (t-SNE), simplify high-dimensional neural data, making them more accessible for interpretation. Bayesian inference introduces a probabilistic approach to understanding neural data, commonly applied to decode sensory information and predict neural responses. Information theory, meanwhile, quantifies the amount of information transmitted within neural circuits, providing insights into the efficiency and mechanisms of neural coding.

These statistical approaches are essential for analyzing data from electrophysiological recordings, neuroimaging, and behavioral experiments. They allow researchers to draw reliable conclusions about brain activity, predict behaviors, and even forecast events like epileptic seizures [10]. Through statistical neuroscience, scientists gain critical insights into the principles of neural organization and function, advancing our understanding of brain dynamics.

Neuroinformatics plays a crucial role in neuroscience by developing algorithms, data management tools, and computational techniques to organize, integrate, and share large datasets, thereby facilitating discovery and enhancing collaboration across studies. This field focuses on establishing standardized formats and databases that enable diverse types of neuroscience data to be combined, compared, and interpreted across studies and institutions. By streamlining the organization and accessibility of complex datasets, neuroinformatics supports efficient data sharing, reproducibility, and broader analyses.

Popular neuroinformatics tools include Brainstorm, Brainsuite, Statistical Parametric Mapping (SPM), and FMRIB Software Library (FSL), containing image analysis and statistical tools for functional, structural, and diffusion MRI. Additionally, platforms such as Neuron and Brain Imaging Data Structure (BIDS) provide standardized data formatting and processing pipelines that enhance consistency in data analysis. Neuroinformatics also involves creating computational models that simulate brain processes, providing valuable insights into brain dynamics, neural circuits, and cognitive functions.

A key goal of neuroinformatics is to promote open science by facilitating data sharing across labs, institutions, and even international boundaries, accelerating discovery, enhancing reproducibility, and allowing for larger-scale and more diverse analyses. Platforms like the NeuroInformatics Framework (NIF) exemplify this approach, providing standardized access to a wide range of neuroscience datasets and tools.

One of the primary applications of neuroinformatics is brain mapping, which involves creating detailed maps of the brain’s structural and functional connectivity to better understand regional interactions. By comparing large datasets from both healthy and diseased brains, neuroinformatics enables the identification of biomarkers and genetic markers associated with neurological and psychiatric disorders. Moreover, neuroinformatics contributes to the development of algorithms for processing data from Brain–Computer Interfaces (BCIs), facilitating direct communication between the brain and external devices [11,12]. Additionally, virtual brain models and curated databases serve as valuable educational tools, providing students, clinicians, and researchers with training in neuroanatomy, neurophysiology, and neural dynamics.

2.2. Experimental Neuroscience

Experimental neuroscience, distinct from theoretical approaches, is centered on empirical studies that directly observe, manipulate, and measure neural function and behavior. This hands-on branch of neuroscience encompasses several key subfields, each focused on specific aspects of the brain and nervous system.

Clinical neuroscience targets neurological, psychiatric, and neurodevelopmental disorders, facilitating collaborations among neurologists, psychiatrists, and neuroscientists to advance diagnostic methods and therapeutic strategies.

Cellular and molecular neuroscience delves into the structure and function of individual neurons, exploring processes such as synaptic transmission, plasticity, and the role of molecular components like neurotransmitters, ion channels, and genetic factors. This foundational research provides insights into the basic units of neural activity.

Systems neuroscience investigates how neural circuits and larger brain systems organize and function, analyzing interactions across brain regions and networks that enable complex capabilities like sensory processing, motor coordination, and emotional regulation.

Developmental neuroscience examines the processes governing nervous system development from embryonic stages through adulthood, including neurogenesis, cell differentiation, and synaptic formation, as well as the effects of genetic and environmental factors on brain maturation.

Cognitive neuroscience studies the neural basis of higher-order cognitive functions, including perception, memory, language, and decision-making. This field often employs neuroimaging techniques such as EEG, MEG, MRI, PET, and fMRI to link brain activity with cognitive processes.

Behavioral neuroscience explores the relationship between neural mechanisms and behavior, investigating how alterations in the brain—whether from injury, disease, or experimental manipulation—impact behavior and psychological processes.

Sensory neuroscience focuses on the neural interpretation of sensory information from the external environment, examining how sensory systems like vision, hearing, and touch process and respond to stimuli.

Social neuroscience examines the neural underpinnings of social behaviors, such as empathy, cooperation, and social decision-making, integrating methodologies from psychology, biology, and neuroscience to understand interpersonal and group dynamics.

Affective neuroscience investigates how the brain processes emotions such as admiration, adoration, aesthetic appreciation, amusement, anger, anxiety, awe, awkwardness, boredom, calm, caring, confusion, craving, disgust, empathic pain, fascination, excitement, fear, horror, interest, joy, lust, nostalgia, play, relief, romance, sadness, satisfaction, seeking, sexual desire, surprise, etc., which are common to all mammals and evolutionarily defined as tools for survival and, in general, fitness.

Social neuroscience and affective neuroscience apply traditional neuroimaging techniques used in experimental neuroscience (e.g., EEG, MEG, and fMRI) to better understand the neural and psychological mechanisms underlying human behavior.

Neuroengineering combines engineering principles with neuroscience to create innovative tools and technologies for studying and manipulating the nervous system, including brain–machine interfaces, neuroprosthetics, and neurostimulation devices.

Each of these branches can also benefit from theoretical neuroscience through the application of mathematical models, computational algorithms, and statistical analyses. Integrating theoretical and experimental approaches allows researchers to investigate the nervous system at all levels, from molecules to behavior, building a comprehensive picture of how the brain enables perception, thought, emotion, and action. Collectively, these subfields deepen our understanding of the brain and hold transformative potential for both medicine and technology, advancing our ability to address neurological disorders and improve human health.

3. Highlights and Key Contributions of Published Articles

This Special Issue comprises 16 papers, which can be broadly categorized into four main areas: medical applications (8 papers), cognitive neuroscience (3 papers), statistical methods (2 papers), and machine learning (5 papers, including 2 focused on medical applications). Below is a brief overview of each paper and its key contributions.

3.1. Medical Applications

Half of the papers in this Special Issue (8 out of 16) focus on medical applications, with 4 specifically addressing Alzheimer’s disease (AD) (contributions 2, 9, 11, and 14). This focus is aligned with the critical importance of early and accurate AD diagnosis, which enables timely therapeutic intervention and management. Brain imaging technologies like MRI and PET scans facilitate the early detection of AD-related structural and functional changes in the brain, often identifying the disease before severe clinical symptoms appear. Early detection provides valuable opportunities for intervention that may slow disease progression. Additionally, brain imaging distinguishes AD from other dementias, such as Lewy body or vascular dementia, by detecting unique patterns like amyloid plaques or hippocampal atrophy. Moreover, imaging allows clinicians to track disease progression over time, informing treatment adjustments and helping to assess therapeutic efficacy.

Among available neuroimaging techniques, MRI is particularly popular in AD research, as it visualizes brain structures, allowing clinicians to detect hippocampal atrophy, a key marker of AD. In this issue, Altwijri et al. (contribution 2) introduce an innovative deep learning approach to automatically diagnose AD using MRI datasets. Leveraging the strengths of deep learning, which often outperforms human detection in assessing AD stages, the authors employ pre-trained convolutional neural networks (CNNs) to classify AD severity with high accuracy, even when dataset quality and quantity are limited. Their method, which preprocesses AD data through an advanced image processing module before training, achieves a 99.3% accuracy rate—an improvement over existing models.

Kozminski and Gniazdowska (contribution 9) review studies on tacrine and its derivatives labeled with radionuclides, exploring their potential as diagnostic radiotracers for AD. While AD is not curable, its progression and symptoms can be managed using treatments like acetylcholinesterase (AChE) inhibitors (e.g., tacrine, rivastigmine, galantamine, and donepezil). The authors analyze radiolabeled tacrine derivatives in early AD diagnosis, with a particular emphasis on computational molecular modeling to visualize tacrine’s interaction with cholinesterase. Their review highlights the limitations of current radiopharmaceuticals based on tacrine derivatives and suggests a shift toward other biomolecules relevant to early AD stages.

Sait (contribution 11) presents a novel integrated model combining LeViT, EfficientNet B7, and Dartbooster XGBoost (DXB) for AD detection using MRI. LeViT is a vision transformer-based hybrid neural network, EfficientNet B7 is a high-performance CNN, and DXB is a robust model blending DART and XGBoost algorithms for predictive accuracy. Using MRI datasets totaling 86,390 images, Sait’s approach achieved 99.8% average generalization accuracy, underscoring the potential of multi-model fusion for high-precision AD detection.

Mattle et al. (contribution 14) examine brain-wide structural connectomics in early AD stages. Analyzing a longitudinal diffusion-weighted imaging dataset of 264 subjects, they apply a tailored machine learning approach that combines exhaustive tractography with neuropsychological data to achieve high classification accuracy. Their model identifies early biomarkers of AD based on hemispheric lateralization of mean tract volume for specific tracts in the supramarginal and paracentral regions, demonstrating the predictive value of diffusion MRI and the importance of multi-modal data integration in neurodegenerative disease research.

Other medical applications in this issue cover cerebral palsy (CP), head tremor, sports medicine, and epilepsy (contributions 5, 6, 13, and 16, respectively).

Roy, Ehrlich, and Lampe (contribution 5) conducted an in-depth EEG study comparing the neural responses of seven patients with cerebral palsy (CP) to a control group of four healthy participants. CP, a movement disorder stemming from early, nonprogressive brain damage, often leads to additional cognitive, communicative, and behavioral symptoms. The study employed two types of tactile stimulation—‘frequent’ and ‘infrequent’—applied to the ring finger and thumb of participants’ left hands, respectively, to elicit event-related potentials (ERPs) recorded at frontal, central, and parietal scalp locations. In the control group, typical mismatch-related ERP responses were observed, while in CP patients, statistically significant differences were detected between the responses to the two stimuli on frontocentral and parietal channels within the 150–250 ms post-stimulus window. Additionally, a distinct late discriminative response appeared on frontal and parietal channels. These findings reveal the presence and potential observability of mismatch-related neural components in CP patients, providing insight into how CP impacts sensory processing. The authors acknowledged certain limitations, including the small sample size, suggesting future studies to build on this work with larger cohorts.

Rossi et al. (contribution 6) investigated head micromovements and body posture to assess vigilance and monitor changes in mental states—an area increasingly relevant due to global population aging trends. With the proportion of individuals over 60 expected to nearly double by 2050 [13], and head tremors being a prevalent symptom in age-related conditions such as Parkinson’s disease, precise monitoring of head movements is increasingly important. Head tremors are commonly experienced by older adults, often as a result of Parkinson’s disease. According to the American Parkinson Disease Association, tremors affect approximately 80% of individuals with Parkinson’s, making them a defining feature of the condition [14]. The miniaturization and widespread use of inertial measurement units (IMUs) in devices like smart glasses have simplified tracking, but self-reports and simple performance measures alone do not provide reliable real-time indicators of vigilance. To address this, the authors examined the relationship between head micromovements, body posture changes, and vigilance reduction during a psychomotor vigilance task. Their results demonstrate that head micromovements are valuable markers for tracking prolonged vigilance decrement and can effectively distinguish between high and low vigilance states, highlighting the potential of IMUs in monitoring cognitive states in aging populations.

Billat et al. (contribution 13) explored the brain’s role in limiting exercise capacity by analyzing EEG recordings taken during incremental exercise tests (IETs) with 42 participants. IETs assess maximal aerobic power and oxygen consumption ($\dot{\mathrm{V}}$O₂max), key indicators in sports medicine. The study aimed to test whether the inability to reach a $\dot{\mathrm{V}}$O₂ plateau ($\dot{\mathrm{V}}$O₂pl) is primarily influenced by central (brain-based) rather than peripheral (muscle-based) factors. The authors observed a general EEG power decline across all frequency bands, irrespective of $\dot{\mathrm{V}}$O₂ plateau occurrence, suggesting depletion of overall “EEG reserve”, while alpha activity in the motor cortex remained relatively preserved. They hypothesize that fatigue-associated EEG changes may reflect the brain’s attempts to conserve neural resources for motor function and that these changes might vary depending on individuals’ sport experience levels. This study opens up the possibility of using EEG as a predictive indicator of exercise exhaustion, which could have applications in optimizing training and managing fatigue.

Ferri et al. (contribution 16) made a significant contribution to epilepsy research by using EEG to study cortical connectivity responses to hyperventilation (HV) in patients with focal epilepsy, a type of epilepsy where seizures originate in specific brain lobes. HV is routinely performed during EEG recording as an activation technique recommended by neurophysiology guidelines. The authors applied phase transfer entropy, an advanced connectivity analysis, to assess how HV affects cortical connectivity. They found that HV-induced connectivity significantly increases, similar to patterns observed during non-REM sleep, which is known to promote epileptic activity. Their findings suggest that HV creates a conductive environment for the spread of epileptiform activities but does not alone trigger seizures in focal epilepsy. This study underscores the role of HV in epilepsy diagnostics and the potential of cortical connectivity measures for understanding seizure propagation and developing targeted interventions.

3.2. Cognitive Neuroscience

The second research focus of the papers in this Special Issue is cognitive neuroscience, with three contributions (1, 7, and 8) exploring key themes: the sense of embodiment (contribution 1), perception (contribution 7), and emotion recognition (contribution 8).

Tomás et al. (contribution 1) reviewed 20 selected studies on BMIs that utilize multisensory feedback to support the sense of embodiment (SoE) in EEG-based applications. The sense of embodiment is fundamental to human perception, allowing individuals to perceive and control their own body parts. Their review indicates that factors such as immersive scenarios, human-like avatars, and coherent sensory feedback significantly enhance the embodiment experience. However, their analysis does not consistently support the idea that incorporating additional sensory modalities leads to stronger SoE or improved BMI performance. The authors underscore a critical gap in the literature: a lack of systematic experimental studies examining how different sensory modalities individually or cumulatively impact SoE and BMI outcomes. They emphasize the need for further empirical research to isolate and measure the contributions of each sensory modality to embodiment in BMIs.

Peña Serrano et al. (contribution 7) make a unique contribution to cognitive neuroscience by applying hypergraph theory to visual perception, marking the first use of hypergraphs in this domain. Hypergraphs are a sophisticated extension of graph theory with diverse applications across cognitive neuroscience and medicine [15]. Using MEG recordings, the authors constructed both traditional graphs and hypergraphs to capture connectivity patterns during the perception of a flickering image. Their analysis considered graph metrics such as degree centrality, betweenness centrality, eigenvector centrality, connected components, shortest-path distances, cycle counts, and node degrees. The hypergraph approach enabled them to capture individual differences across frequency bands, revealing dynamic insights into brain connectivity. The study identified key network features across delta, theta, alpha, beta, and gamma bands, with cortico-cortical interactions across the frontal, parietal, temporal, and occipital lobes. These findings highlight robust activation patterns in specific brain regions, supporting theories of lobe integration and multifunctionality and offering a deeper understanding of neural dynamics in visual perception.

Finally, Yao et al. (contribution 8) introduce a novel approach for constructing complex networks to enhance emotion recognition using EEG data. Unlike conventional methods, which typically rely on ordinal representations of time series as network nodes, their approach leverages dimension and delay to map time series data into phase space, enabling more nuanced network construction. To validate their method, they applied it to two test signals: random noise and Lorenz chaotic signals. Their approach achieved over 91% accuracy in emotion classification, surpassing existing techniques. This contribution offers a promising new pathway for high-accuracy emotion recognition models, with potential applications in affective computing and real-time emotion detection.

3.3. Machine Learning

Machine learning (ML), a transformative branch of Artificial Intelligence (AI), is rapidly advancing data science applications, including neuroscience. Reflecting the impact of ML, its pioneers, John J. Hopfield and Geoffrey E. Hinton, were awarded the Nobel Prize in Physics in 2024. ML has become indispensable in neuroscience, enhancing predictive accuracy in medical diagnostics, advancing BCIs, and serving as a powerful research tool. Five papers in this issue (contributions 2, 3, 8, 10, and 15) apply ML techniques to neuroscience, with two of these (contributions 2 and 8) discussed in previous sections. Here, we explore the remaining three studies (contributions 3, 10, and 15).

Kolodziej et al. (contribution 3) investigated the potential of CNNs to enhance the detection of steady-state visual evoked potentials (SSVEPs) in BCIs. SSVEPs are EEG signals elicited by visual stimuli at specific frequencies, often used in BCIs due to their simplicity and reliability. Typically, users observe flashing lights at designated frequencies, and SSVEPs are detected by analyzing power spectral density. Kolodziej et al. proposed a CNN model capable of classifying SSVEPs effectively, even with limited training data. Their findings indicate that CNNs significantly improve SSVEP-based BCI accuracy, with up to a 20% increase in performance over traditional methods. This improvement is attributed to the CNN classifier’s resilience to artifacts in EEG signals, which often challenge conventional SSVEP detection techniques.

Chen et al. (contribution 10) presented an innovative approach to processing diffusion Magnetic Resonance Imaging (dMRI) data from macaque brains using a custom-designed primary–auxiliary dual GAN network (PadGAN). This end-to-end GAN model extracts latent space features from peak information maps to translate high-b-value images to lower-b-value images. In dMRI, the b-value determines the strength and timing of gradients, with higher b-values emphasizing diffusion effects. By translating these high-b-value images, PadGAN produces computed images that maintain a higher signal-to-noise ratio than directly acquired images [16]. This may enhance the quality and utility of dMRI data in brain connectivity studies.

Finally, Cedron et al. (contribution 15) developed a novel technique for optimizing multilayer perceptrons (MLPs), a form of ANN, to reduce memory usage and improve runtime. Their method involves pruning zero-weight elements from the ANN, creating a sparse matrix that proves advantageous with large datasets and dense networks. Their approach showed that the sparse matrix format is beneficial when non-zero data elements constitute around 10% of the matrix, particularly with data sets containing thousands of entries. This pruning technique prevents exponential memory consumption and shortens processing time, creating ANNs with enhanced efficiency for neuroscience applications. However, the authors noted that this method currently applies only to fully connected feedforward networks.

These papers highlight the growing role of machine learning in advancing neuroscience, offering methods that enhance data processing, analysis accuracy, and computational efficiency in various applications.

3.4. Statistical Methods

Statistical analysis is fundamental to neuroscience, as biological data are inherently noisy and nondeterministic [17]. This variability reflects differences in brain structure and function across individuals and populations, and effective statistical techniques help identify probable patterns and generalize findings from noisy data. However, noise can play a constructive role, as seen in phenomena like coherence resonance, where noise at an optimal level enhances signal coherence [18].

Petzold (contribution 4) introduces a simple yet powerful graphical method, the partial parallelism plot, to illustrate partial parallelism in data. Originally developed for laboratory tests, parallelism plots have been an essential tool for assessing similarity in test results. However, the experimental validation of parallelism remains challenging in bioanalytical method validation. While traditional methods, such as analysis of variance (ANOVA), are commonly applied to evaluate parallelism in linear data sets, they often fall short in identifying nuanced deviations from parallelism. Petzold’s approach extends beyond traditional ANOVA limitations by offering a graphical assessment tool designed for cases where parallelism is only partially present. This method accommodates biomarker tests with subtle deviations, enhancing the evaluation of parallelism and addressing limitations within existing regulatory guidelines.

Gómez et al. (contribution 12) focus on the role of stochasticity in neuronal dynamics, particularly in the opening and closing of ion channels. Neuronal behavior is probabilistic, with neural noise influencing ion channel activity at the cellular level [19] and perceptual switching at the behavioral level [20]. This intrinsic process underscores the complexity of biological systems and highlights that purely random models, while insightful, are approximations. The inherent randomness is likely shaped by hidden or unknown deterministic factors influencing neuronal activity. By studying stochastic models of ion channel behavior, Gómez et al. contribute to a more comprehensive understanding of how noise impacts neural dynamics, shedding light on probabilistic mechanisms that may govern brain function at multiple scales.

These contributions underscore the critical role of statistical methods in neuroscience, providing tools to decipher complex, noisy biological data and elucidate patterns within inherently variable systems.

4. Conclusions

This Special Issue highlights the transformative role of computational and mathematical approaches in advancing neuroscience, showcasing a wide range of state-of-the-art methodologies, such as computational modeling, ML, network analysis, and BCIs, that have deepened our understanding of brain dynamics, network interactions, cognitive processes, and behavior. By addressing core challenges in data integration and model validation, the papers in this issue underscore the potential of these methods to drive breakthroughs with far-reaching implications across medicine, technology, and our understanding of the human mind.

Each contribution demonstrates not only cutting-edge technologies but also valuable applications that bring us closer to decoding the complexity of brain function. From applications in medical diagnostics to insights into cognitive neuroscience and innovative statistical frameworks, these works collectively enhance our capacity to model, predict, and interpret brain activity with increasing accuracy and reliability.

We extend our gratitude to the authors, reviewers, and editors whose dedication has culminated in this comprehensive volume. It is our hope that these collective efforts will enrich our understanding of neural function and inspire further exploration in neuroscience, pushing the field to new and exciting frontiers.