Cyclic Performance of Prefabricated Bridge Piers with Concrete-Filled Steel Tubes and Improved Bracing Connection Detail
Abstract
1. Introduction
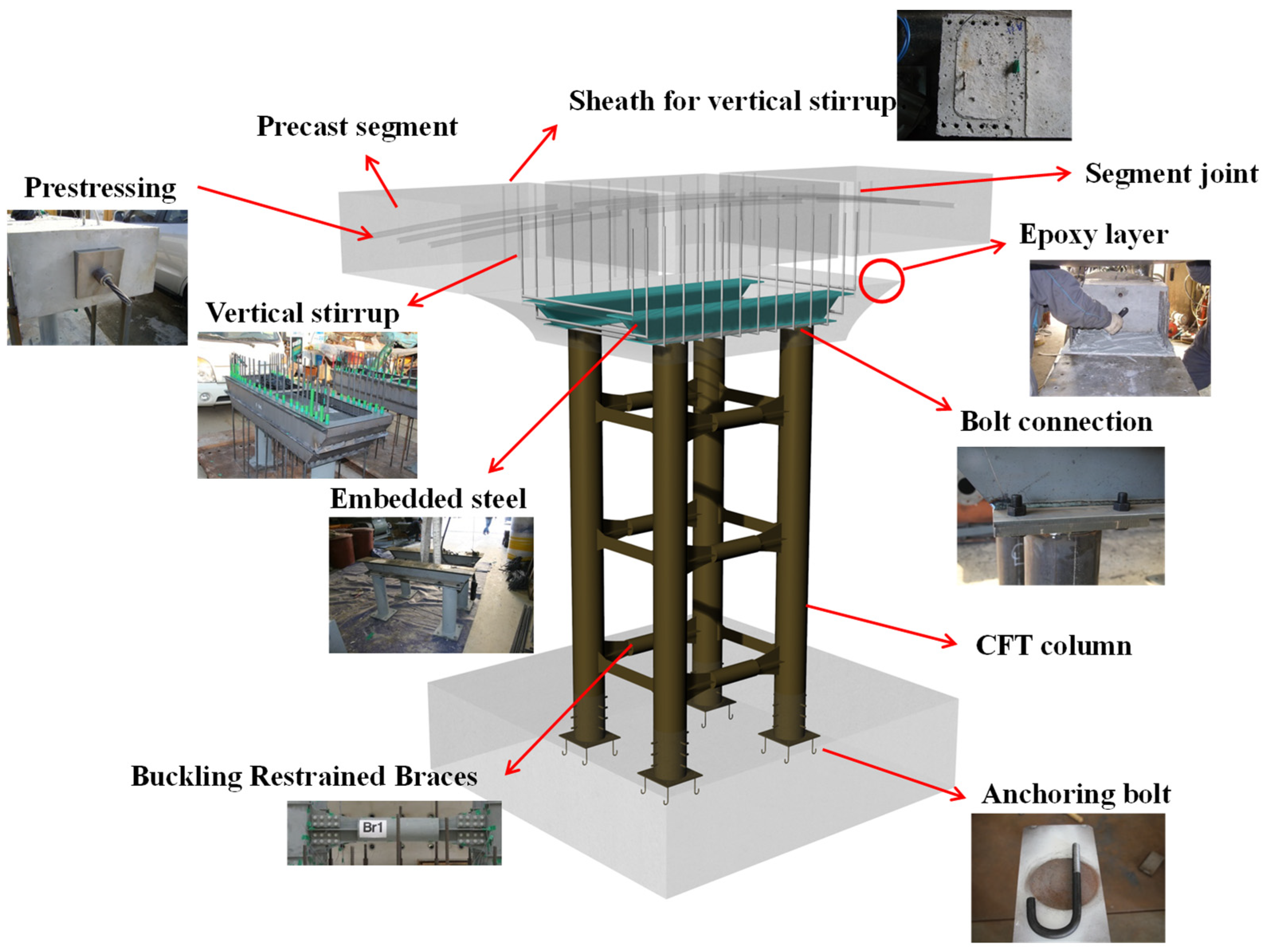
2. Problem Statement
3. Experiments on Connections
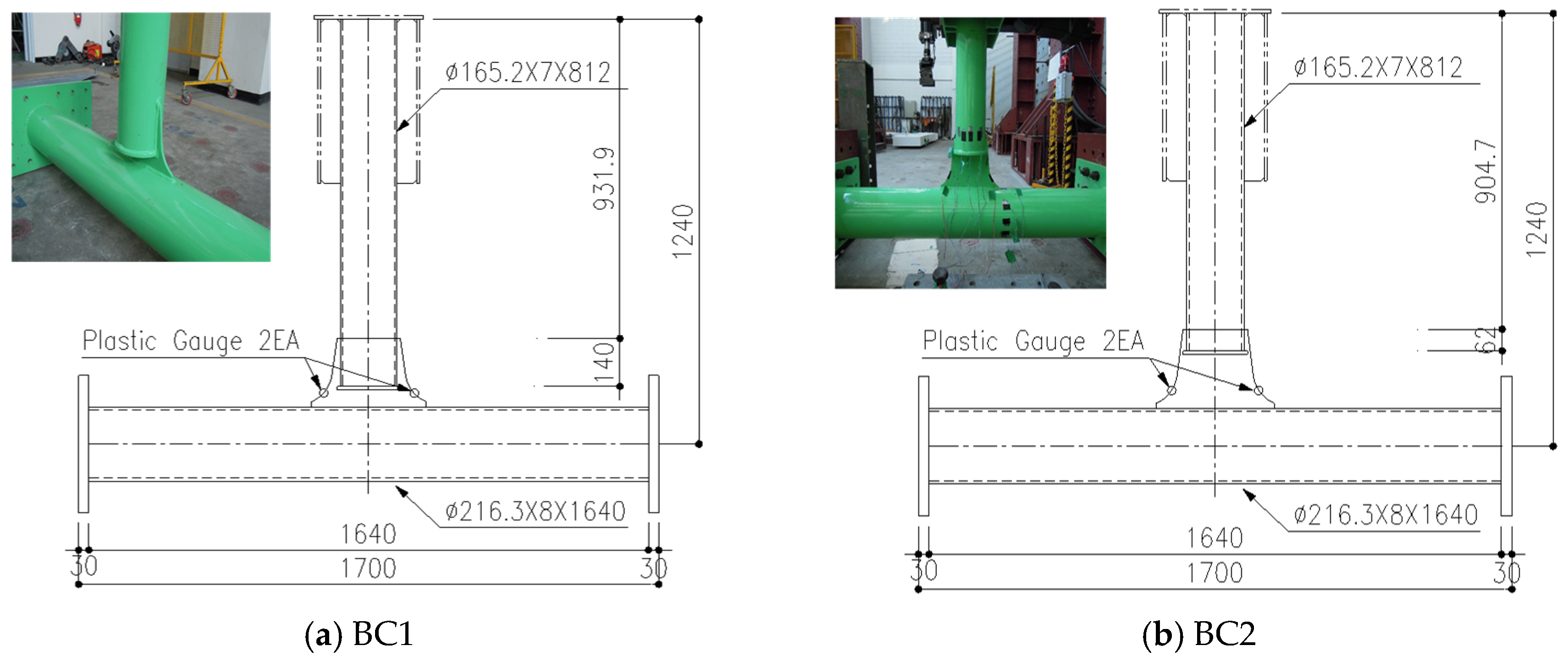
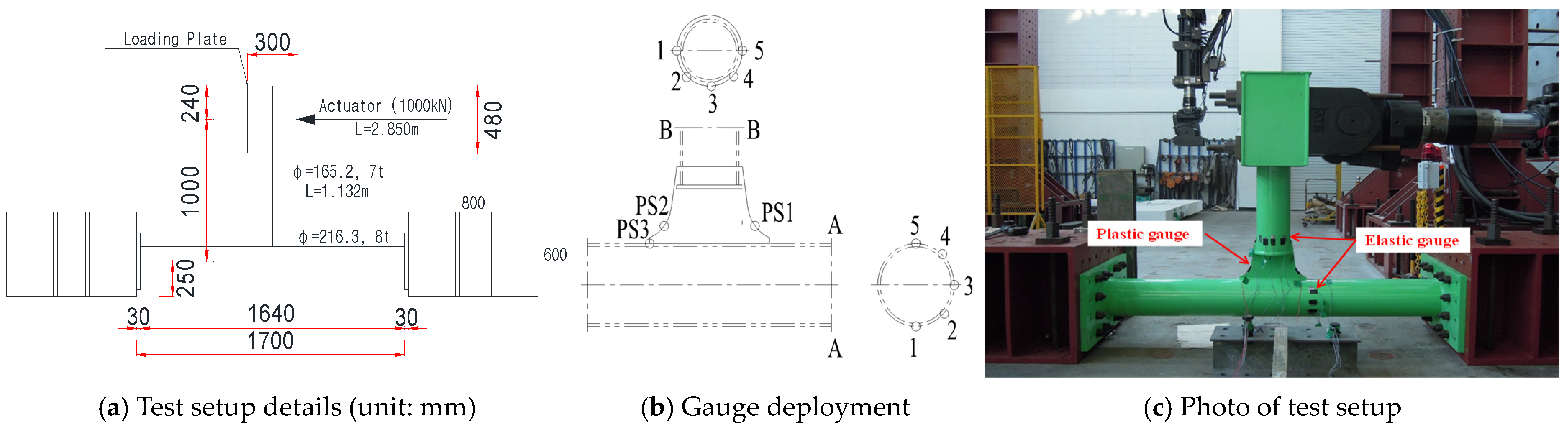
3.1. Connection Test Specimen
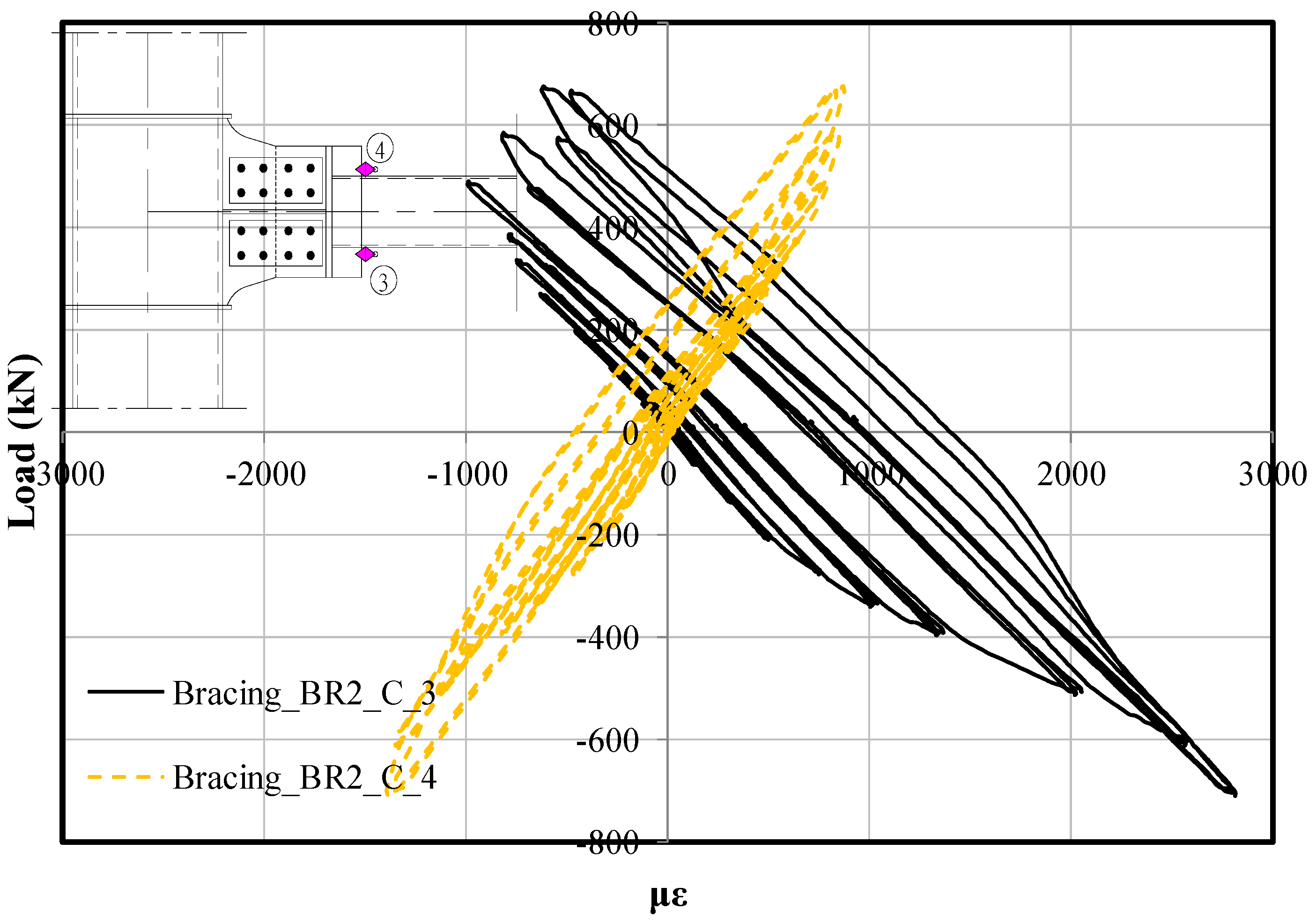
3.2. Connection Test Results
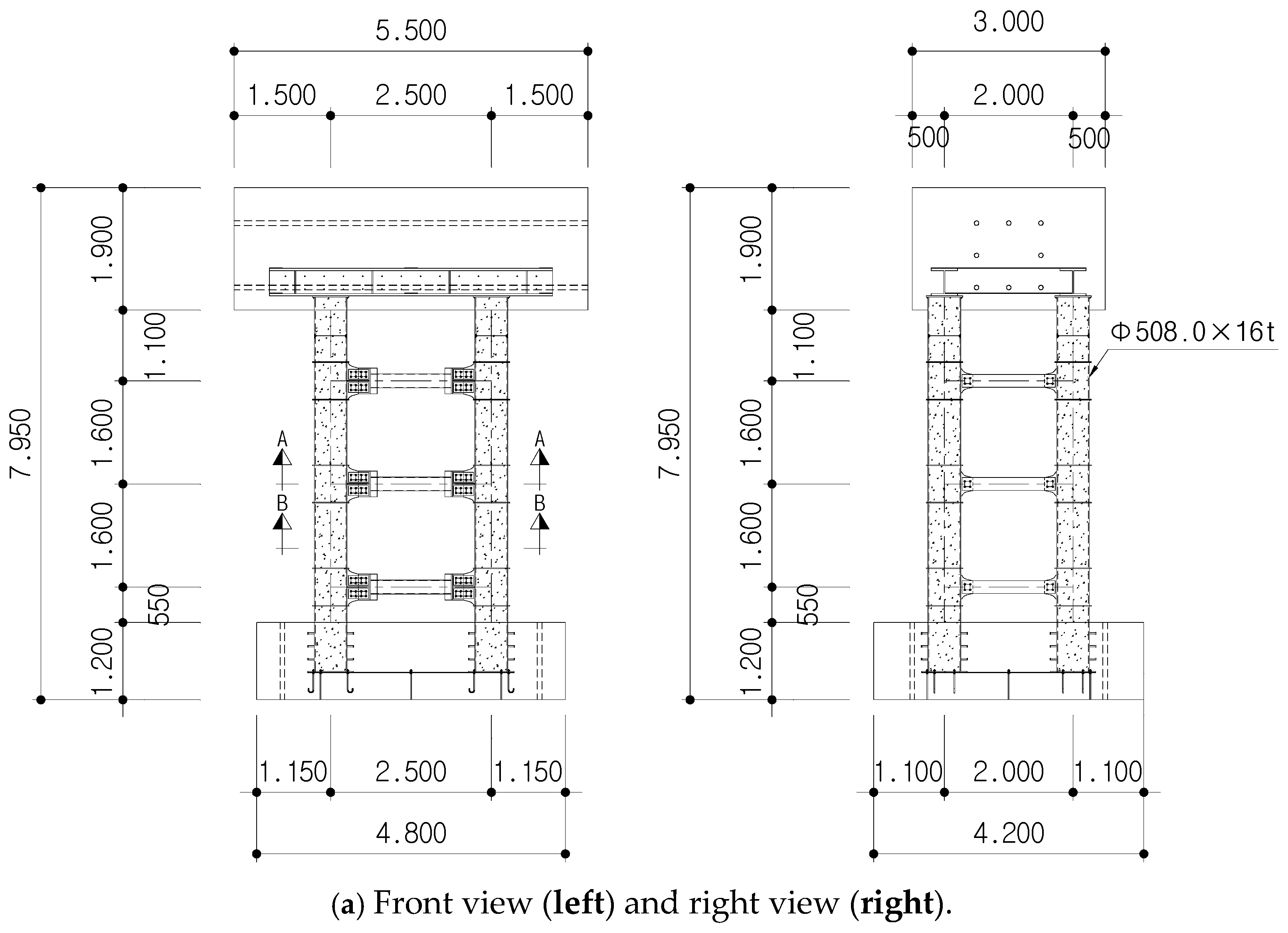
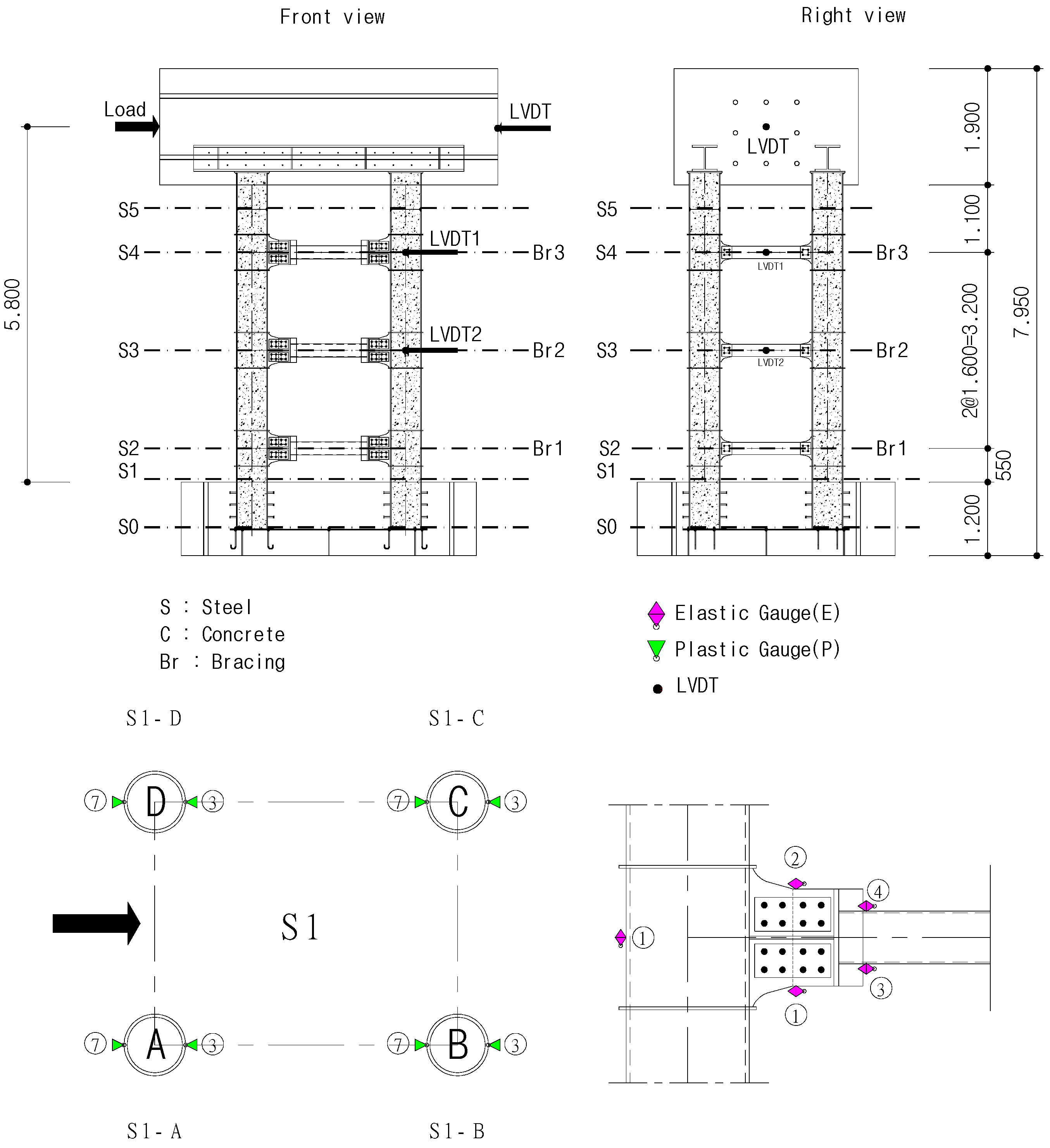
4. Experiments on Full-Scale Modular Bridge Pier
4.1. Full-Scale Test Specimen
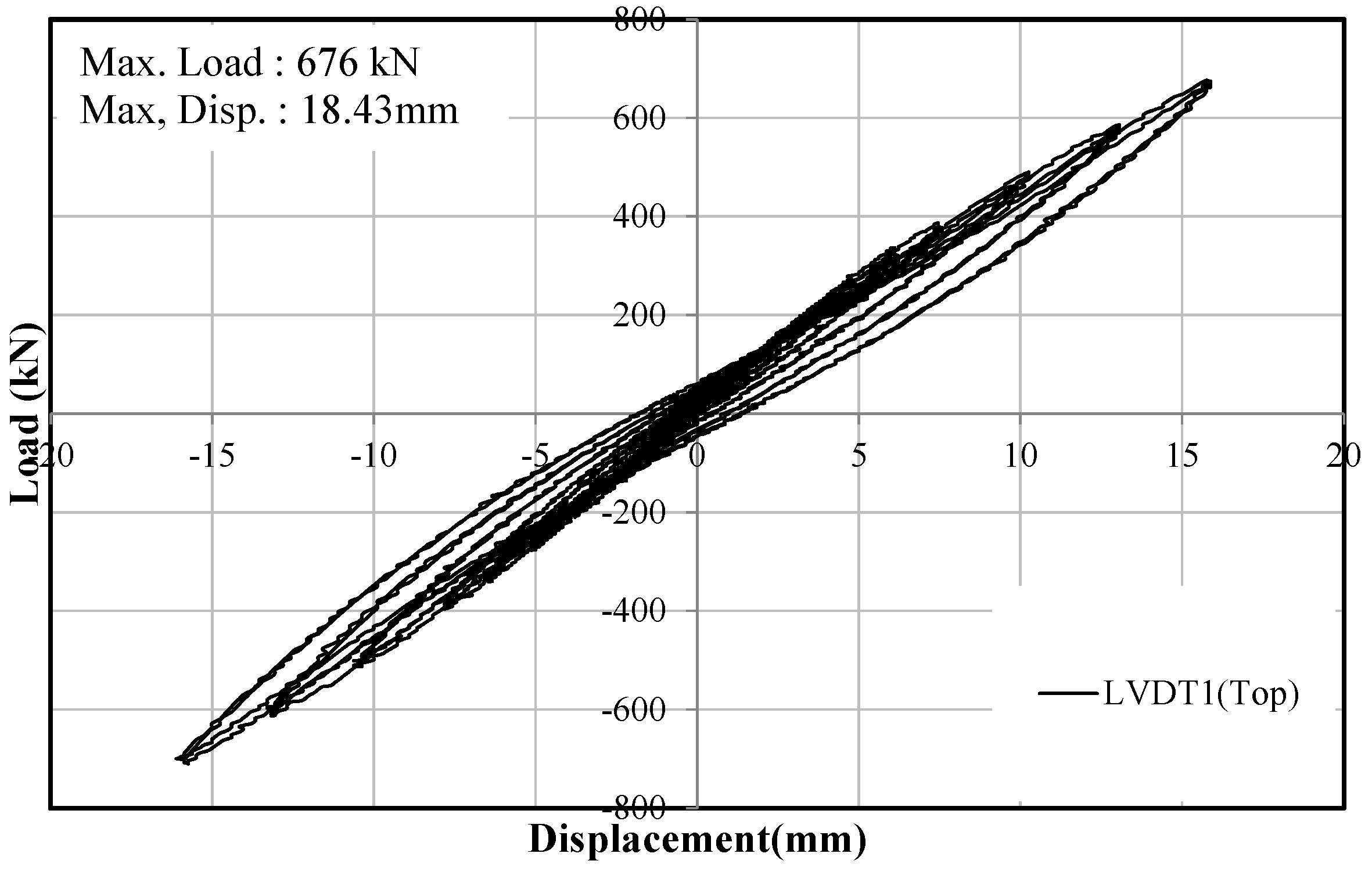
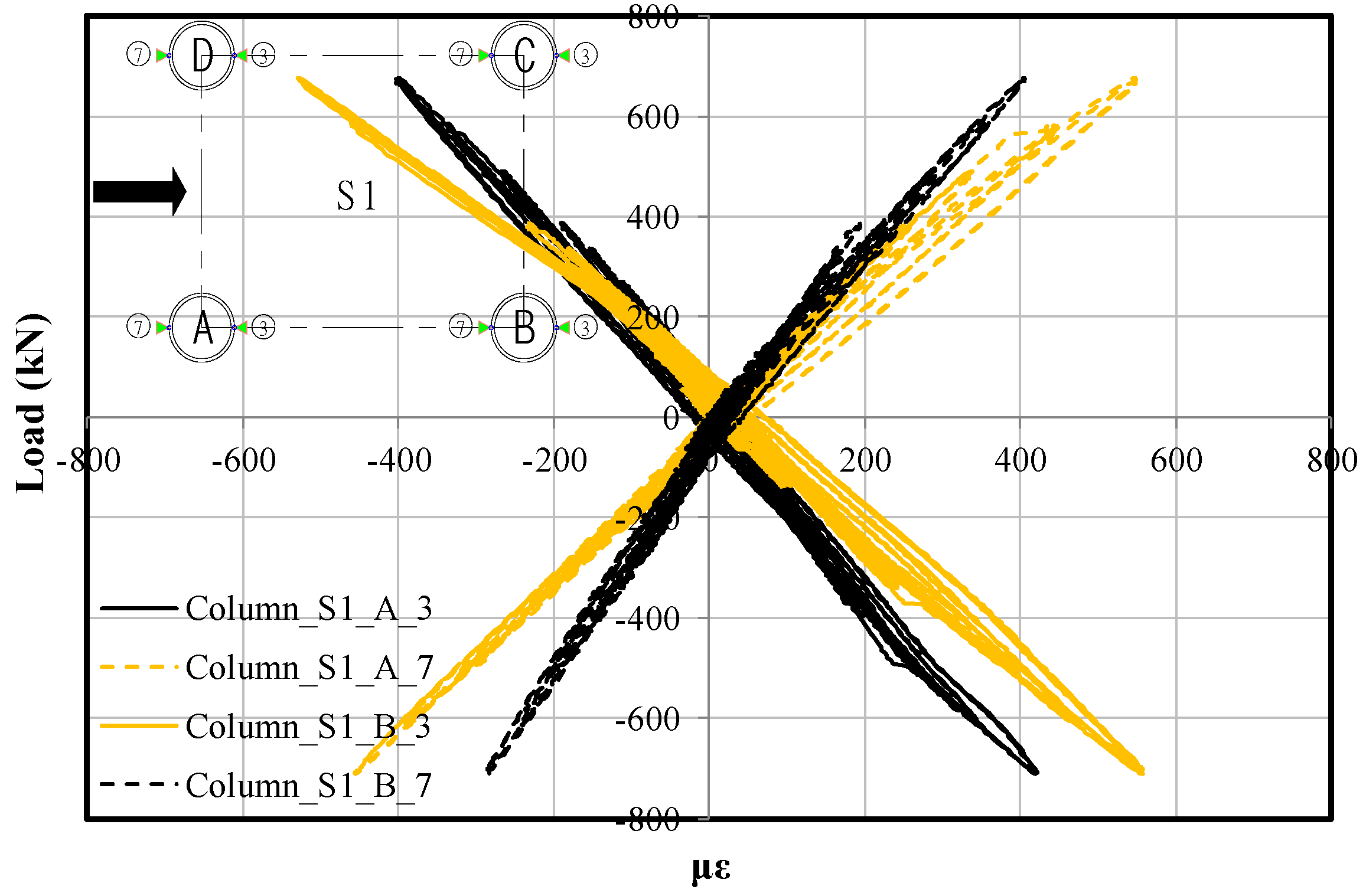
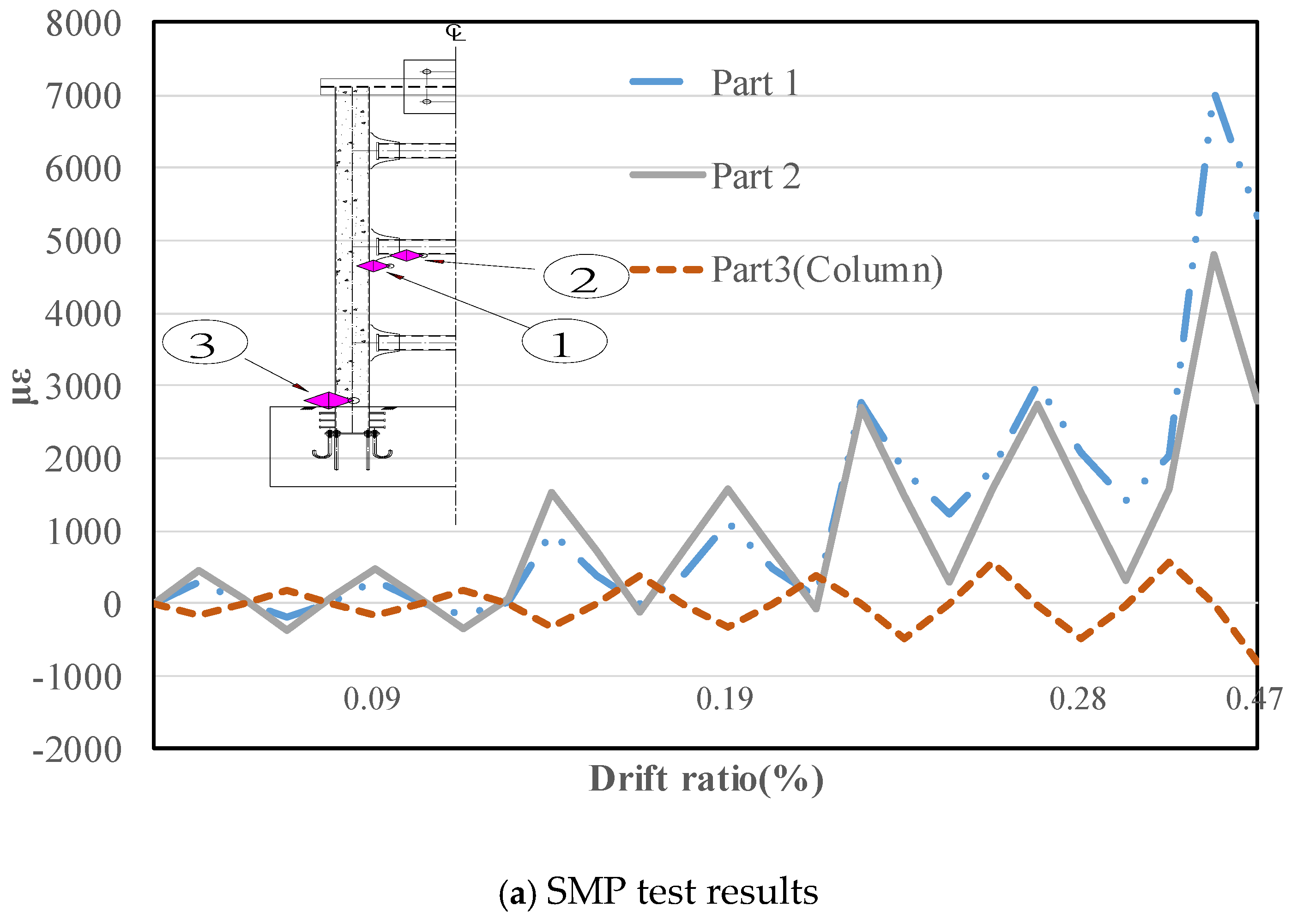
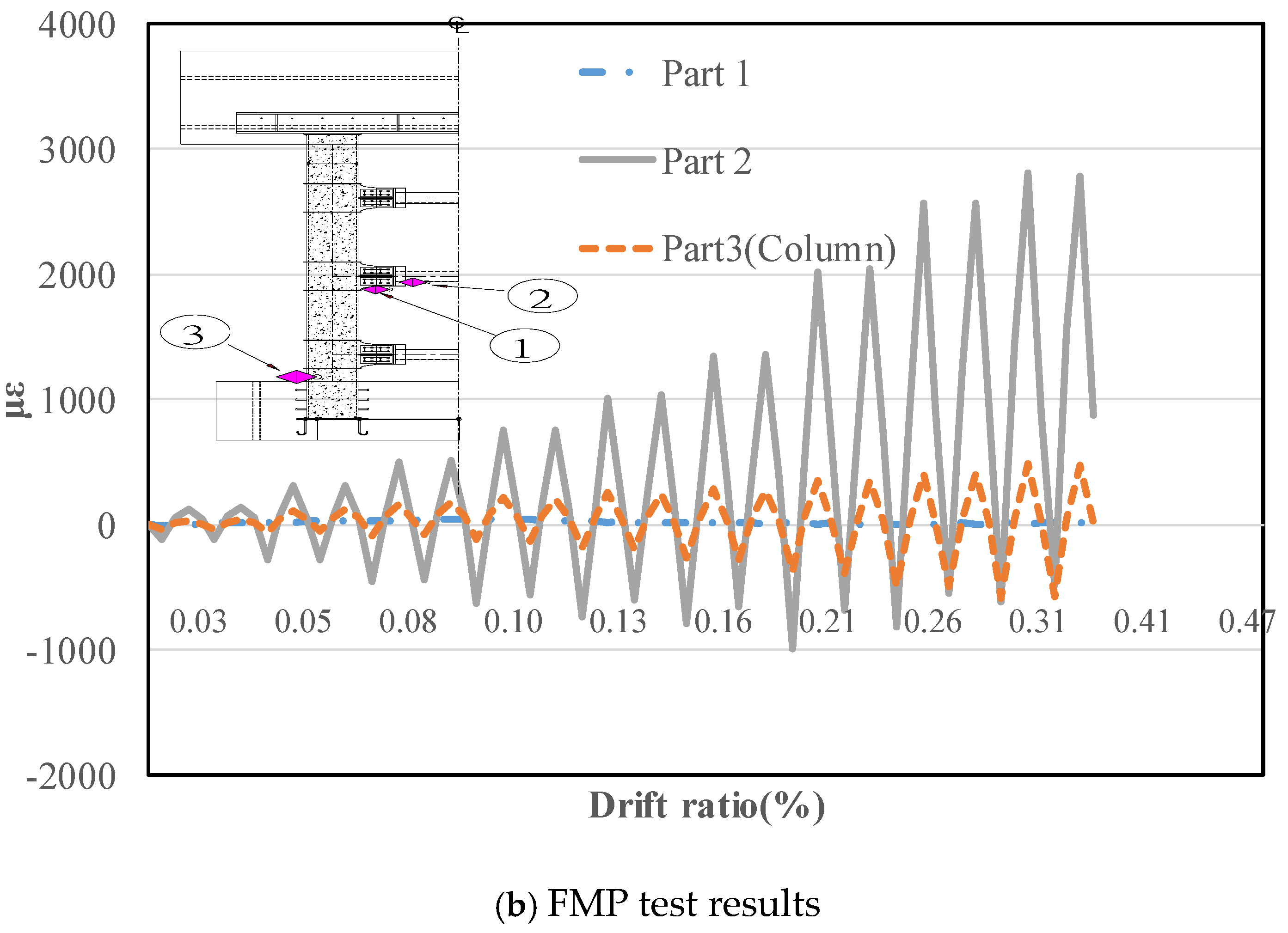
4.2. Full-Scale Test Results
4.3. Comparison of the Full- and Small-Scale Specimens
5. Conclusions
- (1)
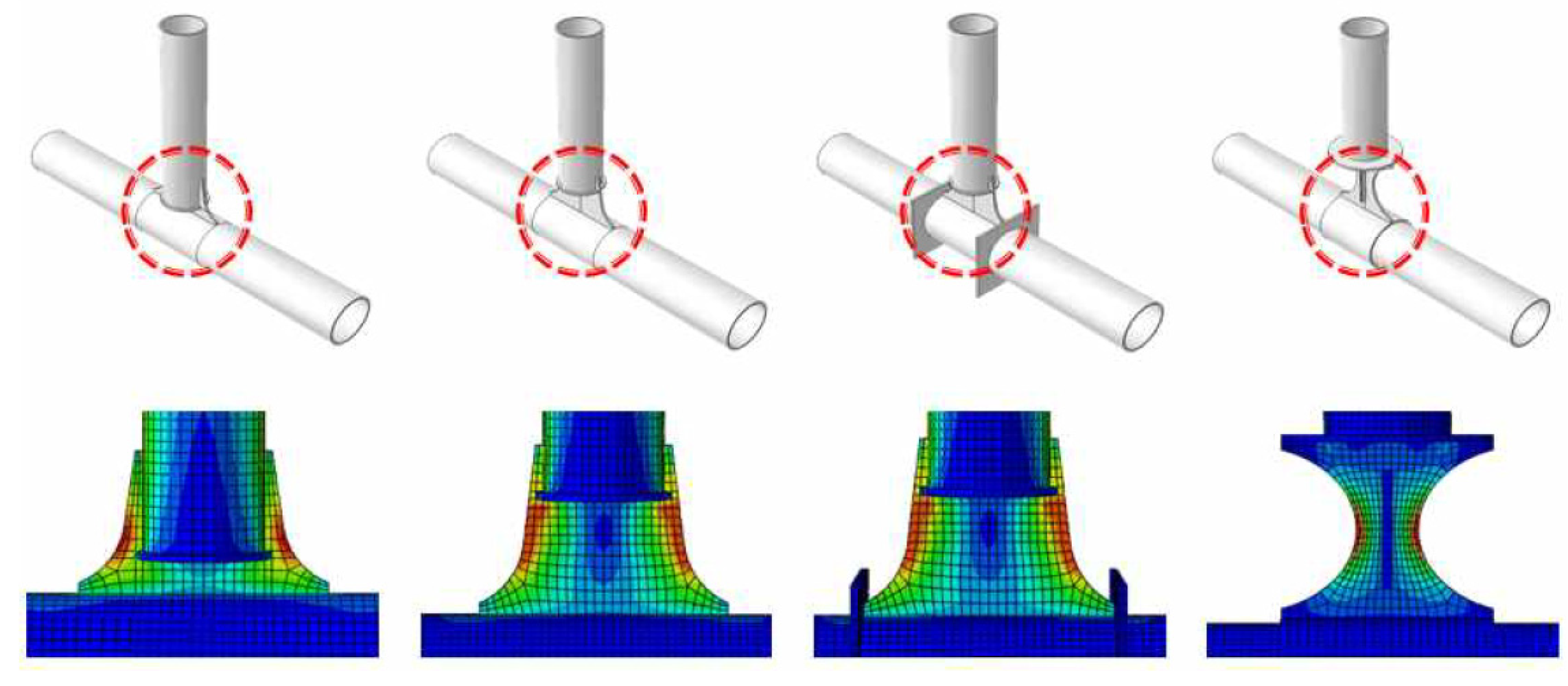
- The connection plates welded to the CFT columns must be made more flexible by extending the plate length to prevent premature fracture of the steel tubes at the welding site.
- (2)
- The moment–rotation curves derived from the component tests can be utilized to design a modular pier with a dog bone-shaped flexible bracing member, which offers greater strength compared with stiffer bracing. The plastification location in the connection can be designed by altering the details to achieve the desired behavior.
- (3)
- Enhanced connection details significantly decreased the stress concentration at the welded section of the connection, improving the energy absorption capacity of the modular pier. The full-scale modular pier demonstrated lower strain values compared with the previous stiffer bracing connection specimen, allowing for the initiation of the yielding of the bracing members before the CFT columns without premature fracture. Therefore, the seismic performance of the modular pier can be designed by adjusting the bracing members and their connection details.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Shim, C.S.; Chung, C.H.; Kim, H.H. Experimental evaluation of seismic performance of precast segmental bridge piers with a circular solid section. Eng. Struct. 2008, 30, 3782–3792. [Google Scholar] [CrossRef]
- Shim, C.S.; Chung, Y.S.; Han, J.H. Cyclic response of concrete-encased composite columns with low steel ratio. Proc. Inst. Civ. Eng. Struct. Build. 2008, 161, 77–89. [Google Scholar] [CrossRef]
- Shim, C.S.; Chugn, C.H.; Kim, I.K.; Kim, Y.J. Shear connections in prestressed beams with precast slabs. Proc. Inst. Civ. Eng. Struct. Build. 2010, 163, 317–330. [Google Scholar] [CrossRef]
- Shim, C.S.; Chung, Y.S.; Yoon, J.Y. Cyclic behavior of prefabricated circular composite columns with low steel ratio. Eng. Struct. 2011, 33, 2525–2534. [Google Scholar] [CrossRef]
- Zeghiche, J.; Chaoui, K. An experimental behaviour of concrete-filled steel tubular columns. J. Constr. Steel Res. 2005, 61, 53–66. [Google Scholar] [CrossRef]
- Tomii, M.; Sakino, K. Experimental Studies on the Ultimate Moment of Concrete Filled Square Steel Tubular Beam-Columns. Trans. Archit. Inst. Jpn. 1979, 275, 55–65. [Google Scholar] [CrossRef] [PubMed]
- AISC. Specification for Structural Steel Buildings; American Institute of Steel Construction: Chicago, IL, USA, 2005. [Google Scholar]
- BSI. Eurocode 4: Design of Composite Steel and Concrete Structures—Part 1-1: General Rules and Rules for Buildings; British Standards Institution: London, UK, 2004. [Google Scholar]
- Nishiyama, I.; Morino, S.; Sakino, K.; Nakahara, H.; Fujimoto, T.; Mukai, A.; Inai, E.; Kai, M.; Tokinoya, H.; Fukumoto, T.; et al. Summary of research on concrete-filled structural steel tube column system carried out under the US–Japan cooperative research program on composite and hybrid structures. Build. Res. Inst. 2002. [Google Scholar]
- Tsuda, K.; Matsui, C.; Mino, E. Strength and Behavior of Slender Concrete Filled Steel Horizontal load. In Proceedings of the 12th World Conference on Earthquake Engineering, Auckland, New Zealand, 30 January–4 February 2000. [Google Scholar]
- Xu, Q.; Sun, H.; Ding, F.; Lyu, F. Analysis of ultimate seismic performance of thin-walled concrete-filled steel tube bridge piers under dynamic load. Eng. Struct. 2023, 292, 116544. [Google Scholar] [CrossRef]
- Zhang, H.S.; Zhao, Y.; Ruan, J.; Nie, X.; Fan, J.S.; Liu, Y.F. Experiment study on temperature field and effect on steel-concrete composite bridge towers. Structures 2023, 50, 937–953. [Google Scholar] [CrossRef]
- Li, X.; Zhang, Z.; Zhou, T.; Xiao, Y.; Sun, Y. Hysteretic behavior of post-tensioned precast segmental CFT double-column piers. Earthq. Eng. Eng. Vib. 2023, 22, 747–762. [Google Scholar] [CrossRef]
- El-Heweity, M.M. On the performance of circular concrete-filled high strength steel columns under axial loading. Alex. Eng. J. 2012, 51, 109–119. [Google Scholar] [CrossRef]
- de Oliveira, W.L.A.; De Nardin, S.; de Cresce El Debs, A.L.H.; El Debs, M.K. Influence of concrete strength and length/diameter on the axial capacity of CFT columns. J. Constr. Steel Res. 2009, 65, 2103–2110. [Google Scholar] [CrossRef]
- Roeder, C.W.; Lehman, D.E.; Thody, R. Composite action in CFT components and connections. Eng. J. 2009, 46, 229–242. [Google Scholar] [CrossRef]
- Lehman, D.E.; Roeder, C.W. Foundation connections for circular concrete-filled tubes. J. Constr. Steel Res. 2012, 78, 212–225. [Google Scholar] [CrossRef]
- Kim, H.J.; Hu, J.W.; Hwang, W.S. Cyclic testing for structural detail improvement of CFT column-foundation connections. Sustainability 2015, 7, 5260–5281. [Google Scholar] [CrossRef]
- Moon, J.; Lehman, D.E.; Roeder, C.W.; Lee, H. Evaluation of embedded concrete-filled tube (CFT) column-to-foundation connections. Eng. Struct. 2013, 56, 22–35. [Google Scholar] [CrossRef]
- Azizinamini, A.; Schneider, S. Moment connections to circular concrete-filled steel tube columns. J. Struct. Eng. 2004, 130, 213–222. [Google Scholar] [CrossRef]
- MacRae, G.; Roeder, C.; Gunderson, C.; Kimura, Y. Brace-Beam-Column Connections for Concentrically Braced Frames with Concrete Filled Tube Columns. J. Struct. Eng. 2004, 130, 233–243. [Google Scholar] [CrossRef]
- Hassan, M.M.; Ramadan, H.M.; Abdel-Mooty, M.N.; Mourad, S.A. Behavior of concentrically loaded CFT braces connections. J. Adv. Res. 2014, 5, 243–252. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Wang, J.; Li, B. Seismic fragility analysis of CFT frames with buckling-restrained braces and steel braces under long- and short-duration ground motions. Structures 2022, 39, 848–865. [Google Scholar] [CrossRef]
- Mata, R.; Nuñez, E. Cyclic Behavior of Concrete-Filled Tube Columns with Bidirectional Moment Connections Considering the Local Slenderness Effect. Buildings 2024, 14, 2240. [Google Scholar] [CrossRef]
- Shim, C.; Kim, D.; Jung, D.; Kim, I.; Chung, C. Cyclic Tests of Modular CFT Bridge Piers. In Proceedings of the 10th National Conference in Earthquake Engineering, Anchorage, AK, USA, 21–25 July 2014; Earthquake Engineering Research Institute: Anchorage, AK, USA, 2014. [Google Scholar]
- Ma, H.W.; Oh, H.C.; Kim, D.W.; Kong, D.; Shim, C.S. Evaluation of Flexural Behavior of a Modular Pier with Circular CFT. J. Korean Soc. Steel Constr. 2012, 24, 725–734. [Google Scholar] [CrossRef][Green Version]
- AASHTO. LRFD Bridge Design Specifications, 5th ed.; American Association of State Highway and Transporta-tion Officials: Washington, DC, USA, 2010. [Google Scholar]
- ACI Committee, 318. Building Code Requirements for Structural Concrete and Commentary; American Concrete Institute: Detroit, MI, USA, 2011. [Google Scholar]



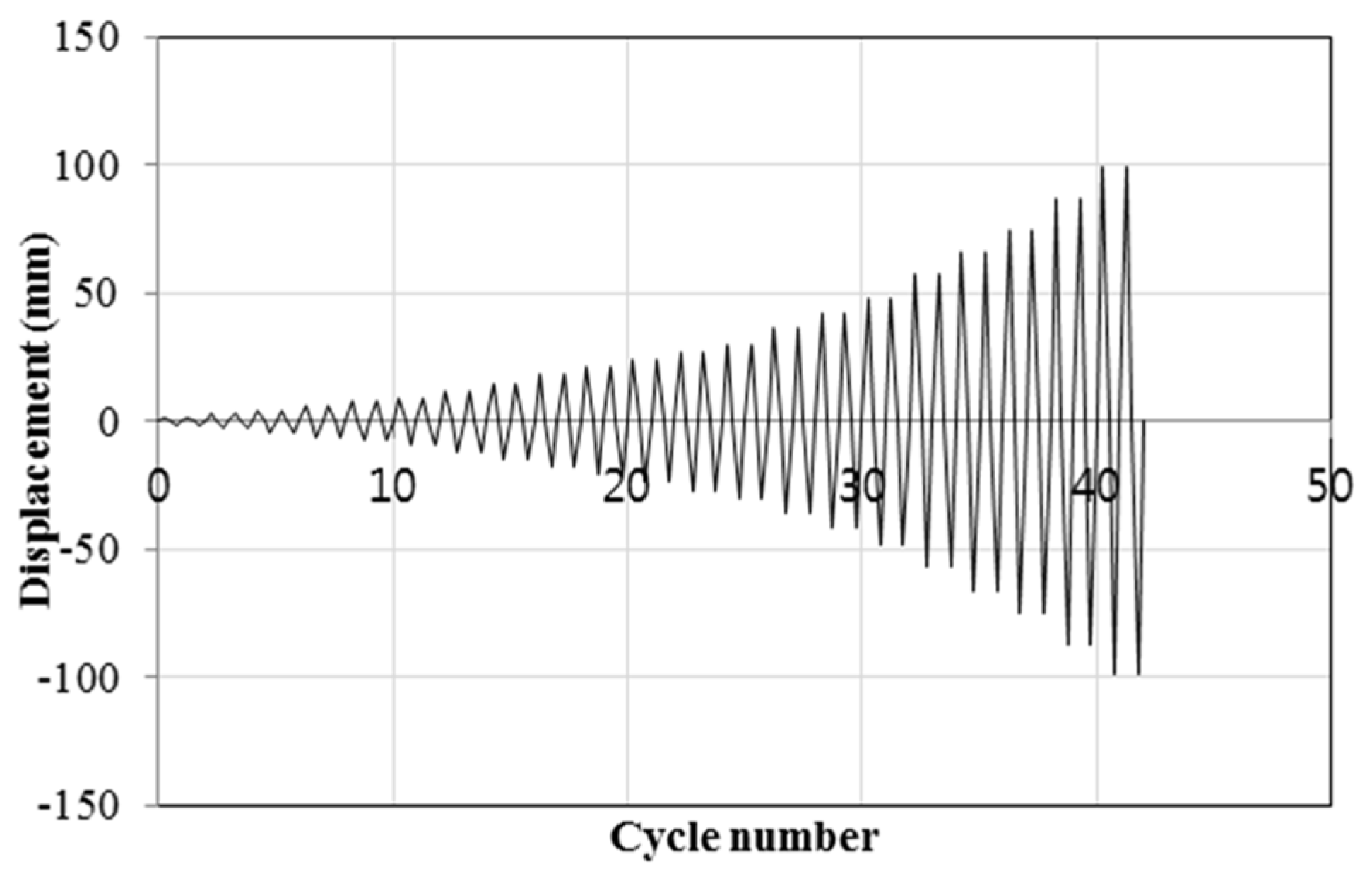
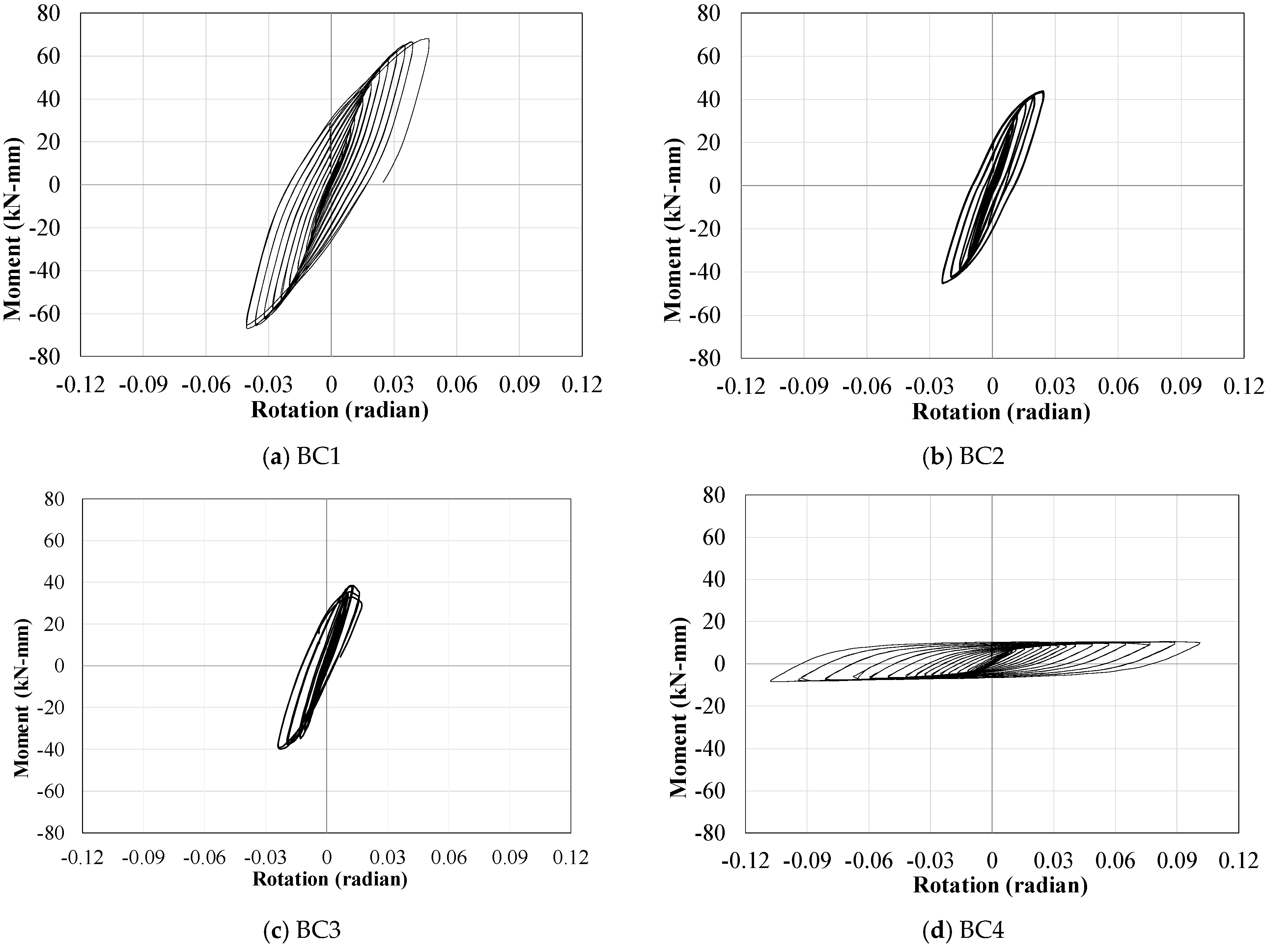
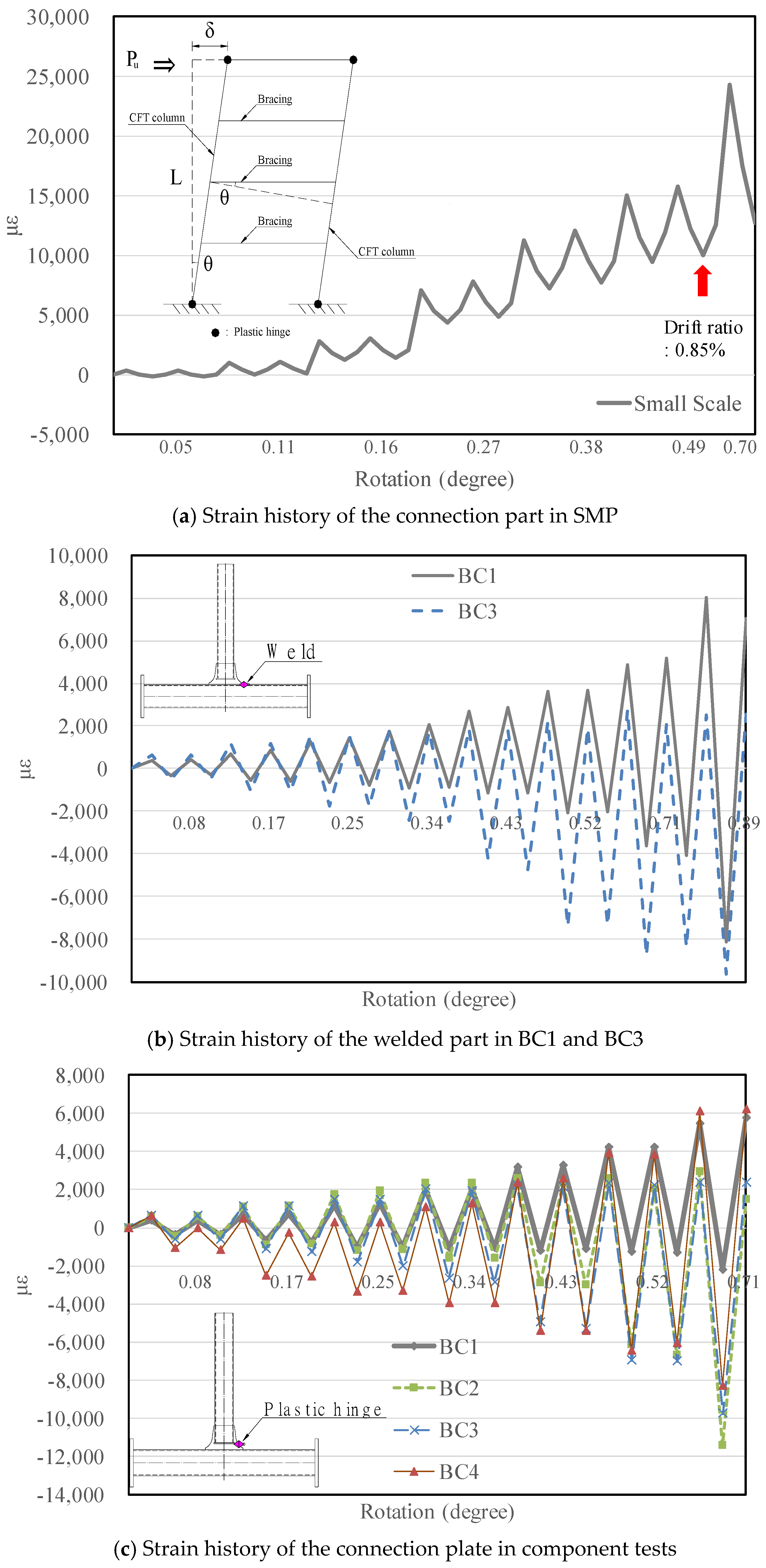
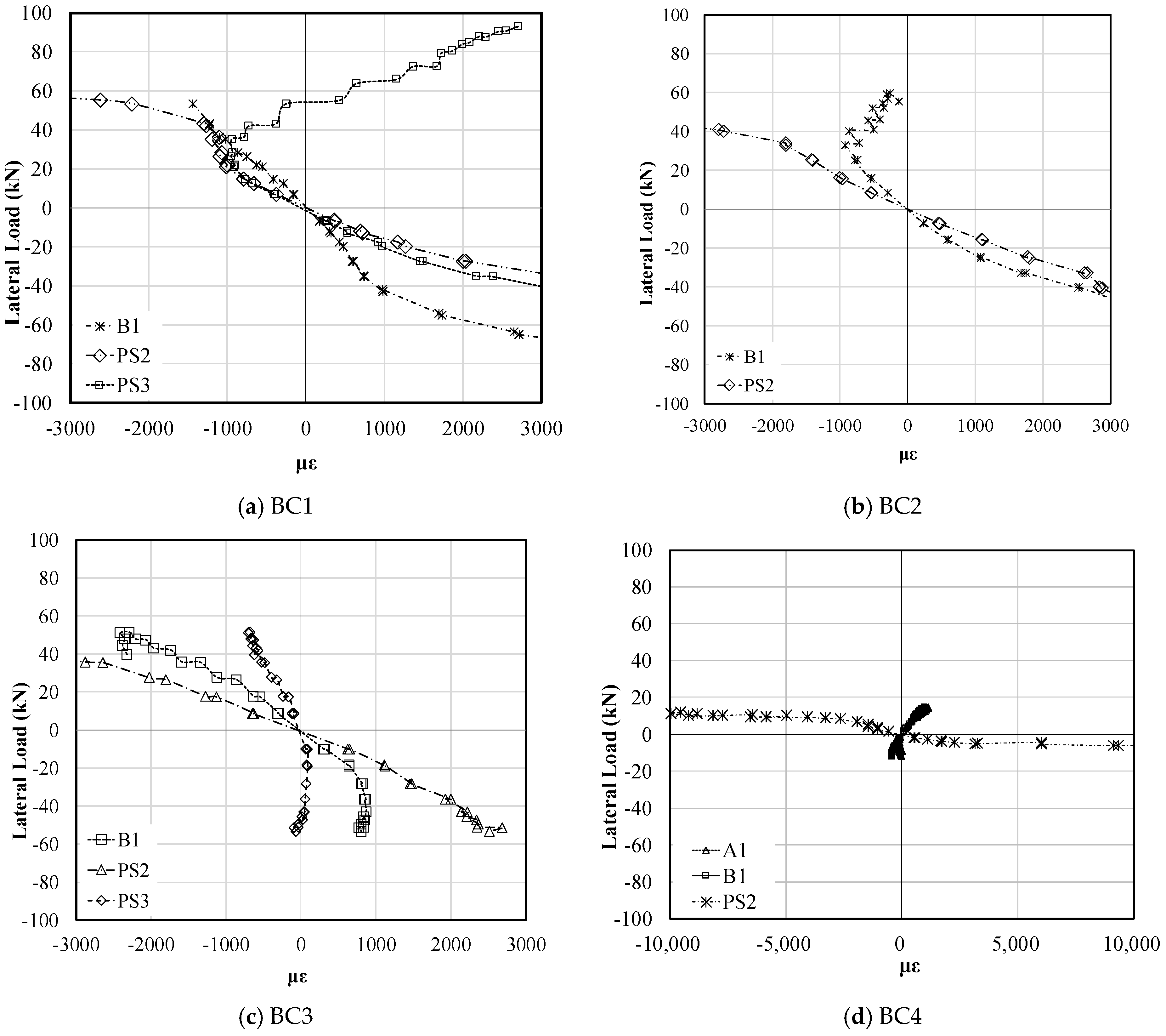


| Cycle | 1~12 | 13~26 | 27~32 | 33~38 | 39~42 |
|---|---|---|---|---|---|
| Displacement (mm) | ±1.5~±9.0 | ±12.0~±30.0 | ±36.0~±48.0 | ±57.0~±75.0 | ±87.0~±99.0 |
| Drift Ratio (%) | ±0.17~±1.01 | ±1.35~±3.36 | ±4.04~±5.38 | ±6.39~±8.41 | ±9.76~±11.1 |
| Velocity Increment (mm/s) | ±0.06 | ±0.12 | ±0.24 | ±0.36 | ±0.48 |
| Specimen | Max. Load (kN) | Displacement (mm) | Energy Absorption (kJ) | Failure Mode |
|---|---|---|---|---|
| BC1 | 93.20 | 32.94 | 8580.68 | Fatigue failure of welding part |
| BC2 | 59.95 | 17.66 | 5244.23 | Lateral buckling without plastic hinge yielding |
| BC3 | 52.39 | 9.26 | 1850.88 | Lateral buckling after plastic hinge yielding |
| BC4 | 14.14 | 74.44 | 4492.59 | No failure with plastic hinge yielding |
| Design Codes | D/t Limits | Test Specimen | |
|---|---|---|---|
| Equations | Calculation | Calculation | |
| LRFD (2010) [7,27] | * | 73.3 | 17.0 |
| ACI-318 (2011) [28] | 73.0 | ||
| Eurocode 4 (2004) [8] | 67.1 | ||
| Displacement (mm) | ±1.5–±18.0 |
| Drift Ratio (%) | ±0.03–±0.31 |
| Velocity Increment (mm/s) | ±1.8 |
| Cycle | 1–17 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, D.; Jeon, C.-H.; Park, K.-T. Cyclic Performance of Prefabricated Bridge Piers with Concrete-Filled Steel Tubes and Improved Bracing Connection Detail. Appl. Sci. 2024, 14, 11810. https://doi.org/10.3390/app142411810
Kim D, Jeon C-H, Park K-T. Cyclic Performance of Prefabricated Bridge Piers with Concrete-Filled Steel Tubes and Improved Bracing Connection Detail. Applied Sciences. 2024; 14(24):11810. https://doi.org/10.3390/app142411810
Chicago/Turabian StyleKim, Dongwook, Chi-Ho Jeon, and Ki-Tae Park. 2024. "Cyclic Performance of Prefabricated Bridge Piers with Concrete-Filled Steel Tubes and Improved Bracing Connection Detail" Applied Sciences 14, no. 24: 11810. https://doi.org/10.3390/app142411810
APA StyleKim, D., Jeon, C.-H., & Park, K.-T. (2024). Cyclic Performance of Prefabricated Bridge Piers with Concrete-Filled Steel Tubes and Improved Bracing Connection Detail. Applied Sciences, 14(24), 11810. https://doi.org/10.3390/app142411810






