A Comprehensive Review on Uncertainty and Risk Modeling Techniques and Their Applications in Power Systems
Abstract
1. Introduction
- While most review articles provide theoretical insights, this case study enhances understanding by showing how these methods perform in real-world scenarios. By applying the techniques to a power system integrating wind farms, we assess their impact on key reliability indices such as loss of load expectation (LOLE), loss of load probability (LOLP), and expected energy not supplied (EENS).
- The case study enables a direct, systematic comparison of modeling techniques, such as Monte Carlo simulation, Markov Chain Monte Carlo (MCMC), RO, and IGDT. This practical analysis helps highlight the suitability of different approaches for varying uncertainty durations and levels.
- Presenting practical examples alongside theoretical discussions fosters greater reader engagement, offering a clearer perspective on the applicability of these techniques in real-world challenges.
2. Risk Modeling Techniques
2.1. Statistical Risk Models
2.1.1. Statistical Risk Models for Renewable Energies
2.1.2. Statistical Reliability Models for Power System
2.2. Qualitative System Analysis
- Start with the top event and break it down using AND/OR gates until basic events are reached.
- Construct a table where each row represents a cut set, and columns represent basic events. Begin by placing the top event in the first row.
- Recursively expand each event in the table:
- AND gate: Add inputs to new columns within the same row.
- OR gate: Add inputs to new rows.
- Apply Boolean algebra to eliminate redundant rows and events, isolating minimal cut sets.
- Review and analyze the minimal cut sets to identify critical failure combinations.
2.3. Stochastic Modeling
2.4. Actuarial Techniques
2.5. Scenario Analysis
2.6. Machine Learning Techniques
2.7. Stress Testing
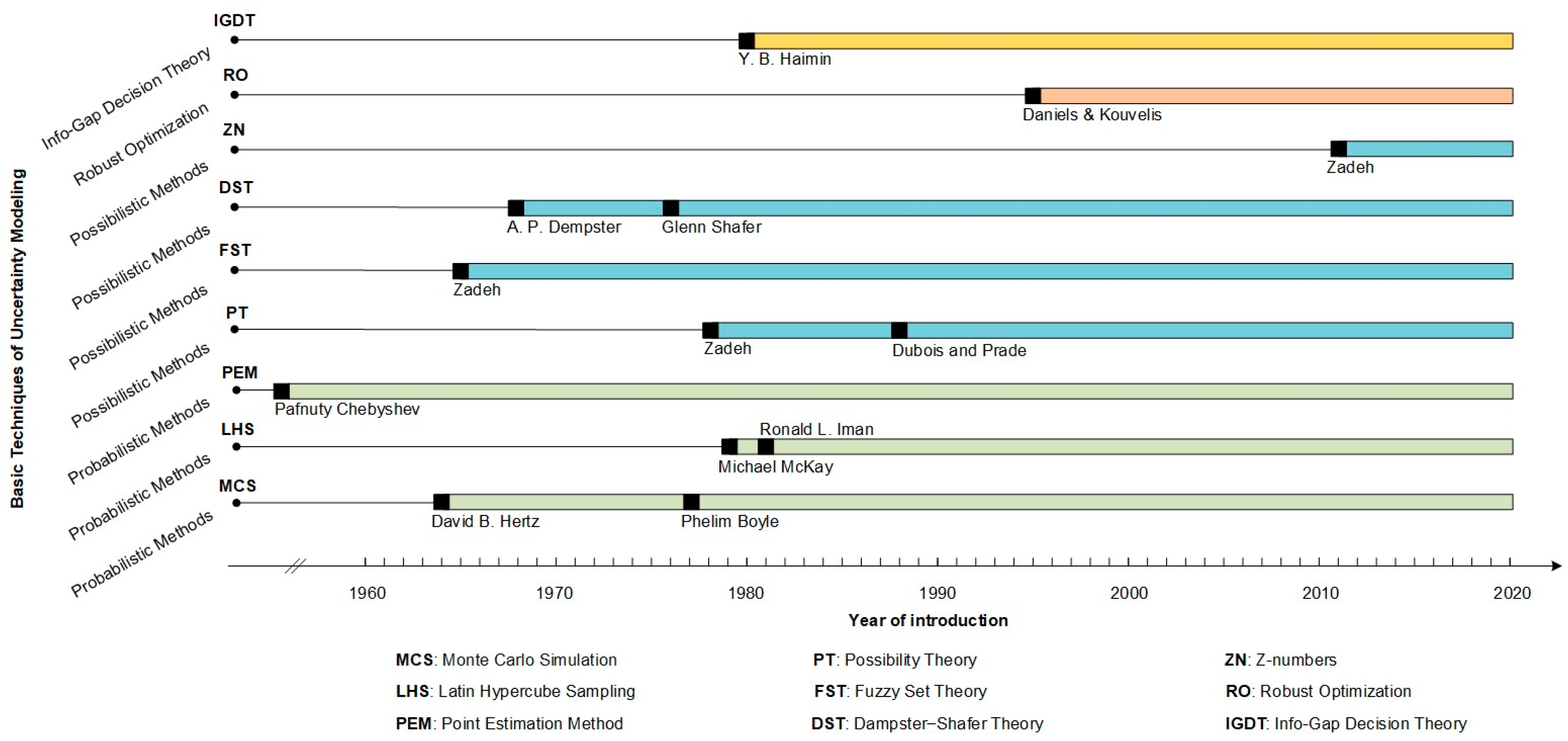
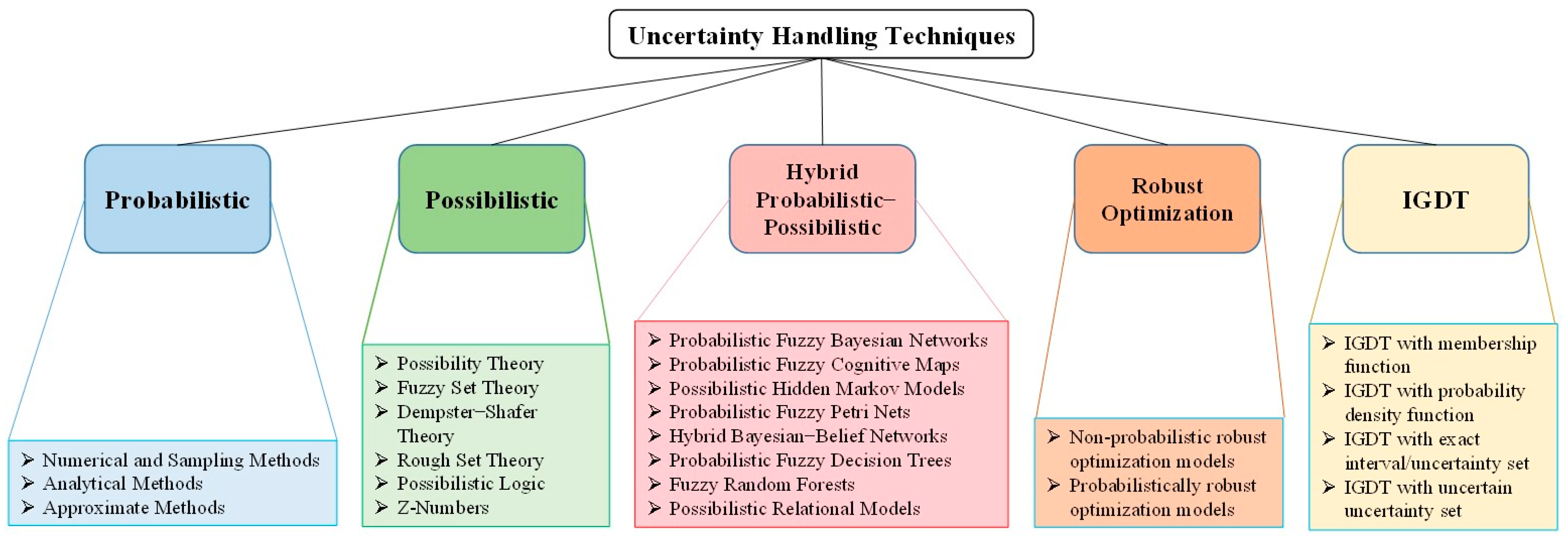
3. Uncertainty Modeling Techniques
3.1. Probabilistic Methods
3.1.1. Numerical and Sampling Methods
- A.
- Monte Carlo Simulation
- B.
- Latin Hypercube Sampling (LHS)
3.1.2. Analytical Methods
- A.
- Point Estimation Methods (PEMs)
3.2. Possibilistic Methods
3.2.1. Possibility Theory
3.2.2. Fuzzy Set Theory
3.2.3. Dempster–Shafer Theory (DST)
3.2.4. Z-Numbers
3.3. Hybrid Probabilistic–Possibilistic Methods
3.4. Robust Optimization (RO)
3.5. Info-Gap Decision Theory (IGDT)
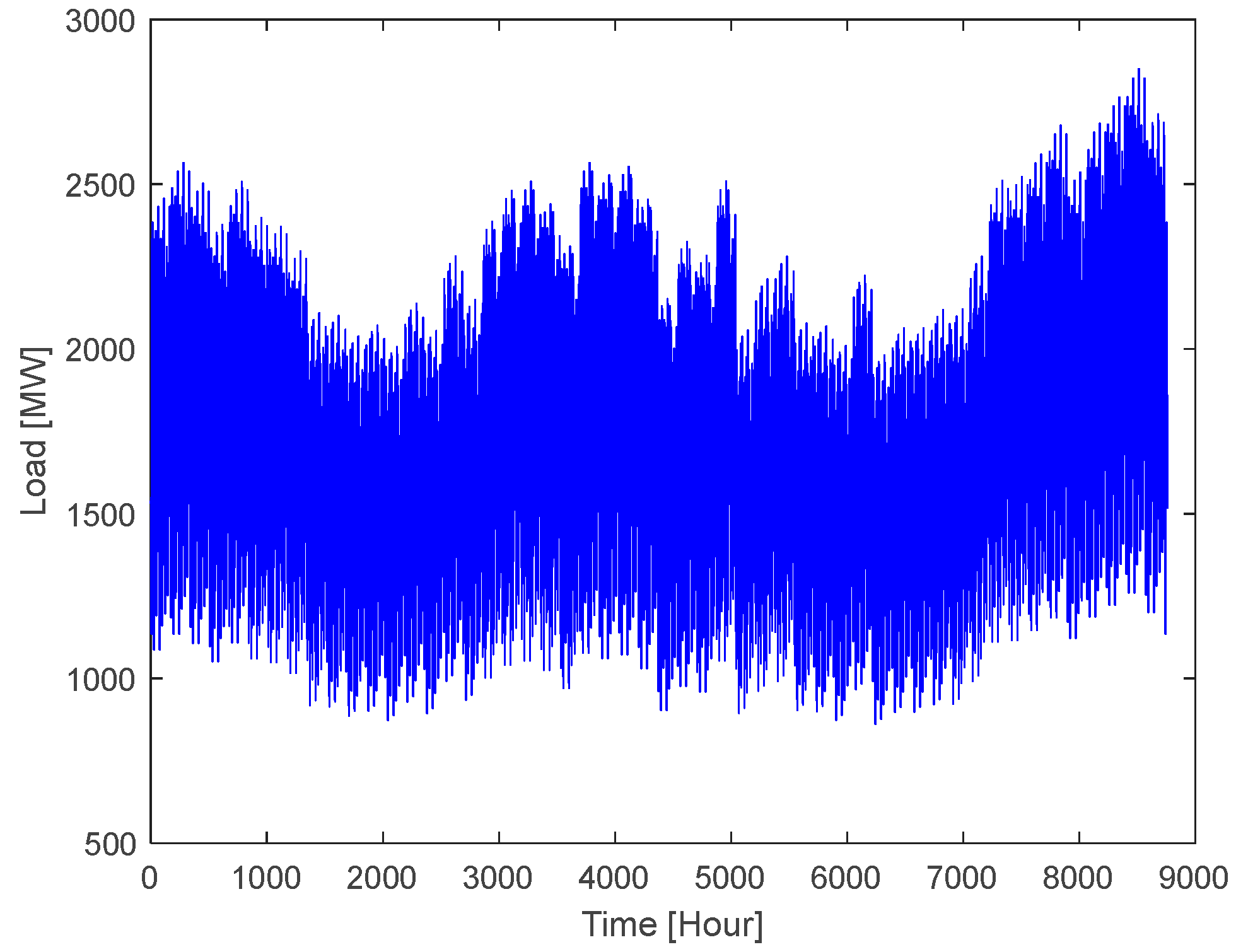
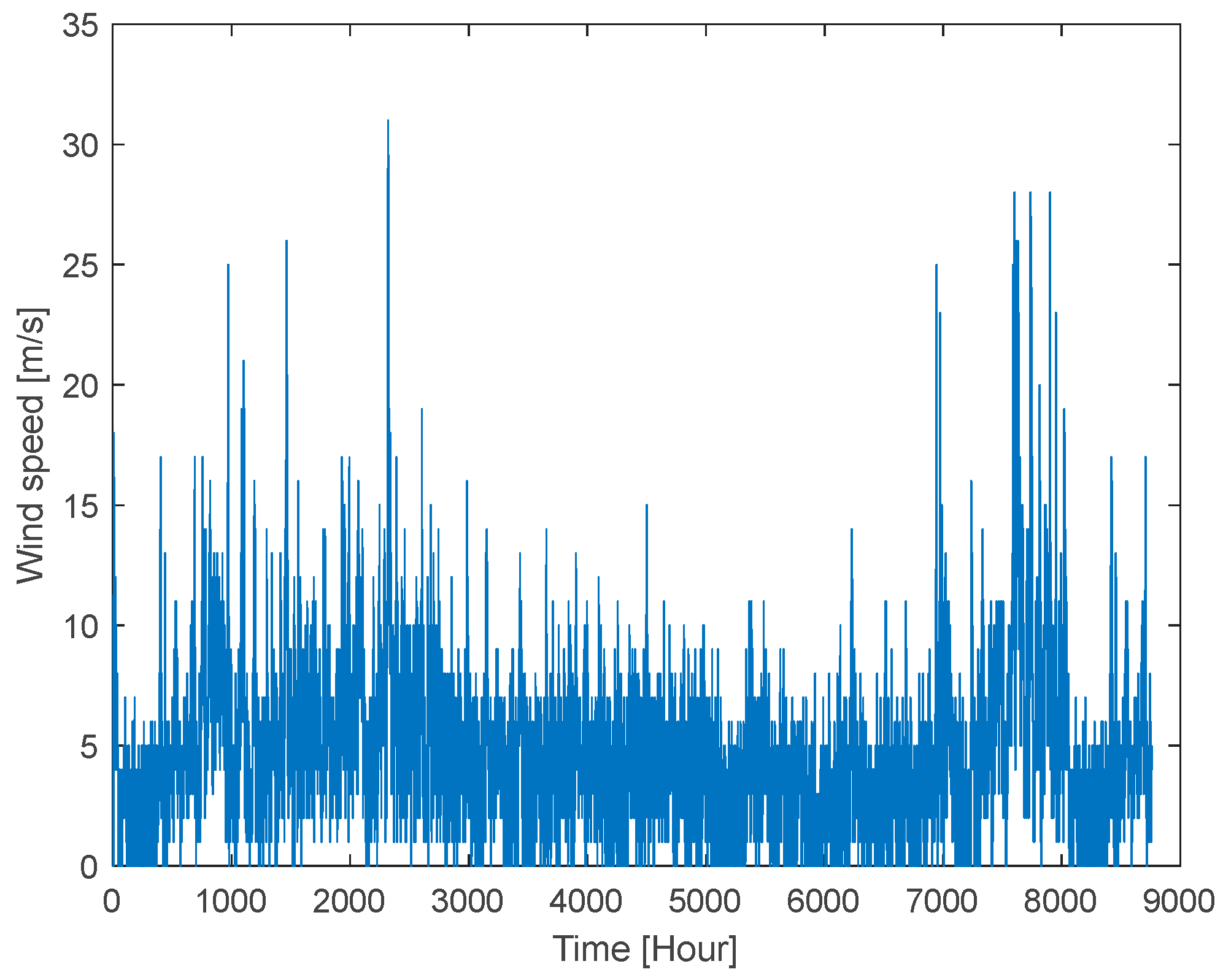
4. Case Study and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| CPP | conventional power plant |
| EENS | expected energy not supplied |
| ENS | energy not supplied |
| IGDT | information-gap decision theory |
| LOLE | loss of load expectation |
| LOLP | loss of load probability |
| MCMC | Markov Chain Monte Carlo |
| PEM | point estimation method |
| RES | renewable energy source |
| RO | robust optimization |
| VoLL | Value of Lost Load |
References
- Billinton, R.; Chu, K. Early evolution of LOLP: Evaluating generating capacity requirements [history]. IEEE Power Energy Mag. 2015, 13, 88–98. [Google Scholar] [CrossRef]
- Skare, E.; Haugdal Jore, S. Hybrid threats in the Norwegian petroleum sector. A new category of risk problems for safety science? Saf. Sci. 2024, 176, 106521. [Google Scholar] [CrossRef]
- Aven, T. A risk and safety science perspective on the precautionary principle. Saf. Sci. 2023, 165, 106211. [Google Scholar] [CrossRef]
- Blokland, P.; Reniers, G. Safety Science, a Systems Thinking Perspective: From Events to Mental Models and Sustainable Safety. Sustainability 2020, 12, 5164. [Google Scholar] [CrossRef]
- Chen, D.; Chen, J.D. Monte-Carlo Simulation-Based Statistical Modeling; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- IEC 61400-26-1:2019; Wind Energy Generation Systems—Part 26-1: Availability for Wind Energy Generation Systems. Swedish Institute for Standards: Stockholm, Sweden, 2019.
- Lutz, M.; Görg, P.; Faulstich, S.; Cernusko, R.; Pfaffel, S. Monetary-based availability: A novel approach to assess the performance of wind turbines. Wind Energy 2020, 23, 77–89. [Google Scholar] [CrossRef]
- Shrestha, T.K.; Karki, R. Utilizing energy storage for operational adequacy of wind-integrated bulk power systems. Appl. Sci. 2020, 10, 5964. [Google Scholar] [CrossRef]
- Wang, M.Q.; Yang, M.; Liu, Y.; Han, X.S.; Wu, Q. Optimizing probabilistic spinning reserve by an umbrella contingencies constrained unit commitment. Int. J. Electr. Power Energy Syst. 2019, 109, 187–197. [Google Scholar] [CrossRef]
- Moghaddam, M.J.H.; Kalam, A.; Nowdeh, S.A.; Ahmadi, A.; Babanezhad, M.; Saha, S. Optimal sizing and energy management of stand-alone hybrid photovoltaic/wind system based on hydrogen storage considering LOEE and LOLE reliability indices using flower pollination algorithm. Renew. Energy 2019, 135, 1412–1434. [Google Scholar] [CrossRef]
- Stephen, G.; Tindemans, S.H.; Fazio, J.; Dent, C.; Acevedo, A.F.; Bagen, B.; Crawford, A.; Klaube, A.; Logan, D.; Burke, D. Clarifying the interpretation and use of the LOLE resource adequacy metric. In Proceedings of the 2022 17th International Conference on Probabilistic Methods Applied to Power Systems (PMAPS), Manchester, UK, 15–12 June 2022; pp. 1–4. [Google Scholar]
- Billinton, R.; Ronald, N.A. Reliability Evaluation of Power Systems; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]
- Sun, D.; Zheng, Z.; Liu, S.; Wang, M.; Sun, Y.; Liu, D. Generation expansion planning considering efficient linear EENS formulation. Glob. Energy Interconnect. 2021, 4, 273–284. [Google Scholar] [CrossRef]
- Bohre, A.K.; Agnihotri, G.; Dubey, M. Optimal sizing and sitting of DG with load models using soft computing techniques in practical distribution system. IET Gener. Transm. Distrib. 2016, 10, 2606–2621. [Google Scholar] [CrossRef]
- Cui, Z.; Zheng, M.; Wang, J.; Liu, J. Reliability Analysis of a Three-Engine Simultaneous Pouring Control System Based on Bayesian Networks Combined with FMEA and FTA. Appl. Sci. 2023, 13, 11546. [Google Scholar] [CrossRef]
- Andrews, J.; Tolo, S. Dynamic and dependent tree theory (D2T2): A framework for the analysis of fault trees with dependent basic events. Reliab. Eng. Syst. Saf. 2023, 230, 108959. [Google Scholar] [CrossRef]
- Chen, M.; Cao, X.; Zhang, Z.; Yang, L.; Ma, D.; Li, M. Risk-averse stochastic scheduling of hydrogen-based flexible loads under 100% renewable energy scenario. Appl. Energy 2024, 370, 123569. [Google Scholar] [CrossRef]
- Ghaffarinasab, N.; Çavuş, Ö.; Kara, B.Y. A mean-CVaR approach to the risk-averse single allocation hub location problem with flow-dependent economies of scale. Transp. Res. Part B Methodol. 2023, 167, 32–53. [Google Scholar] [CrossRef]
- Schneider, I. Jakob Bernoulli, Ars conjectandi (1713). In Landmark Writings in Western Mathematics 1640–1940; Elsevier: Amsterdam, The Netherlands, 2005; pp. 88–104. [Google Scholar]
- Gupta, A.K.; Varga, T. An Introduction to Actuarial Mathematics; Springer Science & Business Media: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Paltrinieri, N.; Comfort, L.; Reniers, G. Learning about risk: Machine learning for risk assessment. Saf. Sci. 2019, 118, 475–486. [Google Scholar] [CrossRef]
- Esposito, S.; Stojadinovic, B.; Mignan, A.; Dolšek, M.; Babič, A.; Selva, J.; Iqbal, S.; Cotton, F.; Iervolino, I. Report on the Proposed Engineering Risk Assessment Methodology for Stress Tests of Non-Nuclear Cis; ETH: Zurich, Switzerland, 2016. [Google Scholar]
- Quiles-Cucarella, E.; Marquina-Tajuelo, A.; Roldán-Blay, C.; Roldán-Porta, C. Particle Swarm Optimization Method for Stand-Alone Photovoltaic System Reliability and Cost Evaluation Based on Monte Carlo Simulation. Appl. Sci. 2023, 13, 11623. [Google Scholar] [CrossRef]
- Reis, D.J.F.; Pessanha, J.E.O. A fast and accurate sampler built on Bayesian inference and optimized Hamiltonian Monte Carlo for voltage sag assessment in power systems. Int. J. Electr. Power Energy Syst. 2023, 153, 109297. [Google Scholar] [CrossRef]
- Liu, C.; Zheng, X.; Yang, H.; Tang, W.; Sang, G.; Cui, H. Techno-economic evaluation of energy storage systems for concentrated solar power plants using the Monte Carlo method. Appl. Energy 2023, 352, 121983. [Google Scholar] [CrossRef]
- Hassani, B.; Hassani, B.K. Scenario Analysis in Risk Management; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Chen, L.; Chen, C.; Wang, L.; Zeng, W.; Li, Z. Uncertainty quantification of once-through steam generator for nuclear steam supply system using latin hypercube sampling method. Nucl. Eng. Technol. 2023, 55, 2395–2406. [Google Scholar] [CrossRef]
- Helton, J.C.; Davis, F.J. Latin hypercube sampling and the propagation of uncertainty in analyses of complex systems. Reliab. Eng. Syst. Saf. 2003, 81, 23–69. [Google Scholar] [CrossRef]
- Cai, J.; Hao, L.; Xu, Q.; Zhang, K. Reliability assessment of renewable energy integrated power systems with an extendable Latin hypercube importance sampling method. Sustain. Energy Technol. Assess. 2022, 50, 101792. [Google Scholar] [CrossRef]
- Bulut, E.; Albak, E.İ.; Sevilgen, G.; Öztürk, F. A new approach for battery thermal management system design based on Grey Relational Analysis and Latin Hypercube Sampling. Case Stud. Therm. Eng. 2021, 28, 101452. [Google Scholar] [CrossRef]
- Hirsch, C.; Wunsch, D.; Szumbarski, J.; Łaniewski-Wołłk, L.; Pons-Prats, J. Uncertainty management for robust industrial design in aeronautics. In Notes on Numerical Fluid Mechanics and Multidisciplinary Design; Springer: Cham, Switzerland, 2019. [Google Scholar]
- Liu, Y.; Wang, J.; Yue, Z. Improved Multi-point estimation method based probabilistic transient stability assessment for power system with wind power. Int. J. Electr. Power Energy Syst. 2022, 142, 108283. [Google Scholar] [CrossRef]
- Pesteh, S.; Moayyed, H.; Miranda, V. Favorable properties of Interior Point Method and Generalized Correntropy in power system State Estimation. Electr. Power Syst. Res. 2020, 178, 106035. [Google Scholar] [CrossRef]
- Kan, R.; Xu, Y.; Li, Z.; Lu, M. Calculation of probabilistic harmonic power flow based on improved three-point estimation method and maximum entropy as distributed generators access to distribution network. Electr. Power Syst. Res. 2024, 230, 110197. [Google Scholar] [CrossRef]
- Aien, M.; Hajebrahimi, A.; Fotuhi-Firuzabad, M. A comprehensive review on uncertainty modeling techniques in power system studies. Renew. Sustain. Energy Rev. 2016, 57, 1077–1089. [Google Scholar] [CrossRef]
- Calderaro, V.; Lamberti, F.; Galdi, V.; Piccolo, A. Power flow problems with nested information: An approach based on fuzzy numbers and possibility theory. Electr. Power Syst. Res. 2018, 158, 275–283. [Google Scholar] [CrossRef]
- Mandal, S.; Maiti, J. Risk analysis using FMEA: Fuzzy similarity value and possibility theory based approach. Expert Syst. Appl. 2014, 41, 3527–3537. [Google Scholar] [CrossRef]
- Murthy, C.; Varma, K.A.; Roy, D.S.; Mohanta, D.K. Mohanta Reliability Evaluation of Phasor Measurement Unit Using Type-2 Fuzzy Set Theory. IEEE Syst. J. 2014, 8, 1302–1309. [Google Scholar] [CrossRef]
- Woo, T.H.; Jang, K.B.; Baek, C.H.; Choi, J.D. Analysis of climate change mitigations by nuclear energy using nonlinear fuzzy set theory. Nucl. Eng. Technol. 2022, 54, 4095–4101. [Google Scholar] [CrossRef]
- Wang, J.; Xu, L.; Cai, J.; Fu, Y.; Bian, X. Offshore wind turbine selection with a novel multi-criteria decision-making method based on Dempster-Shafer evidence theory. Sustain. Energy Technol. Assess. 2022, 51, 101951. [Google Scholar] [CrossRef]
- Tian, W.; de Wilde, P.; Li, Z.; Song, J.; Yin, B. Uncertainty and sensitivity analysis of energy assessment for office buildings based on Dempster-Shafer theory. Energy Convers. Manag. 2018, 174, 705–718. [Google Scholar] [CrossRef]
- Sentz, K.; Ferson, S. Combination of Evidence in Dempster-Shafer Theory; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Wu, Y.; Chen, M.; Shen, K.; Wang, J. Z-number extension of TODIM-CPT method combined with K-means clustering for electric vehicle battery swapping station site selection. J. Energy Storage 2024, 85, 110900. [Google Scholar] [CrossRef]
- Zhang, X.; Goh, M.; Bai, S.; Wang, Q. Green, resilient, and inclusive supplier selection using enhanced BWM-TOPSIS with scenario-varying Z-numbers and reversed PageRank. Inf. Sci. 2024, 674, 120728. [Google Scholar] [CrossRef]
- Zadeh, L.A. A Note on Z-numbers. Inf. Sci. 2011, 181, 2923–2932. [Google Scholar] [CrossRef]
- Zeng, B.; Wei, X.; Zhao, D.; Singh, C.; Zhang, J. Hybrid probabilistic-possibilistic approach for capacity credit evaluation of demand response considering both exogenous and endogenous uncertainties. Appl. Energy 2018, 229, 186–200. [Google Scholar] [CrossRef]
- Khaloie, H.; Abdollahi, A.; Rashidinejad, M.; Siano, P. Risk-based probabilistic-possibilistic self-scheduling considering high-impact low-probability events uncertainty. Int. J. Electr. Power Energy Syst. 2019, 110, 598–612. [Google Scholar] [CrossRef]
- Roukerd, S.P.; Abdollahi, A.; Rashidinejad, M. Probabilistic-possibilistic flexibility-based unit commitment with uncertain negawatt demand response resources considering Z-number method. Int. J. Electr. Power Energy Syst. 2019, 113, 71–89. [Google Scholar] [CrossRef]
- Maulik, A. A hybrid probabilistic information gap decision theory based energy management of an active distribution network. Sustain. Energy Technol. Assess. 2022, 53, 102756. [Google Scholar] [CrossRef]
- Yarmohammadi, H.; Abdi, H. Optimal operation of multi-carrier energy systems considering demand response: A hybrid scenario-based/IGDT uncertainty method. Electr. Power Syst. Res. 2024, 235, 110877. [Google Scholar] [CrossRef]
- Li, J.; Yu, Z.; Mu, G.; Li, B.; Zhou, J.; Yan, G.; Zhu, X.; Li, C. An assessment methodology for the flexibility capacity of new power system based on two-stage robust optimization. Appl. Energy 2024, 376, 124291. [Google Scholar] [CrossRef]
- Zhang, C.; Li, Y.; Zhang, H.; Wang, Y.; Huang, Y.; Xu, J. Distributionally robust resilience optimization of post-disaster power system considering multiple uncertainties. Reliab. Eng. Syst. Saf. 2024, 251, 110367. [Google Scholar] [CrossRef]
- Wang, H.; Yi, Z.; Xu, Y.; Cai, Q.; Li, Z.; Wang, H.; Bai, X. Data-driven distributionally robust optimization approach for the coordinated dispatching of the power system considering the correlation of wind power. Electr. Power Syst. Res. 2024, 230, 110224. [Google Scholar] [CrossRef]
- Dai, J.; Ding, C.; Yan, C.; Tang, Y.; Zhou, X.; Xue, F. Robust optimization method of power system multi resource reserve allocation considering wind power frequency regulation potential. Int. J. Electr. Power Energy Syst. 2024, 155, 109599. [Google Scholar] [CrossRef]
- Li, Z.; Liu, M.; Xie, M.; Zhu, J. Robust optimization approach with acceleration strategies to aggregate an active distribution system as a virtual power plant. Int. J. Electr. Power Energy Syst. 2022, 142, 108316. [Google Scholar] [CrossRef]
- Kang, J.; Wu, Z.; Ng, T.S.; Su, B. A stochastic-robust optimization model for inter-regional power system planning. Eur. J. Oper. Res. 2023, 310, 1234–1248. [Google Scholar] [CrossRef]
- Ben-Tal, A.; El Ghaoui, L.; Nemirovski, A. Robust Optimization; Princeton University Press: Princeton, NJ, USA, 2009. [Google Scholar]
- Sasaki, Y.; Takahashi, N.; Zoka, Y.; Yorino, N.; Bedawy, A.; Krifa, C.; Sekizkai, S. Day-ahead Generation Scheduling with Information Gap Decision Models. IFAC-Pap. 2024, 58, 152–157. [Google Scholar] [CrossRef]
- Seyyedeh-Barhagh, S.; Abapour, M.; Mohammadi-Ivatloo, B.; Shafie-khah, M. Risk-based Peer-to-peer Energy Trading with Info-Gap Approach in the Presence of Electric Vehicles. Sustain. Cities Soc. 2023, 99, 104948. [Google Scholar] [CrossRef]
- Fathi, R.; Tousi, B.; Galvani, S. A new approach for optimal allocation of photovoltaic and wind clean energy resources in distribution networks with reconfiguration considering uncertainty based on info-gap decision theory with risk aversion strategy. J. Clean. Prod. 2021, 295, 125984. [Google Scholar] [CrossRef]
- Ben-Haim, Y. Feedback for energy conservation: An info-gap approach. Energy 2021, 223, 119957. [Google Scholar] [CrossRef]
- Nojavan, S.; Zare, K.; Feyzi, M.R. Optimal bidding strategy of generation station in power market using information gap decision theory (IGDT). Electr. Power Syst. Res. 2013, 96, 56–63. [Google Scholar] [CrossRef]
- Huang, D. Network reliability of a stochastic flow network by wrapping linear programming models into a Monte-Carlo simulation. Reliab. Eng. Syst. Saf. 2024, 252, 110427. [Google Scholar] [CrossRef]
- Karki, R.; Hu, P.; Billinton, R. Reliability evaluation considering wind and hydro power coordination. IEEE Trans. Power Syst. 2009, 25, 685–693. [Google Scholar] [CrossRef]
- Wu, L.; Shahidehpour, M.; Fu, Y. Security-constrained generation and transmission outage scheduling with uncertainties. IEEE Trans. Power Syst. 2010, 25, 1674–1685. [Google Scholar]
- Ge, H.; Asgarpoor, S. Reliability evaluation of equipment and substations with fuzzy Markov processes. IEEE Trans. Power Syst. 2010, 25, 1319–1328. [Google Scholar]
- Papavasiliou, A.; Oren, S.S.; O’Neill, R.P. Reserve requirements for wind power integration: A scenario-based stochastic programming framework. IEEE Trans. Power Syst. 2011, 26, 2197–2206. [Google Scholar] [CrossRef]
- Odat, A.A.; Shawaqfah, M.; Al-Momani, F.; Shboul, B. Data of simulation model for photovoltaic system’s maximum power point tracking using sequential Monte Carlo algorithm. Data Brief 2024, 52, 109853. [Google Scholar] [CrossRef] [PubMed]
- Venkatesh, B.; Yu, P.; Gooi, H.B.; Choling, D. Fuzzy MILP unit commitment incorporating wind generators. IEEE Trans. Power Syst. 2008, 23, 1738–1746. [Google Scholar] [CrossRef]
- Zhang, X.; Pirouzi, A. Flexible energy management of storage-based renewable energy hubs in the electricity and heating networks according to point estimate method. Energy Rep. 2024, 11, 1627–1641. [Google Scholar] [CrossRef]
- Liu, Z.; Wen, F.; Ledwich, G. Optimal siting and sizing of distributed generators in distribution systems considering uncertainties. IEEE Trans. Power Del. 2011, 26, 2541–2551. [Google Scholar] [CrossRef]
- Lojowska, A.; Kurowicka, D.; Papaefthymiou, G.; Van Der Sluis, L. Stochastic modeling of power demand due to EVs using copula. IEEE Trans. Power Syst. 2012, 27, 1960–1968. [Google Scholar] [CrossRef]
- Pantos, M. Exploitation of electric-drive vehicles in electricity markets. IEEE Trans. Power Syst. 2011, 27, 682–694. [Google Scholar] [CrossRef]
- El-Khattam, W.; Hegazy, Y.G.; Salama, M. Investigating distributed generation systems performance using Monte Carlo simulation. IEEE Trans. Power Syst. 2006, 21, 524–532. [Google Scholar] [CrossRef]
- Su, C. Stochastic evaluation of voltages in distribution networks with distributed generation using detailed distribution operation models. IEEE Trans. Power Syst. 2009, 25, 786–795. [Google Scholar] [CrossRef]
- Zhang, H.; Li, P. Probabilistic analysis for optimal power flow under uncertainty. IET Gener. Transm. Distrib. 2010, 4, 553–561. [Google Scholar] [CrossRef]
- Li, X.; Li, Y.; Zhang, S. Analysis of probabilistic optimal power flow taking account of the variation of load power. IEEE Trans. Power Syst. 2008, 23, 992–999. [Google Scholar]
- Kazerooni, A.K.; Mutale, J. Transmission network planning under security and environmental constraints. IEEE Trans. Power Syst. 2010, 25, 1169–1178. [Google Scholar] [CrossRef]
- Yamin, H.Y. Fuzzy self-scheduling for GenCos. IEEE Trans. Power Syst. 2005, 20, 503–505. [Google Scholar] [CrossRef]
- Attaviriyanupap, P.; Kita, H.; Tanaka, E.; Hasegawa, J. A fuzzy-optimization approach to dynamic economic dispatch considering uncertainties. IEEE Trans. Power Syst. 2004, 19, 1299–1307. [Google Scholar] [CrossRef]
- Singh, R.; Pal, B.C.; Vinter, R.B. Measurement placement in distribution system state estimation. IEEE Trans. Power Syst. 2009, 24, 668–675. [Google Scholar] [CrossRef]
- Saric, A.T.; Ciric, R.M. Integrated fuzzy state estimation and load flow analysis in distribution networks. IEEE Trans. Power Del. 2003, 18, 571–578. [Google Scholar] [CrossRef]
- Wang, Y.; Li, W.; Zhang, P.; Wang, B.; Lu, J. Reliability analysis of phasor measurement unit considering data uncertainty. IEEE Trans. Power Syst. 2012, 27, 1503–1510. [Google Scholar] [CrossRef]
- Caro, E.; Morales, J.M.; Conejo, A.J.; Minguez, R. Calculation of measurement correlations using point estimate. IEEE Trans. Power Del. 2010, 25, 2095–2103. [Google Scholar] [CrossRef]
- Perninge, M.; Lindskog, F.; Soder, L. Importance sampling of injected powers for electric power system security analysis. IEEE Trans. Power Syst. 2011, 27, 3–11. [Google Scholar] [CrossRef]
- Duenas, P.; Reneses, J.; Barquin, J. Dealing with multi-factor uncertainty in electricity markets by combining Monte Carlo simulation with spatial interpolation techniques. IET Gener. Transm. Distrib. 2011, 5, 323–331. [Google Scholar] [CrossRef]
- IEEE 24-Bus RTS. Available online: https://matpower.org/docs/ref/matpower5.0/case24_ieee_rts.html (accessed on 3 December 2024).
- Meteoblue. Weather History Download Milwaukee. Available online: https://www.meteoblue.com/en/weather/archive/export/milwaukee_united-states-of%20america_5263045 (accessed on 3 December 2024).








| Type | Probabilistic | Possibilistic | Hybrid | Analytical | RO | IGDT | ||
|---|---|---|---|---|---|---|---|---|
| Application | Monte Carlo | LHS | ||||||
| Reliability evaluation | [63,64,65] | [38,44,66] | [67] | [60] | ||||
| Renewable energy (operation and planning) | [68] | [29] | [40,69] | [50] | [32,70] | [53,54,56] | [58,59] | |
| EV | [71,72] | [43] | [73] | [59] | ||||
| Energy storage | [25] | [30] | ||||||
| DG units | [74] | [34,75] | ||||||
| Load flow/optimal power flow | [76] | [36] | [77] | |||||
| Generation/ transmission/ distribution planning, operation, and control | [24,78] | [27] | [37,79] | [46,47,48,49,80] | [51,52,55] | [58,61] | ||
| State estimation | [81] | [82,83] | [33,84] | |||||
| Electricity market | [85,86] | [79] | [50] | [62] | ||||
| Technique | Monte Carlo and K-Means | MCMC | IGDT | Robust | |||||
|---|---|---|---|---|---|---|---|---|---|
| Index | |||||||||
| Uncertainty duration [month] | 1 | 3 | 1 | 3 | 1 | 3 | 1 | 3 | |
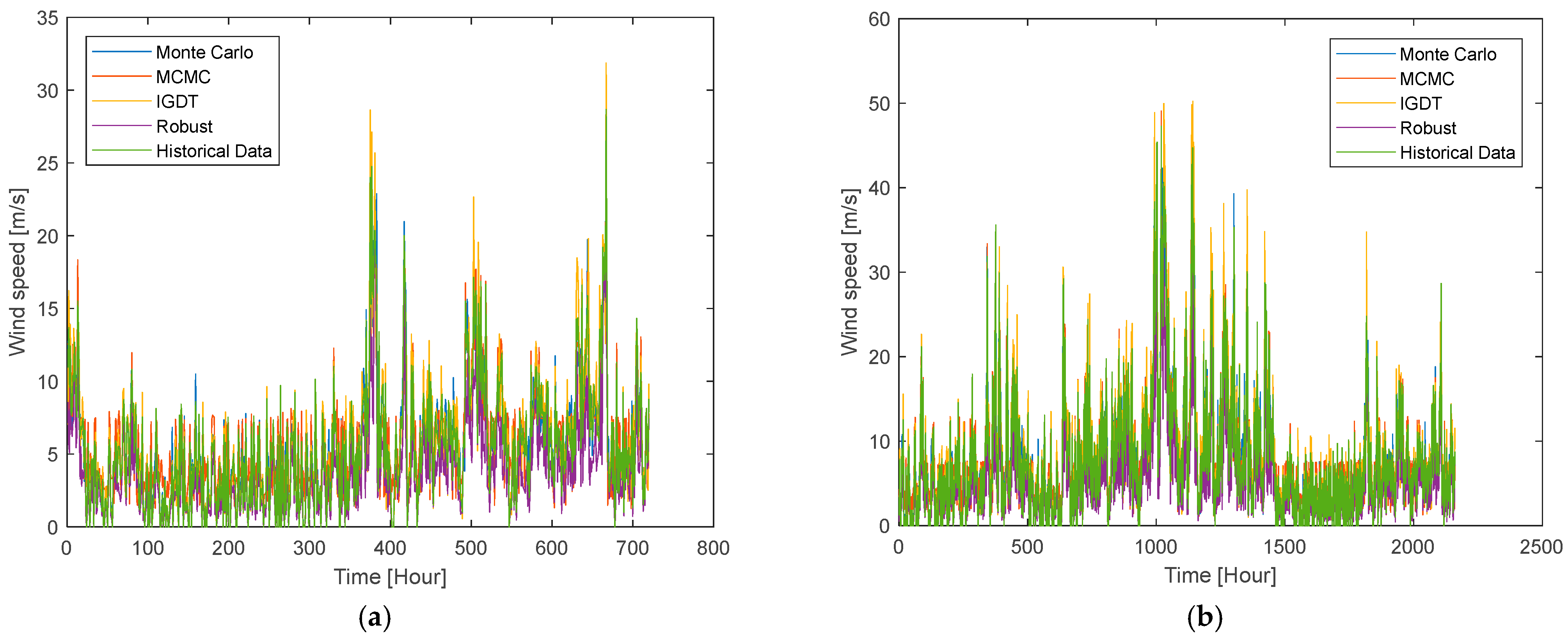
| Correlation coefficient between the wind speeds modeled by the uncertainty modeling technique and real historical data of wind speeds | 0.9682 | 0.9748 | 0.9191 | 0.9711 | 0.9508 | 0.9578 | 0.9272 | 0.9381 | |
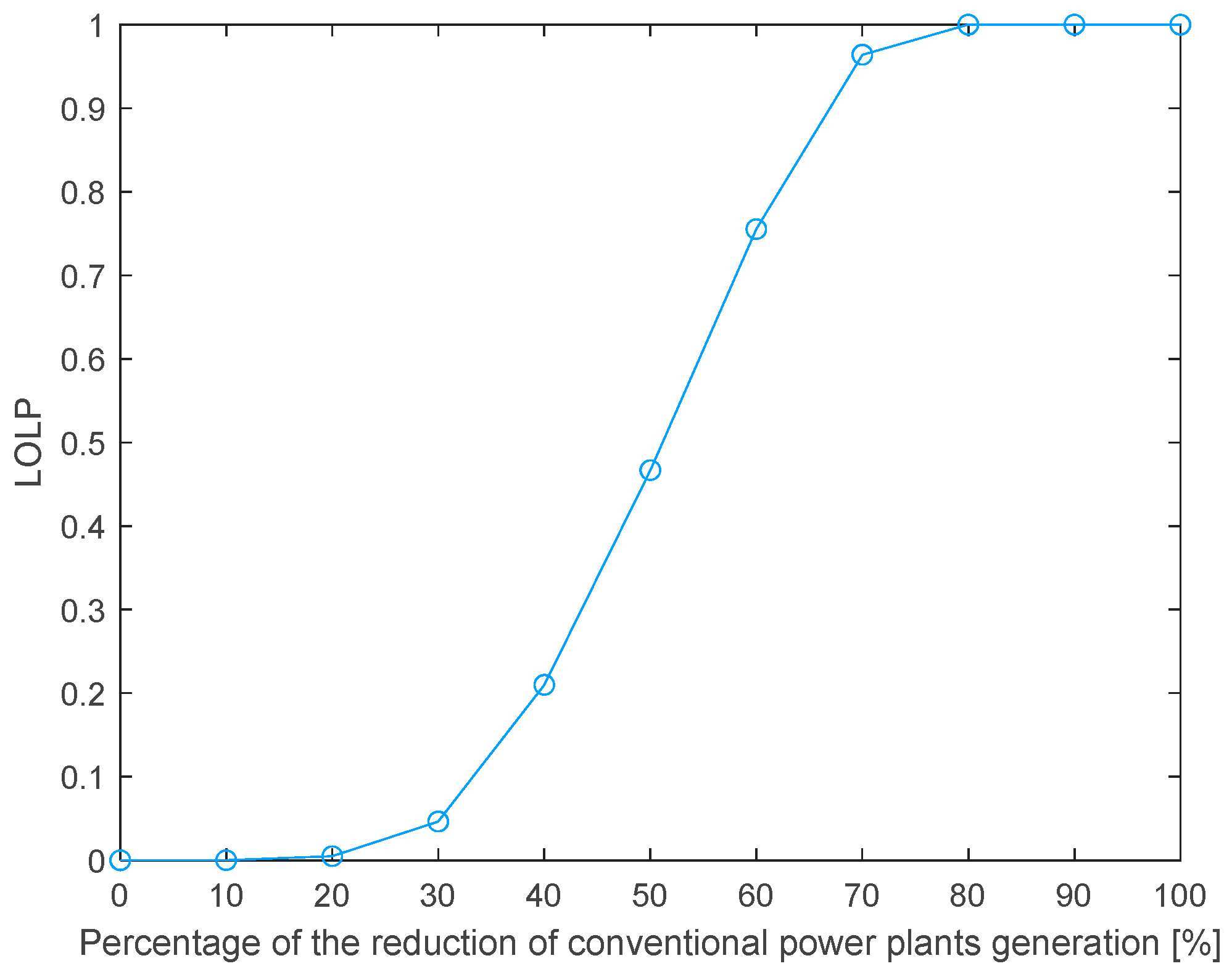
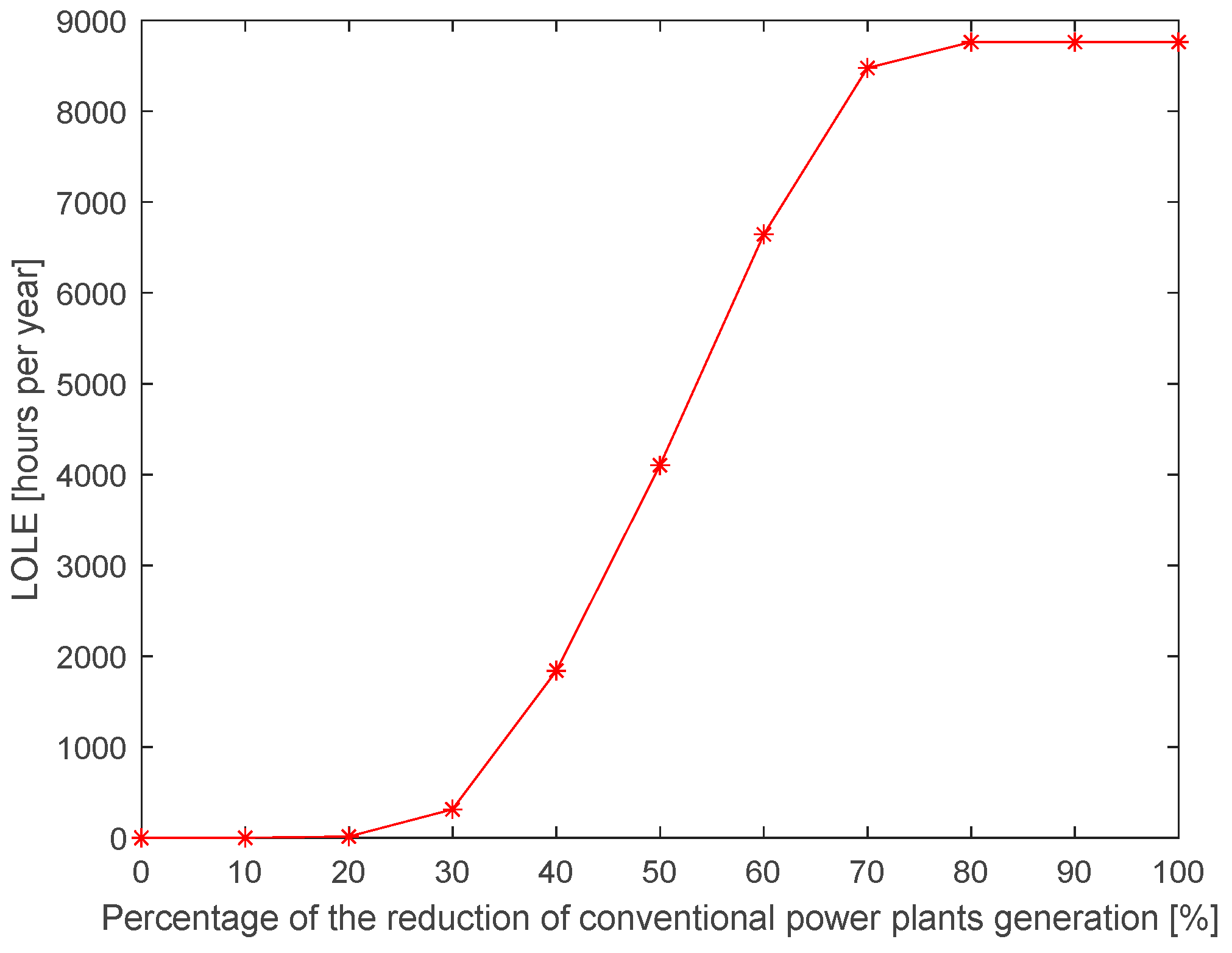
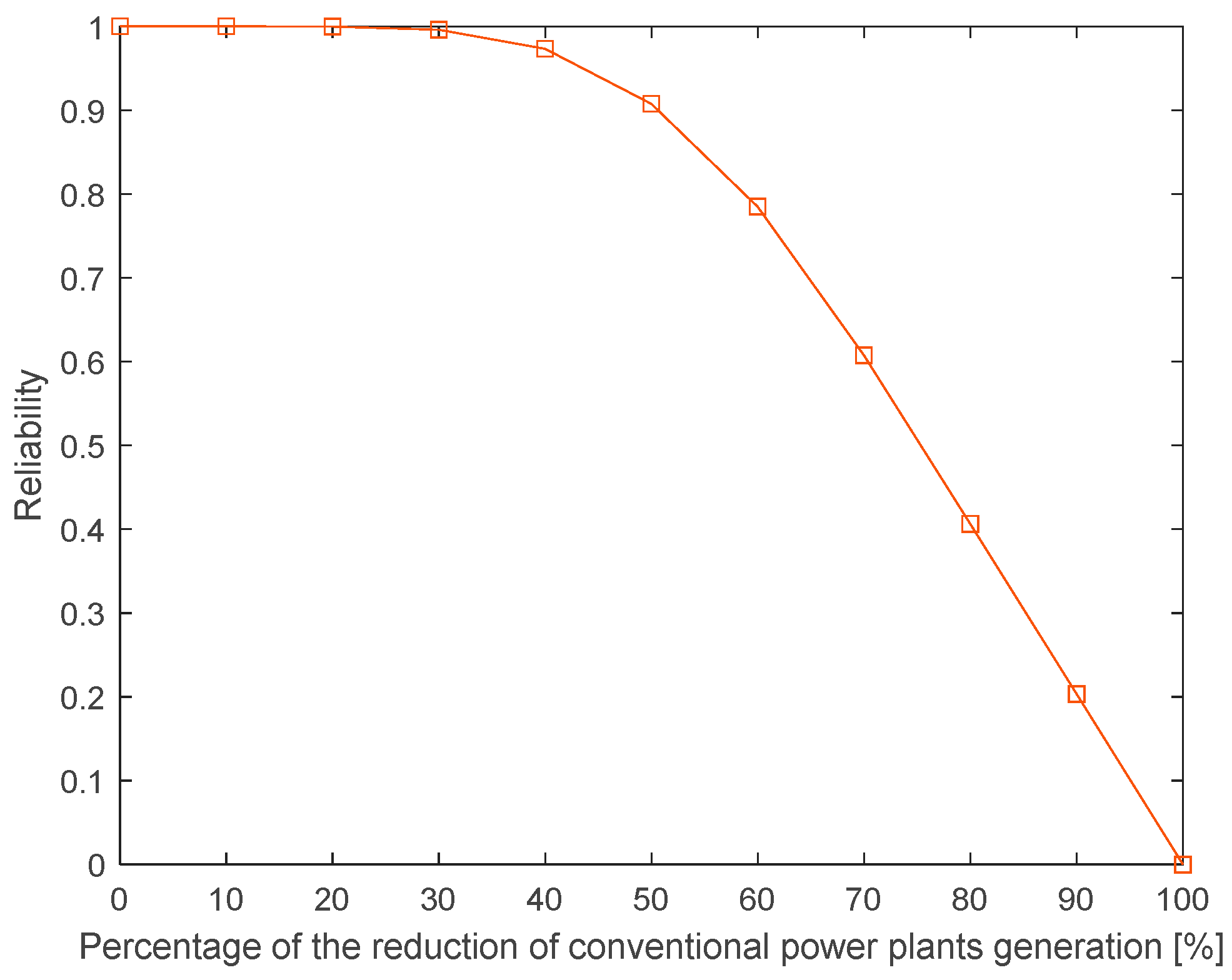
| Index | 20% Reduction in the Generation of CPPs | 30% Reduction in the Generation of CPPs |
|---|---|---|
| LOLE [hours per year] | 14.77 | 314.23 |
| LOLP | 0.00502 | 0.04646 |
| EENS [MWh] | 13.86 | 2423.14 |
| EENS cost [USD] | 4.85 × 104 | 8.48 × 106 |
| Reliability | 0.99969 | 0.99599 |
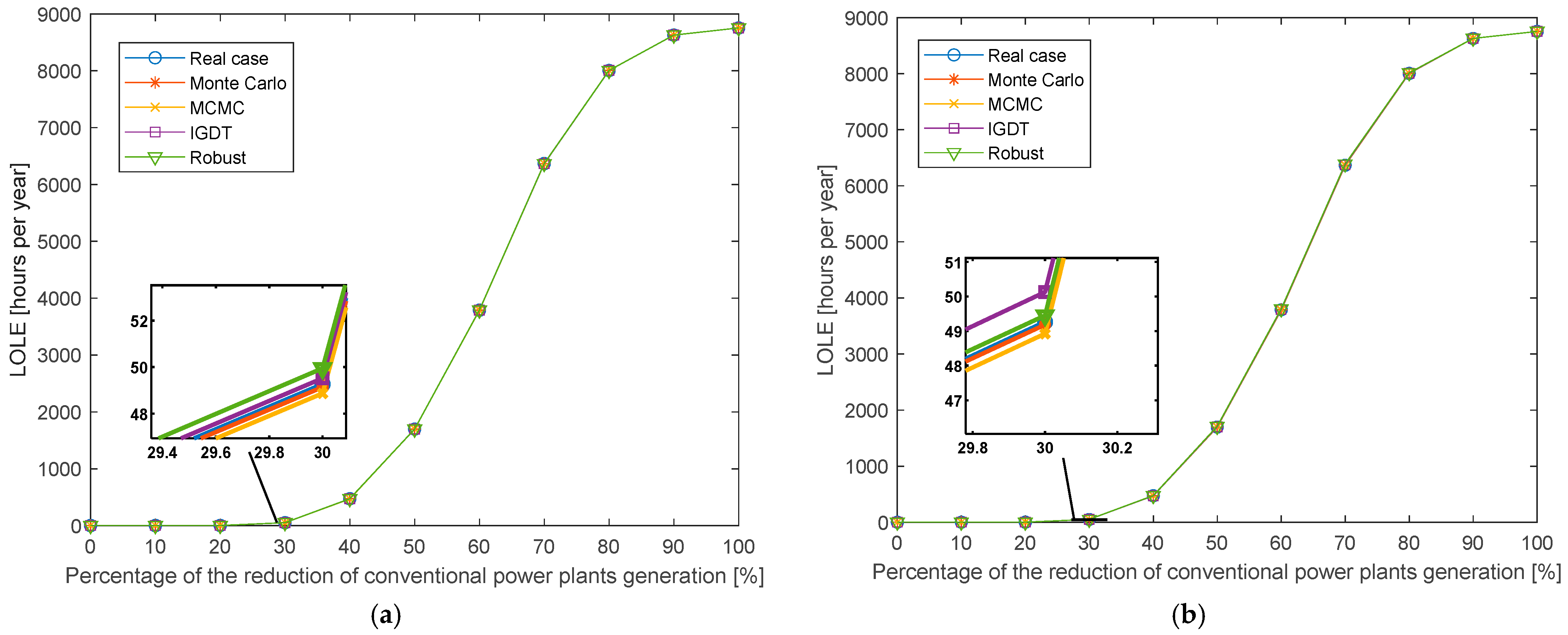
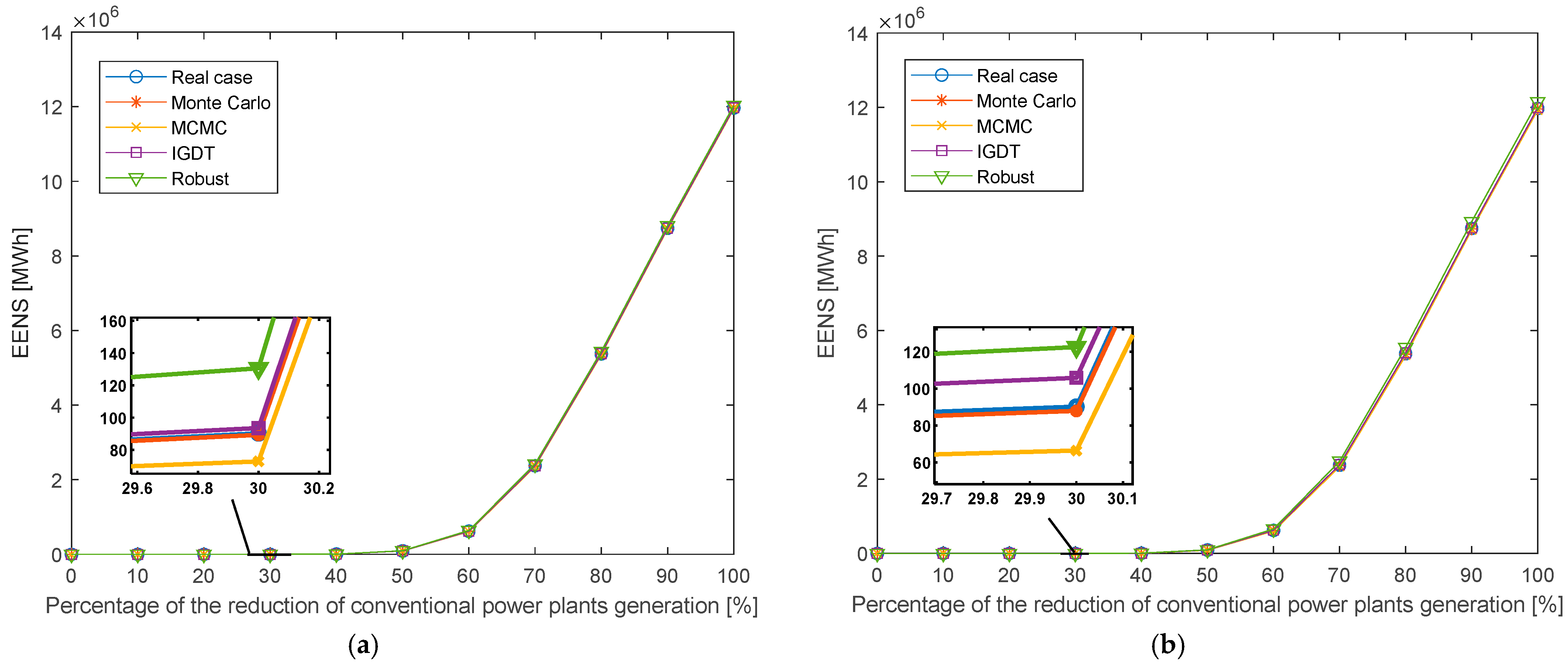
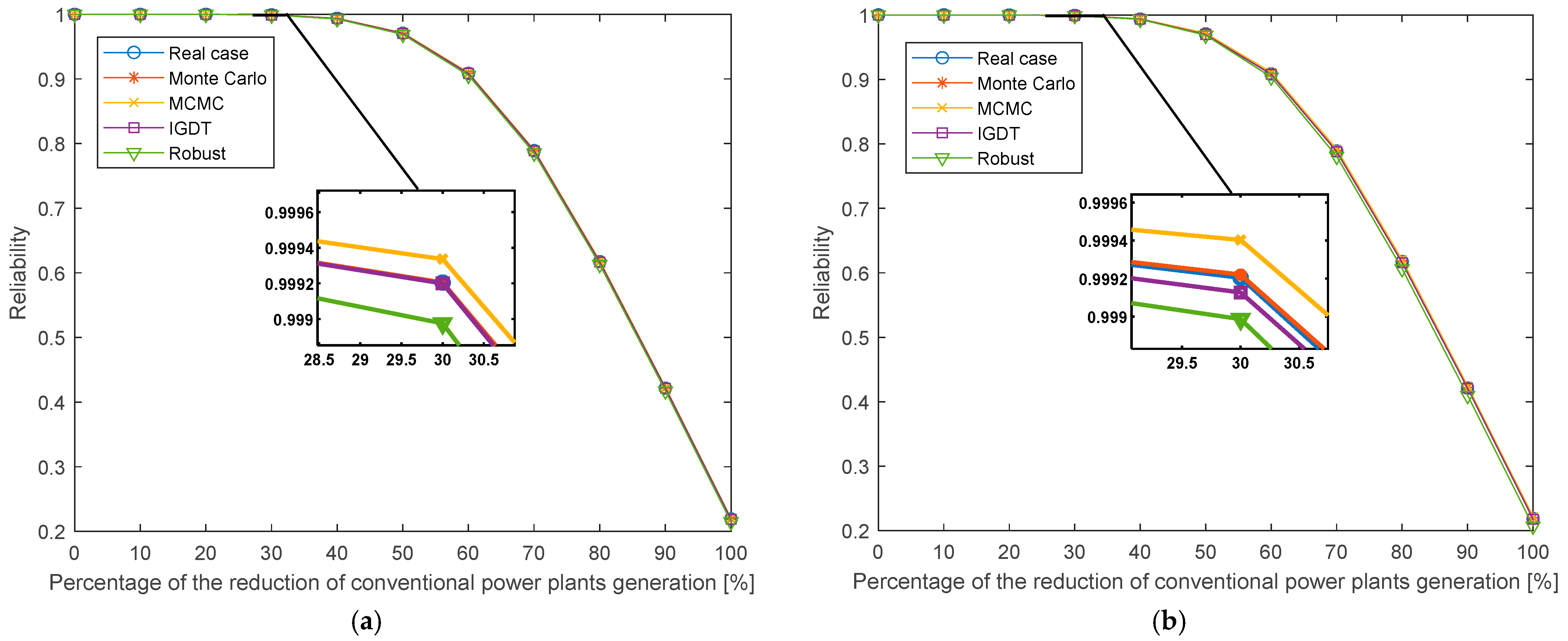
| Case | 20% Reduction in the Generation of CPPs Replaced by 1000 MW (Rated Power) Wind Farm | 30% Reduction in the Generation of CPPs Replaced by 1000 MW (Rated Power) Wind Farm | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Index | Real Case (Without Uncertainty) | Monte Carlo and K-Means | MCMC | IGDT | Robust | Real Case (Without Uncertainty) | Monte Carlo and K-Means | MCMC | IGDT | Robust | |
| LOLE [hours per year] | 0.70 | 0.70 | 0.48 | 0.67 | 0.77 | 49.26 | 49.13 | 48.86 | 49.52 | 49.95 | |
| LOLP | 0.00114 | 0.00114 | 0.00057 | 0.00102 | 0.00136 | 0.01027 | 0.00970 | 0.00913 | 0.01084 | 0.01221 | |
| EENS [MWh] | 0.77 | 0.83 | 0.02 | 0.75 | 1.35 | 90.21 | 89.25 | 72.85 | 93.47 | 130.50 | |
| EENS cost [USD] | 2.69 × 103 | 2.92 × 103 | 0.09 × 103 | 2.64 × 103 | 4.75 × 103 | 3.15 × 105 | 3.12 × 105 | 2.54 × 105 | 3.27 × 105 | 4.56 × 105 | |
| Reliability | 0.99993 | 0.99992 | 0.99999 | 0.99993 | 0.99990 | 0.99920 | 0.99920 | 0.99933 | 0.99919 | 0.99897 | |
| Case | 20% Reduction in the Generation of CPPs Replaced by 1000 MW (Rated Power) Wind Farm | 30% Reduction in the Generation of CPPs Replaced by 1000 MW (Rated Power) Wind Farm | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Index | Real case (Without Uncertainty) | Monte Carlo and K-Means | MCMC | IGDT | Robust | Real case (Without Uncertainty) | Monte Carlo and K-Means | MCMC | IGDT | Robust | |
| LOLE [hours per year] | 0.70 | 0.70 | 0.29 | 0.81 | 0.84 | 49.26 | 49.18 | 48.92 | 50.13 | 49.45 | |
| LOLP | 0.00114 | 0.00114 | 0.00057 | 0.00125 | 0.00159 | 0.01027 | 0.00958 | 0.00890 | 0.01073 | 0.01152 | |
| EENS [MWh] | 0.77 | 0.85 | 0.07 | 0.94 | 1.59 | 90.21 | 87.90 | 66.38 | 105.88 | 122.57 | |
| EENS cost [USD] | 2.69 × 103 | 2.98× 103 | 0.26 × 103 | 3.30 × 103 | 5.57 × 103 | 3.15 × 105 | 3.07 × 105 | 2.32 × 105 | 3.70 × 105 | 4.29 × 105 | |
| Reliability | 0.99993 | 0.99992 | 0.99998 | 0.99992 | 0.99988 | 0.99920 | 0.99922 | 0.99940 | 0.99912 | 0.99898 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Afzali, P.; Hosseini, S.A.; Peyghami, S. A Comprehensive Review on Uncertainty and Risk Modeling Techniques and Their Applications in Power Systems. Appl. Sci. 2024, 14, 12042. https://doi.org/10.3390/app142412042
Afzali P, Hosseini SA, Peyghami S. A Comprehensive Review on Uncertainty and Risk Modeling Techniques and Their Applications in Power Systems. Applied Sciences. 2024; 14(24):12042. https://doi.org/10.3390/app142412042
Chicago/Turabian StyleAfzali, Peyman, Seyed Amir Hosseini, and Saeed Peyghami. 2024. "A Comprehensive Review on Uncertainty and Risk Modeling Techniques and Their Applications in Power Systems" Applied Sciences 14, no. 24: 12042. https://doi.org/10.3390/app142412042
APA StyleAfzali, P., Hosseini, S. A., & Peyghami, S. (2024). A Comprehensive Review on Uncertainty and Risk Modeling Techniques and Their Applications in Power Systems. Applied Sciences, 14(24), 12042. https://doi.org/10.3390/app142412042







