An Improved Cuckoo Search Algorithm under Bottleneck-Degree-Based Search Guidance for Large-Scale Inter-Cell Scheduling Optimization
Abstract
:1. Introduction
2. Inter-Cell Scheduling Model Based on TSCS-BD
2.1. Problem Description
- (1)
- All parts and machines are released at zero moment.
- (2)
- The processing route of a part consists of multiple operations that have sequence constraints.
- (3)
- For any operation, there is at most one machine in a cell that can process it.
- (4)
- Once an operation has started to be processed on a machine, it must not be interrupted until it is finished.
- (5)
- Operation of a job can be performed by only one machine at a time, and each machine can perform only one operation of any job at a time.
- (6)
- Exceptional parts are allowed to be transported to other cells and returned to the original manufacturing cell for subsequent processing.
- (7)
- Processing routes and processing time are known, and transportation time for parts in a cell is ignored.
- (8)
- Inter-cell transport capacity is adequate with no wait time.
2.2. Mathematical Model
2.2.1. Parameter Description
2.2.2. Optimization Objective and Constraints
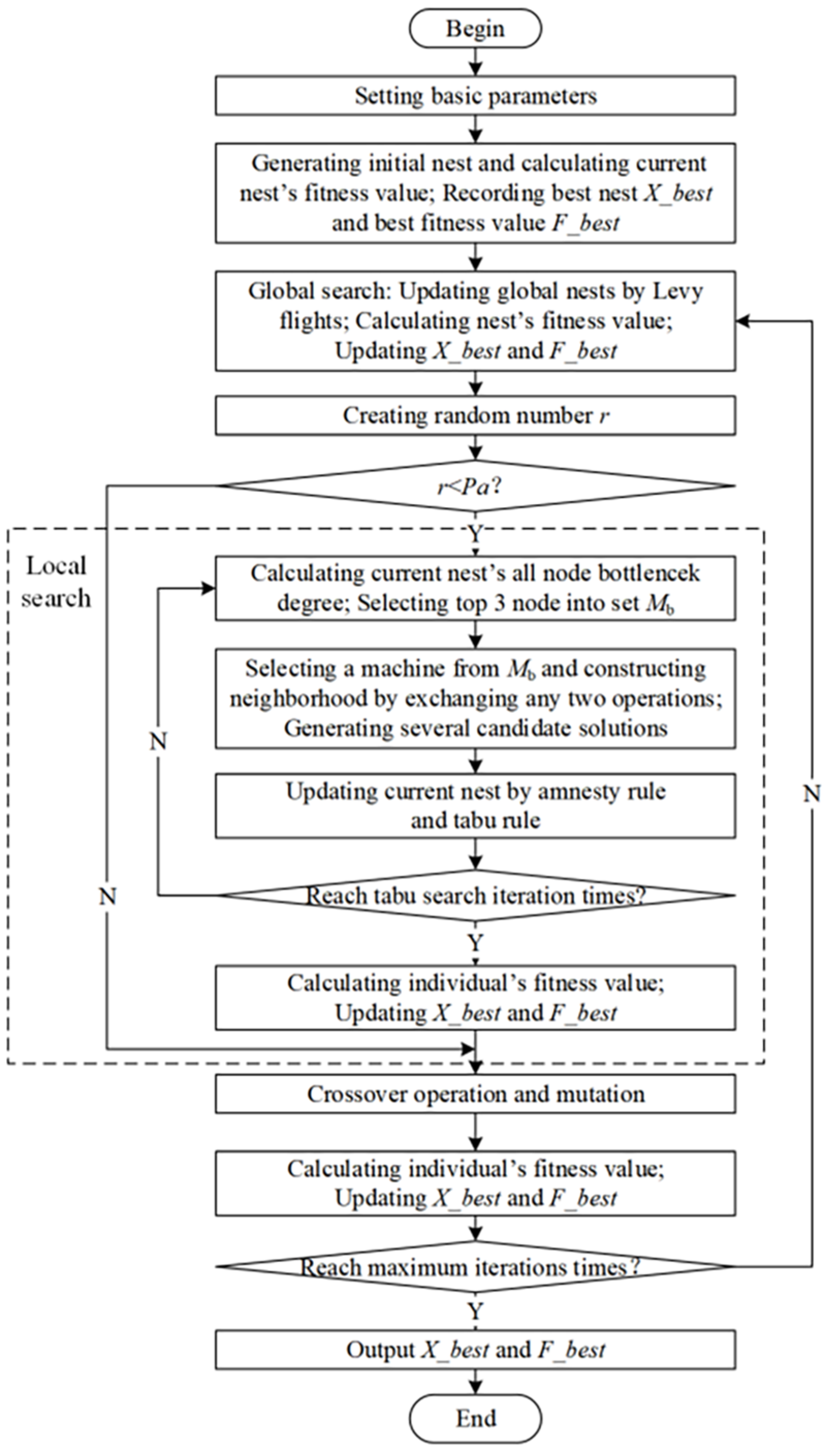
3. An Improved Cuckoo Search Algorithm under Bottleneck-Degree-Based Search Guidance, TSCS-BD
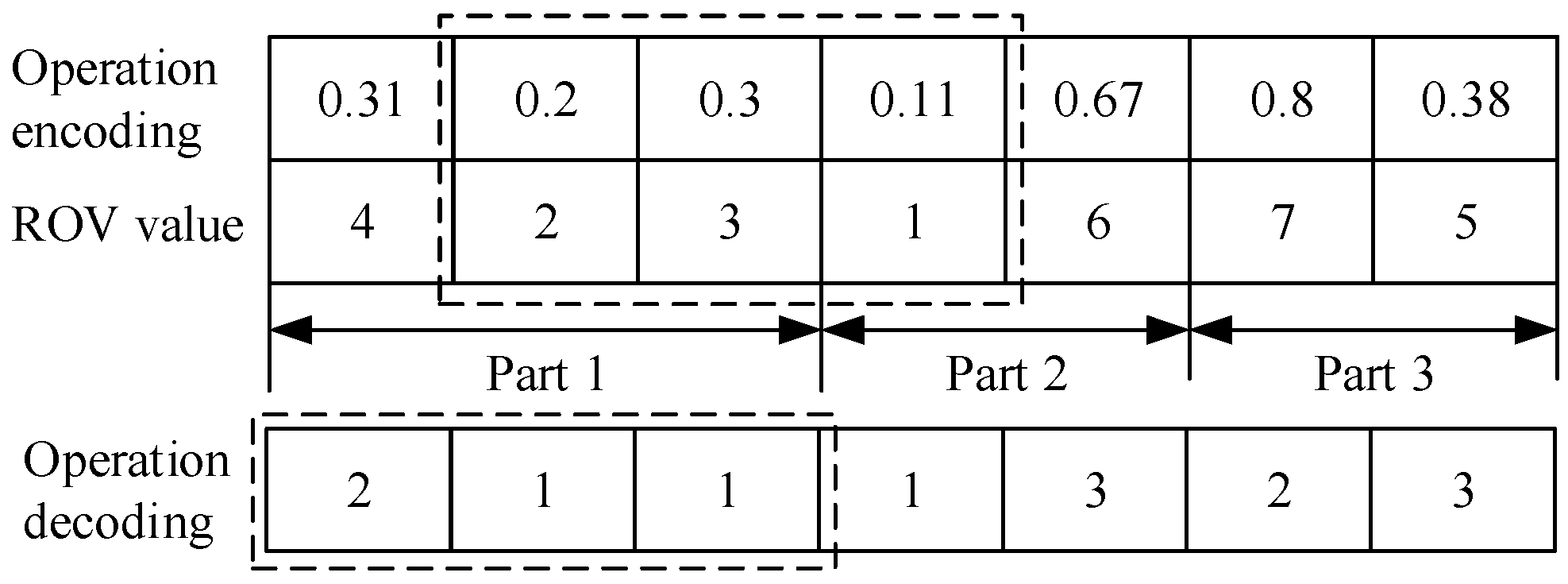
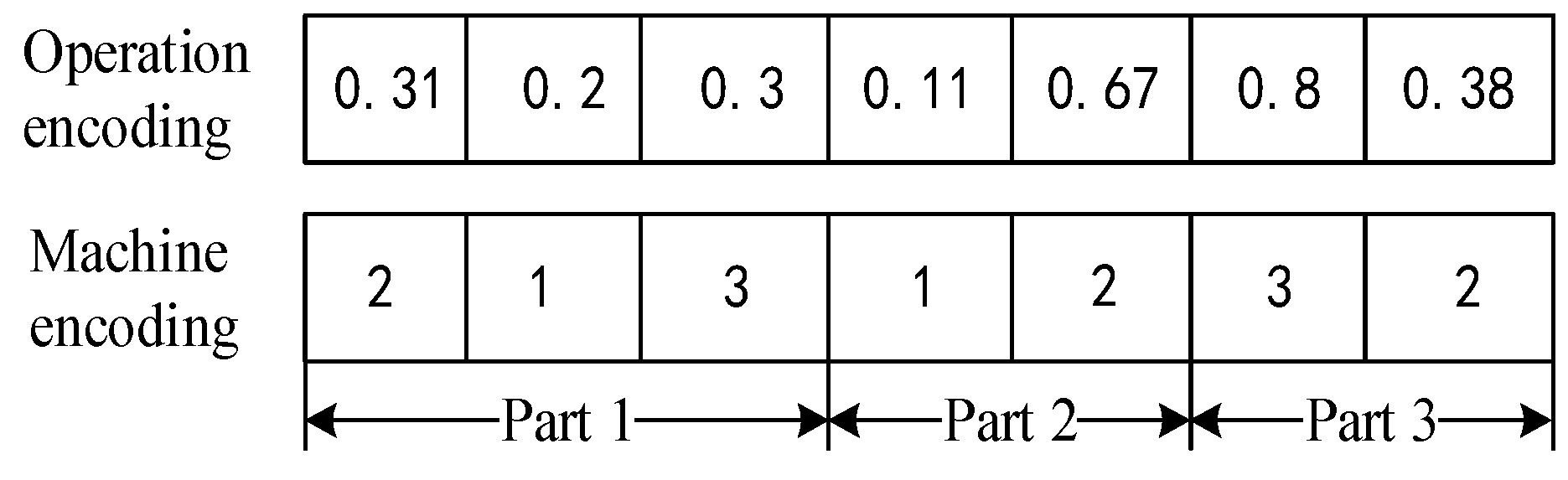
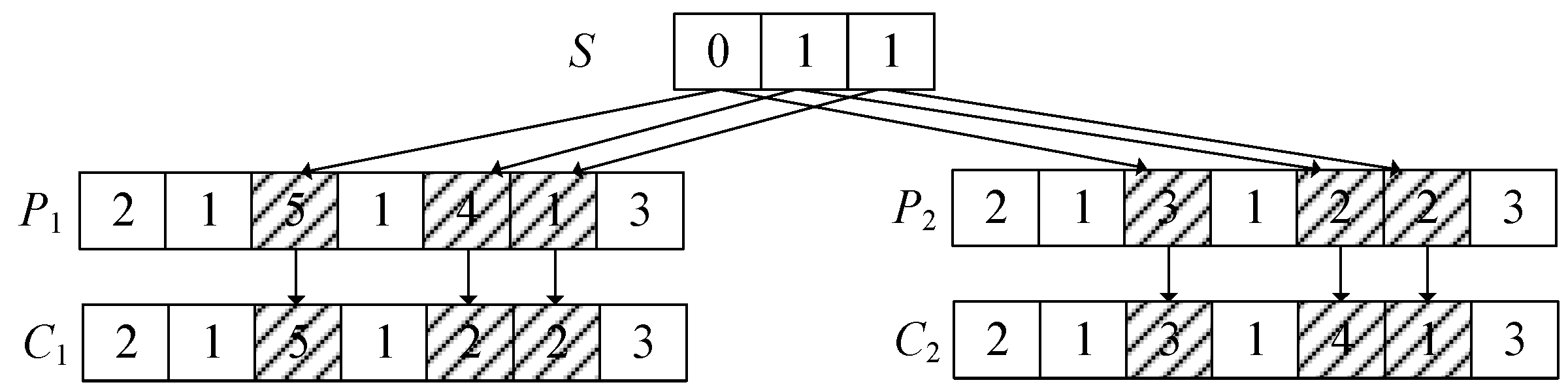
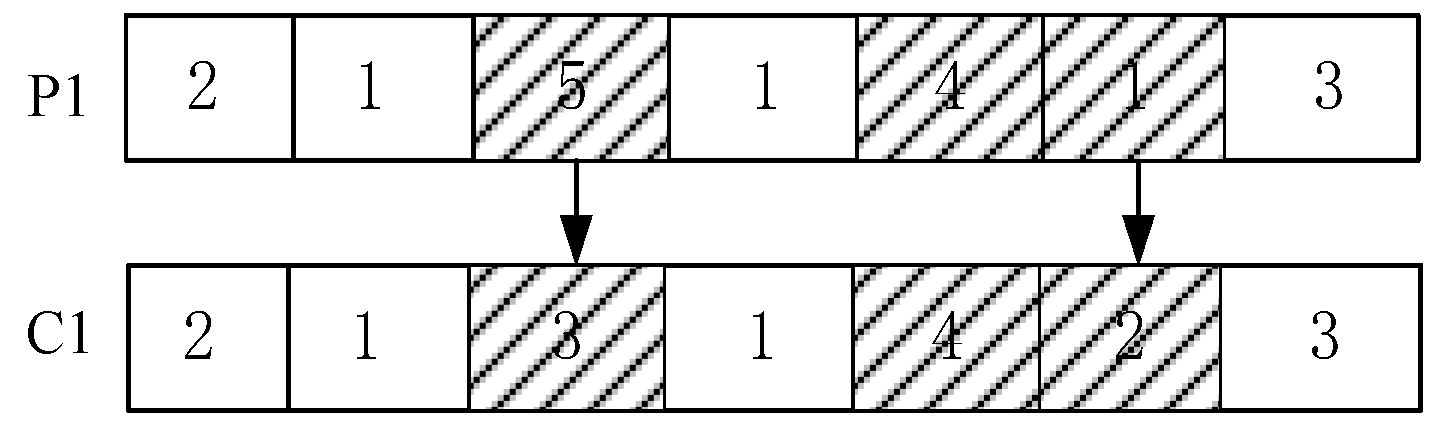
3.1. Coding and Decoding
3.2. Global Search
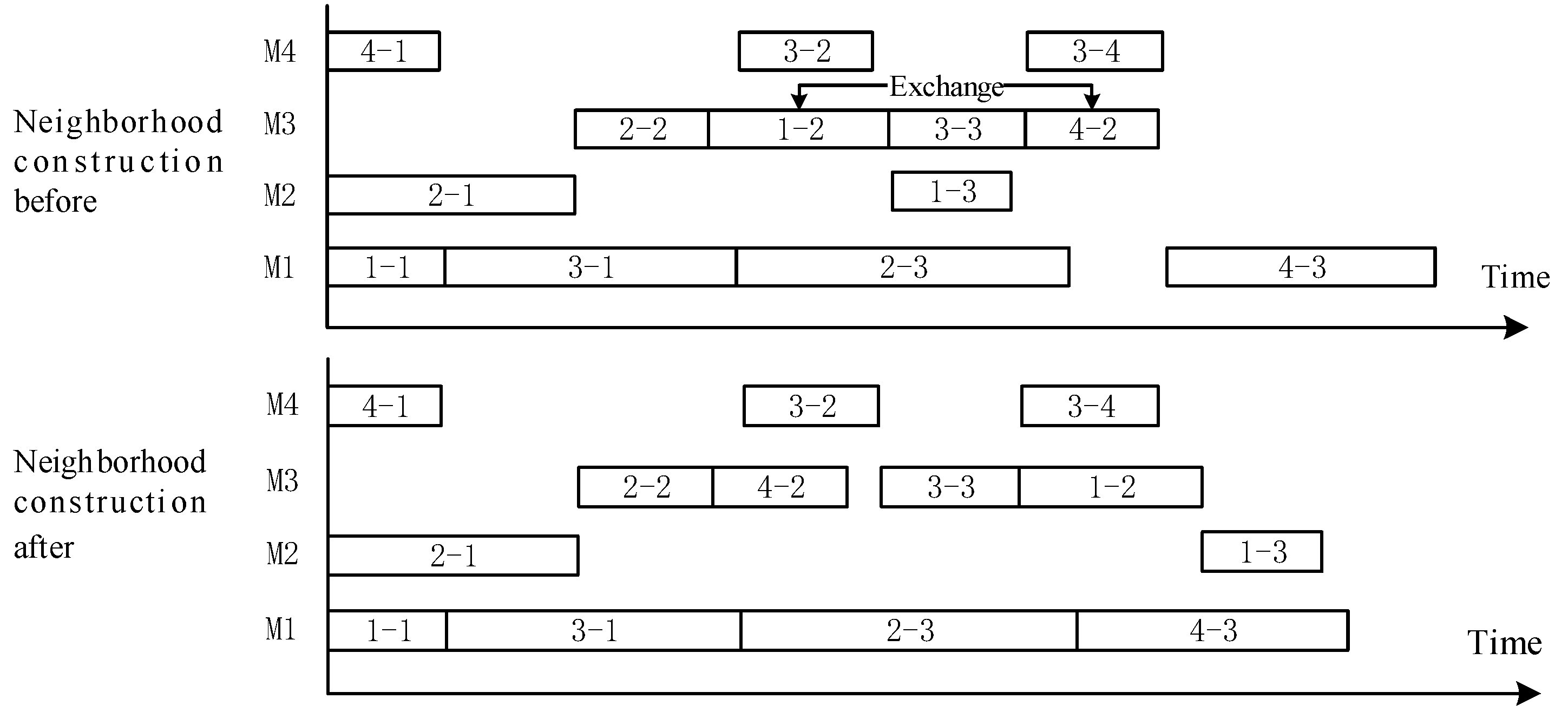
3.3. Tabu Search under Bottleneck-Degree Guidance
3.3.1. Tabu Search
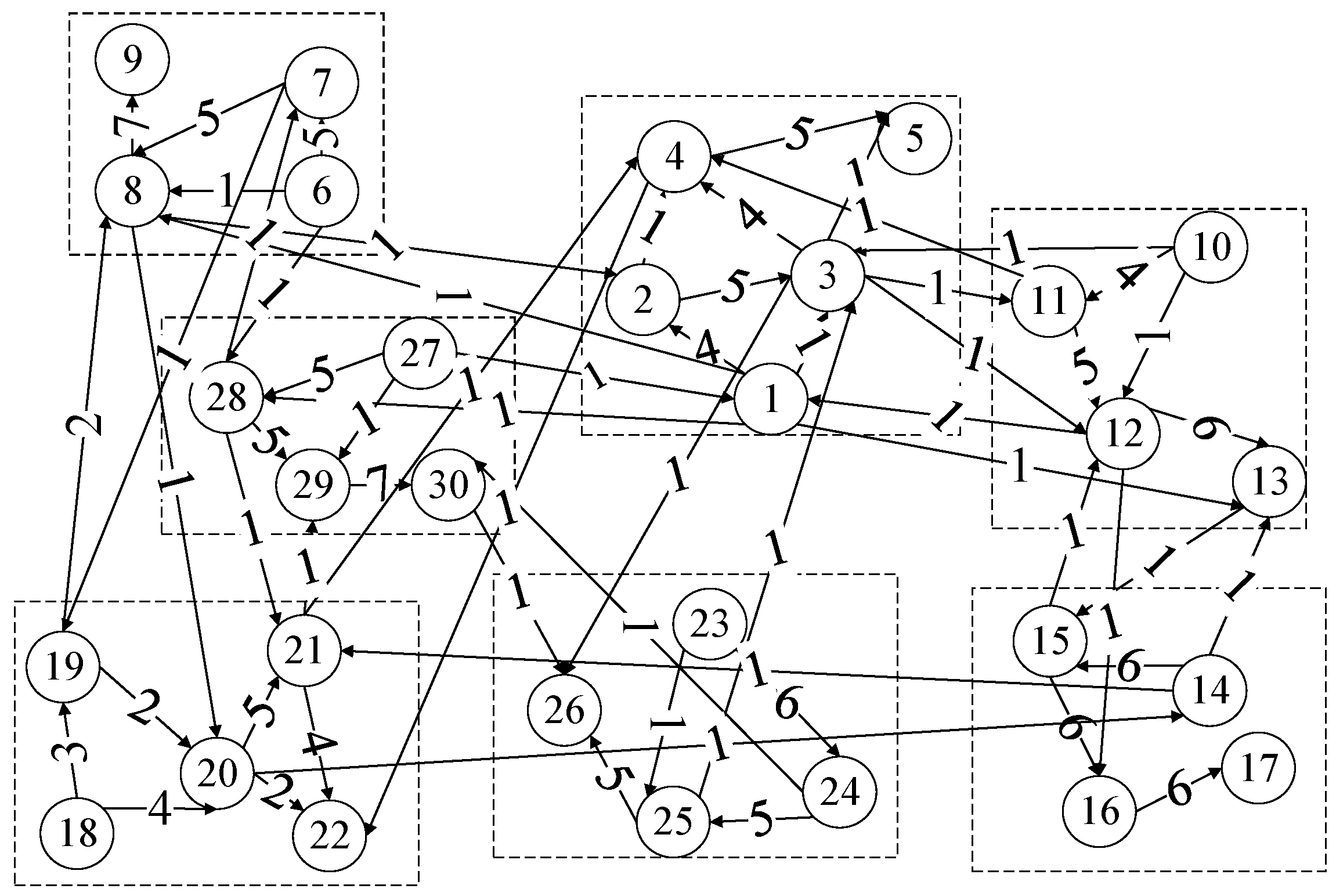
3.3.2. Complex Network Model and Bottleneck Degree
- (1)
- Nodes are the basic elements of the network model, which denote the machines.
- (2)
- Edges are the connections between nodes, which denote the flow of parts among machines.
- (3)
- Edge direction denotes the sequence of operations.
- (4)
- Weights denote the numbers of parts flowing between two machines.
3.3.3. Bottleneck-Degree Guidance for Tabu Search Neighborhood Structure
- (1)
- Selecting an individual to calculate the bottleneck degree with a probability;
- (2)
- Sorting each machine according to the bottleneck degree, with the first three machines with the highest bottleneck degree regarded as bottleneck machines in the current solution;
- (3)
- Randomly selecting one machine from , and constructing the corresponding candidate solution by exchanging the position of any two operations processed on the machine with constraints;
- (4)
- Repeating step (3) until enough candidate solutions are generated.
3.4. Crossover and Mutation
4. Experiments and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Manuel, S.; Sophie, N.P. Solving large scale industrial production scheduling problems with complex constraints: An overview of the state-of-the-art. Procedia Comput. Sci. 2023, 217, 1028–1037. [Google Scholar]
- Mahdavi, S.; Shiri, M.E.; Rahnamayan, S. Metaheuristics in large-scale global continues optimization: A survey. Inf. Sci. 2015, 295, 407–428. [Google Scholar] [CrossRef]
- Feng, Y.; Li, G.; Suresh, P.S. A three-layer chromosome genetic algorithm for multi-cell scheduling with flexible routes and machine sharing. Int. J. Prod. Econ. 2018, 196, 269–283. [Google Scholar] [CrossRef]
- Zhang, R.; Wu, C. A divide-and-conquer strategy with particle swarm optimization for the job shop schedule problem. Eng. Optim. 2010, 42, 641–670. [Google Scholar] [CrossRef]
- Wu, D.; Ierapetritou, M.G. Decomposition approaches for the efficient solution of short-term schedule problems. Comput. Chem. Eng. 2003, 27, 1261–1276. [Google Scholar] [CrossRef]
- El-Kholany, M.M.S.; Gebser, M.; Schekotihin, K. Problem Decomposition and Multi-shot ASP Solving for Job-shop Scheduling. Theory Pract. Log. Program. 2022, 22, 623–639. [Google Scholar] [CrossRef]
- Chu, C.; Portmann, M.C.; Proth, J.M. A splitting-up approach to simplify job-shop schedule problems. Int. J. Prod. Res. 1992, 30, 859–870. [Google Scholar] [CrossRef]
- Zuo, Y.; Gu, H.; Xi, Y. Study on constraint scheduling algorithm for job shop problems with multiple constraint machines. Int. J. Prod. Res. 2008, 46, 4785–4801. [Google Scholar] [CrossRef]
- Sannomiya, N.; Lima, H. Genetic algorithm approach to an optimal scheduling problem for a large-scale complex manufacturing system. In Proceedings of the IEEE International Conference on Systems, Man, and Cybernetics, Tokyo, Japan, 12–15 October 1999; Volume 3, pp. 622–627. [Google Scholar]
- Roslöf, J.; Harjunkoski, I. A short-term scheduling problem in the paper-converting industry. Comput. Chem. Eng. 1999, 23, 871–874. [Google Scholar] [CrossRef]
- Roslöf, J.; Harjunkoski, I. Solving a large-scale industrial scheduling problem using MILP combined with a heuristic procedure. Eur. J. Oper. Res. 2002, 138, 29–42. [Google Scholar] [CrossRef]
- Yang, F.; Gao, K.; Simon, I.W. Decomposition methods for manufacturing system scheduling: A survey. IEEE/CAA J. Autom. Sin. 2018, 5, 389–400. [Google Scholar] [CrossRef]
- Yuan, Y.; Xu, H. An integrated search heuristic for large-scale flexible job shop scheduling problems. Comput. Oper. Res. 2013, 40, 2864–2877. [Google Scholar] [CrossRef]
- Li, Y.; Chen, X.; An, Y. Integrating machine layout, transporter allocation and worker assignment into job-shop scheduling solved by an improved non-dominated sorting genetic algorithm. Comput. Ind. Eng. 2023, 179, 109169. [Google Scholar] [CrossRef]
- Cheng, R.; Jin, Y. A Competitive Swarm Optimizer for Large Scale Optimization. IEEE Trans. Cybern. 2014, 45, 191–204. [Google Scholar] [CrossRef] [PubMed]
- Ali, K.B.; Telmoudi, A.J.; Gattoufi, S. Improved Genetic Algorithm Approach Based on New Virtual Crossover Operators for Dynamic Job Shop Scheduling. IEEE Access 2020, 8, 213318–213329. [Google Scholar] [CrossRef]
- Qiao, Y.; Wu, N.; He, Y. Adaptive genetic algorithm for two-stage hybrid flow-shop scheduling with sequence-independent setup time and no-interruption requirement. Expert Syst. Appl. 2022, 208, 118068. [Google Scholar] [CrossRef]
- Gao, K.; Cao, Z.; Zhang, L. A review on swarm intelligence and evolutionary algorithms for solving flexible job shop scheduling problems. IEEE/CAA J. Autom. Sin. 2019, 6, 904–916. [Google Scholar] [CrossRef]
- Xie, J.; Li, X.; Gao, L. A hybrid algorithm with a new neighborhood structure for job shop scheduling problems. Comput. Ind. Eng. 2022, 169, 108205. [Google Scholar] [CrossRef]
- Sun, K.; Zheng, D.; Song, H. Hybrid genetic algorithm with variable neighborhood search for flexible job shop scheduling problem in a machining system. Expert Syst. Appl. 2023, 215, 119359. [Google Scholar] [CrossRef]
- Majumder, A.; Laha, D.; Suganthan, P.N. A hybrid cuckoo search algorithm in parallel batch processing machines with unequal job ready times. Comput. Ind. Eng. 2018, 124, 65–76. [Google Scholar] [CrossRef]
- Alon, U. Biological networks: The tinkerer as an engineer. Science 2003, 301, 1866–1867. [Google Scholar] [CrossRef]
- Bray, D. Molecular networks: The top-down view. Science 2003, 301, 1864–1865. [Google Scholar] [CrossRef] [PubMed]
- Newman, M.E.J. The structure and function of complex networks. SIAM Rev. 2003, 45, 167–256. [Google Scholar] [CrossRef]
- Barabási, A.L. Emergence of scaling in random networks. Science 1999, 286, 509–512. [Google Scholar] [CrossRef] [PubMed]
- Eric, S.; Michael, P.H.S. Complex networks and simple models in biology. J. R. Soc. Interface 2005, 2, 16849202. [Google Scholar]
- Zhao, Y. Public Opinion Evolution Based on Complex Networks. Cybern. Inf. Technol. 2015, 15, 55–68. [Google Scholar] [CrossRef]
- Rajapakse, I.; Groudline, M.; Mehran, M. Dynamics and control of state-dependent networks for probing genomic organization. Proc. Natl. Acad. Sci. USA 2011, 108, 17257–17262. [Google Scholar] [CrossRef]
- Becker, T.; Wagner, D. Identification of key machines in complex production networks. Procedia CIRP 2016, 41, 69–74. [Google Scholar] [CrossRef]
- Pang, H.; Jiang, X. Solution of Flexible Job Shop Scheduling Problem Based on Ant Colony Algorithm and Complex Network. In Proceedings of the 10th International Symposium on Computational Intelligence and Design, Hangzhou, China, 9–10 December 2017; pp. 463–466. [Google Scholar]
- Zou, M.; Liu, Q.; Yin, Y. Improved small world genetic algorithm for intercell scheduling in network environment. Comput. Integr. Manuf. Syst. 2019, 25, 1991–1999. [Google Scholar]
- Yang, X.S.; Deb, S. Cuckoo search via Lévy flight. In Proceedings of the World Congress on Nature & Biologically Inspired Computing, Coimbatore, India, 9–11 December 2009; pp. 210–214. [Google Scholar]
- Bean, J.C. Genetic Algorithms and Random Keys for Sequencing and Optimization. ORSA J. Comput. 1994, 6, 154–160. [Google Scholar] [CrossRef]
- Mantegna, R.N. Fast accurate algorithm for numerical simulation of Lévy stable stochastic processes. Phys. Rev. E 1994, 49, 4677. [Google Scholar] [CrossRef] [PubMed]
- Sadiq, M.S.; Feras, C.O.; Abdalrahman, M.A. Engineering a Memetic Algorithm from Discrete Cuckoo Search and Tabu Search for Cell Assignment of Hybrid Nanoscale CMOL Circuits. J. Circuits Syst. Comput. 2016, 25, 1650023. [Google Scholar]
- Glover, F. Tabu Search: A Tutorial. Inf. J. Appl. Anal. 1990, 20, 74–94. [Google Scholar] [CrossRef]
- Li, X.; Yuan, Y.; Sun, W. Bottleneck identification in job-shop based on network structure characteristic. Comput. Integr. Manuf. Syst. 2016, 22, 1088–1096. [Google Scholar]
- Golmohammadi, D. A study of scheduling under the theory of constraints. Int. J. Prod. Econ. 2015, 165, 38–50. [Google Scholar] [CrossRef]
- Zou, Y.; Gu, H.; Xi, Y. Modified bottleneck-based heuristic for large-scale job-shop scheduling problems with a single bottleneck. J. Syst. Eng. Electron. 2007, 18, 556–565. [Google Scholar]
- Nieto, J.G.; Alba, E. Restart particle swarm optimization with velocity modulation: A scalability test. Soft Comput. 2011, 15, 2221–2232. [Google Scholar] [CrossRef]


| Parameter | Parameter Meaning |
|---|---|
| The j-th operation of part i | |
| Set of parts, N = {1, 2, ..., n} | |
| Set of machines, M = {1, 2, ..., m} | |
| Processing time of operation on machine m | |
| Starting time of | |
| Completion time of | |
| Transportation time between manufacturing cells of machine m and machine m’ | |
| Completion time of all parts | |
| =1 if the is processed on machine m (=0 otherwise) | |
| =1 if machine m and m’ are located in the same cell (=0 otherwise) |
| Parameter | Parameter Meaning |
|---|---|
| Node load of node m | |
| The shortest distance between nodes s and t | |
| Network efficiency between nodes s and t | |
| Number of shortest paths from node s to node t | |
| Number of shortest paths from node s to node t through node m | |
| Betweenness centrality of node m | |
| Bottleneck degree of node m |
| Experiment | n × m | Cells | Exceptional Parts |
|---|---|---|---|
| L1 | 50 × 30 | 7 | 15 |
| L2 | 70 × 30 | 7 | 15 |
| L3 | 90 × 30 | 7 | 15 |
| L4 | 50 × 40 | 9 | 20 |
| L5 | 70 × 40 | 9 | 20 |
| L6 | 90 × 40 | 9 | 20 |
| L7 | 50 × 50 | 12 | 25 |
| L8 | 70 × 50 | 12 | 25 |
| L9 | 90 × 50 | 12 | 25 |
| Cell | Machines | Cell | Machines | Cell | Machines | Cell | Machines |
|---|---|---|---|---|---|---|---|
| U1 | 1, 2, 3, 4, 5 | U2 | 6, 7, 8, 9 | U3 | 10, 11, 12, 13 | U4 | 14, 15, 16, 17 |
| U5 | 18, 19, 20, 21, 22 | U6 | 23, 24, 25, 26 | U7 | 27, 28, 29, 30 |
| Parts | Manufacturing Cell, Processing Machines | Processing Time (min) |
|---|---|---|
| J1 | (29, 31, 26, 35, 37) | |
| J2 | (27, 33, 34, 28) | |
| ⋮ | ⋮ | ⋮ |
| J48 | (27, 31, 22, 34) | |
| J50 | (28, 32, 28, 25) | |
| Exceptional parts | Manufacturing Cell, Processing Machines | Processing Time (min) |
| J5 | ||
| ⋮ | ⋮ | ⋮ |
| J41 |
| Example IS | TSCS-BD | SWGA | RPSO-VM | CS | TSCS | TSCS-NL | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Ctime | Ctime | P (%) | Ctime | P (%) | Ctime | P (%) | Ctime | P (%) | Ctime | P (%) | |
| L1 | 402.2 | 441.7 | 8.94 | 448.3 | 10.32 | 475.3 | 15.38 | 418.1 | 3.80 | 429 | 6.25 |
| L2 | 527.7 | 584.5 | 9.72 | 580.2 | 9.05 | 635.5 | 16.98 | 550.4 | 4.12 | 557.4 | 5.33 |
| L3 | 654.1 | 728.3 | 10.19 | 721.4 | 9.33 | 795.3 | 17.74 | 685.7 | 4.61 | 673.7 | 2.91 |
| L4 | 365.3 | 403.4 | 9.44 | 407.8 | 10.40 | 427.2 | 14.49 | 372.8 | 2.01 | 368.8 | 0.95 |
| L5 | 469.5 | 521.3 | 9.94 | 528.5 | 11.16 | 564.4 | 16.81 | 482.3 | 2.65 | 500.3 | 6.16 |
| L6 | 578.7 | 641.6 | 9.82 | 632.5 | 8.49 | 708.5 | 18.32 | 602.4 | 3.93 | 615.4 | 5.96 |
| L7 | 348.3 | 379.1 | 8.20 | 389.1 | 10.46 | 411.7 | 15.38 | 356.2 | 2.22 | 359.2 | 3.03 |
| L8 | 424.3 | 469.4 | 9.61 | 478.6 | 11.35 | 513.9 | 17.42 | 437.7 | 3.06 | 428.7 | 1.03 |
| L9 | 507.7 | 562.7 | 9.79 | 572.3 | 11.29 | 618.7 | 17.94 | 526.3 | 3.53 | 529.3 | 4.08 |
| Rank | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Bottleneck Degree | M12 1.00 | M1 0.98 | M3 0.67 | M8 0.43 | M28 0.28 | M20 0.27 | M15 0.23 | M14 0.18 | M25 0.13 | M2 0.13 |
| Node Load | M12 1.00 | M4 0.94 | M30 0.92 | M8 0.90 | M26 0.86 | M13 0.86 | M20 0.84 | M14 0.84 | M16 0.80 | M1 0.80 |
| Network Efficiency | M1 1.00 | M27 0.85 | M3 0.85 | M12 0.81 | M14 0.79 | M8 0.78 | M10 0.75 | M6 0.73 | M28 0.72 | M11 0.69 |
| Betweenness Centrality | M12 1.00 | M1 0.89 | M3 0.73 | M8 0.49 | M28 0.38 | M20 0.35 | M15 0.34 | M25 0.23 | M2 0.23 | M14 0.22 |
| Rank | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| Bottleneck Degree | M7 0.08 | M21 0.06 | M13 0.04 | M19 0.03 | M4 0.02 | M29 0.02 | M16 0.01 | M30 0.01 | M11 0.01 | M24 0.01 |
| Node Load | M6 0.76 | M21 0.76 | M3 0.75 | M15 0.75 | M18 0.73 | M23 0.73 | M27 0.66 | M28 0.66 | M22 0.65 | M29 0.65 |
| Network Efficiency | M20 0.69 | M19 0.67 | M18 0.67 | M25 0.65 | M2 0.64 | M23 0.64 | M15 0.63 | M7 0.63 | M24 0.60 | M13 0.49 |
| Betweenness Centrality | M7 0.16 | M21 0.16 | M29 0.13 | M16 0.11 | M4 0.10 | M19 0.07 | M13 0.06 | M30 0.04 | M24 0.01 | M11 0.01 |
| Rank | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| Bottleneck Degree | M26 0.00 | M17 0.00 | M27 0.00 | M6 0.00 | M5 0.00 | M9 0.00 | M10 0.00 | M23 0.00 | M18 0.00 | M22 0.00 |
| Node Load | M5 0.63 | M9 0.61 | M10 0.57 | M11 0.52 | M17 0.44 | M25 0.43 | M2 0.43 | M24 0.34 | M7 0.34 | M19 0.00 |
| Network Efficiency | M21 0.35 | M4 0.16 | M29 0.12 | M16 0.08 | M30 0.08 | M22 0.00 | M17 0.00 | M26 0.00 | M9 0.00 | M5 0.00 |
| Betweenness Centrality | M22 0.00 | M26 0.00 | M5 0.00 | M6 0.00 | M27 0.00 | M10 0.00 | M23 0.00 | M18 0.00 | M17 0.00 | M9 0.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, P.; Liu, Q.; Xiong, S. An Improved Cuckoo Search Algorithm under Bottleneck-Degree-Based Search Guidance for Large-Scale Inter-Cell Scheduling Optimization. Appl. Sci. 2024, 14, 1011. https://doi.org/10.3390/app14031011
Yang P, Liu Q, Xiong S. An Improved Cuckoo Search Algorithm under Bottleneck-Degree-Based Search Guidance for Large-Scale Inter-Cell Scheduling Optimization. Applied Sciences. 2024; 14(3):1011. https://doi.org/10.3390/app14031011
Chicago/Turabian StyleYang, Peixuan, Qiong Liu, and Shuping Xiong. 2024. "An Improved Cuckoo Search Algorithm under Bottleneck-Degree-Based Search Guidance for Large-Scale Inter-Cell Scheduling Optimization" Applied Sciences 14, no. 3: 1011. https://doi.org/10.3390/app14031011
APA StyleYang, P., Liu, Q., & Xiong, S. (2024). An Improved Cuckoo Search Algorithm under Bottleneck-Degree-Based Search Guidance for Large-Scale Inter-Cell Scheduling Optimization. Applied Sciences, 14(3), 1011. https://doi.org/10.3390/app14031011




