Parametric Analysis on Creep Deformation of Deep-Sea PMMA Observation Window
Abstract
1. Introduction
2. Material and Structure of Frustum Observation Window
2.1. Material
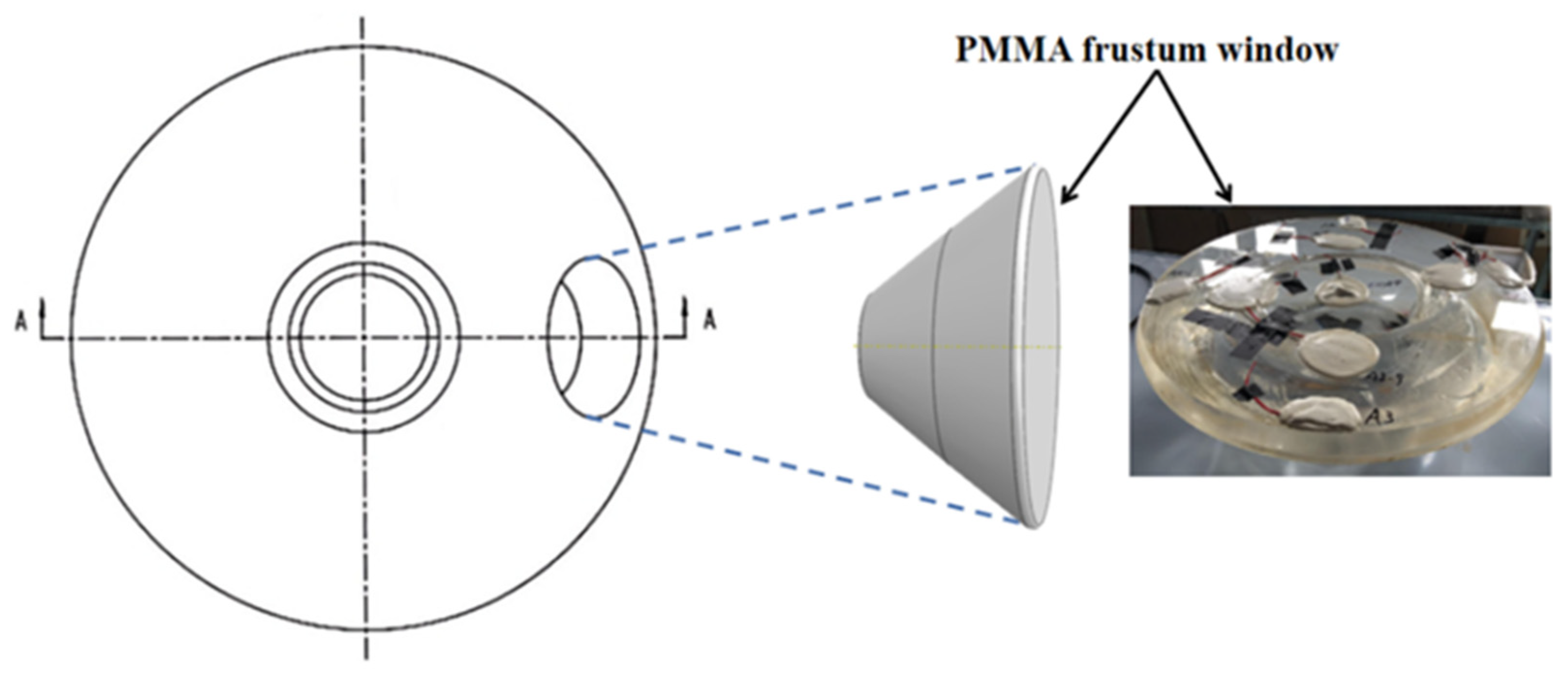
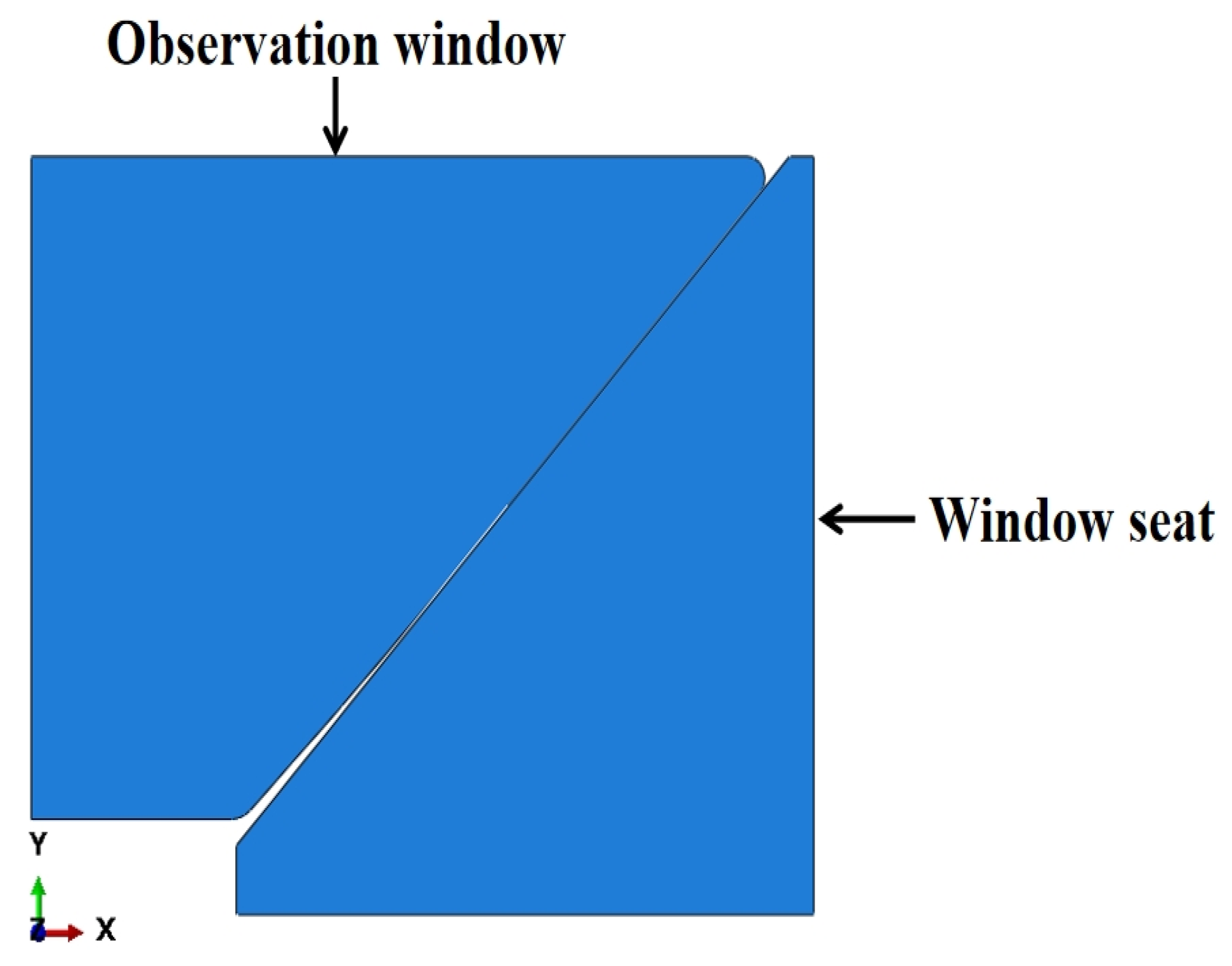
2.2. Structure
3. Temperature-Dependent Time-Hardening Creep Model
4. Parametric Analysis on Creep Deformation of PMMA Frustum Observation Windows
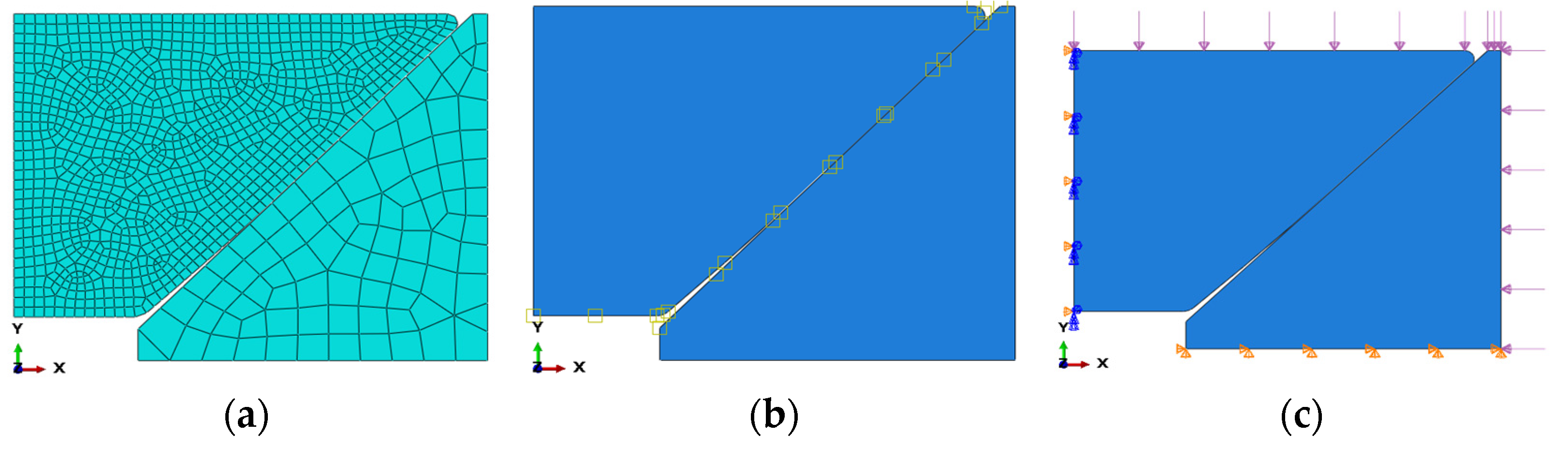
4.1. Finite Element Model and Calculation Methodology for the Observation Window
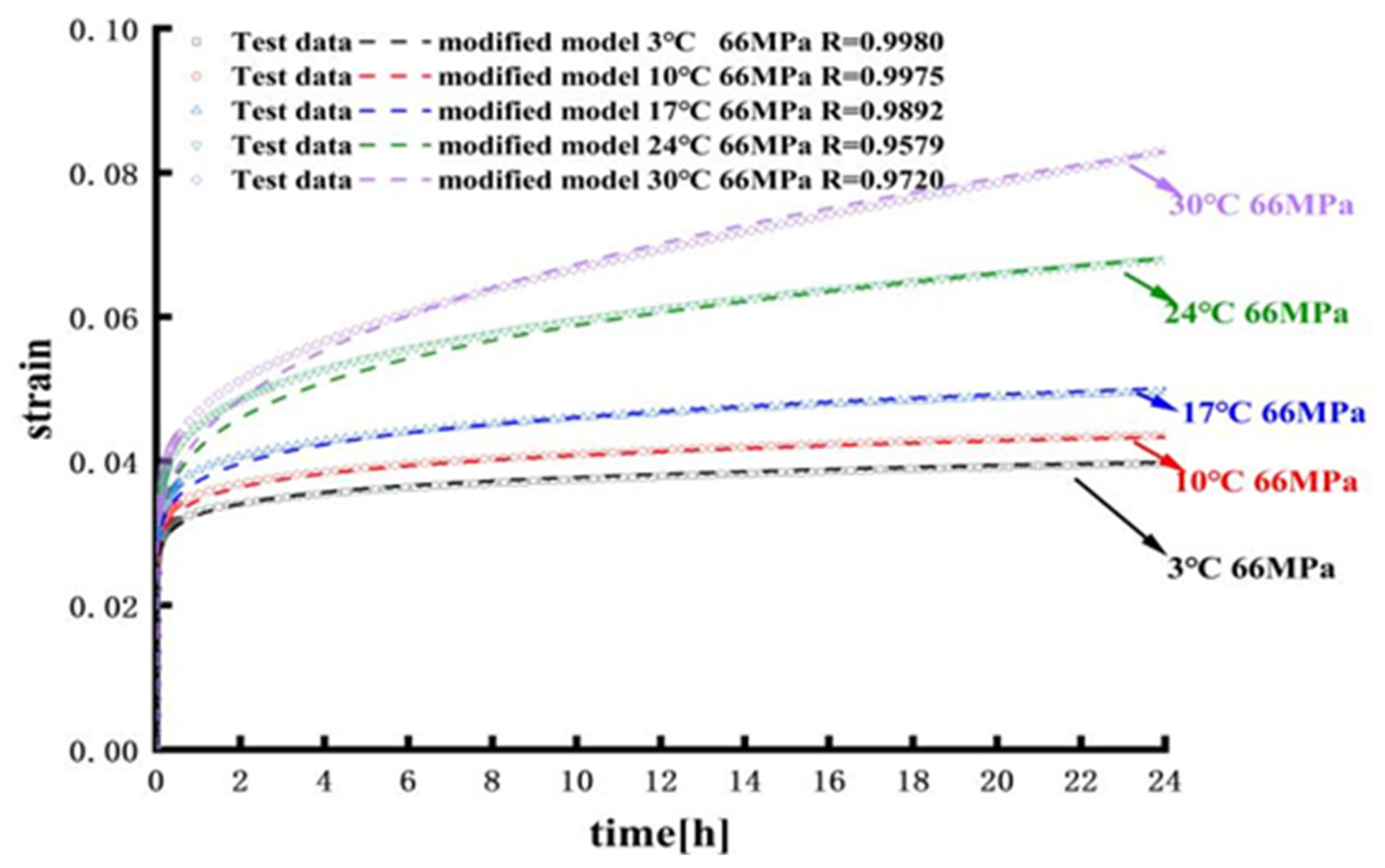
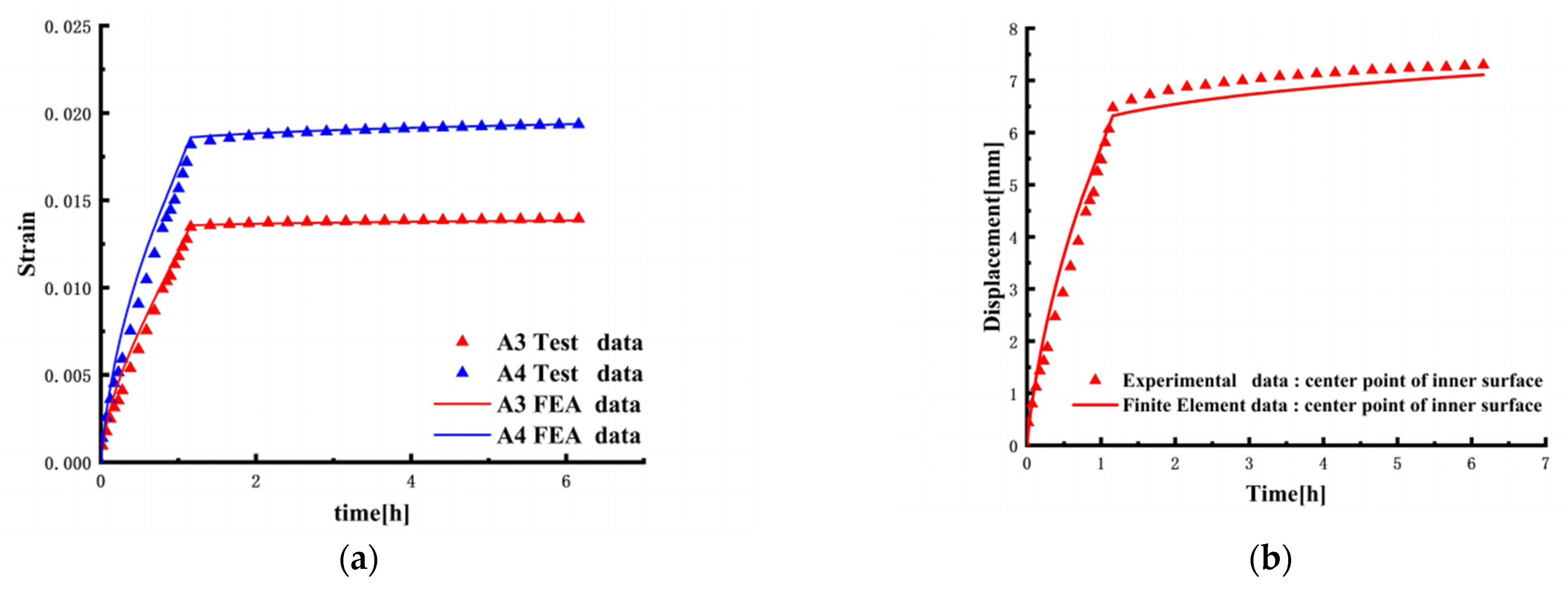
4.2. Simulation Model Validation by Experiment
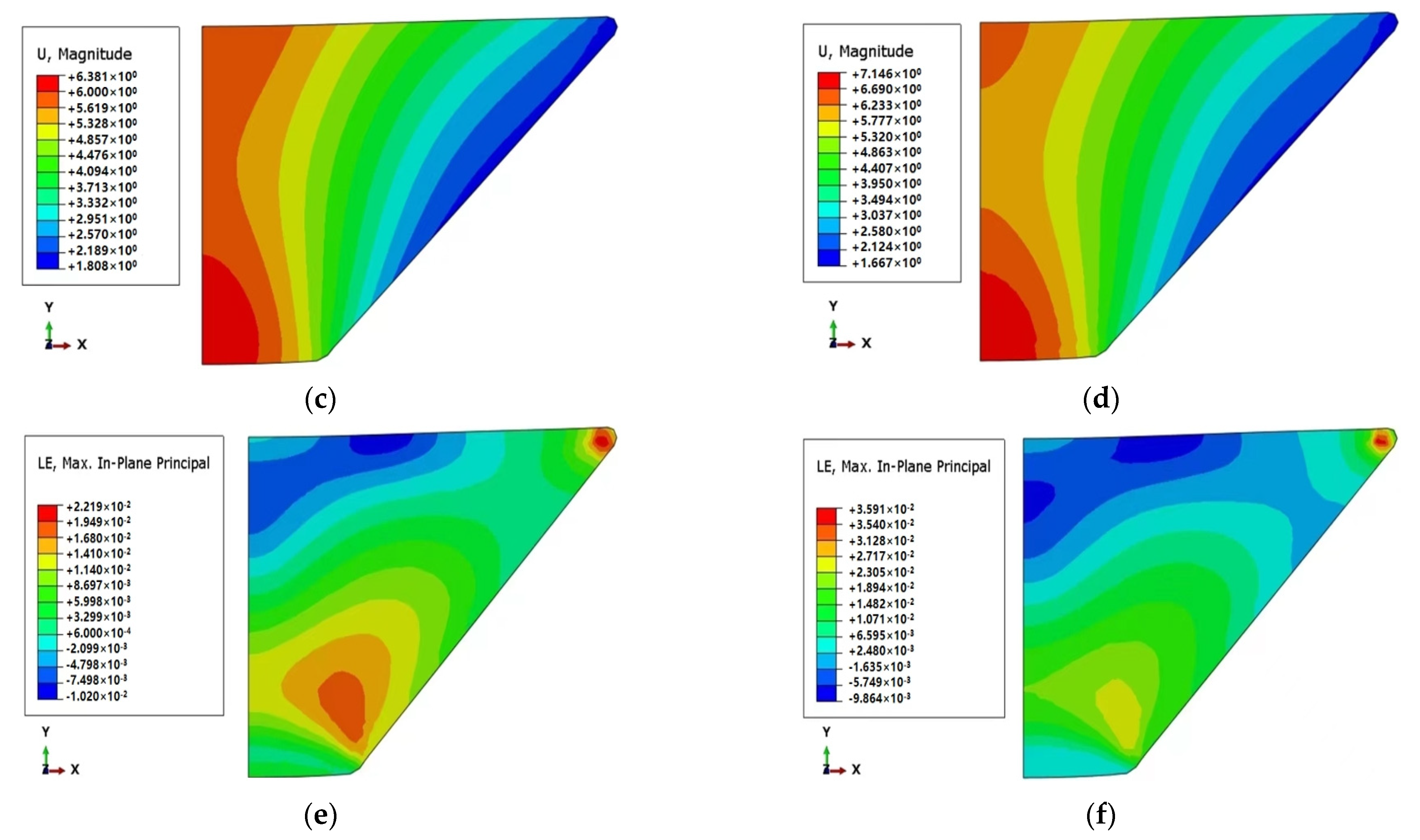
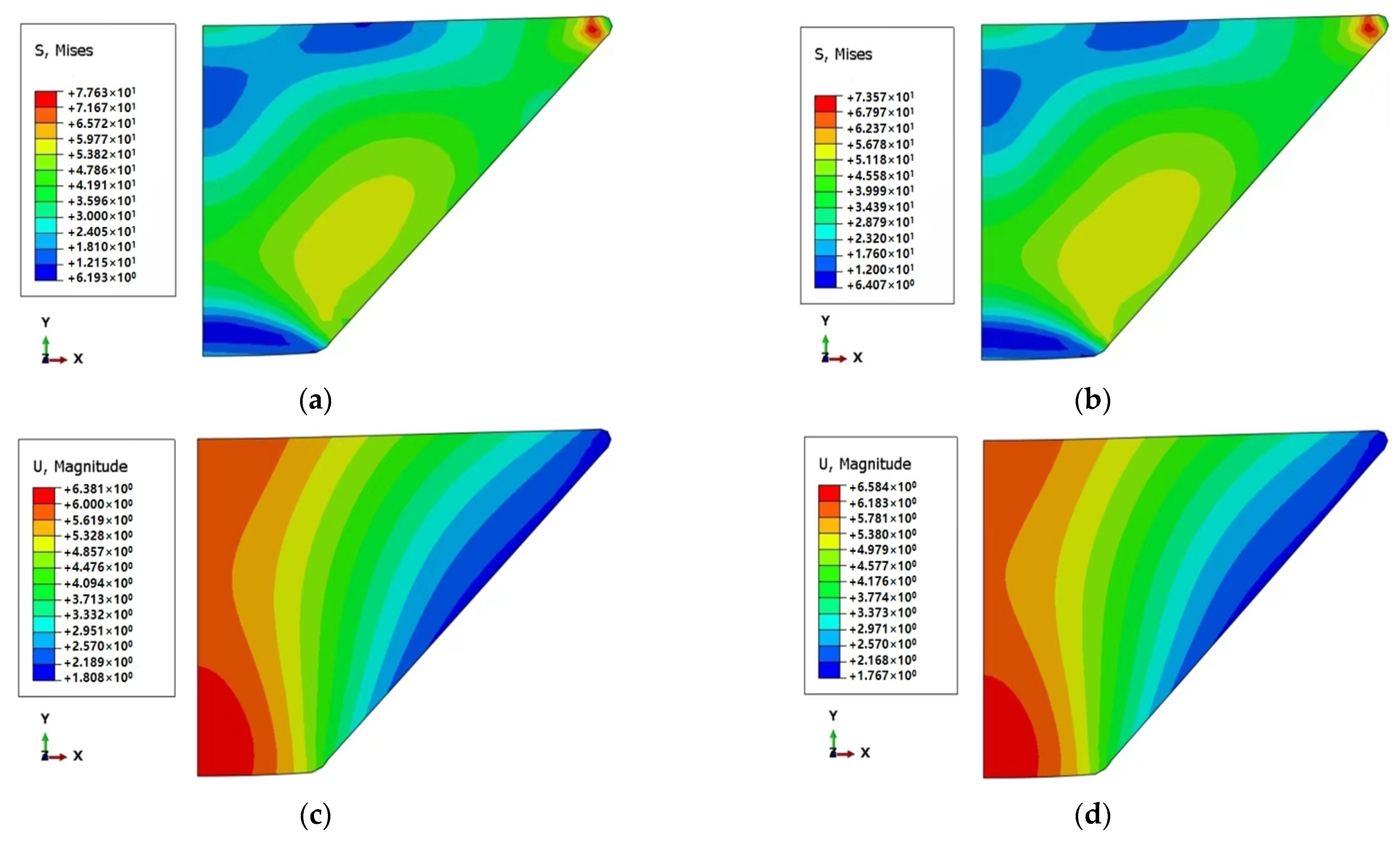
4.3. Effect of Temperature on Creep of Frustum Observation Window
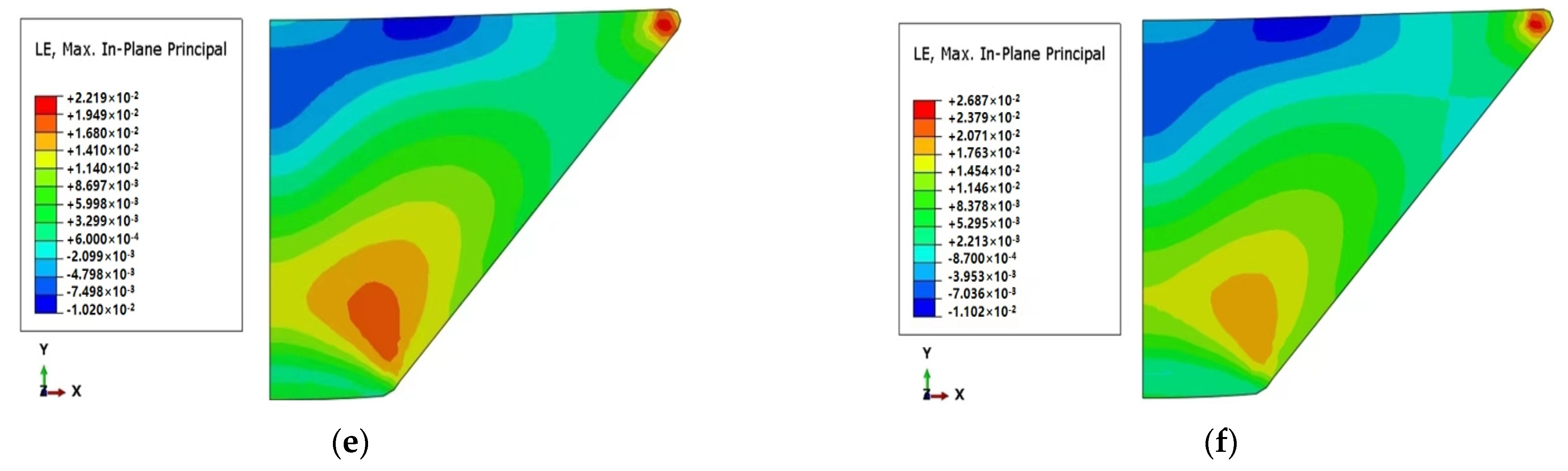
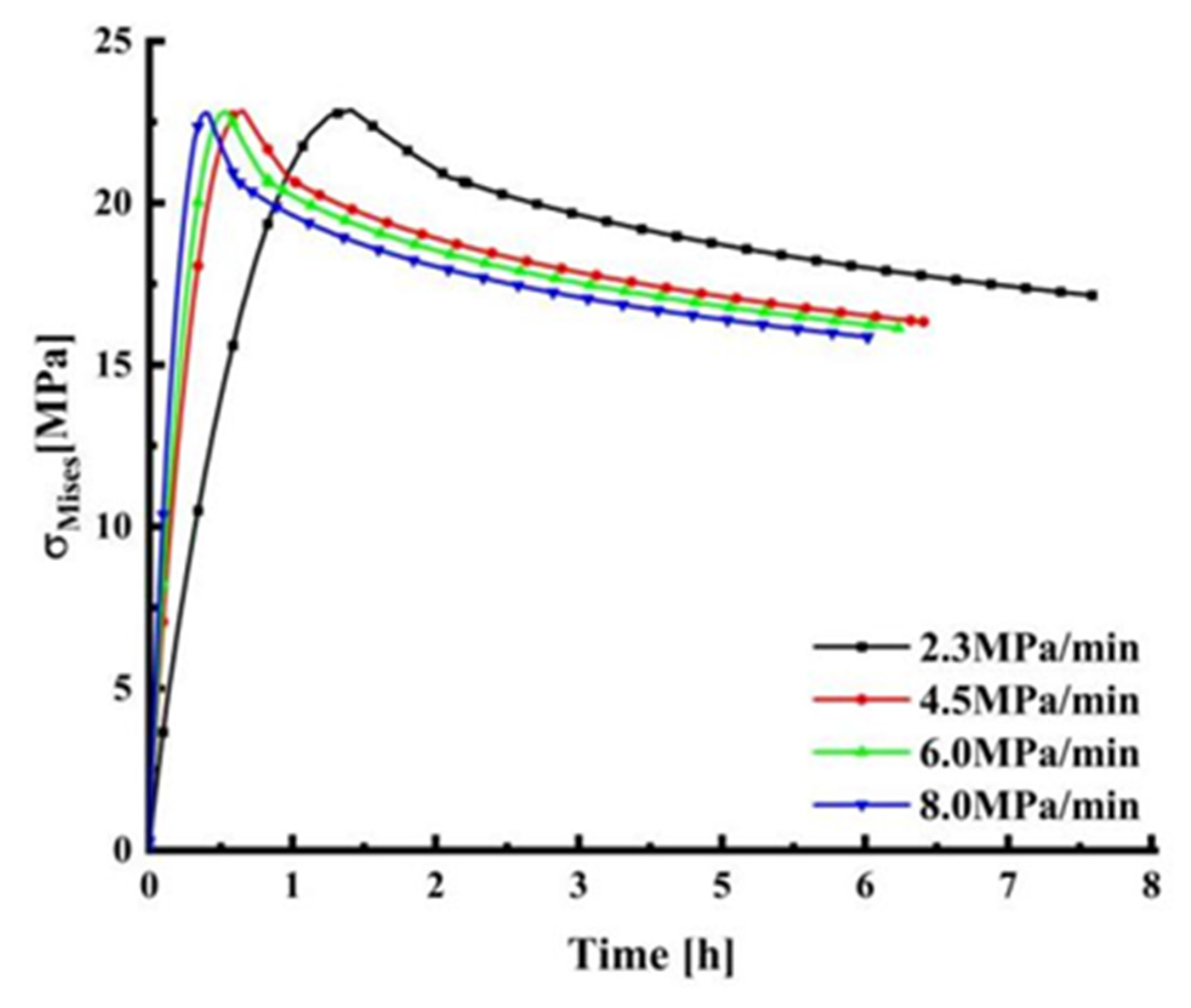
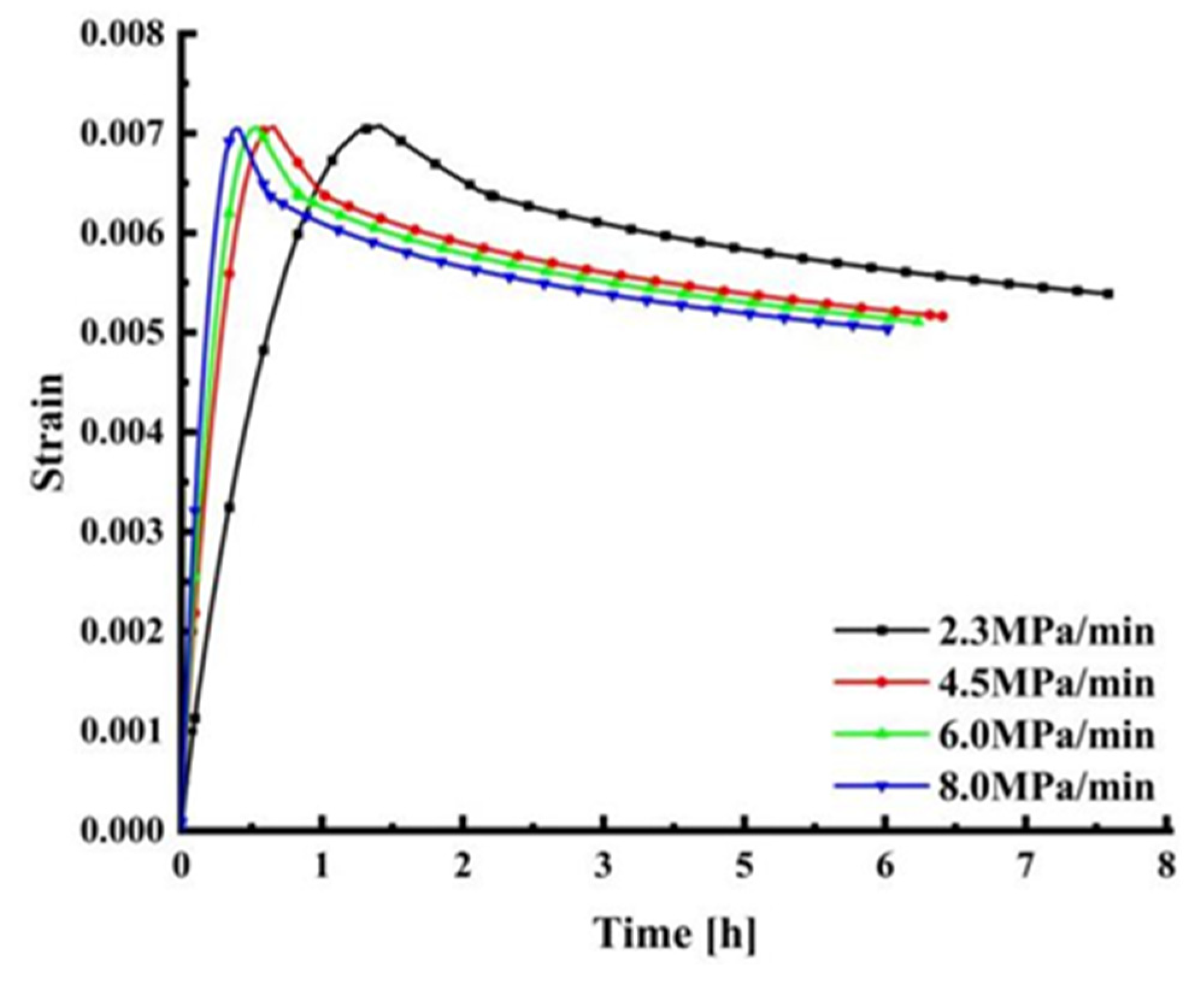
4.4. Effect of Loading Rate on Creep of Frustum Observation Window
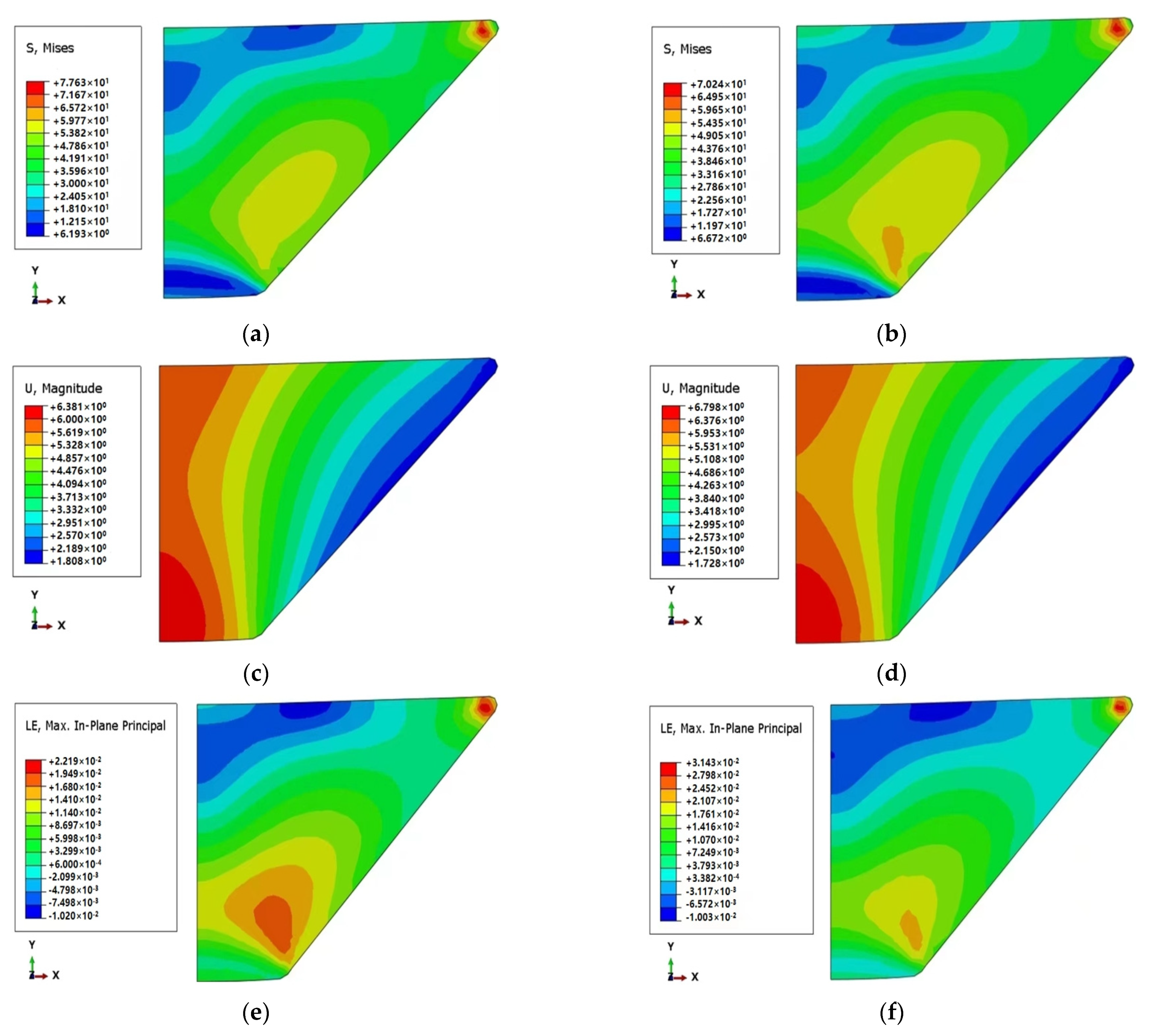
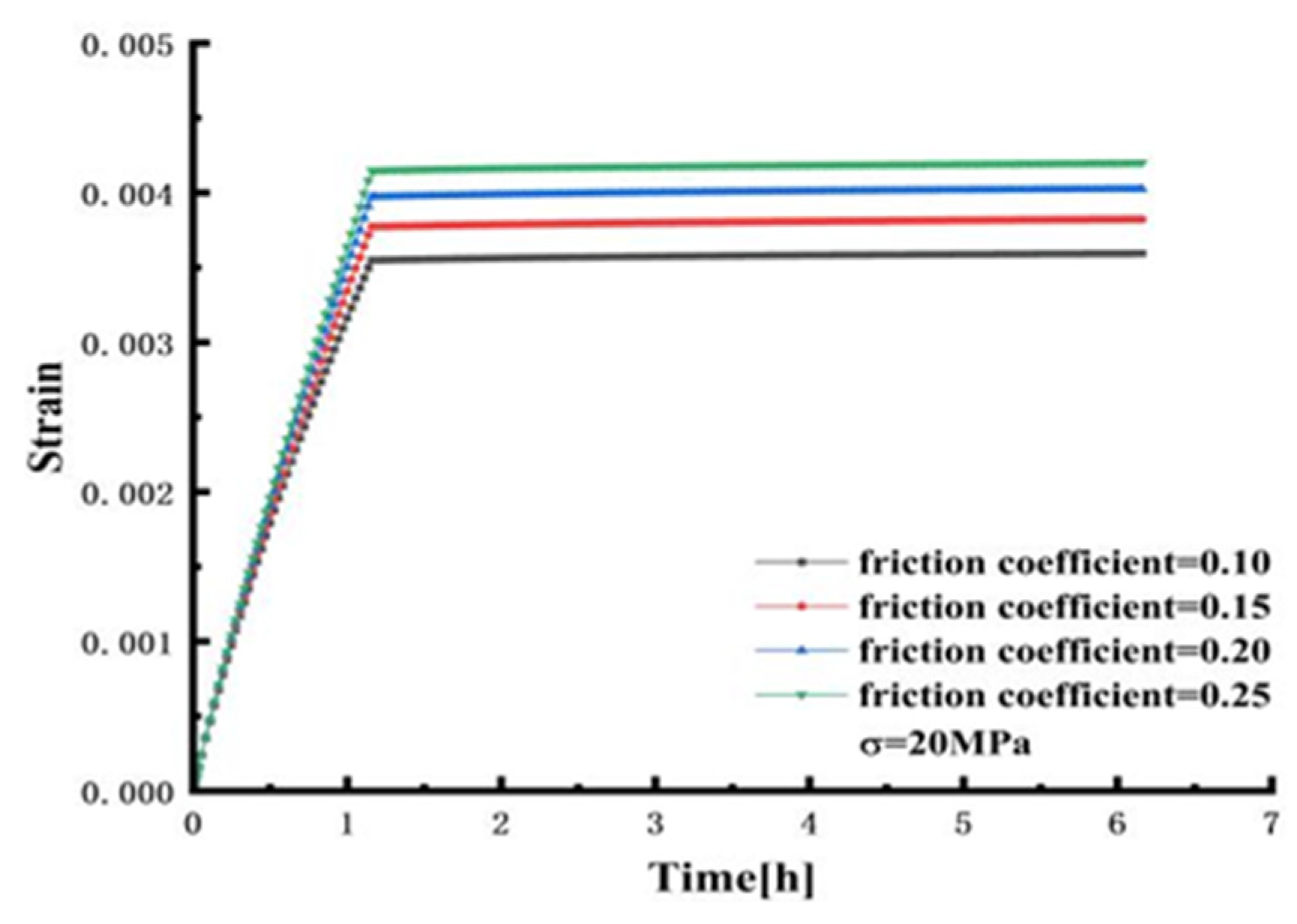
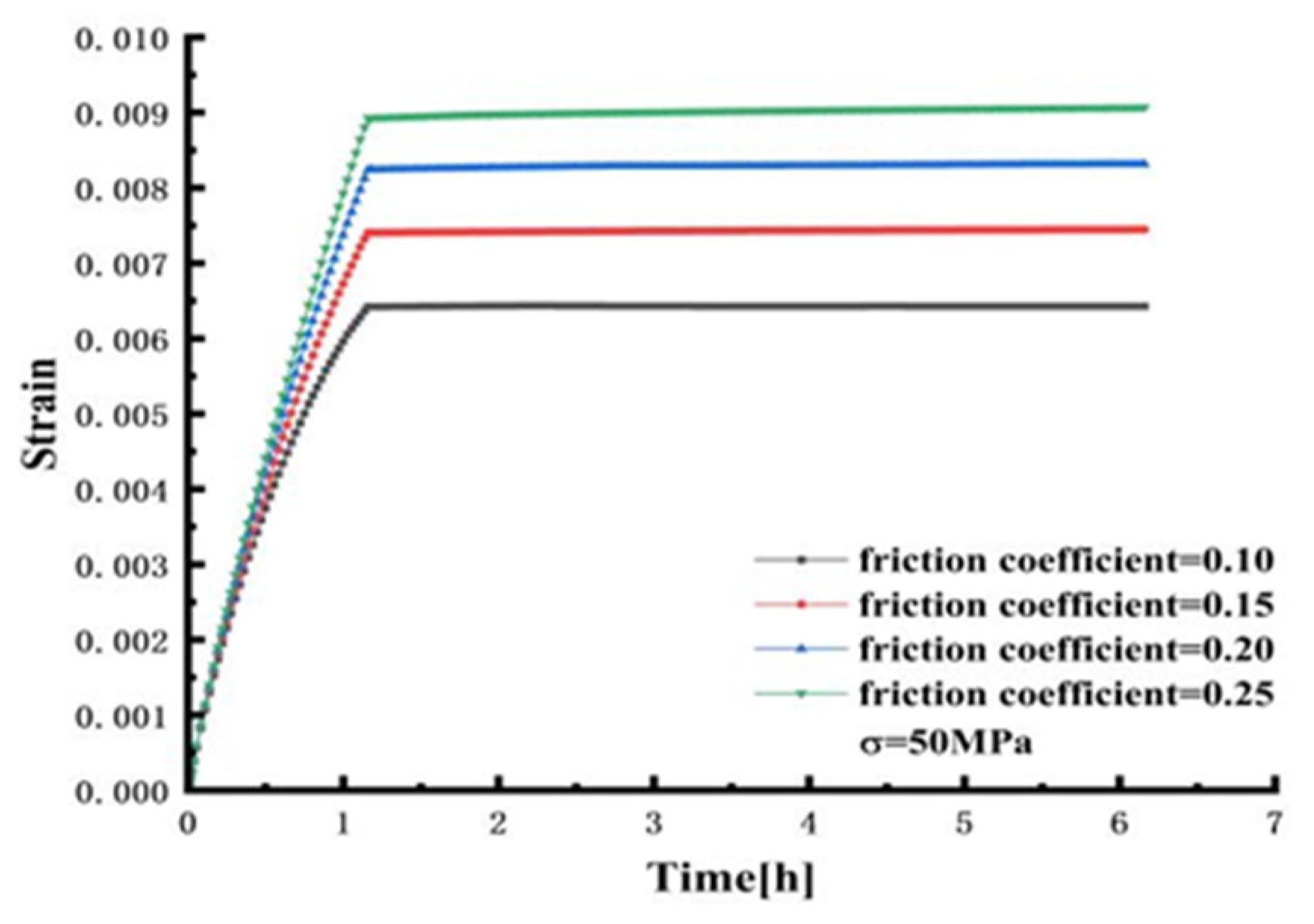
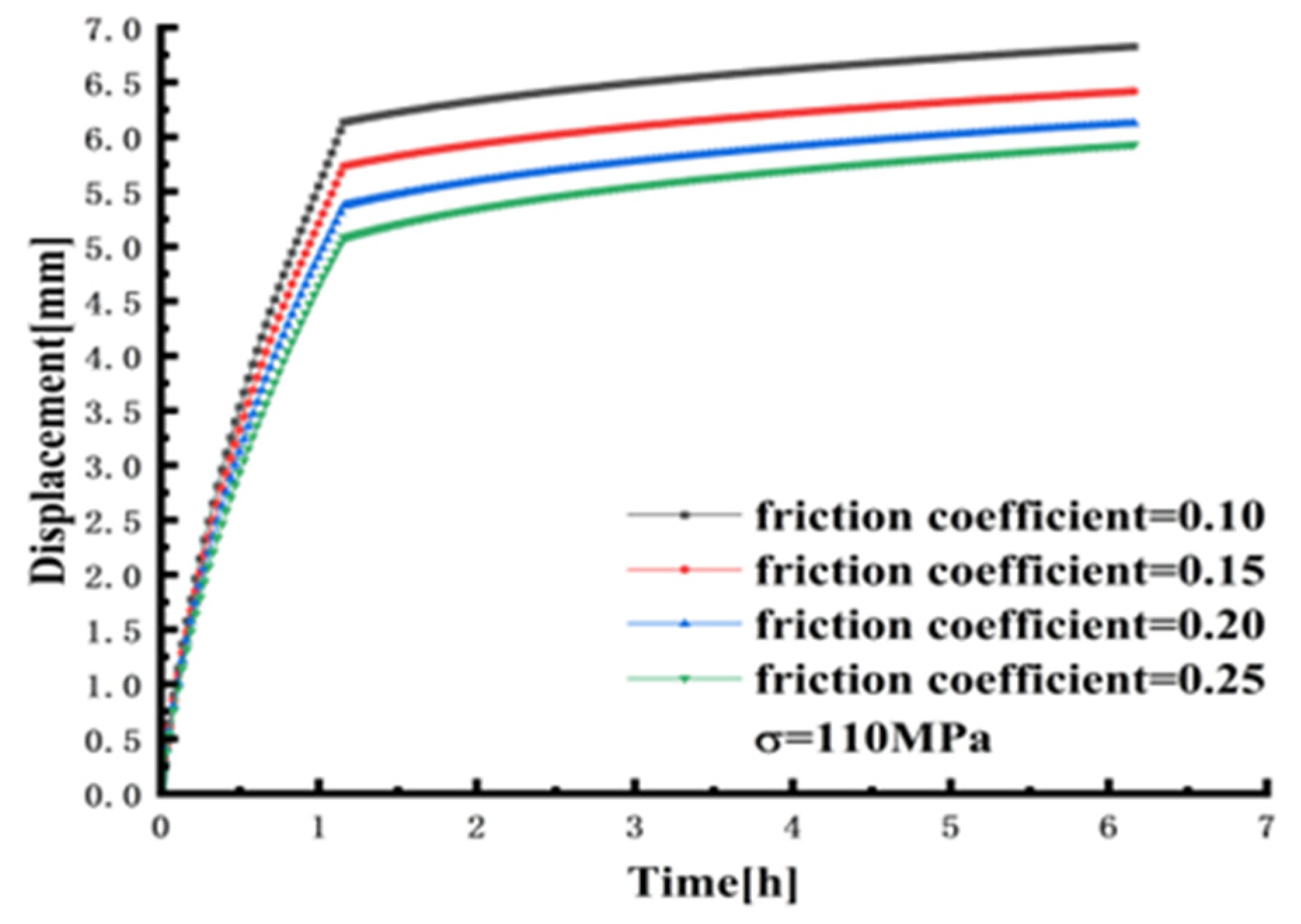
4.5. Effect of Friction Coefficient on Creep of Frustum Observation Window
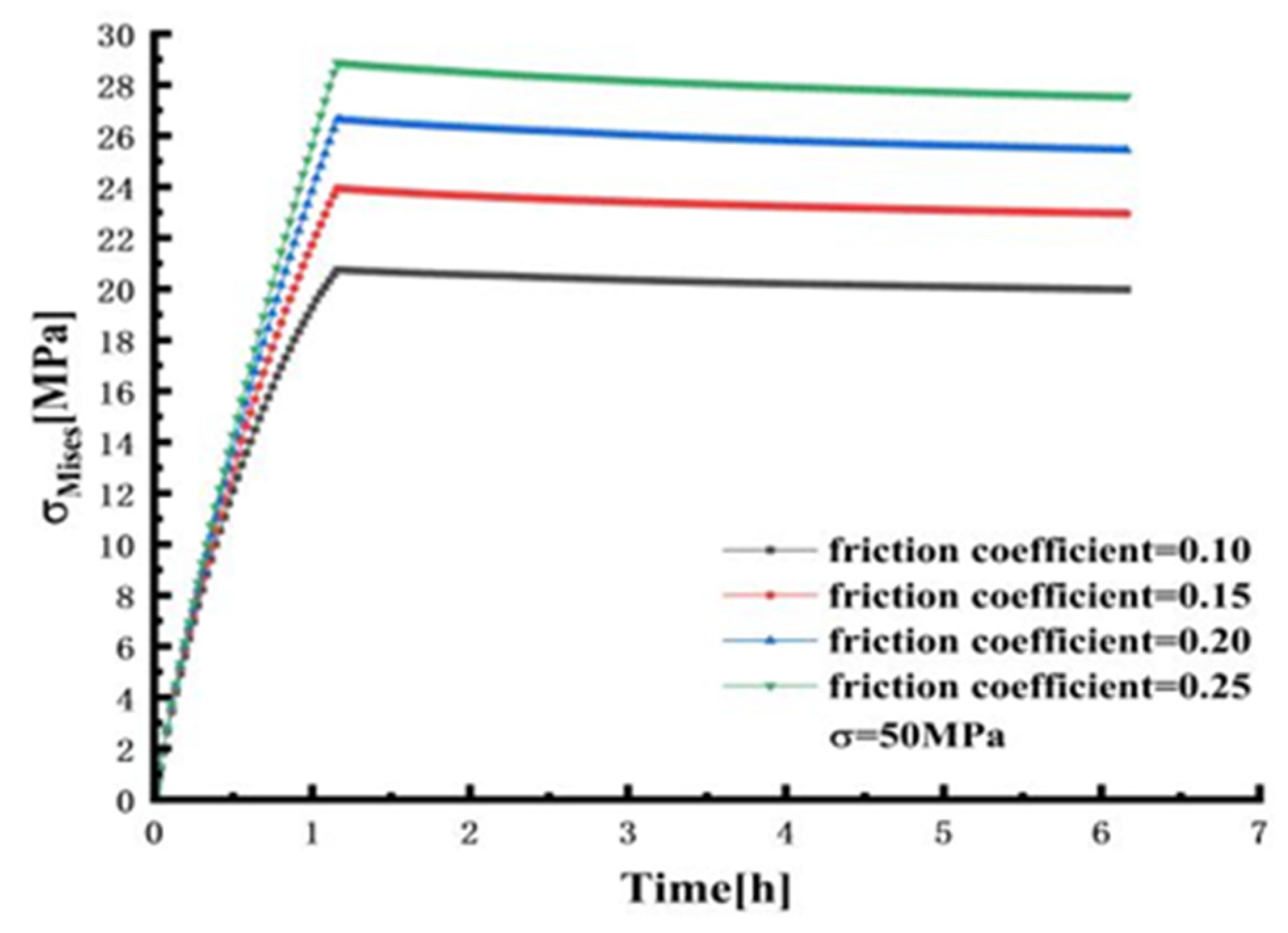
4.6. The Influence of Friction Coefficient Coupling Pressure at Changing Temperature
5. Summary and Conclusions
- (1)
- According to the experimental data at different temperatures, the improved time-hardening creep model is verified to be in good agreement with the experimental data.
- (2)
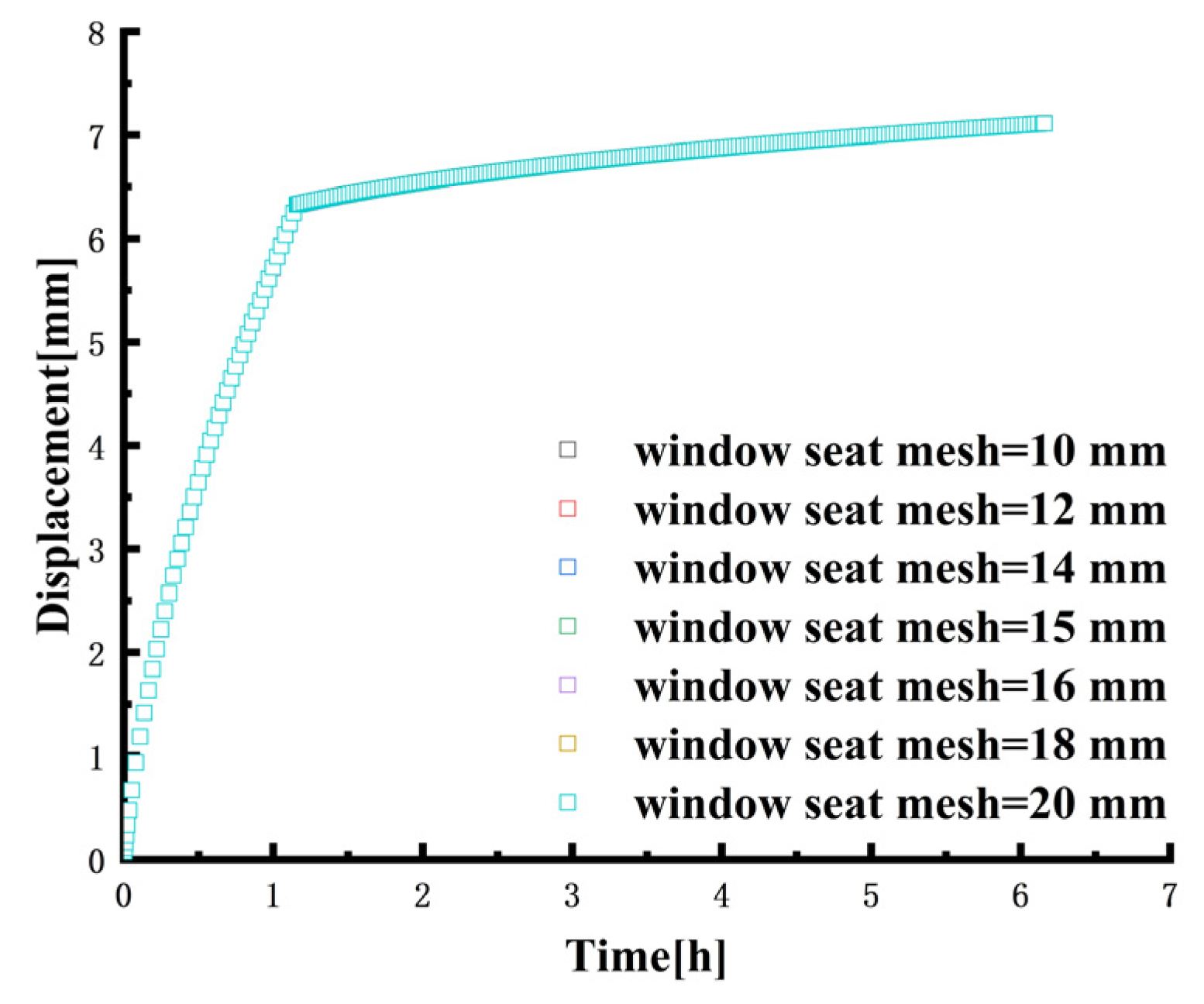
- The mesh convergence of the observation window and the window seat is analyzed. The different mesh sizes have little effect on the axial displacement. The mesh size of the observation window is 5 mm, and the mesh size of the window seat is 15 mm.
- (3)
- The UMAT program is written by the improved time-hardening creep model, and the observation window test data are verified. The curve and the test data are well fitted.
- (4)
- The creep behavior of the observation window considering four temperature changes is analyzed. Under the condition of four kinds of temperature changes, the y-axis displacement difference between 30 °C and 2 °C is the largest in the stage of the maintaining load. The maximum axial displacement at 30 °C is 7.1103 mm, and the minimum axial displacement at 2 °C is 6.5329 mm. The axial displacements of the other two temperature ranges are 6.7667 mm and 6.7532 mm, respectively. As the temperature increases, the total displacement increases, indicating that the temperature effect has a significant effect on the observation window.
- (5)
- The parametric analysis of different loading rates of the observation window was carried out. Under the loading rate of 8 MPa/min and 2.3 MPa/min, the y-axis displacement of the observation window is the largest and the smallest respectively. The y-axis displacement of 8 MPa/min is 7.2213 mm, and the axial displacement of 2.3 MPa/min is 6.9279 mm. As the loading rate continues to increase, the displacement at the center of the lower surface of the observation window continues to increase. However, the stress and strain decrease with the increase of the loading rate of the observation window.
- (6)
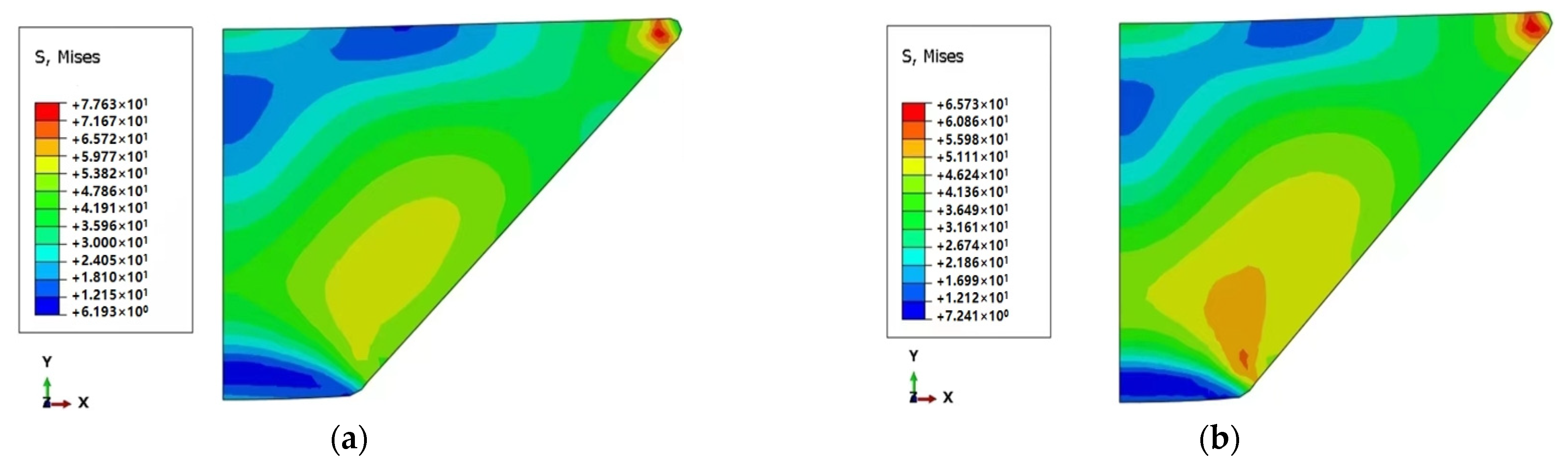
- The parametric analysis of the different friction coefficients of the observation window was carried out. As the friction coefficient increases, the stress and strain at the center of the inner surface of the observation window gradually increase. However, the y-axis displacement at the center of the inner surface gradually decreases with the increase in the friction coefficient. When the friction coefficient (0.05) is the smallest, the y-axis displacement at the center of the lower surface of the observation window is the largest, and the displacement is 7.7638 mm. When the friction coefficient (0.3) is the largest, the y-axis displacement at the center of the lower surface of the observation window is the smallest, and the displacement is 6.0814 mm.
- (7)
- The performance of the PMMA observation window under different friction coefficients, pressures, and temperatures was studied and simulated. The results show that the stress and strain on the observation window increase with the increase in the friction coefficient under different pressure levels. At the same time, the axial displacement at the center of the lower surface gradually decreases with the increase in the friction coefficient.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, F.; Cui, W.C. Experimental investigation on dwell-fatigue property of Ti-6Al-4V ELI used in deep-sea manned cabin. Mater. Sci. Eng. A 2015, 642, 136–141. [Google Scholar] [CrossRef]
- Lin, G.J.; Zhang, W.M.; Feng, Y.L. Review of the research on the observation window of manned submersible. Ship Eng. 2013, 3, 1–5+75. (In Chinese) [Google Scholar]
- Stachiw, J.D. Conical acrylic windows under long term hydrostatic pressure of 20,000 psi. J. Eng. Ind. 1970, 92, 237–256. [Google Scholar] [CrossRef]
- Stachiw, J.D. Conical Acrylic Windows Under Long Term Hydrostatic Pressure of 10,000 psi. J. Eng. Ind. 1972, 94, 1053–1059. [Google Scholar] [CrossRef]
- Stachiw, J.D. Conical Acrylic Windows Under Long-Term Hydrostatic Pressure of 5000 psi. J. Eng. Ind. 1972, 94, 843–848. [Google Scholar] [CrossRef]
- Stachiw, J.D. Handbook of Acrylics for Submersibles, Hyperbaric Chambers and Aquaria; Best Publishing: Flagstaff, AZ, USA, 2003. [Google Scholar]
- Vakili-Tahami, F.; Adibeig, M.R. Using developed creep constitutive model for optimum design of HDPE pipes. Polym. Test. 2017, 63, 392–397. [Google Scholar] [CrossRef]
- Vakili-Tahami, F.; Adibeig, M.R.; Hassanifard, S. Optimizing creep lifetime of friction stir welded PMMA pipes subjected to combined loadings using rheological model. Polym. Test. 2019, 79, 106049. [Google Scholar] [CrossRef]
- Gao, Z.Z.; Liu, W.; Liu, Z.Q.; Yue, Z.F. Experiment and Simulation Study on the Creep Behavior of PMMA at Different Temperatures. Polym.-Plast. Technol. Eng. 2010, 49, 1478–1482. [Google Scholar] [CrossRef]
- Adibeig, M.R.; Hassanifard, S.; Vakili-Tahami, F. Optimum creep lifetime of Polymethyl Methacrylate (PMMA) tube using rheological creep constitutive models based on experimental data. Polym. Test. 2019, 75, 107–116. [Google Scholar] [CrossRef]
- Khan, F.; Yeakle, C. Experimental investigation and modeling of non-monotonic creep behavior in polymers. Int. J. Plast. 2011, 27, 512–521. [Google Scholar] [CrossRef]
- Wang, Y.Y. Research on Fatigue Reliability of Manned Cabin of Full Ocean Depth Submersibles; China Ship Scientific Research Center: Wuxi, China, 2017. (In Chinese) [Google Scholar]
- Tian, C.L.; Hu, Y.; Liu, D.Q. Creep analysis on deep-sea structure’s viewport windows. Ship Mech. 2010, 14, 526–532. (In Chinese) [Google Scholar]
- Du, Q.H.; Hu, Y.; Cui, W.C. Safety assessment of the acrylic conical frustum viewport structure for a deep-sea manned submersible. Ships Offshore Struct. 2017, 12 (Suppl. S1), S221–S229. [Google Scholar] [CrossRef]
- Pranesh, S.B.; Kumar, D.; Anantha Subramanian, V.; Sathianarayanan, D.; Ramadass, G.A. Structural analysis of spherical pressure hull viewport for manned submersibles using biological growth method. Ships Offshore Struct. 2018, 13, 601–616. [Google Scholar]
- Yue, K.; Tian, C.L. Stress analysis method and comparison of different angle of the view-port windows of the deep-sea vehicle. Jiangnan Univ. (Natl. Sci. Ed.) 2011, 5, 015. (In Chinese) [Google Scholar]
- Yue, K.; Tian, C.L. Stress analysis of deep-sea view-port windows and its optimization. Jiangnan Univ. (Natl. Sci. Ed.) 2011, 1, 014. (In Chinese) [Google Scholar]
- Pranesh, S.B.; Kumar, D.; Anantha Subramanian, V.; Sathianarayanan, D.; Ramadass, G.A. Numerical and experimental study on the safety of viewport window in a deep sea manned submersible. Ships Offshore Struct. 2020, 15, 769–779. [Google Scholar] [CrossRef]
- Liu, P.F.; Li, J.X.; Wang, S.B.; Leng, J.X. Finite element analysis of viscoelastic creep behaviors of deep-sea manned submersible viewport windows. Int. J. Press. Vessel. Pip. 2020, 188, 104218. [Google Scholar] [CrossRef]
- Li, J.X.; Liu, P.F.; Tong, X.Y. A simplified method for studying cyclic creep behaviors of deep-sea manned submersible viewport windows. Int. J. Press. Vessel. Pip. 2021, 194, 104565. [Google Scholar] [CrossRef]
- Du, Q.H.; Jiang, H.G.; Hu, X.K. Creep behavior analysis of conical observation window for human occupied vehicle based on ABAQUS. J. Ship Res. 2022, 17, 108–116. (In Chinese) [Google Scholar]
- Wang, F.; Wang, W.W.; Cui, W.C. Effect of temperature and nonlinearity of PMMA material in the design of observation windows for a full ocean depth manned submersible. Mar. Technol. Soc. J. 2019, 53, 27–36. [Google Scholar] [CrossRef]
- Chen, W.; Gu, P.; Zhang, A.F. Study on viewport creep characteristics based on compression creep test. J. Ship Mech. 2021, 25, 73–79. (In Chinese) [Google Scholar]
- ASME PVHO-1; Safety Standard for Pressure Vessels for Human Occupancy: In-Service Guidelines. American Society of Mechanical Engineers: New York, NY, USA, 2016.
- Mu, X.Y. Creep Mechanics; Xi’an Jiaotong University Press: Xi’an, China, 1990; pp. 11–16. (In Chinese) [Google Scholar]

















| Material Property | Value |
|---|---|
| Elastic Modulus, E/MPa | 2740 |
| Density, ρ/kg·m−3 | 1190 |
| Poisson’s ratio, u | 0.38 |
| Compressive yield strength, σs/MPa | 115 |
| a1 | b1 | c1 | d1 | k1 |
| 9.7522 × 10−11 | −8.8688 × 10−8 | 2.6692 × 10−5 | −2.6576 × 10−3 | 6.5806 × 10−9 |
| a2 | b2 | c2 | k2 | |
| 4.7402 × 10−4 | −2.6192 × 10−1 | 3.4994 × 101 | 3.1974 × 10−3 |
| Mesh Size (mm) | Element Number | Displacement (mm) | Relative Error |
|---|---|---|---|
| 1 | 26,516 | 6.9346 | 2.5% |
| 2 | 6422 | 6.9588 | 2.1% |
| 3 | 2888 | 6.9932 | 1.7% |
| 4 | 1618 | 6.9688 | 2.0% |
| 5 | 1059 | 7.1107 | - |
| 6 | 728 | 7.0931 | 0.2% |
| 8 | 400 | 6.9515 | 2.2% |
| Mesh Size (mm) | Element Number | Displacement (mm) | Relative Error |
|---|---|---|---|
| 10 | 198 | 7.1121 | 0.0197% |
| 12 | 144 | 7.1108 | 0.0014% |
| 14 | 109 | 7.1111 | 0.0056% |
| 15 | 90 | 7.1107 | - |
| 16 | 75 | 7.1108 | 0.0014% |
| 18 | 55 | 7.1109 | 0.0028% |
| 20 | 46 | 7.1110 | 0.0042% |
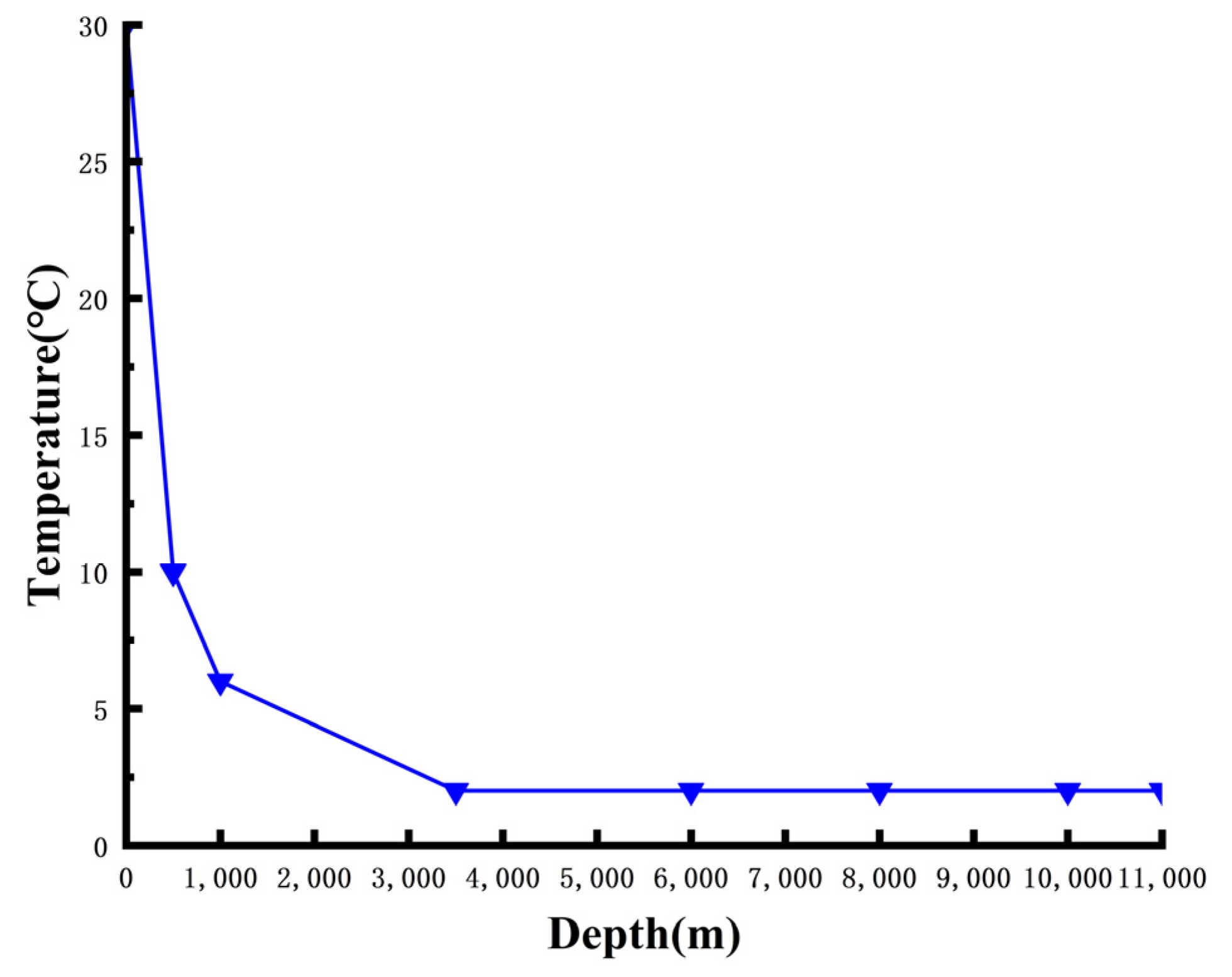
| Working Depth | Temperature/°C | |||
|---|---|---|---|---|
| Spring | Summer | Autumn | Winter | |
| 0 m→500 m | 24 | 30 | 28 | 27 |
| 500 m→1000 m | 8 | 10 | 9 | 8 |
| 1000 m→3500 m | 4.5 | 6 | 5 | 4.5 |
| 3500 m→11,000 m | 2 | 2 | 2 | 2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, Z.; Wang, F.; Wang, H.; Zhao, B. Parametric Analysis on Creep Deformation of Deep-Sea PMMA Observation Window. Appl. Sci. 2024, 14, 1040. https://doi.org/10.3390/app14031040
He Z, Wang F, Wang H, Zhao B. Parametric Analysis on Creep Deformation of Deep-Sea PMMA Observation Window. Applied Sciences. 2024; 14(3):1040. https://doi.org/10.3390/app14031040
Chicago/Turabian StyleHe, Zhihao, Fang Wang, Haoxing Wang, and Bingxiong Zhao. 2024. "Parametric Analysis on Creep Deformation of Deep-Sea PMMA Observation Window" Applied Sciences 14, no. 3: 1040. https://doi.org/10.3390/app14031040
APA StyleHe, Z., Wang, F., Wang, H., & Zhao, B. (2024). Parametric Analysis on Creep Deformation of Deep-Sea PMMA Observation Window. Applied Sciences, 14(3), 1040. https://doi.org/10.3390/app14031040







