A New Car-Body Structure Design for High-Speed EMUs Based on the Topology Optimization Method
Abstract
:1. Introduction
2. Topology Optimization Method of Car-Body Structure
2.1. Homogenization Method
2.2. Variable-Density Method
2.3. Progressive Structural Optimization Method
2.4. Topology Optimization Process of Car-Body Structure
3. Selection of Topology Optimization Design Domain and Model Establishment
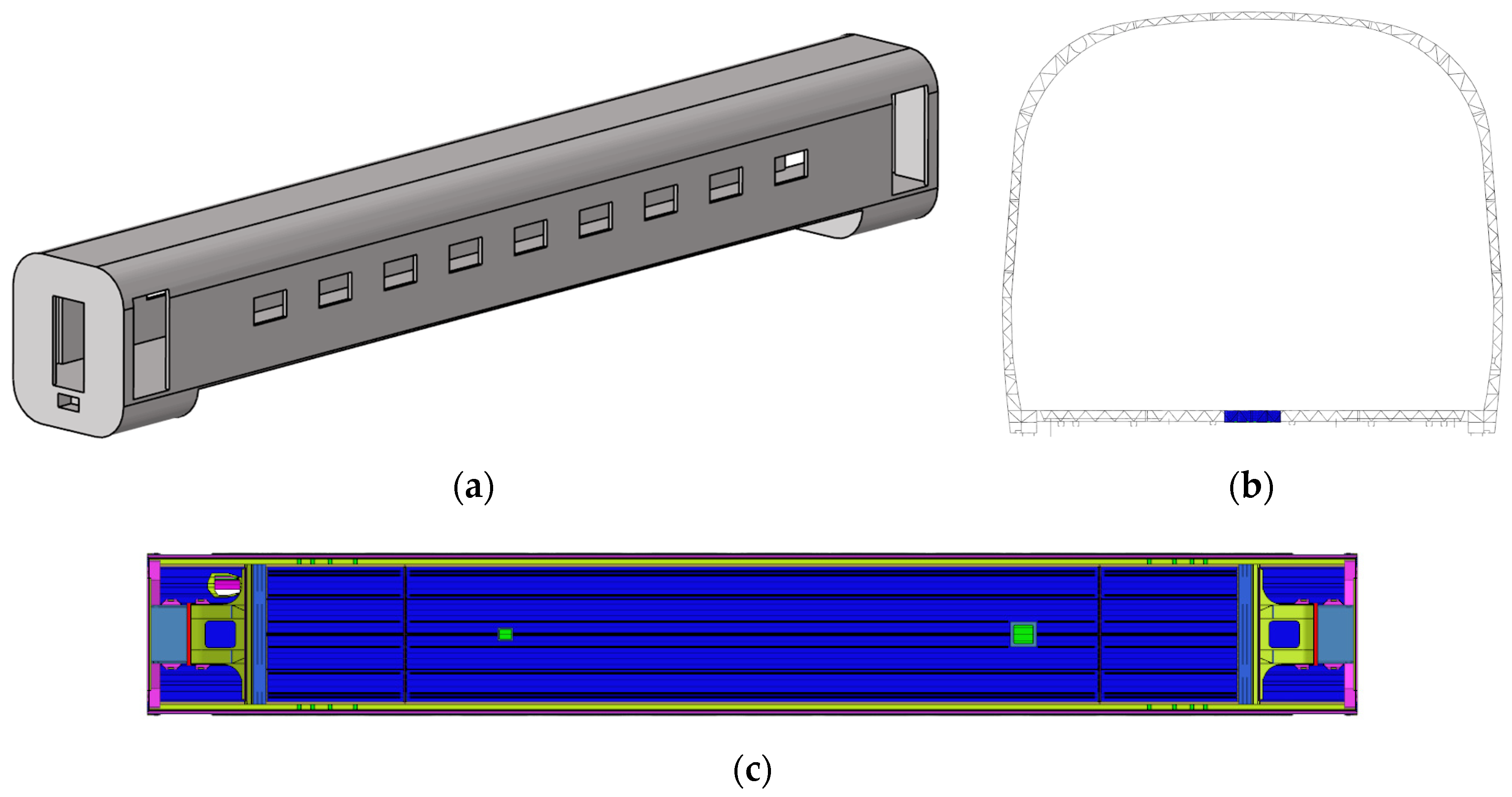
3.1. Selection of Topology Optimization Design Domain
3.2. Establishment of Topology Optimization Design Domain Model
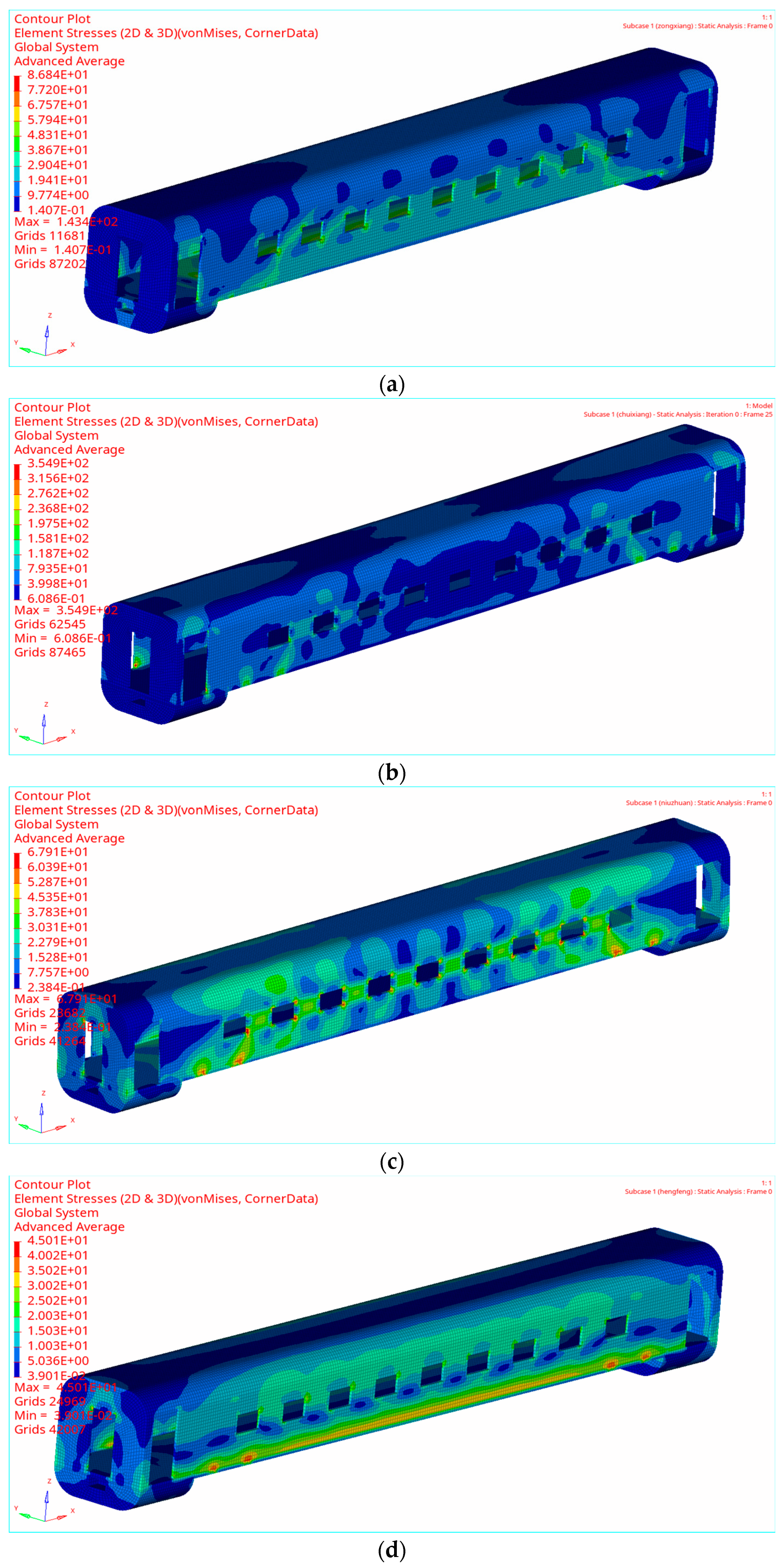
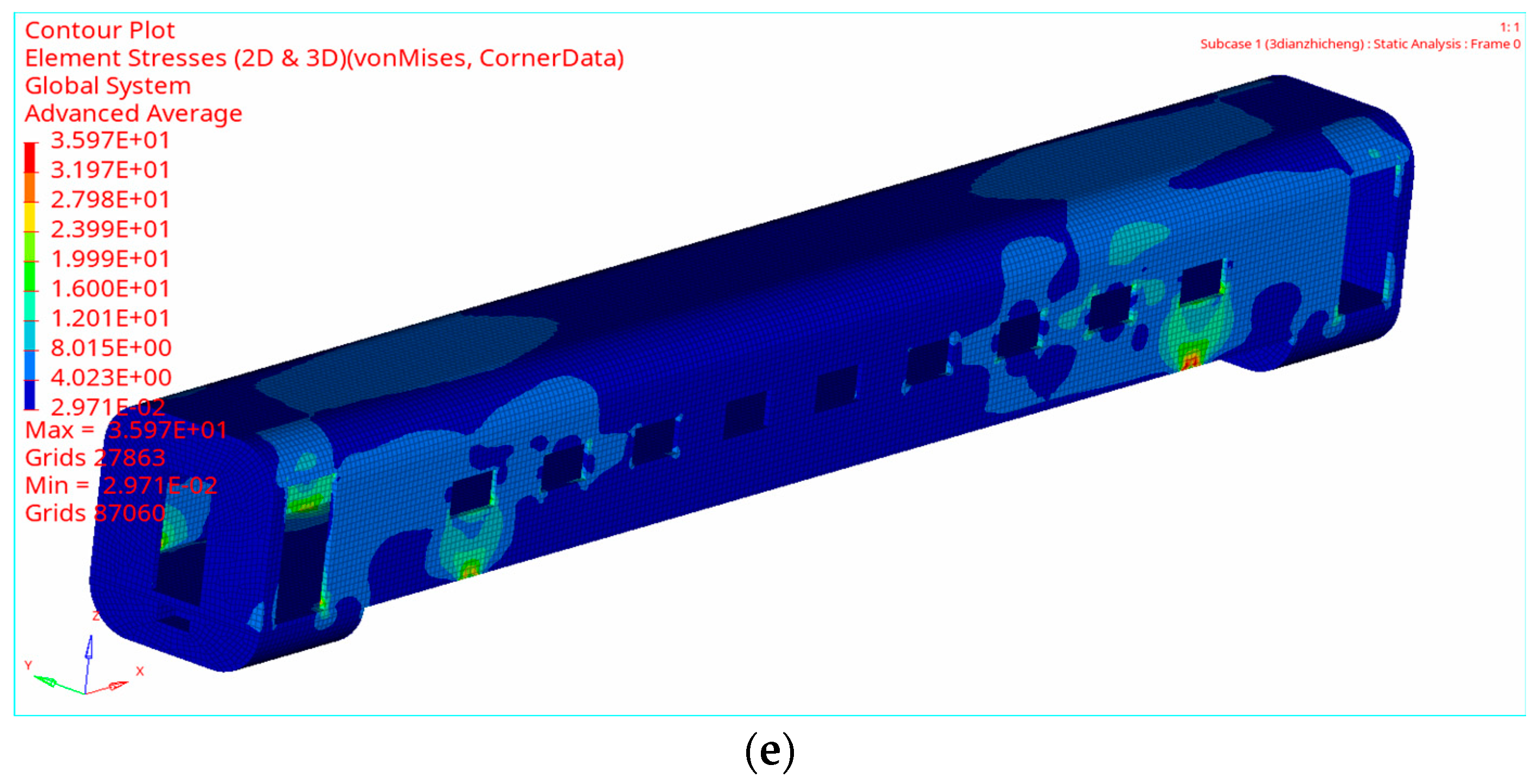
3.3. Results of Static Analysis
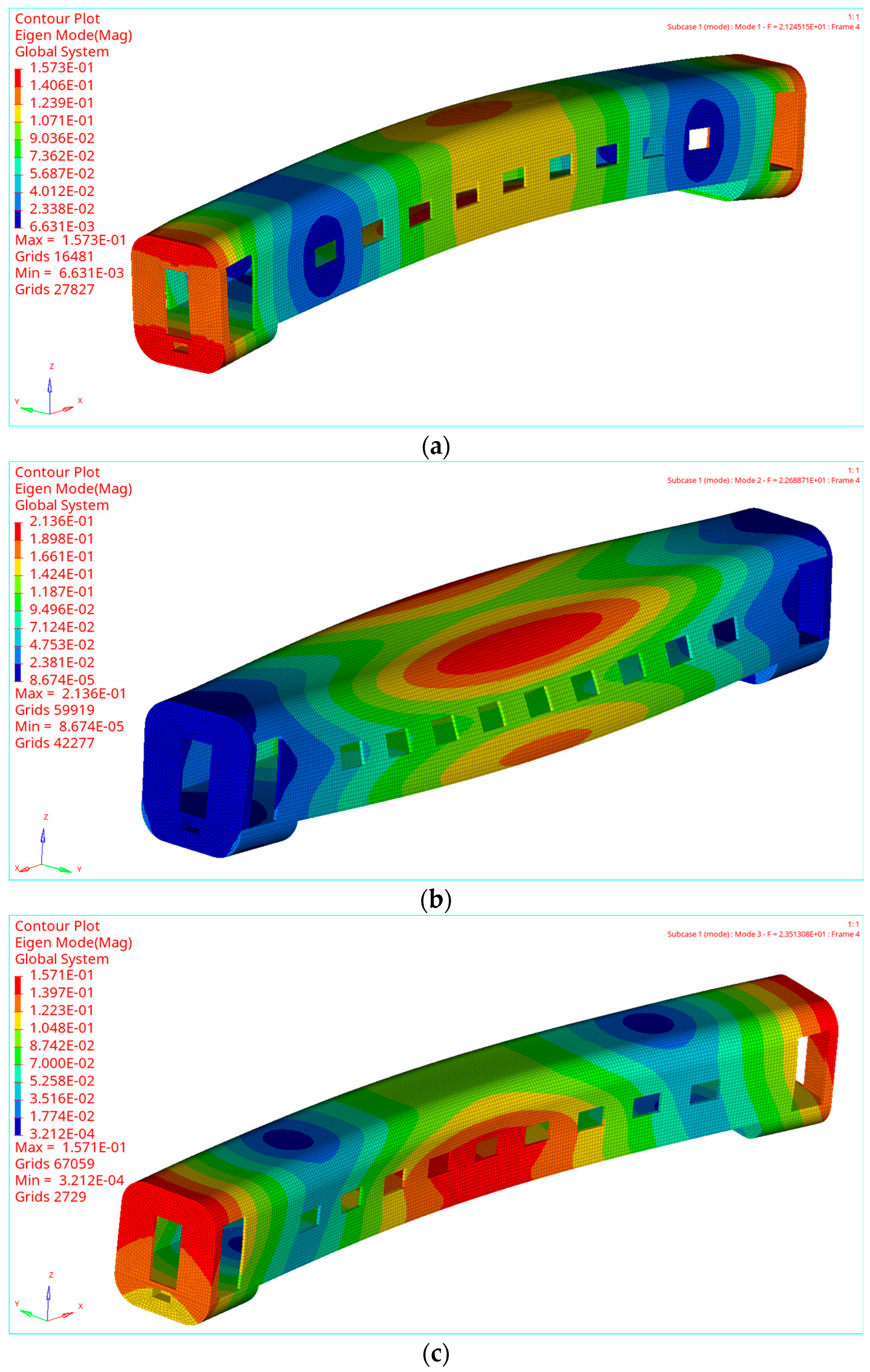
3.4. Results of Modal Analysis
4. Topology Optimization of Car-Body Structure
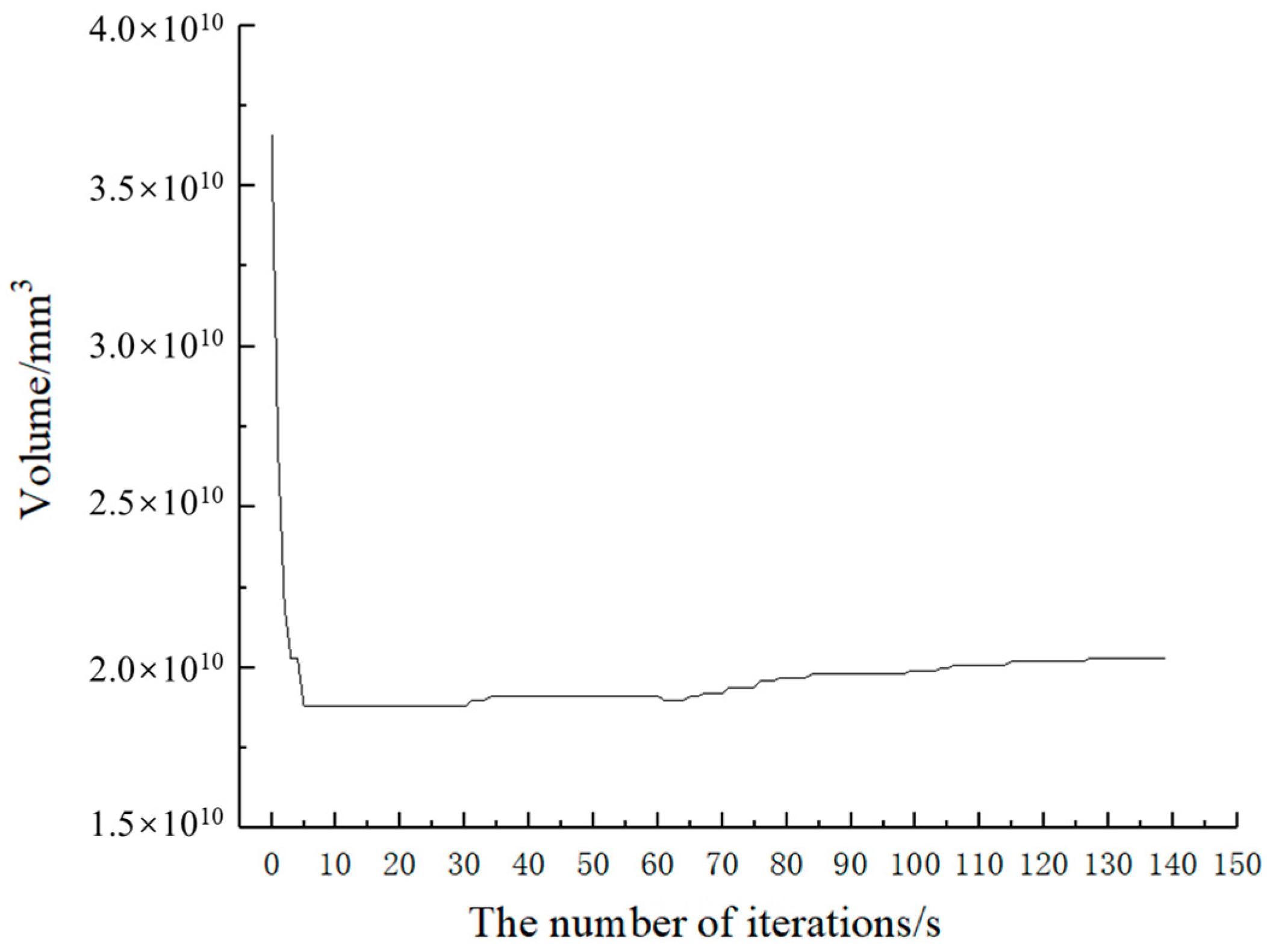
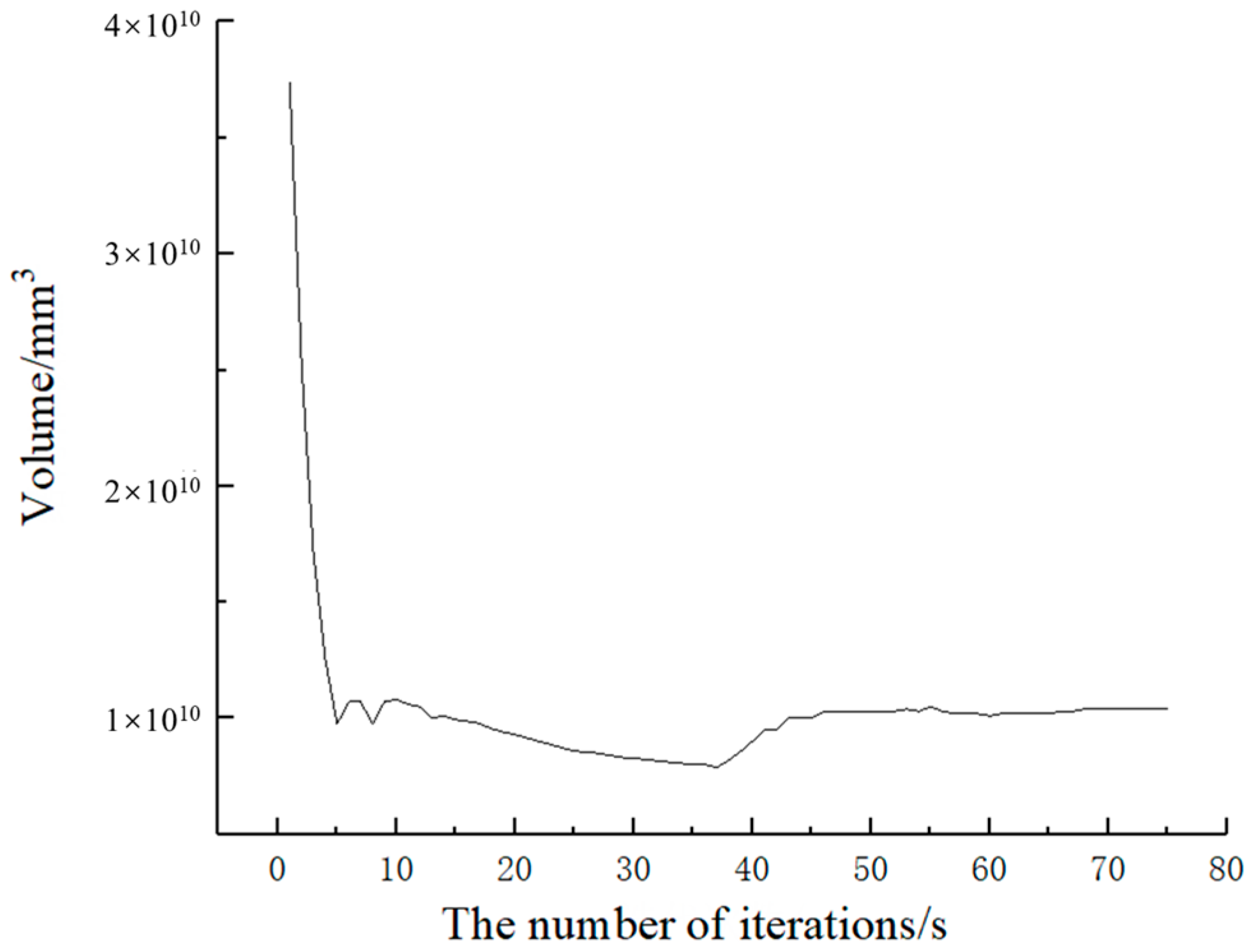
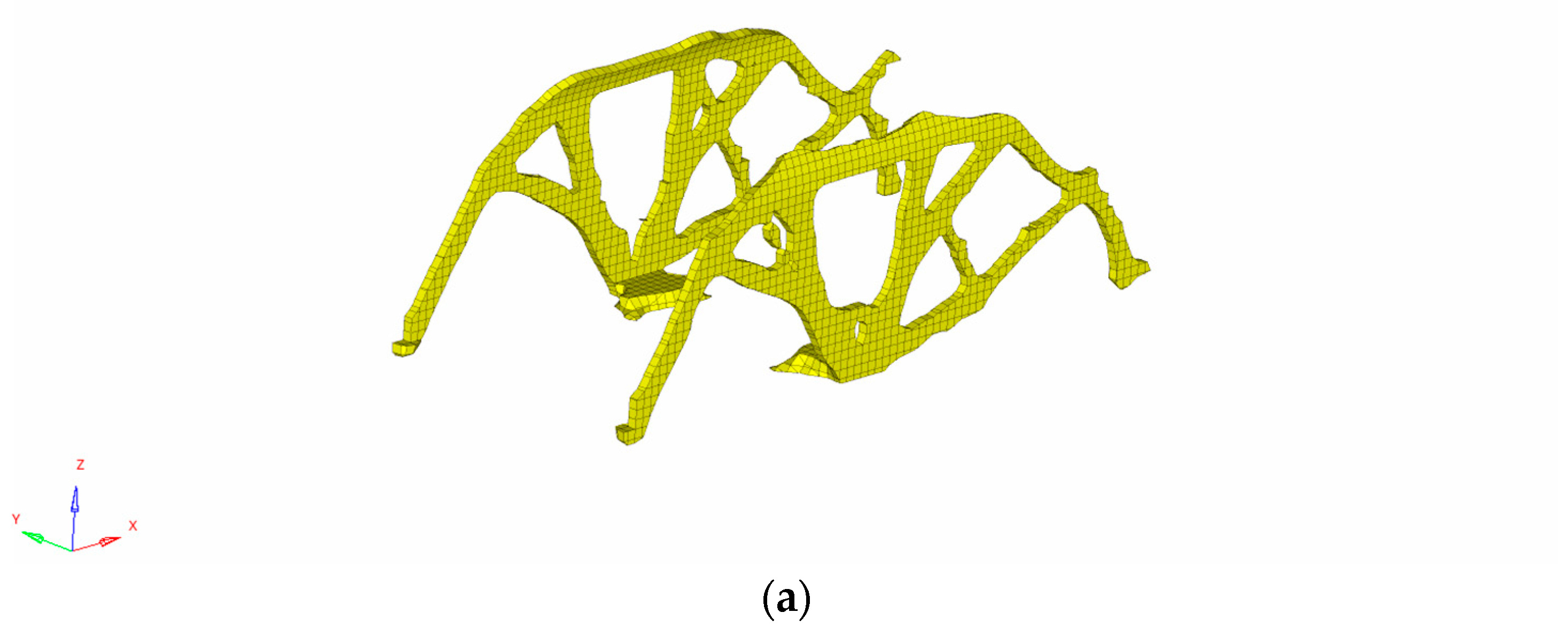
4.1. Topology Optimization Design
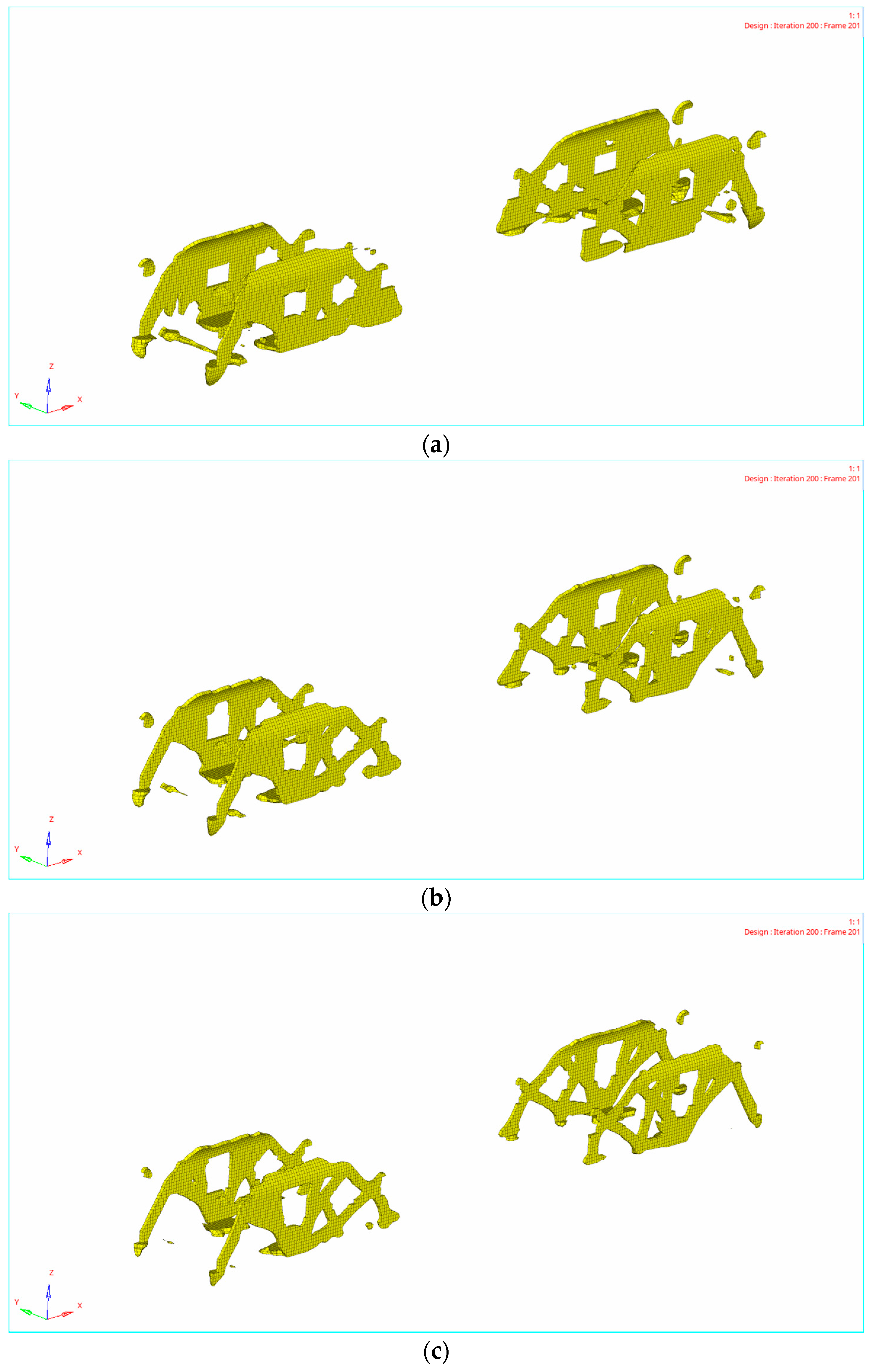
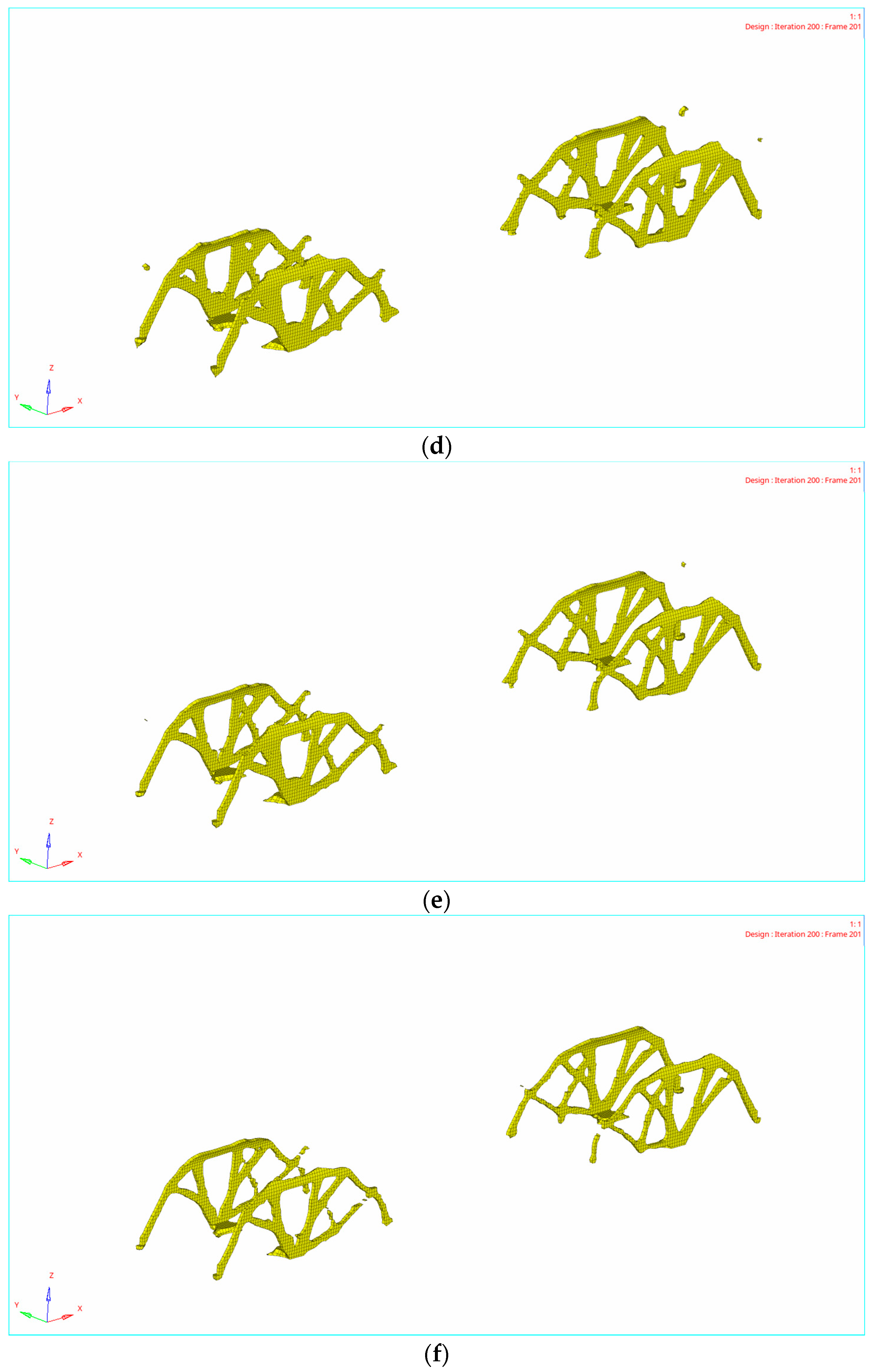
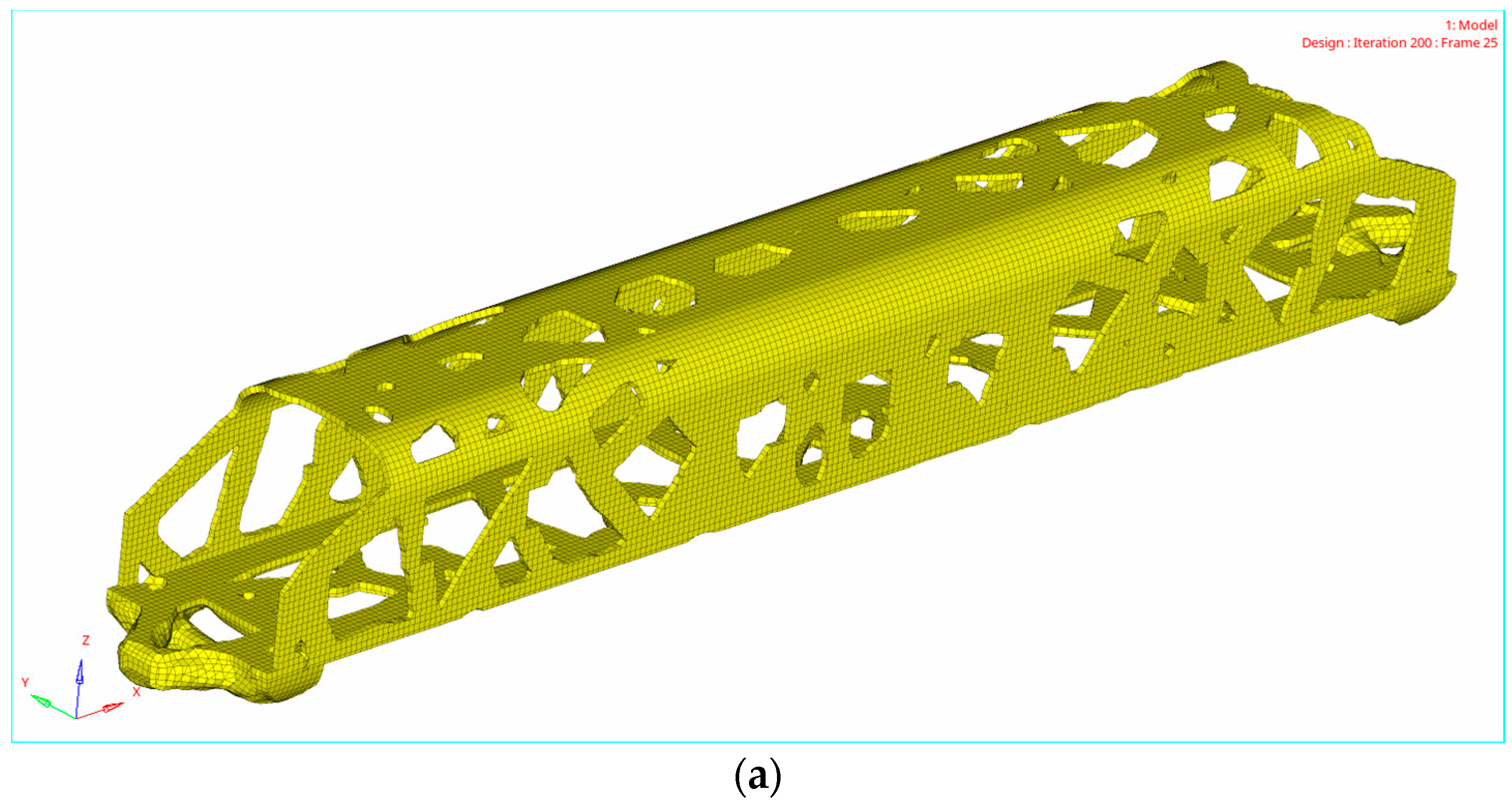
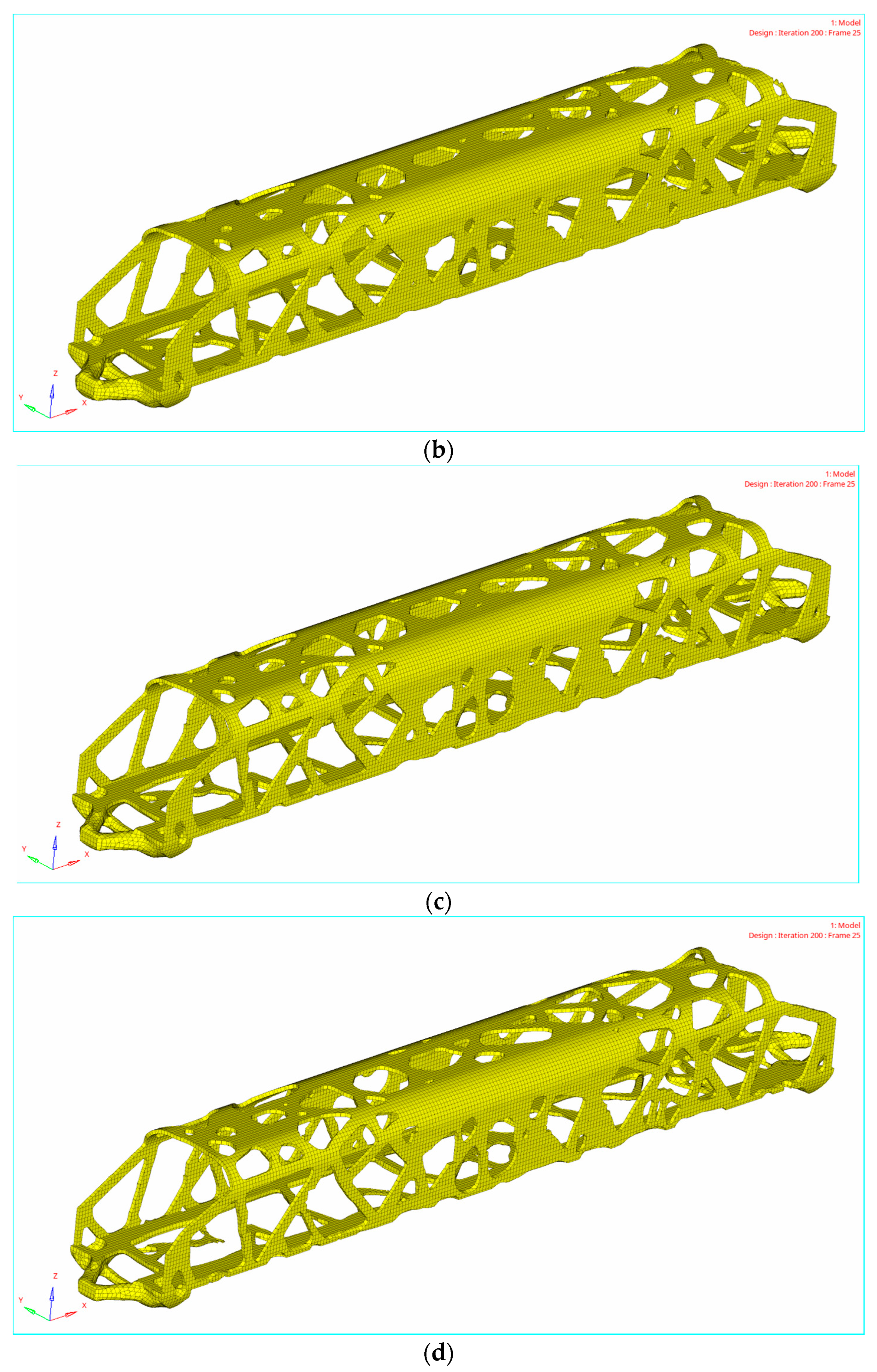
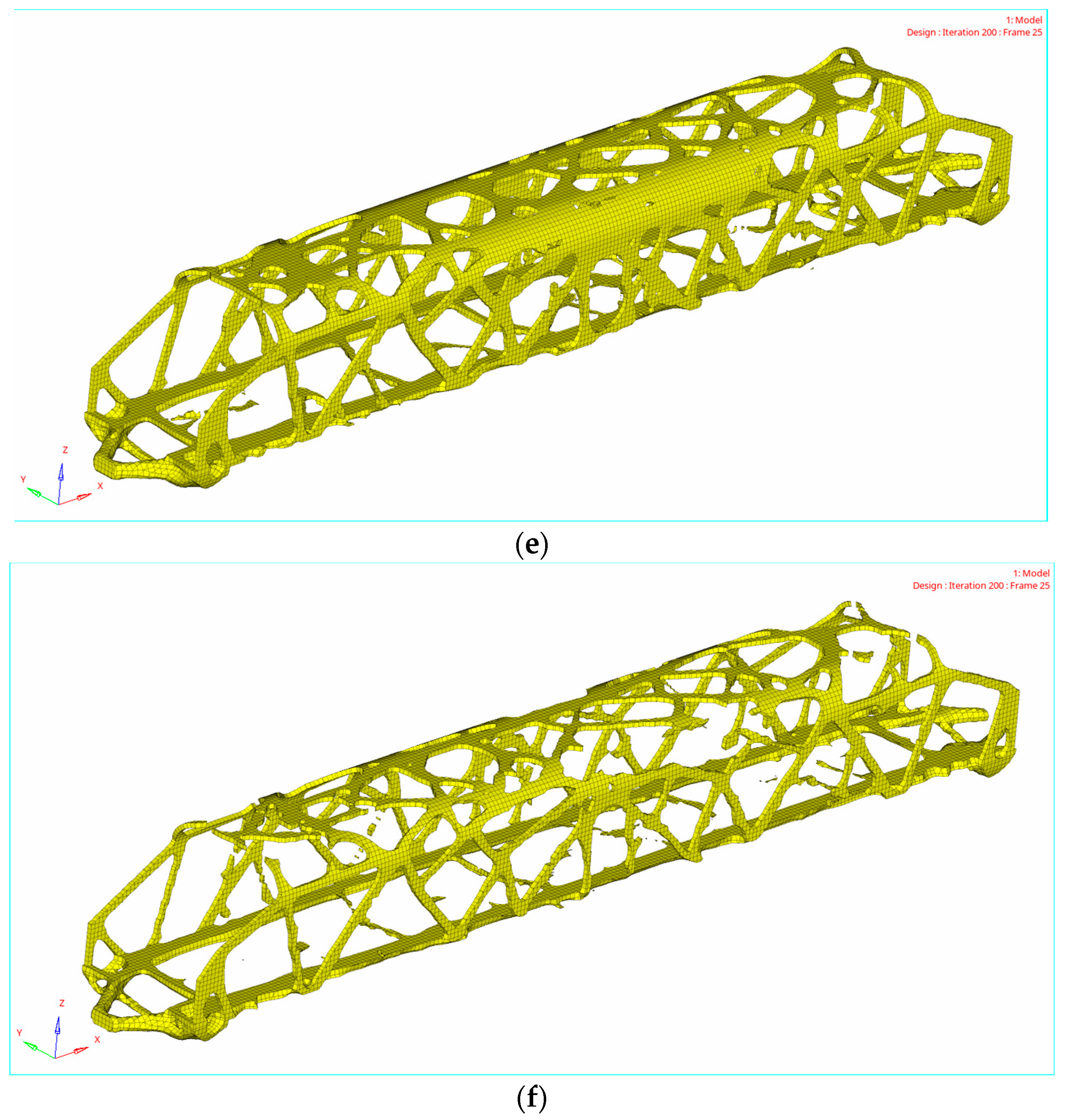
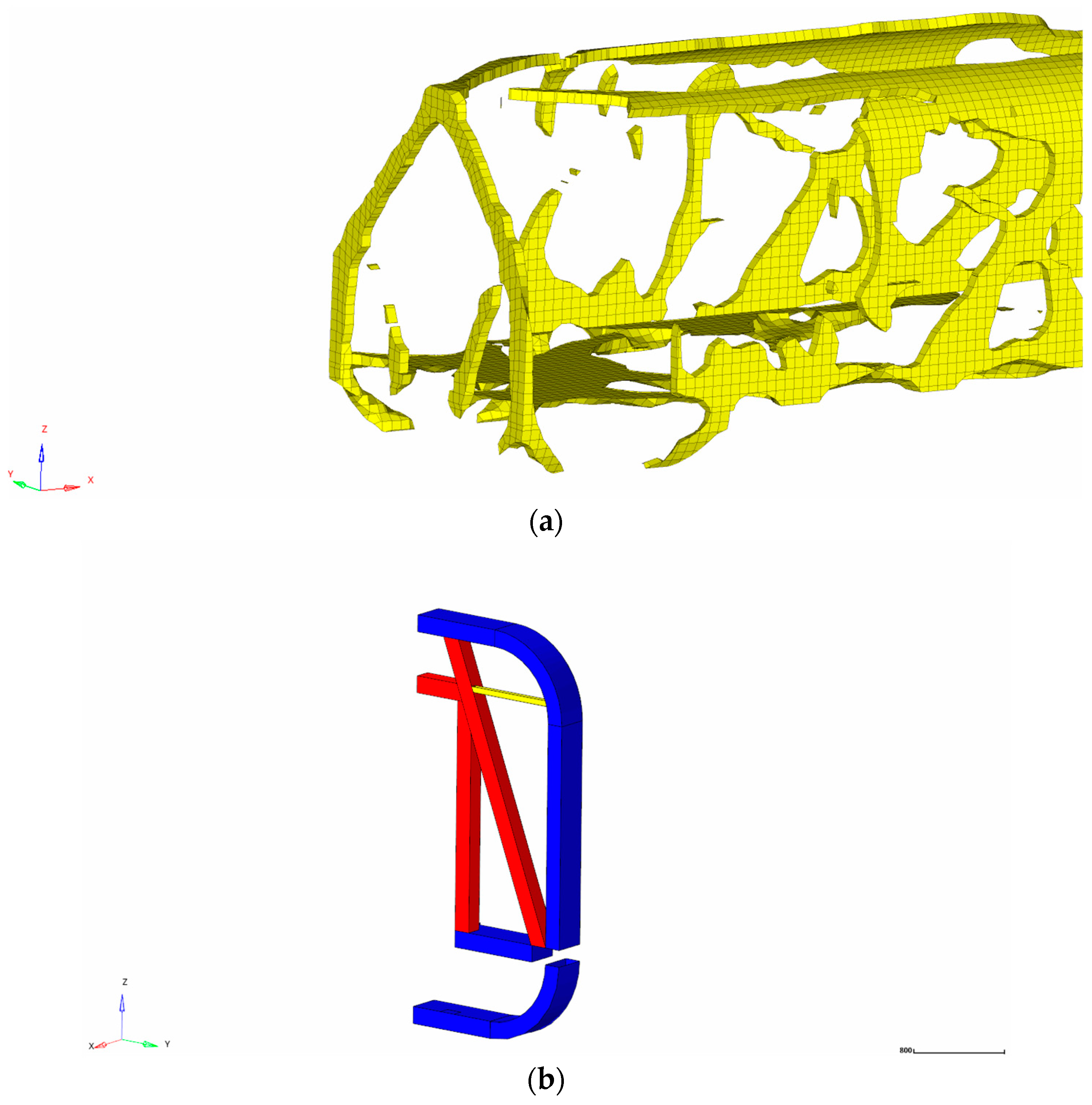
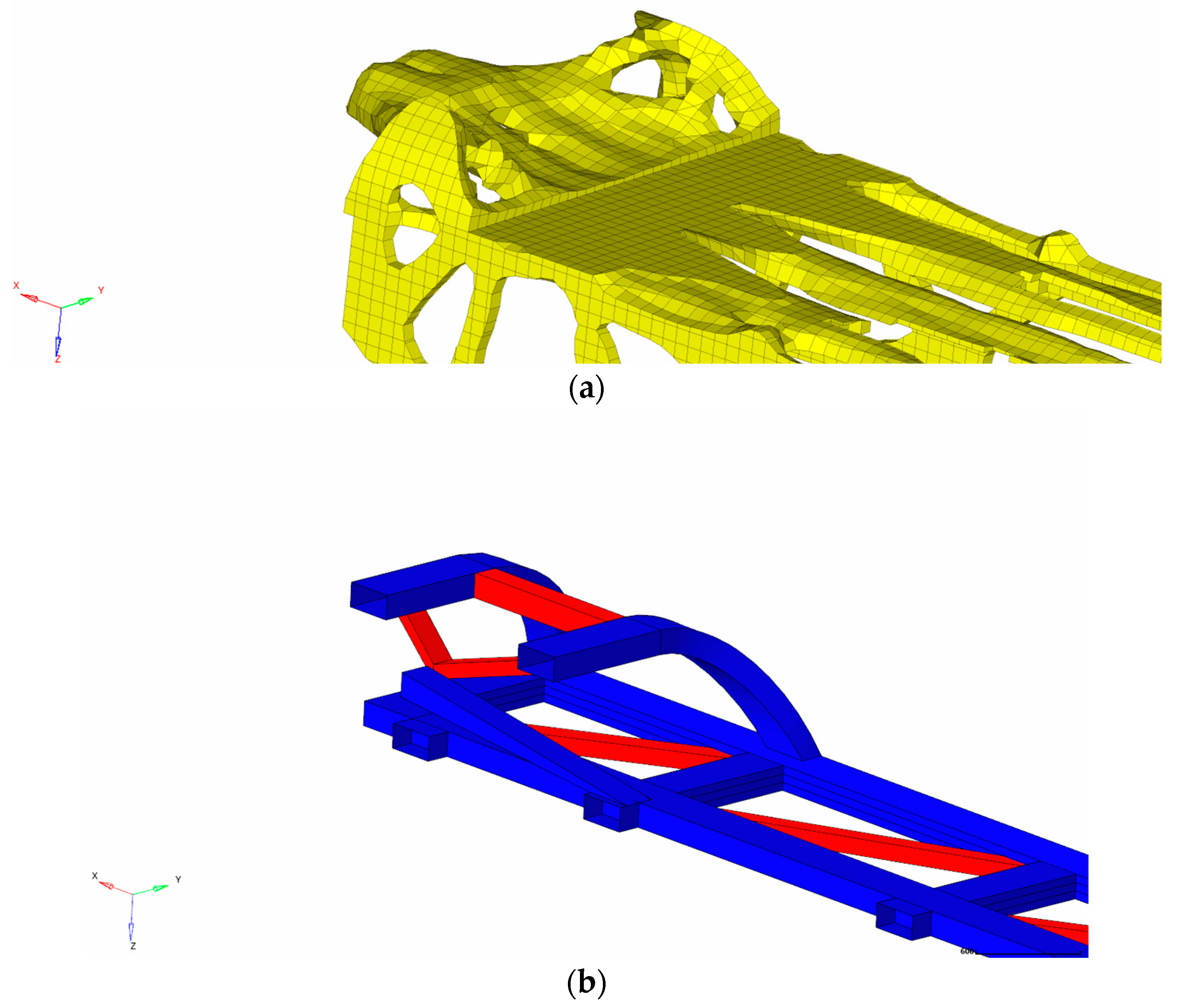
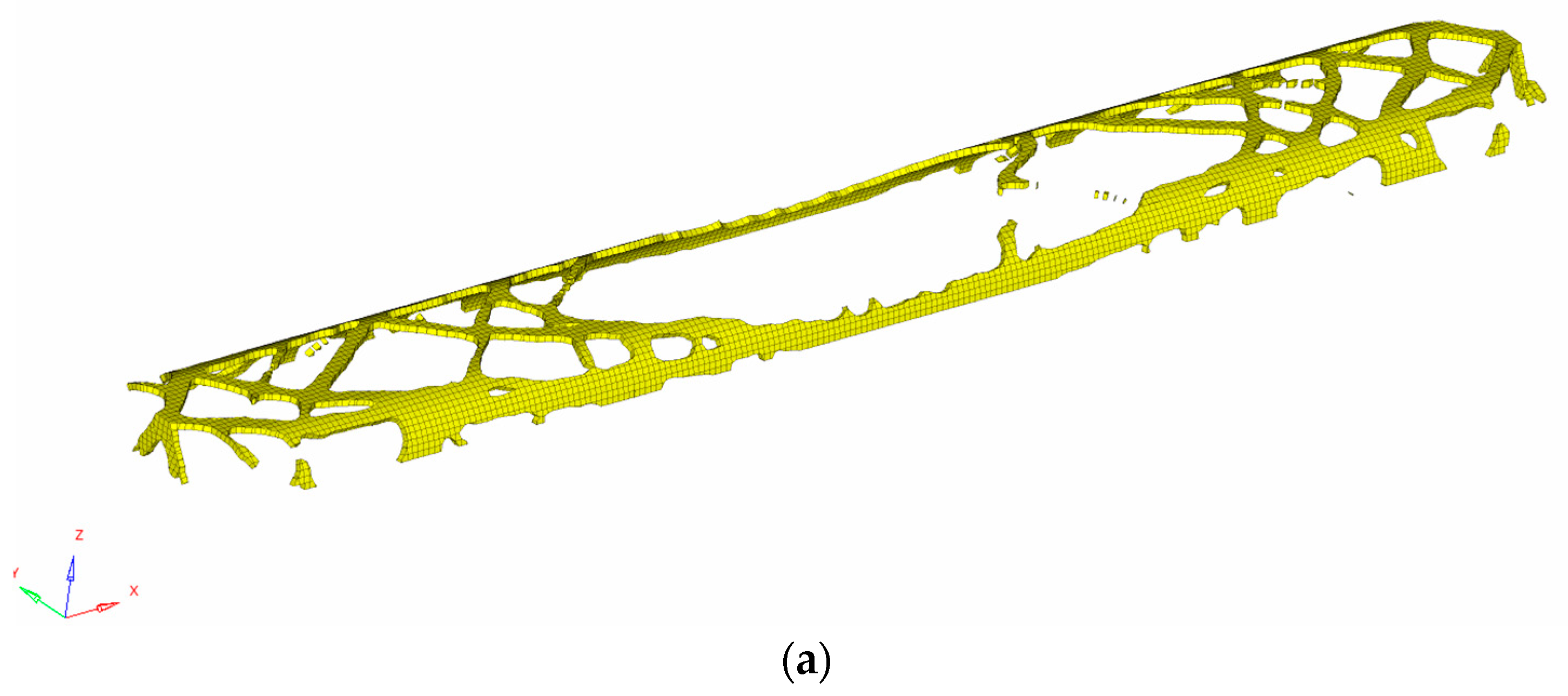
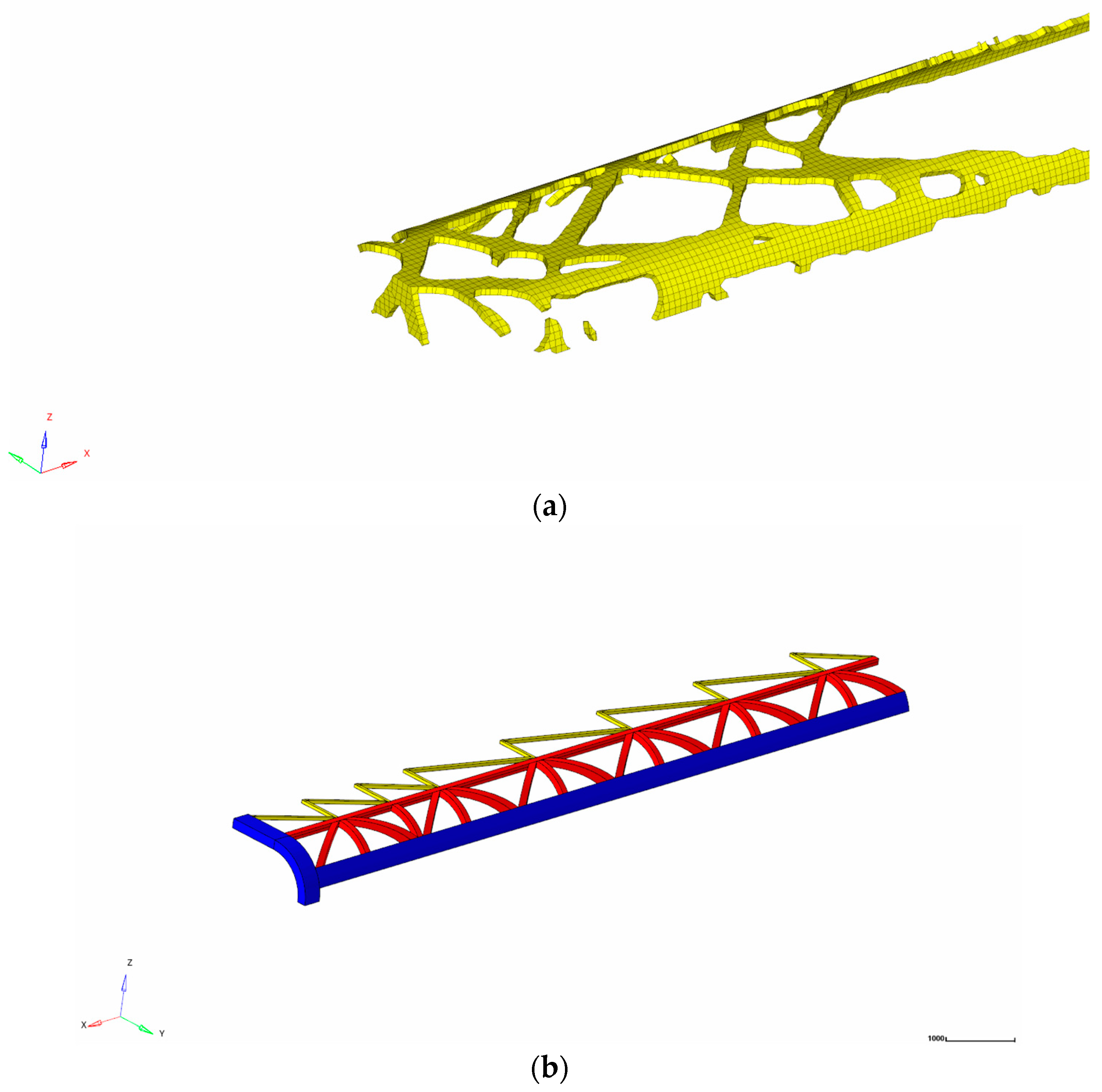
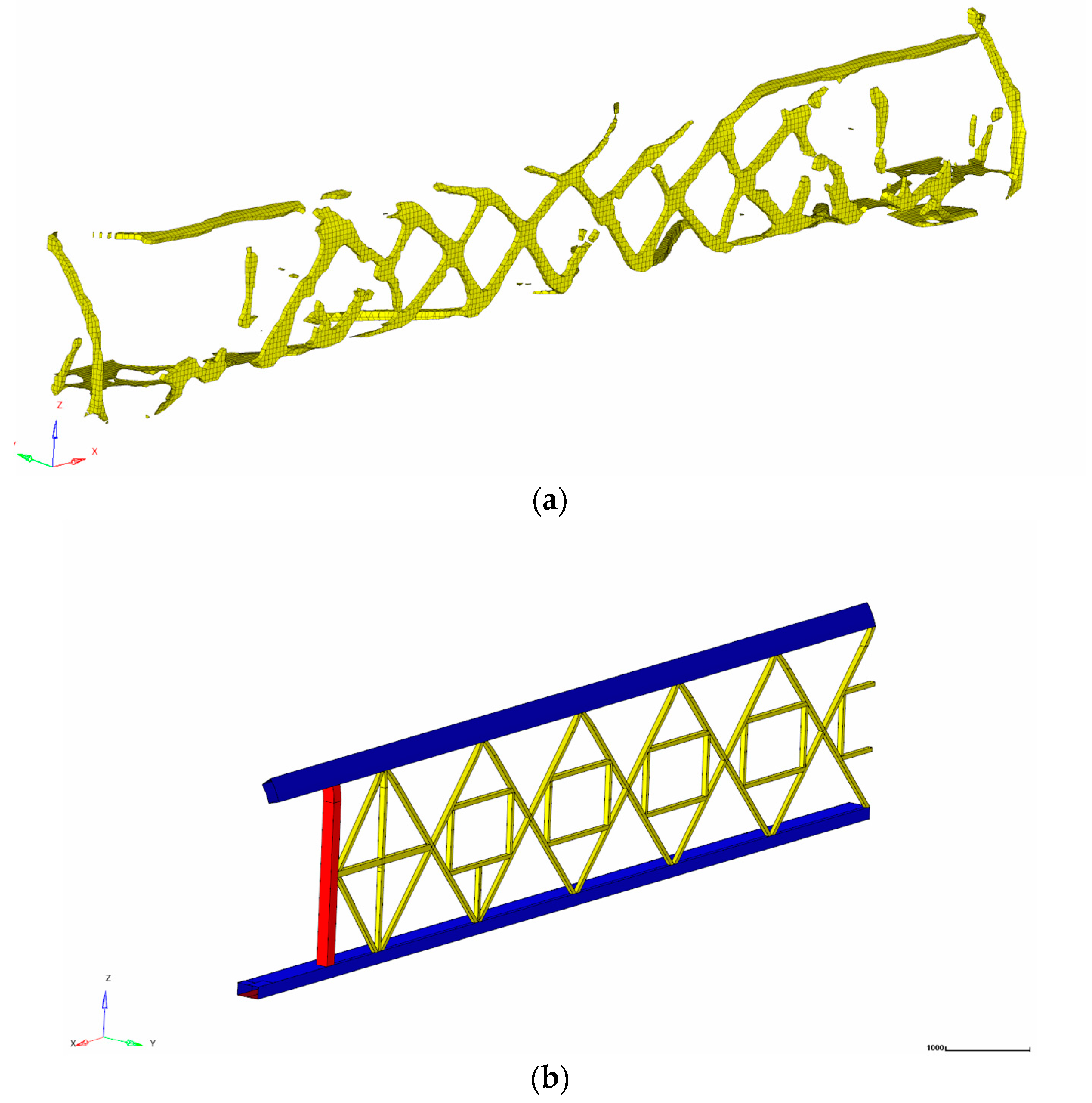
4.2. Topology Optimization Results
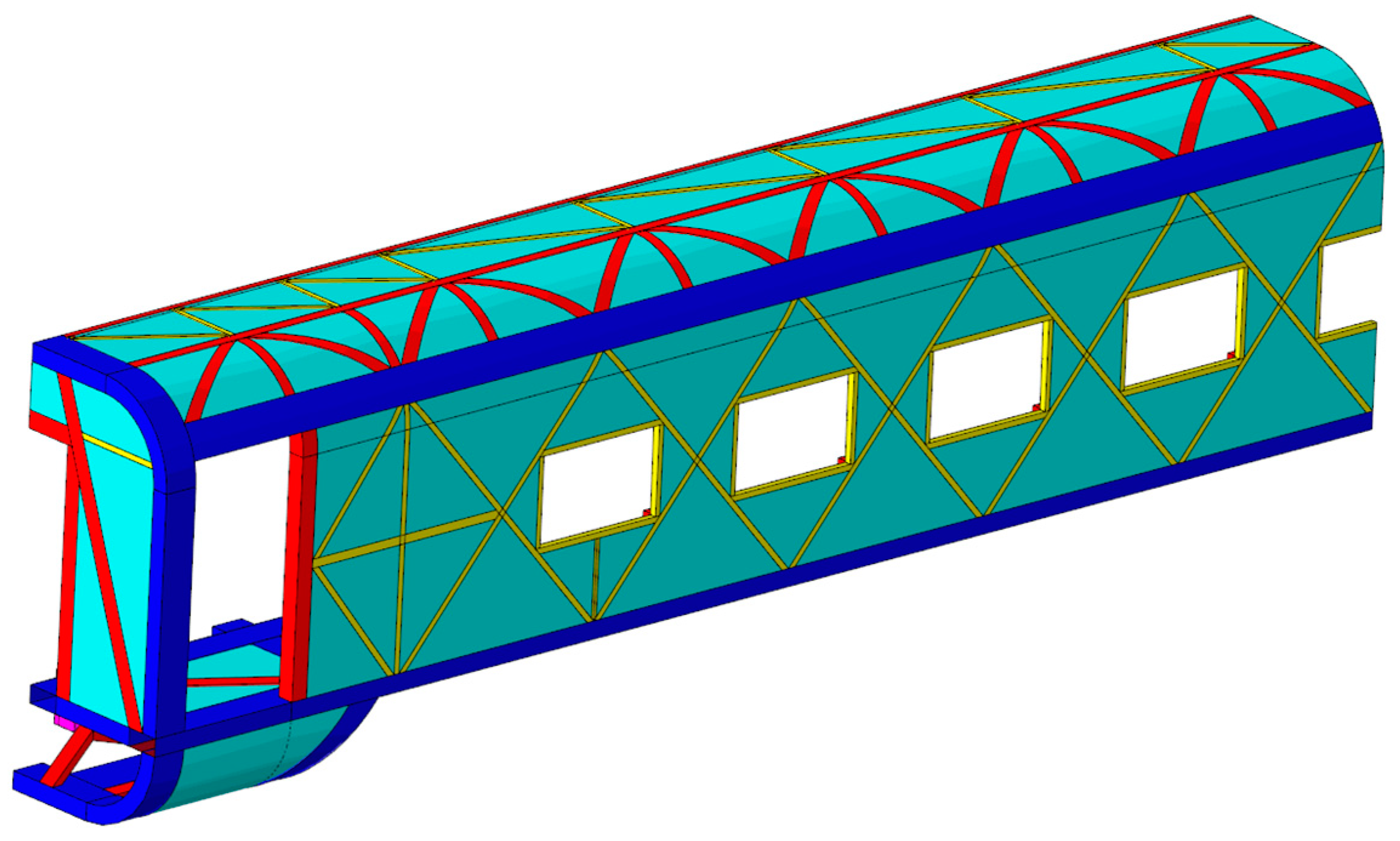
5. Reconstruction of Car-Body Bearing Structure
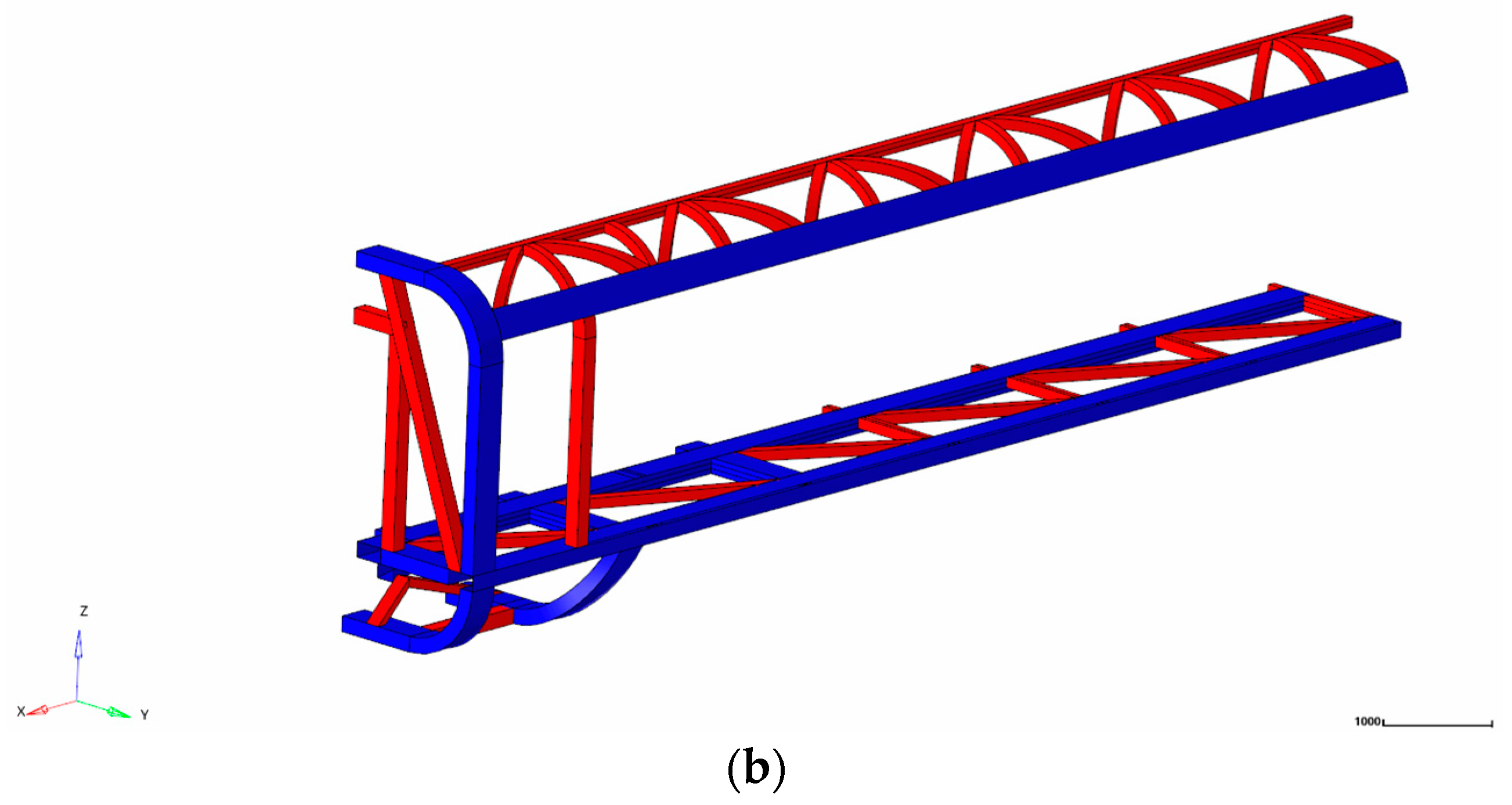
5.1. Design Method of Truss Car-Body Structure Reconstruction
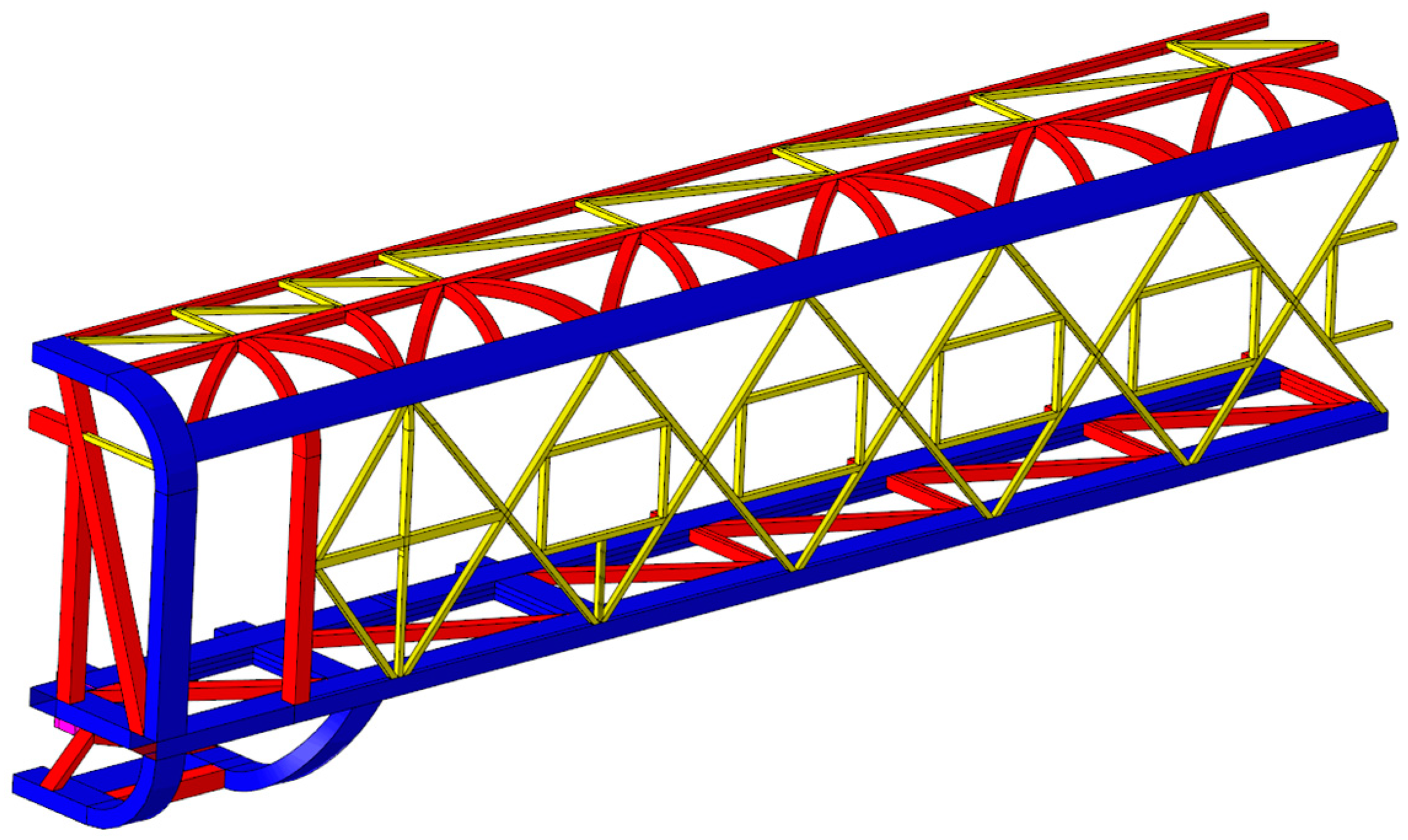
5.2. Establishment of Car-Body Geometry Model and Finite Element Model
5.3. Finite Element Analysis of the Reconstructed Model
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ding, S.S. Research on Key Technology of High-Speed Train Body Design. Ph.D. Thesis, Beijing Jiaotong University, Beijing, China, 2016. [Google Scholar]
- Zhang, Q.G.; Qiao, K.; Cao, Y. The development of foreign high-speed double decker EMU and its inspiration to China. China Railw. 2018, 7, 103–107. [Google Scholar] [CrossRef]
- Liu, C.Q.; Wang, L. 400 km/h cross-country interconnection high-speed EMUs. Electr. Drive Locomot. 2020, 2, 1–6. [Google Scholar] [CrossRef]
- Deng, H.; Zhang, G.Q.; Zhang, Y.; Wang, S.B.; Wang, C. Development Concept of Next Generation High-speed Intelligent EMU. Urban Mass Transit 2022, 25, 11–15. [Google Scholar]
- Harte, A.M.; McNamara, J.F.; Roddy, I.D. A multilevel approach to the optimisation of a composite light rail vehicle bodyshell. Compos. Struct. 2003, 63, 447–453. [Google Scholar] [CrossRef]
- Chiandussi, G.; Gaviglio, I.; Ibba, A. Topology optimisation of an automotive component without final volume constraint specification. Adv. Eng. Softw. 2014, 35, 609–617. [Google Scholar] [CrossRef]
- Chen, B.Z.; Zhang, X.Q.; Qiu, G.Y. Topology Optimization of Underframe for 400km/h High-Speed Train. Mach. Des. Manuf. 2021, 7, 272–275. [Google Scholar] [CrossRef]
- Zhang, Q.; Sun, Q.Z.; Liu, G.F. Finite Element Analysis and Topological Optimization of a Tracked Vehicle Body Based on Hypermesh. J. Jiamusi Univ. (Nat. Sci. Ed.) 2020, 38, 123–126. [Google Scholar]
- Ji, B.K. Research on Topology Optimization Design of High-Speed Train Body Structure Based on CRH EMU. Master’s Thesis, Sichuan University of Science & Engneering, Zigong, China, 2019. [Google Scholar]
- Zhang, L.; Zhang, J.Y.; Li, T.; Zhang, Y.D. Multi-objective aerodynamic optimization design of high-speed train head shape. J. Zhejiang Univ.-Sci. A 2017, 18, 841–854. [Google Scholar] [CrossRef]
- Zhang, L.; Dai, Z.Y.; Li, T.; Zhang, J.Y. Multi-objective aerodynamic shape optimization of a streamlined high-speed train using Kriging model. J. Zhejiang Univ.-Sci. A 2022, 23, 225–245. [Google Scholar] [CrossRef]
- Deb, A.; Chou, C.; Dutta, U.; Gunti, S. Practical Versus RSM-Based MDO in Vehicle Body Design. SAE Int. J. Passeng. Cars-Mech. Syst. 2012, 5, 110–119. [Google Scholar] [CrossRef]
- Chen, X.; Wang, Y.Q.; Sun, K.; Feng, Z.Y.; Zhao, W.H.; Lu, B.H. Multi-Objective Optimization for Section of Sandwich Plate Applied to High-Speed Train Compartments. J. Xi’an Jiaotong Univ. Nat. Sci. Ed. 2013, 47, 62–67. [Google Scholar]
- Sahib, M.M.; Kovács, G. Elaboration of a Multi-Objective Optimization Method for High-Speed Train Floors Using Composite Sandwich Structures. Appl. Sci. 2023, 13, 3876. [Google Scholar] [CrossRef]
- Miao, B.R.; Zhang, L.M.; Zhang, W.H.; Yin, H.T.; Jin, D.C. High-speed Train Carbody Structure Fatigue Simulation Based on Dynamic Characteristics of the Overall Vehilce. J. China Railw. Soc. 2010, 32, 101–108. [Google Scholar] [CrossRef]
- Tang, Q.C.; Ma, L.; Zhao, D.; Lei, J.Y.; Wang, Y.H. A multi-objective cross-entropy optimization algorithm and its application in high-speed train lateral control. Appl. Soft Comput. 2022, 115, 108151. [Google Scholar] [CrossRef]
- Wang, Q.S.; Zeng, J.; Shi, H.L.; Jiang, X.S. Parameter optimization of multi-suspended equipment to suppress carbody vibration of high-speed railway vehicles: A comparative study. Int. J. Rail Transp. 2023, 2023, 2291202. [Google Scholar] [CrossRef]
- Wang, S.M.; Peng, Y.; Wang, T.T.; Che, Q.W.; Xu, P. Collision performance and multi-objective robust optimization of a combined multi-cell thin-walled structure for high speed train. Thin-Walled Struct. 2019, 135, 341–355. [Google Scholar] [CrossRef]
- Peng, Y.; Hou, L.; Che, Q.W.; Xu, P.; Li, F. Multi-objective robust optimization design of a front-end underframe structure for a high-speed train. Eng. Optim. 2019, 51, 753–774. [Google Scholar] [CrossRef]
- Lu, S.S.; Xu, P.; Yan, K.P.; Yao, S.G.; Li, B.H. A force/stiffness equivalence method for the scaled modelling of a highspeed train head car. Thin-Walled Struct. 2019, 137, 129–142. [Google Scholar] [CrossRef]
- Wang, R.; Gao, S.M.; Wu, H.Y. Progress in Hexahedral Mesh Generation and Optimization. J. Comput.-Aided Des. Comput. Graph. 2020, 32, 693–708. [Google Scholar]
- Papanicolau, G.; Bensoussan, A.; Lions, J.L. Asymptotic Analysis for Periodic Structures; Elsevier: New York, NY, USA, 1978; ISBN 978-0-444-85172-7. [Google Scholar]
- Wang, J. Application and Analysis of Asymptotic Homogenization Method in Masonry. Master’s Thesis, Xiangtan University, Xiangtan, China, 2013. [Google Scholar]
- Guedes, J.; Kikuchi, N. Preprocessing and postprocessing for materials based on the homogenization method with adaptive finite element methods. Comput. Method. Appl. M 1990, 83, 143–198. [Google Scholar] [CrossRef]
- Zhang, G.F.; Xu, L.; Li, D.S.; Yu, F.C. Research on Sensitivity Filtering of Continuum Topology Optimization. Modul. Mach. Tool Autom. Manuf. Tech. 2021, 06, 29–32. [Google Scholar] [CrossRef]
- Xie, Y.M.; Steven, G.P. Evolutionary Structural Optimization; Berlin Springer-Verlag: London, UK, 1997; ISBN 978-3-540-76153-2. [Google Scholar]



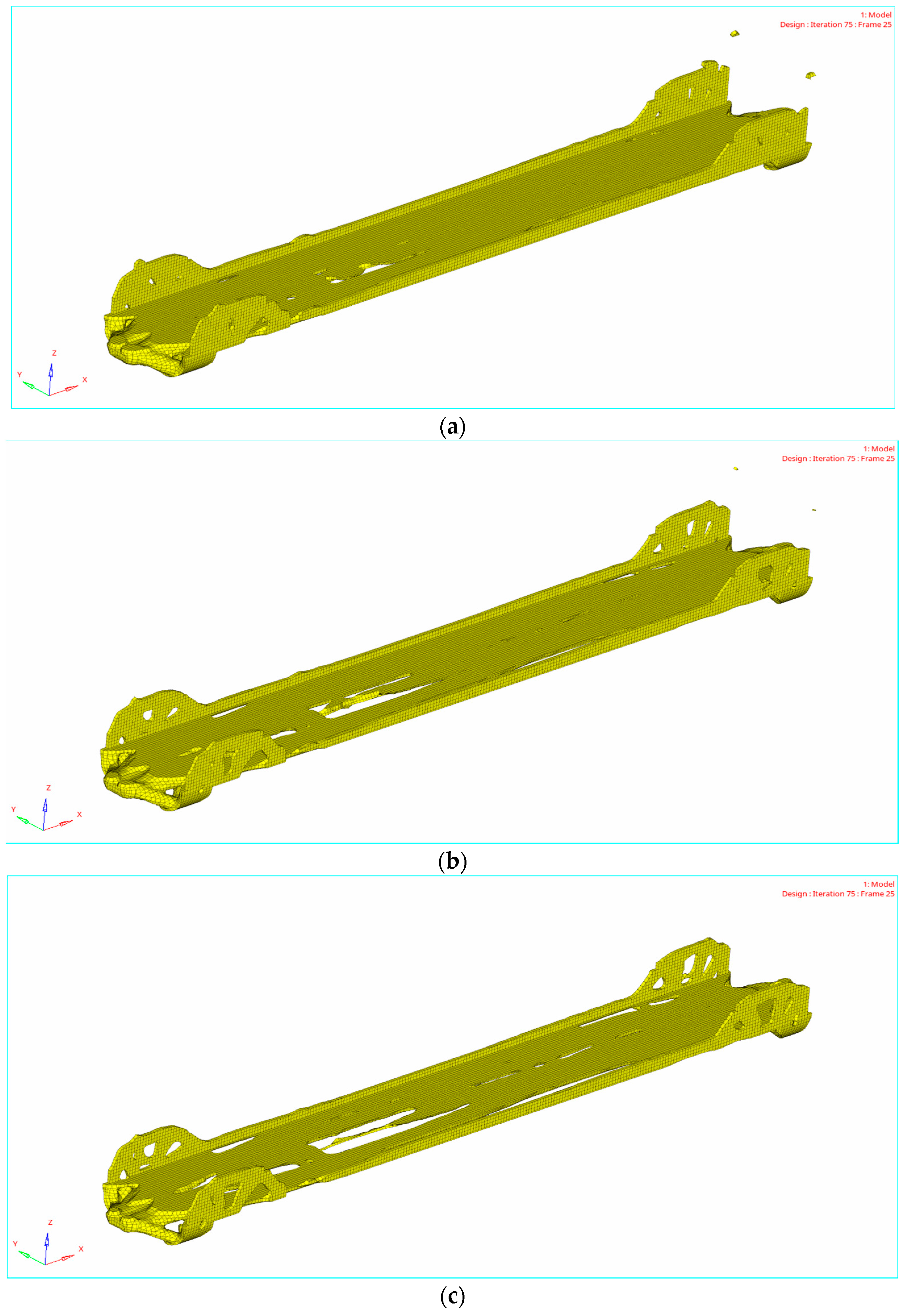
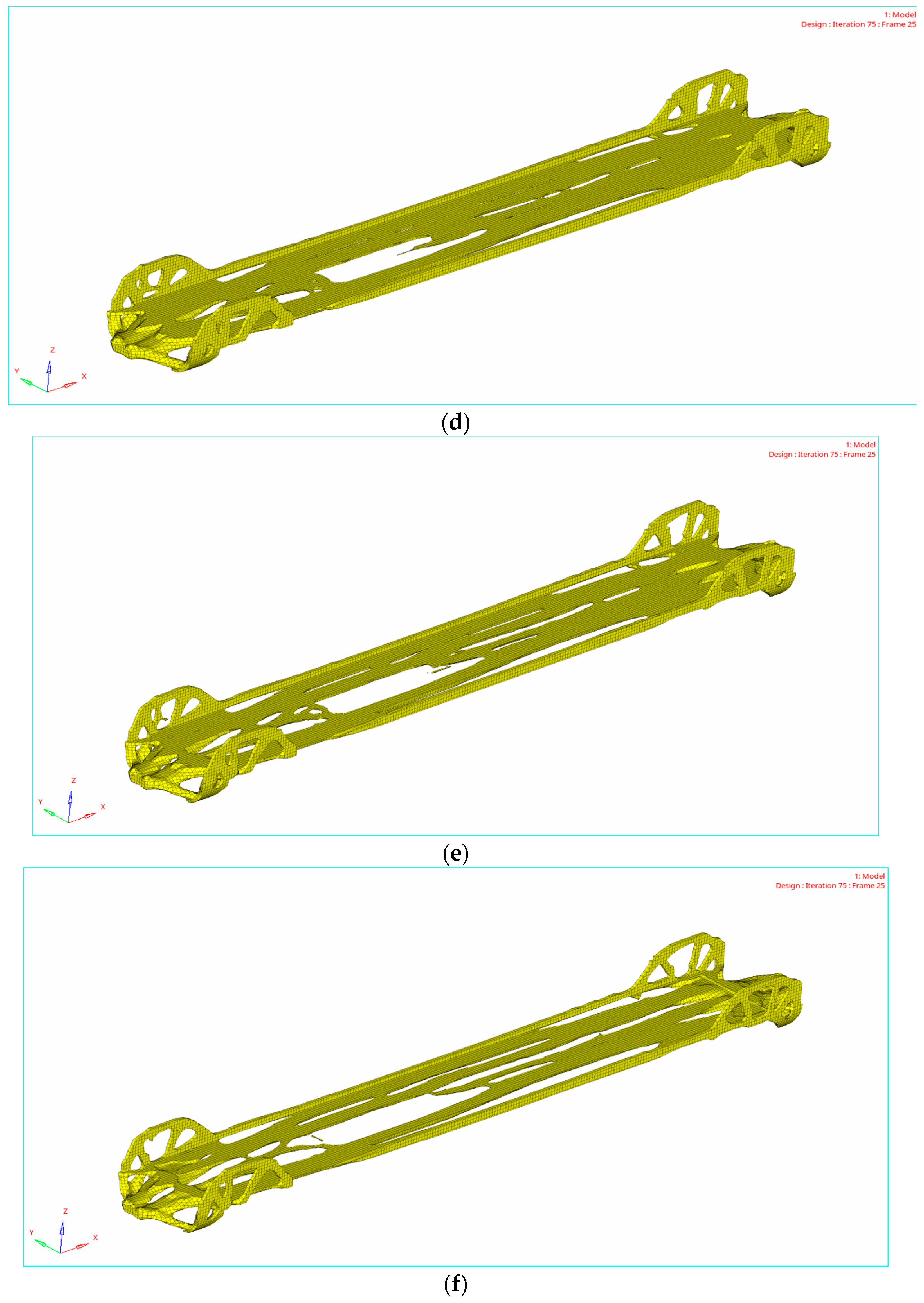

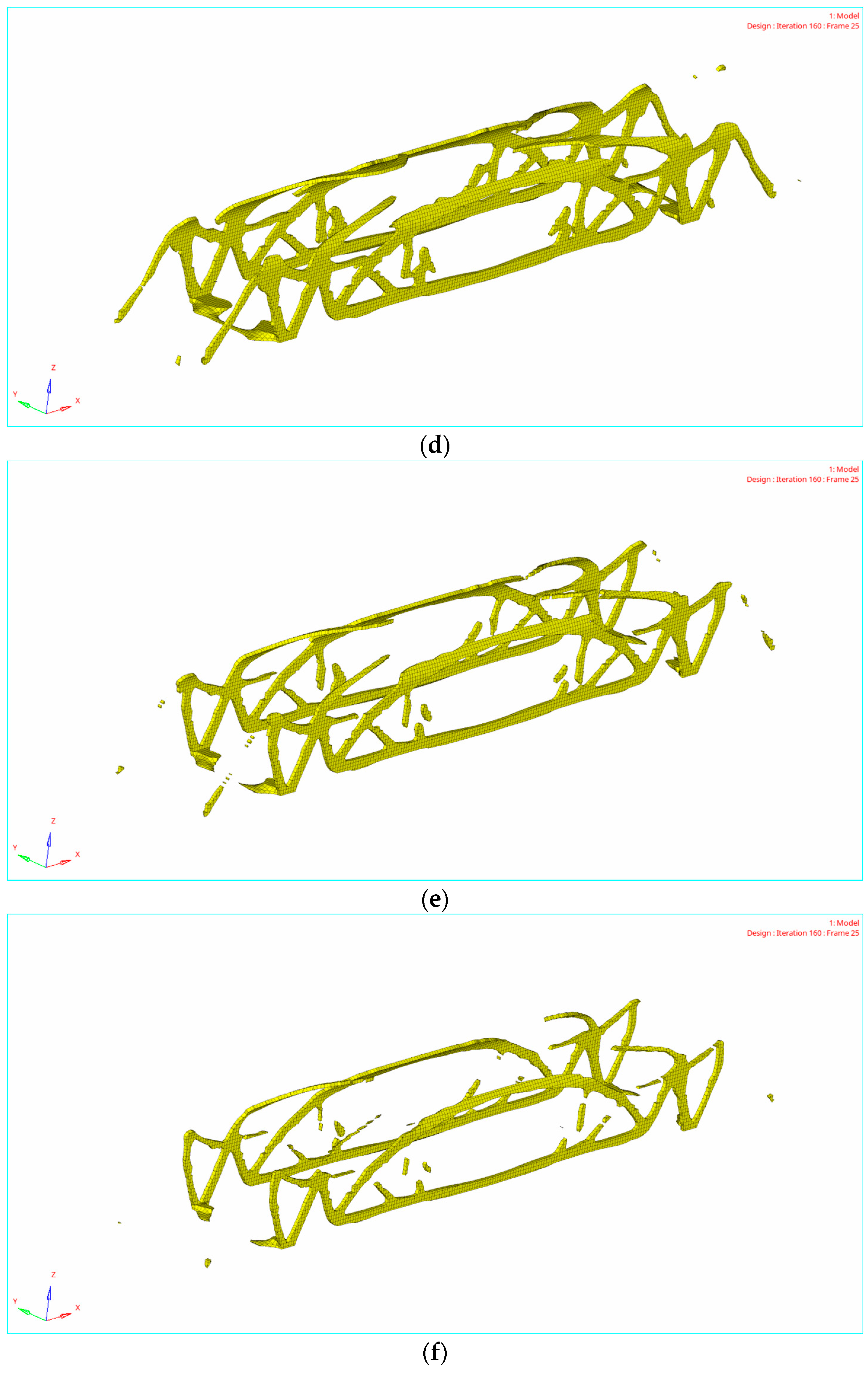

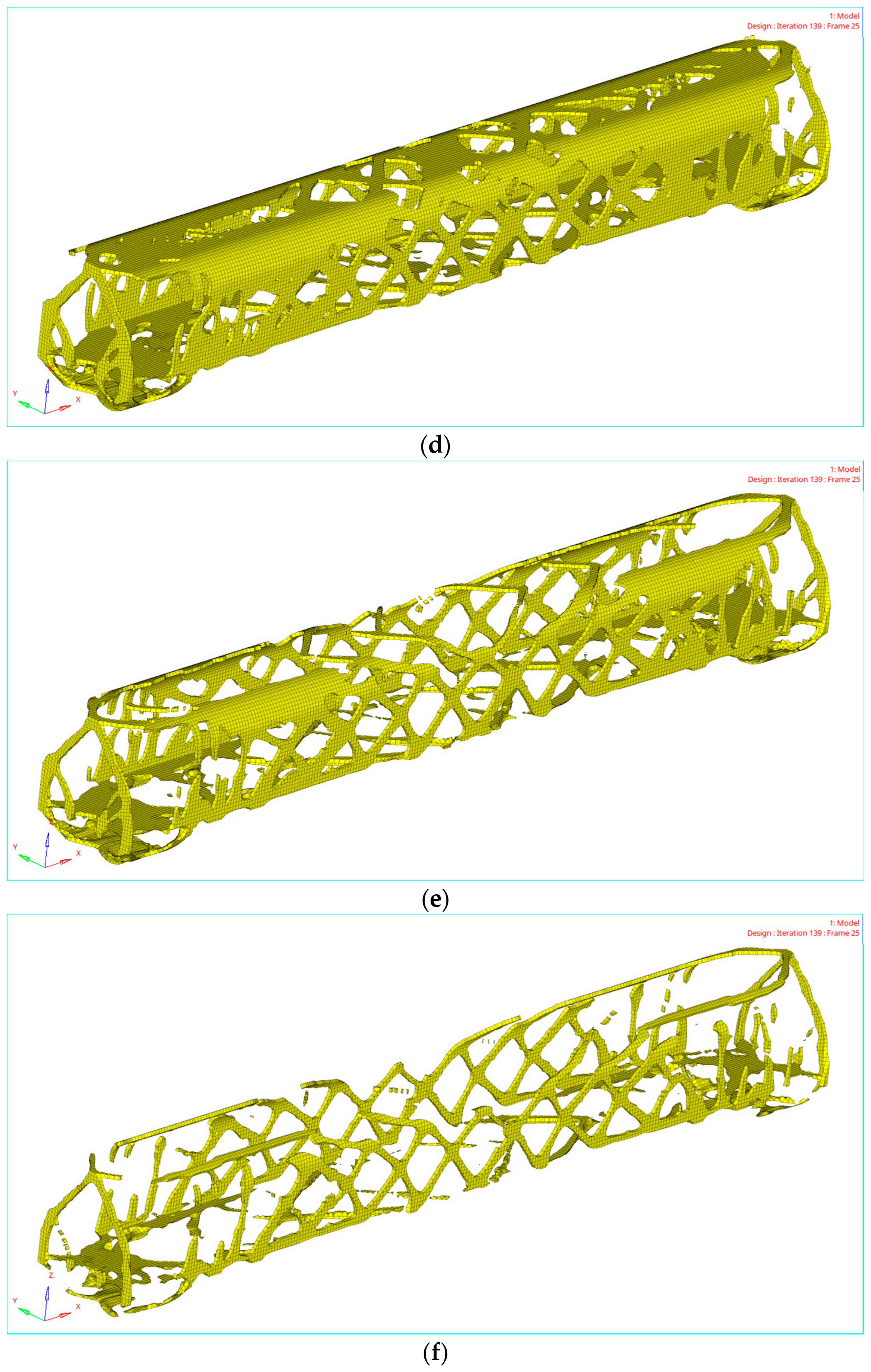







| Structure Size | L/mm |
|---|---|
| Car-body length | 25,000 |
| Fixed distance | 17,800 |
| Car-body width | 3360 |
| Car-body height | 4050 |
| Height from coupler centerline to rail surface | 950 |
| Working Condition | Load | Restraint | Condition Design Diagram |
|---|---|---|---|
| Longitudinal load | Compression force of 1500 kN for front-end coupler seat Compression forces of 300, 300, and 400 kN to the front-end wall near the roof, side wall, and chassis, respectively | Longitudinal constraint at the rear end wall |  |
| Vertical load | 1.3 times the weight of the car body | Vertical restraint at the secondary suspension |  |
| Torsional load | Unit torsional load 1 kN·m | Full restraint at the secondary suspension |  |
| Crosswind load | Unit wind pressure 450 Pa | Full restraint at the secondary suspension | 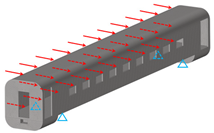 |
| Three-point support load | - | Apply vertical displacement to constrained support points | 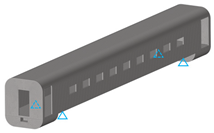 |
| Working Condition | Maximum Von Mises Stress/MPa |
|---|---|
| Longitudinal load | 86.8 |
| Vertical load | 63.3 |
| Torsional load | 67.9 |
| Crosswind load | 45.0 |
| Three-point support load | 36.0 |
| Modal Order Number | Mode Shape of the Car-Body Mode | |
|---|---|---|
| Frequency/Hz | Vibration Mode | |
| 1 | 21.25 | First vertical bending deformation |
| 2 | 22.69 | First diamond deformation |
| 3 | 23.51 | First transverse bending deformation |
| 4 | 30.64 | Breathing deformation |
| Parameter | Description | Value |
|---|---|---|
| MINDIM | Minimum member size | 150 |
| MAXDIM | Maximum member size | 400 |
| OBJTOL | Tolerance of target function | 0.005 |
| CHECKER | Checkerboard parameter | 1 |
| DISCRETE | Discrete parameter | 1 |
| Sequence | Description | Number/t | |
|---|---|---|---|
| 1 | Weight of vehicle maintenance equipment (excluding bogie and car-body structure) | 25.46 | |
| 2 | Weight of bogie | 8.0 | |
| 3 | Passengers (80 kg/per person) | Capacity: 85 | 6.8 |
| Overcrowding: 120 | 9.6 | ||
| 4 | Servicing equipment | 0.4 | |
| 5 | Weight of vehicle with capacity passengers (excluding bogie and car-body structure) | 32.26 | |
| 6 | Weight of vehicle with overcrowding passengers (excluding bogie and car-body structure) | 35.06 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, C.; Ma, K.; Zhu, T.; Ding, H.; Sun, M.; Wu, P. A New Car-Body Structure Design for High-Speed EMUs Based on the Topology Optimization Method. Appl. Sci. 2024, 14, 1074. https://doi.org/10.3390/app14031074
Liu C, Ma K, Zhu T, Ding H, Sun M, Wu P. A New Car-Body Structure Design for High-Speed EMUs Based on the Topology Optimization Method. Applied Sciences. 2024; 14(3):1074. https://doi.org/10.3390/app14031074
Chicago/Turabian StyleLiu, Chunyan, Kai Ma, Tao Zhu, Haoxu Ding, Mou Sun, and Pingbo Wu. 2024. "A New Car-Body Structure Design for High-Speed EMUs Based on the Topology Optimization Method" Applied Sciences 14, no. 3: 1074. https://doi.org/10.3390/app14031074
APA StyleLiu, C., Ma, K., Zhu, T., Ding, H., Sun, M., & Wu, P. (2024). A New Car-Body Structure Design for High-Speed EMUs Based on the Topology Optimization Method. Applied Sciences, 14(3), 1074. https://doi.org/10.3390/app14031074






