This section is devoted to the validation of the new techniques for CCV using several examples. Altogether, five data sets are used.
5.1. Artificial Data Sets
For validation of the newly developed CCV techniques, two artificial data sets were generated. The first one is a good data set with normal distributions where the clusters should be well separated. The second one is an ambiguous data set with one separate cluster and two overlapping clusters based on a normal distribution. Noisy data points were also added based on the uniform distribution. Both data sets have 200 data points each. The artificial good data set was generated with methods that are also used in the data generator [
31]. With this data generator, it is possible to generate multivariate numerical data with arbitrary marginal distributions and arbitrary correlations. The values for the centers of the normal distribution for the good data set are
,
and
. The standard deviation is always 1. Then the x- and y-values were generated based on the three normal distributions. After the data generation, the fuzzy
k-means clustering algorithm is applied using the package fkm provided in the statistics software R (Version 4.2.2) to determine the clustering results [
10]. To visualize the clustering results, CCV techniques are applied. The following figures show the results of the visualization for the artificial good data set with 2, 3, and 4 clusters. The CPC method always puts the first cluster center in the middle, all other centers on the edge, and all data points inside the circle. The A2C method always uses the first and second cluster centers for the angle-based visualization. The AM method also always uses the first cluster center for the angle-based visualization. The colors of the clusters for all following figures are black for the first, red for the second, green for the third, and blue for the fourth cluster.
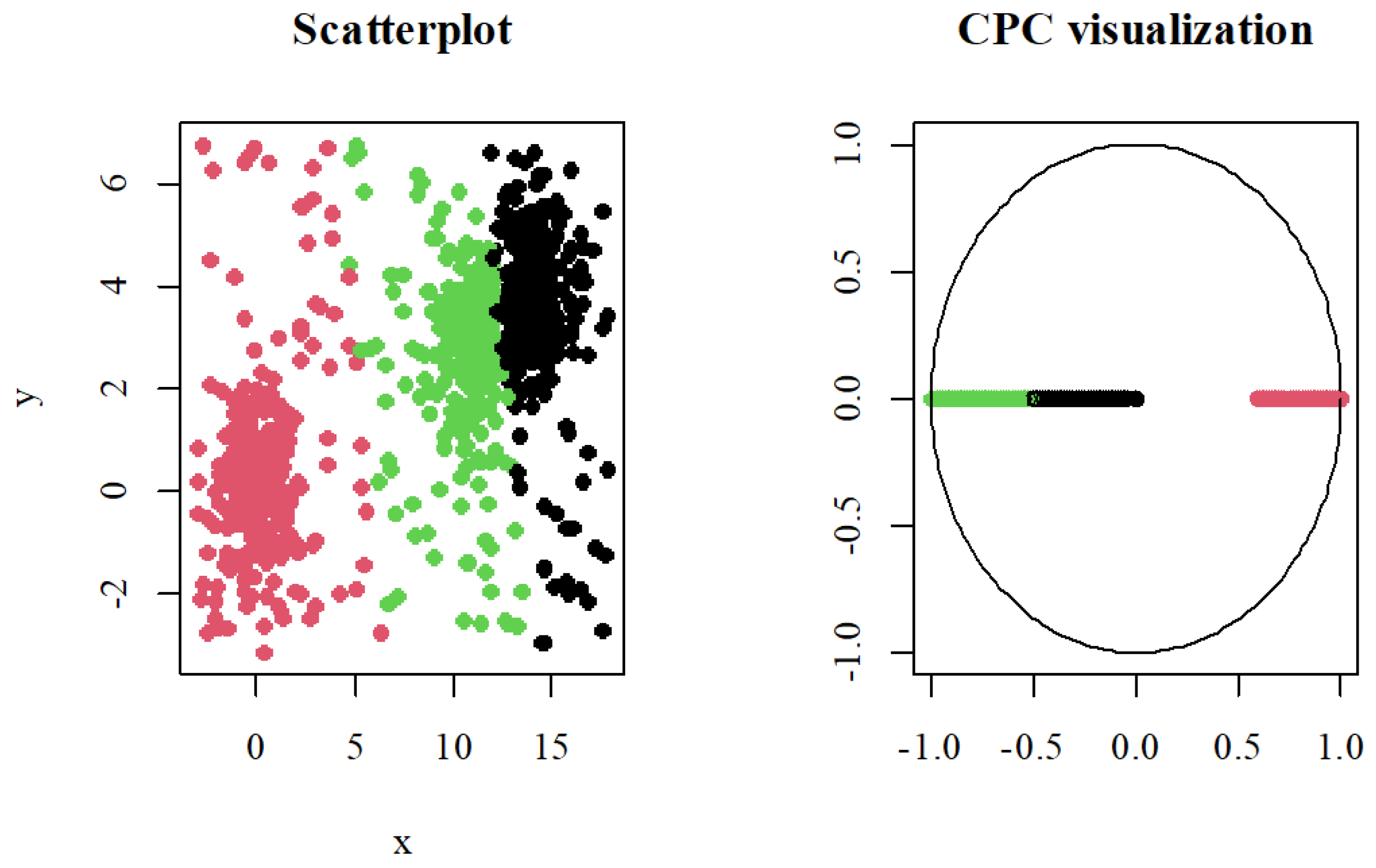
Figure 2 shows the artificially good data set with two clusters. The clustered data are located in the top left. The centers of the three normal distributions are very well separated, and the fuzzy
k-means algorithm identified two clusters. With the CPC method in the top right, both clusters are clearly separated in the visualization. The cluster center of the black cluster is in the middle of the circle, and the red cluster center is on the edge. The A2C method in the bottom left also delivers a clear separation of the two clusters. The AM method in the bottom right leads to a clear separation of the clusters.
Figure 3 shows the artificial good data set with three clusters. The clustered data is located again at the top left. The centers of the three normal distributions are very well separated, and the fuzzy k-means algorithm identified three clusters. With the CPC method in the top right, the three clusters are clearly separated in the visualization. The black cluster center is in the middle of the circle, and the red and green cluster centers are on the edges. The A2C method in the bottom left also delivers a clear separation of the three clusters. The AM method in the bottom right leads to separation of the black cluster, but some data points of the red and green clusters are mixed.
Figure 4 shows the artificial good data set with four clusters. The clustered data is located again at the top left. The centers of the three normal distributions are more or less clearly separated, and the fuzzy
k-means algorithm identified four clusters. But two clusters are very close to each other, and some data points could theoretically be in the other cluster. With the CPC method in the top right, the four clusters are separated in the visualization. The black cluster center is in the middle of the circle, and the red, green, and blue cluster centers are on the edge. The visualization shows clearly that the black, red, and green clusters are clearly separated. But some data points in the black cluster are attracted to the red cluster, and vice versa. Therefore, some data points overlap toward the respective cluster center. The A2C method in the bottom left does not indicate a clear separation of the four clusters either. It is also visible that the data points of the black and red clusters are mixed together. The AM method in the bottom right delivers the same mixed separation of the clusters and, additionally, a mix between the blue and green clusters.
For the artificially ambiguous data set, the values for the center of the separated cluster based on the normal distribution is and and for the two overlapping clusters. The standard deviation is also always 1. The interval of the uniform distribution is from −3 to 18 to cover the three clusters with noisy data points. Then the x- and y-values were generated based on the distributions. To achieve the clustering results, the fuzzy k-means algorithm is also applied, and the CCV techniques are used for the visualization. The following figures show the results of the visualization for the artificially ambiguous data set with 2, 3, and 4 clusters. All three CCV techniques show the dependencies always in the direction of the first cluster.
Figure 5 shows the artificially ambiguous data set with two clusters. The clustered data are located in the top left. The center of the separated red cluster is clearly visible, but the fuzzy
k-means algorithm seems to be able to identify two clusters. With the CPC method in the top right, both clusters are also not clearly separated in the visualization. Although the black cluster center is in the middle and the red cluster center is at the edge of the circle, there is a smooth transition between the data points. Some data points of the black cluster are attracted to the red cluster center, so a separation is not clearly visible. The A2C method in the bottom left delivers a better visualization result, but there are also some data points very close to the black and red clusters, respectively, and the two generated overlapping clusters are identified as one cluster. The same applies for the AM method in the bottom right.
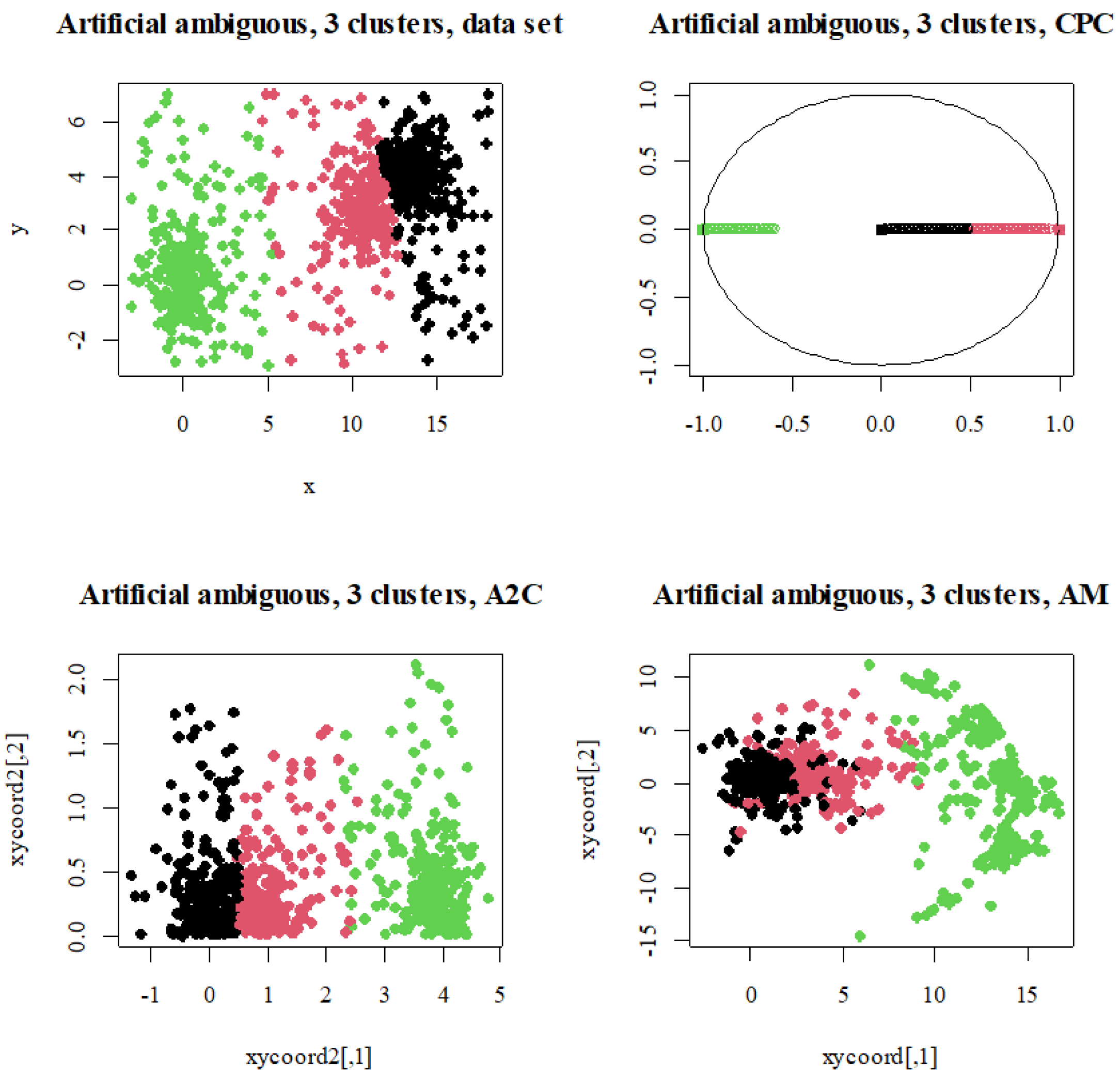
Figure 6 shows the artificially ambiguous data set with three clusters. The clustered data is located again at the top left. The center of the separated green cluster is theoretically well separated, and the fuzzy
k-means algorithm identified three clusters. With the CPC method in the top right, the three clusters are partially clearly separated in the visualization. The black cluster center is in the middle of the circle, and the red and green cluster centers are on the edge. Some data points in the red cluster are attracted to the black cluster. The A2C method in the bottom left delivers a not-clear separation of the clusters. Only the green cluster, in contrast to the black and red clusters, is generally separated. The black and red clusters are very close to each other, with no clear separation. The AM method in the bottom right leads to a clear separation of the separated green cluster. The data points of the red and black clusters are mixed.
Figure 7 shows the artificially ambiguous data set with four clusters. The clustered data are located again at the top left. The center of the separated black cluster and both centers of the overlapping clusters are visible. Due to the noisy data points, the fuzzy
k-means algorithm seems to be able to identify four clusters. The majority of the noisy data points are in their own cluster. With the CPC method in the top right, the four clusters are separated in the visualization. The black cluster center is in the middle of the circle, and the red, green, and blue cluster centers are on the edge. The visualization shows clearly that the black, red, and blue clusters are clearly separated. But some data points in the black cluster are attracted to the blue cluster, and vice versa. Therefore, some data points overlap toward the respective cluster center. The A2C method in the bottom left delivers a not very clear separation of the four clusters because of some mixed data points for the black and blue clusters. The green and red clusters are also overlapping. The AM method in the bottom right delivers the same mixed separation of the black and blue clusters but a significantly better separation of the green and red clusters.
The use of the three newly developed CCV techniques has indicated that the results based on the k-means clustering algorithm deliver more information about the dependencies between the individual clusters when focusing on a single cluster. With two or three clusters, the separation is visible both for the artificial good and partially for the ambiguous data set. But with four clusters, the data points are overlapping between some clusters. Therefore, it is not possible to separate the data points correctly. But with only two clusters, one larger cluster is created, into which all close data points are classified. However, it should be noted that if the initial data set is better, the easier it can be clearly clustered than poorer initial data. With the black cluster as the center, all three CCV techniques achieved a good separation of the three other clusters.
5.2. Iris Data Set
In addition to the two artificial data sets, the CCV techniques are also applied to a real data set. The data set is the simple Iris data set [
32]. This data set was created as part of the investigation of Iris flowers in 1935. The data set contains measured data from 150 iris plants. These are divided into 50 Virginia irises (Iris Virginica), bristly irises (Iris setosa), and irises of different colors (iris versicolor) each. The length and width of the sepal leaves are included, as well as the petal leaves of each individual plant. The categorical attribute species will not be considered here. The fuzzy
k-means clustering algorithm is also applied to determine the clustering results. For the visualization of the clustering results, CCV techniques are used. The following figures show the results of the visualization for the Iris data set with 2, 3, and 4 clusters. The CPC method always puts the first cluster center in the middle, all other centers on the edge, and all data points inside the circle. The A2C method always uses the first and second cluster centers for the angle-based visualization. The AM method also always uses the first cluster center for the angle-based visualization. The colors of the clusters are red for the first, black for the second, and green for the third. and blue for the fourth cluster.
Figure 8 shows the Iris data set with two clusters. With the CPC method (left), two clusters are separated, but some data points from the red cluster are attracted to the black cluster. Therefore, a clear separation is not visible. The A2C method (middle) leads to a better visualization because the two clusters are partially separated, but some data points of the red cluster are also attracted to the black cluster. The AM method (right) shows the same result.
Figure 9 shows the Iris data set with three clusters. With the CPC method (left), three clusters are clearly separated, and the black cluster is very well distinguished from the other two clusters. The A2C method (middle) also shows that the red cluster is clearly separated. But the black and green clusters are slightly mixed. With the AM method (right), the same results are indicated.
Figure 10 shows the Iris data set in four clusters. The CPC method (left) leads to a clear separation of the different clusters. But the green and red clusters are attracted to each other. With the A2C method (middle), the black and blue cluster are slightly mixed, and the other two clusters are mixed with no distinction. The same applies to the AM method (right).
The use of the three newly developed CCV techniques has indicated that the results based on the k-means clustering algorithm deliver more information about the dependencies between the individual clusters when focusing on a single cluster. This was also demonstrated with the artificial data sets. In general, two clusters could be too few for the Iris dataset because there are three iris plants. With three clusters, one cluster is clearly separated but not the other two clusters. With four clusters, a large part of the data points are mixed, and only one cluster differs from the others. With the red cluster as the center, all three CCV techniques achieved a good separation of the three other clusters.
5.3. Hepatitis-C-Virus Data Set
In addition to the already-mentioned data sets, the CCV techniques are also applied to a second real data set. The HCV data set contains laboratory values of blood donors, Hepatitis C patients, and demographic values like age [
33]. The target attribute contains normal blood donors vs. Hepatitis C patients, including its progress with ‘just’ Hepatitis C, Fibrosis, Cirrhosis. The fuzzy
k-means clustering algorithm is also applied to determine the clustering results. For the visualization of the clustering results, CCV techniques are used. The following figures show the results of the visualization for the HCV data set with 2, 3, and 4 clusters. The CPC method always puts the first cluster center in the middle, all other centers on the edge, and all data points inside the circle. The A2C method always uses the first and second cluster centers for the angle-based visualization. The AM method also always uses the first cluster center for the angle-based visualization. The colors of the clusters are red for the first, black for the second, green for the third, and blue for the fourth cluster.
Figure 11 shows the HCV data set with two clusters. With the CPC method (left), two clusters are separated, but the data points seem to merge smoothly from the red cluster to the black cluster. Therefore, a clear separation is not visible. The A2C method (middle) leads to a better visualization of the fact that the two clusters are partially separated. The AM method (right) shows the same result.
Figure 12 shows the HCV data set with three clusters. With the CPC method (left), three clusters are separated, but some data points from the red cluster are attracted to the green and black cluster. The A2C method (middle) shows a better, more clear separation. With the AM method (right), the same result is visible.
Figure 13 shows the HCV data set with four clusters. The CPC method (left) leads to a clear separation of the different clusters. But the read and blue clusters are attracted to each other. With the A2C method (middle), again, a better, clearer separation is visible. The same applies to the AM method (right).
The use of the three newly developed CCV techniques has indicated that the results based on the k-means clustering algorithm deliver more information about the dependencies between the individual clusters when focusing on a single cluster. In general, two clusters could be too few for the HCV dataset because there are four categories. With three clusters, the clusters are close together but more or less clearly separated. Four clusters lead to a more or less clear separation with no mixing data points. With the red cluster as the center, all three CCV techniques achieved a good separation of the three other clusters.
5.4. Sugar Production Data Set
The CCV techniques are also applied to a third real data set. The data was collected in a sugar factory of Nordzucker AG, where the sugar production process consists of several stages that are monitored automatically. The sugar production data set contains 43 parameters that influence a target parameter during sugar production. The parameters represent the sugar production over a period of four weeks. The collected data was completely anonymized and additionally manipulated with normally distributed noise. The fuzzy k-means clustering algorithm is also applied to determine the clustering results. For the visualization of the clustering results, CCV techniques are used. The following figures show the results of the visualization for the sugar production data set with 2, 3, and 4 clusters. The CPC method always puts the first cluster center in the middle, all other centers on the edge, and all data points inside the circle. The A2C method always uses the first and second cluster centers for the angle-based visualization. The AM method also always uses the first cluster center for the angle-based visualization. The colors of the clusters are red for the first, black for the second, green for the third, and blue for the fourth cluster.
Figure 14 shows the sugar production data set with two clusters. With the CPC method (left), two clusters are separated, but the points are placed in the middle of both clusters and are very close to each other. Therefore, a clear separation is not visible. The A2C method (middle) leads to a better visualization of the fact that the two clusters are partially separated. The AM method (right) indicates that the points of the black cluster are distributed in a circle around the center, even if some points deviate from this. The points of the red cluster are distributed around the black cluster.
Figure 15 shows the sugar production data set in three clusters. With the CPC method (left), three clusters are separated, but the data points of the green cluster are near the center between the green and red clusters. The data points of the black cluster are in the center between the red and the black cluster but are more attracted to the black cluster. The A2C method (middle) shows a better separation where the points of the black and green clusters are close to each other. The red cluster is more separated. The AM method (right) shows that the data points of the black cluster are also distributed in a circle around the center with no deviations. The data points of the red and green clusters are distributed around the black data points.
Figure 16 shows the sugar production data set with four clusters. The CPC method (left) leads to a clear separation of the different clusters, with green data points in the center of the green and red clusters. With the A2C method (middle), a clear separation is also visible even if the red and blue clusters are slightly mixed. The AM method (right) shows that the points of the blue cluster are distributed in a circle around the center with slight deviations from some data points. The data points of the red, green, and black clusters are distributed around the blue cluster.
The use of the three newly developed CCV techniques has indicated that the results based on the k-means clustering algorithm deliver more information about the dependencies between the individual clusters when focusing on a single cluster. Only two clusters could be too few for the sugar production dataset because the whole process varies and the influence of the parameters on the target variables cannot be divided into only two classes. With three clusters, the clusters are close together but more or less clearly separated. This is possible because the data show the parameters of four weeks when the sugar factory is running in a balanced mode, in contrast to the start of the factory, where all parameters have to be set first. With four clusters, there is also a more or less clear separation, but two clusters have mixing data points. With the red cluster as the center, all three CCV techniques achieved a good separation of the three other clusters.