A High-Capacity and High-Security Image Steganography Network Based on Chaotic Mapping and Generative Adversarial Networks
Abstract
1. Introduction
- Designing CHASE, a novel invertible high-capacity image steganography network capable of hiding a multi-channel colour secret image within a single-channel grey cover image in a single steganography process.
- Proposing an image permutation algorithm based on Logistic chaotic mapping, utilising encrypted secret images in the steganography process to enhance security.
- Combining encoder-decoder steganography structure and the adversarial learning concept of generative adversarial networks to improve image quality in stego and revealed secret images at large-capacity scales, with generated stego images exhibiting high resistance to steganalysis.
2. Related Work
2.1. Image Steganography
2.2. Invertible Neural Network
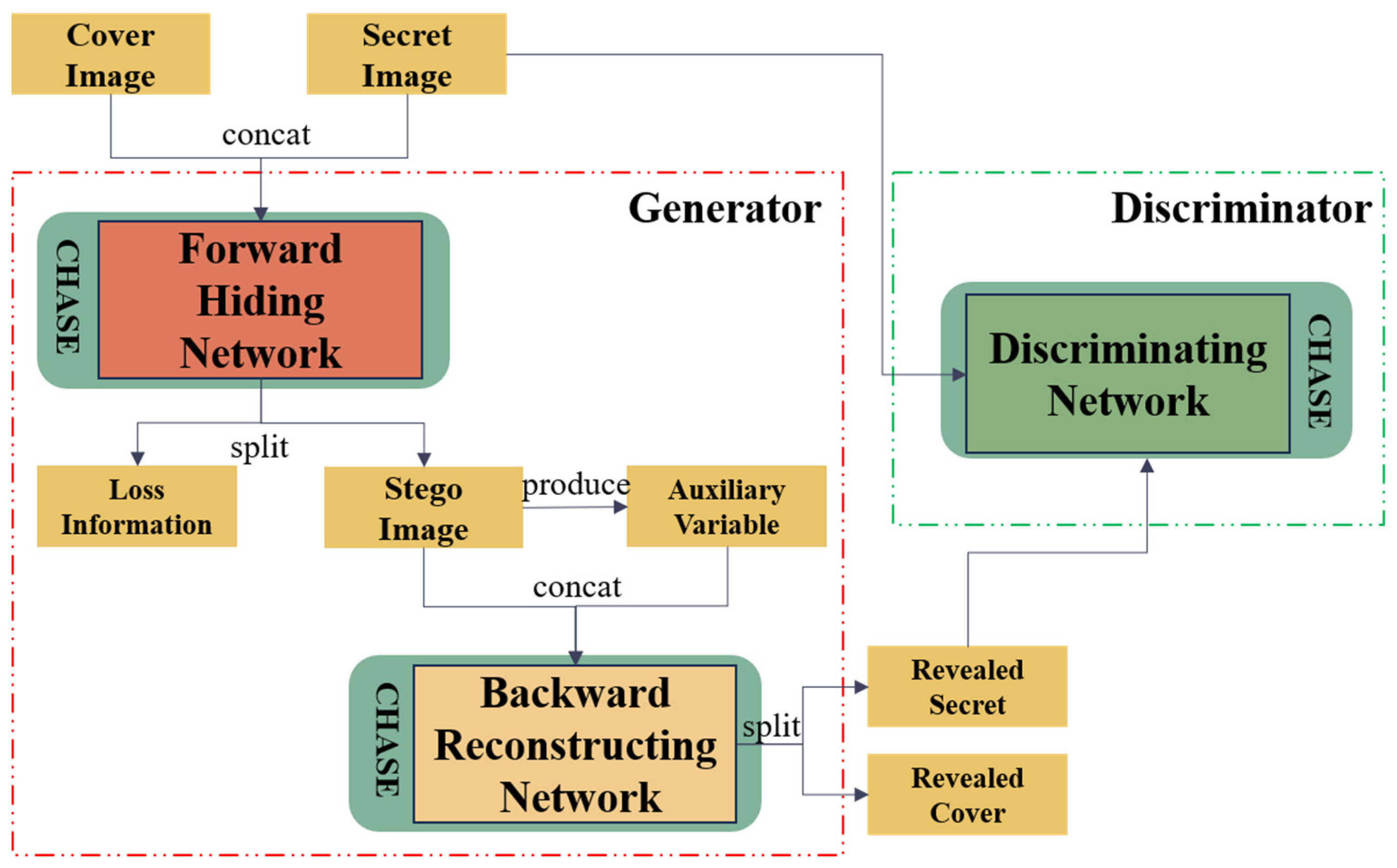
3. Proposed Approach
3.1. Overview
3.2. Network Architecture
3.2.1. Steganography Position
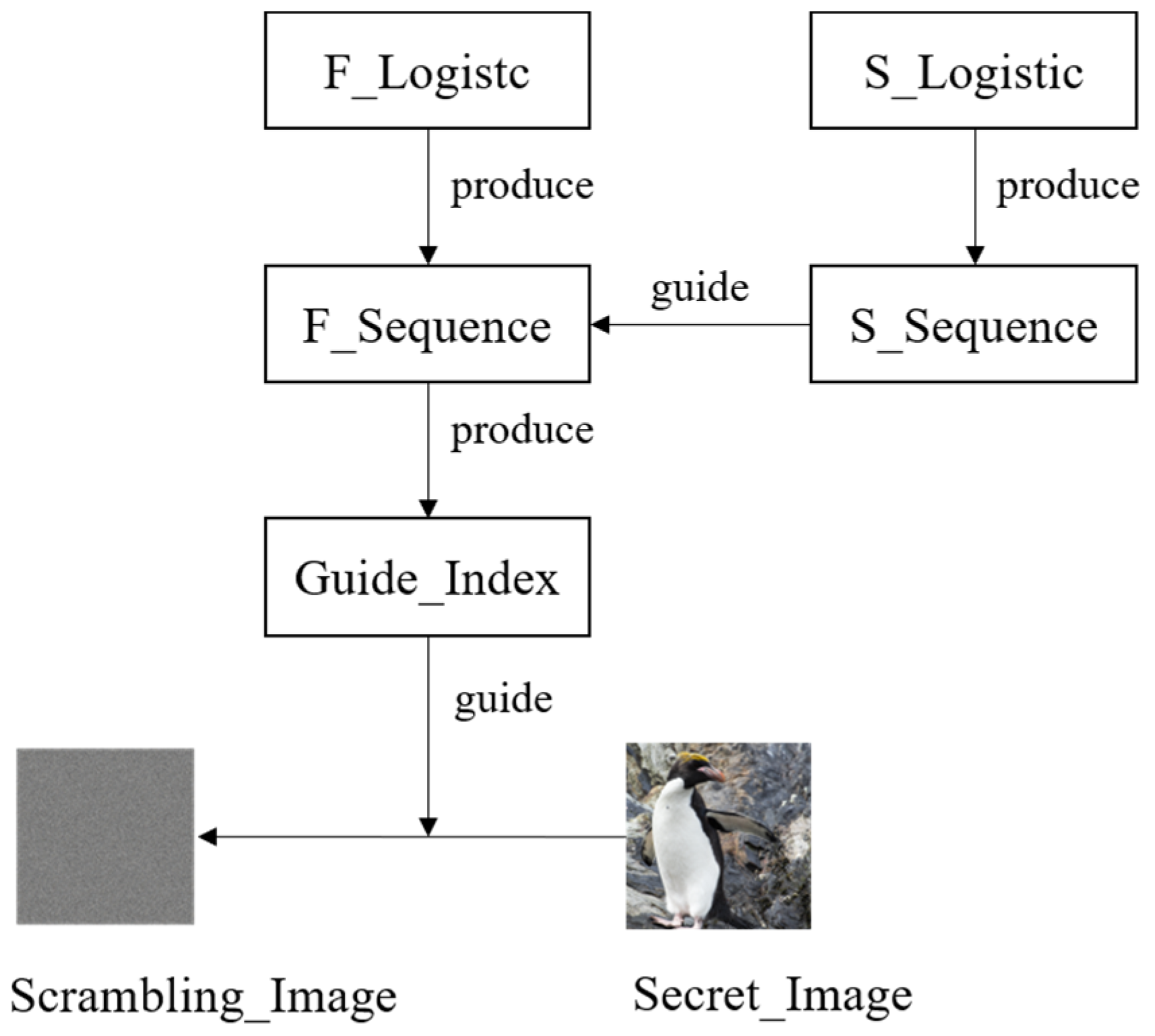
3.2.2. Image Permutation
- Step 1: Pixel Position Choosing
- Step 2: Chaotic Sequence Generation
- Step 3: Iterative Scrambling of Sub-Images
- Step 4: Random Exchange of Sub-Images
3.2.3. Chaos Mapping Enhanced Image Steganography Network (CHASE)
3.3. Optimization Strategy
- Hiding Loss. In the forward hiding process, the network conceals the secret information within the cover image to generate the stego image. The objective is to make the stego image visually close to the cover image. Hence, the hiding loss is defined as follows, where N represents the number of reversible blocks:
- Reconstruction Loss. The secret image reconstructed by the backward reconstruction process should be kept consistent with the original secret image, and for this purpose, the reconstruction loss is defined in the following form, where N represents the number of reversible blocks:And the next two loss functions are used in each of the two stages of training.
- Loss information r loss. In stage 1, we performed L2 regularization of the loss information r as a distribution loss function to constrain the loss information distribution to be more concentrated around values close to zero, thus reducing the complexity of the model, making the model smoother and the training more stable.So, the total loss function at stage 1 is expressed as:
- GAN Loss. In Stage 2, the cross-entropy loss function is employed as the distribution loss to quantify the disparity between the distribution of the reconstructed secret image and the original secret image. By considering the original secret image as the ground truth and the reconstructed secret image as the predicted distribution in the GAN model, minimizing the cross-entropy loss encourages the model to align its predicted distribution closely with the ground truth distribution. The GAN loss is defined in the following form, where N represents the number of reversible blocks.Therefore, the total loss function at stage 2 is expressed as:
4. Experimental Results
4.1. Implementation and Setup Details
4.2. Comparison
4.3. Ablation Study
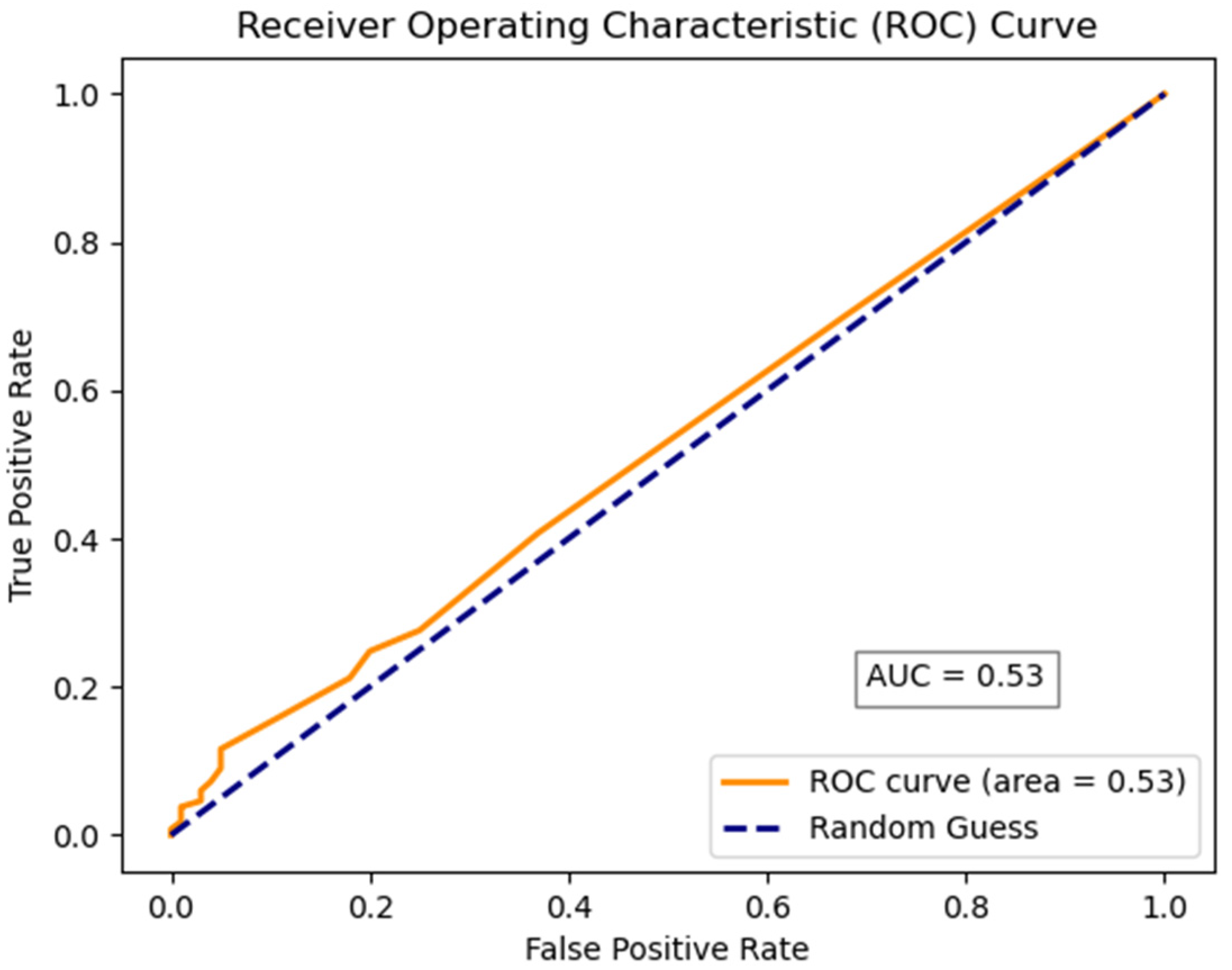
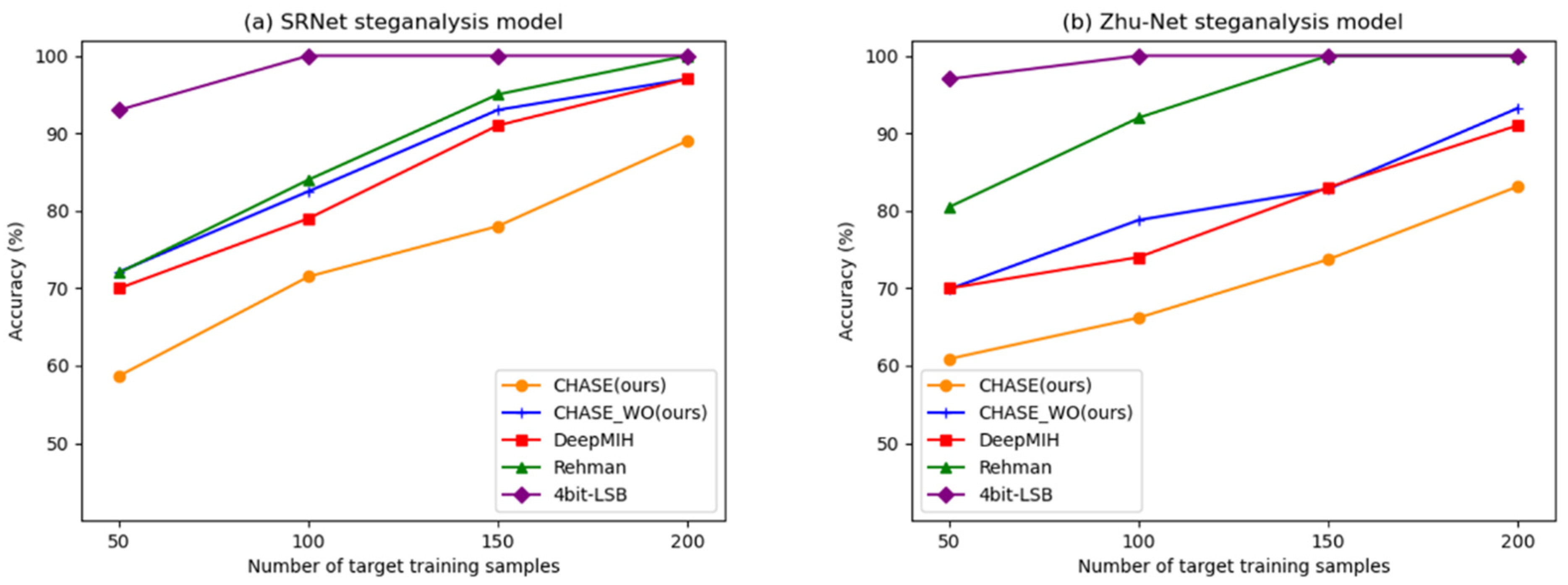
4.4. Steganalysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Subramanian, N.; Elharrouss, O.; Al-Maadeed, S.; Bouridane, A. Image steganography: A review of the recent advances. IEEE Access 2021, 11, 23409–23423. [Google Scholar] [CrossRef]
- Cheddad, A.; Condell, J.; Curran, K.; Mc Kevitt, P. Digital image steganography: Survey and analysis of current methods. Signal Process. 2010, 90, 727–752. [Google Scholar] [CrossRef]
- Evstutin, O.; Melman, A.; Meshcheryakov, A. Digital Steganography and Watermarking for Digital Images: A Review of Current Research Directions. IEEE Access 2020, 8, 166589–166611. [Google Scholar] [CrossRef]
- Tamimi, A.A.; Abdalla, A.M.; Al-Allaf, O. Hiding an image inside another image using variable-rate steganography. Int. J. Adv. Comput. Sci. Appl. (IJACSA) 2013, 4, 18–21. [Google Scholar]
- Asad, M.; Gilani, J.; Khalid, A. An enhanced least significant bit modification technique for audio steganography. In Proceedings of the International Conference on Computer Networks and Information Technology, Abbottabad, Pakistan, 11–13 July 2011; pp. 143–147. [Google Scholar]
- Ruanaidh, J.J.K.O.; Dowling, W.J.; Boland, F.M. Phase watermarking of digital images. In Proceedings of the 3rd IEEE International Conference on Image Processing, Lausanne, Switzerland, 19 September 1996; Volume 3, pp. 239–242. [Google Scholar]
- Hsu, C.T.; Wu, J.L. Hidden digital watermarks in images. IEEE Trans. Image Process. 1999, 8, 58–68. [Google Scholar]
- Barni, M.; Bartolini, F.; Piva, A. Improved wavelet-based watermarking through pixel-wise masking. IEEE Trans. Image Process. 2001, 10, 783–791. [Google Scholar] [CrossRef]
- Volkhonskiy, D.; Borisenko, B.; Burnaev, E. Generative adversarial netwoks for image steganography. In Proceedings of the Open Review Conference on Learning Representations(ICLR 2016), San Juan, PR, USA, 2–4 May 2016. [Google Scholar]
- Tang, W.; Tan, S.; Li, B.; Huang, J. Automatic steganographic distortion learning using a generative adversarial network. IEEE Signal Process. Lett. 2017, 24, 1547–1551. [Google Scholar] [CrossRef]
- Yang, J.; Liu, K.; Kang, X.; Wong, E.K.; Shi, Y.Q. Spatial image steganography based on generative adversarial network. arXiv 2018, arXiv:1804.07939. [Google Scholar] [CrossRef]
- Yang, J.; Ruan, D.; Huang, J.; Kang, X.; Shi, Y.Q. An embedding cost learning framework using GAN. IEEE Trans. Inf. Forensics Secur. 2018, 15, 839–851. [Google Scholar] [CrossRef]
- Hayes, J.; Danezis, G. Generating steganographic images via adversarial training. In Proceedings of the Advances in Neural Information Processing Systems, Los Angeles, CA, USA, 4–9 December 2017; pp. 1954–1963. [Google Scholar]
- Wang, Y.; Niu, K.; Yang, X. Information hiding scheme based on generative adversarial network. J. Comput. Appl. 2018, 38, 2923–2928. [Google Scholar]
- Baluja, S. Hiding images in plain sight: Deep steganography. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 2069–2079. [Google Scholar]
- Baluja, S. Hiding images within images. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 42, 1685–1697. [Google Scholar] [CrossRef]
- Holub, V.; Fridrich, J.; Denemark, T. Universal distortion function for steganography in an arbitrary domain. EURASIP J. Inf. Secur. 2014, 2014, 1–13. [Google Scholar] [CrossRef]
- Holub, V.; Fridrich, J. Designing steganographic distortion using directional filters. In Proceedings of the 2012 IEEE International Workshop on Information Forensics and Security, Tenerife, Spain, 2–5 December 2012; pp. 234–239. [Google Scholar]
- Pevný, T.; Filler, T.; Bas, P. Using high-dimensional image models to perform highly undetectable steganography. In Proceedings of the International Workshop on Information Hiding, Calgary, AB, Canada, 28–30 June 2010; pp. 161–177. [Google Scholar]
- Shi, H.; Dong, J.; Wang, W.; Qian, Y.; Zhang, X. SSGAN: Secure steganography based on generative adversarial networks. In Proceedings of the Pacific Rim Conference on Multimedia, Harbin, China, 28–29 September 2017; pp. 534–544. [Google Scholar]
- Zhang, K.A.; Cuesta-Infante, A.; Xu, L.; Veeramachaneni, K. SteganoGAN:High capacity image steganography with gans. arXiv 2019, arXiv:1901.03892. [Google Scholar] [CrossRef]
- Rehman, R.; Nadeem, S.; Nadeem, M.S.; ul Hussain, S. End-to-End Trained CNN Encoder-Decoder Networks for Image Steganography. arXiv 2017, arXiv:1711.07201. [Google Scholar] [CrossRef]
- Zhang, R.; Dong, S.; Liu, J. Invisible steganography via generative adversarial networks. Multimed. Tools Appl. 2019, 78, 8559–8575. [Google Scholar] [CrossRef]
- Dinh, L.; Krueger, D.; Bengio, Y. Nice: Nonlinear independent components estimation. arXiv 2014, arXiv:1410.8516. [Google Scholar] [CrossRef]
- Dinh, L.; Sohl-Dickstein, J.; Bengio, S. Density estimation using real NVP. In Proceedings of the 5th International Conference on Learning Representations(ICLR 2017), Toulon, France, 24–26 April 2017. [Google Scholar]
- Kingma, D.P.; Dhariwal, P. Glow: Generative flow with invertible 1×1 convolutions. arXiv 2018, arXiv:1807.03039. [Google Scholar] [CrossRef]
- Lugmayr, A.; Danelljan, M.; Van Gool, L.; Timofte, R. SRFlow: Learning the super-resolution space with normalizing flow. In European Conference on Computer Vision; Springer: Berlin/Heidelberg, Germany, 2020; pp. 715–732. [Google Scholar]
- Ardizzone, L.; Lüth, C.; Kruse, J.; Rother, C.; Köthe, U. Guided image generation with conditional invertible neural networks. arXiv 2019, arXiv:1907.02392. [Google Scholar] [CrossRef]
- Denker, A.; Schmidt, M.; Leuschner, J.; Maass, P. Conditional Invertible Neural Networks for Medical Imaging. J. Imaging 2021, 7, 243. [Google Scholar] [CrossRef] [PubMed]
- Xing, Y.; Qian, Z.; Chen, Q. Invertible Image Signal Processing 2021. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021. [Google Scholar]
- Xiao, M.; Zheng, S.; Liu, C.; Wang, Y.; He, D.; Ke, G.; Bian, J.; Lin, Z.; Liu, T.Y. Invertible image rescaling. In Proceedings of the European Conference on Computer Vision (ECCV), Glasgow, UK, 23–28 August 2020. [Google Scholar]
- Lu, S.P.; Wang, R.; Zhong, T. Large-Capacity Image Steganography Based on Invertible Neural Networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021. [Google Scholar]
- Jing, J.; Deng, X.; Xu, M.; Wang, J.; Guan, Z. Hinet: Deep image hiding by invertible network. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, BC, Canada, 11–17 October 2021. [Google Scholar]
- Guan, Z.; Jing, J.; Deng, X. DeepMIH: Deep Invertible Network for Multiple Image Hiding. IEEE Trans. Pattern Anal. Mach. Intell 2023, 45, 372–390. [Google Scholar] [CrossRef] [PubMed]
- Gu, G.S.; Liu, F.C. Contourlet domain image encryption based on chaos on mapping. J. Comput. Appl. 2011, 31, 771–773. [Google Scholar] [CrossRef]
- May, R.M. Simple mathematical models with very complicated dynamics. Nature 1976, 261, 459–467. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Yu, K.; Wu, S.; Gu, J.; Liu, Y.; Dong, C.; Qiao, Y.; Loy, C.C. Esrgan: Enhanced super-resolution generative adversarial networks. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; Volume 4. [Google Scholar]
- Zhang, C.; Benz, P.; Karjauv, A.; Sun, G.; Kweon, I.S. UDH: Universal Deep Hiding for Steganography Watermarking, and Light Fieled Messaging. Adv. Neural Inf. Process. Syst. 2020, 33, 10223–10234. [Google Scholar]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. Adv. Neural Inf. Process. Syst. 2014, 27, 2672–2680. [Google Scholar]
- Woo, S.; Park, J.; Lee, J.Y.; Kweon, I.S. CBAM: Convolutional Block Attention Module. arXiv 2018, arXiv:1807.06521. [Google Scholar] [CrossRef]
- Agustsson, E.; Timofte, R. Ntire 2017 challenge on single image super-resolution: Dataset and study. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Honolulu, HI, USA, 21–26 July 2017; pp. 126–135. [Google Scholar]
- Lin, T.Y.; Maire, M.; Belongie, S.; Hays, J.; Perona, P.; Ramanan, D.; Dollár, P.; Zitnick, C.L. Microsoft coco: Common objects in context. In Proceedings of the European Conference on Computer Vision, Zurich, Switzerland, 6–12 September 2014; Springer: Berlin/Heidelberg, Germany, 2014; Volume 5, pp. 740–755. [Google Scholar]
- Russakovsky, O.; Deng, J.; Su, H.; Krause, J.; Satheesh, S.; Ma, S.; Huang, Z.; Karpathy, A.; Khosla, A.; Bernstein, M.; et al. Imagenet large scale visual recognition challenge. Int. J. Comput. Vis. 2015, 115, 211–252. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Simoncelli. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef]
- Boehm, B. Stegexpose—A tool for detecting LSB Steganography. arXiv 2014, arXiv:1410.6656. Available online: https://github.com/b3dk7/StegExpose (accessed on 16 December 2023).
- Boroumand, M.; Chen, M.; Fridrich, J. Deep residual network for steganalysis of digital images. IEEE Trans. Inf. Forensics Secur. 2018, 14, 1181–1193. [Google Scholar] [CrossRef]
- Zhang, R.; Zhu, F.; Liu, J.; Liu, G. Depth-wise separable convolutions and multi-level pooling for an efficient spatial cnn-based steganalysis. IEEE Trans. Inf. Forensics Secur. 2020, 15, 1138–1150. [Google Scholar] [CrossRef]
- Weng, X.; Li, Y.; Chi, L.; Mu, Y. Highcapacity convolutional video steganography with temporal residual modeling. In Proceedings of the 2019 on International Conference on Multimedia Retrieval, Ottawa, ON, Canada, 10–13 June 2019; pp. 87–95. [Google Scholar]





| Notation | Description |
|---|---|
| Cover image | |
| Secret image | |
| Stego image | |
| Image scrambling process/Image inverse scrambling process | |
| / | Hiding process/Reconstruction process |
| Reconstructed secret image | |
| Inverse Scrambling reconstructed secret image | |
| Reconstructed host image | |
| r | Loss function generated during forward hiding process |
| z | Auxiliary variable used to assist in reconstructing images |
| Layers | Process | Output Size |
|---|---|---|
| Input | / | 3 × 256 × 256 |
| Layer 1 | 3 × 3 Conv + LeakyReLu | 64 × 256 × 256 |
| Layer 2 | 4 × 4 Conv + BatchNorm + LeakyReLu | 64 × 128 × 128 |
| Layer 3 | 3 × 3 Conv + BatchNorm + LeakyReLu | 128 × 128 × 128 |
| Layer 4 | 4 × 4 Conv + BatchNorm + LeakyReLu | 128 × 64 × 64 |
| Layer 5 | 3 × 3 Conv + BatchNorm + LeakyReLu | 256 × 64 × 64 |
| Layer 6 | 4 × 4 Conv + BatchNorm + LeakyReLu | 256 × 32 × 32 |
| Layer 7 | 3 × 3 Conv + BatchNorm + LeakyReLu | 512 × 32 × 32 |
| Layer 8 | 4 × 4 Conv + BatchNorm + LeakyReLu | 512 × 16 × 16 |
| Layer 9 | 3 × 3 Conv + BatchNorm + LeakyReLu | 512 × 16 × 16 |
| Layer 10 | 4 × 4 Conv + BatchNorm + LeakyReLu | 512 × 8 × 8 |
| Layer 11 | CBAM | 1 × 32,768 |
| Layer 12 | FC | 1 × 100 |
| Output | FC | 1 × 1 |
| Methods | RP | Cover/Stego Image Pair | |||||
|---|---|---|---|---|---|---|---|
| DIV2K | COCO | ImageNet | |||||
| PSNR (dB) ↑ | SSIM ↑ | PSNR (dB) ↑ | SSIM ↑ | PSNR (dB) ↑ | SSIM ↑ | ||
| 4bit-LSB | 50% | 33.19 | 0.94 | 33.79 | 0.94 | 33.68 | 0.94 |
| Rehman et al. [22] | 33.3% | 30.70 | 0.92 | 30.18 | 0.91 | 32.68 | 0.93 |
| DeepMIH [34] | 300% | 34.13 | 0.94 | 34.29 | 0.94 | 33.39 | 0.93 |
| CHASE_WO | 300% | 35.98 | 0.94 | 33.59 | 0.92 | 33.34 | 0.93 |
| CHASE | 300% | 33.09 | 0.91 | 31.34 | 0.90 | 30.03 | 0.92 |
| Methods | RP | Secret/Reconstructed Image Pair | |||||
| DIV2K | COCO | ImageNet | |||||
| PSNR (dB) ↑ | SSIM ↑ | PSNR (dB) ↑ | SSIM ↑ | PSNR (dB) ↑ | SSIM ↑ | ||
| 4bit-LSB | 50% | 30.81 | 0.90 | 32.04 | 0.91 | 31.26 | 0.90 |
| Rehman et al. [22] | 33.3% | 32.11 | 0.93 | 32.13 | 0.92 | 34.75 | 0.93 |
| DeepMIH [34] | 300% | 33.47 | 0.93 | 33.87 | 0.93 | 32.21 | 0.92 |
| CHASE_WO | 300% | 36.02 | 0.95 | 34.41 | 0.94 | 32.07 | 0.93 |
| CHASE | 300% | 32.23 | 0.93 | 33.47 | 0.93 | 31.62 | 0.91 |
| Image-Premutation | GAN | Cover/Stego Pair | Secret/Reconstructed Pair |
|---|---|---|---|
| × | × | 33.82/0.92 | 35.18/0.93 |
| × | √ | 35.98/0.94 | 36.02/0.95 |
| √ | × | 33.61/0.92 | 30.41/0.90 |
| √ | √ | 33.09/0.91 | 32.23/0.93 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huo, L.; Chen, R.; Wei, J.; Huang, L. A High-Capacity and High-Security Image Steganography Network Based on Chaotic Mapping and Generative Adversarial Networks. Appl. Sci. 2024, 14, 1225. https://doi.org/10.3390/app14031225
Huo L, Chen R, Wei J, Huang L. A High-Capacity and High-Security Image Steganography Network Based on Chaotic Mapping and Generative Adversarial Networks. Applied Sciences. 2024; 14(3):1225. https://doi.org/10.3390/app14031225
Chicago/Turabian StyleHuo, Lin, Ruipei Chen, Jie Wei, and Lang Huang. 2024. "A High-Capacity and High-Security Image Steganography Network Based on Chaotic Mapping and Generative Adversarial Networks" Applied Sciences 14, no. 3: 1225. https://doi.org/10.3390/app14031225
APA StyleHuo, L., Chen, R., Wei, J., & Huang, L. (2024). A High-Capacity and High-Security Image Steganography Network Based on Chaotic Mapping and Generative Adversarial Networks. Applied Sciences, 14(3), 1225. https://doi.org/10.3390/app14031225







