A Robust Generator–Harvester for Independent Sensor Systems †
Abstract
1. Introduction
2. State of the Research Field and Topics Analyzed
2.1. Problems Relating to the Electromagnetic Component of the Designed Harvester
2.2. Designing an Electromagnetic Transformation Method: Renewable Energy
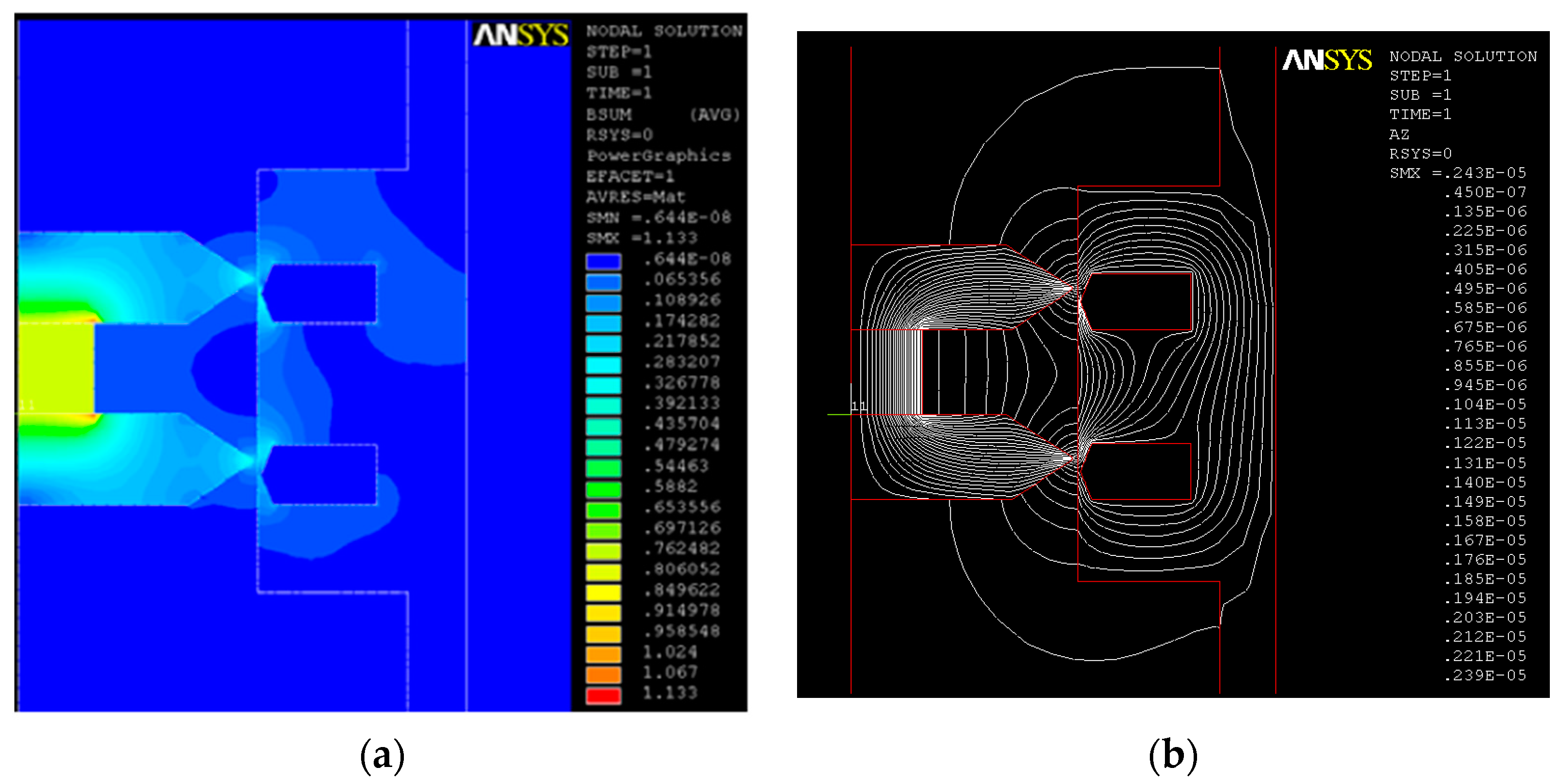
3. Mathematical–Physical Model
4. Experiments
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Stratton, J.A. Theory of Electromagnetic Field; SNTL: Prague, Czech Republic, 1961. [Google Scholar]
- Cawthorne, W.R. Optimization of a Brushless Permanent Magnet Linear Alternator for Use with a Linear Internal Combustion Engine. Ph.D. Thesis, Dissertations, and Problem Reports, 1999; p. 3160. Available online: https://researchrepository.wvu.edu/etd/3160 (accessed on 25 May 2022).
- Jirků, T.; Fiala, P.; Kluge, M. Magnetic resonant harvesters and power management circuit for magnetic resonant harvesters. Microsyst. Technol. 2010, 16, 677–690. [Google Scholar] [CrossRef]
- Cawthorne, W.R.; Famouri, P.; Chen, J.; Clark, N.N.; McDaniel, T.I.; Atkinson, R.J.; Nandkumar, S.; Atkinson, C.M.; Petreanu, S. Development of a linear alternator-engine for hybrid electric vehicle applications. IEEE Trans. Veh. Technol. 1999, 48, 1797–1802. [Google Scholar] [CrossRef]
- Famouri, P.; Cawthorne, W.R.; Clark, N.; Nandkumar, S.; Atkinson, C.; Atkinson, R.; Petreanu, S. Design and testing of a novel linear alternator and engine system for remote electrical power generation. In Proceedings of the IEEE Engineering Society, Winter Meeting, New York, NY, USA, 31 January–4 February 1999; Volume 1, pp. 108–112. [Google Scholar]
- Nor, K.M.; Arof, H.; Wijono. Design of a 5 kW tubular permanent magnet linear generator. In Proceedings of the 39th International Universities Power Engineering Conference, UPEC 2004, Bristol, UK, 6–8 September 2004; Volume 1, pp. 528–532. [Google Scholar]
- Hernandez, I.; Segundo, J.; Gonzalez, X.; Luna, D.; Juarez, Z. Performance and power quality assessment of a linear electric generator focused on microgeneration applications. Int. Trans. Electr. Energ. Syst. 2017, 27, e2326. [Google Scholar] [CrossRef]
- Fiala, P.; Szabo, Z.; Marcon, P.; Roubal, Z. Mini- and microgenerators applicable in the MEMS technology. In Proceedings of the SPIE—The International Society for Optical Engineering, San Diego, CA, USA, 6–10 August 2017; p. 10246. [Google Scholar] [CrossRef]
- Atkinson, C.M.; Petreanu, S.; Clark, N.N.; Atkinson, R.J.; McDaniel, T.I.; Nandkumar, S.; Famouri, P. Numerical Simulation of a Two-Stroke Linear Engine-Alternator Combination; SAE Technical Papers; SAE International: Warrendale, PA, USA, 1999. [Google Scholar] [CrossRef]
- Mikalsen, R.; Roskilly, A.P. Performance simulation of a spark ignited free-piston engine generator. Appl. Therm. Eng. 2008, 28, 1726–1733. [Google Scholar] [CrossRef]
- Clark, N.N.; McDaniel, T.I.; Atkinson, R.J.; Nandkumar, S.; Atkinson, C.; Petreanu, S.; Famouri, P. Modeling and development of a linear engine. Paper No. 98-ICE-95. In Proceedings of the Spring Technical Conference, ASME, Fort Lauderdale, FL, USA, 26–29 April 1998. [Google Scholar]
- Fredriksson, J.; Denbratt, I. Simulation of a Two-Stroke Free Piston Engine. Paper No. 2004-01-187; SAE International: Warrendale, PA, USA, 2004. [Google Scholar]
- Van Blarigan, P.; Sandia National Laboratories. Advanced Internal Combustion Electrical Generator. In Proceedings of the 2001 DOE Hydrogen Program Review, NREL/CP-570-30535, Baltimore, MD, USA, 17–19 April 2001. [Google Scholar]
- Pavelka, J. Analysis of combustion engine—Electric linear generator set operation. In Proceedings of the 13th International Power Electronics and Motion Control Conference (EPE/PEMC 2008), IEEE, Poznan, Poland, 1–3 September 2008; pp. 988–993. [Google Scholar] [CrossRef]
- Mikalsen, R.; Roskilly, A.P. A review of free-piston engine history and applications. Appl. Therm. Eng. 2007, 27, 2339–2352. [Google Scholar] [CrossRef]
- Virsik, R.; Heron, A. Free piston linear generator in comparison to other range-extender technologies. World Electr. Veh. J. 2013, 6, 426–435. [Google Scholar] [CrossRef]
- Lim, O.; Hung, N.B.; Iida, N. A power generation study of a power pack based on operating parameters of the linear engine fuelled with propane. Energy Procedia 2014, 61, 1581–1584. [Google Scholar] [CrossRef]
- Szabo, Z.; Fiala, P.; Dohnal, P. Magnetic circuit modifications in resonant vibration harvesters. Mech. Syst. Signal Process. 2018, 99, 832–845. [Google Scholar] [CrossRef]
- Zukal, J.; Fiala, P.; Szabó, Z.; Dedková, J.; Pernica, R. Coupled numerical model of vibration-based harvester. Appl. Sci. 2020, 10, 2725. [Google Scholar] [CrossRef]
- Szabó, Z.; Fiala, P.; Zukal, J.; Dědková, J.; Dohnal, P. Optimal structural design of a magnetic circuit for vibration harvesters applicable in MEMS. Symmetry 2020, 12, 110. [Google Scholar] [CrossRef]
- Zukal, J.; Szabo, Z.; Pernica, R.; Kadlec, R.; Dedkova, J.; Klima, M.; Fiala, P. Designing a Robust Model of a Linear Motion-driven Harvester. In Proceedings of the Photonics & Electromagnetics Research Symposium (PIERS), Prague, Czech Republic, 3–6 July 2023; pp. 732–738. [Google Scholar] [CrossRef]
- Schillingmann, H.; Maurus, Q.; Henke, M. Linear generator design for a free-piston engine with high force density. In Proceedings of the 12th International Symposium on Linear Drives for Industry Applications, LDIA, Neuchatel, Switzerland, 1–3 July 2019. [Google Scholar] [CrossRef]
- Baker, N.J.; Sa Jalal, A.; Wang, J.; Korbekandi, R.M. Experimental comparison of two linear machines developed for the free piston engine. J. Eng. 2019, 4406–4410. [Google Scholar] [CrossRef]
- Baker, N.J.; Korbekandi, R.M.; Wu, D.; Jalal, A.S. An investigation of short translator linear machines for use in a free piston engine. In Proceedings of the IEEE International Electric Machines and Drives Conference, IEMDC, San Diego, CA, USA, 12–15 May 2019; pp. 68–73. [Google Scholar] [CrossRef]
- Subramanian, J.; Heiskell, G.; Mahmudzadeh, F.; Famouri, P. Study of radial and axial magnets for linear alternator—Free piston engine system. In Proceedings of the 2017 North American Power Symposium, NAPS 2017, Morgantown, WV, USA, 17–19 September 2017. [Google Scholar] [CrossRef]
- Hansson, J. Analysis and Control of a Hybrid Vehicle Powered by a Free-Piston Energy Converter, Electrical Machines and Power Electronics. Licentiate Thesis, School of Electrical Engineering, Royal Institute of Technology (KTH), Stockholm, Sweden, 2006. [Google Scholar]
- Kulkarni, S.; Koukharenko, E.; Torah, R.; Tudor, M.J.; Beeby, S.; O’Donnell, T. Design, fabrication and test of integrated micro-scale vibration-based electromagnetic generator. Sens. Actuators A Phys. 2008, 145–146, 336–342. [Google Scholar] [CrossRef]
- Beeby, S.P.; Torah, R.N.; Torah, M.J.; O’ Donnell, T.; Saha, C.R.; Roy, S. A microelectromagnetic generator for vibration energy harvesting. J. Micromech. Microeng. 2007, 17, 1257–1265. [Google Scholar] [CrossRef]
- Zhu, D.; Roberts, S.; Tudor, M.J.; Beeby, S.P. Design and experimental characterization of a tunable vibration-based electromagnetic microgenerator. Sens. Actuators A Phys. 2010, 158, 284–293. [Google Scholar] [CrossRef]
- Elvin, N.G.; Elvin, A.A. An experimentally validated electromagnetic energy harvester. J. Sound. Vib. 2011, 330, 2314–2324. [Google Scholar] [CrossRef]
- Wang, P.H.; Dai, X.H.; Fang, D.M.; Zhao, X.L. Design, fabrication and performance of a new vibration-based electromagnetic micro power generator. Microelectron. J. 2007, 38, 1175–1180. [Google Scholar] [CrossRef]
- Yang, J.; Yu, Q.; Zhao, J.; Zhao, N.; Wen, Y.; Li, P.; Qiu, J. Design and optimization of a biaxial vibration-driven electromagnetic generator. J. Appl. Phys. 2014, 116, 114506. [Google Scholar] [CrossRef]
- Lee, B.C.; Rahman, M.A.; Hyun, S.; Chung, S.G. Low frequency driven electromagnetic energy harvester for self-powered system. Smart Mater. Struct. 2012, 21, 125024. [Google Scholar] [CrossRef]
- Quinn, J.B.; Waldmann, T.; Richter, K.; Kasper, M.; Wohlfahrt-Mehrens, M. Energy Density of Cylindrical Li-Ion Cells: A Comparison of Commercial 18650 to the 21700 Cells. J. Electrochem. Soc. 2018, 165, A3284–A3291. [Google Scholar] [CrossRef]
- Liu, C.; Yu, Z.; Liu, C.; Yu, Z.; Neff, D.; Zhamu, A.; Jang, B.Z. Graphene-Based Supercapacitor with an Ultrahigh Energy Density. Nano Lett. 2010, 10, 4863–4868. [Google Scholar] [CrossRef]
- Yamanaka, Y.; Nirei, M.; Sato, M.; Murata, H.; Yinggang, B.; Mizuno, T. Design of linear synchronous generator suitable for free-piston engine linear generator system. In Proceedings of the 11th International Symposium on Linear Drives for Industry Applications (LDIA), IEEE, Osaka, Japan, 6–8 February 2017; pp. 1–4. [Google Scholar] [CrossRef]
- Subramanian, J.; Mahmudzadeh, F.; Bade, M.; Famouri, P. Simulation and Experimental Validation of Equivalent Circuit Parameters and Core Loss in a Tubular Permanent Magnet Linear Generator for Free Piston Engine Applications. In Proceedings of the IEEE International Electric Machines & Drives Conference (IEMDC), IEEE, San Diego, CA, USA, 12–15 May 2019; pp. 57–62. [Google Scholar] [CrossRef]
- Zhang, X.; Cooke, K.B.; Kos, J. Modeling and simulation of a hybrid-engine. In Proceedings of the IEEE WESCANEX 97 Communications, Power and Computing. Conference Proceedings, Winnipeg, MB, Canada, 22–23 May 1997; pp. 286–291. [Google Scholar] [CrossRef]
- Fazal, I.; Karsiti, M.N.; Zulkifli, S.A.; Ibrahim, T.; Rao, K.S.R. Modeling and simulation of a moving-coil linear generator. In Proceedings of the Advanced Systems (ICIAS 2010), IEEE, Kuala Lumpur, Malaysia, 15–17 June 2010; pp. 1–5. [Google Scholar] [CrossRef]
- Graef, M.; Treffinger, P.; Pohl, S.-E.; Rinderknecht, F. Investigation of a high efficient Free Piston Linear Generator with variable Stroke and variable Compression Ratio A new Approach for Free Piston Engines. World Electr. Veh. J. 2007, 1, 116–120. [Google Scholar] [CrossRef]
- Tikkanen, R.S.; Vilenius, M. Hydraulic free piston engine—Challenge for control. In Proceedings of the 1999 European Control Conference (ECC), IEEE, Karlsruhe, Germany, 31 August–3 September 1999; pp. 2943–2948. [Google Scholar] [CrossRef]
- Zou, H.; Wang, M.; Tang, M.; Li, C.; Tian, C. Experimental investigation and performance analysis of a direct-driven linear generator. Energy Procedia 2017, 142, 284–290. [Google Scholar] [CrossRef]
- Seo, U.-J.; Riemer, B.; Appunn, R.; Hameyer, K. Design considerations of a linear generator for a range extender application. Arch. Electr. Eng. 2015, 64, 581–592. [Google Scholar] [CrossRef]
- Takahara, K.; Ohsaki, S.; Itoh, Y.; Ohyama, K.; Kawaguchi, H. Characteristic analysis and trial manufacture of permanent-magnetic type linear generator. Electr. Eng. Jpn. 2008, 166, 94–100. [Google Scholar] [CrossRef]
- Nguyen, V.T.; Ta, Q.T.H.; Nguyen, P.K.T. Artificial intelligence-based modeling and optimization of microbial electrolysis cell-assisted anaerobic digestion fed with alkaline-pretreated waste-activated sludge. Biochem. Eng. J. 2022, 187. [Google Scholar] [CrossRef]
- Talib, N.H.H.A.; Salleh, H.; Youn, B.D.; Resali, M.S.M. Comprehensive Review on Effective Strategies and Key Factors for High Performance Piezoelectric Energy Harvester at Low Frequency. Int. J. Automot. Mech. Eng. 2019, 16, 7181–7210. [Google Scholar] [CrossRef]
- ANSYS. 1990–2023, USA. Available online: www.ansys.com (accessed on 12 November 2023).
- Available online: https://www.greencarcongress.com/2016/05/20160506-toyotafpeg.html (accessed on 8 January 2024).
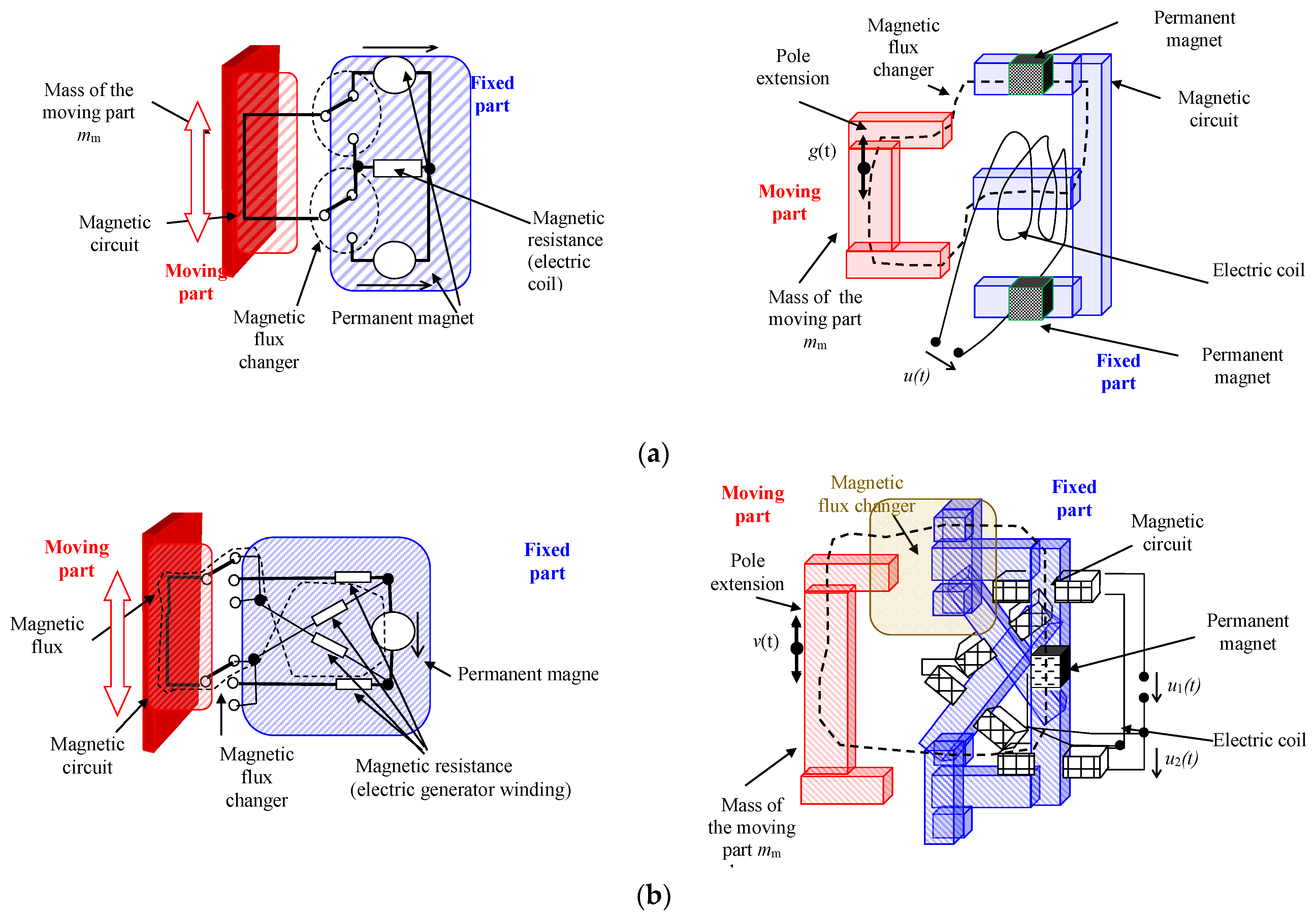
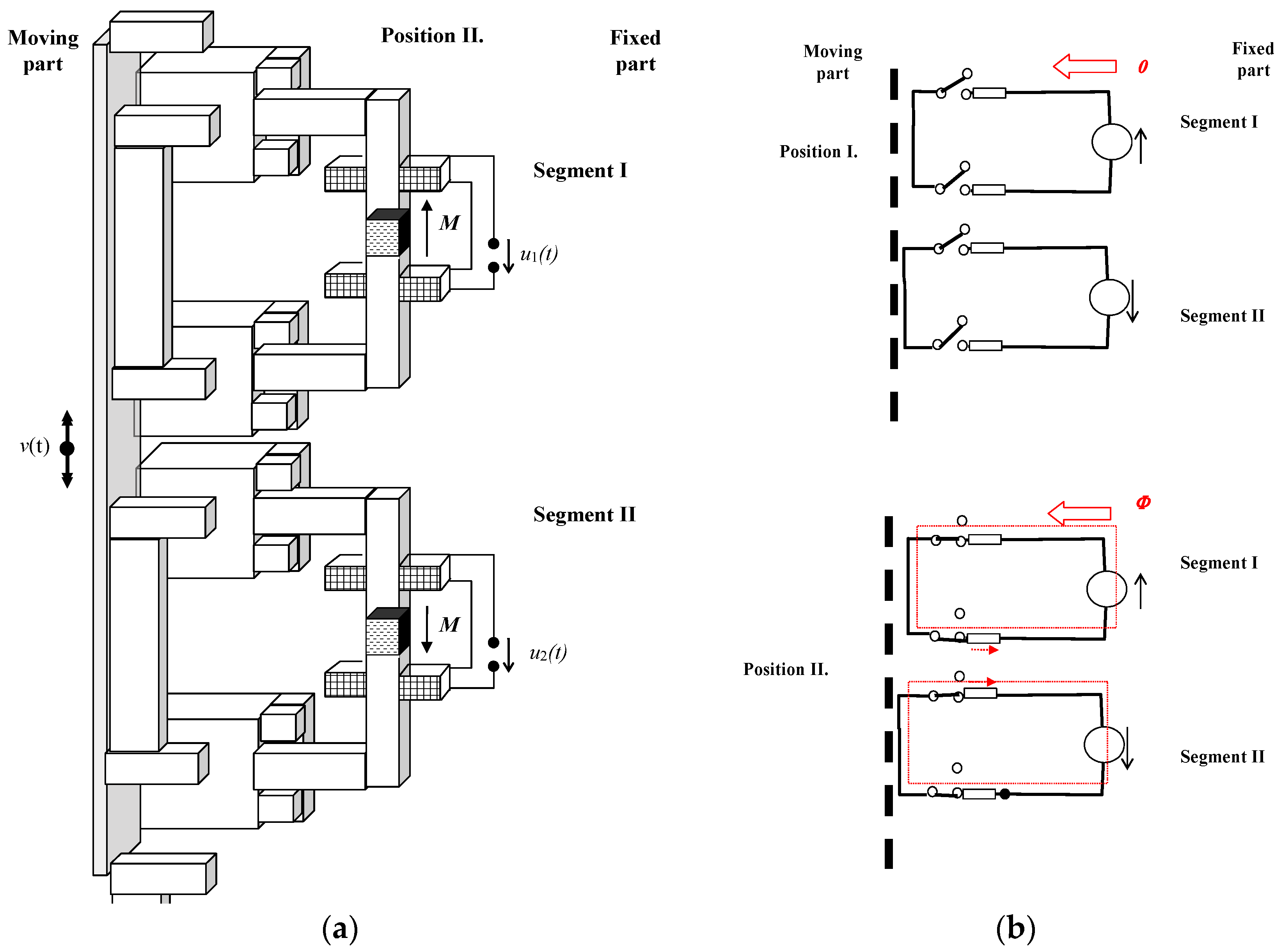
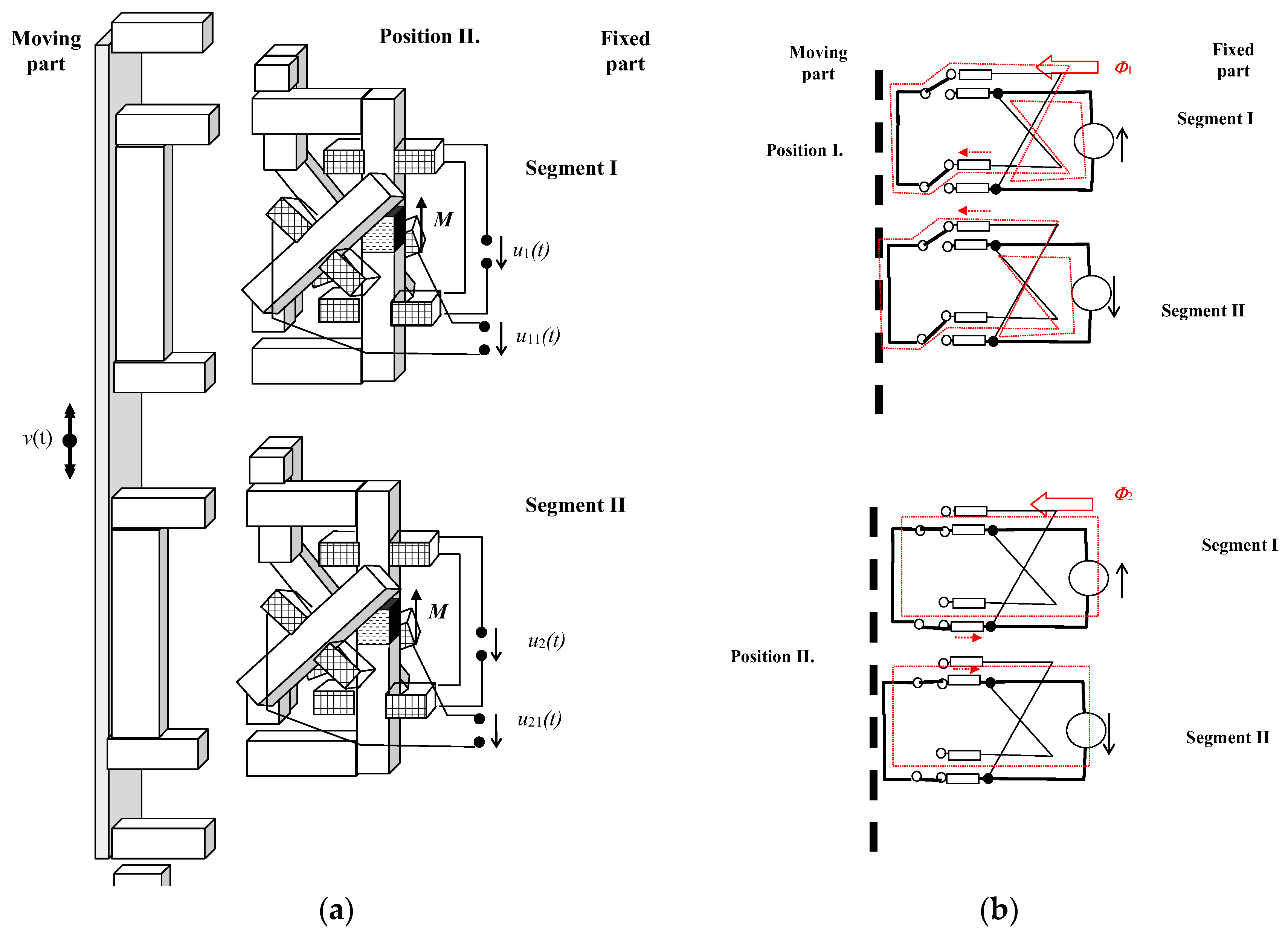
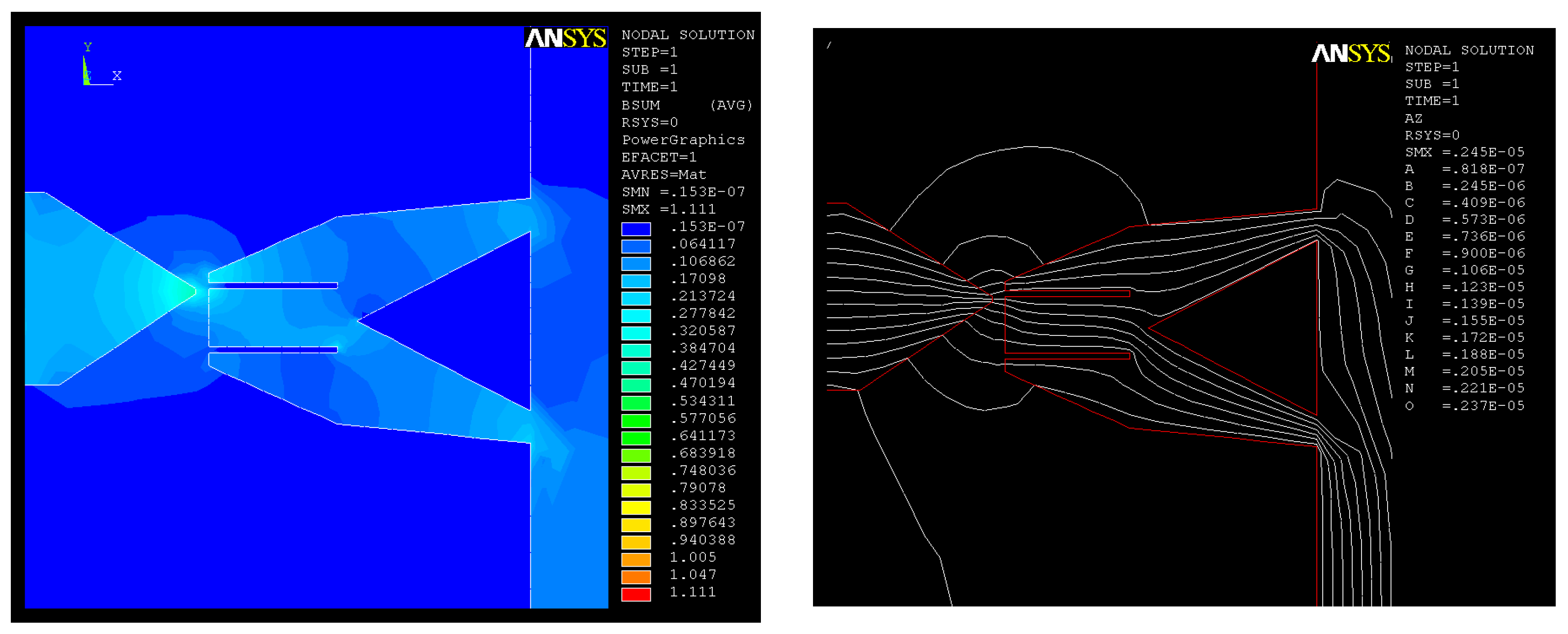





| Reference | Permanent Magnet Type | Generator Body Size x,y,z [m] | Output Power Pout [W] | Output Voltage Uout [V] | Effective Power Density pefd [W/m3] |
|---|---|---|---|---|---|
| Beeby et al. [28], 2007 | − | 375 mm3 | 2 × 10−6 | 0.428 RMS | ≈6 |
| Zhu et al. [29], 2010 | FeNdB | 2000 mm3 | 61.6–156.6 × 10−6 | − | ≈30−80 |
| Kulkarni et al. [27], 2008 | FeNdB | 3375 mm3 | 0.6 × 10−6 | 0.025 | ≈0.2 |
| Wang et al. [31], 2007 | FeNdB | 256 mm3 | - | 0.06 | - |
| Lee et al. [33], 2012 | FeNdB | 1.4 × 10−4 m3 | 1.52 × 10−3 | 4.8 | ≈10 |
| Yang et al. [32], 2014. | − | 50,000 mm3 | 13.4 × 10−3 | 0.7−2.0 | ≈270 |
| Elvin et al. [30], 2011 | − | 15,000 mm3 | 4 × 10−6 | 0.007 | ≈0.26 |
| MG I [18], 2006 | FeNdB | 90, 40, 30 mm | 70 × 10−3 | 4−60 (300) p-p | ≈650 |
| MG II [18], 2006 | FeNdB | 50, 27, 25 mm | 19.5 × 10−3 | 6−15 | ≈60 |
| MG III | FeNdB | 50, 25, 25 mm | 5.0 × 10−3 | 1.0−2.5 | ≈15 |
| MG IV | FeNdB | 50, 35, 25 mm | 8.0 × 10−3 | 1.0−2.5 | ≈18 |
| * Lith. battery [34], 2018 | * Lith. battery | ≈40 × 106 | |||
| * Supercap [35], 2010 | * Supercap | ≈3−5 | |||
| * Fuel | * Fuel | ≈4 × 109 | |||
| * U235 | * U235 | ≈9 × 1016 |
| Measurement HV@n = 30 | * Type I | nA,I | ** Type II | nA,II | *** Type III | nA,III |
|---|---|---|---|---|---|---|
| U0[V]@Z1 = ∞ Ω | 0.200 | 0.018 | 0.300 | 9.13 × 10−4 | 0.800 | 6.39 × 10−4 |
| Uz[V]@Z1,Re = 150 Ω | 0.0100 | 1.82 × 10−5 | 0.0200 | 3.65 × 10−5 | 0.500 | 0.0016 |
| I0[A]@Z1 = ∞ Ω | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| Iz[A]@Z1,Re =150 Ω | 6.66 × 10−5 | 1.22 × 10−7 | 1.33 × 10−4 | 2.43 × 10−7 | 0.500 | 1.06 × 10−5 |
| P0[W]@Z1 = ∞ Ω | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| Pz[W]@Z1,Re =150 Ω | 6.66 × 10−7 | 1.217 × 10−11 | 2.66 × 10−6 | 4.86 × 10−11 | 0.00166 | 9.21 × 10−8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zukal, J.; Szabó, Z.; Kříž, T.; Kadlec, R.; Dědková, J.; Fiala, P. A Robust Generator–Harvester for Independent Sensor Systems. Appl. Sci. 2024, 14, 1246. https://doi.org/10.3390/app14031246
Zukal J, Szabó Z, Kříž T, Kadlec R, Dědková J, Fiala P. A Robust Generator–Harvester for Independent Sensor Systems. Applied Sciences. 2024; 14(3):1246. https://doi.org/10.3390/app14031246
Chicago/Turabian StyleZukal, Jiří, Zoltán Szabó, Tomáš Kříž, Radim Kadlec, Jamila Dědková, and Pavel Fiala. 2024. "A Robust Generator–Harvester for Independent Sensor Systems" Applied Sciences 14, no. 3: 1246. https://doi.org/10.3390/app14031246
APA StyleZukal, J., Szabó, Z., Kříž, T., Kadlec, R., Dědková, J., & Fiala, P. (2024). A Robust Generator–Harvester for Independent Sensor Systems. Applied Sciences, 14(3), 1246. https://doi.org/10.3390/app14031246







