Research on Mechanical Model and Torsional Stiffness Properties of Leaf Spring Torsional Vibration Dampers for Marine Diesel Engines

Abstract

The torsional stiffness parameter significantly influences the natural frequency of a leaf spring torsional vibration damper and its proper match with a diesel engine, and the nonlinear characteristics of torsional stiffness avoid reduced reliability due to the excessive torsion angle of the damper. An efficient mechanical model for the damper with nonlinear characteristics is established by integrating the Euler–Bernoulli beam theory and accounting for the geometric nonlinearity of leaf spring deformation during operation. The model’s validity is confirmed through finite element analysis. This study then explores the influence of design parameters on the mechanical characteristics of the damper. The results reveal a gradual increase in the torsional stiffness of the damper with the expanding arc radius of the clamping groove. Simultaneously, the torsional stiffness curve exhibits more pronounced nonlinear characteristics. In contrast, an elongation of the leaf spring leads to a sharp decline in torsional stiffness, accompanied by a diminishing prominence of nonlinear traits. Thus, both the arc radius of the clamping groove and the spring length significantly impact the torsional stiffness and nonlinear features of the leaf spring torsional vibration damper. The nonlinear characteristics intensify with an enlarged arc radius of the clamping groove and a reduced leaf spring length. Additionally, the damper’s torsional stiffness is influenced by the leaf spring thickness and the red copper gasket length. Future damper designs should comprehensively consider these relevant parameters.

1. Introduction

The stability and reliability of marine diesel engines, serving as the primary power source for maritime vessels, hold significant importance. During diesel engine operation, the crankshaft system generates cyclic torsional vibrations due to fluctuating torque. Due to the longer length of the crankshaft in marine high-power diesel engines and the larger moment of inertia within the crankshaft system, there is smaller torsional stiffness and lower natural frequency, making it highly susceptible to resonance within its operational speed [1,2,3,4,5]. Hence, preventive measures must be incorporated into diesel engine design to avoid severe noise and potential crankshaft fractures. The leaf spring torsional vibration damper, a pivotal component of the diesel engine, is positioned at the crankshaft’s free end. When appropriately selected, it efficiently absorbs vibration energy, diminishing vibration and noise at the engine’s limit speed [6,7,8,9]. The occurrence of torsional vibration in diesel engines prompts the inner and outer rings of the leaf spring torsional vibration damper to exhibit relative movement, resulting in bending and deformation of the damper’s leaf spring. Simultaneously, the combined effect of friction from the red copper gasket between the leaf springs and the flow of cooling oil absorbs vibration energy, effectively mitigating structural vibrations in the crankshaft system and the hull [10,11,12]. For the damper, the torsional stiffness parameter plays a crucial role in calculating its natural frequency, thereby influencing the damper’s design and ensuring its compatibility with the engine. Typically, the natural frequency of the damper is selected to be close to a specific vibration frequency. The selected natural frequency of the damper is closely tied to the torsional vibration frequency of the diesel engine shaft system, which, in turn, depends on the speed and structure of the engine. During the operation of the diesel engine, the torsional vibration frequency typically falls within the range of 50–300 Hz. The torsional stiffness of the damper is dictated by the stiffness and force exerted by the leaf spring group.

The leaf spring group within the torsional vibration damper is structured as a double-laminated beam, attracting continuous scholarly attention to its mechanical model and calculations. The Newmark model [13], a classical calculation model, simplifies the upper and lower sections of the composite beam as Euler–Bernoulli beams derived from their elastic interaction. This classic model remains extensively utilized in current research. Girhammar et al. [14] utilized the Hamilton principle to derive partial differential equations, general solutions for deflection and internal forces, and corresponding consistent boundary conditions for the Euler–Bernoulli composite beam structure with interlayer slip subjected to general dynamic loads. Building upon Reddy’s high-order beam theory, He et al. [15] introduced the implicit kinematic hypothesis for small deformation double-laminated beams. The Lagrange multiplier method was utilized to incorporate this assumption as a constraint within the minimum potential energy variational principle of high-order composite beams, resulting in a nonlinear displacement method for high-order composite beams that can be converted into nonlinear Euler–Bernoulli composite beams. Shen et al. [16] utilized the differential quadrature element method to derive the complete Lagrange formulation for analyzing quadrature elements in composite beams, considering interface slip. This method is grounded in the small-strain Euler–Bernoulli beam theory and incorporates assumptions of large displacement and finite rotation. Furthermore, Nguyen et al. [17] introduced the direct stiffness method to address partial interaction behavior within double-laminated beams and performed linear static analyses on such beams.

The thickness of the damper leaf spring is uniformly varied, which is typical of a variable cross-section leaf spring. The study of variable cross-section leaf springs commonly employs the Euler–Bernoulli beam model. Currently, empirical formulas and macroscopic mechanical property tests remain the primary methods for summarizing its mechanical properties. The existing empirical formulas only calculate linear stiffness with limited considerations, lacking the ability to evaluate nonlinear properties. The shape of a leaf spring significantly influences its properties [18]. Various methods exist for calculating the variable stiffness of leaf springs. These include the common curvature method [19,20], which assumes continuous contact along the entire length of each leaf spring without gaps under any load, with each leaf spring in the same cross-section sharing a common radius of curvature, and the centralized load method [21,22,23], which presumes contact solely at the end of each leaf spring for force transfer among them. Additionally, the finite element method [24,25,26] is available. Numerous engineering application data indicate that the centralized load method exhibits higher accuracy in calculating short leaf springs, while the common curvature method demonstrates better accuracy for long leaf springs. Nevertheless, both the common curvature method and the concentrated load method display limited adaptability and lower accuracy in determining the stiffness of variable-section leaf springs, posing challenges in meeting engineering practice requirements. In response, Hu et al. [27] developed a comprehensive mechanical model for the gradual stiffness of leaf springs, considering the distinct operational characteristics of the main and auxiliary springs, and proposed a hybrid method, amalgamating the common curvature and concentrated load methods. Shi et al. [28] introduced an efficient method to calculate the comprehensive stiffness of parabolic leaf springs with variable stiffness. The calculation method for their composite stiffness was derived using numerical integration. Zhou et al. [29] proposed a curved beam model considering thickness variation along the leaf spring’s length and accounted for end displacement in determining the overall stiffness. Hwang et al. [30] deduced the linear stiffness of leaf springs, treating the stiffness of multiple groups as the cumulative stiffness of all individual leaf springs.

The analytical method proves more efficient than the finite element method for calculating the torsional stiffness of the damper, offering better support for damper design and mechanical property research. This paper introduces, for the first time, an efficient mechanical model for the torsional stiffness of the leaf spring’s torsion damper with nonlinear characteristics (as defined in Appendix A), integrating the Euler–Bernoulli beam theory [31,32] and considering the geometric nonlinearity in spring deformation during operation. This model is then employed to investigate the influence of damper design parameters on its torsional stiffness properties.

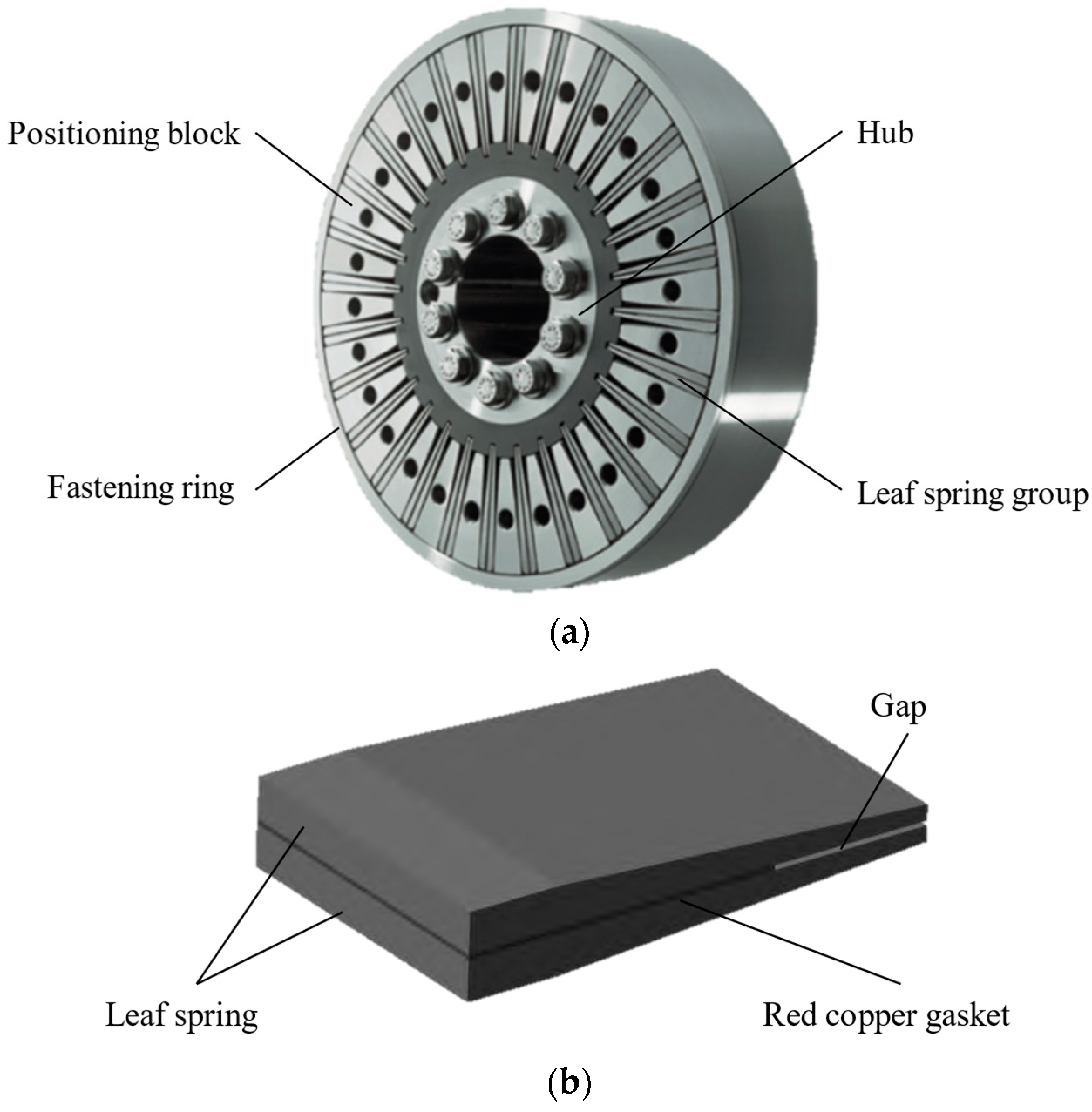
2. Structure and Parametric Model of Leaf Spring Torsional Vibration Damper

Figure 1a depicts the typical composition of the current marine diesel engine leaf spring torsional vibration damper, comprising a leaf spring group (refer to Figure 1b), hub, positioning block, fastening ring, etc. The leaf spring, hub, and fastening ring are constructed from chromium alloy, while the positioning block is crafted from 45 steel. The leaf spring group serves as the primary component influencing the damper’s crucial performance aspects. Torsional vibrations in the diesel engine cause reciprocal torsional displacement in the hub concerning the outer ring (comprising the leaf spring group, positioning block, fastening ring, etc.). The hub’s clamping groove applies force to the leaf spring’s end, inducing bending and deformation in the leaf spring group. A well-designed, manufactured, and installed leaf spring torsional vibration damper ensures that the thin edge of the leaf spring group embeds into the clamping groove, while the thick edge remains securely fixed by the fastening ring and positioning block.

In Figure 2, the parameter model of the leaf spring torsional vibration damper is depicted. In this figure, marked as 1 and 2 are the leaf springs. In this figure, components labeled 1 and 2 represent leaf springs, with a red copper gasket positioned between their middle sections, while their left ends are fixed at T₁. O denotes the coordinate origin; O₁ represents the center of the circular arc on both sides of the clamping groove, originating from point O_r with a radius r; N marks the contact point between the leaf spring and the arc; a₁ and a₂ stand for the thicknesses of the leaf spring’s left and right ends; L signifies the horizontal distance of point N. F_c denotes the interaction force between the two leaf springs at the red copper gasket’s end, where S represents the bending part’s length of the red copper gasket, and b stands for the leaf spring’s width. Additionally, the force acting on leaf spring 1 during the deformation process aligns with the O₁N direction. Due to the small magnitude of the horizontal component force and its negligible impact on spring bending, this component force is disregarded. Only the vertical component force is considered and denoted as force F.

3. Mechanical Modeling

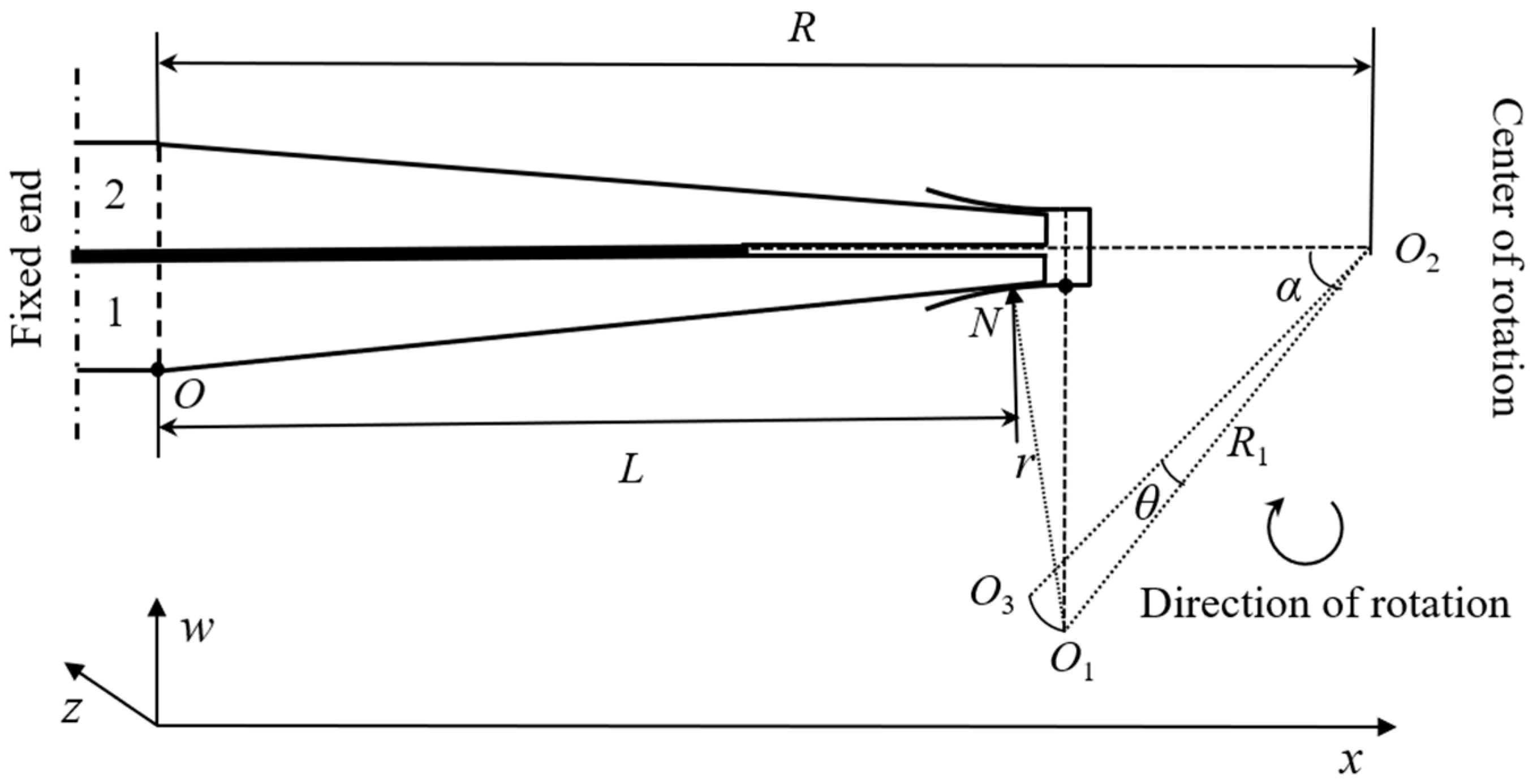
3.1. Modeling for Leaf Spring Group Deformation

Euler–Bernoulli beam theory is a classical beam theory [33]. The displacement field of this theory can be expressed as:

$$\{\begin{array}{l}u\left(x,z\right)=-z\frac{\mathrm{d}{w}_0}{\mathrm{d}x}\hfill \\ w\left(x,z\right)=w_0\left(x\right)\hfill \end{array}$$

(1)

where w₀ represents the transverse displacement of every point along the neutral axis, synonymous with deflection. The utilization of Euler–Bernoulli beam theory relies on two fundamental assumptions: firstly, the cross-section of the beam remains flat both before and after deformation, and secondly, the cross-section remains perpendicular to the neutral layer post-deformation. The primary strength of this theoretical beam model lies in having a single generalized displacement, typically necessitating only one positional function during solving, significantly simplifying the calculation process [34,35]. Figure 3 illustrates the state of the Euler–Bernoulli beam pre- and post-deformation.

Figure 1b illustrates that within the leaf spring group’s structure, a red copper gasket is positioned between the two leaf springs to prevent contact wear between identical materials. During the bending deformation of the leaf spring group, the red copper gasket undergoes bending, ensuring that it only makes contact with the two leaf springs at T₂ in Figure 2, facilitating force transmission. Consequently, during model establishment, we segment the function at T₂ to more effectively address the impact of the force at this point on the bending moment of the leaf spring. In the coordinate system depicted in Figure 2, the bending moments M₁(x) and M₂(x) of leaf springs 1 and 2 are expressed as follows:

$$M_1\left(x\right)=\{\begin{array}{cc}F\left(L-x\right)-F_{\mathrm{c}}\left(S-x\right),& x\in \left[0,S\right]\\ F\left(L-x\right),& x\in \left(S,L\right]\end{array}$$

(2)

$$M_2\left(x\right)=\{\begin{array}{cc}{F}_{\mathrm{c}}\left(S-x\right),& x\in \left[0,S\right]\\ 0,& x\in \left(S,L\right]\end{array}$$

(3)

Based on Euler–Bernoulli beam theory, the bending mechanical model of two leaf springs is:

$$M_1\left(x\right)=EI\frac{{\mathrm{d}}^2{w}_1\left(x\right)}{\mathrm{d}{x}^2}$$

(4)

$$M2\left(x\right)=EI\frac{{\mathrm{d}}^2{w}_2\left(x\right)}{\mathrm{d}{x}^2}$$

(5)

where w₁ and w₂ are the deflections of leaf spring 1 and leaf spring 2, respectively, in m.

$$\frac{{\mathrm{d}}^2{w}_1\left(x\right)}{\mathrm{d}{x}^2}=\{\begin{array}{cc}\frac{F\left(L-x\right)-F_{\mathrm{c}}\left(S-x\right)}{EI},& x\in \left[0,S\right]\\ \frac{F\left(L-x\right)}{EI},& x\in \left(S,L\right]\end{array}$$

(6)

$$\frac{{\mathrm{d}}^2{w}_2\left(x\right)}{\mathrm{d}{x}^2}=\{\begin{array}{cc}\frac{F_{\mathrm{c}}\left(S-x\right)}{EI},& x\in \left[0,S\right]\\ 0,& x\in \left(S,L\right]\end{array}$$

(7)

where E is the elastic modulus of spring material, in MPa. The sectional moment of inertia I is:

$$I\left(x\right)=\frac{b{h}^3\left(x\right)}{12}$$

(8)

h(x) is the thickness of any position of the leaf spring,

$$h\left(x\right)=a_1+kx$$

(9)

where k is the thickness change rate of the leaf spring,

$$k=\frac{\left(a_2-a_1\right)}{l}$$

(10)

where l is the length of the curved portion of the leaf spring. Substitute Formulas (8)–(10) into Formulas (6) and (7) to obtain:

$$\frac{{\mathrm{d}}^2{w}_1\left(x\right)}{\mathrm{d}{x}^2}=\{\begin{array}{cc}\frac{12\left[F\left(L-x\right)-F_{\mathrm{c}}\left(S-x\right)\right]}{Eb{\left(a_1+kx\right)}^3},& x\in \left[0,S\right]\\ \frac{12F\left(L-x\right)}{Eb{\left(a_1+kx\right)}^3},& x\in \left(S,L\right]\end{array}$$

(11)

$$\frac{{\mathrm{d}}^2{w}_2\left(x\right)}{\mathrm{d}{x}^2}=\{\begin{array}{cc}\frac{12F_{\mathrm{c}}\left(S-x\right)}{Eb{\left(a_1+kx\right)}^3},& x\in \left[0,S\right]\\ 0,& x\in \left(S,L\right]\end{array}$$

(12)

Considering boundary conditions $\frac{\mathrm{d}{w}_1\left(x\right)}{\mathrm{d}x}{|}_{x=0}=\frac{\mathrm{d}{w}_2\left(x\right)}{\mathrm{d}x}{|}_{x=0}=0$, the angle function of the leaf spring group is obtained by integrating expressions (11) and (12) once:

$$\frac{\mathrm{d}{w}_1\left(x\right)}{\mathrm{d}x}={\phi }_1\left(x\right)=\{\begin{array}{c}{\phi }_{11}\left(x\right), x\in \left[0,S\right]\\ {\phi }_{12}\left(x\right), x\in \left[S,L\right]\end{array}$$

(13)

$$\frac{\mathrm{d}{w}_2\left(x\right)}{\mathrm{d}x}={\phi }_2\left(x\right)=\{\begin{array}{c}{\phi }_{21}\left(x\right), x\in \left[0,S\right]\\ {\phi }_{22}\left(x\right), x\in \left[S,L\right]\end{array}$$

(14)

where:

$$\begin{array}{l}{\phi }_{11}\left(x\right)={\displaystyle {\int }_{ 0}^x \frac{12\left[F\left(L-t\right)-F_{\mathrm{c}}\left(S-t\right)\right]}{Eb{\left(a_1+kt\right)}^3}\mathrm{d}t}\\ =6x(FLkx-F_{c}Skx+2FL{a}_1-F{a}_{1}x-2F_{c}S{a}_1+F_c{a}_{1}x)/[Eb{(kx+a_1)}^2{a_1}^2]\end{array}$$

(15)

$$\begin{array}{l}{\phi }_{12}\left(x\right)={\displaystyle {\int }_{ 0}^S \frac{12\left[F\left(L-t\right)-F_{\mathrm{c}}\left(S-t\right)\right]}{Eb{\left(a_1+kt\right)}^3}\mathrm{d}t}+{\displaystyle {\int }_{ S}^x \frac{12F\left(L-t\right)}{Eb{\left(a_1+kt\right)}^3}\mathrm{d}t}\\ =6S(FLSk-F_C{S}^{2}k+2FL{a}_1-FS{a}_1-F_{C}S{a}_1)/[Eb{(Sk+a_1)}^2{a_1}^2]-\\ 6F(L{S}^{2}k-Lk{x}^2-2S^{2}kx+2Sk{x}^2+2LS{a}_1-2L{a}_{1}x-S^2{a}_1+a_1{x}^2)/\\ [Eb{(kx+a_1)}^2{(Sk+a_1)}^2]\end{array}$$

(16)

$${\phi }_{21}\left(x\right)={\displaystyle {\int }_{ 0}^x \frac{12F_{\mathrm{c}}\left(S-t\right)}{Eb{\left(a_1+kt\right)}^3}}\mathrm{d}t=6F_{C}x(Skx+2S{a}_1-a1x)/[Eb{\left(kx+a_1\right)}^2{a_1}^2]$$

(17)

$${\phi }_{22}\left(x\right)={\displaystyle {\int }_{ 0}^S \frac{12F_{\mathrm{c}}\left(S-t\right)}{Eb{\left(a_1+kt\right)}^3}}\mathrm{d}t+{\displaystyle {\int }_{ S}^x 0 }\mathrm{d}t=6F_C{S}^2/[{a_1}^2(Sk+a_1)bE]$$

(18)

After inspection, ${\phi }_{11}\left(S\right)-{\phi }_{12}\left(S\right)=0$, ${\phi }_{21}\left(S\right)-{\phi }_{22}\left(S\right)=0$. Similarly, considering boundary conditions $w_1(x){|}_{x=0}=w_2(x){|}_{x=0}=0$, integrate Equations (13) and (14) again to obtain the deflection function of the two leaf springs:

$$w_1\left(x\right)=\{\begin{array}{l}{w}_{11}\left(x\right), x\in \left[0,S\right]\\ w_{12}\left(x\right), x\in \left(S,L\right]\end{array}$$

(19)

$$w_2\left(x\right)=\{\begin{array}{l}{w}_{21}\left(x\right), x\in \left[0,S\right]\\ w_{22}\left(x\right), x\in \left(S,L\right]\end{array}$$

(20)

The functions in the leaf spring deflection expressions (19) and (20) are calculated. See Appendix A for details.

3.2. Modeling for Torsional Stiffness

As the hub rotates relative to the outer ring, the contact points between the arcs on both sides of the clamping groove and the leaf spring undergo continuous positional changes. In Figure 4, O₂ signifies the rotation center of the damper hub; O₃ denotes the position of O₁ after the torsion angle $\theta$.

The coordinates of point O₁ are (O_1x, O_1y), and the coordinates of point O₃ are (O_3x, O_3y), where:

$$\{\begin{array}{l}{O}_{1x}=R-R_1\cos \alpha \\ O_{1y}=-R_1\sin \alpha \\ O_{3x}=R-R_1\cos (\alpha -\theta )\\ O_{3y}=-R_1\cos (\alpha -\theta )\end{array}$$

(21)

From Equations (9) and (19), it is easy to know that the coordinate of contact point N is $(L , {\epsilon }_{12}(L))$, where ${\epsilon }_{12}(L)=w_{12}(L)-kx$. It can be seen from the structure of the damper that there is the following positional relation during the rotation process: (1) the length of $\overrightarrow{O_{1}N}$ is always the arc radius r; (2) the tangent of the contact point N is always perpendicular to $\overrightarrow{O_{1}N}$. Therefore, the following equations can be obtained:

$$\{\begin{array}{c}{(L-R+R_1\cos (\alpha -\theta ))}^2+{({\epsilon }_{12}(L)+R_1\sin (\alpha -\theta ))}^2-r^2=0\\ {\delta }_{12}\left(L) ({\epsilon }_{12}\right(L)+R_1\sin (\alpha -\theta \left)\right)+L - \mathrm{R}+R_1\cos (\alpha -\theta )=0\end{array}$$

(22)

where ${\delta }_{12}(L)={\phi }_{12}(L)-k$. Based on the deformation compatibility conditions of two leaf springs at the T₂ point:

$$w_{11}\left(T_2\right)-w_{21}\left(T_2\right)=0$$

(23)

Simultaneously, Equations (22) and (23) are introduced into the specific damper parameters, and the numerical solution of relevant parameters is obtained by solving the nonlinear equations with mathematical tools. Then, the total hub torque $M_Z$ of the damper is:

$$M_Z=nF\left(R-L\right)$$

(24)

where n is the number of circumferential leaf spring groups. The torsion angle of the hub is $\theta$, so the torsional stiffness of the damper is:

$$K=\frac{M_Z}{\theta }=\frac{nF\left(R-L\right)}{\theta }$$

(25)

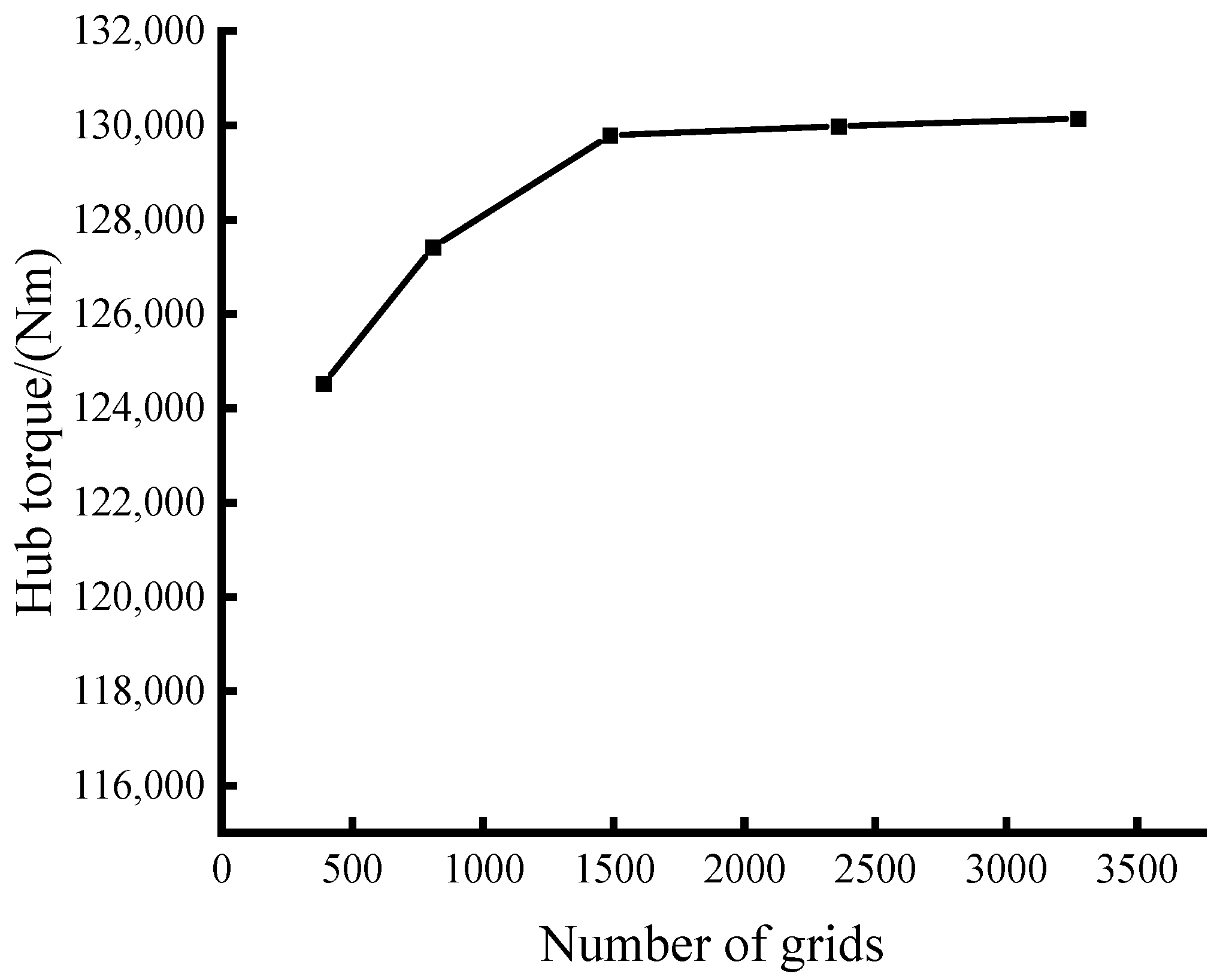
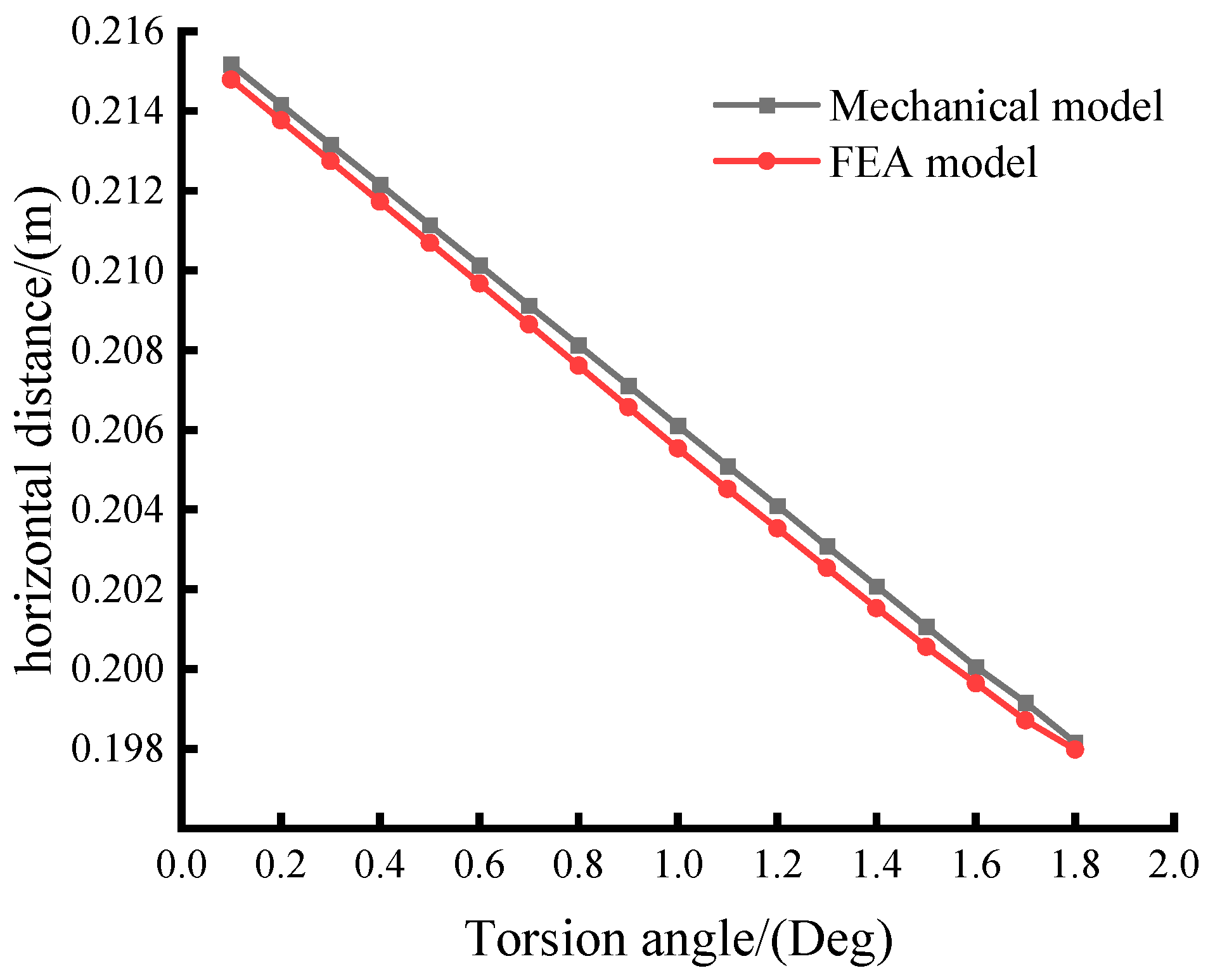
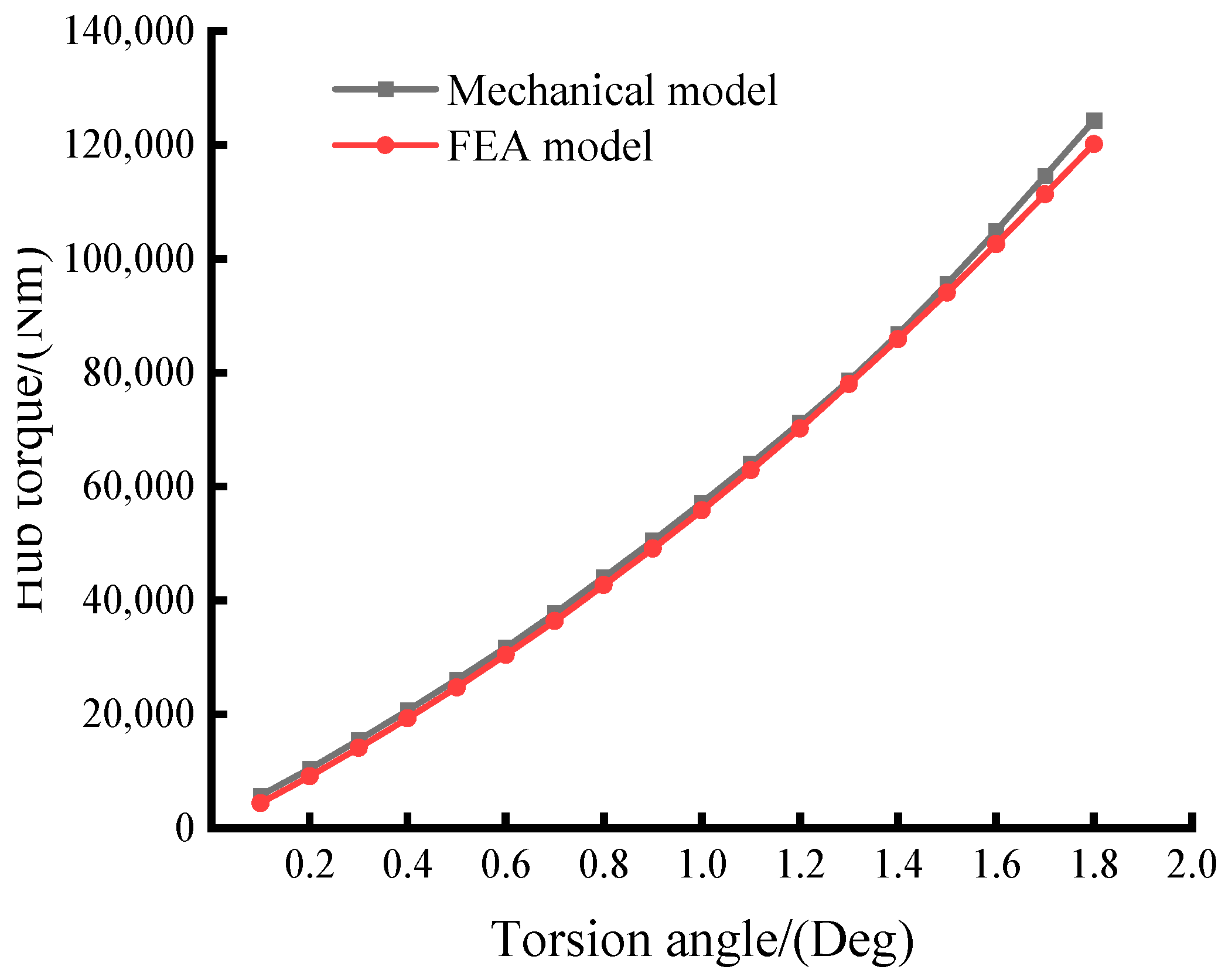
4. Verification of Model

The leaf spring torsional vibration damper used in marine diesel engines is sizable and heavy, demanding considerable resources for testing. The extensively employed finite element analysis method has matured and proven reliable in theoretical research, commercial software, and simulation of contact surfaces. This paper utilizes Ansys 2022R1 software to validate the established mechanical model governing the damper’s torsional stiffness. The key aspects encompass the following: (1) The leaf spring group exhibits typical plane strain characteristics, with the four-node quadrilateral plane strain element chosen for the finite element analysis. (2) There are degrees of freedom of the coupled Y-axis at the end of the red copper gasket (at T₂ in Figure 2). (3) The thicker edge of the leaf spring group is fixed by the positioning block, treating the finite element model as a fixed constraint. (4) As observed in Section 2, both the hub and leaf spring are crafted from chrome alloy. Nonetheless, due to the considerable discrepancy in contact area sizes between the hub clamping groove and the leaf spring length, and the greater stiffness of the clamping groove compared to the leaf spring, the clamping groove’s deformation is disregarded and treated as a rigid body. (5) Classify the contact region between the leaf spring and the clamping groove as frictional contact, with a friction coefficient of 0.1. (6) Rotate the hub clockwise around the damper center shaft in 0.1° steps to reach 1.8°.

The geometry of the damper is interconnected with the structure, size, power, and other factors of the diesel engine. The geometric dimensions of various parts in different dampers vary significantly. While ensuring optimal performance, researchers are tasked with designing parameters and sizes in a manner that aligns reasonably with the diesel engine’s space constraints. In general, the maximum diameter of the damper body typically falls within a range of 500 to 1500 mm. Using the leaf spring torsional vibration damper structure (depicted in Figure 5) as an example, the specific parameters include a thick edge leaf spring thickness of 0.016 m, thin edge thickness of 0.006 m, red copper gasket’s bending part length of 0.14 m, arc radius of 0.16 m, leaf spring bending part length of 0.22 m, leaf spring width of 0.15 m, O₁O₂ center distance of 0.261 m, rotation center horizontal distance of 0.426 m, angle between O₁O₂ line and horizontal direction at 39.48°, leaf spring elastic modulus of 2.1 × 10⁵ MPa, and Poisson’s ratio of 0.3, with 20 leaf spring groups. Typically, the damper’s torsion angle remains below 2°, with this example’s maximum torsion angle capped at 1.8°. Figure 6 demonstrates grid independence, confirming the upper limit criterion for the maximum hub torque with the specified parameters at a 1.8° torsion angle. Findings reveal that when the element count surpasses 1485, the maximum hub torque variation remains within 1%. Given the minimal influence of heightened mesh density on the outcomes, a meshing strategy with 1485 elements is employed. Validation outcomes for additional parameters are depicted in Figure 7, Figure 8 and Figure 9. The numerical outcomes for transverse force F, horizontal distance L, and hub torque M_z align well with the finite element simulation’s results in this mechanical model. At a torsion angle of 1.8°, the maximum error of these parameters remains within 3%.

At a torsion angle of 1.8°, the mentioned parameters exhibit their maximum error but remain within 3%. The damper’s torsional stiffness is determined based on its natural frequency. During the design process, the torsional stiffness is calculated under various torsion angles, based on the required natural frequency of the damper. This difference is substantial, and the range is extensive. Through verification of our established mechanical model, it is observed that the torsional stiffness, when the maximum torsion angle is within 1.8° and parameters are positive real numbers within a reasonable range, exhibits high accuracy. This verifies the effectiveness of the torsional stiffness mechanical model of the leaf spring torsional vibration damper presented in this paper. Furthermore, Figure 8 illustrates that the torsional stiffness of the torsional vibration damper is nearly linear when the torsion angle is below 0.6°, with nonlinearity emerging as the torsion angle increases.

5. Analysis for Torsional Stiffness Properties of Leaf Spring Torsional Vibration Damper

The torsional stiffness of a leaf spring torsional vibration damper is determined by its natural frequency. In the design process, the torsional stiffness is calculated at various torsion angles based on the required natural frequency of the damper. With the establishment of an efficient mechanical model for the torsional stiffness of a leaf spring torsional vibration damper, it becomes possible not only to calculate the damper’s torsional stiffness but also to conveniently study the influence of design parameters on the torsional stiffness characteristics. Using the damper depicted in Figure 5 as an example, the impact of pertinent parameters on the torsional stiffness characteristics is investigated.

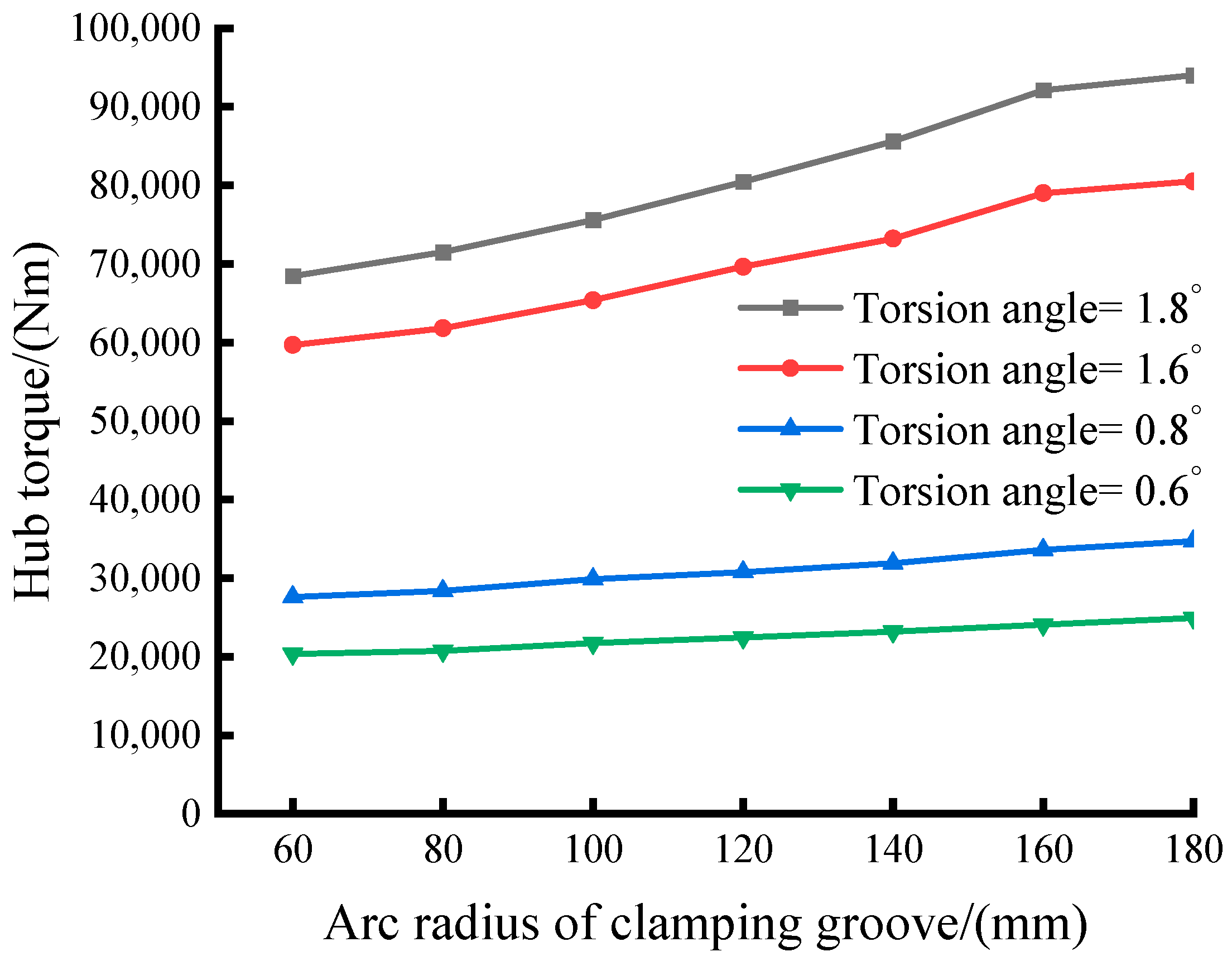
5.1. Influence of Clamping Groove Arc Radius on Torsional Stiffness Properties

The clamping groove, crucial in the interaction between the leaf spring group and the hub, necessitates an investigation into its design parameters for the damper’s torsional stiffness properties. Altering solely the arc radius of the clamping groove while maintaining other parameters reveals its impact on the damper’s torsional stiffness (Figure 10 and Figure 11). The figures illustrate a notable variance among the damper’s torsional stiffness curves at varying radii, with this variance amplifying as the radius expands. Notably, a smaller arc radius renders a less obvious nonlinear property in the torsional stiffness curve, almost remaining linear at 60 mm. However, with increasing radii, the nonlinear characteristics become more conspicuous. Around 160 mm, this nonlinearity peaks; further increments to 180 mm produce marginal changes in the curve. In Figure 10, the torsional stiffness curve under varied clamping groove arc radii starts displaying nonlinear changes at approximately 0.6° of torsion angle. This illustrates the considerable influence of the clamping groove arc radius on both the torsional stiffness and its nonlinear traits. Extremely small radii result in nearly linear stiffness curves, losing the benefit of nonlinear effects. Conversely, beyond a certain arc radius, the damper’s torsional stiffness nearly plateaus. Determining an optimal clamping groove arc radius based on torsional stiffness requirements is pivotal for future leaf spring damper design.

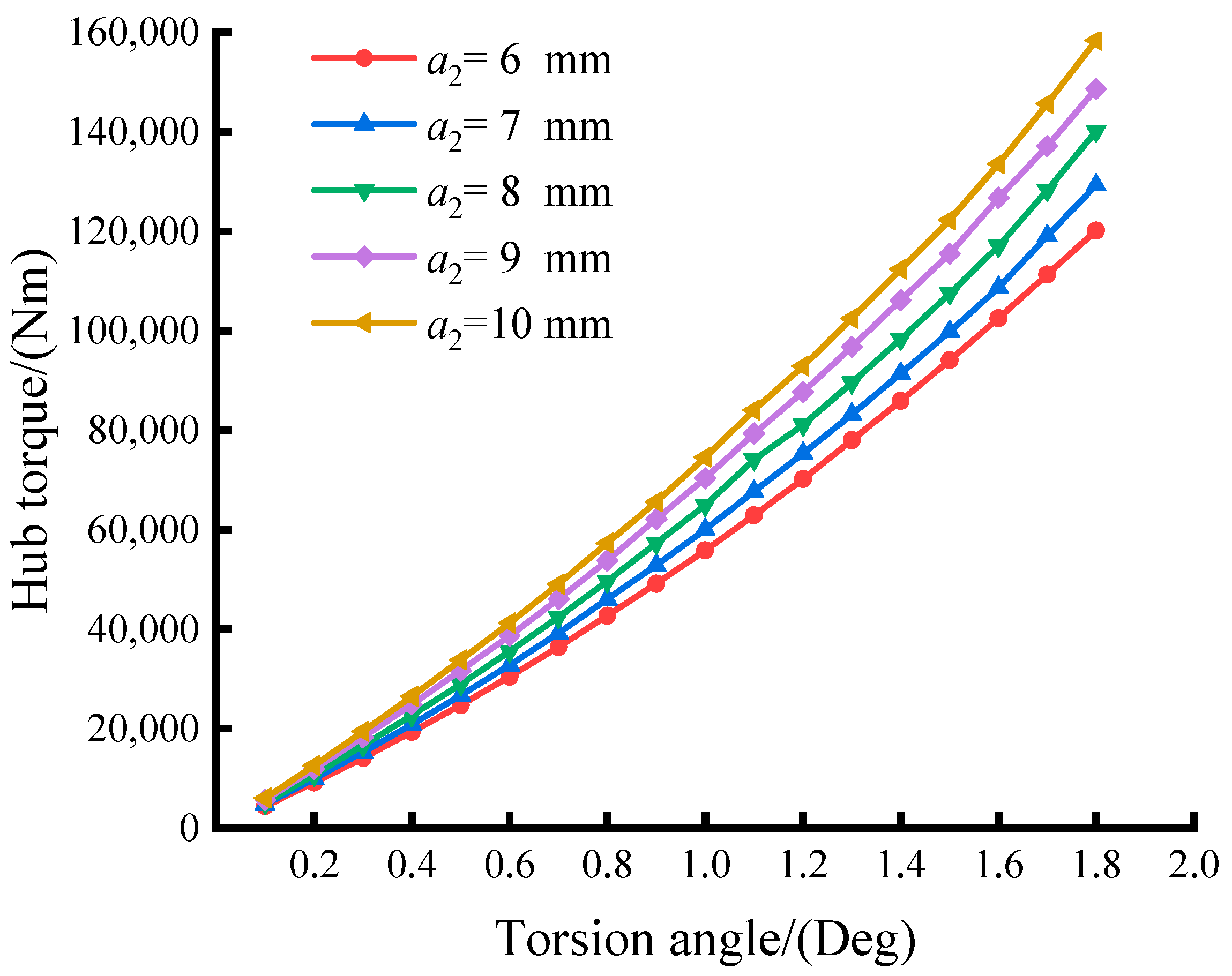
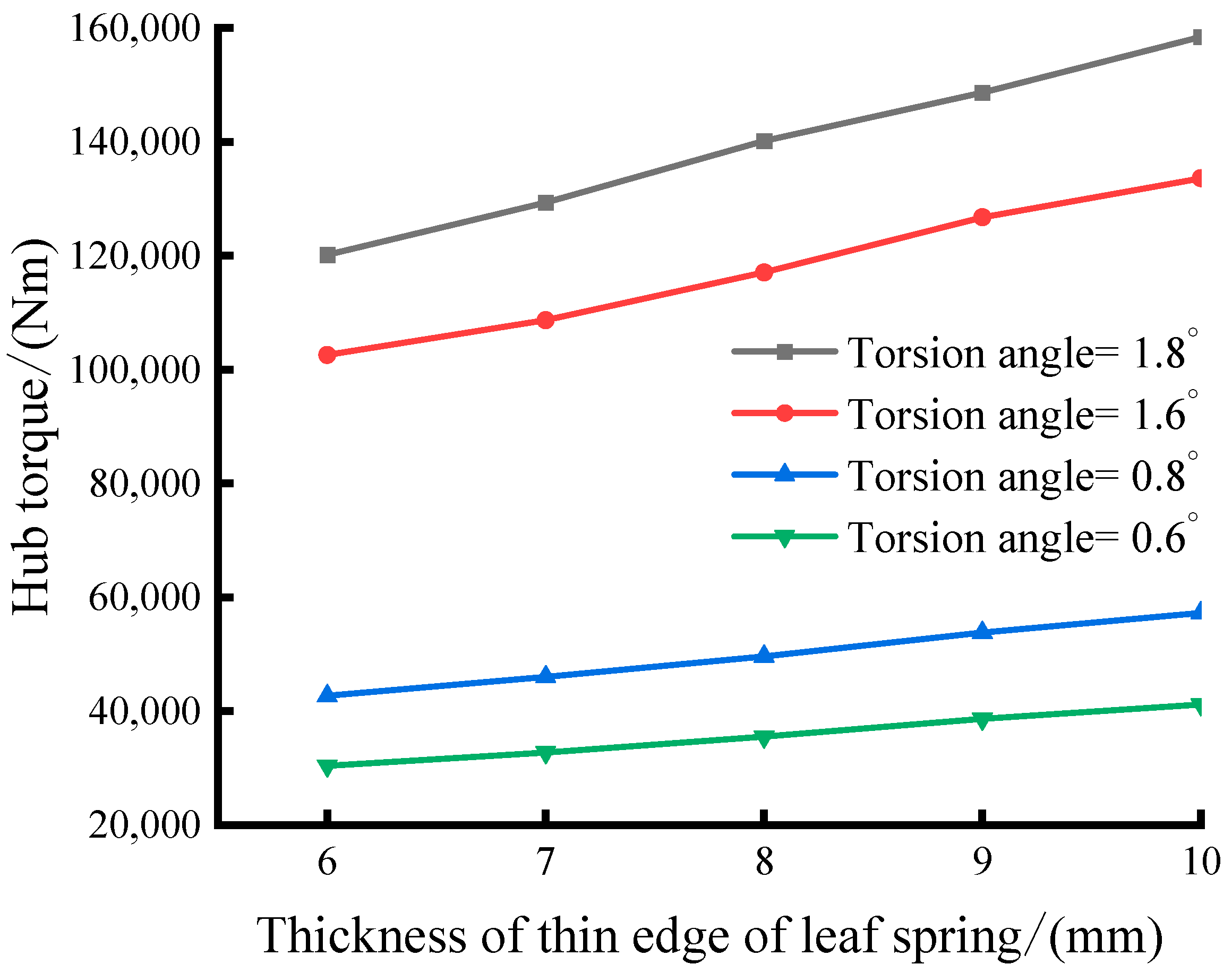
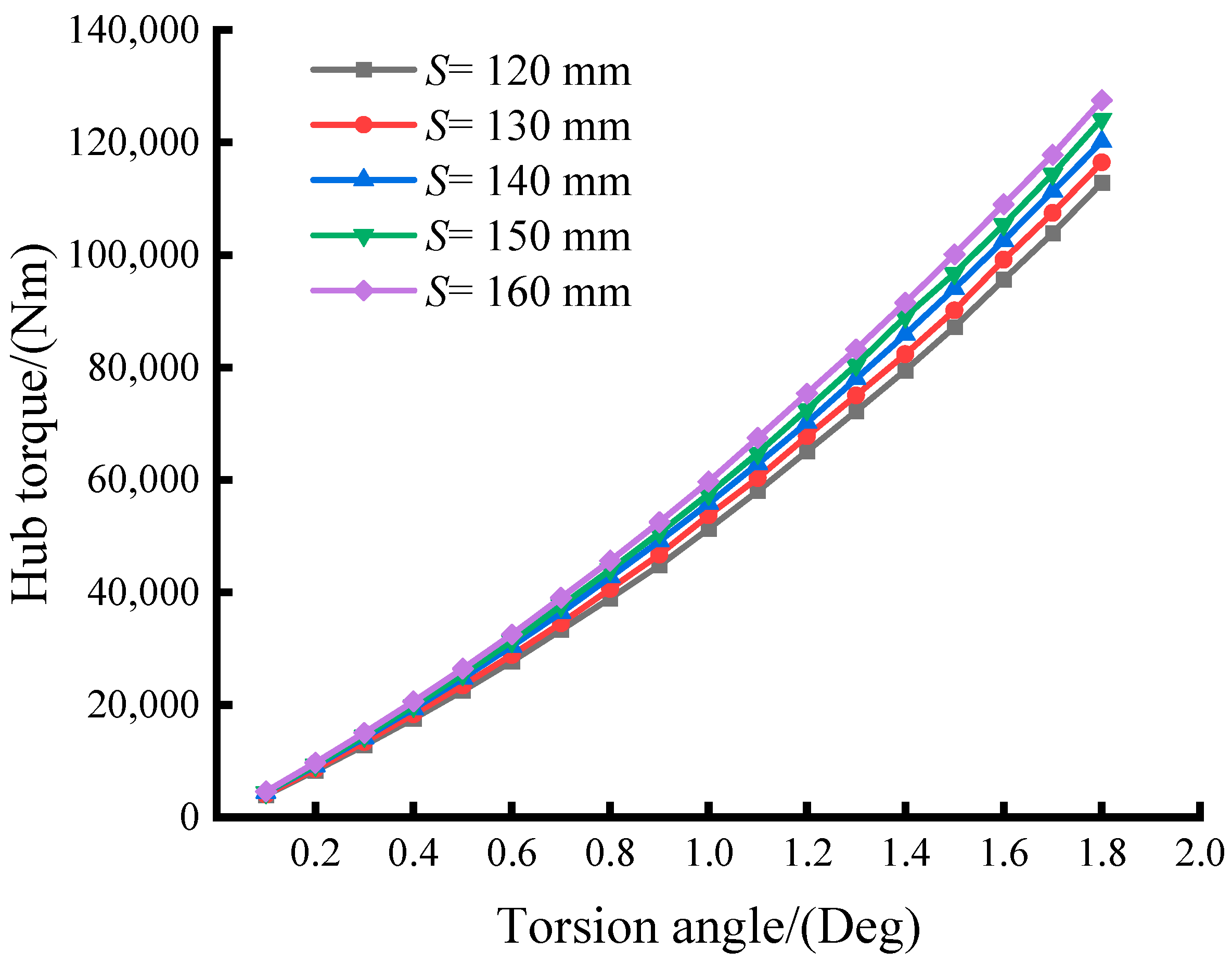
5.2. Influence of Leaf Spring Size on Torsional Stiffness Properties

The stiffness of the leaf spring group governs the torsional stiffness of the torsional vibration damper. From the leaf spring group’s structure, it is evident that the spring’s length and thickness impact its stiffness. Maintaining the other parameters constantly, altering the leaf spring length reveals its impact on the damper’s torsional stiffness, illustrated in Figure 12 and Figure 13. Figure 12 highlights the considerable influence of spring length on the damper’s torsional stiffness. When the spring length is shorter, the damper’s torsional stiffness curve displays pronounced nonlinear characteristics. However, as the leaf spring length increases, the curve’s nonlinear aspects gradually diminish. At a leaf spring length of 260 mm, the curve tends towards linearity. Figure 13 demonstrates the significant influence of leaf spring length on torsional stiffness at equivalent torsion angles, with this influence amplifying as the torsion angle increases. At smaller torsion angles, increasing the leaf spring length leads to a gradual decline in torsional stiffness. Yet, at torsion angles of 1.6° and 1.8°, extending the leaf spring sharply reduces torsional stiffness. Shorter springs exhibit increased stiffness in the spring group, resulting in conspicuous nonlinear characteristics in the torsional stiffness of the damper.

Given a uniform change in the thickness of the leaf spring, Figure 14 and Figure 15 illustrate the impact on the torsional stiffness of the leaf spring torsional vibration damper by altering the thickness of the thin edge while maintaining the thickness of the thick edge. The curves in Figure 14 exhibit noticeable nonlinear characteristics, and these properties become more pronounced as the thickness of the thin edge of the leaf spring increases. Figure 15 indicates that, under the same torsion angle, the impact of leaf spring thickness on the torsional stiffness of the damper is as follows: when the torsion angle is small, the effect of spring thickness on torsional stiffness is relatively modest; with an increase in torsion angle, the influence of spring thickness on torsional stiffness also grows. Consequently, the thickness of the spring has a discernible impact on the torsional stiffness and nonlinear characteristics of the damper.

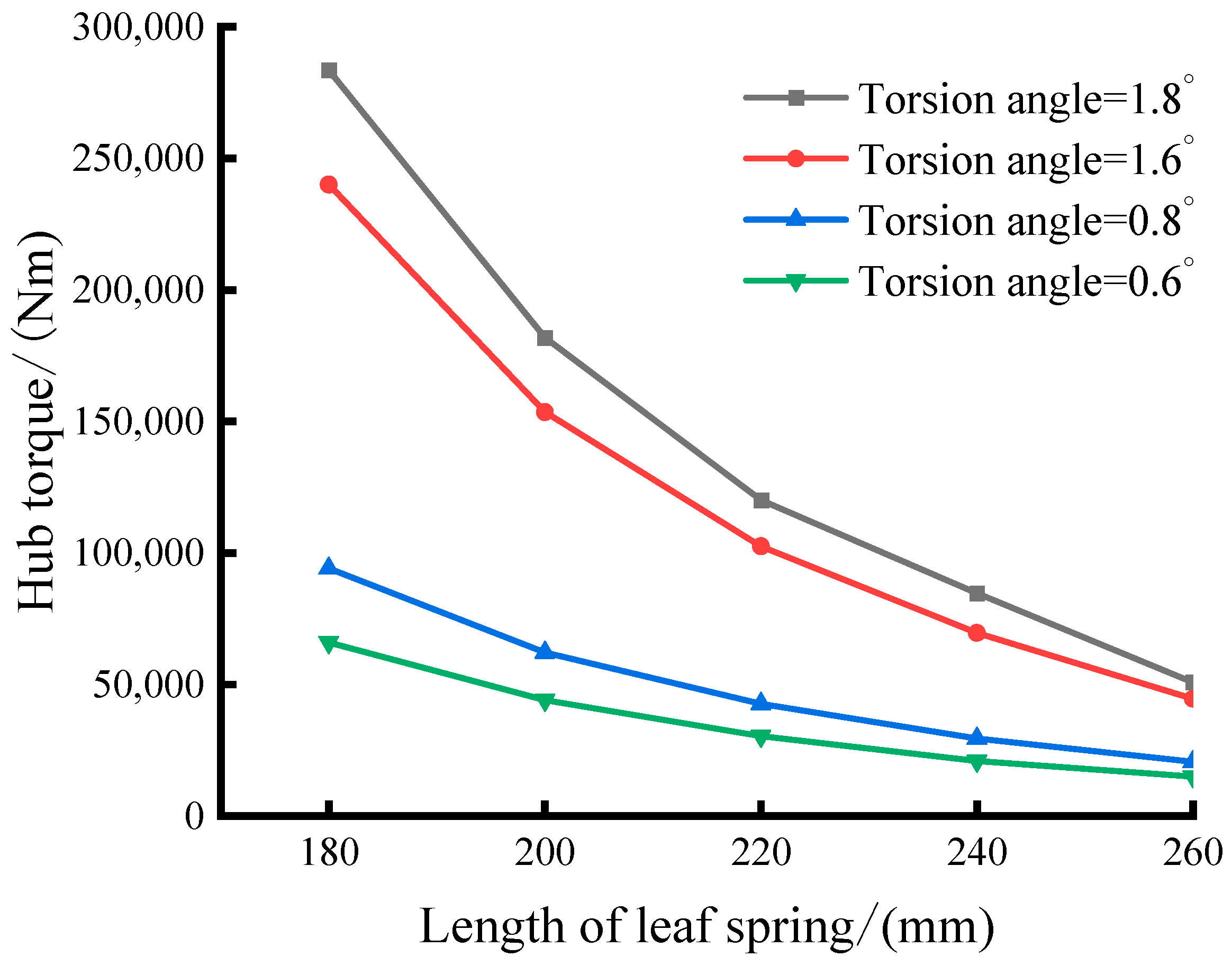
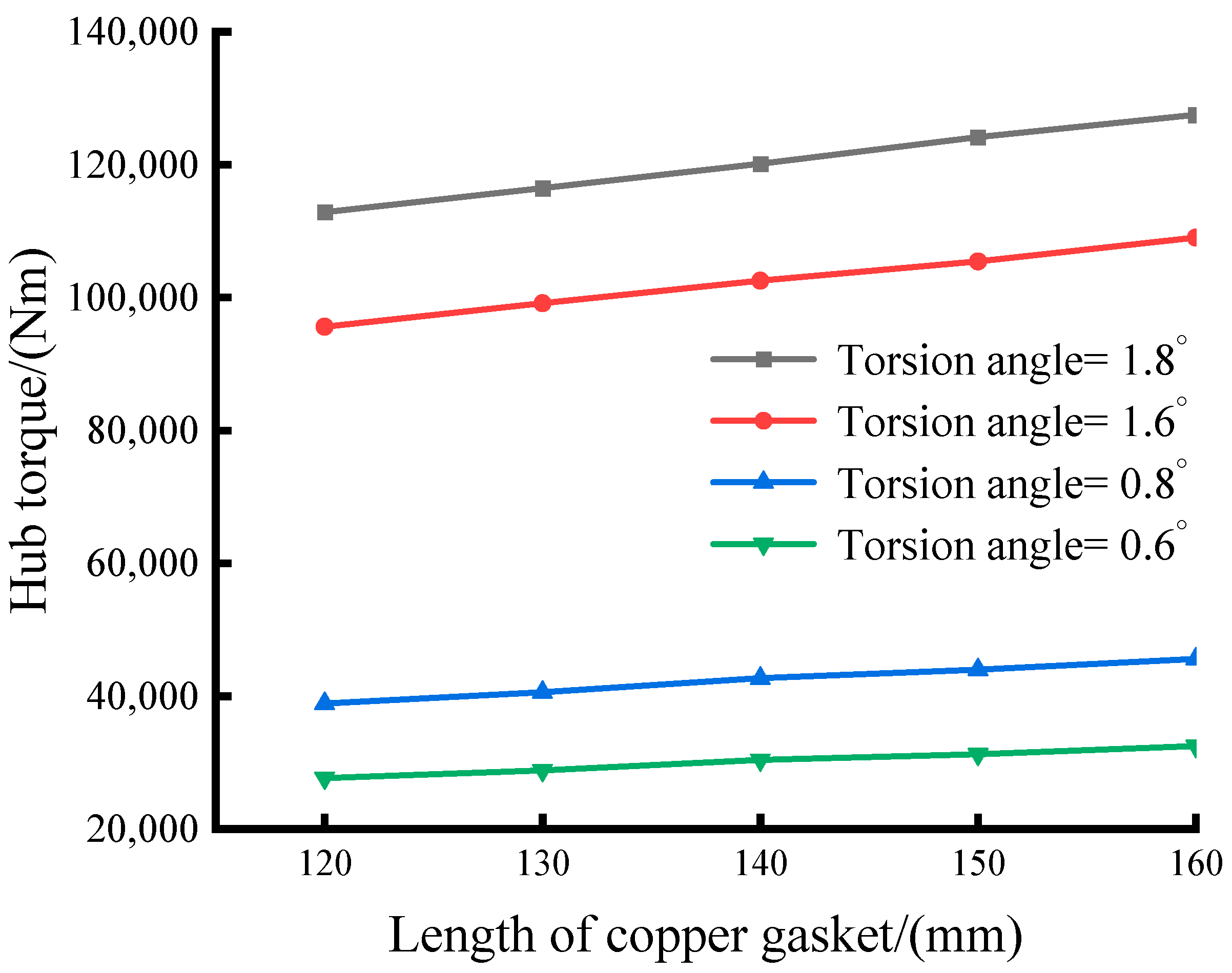
5.3. Influence of Red Copper Gasket Length on Torsional Stiffness Properties

Figure 16 depicts the impact of the red copper gasket length on the damper’s torsional stiffness. The figure reveals distinct nonlinear properties across all curves. Notably, when the torsion angle surpasses 1.4°, the minimal disparity in curvature radius is observed among the curves, suggesting the negligible influence of the red copper gasket’s length on the damper’s torsional stiffness nonlinear characteristics. Figure 17 demonstrates a marginal increase in torsional stiffness with the elongation of the red copper gasket at identical torsion angles. Consequently, in the prospective design of leaf spring torsional vibration dampers, the effect of red copper gasket length on the damper’s torsional stiffness nonlinear characteristics may be disregarded.

6. Conclusions

This study establishes an efficient mechanical model for the torsional stiffness of the leaf spring torsional vibration damper by integrating the Euler–Bernoulli beam theory with the geometric nonlinearity observed during spring deformation. Subsequently, the research investigates the impact of clamping groove arc radius, leaf spring thickness and length, and red copper gasket length on torsional stiffness properties. The principal conclusions are as follows:

(1)

The analytical outcomes from the mechanical model proposed in this article exhibit a high level of concordance with the results obtained through finite element analysis, validating the reliability of the model. The model can not only compute the torsional stiffness of the damper but also facilitate the study of how design parameters affect the torsional stiffness characteristics, thereby assisting in the design of dampers.

(2)

The damper’s torsional stiffness and nonlinear features undergo significant influence from the clamping groove arc radius. Specifically, nonlinear traits become more pronounced with increasing arc radius. This serves to prevent damage and failure due to excessive torsion angles within the damper.

(3)

The length of the leaf spring significantly impacts the damper’s torsional stiffness. Longer leaf springs result in reduced stiffness within the leaf spring group, sharply diminishing the damper’s torsional stiffness and displaying pronounced nonlinear characteristics. Leaf spring thickness minimally affects the damper’s nonlinear characteristics but strongly influences its torsional stiffness. Decreasing the thickness of the leaf spring’s thin side leads to a reduction in the damper’s torsional stiffness.

(4)

The length of the red copper gasket minimally affects the damper’s torsional stiffness nonlinearity but moderately influences its stiffness.

(5)

During the design of leaf spring torsional vibration dampers, attention must be given to the impact of clamping groover radius, spring length, and spring thickness on torsional stiffness and its nonlinear characteristics. If researchers observe a significant deviation in torsional stiffness from the anticipated value during the design phase, their priority should be adjusting the spring length, followed by reasonable adjustments to other parameters. Additionally, the impact of the red copper gasket length on torsional stiffness can be taken into account, but there is no need to consider its influence on the nonlinear characteristics of torsional stiffness.