A Practical Approach to Using Energy Integration in the Simulation of Biomass Thermochemical Processes: Application to Supercritical Water Gasification
Abstract
:Featured Application
Abstract
1. Introduction
2. Methodology
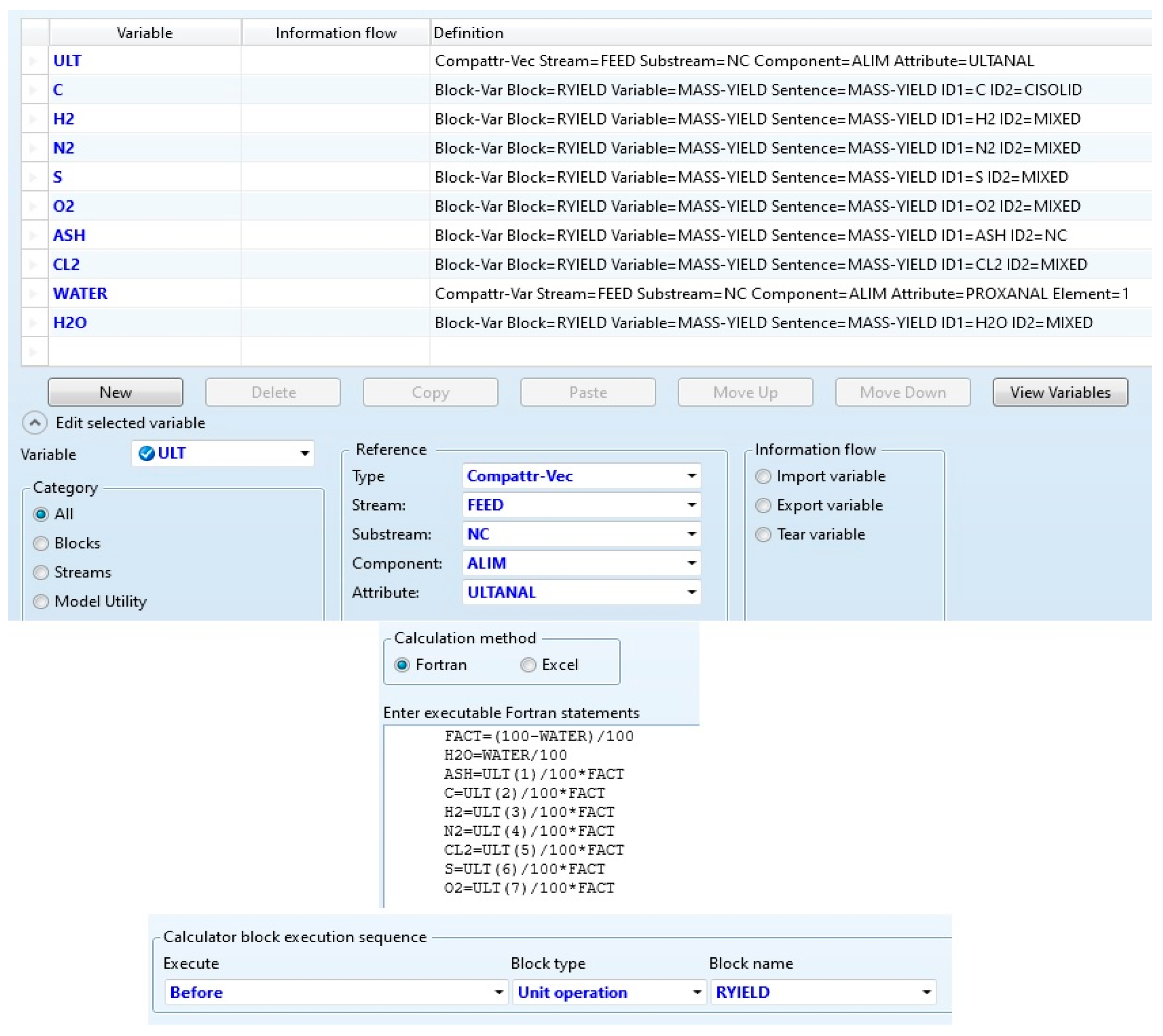
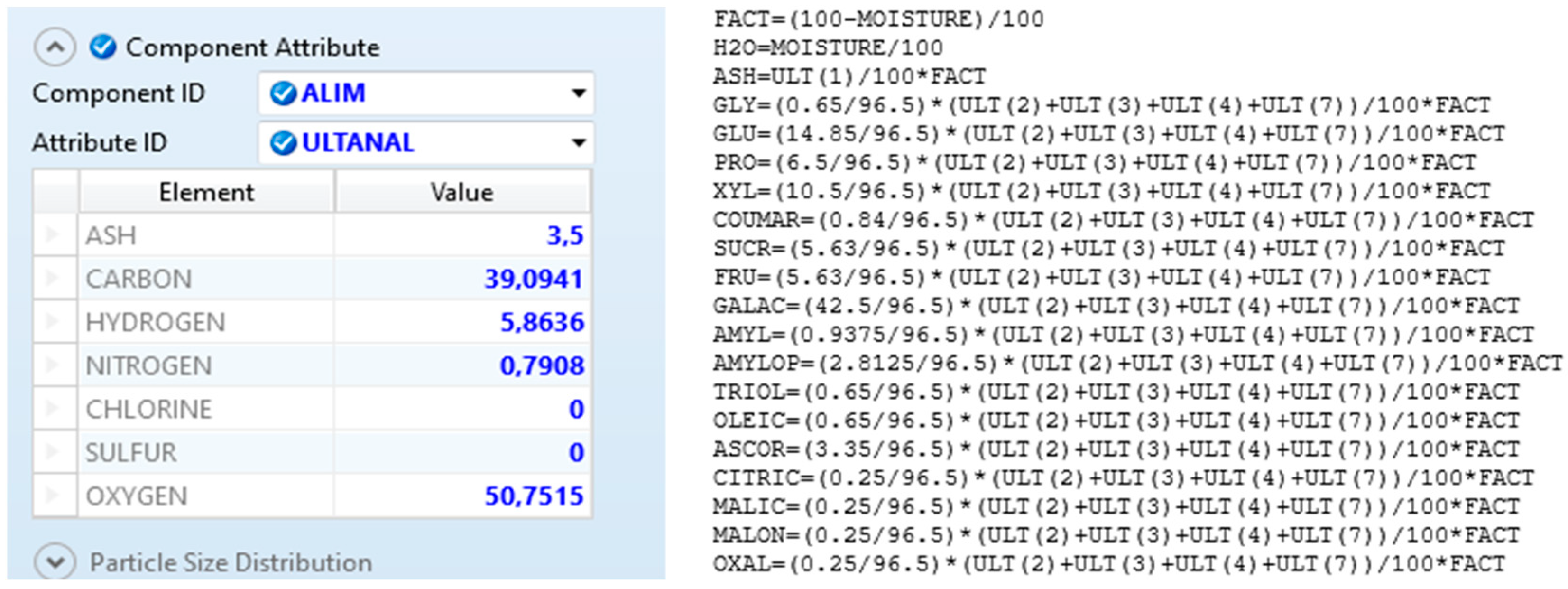
2.1. The Current Simulation Method and the New Approach Applied to Solid Biomass
2.2. Process Arrangements from the Feed Stream to the Reactor
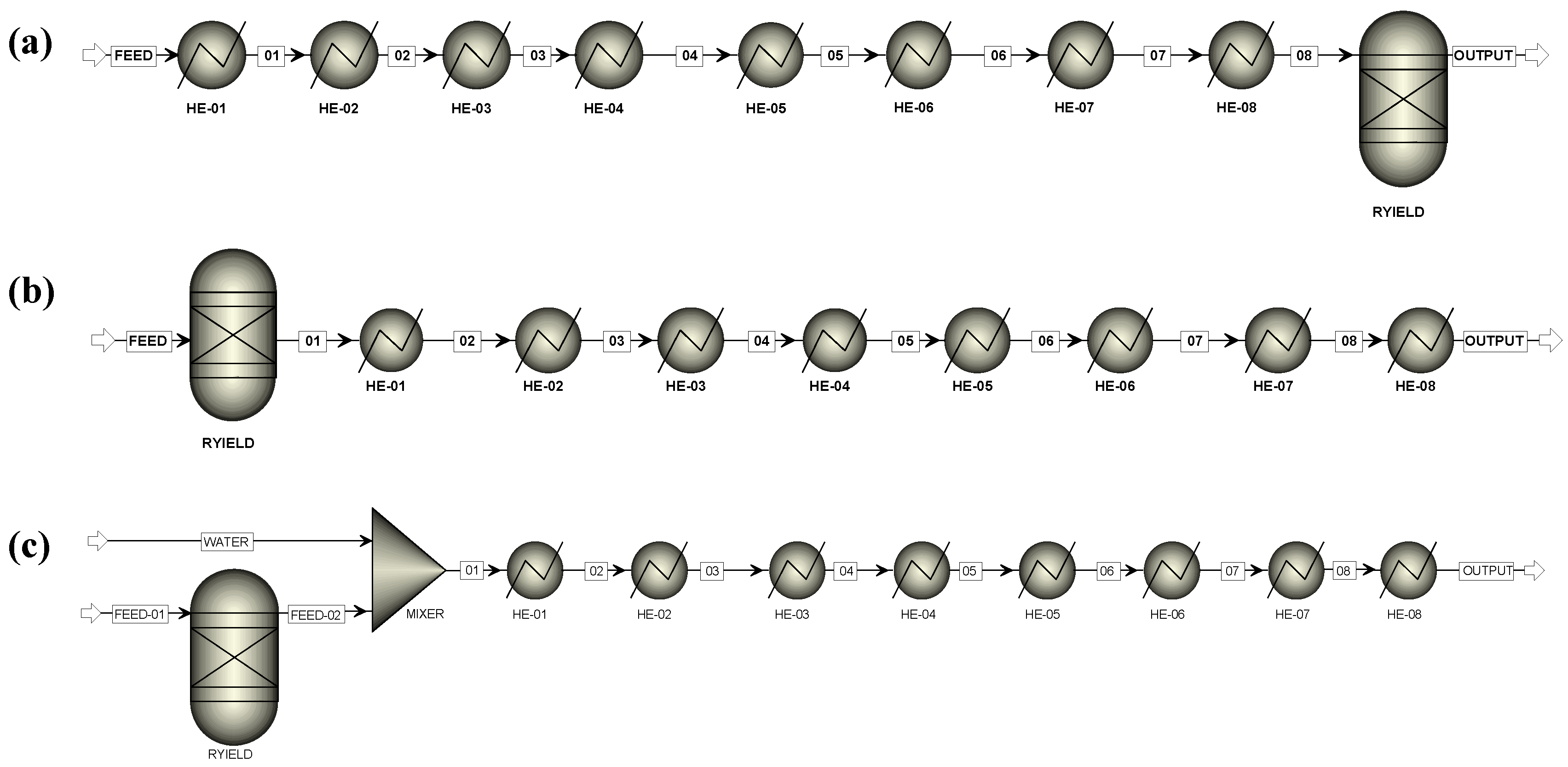
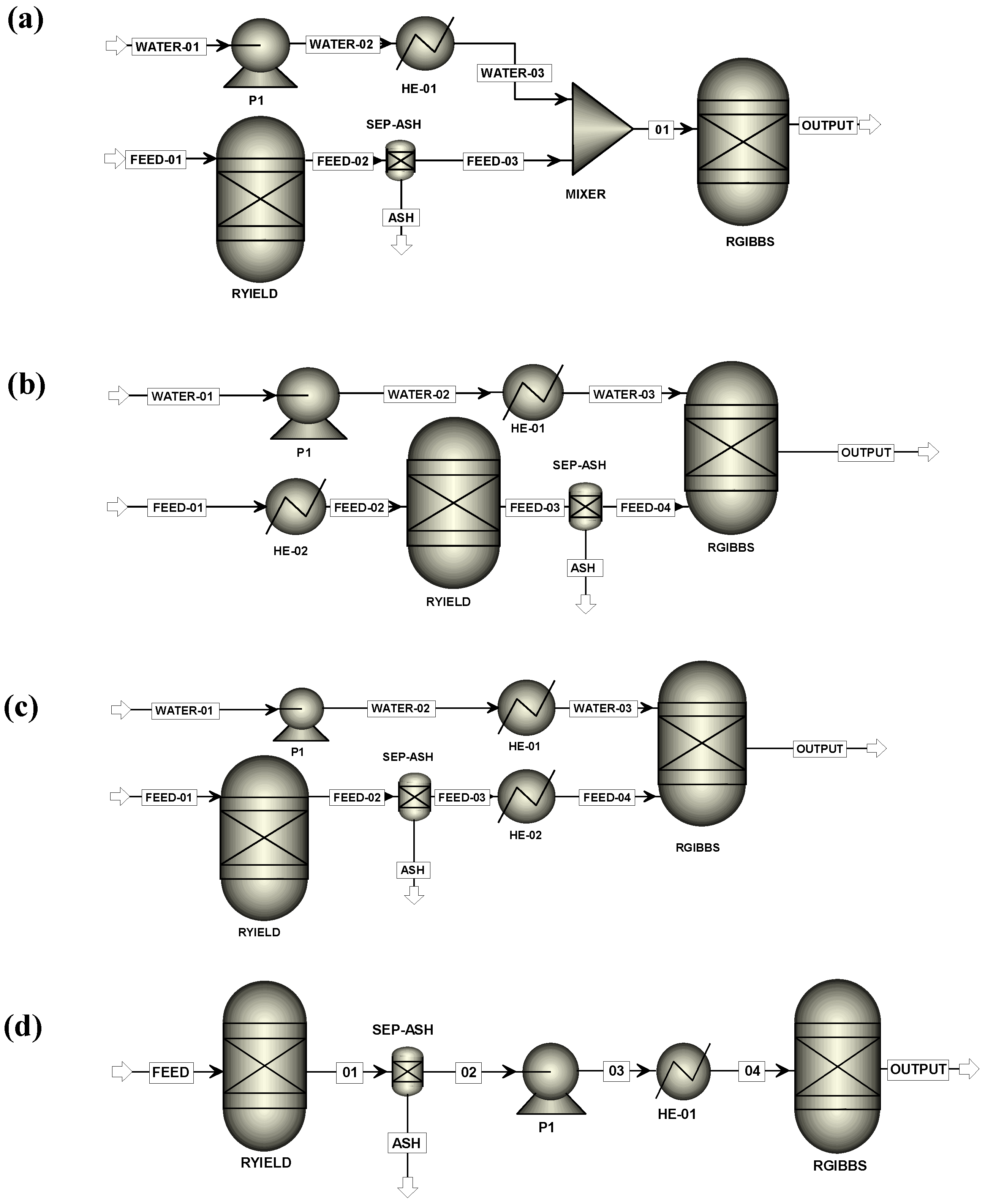
- ARR-1: The RYield plus RGibbs blocks operate under reactor conditions. The RYield block decomposes the feedstock into C, H2, and O2 (Figure 5a).
- ARR-2: The same as ARR-1, but RYield operates at the RGibbs inlet temperature using a preheater for the feed stream (Figure 5b).
- ARR-3: The same as ARR-2, but RYield operates at ambient temperature, and the stream that leaves the block is heated (Figure 5c).
- ARR-4: The same as ARR-3, but RYield decomposes solid biomass into its representative liquid model compounds (Figure 5c).
- ARR-5: There is a unique feed stream for RYield since water is considered as moisture in the solid, thus simulating wet solid biomass. RYield operates at ambient temperature, and the stream leaving the block is heated. Solid biomass is decomposed into C, H2, and O2 (Figure 5d). A pump cannot be added because the stream is a mixture of solid and gas.
- ARR-6: The same as ARR-5, but RYield decomposes the wet solid biomass into a series of representative liquid model compounds (Figure 5d). A pump is added to the system to increase the pressure to 240 bar, so the electrical input is calculated.
2.3. Validation of the New Approach
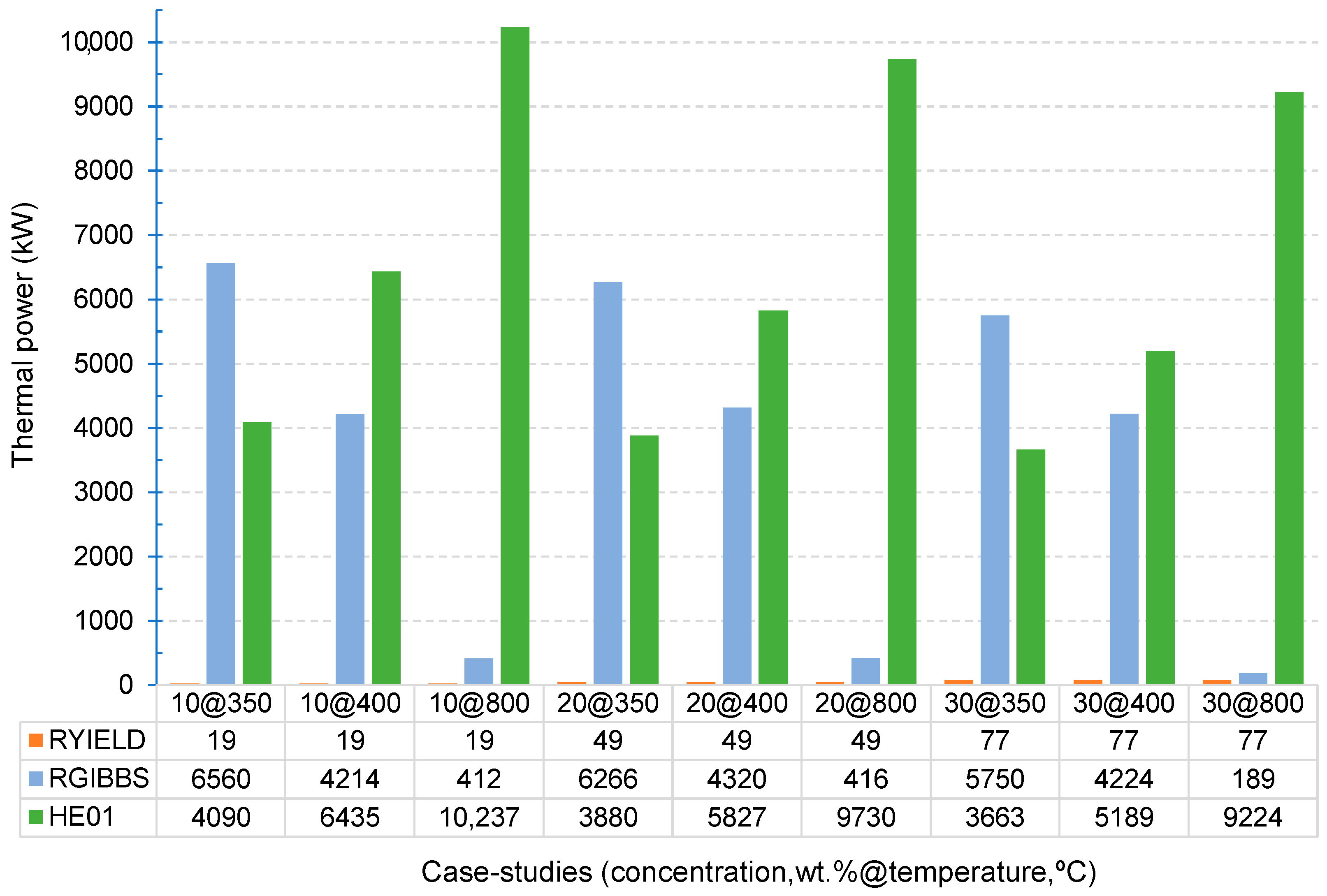
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pinkard, B.R.; Gorman, D.J.; Tiwari, K.; Kramlich, J.C.; Reinhall, P.G.; Novosselov, I.V. Review of Gasification of Organic Compounds in Continuous-Flow, Supercritical Water Reactors. Ind. Eng. Chem. Res. 2018, 57, 3471–3481. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, L.; Xu, P.; Liu, B.; Shuai, Y.; Li, B. Hydrogen production through biomass gasification in supercritical water: A review from exergy aspect. Int. J. Hydrogen Energy 2019, 44, 15727–15736. [Google Scholar] [CrossRef]
- Gutiérrez Ortiz, F.J. Biofuel production from supercritical water gasification of sustainable biomass. Energy Convers. Manag. X 2022, 14, 100164. [Google Scholar] [CrossRef]
- Gutiérrez Ortiz, F.J.; Kruse, A. The use of process simulation in supercritical fluids applications. React. Chem. Eng. 2020, 5, 424–451. [Google Scholar] [CrossRef]
- Aspen Plus. 2023. Available online: https://www.aspentech.com/en/products/engineering/aspen-plus (accessed on 1 February 2024).
- Haydary, J. Processes with Nonconventional Solids. Chem. Process Des. Simulation. In Aspen Plus Aspen HYSYS Applications; JohnWiley & Sons, Inc.: Hoboken, NJ, USA, 2019; pp. 321–346. [Google Scholar] [CrossRef]
- Khumalo, N.L. Process Simulation of the Co-Gasification of Biomass and Polyethylene. Ph.D. Thesis, University of South Africa, Pretoria, South Africa, 2021; pp. 1–286. [Google Scholar]
- Wooley, R.J.; Putsche, V. Development of an ASPEN PLUS. Physical Property Database for Biofuels Components; NREL: Golden, CO, USA; U.S. Department of Energy: Washington, DC, USA, 1996.
- Zheng, H.; Kaliyan, N.; Morey, R.V. Aspen Plus simulation of biomass integrated gasification combined cycle systems at corn ethanol plants. Biomass Bioenergy 2013, 56, 197–210. [Google Scholar] [CrossRef]
- Lan, W.; Chen, G.; Zhu, X.; Wang, X.; Liu, C.; Xu, B. Biomass gasification-gas turbine combustion for power generation system model based on ASPEN PLUS. Sci. Total Environ. 2018, 628–629, 1278–1286. [Google Scholar] [CrossRef] [PubMed]
- Aghaalikhani, A.; Schmid, J.C.; Borello, D.; Fuchs, J.; Benedikt, F.; Hofbauer, H.; Rispoli, F.; Henriksen, U.B.; Sarossy, Z.; Cedola, L. Detailed modelling of biomass steam gasification in a dual fluidized bed gasifier with temperature variation. Renew. Energy 2019, 143, 703–718. [Google Scholar] [CrossRef]
- Gündüz Han, D.; Erdem, K.; Midilli, A. Investigation of hydrogen production via waste plastic gasification in a fluidized bed reactor using Aspen Plus. Int. J. Hydrogen Energy 2023, 48, 39315–39329. [Google Scholar] [CrossRef]
- Louw, J.; Schwarz, C.E.; Knoetze, J.H.; Burger, A.J. Thermodynamic modelling of supercritical water gasification: Investigating the effect of biomass composition to aid in the selection of appropriate feedstock material. Bioresour. Technol. 2014, 174, 11–23. [Google Scholar] [CrossRef] [PubMed]
- Ruya, P.M.; Purwadi, R.; Lim, S.S. Supercritical water gasification of sewage sludge for power generation– thermodynamic study on auto-thermal operation using Aspen Plus. Energy Convers. Manag. 2020, 206, 112458. [Google Scholar] [CrossRef]
- Liang, J.; Liu, Y.; Chen, J.; Jiaqiang, E.; Leng, E.; Zhang, F.; Liao, G. Performance comparison of black liquor gasification and oxidation in supercritical water from thermodynamic, environmental, and techno-economic perspectives. Fuel 2023, 334, 126787. [Google Scholar] [CrossRef]
- Martins, A.H.; Rouboa, A.; Monteiro, E. On the green hydrogen production through gasification processes: A techno-economic approach. J. Clean. Prod. 2023, 383, 135476. [Google Scholar] [CrossRef]
- Chen, J.; Xu, W.; Zhang, F.; Zuo, H.; Jiaqiang, E.; Wei, K.; Liao, G.; Fan, Y. Thermodynamic and environmental analysis of integrated supercritical water gasification of coal for power and hydrogen production. Energy Convers. Manag. 2019, 198, 111927. [Google Scholar] [CrossRef]
- Okolie, J.A.; Nanda, S.; Dalai, A.K.; Kozinski, J.A. Techno-economic evaluation and sensitivity analysis of a conceptual design for supercritical water gasification of soybean straw to produce hydrogen. Bioresour. Technol. 2021, 331, 125005. [Google Scholar] [CrossRef]
- Gutiérrez Ortiz, F.J.; Ollero, P.; Serrera, A.; Sanz, A. Thermodynamic study of the supercritical water reforming of glycerol. Int. J. Hydrogen Energy 2011, 36, 8994–9013. [Google Scholar] [CrossRef]
- Okolie, J.A.; Nanda, S.; Dalai, A.K.; Kozinski, J.A. Hydrothermal gasification of soybean straw and flax straw for hydrogen-rich syngas production: Experimental and thermodynamic modeling. Energy Convers. Manag. 2020, 208, 112545. [Google Scholar] [CrossRef]
- Panichkittikul, N.; Mariyappan, V.; Wu, W.; Patcharavorachot, Y. Improvement of biohydrogen production from biomass using supercritical water gasification and CaO adsorption. Fuel 2024, 361, 130724. [Google Scholar] [CrossRef]
- Lopez-Velazquez, M.A.; Santes, V.; Balmaseda, J.; Torres-Garcia, E. Pyrolysis of orange waste: A thermo-kinetic study. J. Anal. Appl. Pyrolysis 2013, 99, 170–177. [Google Scholar] [CrossRef]
- Ortiz-Sanchez, M.; Solarte-Toro, J.C.; González-Aguirre, J.A.; Peltonen, K.E.; Richard, P.; Cardona Alzate, C.A. Pre-feasibility analysis of the production of mucic acid from orange peel waste under the biorefinery concept. Biochem. Eng. J. 2020, 161, 107680. [Google Scholar] [CrossRef]
- Siles López, J.A.; Li, Q.; Thompson, I.P. Biorefinery of waste orange peel. Crit. Rev. Biotechnol. 2010, 30, 63–69. [Google Scholar] [CrossRef]
- Rivas, B.; Torrado, A.; Torre, P.; Converti, A.; Domínguez, J.M. Submerged citric acid fermentation on orange peel autohydrolysate. J. Agric. Food Chem. 2008, 56, 2380–2387. [Google Scholar] [CrossRef]
- Huang, Y.B.; Fu, Y. Hydrolysis of cellulose to glucose by solid acid catalysts. Green Chem. 2013, 15, 1095–1111. [Google Scholar] [CrossRef]
- Stark, N.M.; Yelle, D.J.; Agarwal, U.P. Techniques for Characterizing Lignin. In Lignin in Polymer Composites; Elsevier Inc.: Amsterdam, The Netherlands, 2016; pp. 49–66. [Google Scholar] [CrossRef]
- Karthäuser, J.; Biziks, V.; Mai, C.; Militz, H. Lignin and lignin-derived compounds for wood applications—A review. Molecules 2021, 26, 2533. [Google Scholar] [CrossRef]
- Sasaki, M.; Adschiri, T.; Arai, K. Kinetics of Cellulose Conversion at 25 MPa in Sub- and Supercritical Water. AIChE J. 2004, 50, 192–202. [Google Scholar] [CrossRef]
- Pathak, P.D.; Mandavgane, S.A.; Kulkarni, B.D. Fruit peel waste: Characterization and its potential uses. Curr. Sci. 2017, 113, 444–454. [Google Scholar] [CrossRef]
- Mahato, N.; Sinha, M.; Sharma, K.; Koteswararao, R.; Cho, M.H. Modern extraction and purification techniques for obtaining high purity food-grade bioactive compounds and value-added co-products from citrus wastes. Foods 2019, 8, 523. [Google Scholar] [CrossRef]
- Mamma, D.; Christakopoulos, P. Biotransformation of Citrus By-Products into Value Added Products. Waste Biomass Valorization 2014, 5, 529–549. [Google Scholar] [CrossRef]
- Brown, W.H.; Poon, T. Introduction to Organic Chemistry, 6th ed.; Wiley: Hoboken, NJ, USA, 2016. [Google Scholar] [CrossRef]
- Lee, S.J. Process simulation, economic analysis and synthesis of biodiesel from waste vegetable oil using supercritical methanol. Chem. Eng. Res. Des. 2011, 131, 2626–2642. [Google Scholar] [CrossRef]
- Kick, C.; Kline, A.; Hladky, H.; Aller, B. Using AspenPlus Resources to Model Biodiesel Production Applicable for a Senior Capstone Design Project. ASEE North-Central Section Conference. 2013. Available online: https://asee-ncs.org/proceedings/2013/papers/51.pdf (accessed on 15 January 2024).
- Nanda, S.; Isen, J.; Dalai, A.K.; Kozinski, J.A. Gasification of fruit wastes and agro-food residues in supercritical water. Energy Convers. Manag. 2016, 110, 296–306. [Google Scholar] [CrossRef]
- Susanti, R.F.; Dianningrum, L.W.; Yum, T.; Kim, Y.; Lee, Y.; Kim, J. High-yield hydrogen production by supercritical water gasification of various feedstocks: Alcohols, glucose, glycerol and long-chain alkanes. Chem. Eng. Res. Des. 2014, 92, 1834–1844. [Google Scholar] [CrossRef]
- Cao, C.; Xu, L.; He, Y.; Guo, L.; Jin, H.; Huo, Z. High-Efficiency Gasification of Wheat Straw Black Liquor in Supercritical Water at High Temperatures for Hydrogen Production. Energy Fuels 2017, 31, 3970–3978. [Google Scholar] [CrossRef]
- Gutiérrez Ortiz, F.J.; Campanario, F.J.; Aguilera, P.G.; Ollero, P. Hydrogen production from supercritical water reforming of glycerol over nickel catalysts. Energy 2015, 84, 634–642. [Google Scholar] [CrossRef]
- Gutiérrez Ortiz, F.J.; Campanario, F.J. Hydrogen production from supercritical water reforming of acetic acid, acetol, 1-butanol and glucose over Ni-based catalyst. J. Supercrit. Fluids 2018, 138, 259–270. [Google Scholar] [CrossRef]
- Antal, M.J.; Allen, S.G.; Schulman, D.; Xu, X. Biomass gasification in supercritical water. Ind. Eng. Chem. Res. 2000, 39, 4040–4053. [Google Scholar] [CrossRef]
- Arpornwichanopa, A.; Boonpithaka, N.; Kheawhoma, S.; Ponpesha, P.; Authayanunb, S. Performance analysis of a biomass supercritical water gasification process under energy self-sufficient condition. Comput. Aided Chem. Eng. 2014, 33, 1699–1704. [Google Scholar] [CrossRef]
- Reynolds, W.C. The Element Potential Method for Chemical Analysis. 1986. Available online: https://web.stanford.edu/~cantwell/AA283_Course_Material/AA283_Resources/STANJAN_write-up_by_Bill_Reynolds.pdf (accessed on 15 January 2024).
- Tsanas, C.; Stenby, E.H.; Yan, W. Calculation of simultaneous chemical and phase equilibrium by the method of Lagrange multipliers. Chem. Eng. Sci. 2017, 174, 112–126. [Google Scholar] [CrossRef]
- Binous, H.; Bellagi, A. Calculations of complex chemical reaction equilibria using stoichiometric and non-stoichiometric approaches in combination with arc-length continuation. Eng. Rep. 2022, 4, e12506. [Google Scholar] [CrossRef]


| Compound | Experimental Yield (mol/mol) | Equilibrium Yield (mol/mol) | Deviation | Reference |
|---|---|---|---|---|
| H2 | 5.27 | 5.320 | −0.050 | [39] |
| CO2 | 2.11 | 1.990 | 0.120 | [39] |
| CO | 0.27 | 0.790 | −0.520 | [39] |
| CH4 | 0.32 | 0.220 | 0.100 | [39] |
| H2 | 2.41 | 2.400 | 0.010 | [40] |
| CO2 | 1.48 | 1.290 | 0.190 | [40] |
| CO | 0.29 | 0.580 | −0.290 | [40] |
| CH4 | 0.45 | 0.430 | 0.020 | [40] |
| H2 | 0.55 | 0.552 | −0.002 | [42] |
| CO2 | 0.35 | 0.345 | 0.005 | [42] |
| CO | 0.03 | 0.027 | 0.003 | [42] |
| CH4 | 0.06 | 0.076 | −0.016 | [42] |
| ARR-1, 2 | ARR-3 | ARR-4 | ARR-5 | ARR-6 | |
|---|---|---|---|---|---|
| RYIELD | 2279.75 | 1816.67 | 40.49 | 1867.31 | 18.99 |
| SEP-ASH | balance | balance | balance | balance | balance |
| PUMP (*) | 177.40 | 177.40 | 177.40 | - | 186.65 |
| HE01 | 3855.61 | 3855.61 | 3855.61 | 5950.79 | 4089.70 |
| HE02 | - | 165.44 | 211.37 | - | - |
| RGIBBS | 4560.36 | 4850.45 | 6580.75 | 3036.75 | 6559.52 |
| RYIELD + RGIBBS | 6840.11 | 6667.12 | 6621.24 | 4904.05 | 6578.51 |
| SYSTEM | 10,873.45 | 10,873.45 | 10,873.45 | 10,873.45 | 10,873.45 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gutiérrez Ortiz, F.J.; López-Guirao, F. A Practical Approach to Using Energy Integration in the Simulation of Biomass Thermochemical Processes: Application to Supercritical Water Gasification. Appl. Sci. 2024, 14, 1577. https://doi.org/10.3390/app14041577
Gutiérrez Ortiz FJ, López-Guirao F. A Practical Approach to Using Energy Integration in the Simulation of Biomass Thermochemical Processes: Application to Supercritical Water Gasification. Applied Sciences. 2024; 14(4):1577. https://doi.org/10.3390/app14041577
Chicago/Turabian StyleGutiérrez Ortiz, Francisco Javier, and F. López-Guirao. 2024. "A Practical Approach to Using Energy Integration in the Simulation of Biomass Thermochemical Processes: Application to Supercritical Water Gasification" Applied Sciences 14, no. 4: 1577. https://doi.org/10.3390/app14041577
APA StyleGutiérrez Ortiz, F. J., & López-Guirao, F. (2024). A Practical Approach to Using Energy Integration in the Simulation of Biomass Thermochemical Processes: Application to Supercritical Water Gasification. Applied Sciences, 14(4), 1577. https://doi.org/10.3390/app14041577







