New Approaches of Stochastic Models to Examine the Vibration Features in Roller Bearings
Abstract
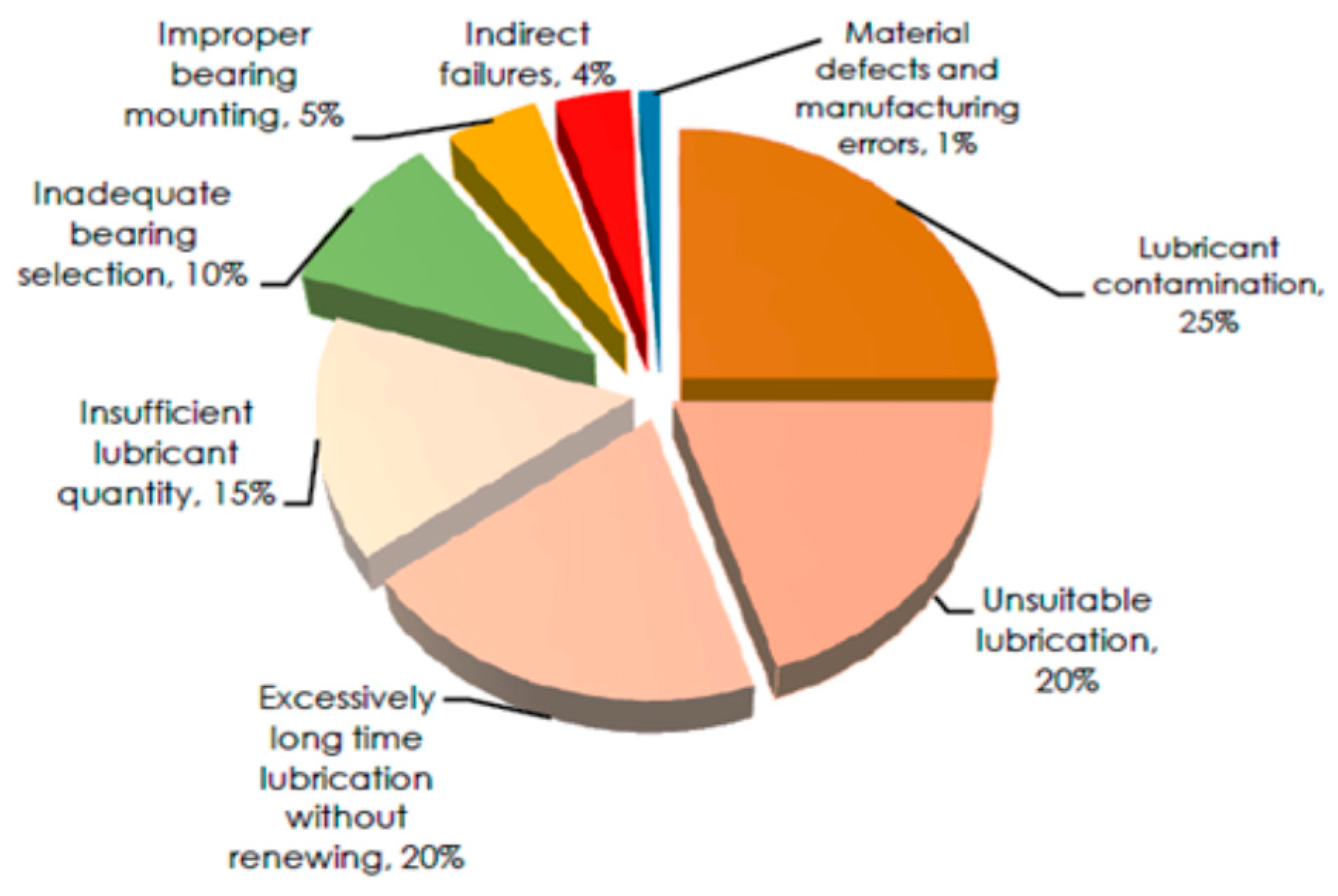
:1. Introduction
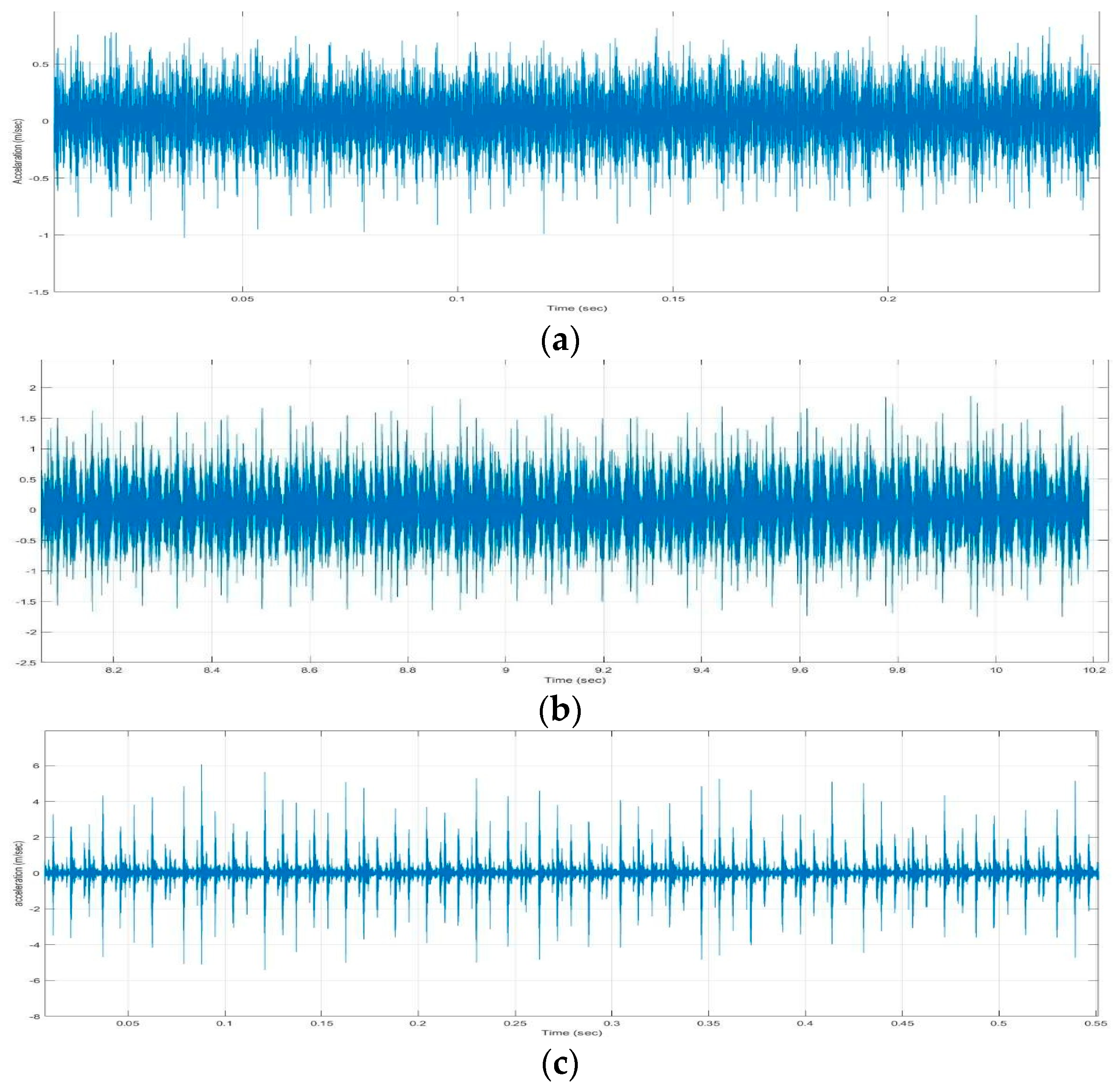
2. Experimental Setup
3. Spectral Analysis
4. Methodology
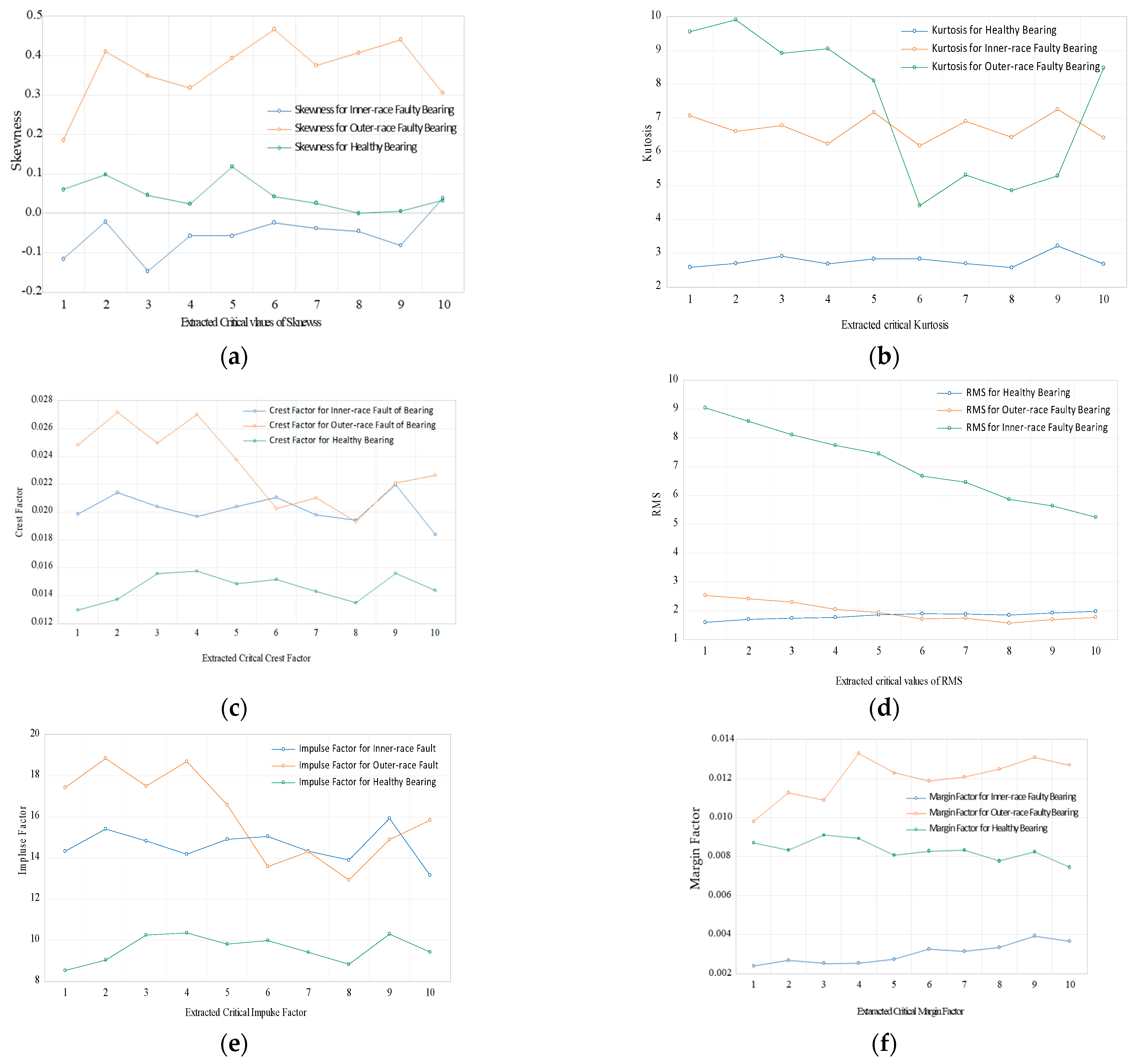
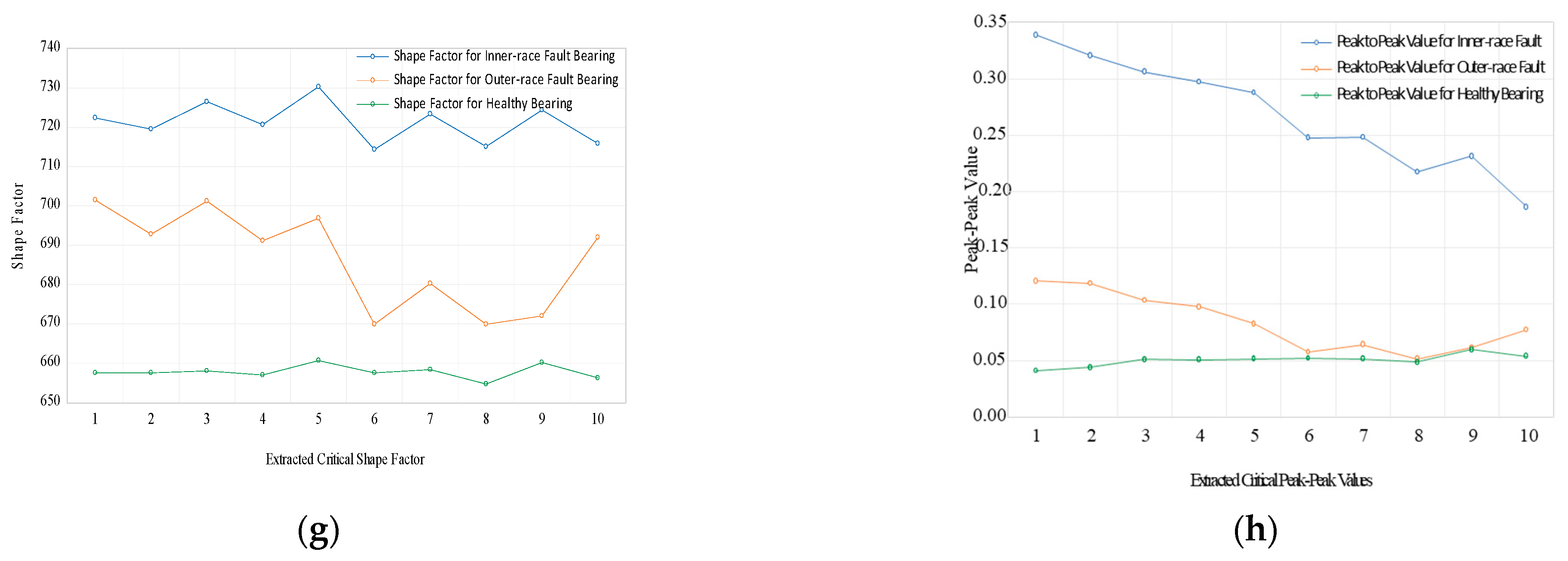
5. Feature Extraction
6. Stochastic Modelling of Vibration Features
6.1. Stochastic Association amongst Inner-Race Faulty Features with Healthy Features
- (a)
- Impulse Factor
- (b)
- Crest Factor
- (c)
- Shape Factor
- (d)
- Margin Factor
- (e)
- Peak–Peak Factor
- (f)
- RMS Value
- (g)
- Kurtosis
6.2. Stochastic Association amongst Outer-Race Faulty Features with Healthy Features
- (a)
- Impulse Factor
- (b)
- Crest Factor
- (c)
- Shape Factor
- (d)
- Margin Factor
- (e)
- Peak-Peak Factor
- (f)
- RMS Value
- (g)
- Kurtosis
7. Optimization Result and Discussion
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Impulse factor for inner-race fault | |
| Impulse factor for outer-race fault | |
| Impulse factor for healthy state | |
| Inner-race impulse factor white-noise term with | |
| Crest factor for inner-race fault | |
| Crest factor for outer-race fault | |
| Crest factor for healthy state | |
| Inner-race crest factor white-noise term with | |
| Shape factor for inner-race fault | |
| Shape factor for outer-race fault | |
| Shape factor for healthy state | |
| Inner-race shape factor white-noise term with | |
| Margin factor for inner-race fault | |
| Margin factor for outer-race fault | |
| Margin factor for healthy state | |
| Inner-race margin factor white-noise term with | |
| Peak-to-peak factor for inner-race fault | |
| Peak-to-peak factor for outer-race fault | |
| Peak-to-peak factor for healthy state | |
| Inner-race peak to peak factor white-noise term with | |
| RMS for inner-race fault | |
| RMS for outer-race fault | |
| RMS for healthy state | |
| Inner-race RMS white-noise term with | |
| Kurtosis for inner-race fault | |
| Kurtosis for outer-race fault | |
| Kurtosis for healthy state | |
| Inner-race kurtosis white-noise term with |
References
- Hua, L. Ring Rolling Forming Theory and Technology for Bearing. J. Mech. Eng. 2014, 50, 70. [Google Scholar] [CrossRef]
- Harris, T.; Anderson, W. Rolling Bearing Analysis. J. Lubr. Technol. 1967, 89, 521. [Google Scholar] [CrossRef]
- Kim, N.-H.; An, D.; Choi, J.-H. Prognostics and Health Management of Engineering Systems; Springer International Publishing: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Ompusunggu, A.P. Systematic methodology for generating natural spall faults on rolling element bearings. In Proceedings of the 5th International Conference on Maintenance, Condition Monitoring and Diagnostics 2021, Oulu, Finland, 16–17 February 2021. [Google Scholar]
- Kim, T.; Olver, A.; Pearson, P. Fatigue and Fracture Mechanisms in Large Rolling Element Bearings. Tribol. Trans. 2001, 44, 583–590. [Google Scholar] [CrossRef]
- McDonald, C.; Temby, A.; Hargreaves, M.; Moore, A. Failure of a set of roller bearings. Wear 1957, 1, 64–70. [Google Scholar] [CrossRef]
- Hussain, M.; Mansoor, A.; Qureshi, S.; Nisar, S. Bearing degradation prognosis using structural break classifier. Mechanika 2018, 24, 456–461. [Google Scholar] [CrossRef]
- Randall, R.B. Vibration-Based Condition Monitoring, 2nd ed.; Wiley: Hoboken, NJ, USA, 2021. [Google Scholar]
- Guo, L.; Li, N.; Jia, F.; Lei, Y.; Lin, J. Are current neural network-based health indicator for remaining useful life prediction of bearings. Neurocomputing 2017, 240, 98–109. [Google Scholar] [CrossRef]
- Al Masry, Z.; Schaible, P.; Zerhouni, N.; Varnier, C. Remaining useful life prediction for ball bearings based on health indicators. MATEC Web Conf. 2019, 261, 02003. [Google Scholar] [CrossRef]
- Wang, B.; Lei, Y.; Li, N.; Li, N. A Hybrid Prognostics Approach for Estimating Remaining Useful Life of Rolling Element Bearings. IEEE Trans. Reliab. 2020, 69, 401–412. [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, J.; Yang, C.; Xu, D.; Ge, J. Remaining useful life prediction of rolling bearings based on Pearson correlation-KPCA multi-feature fusion. Measurement 2022, 201, 111572. [Google Scholar] [CrossRef]
- Widodo, A.; Yang, B.-S. Application of relevance vector machine and survival probability to machine degradation assessment. Expert Syst. Appl. 2011, 38, 2592–2599. [Google Scholar] [CrossRef]
- Stepanova, M.; Thomas, L. Censoring issues in survival analysis. Oper. Res. 2002, 50, 277–289. [Google Scholar] [CrossRef]
- Gareth, J.; Daniela, W.; Trevor, H.; Robert, T. An Introduction to Statistical Learning: With Applications in R, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar]
- Almutairi, K.M.; Sinha, J.K. Experimental Vibration Data in Fault Diagnosis: A Machine Learning Approach to Robust Classification of Rotor and Bearing Defects in Rotating Machines. Machines 2023, 11, 943. [Google Scholar] [CrossRef]
- Lei, Y.; He, Z.; Zi, Y. Application of an intelligent classification method to mechanical fault diagnosis. Expert Syst. Appl. 2009, 36, 9941–9948. [Google Scholar] [CrossRef]
- Dron, J.-P.; Bolaers, F.; Rasolofondraibe, L. Improvement of the sensitivity of the scalar indicators (crest factor, kurtosis) using a de-noising method by spectral subtraction: Application to the detection of defects in ball bearings. J. Sound Vib. 2004, 270, 61–73. [Google Scholar] [CrossRef]
- Ovacikli, A.K.; Paajarvi, P.; LeBlanc, J.; Carlson, J. Uncovering harmonic content via skewness maximization-a Fourier analysis. In Proceedings of the 2014 22nd European Signal Processing Conference (EUSIPCO), IEEE, Lisbon, Portugal, 1–5 September 2014; pp. 481–485. [Google Scholar]
- Antoni, J. The infogram: Entropic evidence of the signature of repetitive transients. Mech. Syst. Signal Process. 2016, 74, 73–94. [Google Scholar] [CrossRef]
- Antoni, J.; Borghesani, P. A statistical methodology for the design of condition indicators. Mech. Syst. Signal Process. 2019, 114, 290–327. [Google Scholar] [CrossRef]
- Dyer, V.; Stewart, R.M. Detection of Rolling Element Bearing Damage by Statistical Vibration Analysis. J. Mech. Des. 1978, 100, 229–235. [Google Scholar] [CrossRef]
- Antoni, J. Fast computation of the kurtogram for the detection of transient faults. Mech. Syst. Signal Process. 2007, 21, 108–124. [Google Scholar] [CrossRef]
- Bishop, C. Pattern Recognition and Machine Learning; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Baum, L.E.; Eagon, J.A. An inequality with applications to statistical estimation for probabilistic functions of Markov processes and to a model forecology. Bull. Am. Math. Soc. 1967, 5, 360–363. [Google Scholar] [CrossRef]
- Baum, L.E.; Petrie, T. Statistical inference for probabilistic functions of finite state Markov chains. Ann. Math. Stat. 1966, 37, 1554–1563. [Google Scholar] [CrossRef]
- Li, X.; Liang, M. Bearing fault diagnosis using a hidden Markov model based on vibration signals. IEEE Access 2019, 7, 105151–105160. [Google Scholar]
- Dong, J.; Chen, J. Bearing fault diagnosis based on the hidden Markov model and the support vector machine. Measurement 2018, 128, 354–361. [Google Scholar]
- Qiu, Z.; Cao, L.; Li, X. Bearing fault diagnosis using a Markov chain model and improved ensemble empirical mode decomposition. Measurement 2018, 117, 167–176. [Google Scholar]
- Li, H.; Liang, M.; Li, X. Bearing fault diagnosis based on a hidden Markov model and multiscale permutation entropy. Mech. Syst. Signal Process. 2017, 92, 432–447. [Google Scholar]
- Guo, W.; Chen, J.; Dong, J. Bearing fault diagnosis based on hidden Markov model with hybrid feature extraction. Measurement 2017, 97, 96–105. [Google Scholar]
- Lei, Y.; Li, N.; Lin, J. A New Method Based on Stochastic Process Models for Machine Remaining Useful Life Prediction. IEEE Trans. Instrum. Meas. 2016, 65, 2671–2684. [Google Scholar] [CrossRef]
- Randall, R.; Antoni, J. Rolling element bearing diagnostics—A tutorial. Mech. Syst. Signal Process. 2011, 25, 485–520. [Google Scholar] [CrossRef]
- Chen, Y.; Rao, M.; Feng, K.; Niu, G. Modified Varying Index Coefficient Autoregression Model for Representation of the Nonstationary Vibration from a Planetary Gearbox. IEEE Trans. Instrum. Meas. 2023, 72, 3511812. [Google Scholar] [CrossRef]
- Han, T.; Xie, W.; Pei, Z. Semi-supervised adversarial discriminative learning approach for intelligent fault diagnosis of wind turbine. Inf. Sci. 2023, 648, 3511812. [Google Scholar] [CrossRef]
- El-Thalji, I.; Jantunen, E. A summary of fault modelling and predictive health monitoring of rolling element bearings. Mech. Syst. Signal Process. 2015, 60, 252–272. [Google Scholar] [CrossRef]
- Liu, C.; Xie, L.; Wang, D.; Zhou, G.; Zhou, Q.; Miao, Q. Application of stochastic resonance in bearing fault diagnosis. In Proceedings of the 2014 Prognostics and System Health Management Conference (PHM-2014), Zhangjiajie, China, 24–27 August 2014; pp. 223–228. [Google Scholar]
- Akaike, H. Fitting autoregressive model models for prediction. Ann. Inst. Stat. Math. 1969, 21, 243–247. [Google Scholar] [CrossRef]
- Schwarz, G. Estimating the dimension of a model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]


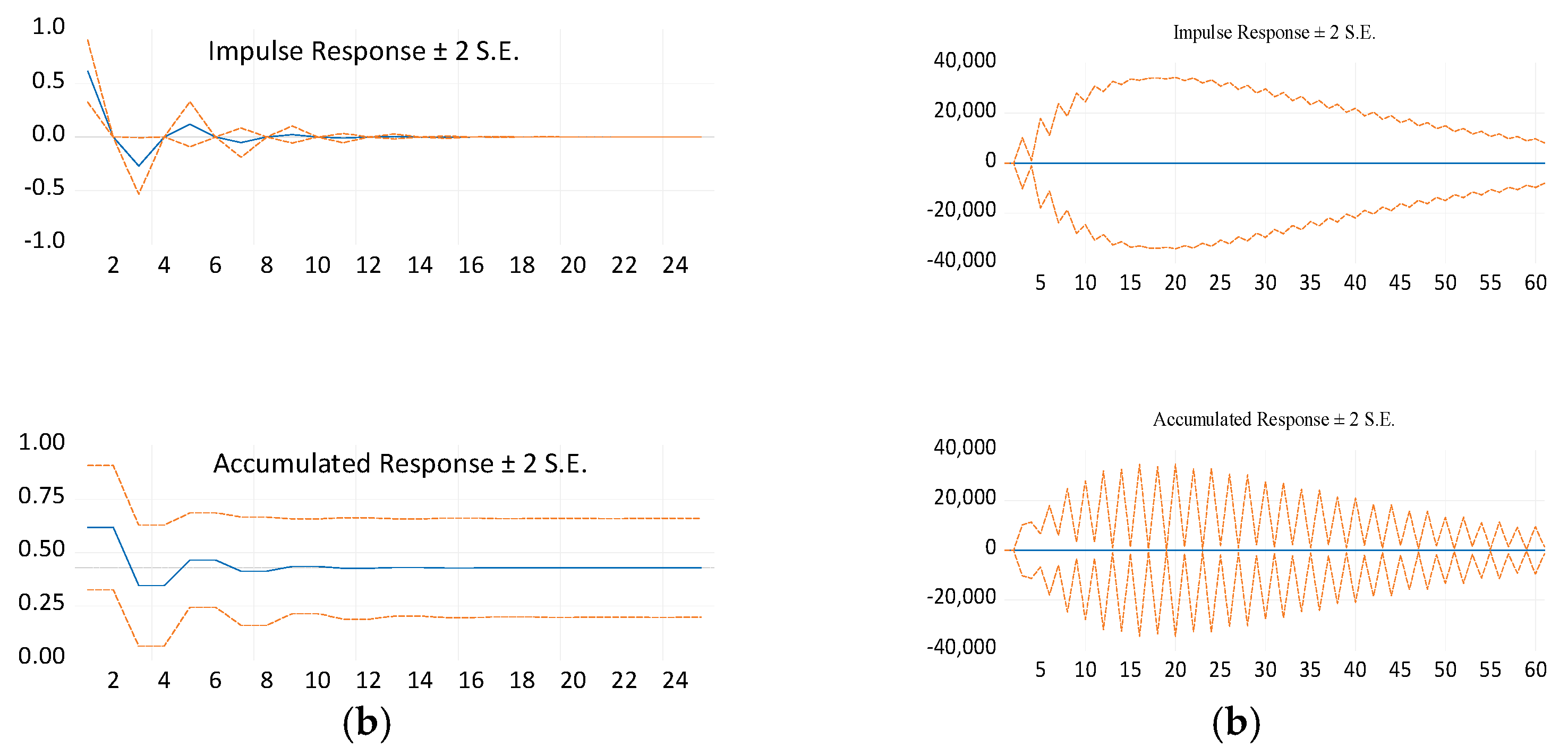
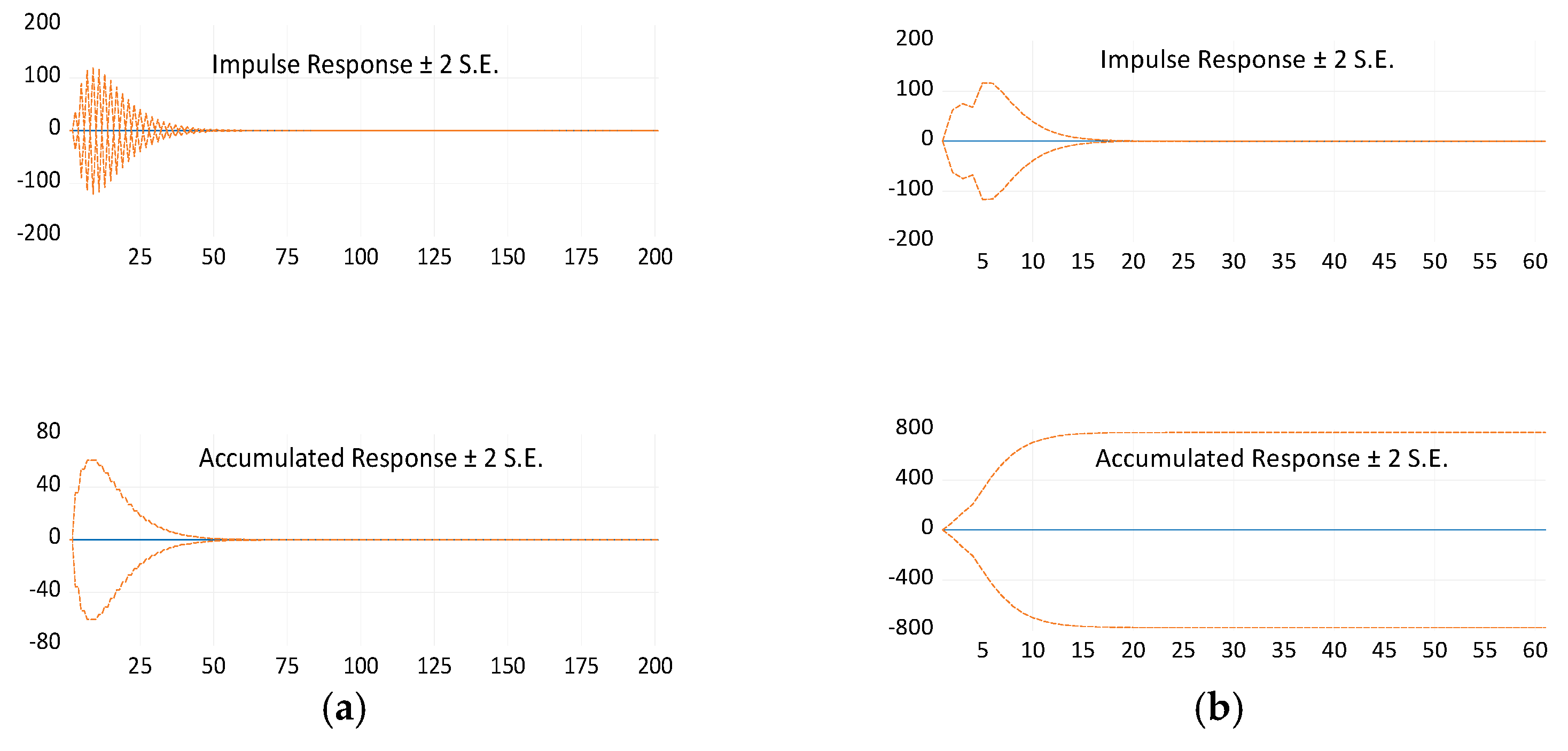
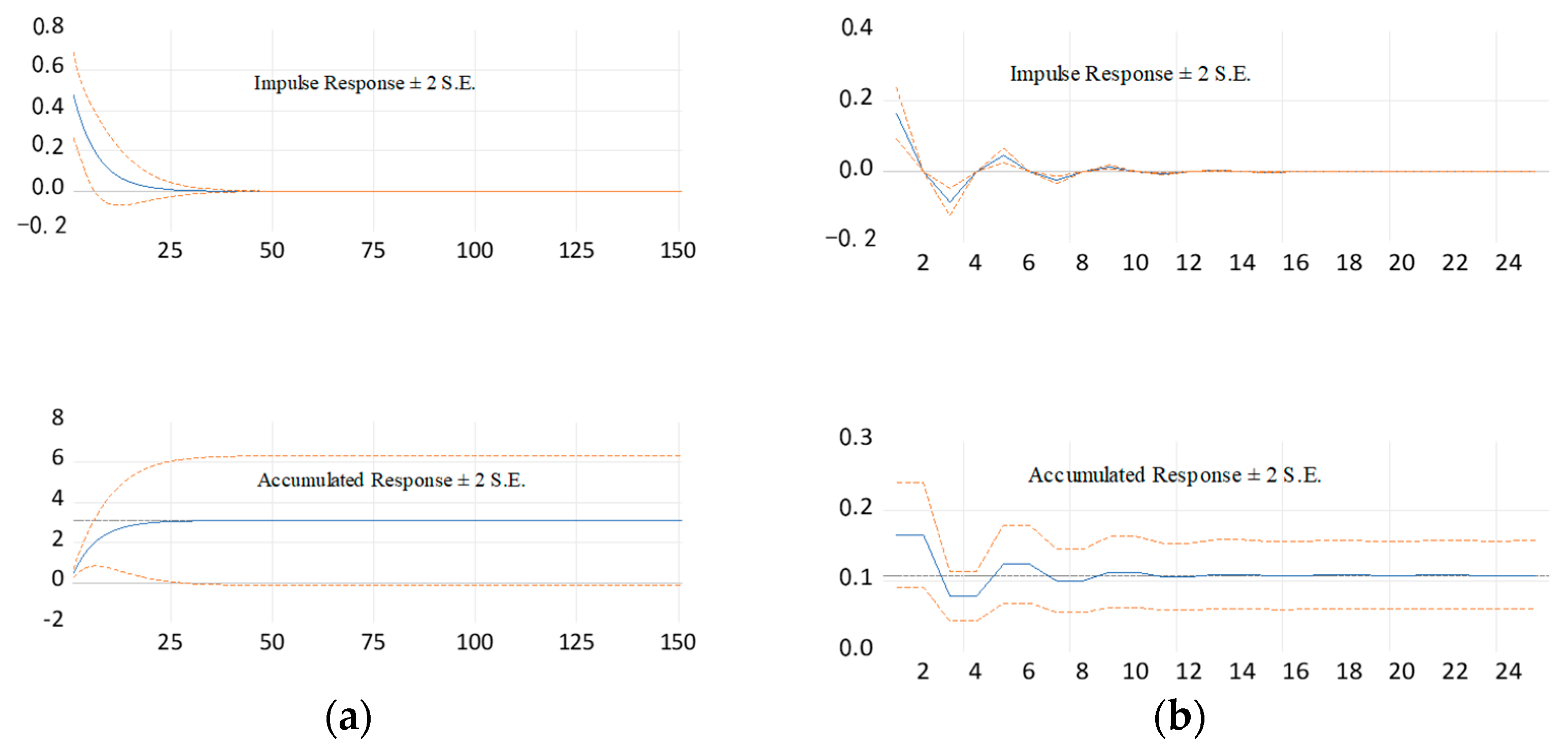
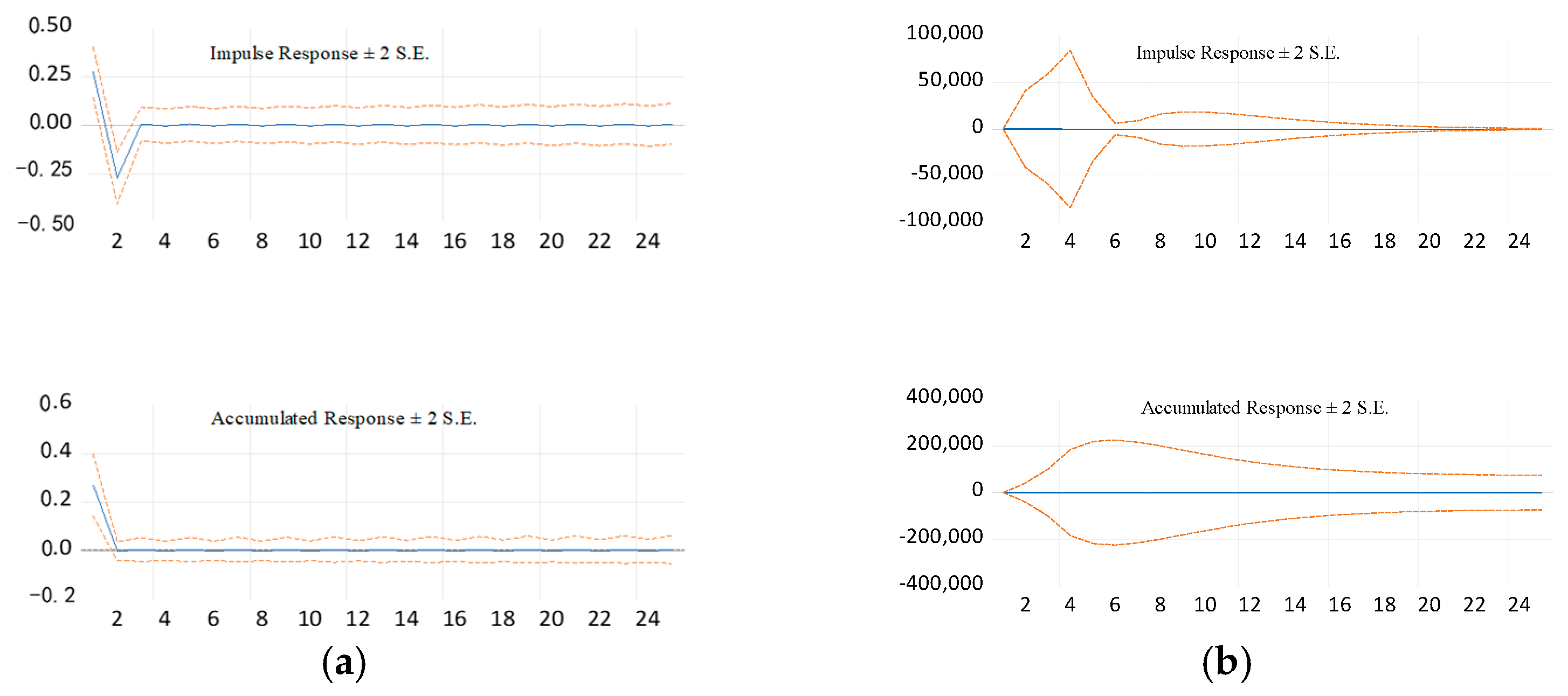

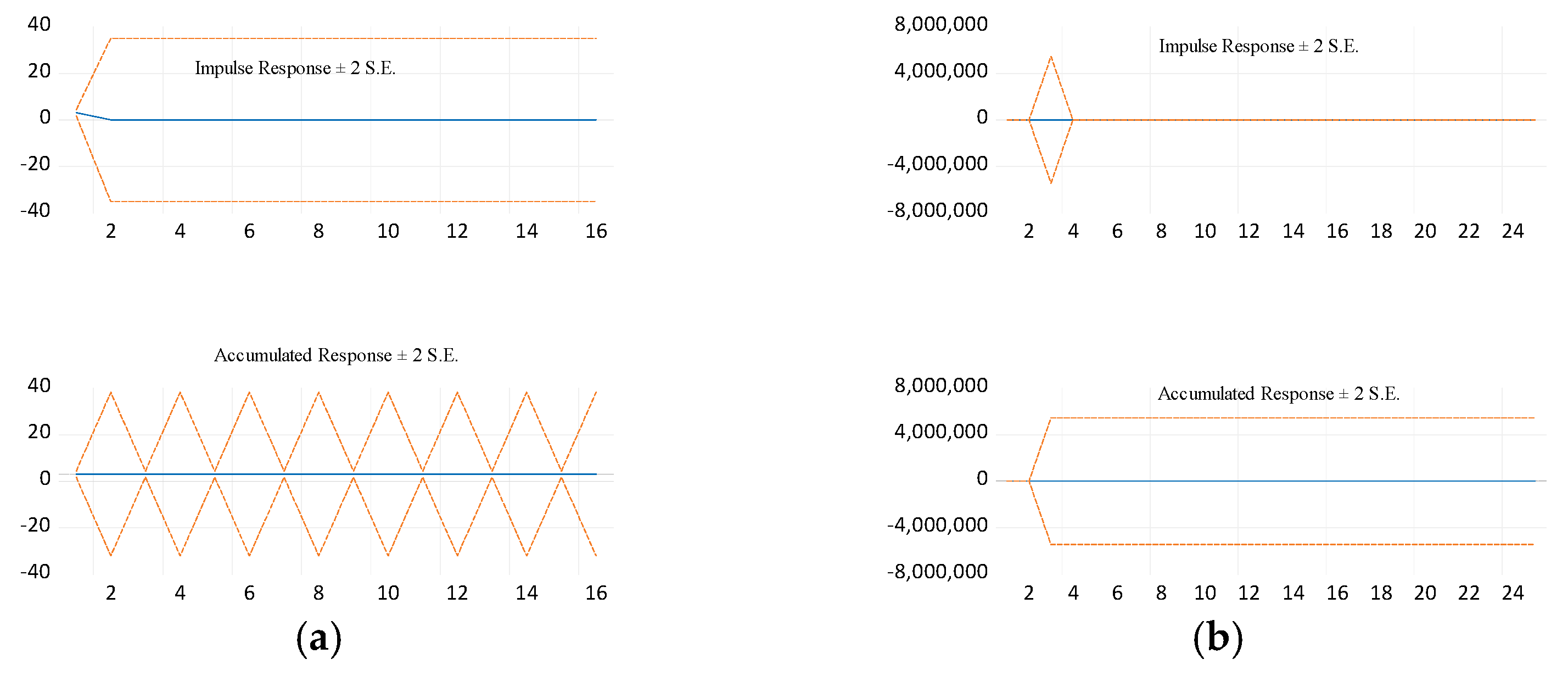
| S.No | Radial Loading (mm) | Defect Width (mm) | Defect Depth (mm) |
|---|---|---|---|
| 1 | 30 | 38 | 12 |
| 2 | 45 | 38 | 12 |
| 3 | 60 | 383 | 12 |
| Models | p-Values | ||||
|---|---|---|---|---|---|
| Stochastic model of impulse factor | 0.042 | 0.015 | 0.026 | 0.047 | 0.75 |
| Stochastic model of crest factor | 0.021 | 0.0151 | 0.0136 | 0.057 | 0.73 |
| Stochastic model of shape factor | 0.001 | 0.001 | 0.001 | 0.77 | |
| Stochastic model of margined factor | 0.005 | 0.014 | 0.056 | 0.075 | 0.75 |
| Stochastic model of peak to peak value | 0.006 | 0.087 | 0.042 | 0.099 | 0.90 |
| Stochastic model of root mean square | 0.012 | 0.091 | 0.076 | 0.91 | |
| Stochastic model of kurtosis | 0.001 | 0.001 | 0.001 | 0.70 | |
| Models | p-Values | ||||
|---|---|---|---|---|---|
| Stochastic model of impulse factor | 0.001 | 0.057 | 0.056 | 0.701 | |
| Stochastic model of crest factor | 0.001 | 0.063 | 0.044 | 0.699 | |
| Stochastic model of shape factor | 0.001 | 0.081 | 0.68 | ||
| Stochastic model of margined factor | 0.046 | 0.049 | 0.089 | 0.091 | 0.66 |
| Stochastic model of peak to peak value | 0.050 | 0.069 | 0.092 | 0.68 | |
| Stochastic model of root mean square | 0.001 | 0.002 | 0.089 | 0.84 | |
| Stochastic model of kurtosis | 0.071 | 0.022 | 0.078 | 0.088 | 0.76 |
| Models | Order | AIC | BIC |
|---|---|---|---|
| Impulse Factor Inner Race Fault | ARMA (2,3) | 2.6516 | 2.8029 |
| Impulse Factor Outer Race Fault | ARMA (1,3) | 4.3337 | 4.4547 |
| Crest Factor Inner Race Fault | ARMA (2,2) | −10.6074 | −10.4561 |
| Crest Factor Outer Race Fault | ARMA (1,3) | −8.8708 | −8.7498 |
| Shape Factor Inner Race Fault | ARMA (1,1) | 5.6182 | 5.7392 |
| Shape Factor Outer Race Fault | ARMA (0,2) | 7.9342 | 7.9987 |
| Margin Factor Inner Race Fault | ARMA (1,2) | −12.4488 | −12.2974 |
| Margin Factor Outer Race Fault | ARMA (2,1) | −10.4902 | −10.3806 |
| Peak–Peak Factor Inner Race Fault | ARMA (2,3) | 2.6516 | 2.4857 |
| Peak–Peak Factor Outer Race Fault | ARMA (1,3) | 4.3337 | 4.4547 |
| RMS Inner Race Fault | ARMA (1,0) | 1.7768 | 1.8978 |
| RMS Outer Race Fault | ARMA (2,0) | −0.4051 | −0.2341 |
| Kurtosis Inner Race Fault | ARMA (1,2) | 1.1191 | 1.2067 |
| Kurtosis Outer Race Fault | ARMA (1,3) | 4.2627 | 4.4141 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bhatti, S.; Shaikh, A.A.; Mansoor, A.; Hussain, M. New Approaches of Stochastic Models to Examine the Vibration Features in Roller Bearings. Appl. Sci. 2024, 14, 1616. https://doi.org/10.3390/app14041616
Bhatti S, Shaikh AA, Mansoor A, Hussain M. New Approaches of Stochastic Models to Examine the Vibration Features in Roller Bearings. Applied Sciences. 2024; 14(4):1616. https://doi.org/10.3390/app14041616
Chicago/Turabian StyleBhatti, Saima, Asif Ali Shaikh, Asif Mansoor, and Murtaza Hussain. 2024. "New Approaches of Stochastic Models to Examine the Vibration Features in Roller Bearings" Applied Sciences 14, no. 4: 1616. https://doi.org/10.3390/app14041616
APA StyleBhatti, S., Shaikh, A. A., Mansoor, A., & Hussain, M. (2024). New Approaches of Stochastic Models to Examine the Vibration Features in Roller Bearings. Applied Sciences, 14(4), 1616. https://doi.org/10.3390/app14041616







