Large Eddy Simulation of the Effect of Hydrogen Ratio on the Flame Stabilization and Blow-Off Dynamics of a Lean CH4/H2/Air Bluff-Body Flame
Abstract
1. Introduction
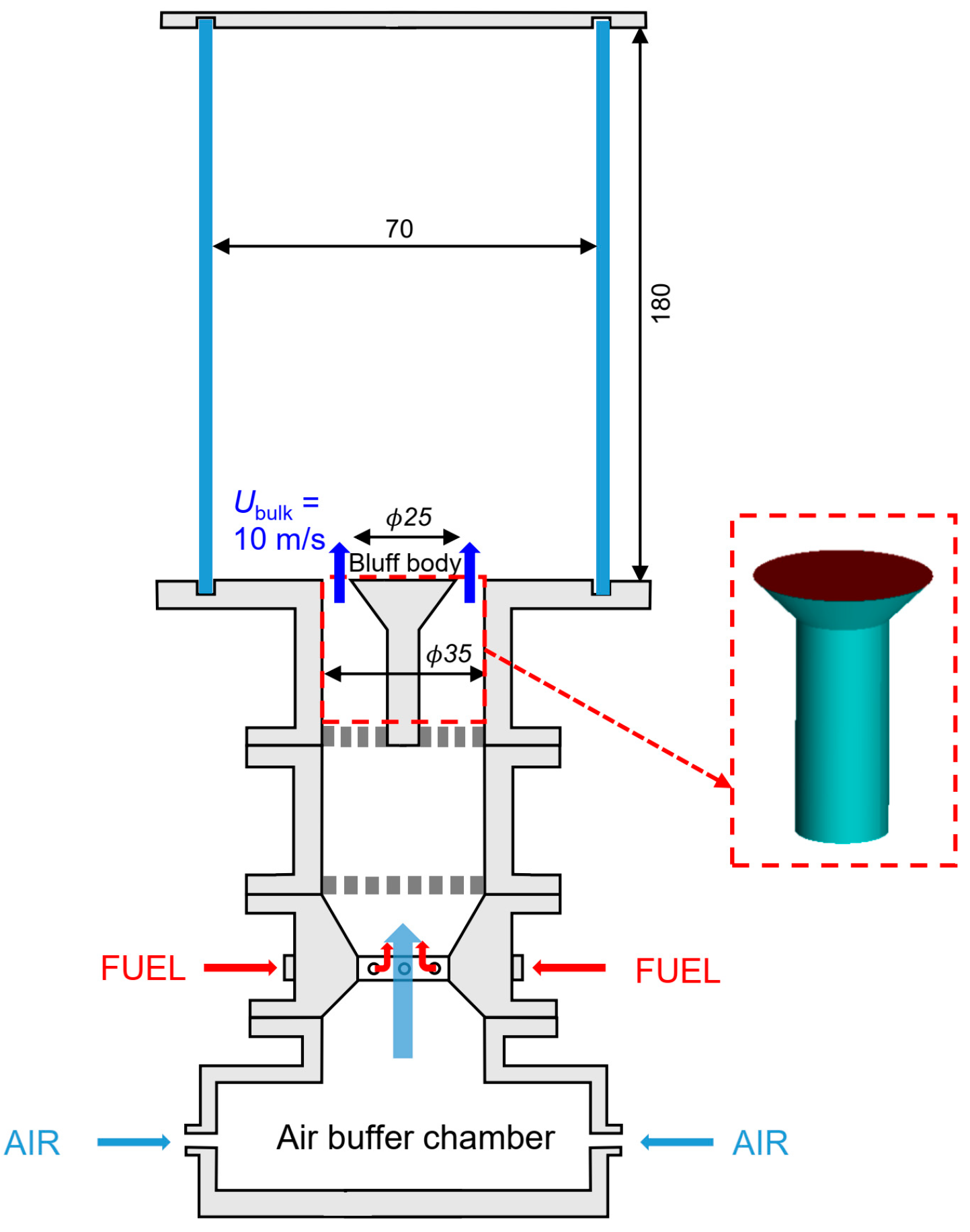
2. Experimental Methodology
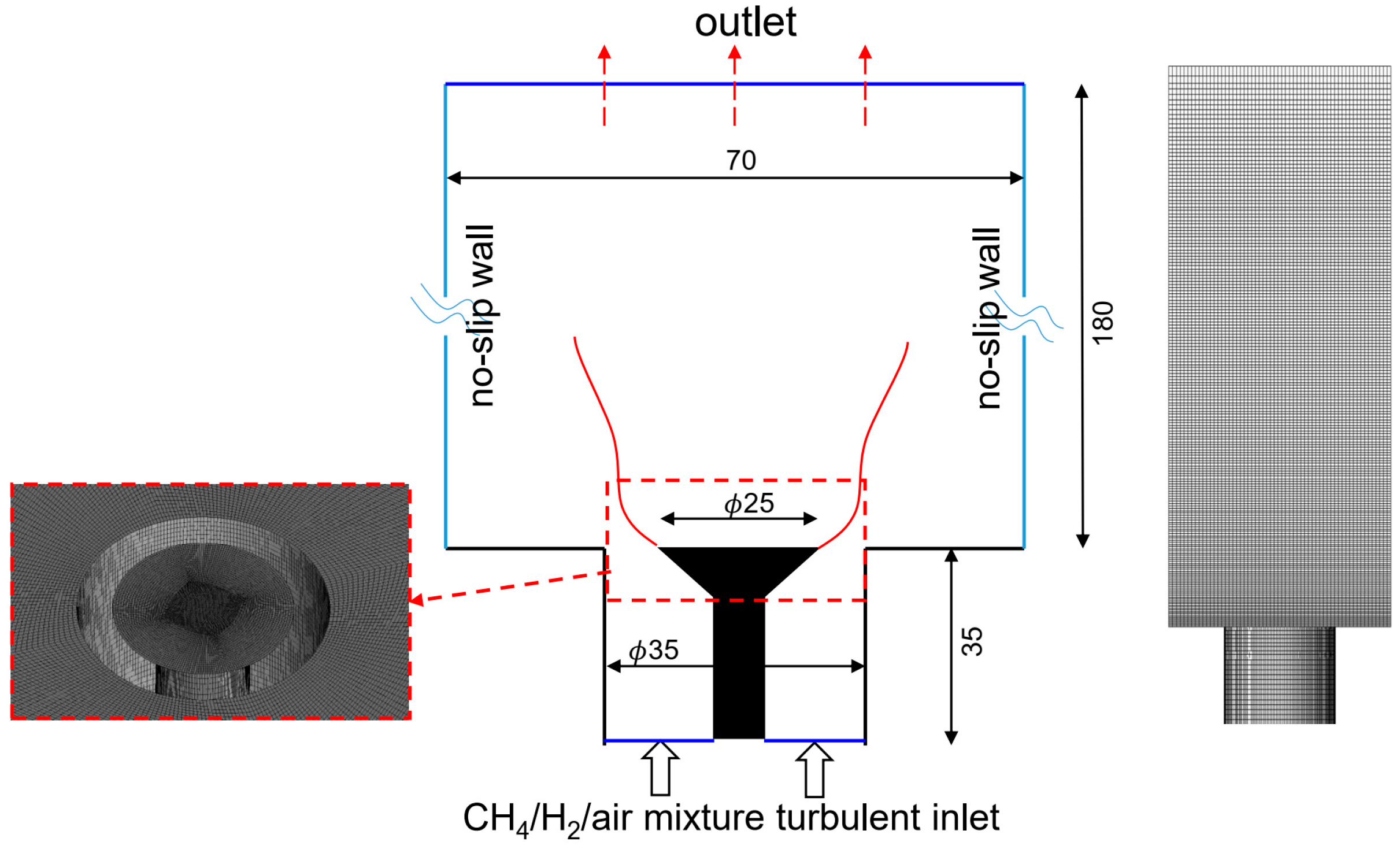
3. Simulation Setup
4. Results and Discussion
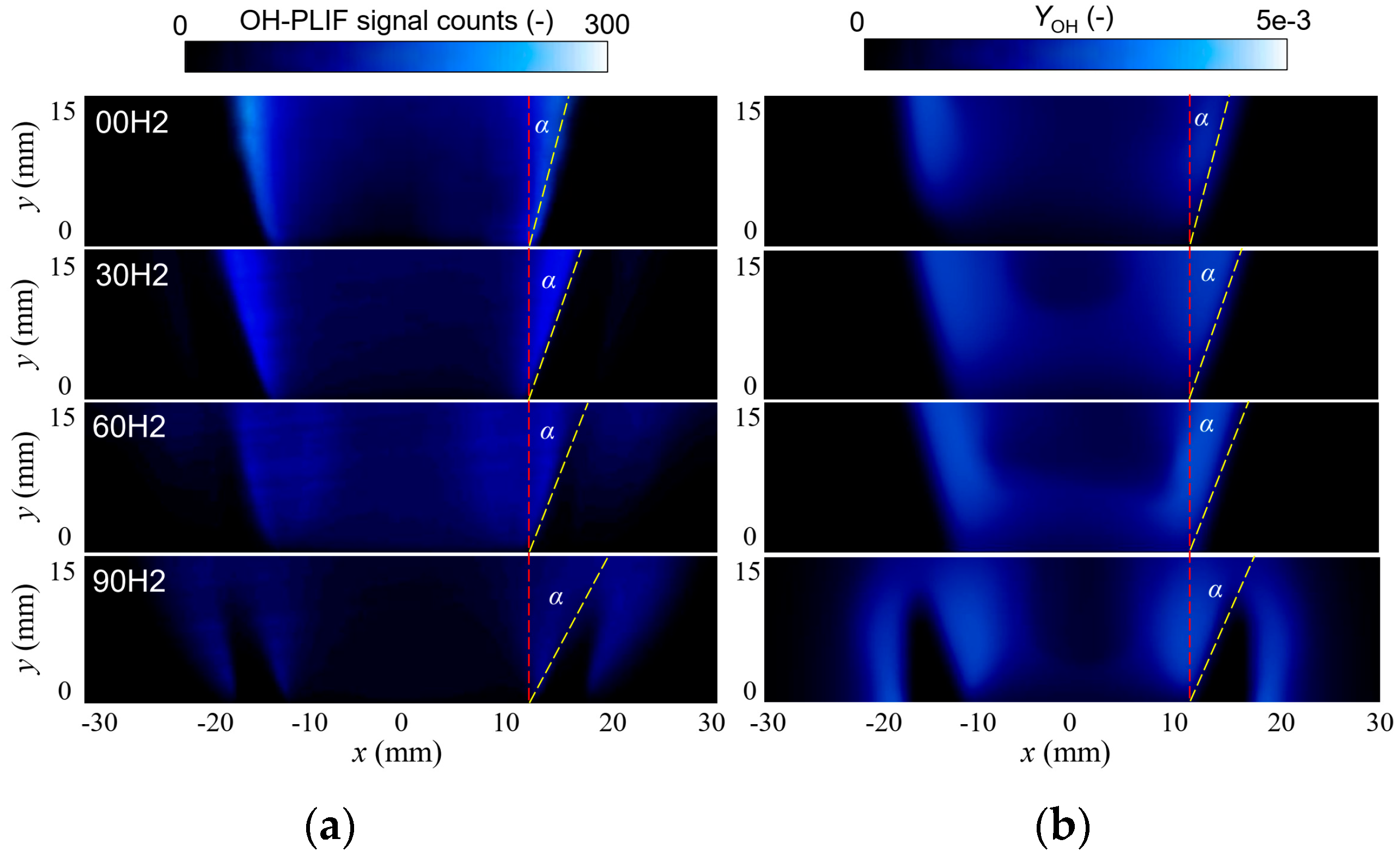
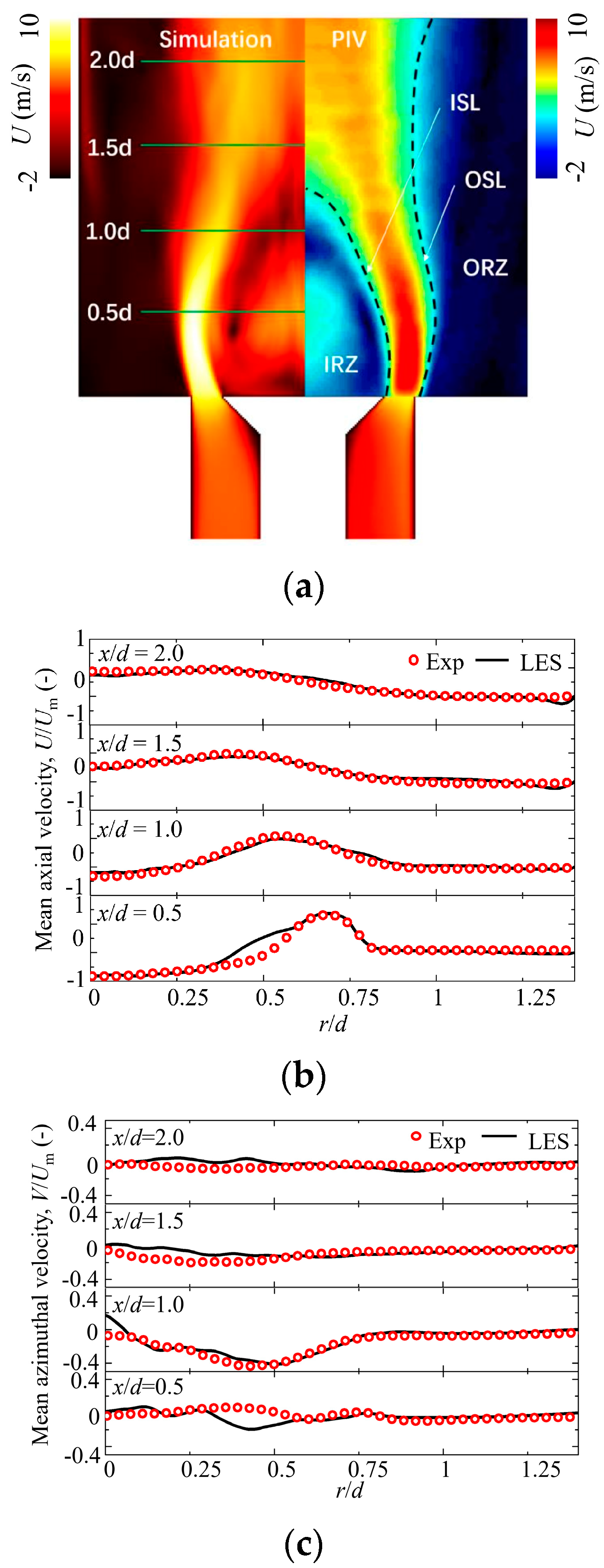
4.1. Model Validation
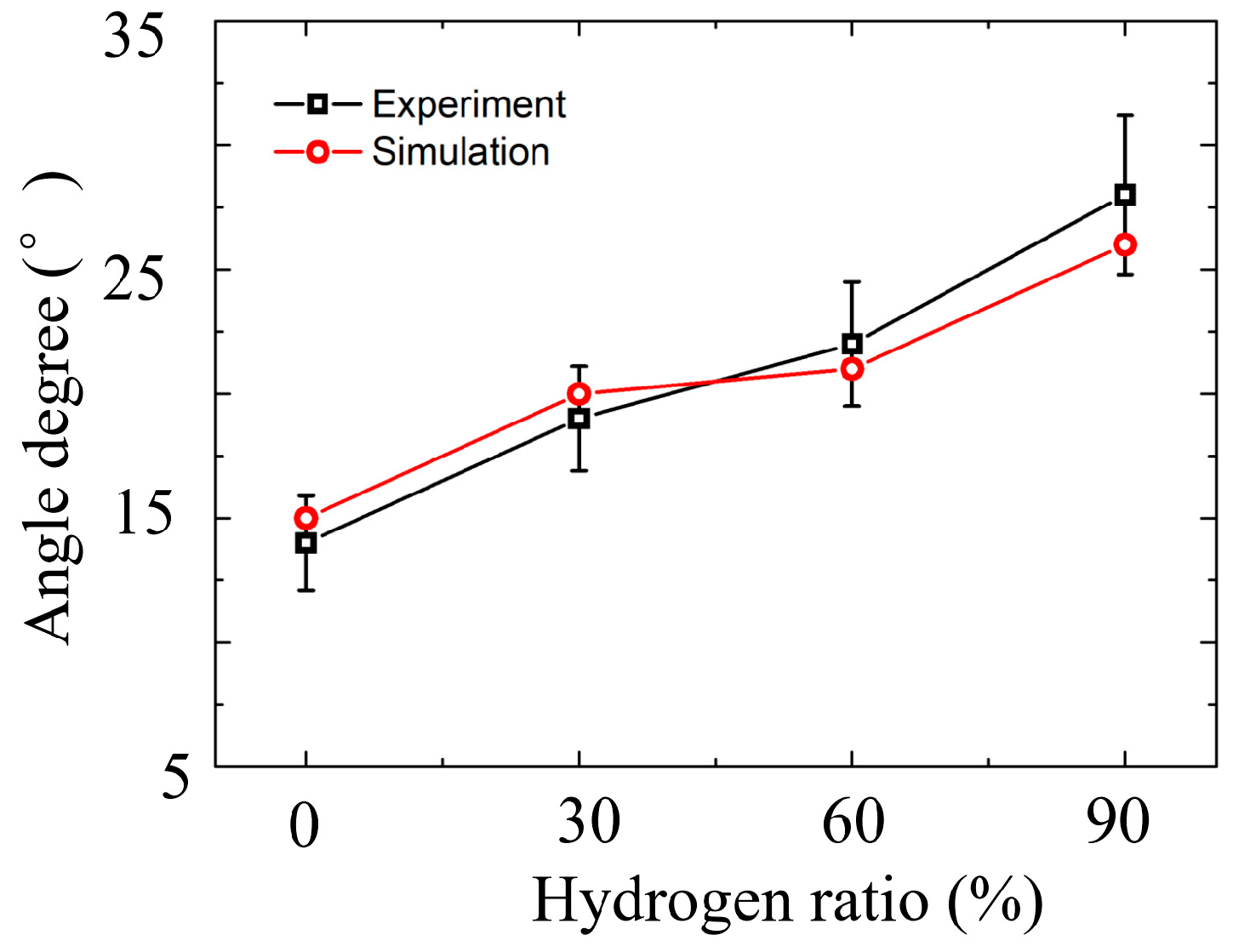
4.2. Flame Stabilization
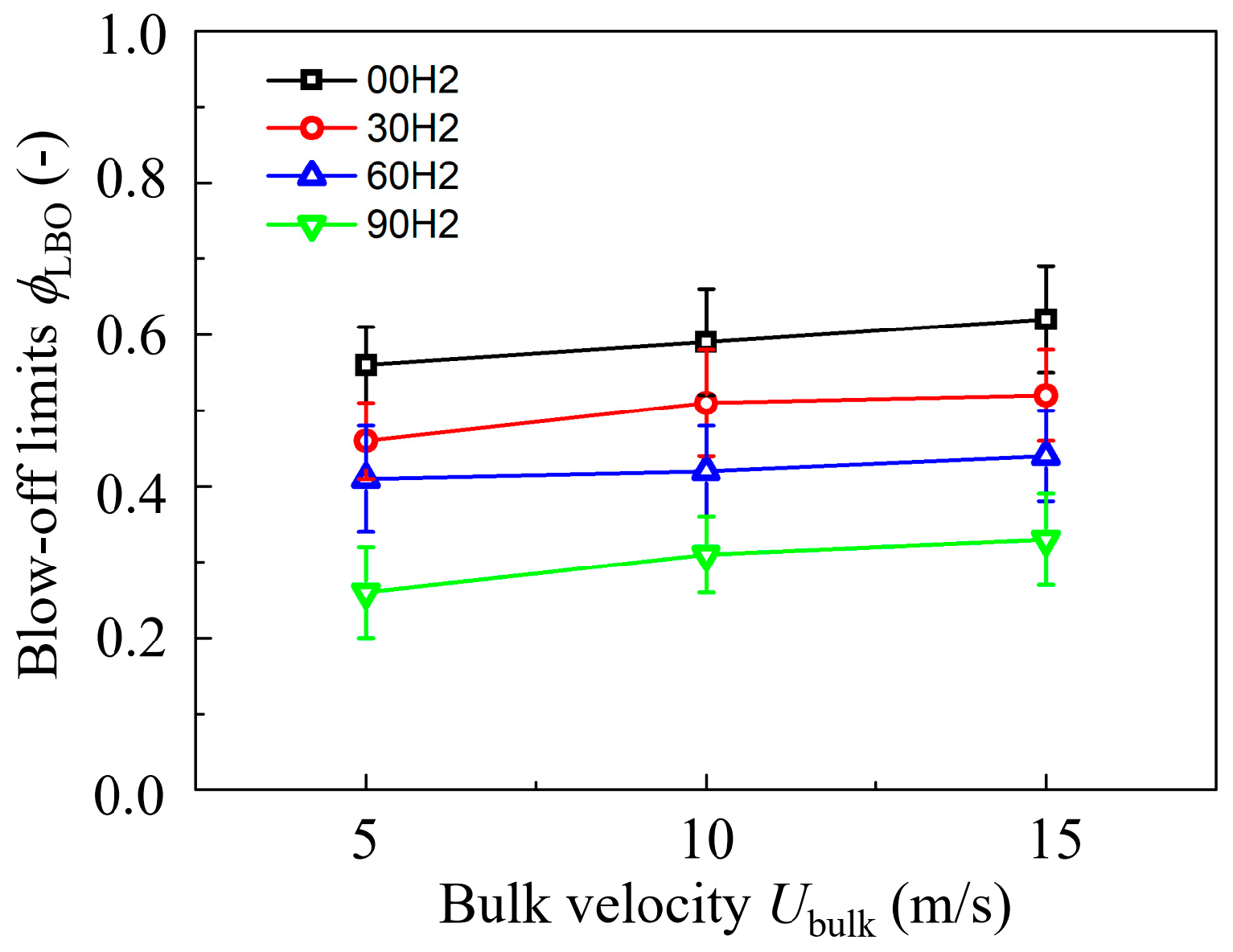
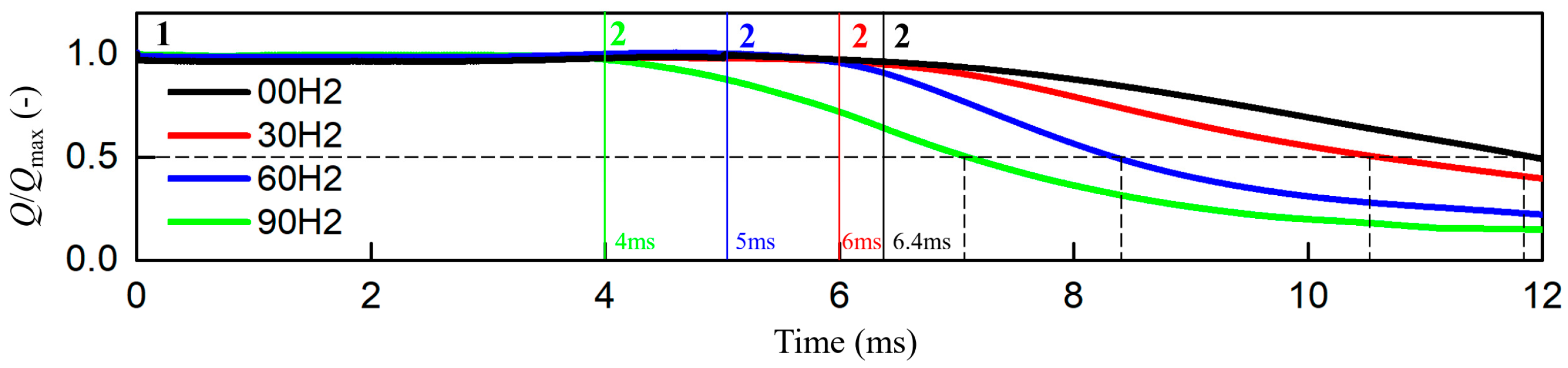
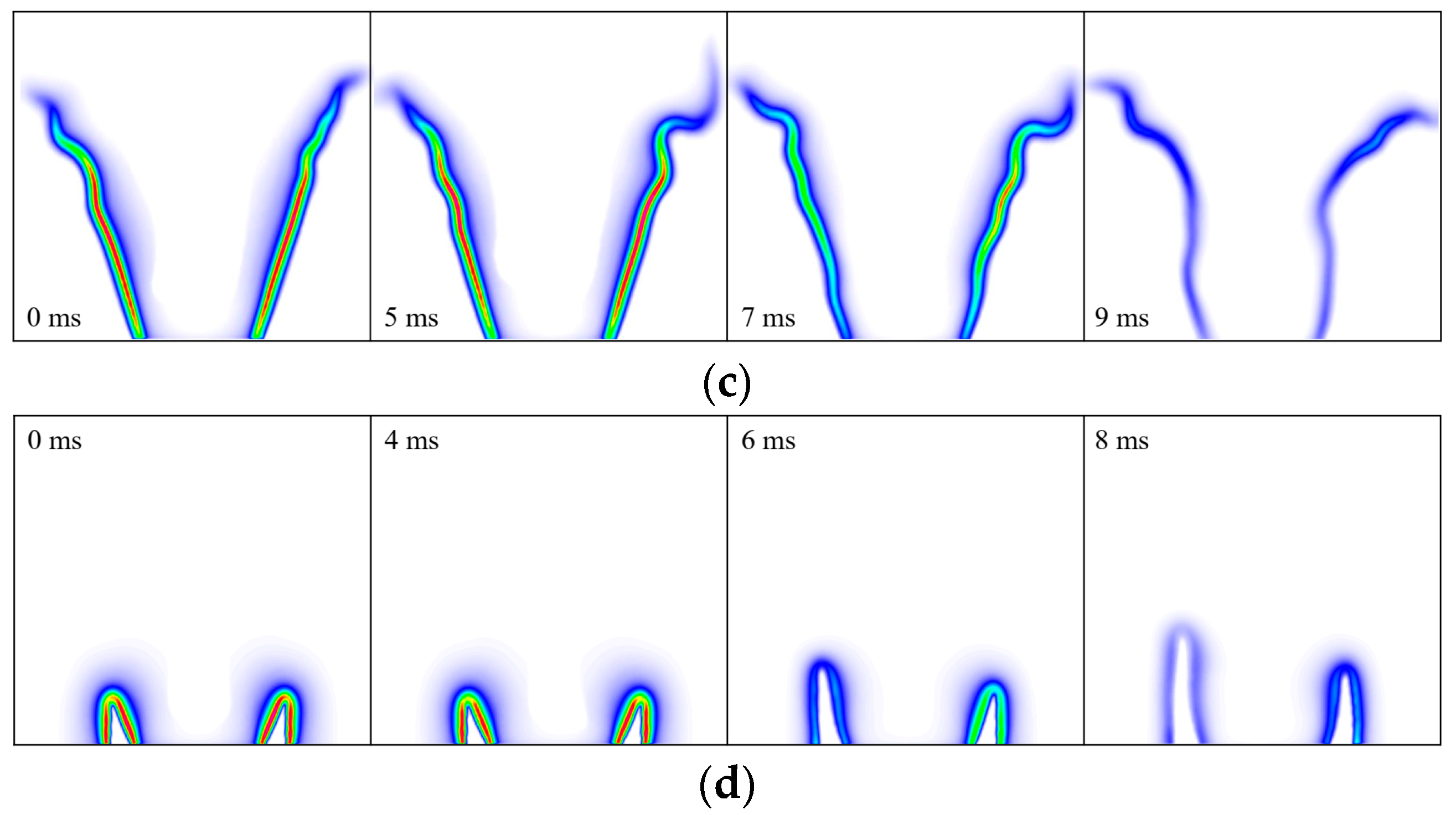
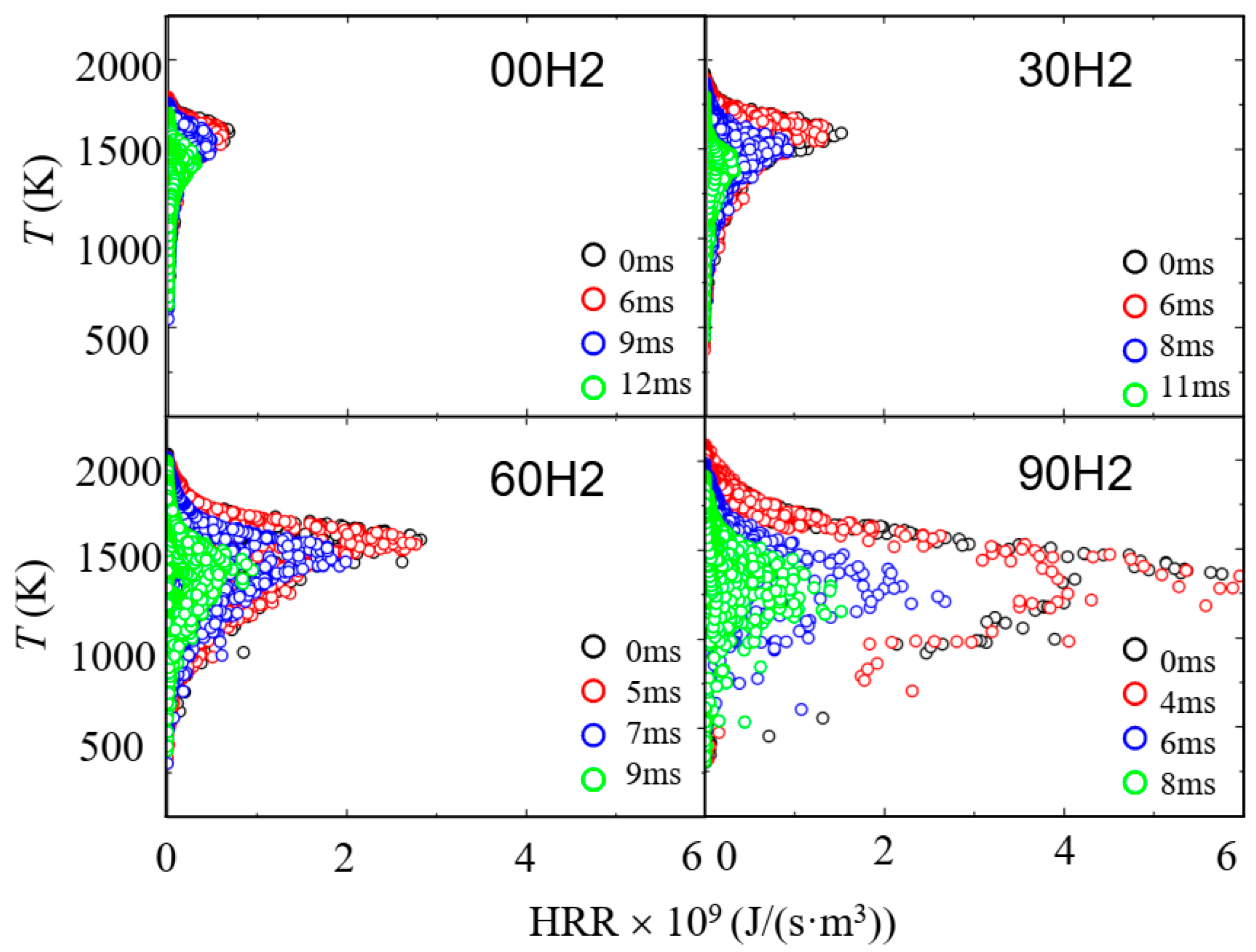
4.3. Blow-Off Dynamics
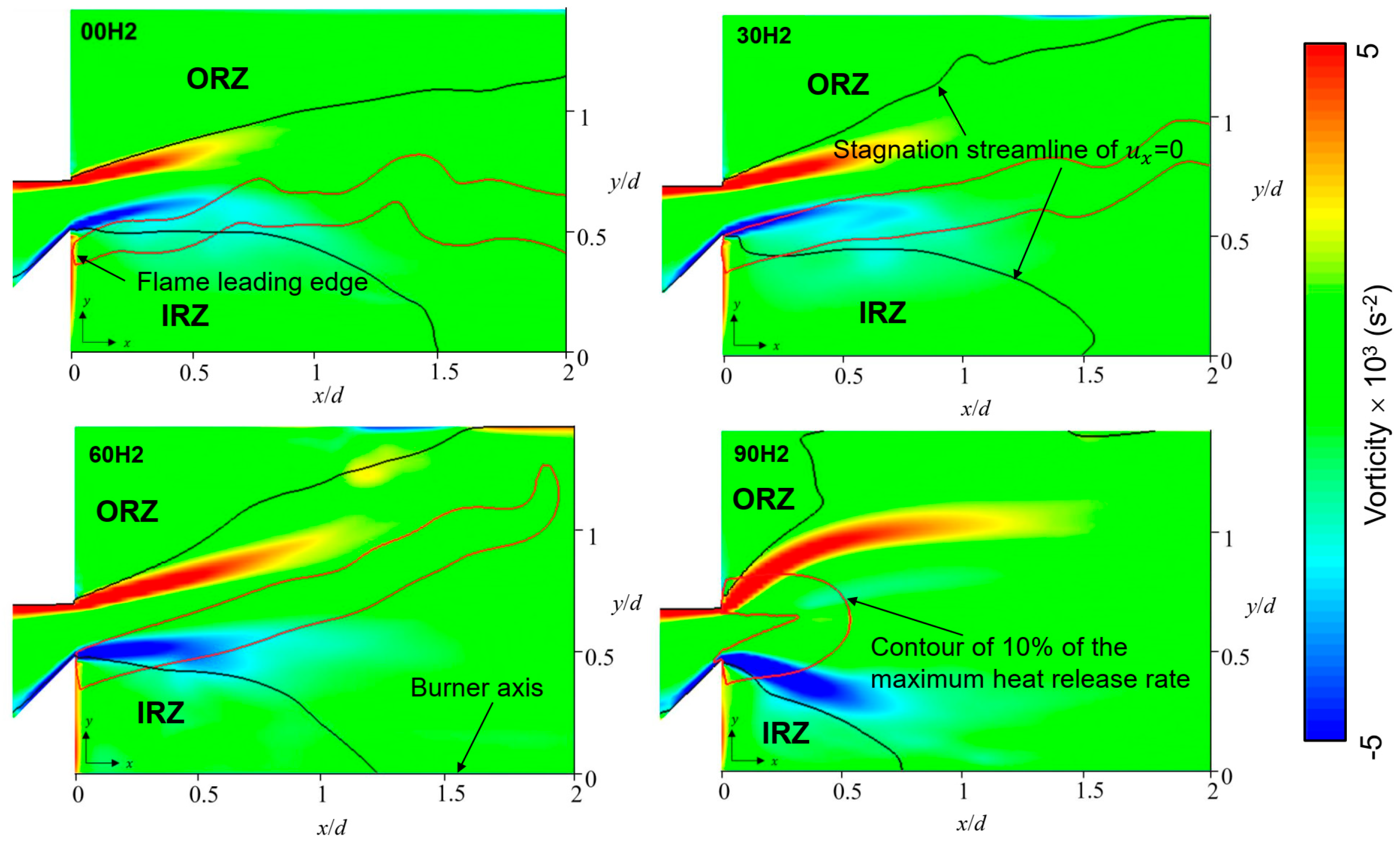
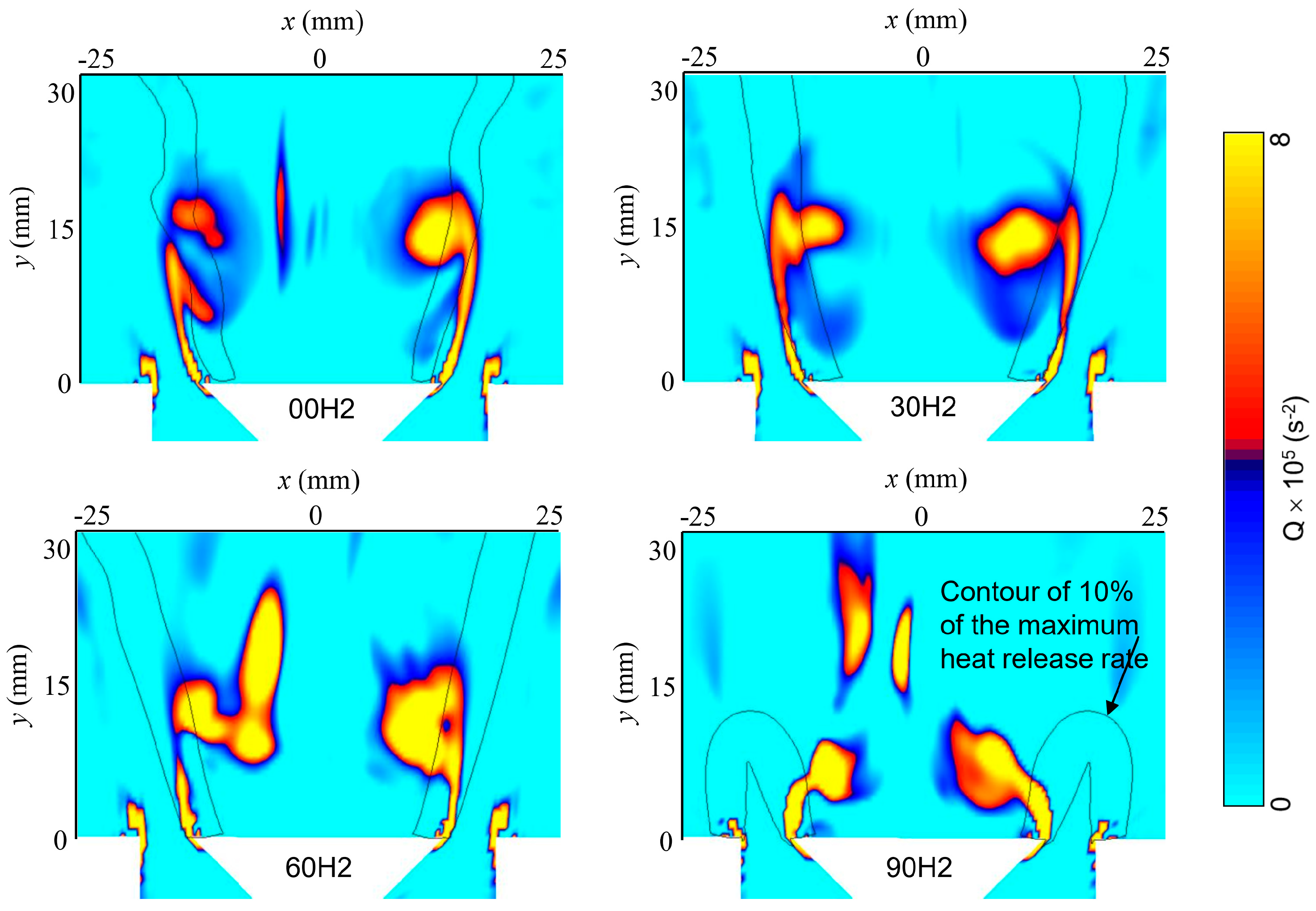
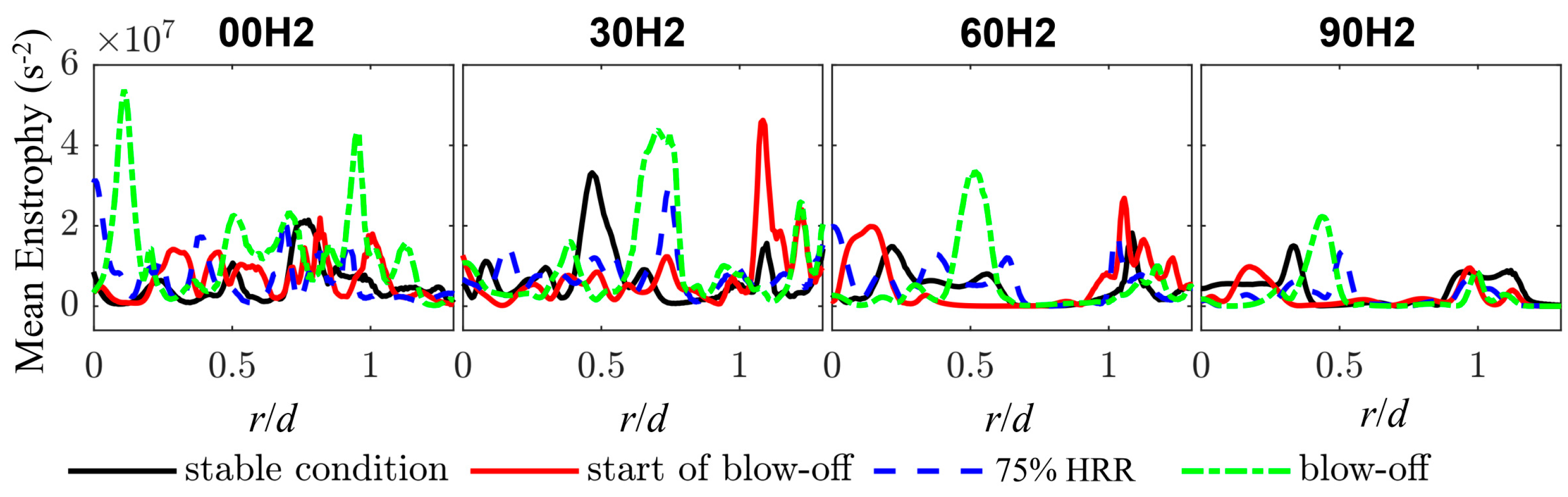
4.4. Vorticity Field during Blow-Off
5. Conclusions
- Under stable conditions, both the flame height and the inner/outer recirculation zone decrease with an increase in the hydrogen ratio. The angle between the flame edge and centerline increases linearly, and the ability of the flame to stabilize in higher-strain-rate locations is enhanced. The location of the flame moves away from the vortex concentration area. This implies that the flame tends to attach to the bluff body more strongly.
- For blow-off conditions, a specific precursor event that triggers blow-off is identifiable by the rate of HRR decrease. The blow-off process is separated into two stages. With an increase in the hydrogen ratio, the duration of each stage decreases. The decrease in the heat release rate is one of the main factors that cause blow-off in lean CH4/H2/air flames and also influences flame temperature.
- An increase in enstrophy during the blow-off sequence was observed in all cases. The mean value of enstrophy decreased with hydrogen blending. Our enstrophy budget analysis showed that the vortex stretching source term was significantly reduced in magnitude with an increase in hydrogen ratio, which corresponded to a decrease in the absolute enstrophy value. The dilatation and baroclinic torque terms suddenly decreased close to blow-off, but their decline was not significant in high-hydrogen-ratio conditions.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. PIV and PLIF Measurement

Appendix B. Chemical Reaction Mechanism

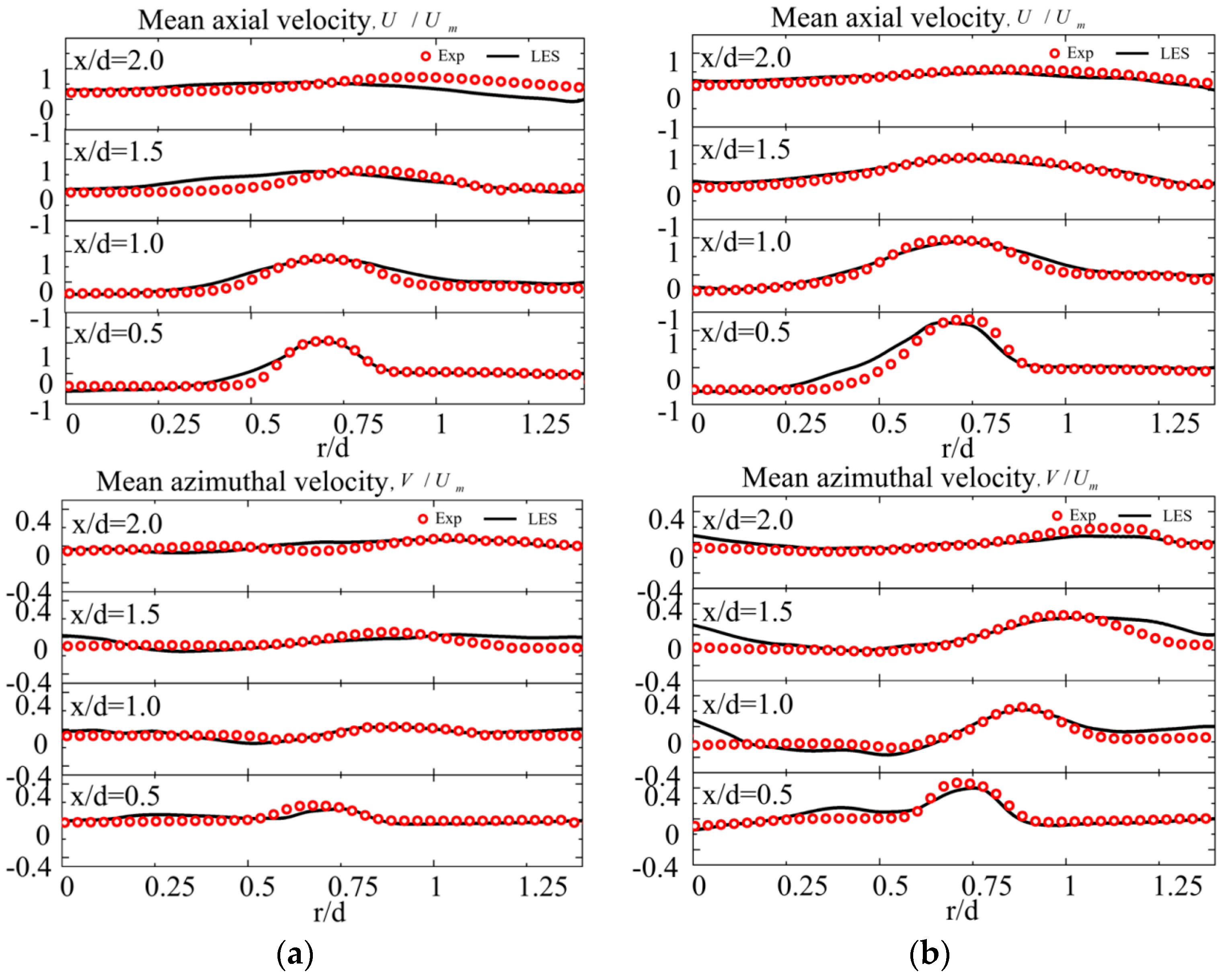
Appendix C. Velocity Field Validation

References
- Lund, H.; Muenster, E. Management of surplus electricity-production from a fluctuating renewable-energy source. Appl. Energy 2003, 76, 65–74. [Google Scholar] [CrossRef]
- Bothien, M.R.; Ciani, A.; Wood, J.P.; Fruechtel, G. Sequential combustion in gas turbines: The key technology for burning high hydrogen contents with low emissions. In Proceedings of the ASME Turbo Expo 2019: Turbomachinery Technical Conference and Exposition, Phoenix, AZ, USA, 17–21 June 2019. [Google Scholar]
- Birol, F. The Future of Hydrogen, Seizing Today’s Opportunities, Report Prepared by the IEA for the G20, 82–83, Japan; IEA: Paris, France, 2019. [Google Scholar]
- Lee, M.C.; Seo, S.B.; Chung, J.H.; Kim, S.M.; Joo, Y.J.; Ahn, D.H. Gas turbine combustion performance test of hydrogen and carbon monoxide synthetic gas. Fuel 2010, 89, 1485–1491. [Google Scholar] [CrossRef]
- Valera-Medina, A.; Gutesa, M.; Xiao, H.; Pugh, D.; Giles, A.; Goktepe, B.; Marsh, R.; Bowen, P. Premixed ammonia/hydrogen swirl combustion under rich fuel conditions for gas turbines operation. Int. J. Hydrogen Energy 2019, 44, 8615–8626. [Google Scholar] [CrossRef]
- Tao, C.; Zhou, H. Dilution effects of CO2, Ar, N2 and He microjets on the combustion dynamic and emission characteristics of unsteady premixed flame. Aerosp. Sci. Technol. 2021, 111, 106537. [Google Scholar] [CrossRef]
- Ying, H.; Yang, V. Dynamics and stability of lean-premixed swirl-stabilized combustion. Prog. Energy Combust. Sci. 2009, 35, 293–364. [Google Scholar]
- Salvador, F.; Carreres, M.; García-Tíscar, J.; Belmar-Gil, M. Modal decomposition of the unsteady non-reactive flow field in a swirl-stabilized combustor operated by a Lean Premixed injection system. Aerosp. Sci. Technol. 2021, 112, 106622. [Google Scholar] [CrossRef]
- Ruan, C.; Chen, F.; Cai, W.; Qian, Y.; Yu, L.; Lu, X. Principles of non-intrusive diagnostic techniques and their applications for fundamental studies of combustion instabilities in gas turbine combustors: A brief review. Aerosp. Sci. Technol. 2019, 84, 585–603. [Google Scholar] [CrossRef]
- Zhao, D.; Lu, Z.; Zhao, H.; Li, X.; Wang, B.; Liu, P. A review of active control approaches in stabilizing combustion systems in aerospace industry. Prog. Aerosp. Sci. 2018, 97, 35–60. [Google Scholar] [CrossRef]
- Li, L.; Zhao, D. Prediction of stability behaviors of longitudinal and circumferential eigenmodes in a choked thermoacoustic combustor. Aerosp. Sci. Technol. 2015, 46, 12–21. [Google Scholar] [CrossRef]
- Hawkes, E.R.; Chen, J.H. Direct numerical simulation of hydrogen-enriched lean premixed methane–air flames. Combust. Flame 2004, 138, 242–258. [Google Scholar] [CrossRef]
- Schefer, R.W.; Wicksall, D.; Agrawal, A. Combustion of hydrogen-enriched methane in a lean premixed swirl-stabilized burner. Proc. Combust. Inst. 2002, 29, 843–851. [Google Scholar] [CrossRef]
- Zhao, T.; Zhang, J.; Ju, D.; Huang, Z.; Han, D. Exergy losses in premixed flames of dimethyl ether and hydrogen blends. Front. Energy 2019, 13, 658–666. [Google Scholar] [CrossRef]
- Wang, Z.; Hu, B.; Fang, A.; Zhao, Q.; Chen, X. Analyzing lean blow-off limits of gas turbine combustors based on local and global Damköhler number of reaction zone. Aerosp. Sci. Technol. 2021, 111, 106532. [Google Scholar] [CrossRef]
- Sacramento, E.M.D.; Lima, L.C.D.; Oliveira, C.J.; Veziroglu, T.N. A hydrogen energy system and prospects for reducing emissions of fossil fuels pollutants in the Ceará state—Brazil. Int. J. Hydrogen Energy 2008, 33, 2132–2137. [Google Scholar] [CrossRef]
- Koç, Y.; Yağlı, H.; Goerguelue, A.; Koc, A. Analysing the performance, fuel cost and emission parameters of the 50 MW simple and recuperative gas turbine cycles using natural gas and hydrogen as fuel. Int. J. Hydrogen Energy 2020, 45, 22138–22147. [Google Scholar] [CrossRef]
- Giacomazzi, E.; Battaglia, V.; Bruno, C. The coupling of turbulence and chemistry in a premixed bluff-body flame as studied by LES. Combust. Flame 2004, 138, 320–335. [Google Scholar] [CrossRef]
- Ruan, C.; Chen, F.; Yu, T.; Cai, W.; Li, X.; Lu, X. Experimental characterization of flame/flow dynamics during transition between stable and thermo-acoustically unstable conditions in a gas turbine model combustor. Aerosp. Sci. Technol. 2020, 102, 105858. [Google Scholar] [CrossRef]
- Shanbhogue, S.J.; Husain, S.; Lieuwen, T. Lean blowoff of bluff body stabilized flames: Scaling and dynamics. Prog. Energy Combust. Sci. 2009, 35, 98–120. [Google Scholar] [CrossRef]
- Wan, J.; Fan, A. Recent progress in flame stabilization technologies for combustion-based micro energy and power systems. Fuel 2020, 286, 119391. [Google Scholar] [CrossRef]
- Dawson, J.; Gordon, R.; Kariuki, J.; Mastorakos, E.; Masri, A.; Juddoo, M. Visualization of blow-off events in bluff-body stabilized turbulent premixed flames. Proc. Combust. Inst. 2011, 33, 1559–1566. [Google Scholar] [CrossRef]
- Tong, Y.; Liu, X.; Wang, Z.; Richter, M.; Klingmann, J. Experimental and numerical study on bluff-body and swirl stabilized diffusion flames. Fuel 2018, 217, 352–364. [Google Scholar] [CrossRef]
- Kim, H.S.; Arghode, V.K.; Linck, M.B.; Gupta, A.K. Hydrogen addition effects in a confined swirl-stabilized methane-air flame. Int. J. Hydrogen Energy 2009, 34, 1054–1062. [Google Scholar] [CrossRef]
- Michaels, D.; Shanbhogue, S.J.; Ghoniem, A.F. The impact of reactants composition and temperature on the flow structure in a wake stabilized laminar lean premixed CH4/H2/air flames; mechanism and scaling. Combust. Flame 2017, 176, 151–161. [Google Scholar] [CrossRef]
- Denaro, F.M. What Is the Basic Physical Meaning of Enstrophy? Available online: https://www.researchgate.net/post/What_is_the_basic_physical_meaning_of_enstrophy (accessed on 25 January 2024).
- Balachandran, R.; Ayoola, B.O.; Kaminski, C.F.; Dowling, A.P.; Mastorakos, E. Experimental investigation of the nonlinear response of turbulent premixed flames to imposed inlet velocity oscillations. Combust. Flame 2005, 143, 37–55. [Google Scholar] [CrossRef]
- Immer, M.C. Time-Resolved Measurement and Simulation of Local Scale Turbulent Urban Flow. Ph.D. Thesis, ETH Zurich, Zürich, Switzerland, 2016. [Google Scholar]
- Veynante, D.; Vervisch, L. Turbulent combustion modeling. Prog. Energy Combust. Sci. 2002, 28, 193–266. [Google Scholar] [CrossRef]
- Colin, O.; Ducros, F.; Veynante, D.; Poinsot, T. A thickened flame model for large eddy simulations of turbulent premixed combustion. Phys. Fluids 2000, 12, 1843–1863. [Google Scholar] [CrossRef]
- Wei, X.; Zhang, M.; An, Z.; Wang, J.; Huang, Z.; Tan, H. Large eddy simulation on flame topologies and the blow-off characteristics of ammonia/air flame in a model gas turbine combustor. Fuel 2021, 298, 120846. [Google Scholar] [CrossRef]
- Wang, G.; Boileau, M.; Veynante, D.; Truffin, K. Large eddy simulation of a growing turbulent premixed flame kernel using a dynamic flame surface density model. Combust. Flame 2012, 159, 2742–2754. [Google Scholar] [CrossRef]
- Charlette, F.; Meneveau, C.; Veynante, D. A power-law flame wrinkling model for LES of premixed turbulent combustion Part II: Dynamic formulation. Combust. Flame 2002, 131, 181–197. [Google Scholar] [CrossRef]
- Han, W.; Wang, H.; Kuenne, G.; Hawkes, E.R.; Chen, J.H.; Janicka, J.; Hasse, C. Large eddy simulation/dynamic thickened flame modeling of a high Karlovitz number turbulent premixed jet flame. Proc. Combust. Inst. 2019, 37, 2555–2563. [Google Scholar] [CrossRef]
- Ansys Chemkin-Pro. ANSYS React Des San Diego, version 17.2; Ansys Chemkin-Pro: Canonsburg, PA, USA, 2016.
- Martin, C.E.; Benoit, L.; Sommerer, Y.; Nicoud, F.; Poinsot, T. Large-eddy simulation and acoustic analysis of a swirled staged turbulent combustor. AIAA J. 2006, 44, 741–750. [Google Scholar] [CrossRef]
- Kitano, T.; Kaneko, K.; Kurose, R.; Komori, S. Large-eddy simulations of gas- and liquid-fueled combustion instabilities in back-step flows. Combust. Flame 2016, 170, 63–78. [Google Scholar] [CrossRef]
- Guo, S.; Wang, J.; Wei, X.; Yu, S.; Zhang, M.; Huang, Z. Numerical simulation of premixed combustion using the modified dynamic thickened flame model coupled with multi-step reaction mechanism. Fuel 2018, 233, 346–353. [Google Scholar] [CrossRef]
- Issa, R.I. Solution of the implicitly discretised fluid flow equations by operator-splitting. J. Comput. Phys. 1986, 62, 40–65. [Google Scholar] [CrossRef]
- Karalus, M.F.; Fackler, K.B.; Novosselov, I.V.; Kramlich, J.C.; Malte, P.C. A skeletal mechanism for the reactive flow simulation of methane combustion. In Proceedings of the Turbo Expo: Power for Land, Sea, and Air, San Antonio, TX, USA, 3–7 June 2013; p. V01BT04A065. [Google Scholar]
- Lee, C.Y.; Cant, S. Assessment of LES subgrid-scale models and investigation of hydrodynamic behaviour for an axisymmetrical bluff body flow. Flow Turbul. Combust. 2017, 98, 155–176. [Google Scholar] [CrossRef] [PubMed]
- Chen, Q.; Zhong, Q.; Qi, M.; Wang, X. Comparison of vortex identification criteria for planar velocity fields in wall turbulence. Phys. Fluids 2015, 27, 085101. [Google Scholar] [CrossRef]
- Guo, S.; Wang, J.; Zhang, W.; Zhang, M.; Huang, Z. Effect of hydrogen enrichment on swirl/bluff-body lean premixed flame stabilization. Int. J. Hydrogen Energy 2020, 45, 10906–10919. [Google Scholar] [CrossRef]
- Hunt, J.C.R.; Wray, A.A.; Moin, P. Eddies, streams, and convergence zones in turbulent flows. In Proceedings of the 1988 Summer Program, Stanford, CA, USA, 8–10 April 1988; pp. 193–208. [Google Scholar]
- Fu, W.-S.; Lai, Y.-C.; Li, C.-G. Estimation of turbulent natural convection in horizontal parallel plates by the Q criterion. Int. Commun. Heat Mass Transf. 2013, 45, 41–46. [Google Scholar] [CrossRef]
- Panesi, M. Influences Of The Darrieus-Landau Instability On Premixed Turbulent Flames. In Proceedings of the 70th Annual Meeting of the APS Division of Fluid Dynamics, Denver, CO, USA, 19–21 November 2017. [Google Scholar]


| ID | (m/s) | (mm) | Tad (K) | (mm) | n | F | |
|---|---|---|---|---|---|---|---|
| 00H2 | 0.2468 | 0.573 | 1919.71 | 0.5 | 0.872 | 7 | 6 |
| 30H2 | 0.2970 | 0.510 | 1927.91 | 0.5 | 0.980 | 7 | 7 |
| 60H2 | 0.4112 | 0.429 | 1944.72 | 0.5 | 1.166 | 7 | 8 |
| 90H2 | 0.8599 | 0.363 | 2001.72 | 0.5 | 1.377 | 7 | 9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, L.; Zhang, M.; Peng, S.; Wang, J.; Huang, Z. Large Eddy Simulation of the Effect of Hydrogen Ratio on the Flame Stabilization and Blow-Off Dynamics of a Lean CH4/H2/Air Bluff-Body Flame. Appl. Sci. 2024, 14, 1846. https://doi.org/10.3390/app14051846
Cheng L, Zhang M, Peng S, Wang J, Huang Z. Large Eddy Simulation of the Effect of Hydrogen Ratio on the Flame Stabilization and Blow-Off Dynamics of a Lean CH4/H2/Air Bluff-Body Flame. Applied Sciences. 2024; 14(5):1846. https://doi.org/10.3390/app14051846
Chicago/Turabian StyleCheng, Lei, Meng Zhang, Shiyao Peng, Jinhua Wang, and Zuohua Huang. 2024. "Large Eddy Simulation of the Effect of Hydrogen Ratio on the Flame Stabilization and Blow-Off Dynamics of a Lean CH4/H2/Air Bluff-Body Flame" Applied Sciences 14, no. 5: 1846. https://doi.org/10.3390/app14051846
APA StyleCheng, L., Zhang, M., Peng, S., Wang, J., & Huang, Z. (2024). Large Eddy Simulation of the Effect of Hydrogen Ratio on the Flame Stabilization and Blow-Off Dynamics of a Lean CH4/H2/Air Bluff-Body Flame. Applied Sciences, 14(5), 1846. https://doi.org/10.3390/app14051846






