A Bearing Fault Diagnosis Method Based on Improved Transfer Component Analysis and Deep Belief Network
Abstract
1. Introduction
- The divergence factor is proposed to measure the compactness of samples within a category. Considering subdomain adaptation and divergence factors aims to improve the TCA, reducing subdomain discrepancies and increasing sample compactness;
- A simple method named SRPLC-K-means was designed to filter the noisy samples and correct the pseudo labels. The experimental results have verified that the SRPLC-K-means method is helpful in overcoming the issue of false pseudo labels;
- The experimental results on Case Western Reserve University and underground drum motor bearing datasets have demonstrated that the proposed method can reduce the time required for a fault diagnosis and increase accuracy.
2. Basic Theory
2.1. Transfer Component Analysis
2.2. Subdomain Adaptation
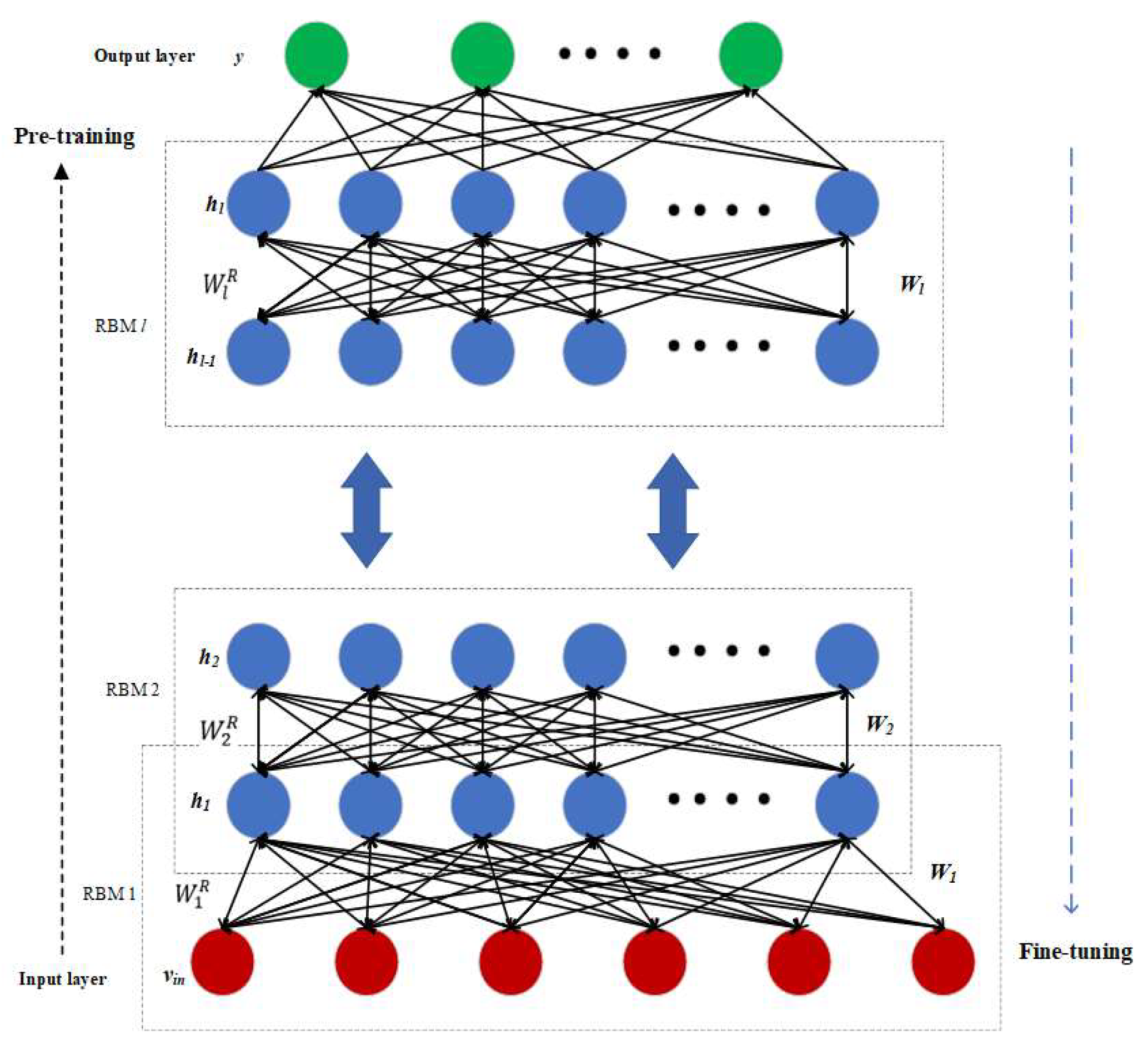
2.3. Deep Belief Networks
3. Proposed Method
3.1. Improved Transfer Component Analysis
3.1.1. Dispersion Factor
3.1.2. Improved Transfer Component Analysis
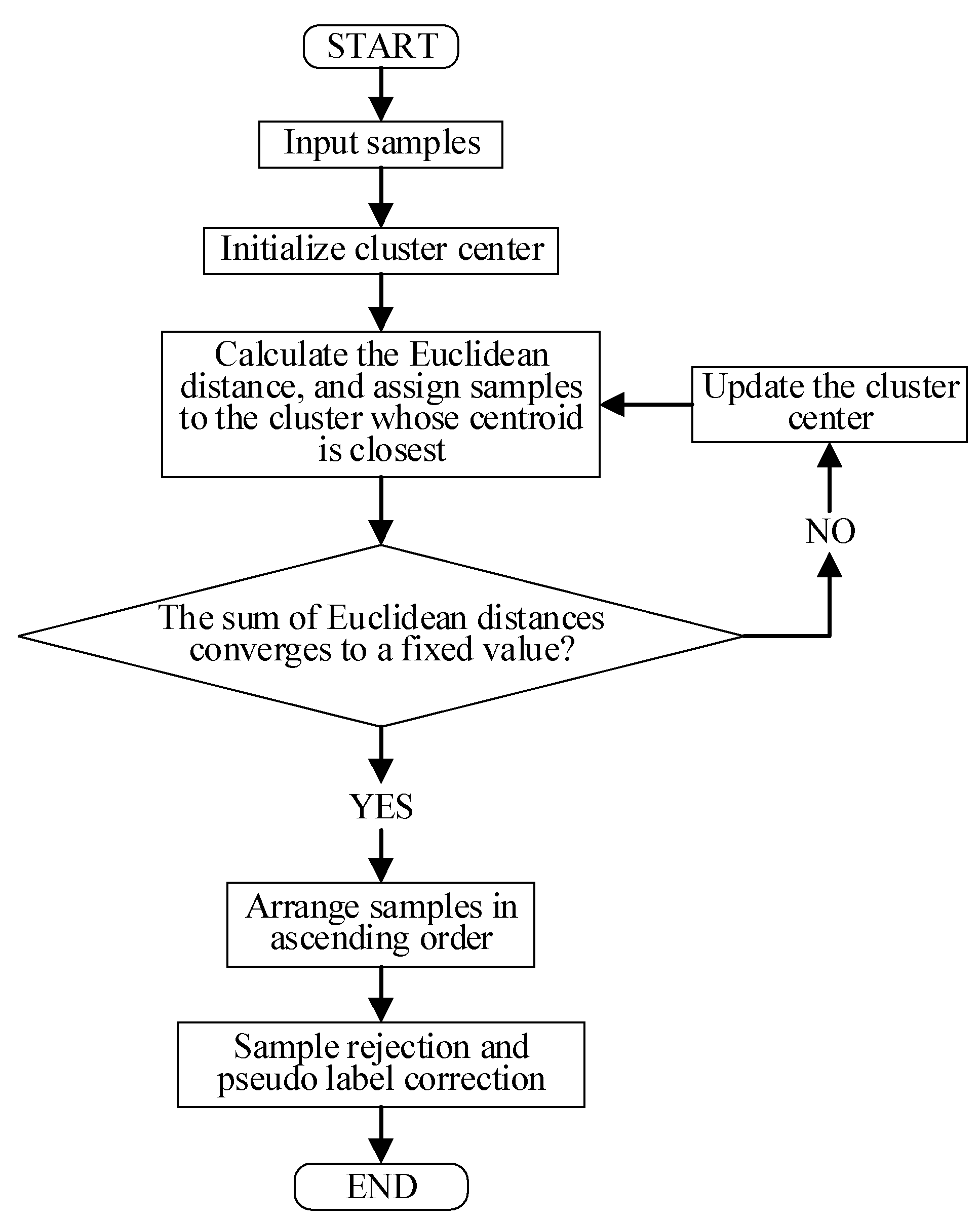
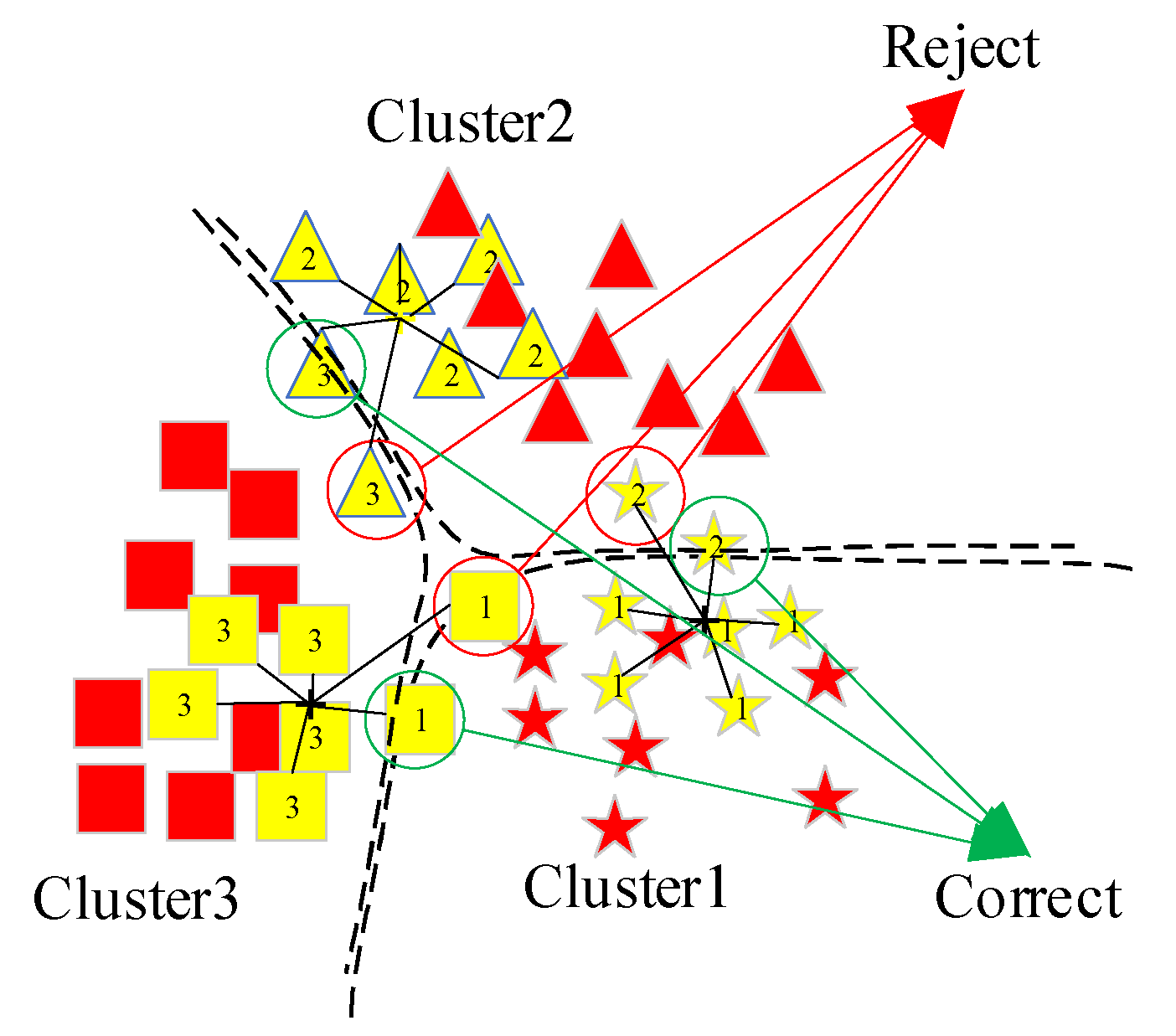
3.2. SRPLC-K-Means
- Randomly select k initial cluster centers from N samples;
- Calculate the Euclidean distance from each sample to the nearest cluster center and assign the sample to the cluster where is located. The calculation of the Euclidean distance from the center is shown in Equation (14);where is the coordinates of the cluster center, is the coordinates of the sample, and n is the feature dimension of the sample;
- Update the cluster center and recalculate the distance between each sample and the cluster center it belongs to;
- Repeat steps 2 and 3 until the sum of the Euclidean distances from all the samples to their respective cluster centers converges to a fixed value;
- Arrange the samples of each cluster in ascending order based on their Euclidean distance from the cluster center they belong to;
- Reserve the samples in the top d% of the sequence number. Adopting the idea of the minority obeying the majority, modify the pseudo labels of minority classes in the new sample set to those of majority classes.
3.3. The Fault Diagnosis Model of the Proposed Method
4. Experimental Analysis and Verification
4.1. Preparation of the Experimental Data
4.1.1. Introduction of the Dataset
4.1.2. Feature Extraction
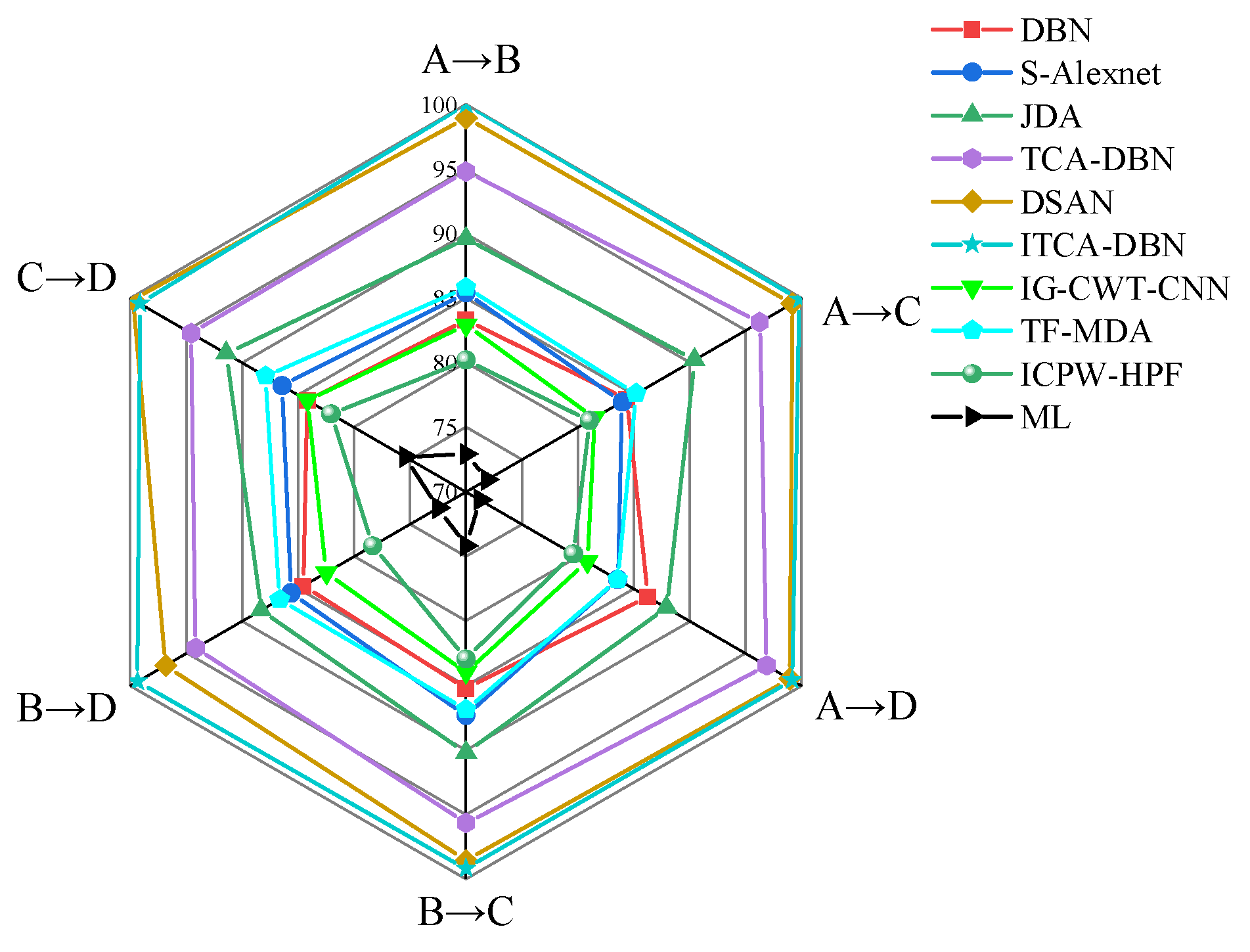
4.2. Test Ⅰ
4.3. Test Ⅱ
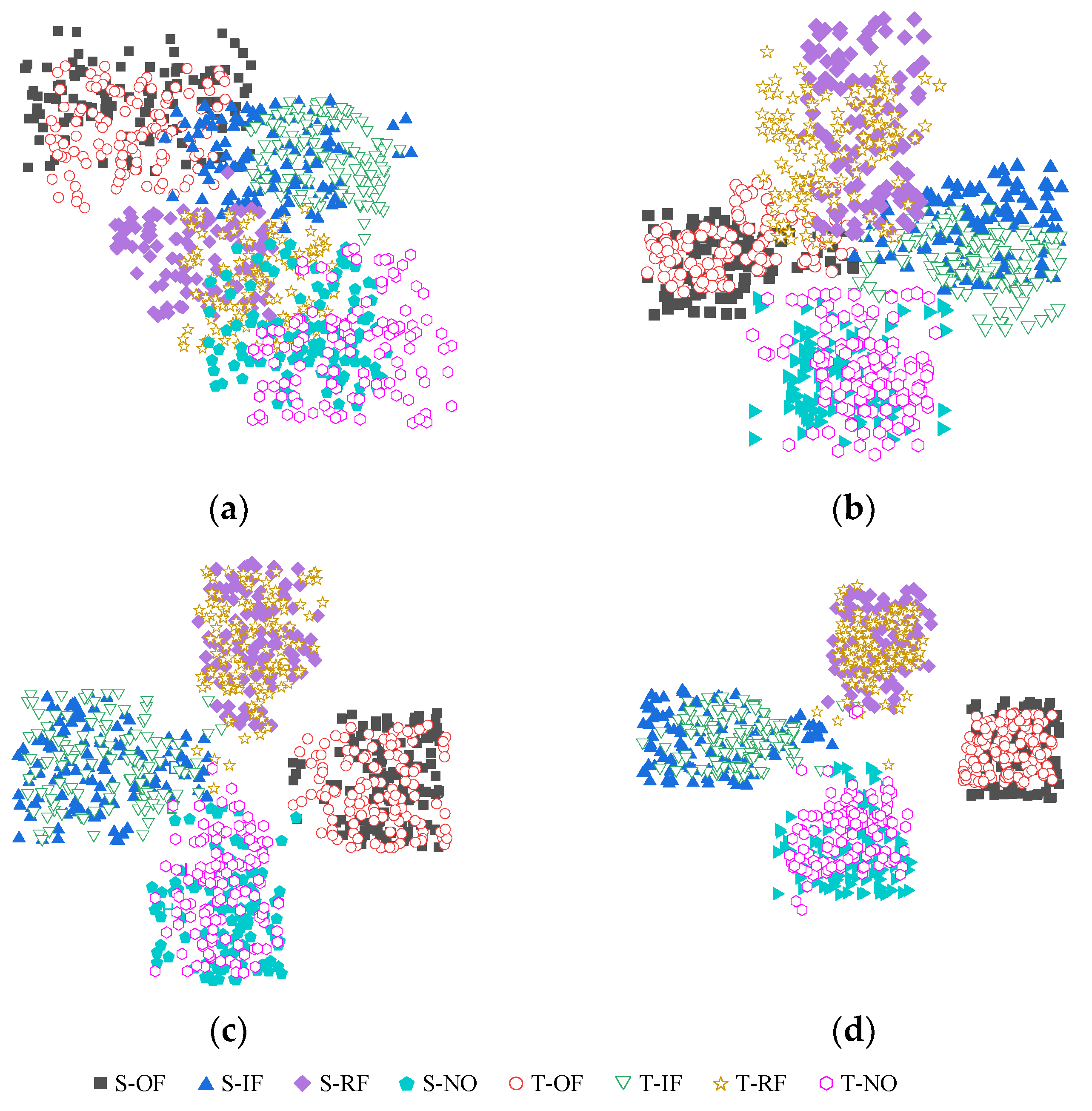
4.4. Feature Visualization
4.5. Test Ⅲ
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yin, C.; Wang, Y.; Ma, G.; Wang, Y.; Sun, Y.; He, Y. Weak fault feature extraction of rolling bearings based on improved ensemble noise-reconstructed EMD and adaptive threshold denoising. Mech. Syst. Signal Process. 2022, 171, 108834. [Google Scholar] [CrossRef]
- Liu, Q.; Chen, F.; Zhou, Z.; Wei, Q. Fault diagnosis of rolling bearing based on wavelet package transform and ensemble empirical mode decomposition. Adv. Mech. Eng. 2019, 5 Pt 2, 792584. [Google Scholar] [CrossRef]
- Liang, P.; Wang, W.; Yuan, X.; Liu, S.; Zhang, L.; Cheng, Y. Intelligent fault diagnosis of rolling bearing based on wavelet transform and improved ResNet under noisy labels and environment. Eng. Appl. Artif. Intell. 2022, 115, 105269. [Google Scholar] [CrossRef]
- Lei, C.; Xia, B.; Xue, L. Rolling bearing fault diagnosis method based on MTF-CNN. J. Vib. Shock 2022, 41, 151–158. [Google Scholar]
- Xu, X.; Cao, D.; Zhou, Y. Application of neural network algorithm in fault diagnosis of mechanical intelligence. Mech. Syst. Signal Process. 2020, 141, 106625. [Google Scholar] [CrossRef]
- Umang, P.; Pandya, D. Experimental investigation of cylindrical bearing fault diagnosis with SVM. J. Vib. Shock 2021, 44, 1286–1290. [Google Scholar]
- Mohammad, H.; Mahmoud, O.; Ebrahim, B. Fault diagnosis of tractor auxiliary gearbox using vibration analysis and random forest classifier. Inf. Process. Agric. 2022, 9, 60–67. [Google Scholar]
- Gong, M.; Guo, Y.; Yan, P.; Wu, N.; Zhang, C. A new fault diagnosis method of rolling bearings of shearer. Ind. Mine Autom. 2017, 43, 50–53. [Google Scholar]
- Lei, X.; Lu, N.; Chen, C. An AVMD-DBN-ELM model for bearing fault diagnosis. Sensors 2022, 22, 9369. [Google Scholar] [CrossRef]
- Zhang, J.; Ren, C. Rolling bearing feature transfer diagnosis based on deep belief network. J. Vib. Meas. Diagn. 2022, 42, 277–284+407. [Google Scholar]
- Ye, N.; Chang, P.; Zhang, L.; Wang, J. Research on multi-condition bearing fault diagnosis based on improved semi-supervised deep belief network. J. Mech. Eng. 2021, 57, 80–90. [Google Scholar]
- Wang, C.; Chen, D.; Chen, J.; Lai, X.; He, T. Deep regression adaptation networks with model-based transfer learning for dynamic load identification in the frequency domain. Eng. Appl. Artif. Intell. 2021, 102, 104244. [Google Scholar] [CrossRef]
- Pang, B.; Liu, Q.; Sun, Z.; Xu, Z.; Hao, Z. Time-frequency supervised contrastive learning via pseudo-labeling: An unsupervised domain adaptation network for rolling bearing fault diagnosis under time-varying speeds. Adv. Eng. Inform. 2024, 59, 102304. [Google Scholar] [CrossRef]
- Li, X.; Hu, Y.; Zheng, J.; Li, M.; Ma, W. Central moment discrepancy based domain adaptation for intelligent bearing fault diagnosis. Neurocomputing 2021, 429, 12–24. [Google Scholar] [CrossRef]
- Ma, W.; Zhang, Y.; Ma, L. Sliced An unsupervised domain adaptation approach with enhanced transferability and discriminability for bearing fault diagnosis under few-shot samples. Expert Syst. Appl. 2023, 225, 120084. [Google Scholar] [CrossRef]
- Kmjad, Z.; Sikora, A. Bearing fault diagnosis with intermediate domain based Layered Maximum Mean Discrepancy: A new transfer learning approach. Eng. Appl. Artif. Intell. 2021, 105, 104415. [Google Scholar]
- Chen, C.; Fu, Z.; Chen, Z.; Jin, S.; Cheng, Z.; Jin, X.; Hua, X.-S. HoMM: Higher-order moment matching for unsupervised domain adaptation. Proc. AAAI Conf. Artif. Intell. 2020, 34, 3422–3429. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhuang, F.; Wang, J.; Ke, G.; Chen, J.; Bian, J.; Xiong, H.; He, Q. Deep subdomain adaptation network for image classification. IEEE Trans. Neural Netw. Learn. Syst. 2020, 32, 1713–1722. [Google Scholar] [CrossRef] [PubMed]
- Wang, P.; Yang, G.; Li, Y.; Li, P.; Guo, Y.; Chen, R. Deep sample clustering domain adaptation for breast histopathology image classification. Biomed. Signal Process. Control 2024, 87, 105500. [Google Scholar] [CrossRef]
- Tian, M.; Su, X.; Chen, C.; An, W.; Sun, X. Research on domain adaptive fault diagnosis method for wind turbine generator bearings. Acta Energiae Solaris Sin. 2023, 44, 310–317. [Google Scholar]
- Chen, P.; Zhao, R.; He, T.; Wei, K.; Yang, Q. Unsupervised domain adaptation of bearing fault diagnosis based on Join Sliced Wasserstein Distance. ISA Trans. 2022, 129, 504–519. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, Y.; Chow, T.W.S.; Li, B. Deep adversarial subdomain adaptation network for intelligent fault diagnosis. IEEE Trans. Ind. Inform. 2022, 18, 6038–6046. [Google Scholar] [CrossRef]
- Kouw, W.M.; Loog, M. A review of single-source unsupervised domain adaptation. arXiv 2019, arXiv:1901.05335. [Google Scholar]
- Pan, S.J.; Tsang, I.W.; Kwok, J.T.; Yang, Q. Domain adaptation via transfer component analysis. IEEE Trans. Neural Netw. 2011, 22, 199–210. [Google Scholar] [CrossRef] [PubMed]
- Su, Y.; Huang, H.; Lai, X.; Chen, Y.; Yang, L.; Lin, C.; Xie, X.; Huang, B. Evaluation of landslide susceptibility of reservoir bank trans-regional Based on transfer component analysis. Earth Sci. 2023, 1–21. [Google Scholar] [CrossRef]
- Sujatha, K.; Yu, W.; Jin, L.; Seifedine, K. GO-DBN: Gannet optimized deep belief network based wavelet kernel elm for detection of diabetic retinopathy. Expert Syst. Appl. 2023, 229, 120408. [Google Scholar]
- Wang, G.; Qiao, J.; Bi, J.; Li, W.; Zhou, M. TL-GDBN: Growing deep belief network with transfer learning. IEEE Trans. Autom. Sci. Eng. 2019, 16, 874–885. [Google Scholar] [CrossRef]
- Sharma, A.; Kalluri, T.; Chandraker, M. Instance level affinity-based transfer for unsupervised domain adaptation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 5361–5371. [Google Scholar]
- Smith, W.A.; Randall, R.B. Rolling element bearing diagnostics using the Case Western Reserve University data: A benchmark study. Mech. Syst. Signal Process. 2015, 64–65, 100–113. [Google Scholar] [CrossRef]
- Jiao, J.; Yue, J.; Pei, D. Rolling bearing fault diagnosis method based on MSK-SVM. J. Electron. Meas. Instrum. 2022, 36, 109–117. [Google Scholar]
- Du, J.; Li, X.; Gao, Y.; Gao, L. Integrated Gradient-Based Continuous Wavelet Transform for Bearing Fault Diagnosis. Sensors 2022, 22, 8760. [Google Scholar] [CrossRef]
- Kim, Y.; Kim, Y. Time-Frequency Multi-Domain 1D Convolutional Neural Network with Channel-Spatial Attention for Noise-Robust Bearing Fault Diagnosis. Sensors 2023, 23, 9311. [Google Scholar] [CrossRef] [PubMed]
- Kiakojouri, A.; Lu, Z.; Mirring, P.; Powrie, H.; Wang, L. A Novel Hybrid Technique Combining Improved Cepstrum Pre-Whitening and High-Pass Filtering for Effective Bearing Fault Diagnosis Using Vibration Data. Sensors 2023, 23, 9048. [Google Scholar] [CrossRef] [PubMed]
- Bertocco, M.; Fort, A.; Landi, E.; Mugnaini, M.; Parri, L.; Peruzzi, G.; Pozzebon, A. Roller Bearing Failures Classification with Low Computational Cost Embedded Machine Learning. In Proceedings of the 2022 IEEE International Workshop on Metrology for Automotive (MetroAutomotive), Modena, Italy, 4–6 July 2022; pp. 12–17. [Google Scholar]
- Han, T.; Liu, C.; Yang, W.; Jiang, D. Deep transfer network with joint distribution adaptation: A new intelligent fault diagnosis framework for industry application. ISA Trans. 2020, 97, 269–281. [Google Scholar] [CrossRef] [PubMed]
- Duan, L.; Xie, J.; Wang, K.; Wang, J. Gearbox diagnosis based on auxiliary monitoring datasets of different working conditions. J. Vib. Shock 2017, 36, 104–108+116. [Google Scholar]
- Ding, X.; Wang, H.; Cao, Z.; Liu, X.; Liu, Y.; Huang, Z. An Edge Intelligent Method for Bearing Fault Diagnosis Based on a Parameter Transplantation Convolutional Neural Network. Electronics 2023, 12, 1816. [Google Scholar] [CrossRef]
- Bibal, A.; Delchevalerie, V.; Frénay, B. DT-SNE: T-SNE discrete visualizations as decision tree structures. Neurocomputing 2023, 529, 101–112. [Google Scholar] [CrossRef]




| Types of Bearing | Working Conditions | Rotational Speeds | Loads | Health Status |
|---|---|---|---|---|
| SKF6205 | A | 1797 r/min | 0 HP | Normal state Inner ring fault Rolling element fault Outer ring fault |
| B | 1772 r/min | 1 HP | ||
| C | 1750 r/min | 2 HP | ||
| D | 1730 r/min | 3 HP | ||
| SKF6203 | E | 1797 r/min | 0 HP | |
| F | 1772 r/min | 1 HP | ||
| G | 1750 r/min | 2 HP | ||
| H | 1730 r/min | 3 HP |
| Name | Definition | Name | Definition |
|---|---|---|---|
| Average | Standard deviation | ||
| Margin index | Skewness index | ||
| Root mean square | Kurtosis index | ||
| Pulse index | Waveform entropy |
| Methods | A → B | A → C | A → D | B → C | B → D | C → D | Average Accuracy |
|---|---|---|---|---|---|---|---|
| DBN | 83.333 | 84.375 | 86.25 | 85.208 | 84.583 | 84.167 | 84.653 |
| S-Alexnet | 85.417 | 83.958 | 83.542 | 87.292 | 85.625 | 86.458 | 85.382 |
| IG-CWT-CNN | 82.917 | 81.458 | 80.833 | 83.958 | 82.5 | 84.167 | 82.639 |
| TF-MDA | 85.833 | 85.208 | 83.542 | 86.875 | 86.667 | 87.927 | 86.009 |
| ICPW-HPF | 80.209 | 81.0417 | 79.583 | 82.917 | 78.333 | 82.083 | 80.694 |
| ML | 72.927 | 71.875 | 71.25 | 74.167 | 72.5 | 75.417 | 73.023 |
| JDA | 89.583 | 90.417 | 87.917 | 90.208 | 88.333 | 91.458 | 89.653 |
| TCA-DBN | 94.792 | 96.25 | 96.875 | 95.625 | 94.167 | 94.583 | 95.382 |
| DSAN | 98.958 | 99.167 | 98.958 | 98.542 | 96.875 | 99.792 | 98.715 |
| ITCA-DBN | 100 | 99.792 | 99.167 | 99.167 | 99.375 | 99.167 | 99.445 |
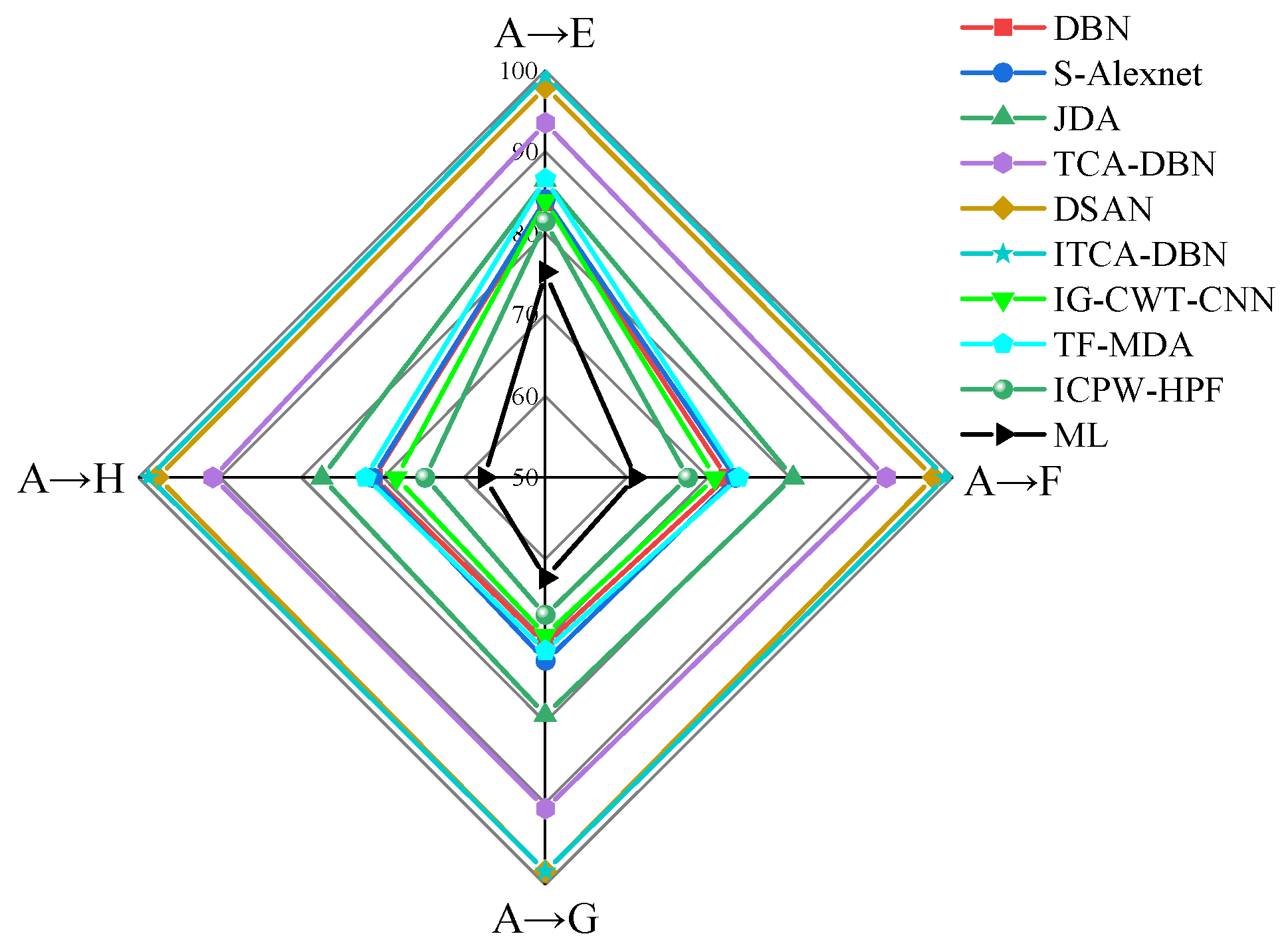
| Methods | A → E | A → F | A → G | A → H | Average Accuracy |
|---|---|---|---|---|---|
| DBN | 83.75 | 72.292 | 70.417 | 71.042 | 74.375 |
| S-Alexnet | 84.167 | 73.333 | 72.5 | 71.25 | 75.313 |
| IG-CWT-CNN | 83.958 | 70.833 | 69.375 | 68.333 | 73.125 |
| TF-MDA | 86.667 | 73.75 | 71.25 | 72.083 | 75.938 |
| ICPW-HPF | 81.458 | 67.5 | 66.875 | 64.792 | 70.156 |
| ML | 75.208 | 61.042 | 62.292 | 57.5 | 64.01 |
| JDA | 86.458 | 80.417 | 79.167 | 77.5 | 80.886 |
| TCA-DBN | 93.542 | 91.875 | 90.625 | 90.833 | 91.719 |
| DSAN | 97.917 | 97.708 | 98.333 | 97.708 | 97.916 |
| ITCA-DBN | 99.375 | 99.167 | 98.333 | 98.75 | 98.906 |
| Working Conditions | Rotational Speeds | Health Status |
|---|---|---|
| I | 500 r/min | Normal state Inner ring fault Rolling element fault Outer ring fault |
| J | 750 r/min | |
| K | 1000 r/min |
| Methods | I → J | I → K | J → K | Average Accuracy |
|---|---|---|---|---|
| DBN | 68.125 | 66.25 | 71.042 | 68.472 |
| S-Alexnet | 70.625 | 66.042 | 67.083 | 67.917 |
| IG-CWT-CNN | 67.292 | 66.875 | 65.417 | 66.528 |
| TF-MDA | 71.042 | 72.083 | 69.167 | 70.764 |
| ICPW-HPF | 64.792 | 63.75 | 62.292 | 63.611 |
| ML | 55.625 | 53.75 | 54.375 | 54.583 |
| JDA | 71.25 | 67.083 | 70.625 | 69.653 |
| TCA-DBN | 82.083 | 78.958 | 80.625 | 80.555 |
| DSAN | 86.875 | 84.167 | 88.125 | 86.389 |
| ITCA-DBN | 92.083 | 90.833 | 92.917 | 91.944 |
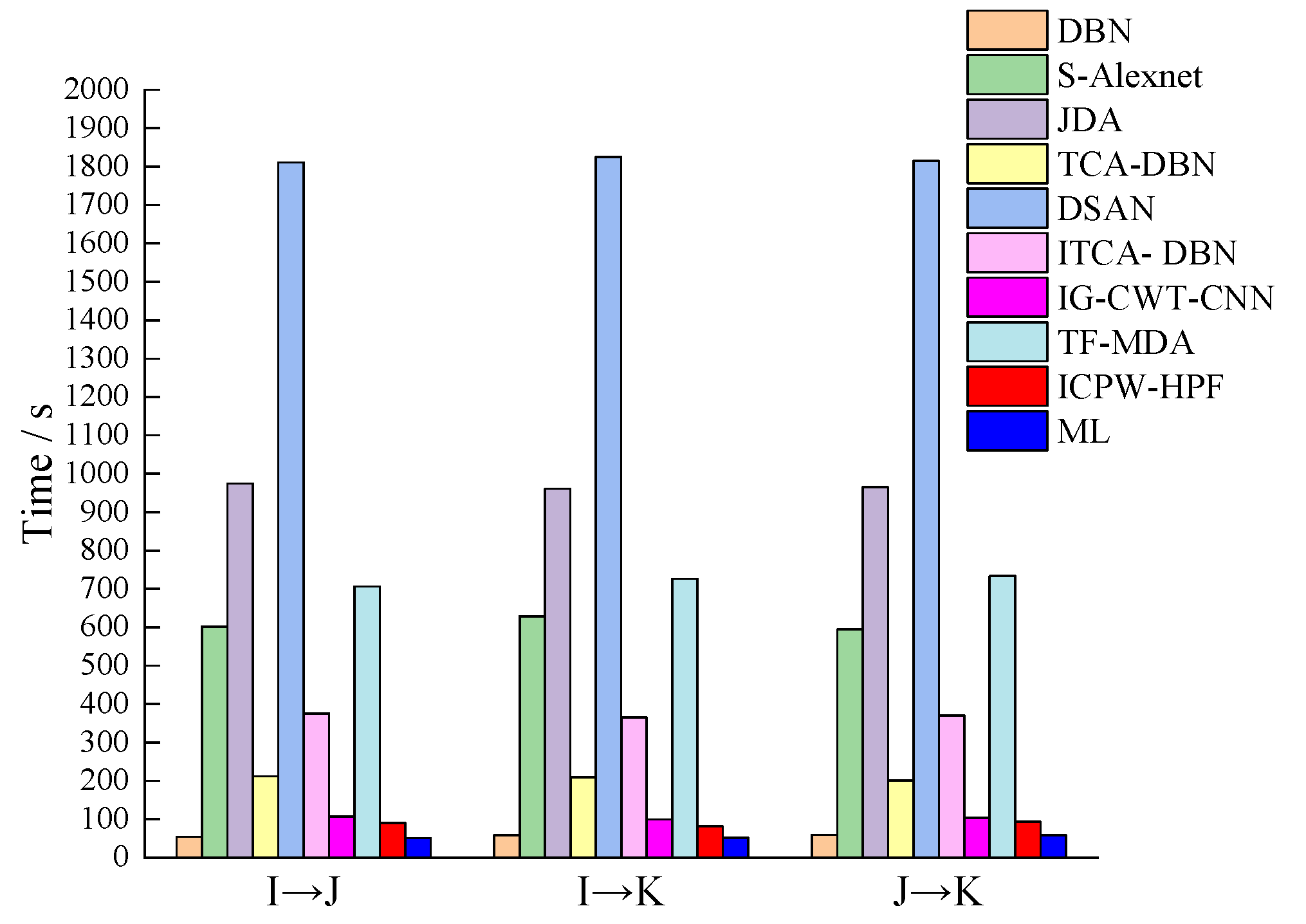
| Methods | I → J | I → K | J → K | Average Time |
|---|---|---|---|---|
| DBN | 54.3 | 58.7 | 59.6 | 57.5 |
| S-Alexnet | 601.6 | 628.4 | 594.5 | 608.7 |
| IG-CWT-CNN | 106.7 | 99.6 | 103.4 | 103.2 |
| TF-MDA | 706.6 | 726.5 | 733.8 | 722.3 |
| ICPW-HPF | 89.8 | 81.5 | 93.4 | 88.2 |
| ML | 50.9 | 51.3 | 58.8 | 53.7 |
| JDA | 974.5 | 961.2 | 965.2 | 967 |
| TCA-DBN | 212.3 | 209.7 | 200.7 | 207.6 |
| DSAN | 1811.2 | 1825.4 | 1814.3 | 1817 |
| ITCA-DBN | 375.6 | 364.9 | 370.7 | 370.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, D.; Ma, M. A Bearing Fault Diagnosis Method Based on Improved Transfer Component Analysis and Deep Belief Network. Appl. Sci. 2024, 14, 1973. https://doi.org/10.3390/app14051973
Li D, Ma M. A Bearing Fault Diagnosis Method Based on Improved Transfer Component Analysis and Deep Belief Network. Applied Sciences. 2024; 14(5):1973. https://doi.org/10.3390/app14051973
Chicago/Turabian StyleLi, Dalin, and Meiling Ma. 2024. "A Bearing Fault Diagnosis Method Based on Improved Transfer Component Analysis and Deep Belief Network" Applied Sciences 14, no. 5: 1973. https://doi.org/10.3390/app14051973
APA StyleLi, D., & Ma, M. (2024). A Bearing Fault Diagnosis Method Based on Improved Transfer Component Analysis and Deep Belief Network. Applied Sciences, 14(5), 1973. https://doi.org/10.3390/app14051973






