Hi-RCA: A Hierarchy Anomaly Diagnosis Framework Based on Causality and Correlation Analysis
Abstract
:1. Introduction
- Limitation by anomaly data volume. Most of the existing research adopts causal inference techniques to obtain the variables’ causality, which requires sufficient length of the anomaly data. However, in real situations, the anomaly duration is an uncontrollable variable. When anomaly data do not satisfy the requirements of causal inference methods, untrusted pseudo-causality will arise, which limits, or even worsens, the diagnosis performance.
- Over-simplification of metric relationships. Since the relationship between diverse monitored metrics is complex, causation and correlation exist simultaneously. Existing research oversimplifies the metric relationship either as causation or correlation. In fact, correlation does not imply causation.
- Lack of diagnosing interpretability. Under multiple anomaly types and anomaly cascading, anomaly symptoms are diverse; hence, interpretability for the diagnosis results is important. Anomaly diagnosis requires not only locating the root cause, but also explaining the logic behind anomaly symptoms. For example, a CPU hog occurs at a microservice, causing both CPU metrics and memory metrics to increase. Without the explanation of anomaly symptoms, i.e., the original CPU anomaly propagates to memory, engineers may not trust the diagnosis results, because memory can also be a possible cause.
- We propose a general anomaly evaluator using Kalman filtering, which requires no expert knowledge and is general for various metrics with different characteristics.
- We use the intervention recognition task to identify anomalous metrics, to avoid the causal inference performance being limited by anomaly data distribution, which utilizes the causation change in metrics for accurate anomaly diagnosis.
- We analyze the causation and correlation separately. We characterize anomaly symptoms from the global perspective where all metrics are considered jointly. Based on the correlation-based anomaly knowledge graph, diverse anomaly symptoms can be explained.
2. Related Work
3. Model
3.1. Problem Formulation
3.2. System Framework
3.3. Anomalous Microservice Locator
3.4. Anomalous Reason Diagnoser
4. Experiment
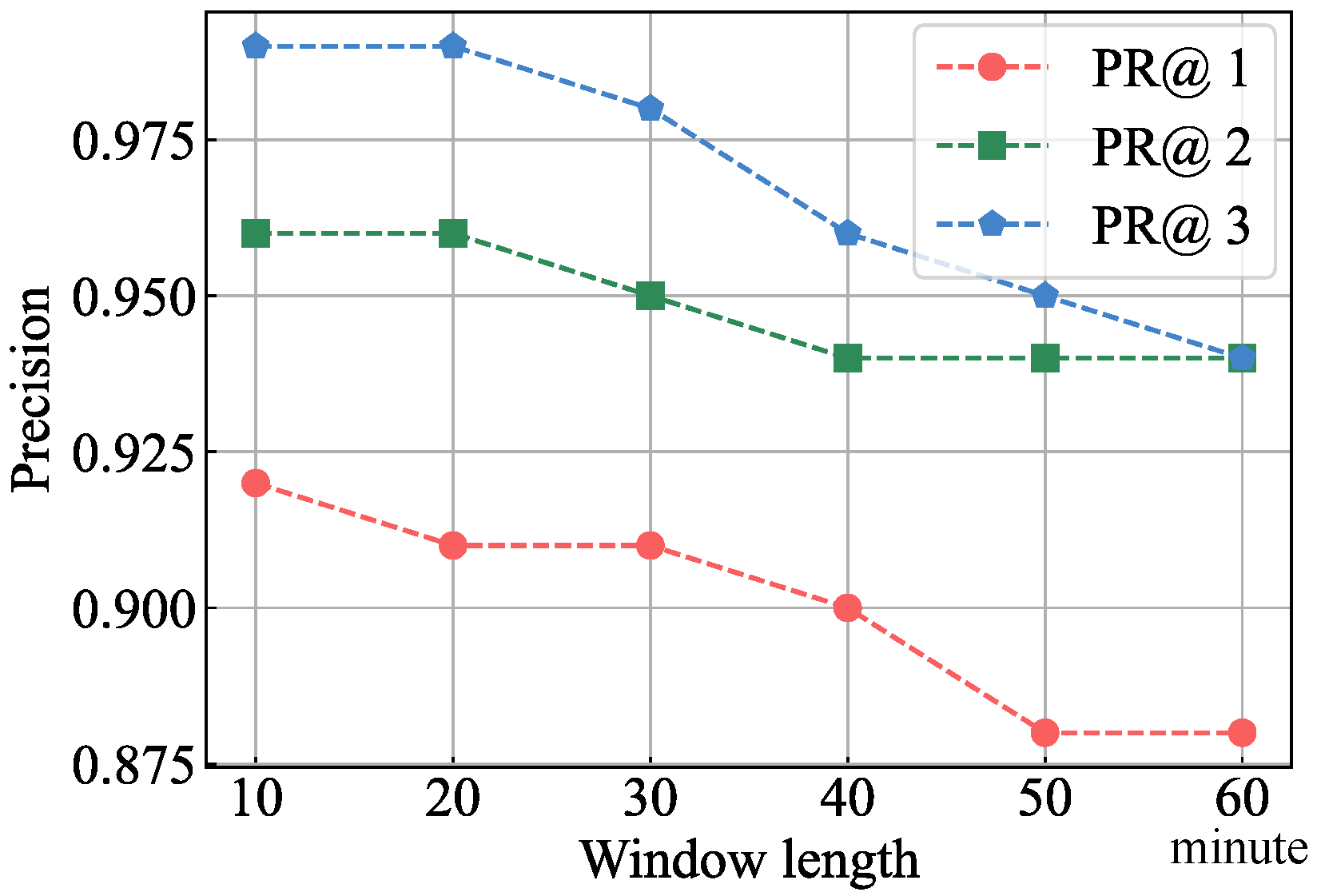
4.1. Experiment Setup
4.2. Evaluation of Anomalous Microservice Locator
- Quantile anomaly detector [47] compares each time series value with historical quantiles. In our experiment, we detect anomalies if their value is above 99% or below 1%.
- Level-shift anomaly detector [47] detects a shift of value level by tracking the difference between median values at two sliding time windows next to each other.
- Cauchy detector [48] detects an anomaly by comparing the current value and the history-smoothed value in a sliding window.
4.3. Evaluation of Hi-RCA
- MicroDiag [30]: MicroDiag locates the culprit metric based on the metric’s causality graph. It identifies the potential propagation among components first, considers different methods of anomaly propagation, and uses two types of causal inference methods to construct the propagation graph among different components and metrics. The root cause metric is localized based on the PageRank algorithm of the causality graph.
- MicroDiag-V1: Since MicroDiag directly locates the root cause metric from diverse components, to eliminate the distractions of diverse microservices, we implement it in a simplified scenario where the anomalous microservice has been located, to compare the effectiveness of MicroDiag.
- Loud [8]: Loud localizes the culprit metrics based on a propagation graph of anomalous metrics. The graph is constructed by the Granger causality test of metrics. To implement Loud, the anomalous metrics are chosen by the Cauchy Detector [48], the propagation graph is built using the Granger test, and the root cause is located based on the PageRank result of the propagated graph with weighted edges.
- Cauchy [48]: An anomaly detector that can quantify the time series abnormality and detects an anomaly by comparing the current value and the history-smoothed value in a sliding window. We compute all metrics’ Cauchy anomaly scores and locate the metric with the highest anomaly score as the root cause. Cauchy is chosen as a baseline to show the result where metrics are observed in isolation, regardless of the association between them.
- Random Selection (RS): Random selection is a method engineers use when lacking domain-specific knowledge of the system. Every time, they randomly select an unchecked metric to investigate until the root cause is found.
- Hi-RCA-w/o-1: Hi-RCA algorithm without the causal inference, i.e., the anomaly knowledge graph is constructed as a static knowledge graph manually, not from the intervention recognition task used in Hi-RCA. Then, the reason for the anomaly is inferred based on the graph comparison between CPG and the static knowledge graph.
- Hi-RCA-w/o-2: Hi-RCA algorithm with a variant version of the Anomalous Reason Diagnoser, instead of the graph comparison method. The root cause is located based on the PageRank algorithm [49] in the CPG where nodes are the anomaly metrics and edges denote their dependencies.
4.4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Butzin, B.; Golatowski, F.; Timmermann, D. Microservices approach for the internet of things. In Proceedings of the IEEE 21st International Conference on Emerging Technologies and Factory Automation (ETFA), Berlin, Germany, 6–9 September 2016; pp. 1–6. [Google Scholar]
- Di Francesco, P.; Malavolta, I.; Lago, P. Research on architecting microservices: Trends, focus, and potential for industrial adoption. In Proceedings of the IEEE International Conference on Software Architecture (ICSA), Gothenburg, Sweden, 3–7 April 2017; pp. 21–30. [Google Scholar]
- Newman, S. Building Microservices; O’Reilly Media, Inc.: Sebastopol, CA, USA, 2021. [Google Scholar]
- Wang, P.; Xu, J.; Ma, M.; Lin, W.; Pan, D.; Wang, Y.; Chen, P. Cloudranger: Root cause identification for cloud native systems. In Proceedings of the 18th IEEE/ACM International Symposium on Cluster, Cloud and Grid Computing (CCGRID), Washington, DC, USA, 1–4 May 2018; pp. 492–502. [Google Scholar]
- Ma, M.; Lin, W.; Pan, D.; Wang, P. Ms-rank: Multi-metric and self-adaptive root cause diagnosis for microservice applications. In Proceedings of the IEEE International Conference on Web Services (ICWS), Milan, Italy, 8–13 July 2019; pp. 60–67. [Google Scholar]
- Ma, M.; Xu, J.; Wang, Y.; Chen, P.; Zhang, Z.; Wang, P. Automap: Diagnose your microservice-based web applications automatically. In Proceedings of the Web Conference 2020, Taipei, Taiwan, 20–24 April 2020; pp. 246–258. [Google Scholar]
- Lin, J.; Chen, P.; Zheng, Z. Microscope: Pinpoint performance issues with causal graphs in micro-service environments. In Proceedings of the Service-Oriented Computing: 16th International Conference—ICSOC 2018, Hangzhou, China, 12–15 November 2018; pp. 3–20. [Google Scholar]
- Mariani, L.; Monni, C.; Pezzé, M.; Riganelli, O.; Xin, R. Localizing faults in cloud systems. In Proceedings of the IEEE 11th International Conference on Software Testing, Verification and Validation (ICST), Västerås, Sweden, 9–13 April 2018; pp. 262–273. [Google Scholar]
- Wu, L.; Tordsson, J.; Elmroth, E.; Kao, O. Microrca: Root cause localization of performance issues in microservices. In Proceedings of the NOMS 2020–2020 IEEE/IFIP Network Operations and Management Symposium, Budapest, Hungary, 20–24 April 2020; pp. 1–9. [Google Scholar]
- Wu, L.; Bogatinovski, J.; Nedelkoski, S.; Tordsson, J.; Kao, O. Performance diagnosis in cloud microservices using deep learning. In Proceedings of the International Conference on Service-Oriented Computing, Dubai, United Arab Emirates, 14 December 2020; pp. 85–96. [Google Scholar]
- Samir, A.; Pahl, C. DLA: Detecting and localizing anomalies in containerized microservice architectures using markov models. In Proceedings of the 7th International Conference on Future Internet of Things and Cloud (FiCloud), Istanbul, Turkey, 26–28 August 2019; pp. 205–213. [Google Scholar]
- Su, Y.; Zhao, Y.; Xia, W.; Liu, R.; Bu, J.; Zhu, J.; Cao, Y.; Li, H.; Niu, C.; Zhang, Y.; et al. Coflux: Robustly correlating kpis by fluctuations for service troubleshooting. In Proceedings of the International Symposium on Quality of Service, Phoenix, AZ, USA, 24–25 June 2019; pp. 1–10. [Google Scholar]
- Shang, Z.; Zhang, Y.; Zhang, X.; Zhao, Y.; Cao, Z.; Wang, X. Time series anomaly detection for kpis based on correlation analysis and hmm. Appl. Sci. 2021, 11, 11353. [Google Scholar] [CrossRef]
- Eddy, S.R. Hidden markov models. Curr. Opin. Struct. Biol. 1996, 6, 361–365. [Google Scholar] [CrossRef] [PubMed]
- Shan, H.; Chen, Y.; Liu, H.; Zhang, Y.; Xiao, X.; He, X.; Li, M.; Ding, W. ?-Diagnosis: Unsupervised and real-time diagnosis of small-window long-tail latency in large-scale microservice platforms. In Proceedings of the World Wide Web Conference, San Francisco, CA, USA, 13–17 May 2019; pp. 3215–3222. [Google Scholar]
- Candès, E.J.; Li, X.; Ma, Y.; Wright, J. Robust principal component analysis? J. ACM 2011, 58, 1–37. [Google Scholar] [CrossRef]
- Mi, H.; Wang, H.; Zhou, Y.; Lyu, M.R.; Cai, H. Toward fine-grained, unsupervised, scalable performance diagnosis for production cloud computing systems. IEEE Trans. Parallel Distrib. Syst. 2013, 24, 1245–1255. [Google Scholar] [CrossRef]
- Nguyen, H.; Tan, Y.; Gu, X. Pal: P ropagation-aware a nomaly l ocalization for cloud hosted distributed applications. In Managing Large-Scale Systems via the Analysis of System Logs and the Application of Machine Learning Techniques; Association for Computing Machinery: New York, NY, USA, 2011; pp. 1–8. [Google Scholar]
- Nguyen, H.; Shen, Z.; Tan, Y.; Gu, X. Fchain: Toward black-box online fault localization for cloud systems. In Proceedings of the IEEE 33rd International Conference on Distributed Computing Systems, Philadelphia, PA, USA, 8–11 July 2013; pp. 21–30. [Google Scholar]
- Nedelkoski, S.; Cardoso, J.; Kao, O. Anomaly detection and classification using distributed tracing and deep learning. In Proceedings of the 19th IEEE/ACM international symposium on cluster, cloud and grid computing (CCGRID), Larnaca, Cyprus, 14–17 May 2019; pp. 241–250. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Gan, Y.; Zhang, Y.; Hu, K.; Cheng, D.; He, Y.; Pancholi, M.; Delimitrou, C. Seer: Leveraging big data to navigate the complexity of performance debugging in cloud microservices. In Proceedings of the 24th International Conference on Architectural Support for Programming Languages and Operating Systems, Providence, RI, USA, 13–17 April 2019; pp. 19–33. [Google Scholar]
- Scheinert, D.; Acker, A.; Thamsen, L.; Geldenhuys, M.K.; Kao, O. Learning dependencies in distributed cloud applications to identify and localize anomalies. In Proceedings of the IEEE/ACM International Workshop on Cloud Intelligence (CloudIntelligence), Madrid, Spain, 29–29 May 2021; pp. 7–12. [Google Scholar]
- Gan, Y.; Liang, M.; Dev, S.; Lo, D.; Delimitrou, C. Sage: Practical and scalable ml-driven performance debugging in microservices. In Proceedings of the 26th ACM International Conference on Architectural Support for Programming Languages and Operating Systems, Virtual, 19–23 April 2021; pp. 135–151. [Google Scholar]
- Deng, A.; Hooi, B. Graph neural network-based anomaly detection in multivariate time series. Proc. AAAI Conf. Artif. Intell. 2021, 35, 4027–4035. [Google Scholar] [CrossRef]
- Dean, D.J.; Nguyen, H.; Gu, X. UBL: Unsupervised behavior learning for predicting performance anomalies in virtualized cloud systems. In Proceedings of the 9th International Conference on Autonomic Computing, San Jose, CA, USA, 18–20 September 2012; pp. 191–200. [Google Scholar]
- Lin, W.; Ma, M.; Pan, D.; Wang, P. Facgraph: Frequent anomaly correlation graph mining for root cause diagnose in micro-service architecture. In Proceedings of the IEEE 37th International Performance Computing and Communications Conference (IPCCC), Orlando, FL, USA, 17–19 November 2018; pp. 1–8. [Google Scholar]
- Spirtes, P.; Glymour, C.N.; Scheines, R. Causation, Prediction, and Search; MIT Press: Cambridge, MA, USA, 2000. [Google Scholar]
- Wu, L.; Tordsson, J.; Bogatinovski, J.; Elmroth, E.; Kao, O. Microdiag: Fine-grained performance diagnosis for microservice systems. In Proceedings of the IEEE/ACM International Workshop on Cloud Intelligence (CloudIntelligence), Madrid, Spain, 29 May 2021; pp. 31–36. [Google Scholar]
- Shimizu, S.; Inazumi, T.; Sogawa, Y.; Hyvarinen, A.; Kawahara, Y.; Washio, T.; Hoyer, P.O.; Bollen, K.; Hoyer, P. Directlingam: A direct method for learning a linear non-gaussian structural equation model. J. Mach. Learn. Res.-JMLR 2011, 12, 1225–1248. [Google Scholar]
- Granger, C.W.J. Investigating causal relations by econometric models and cross-spectral methods. Econom. J. Econom. Soc. 1969, 37, 424–438. [Google Scholar] [CrossRef]
- Meng, Y.; Zhang, S.; Sun, Y.; Zhang, R.; Hu, Z.; Zhang, Y.; Jia, C.; Wang, Z.; Pei, D. Localizing failure root causes in a microservice through causality inference. In Proceedings of the IEEE/ACM 28th International Symposium on Quality of Service (IWQoS), Hangzhou, China, 15–17 June 2020; pp. 1–10. [Google Scholar]
- Qiu, J.; Du, Q.; Yin, K.; Zhang, S.; Qian, C. A causality mining and knowledge graph based method of root cause diagnosis for performance anomaly in cloud applications. Appl. Sci. 2020, 10, 2166. [Google Scholar] [CrossRef]
- Nie, X.; Zhao, Y.; Sui, K.; Pei, D.; Chen, Y.; Qu, X. Mining causality graph for automatic web-based service diagnosis. In Proceedings of the IEEE 35th International Performance Computing and Communications Conference (IPCCC), Las Vegas, NV, USA, 9–11 December 2016; pp. 1–8. [Google Scholar]
- Ma, M.; Lin, W.; Pan, D.; Wang, P. Servicerank: Root cause identification of anomaly in large-scale microservice architectures. IEEE Trans. Dependable Secur. Comput. 2021, 19, 3087–3100. [Google Scholar] [CrossRef]
- Chen, P.; Qi, Y.; Zheng, P.; Hou, D. Causeinfer: Automatic and distributed performance diagnosis with hierarchical causality graph in large distributed systems. In Proceedings of the IEEE INFOCOM 2014-IEEE Conference on Computer Communications, Toronto, ON, Canada, 27 April–2 May 2014; pp. 1887–1895. [Google Scholar]
- Kim, M.; Sumbaly, R.; Shah, S. Root cause detection in a service-oriented architecture. ACM Sigmetrics Perform. Eval. Rev. 2013, 41, 93–104. [Google Scholar] [CrossRef]
- Liu, D.; He, C.; Peng, X.; Lin, F.; Zhang, C.; Gong, S.; Li, Z.; Ou, J.; Wu, Z. Microhecl: High-efficient root cause localization in large-scale microservice systems. In Proceedings of the IEEE/ACM 43rd International Conference on Software Engineering: Software Engineering in Practice (ICSE-SEIP), Madrid, Spain, 25–28 May 2021; pp. 338–347. [Google Scholar]
- Liu, P.; Zhang, S.; Sun, Y.; Meng, Y.; Yang, J.; Pei, D. Fluxinfer: Automatic diagnosis of performance anomaly for online database system. In Proceedings of the IEEE 39th International Performance Computing and Communications Conference (IPCCC), Austin, TX, USA, 6–8 November 2020; pp. 1–8. [Google Scholar]
- Chui, C.K.; Chen, G. Kalman filtering with real time applications. Appl. Opt. 1989, 28, 1841. [Google Scholar]
- Bareinboim, E.; Correa, J.D.; Ibeling, D.; Icard, T. On pearl’s hierarchy and the foundations of causal inference. In Probabilistic and Causal Inference: The Works of Judea Pearl; Association for Computing Machinery: New York, NY, USA, 2022; pp. 507–556. [Google Scholar]
- Zelterman, D. Causality: Models, Reasoning, and Inference; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Li, M.; Li, Z.; Yin, K.; Nie, X.; Zhang, W.; Sui, K.; Pei, D. Causal inference-based root cause analysis for online service systems with intervention recognition. In Proceedings of the 28th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, 14–18 August 2022; pp. 3230–3240. [Google Scholar]
- AIOps Challenge 2022. Available online: https://competition.aiops-challenge.com/home/competition (accessed on 1 September 2023).
- Hipster-Shop with OpenTelemetry. Available online: https://github.com/yuxiaoba/Hipster-Shop (accessed on 1 September 2023).
- ADTK. Available online: https://adtk.readthedocs.io/en/stable (accessed on 1 September 2023).
- Cao, W.; Gao, Y.; Lin, B.; Feng, X.; Xie, Y.; Lou, X.; Wang, P. Tcprt: Instrument and diagnostic analysis system for service quality of cloud databases at massive scale in real-time. In Proceedings of the 2018 International Conference on Management of Data, Houston, TX, USA, 10–15 June 2018; pp. 615–627. [Google Scholar]
- Page, L. The Pagerank Citation Ranking: Bringing Order to the Web. In Stanford Digital Library Technologies Project; Technical Report; University of Pennsylvania: Philadelphia, PA, USA, 1998. [Google Scholar]
- Montella, C. The Kalman filter and related algorithms: A literature review. Res. Gate 2011, 1–17. [Google Scholar]


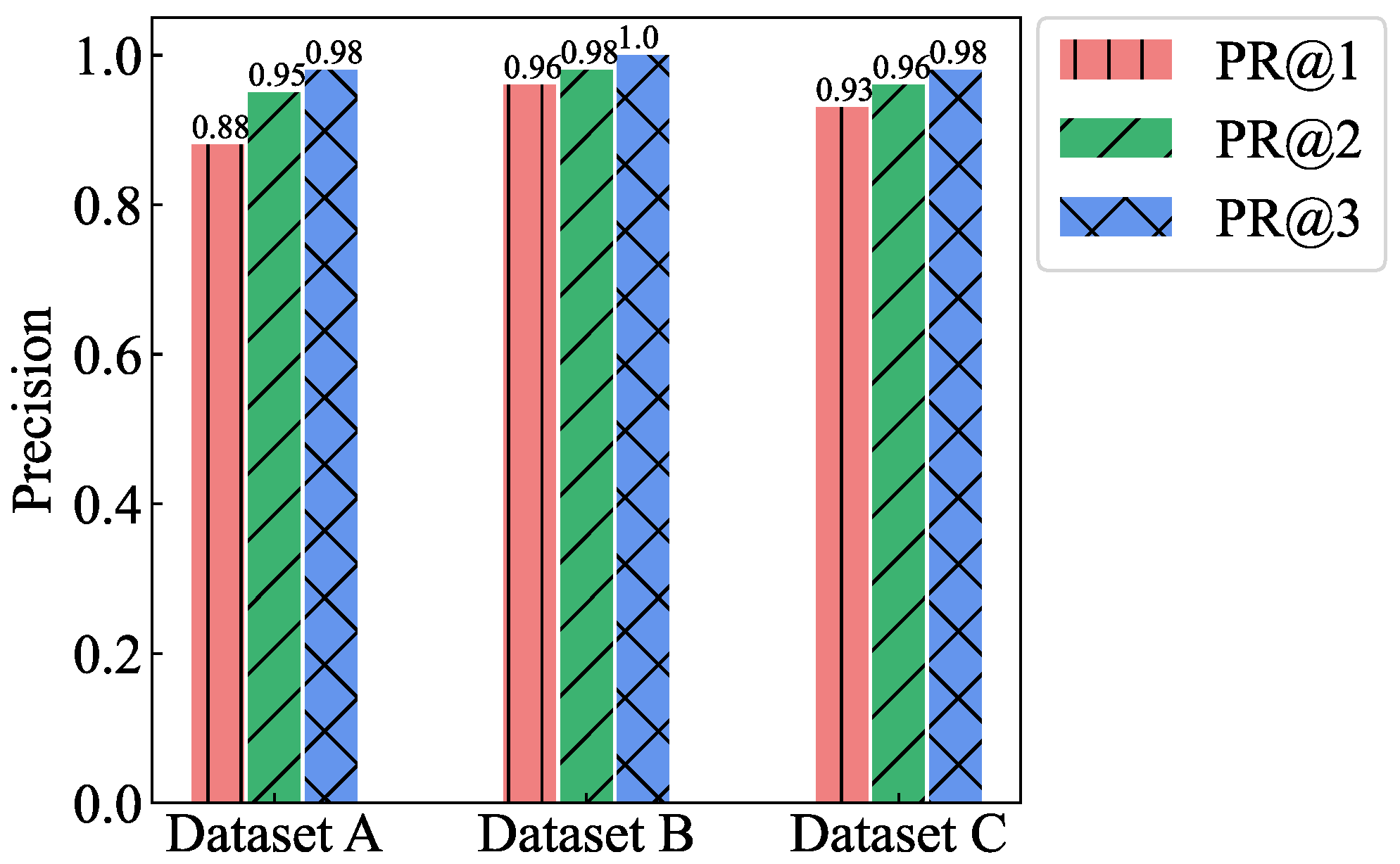

| Method | Dataset A | Dataset B | Dataset C | ||||||
|---|---|---|---|---|---|---|---|---|---|
| PR@1 | PR@2 | PR@3 | PR@1 | PR@2 | PR@3 | PR@1 | PR@2 | PR@3 | |
| Quantile | 0.25 | 0.29 | 0.37 | 0.26 | 0.42 | 0.48 | 0.27 | 0.31 | 0.35 |
| Level-shift | 0.66 | 0.76 | 0.78 | 0.82 | 0.84 | 0.90 | 0.71 | 0.80 | 0.85 |
| Cauchy | 0.73 | 0.86 | 0.90 | 0.84 | 0.96 | 0.96 | 0.82 | 0.87 | 0.89 |
| Kalman filtering | 0.88 | 0.95 | 0.98 | 0.96 | 0.98 | 1.0 | 0.93 | 0.96 | 0.98 |
| Method | Dataset A | Dataset B | Dataset C | ||||||
|---|---|---|---|---|---|---|---|---|---|
| PR@1 | PR@2 | PR@3 | PR@1 | PR@2 | PR@3 | PR@1 | PR@2 | PR@3 | |
| RS | 0.03 | 0.08 | 0.19 | 0.14 | 0.14 | 0.18 | 0.05 | 0.15 | 0.18 |
| Loud | 0.29 | 0.34 | 0.39 | 0.18 | 0.34 | 0.38 | 0.31 | 0.36 | 0.38 |
| Cauchy | 0.15 | 0.2 | 0.24 | 0.14 | 0.16 | 0.18 | 0.11 | 0.16 | 0.24 |
| MicroDiag | 0.22 | 0.46 | 0.64 | 0.24 | 0.48 | 0.66 | 0.22 | 0.53 | 0.76 |
| MicroDiag-V1 | 0.27 | 0.54 | 0.71 | 0.22 | 0.38 | 0.6 | 0.22 | 0.45 | 0.84 |
| Hi-RCA | 0.75 | 0.85 | 0.88 | 0.86 | 0.89 | 0.98 | 0.76 | 0.8 | 0.89 |
| Hi-RCA-w/o-1 | 0.75 | 0.75 | 0.85 | 0.82 | 0.90 | 0.92 | 0.73 | 0.78 | 0.82 |
| Hi-RCA-w/o-2 | 0.07 | 0.25 | 0.32 | 0.2 | 0.32 | 0.38 | 0.11 | 0.25 | 0.29 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, J.; Guo, Y.; Chen, Y.; Zhao, Y. Hi-RCA: A Hierarchy Anomaly Diagnosis Framework Based on Causality and Correlation Analysis. Appl. Sci. 2023, 13, 12126. https://doi.org/10.3390/app132212126
Yang J, Guo Y, Chen Y, Zhao Y. Hi-RCA: A Hierarchy Anomaly Diagnosis Framework Based on Causality and Correlation Analysis. Applied Sciences. 2023; 13(22):12126. https://doi.org/10.3390/app132212126
Chicago/Turabian StyleYang, Jingjing, Yuchun Guo, Yishuai Chen, and Yongxiang Zhao. 2023. "Hi-RCA: A Hierarchy Anomaly Diagnosis Framework Based on Causality and Correlation Analysis" Applied Sciences 13, no. 22: 12126. https://doi.org/10.3390/app132212126
APA StyleYang, J., Guo, Y., Chen, Y., & Zhao, Y. (2023). Hi-RCA: A Hierarchy Anomaly Diagnosis Framework Based on Causality and Correlation Analysis. Applied Sciences, 13(22), 12126. https://doi.org/10.3390/app132212126





