Multi-Objective Optimization of Cyclone Separators Based on Geometrical Parameters for Performance Enhancement
Abstract
1. Introduction
2. Mathematical Modeling
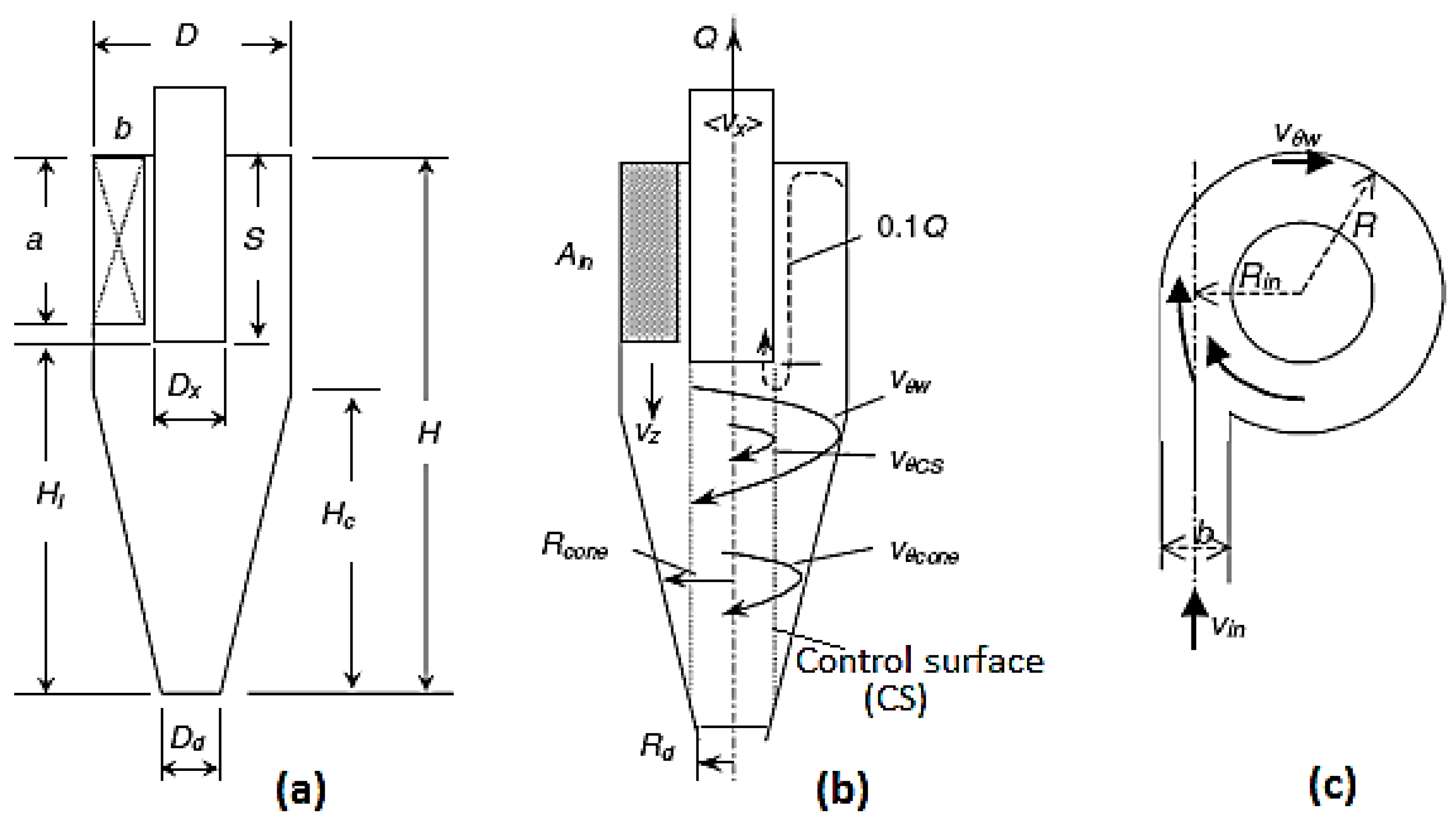
2.1. The Geometric Details
2.2. Muschelknautz Model
- (a)
- The wall roughness.
- (b)
- The variation in the feed of the particle size distribution.
- (c)
- The solid particle loading.
2.2.1. Prediction of the Pressure Drop
2.2.2. Prediction of the Cut-Off Size
2.3. Genetic Algorithms
2.4. Computational Fluid Dynamics
2.4.1. Continuous Phase
Large Eddy Simulation
Modeling the Particulate Phase
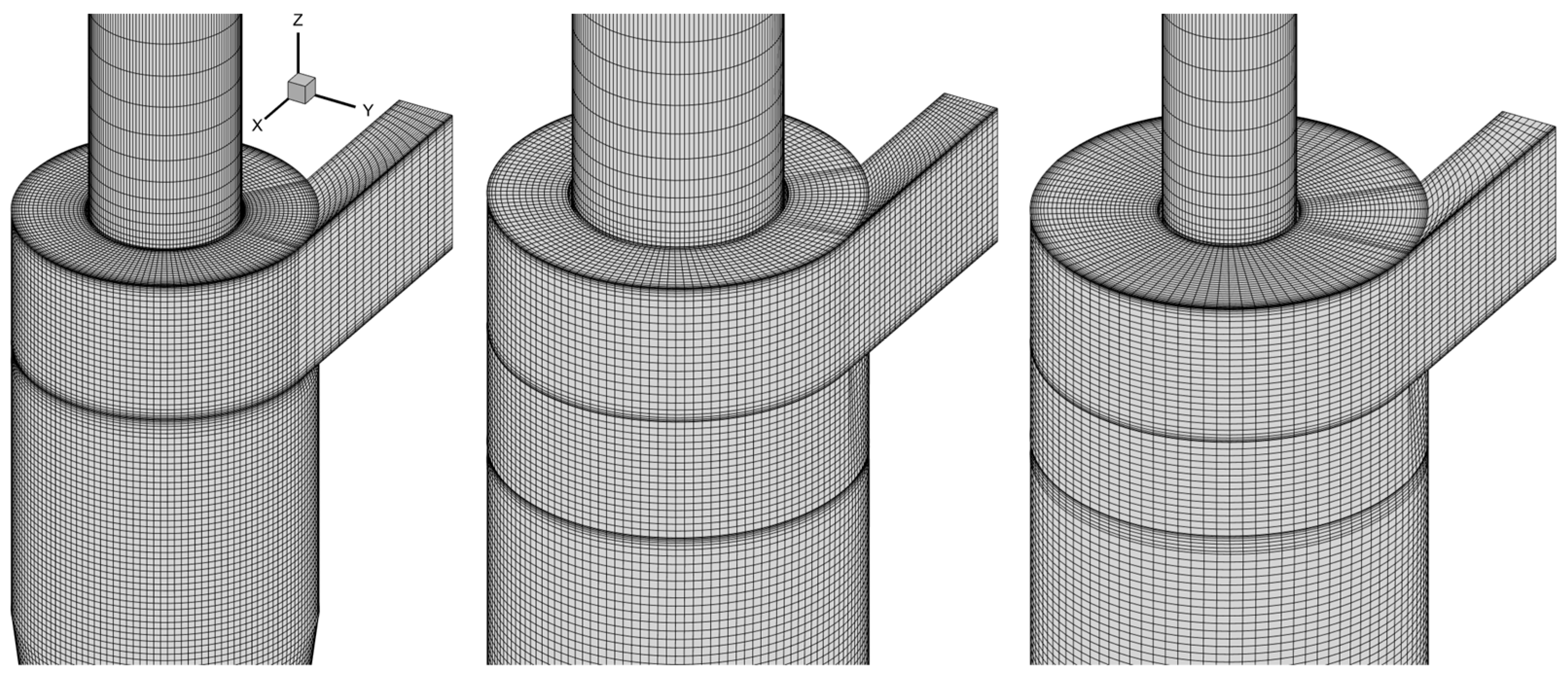
Meshing
Numerical Settings
Settings for the Genetic Algorithm
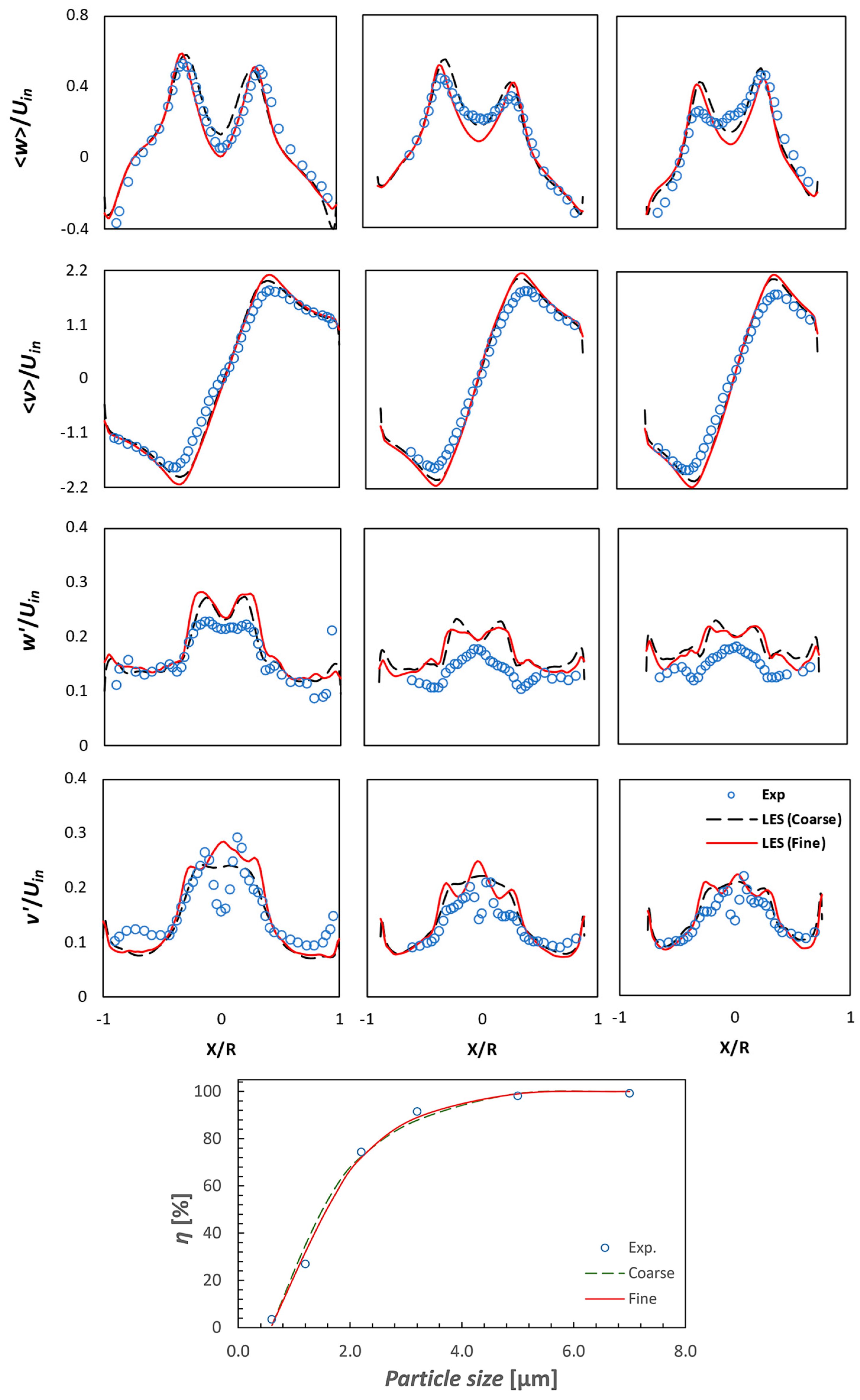
2.5. Validation
3. Results and Discussion
3.1. Pareto Front Points
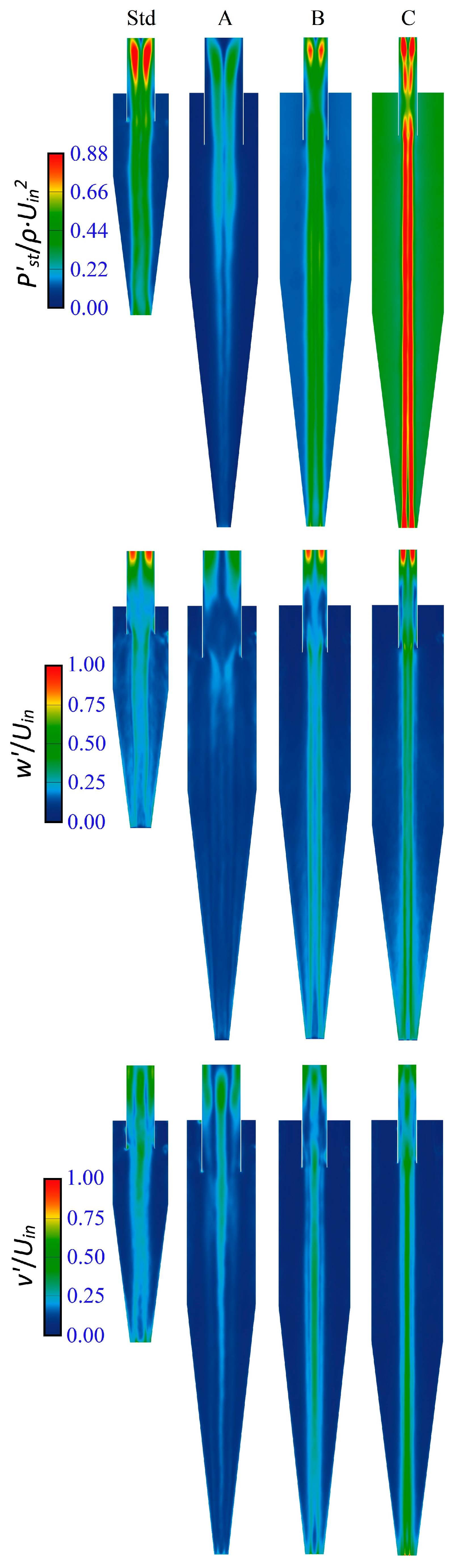
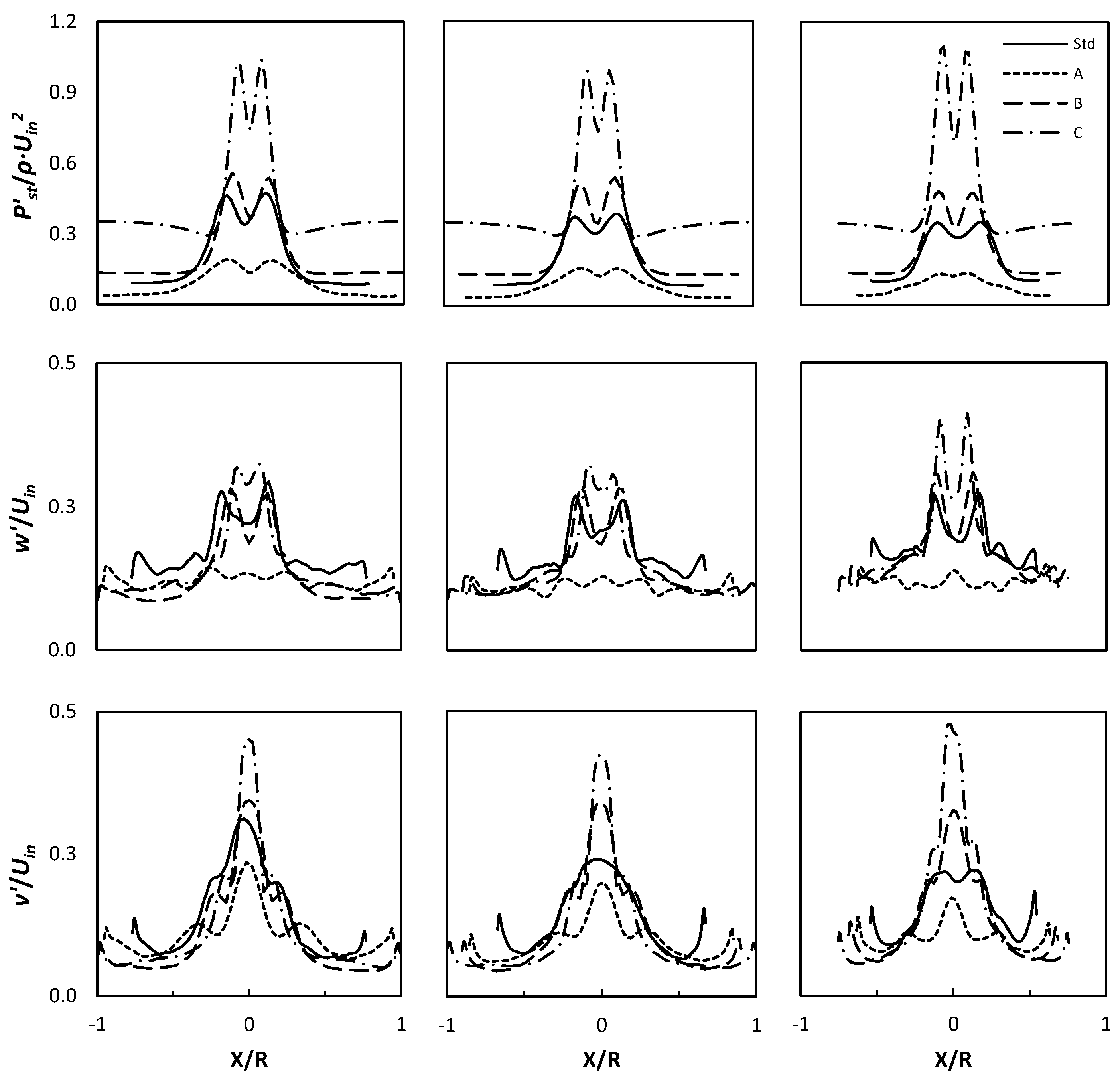
3.1.1. Mean Flow Field
3.1.2. Fluctuating Flow Field
3.1.3. Vortex Core Representation
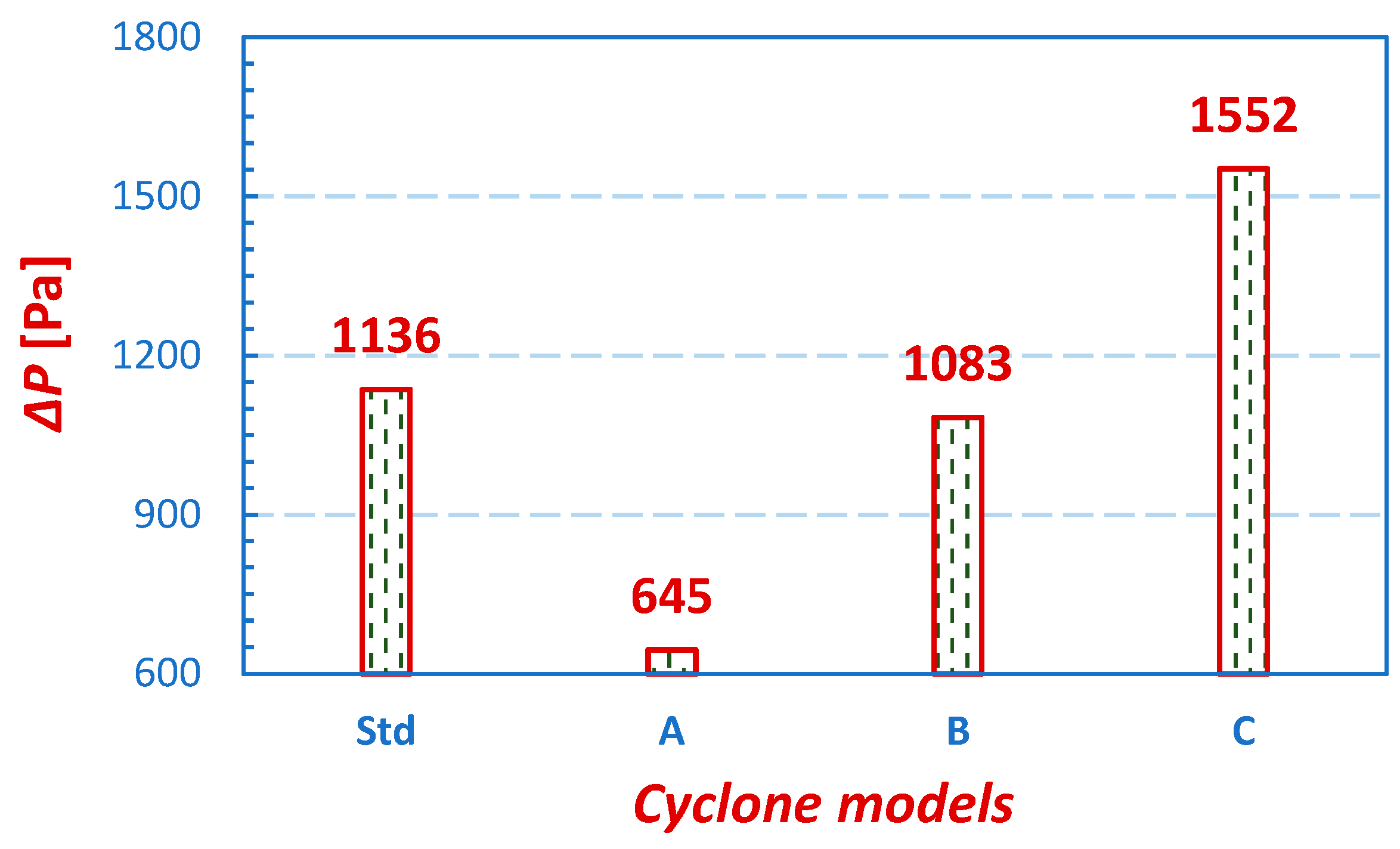
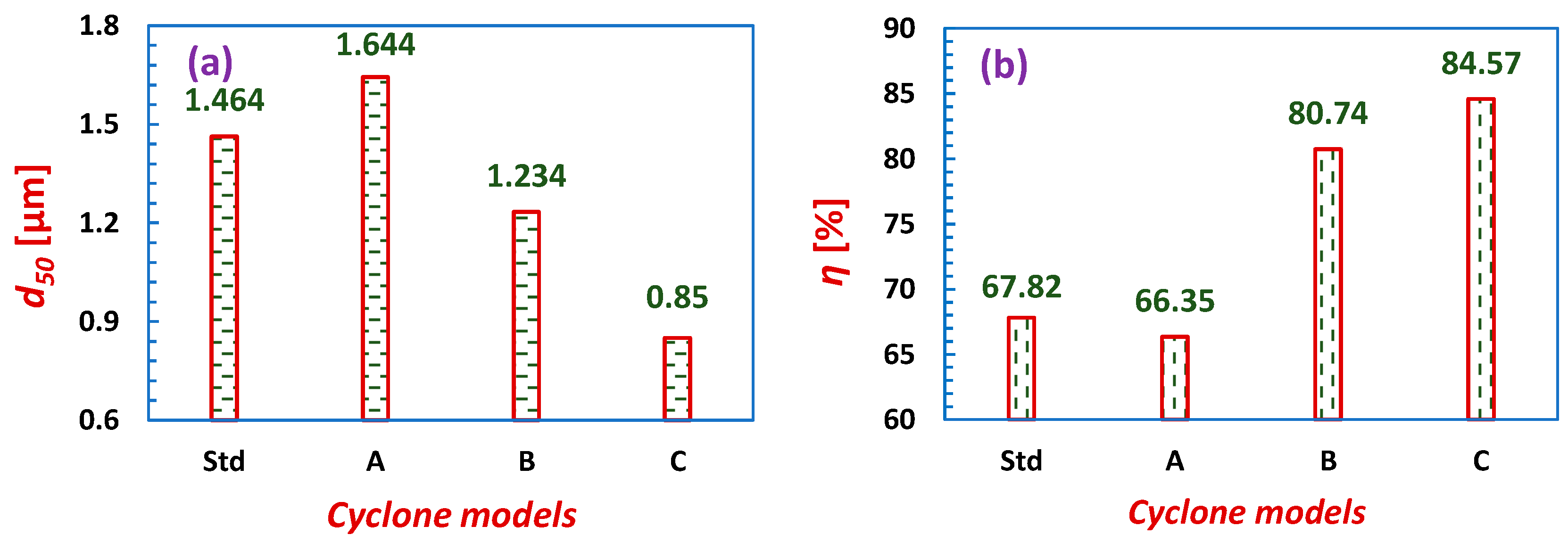
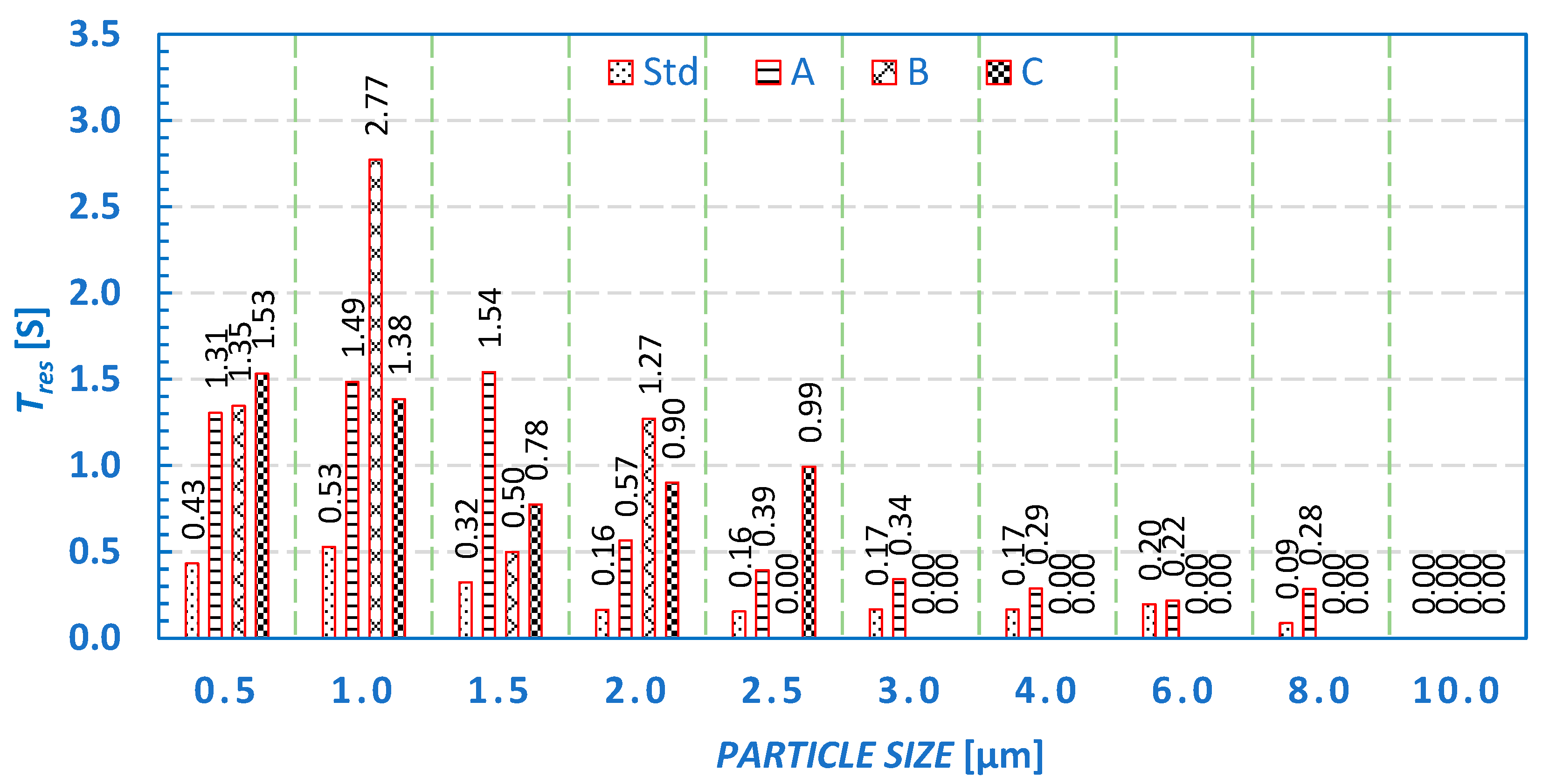
3.1.4. Cyclone Performance
4. Conclusions
- In cyclone model A, the pressure losses decreased significantly by 43.22%, with a marginal reduction of 2.16% in the overall collection efficiency and an increase in the cut-off size by 12.3%.
- In model B, with a reduction in the pressure drop by 4.67%, cut-off sizes decreased by 15.71%, with a 19.05% enhancement in the collection efficiency.
- In Model C, with an increase in the pressure drop by 36.62%, the cut-off size decreased by 41.94%, and the collection efficiency increased by 24.69%.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| a | height of the cyclone inlet |
| A | inlet area of the cyclone |
| b | width of the cyclone inlet |
| Bc | cone tip diameter of the cyclone |
| CD | drag force coefficient |
| Cs | Smagorinsky constant |
| dp | particle diameter |
| d50 | cut-off size |
| D | diameter of the standard cyclone model/characteristic diameter |
| Dc | (optimized) cyclone diameter |
| DL,ij | molecular diffusive transport term |
| DT,ij | turbulent diffusive transport term |
| Dx | vortex finder diameter |
| f | frequency of oscillation of the PVC |
| Fi | additional forces per unit mass |
| FD | drag force |
| g | gravitational accelerations |
| Hc | length of the cylindrical segment of the cyclone |
| k | von Kármán constant |
| l | characteristic length |
| Ls | length scale of subgrid-scales |
| Lv, S | insertion length of the vortex finder diameter inside the cyclone |
| mp | particle mass |
| p | instantaneous gas static pressure |
| P | mean static pressure of the gas |
| p0 | pressure at the symmetric axis |
| p’ | fluctuating gas pressure |
| resolved static pressure | |
| ∆P | differential pressure measurement |
| Pij | stress generation term |
| Q | the volume flow rate of air |
| R | the radius of the cyclone body |
| Re | Reynolds number |
| S | vortex finder insertion length |
| Sw | geometric swirl number |
| t | time |
| tη | the time scale for smaller eddies |
| TL | Lagrangian integral time scale |
| u | characteristic velocity |
| ui | velocity vector in the i-coordinate direction/instantaneous velocity |
| the mean velocity component | |
| the fluctuating velocity component | |
| particle velocity | |
| U | mean gas velocity |
| V | the volume of a cell |
| vθ | tangential velocity |
| xi | position in the i-direction |
| f | friction factor |
| ρ | gas density |
| Q | volume flow rate |
| velocity at the wall | |
| tangential velocity of the rotating fluid in the inner core radius | |
| AR | the total inside surface area |
| average axial velocity of the gas exiting via the vortex finder | |
| vin | gas velocity at the inlet |
| density of the particulate phase | |
| µ | fluid viscosity |
| Ht | cyclone length |
| S | Insertion depth of the outlet tube |
| µsgs | sub-grid scale viscosity |
| velocity of the particle | |
| acceleration due to gravity | |
| additional forces (e.g., the Saffman lift force, Brownian force, etc.) | |
| Rep | Reynolds number of the particle |
| Tres | residence time |
Appendix A
Appendix A.1. Modeling Pressure Drop and Cut-Off Size Using the Muschelknautz Method (MM) of Modeling
Appendix A.1.1. Evaluating the Pressure Drop Inside a Cyclone
Appendix A.1.2. Evaluating the Cut-Off Diameter of a Cyclone
References
- Stewart, B.W.; Kleihues, P. World Cancer Report; IARC Press: Lyon, France, 2003. [Google Scholar]
- Kloog, B.; Ridgway, P.; Koutrakis, B.; Coull, A.; Schwartz, J.D. Long- and short-term exposure to PM2.5 and mortality. Epidemiology 2013, 24, 555–561. [Google Scholar] [CrossRef]
- Knibbs, L.D.; Cole-Hunter, T.; Morawska, L. A review of commuter exposure to ultrafine particles and its health effects. Atmos. Environ. 2011, 45, 2611–2622. [Google Scholar] [CrossRef]
- Neumann, J.E.; Amend, M.; Anenberg, S.; Kinney, P.L.; Sarofim, M.; Martinich, J.; Lukens, J.; Xu, J.-W.; Roman, H. Estimating PM2.5-related premature mortality and morbidity associated with future wildfire emissions in the western US. Environ. Res. Lett. 2021, 16, 035019. [Google Scholar] [CrossRef] [PubMed]
- Broome, R.A.; Powell, J.; Cope, M.E.; Morgan, G. The mortality effect of PM 2.5 sources in the Greater Metropolitan Region of Sydney, Australia. Environ. Int. 2020, 137, 105429. Available online: https://www.ncbi.nlm.nih.gov/pubmed/32062440 (accessed on 15 December 2023). [CrossRef] [PubMed]
- Wasilewski, M.; Brar, L.S. Optimization of the geometry of cyclone separators used in clinker burning process: A case study. Powder Technol. 2017, 313, 293–302. [Google Scholar] [CrossRef]
- Luciano, R.D.; Silva, B.L.; Rosa, L.M.; Meier, F.H. Multi-objective optimization of cyclone separators in series based on computational fluid dynamics. Powder Technol. 2018, 325, 452–466. [Google Scholar] [CrossRef]
- Singh, P.; Couckuyt, I.; Elsayed, K.; Deschrijver, D.; Dhaene, T. Multi-objective geometry optimization of a gas cyclone using triple-fidelity co-kriging surrogate models. J. Optim. Theory Appl. 2017, 175, 172–193. [Google Scholar] [CrossRef]
- Sabareesh, S.P.; Krishna, P.R. Process modeling and particle flow simulation of sand separation in cyclone separator. Part. Sci. Technol. 2015, 33, 385–392. [Google Scholar] [CrossRef]
- Pishbin, S.I.; Moghiman, M. Optimization of cyclone separators using genetic algorithm. Int. Rev. Chem. Eng. 2018, 6, 91–99. [Google Scholar] [CrossRef]
- Balan, S.A.; Burov, A.A.; Burov, A.I. Distribution dust flow along the curved boundary of a closed loop. Odessa 2000, 2, 56–59. [Google Scholar]
- Jakštonienė, I. Researches and Development of Cylindrical Multichannel Cyclone with Adjustable Half Rings. Ph.D. Thesis, Technika, Vilnius, Lithuania, 2012; 155p. [Google Scholar]
- Burov, A.A.; Burov, A.I.; Silin, A.V.; Cabiev, O.N. Centrifugal purification of industrial emissions into the atmosphere. Environ. Ecol. Saf. Life Act. 2005, 6, 44–51. [Google Scholar]
- Winfield, D.; Mark, C.; Nick, C.; David, P.; Ian, C. Performance comparison of a single and triple tangential inlet gas separation cyclone: A CFD Study. Powder Technol. 2013, 235, 520–531. [Google Scholar] [CrossRef]
- Sophie, A.; Mathieu, V.; Jullemier, S.; Contal, P.; Midoux, N.; Rode, S.; Leclerc, J.-P. Comparison of different models of cyclone prediction performance for various operating conditions using a general software. Chem. Eng. Process. Process Intensif. 2004, 43, 511–522. [Google Scholar] [CrossRef]
- Baltėrnas, P.; Vaitiekūnas, P.; Jakštonienė, I.; Konoverskytė, S. Study of Gas–Solid Flow in a Multichannel Cyclone. J. Environ. Eng. Landsc. Manag. 2012, 20, 129–137. [Google Scholar] [CrossRef]
- Plashihin, S.V.; Serebryanskyy, D.O. Bench testing centrifugal filter and capture tsyklofiltra in ash solid fuel boilers. Mater. Eng. 2011, 5, 89–94. [Google Scholar]
- Baltrėnas, P.; Chlebnikovas, A. Removal of fine solid particles in aggressive gas flows in a newly designed multi-channel cyclone. Powder Technol. 2019, 356, 480–492. [Google Scholar] [CrossRef]
- Jasevičius, R.; Emden, H.K.; Baltrėnas, P. Numerical simulation of the sticking process of glass-microparticles to a flat wall to represent pollutant-particles treatment in a multi-channel cyclone. Particuology 2017, 32, 112–131. [Google Scholar] [CrossRef]
- Parvaz, F.; Hosseini, S.H.; Ahmadi, G.; Elsayed, K. Impacts of the vortex finder eccentricity on the flow pattern and performance of a gas cyclone. Sep. Purif. Technol. 2017, 187, 1–13. [Google Scholar] [CrossRef]
- Parvaz, F.; Hosseini, S.H.; Elsayed, K.; Ahmadi, G. Influence of the dipleg shape on the performance of gas cyclones. Sep. Puri. Technol. 2020, 233, 116000. [Google Scholar] [CrossRef]
- Sun, X.; Kim, S.; Yang, S.D.; Kim, H.S.; Yoon, J.Y. Multi-objective optimization of a Stairmand cyclone separator using response surface methodology and computational fluid dynamics. Powder Technol. 2017, 320, 51–65. [Google Scholar] [CrossRef]
- Brar, L.S.; Elsayed, K. Analysis and optimization of multi-inlet gas cyclones using large eddy simulation and artificial neural network. Powder Technol. 2017, 311, 465–483. [Google Scholar] [CrossRef]
- Guo, M.; Xue, H.; Pang, J.; Le, D.K.; Sun, X.; Yoon, J.Y. Numerical investigation on the swirling vortical characteristics of a Stairmand cyclone separator with slotted vortex finder. Powder Technol. 2022, 416, 118236. [Google Scholar] [CrossRef]
- Elsayed, K.; Parvaz, F.; Hosseini, S.H.; Ahmadi, G. Influence of the dipleg and dustbin dimensions on performance of gas cyclones: An optimization study. Sep. Puri. Technol. 2020, 239, 116553. [Google Scholar] [CrossRef]
- Kumar, V.; Jha, K. Multi-objective shape optimization of vortex finders in cyclone separators using response surface methodology and genetic algorithms. Sep. Purif. Technol. 2019, 215, 25–31. [Google Scholar] [CrossRef]
- Brar, L.S.; Elsayed, K. Analysis and optimization of cyclone separators with eccentric vortex finders using large eddy simulation and artificial neural network. Sep. Purif. Technol. 2018, 207, 269–283. [Google Scholar] [CrossRef]
- Shastri, R.; Brar, L.S.; Elsayed, K. Multi-objective optimization of cyclone separators using mathematical modelling and large-eddy simulation for a fixed total height condition. Sep. Purif. Technol. 2022, 291, 120968. [Google Scholar] [CrossRef]
- Muschelknautz, E.; Gase, D.B.V.Z. Die Berechnung von Zyklonabscheidern für Gase. Chem-Ing-Tech. 1972, 44, 63–71. [Google Scholar] [CrossRef]
- Muschelknautz, E.; Trefz, M. Design and calculation of higher and highest loaded gas cyclones. In Proceedings of the Second World Congress on Particle Technology, Kyoto, Japan, 19–22 September 1990; pp. 52–71. [Google Scholar]
- Brar, L.S.; Sharma, R.P. Effect of varying diameter on the performance of industrial-scale gas cyclone dust separators. Mater. Today Proc. 2015, 2, 3230–3237. [Google Scholar] [CrossRef]
- Brar, L.S.; Sharma, R.P.; Elsayed, K. The effect of the cyclone length on the performance of Stairmand high-efficiency cyclone. Powder Technol. 2015, 286, 668–677. [Google Scholar] [CrossRef]
- Stairmand, C.J. The design and performance of cyclone separators. Trans. Instn. Chem. Engrs. 1951, 29, 356–383. [Google Scholar]
- Hoffman, A.C.; Stein, L.E. Gas Cyclones and Swirl Tubes: Principles, Design and Operation; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar] [CrossRef]
- Ferziger, J.H.; Perić, M. Computational Methods for Fluid Dynamics; Springer: Berlin, Germany, 2002. [Google Scholar] [CrossRef]
- Zhao, B.; Su, Y.; Zhang, J. Simulation of gas flow pattern and separation efficiency in cyclone with conventional single and spiral double inlet configuration. Chem Eng. Res. Des. 2006, 84, 1158–1165. [Google Scholar] [CrossRef]
- Morsi, S.A.; Alexander, A.J. An investigation of particle trajectories in two-phase flow systems. J. Fluid Mech. 1972, 55, 193–208. [Google Scholar] [CrossRef]
- Dukowwicz, J.K.; Dvinsky, A.S. Approximate Factorization as a High-Order Splitting for the Implicit Incompressible Flow Equations. J. Comput. Phys. 1992, 102, 336–347. [Google Scholar] [CrossRef]
- Patankar, S. Numerical Heat Transfer and Fluid Flow; CRC Press: Boca Raton, FL, USA, 1980. [Google Scholar] [CrossRef]
- Brar, L.S.; Derksen, J.J. Revealing the details of vortex core precession in cyclones by means of large-eddy simulation. Chem. Eng. Res. Des. 2020, 159, 339–352. [Google Scholar] [CrossRef]
- Brar, L.S.; Wasilewski, M. Investigating the effects of temperature on the performance of novel cyclone separators using large-eddy simulation. Powder Technol. 2023, 416, 118213. [Google Scholar] [CrossRef]
- de Souza, F.J.; Salvo, R.D.V.; Martins, D.A.D.M. Large Eddy Simulation of the gas–particle flow in cyclone separators. Sep. Purif. Technol. 2012, 94, 61–70. [Google Scholar] [CrossRef]
- Kumar, M.; Vanka, S.P.; Banerjee, R.; Mangadoddy, N. Dominant Modes in a Gas Cyclone Flow Field Using Proper Orthogonal Decomposition. Ind. Eng. Chem. Res. 2022, 61, 2562–2579. [Google Scholar] [CrossRef]
- Pandey, S.; Brar, L.S. Performance analysis of cyclone separators with bulged conical segment using large-eddy simulation. Powder Technol. 2023, 425, 118584. [Google Scholar] [CrossRef]
- Pandey, S.; Brar, L.S. The impact of increasing the length of the conical segment on the cyclone performance using large-eddy simulation. Symmetry 2023, 15, 682. [Google Scholar] [CrossRef]
- Shastri, R.; Brar, L.S. Numerical investigations of the flow-field inside cyclone separators with different cylinder-to-cone ratios using large-eddy simulation. Sep. Purif. Technol. 2020, 249, 117149. [Google Scholar] [CrossRef]
- Shastri, R.; Wasilewski, M.; Brar, L.S. Analysis of the novel hybrid cyclone separators using large-eddy simulation. Powder Technol. 2021, 394, 951–969. [Google Scholar] [CrossRef]
- Wasilewski, M.; Brar, L.S.; Ligus, G. Experimental and numerical investigation on the performance of square cyclones with different vortex finder configurations. Sep. Purif. Technol. 2020, 239, 116588. [Google Scholar] [CrossRef]
- Wasilewski, M.; Brar, L.S.; Ligus, G. Effect of the central rod dimensions on the performance of cyclone separators—Optimization study. Sep. Purif. Technol. 2021, 274, 119020. [Google Scholar] [CrossRef]
- Wasilewski, M.; Brar, L.S. Performance analysis of the cyclone separator with a novel clean air inlet installed on the roof surface. Powder Technol. 2023, 428, 118849. [Google Scholar] [CrossRef]
- Hoekstra, A.J. Gas Flow Field and Collection Efficiency of Cyclone Separators. Ph.D. Thesis, Technical University Delft, Delft, The Netherlands, 2000. Available online: http://resolver.tudelft.nl/uuid:67b8f405-eef0-4c2d-9646-80200e5274c6 (accessed on 3 May 2023).
- Derksen, J.J.; Akker, H.E.A.V.D.; Sundaresan, S. Two-way coupled large-eddy simulations of the gas-solid flow in cyclone separators. AIChE J. 2008, 54, 872–885. [Google Scholar] [CrossRef]







| Geometrical Parameter | Notation | Lower Bound | Upper Bound |
|---|---|---|---|
| Cyclone diameter | * Dc/D | 1.000 | 1.300 |
| Total cyclone length | Ht/D | 4.000 | 8.000 |
| Vortex finder diameter | Dx/D | 0.300 | 0.700 |
| Length of conical segment | Hc/D | 1.000 | 4.000 |
| Cone tip diameter | Bc/D | 0.010 | 0.040 |
| Insertion length of vortex finder | S/D | 0.345 | 0.690 |
| Solver | Gamultiobj |
|---|---|
| Population type | Double vector |
| Population size | 90 (defined as 15× number of variables) |
| Number of variables | 6 |
| Selection operation | Tournament (size equal to 2 (default)) |
| Crowding distance fraction | 0.35 |
| Crossover fraction | 0.8 (default) |
| Crossover operation | Intermediate (with a ratio equal to 0.2 (default)) |
| Number of generations (iterations) | 1200 (defined as 200× number of variables) |
| User function evaluation | In parallel |
| Sl. No. | Dx/D | Dc/D | Ht/D | Bc/D | S/D | Hc/D | ∆P (Pa) | d50 (µm) |
|---|---|---|---|---|---|---|---|---|
| 1 | 0.700 | 1.041 | 7.628 | 0.135 | 1.386 | 1.090 | 328.250 | 1.727 |
| 2 | 0.700 | 1.052 | 7.814 | 0.195 | 0.990 | 1.621 | 335.360 | 1.626 |
| 3 | 0.683 | 1.076 | 7.817 | 0.169 | 1.138 | 2.217 | 354.440 | 1.573 |
| 4 | 0.690 | 1.145 | 7.748 | 0.224 | 1.010 | 2.052 | 362.560 | 1.498 |
| 5 | 0.693 | 1.221 | 7.659 | 0.207 | 1.072 | 2.917 | 378.640 | 1.445 |
| * 6 A | 0.690 | 1.241 | 7.841 | 0.252 | 0.934 | 3.321 | 385.830 | 1.383 |
| 7 | 0.655 | 1.207 | 7.800 | 0.228 | 1.028 | 3.310 | 408.880 | 1.361 |
| 8 | 0.645 | 1.266 | 7.814 | 0.269 | 0.852 | 3.179 | 425.630 | 1.280 |
| 9 | 0.621 | 1.293 | 7.852 | 0.331 | 0.779 | 3.276 | 453.010 | 1.206 |
| 10 | 0.562 | 1.183 | 7.790 | 0.228 | 0.962 | 2.314 | 495.470 | 1.206 |
| 11 | 0.555 | 1.255 | 7.776 | 0.279 | 0.900 | 2.121 | 514.470 | 1.140 |
| 12 | 0.534 | 1.293 | 7.821 | 0.359 | 0.917 | 2.493 | 550.880 | 1.075 |
| 13 | 0.517 | 1.248 | 7.852 | 0.324 | 0.855 | 3.369 | 588.540 | 1.051 |
| 14 | 0.503 | 1.290 | 7.814 | 0.290 | 0.828 | 2.921 | 615.830 | 1.006 |
| 15 | 0.476 | 1.290 | 7.807 | 0.317 | 0.828 | 3.152 | 682.930 | 0.951 |
| 16 | 0.452 | 1.290 | 7.817 | 0.324 | 0.834 | 1.852 | 716.070 | 0.924 |
| * 17 B | 0.438 | 1.293 | 7.831 | 0.331 | 0.852 | 3.348 | 783.340 | 0.883 |
| 18 | 0.417 | 1.245 | 7.834 | 0.293 | 0.841 | 2.762 | 837.250 | 0.870 |
| 19 | 0.407 | 1.297 | 7.828 | 0.359 | 0.831 | 3.069 | 885.880 | 0.828 |
| 20 | 0.393 | 1.293 | 7.821 | 0.328 | 0.907 | 1.769 | 913.240 | 0.821 |
| 21 | 0.390 | 1.293 | 7.831 | 0.328 | 0.852 | 1.938 | 939.900 | 0.807 |
| 22 | 0.372 | 1.293 | 7.831 | 0.321 | 0.841 | 3.828 | 1068.410 | 0.760 |
| 23 | 0.366 | 1.300 | 7.862 | 0.359 | 0.803 | 3.724 | 1109.230 | 0.741 |
| 24 | 0.345 | 1.297 | 7.845 | 0.345 | 0.807 | 3.748 | 1242.890 | 0.707 |
| 25 | 0.334 | 1.290 | 7.848 | 0.338 | 0.845 | 3.403 | 1315.360 | 0.695 |
| 26 | 0.334 | 1.293 | 7.852 | 0.321 | 0.783 | 3.848 | 1355.670 | 0.681 |
| * 27 C | 0.328 | 1.293 | 7.859 | 0.338 | 0.776 | 3.972 | 1402.080 | 0.671 |
| 28 | 0.321 | 1.293 | 7.855 | 0.338 | 0.807 | 3.659 | 1470.930 | 0.660 |
| 29 | 0.303 | 1.297 | 7.848 | 0.341 | 0.807 | 3.879 | 1665.690 | 0.628 |
| 30 | 0.300 | 1.300 | 7.862 | 0.362 | 0.769 | 3.986 | 1713.050 | 0.618 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pandey, S.; Wasilewski, M.; Mukhopadhyay, A.; Prakash, O.; Ahmad, A.; Brar, L.S. Multi-Objective Optimization of Cyclone Separators Based on Geometrical Parameters for Performance Enhancement. Appl. Sci. 2024, 14, 2034. https://doi.org/10.3390/app14052034
Pandey S, Wasilewski M, Mukhopadhyay A, Prakash O, Ahmad A, Brar LS. Multi-Objective Optimization of Cyclone Separators Based on Geometrical Parameters for Performance Enhancement. Applied Sciences. 2024; 14(5):2034. https://doi.org/10.3390/app14052034
Chicago/Turabian StylePandey, Satyanand, Marek Wasilewski, Arkadeb Mukhopadhyay, Om Prakash, Asim Ahmad, and Lakhbir Singh Brar. 2024. "Multi-Objective Optimization of Cyclone Separators Based on Geometrical Parameters for Performance Enhancement" Applied Sciences 14, no. 5: 2034. https://doi.org/10.3390/app14052034
APA StylePandey, S., Wasilewski, M., Mukhopadhyay, A., Prakash, O., Ahmad, A., & Brar, L. S. (2024). Multi-Objective Optimization of Cyclone Separators Based on Geometrical Parameters for Performance Enhancement. Applied Sciences, 14(5), 2034. https://doi.org/10.3390/app14052034







