Analysis of Electroencephalograms Based on the Phase Plane Method
Abstract
:1. Introduction
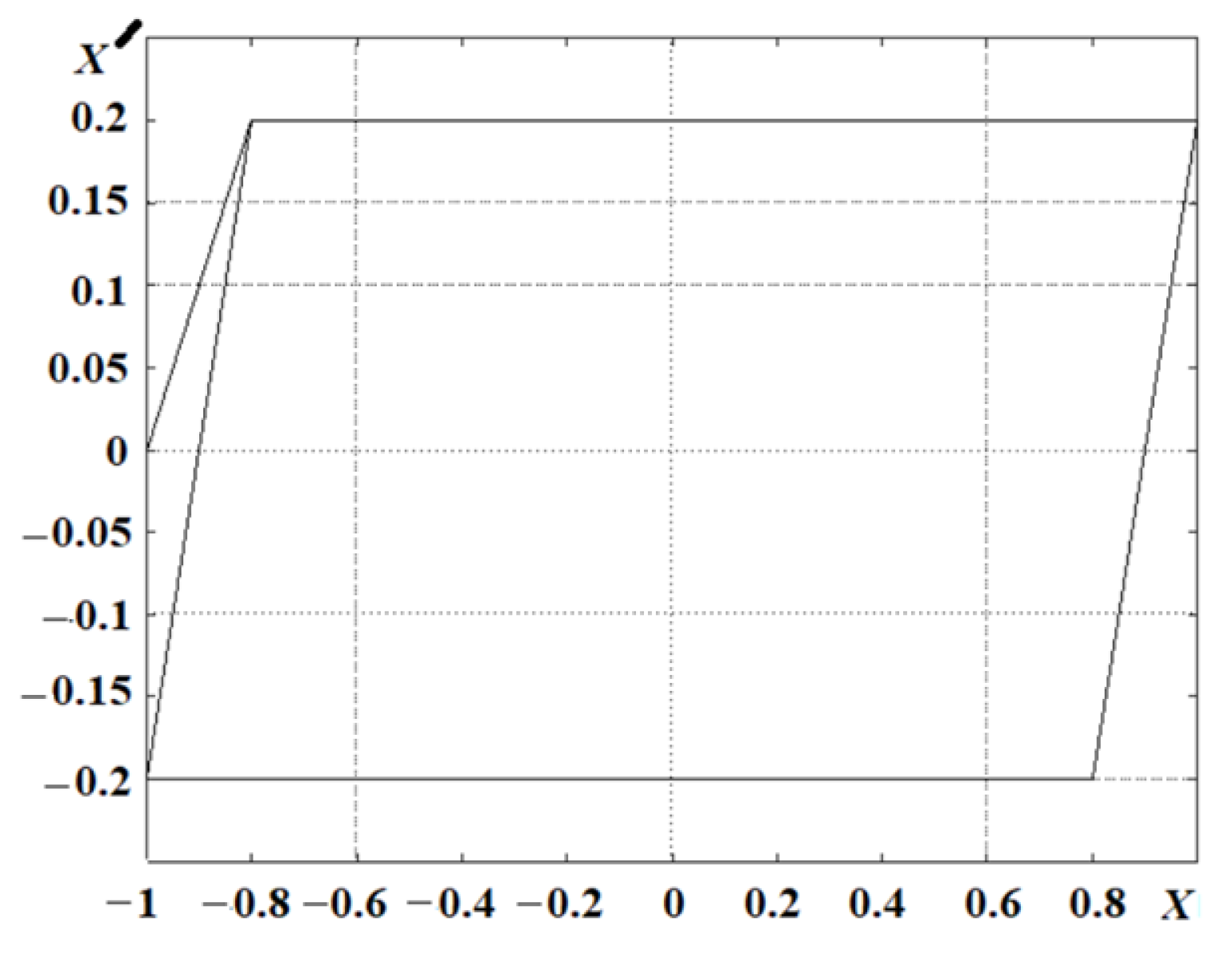
2. Phase Plane Method
- Define the system state variables. These can be physical quantities such as position, speed, temperature, etc.;
- Define differential equations that describe how the variables of the state of the system change over time. These equations can be derived from physical laws or experimental data;
- Solve the differential equations for different initial conditions to obtain the values of the variables of the state of the system at different points in time;
- Draw points corresponding to the values of the state variables on the coordinate plane. Each point represents the state of the system at a particular point in time;
- Connect the points with lines or curves to obtain a phase portrait. The shape and nature of these lines or curves can provide information about the behavior of the system.
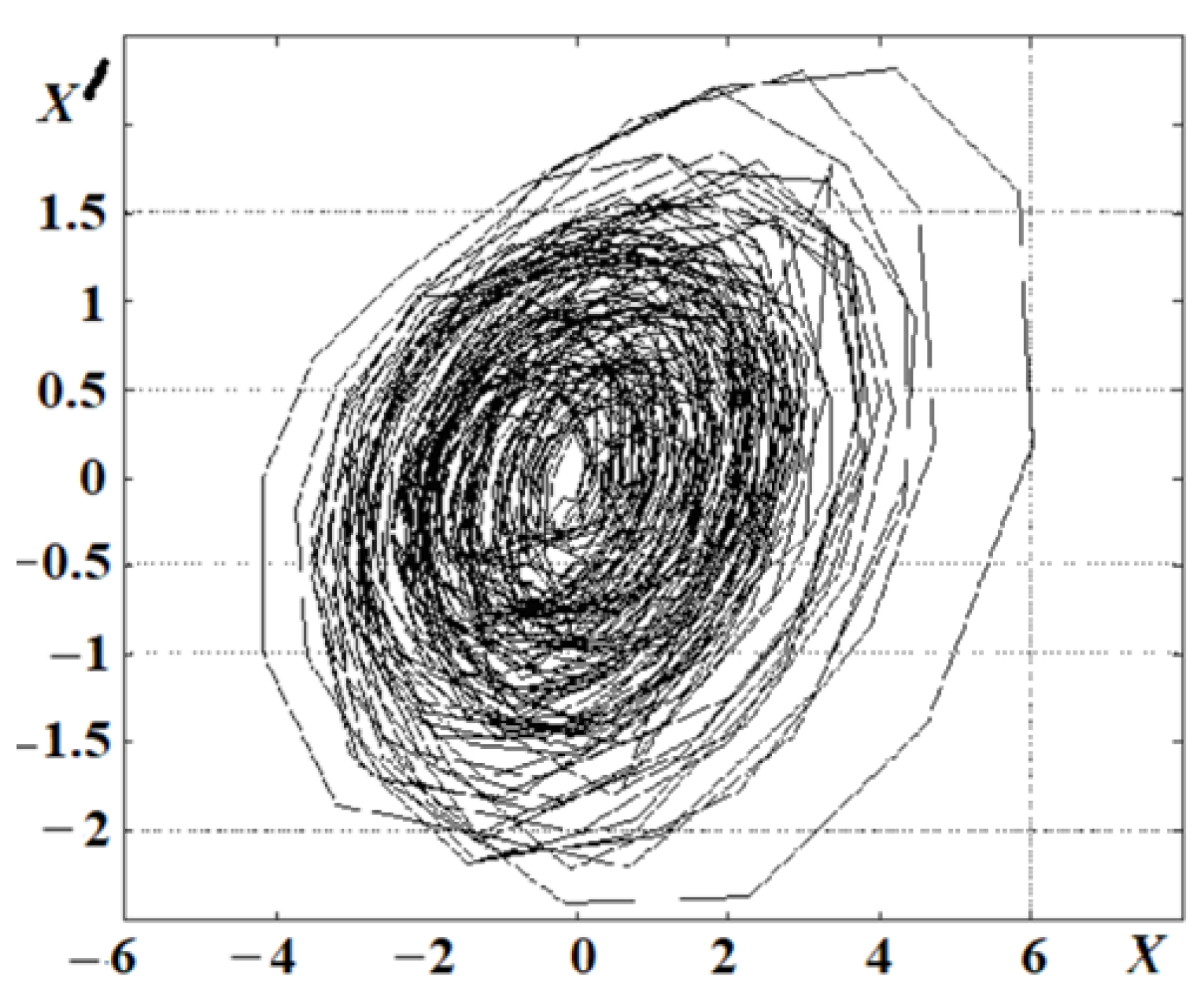
3. Determination of the Signal-to-Noise Ratio Based on the Phase Portrait
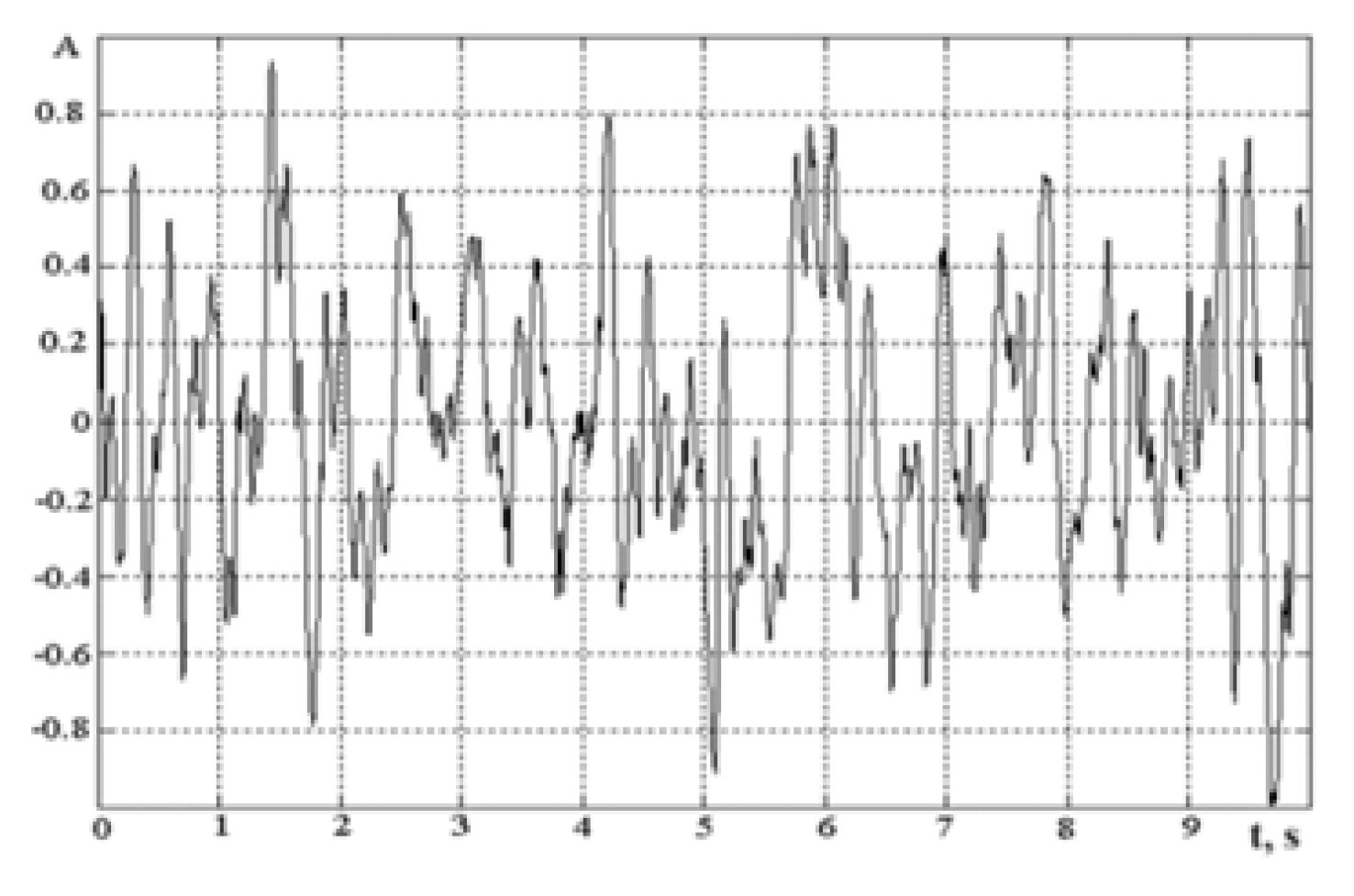
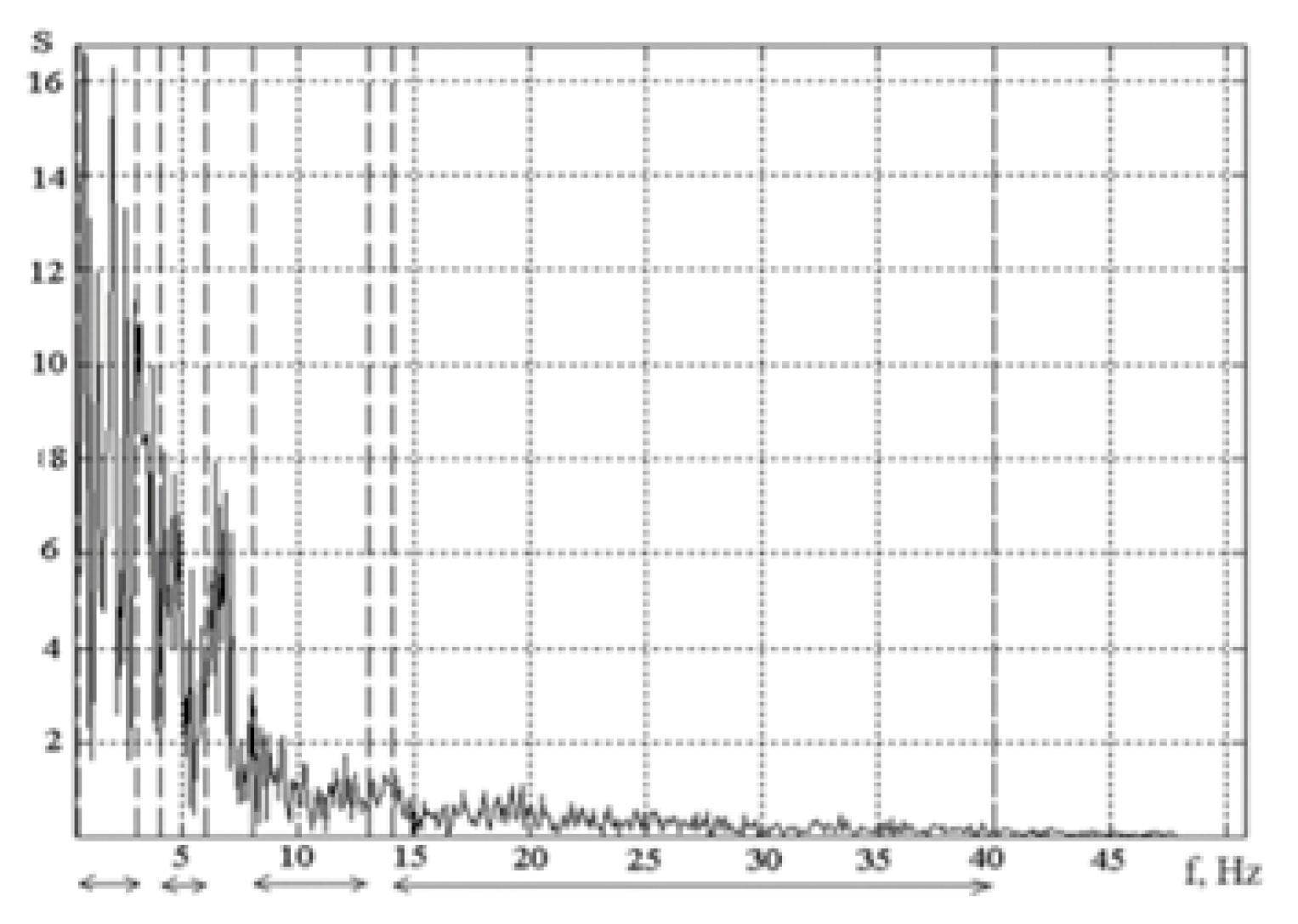
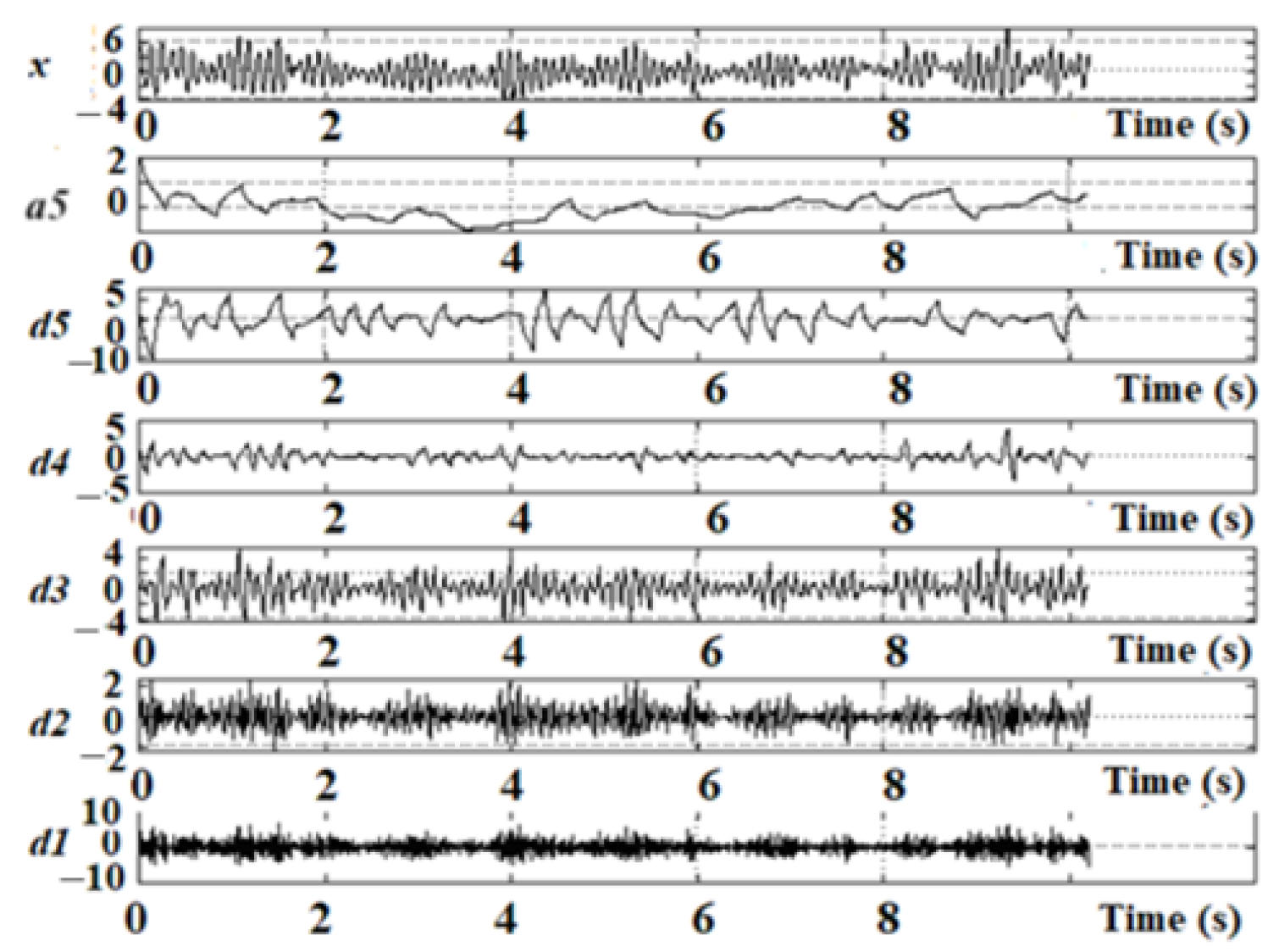
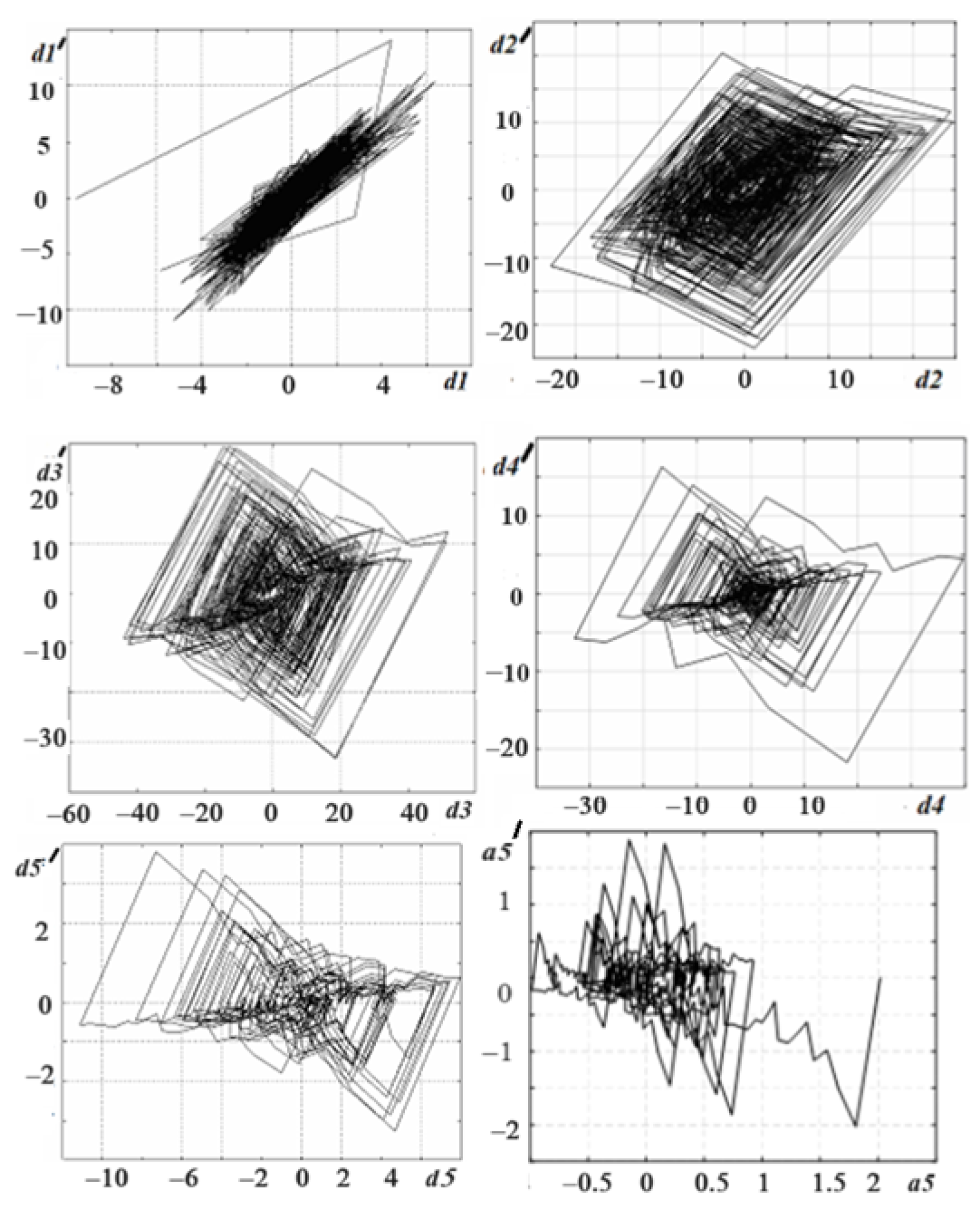
4. Electroencephalogram Phase Portrait and Wavelet Analysis
- Signal space can be divided into nested subspaces that do not intersect;
- For any function , its compressed version belongs to the space ;
- There is a function , the shifts of which create the orthonormal basis of space .
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Collura, T.F.; Morris, H.H.; Burgess, R.C.; Jacobs, E.C.; Klem, G.H. Phase-plane trajectories of EEG seizure patterns in epilepsy. Am. J. EEG Technol. 1992, 32, 295–307. [Google Scholar] [CrossRef]
- Akilli, M.; Yilmaz, N. Study of weak periodic signals in the EEG signals and their relationship with postsynaptic potentials. IEEE Trans. Neural Syst. Rehabil. Eng. 2018, 26, 1918–1925. [Google Scholar] [CrossRef]
- Jarray, R.; Jmail, N.; Hadriche, A.; Frikha, T. A Comparison between modeling a normal and an epileptic state using the FHN and the epileptor model. In Innovations in Bio-Inspired Computing and Applications, Proceedings of the 8th International Conference on Innovations in Bio-Inspired Computing and Applications (IBICA 2017), Marrakech, Morocco, 11–13 December 2017; Springer International Publishing: Berlin/Heidelberg, Germany, 2018; pp. 245–254. [Google Scholar]
- Kako, T.; Ohishi, Y.; Kameoka, H.; Kashino, K.; Takeda, K. Automatic Identification for Singing Style based on Sung Melodic Contour Characterized in Phase Plane. In Proceedings of the 10th International Society for Music Information Retrieval Conference, Kobe, Japan, 26–30 October 2009; pp. 393–398. [Google Scholar]
- Voloshchuk, Y.I. Signals and Processes in Radiotechnics; OO “Company Smith”: Kharkiv, Ukraine, 2005; Volume 2, pp. 102–121. [Google Scholar]
- Vidyasagar, M. Nonlinear Systems Analysis; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2002; p. 515. [Google Scholar]
- Reyn, J. Phase Portraits of Planar Quadratic Systems; Springer: Berlin/Heidelberg, Germany, 2007; pp. 35–115. [Google Scholar]
- Kudryashov, N.A.; Lavrova, S.F. Painlevé Test, Phase Plane Analysis and Analytic Solutions of the Chavy–Waddy–Kolokolnikov Model for the Description of Bacterial Colonies. Mathematics 2023, 11, 3203. [Google Scholar] [CrossRef]
- Melka, R.F.; Yousif, H.A. Imaging phase plane models. Int. J. Math. Educ. Sci. Technol. 2023, 54, 2281–2303. [Google Scholar] [CrossRef]
- Tenreiro Machado, J.A.; Costa, A.C.; Quelhas, M.D. Shannon, Rényie and Tsallis entropy analysis of DNA using phase plane. Nonlinear Anal. Real World Appl. 2011, 12, 3135–3144. [Google Scholar] [CrossRef]
- Tamang, J.; Abdikian, A.; Saha, A. Phase plane analysis of small amplitude electron-acoustic supernonlinear and nonlinear waves in magnetized plasmas. Phys. Scr. 2020, 95, 105604–105623. [Google Scholar] [CrossRef]
- Amir, M. Phase-plane analysis of test particle orbits in regular black holes. Commun. Theor. Phys. 2020, 72, 15404–15411. [Google Scholar] [CrossRef]
- Mantaras, D.; Luque, P.; Alonso, M. Phase plane analysis applied to non-explicit multibody vehicle models. Multibody Syst. Dyn. 2022, 56, 173–188. [Google Scholar] [CrossRef]
- Isojima, S.; Suzuki, S. Ultradiscrete hard-spring equation and its phase plane analysis. Jpn. J. Ind. Appl. Math. 2023, 40, 1083–1105. [Google Scholar] [CrossRef]
- Streipert, S.; Wolkowicz, G. An augmented phase plane approach for discrete planar maps: Introducing next-iterate operators. Math. Biosci. 2023, 355, 121–132. [Google Scholar] [CrossRef]
- Tchernichovski, O.; Benjamini, Y.; Golani, I. The dynamics of long-term exploration in the rat. Part I. A phase-plane analysis of the relationship between location and velocity. Biol. Cybern. 1998, 78, 423–432. [Google Scholar] [CrossRef]
- Encyclopedia of Mathematics. “Three-Sigma Rule”. Available online: https://encyclopediaofmath.org/wiki/Three-sigma_rule (accessed on 20 December 2023).
- Middleton, D. An Introduction to Statistical Communication Theory: An IEEE Press Classic Reissue; Wiley-IEEE Press: Hoboken, NJ, USA, 1996; pp. 275–351. [Google Scholar]
- Levin, B.R. Theoretical Foundations of Statistical Radiotechnics; Radio and Communications: Moscow, Russia, 1989; pp. 57–104. [Google Scholar]
- Zenkov, L.R. Pharmacoresistent Epilepsy; Medpress-Inform: Vydavets, Russia, 2003; pp. 11–21. [Google Scholar]
- Zenkov, L.R. Clinical Encephalography with Elements of Epileptology; Medpress-Inform: Vydavets, Russia, 2016; pp. 13–31. [Google Scholar]
- Purdon, P.; Pavone, K.; Akeju, O. The Ageing Brain: Age-dependent changes in the electroencephalogram during propofol and sevoflurane general anaesthesia. Br. J. Anaesth. BJA 2015, 115, i46–i57. [Google Scholar] [CrossRef]
- Struck, A.; Osman, G.; Rampal, N. Time-dependent risk of seizures in critically ill patients on continuous electroencephalogram. Ann. Neurol. 2017, 82, 177–185. [Google Scholar] [CrossRef]
- Gao, Y.; Gao, B.; Chen, Q. Deep Convolutional Neural Network-Based Epileptic Electroencephalogram (EEG) Signal Classification. Front. Neurol. 2020, 11, 375. [Google Scholar] [CrossRef]
- Friedman, D. Continuous Electroencephalogram Monitoring in the Intensive Care Unit. Anesth. Analg. 2009, 109, 506–523. [Google Scholar] [CrossRef]
- Runnova, A.; Zhuravlev, M.; Ukolov, R.; Blokhina, I.; Dubrovski, A.; Lezhnev, N.; Sitnikova, E.; Saranceva, E.; Kiselev, A.; Karavaev, A.; et al. Modified wavelet analysis of ECoG-pattern as promising tool for detection of the blood–brain barrier leakage. Sci. Rep. 2021, 11, 18505. [Google Scholar] [CrossRef]
- Rossetti, A.O.; Schindler, K.; Sutter, R.; Rüegg, S.; Zubler, F.; Novy, J.; Oddo, M.; Warpelin-Decrausaz, L.; Alvarez, V. Continuous vs. Routine Electroencephalogram in Critically Ill Adults with Altered Consciousness and No Recent Seizure. A Multicenter Randomized Clinical Trial. JAMA Neurol. 2020, 77, 1225–1232. [Google Scholar] [CrossRef] [PubMed]
- Chaumon, M. A practical guide to the selection of independent components of the electroencephalogram for artifact correction. J. Neurosci. Methods 2015, 250, 47–63. [Google Scholar] [CrossRef] [PubMed]
- Kharchenko, O.I.; Lonin, Y.F.; Zabrodina, L.P. Separation of electroencephalogram low-frequency components on the basis of the stochastic resonance effect. Probl. At. Sci. Technol. 2021, 134, 135–137. [Google Scholar] [CrossRef]
- Sidorenko, A.V.; Voitikova, M.V. Wavelet analysis of electroencephalographic signals in microwaves. In Biomedical Technology in Radioelectronics; Radiotekhnika: Moscow, Russia, 2004; pp. 50–57. [Google Scholar]
- Bassam, N.A.; Ramachanrad, V.; Parameswaram, S.E. Wavelet theory and application in communication and signal processing. In Wavelet Theory; Mohammady, S., Ed.; IntechOpen: London, UK, 2021; pp. 145–256. [Google Scholar]
- Chao, B.; Chung, W.; Shih, Z. Earth’s rotation variations: A wavelet analysis. Terra Nova 2014, 26, 260–264. [Google Scholar] [CrossRef]
- Bing, J.; Hosseini, Z.; Wang, L. Spectral Wavelet-feature Analysis and Classification Assisted Denoising for enhancing magnetic resonance spectroscopy. NMR Biomed. 2021, 34, e4497–e4511. [Google Scholar]
- Al-Badour, F.; Sunar, M.; Cheded, L. Vibration analysis of rotating machinery using time–frequency analysis and wavelet techniques. Mech. Syst. Signal Process. 2011, 25, 2083–2101. [Google Scholar] [CrossRef]
- Arfaou, S.; Mabrouk, A.B.; Cattani, C. Wavelet Analysis. Basic Concepts and Applications; Chapman and Hall, CRC: Boca Raton, FL, USA, 2021; pp. 139–254. [Google Scholar]
- Merry, R.J.E. Wavelet Theory and Applications, a Literature Study; Eindhoven University of Technology, Department of Mechanical Engineering Control Systems Technology Group: Eindhoven, The Netherlands, 2005; pp. 5–41. [Google Scholar]


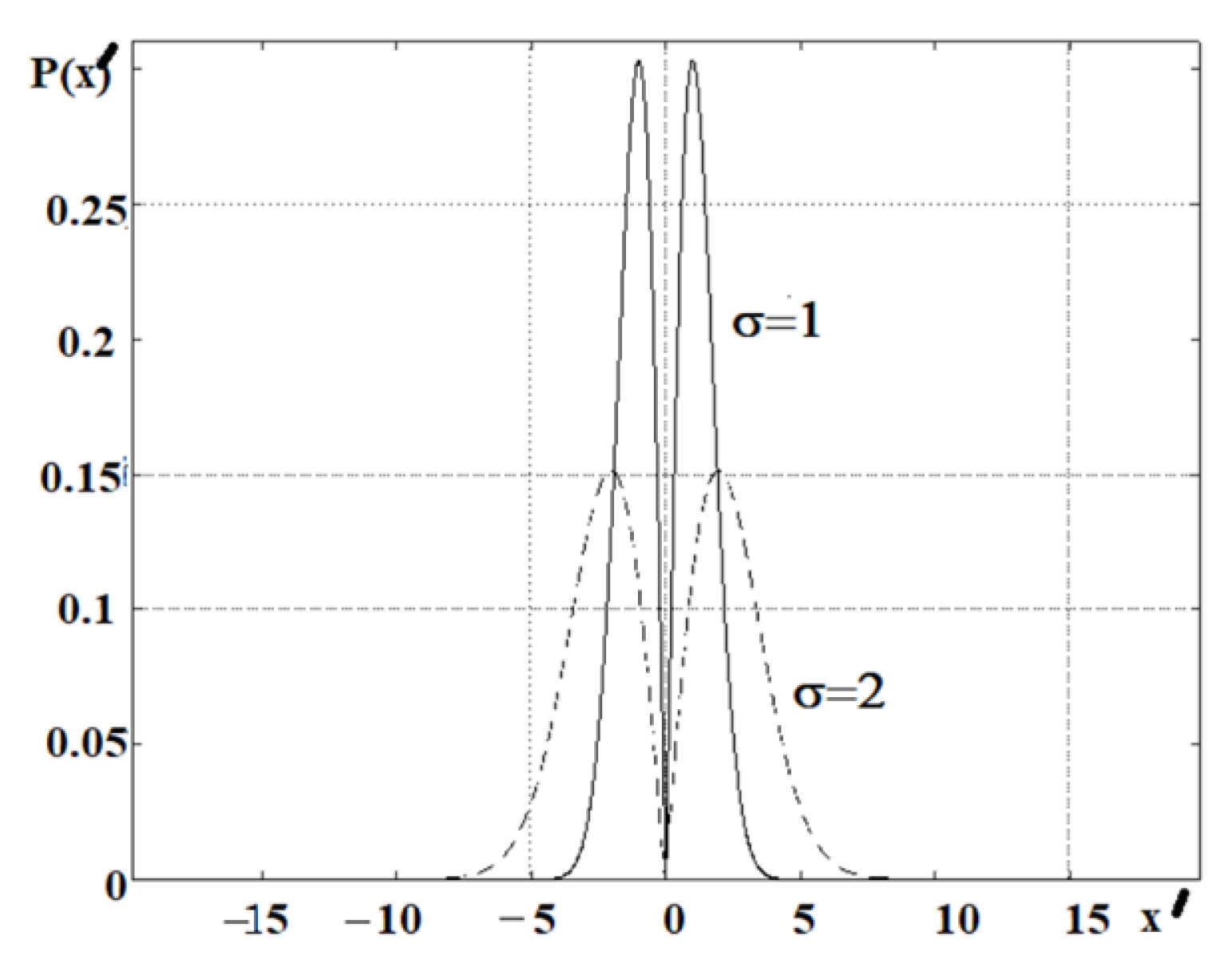





| Probability Density Function | Mean Value | Dispersion |
|---|---|---|
| 0 |
| a | |||
|---|---|---|---|
| 0.8647 | 0.9889 | 0.9997 |
| EEG rhythms of an awake adult | ||
| rhythm | Frequency (Hz) | Amplitude (V) |
| up to 100 | ||
| up to 15 normally | ||
| Types of pathological activity for an awake adult | ||
| exceeds 40 , reaching 300 or more in some pathological conditions | ||
| Number of Realizations of EEG | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| SNR |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kharchenko, O.; Kovacheva, Z.; Andonov, V. Analysis of Electroencephalograms Based on the Phase Plane Method. Appl. Sci. 2024, 14, 2204. https://doi.org/10.3390/app14052204
Kharchenko O, Kovacheva Z, Andonov V. Analysis of Electroencephalograms Based on the Phase Plane Method. Applied Sciences. 2024; 14(5):2204. https://doi.org/10.3390/app14052204
Chicago/Turabian StyleKharchenko, Oksana, Zlatinka Kovacheva, and Velin Andonov. 2024. "Analysis of Electroencephalograms Based on the Phase Plane Method" Applied Sciences 14, no. 5: 2204. https://doi.org/10.3390/app14052204
APA StyleKharchenko, O., Kovacheva, Z., & Andonov, V. (2024). Analysis of Electroencephalograms Based on the Phase Plane Method. Applied Sciences, 14(5), 2204. https://doi.org/10.3390/app14052204











