A Model for Simulating the Upward Flow of a Viscous Fluid in a Fracture Network
Abstract
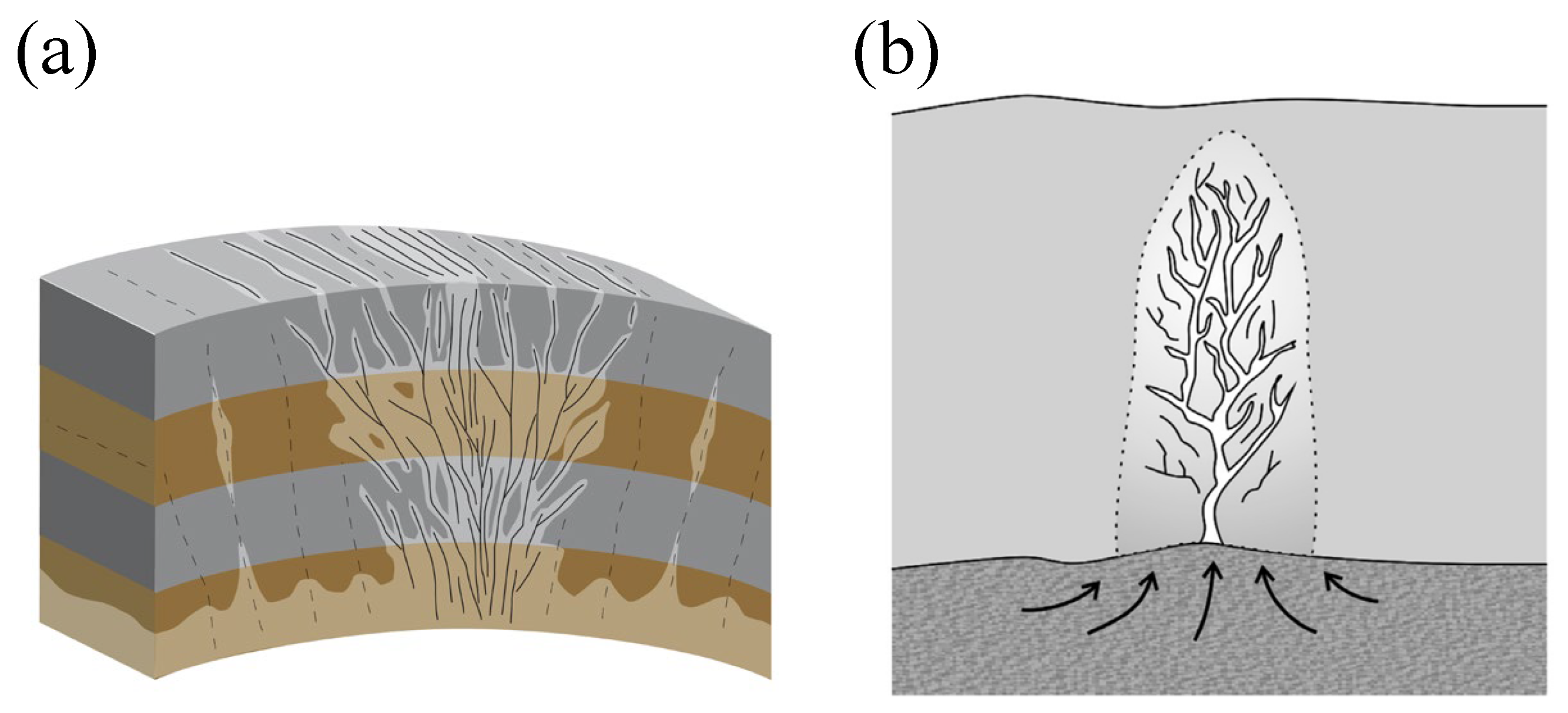
1. Introduction
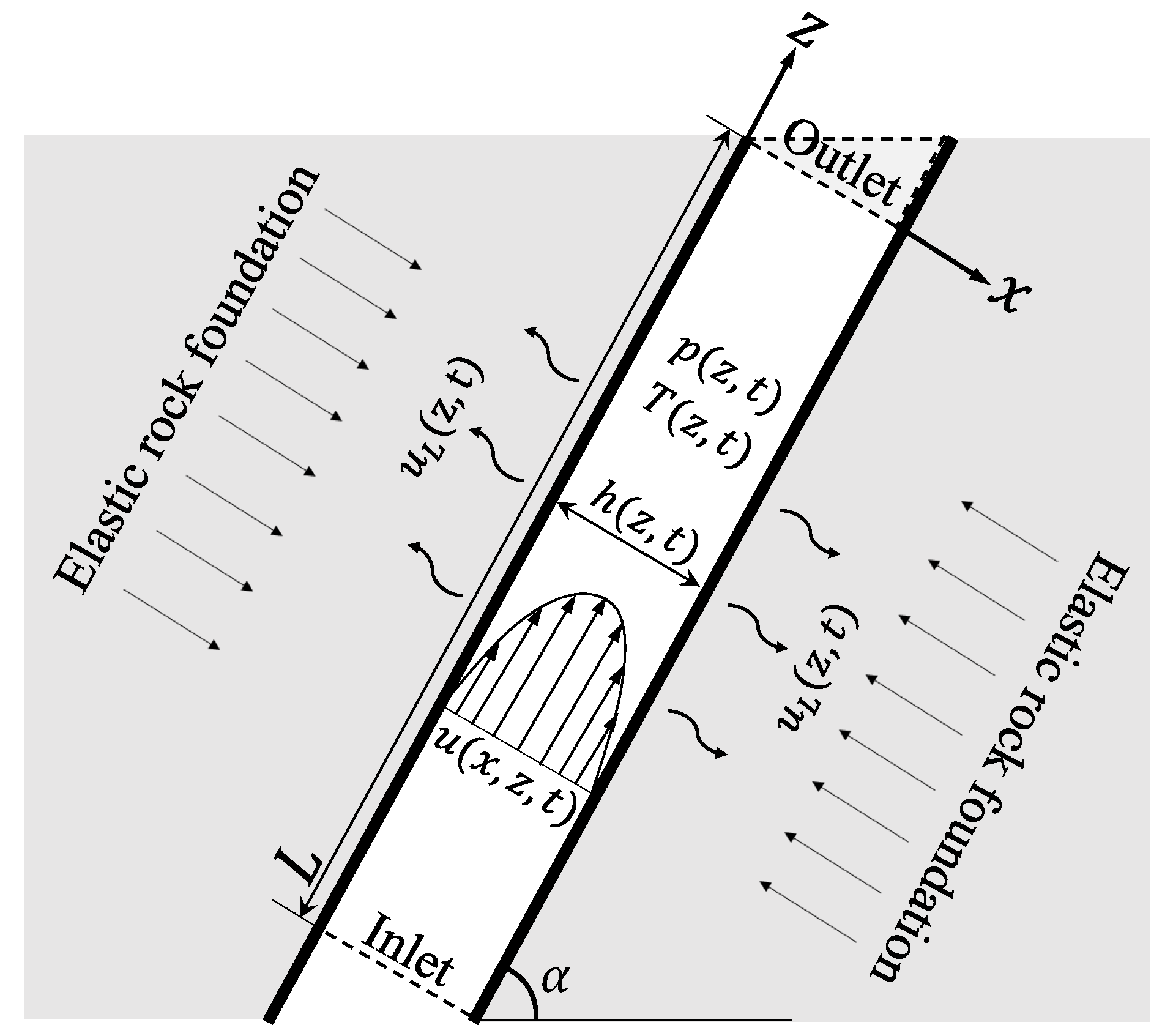
2. The Upward Flow of a Viscous Liquid in a Single Fracture
2.1. Model
2.1.1. Governing Equations
2.1.2. The Numerical Scheme, Boundary and Initial Conditions, and Parameters
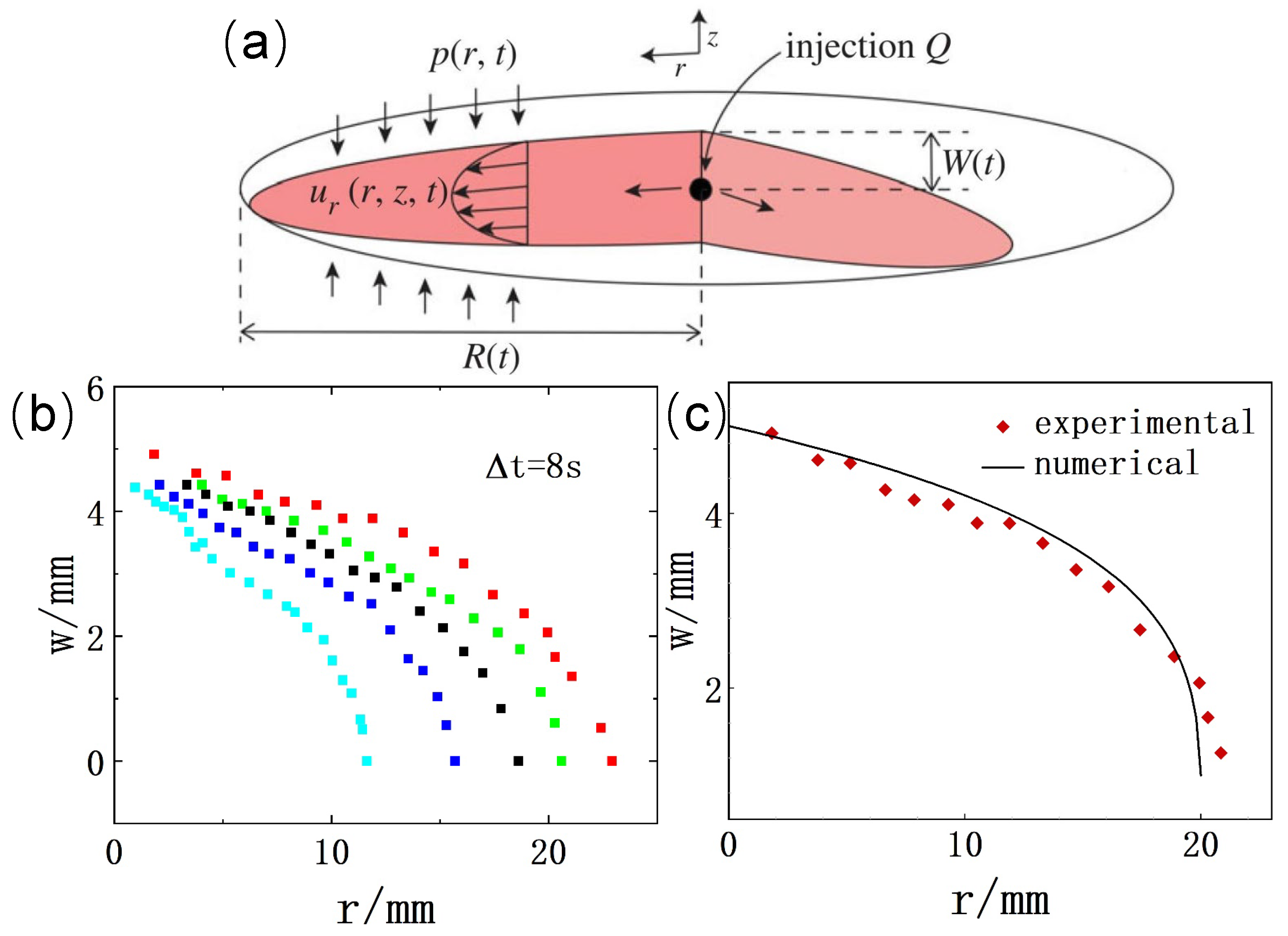
2.2. The Validation of Our Model
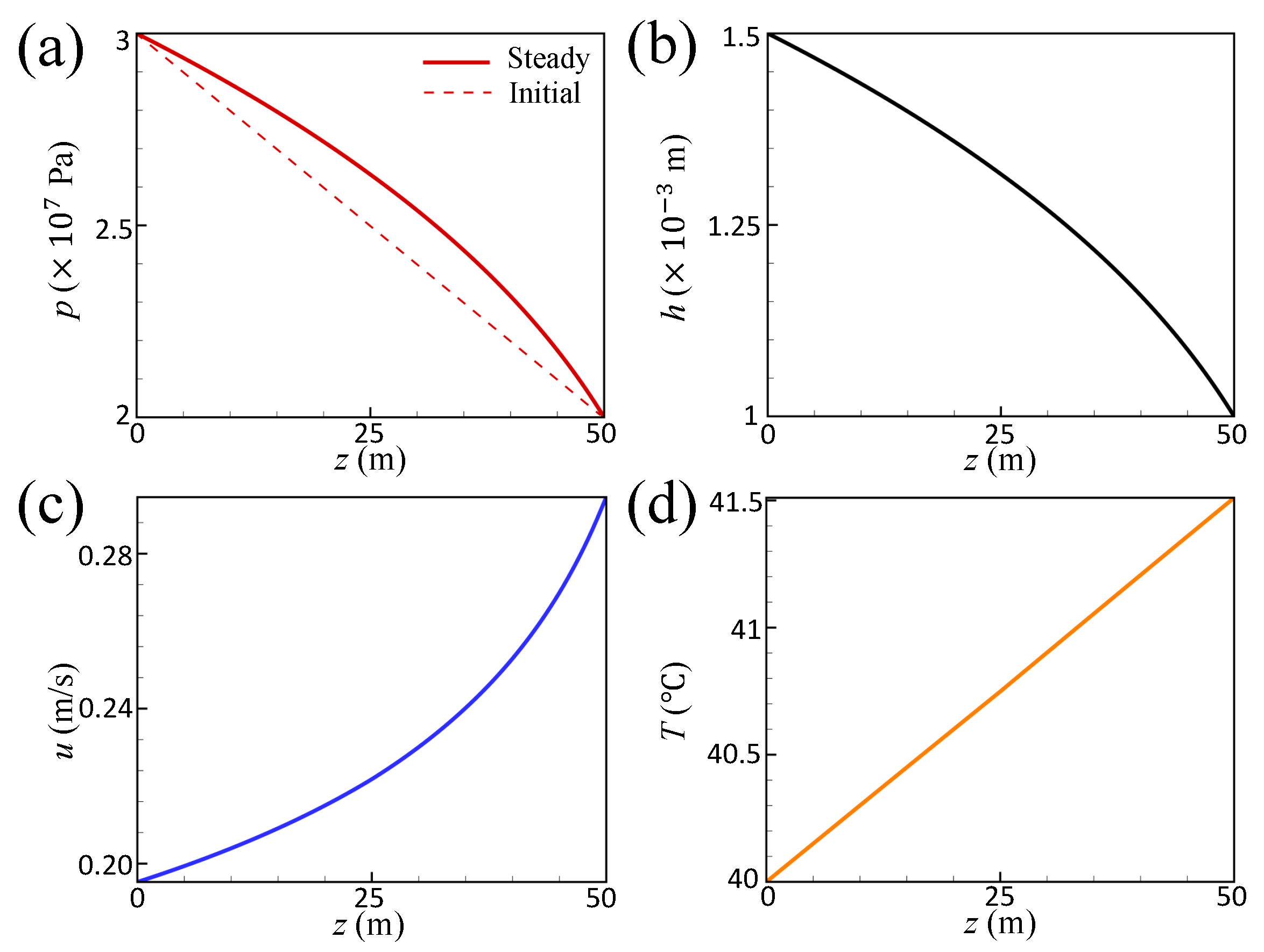
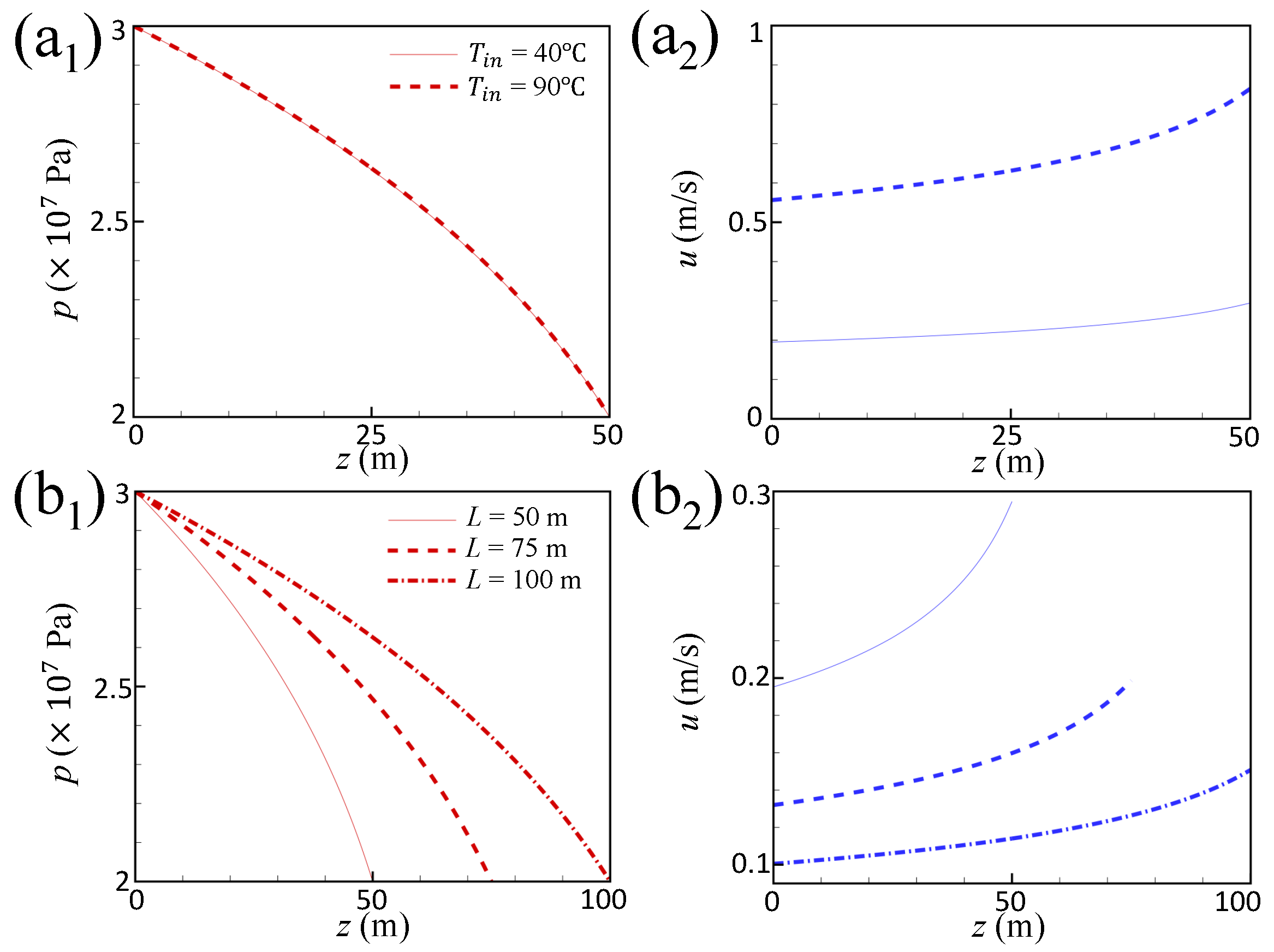
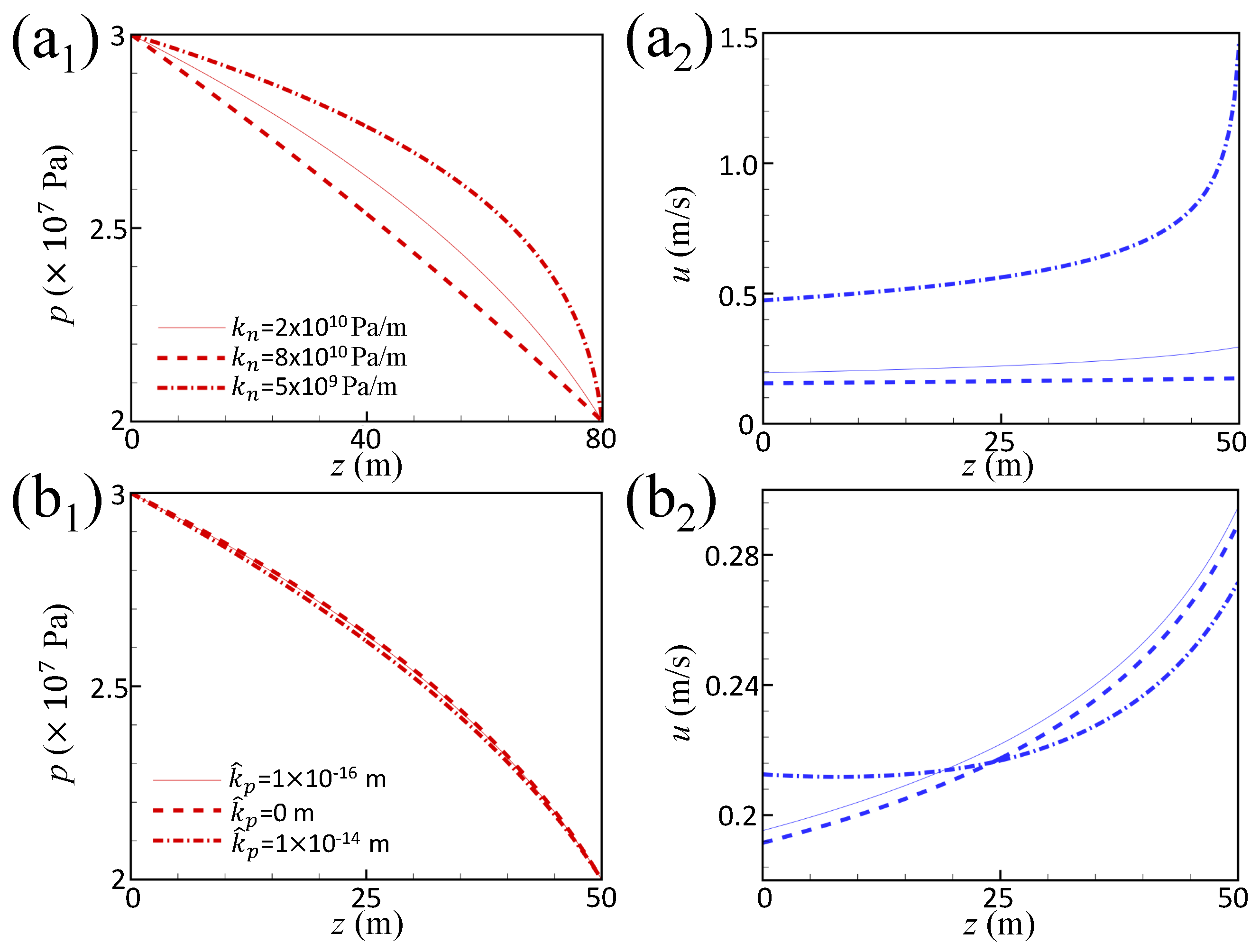
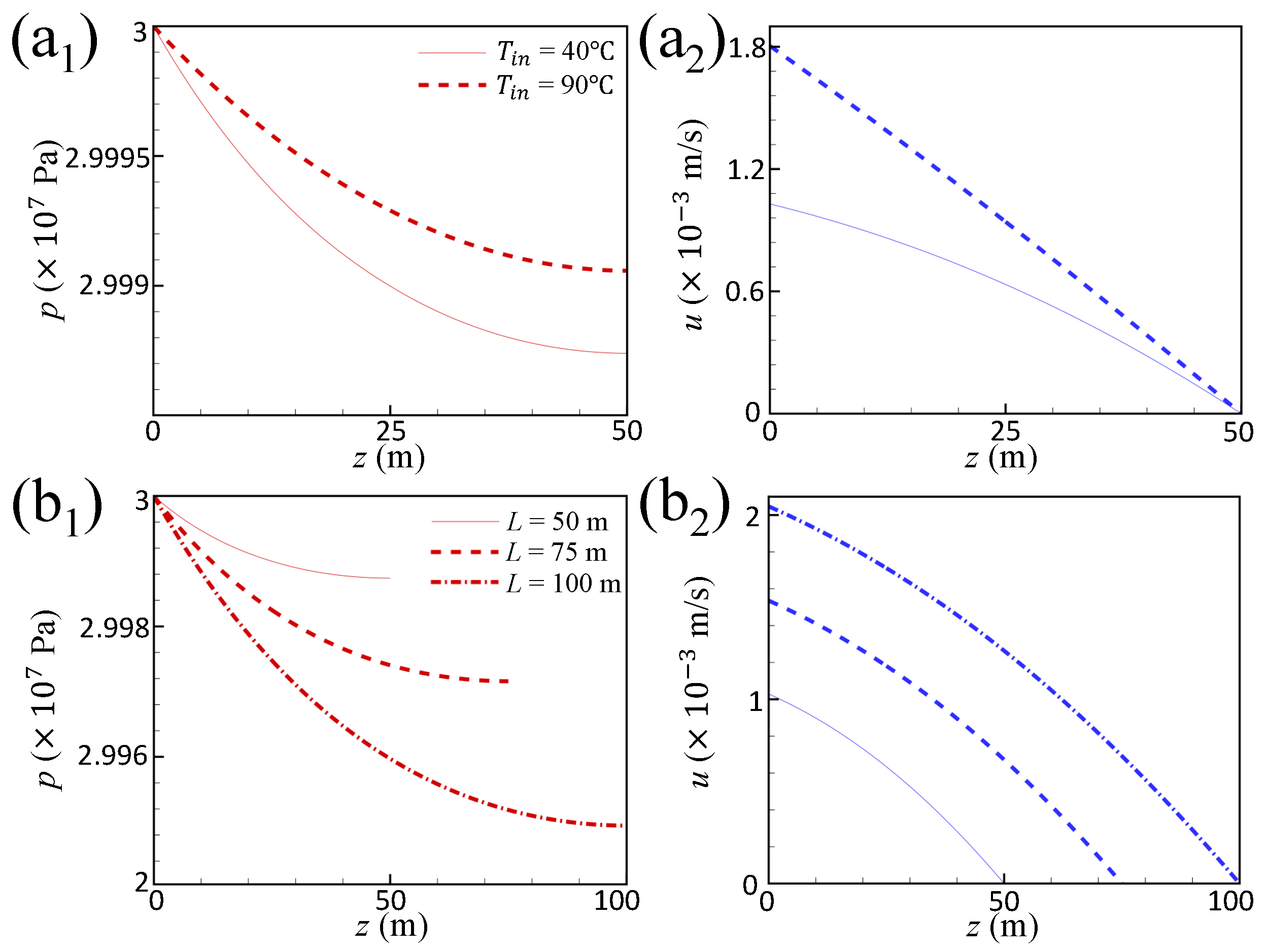
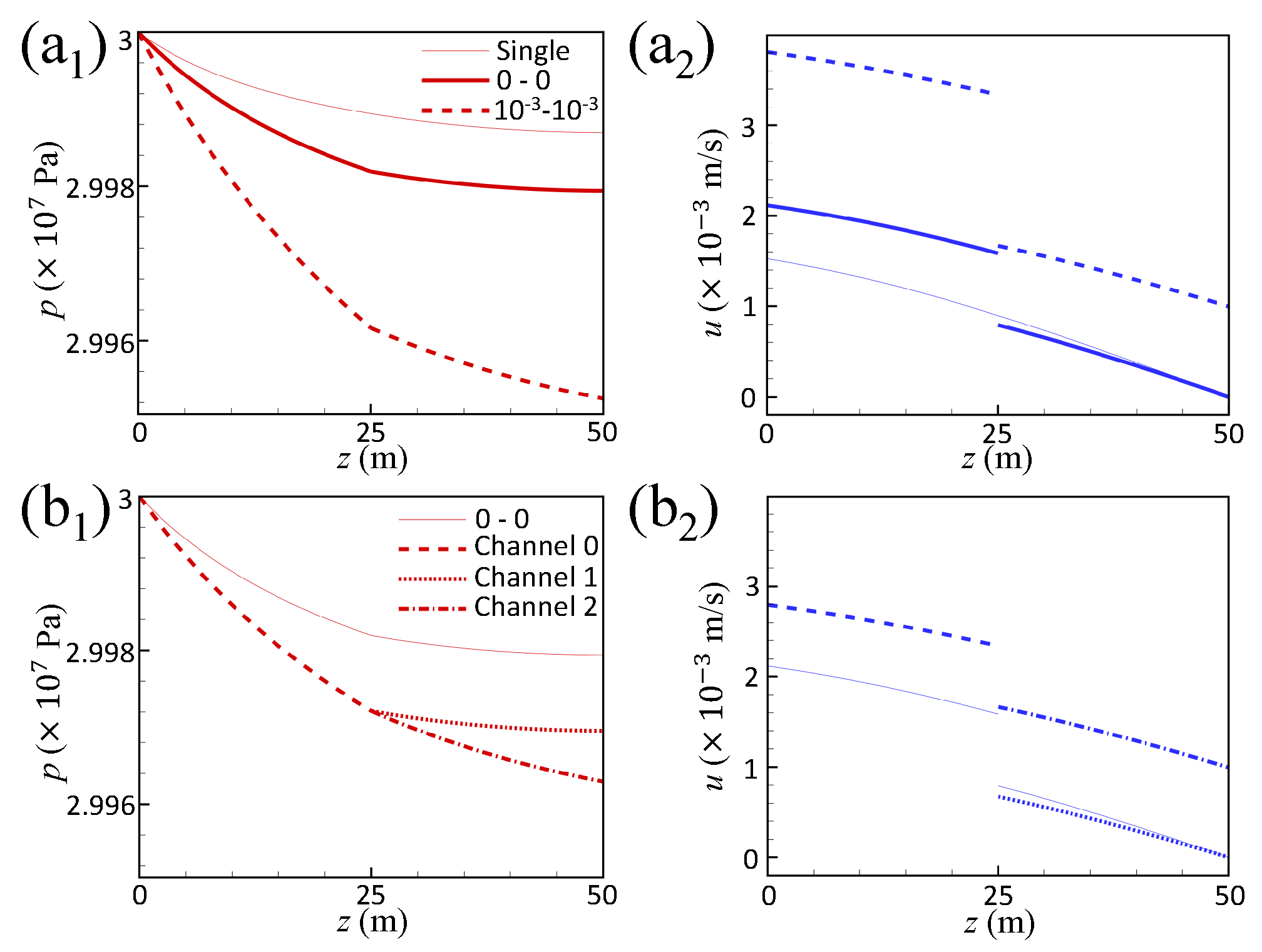
2.3. Result
3. The Upward Flow of Liquid in a Bifurcated Fracture
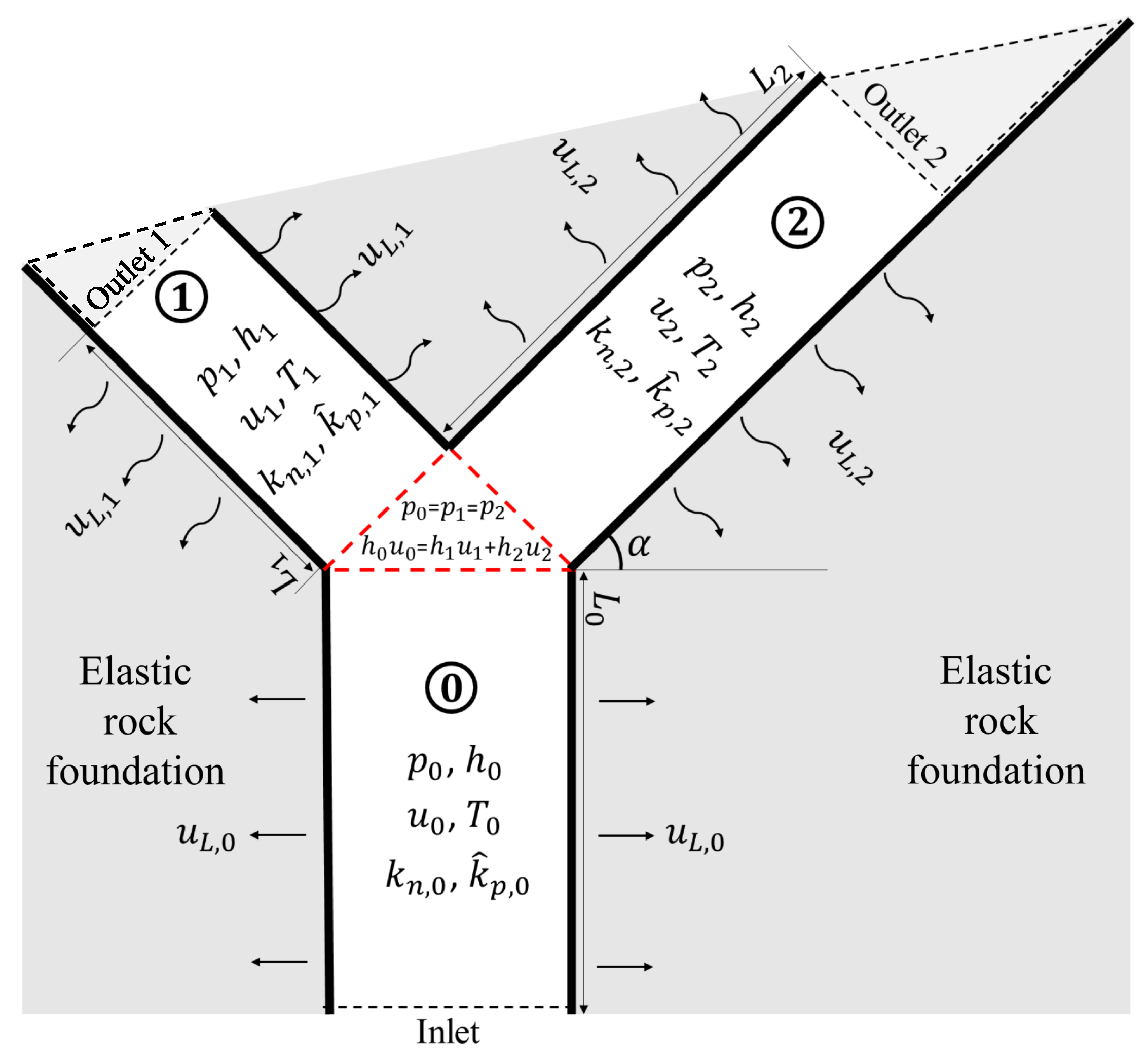
3.1. Model
3.1.1. Governing Equations
3.1.2. The Boundary and Initial Conditions
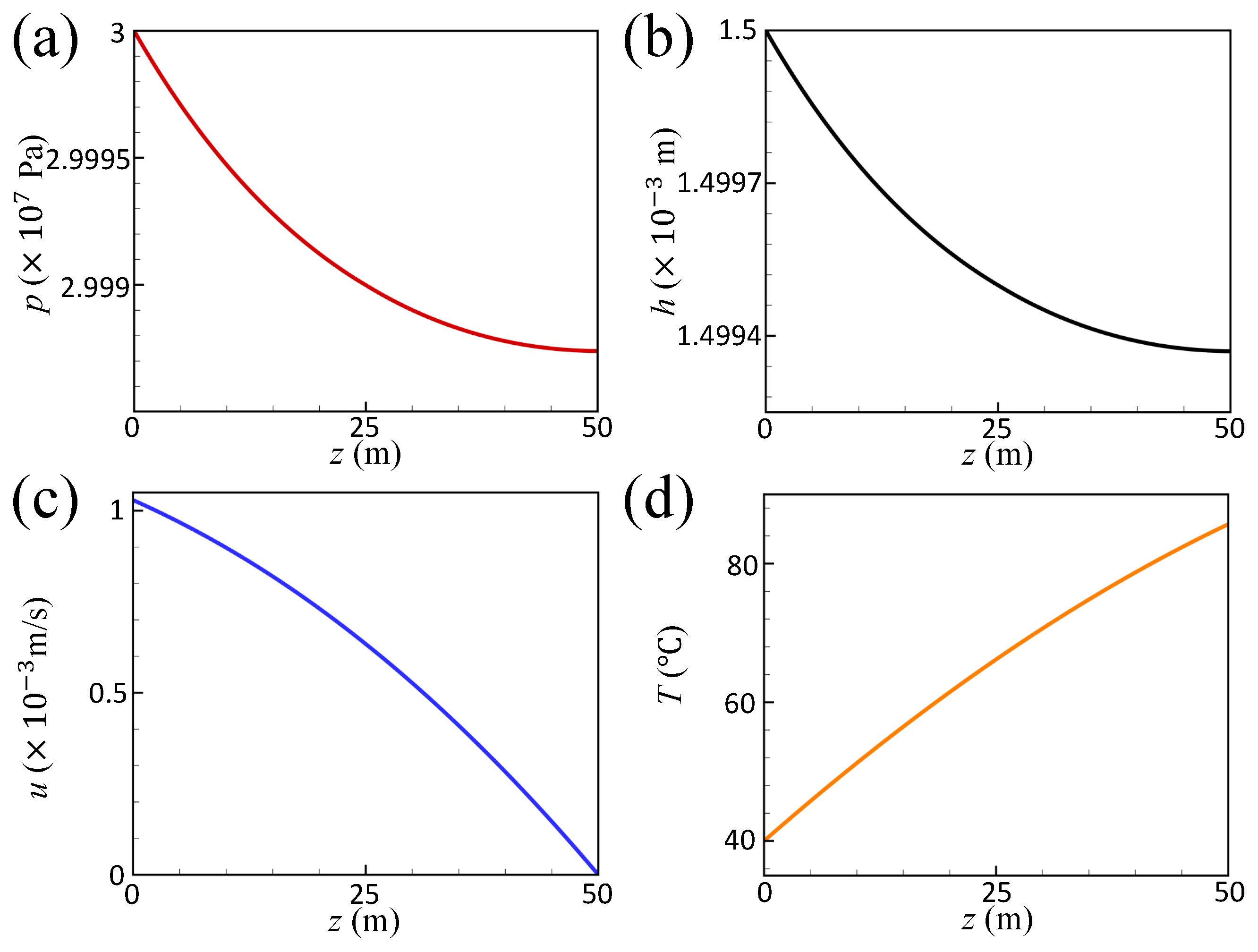
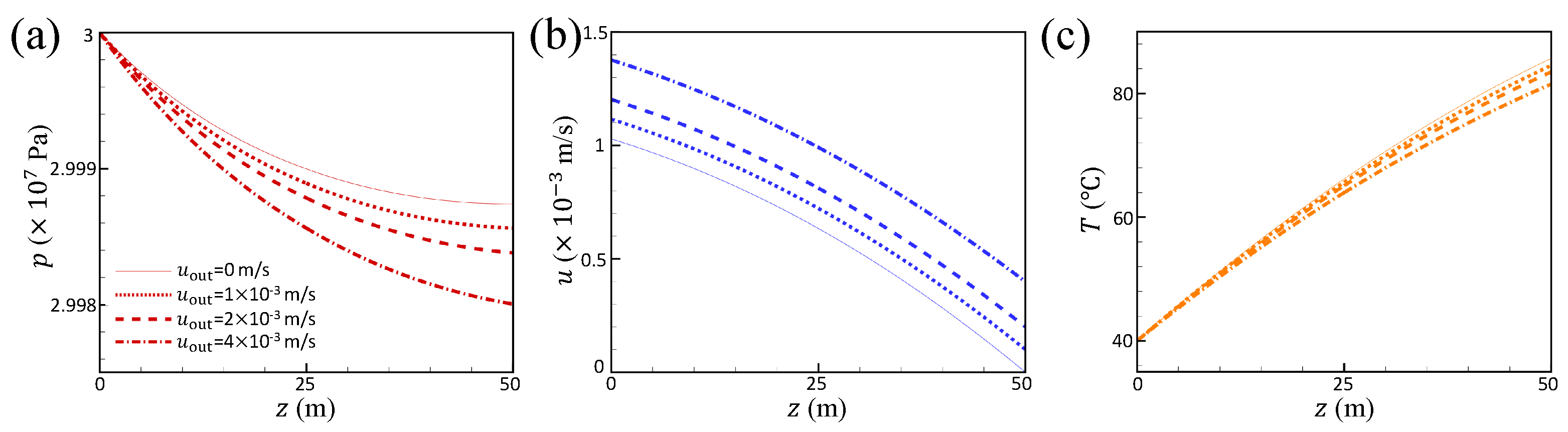
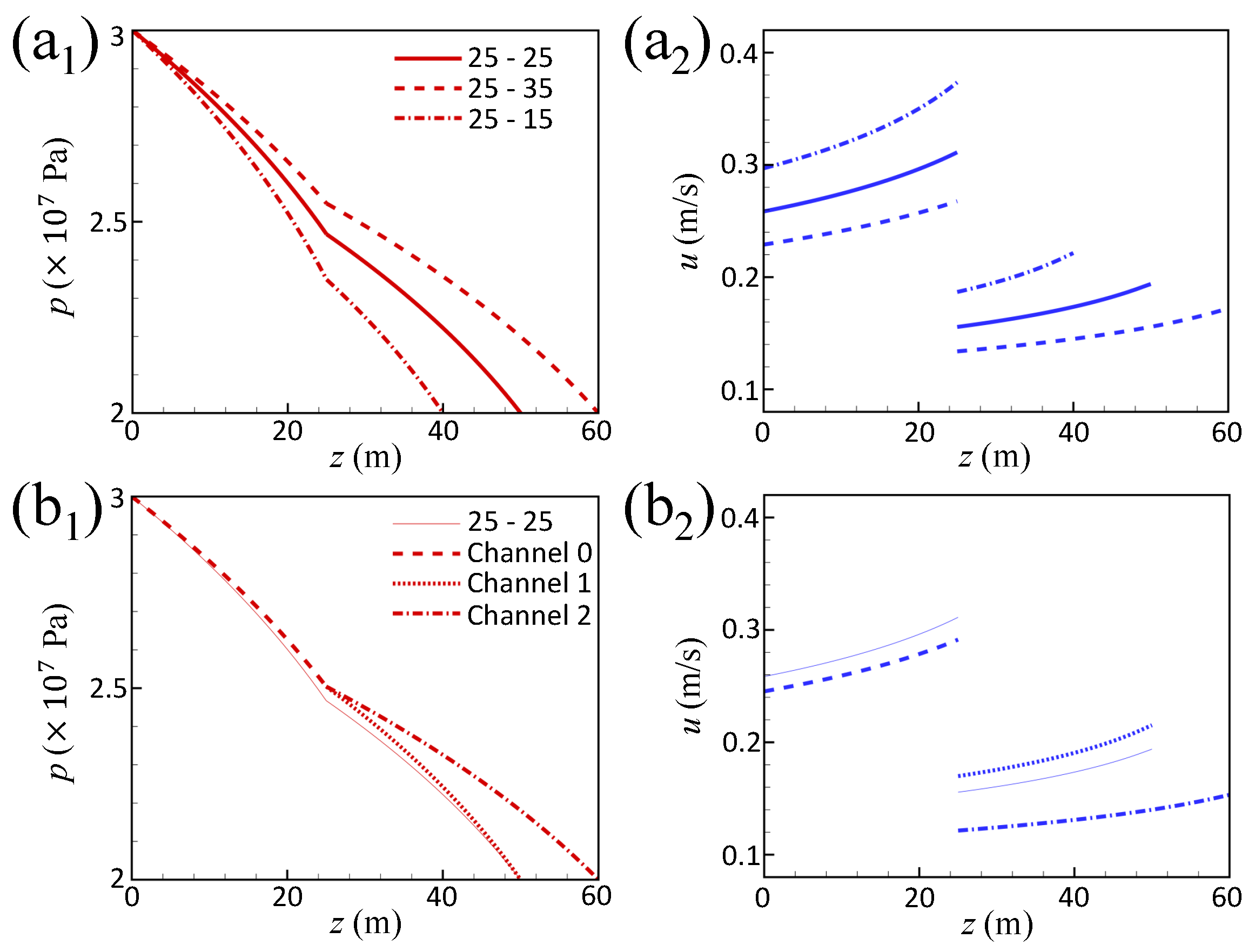
3.2. Results
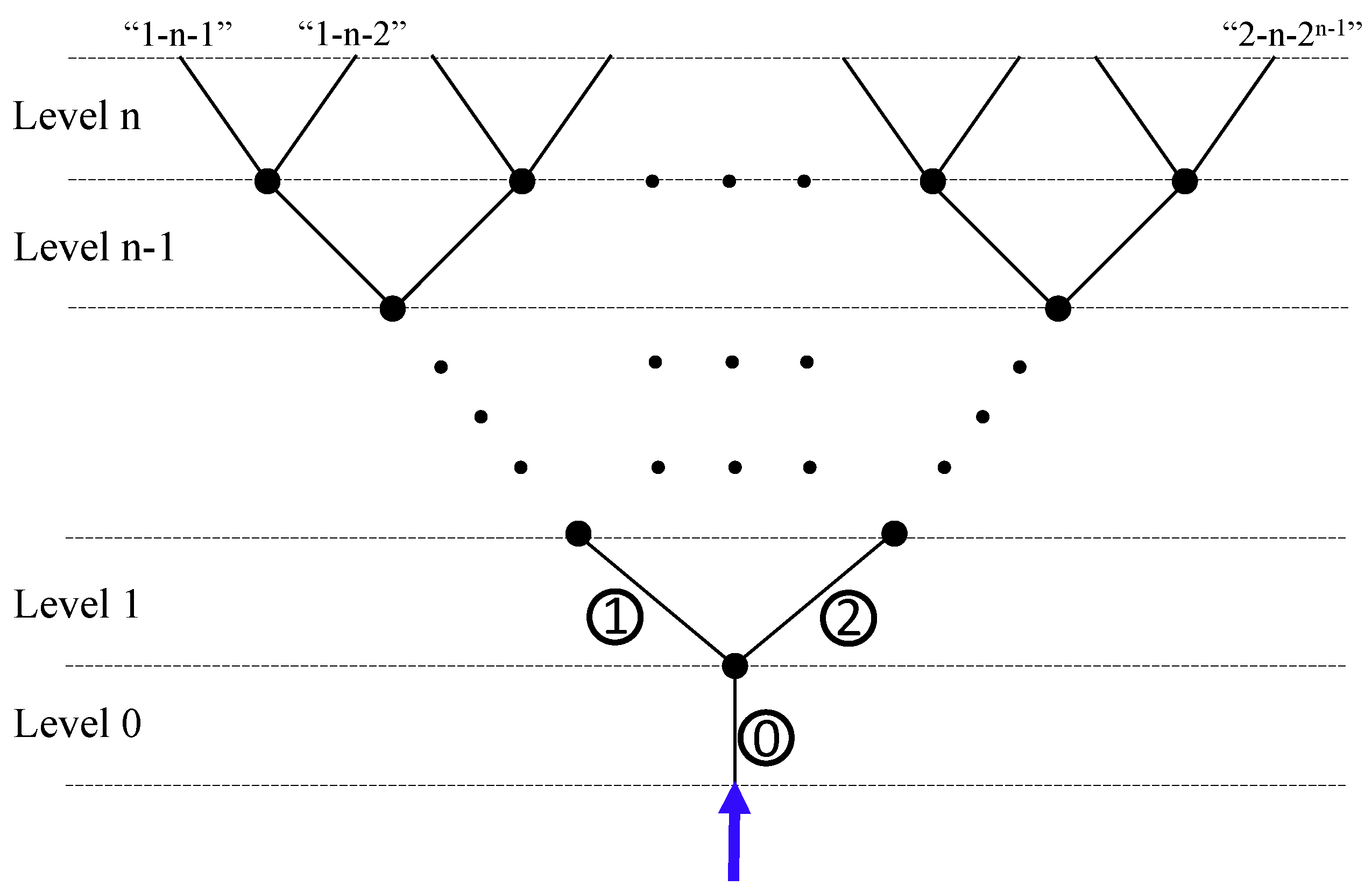
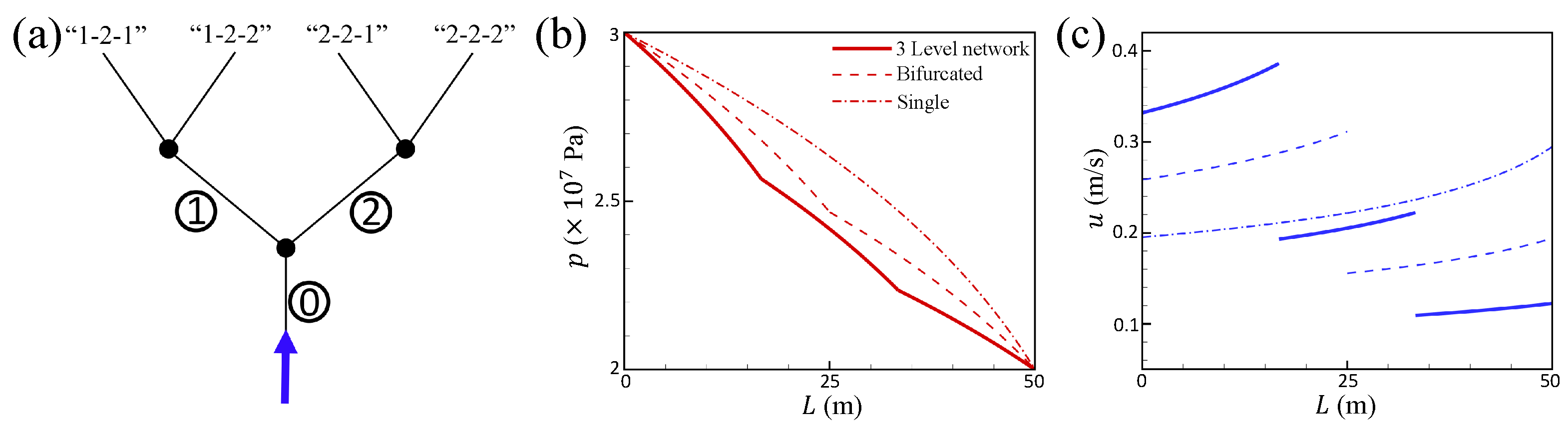
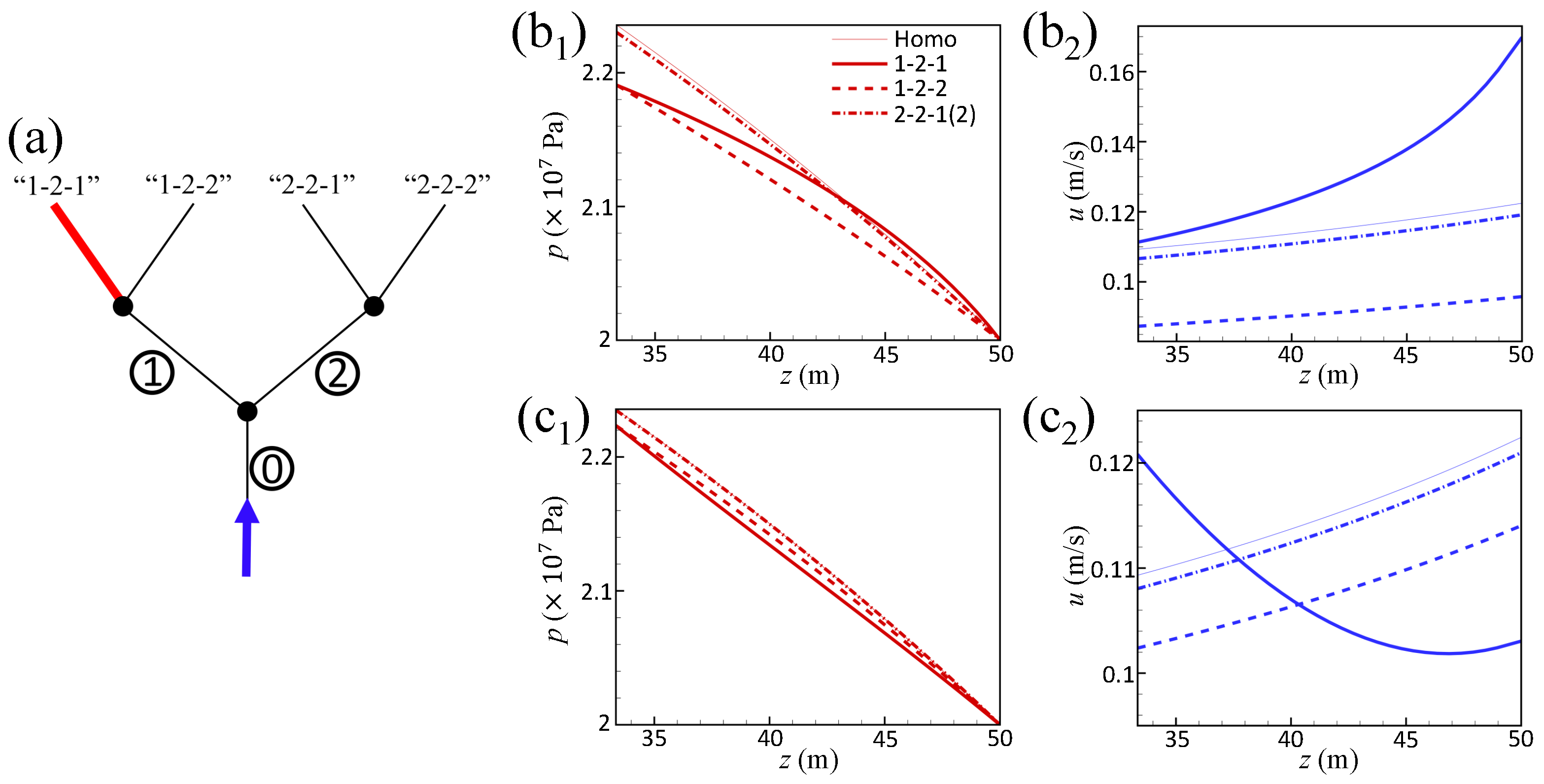
4. The Upward Flow in a Fracture Network
4.1. Model
4.1.1. Governing Equation
4.1.2. The Boundary and Initial Condition
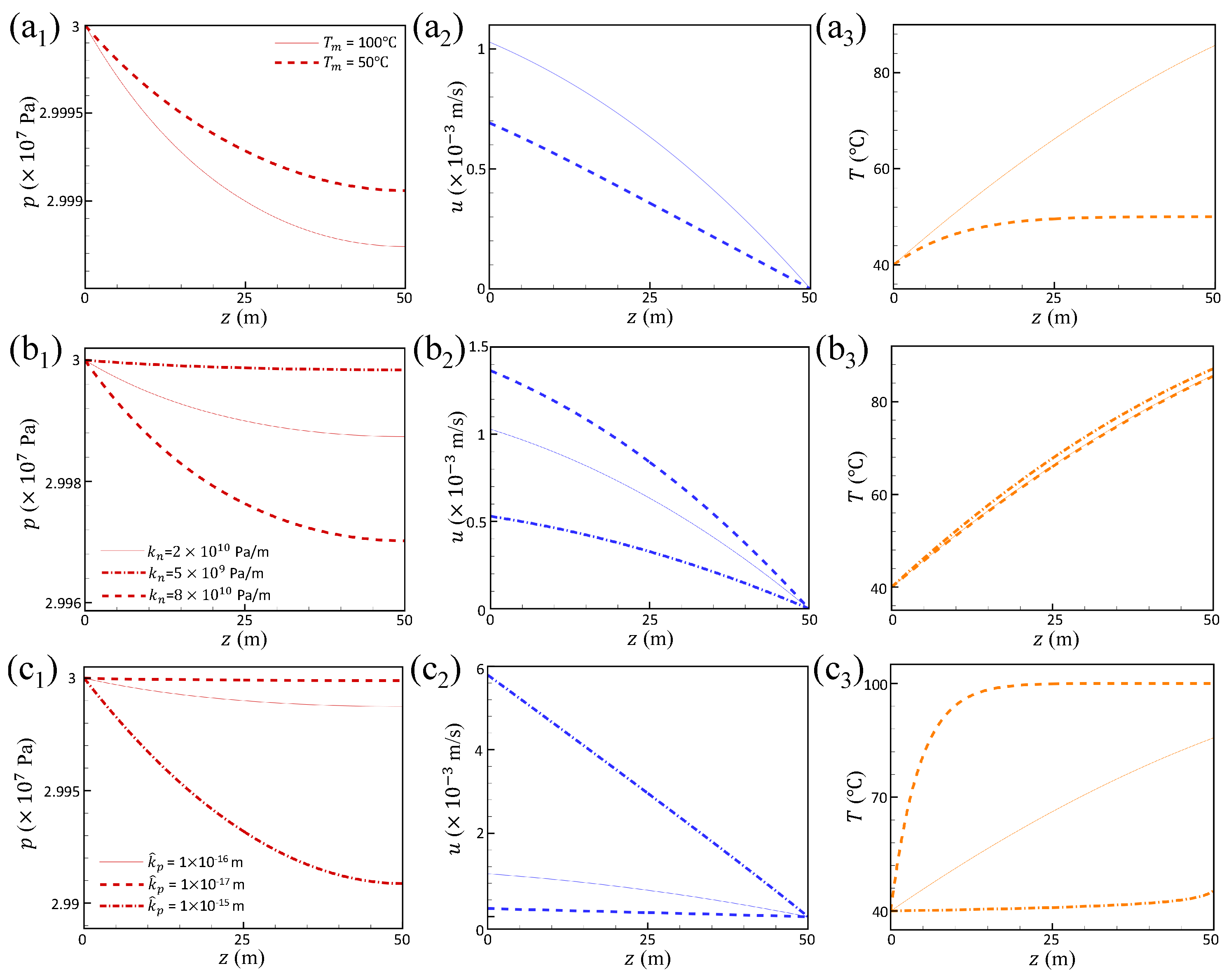
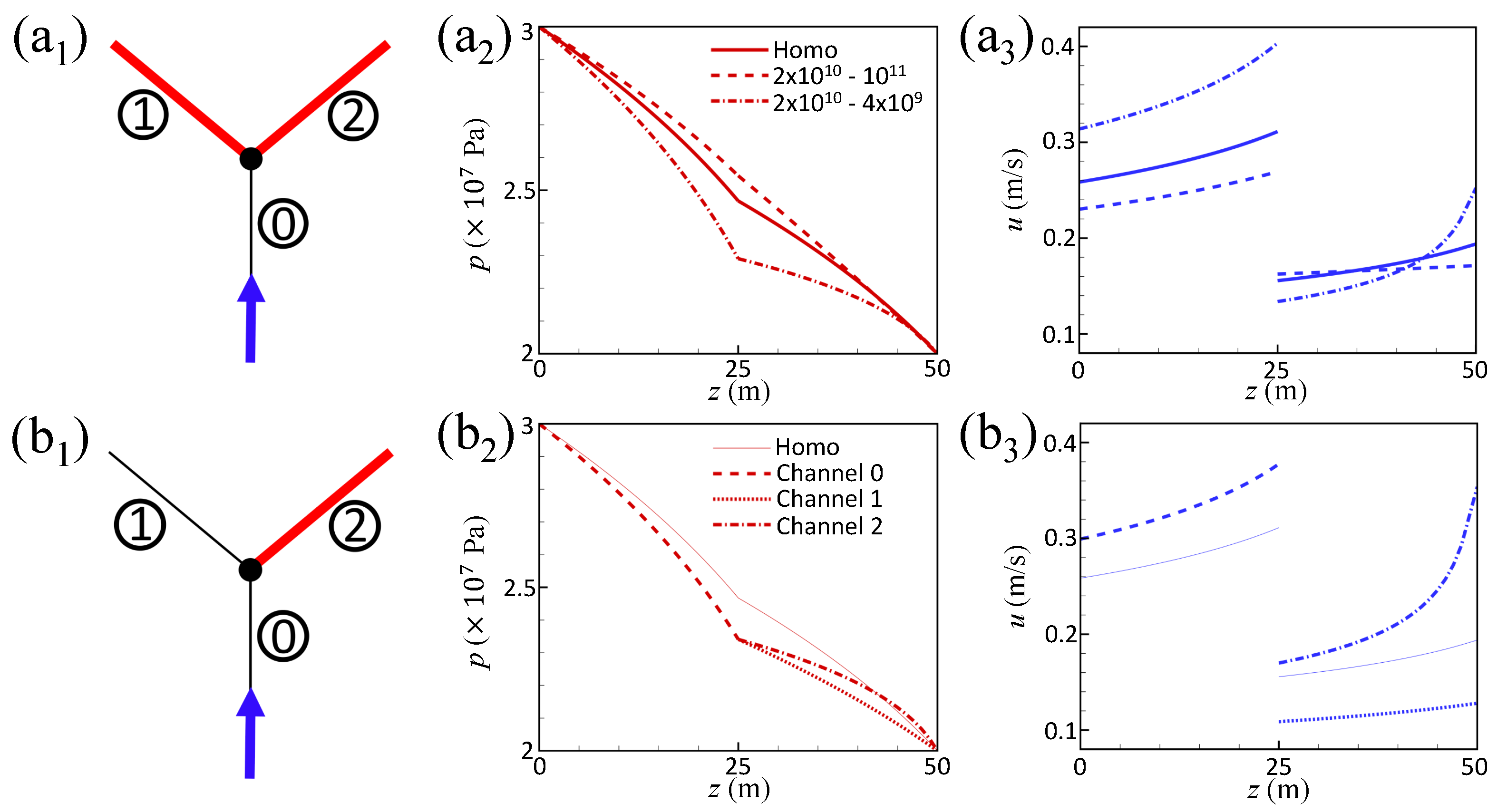
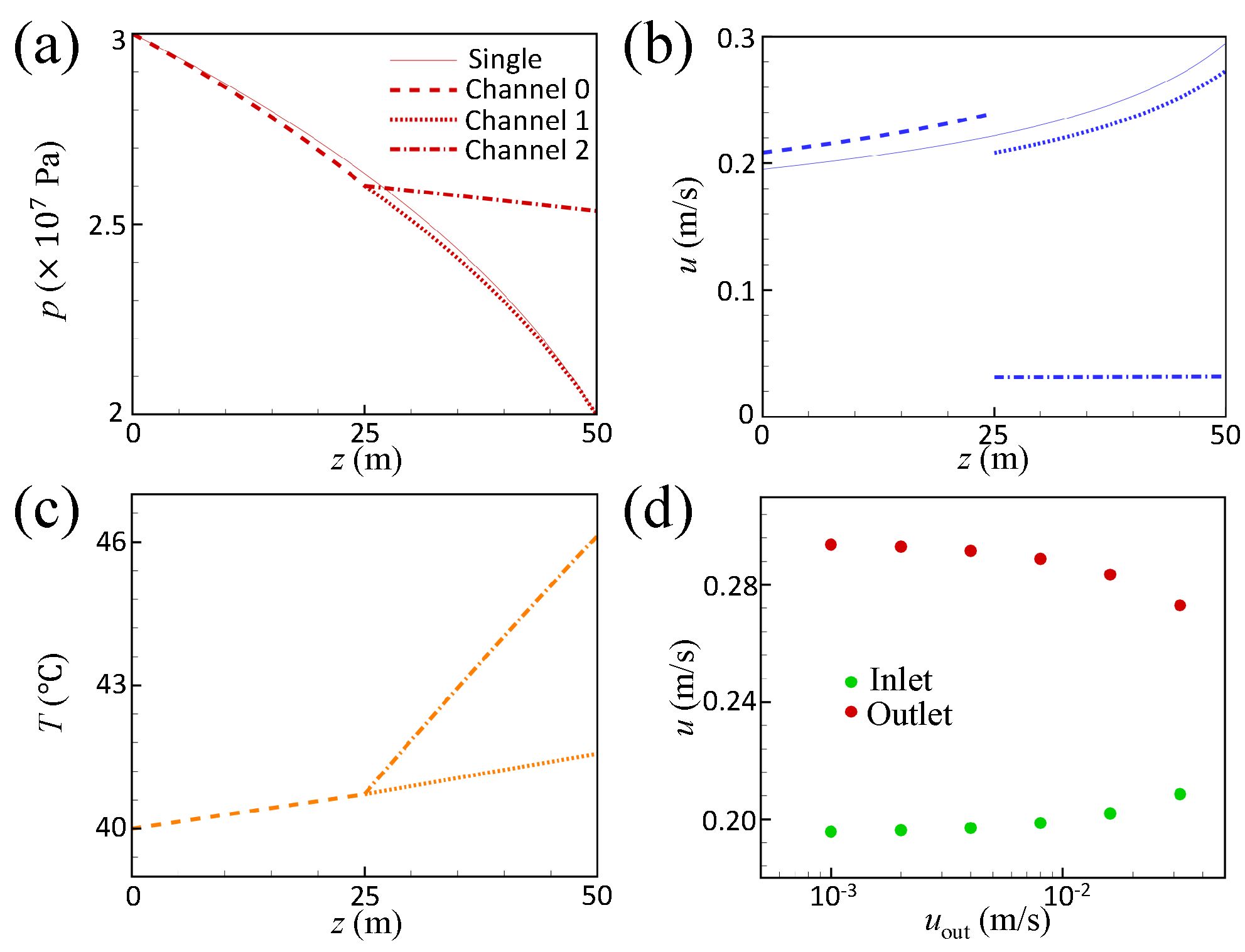
4.2. Result
5. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. The Discretization of Our Governing Equation
References
- Zou, C.; Zhai, G.; Zhang, G.; Wang, H.; Zhang, G.; Li, J.; Wang, Z.; Wen, Z.; Ma, F.; Liang, Y.; et al. Formation, distribution, potential and prediction of global conventional and unconventional hydrocarbon resources. Shiyou Kantan Kaifa/Petroleum Explor. Dev. 2015, 42, 13–25. [Google Scholar] [CrossRef]
- Sieminski, A. EIA Overview; Energy Information Administration: Washington, DC, USA, 2016.
- Gas transport and storage capacity in shale gas reservoirs—A review. Part A: Transport processes. J. Unconv. Oil Gas Resour. 2015, 12, 87–122. [CrossRef]
- Jiang, Q.; Cui, J.; Feng, X.T.; Zhang, Y.H.; Zhang, M.Z.; Zhong, S.; Ran, S.G. Demonstration of spatial anisotropic deformation properties for jointed rock mass by an analytical deformation tensor. Comput. Geotech. 2017, 88, 111–128. [Google Scholar] [CrossRef]
- Zhou, T.; Zhu, J.; Xie, H. Mechanical and Volumetric Fracturing Behaviour of Three-Dimensional Printing Rock-like Samples Under Dynamic Loading. Rock Mech. Rock Eng. 2020, 53, 2855–2864. [Google Scholar] [CrossRef]
- Zhang, S.; Yan, J.; Cai, J.; Zhu, X.; Hu, Q.; Wang, M.; Geng, B.; Zhong, G. Fracture characteristics and logging identification of lacustrine shale in the Jiyang Depression, Bohai Bay Basin, Eastern China. Mar. Pet. Geol. 2021, 132, 105192. [Google Scholar] [CrossRef]
- Gong, L.; Wang, J.; Gao, S.; Fu, X.; Liu, B.; Miao, F.; Zhou, X.; Meng, Q. Characterization, controlling factors and evolution of fracture effectiveness in shale oil reservoirs. J. Pet. Sci. Eng. 2021, 203, 108655. [Google Scholar] [CrossRef]
- Ogata, K.; Senger, K.; Braathen, A.; Tveranger, J. Fracture corridors as seal-bypass systems in siliciclastic reservoir-cap rock successions: Field-based insights from the Jurassic Entrada Formation (SE Utah, USA). J. Struct. Geol. 2014, 66, 162–187. [Google Scholar] [CrossRef]
- Wang, X.; Zhou, X.; Li, S.; Zhang, N.; Ji, L.; Lu, H. Mechanism Study of Hydrocarbon Differential Distribution Controlled by the Activity of Growing Faults in Faulted Basins: Case Study of Paleogene in the Wang Guantun Area, Bohai Bay Basin, China. Lithosphere 2022, 2022, 7115985. [Google Scholar] [CrossRef]
- Cartwright, J.; Huuse, M.; Aplin, A. Seal bypass systems. Am. Assoc. Pet. Geol. Bull. 2007, 91, 1141–1166. [Google Scholar] [CrossRef]
- Cartwright, J.; Santamarina, C. Seismic characteristics of fluid escape pipes in sedimentary basins: Implications for pipe genesis. Mar. Pet. Geol. 2015, 65, 126–140. [Google Scholar] [CrossRef]
- Oda, M. An equivalent continuum model for coupled stress and fluid flow analysis in jointed rock masses. Water Resour. Res. 1986, 22, 1845–1856. [Google Scholar] [CrossRef]
- Chaudhary, A.S.; Ehlig-Economides, C.; Wattenbarger, R. Shale oil production performance from a stimulated reservoir volume. In Proceedings of the SPE Annual Technical Conference and Exhibition, Denver, CO, USA, 30 October–2 November 2011; OnePetro: Richardson, TX, USA, 2011. [Google Scholar]
- Agboada, D.K.; Ahmadi, M. Production decline and numerical simulation model analysis of the Eagle Ford Shale oil play. In Proceedings of the SPE Western Regional & AAPG Pacific Section Meeting 2013 Joint Technical Conference, Monterey, CA, USA, 19–25 April 2013; OnePetro: Richardson, TX, USA, 2013. [Google Scholar]
- Karimi-Fard, M.; Durlofsky, L.J.; Aziz, K. An efficient discrete-fracture model applicable for general-purpose reservoir simulators. SPE J. 2004, 9, 227–236. [Google Scholar] [CrossRef]
- Jiang, J.; Younis, R.M. Hybrid coupled discrete-fracture/matrix and multicontinuum models for unconventional-reservoir simulation. SPE J. 2016, 21, 1009–1027. [Google Scholar] [CrossRef]
- Wu, Y.s.; Wang, C.; Li, J.; Fakcharoenphol, P. Transient Gas Flow in Unconventional Gas Reservoir. SPE Annu. 2012, 4–7. [Google Scholar]
- Liu, Y.; Guo, J.; Chen, Z. Leakoff characteristics and an equivalent leakoff coefficient in fractured tight gas reservoirs. J. Nat. Gas Sci. Eng. 2016, 31, 603–611. [Google Scholar] [CrossRef]
- Xu, W.; Thiercelin, M.; Ganguly, U.; Weng, X.; Gu, H.; Onda, H.; Sun, J.; Le Calvez, J. Wiremesh: A novel shale fracturing simulator. In Proceedings of the International Oil and Gas Conference and Exhibition in China, Beijing, China, 8–10 June 2010; OnePetro: Richardson, TX, USA, 2010. [Google Scholar]
- Weng, X.; Kresse, O.; Cohen, C.; Wu, R.; Gu, H. Modeling of hydraulic-fracture-network propagation in a naturally fractured formation. SPE Prod. Oper. 2011, 26, 368–380. [Google Scholar]
- Geng, L.; Li, G.; Wang, M.; Li, Y.; Tian, S.; Pang, W.; Lyu, Z. A fractal production prediction model for shale gas reservoirs. J. Nat. Gas Sci. Eng. 2018, 55, 354–367. [Google Scholar] [CrossRef]
- Zhang, L.; Cui, C.; Ma, X.; Sun, Z.; Liu, F.; Zhang, K. A fractal discrete fracture network model for history matching of naturally fractured reservoirs. Fractals 2019, 27, 1940008. [Google Scholar] [CrossRef]
- Ozdemirtas, M.; Babadagli, T.; Kuru, E. Experimental and numerical investigations of borehole ballooning in rough fractures. SPE Drill. Complet. 2009, 24, 256–265. [Google Scholar] [CrossRef]
- Lai, C.Y.; Zheng, Z.; Dressaire, E.; Wexler, J.S.; Stone, H.A. Experimental study on penny-shaped fluid-driven cracks in an elastic matrix. Proc. R. Soc. Math. Phys. Eng. Sci. 2015, 471, 2182. [Google Scholar] [CrossRef]
- Leythaeuser, D.; Schaefer, R.G.; Yukler, A. Role of diffusion in primary migration of hydrocarbons. AAPG Bull. 1982, 66, 408–429. [Google Scholar]
- Yuan, L.; Zhou, F.; Li, B.; Gao, J.; Yang, X.; Cheng, J.; Wang, J. Experimental study on the effect of fracture surface morphology on plugging efficiency during temporary plugging and diverting fracturing. J. Nat. Gas Sci. Eng. 2020, 81, 103459. [Google Scholar] [CrossRef]
- Li, M.; Zhou, F.; Sun, Z.; Dong, E.; Zhuang, X.; Yuan, L.; Wang, B. Experimental study on plugging performance and diverted fracture geometry during different temporary plugging and diverting fracturing in Jimusar shale. J. Pet. Sci. Eng. 2022, 215, 110580. [Google Scholar] [CrossRef]
- Wang, B.; Zhou, F.; Wang, D.; Liang, T.; Yuan, L.; Hu, J. Numerical simulation on near-wellbore temporary plugging and diverting during refracturing using XFEM-Based CZM. J. Nat. Gas Sci. Eng. 2018, 55, 368–381. [Google Scholar] [CrossRef]
- Dana, A.; Peng, G.G.; Stone, H.A.; Huppert, H.E.; Ramon, G.Z. Backflow from a model fracture network: An asymptotic investigation. J. Fluid Mech. 2019, 864, 899–924. [Google Scholar] [CrossRef]
- Guo, J.; Liu, Y. A comprehensive model for simulating fracturing fluid leakoff in natural fractures. J. Nat. Gas Sci. Eng. 2014, 21, 977–985. [Google Scholar] [CrossRef]
- Biot, M.A.; Masse, L.; Medlin, W.L. Temperature analysis in hydraulic fracturing. J. Pet. Technol. 1987, 39, 1389–1397. [Google Scholar] [CrossRef]
- Kamphuis, H.; Davies, D.R.; Roodhart, L. A new simulator for the calculation of the in situ temperature profile during well stimulation fracturing treatments. J. Can. Pet. Technol. 1993, 32. [Google Scholar] [CrossRef]
- Wenzheng, L.; Qingdong, Z.; Jun, Y. Numerical simulation of elasto-plastic hydraulic fracture propagation in deep reservoir coupled with temperature field. J. Pet. Sci. Eng. 2018, 171, 115–126. [Google Scholar]
- Whitsitt, N.F.; Dysart, G.R. The effect of temperature on stimulation design. J. Pet. Technol. 1970, 22, 493–502. [Google Scholar] [CrossRef]
- Kovalyshen, Y.; Detournay, E. A reexamination of the classical PKN model of hydraulic fracture. Transp. Porous Media 2010, 81, 317–339. [Google Scholar] [CrossRef]
- Lu, C.; Jiang, H.; Qu, S.; Zhang, M.; He, J.; Xiao, K.; Yang, H.; Yang, J.; Li, J. Hydraulic fracturing design for shale oils based on sweet spot mapping: A case study of the Jimusar formation in China. J. Pet. Sci. Eng. 2022, 214, 110568. [Google Scholar] [CrossRef]
- Zhi, D.; Xiang, B.; Zhou, N.; Li, E.; Zhang, C.; Wang, Y.; Cao, J. Contrasting shale oil accumulation in the upper and lower sweet spots of the lacustrine Permian Lucaogou Formation, Junggar Basin, China. Mar. Pet. Geol. 2023, 150, 106178. [Google Scholar] [CrossRef]
- Wang, Y.; Li, T.; Chen, Y.; Ma, G. A three-dimensional thermo-hydro-mechanical coupled model for enhanced geothermal systems (EGS) embedded with discrete fracture networks. Comput. Methods Appl. Mech. Eng. 2019, 356, 465–489. [Google Scholar] [CrossRef]
- Detournay, E.; Garagash, D.I. The near-tip region of a fluid-driven fracture propagating in a permeable elastic solid. J. Fluid Mech. 2003, 494, 1–32. [Google Scholar] [CrossRef]
- Ma, C.; Dong, C.; Luan, G.; Lin, C.; Liu, X.; Elsworth, D. Types, characteristics and effects of natural fluid pressure fractures in shale: A case study of the Paleogene strata in Eastern China. Pet. Explor. Dev. 2016, 43, 634–643. [Google Scholar]
- Xu, S.; Hao, F.; Xu, C.; Zou, H.; Zhang, X.; Zong, Y.; Zhang, Y.; Cong, F. Hydrocarbon migration and accumulation in the northwestern Bozhong subbasin, Bohai Bay Basin, China. J. Pet. Sci. Eng. 2019, 172, 477–488. [Google Scholar] [CrossRef]
- Chen, X.; Zhao, J.; Chen, L. Experimental and numerical investigation of preferential flow in fractured network with clogging process. Math. Probl. Eng. 2014, 2014, 879189. [Google Scholar] [CrossRef]
- Wang, W.; Su, Y.; Zhang, X.; Sheng, G.; Ren, L. Analysis of the complex fracture flow in multiple fractured horizontal wells with the fractal tree-like network models. Fractals 2015, 23, 1550014. [Google Scholar] [CrossRef]
- Umar, I.A.; Negash, B.M.; Quainoo, A.K.; Ayoub, M.A. An outlook into recent advances on estimation of effective stimulated reservoir volume. J. Nat. Gas Sci. Eng. 2021, 88, 103822. [Google Scholar] [CrossRef]
- Feng, P.; Ma, H.; Qian, J.; Wang, J.; Cao, Y.; Ma, L.; Luo, Q. Influence of Bifurcated Fracture Angle on Mechanical Behavior of Rock Blocks. Indian Geotech. J. 2023, 53, 622–633. [Google Scholar] [CrossRef]
- LeVeque, R.; Oliger, J. Numerical methods based on additive splittings for hyperbolic partial differential equations. Math. Comput. 1983, 40, 469–497. [Google Scholar] [CrossRef]


| Parameter | Symbol | Unit | Value |
|---|---|---|---|
| Fracture length | L | m | 50 |
| Original fracture aperture | m | 0.001 | |
| Original pressure | Pa | 2 × 107 | |
| Inlet pressure | Pa | 3 × 107 | |
| Fracture stiffness | Pa/m | 2 ×10 10 | |
| Permeability per thickness | m | 1 × 10−16 | |
| Liquid density | kg/m3 | 1000 | |
| Liquid specific heat | C | J/(kg·K) | 4199.2 |
| Reference viscosity module | Pa s | 0.2 | |
| Rock density | kg/m3 | 2650 | |
| Rock specific heat | J/(kg·K) | 1003.8 | |
| Rock thermal conductivity | W/(m·K) | 5.23 | |
| Inlet temperature | °C | 40 | |
| Rock matrix temperature | °C | 100 | |
| Reference temperature | °C | 20 | |
| Arrhenius activation energy | J/(g) | 20,091.84 | |
| Reservoir porosity | - | 0.1 | |
| Universal gas constant | R | J/(g··K) | 8.31 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, Z.; Li, Y.; Li, H.; Men, J.; Zhang, S. A Model for Simulating the Upward Flow of a Viscous Fluid in a Fracture Network. Appl. Sci. 2024, 14, 2288. https://doi.org/10.3390/app14062288
Qin Z, Li Y, Li H, Men J, Zhang S. A Model for Simulating the Upward Flow of a Viscous Fluid in a Fracture Network. Applied Sciences. 2024; 14(6):2288. https://doi.org/10.3390/app14062288
Chicago/Turabian StyleQin, Zhipeng, Yang Li, Huifen Li, Jiakun Men, and Shuhang Zhang. 2024. "A Model for Simulating the Upward Flow of a Viscous Fluid in a Fracture Network" Applied Sciences 14, no. 6: 2288. https://doi.org/10.3390/app14062288
APA StyleQin, Z., Li, Y., Li, H., Men, J., & Zhang, S. (2024). A Model for Simulating the Upward Flow of a Viscous Fluid in a Fracture Network. Applied Sciences, 14(6), 2288. https://doi.org/10.3390/app14062288






