Affine Formation Maneuver Control for Multi-Agent Based on Optimal Flight System

Abstract

The use of affine maneuver control to maintain the desired configuration of unmanned aerial vehicle (UAV) swarms has been widely practiced. Nevertheless, the lack of capability to interact with obstacles and navigate autonomously could potentially limit its extension. To address this problem, we present an innovative formation flight system featuring a virtual leader that seamlessly integrates global control and local control, effectively addressing the limitations of existing methods that rely on fixed configuration changes to accommodate real-world constraints. To enhance the elasticity of an algorithm for configuration change in an obstacle-laden environment, this paper introduces a second-order differentiable virtual force-based metric for planning local trajectories. The virtual field comprises several artificial potential field (APF) forces that adaptively adjust the formation compared to the existing following control. Then, a distributed and decoupled trajectory optimization framework that considers obstacle avoidance and dynamic feasibility is designed. This novel multi-agent agreement strategy can efficiently coordinate the global planning and local trajectory optimizations of the formation compared to a single method. Finally, an affine-based maneuver approach is employed to validate an optimal formation control law for ensuring closed-loop system stability. The simulation results demonstrate that the proposed scheme improves track accuracy by 32.92% compared to the traditional method, while also preserving formation and avoiding obstacles simultaneously.

1. Introduction

The use of unmanned aerial vehicle (UAV) swarms [1,2] has significantly expanded the range of applications and possibilities in the unmanned field, surpassing the capabilities of single-vehicle systems. Formation-based control algorithms aim to guide all vehicles to form specific configurations while maintaining relative velocity and distance. However, relying on fixed formation patterns limits the adaptability of formation control in different environments. Hence, the notion of dynamically altering configurations in UAV formation control has garnered significant attention from researchers, particularly the maneuver control for the purpose of achieving continuous formation change [3,4,5,6]. This approach possesses the ability to autonomously navigate aerial formations in cluttered and wild environments, effectively providing assistance during natural disasters like earthquakes and floods. Maneuver control can aid in formation search and guidance [7]. Additionally, researchers can inspect restricted areas such as documenting structural and cultural artifacts within historical buildings [8] or autonomously searching subterranean environments [9], which can gain situational awareness and assist specialized personnel in specific missions, such as assessing the structural integrity of collapsed buildings, tunnels, mines, exploration of a newly discovered branch in a cave network, and searching for lost persons. Formation configurations can be associated with different tasks and environments, such as collective animal behavior [10] in nature or reconnaissance and strike missions [11,12]. However, continuous configuration changes increase system complexity and communication requirements among UAV agents, particularly when adjusting and preserving the position and orientation of each agent in motion [13]. Additionally, the effectiveness of configuration change may be hindered by various external and internal constraints.

Therefore, various methods combining formation control with configuration changes have been extended to multi-agent systems, resulting in more versatile forms of unmanned vehicles, including maneuvering [13,14], surveillance [15], reconnaissance [16], and traffic monitoring and management [17]. In addition to researching practical constraints and scenarios, distributed methods have proven to be more adaptable and consider mutual autonomy coordination for configuration changes, in contrast to centralized approaches [3,17]. This suggests that the characteristics of the distributed strategy are better suited for the dynamic configuration changes of formations. Distributed formation control strategies closely related to configurations can be broadly categorized into position, displacement, and distance-based methods, based on the types of sensed and controlled variables used thus far. However, these methods have limited effectiveness in accurately tracking the target formation [18], which restricts configuration changes to variations in time, scales, and orientation of the target configuration [19,20,21]. From a control perspective, the dynamic change of configuration can be specified at the global formation level [19,20,21,22] or the local level [23,24]. The global approach involves presetting the path points of the formation’s center of gravity for agents to follow, maintaining the rigid body structure by preserving relative positions and transitioning between different formation shapes. On the other hand, the local approach focuses on agent-level control, which is more adaptable to tasks and collision avoidance. The first approach involves maintaining the rigid structure of the configuration with constant constraints, requiring a configuration with a predefined change scale and nominal configuration. Ref. [6] proposed an affine-based generation method for target configuration using an interaction law with both designed positive and negative weights (different from consensus control law). Ref. [22] extended the affine-based method by introducing a stress matrix to enable general linear transformations involving translation, rotation, scaling, shear, or compositions of these transformations. These methods ensure that the configuration maintains the rigid graph structure in each step, preserving collinearity and distance ratios, while also enabling maneuver control. The second approach is more adaptable, aiming to maximize the observation capabilities of the robot team and facilitate obstacle avoidance. This method focuses on actively moving mobile agents to improve the accuracy of target detection with a dynamically adjustable geometry. Ref. [25] studied a formation loop that forms an un-rigid configuration using a distributed non-linear model predictive controller (DNMPC) and an estimator module. Ref. [26] discussed the use of artificial potential fields (APF) as a cost function in a non-linear model predictive controller (NMPC) with a modified A* path planner method for configuration changes. These methods exhibit generality, allowing adaptation to both static and dynamic environments, where the value and direction of velocity can be adjusted based on the current cost.

However, these methods have limitations in terms of generality. The first method fails to address sudden changes in an agent’s velocity in terms of value and direction. The velocity is directly designed in each step of the configuration transformation, relying on prior information about the environment. The second approach heavily relies on strong communication interaction, which may lead to reconstruction failures in the event of breakdowns in one or more agents. Therefore, the goal of formation control with continuous configuration changes is to ensure low communication costs, an adaptable change model, as well as equilibrium and stability within the system.

Thus, this paper presents an algorithm that integrates APF-based leader control [27,28,29,30] with the affine formation, while utilizing behavior optimization for local trajectory calculation. This algorithm enables efficient navigation for multi-agents within a formation by incorporating artificial potentials to guide agent movement, a virtual leader for formation path planning, and geometric pattern modeling for obstacle avoidance. Moreover, the agents within the formation are initially placed randomly and are adjusted applying additional forces to move individual agents to their new equilibrium positions in various configurations.

The objective of employing potential functions is to guide agents away from obstacles and towards or away from the virtual leader, while also ensuring cohesion among agents as they navigate through the environment [31,32,33]. In other words, the configuration of the formation can be adjusted based on the error in the velocity vector of agents and the virtual leader. Therefore, the potential functions used in our methodology consist of virtual leader forces and obstacle forces. As the virtual leader’s position moves, the artificial potential relationships guide the group along the path defined by the virtual leader’s motion. By relying on the global motion of a virtual leader, the complexity of planning multiple collision-free paths for numerous vehicles is reduced to planning just one collision-free path. Consequently, the interacting agents enter optimization procedures, where the explicit fourth-order Runge–Kutta methods [34] are introduced into the local control law. This method is commonly used to solve ordinary differential equations (ODE) and estimates the value of the next step by utilizing the slope of the midpoint with truncation error O ($L^4$) in each step size. Subsequently, the local trajectory [35] of each agent estimates the value of the function at the next step by calculating the slopes of multiple intermediate points to obtain the numerical solution.

The virtual leader abstraction is utilized to guide the formation through the environment. It is important to note that the virtual leader is not a physical vehicle, but an imaginary point used as a reference for the movement of the formation. The construction of the virtual leader is similar to Leonard [3]. The virtual leader abstraction offers a significant advantage by eliminating the need for individual node trajectories, focusing solely on planning the path of the virtual leader through areas of interest for the entire team. This approach greatly reduces communication requirements. Additionally, the motion of the virtual leader is limited to a distance that prevents any of the vehicles from experiencing excessive total forces in the direction of the virtual leader’s motion.

Furthermore, the communication requirements among agents may vary depending on the level of precision needed for configuration changes. Each agent updates its trajectory within the formation based on the positions of other agents, obstacles, and the virtual leader each time step. The position of the virtual only needs to be transmitted to each agent once per update at most, regardless of whether there is a need to recalculate the position to adjust the local trajectory. This approach ensures that the bandwidth requirements for all agents interacting with their positions remain manageable in small formations (less than 20 agents), as it considers only horizontal motion consensus. However, for larger groups, the position information would be limited to agents within a nearby radius.

This paper investigates the generality of formation-desired configurations and proposes an adaptable algorithm for local trajectory planning. The algorithm ensures the continuous change of geometric patterns and improves the consistency of local trajectory planning with realistic constraints. Consequently, the formation control relies less on prior information and enhances the ability to avoid obstacles and other agents in real-time, particularly in situations involving sudden obstacles. Additionally, the combination of formation control methods and optimal techniques expands the utilization of formation configuration variations and definitions to adapt to more complex environments.

The contributions of this article could be summarized as follows:

• A novel non-linear and dynamical system for formation configurations changing is created by the combination of the global and local control law, which could relieve the dependence on the rigid body of formation.
• An APF-based adjustment metric is developed for local trajectory planning through various forces. It could solve the problem of local minimum value of APF and update the local navigation to filter the discrete value due to a sudden change of velocity.
• A novel optimal framework has been integrated, combining a virtual leader to consider dynamic feasibility, obstacle avoidance, and flexibility. This framework can improve the elasticity of configuration variations in potential collision.

The paper is organized as follows. Section 2 describes the preliminaries. In Section 3, the description of the interaction forces among agents, virtual leader, and obstacles is presented. The description and proof of the main results for local control laws are given in Section 4. The results of the simulation and discussions are drawn in Section 5. Section 6 concludes the entire paper and provides a glimpse into future prospects.

2. Preliminaries

This section mainly introduces the preliminary knowledge of unmanned aerial vehicles, containing graph theory to depict the inner relationship of the system and the state–space equation of the UAV system.

2.1. Graph Theory

A weighted undirected graph is denoted as $G=(V,E,A)$, where $V=(v_1,v_2,\dots ,v_n)$ represents the set of all vertices in the undirected graph, and each vertex represents an agent. $E=\{e_{ij}=(v_i,v_j)\}\subseteq v\times v$ represents the edge set between vertices, and $e_{ij}=(v_i,v_j)$ represents the edge from $v_i$ vertex to $v_j$ vertex; an edge connection between two vertices indicates that there is an information interaction between these two vertices. The graph is undirected if it allows two-way communication; otherwise, it is directed. $A={[a_{ij}]}_{n\times n}$ represents the adjacency matrix indicating the relationship between agents, where $a_{ij}$ is the weight of the side $e_{ij}=(v_i,v_j)$ and where the diagonal elements of the matrix are $A$ all 0. For $i,j=1,2,3,\dots ,n(i\ne j)$, if the agents $v_i$ and $v_j$ can receive information from each other, then the elements in the adjacency matrix are $a_{ij}=a_{ji}>0$; otherwise, the element in the adjacency matrix is 0. This paper has only considered an undirected graph, in which $e_{ij}\in E\iff e_{ji}\in E$.

2.2. Kinematic and Dynamic Models of UAV

The multi-agent formation is denoted as $(G,p)$, where the vertex $v_i$ within graph $G$ is mapped to point $p_i$. In addition, it is assumed that the first agents $n_l$ are leaders and the rest $n_f$ are followers. Let $V_l=\{v_1,v_2,\dots ,v_l\}$ and $V_f=\{v_{l+1},v_{l+2},\dots ,v_n\}$ be the sets of leaders and followers, respectively, where $l,f\in n$.

A mass-point [18,36] can be used to describe the UAV agent and the motion of the formation. The fixed-wing agent model is described as Figure 1 shows:

It is shown that all these variables are presented to depict the agent motion from the inertial coordinate frame $(x,y,z)$; thus, the kinematic motion equations for UAV can be expressed as

$$\begin{array}{l}{\dot{x}}_i=V_i\cos {\gamma }_i\cos {\chi }_i\\ {\dot{y}}_i=V_i\cos {\gamma }_i\sin {\chi }_i\\ {\dot{h}}_i=V_i\sin {\gamma }_i\end{array}$$

(1)

Meanwhile, the dynamic of UAV is given by

$$\begin{array}{l}{\dot{V}}_i=\frac{T_i-D_i}{m_i}-g\sin {\gamma }_i\\ {\dot{\gamma }}_i=\frac{g}{V_i}(n_{gi}\cos {\varphi }_i-\cos {\gamma }_i)\\ \dot{\chi }=\frac{L_i\sin {\varphi }_i}{m_i{V}_i\cos {\gamma }_i}\end{array},$$

(2)

where $x_i$ and $y_i$ are the range displacement projected on the $X$ and $Y$ axes separately, $h_i$ is the flight altitude, and $V_i$ is the speed which is assumed as ground speed in the paper, ${\chi }_i$ and ${\gamma }_i$ are the heading angle and the flight one. $T_i$ is the engine thrust vector directed with the velocity vector, $D_i$ is a general term for drag. Additionally, $m_{i}g$ is used to describe the gravity of the agent, the $g$ load $n_{gi}=L_i/m_{i}g$ is contained by an elevator, ${\varphi }_i$ the banking angle and the engine thrust $T_i$ are considered as the control inputs.

Therefore, by the use of the feedback linearization technology, the non-linear UAV model Formulation (1) and (2) can be simplified to a linear constant system

$$\left\{\begin{array}{l}{x}_i(t)=u_{xi}(t)\\ y_i(t)=u_{yi}(t)\\ h_i(t)=u_{hi}(t)\end{array}\right.$$

(3)

However, $u_{xi}(t)$, $u_{yi}(t)$, and $u_{hi}(t)$ are virtual control inputs to describe the accelerations in each way. The actual control input is given as

$$\begin{array}{l}{\varphi }_i={\tan }^{-1}[\frac{u_{yi}\cos {\chi }_i-u_{xi}\sin {\chi }_i}{\cos {\gamma }_i(u_{hi}+g)-\sin {\gamma }_i(u_{xi}\cos {\chi }_i-u_{yi}\sin {\chi }_i)}]\\ n_{gi}=\frac{\cos {\gamma }_i(u_{hi}+g)-\sin {\gamma }_i(u_{xi}\cos {\chi }_i-u_{yi}\sin {\chi }_i)}{g\cos {\varphi }_i}\\ T_i=[\sin {\gamma }_i(u_{hi}+g)+\cos {\gamma }_i(u_{xi}\cos {\chi }_i+u_{yi}\sin {\chi }_i)]m_i+D_i\end{array},$$

(4)

where the heading angle ${\chi }_i$ can be expressed as $\tan {\chi }_i={\dot{y}}_i/{\dot{x}}_i$, the fight one ${\gamma }_i$ is $\sin {\gamma }_i={\dot{h}}_i/V_i$. Thus, in terms of the state–space representation, denoting ${\mathit{p}}_i=[x_i y_i h_i]$, ${\mathit{v}}_i=[v_{xi} v_{yi} v_{hi}]$, and ${\mathit{u}}_i=[u_{xi} u_{yi} u_{hi}]$, which are the position, velocity, and acceleration control vector, the double-integrator system is reduced as

$$\left\{\begin{array}{l}{\dot{\mathit{p}}}_i(t)={\mathit{v}}_i(t)\\ {\dot{\mathit{v}}}_i(t)={\mathit{u}}_i(t)\end{array}\right.$$

(5)

where ${\mathit{p}}_i\in R^n$, ${\mathit{v}}_i\in R^n$, ${\mathit{u}}_i\in R^n$. Consider a flock of $n$ agents in $R^d$ and ${\mathit{p}}_i\in R^d$ as the position of agent $i$ and $\mathit{p}=[p_1^T,p_2^T,\dots ,p_n^T]\in R^{dn}$ is the configuration of all the agents, where $d\ge 2$ and $n\ge d+1$. Let $m$ be the number of edges in an undirected graph and the orientation of which is the direction assignment to each edge.

Given the substantial difference in time constants between the horizontal and vertical trajectory controllers, configuration control can be concentrated primarily on achieving consensus in the horizontal positional and velocity motion. Meanwhile, the control input is composed of anticipated configuration, reference trajectory, velocity, and state information of adjacent entities.

It is presupposed that all followers possess a restricted situational awareness, and their capability to detect fellows is constrained by their sensing range. Supposing all Unmanned Aerial Vehicles (abbreviated as UAV) possess an equivalent efficacious sensing range, thus the neighbor set of agent $i$ can be depicted as:

$$N_i=\{j:\parallel {\mathit{p}}_{ij}\parallel <R,j=1,\dots ,n;j\ne i\}$$

(6)

where ${\mathit{p}}_{ij}={\mathit{p}}_i-{\mathit{p}}_j$ is the position vector from UAV $i$ to UAV $j$, $\parallel \cdot \parallel$ is the Euclidean norm, $R$ is the sensing range.

Let $U_{ij}$ denote the artificial potential between UAV $i$ and $j$, $R_0$ and $R_1,R_2$ are sensing range and desired distance, respectively. $\otimes$ is the Kronecker product and $\parallel \cdot \parallel$ as the Euclidean norm of vector notation, $I_n\in R^{n\times n}$ is the identity matrix of order $n$, and $\dim (\cdot )$ is the dimension of a linear space. For any vector $x$, $diag(x)$ denotes the diagonal matrix whose $ii\mathrm{th}$ diagonal entry is the $i\mathrm{th}$ entry of $x$. ${\mathrm{Z}}_i$ denotes the total artificial potential of UAV $i$.

2.3. Affine Transformation Description

Based on the undirected graph $G$ to describe the communication topology of multi-agent formation, denote the $R={[R_l,R_f]}^T={[r_1,r_2,\dots ,r_N]}^T$ as the nominal configuration and let $S$ be the affine span. Let the dimension be $d=2$ and $P={\left\{p_i\right\}}_{i=1}^n$ in ${ℝ}^2$ be the affine image set and the associated definitions and lemmas about affine transformation are presented as follow [22].

Definitions 1 (Affine Span). 

A linear space can be obtained by any affine span. Thus, provided with the nominal configuration ${\left\{r_i\right\}}_{i=1}^N$ for formation $G$, the affine span $S$ is:

$$S=\left\{{\displaystyle {\sum }_{i=1}^N\alpha r_i:{\alpha }_i\in {ℝ}^2 \mathrm{and} }{\displaystyle {\sum }_{i=1}^N{\alpha }_i=1}\right\}$$

(7)

Lemma 1 (Affine Span with Rank condition). 

The nominal configuration ${\left\{r_i\right\}}_{i=1}^N$ affinely span ${ℝ}^2$ if and only if $N\ge 3$ and $rank(\overline{R}(r))=3$, where $\overline{R}(r)=[R,1_N]\in {ℝ}^{N\times 3}$.

Definitions 2 (Affine Image). 

The affine image set consisting of all the affine transformations of the nominal configuration ${\left\{r_i\right\}}_{i=1}^N$, which is defined as follows:

$$I(r)=\{P={[p_1^T,p_2^T,\dots ,p_N^T]}^T\in {ℝ}^{2N}|p_i=A^{\prime }{r}_i+b\}$$

(8)

where $I(R)$ is the predefined affine image and can be applied to all time-varying target configurations, and a linear subspace because it is closed under addition and scalar multiplication, $A^{\prime }\in {ℝ}^{2\times 2}$ and $b\in {ℝ}^2$ are the linear affine transformation.

Lemma 2 (General Rigid). 

The nominal configuration is universally rigid if and only if the stress matrix is positive semi-definite and satisfies $\mathrm{rank}(\mathrm{\Omega })=N-3$.

Definitions 3 (Stress Matrix). 

The stress matrix can be viewed as generalized graph Laplacian matrices with both positive and negative edge weights. Let graph stress denote as the scalar ${\left\{{\omega }_{ij}\right|{\omega }_{ij}={\omega }_{ji},{\omega }_{ij}\in ℝ\}}_{ij\in E}$, ${\omega }_{ij}>0$ represents the attractive force and ${\omega }_{ij}<0$ the opposite, and denote if:

$${\displaystyle {\sum }_{j\in N_i}{\omega }_{ij}({\mathit{p}}_j-{\mathit{p}}_i)}=0$$

(9)

the equilibrium set $\mathrm{\Omega }\in {ℝ}^{N\times N}$ satisfies:

$${[\mathrm{\Omega }]}_{ij}=\left\{\begin{array}{l}0, i\ne j,(i,j)\notin E,\\ -{\omega }_{ij} i\ne j,(i,j)\in E,\\ {\displaystyle {\sum }_{k\in N_i}{\omega }_{ik}} i=j.\end{array}\right.$$

(10)

Equation (10) can be expressed in a matrix form as $(\mathrm{\Omega }\otimes I_2)R=0$, denote the $\overline{\mathrm{\Omega }}=\mathrm{\Omega }\otimes I_2$:

$$\overline{\mathrm{\Omega }}=\mathrm{\Omega }\otimes I_2=\left[\begin{array}{l}{\overline{\mathrm{\Omega }}}_{ll} {\overline{\mathrm{\Omega }}}_{lf}\\ {\overline{\mathrm{\Omega }}}_{fl} {\overline{\mathrm{\Omega }}}_{ff}\end{array}\right]$$

(11)

Definitions 4 (Affine Localizability). 

Denote the nominal formation $(G,r)$ as affinely localizable if and only if ${\left\{r_i\right\}}_{i=1}^N$ affinely span ${ℝ}^2$ (Lemma 1) and any $p={[p_l^T,p_f^T]}^T\in I(r)$, $p_f^T$ can be uniquely determined by $p_l^T$.

Lemma 3 (Affine Localizability of Nominal Formation). 

If the nominal configuration ${\left\{r_i\right\}}_{i=1}^N$ affinely span ${ℝ}^2$ and $\mathrm{\Omega }$ is positive semi-definite, $(G,r)$ is affinely localizable if and only if ${\overline{\mathrm{\Omega }}}_{ff}$ is nonsingular.

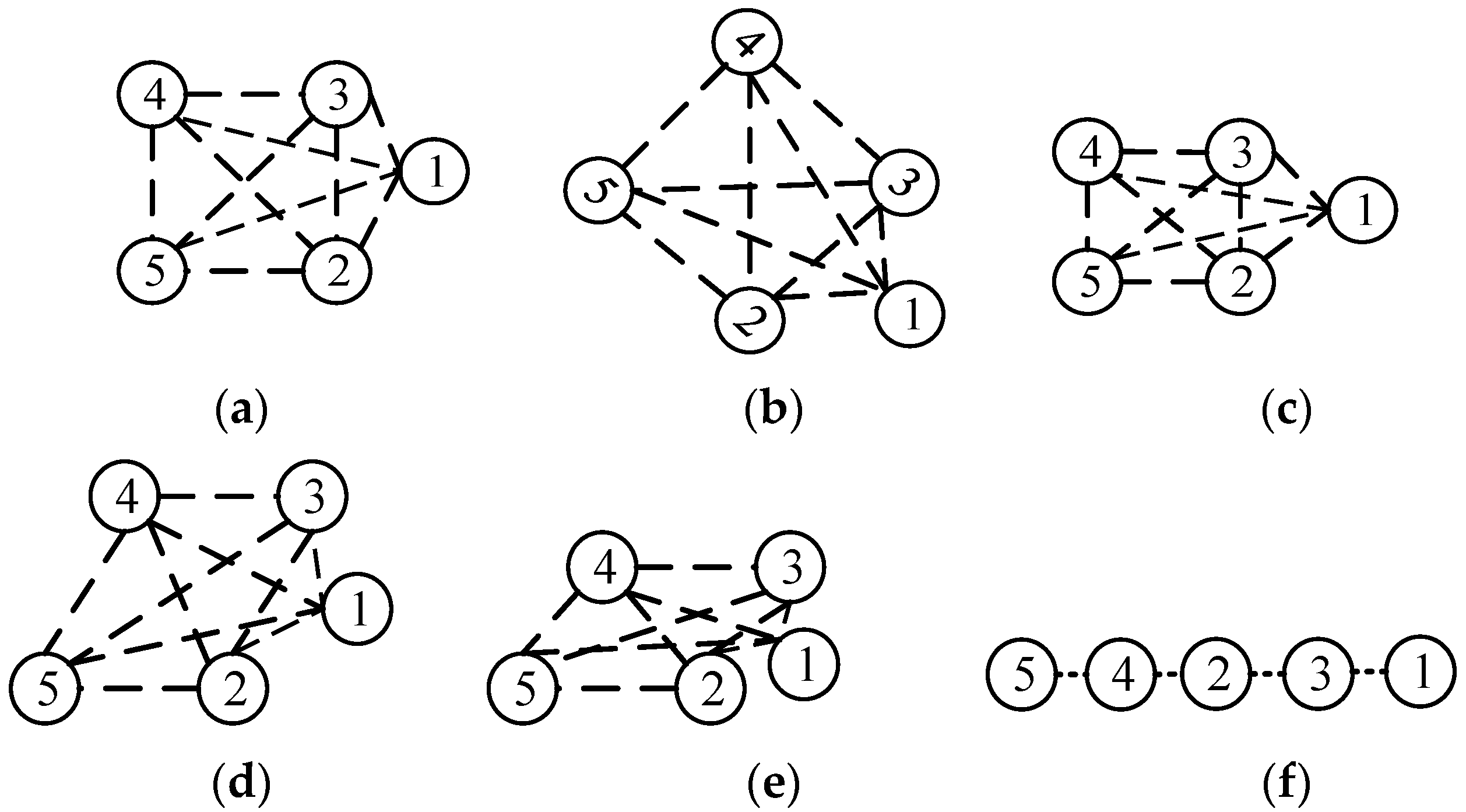
From Figure 2, it can be seen that Figure 2b–d are obtained by rotating, scaling, and shearing the original formation Figure 2a, respectively. Figure 2e is obtained from Figure 2d by reducing the scale in the vertical direction. Figure 2f, where the four points are collinear, is obtained from Figure 2e by reducing the scale in the vertical direction to zero.

Due to the simplification of the communication complexity, only leaders need to be aware of the affine transformation $(A,b)$ and controlled only. Thus, the leader–follower strategy can be well adopted as the control law, and the leaders’ positions will have a one-to-one correspondence to the affine transformation $[A(t),b(t)]$.

3. Agent Motion by Forces

In this section, we propose the concept of an artificial potential function (APF)-based virtual leader strategy with the extraordinary ability to abruptly alter the position of others, which is absolutely essential for executing intricate maneuvers within the swarm.

3.1. APF-Based Virtual Leader Forces

Previous research on affine-based formation control [21,22] primarily relies on prior information about obstacles. However, when realistic constraints are introduced into the control law, such as communication loss or sudden situations, the proposed algorithm may not successfully navigate. This is due to the unknown obstacles causing the loss of rigidity during the transition to a predefined configuration. To address this issue, this paper introduces the APF-based virtual leader, which is more suitable for driving a large group of UAVs to make sudden changes in flight direction. The APF assists agents in local trajectory planning, ensuring that the force range between the virtual leader and the real agents remains appropriate.

The dynamic generation of control forces for smooth group navigation is achieved through the use of APF, which effortlessly enables the swarm to navigate around obstacles while maintaining cohesion. The APF of the virtual leader is determined by each agent’s position and the current placement of the virtual leader. The initial position of the virtual leader can be defined as the centroid of the real leaders group. To achieve the desired formation with a rigid body and ensure equilibrium for all agents, the virtual leader should be placed at the centroid, which can be defined as follows:

$$p_{vl}=1/N{\displaystyle {\sum }_{i=1}^N{p}_l}$$

(12)

As illustrated in Figure 3, our approach enhances the maneuverability of the affine-based formation by incorporating a virtual leader alongside conventional leader. This enables agents to change their flight direction and replan their local trajectories. Consequently, agents can interact with multiple obstacles, adaptively adjusting their local trajectories while iteratively evaluating collision possibilities. This concept allows for responsive behavior to environmental changes, as the APF directs agents away from obstacle positions towards new equilibrium positions. The equilibrium position for each agent is determined by following the steepest gradient towards the geometric point where the sum of these virtual forces is zero. The followers then track the plan of the virtual leader at the local level, seamlessly integrating trajectory planning with formation control. The virtual leader is initially positioned at the centroid of the leaders.

The use of artificial potential between the virtual leader and the agents is illustrated in Figure 4. The virtual leader potential function is simply a function of each agent’s position and the virtual leader’s current placement. Let $U_{ij}(|\left|{\mathit{p}}_{ij}\right||)$ represent a non-negative smooth pairwise artificial potential function associated with the relative distance between agent $(i,j)$. It governs the collective and individual movement within the swarm, which satisfies:

$$U_{ij}(||{\mathit{p}}_{ij}||)=\left\{\begin{array}{l}a\ln (||{\mathit{p}}_{ij}||)+\frac{b}{c{(||{\mathit{p}}_{ij}||)}^2}\hspace{1em}||{\mathit{p}}_{ij}||\le d_{sen}\\ a\ln (r)+\frac{b}{c{(r)}^2}\hspace{1em}\hspace{1em}\hspace{1em} ||{\mathit{p}}_{ij}||>d_{sen}\end{array}\right.$$

(13)

where $i,j=1,2,\dots ,N,i\ne j$, $a$, $b$ and $c$ are positive constants, $U_{ij}(|\left|{\mathit{p}}_{ij}\right||)$ is bounded and continuously differentiable over interval $[0,+\infty )$. $\nabla (b/{(|\left|{\mathit{p}}_{ij}\right||)}^2)$ describes the gradient negative cube odd function, which is not defined at 0 point. Therefore, $U_{ij}(|\left|{\mathit{p}}_{ij}\right||)$ would obtain its boundary maximum value $U_0$ when $\left|\right|{\mathit{p}}_{ij}\left|\right|\to 0$; minimum $U_d$ when $(i,j)$ satisfies the desired position; that is, $\left|\right|{\mathit{p}}_{ij}\left|\right|=d$; and the constant $U_r$ when $\left|\right|{\mathit{p}}_{ij}\left|\right|>d_{sen}$. Formulation (13) can describe both the fundamental forces of attraction and repulsion between agents, agents and virtual leaders, and agents and obstacles, $a$, $b$, and $c$ are the positive constants.

Meanwhile, the obstacles could generate a repulsive force solely to prevent collisions and enable the formation to traverse smoothly among multiple obstacles. The obstacles then produce a repulsive force between the agents and polygon edges of obstacles (inversely related to the distance), as follows:

$$U_{ob}={\displaystyle \sum _{k=1}^m\frac{b}{c{(|\left|{\mathit{p}}_{io}\right||)}^2}},{(b,c)}_{ob}$$

(14)

It is important to note that the system does not include a specific obstacle detection law. Instead, it assumes that information about obstacle position and shape is available, for example, through system perception and 3D modeling. However, it is observed that the value and direction can change suddenly to potential forces within the formation. As a result, some may find that their newly calculated trajectory could potentially lead to collisions with other agents or obstacles, when the formation is striving to reach an equilibrium point. Therefore, trajectory planning should be incorporated into the motion of the agents at each time step.

3.2. Local Trajectory Planning

In order to avoid the system oscillations resulted from the sudden change of velocity, the receding horizon strategy is utilized to reduce the settling time in formation control of UAVs swarm navigation in the presence of obstacles. Therefore, the Runge–Kutta of order 4 (RK4) method is introduced in the paper for kinematic discretization description to update the agents’ state.

The purpose of employing this method is to facilitate the adaptability of local trajectories, meaning that new trajectories are smoothed and discretized within the time step prior to the agents reaching new target points. As a result, the agents ultimately converge towards an equilibrium point, where the total sum of virtual forces becomes zero, effectively preventing any potential collisions. The description of local control law is as follows:

$${\mathit{u}}_{local}^i=\underset{f_i^p}{\underbrace{-{\displaystyle {\sum }_{j=1,j\ne i}^N{\nabla }_i[{\lambda }_{ij}{U}_{ij}(\left|\right|{\tilde{\mathit{p}}}_{ij}\left|\right|)+{\lambda }_{io}{U}_{io}(\left|\right|{\tilde{\mathit{p}}}_{io}\left|\right|)+{\lambda }_{iv}{U}_{iv}(\left|\right|{\tilde{\mathit{p}}}_{iv}\left|\right|)]}}}+\underset{f_i^v}{\underbrace{C_1{\displaystyle {\sum }_{j=1,j\ne i}^N({\mathit{v}}_i-{\mathit{v}}_j)}+({\mathit{v}}_i-{\mathit{v}}_{vl})}}$$

(15)

where $C_1$ is the constant value, ${\lambda }_{ij}$, ${\lambda }_{io}$, and ${\lambda }_{iv}$ are different spring constants. ${\mathit{f}}_i^p$ is the gradient-based term, which regulates position consensus by employing local repulsive and attractive forces, ensuring collision avoidance and cohesion maintenance, and ${\mathit{f}}_i^v$ means the agent’s velocity is adjusted by utilizing the weighted average velocity of its neighbors as a reference. Denote $\mathrm{X}\{{\mathit{p}}_i,{\mathit{v}}_i\}$ as the state of the agent, and the state is updated within a time step. Thus, the process of updating is described as follows:

$$X_{n+1}=X_n+h_{n+1}{\displaystyle {\sum }_{i=1}^s{a}_i{k}_i},i=1,2,\dots ,s$$

(16)

$$k_i=f(t_s,x_n^j,x_{n+1}^j),j=1,2,\dots ,s$$

(17)

where the $k_i$ is a slope of four points in the time step interval, calculated at both ends and two midpoints of the interval. Hence, input ${\mathit{u}}_l^i$ is initially derived through the application of the local control law. Subsequently, the acquired position and velocity are discretized to facilitate the update of the local trajectory as Figure 5 shows.

As depicted in Figure 5, the agent interacts with other agents, obstacles (with d-react), and the virtual leader, which generates the three kinds of artificial potential forces $U_i$ to obtain the fast gradient descent direction $\nabla (U_i)$ to equilibrium state $X_i$. Then, the state of the formation would be constantly updated $X_{n+1}^i$ in a receding horizon to avoid the collision. The following Algorithm 1 summarizes the local control.

Algorithm 1: Local Trajectory Planning

Count the error sum ${\tilde{\mathit{p}}}_i$, ${\tilde{\mathit{v}}}_i$ in time step

${\mathit{p}}_{io}={\overrightarrow{p}}_{io}\ast {(d\_react/\left|\right|p_{io}\left|\right|)}^2$ ${\mathit{p}}_{iv}={\overrightarrow{p}}_{iv}\ast \left|\right|p_{iv}\left|\right|$

${\mathit{p}}_{ij}={\overrightarrow{p}}_{ij}\ast \left|\right|p_{ij}\left|\right|$

${\mathit{v}}_{ij}=v_i-v_j$, ${\mathit{v}}_{iv}=v_i-v_{vl}$

Calculate equilibrium location ${\mathit{p}}_i$

${\nabla }_i[U_{ij}(\left|\right|{\tilde{\mathit{p}}}_{ij}\left|\right|)+U_{io}(\left|\right|{\tilde{\mathit{p}}}_{io}\left|\right|)+U_{iv}(\left|\right|{\tilde{\mathit{p}}}_{iv}\left|\right|)]$

Calculate the state $X_{n+1}\{p_i,v_i\}$ in next time

$X_{n+1}=X_n+h{\displaystyle {\sum }_{i=1}^4{a}_i{k}_i}$

Check

$\left|\right|p_{io}\left|\right|<d\_\min$

$\left|\right|v_i\left|\right|<v\_\min$

end

Where $d\_react$ is the sensing distance based on the radius of the obstacles, $d\_\min$ is the minimum distance between agents and obstacles, and $v\_\min$ is the lower bounds of velocity, which can be described as:

$$\left\{\begin{array}{l}{v}_{\min }\le \left|\right|{\mathit{v}}_i\left|\right|\le v_{\max }\\ u_{\min }\le {\mathit{u}}_i\le u_{\max }\end{array}\right.$$

(18)

Furthermore, to mitigate the impact of local minima limitations in the implementation of APF, such as a formation navigating through narrow openings between obstacles, it is essential to reduce the velocity of the virtual leader as the forces applied to the real agents increase.

4. Formation Control with Virtual Leader

4.1. Algorithm Description

If we assume that only a subset of agents in the formation can receive global information, then a widely used distributed controller protocol with a three-component controller protocol can be defined as follows:

$${\mathit{u}}_i=\underset{{\mathit{u}}_{local}}{\underbrace{{\mathit{f}}_i^p+{\mathit{f}}_i^v}}+{\mathit{f}}_i^l$$

(19)

where the first component ${\mathit{f}}_i^p$ and the second one ${\mathit{f}}_i^v$ are the same as (15) in local formation control for input and ${\mathit{f}}_i^l$ is the navigational feedback which would drive the agent to track the global path.

Therefore, the distributed control protocol for an agent based on virtual leader and APF is designed as follows:

$${\mathit{u}}_i=\underset{f_i^p}{\underbrace{-{\displaystyle {\sum }_{j=1,j\ne i}^N{\nabla }_i(U_{ij}+U_{io}+U_{iv})}}}+\underset{f_i^v}{\underbrace{C_1{\displaystyle {\sum }_{j=1,j\ne i}^N({\mathit{v}}_i-{\mathit{v}}_j)+({\mathit{v}}_i-{\mathit{v}}_{vl})}}}+\underset{f_i^l}{\underbrace{f({\mathit{u}}_d,{\mathit{v}}_d,{\mathit{p}}_d)}}$$

(20)

$$f({\mathit{u}}_d,{\mathit{v}}_d,{\mathit{p}}_d)={\mathit{u}}_d-C_2({\mathit{p}}_i-{\mathit{p}}_d)-C_3({\mathit{v}}_i-{\mathit{v}}_d)$$

(21)

where $f({\mathit{u}}_d,{\mathit{v}}_d,{\mathit{p}}_d)$ represents the global path, in which ${\mathit{u}}_d$ and ${\mathit{v}}_d$ are desired velocity and obtained from desired path ${\mathit{p}}_d$. The global path ${\mathit{p}}_d$ is designed by the affine-based control algorithm and the corresponding configurations must be pre-defined.

From Equation (8), the constant is defined as follows:

$$p^{*}(t)=[I_n\otimes A(t)]r+I_{n}b(t)$$

(22)

where $A(t)\in {ℝ}^{d\times d}$ and $b(t)\in {ℝ}^d$ are continuous of $t$. The desired position $p^{*}(t)$ of agent $i\in V$ in the target formation is $p_i^{*}(t)=A(t)r_i+b(t)$, where $r$ is the constant configuration and $(G,r)$ the nominal formation for a typical geometric pattern, such as the standard geometric graph, as illustrated in Figure 2. Thus, the desired control input ${\mathit{u}}_d$ would be:

$${\mathit{u}}_d=-1/{\gamma }_i{\displaystyle {\sum }_{j\in N_i}{\mathrm{\Omega }}_{ij}({\dot{\mathit{p}}}_{id}-{\dot{\mathit{p}}}_{jd})}$$

(23)

where ${\gamma }_i={\displaystyle {\sum }_{j\in N_i}{\omega }_{ij}}$, motion consensus is only considered in the paper; thus, we have ${\mathit{v}}_{1d}=\cdots ={\mathit{v}}_{Nd}={\mathit{v}}_d,$ ${\mathit{p}}_{1d}=\cdots ={\mathit{p}}_{Nd}={\mathit{p}}_d$. Formulations (22) and (23) describe the pre-defined configuration and the formation moves to the desired position ${\mathit{p}}_i(t)\to {\mathit{p}}^{*}(t)(t\to \infty )$. This strategy primarily focuses on ensuring that various pre-defined configurations can be achieved even in the presence of obstacles. Additionally, the locally planned trajectory can be adjusted to avoid collisions if necessary and the sudden change of velocity. The following Algorithm 2 summarizes the desired input control.

Algorithm 2: Formation Control

Pre-define the nominal configurations image

$I(r)=\{P={[p_1^T,p_2^T,\dots ,p_N^T]}^T\in {ℝ}^{2N}|p_i=A^{\prime }{r}_i+b\}$

Regulate the change of formation

${\mathit{p}}^{*}(t)=[I_n\otimes A(t)]r+I_{n}b(t)$

Calculate the desired inputs ${\mathit{u}}_d$ for leaders’ path

${\mathit{u}}_d=-1/{\gamma }_i{\displaystyle {\sum }_{j\in N_i}{\mathrm{\Omega }}_{ij}({\dot{\mathit{p}}}_i-{\dot{\mathit{p}}}_j)}$

Calculate virtual leader trajectory in single-integrator

${\mathit{u}}_{vl}={\dot{\mathit{p}}}_{t+1}-{\dot{\mathit{p}}}_t$

Calculate the real input for followers

${\mathit{u}}_i={\mathit{f}}_i^p+{\mathit{f}}_i^v+{\mathit{f}}_i^l$

Optimize the trajectory (state) in Algorithm 1

$X_{n+1}=X_n+h{\displaystyle {\sum }_{i=1}^4{a}_i{k}_i}$

Nonlinear programming for the spring constant

${\lambda }_{ij}$, ${\lambda }_{io}$ and ${\lambda }_{iv}$ by fmincon in Matlab toolboxes

end

This paper creatively integrates the local control and affine-based global control into a unique optimal control framework. Hence, the approach involves using an affine-based method to generate multiple geometric patterns for all agents, followed by online calculation of local trajectories to update the trajectory and avoid collisions. The aim of this model would achieve collective maneuvers simultaneously and efficiently.

Moreover, the use of virtual leader forces has been considered as an adjustment metric to prevent the collision from agents and obstacles, which would enhance the realistic functional and generality of UAV formation flight. This method can also solve the problem of much communication and feedback between leaders and followers to some extent, as Figure 5 shows.

The following assumptions are made in this paper:

• The obstacle avoidance maneuvers are primarily in the horizontal plane.
• To simplify the calculations of obstacle forces, the obstacles are enclosed within a circle.
• The communication among UAVs is not limited by the information transmission distance.
• The nominal configuration is affinely spanned ${ℝ}^d$ and designed to be generically universally rigid, leaders must satisfy the desired condition of $d+1$ agents affinely spanning ${ℝ}^d$ at least.
• The formation $(G,p)$ maintains the connection relation within the graph $G=(V,E,A)$ through the whole flight.

4.2. Proof of Main Results

In this subsection, the primary outcomes of the motion consensus and formation control protocol for a UAV swarm with virtual agents are presented, supported by the following theorem. The formation stability of the novel control protocol is theoretically analyzed and proved, as stated in the following theorem.

Theorem 1. 

Supposing a disordered swarm of nagents is described by (5) in dynamics and steered by protocol (20) in formation control, if the interaction between agents within the graph $(G,p)$ is undirected and connected for the whole time, ${\mathrm{Z}}_0$ is denoted as the sum of total artificial potential (formation, virtual agent and obstacles), and then the following conclusions are:

• The graph is connected mutually if $Z_0<U_r$ for all $t\ge 0$.
• Obstacles collision can be prevented between the agent and obstacles if $Z_t<U_0$.
• The trajectories of all agents converge to the desired values asymptotically.

Proof of Theorem 1. 

We firstly prove part 1 of Theorem 1.

For the sake of simplicity and without sacrificing generality, it is assumed that $M(1\le M\le N)$ agents function as leaders. Therefore, the kinematic error of the leaders in the system is defined as follows:

$$\left\{\begin{array}{l}{\tilde{\mathit{p}}}_i={\mathit{p}}_i-{\mathit{p}}_d\\ {\tilde{\mathit{v}}}_i={\mathit{v}}_i-{\mathit{v}}_d\end{array}\right.,i=1,2,\dots ,M$$

(24)

based on the fact that the global trajectory is twice differentiable with respect to time and all agents have access to global information. It also satisfies that ${\dot{\mathit{p}}}_d={\mathit{v}}_d$, ${\dot{\mathit{v}}}_d={\mathit{u}}_d$ and we have ${\tilde{\mathit{p}}}_{ij}={\tilde{\mathit{p}}}_i-{\tilde{\mathit{p}}}_j$, ${\dot{\tilde{\mathit{p}}}}_i={\tilde{\mathit{v}}}_i,{\dot{\tilde{\mathit{v}}}}_i={\tilde{\mathit{u}}}_i$.

Given that $Z_t$ represents the summation of the total relative kinetic energy of an agent at time $t$, it can be deduced that:

$${\rm Z}(t)=1/2{\displaystyle {\sum }_{i=1,i\in O}^N\left\{[U_i(\left|\right|{\tilde{\mathit{p}}}_{i{j}^{\prime }}\left|\right|)]+C_2{({\mathit{p}}_i-{\mathit{p}}_d)}^T({\mathit{p}}_i-{\mathit{p}}_d)\left.+C_3{({\mathit{v}}_i-{\mathit{v}}_d)}^T({\mathit{v}}_i-{\mathit{v}}_d)\right\}\right.}$$

(25)

Denote $V_i={\displaystyle {\sum }_{i=1,i\in O}^N\left\{{\tilde{\mathit{p}}}_i^T{\tilde{\mathit{p}}}_i+U(‖{\tilde{\mathit{p}}}_i‖)\right\}}$ as the total artificial of agent $i$. Then in the error system, $\mathrm{Z}(t)$ can be re-written as follows:

$$\mathrm{Z}(t)=\frac{1}{2}{\displaystyle {\sum }_{i=1,i\in O}^N[V_i+{\tilde{\mathit{v}}}_i^T{\tilde{\mathit{v}}}_i]}$$

(26)

It can be easily demonstrated that $Z(t)$ is positive semi-definite, making it a suitable candidate function for Lyapunov analysis. Considering the symmetry of $U_{ij}$ with respect to ${\tilde{\mathit{p}}}_{ij}$, we have the following:

$$\frac{\partial U_i}{\partial {\tilde{\mathit{p}}}_{i{j}^{\prime }}}=\frac{\partial U_i}{\partial {\tilde{\mathit{p}}}_i}=-\frac{\partial U_i}{\partial {\tilde{\mathit{p}}}_{j^{\prime }}}$$

(27)

Thus, we have

$$\frac{d}{dt}\left(\frac{1}{2}{\displaystyle {\sum }_{i=1,i\in O}^N{V}_i}\right)={\displaystyle {\sum }_{i=1,i\in O}^N\left\{{\tilde{\mathit{v}}}_{\mathit{i}}^T({\nabla }_{p_i}{U}_i)+C_2{\tilde{\mathit{v}}}_i^T{\tilde{\mathit{p}}}_i\right\}}$$

(28)

where $U_i={\displaystyle {\sum }_{i\in O}^N{U}_{i{j}^{\prime }}(|\left|{\tilde{\mathit{p}}}_{i{j}^{\prime }}\right||)}$, $j^{\prime }$ means other agents, obstacles, and virtual leaders. Then, obtaining the derivative to time $t$ for $Z(t)$ as follows:

$$\dot{Z}(t)={\displaystyle {\sum }_{i=1,i\in O}^N({\nabla }_{{\mathit{p}}_i}{U}_i)+C_2{\tilde{\mathit{v}}}_i^T{\tilde{\mathit{p}}}_i+{\tilde{\mathit{v}}}_i^T{\dot{\tilde{\mathit{v}}}}_i}$$

(29)

thus, via substituting (20) to (30), we might have:

$$\dot{Z}(t)={\displaystyle {\sum }_{i=1}^N{\tilde{\mathit{v}}}_i^T}{\displaystyle {\sum }_{j=1,j\ne i}^N{C}_1{a}_{ij}({\mathit{v}}_{ij}-{\mathit{v}}_{iv})}+{\displaystyle {\sum }_{i=1}^N{C}_3{\tilde{\mathit{v}}}_i^T{\dot{\tilde{\mathit{v}}}}_i}$$

(30)

and Equation (31) can be expressed in matrix form as follows:

$$\dot{Z}(t)=-{\tilde{\mathit{v}}}^T[(C_{1}Y(t)+C_3\mathrm{\Omega }(t))\otimes I_n]\tilde{\mathit{v}}$$

(31)

where $\mathrm{\Omega }(t)$ is the stress matrix, $Y(t)=diag[{\gamma }_1,{\gamma }_2,\dots ,{\gamma }_N]$, $\tilde{\mathit{v}}={({\tilde{\mathit{v}}}_1^T,{\tilde{\mathit{v}}}_2^T,\dots ,{\tilde{\mathit{v}}}_N^T)}^T$. Apparently, $\mathrm{\Omega }(t)$ and $Y(t)$ are positive semi-definite, these two factors would explain that $Z(t\ge 0)$ is non-increasing function with $\dot{Z}(t)\le 0$.

Thus, the level set $\psi =\{{[{\tilde{\mathit{p}}}^T,{\tilde{\mathit{v}}}^T]}^T\in R^{2nN}:Z(t)\le Z(0),t\ge 0\}$ can been seen as a positively invariant set. Then, supposing that $Z(0)<U_r$, the equation can possibly meet $U_i(|\left|{\tilde{\mathit{p}}}_{i{j}^{\prime }}\right||)\le Z(t)\le Z(0)<U_r$ ($i\in O$, $t\ge 0$) in each edge $[e_{ij}]$. Therefore, the connectivity of graph $G$ of all agents ${\mathit{p}}_i$ for swarm is shown within $t\ge 0$ and $i\in O$; that is to say, the part 1 of Theorem 1 is proved.

As for part 2 of Theorem 1, it is obvious that $U_i(|\left|{\tilde{\mathit{p}}}_{i{j}^{\prime }}\right||)\le Z(t)\le Z(0)<U_r<U_0$ from above; thus, the obstacles collision is proved.

The part 3 of the theorem, $\left|\right|{\tilde{\mathit{p}}}_i\left|\right|$ and $\left|\right|{\tilde{\mathit{v}}}_i\left|\right|$ are all bounded and level set $\psi$ is tight from the above analysis. Moreover, all trajectories of agents would finally converge and satisfy the invariant set ${\psi }^{\prime }=\{{[{\tilde{\mathit{p}}}^T,{\tilde{\mathit{v}}}^T]}^T:\dot{Z}(t)=0,t\ge 0\}$. As $Y(t)$ and $\mathrm{\Omega }(t)$ are positive semi-definite from the definition, based on Formulation (31) and as $\dot{Z}(t)=0$, we could obtain ${\tilde{\mathit{v}}}^T[Y(t)\otimes I_n]\tilde{\mathit{v}}=0$ and ${\tilde{\mathit{v}}}^T[\mathrm{\Omega }(t)\otimes I_n]\tilde{\mathit{v}}=0$. Since the stress matrix $\mathrm{\Omega }(t)$ can be considered as generalized graph Laplacian matrices with both positive and negative edge weights, $\mathrm{\Omega }(t)$ can thus also meet the sum of squares property [30]; therefore, ${\tilde{\mathit{v}}}^T[(C_{1}Y(t)+C_3\mathrm{\Omega }(t))\otimes I_n]\tilde{\mathit{v}}$ can be equivalent to ${\tilde{\mathit{v}}}_1={\tilde{\mathit{v}}}_2=\dots ={\tilde{\mathit{v}}}_N$. To be more specific, this result can demonstrate that the errors of all agents’ velocity would converge to 0 asymptotically. Thus, it can imply the ${\tilde{\mathit{v}}}_1={\tilde{\mathit{v}}}_2=\dots ={\tilde{\mathit{v}}}_N=0$, such that part 3 of the Theorem 1 is proved. □

Remark 1. 

After examining the proof process, it has been determined that parts 1–3 of the theorem align with the fundamental principles of swarm algorithms, namely cohesion, separation, and alignment as proposed by Reynolds. Furthermore, these essential criteria have been employed to validate the algorithm presented in this paper.

Remark 2. 

Despite the similarities between certain terms in Equation (20) and existing protocols, the swarm behavior guided by Equation (20) would be distinctively unique. This is due to the presence of a virtual agent serving as an evaluation index through the local trajectory. Consequently, each agent is required not only to track the global trajectory but also to actively adjust its own local trajectory.

Remark 3. 

Although the paper does not specifically analyze the impact of acceleration and turning rate as inputs, it is important to note that these two factors are influenced by the agents themselves. Therefore, assuming that the initial distance and interaction range between agents meet the required range, $Z(0)<U_r$ and $Z(0)<U_0$ can effectively avoid collisions within the agent swarm and ensure the overall stability of the system.

The controller protocol (20) offers several advantages to a certain extent. Firstly, it integrates protocols for leaders/followers and virtual agents, enabling simultaneous operation. This distinguishes it from existing control protocols and enhances the adaptability and scalability of the system. Secondly, the local adjustment eliminates the need for additional feedback information interaction among leaders and followers, thereby greatly reducing communication consumption. Thirdly, based on the aforementioned local protocol, each UAV can be dynamically and randomly assigned as a leader in complex environments, ensuring continuity in the event that leaders are shot down or destroyed.

5. Simulation and Analysis

In this section, we proceed to conduct numerical simulations to illustrate the theoretical results and validate the effectiveness of the novel formation control algorithm.

The whole experimental process is shown in Figure 6, and the algorithm in two-dimensional is described as follows:

• The randomly distributed generated agents denoted as $\left\{\mathit{p}\right|{\mathit{p}}_{ij}\in {ℝ}^d,\forall (i,j)\in ℝ\}$, $(i,j)\in (1,\dots ,n)$ are steered to rendezvous and make a swarm formation as the nominal configuration ${\mathit{p}}_0\in (\mathit{P},r)$. The leaders are set and then time-varying velocity $\mathit{v}(t)$ (10) starts to change in this stage for all agents ${\mathit{u}}_i$ (20).
• Desired geometric patterns $A(r)$ are predefined and generated with desired trajectories and corresponding positions of the formation $p^{\ast }(t)$ based on the knowledge of obstacle position and shape available.
• A trajectory through all the barycenter of leaders of each predefined configuration; thus, this virtual agent motives with constant velocity $\mathrm{X}({\mathit{v}}_{vl},{\mathit{p}}_{vl})$ in a single-integrator differentiable.
• Based on the available knowledge of obstacles, using constant interaction with other agents and obstacle constraints (20) to trigger local trajectory planning in Algorithm 1 (15) and (16).
• The formation operated the (20) control law to adjust the trajectories of agents possibly entering collide zones of obstacles while changing the configuration of formation $p(t)\to p^{*}(t)$, which can demonstrate the tracking ability of the algorithm (21).

It is noted that only the leaders possess global information regarding the desired trajectory (${\mathit{u}}_d$). The focus on the position error relative to the reference trajectory is solely on the leaders. Consequently, the control laws for the leaders are not explicitly designed in this paper.

In order to evaluate the performance of our proposed methods, all the experiments are simulated on PC with MATLAB R2020a Windows 10. Protocol (20) is used to steer seven UAV agents moving in a two-dimensional space with five processes above through Algorithms 1 and 2.

The number of agents $N=7$, the sensing range $d_{\mathit{react}}=30$, desired distance from the virtual leader $d_0=30$, obstacles radius $ob{s}_{\mathit{rad}}=20$, maximum velocity $v_{\max }=80 \mathrm{m}\mathrm{/}\mathrm{s}$, max acceleration $u_{\max }=2 \mathrm{m}\mathrm{/}{\mathrm{s}}^2$, max velocity error $e_{v\max }=0.5 \mathrm{m}\mathrm{/}\mathrm{s}$, max trajectory error $e_{x\max }=10 \mathrm{m}$, the timestep $d_t=0.1 \mathrm{s}$. Other parameters were set as $a=1.5$, $b=2$, $c=0.5$, $\delta =0.6$, ${\omega }_{ij}=1$. All the above parameters remained fixed throughout the simulation.

The experiment is divided into three phases: Firstly, the desired path of the formation, the position of configuration, and the obstacles are pre-defined. The experiment could be conducted by affine maneuvering by single-integrator control law from (20) in Zhao [22]. Secondly, the obstacle is randomly located in the trajectory of formation to test the effect of a local trajectory planning method (Algorithm 1). Finally, the formation with seven agents is operated as Algorithm 2 and the experiment process acts as Figure 6.

5.1. Phase I

With the available information regarding obstacles, it becomes feasible to pre-define the desired path and its corresponding configuration. The purpose of this part is to generate the nominal configurations during each time interval, which can provide the desired path for the leaders of the formation and the desired tracking velocity. The positions of agents are randomly selected from the box $[-3 \mathrm{m},3 \mathrm{m}]\times [-3 \mathrm{m},3 \mathrm{m}]$, as Figure 7b shows. Their velocities of leaders are set as constant $v_d=45 \mathrm{m}\mathrm{/}\mathrm{s}$ and directions in intervals $[-\pi /2,\pi /2]$. Agents 1, 2, and 3 are assigned as leaders illustrated in red through the whole simulation and the four change forms of configuration are calculated, scaling, rotation, shear, and translation. It is shown that the affine-based leader/follower consensus protocol can form the continuous configuration change for the formation. The nominal configuration is established prior to 6 s. At the moment $t=6 \mathrm{s}$ and $t=13 \mathrm{s}$ the formation is expected to undergo scaling in the y-direction, with shrinking and enlargement occurring, respectively. Starting from $t=19 \mathrm{s}$ and $t=24 \mathrm{s}$, the formation initiates rotation. Additionally, there is shearing at $t=28 \mathrm{s}$ and $t=36 \mathrm{s}$, while the formation translates during other time intervals within the given range.

One can see that the velocity for followers would have suddenly changed to meet the requirement in each time interval of the different configuration changes. The scale of change could not be controlled effectively in any case.

5.2. Phase II

The aim of the second part is mainly to test the effect of the algorithm of local trajectory planning. The position of the obstacle is located randomly at $[-10,-5,60,6]$ (x, y, width, height) and agents are from the box $[-50 \mathrm{m},-40 \mathrm{m}]\times [-60 \mathrm{m},-50 \mathrm{m}]$ as Figure 8a shows; the acceleration, velocity, and the angle of drift are in intervals $[0 \mathrm{m}\mathrm{/}{\mathrm{s}}^2,2 \mathrm{m}\mathrm{/}{\mathrm{s}}^2]$, $[1 \mathrm{m}\mathrm{/}\mathrm{s},15 \mathrm{m}\mathrm{/}\mathrm{s}]$ and $[-\pi /2,\pi /2]$, the velocity of the virtual leader is $v^l=[5 \mathrm{m}\mathrm{/}\mathrm{s},5 \mathrm{m}\mathrm{/}\mathrm{s}]$. The formation has started at the nominal configuration and encounters the obstacle along the desired path $x_d$, as Figure 8b shows. The state ${\mathrm{X}}_{vl}$ of the virtual leader is the desired state for agents, as Figure 8b shows, and the formation would generate Algorithm 1 to steer agents to avoid obstacles. The velocity and its error related to the virtual leader are given in Figure 8c,d; as can been seen, the velocity fluctuates greater at $t=10 \mathrm{s}$ and $t=20 \mathrm{s}$ moving through the obstacle and the velocity change interval is from $v=5 \mathrm{m}\mathrm{/}\mathrm{s}$ to $v=[1 \mathrm{m}\mathrm{/}\mathrm{s},14 \mathrm{m}\mathrm{/}\mathrm{s}]$. Figure 8d illustrates the change in velocity error during the same time interval. The primary reason for this is that the desired trajectory, as moved by the virtual leader, would directly pass through the obstacle. However, the formation manages to avoid collision and maintain its configuration due to the forces exerted by the virtual leader. In Figure 8e, the trajectory error of all agents is depicted, with the note that the X and Y axes have different scales. It can be observed that the leaders and followers exhibit smaller average position errors, while the overall formation has a relatively larger error. The desired trajectory is not fully matched due to the influence of uninformed followers on the leaders, but it remains within an acceptable range. Lastly, Figure 8f demonstrates the total velocity error for all agents, indicating that the protocol will converge eventually.

5.3. Phase III

The purpose of this part is to test the affine-based local trajectory planning algorithm in the pre-defined positions of obstacles to follow the desired path without collision. The positions of three obstacles are located at $[-10,-5,30,6]$, $[-10,-30,30,50]$, and $[-10,-40,30,6]$. The initial velocity of the virtual leader is set $v^l=[40 \mathrm{m}\mathrm{/}\mathrm{s},0 \mathrm{m}\mathrm{/}\mathrm{s}]$ and it moves with constant velocity through all the paths with direction intervals $[-\pi /2,\pi /2]$. Meanwhile, based on the velocity of the virtual leader $v^l=[45 \mathrm{m}\mathrm{/}\mathrm{s},0 \mathrm{m}\mathrm{/}\mathrm{s}]$, the velocities of agents in the formation are randomly generated with a standard normal distribution. The initial acceleration of the agents is set $[0 \mathrm{m}\mathrm{/}{\mathrm{s}}^2]$. The formation starts at the random positions $[p_1,p_2,\dots ,p_7]$ to follow the desired path $p_d$, planning the local trajectory. From Figure 9a, it is known that all the accelerations of agents have changed drastically and unpredictably, especially in the interval of $t=200 \mathrm{s}–300 \mathrm{s}$, and would converge in the final. The main reason is that input of agents would increase or decrease suddenly when the forces among agents undergo changes. Figure 9b depicts the velocity error of the agents, indicating that the reference velocity is well tracked by both leaders and followers throughout the trajectory tracking process. The experimental results particularly demonstrate that the proposed algorithm enables the asymptotic tracking of the desired trajectory and remains effective even when the trajectory changes suddenly due to the formation steering local planning to avoid collisions during the motion process. Figure 9c illustrates that the minimum distance between agents consistently remains greater than 0, indicating successful collision avoidance for the formation and the maintenance of the desired configuration within the acceptable error range. Additionally, Figure 9d indicates that trajectory tracking is achieved satisfactorily.

5.4. Discussion

The experiments primarily focused on determining the optimal trajectory of each agent for affine maneuver control, revealing that a single mode of control may lack generality in complex environments to some extent. The proposed algorithm has been validated to be effective, particularly in addressing situations involving colliding obstacles. From the experiments, it was observed that each agent in the swarm autonomously carried out obstacles’ detection, judgment, and decision-making, compared with the original algorithm. The virtual leader mainly influenced an agent if it was likely to enter the zone where obstacles react, while the other agents continued to track desired trajectories with less effect from the virtual leader forces and reach predefined positions. Notably, even in the presence of abrupt changes in trajectories or obstacles, the proposed algorithm remained effective.

From Figure 7, Figure 8 and Figure 9, it is demonstrated that the purpose of the proposed algorithm is to guarantee the configuration change to avoid the collision autonomously and maneuver continuously to track the predefined trajectory of an affine image set $A(r)$. Thus, Figure 7b shows that the random formation is generated at the beginning and starts to form the nominal configuration and then reach each $A(r)$ (${[p_i^{*}]}^T$ from ${[p_i]}^T$). However, a pre-defined trajectory would not avoid the obstacles effectively and could not provide the capability of changing velocity $\mathit{v}$ suddenly.

Therefore, the proposed model is introduced to deal with the problem. It is shown that 11 desired positions have been pre-defined in Figure 7, and the original path shows the possibility of collision. Note that system of detecting and steering each agent is determined by distance $\left|\right|p_i-p_{obstacle}\left|\right|$ only. In any case, the formation steered by an affine-based maneuvering method would fall apart and lose the body integrity when encountering the obstacles. Moreover, a virtual leader is designed to operate based on the pre-defined trajectory of the centroid of the pre-defined configurations as Figure 3 demonstrates, denoted as $p_d^{vl}$ (12).

The advantage of this virtual strategy lies in its ability to enhance system functionality without significantly increasing complexity. Firstly, this strategy does not interfere with the formation motion. Secondly, the trajectory of the virtual agent is constructed based on the existing pre-defined trajectory. Lastly, this virtual agent can be seamlessly integrated into the control protocol, serving as an adjustment metric. Thus, the virtual leader introduced into the algorithm can modify the formation motion and improve the effectiveness of formation maneuvering.

In order to evaluate the effectiveness of the proposed method, we use two indexes to evaluate the motion results.

Table 1. Evaluation tests (mean value).

Methods	Speed (s)	Track Accuracy (%)
Affine-based maneuvering	40	67.34
The proposed method	450	89.51

intuitively shows the average value of all the experimental results with motion speed and track accuracy. It can been seen from Table 1 that the proposed method had the highest accuracy value. However, the time has been taken larger than that of the affine-based maneuvering method, which is due to the complexity of the proposed being higher than the affine-based maneuvering method ($O(L^2)$ and $O(2L)$).

The second term Speed shows that the affine-based maneuvering took up 40 s, and the proposed method used 450 s. Obviously, the proposed method would use more time than the classic one with higher computational cost. Firstly, based on $p^{\ast }(t)=[I_n\otimes A(t)]r+I_{n}b(t)$ (22), the classic method basically solved the changeable problem of formation configurations for multi-agent. Then, the proposed method took more within each time step due to the calculation from Algorithm 1 (15).

The obstacle added to the experiment scenario is depicted in Figure 10a, which is based on Figure 7a. As illustrated in Figure 7b, the new obstacle is inserted between $t=13 \mathrm{s}$ to $t=19 \mathrm{s}$. The experimental results primarily focus on the formation maneuvering $t=0 \mathrm{s}–40 \mathrm{s}$ and are obtained as follows.

It has been shown that the proposed method improves the maneuvering ability of the formation. From Figure 10b, it is evident that the trajectory error is reduced by the proposed method. Furthermore, the velocity of the X axis in the classic method undergoes more drastic changes compared to the proposed method, as observed in Figure 10c,e. Similarly, Figure 10d,f demonstrate that the velocity of the Y axis in the proposed method changes smoothly.

6. Conclusions

The changes in formation configuration have been confirmed to be feasible. However, the challenge of maneuvering the formation while avoiding obstacles and converging to desired values has not been adequately addressed to enhance practical application. Moreover, the concept of a rigid body may not suffice in diverse environmental situations. Although the affine technique has somewhat resolved this issue by continuously providing multiple geometric patterns for configuration changes, it requires an adjustable environment and the maintenance of a rigid body at all times. As a result, this method lacks some generality for practical application, particularly in complex environments.

Therefore, this paper introduces a new consensus protocol based on a hybrid control model to enhance the effectiveness of formation maneuver control and obstacle avoidance in complex environments. The protocol employs distributed control laws with a virtual leader for double-integrator control and establishes the system’s stability. The presented algorithm showcases the capability to autonomously adjust each local trajectory of a formation based on potential forces when encountering obstacle colliding zones. Crucially, the control law is confined to each agent’s local reference frame, thereby improving the adaptability and scalability of the formation in realistic environments. Furthermore, the results show that the formation, steered by the proposed control algorithm, can still reach the predefined configuration even in the presence of violent trajectory changes. Additionally, the algorithm effectively reduces communication consumption.

In the future, there are several important topics that require attention. These include investigating more intricate graph structures, dynamic leader reassignment, and transitioning between distributed and decentralized control laws to enhance autonomy. Moreover, it is crucial to develop more autonomous control laws for adapting to environmental changes, improve deep learning techniques to establish rule-based response mechanisms, explore the interconnections between agents in complex networks, utilize the MPC method for local environment prediction, and delve into other related areas.