Next Article in Journal
Enhanced Conversion Efficiency in MAPbI3 Perovskite Solar Cells through Parameters Optimization via SCAPS-1D Simulation
Previous Article in Journal
Triple Time Interval Hybridization Strategy for Rapidly Calculating Regional Target–Visible Time Window of Earth Observation Payloads on Space Station
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Applied Sciences
Volume 14
Issue 6
10.3390/app14062389
applsci-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Physical and Finite Element Models for Determining the Capacity and Failure Mechanism of Helical Piles Placed in Weak Soil

by
Buse Emirler
Department of Civil Engineering, Cukurova University, Adana 01250, Turkey
Appl. Sci. 2024, 14(6), 2389; https://doi.org/10.3390/app14062389
Submission received: 19 January 2024 / Revised: 2 March 2024 / Accepted: 4 March 2024 / Published: 12 March 2024
(This article belongs to the Section Civil Engineering)
Browse Figures
Versions Notes

Abstract

:
The foundations of particular engineering structures, including marine and jetty structures, mooring systems for submerged platforms or those on the ocean surface, and transmission towers, are subjected to various external loads including compression, uplift, and lateral loads. In such cases, to improve the soil resistance below foundations, pile foundations such as helical piles, anchored piles, and batter piles are commonly preferred, depending on the in situ conditions. Helical piles, increasingly used as an alternative foundation to conventional piles, are placed in the soil body by rotating with torque. This paper deals with the contribution of a helical pile in improving loose sandy soil, and the main purpose is to study the effect of the helix-buried depth on the load-bearing capacity and failure mechanism. The investigated variables include the distance between helixes, the number of helixes, and the diameter of the upper helix. Physical model tests were conducted, and two- and three-dimensional numerical analyses were performed by using the finite element method with an advanced soil model to illustrate the failure mechanisms of helical piles. The aim was to reveal the efficiency of the finite element method in modelling helical piles placed in weak sandy soil. A simplified linear geometry for helixes was established in a two-dimensional finite element model whereas a real geometry for helixes, which was a more realistic approach, was created in a three-dimensional finite element model. The results show that the three-dimensional model indicates better agreement with the physical model compared to the two-dimensional model, and all investigated variables highly affect the load-bearing capacity of helical piles.

1. Introduction

Helical piles, which are one of the special deep foundation types, are widely used in many fields of geotechnical engineering due to their ease of application and functionality. These types of piles that can resist various forces, such as compression and uplift forces, are manufactured effortlessly and brought to the relevant region via preparation outside the project site, and they are placed into the soil body by pushing or turning in an inclined or perpendicular way through a hydraulic torque machine. Helical piles were recommended by Alexander Mitchell in the first half of the 1800s with the idea of finding a solution for safely anchoring ships in harbors and supplying strong foundations for lighthouses in weak soil in shallow water [1]. Since that time, helical piles have been applied in the foundations of marine structures (bridges, oceanfront piers, lighthouses, etc.), electricity transmission and telecommunication towers, structures on slopes, buried pipelines, renewable energy source structures such as solar panels and wind turbines, shoring structures, damaged or long-term damaged structures, historical structures, and the construction of many other structures [2,3,4,5]. Piles that support the offshore jacked/tripod structures are exposed to combined axial (uplift and compression) and lateral forces (Figure 1). However, helical piles are superior to conventional pile foundations [6,7,8] because they provide more resistance due to the helix [9,10].
Despite the abundance of usage areas of helical piles, the increase in application, and the advantages they provide, it can be seen that research and design methods for helical piles are relatively limited compared to conventional pile foundations, and previous studies mostly focus on the uplift behavior [11,12,13,14,15,16,17,18,19]. In addition, it can be expressed that numerical efforts regarding the failure mechanism of helical piles are quite limited [11,20,21,22,23,24,25,26,27,28]. Therefore, since there is a necessity in the literature, albeit at a limited level, the compression behavior of helical piles has been investigated using physical model tests and two-dimensional (2D) and three-dimensional (3D) finite element models.
This study may be assessed as a reasonable effort where the behavior of helical piles has been investigated via a physical model test first in the laboratory, and following that, 2D and 3D numerical analyses have been performed in order to observe the performance of the finite element method. A simplified linear geometry for helixes was established in a 2D finite element model whereas a real geometry for helixes, which was a more realistic approach, was created in a 3D finite element model. It has been observed that the valuable previous efforts on the subject so far are generally concentrated in the theoretical and experimental framework. However, in addition to the limited number of 3D numerical studies on the subject, the number of parameters investigated in such studies was quite limited compared to experimental studies. Moreover, theoretical studies related to helical piles focused on determining the net value of the bearing capacity by considering several assumptions while experimental studies generally focused on the parameters that affect the bearing capacity (number of helixes, spacing ratio between helixes, helix diameter, soil density, etc.) [29,30,31,32]. In the experimental studies, where the effect of helix number on the bearing capacity was investigated, the helix diameter was generally kept constant, whereas the number of studies in which the effect of the location of the upper helix plate was investigated was quite limited. Therefore, it is thought that it is quite essential to study the effect of a large number of spacing ratios between helixes on the bearing capacity experimentally, and this effort provides notable novelty to the present study. In addition, it is believed that when this problem, which has been studied experimentally, is also successfully modelled numerically and valuable results are obtained, the originality of the study will improve.
To briefly mention the scope of the study, it aims to assess the behavior of helical piles with the physical model tests and also to present the results obtained from 2D and 3D finite element models. The behavior of single and multiple helical piles placed in loose sandy soil (RD = 30–35%) will be examined under the compression load; and in this regard, the effects of parameters such as helix number, helix distance, and upper helix diameter will be investigated in terms of bearing capacity and failure mechanism, experimentally and numerically. As a result of this effort, the performance of the finite element models established with simplified linear geometry (2D) and real geometry (3D) was evaluated by comparing the physical model test results.

2. Materials and Methods

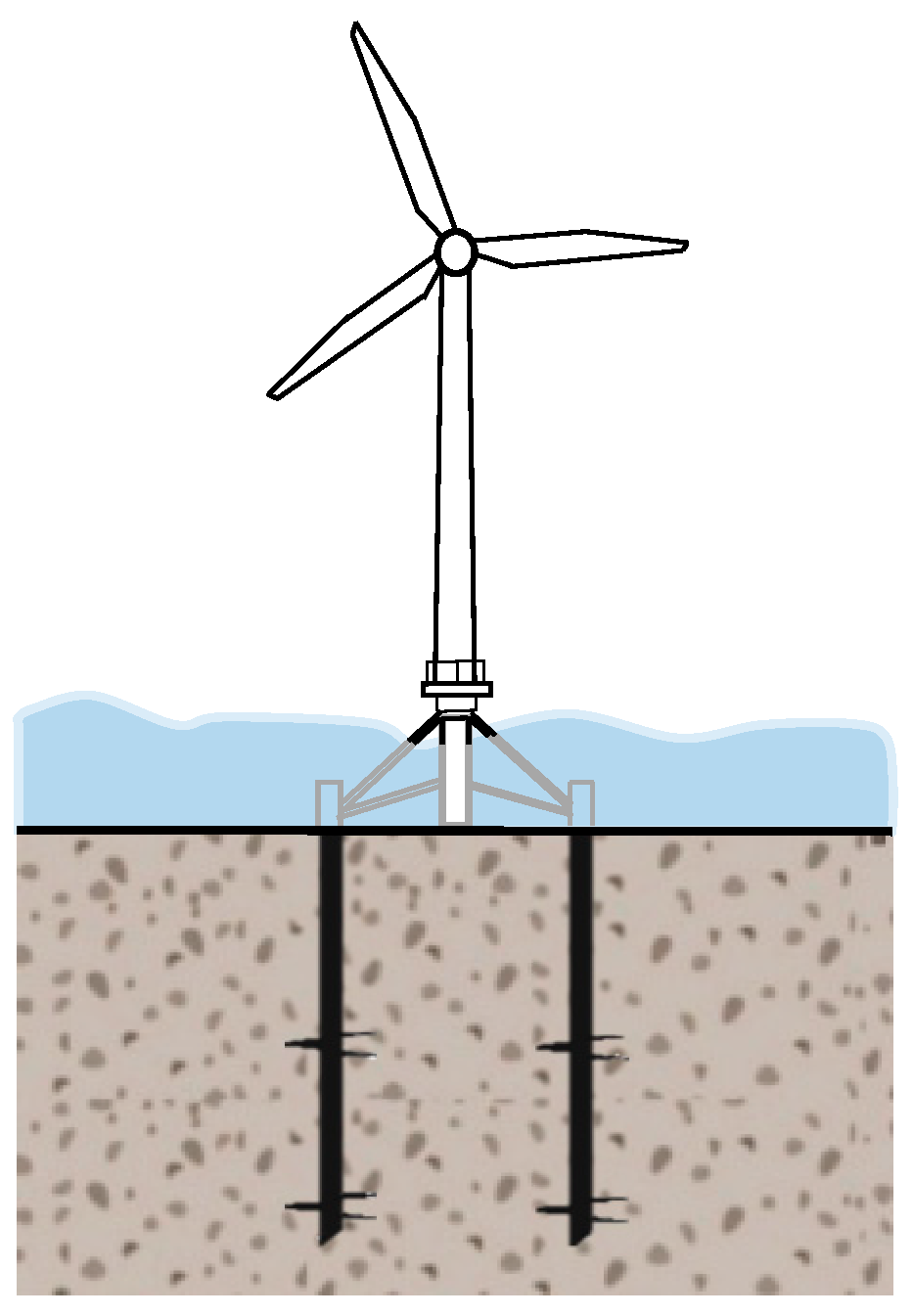
2.1. Physical Model Test

The physical model tests were performed in the Geotechnical Laboratory of the Department of Civil Engineering of Iskenderun Technical University. In the physical model tests, the compression force was applied by the load motor fixed to the test box. While the loading device with speed control is employed, the loading arm can be moved up and down in different directions. Whilst performing the tests, the load was applied gradually, and the speed of the compression load was kept constant at each step.
A rectangular steel-framed test box with internal dimensions of 1500 mm (length), 1200 mm (width), and 1000 mm (depth) was used. During the tests, an electronic load cell with a capacity of 20 kN was preferred to read the load values applied to model piles. The displacements of the model piles were measured by employing two different displacement transducers (LVDTs). The displacement values of the pile system were obtained for each load stage by calculating the arithmetic mean of the displacement considered at two different points that were equal distances to the center of the system.
During the tests, the displacement and load values saved by the data logger were conveyed to the software, and they were converted into numerical values. In addition, the test apparatus with all related attachments is presented in Figure 2 to show the test setup consisting of the test box, loading system, sandy soil, model pile, load cell, and displacement transducers. The shaft lengths of model steel pipe piles employed in the tests were equal to 600 mm and the outer diameters of them were equal to 22 mm. Since the effect of upper helix diameter on the bearing capacity was one of the parameters investigated, the diameter of the lower helixes (D1) was kept constant at 60 mm while the diameters of the upper helixes (D2) were considered as 60 mm, 80 mm, 100 mm, and 120 mm. The pitch of the helix for the lower and upper plates was accepted as 0.3D1 and 0.3D2, respectively. To mention the investigated parameters and the test program, the number of helixes (N = 0, 1, 2), the spacing ratio between helixes (S/D1 = 1–8), and the diameter of the upper helix (D2 = 60 mm, 80 mm, 100 mm, and 120 mm) were considered as the variables. The test program is given in Table 1, and the effects of these parameters on the bearing capacity of the helical piles are presented in detail thereafter.
Various methods are available to prepare a sand body in the laboratory like vibration, compaction, and the raining technique. In physical model tests, having uniform strata is significant to allow for the repeatability of tests [33]. Considering the foregoing methods, the raining technique was selected to acquire the required relative density of the sand. In the physical model tests, sand samples brought from Iskenderun sand quarry were used. In accordance with ASTM D2487-11 [34], they were washed and sieved through sieve number 10 (2 mm dia.) and sieve number 80 (0.18 mm dia.). Following this, they were dried in an oven at the end of the sieving process. Afterward, sand samples were sieved through predetermined sieves, taking into account the standard mentioned above, and the grain size distribution was determined (see Figure 3). The soil class was identified as SP based on the grain size distribution curve. The sieve analysis results are presented in Table 2.
To obtain the specific unit weight of the sand, the density bottle test was performed, and γs was calculated to be 27.2 kN/m3. Dry unit weights of sandy soil for maximum (γdmax) and minimum (γdmin) values were decided according to ASTM D4253-16 [35] and ASTM D4254-16 [36]. In the shear box tests, the sand sample was placed into the box with the relative density as RD = 30–35% (γdmin = 15.52 kN/m3) for the loose sand condition. From the shear box tests repeated more than once, the internal friction angle of the loose sand was between ϕ = 30–32°.

2.2. Finite Element Model

Conducting a laboratory test in geotechnical foundation engineering is both a difficult and time-consuming procedure along with quite expensive. Nevertheless, the results acquired from such tests are the closest to those procured from field tests. As a result, establishing a numerical model that is less costly and not time-consuming, as well as being in good consistency with the test results, can provide a significant benefit to geotechnical designers. Therefore, a series of 2D and 3D numerical analyses were performed to study the load–displacement behavior of helical piles and to demonstrate their failure mechanisms. For numerical analyses, PLAXIS 2D (Version 2023.2) [37] and PLAXIS 3D (Version 2023.2) [38] software, based on the finite element method frequently used by researchers [39,40], were chosen due to some of their advantages. One of the advantages of the software is that it includes the ability to create different complicated material models to reflect soil behaviors; plus, it covers some specific structural elements for foundations, piles, anchors, geogrids, retaining walls, etc. [41].
Two-dimensional and three-dimensional finite element models established for the problem are presented in Figure 4, respectively. In the 2D model, it was enough to define the length (x = 750 mm; half of the length was considered since the axisymmetric model was used) and the depth (y = 1000 mm), whereas in the 3D model, the length (x = 1500 mm), width (y = 1200 mm), and depth (z = 1000 mm) values must be entered into the model. Within the scope of the study, the properties of the investigated loose sandy soil were introduced to the software, and the soil was assigned to the defined area for 2D modelling and assigned to the defined volume for 3D modelling. Since it is essential to use an appropriate soil model for the prediction of soil behaviors, the numerical analyses were accomplished using the Hardening Soil model which can represent the behavior of different soils, both soft soil and stiff soils [42]. The model was established in the frame of the theory of elasticity, and the material behavior is non-linear before failure, but after failure, it is considered based on Mohr–Coulomb strength parameters [43,44]. Following the definition of soil properties, the properties of the pile element were introduced to the software, and the relevant structural element was assigned to the relevant region.
The helical pile element was modelled in both 2D and 3D using the plate element. While in 2D modelling the axisymmetric approach was considered to create the finite element model, in 3D modelling the finite element model was established identically to the physical model test setup. In addition, in 3D modelling, SOLIDWORKS 2016 [45] software was used to create the helix structure of the pile element identically, and then, the pile element was transferred to the PLAXIS 3D software, where the analyses were performed. The pile shaft with an outer diameter (d) of 22 mm, a thickness of 2.5 mm, and a length (L) of 600 mm was created for the straight pile as it was compatible with the test. Helix plates were modelled as well as the shaft for different diameters of helical piles such as D2 = 60 mm, 80 mm, 100 mm, and 120 mm. The distance between the bottom and top point of the plate (pitch) is related to the diameter of the relevant helix, and they were determined for the lower and upper plates as 0.3D1 and 0.3D2, respectively. In the 2D and 3D mesh procedures, the soil region is created using 15-node triangle elements and 10-node tetrahedral elements, respectively. Also, medium mesh density and enhanced mesh refinement were selected for the finite element models to save computer effort and time.
The sandy soil and pile properties considered in the software are presented in detail in Table 3. Several soil parameters (e.g., saturated and unsaturated unit weights, internal friction angle, specific unit weight, etc.) required by constitutive models were acquired through conventional laboratory experiments based on the relevant ASTM standards. Moreover, for other sandy soil parameters related to the stiffness that require more comprehensive laboratory effort like secant stiffness, tangent stiffness, unloading/reloading stiffness, power for the stress-level dependency of stiffness, and the failure ratio belonging to the Hardening Soil model, they were determined by considering the values that are in best agreement with the test data.
The software employed in this paper offers negative and positive interface elements to model the interaction between soil and helical piles (see Figure 4). The value of the strength reduction factor (Rinter) changes from 0 to 1, and if the Rinter is accepted as 0, then no interaction occurs between the soil and helical pile. On the other hand, if the Rinter is accepted as 1, then the interaction between the soil and helical pile is rigid. In this study, Rinter was accepted as 0.4 to successfully reflect the interaction between the loose sandy soil and the helical pile, and as determined in a previous study [46], this value was determined parametrically to give the most compatible result with the physical test results.

3. Findings and Discussion

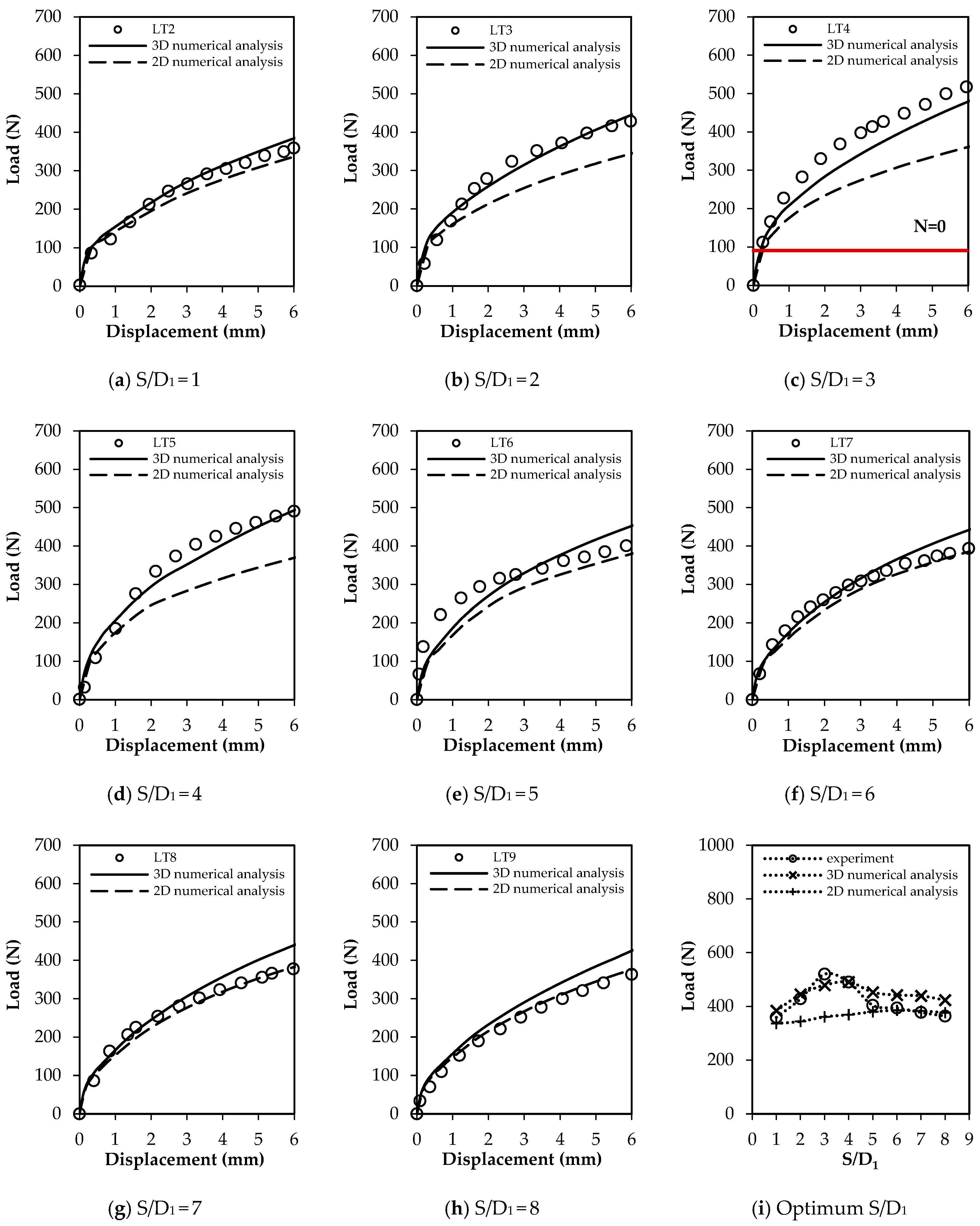
3.1. The Effect of the Distance between Helixes

The effect of the distance between helixes was expressed with the spacing ratio between helixes (S/D1), which is a dimensionless term, where S and D1 refer to the distance between helixes and the diameter of the lower helix, respectively. The effect of this parameter on the bearing capacity of the helical piles was investigated using physical model tests and compared to the results obtained from 2D and 3D finite element models. In accordance with this purpose, the multiple helical pile (N = 2) was used in this series of tests by considering the diameters of helixes of D1 = D2 = 60 mm. While examining the spacing ratio between helixes, the diameter of helixes was kept constant to eliminate the effect of other parameters on the results. The physical model tests were conducted for eight different spacing ratios as S/D1 = 1–8. The reason as to why such different spacing ratios are considered in this study is that there is still uncertainty on the subject. Several researchers have stated that if the buried depth is between 3 and 8 times the foundation diameter, these types of foundations can be considered deep foundations. On the other hand, the recommended minimum buried depth of helical piles was expressed as 5 times the upper helix diameter [47]. Therefore, the aim of this section, both the optimum spacing ratio between helixes and the efficient depth of the upper helix specified. In this study, the physical model tests were continued until the displacement of 10% of the helix diameter, and the failure load was determined as the load corresponding to this displacement. The results of the load–displacement relationship obtained from the physical model tests and 2D/3D finite element models are presented in Figure 5; also, the failure mechanism results obtained from the 3D finite element model, which shows better agreement with the physical model test results, are given in Figure 6.
The load–displacement results acquired from the physical model tests were more consistent with the 3D finite element model results compared to the 2D finite element model results (see Figure 5). The reason for this result can be shown in the more realistic modelling for helixes in the 3D analyses compared to the 2D analyses. However, from all results, it was seen that even if the approach of modelling the helix as a horizontal plate in two dimensions is not good enough, this approach shows that it is possible to have a rough idea about the behavior of helical piles. In addition, the pile capacity increased with the increase in the distance between helixes, and this increase continued up to a certain ratio. While the physical model test and 3D numerical analysis results showed similar behavior, no significant capacity increase was found in the 2D numerical analysis results (see Figure 5i). In other words, the optimum spacing ratio between helixes was obvious in the results of the physical model tests and 3D analyses, whereas this finding was not observed in the results obtained from the 2D analyses.
Based on the physical model test results, a failure load of 359 N was obtained at S/D1 = 1, 520 N was obtained at S/D1 = 3, and 364 N was obtained at S/D1 = 8, and therefore, the maximum load was found at S/D1 = 3. In the 3D numerical analysis results, the maximum pile capacity was determined to be S/D1 = 3–4. In other words, in the case where the buried depth of the upper helix was more than 5D2, the pile capacity was determined to be the maximum in both the physical model test and the 3D numerical analysis. It was understood from the results that the effect of the soil zone over the upper helix on the pile capacity is more important than the distance between the helixes. It can be said that in helical piles at a buried depth of less than 5D2, a shallow foundation behavior rather than a deep foundation behavior is effective for the upper helix, and therefore, the contribution of the upper helix plate to the capacity is less. Plus, there was not a significant capacity increment in the 2D analysis results as the spacing ratio between helixes increased.
According to these results, if the multiple helical pile is to be used, it is recommended that the distance between the helixes and the buried depth of the upper helix be adjusted to be more efficient. Therefore, the recommended buried depth of the upper helix for this study is a value greater than 5D2.
The effect of the distance between helixes on the failure mechanisms obtained from the 3D finite element model is presented in Figure 6. It is known that multiple helical piles have cylindrical or individual failure mechanisms depending on the distance between helixes [20,30,48]. Therefore, this situation was clearly confirmed when the failure mechanisms were examined. While the failure mechanism in closely spaced multiple helical piles exhibited cylindrical behavior, as the distance between the helixes increased, an individual failure mechanism was obtained (see Figure 6). The intensity in the cylindrical failure mechanism was more pronounced at the spacing ratio between helixes of S/D1 = 1. As the distance between helixes increased (e.g., S/D1 = from 1 to 2), although the failure mechanisms appeared to be roughly cylindrical, the intensity began to cluster around the helixes, and this intensity decreased along the shaft between two helixes. It was observed that at S/D1 = 3, the most intense zone was still around the helix, and this intensity around the helixes was preserved at all increasing spacing ratios. It was noticed that the interaction between the helixes decreased, and the failure mechanism reached the soil surface along with the spacing ratio of S/D1 = 4. In other words, the failure mechanism showed a transition from a deep foundation to a shallow foundation at this spacing ratio. The decreases in helical pile capacity occurring after these spacing ratios (e.g., S/D1 = 4, 5, 6, 7, and 8) can be explained by this behavior change observed in the failure mechanisms.

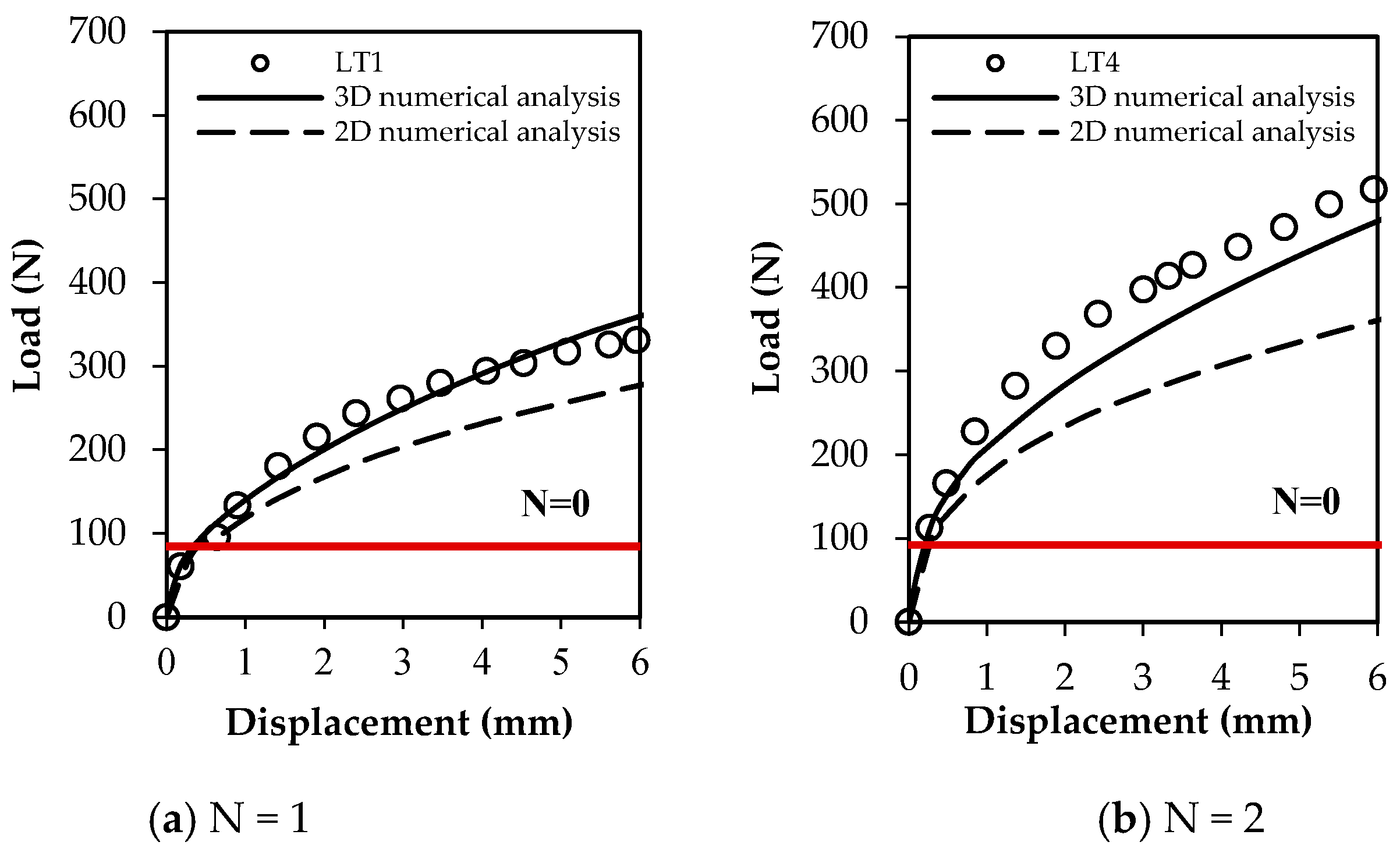
3.2. The Effect of the Number of Helixes

The effect of the number of helixes (N = 0, 1, 2) was investigated in this section considering the physical model tests and numerical analyses. In the case of the multiple helical pile, the spacing ratio between helixes was constant at S/D1 = 3, which is the optimum spacing ratio between helixes. The results for load–displacement obtained from the physical model tests and 2D/3D finite element models are presented in Figure 7; also, the failure mechanism results of the 3D finite element model, which is in better agreement with the physical model test results, are given in Figure 8.
The capacity of the straight pile (N = 0; with no helix) was determined to be approximately 86 N, and the effect of the presence of a helix on the capacity was interpreted by comparing it with a straight pile in the test. In the case of using single (N = 1) and multiple helixes (N = 2), the capacities were found to be 335 N and 520 N, respectively. When compared to the straight pile, these situations offered a capacity increase of 3.9 and 6 times, respectively (Figure 7). In the transition from the straight pile to the helical pile, the increase in capacity originated from the helix plate in a single helical pile, but in a multiple helical pile, this increase originated from either the total bearing capacity of the helix plates or the cylindrical region formed between the helixes depending on the distance between the helixes [49,50,51]. With the transition from a single helix to multiple helixes, the pile capacity increased by approximately 55%. The level of this increase was directly related to the distance between the helixes and the location of the upper helix plate (buried depth). Hence, it was recommended to choose an optimum distance to achieve maximum efficiency.
From the physical model test results, it could be seen that the capacity of the helical pile increased significantly compared to the straight pile. When all results were examined, it was determined that the physical model test and 3D finite element results had better agreement; on the other hand, the 2D finite element results were slightly below the physical model test results.
The effect of the number of helixes on the failure mechanisms obtained from the 3D finite element model is presented in Figure 8. In the case of N = 1 (single helical pile), the displacement intensity on the failure mechanism occurred around the helix and exhibited deep foundation behavior. At N = 2 (i.e., multiple helical piles), the displacement intensity decreased significantly and dropped by almost half compared to N = 1. It can be expressed that the use of multiple helixes caused a cylindrical formation on the failure mechanism between the helixes. The presence of the upper helix plate ensured that the failure mechanism was effective almost along the shaft and the mechanism moved towards the soil surface. When the failure mechanisms of single and multiple helical piles were compared, it was observed that the upper helix plate belonging to the multiple helical piles was positioned where the displacements originating from the single helical pile disappeared. As a result of this, it was understood that the upper helix in the multiple helical pile was placed at the optimum distance where the displacements were damped in the failure mechanism.

3.3. The Effect of the Upper Helix Diameter

In this section, the effect of the upper helix diameter was investigated using the physical model tests and 2D/3D finite element models. In accordance with this purpose, the multiple helical pile (N = 2) was considered in this series of tests. While examining the upper helix diameter, the distance between helixes was kept constant at S/D1 = 3, which is the optimum spacing ratio, to eliminate the effect of other parameters on the results. The physical model tests were carried out for four different upper helix diameters such as D2 = 60 mm, 80 mm, 100 mm, and 120 mm. The results of the load–displacement relationship obtained from the physical model tests and 2D/3D finite element models are presented in Figure 9; also, the failure mechanism results acquired from the 3D finite element model, which is in better agreement with the physical model tests, are given in Figure 10.
With the increase in the upper helix diameter, the pile capacity increased significantly. When the lower and upper helix diameters were the same, the helical pile capacity was approximately 520 N. As the upper helix diameter increased, the capacity was determined to be 580 N, 690 N, and 875 N, respectively. When the upper helix diameter was twice the lower helix diameter, the capacity increased by approximately 70% (Figure 9). This increase in capacity can be explained by the growth of the soil zone which the upper helix plate resists while compressive load is being applied. Thus, the upper helix plate in the multiple helical piles became a determining parameter for the capacity. Based on this result, in cases where multiple helical piles will be used in loose sandy soils, it may be recommended to make the upper helix plate larger compared to the lower helix plate to obtain maximum efficiency from the helical pile and to generate the required torque/capacity. When the results obtained from the physical model tests and finite element models were examined, it was determined that the physical model test and 3D finite element model results were in good agreement, and therefore, it can be expressed that the 3D model quite successfully reflected the physical model test behavior. On the other hand, the results of the 2D model were slightly below the test results.
The effect of the upper helix diameter on the failure mechanisms obtained from the 3D finite element model is presented in Figure 10. When the failure mechanisms were examined, it was seen that in the helical pile with helixes of equal diameter, the failure mechanism showed an individual intensity around the helixes but created a cylindrical behavior with low intensity along the shaft between the helixes. As the upper helix diameter increased, the increase in capacity was reflected in the failure mechanism as a decrease in displacement intensity. With the upper helix diameter of D2 = 80 mm in the helical pile, there was displacement intensity around the helix plates even though it was not as intense as with the diameter of D2 = 60 mm. This intensity reached its minimum level at D2 = 120 mm. It can be stated that the increase in plate diameter caused a change in the failure mechanism behavior. As a result of this, the cylindrical formation changed to an hourglass appearance that widens in the area where the upper helix is located and narrows in the area where the lower helix is located.

4. Conclusions

This paper focuses on behavior of helical piles placed in weak (loose sandy) soil. With this purpose, the effects of the spacing ratio between helixes (S/D1 = 1–8), the number of helixes (N = 0, 1, 2), and the upper helix diameter (D2 = 60 mm, 80 mm, 100 mm, and 120 mm) on the load–displacement and failure mechanism were investigated using physical model tests and 2D/3D finite element models.
Based on the outputs acquired from this effort, the following conclusions are provided.
  • The Hardening Soil model employed successfully demonstrates the behavior of the helical pile placed in weak soil.
  • The 3D finite element model is quite successful in replicating the behavior of helical piles but the 2D finite element model remains slightly less successful in reflecting the physical model test results.
  • The distance between helixes is quite an important parameter, and the helical pile capacity increases as the distance between helixes increases until the S/D1 = 3–4.
  • In the case of multiple helical piles, the buried depth of the upper helix should be selected as a value greater than 5D2.
  • The displacement intensity in the cylindrical failure mechanism is more pronounced at S/D1 = 1. Also, at S/D1 = 3, the most intense zone is still around the helix, and this intensity around the helixes is preserved at all increasing spacing ratios. The interaction between the helixes decreases and the failure mechanism reaches the soil surface along with the spacing ratio of S/D1 = 4.
  • The capacity of the helical pile increases with the increase in the number of helixes. At N = 2, the displacement intensity decreases significantly and drops by almost half compared to N = 1.
  • With the increase in the diameter of the upper helix, the capacity of helical piles increases significantly.
  • As the upper helix diameter increases, the increase in capacity is reflected in the failure mechanism as a decrease in displacement intensity. The increase in helix diameter causes a change in the failure mechanism behavior. As a result of this, the cylindrical formation changes to an hourglass appearance.

Funding

This study was supported by the Cukurova University Scientific Research Projects Coordination Unit (Project No. FBA-2021-13948).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Dataset available on request from the author. The raw data supporting the conclusions of this article will be made available by the author on request.

Acknowledgments

The author would like to thank the authorities of the Geotechnical Laboratory of the Department of Civil Engineering of Iskenderun Technical University where the physical model tests were performed. The author would also like to thank Mustafa Tolun, who was a researcher in the other part of this two-part project but also supported this study with his ideas.

Conflicts of Interest

The author declares no conflicts of interest.

References

  1. Lutenegger, A.J. Historical development of iron screw-pile foundations: 1836–1900. Int. J. Hist. Eng. Technol. 2011, 81, 108–128. [Google Scholar] [CrossRef]
  2. Tsuha, C.H.C.; Aoki, N.; Rault, G.; Thorel, L.; Garnier, J. Evaluation of the efficiencies of helical anchor plates in sand by centrifuge model tests. Can. Geotech. J. 2012, 49, 1102–1114. [Google Scholar] [CrossRef]
  3. Nazir, R.; Chuan, H.S.; Niroumand, H.; Kassim, K.A. Performance of single vertical helical anchor embedded in dry sand. Measurement 2013, 49, 42–51. [Google Scholar] [CrossRef]
  4. Sakr, M.A.; Nazir, A.K.; Azzam, W.R.; Sallam, A.F. Behavior of grouted single screw piles under inclined tensile loads in sand. Electron. J. Geotech. Eng. 2016, 21, 571–591. [Google Scholar]
  5. Cortes Garcia, L.D. Assessment of Helical Anchors Bearing Capacity for Offshore Aquaculture Applications. Master’s Thesis, University of Maine, Orono, ME, USA, 2019. [Google Scholar]
  6. Conte, E.; Pugliese, L.; Troncone, A.; Vena, M. A simple approach for evaluating the bearing capacity of piles subjected to inclined loads. Int. J. Geomech. 2021, 21, 04021224. [Google Scholar] [CrossRef]
  7. Li, Z.; Zhao, J.; Liu, T.; Guan, C.; Liu, Y.; Zhu, W.; Liu, L. Capacity change of piles in loess under cyclic axial tension or compression load. Int. J. Geomech. 2023, 23, 04023182. [Google Scholar] [CrossRef]
  8. Han, M.; Jia, J.; Li, Z.; Zhu, Z.; Tu, B.; Liu, L. Improved analytical method for stabilizing piles in loess slope considering nonlinear pile-soil interactions. Int. J. Geomech. 2024, 24, 04024002. [Google Scholar] [CrossRef]
  9. Spagnoli, G.; Gavin, K.; Brangan, C.; Bauer, S. In situ and laboratory tests in dense sand investigating the helix-to-shaft ratio of helical piles as a novel offshore foundation system. In Frontiers in Offshore Geotechnics III, 1st ed.; Meyer, V., Ed.; CRC Press/Balkema: Leiden, The Netherlands, 2015; Volume 1, pp. 643–648. [Google Scholar]
  10. Pavan Kumar, P.V.; Patra, S.; Haldar, S. Behaviour of screw pile under axial compressive and lateral loading in sand for offshore energy foundations. In Advances in Offshore Geotechnics: Proceedings of ISOG2019, 1st ed.; Haldar, S., Patra, S., Ghanekar, R.K., Eds.; Springer: Singapore, 2020; Volume 92, pp. 393–403. [Google Scholar]
  11. Livneh, B.; El Naggar, M.H. Axial testing and numerical modeling of square shaft helical piles under compressive and tensile loading. Can. Geotech. J. 2008, 45, 1142–1155. [Google Scholar] [CrossRef]
  12. Demir, A.; Ok, B. Uplift response of multi-plate helical anchors in cohesive soil. Geomech. Eng. 2015, 8, 615–630. [Google Scholar] [CrossRef]
  13. Harnish, J.L. Helical Pile Installation Torque and Capacity Correlations. Master’s Thesis, Western University, London, ON, Canada, 2015. [Google Scholar]
  14. Mohajerani, A.; Bosnjak, D.; Bromwich, D. Analysis and design methods of screw piles: A review. Soils Found. 2016, 56, 115–128. [Google Scholar] [CrossRef]
  15. Rawat, S.; Gupta, A.K. Numerical modelling of pullout of helical soil nail. J. Rock Mech. Geotech. Eng. 2017, 9, 648–658. [Google Scholar] [CrossRef]
  16. Khaleel, O.B. Pull-out Capacity of Double-Helix Screw Pile in Organic Soil. Master’s Thesis, Gaziantep University, Gaziantep, Türkiye, 2018. [Google Scholar]
  17. Vignesh, V.; Muthukumar, M. Experimental and numerical study of group effect on the behavior of helical piles in soft clays under uplift and lateral loading. Ocean. Eng. 2023, 268, 113500. [Google Scholar] [CrossRef]
  18. Huang, Y.; Mu, L.; Wang, P. Three-dimensional finite element analysis for uplifting independent helix plate anchor in uniform clay. Ocean. Eng. 2023, 285, 115455. [Google Scholar] [CrossRef]
  19. Venkatesan, V.; Mayakrishnan, M. Behavior of mono helical pile foundation in clays under combined uplift and lateral loading conditions. Appl. Sci. 2022, 12, 6827. [Google Scholar] [CrossRef]
  20. Sprince, A.; Pakrastinsh, L. Helical Pile Behaviour and Load Transfer Mechanism in Different Soils. In Proceedings of the 10th International Conference Modern Building Materials, Structures and Techniques, Vilnius, Lithuania, 19–21 May 2010. [Google Scholar]
  21. Elsherbiny, Z.H.; El Naggar, M.H. Axial compressive capacity of helical piles from field tests and numerical study. Can. Geotech. J. 2013, 50, 1191–1203. [Google Scholar] [CrossRef]
  22. Salhi, L.; Nait-Rabah, O.; Deyrat, C.; Roos, C. Numerical modeling of single helical pile behavior under compressive loading in sand. Electron. J. Geotech. Eng. 2013, 18, 4319–4338. [Google Scholar]
  23. Gavin, K.; Doherty, P.; Tolooiyan, A. Field investigation of the axial resistance of helical piles in dense sand. Can. Geotech. J. 2014, 51, 1343–1354. [Google Scholar] [CrossRef]
  24. Polishchuk, A.I.; Maksimov, F.A. Numerical Analysis of Helical Pile-Soil Interaction under Compressive Loads. IOP Conf. Ser. Mater. Sci. Eng. 2017, 262, 012099. [Google Scholar] [CrossRef]
  25. Bak, H.M.; Halabian, A.M.; Hashemolhosseini, H.; Rowshanzamir, M. Axial response and material efficiency of tapered helical piles. J. Rock Mech. Geotech. Eng. 2021, 13, 176–187. [Google Scholar] [CrossRef]
  26. Nowkandeh, M.J.; Choobbasti, A.J. Numerical study of single helical piles and helical pile groups under compressive loading in cohesive and cohesionless soils. Bull. Eng. Geol. Environ. 2021, 80, 4001–4023. [Google Scholar] [CrossRef]
  27. Shao, K.; Su, Q.; Liu, J.; Liu, K.; Xiong, Z.; Wang, T. Optimization of inter-helix spacing for helical piles in sand. J. Rock Mech. Geotech. Eng. 2022, 14, 936–952. [Google Scholar] [CrossRef]
  28. Zhuang, X.; Zong, Z.; Huang, Y.; Wang, C.; Lin, X. Parametric study on analyzing the effect of soil-cement strength on the uplifting behavior of HSCM piles installed in marine soft clay. Appl. Sci. 2023, 13, 330. [Google Scholar] [CrossRef]
  29. Narasimha Rao, S.; Prasad, Y.V.S.N.; Shetty, D. The behaviour of model screw piles in cohesive soils. Soils Found. 1991, 31, 35–50. [Google Scholar]
  30. Perko, H.A. Helical Piles: A Practical Guide to Design and Installation, 1st ed.; John Wiley & Sons: Hoboken, NJ, USA, 2009; pp. 1–528. [Google Scholar]
  31. Ha, T.S.; Moon, H.R.; Moon, H.M. An Analysis of Correlation between Predicted and Measured Bearing Capacity in Rotary (Helical) Pile Method. In Proceedings of the KGS Fall National Conference, Seoul, Republic of Korea, 17 October 2013. [Google Scholar]
  32. Ding, H.; Wang, L.; Zhang, P.; Liang, Y.; Tian, Y.; Qi, X. The recycling torque of a single-plate helical pile for offshore wind turbines in dense sand. Appl. Sci. 2019, 9, 4105. [Google Scholar] [CrossRef]
  33. Asakereh, A.; Ghazavi, M.; Moghaddas Tafreshi, S.N. Cyclic response of footing on geogrid-reinforced sand with void. Soils Found. 2013, 53, 363–374. [Google Scholar] [CrossRef]
  34. ASTM D2487-11; Standard Practice for Classification of Soils for Engineering Purposes (Unified Soil Classification System). ASTM International: West Conshohocken, PA, USA, 2011.
  35. ASTM D4253-16; Standard Test Methods for Maximum Index Density and Unit Weight of Soils Using a Vibratory Table. ASTM International: West Conshohocken, PA, USA, 2016.
  36. ASTM D4254-16; Standard Test Methods for Minimum Index Density and Unit Weight of Soils and Calculation of Relative Density. ASTM International: West Conshohocken, PA, USA, 2016.
  37. PLAXIS 2D, PLAXIS 2D Version 2023.2; Plaxis-Bentley Systems: Delft, The Netherlands, 2023.
  38. PLAXIS 3D, PLAXIS 3D Version 2023.2; Plaxis-Bentley Systems: Delft, The Netherlands, 2023.
  39. Zhang, W.; Gu, X.; Ou, Q. Bearing capacity and failure mechanism of strip footings lying on slopes subjected to various rainfall patterns and intensities. Geol. J. 2023; in press. [Google Scholar] [CrossRef]
  40. Zhang, W.; Li, Y.; Goh, A.T.C.; Zhang, R. Numerical study of the performance of jet grout piles for braced excavations in soft clay. Comput. Geotech. 2020, 124, 103631. [Google Scholar] [CrossRef]
  41. Emirler, B.; Tolun, M.; Yildiz, A. Investigation on determining uplift capacity and failure mechanism of the pile groups in sand. Ocean. Eng. 2020, 218, 108145. [Google Scholar] [CrossRef]
  42. Schanz, T. Zur Modellierung des Mechanischen Verhaltens von Reibungsmaterialien. Master’s Thesis, Institut für Geotechnik-Universität Stuttgart, Stuttgart, Germany, 1998. (In German). [Google Scholar]
  43. Çelik, S. Comparison of Mohr-Coulomb and Hardening Soil models’ numerical estimation of ground surface settlement caused by tunneling. Iğdır Univ. J. Inst. Sci. Technol. 2017, 7, 95–102. [Google Scholar] [CrossRef]
  44. Lv, Y.; Liu, H.; Ng, C.W.W.; Ding, X.; Gunawan, A. Three-dimensional numerical analysis of the stress transfer mechanism of XCC piled raft foundation. Comput. Geotech. 2014, 55, 365–377. [Google Scholar] [CrossRef]
  45. SOLIDWORKS; SOLIDWORKS 2016; Dassault Systèmes: Waltham, MA, USA, 2015.
  46. Liu, W.; Liang, J.; Xu, T. Tunnelling-induced ground deformation subjected to the behavior of tail grouting materials. Tunn. Undergr. Space Technol. 2023, 140, 105253. [Google Scholar] [CrossRef]
  47. Hubbell Power Systems. Technical Design Manual Edition 3: Bulletin 01-0605; Hubbell Power Systems, Inc.: Centralia, MO, USA, 2014. [Google Scholar]
  48. AC358; Acceptance Criteria for Helical Foundation Systems and Devices. ICC Evaluation Service: Brea, CA, USA, 2007.
  49. Mitsch, M.P.; Clemence, S.P. Uplift capacity of helix anchors in sand. In Uplift Behavior of Anchor Foundations in Soil: Proceedings of a Session Held in Conjunction with the ASCE Convention, 1st ed.; Clemence, S.P., Ed.; ASCE: New York, NY, USA, 1985; pp. 26–47. [Google Scholar]
  50. Ghaly, A.; Hanna, A.; Hanna, M. Uplift behavior of screw anchors in sand. I: Dry sand. J. Geotech. Eng. 1991, 117, 773–793. [Google Scholar] [CrossRef]
  51. Narasimha Rao, S.; Prasad, Y.V.S.N.; Veeresh, C. Behaviour of embedded model screw anchors in soft clays. Géotechnique 1993, 43, 605–614. [Google Scholar]
Applsci 14 02389 g001
Figure 1. A foundation system with a helical pile for an offshore wind turbine.
Figure 1. A foundation system with a helical pile for an offshore wind turbine.
Applsci 14 02389 g001
Applsci 14 02389 g002aApplsci 14 02389 g002b
Figure 2. Test setup.
Figure 2. Test setup.
Applsci 14 02389 g002aApplsci 14 02389 g002b
Applsci 14 02389 g003
Figure 3. Grain size distribution curve of the sand sample.
Figure 3. Grain size distribution curve of the sand sample.
Applsci 14 02389 g003
Applsci 14 02389 g004
Figure 4. Numerical analysis models: (a) two-dimensional and (b) three-dimensional.
Figure 4. Numerical analysis models: (a) two-dimensional and (b) three-dimensional.
Applsci 14 02389 g004
Applsci 14 02389 g005
Figure 5. The effect of the distance between helixes on the load–displacement relationship.
Figure 5. The effect of the distance between helixes on the load–displacement relationship.
Applsci 14 02389 g005
Applsci 14 02389 g006
Figure 6. The effect of the distance between helixes on the failure mechanism.
Figure 6. The effect of the distance between helixes on the failure mechanism.
Applsci 14 02389 g006
Applsci 14 02389 g007
Figure 7. The effect of the number of helixes on the load–displacement relationship.
Figure 7. The effect of the number of helixes on the load–displacement relationship.
Applsci 14 02389 g007
Applsci 14 02389 g008
Figure 8. The effect of the number of helixes on the failure mechanism.
Figure 8. The effect of the number of helixes on the failure mechanism.
Applsci 14 02389 g008
Applsci 14 02389 g009
Figure 9. The effect of the upper helix diameter on the load–displacement relationship.
Figure 9. The effect of the upper helix diameter on the load–displacement relationship.
Applsci 14 02389 g009
Applsci 14 02389 g010
Figure 10. The effect of the upper helix diameter on the failure mechanism.
Figure 10. The effect of the upper helix diameter on the failure mechanism.
Applsci 14 02389 g010
Table 1. Test program.
Table 1. Test program.
Test No.Lower Helix Diameter
D1 (mm)		Upper Helix Diameter
D2 (mm)		Number of Helixes
N		S/D1Applsci 14 02389 i001
LT0Straight pile (only shaft)--
LT160-1-
LT2606021
LT32
LT43 *
LT54
LT65
LT76
LT87
LT98
LT106080
LT1110023
LT12120
* The value indicates the optimum spacing ratio between helixes. In all tests, shaft geometry, length (L), and diameter (d) were selected as circular (pipe), 600 mm, and 22 mm, respectively. LT refers to the abbreviation laboratory test.
Table 2. Results of the sieve analysis.
Table 2. Results of the sieve analysis.
ParametersValues
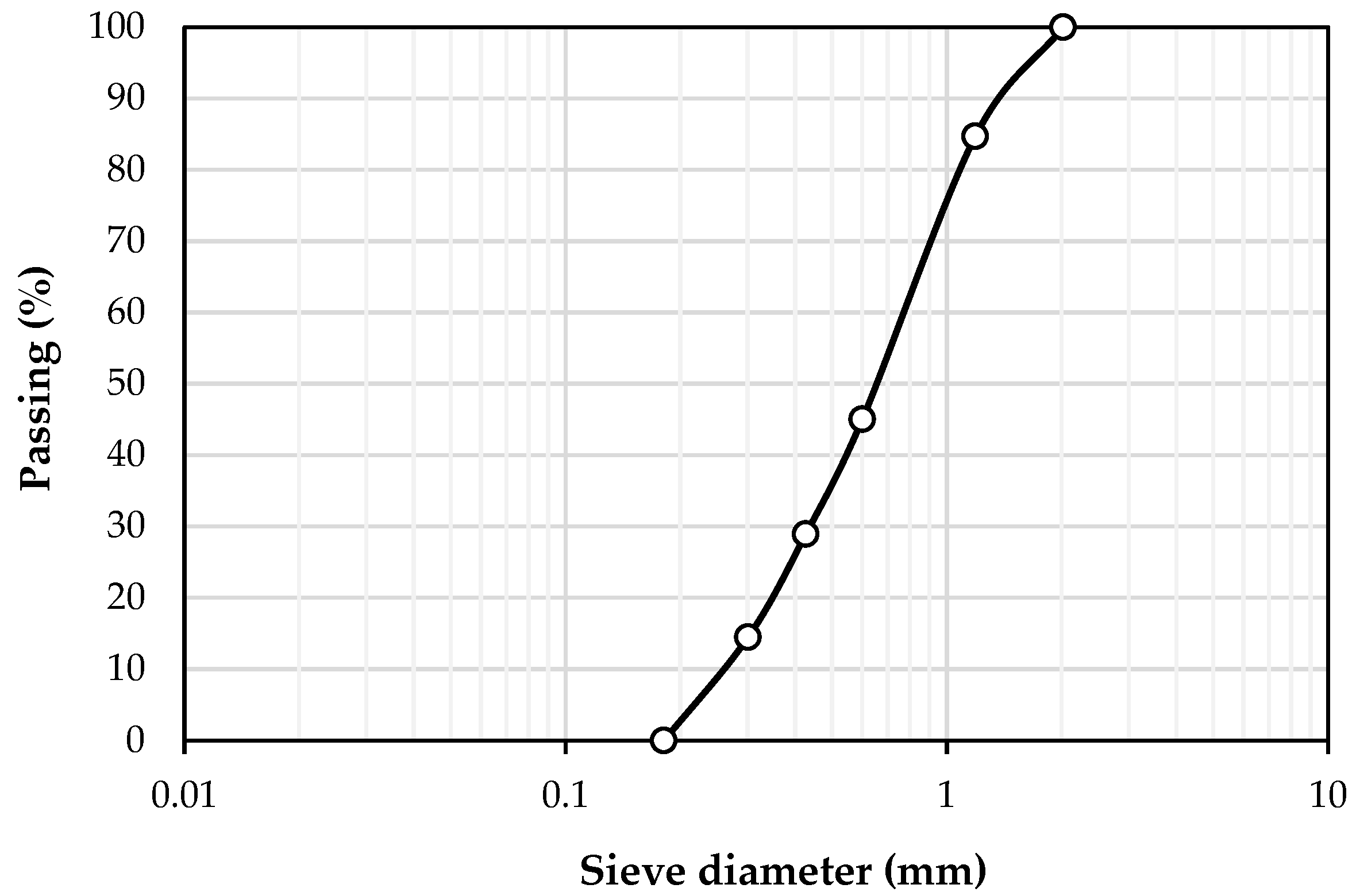
Effective grain size, D10 (mm)0.26
D30 (mm)0.44
D60 (mm)0.78
Coefficient of uniformity, Cu2.97
Coefficient of curvature, Cc0.96
Soil class (USCS)SP
Table 3. Material properties used in the numerical analysis.
Table 3. Material properties used in the numerical analysis.
ParametersValues
Soil
Material modelHardening Soil
Drainage typeDrained
Unit weight above phreatic level, γunsat (kN/m3)15.2
Unit weight below phreatic level, γsat (kN/m3)18.0
Sec ant   stiffness ,   E 50 ref (kN/m2)9000
Tan gent   stiffness ,   E oed ref (kN/m2)9000
Unloading / reloading   stiffness ,   E ur ref (kN/m2)27,000
Power, m0.68
Poisson’s ratio, v0.3
Friction angle, ϕ (°)30
Dilatancy angle, Ψ (°)0
Failure ratio, Rf0.99
Strength reduction factor, Rinter0.4
Pile
Thickness, d (mm)2.5
Unit weight, γ (kN/m3)77
Young’s modulus, E (kN/m2)2.1 × 108
Poisson’s ratio, v0.3
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Emirler, B. Physical and Finite Element Models for Determining the Capacity and Failure Mechanism of Helical Piles Placed in Weak Soil. Appl. Sci. 2024, 14, 2389. https://doi.org/10.3390/app14062389

AMA Style

Emirler B. Physical and Finite Element Models for Determining the Capacity and Failure Mechanism of Helical Piles Placed in Weak Soil. Applied Sciences. 2024; 14(6):2389. https://doi.org/10.3390/app14062389

Chicago/Turabian Style

Emirler, Buse. 2024. "Physical and Finite Element Models for Determining the Capacity and Failure Mechanism of Helical Piles Placed in Weak Soil" Applied Sciences 14, no. 6: 2389. https://doi.org/10.3390/app14062389

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop