Risk Assessment for Linear Regression Models in Metrology
Abstract
Featured Application
Abstract
1. Introduction
2. Materials and Methods
2.1. Measurement Description
2.2. Model Parameters
2.2.1. Best Estimate of a Measurand
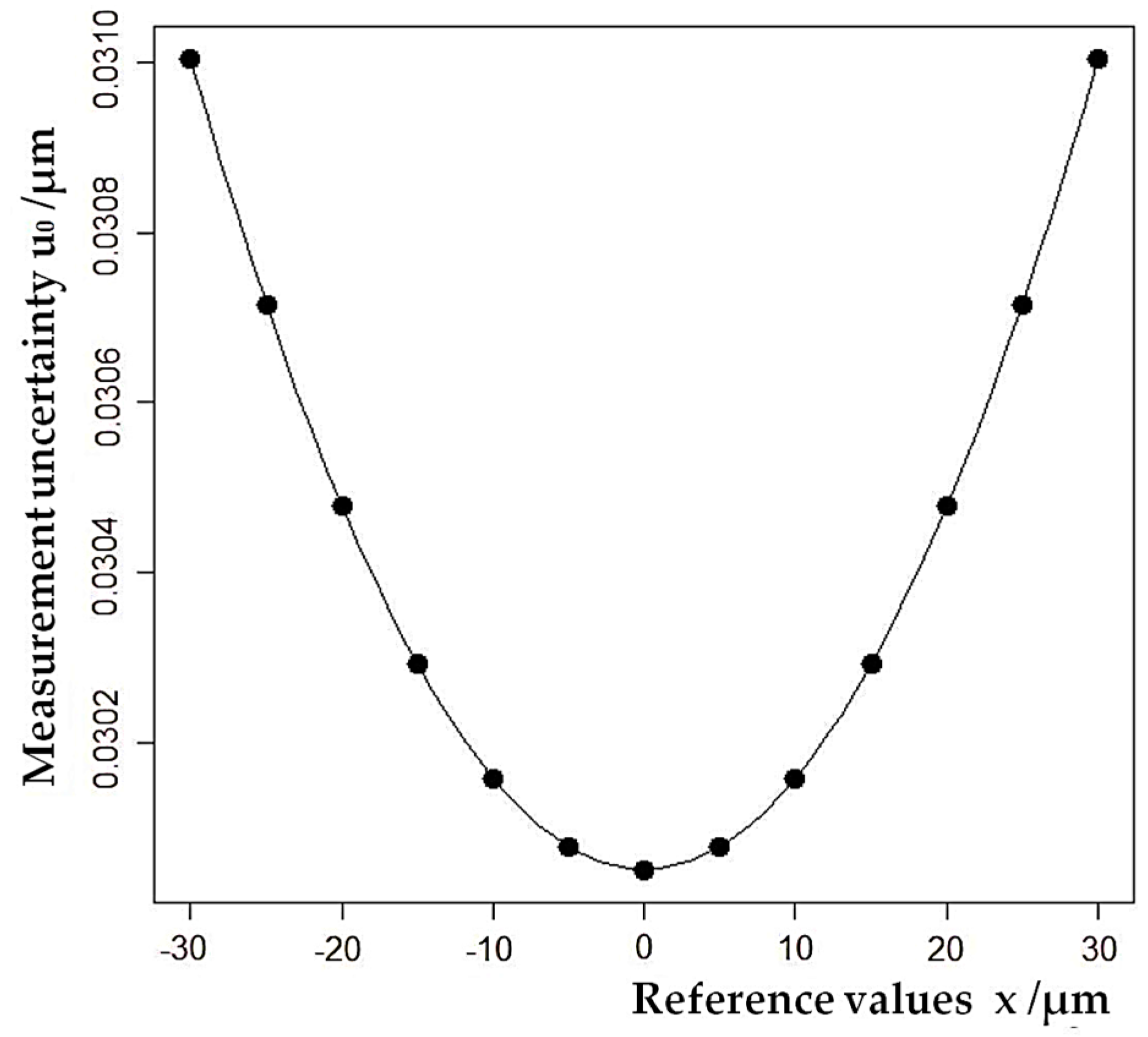
2.2.2. Measurement Uncertainty
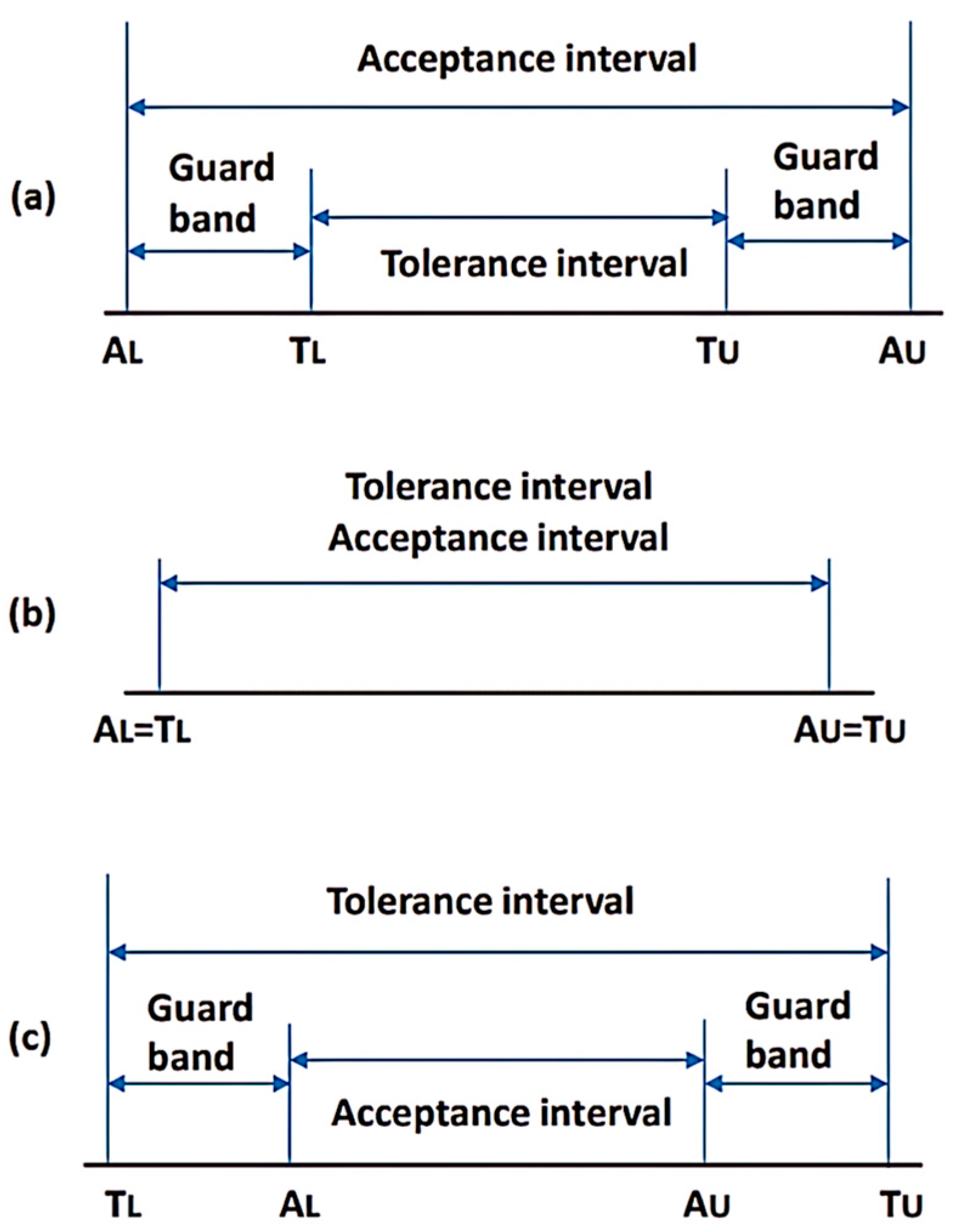
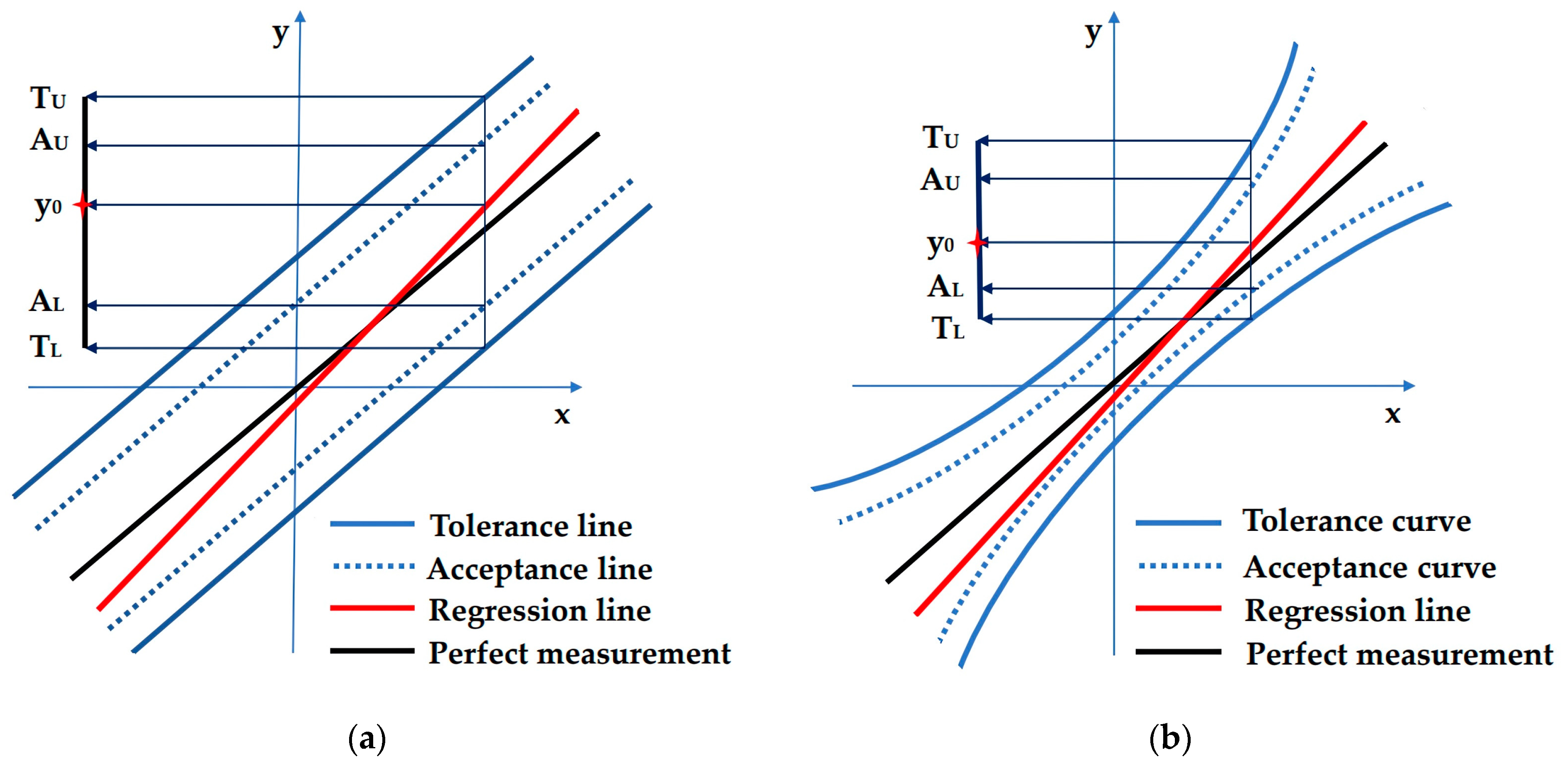
2.2.3. Tolerance and Acceptance Interval
2.3. Risk Calculation
3. Results and Discussion
3.1. Graphical Risk Analysis
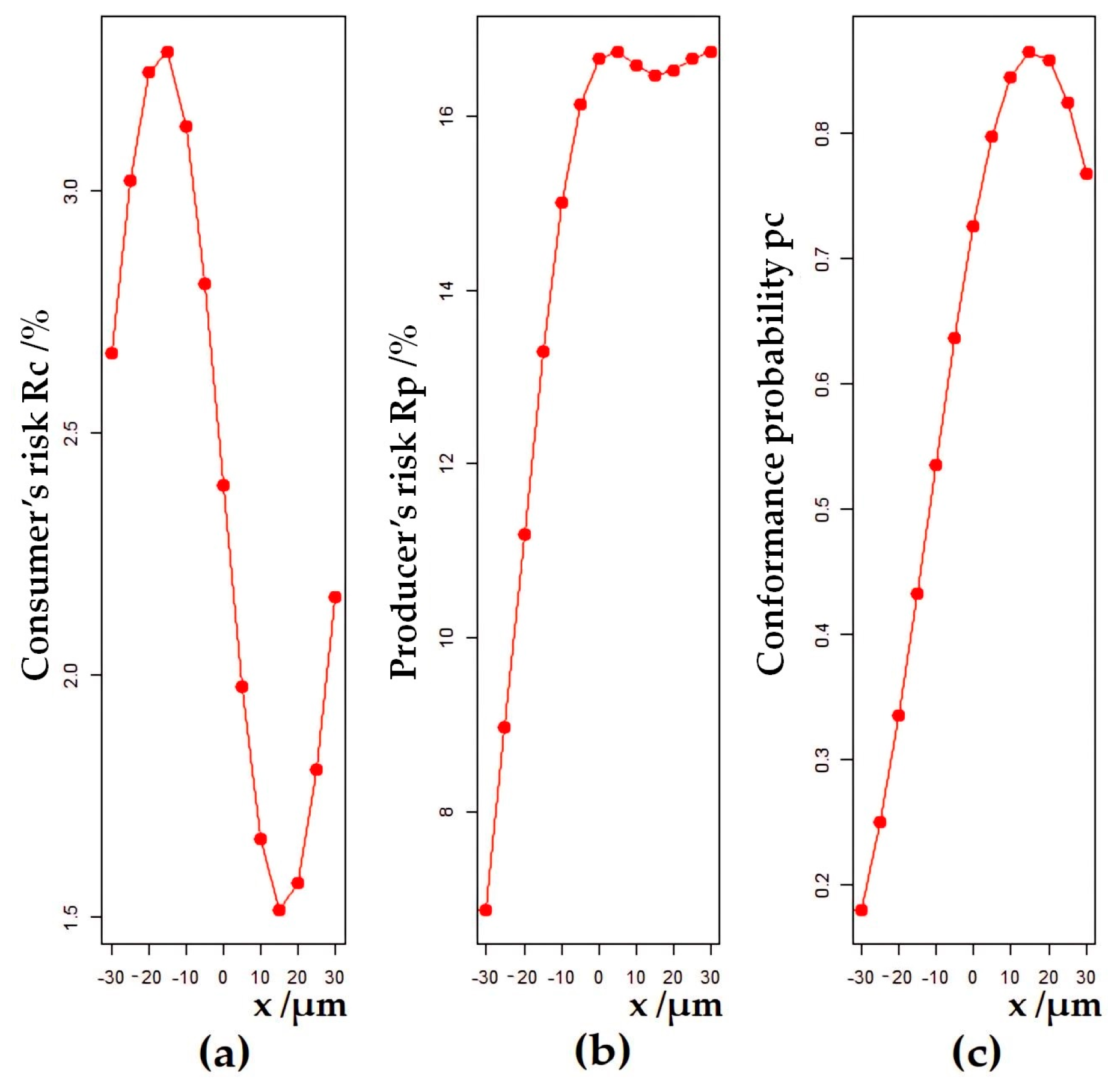
3.1.1. Behaviors of a Global Consumer and Producer Risk along the Moderate Scale
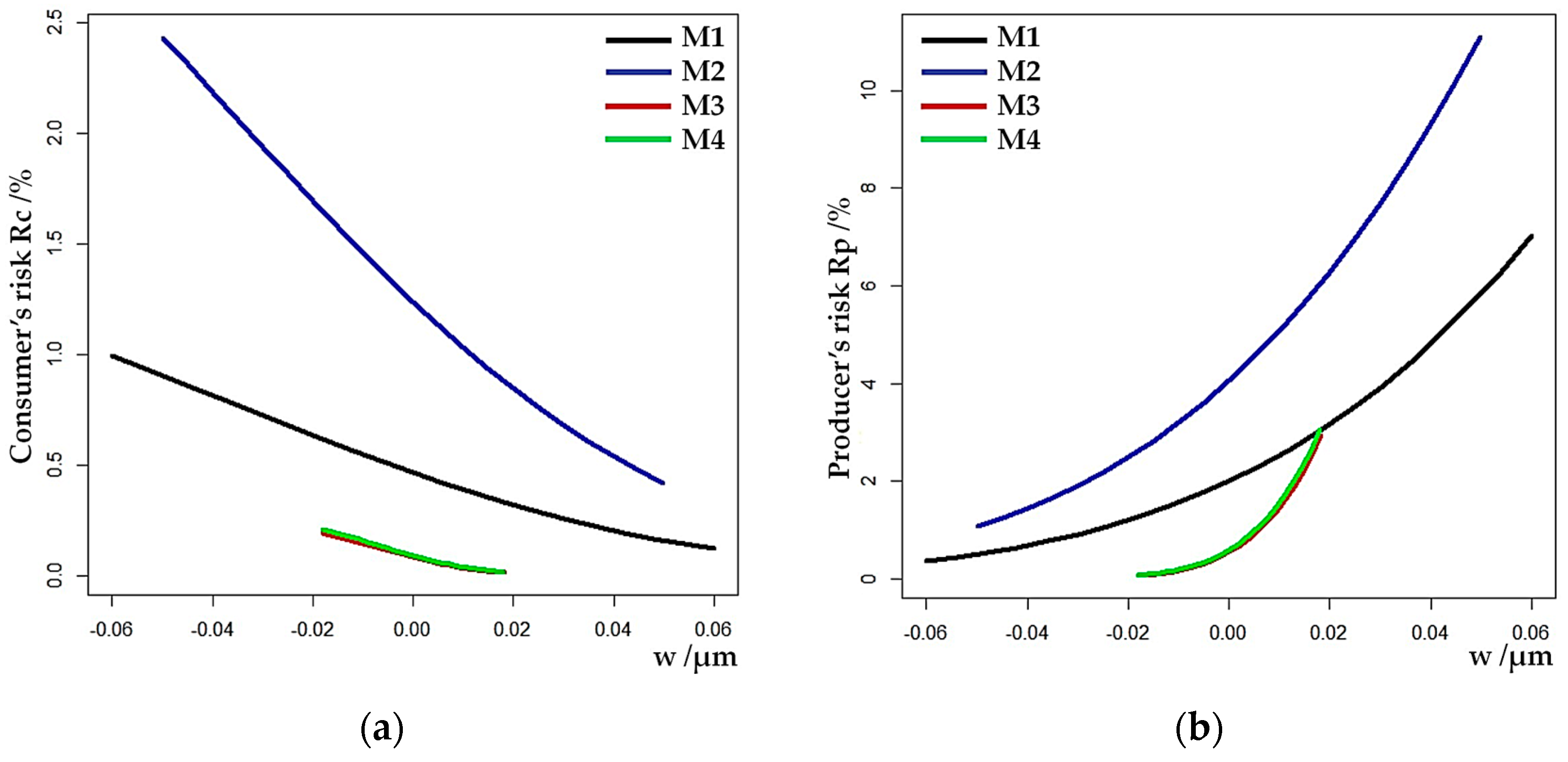
3.1.2. Behaviors of Global Consumer and Producer Risk along the Guard Band Axis
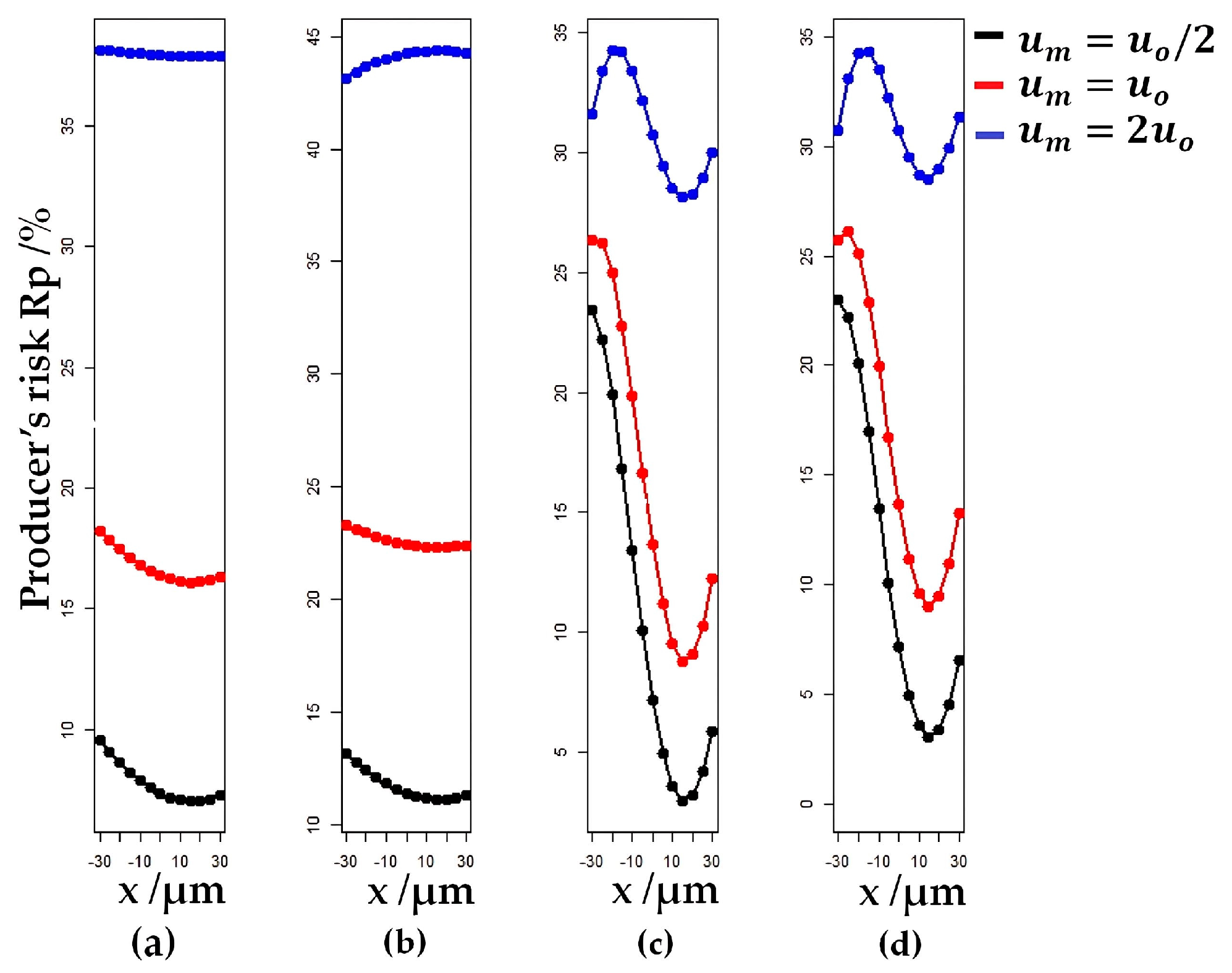
3.1.3. Behavior of Global Consumer’s and Producer’s Risk with the Changes in Measurement Uncertainty of a Future Inspection Process
3.2. Comparison of Models by Root Mean Squared Error
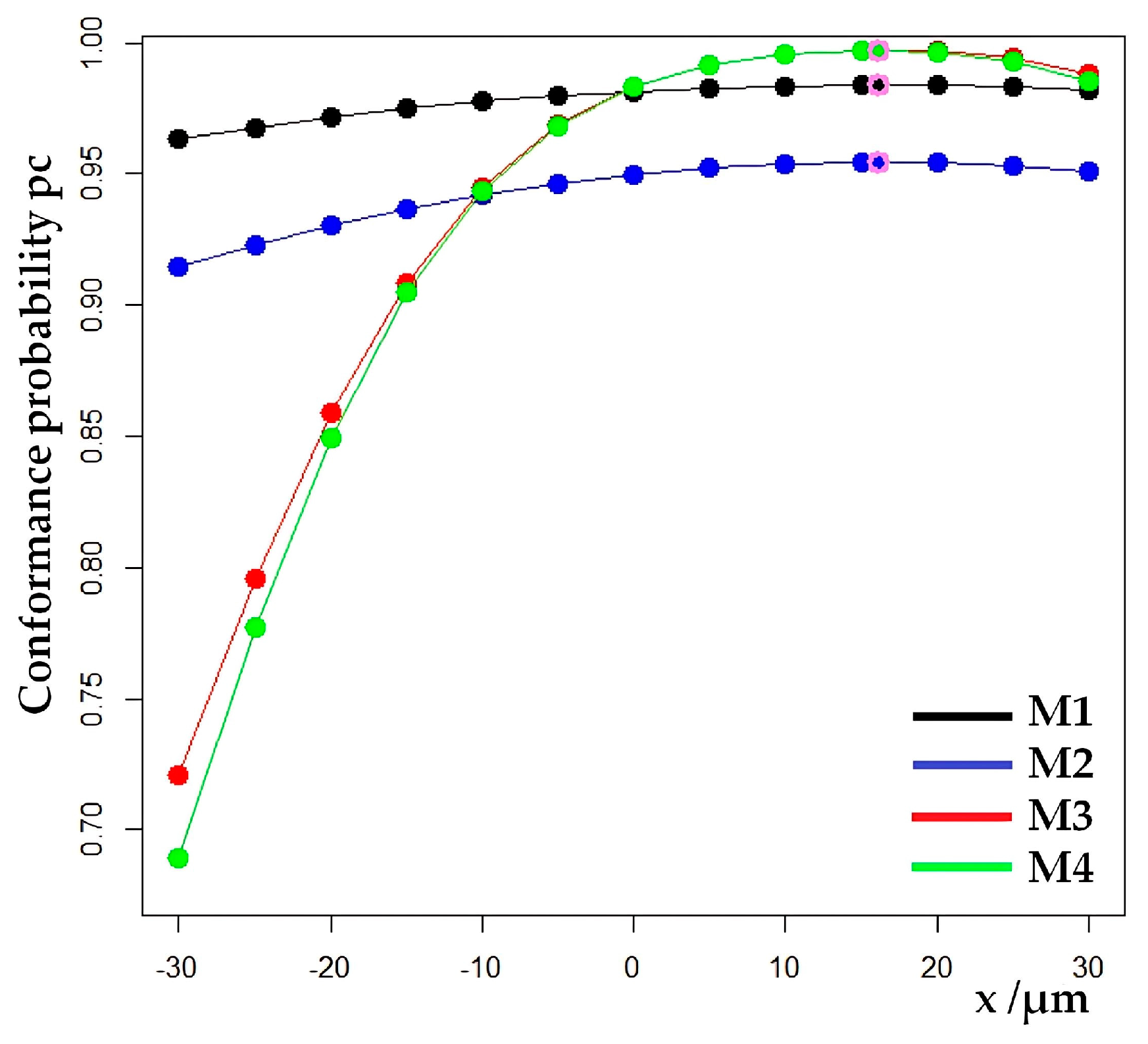
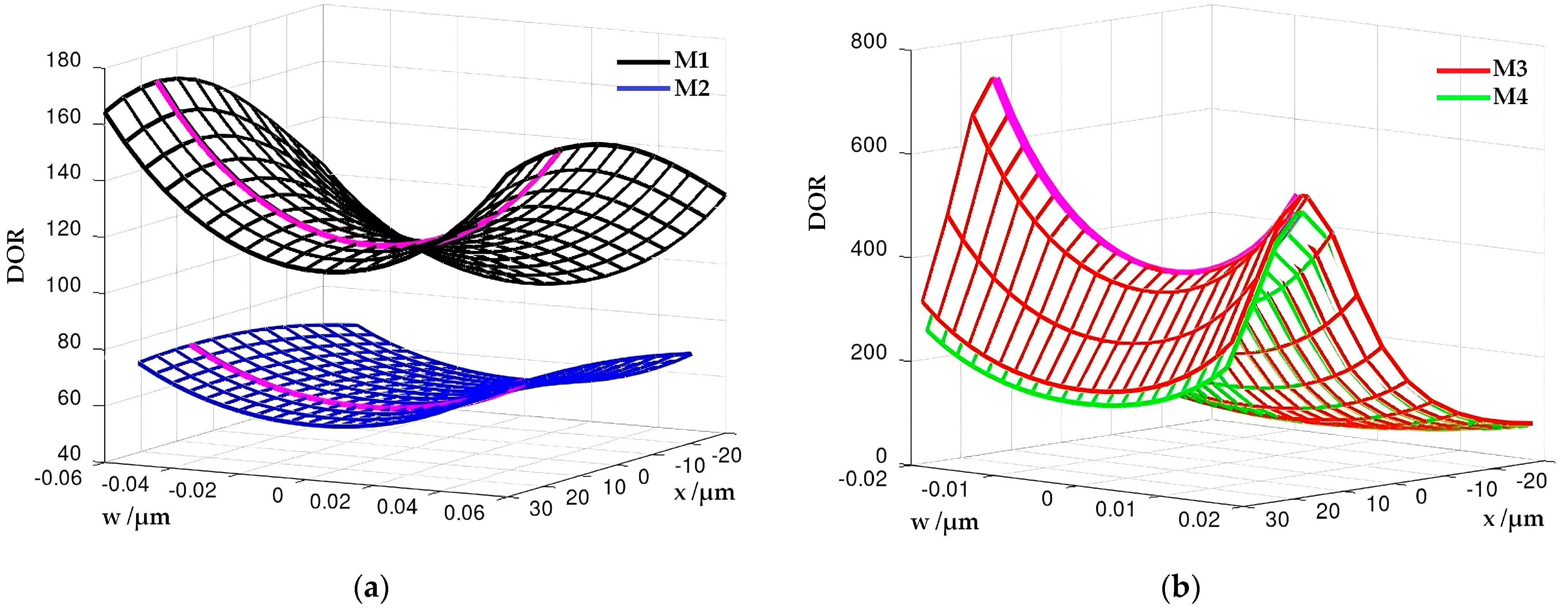
3.3. Comparison of Models Using Metrics Related to the Confusion Matrix
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Savković, B.; Kovač, P.; Rodić, D.; Štrbac, B.; Klančnik, S. Comparison of artificial neural network, fuzzy logic, and genetic algorithm for cutting temperature and surface roughness prediction during the face milling process. Adv. Prod. Eng. Manag. 2020, 15, 137–150. [Google Scholar] [CrossRef]
- Sheth, S.; Modi, B.; Patel, D.; Chaudhari, A. Modeling and Prediction Using Regression, ANN, and Fuzzy Logic of Real Time Vibration Monitoring on Lathe Machine in Context of Machining Parameters. Bonfring. Int. J. Man. Mach. Interface 2015, 3, 30–35. [Google Scholar] [CrossRef][Green Version]
- Razumić, A.; Runje, B.; Lisjak, D.; Kolar, D.; Horvatić Novak, A.; Štrbac, B.; Savković, B. Atomic force microscopy: Step height measurement uncertainty evaluation. In Proceedings of the International Conference MATRIB 2023—Materials, Tribology & Recycling, Vela Luka, Croatia, 29 June–1 July 2023. [Google Scholar]
- Papafotis, K.; Nikitas, D.; Sotiriadis, P.P. Magnetic Field Sensors’ Calibration: Algorithms’ Overview and Comparison. Sensors 2021, 21, 5288. [Google Scholar] [CrossRef] [PubMed]
- Shen, G.; Wang, Y.; Dewaele, A.; Wu, C.; Fratanduono, D.E.; Eggert, J.; Klotz, S.; Dziubek, K.F.; Loubeyre, P.; Fat’yanov, O.V.; et al. Toward an international practical pressure scale: A proposal for an IPPS ruby gauge (IPPS-Ruby2020). High Press. Res. 2020, 40, 299–314. [Google Scholar] [CrossRef]
- Aime, L.F.J.; Kissinger, T.; James, S.W.; Chehura, E.; Verzeletti, A.; Tatam, R.P. High sensitivity pressure measurement using optical fibre sensors mounted on a composite diaphragm. Opt. Express. 2021, 29, 4105–4123. [Google Scholar] [CrossRef] [PubMed]
- Greaves, M.; Caillon, N.; Rebaubier, H.; Bartoli, G.; Bohaty, S.; Cacho, I.; Clarke, L.; Cooper, M.; Daunt, C.; Delaney, M.; et al. Interlaboratory comparison study of calibration standards for foraminiferal Mg/Ca thermometry. Geochem. Geophys. Geosyst. 2008, 9, Q08010. [Google Scholar] [CrossRef]
- Velychko, O.; Shevkun, S.; Gordiyenko, T.; Mescheriak, O. Interlaboratory comparisons of the calibration results of time meters. East. Eur. J. Enterp. Technol. 2018, 1, 4–11. [Google Scholar] [CrossRef][Green Version]
- Wübbeler, G.; Bodnar, O.; Elster, C. Robust Bayesian linear regression with application to an analysis of the CODATA values for the Planck constant. Metrologia 2018, 55, 20. [Google Scholar] [CrossRef]
- Liao, K.; Shafieloo, A.; Keeley, R.E.; Linder, E.V. A Model-independent Determination of the Hubble Constant from Lensed Quasars and Supernovae Using Gaussian Process Regression. Astrophys. J. Lett. 2019, 886, L23. [Google Scholar] [CrossRef]
- Cox, M.G.; Forbes, A.B.; Harris, P.M.; Smith, I.M. The Classification and Solution of Regression Problems for Calibration, NPL Report CMSC 24/03; National Physical Laboratory: Teddington, UK, 2004; Available online: https://eprintspublications.npl.co.uk/2772/1/cmsc24.pdf (accessed on 4 January 2024).
- Fernández-Delgado, M.; Sirsat, M.S.; Cernadas, E.; Alawadi, S.; Barro, S.; Febrero-Bande, M. An extensive experimental survey of regression methods. Neural Netw. 2019, 111, 11–34. [Google Scholar] [CrossRef]
- BIPM; IEC; IFCC; ILAC; ISO; IUPAC; IUPAP; OIML. Evaluation of Measurement Data—The Role of Measurement Uncertainty in Conformity Assessment. Joint Committee for Guides in Metrology, JCGM 106:2012. BIPM. 2012. Available online: https://www.bipm.org/documents/20126/2071204/JCGM_106_2012_E.pdf/fe9537d2-e7d7-e146-5abb-2649c3450b25 (accessed on 4 January 2024).
- BIPM; IEC; IFCC; ILAC; ISO; IUPAC; IUPAP; OIML. Evaluation of Measurement Data—An Introduction to the “Guide to the Expression of Uncertainty in Measurement” and Related Documents. Joint Committee for Guides in Metrology, JCGM 104:2009. BIPM. 2009. Available online: https://www.bipm.org/en/committees/jc/jcgm/publications (accessed on 4 January 2024).
- Expression of uncertainty in measurement. Chem. Int. 2018, 40, 30–31. [CrossRef]
- GUM-Introduction. Available online: https://www.iso.org/sites/JCGM/GUM-introduction.htm (accessed on 4 January 2024).
- ILAC-G8:09/2019; Guidelines on Decision Rules and Statements of Conformity. ILAC Secretariat: Newton, SA, Australia, 2019. Available online: https://ilac.org/publications-and-resources/ilac-guidance-series/ (accessed on 5 January 2024).
- Božić, D.; Runje, B.; Lisjak, D.; Kolar, D. Metrics Related to Confusion Matrix as Tools for Conformity Assessment Decisions. Appl. Sci. 2023, 13, 8187. [Google Scholar] [CrossRef]
- Pendrill, L.R. Using measurement uncertainty in decision-making and conformity assessment. Metrologia 2014, 51, 3206. [Google Scholar] [CrossRef]
- Dias, F.R.S.; Lourenço, F.R. Measurement uncertainty evaluation and risk of false conformity assessment for microbial enu-meration tests. J. Microbiol. Methods 2021, 189, 106312. [Google Scholar] [CrossRef]
- Williams, A.; Magnusson, B. (Eds.) Eurachem/CITAC Guide: Use of Uncertainty Information in Compliance Assessment. Available online: https://www.eurachem.org/images/stories/Guides/pdf/MUC2021_P1_EN.pdf (accessed on 9 January 2024).
- Young, D.S. Tolerance: An R Package for Estimating Tolerance Intervals. J. Stat. Softw. 2010, 36, 1–39. [Google Scholar] [CrossRef]
- Wallis, A.W. Tolerance intervals for linear regressions. In Proceedings of the Second Berkeley Symposium on Mathematical Statistics and Probability, Berkeley, CA, USA, 31 July–12 August 1950; Available online: https://digicoll.lib.berkeley.edu/record/112745/files/math_s2_article-04.pdf (accessed on 5 January 2024).
- EUROLAB. Technical Report No.1/2017-Decision Rules Applied to Conformity Assessment. Available online: https://www.eurolab.org/pubs-techreports (accessed on 7 January 2024).
- Božić, D.; Samardžija, M.; Kurtela, M.; Keran, Z.; Runje, B. Risk Evaluation for Coating Thickness Conformity Assessment. Materials 2023, 16, 758. [Google Scholar] [CrossRef]
- Runje, B.; Horvatić Novak, A.; Razumić, A.; Piljek, P.; Štrbac, B.; Orošnjak, M. Evaluation of Consumer and Producer Risk in Conformity Assessment Decision. In Proceedings of the 30th DAAAM International Symposium “Intelligent Manufacturing & Automation”, Zadar, Croatia, 23–26 October 2019. [Google Scholar] [CrossRef]
- Božić, D.; Runje, B. Data Modelling in Risk Assessment. In Proceedings of the Laboratory Competence-2022, Cavtat, Croatia, 9–12 November 2022; Available online: https://www.crolab.hr/userfiles/file/cavtat2022/CROLAB_Cavtat%202022_zbornik%20radova_final_B.pdf (accessed on 9 January 2024).
- Toczek, W.; Smulko, J. Risk Analysis by a Probabilistic Model of the Measurement Process. Sensors 2021, 21, 2053. [Google Scholar] [CrossRef]
- Rajan, A.; Kuang, Y.C.; Po-Leen Ooi, M.; Demidenko, S.N. Moments and Maximum Entropy Method for Expanded Uncertainty Estimation in Measurements. In Proceedings of the IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Turin, Italy, 22–25 May 2017. [Google Scholar] [CrossRef]
- Weise, K.; Woger, W. A Bayesian theory of measurement uncertainty. Meas. Sci. Technol. 1993, 4, 1. [Google Scholar] [CrossRef]
- BIPM; IEC; IFCC; ILAC; ISO; IUPAC; IUPAP; OIML. Evaluation of Measurement Data—Supplement 1 to the “Guide to the Expression of Uncertainty in Measurement”—Propagation of Distributions Using a Monte Carlo Method. Joint Committee for Guides in Metrology, JCGM 101:2008. BIMP. 2008. Available online: https://www.bipm.org/documents/20126/2071204/JCGM_101_2008_E.pdf/325dcaad-c15a-407c-1105-8b7f322d651c (accessed on 9 January 2024).
- Lira, I. A Bayesian approach to the consumer’s and producer’s risks in measurement. Metrologia 1999, 36, 397–402. [Google Scholar] [CrossRef]
- Cox, M.G.; Forbes, A.B.; Harris, P.M. Bayesian estimation methods in metrology. In Proceedings of the 24th International Workshop on Bayesian Inference and Maximum Entropy Methods in Science and Engineering, Garching, Germany, 25–30 July 2004. [Google Scholar] [CrossRef]
- Božić, D.; Runje, B. Selection of an Appropriate Prior Distribution in Risk Assessment. In Proceedings of the 33rd International DAAAM Virtual Symposium “Intelligent Manufacturing & Automation”, Vienna, Austria, 26–27 October 2022. [Google Scholar] [CrossRef]
- Brandão, L.P.; Silva, V.F.; Bassi, M.; de Oliveira, E.C. Risk Assessment in Monitoring of Water Analysis of a Brazilian River. Molecules 2022, 27, 3628. [Google Scholar] [CrossRef]
- Kuselman, I.; Pennecchi, F.; Bettencourt da Silva, R.J.N.; Brynn Hibbert, D. Conformity assessment of multicomponent materials or objects: Risk of false decisions due to measurement uncertainty—A case study of denatured alcohols. Talanta 2017, 164, 189–195. [Google Scholar] [CrossRef]
- Pennecchi, F.R.; Kuselman, I.; Hibbert, B.D.; Sega, M.; Rolle, F.; Altshul, V. Fit-for-purpose risks in conformity assessment of a substance or material—A case study of synthetic air. Measurement 2022, 188, 110542. [Google Scholar] [CrossRef]
- Pennecchi, F.R.; Kuselman, I.; Di Rocco, A.; Brynn Hibbert, D.; Semenova, A.A. Risks in a sausage conformity assessment due to measurement uncertainty, correlation, and mass balance constraint. Food Control 2021, 125, 107949. [Google Scholar] [CrossRef]
- Separovic, L.; de Godoy Bertanha, M.L.; Saviano, A.M.; Lourenço, F.R. Conformity Decisions Based on Measurement Uncertainty—A Case Study Applied to Agar Diffusion Microbiological Assay. J. Pharm. Innov. 2020, 15, 110–115. [Google Scholar] [CrossRef]
- Lombardo, M.; Margueiro da Silva, S.; Lourenço, F.R. Conformity assessment of medicines containing antibiotics—A multi-variate assessment. Regul. Toxicol. Pharmacol. 2022, 136, 105279. [Google Scholar] [CrossRef]
- Pennecchi, F.R.; Kuselman, I.; Bettencourt da Silva, R.J.N.; Brynn Hibbert, D. Risk of a false decision on conformity of an environmental compartment due to measurement uncertainty of concentrations of two or more pollutants. Chemosphere 2018, 202, 165–176. [Google Scholar] [CrossRef]
- Separovic, L.; Lourenço, F.R. Measurement uncertainty and risk of false conformity decision in the performance evaluation of liquid chromatography analytical procedures. J. Pharm. Biomed. Anal. 2019, 171, 73–80. [Google Scholar] [CrossRef]
- Caffaro, A.M.; Lourenço, F.R. Total combined global risk assessment applied to pharmaceutical equivalence—A case study of ofloxacin medicines. Chemom. Intell. Lab. Syst. 2023, 241, 104935. [Google Scholar] [CrossRef]
- Bednjanec, F. Umjeravanje Uređaja za Mjerenje Kružnosti. Diplomski rad, Fakultet Strojarstva i Brodogradnje, Sveučilište u Zagrebu 2016. 24 March 2016. Available online: https://urn.nsk.hr/urn:nbn:hr:235:701539 (accessed on 10 January 2024).
- Huzak, M. Vjerojatnost i Matematička Statistika, Predavanja; Poslijediplomski Specijalistički Sveučilišni Studij Aktuarske Matematike; Specialist u Zagrebu, PMF-Matematički Odjel: Zagreb, Croatia, 2006; Available online: http://aktuari.math.pmf.unizg.hr/docs/vms.pdf (accessed on 11 January 2024).
- Ortiz, M.C.; Sánchez, M.S.; Sarabia, L.A. 1.05—Quality of Analytical Measurements: Univariate Regression. In Comprehensive Chemometrics. Chemical and Biochemical Data Analysis, 1st ed.; Brown, S.D., Tauler, R., Walczak, B., Eds.; Elsevier: Amsterdam, The Netherlands, 2009; Volume 1, pp. 127–169. [Google Scholar] [CrossRef]
- Ellison, S.R.; Williams, A. (Eds.) Eurachem/CITAC Guide: Quantifying Uncertainty in Analytical Measurement. Available online: https://www.eurachem.org/images/stories/Guides/pdf/QUAM2012_P1.pdf (accessed on 11 January 2024).
- Miller, S.J. The Method of Least Squares; Mathematics Department Brown University: Providence, RI, USA, 2006; Available online: https://web.williams.edu/Mathematics/sjmiller/public_html/105Sp10/handouts/MethodLeastSquares.pdf (accessed on 15 January 2024).
- BIPM; IEC; IFCC; ILAC; ISO; IUPAC; IUPAP; OIML. Evaluation of Measurement Data—Guide to the Expression of Uncertainty in Measurement. Joint Committee for Guides in Metrology, JCGM 100:2008. BIPM. 2008. Available online: https://www.bipm.org/documents/20126/2071204/JCGM_100_2008_E.pdf/cb0ef43f-baa5-11cf-3f85-4dcd86f77bd6 (accessed on 16 January 2024).
- Taylor, B.N.; Kuyatt, C.E. Guidelines for Evaluating and Expressing the Uncertainty of NIST Measurement Results; NIST Technical Note 1297; US Department of Commerce, Technology Administration, National Institute of Standards and Technology: Gaithersburg, MD, USA, 1994. Available online: https://emtoolbox.nist.gov/publications/nisttechnicalnote1297s.pdf (accessed on 16 January 2024).
- Farrance, I.; Frenkel, R. Uncertainty of Measurement: A Review of the Rules for Calculating Uncertainty Components through Functional Relationships. Clin. Biochem. Rev. 2012, 33, 49–75. Available online: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC3387884/ (accessed on 16 January 2024).
- Klauenberg, K.; Martens, S.; Bošnjaković, A.; Cox, M.G.; Van der Veen, A.M.; Elster, C. The GUM perspective on straight-line errors-in-variables regression. Measurement 2021, 187, 110340. [Google Scholar] [CrossRef]
- Croarkin, C.; Tobias, P.; Zey, C. Engineering Statistics Handbook; The Institute Gaithersburg: Gaithersburg, MD, USA, 2001. Available online: https://www.itl.nist.gov/div898/handbook/dtoc.htm (accessed on 16 January 2024).
- Krishnamoorthy, K.; Mathew, T. Statistical Tolerance Regions: Theory, Applications, and Computation; Wiley: Hoboken, NJ, USA, 2009. [Google Scholar]
- Splinter, K.; Sigler, G.; Harman, M.; Kolsti, K. Tolerance Intervals Demystified; STAT Center of Excellence Air Force Institute of Technology: Wright-Patterson AFB, OH, USA. Available online: https://www.afit.edu/STAT/statcoe_files/Tolerance%20Intervals%20Demystified.pdf (accessed on 23 January 2024).
- Greenwell, B.M. Topics in Statistical Calibration. Ph.D. Thesis, Air Force Institute of Technology, Hobson Way, OH, USA, 3 March 2014. Available online: https://apps.dtic.mil/sti/pdfs/ADA598921.pdf (accessed on 23 January 2024).
- R Core Team. R: A Language and Environment for Statistical Computing; The R Foundation for Statistical Computing: Vienna, Austria, 2022; Available online: https://www.R-project.org/ (accessed on 13 February 2024).
- Borchers, H.W. Pracma: Practical Numerical Math Functions. R Package Version 2.4.2/r532. Available online: https://R-Forge.R-project.org/projects/optimist/ (accessed on 13 February 2024).
- Eaton, J.W.; Bateman, D.; Hauberg, S.; Wehbring, R. GNU Octave Version 8.4.0 Manual: A High-Level Interactive Language for Numerical Computations. Available online: https://www.gnu.org/software/octave/doc/v8.4.0/ (accessed on 13 February 2024).
- Botchkarev, A. A new typology design of performance metrics to measure errors in machine learning regression algorithms. Interdiscip. J. Inf. Knowl. Manag. 2019, 14, 45–76. [Google Scholar] [CrossRef]
- Abhishek, T. Comparative Assessment of Regression Models Based on Model Evaluation Metrics. Int. Res. J. Eng. Technol. 2021, 9, 853–860. [Google Scholar]
- Hodson, T.O. Root-mean-square error (RMSE) or mean absolute error (MAE): When to use them or not. Geosci. Model Dev. 2022, 15, 5481–5487. [Google Scholar] [CrossRef]
- Chicco, D.; Warrens, M.J.; Jurman, G. The coefficient of determination R-squared is more informative than SMAPE, MAE, MAPE, MSE and RMSE in regression analysis evaluation. PeerJ Comput. Sci. 2021, 7, e623. [Google Scholar] [CrossRef] [PubMed]
- Chai, T.; Draxler, R.R. Root mean square error (RMSE) or mean absolute error (MAE)?—Arguments against avoiding RMSE in the literature. Geosci. Model Dev. 2014, 7, 1247–1250. [Google Scholar] [CrossRef]
- Jeni, L.A.; Cohn, J.F.; de la Torre, F. Facing Imbalanced Data—Recommendations for the Use of Performance Metrics. In Proceedings of the 2013 Humaine Association Conference on Affective Computing and Intelligent Interaction (ACII), Geneva, Switzerland, 2–5 September 2013. [Google Scholar] [CrossRef]
- De Diego, I.M.; Redondo, A.R.; Fernández, R.R.; Navarro, J.; Moguerza, J.M. General Performance Score for Classification Problems. Appl. Intell. 2022, 52, 12049–12063. [Google Scholar] [CrossRef]
- Grandini, M.; Bagli, E.; Visani, G. Metrics for Multi-Class Classification: An Overview. arXiv 2020, arXiv:2008.05756. [Google Scholar] [CrossRef]
- Chicco, D.; Tötsch, N.; Jurman, G. The Matthews correlation coefficient (MCC) is more reliable than balanced accuracy, bookmaker informedness, and markedness in two-class confusion matrix evaluation. BioData Min. 2021, 14, 13. [Google Scholar] [CrossRef]
- McHugh, M.L. The odds ratio: Calculation, usage, and interpretation. Biochem. Medica 2009, 19, 120–126. Available online: https://hrcak.srce.hr/37593 (accessed on 1 February 2024). [CrossRef]
- Glas, A.S.; Lijmer, J.G.; Prins, M.H.; Bonsel, G.J.; Bossuyt, P.M.M. The diagnostic odds ratio: A single indicator of test performance. J. Clin. Epidemiol. 2003, 56, 1129–1135. [Google Scholar] [CrossRef]
- Šimundić, A.M. Measures of Diagnostic Accuracy: Basic Definitions. Ejifcc 2009, 19, 203. Available online: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC4975285/ (accessed on 1 February 2024).








| Reference Value x/µm | 1st Measurement y1/µm | 2nd Measurement y2/µm | 3rd Measurement y3/µm |
|---|---|---|---|
| −30 | −30.10 | −30.02 | −30.05 |
| −25 | −25.12 | −25.05 | −25.05 |
| −20 | −20.10 | −20.05 | −20.05 |
| −15 | −15.10 | −15.00 | −15.05 |
| −10 | −10.10 | −10.00 | −10.05 |
| −5 | −5.10 | −5.05 | −5.06 |
| 0 | 0.00 | 0.00 | 0.00 |
| 5 | 4.98 | 4.98 | 5.00 |
| 10 | 9.99 | 10.00 | 10.02 |
| 15 | 14.99 | 15.00 | 15.00 |
| 20 | 20.00 | 20.00 | 20.05 |
| 25 | 25.00 | 25.02 | 25.00 |
| 30 | 30.00 | 30.05 | 30.00 |
| Source of Uncertainty | Probability Distribution | Standard Uncertainty/µm |
|---|---|---|
| ULM device | Normal | 0.1 |
| Linear error of the probe I | Rectangular | 0.000184462 |
| Linear error of the dial probe II | Rectangular | 0.065909762 |
| Resolution | Rectangular | 0.034641016 |
| Combined measurement uncertainty of the probe | 0.1247 | |
| Model | Uncertainty | Tolerance Interval |
|---|---|---|
| M1 Linearized model | µm | |
| M2 Linearized model | ||
| M3 Non-linearized model | ||
| M4 Linearized model |
| RMSE, Global Consumer’s Risk | ||||
| /µm | /% | /% | /% | /% |
| 0.63 | 0.94 | 5.40 | 5.27 | |
| 0.22 | 0.35 | 2.55 | 2.68 | |
| 0.17 | 0.27 | 2.11 | 2.16 | |
| 0.40 | 0.60 | 3.66 | 3.63 | |
| RMSE, Global Producer’s Risk | ||||
| /µm | /% | /% | /% | /% |
| 1.16 | 0.97 | 2.40 | 2.52 | |
| 0.46 | 0.42 | 4.03 | 3.97 | |
| 0.35 | 0.32 | 2.92 | 2.87 | |
| 0.75 | 0.64 | 3.19 | 3.18 | |
| RMSE, Conformance Probability | ||||
| /µm | ||||
| 0.022 | 0.039 | 0.356 | 0.358 | |
| 0.007 | 0.014 | 0.092 | 0.100 | |
| 0.005 | 0.010 | 0.078 | 0.083 | |
| 0.013 | 0.025 | 0.217 | 0.220 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Božić, D.; Runje, B.; Razumić, A. Risk Assessment for Linear Regression Models in Metrology. Appl. Sci. 2024, 14, 2605. https://doi.org/10.3390/app14062605
Božić D, Runje B, Razumić A. Risk Assessment for Linear Regression Models in Metrology. Applied Sciences. 2024; 14(6):2605. https://doi.org/10.3390/app14062605
Chicago/Turabian StyleBožić, Dubravka, Biserka Runje, and Andrej Razumić. 2024. "Risk Assessment for Linear Regression Models in Metrology" Applied Sciences 14, no. 6: 2605. https://doi.org/10.3390/app14062605
APA StyleBožić, D., Runje, B., & Razumić, A. (2024). Risk Assessment for Linear Regression Models in Metrology. Applied Sciences, 14(6), 2605. https://doi.org/10.3390/app14062605







