Assessment of Non-Linear Analyses of RC Buildings Retrofitted with Hysteretic Dampers According to the Italian Building Code

Abstract

While the use of steel hysteretic dampers has spread in the last decade for both new and retrofitted constructions, the Italian Building Code (IBC), as well as the Eurocode 8, does not provide specific recommendations for the design and verification of structures equipped with this technology. Due to their strong non-linear behavior, the effectiveness of the design with these systems must be verified through non-linear analyses. Non-Linear Time-History analyses (NLTHAs) are the most reliable method, but they are computationally expensive. The aim of the study is to investigate the reliability of non-linear static procedures, allowed by the IBC as an alternative to NLTHAs, for the analysis of buildings equipped with hysteretic devices provided with high damping capability. A parametric study is conducted on two reinforced concrete residential buildings, typical of the Italian residential heritage, retrofitted with hysteretic braces characterized by different stiffness and ductility values. The retrofit design is verified using non-linear analyses, both static and dynamic, considering either natural or artificial accelerograms, as the IBC deems them as equivalent. Within this work, reference is made only to the IBC; however, given the significant similarity between the IBC and the European code, the outcomes are expected to have a broader impact and to be not limited to the Italian context. Therefore, although this work is a preliminary study, it is believed to offer some initial insights on the topic and serve as the foundation for a more in-depth study that could lead to a regulatory revision on the subject.

1. Introduction

Hysteretic dampers are widely used for seismic passive protection of both new and existing structures [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15]. According to the European standard EN 15129 [16], hysteretic dampers, which are further classified in steel hysteretic dampers, friction dampers and metal extrusion dampers, belong to the category of Displacement-Dependent Devices (DDDs). These systems are characterized by constitutive behavior which is mainly dependent on displacement. Among DDDs, steel hysteretic dampers are the most popular devices for the seismic protection of ordinary structures, such as school, residential and industrial buildings, as proved by the large number of studies and applications [17,18,19,20,21,22,23,24,25], thanks to their good damping capacity and predictable behavior combined with ease of manufacturing and installation [26,27,28,29]. Focusing on the Italian scenario, recommendations on anti-seismic devices are given in Chapter 11 of the Italian Building Code, the IBC [30,31]. In particular, the code requires that devices designed to satisfy the performance requirements at the ultimate limit state (seismic action with probability of exceedance of 10% over the reference period of the structure V_R, corresponding to the Life safety Limit State, LLS according to IBC [30]) must be able to resist earthquakes of higher intensity with probability of exceedance of 5% over V_R, corresponding to the Collapse Limit State, CLS. Therefore, with d_bd being the design displacement at LLS, the device must be designed to withstand the maximum between γ_x·d_bd and d₂, where γ_x = 1.1 is the amplification factor specified by EN 15129 [16] and d₂ is the displacement at the CLS [30,31].

As hysteretic devices introduce significant non-linear behavior and energy dissipation into the structure, such features should be taken into account in the modelling and analyses of structural systems incorporating such devices [16].

Therefore, the effectiveness of the retrofitted system is verified through non-linear analyses, which can be performed according to either static or dynamic methods.

The Commentary to the IBC [31], in paragraph §C7.3.4.2, provides guidance for the application of Non-Linear Static Analyses (NLSAs). In such analyses, the structure is described through its capacity curve F_b–d_c, where F_b is the shear force at the base and d_c is the displacement of a control point, which usually coincides with the center of mass of the top floor. For each limit state, the performance level is determined by comparing the capacity curve to the spectral demand. To perform such comparison, the structural system is replaced by an equivalent Single-Degree-of-Freedom (SDOF) system through Equations (1)–(3), and capacity curve F_b–d_c of the physical Multi-Degree-of-Freedom (MDOF) system is replaced by the “reduced” capacity curve F*–d* of the equivalent SDOF system shown in Figure 1.

$$\Gamma =\frac{{\phi }^{T}M\tau }{{\phi }^{T}M\phi }$$

(1)

$$d^{\ast }=\frac{d_c}{\Gamma }$$

(2)

$$F^{\ast }=\frac{F_b}{\Gamma }$$

(3)

For practical purposes, according to [31], the amount of energy dissipated by the system, and therefore the equivalent viscous damping ratio ξ_eq, is evaluated by replacing the capacity curve of the equivalent SDOF system by an equivalent bilinear curve, determined based on the principle of energetic equivalence. The performance point (PP) of the system can be determined by applying either Method A, based on the principle of equal displacements or equal energies, or Method B, which is based on the Capacity Spectrum Method. In this study, Method B is considered, and the PP is evaluated through an iterative procedure in the acceleration–displacement response spectrum (ADRS) space. As the first step, the displacement at the PP is set equal to $d_{max}^{\ast }$, correspondent to the target seismic displacement of the analyzed structure, where $F_{max}^{\ast }$ is the corresponding force determined on the SDOF capacity curve. The equivalent bilinear curve of the equivalent SDOF system is then obtained by imposing same initial stiffness as the initial stiffness of the SDOF capacity curve and identifying the yield point ($d_y^{\ast }$; $F_y^{\ast }$) through the equivalence of areas A₁ and A₂, as shown in Figure 2.

Through the equivalent bilinear capacity curve, the equivalent viscous damping ratio ξ_eq is determined with Equation [C7.3.10] of [31]:

$${\xi }_{eq}=k\frac{63.7(F_y^{\ast }{d}_{max}^{\ast }-F_{max}^{\ast }{d}_y^{\ast })}{F_{max}^{\ast }{d}_{max}^{\ast }}+5$$

(4)

where parameter k accounts for the actual energy dissipation capacity of the structural system. In principle, k should be calibrated based on experimental data, but when relevant data are missing, it can be taken as 1.0 for structures with high damping capability (characterized by wide and stable hysteresis loops), 0.66 for structures with moderate damping capability (moderate change of the hysteresis loops), and 0.33 for structures with low damping capability (hysteresis loops affected by substantial pinching and decrease in area). Through ξ_eq, the damping reduction factor η is determined to evaluate the damped demand spectrum according to the equation [3.2.4] of the IBC [30]:

$$\eta =\sqrt{10/(5+{\xi }_{eq})}\ge 0.55$$

(5)

The equivalent bilinear curve and the damped spectrum demand are compared in the ADRS plane; their crossing point is the new PP, and Method B is iteratively applied until the difference between two consecutive PPs is sufficiently small.

According to Equation (5), the minimum value of the damping factor η is 0.55, which corresponds to an equivalent viscous damping ratio ξ_eq = 28%. In a structure equipped with damped braces, ξ_eq, and consequently η, depends upon the damping capacity of the dampers. In this regard, it must be emphasized that steel hysteretic dampers available nowadays, such as Buckling Restrained Braces (BRBs), friction and extrusion dampers, are characterized by high damping capacity, with ξ_eq > 28% [3,4,5,6,32,33,34,35,36]. Therefore, the contribution of such dampers to increase the overall damping ξ_eq of the combined structural system may be not completely considered in the analyses due to the limitation on η [30].

Non-Linear dynamic, or Time-History, analyses (NLTHAs) are acknowledged, by far, to be the most reliable method for predicting the seismic response of structures. However, they involve the formulation of accurate mathematical models of the real structure, are time consuming and the accuracy of the results depends on the assumptions made on the seismic action. Therefore, for ordinary structures, NLTHAs are usually replaced by simpler and computationally less onerous static analyses. Regarding the representation of the seismic input in NLTHAs, the IBC [30] §3.2.3.6 allows for consideration of either natural or artificial accelerograms. The use of artificial accelerograms was attractive in the past years since it allowed for the generation of spectrum compatible time-series even in those cases where the elastic design spectrum was the only available information [37]. Today, thanks to the growing availability of strong motions databases, the use of real accelerograms recorded during earthquakes is preferred [38]. According to the IBC [30] §3.2.3.6, natural accelerograms must be selected and properly scaled in magnitude in order to match, on average, the target elastic spectrum at a 5% equivalent viscous damping ratio (with lower and upper tolerances of −10% and +30%, respectively) in the range of periods relevant for the specific case study, which is the largest between 0.15 ÷ 2 s and 0.15 ÷ 2 T, where T is the fundamental elastic period of the structure in the direction where the accelerogram is applied. In case artificial accelerograms are used, they are generated to match, on average, the elastic response at 5% viscous damping, with lower tolerance of −10% over the period range. The duration of the accelerograms is consistent with the magnitude and the other relevant features of the seismic event, but when site-specific data are not available, the pseudo-stationary part should be equal to 10 s and the total duration must not be less than 25 s. NLTHAs calculate the actual response of the system over the whole duration of the ground motion time-history and therefore permit to account for the actual dissipation capacity of the hysteretic dampers, overcoming the limitations on the maximum equivalent viscous damping ratio which affect NLSAs in the case of hysteretic dampers with high dissipation capability.

However, in spite of the increasing spread of hysteretic dampers for both new and retrofitted buildings [17,18,19,20,21,22,23,24,25], the IBC [30,31] does not provide specific recommendations for the analyses of structures provided with such devices but refers to the general provisions for buildings in seismic areas. The same consideration is valid also referring to the European design code [39]. In fact, the IBC [30,31] and the European code [39] adopt similar provisions regarding non-linear static and dynamic analyses for structures subjected to seismic actions. This highlights that at the European level, there is also a lack of a clear guidance for practitioners who must tackle the design of damping systems for buildings, including instructions on the type of analyses to be performed. The present study aims at providing some guidance in this regard by comparing the results on NLSAs and NLTHAs of two archetype reinforced concrete (RC) frame buildings retrofitted with hysteretic steel braces in accordance with the requirements of the code [30,31].

A parametric study is performed exploring various design solutions that consider hysteretic dampers with different ductility and stiffness, and two sites, with the goal of assessing the accuracy of NLSAs for buildings retrofitted with energy dissipation systems. To better highlight the limitations of the non-linear static procedure, the analyses are performed either considering limitation η ≥ 0.55 or using the actual η resulting from the equivalent viscous damping ratio of the retrofitted system. Additionally, since according to the code [30,31] either natural or artificial accelerograms can be used in NLTHAs, a secondary goal of the study is to compare the results obtained using either time-histories. It is important to emphasize that within this article, reference is made exclusively to the IBC [30,31]. Nevertheless, given the similarity between the Italian and European codes concerning the non-linear analysis methods, the relevance of this work should not be interpreted as solely limited to the Italian context.

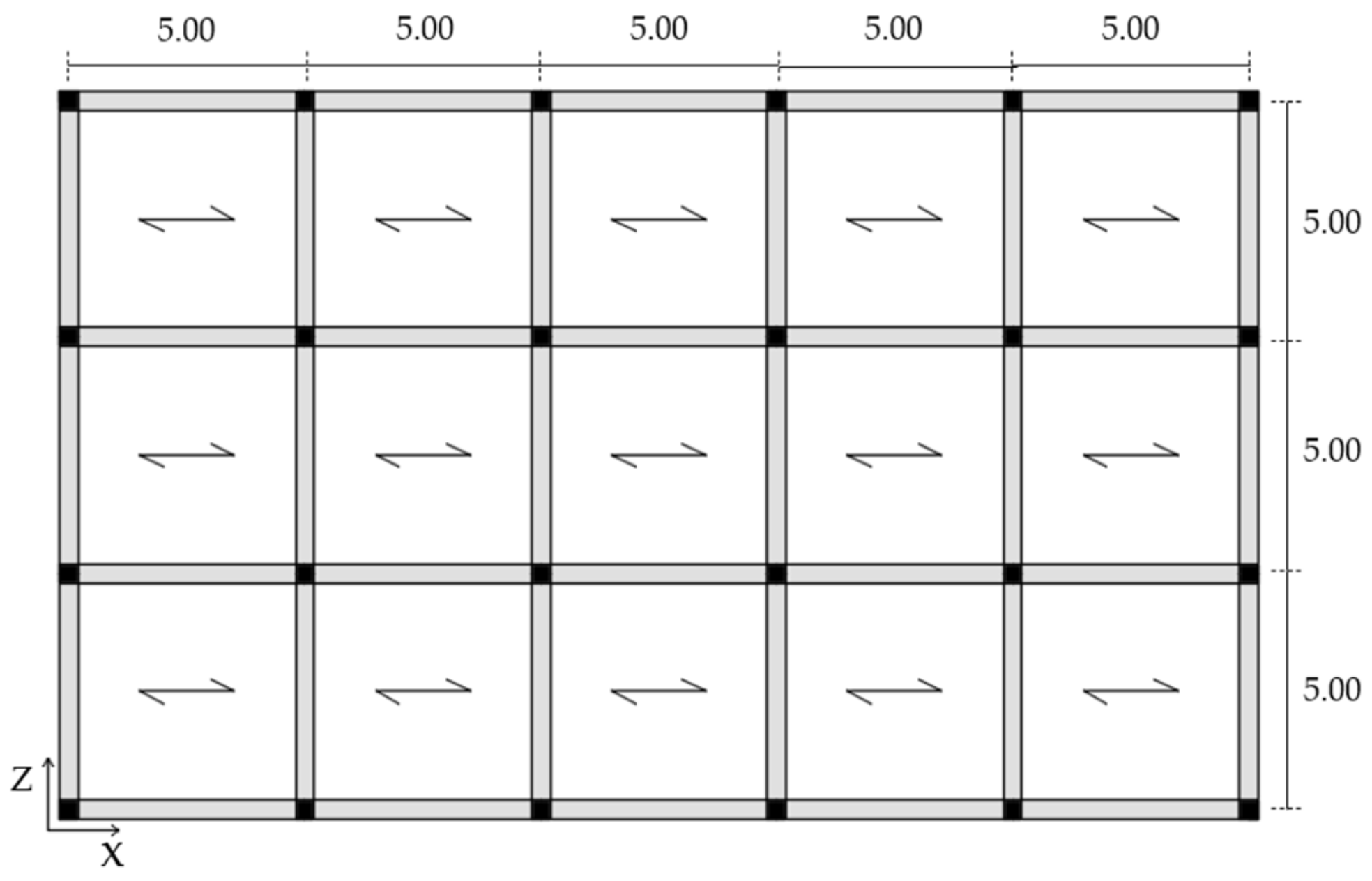
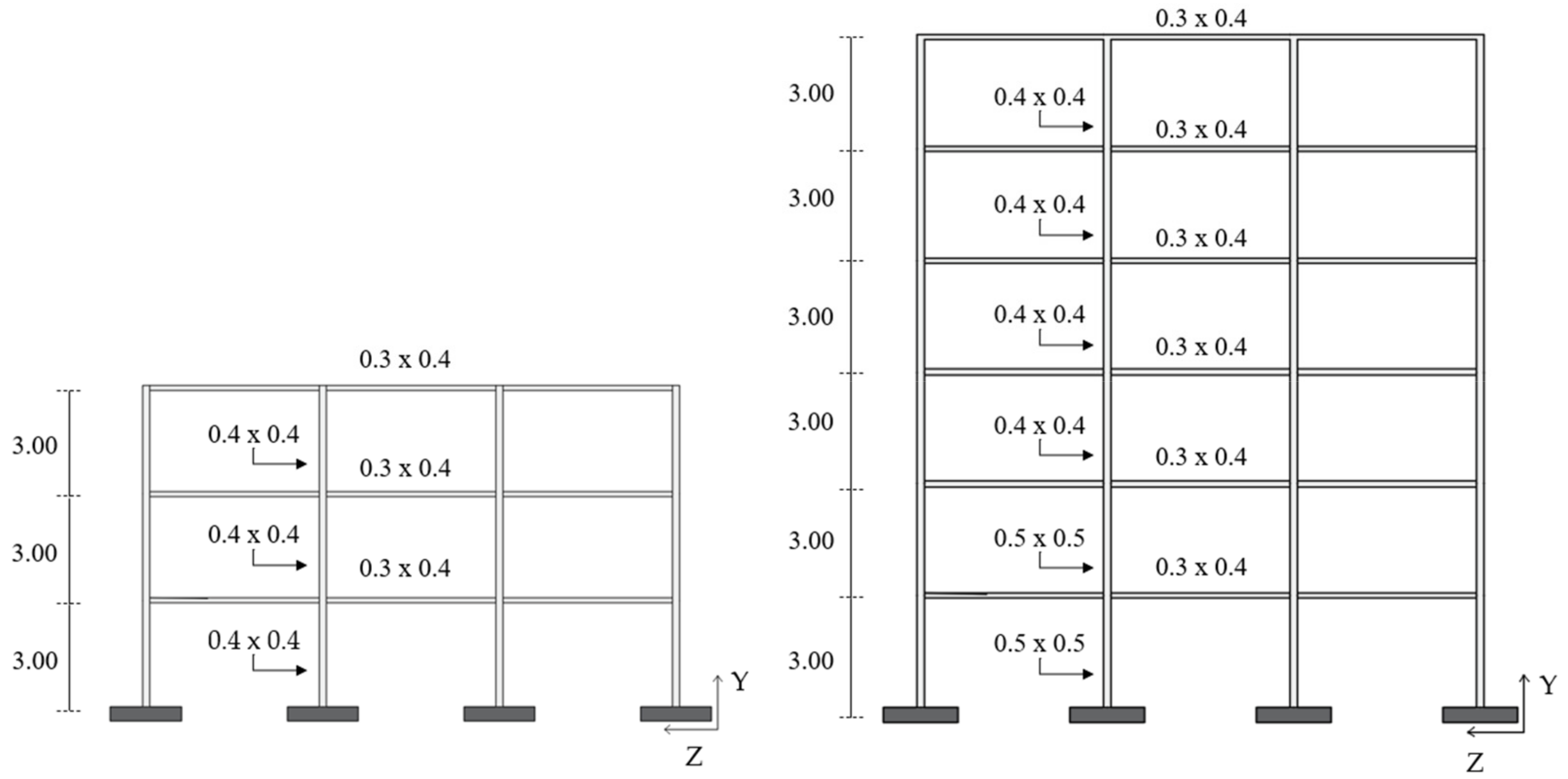
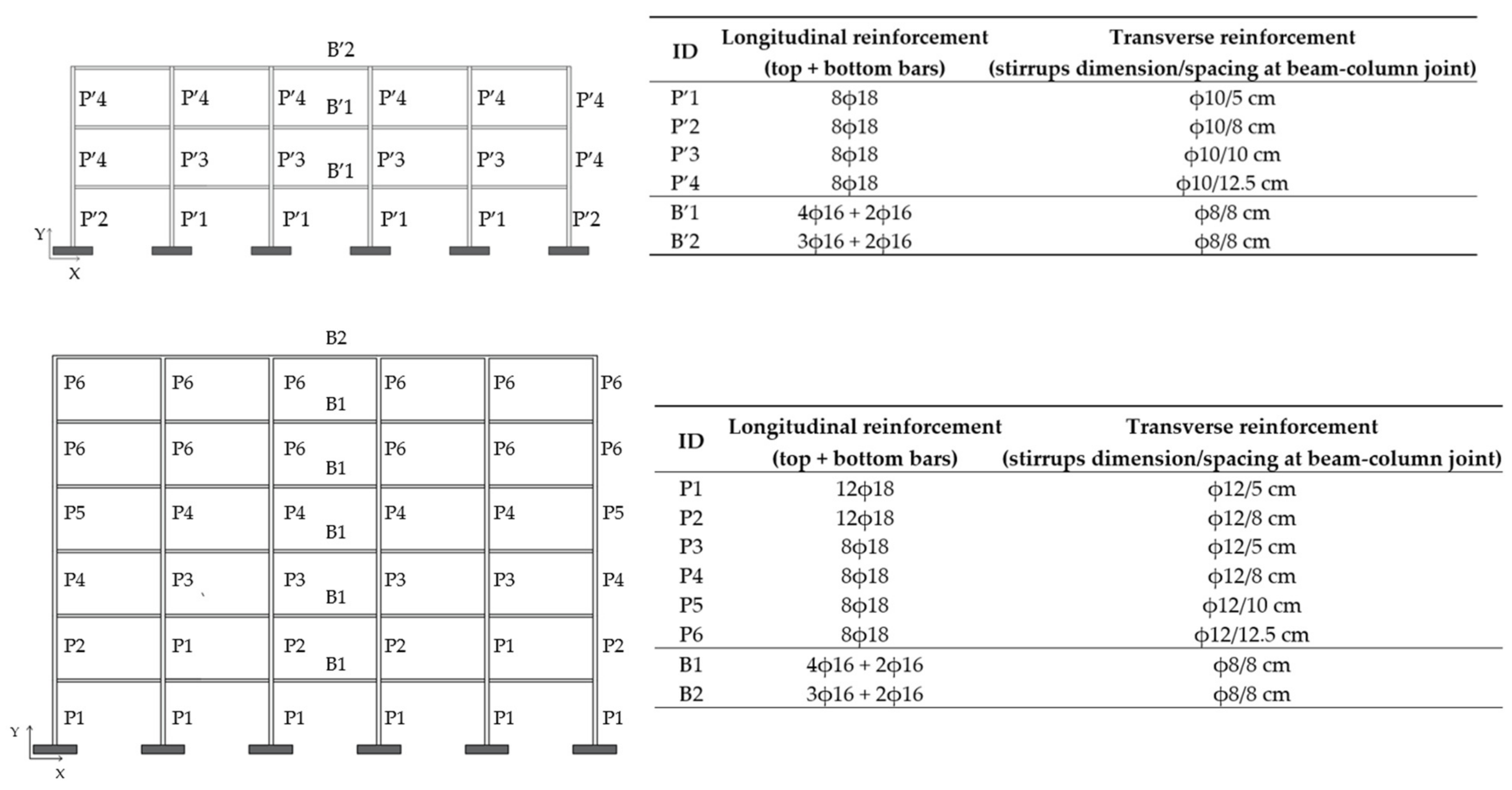
2. RC Case Study Structures

Two archetype buildings characterized by a RC moment-resisting frame taken from the literature [40] are assumed to be case studies. The first is a three-story building, and the second is a six-story building. Both buildings have the same 25 × 15 m² plan shown in Figure 3 and composed by bays of 5 m in each horizontal direction.

Figure 4 shows the elevation views with indication of the inter-story height and cross-sections of the structural members, while Figure 5 reports the reinforcement of beams and columns.

Both structures are designed following the prescriptions of the IBC [30] for residential building use, considering a moderate seismicity area with a PGA = 1.91 m/s² and a B soil type. The design is performed for a low ductility class (Class B) assuming C25/30 concrete and B450C steel [30] for reinforcement. Permanent non-structural loads comprise a 20 cm thick reinforced concrete slab supporting a 5 cm screed (0.95 kN/m²), flooring (0.4 kN/m²), and partition walls (1.6 kN/m²) for intermediate stories, while live loads equal to 2 kN/m² are assumed in accordance with IBC [30] for residential buildings.

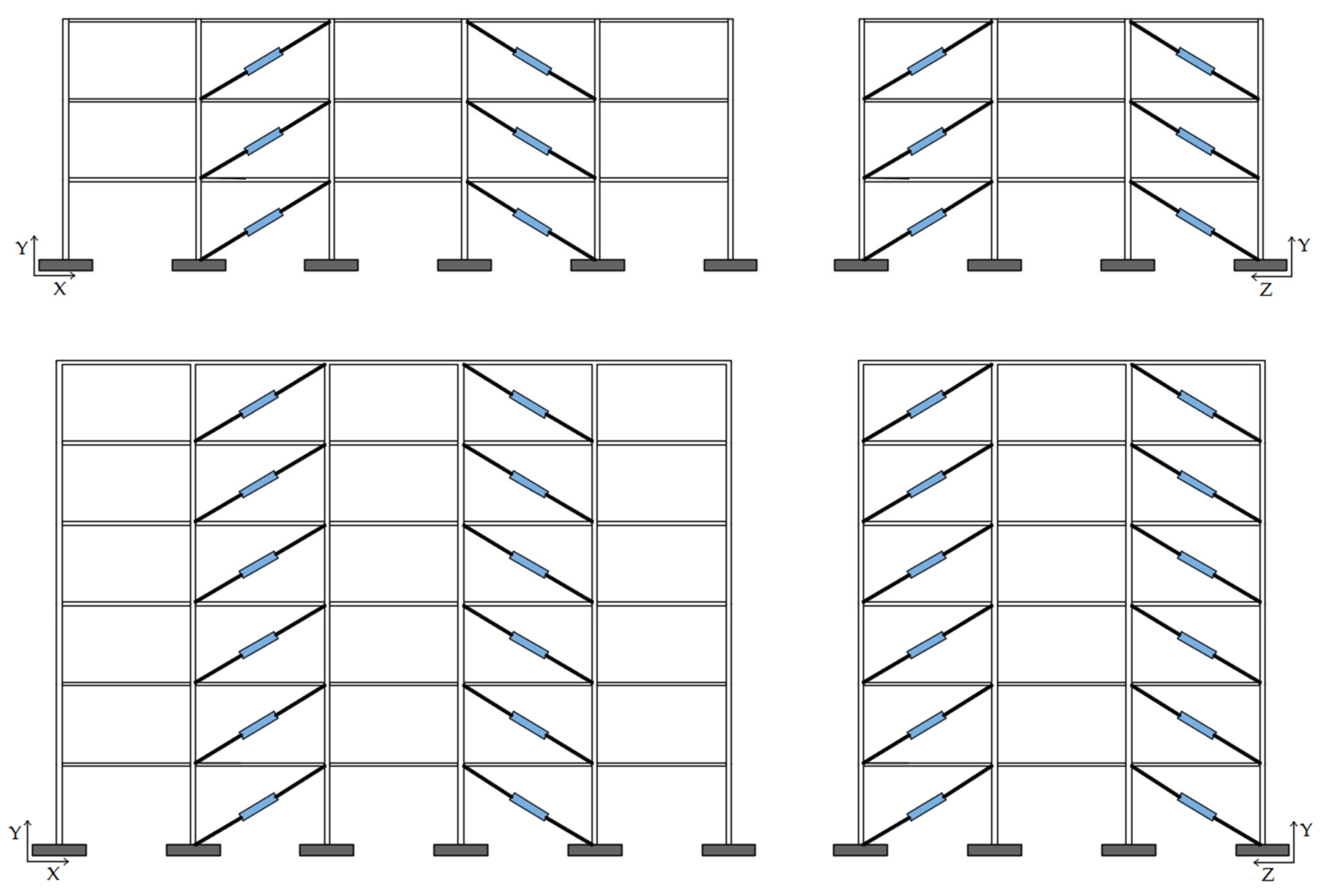
3. Design of the Seismic Retrofit

The case study structures are retrofitted in accordance with the IBC [30] referring to the seismic loads for Life safety limit state (LLS) related to the municipalities of Benevento (Long 14.787°, Lat 41.1305°) and Tramutola (Long 15.7919°, Lat 40.3176°), which are two sites of high seismicity in southern Italy. The design is performed assuming a typical residential building use with nominal life V_N = 50 years and functional class cu = II. A T₁ topography, and soil type B is considered for Benevento resulting in a PGA equal to 2.94 m/s², while T₁ topography and soil type C are assumed for Tramutola for a PGA = 3.41 m/s². The retrofit design is carried out applying a procedure developed by the authors of work [1,41]. This methodology is implemented in the ADRS space, where the structural system composed of the RC frame and the hysteretic dampers is modelled through an equivalent SDOF system, characterized by its secant stiffness and equivalent viscous damping ratio. It is important to recall that a pre-requisite for this procedure is that the behavior of the building is governed by the first mode, legitimating the condensation of the MDOF structure to the equivalent SDOF system. Therefore, this methodology is valid for low-rise and medium-rise buildings, regular in plan and in elevation, as the case studies analyzed in the present work. The sizing of the dampers is carried out in order to reach a desired structural performance level, which is expressed in terms of target displacement d_p, evaluated at the top of the structure. In the present study, d_p is selected with the aim of guaranteeing the Immediate Occupancy performance level [42] by keeping the main frame in the elastic range or by conceiving at most a controlled concrete cracking, limiting structural damage as much as possible. Therefore, the structures are immediately accessible after a main earthquake correspondent to the LLS according to the IBC [30], characterized by return period T_R of 475 years, with a probability of non-exceedance of 10% for nominal life V_N = 50 years of a residential building (cu = II). Figure 6 shows the capacity curves of the case study buildings and the relative d_ps which correspond to the ending point of the elastic branch, or at most at the beginning of the second branch relevant to the cracked concrete [43].

In this study, the two structures are retrofitted by using hysteretic steel dampers installed into diagonal steel braces (Figure 7), which is a common configuration for frame buildings [1,5,6,43,44,45]. An elastic–perfectly plastic constitutive behavior is assumed for the dampers, similarly to other studies [1,6,41,43,44]. Four units on each floor in both X and Z directions are installed in the external bays according to the layout shown in Figure 7.

The mechanical properties of each diagonal steel brace and the encased hysteretic steel damper form an in-series system can be expressed as a combination of the properties of the linear elastic brace (B) and of the elasto-plastic damper (D), as shown in Figure 8, where K_B and K_D are the elastic stiffnesses of the brace and of the damper, V_y is the maximum force of the damper, d_y, d_bd and d₂ are the yield displacement, the design seismic displacement calculated at LLS and the ultimate displacement of the damper at CLS, respectively. Damper ductility μ_D, defined as the ratio between d_bd and yield deflection d_y, for standard steel hysteretic dampers typically ranges between $4$ and 16 [1,15,41,43]. The properties of the single damped brace (DB), in terms of stiffness K_DB, ductility μ_DB, and damping capacity ξ_DB, are determined through the Equations (6)–(8), where ratio K_B/K_D between the stiffnesses of the steel brace and the damper should be taken ≥2 in order to guarantee that the largest part of the deformation of the story is concentrated in the damper [45,46]. Typical values of μ_DB and ξ_DB for damped bracing systems according to current practice are reported in

Table 1. Properties of damped braces for different values of K_B/K_D and μ_D.

μD (-)	KB/KD = 2		KB/KD = 3		KB/KD = 4		KB/KD = 5
	μDB (-)	ξDB (%)	μDB (-)	ξDB (%)	μDB (-)	ξDB (%)	μDB (-)	ξDB (%)
4	3.0	42.4	3.3	44.1	3.4	44.9	3.5	45.5
6	4.3	49.0	4.8	50.3	5.0	50.9	5.2	51.3
8	5.7	52.4	6.3	53.5	6.6	54.0	6.8	54.3
10	7.0	54.6	7.8	55.4	8.2	55.9	8.5	56.2
12	8.3	56.0	9.3	56.8	9.8	57.2	10.2	57.4
14	9.7	57.1	10.8	57.7	11.4	58.1	11.8	58.3
16	11.0	57.9	12.3	58.5	13.0	58.8	13.5	58.9
4	3.0	42.4	3.3	44.1	3.4	44.9	3.5	45.5
6	4.3	49.0	4.8	50.3	5.0	50.9	5.2	51.3

[15,43,44]. Therefore, in the study, the seismic upgrade of the case study buildings is performed considering damped brace systems characterized by values of ductility μ_DB ranging from 3 to 13.5; more specifically, μ_DBs equal to 3, 5, 7, 9, 11, and 13.5 are assumed.

$$K_{DB}=\frac{K_D{K}_B}{K_D+K_B}$$

(6)

$${\mu }_{DB}=1+\frac{{\mu }_D-1}{1+\frac{K_D}{K_B}}$$

(7)

$${\xi }_{DB}=\frac{2}{\pi }·\frac{{\mu }_{DB}-1}{{\mu }_{DB}}$$

(8)

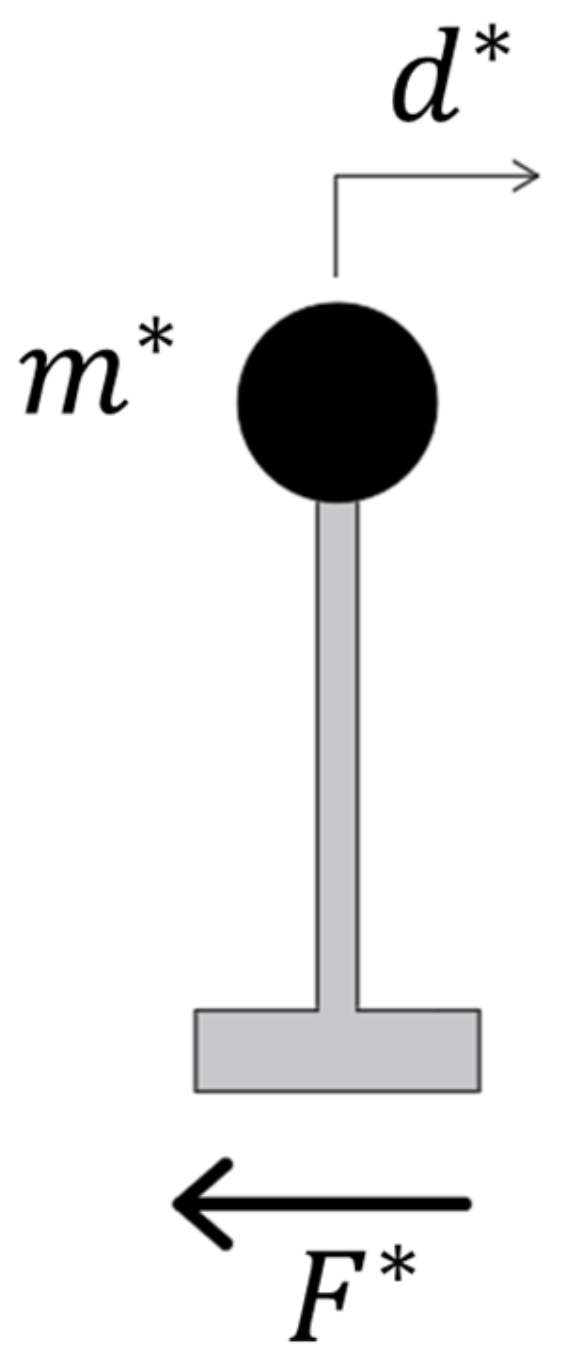
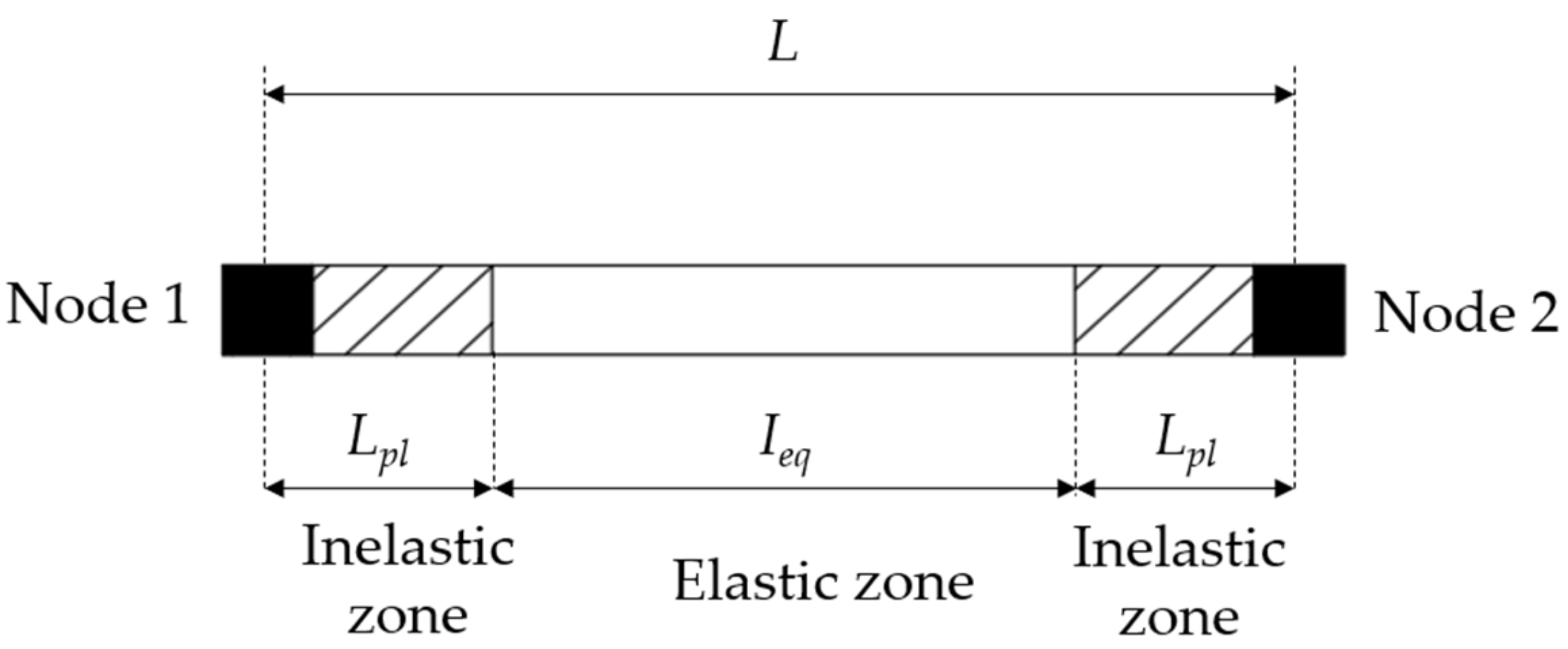
4. OpenSees Numerical Model

The case study structures are modelled as 3D buildings in the OpenSees software program version 3.6.0 [47,48], adopting the modelling procedure presented in [49] and validated in [1,5,6,41,43]. Beams and columns are implemented through the forceBeamColumn element object [50], assigning a non-linear behavior to the external sections and a linear elastic behavior to the internal section of the element, as shown in Figure 9. Since the case study structures are designed to fail in flexure in accordance with the requirements of the IBC [30], the external sub-elements correspond to the dissipative areas in which plastic flexural mechanisms are expected to be activated and concrete is defined with a well-detailed confinement model, correspondent to the Concrete04 material model, which is based on the model proposed by Popovics [51]. In particular, concrete is assumed nonresistant under tension, and the core region is characterized by concrete strength f_cc and deformations ε_cc and ε_cu defined according to Equations (A.6)–(A.8) of Part 3 of Eurocode 8 [52]. The length of dissipative zones L_pl (plastic hinge length) is defined according to Equation (A.9) of Eurocode 8 [52]. Regarding the reinforcement, the single steel bar is modelled as a fiber defined through the material model Steel02 with isotropic strain hardening [53,54], assuming a strain-hardening ratio b equal to 0.005 [40] and the parameters that control the transition from the elastic to the plastic branch as R₀ = 18, C_R1 = 0.925, C_R2 = 0.15. An effective area moment of inertia, I_eq = 0.5I_g, where I_g is the area moment of inertia of the gross section, is assigned to the internal elastic section to account for concrete cracking.

The floor slabs are defined as rigid diaphragms where the masses of the structural members are concentrated in the center of mass of each story. Since the rigid diaphragms constrains the nodes belonging to the same floor to have the same displacement, a fictitious axial force is generated in the beams, as demonstrated in [55]. Therefore, it is necessary to add an axial release in the form of an axial buffer (defined through a zeroLength element object [56]) between one end of each beam and the adjacent node.

Dead and live loads are calculated according to the tributary area concept and introduced in the model as uniformly distributed loads on the beams. The analyses consider the P-Delta effects, while they disregard bond slip and low-cycle fatigue effects. The columns are designed to be rigidly connected to the ground; thus, fixed base supports are defined in the model. The Rayleigh method defined as a function of the tangent stiffness matrix with a 5% viscous damping ratio is used to consider the damping of the frame, as reported in Ref. [40].

The diagonal steel braces equipped with the hysteretic dampers are modelled by means of a truss element object [48] with an assigned uniaxialMaterial elastic–perfectly plastic behavior, as commonly implemented in other studies (e.g., [43,44,57,58,59]).

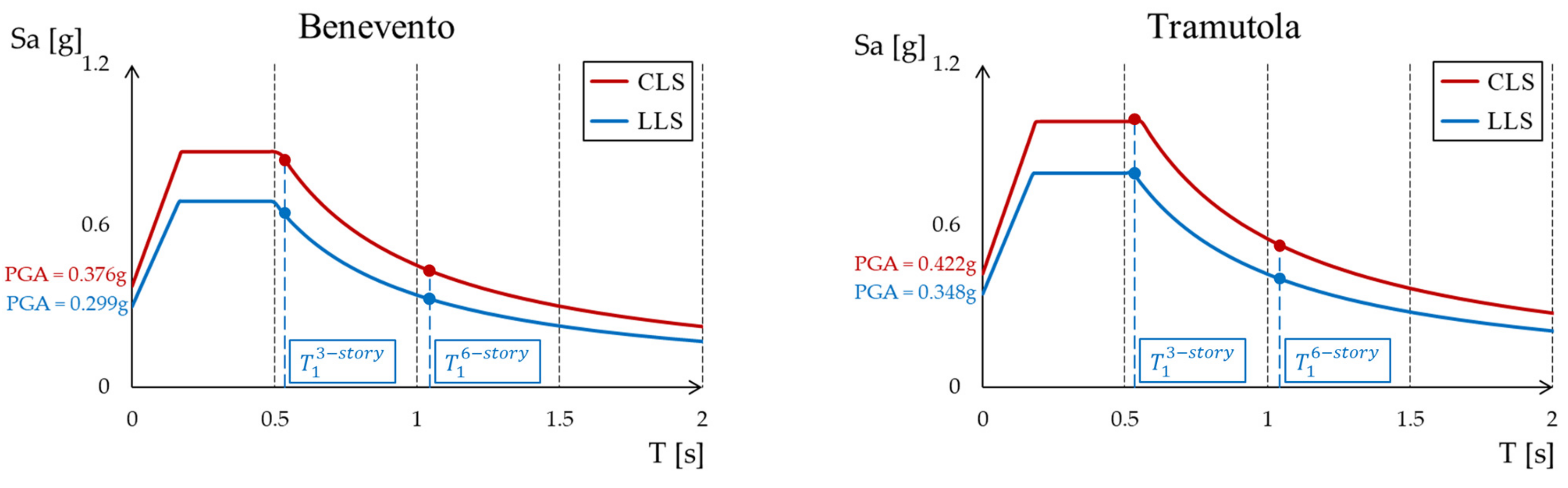
5. Selection of the Accelerograms for the Non-Linear Time-History Analyses

The NLTHAs are conducted in accordance with the provisions of the IBC [30] referring to the seismic action in the municipalities of Benevento (soil type B and T₁ category) and Tramutola (soil type C and T₁ category). Two limit states characterized from different return periods of the design earthquake are considered, namely (i) the Life safety Limit State (LLS) with return period T_R = 475 years and (ii) the Collapse Limit State (CLS) with return period T_R = 975 years. Figure 10 shows the ξ = 5% damped spectra with indication of the PGAs at either site for the two limit states and the fundamental period of each building.

Following the prescriptions at §3.2.3.6 of the IBC [30], a suite of seven independent accelerograms is needed to perform NLTHAs. In the study, for each site and limit state, two sets of bidirectional accelerograms, both artificial and natural, were considered. Seven pairs of artificial accelerograms with a pseudo-stationary part of 10 s and a total duration of 30 s were generated using SIMQKE software program version 2.7 [60]. Seven pairs of natural ground motions were selected from the European Ground Motion Database [61] using REXEL software program version 3.5 [62]; the natural accelerograms are characterized by a magnitude (Mw) within the interval of [5,6,7] and an epicentral distance (R_ep) in the range of 0–30 km. The selected accelerograms are compatible with the elastic design spectrum from the IBC [30] with 5% equivalent viscous damping ratio for an ordinary structure with cu = II and V_N = 50 years.

With the aim of obtaining results independent from the directionality of the excitations, two analyses were carried out for each bidirectional ground motion by switching the two components of the seismic input with respect to the main plan directions (X and Z) of the building.

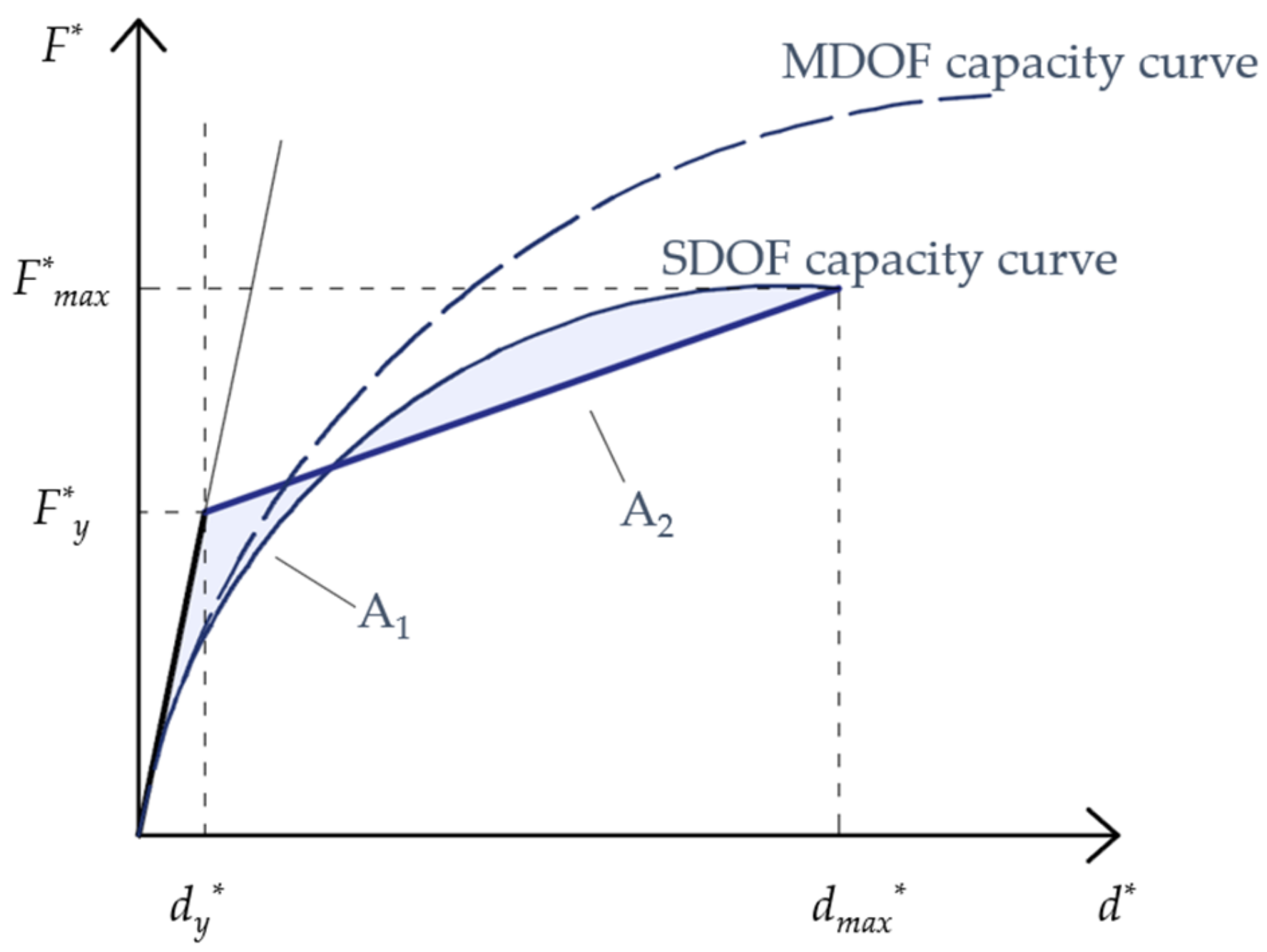
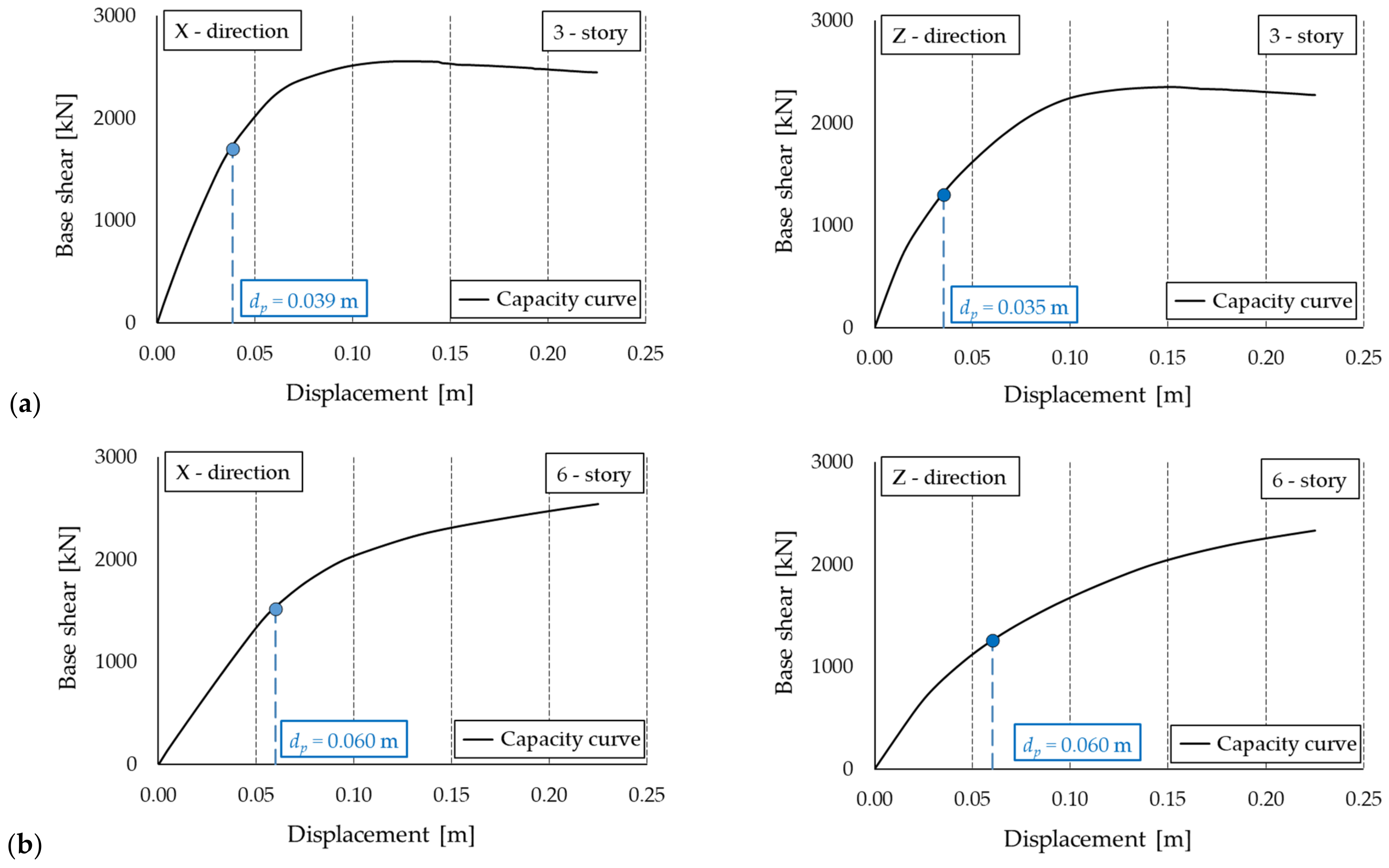
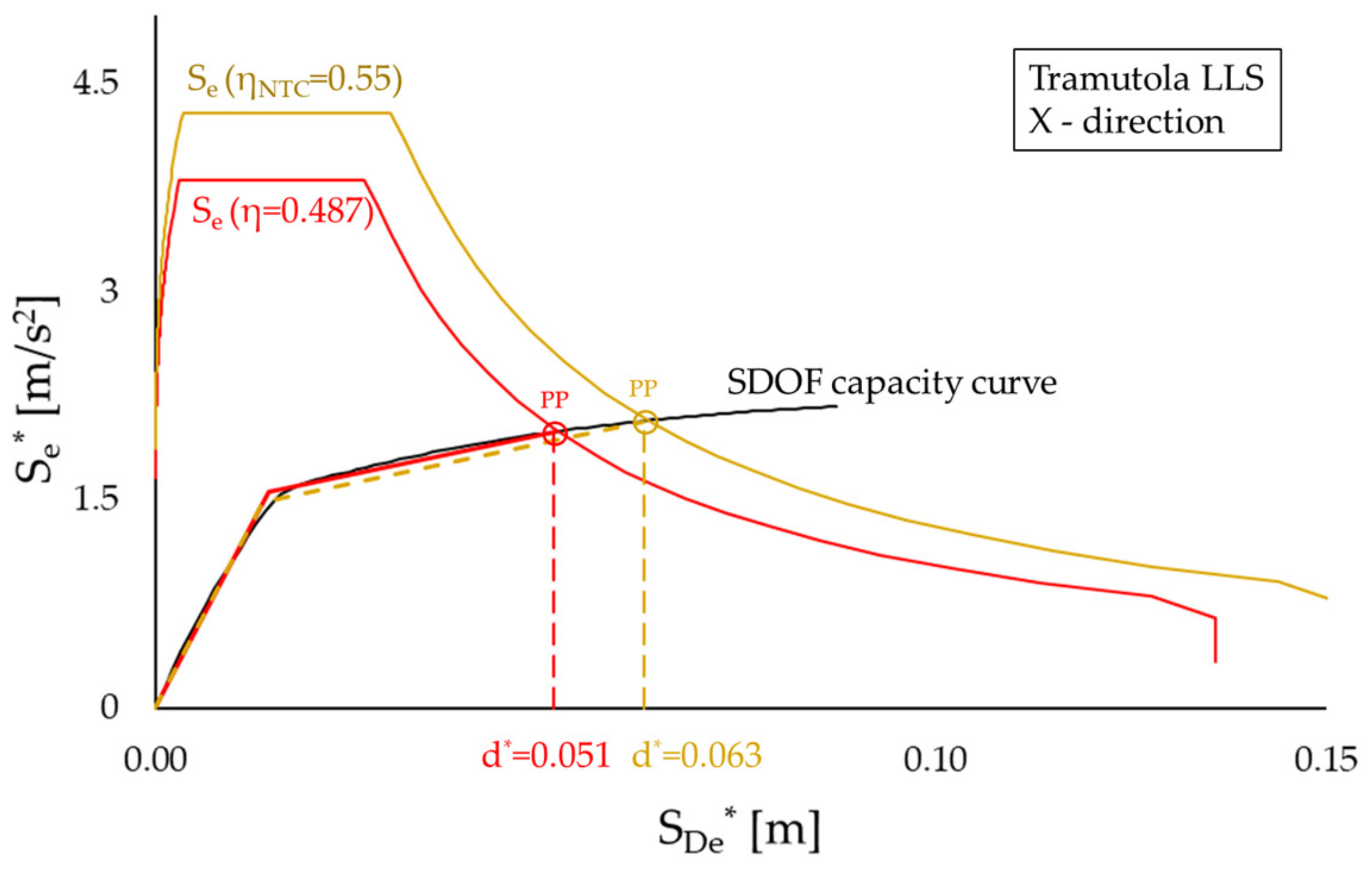
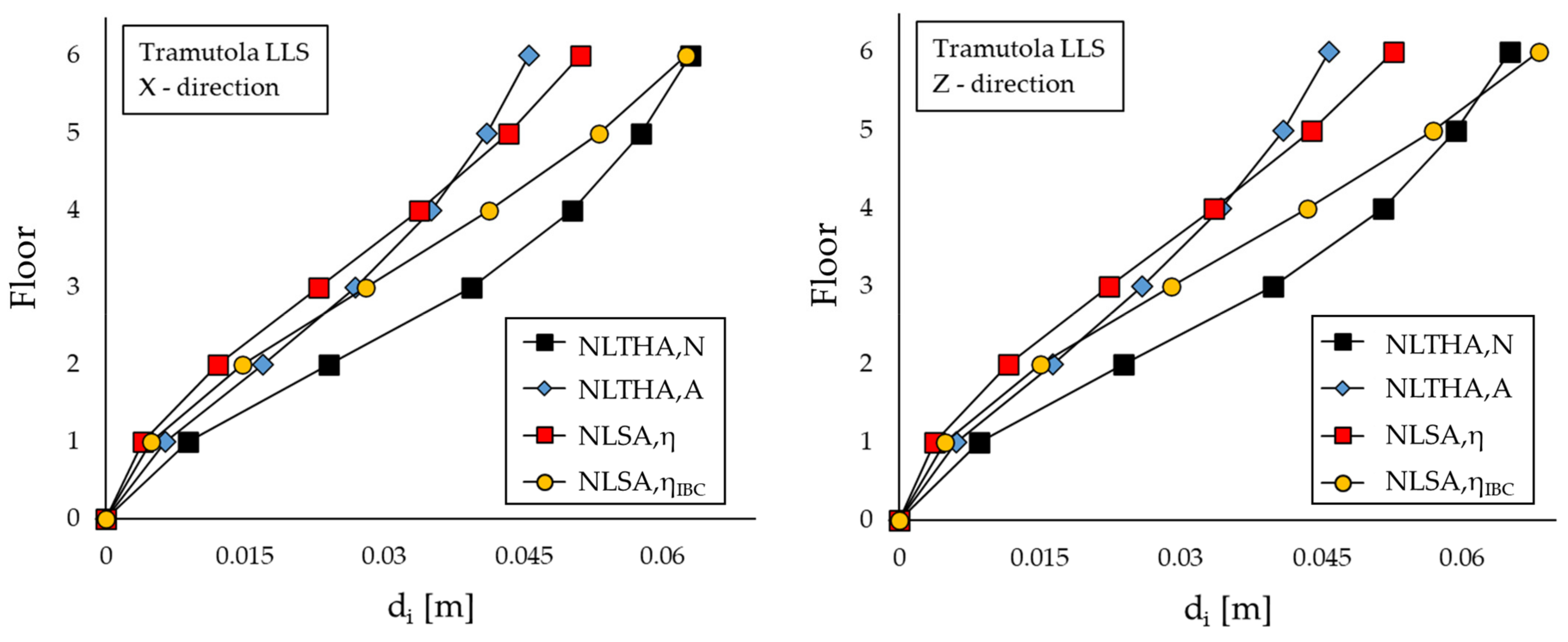
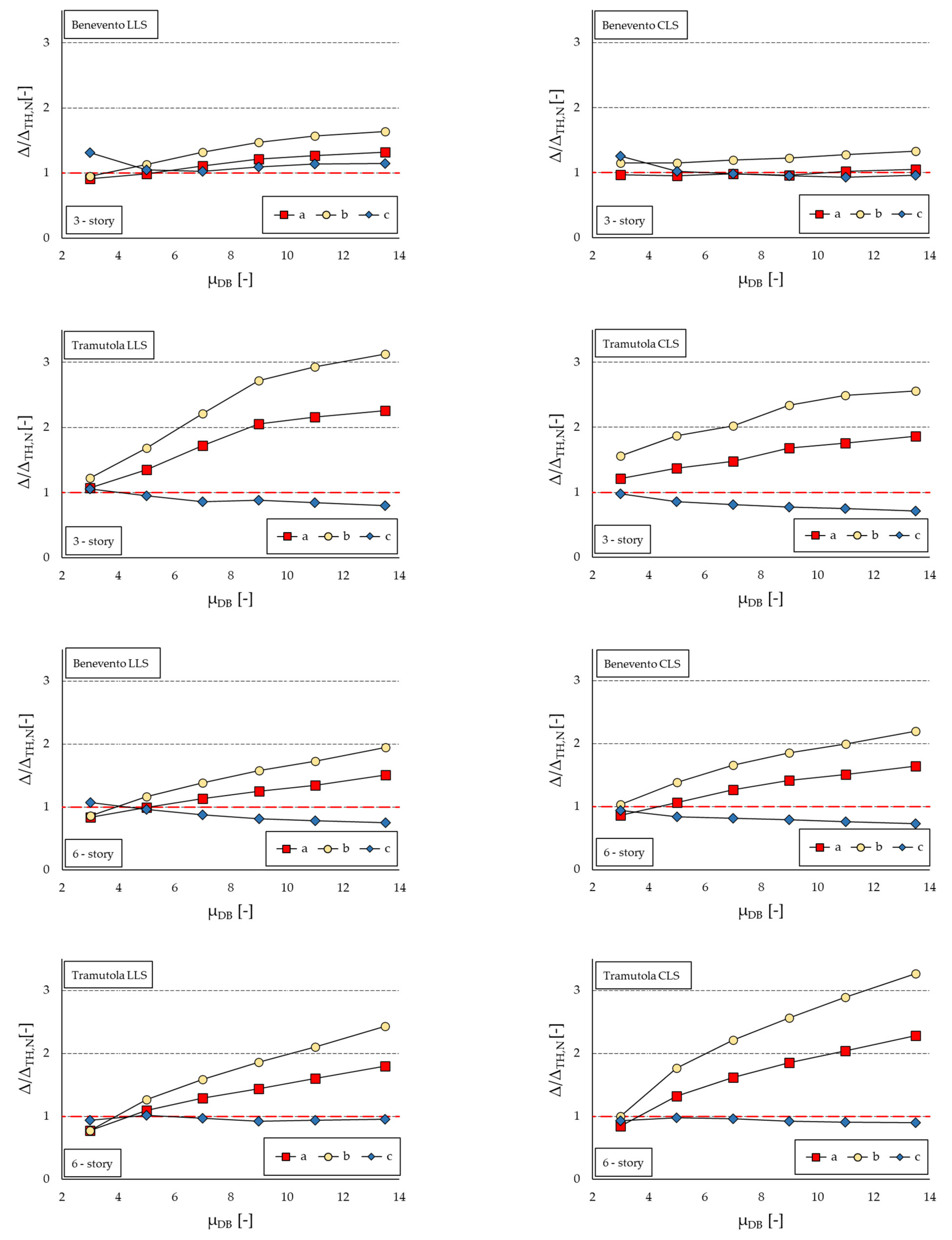
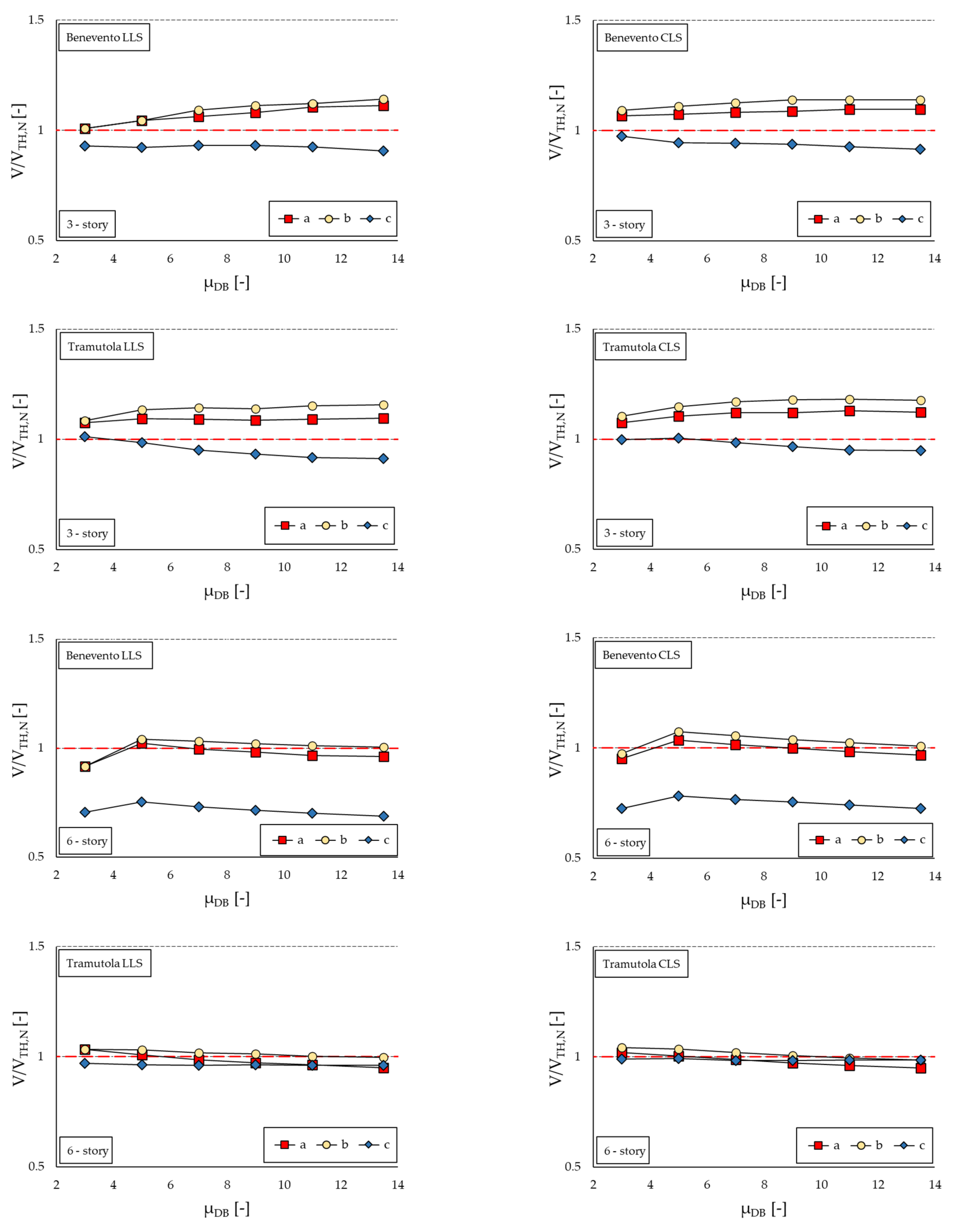
6. Results of Non-Linear Analyses

The results of the non-linear analyses are evaluated in terms of maximum displacement at the roof level (d), selected as control point, maximum inter-story drift ratio (Δ), and maximum shear force at the base (V), which are engineering demand parameters (EDPs) usually considered to investigate the performance of the structural system and the effectiveness of the retrofit design [1,5,6,15,17,18,41,43,44].

As an example, Figure 11 shows the results at LLS for the six-story building in Tramutola retrofitted with damped braces with ductility μ_DB = 9. The damped spectrum depicted in red corresponds to the damping reduction factor η resulting from the actual ${\xi }_{eq}$ evaluated as $\sqrt{10/(5+{\xi }_{eq})}$ which in this case amounts to 0.487. The yellow curve refers to the case in which the damping reduction factor is evaluated in accordance with the IBC [30] as ${\eta }_{IBC}=\mathrm{m}\mathrm{a}\mathrm{x}(0.55;\sqrt{10/(5+{\xi }_{eq})})$. The actual η results in a −22.4% in the displacement at roof level and −4.1% in the global shear force in comparison to the values calculated by assuming η_IBC.

For the same case study structure, Figure 12 shows the comparison between the maximum displacements at each floor obtained from static and dynamic non-linear analyses in X and Z directions. In the graph, NLTHA,N and NLTHA,A stand for Non-Linear Time-History analyses with either natural (N) or artificial (A) accelerograms, while NLSA,η and NLSA,η_IBC refer to non-linear static analyses considering either η or η_IBC, respectively. NLTHA,N calculates the largest displacements at each floor, but the last one where its results are similar (or even smaller than) to NLSA,η_IBC. For the first three floors, NLTHA,A, NLSA,η, and NLSA,η_IBC provide consistent results, smaller than those calculated from NLTHA,N, but their estimates diverge at the upper floors. Regarding the displacement of the control point, curiously, in the X direction, the maximum and minimum values are calculated by the two time-history analyses, with a deviation of about 27% in the X direction and 29% in the Z direction; in the Z direction, the largest displacement is calculated by NLSA,η_IBC. There is a deviation of approximately 19% in both directions between NLSA,η and NLTHA,N, while NLSA,η_IBC yields results quite similar to those of NLTHA,N, with a difference of about 5% at the top floor in the Z direction.

For each analysis, results similar to those shown in Figure 12 are obtained for displacements, inter-story drift ratio and shear forces in the columns at the base floors. Hereinafter, the results of the non-linear analyses are compared to the values obtained from NLTHAs with natural accelerograms, assumed as benchmark by means of some simple indexes. Specifically, the three dimensionless ratios, d/dTH,N, Δ/ΔTH,N, and V/VTH,N are introduced. In these ratios, d, Δ and V represent the maximum displacement at the roof level, the maximum inter-story drift ratio, and the maximum shear force at the base, respectively. Each response parameter (d, Δ and V) is calculated in a non-linear analysis (NLSA with actual η, NLSA with ηIBC, and NLTHA,A) and then compared to the corresponding quantity determined from the NLTHAs with natural accelerograms (dTH,N, ΔTH,N and VTH,N, respectively).

Figure 13, Figure 14 and Figure 15 show the dimensionless ratios for the two buildings associated to the examined μ_DBs (for each index, the largest between the values for the X and Z directions is reported). The curves are labelled as follows: curve (a) shows the results from NLSAs where the actual damping reduction factor $\eta =\sqrt{10/(5+{\xi }_{eq})}$ is considered; curve (b) reports the results from NLSAs in which ${\eta }_{IBC}=\mathrm{m}\mathrm{a}\mathrm{x}(0.55;\sqrt{10/(5+{\xi }_{eq})})$ is used; curve (c) shows the results from NLTHAs with artificial accelerograms.

The deviation on the top building displacement is examined in Figure 13. For the three-story building, NLSAs overestimate the top building displacement calculated by NLTHA,N except for Benevento (CLS) where d/d_TH,N is approximately equal to unity for NLSA,η_IBC, and about 0.8 for NLSA,η. Also, in the case of Benevento (LLS), for μ_DB = 3, NLSA,η_IBC underestimates the results from NLTHA,N. Considering the site of Tramutola, for both limit states, d/d_TH,N ranges from 1.05 to 1.40 for NLSA,η and from 1.20 to about 2.0 for NLSA,η_IBC.

The opposite trend is revealed for the six-story building: NLSA,η underestimates the benchmark displacement for both sites; d/d_TH,N is approximately constant at LLS, while it tends to increase with μ_DB at CLS and approaches unity for the case of Tramutola when μ_DB ≥ 9. In general, NLSA,η_IBC yields conservative results at CLS when μ_DB ≥ 5 (Tramutola) or μ_DB ≥ 7 (Benevento), while at LLS it underestimates the displacement of the top floor for small μ_DB.

NLTHA,A always estimates lower values than NLSAs. More specifically, when referring to d/d_TH,N (Figure 13), NLTHA,A underestimates the top displacement calculated from NLTHA,N in either building. Only in the particular case of the three-story building in Benevento do artificial accelerograms provide larger (for μ_DB = 3) or similar displacements than natural ones. As a general trend, for the three-story building, ratio d/d_TH,N decreases as μ_DB increases, while for the six-story building the ratio is virtually independent of the properties of the damped brace system, at least when μ_DB ≥ 5. Additionally, for the six-story building at both sites, similar values of d/d_TH,N are obtained at LLS and CLS, showing that the accuracy is little affected by the intensity of the earthquake. Disregarding the case of μ_DB = 3, for the three-story building, the maximum deviation from the benchmark is about −20% in Benevento and −22% in Tramutola, while for the six-story buildings the corresponding figures are −28% and −25%, respectively. It is worth noticing that for the three-story building in Benevento, NLTHA,A and NLSA,η provide results remarkably close to each other, and this similarity increases with the increase in the ductility of the damping system.

By looking at Figure 14 relevant to Δ/Δ_TH,N, non-linear static analyses provide rough estimates of the maximum inter-story drift, with overestimates that increase almost proportionally with μ_DB, with the only exception of Benevento CLS where Δ/Δ_TH,N is close to unity. Notably, for low damper ductility (μ_DB = 3), Δ/Δ_TH,N is always close to one. The ratio between inter-story drifts calculated by NLSA,η and by NLSA,η_IBC is as large as 1.3 (Benevento)/1.6 (Tramutola) for the three-story building, and 2.0 (both Benevento and Tramutola) for the six-story building. Again, NLTHA,A provides better estimates, with maximum deviations of about 25% to 30% (three-story building in Tramutola and six-story building in Benevento). It is noteworthy that for both buildings equipped with the retrofitting system with μ_DB = 3 in the sites of Tramutola (at both LLS and CLS) and Benevento (at LLS), all analyses yield consistent results.

In terms of maximum shear force at base V (Figure 15), NLSA,η and NLSA,η_IBC show a fair performance, with V/V_TH,N ratios approaching unity: the maximum relative deviations from the benchmark are of the order of +10% (NLSA,η)/+15% (NLSA,η_IBC) for the three-story building and −5% (NLSA,η)/0% (NLSA,η_IBC) for the six-story building. The influences of the seismic scenario and of the ductility of the damping system are negligible. On the other hand, NLTHA,A underestimates the shear force by 10% for the three-story building (Benevento and Tramutola), by 25–30% for the six-story building in Benevento and by less than 5% for the six-story building in Tramutola. Also, for NLTHA,A, virtually no influence of μ_DB is shown.

The main trends highlighted from the results shown in Figure 13, Figure 14 and Figure 15 are summarized as follows:

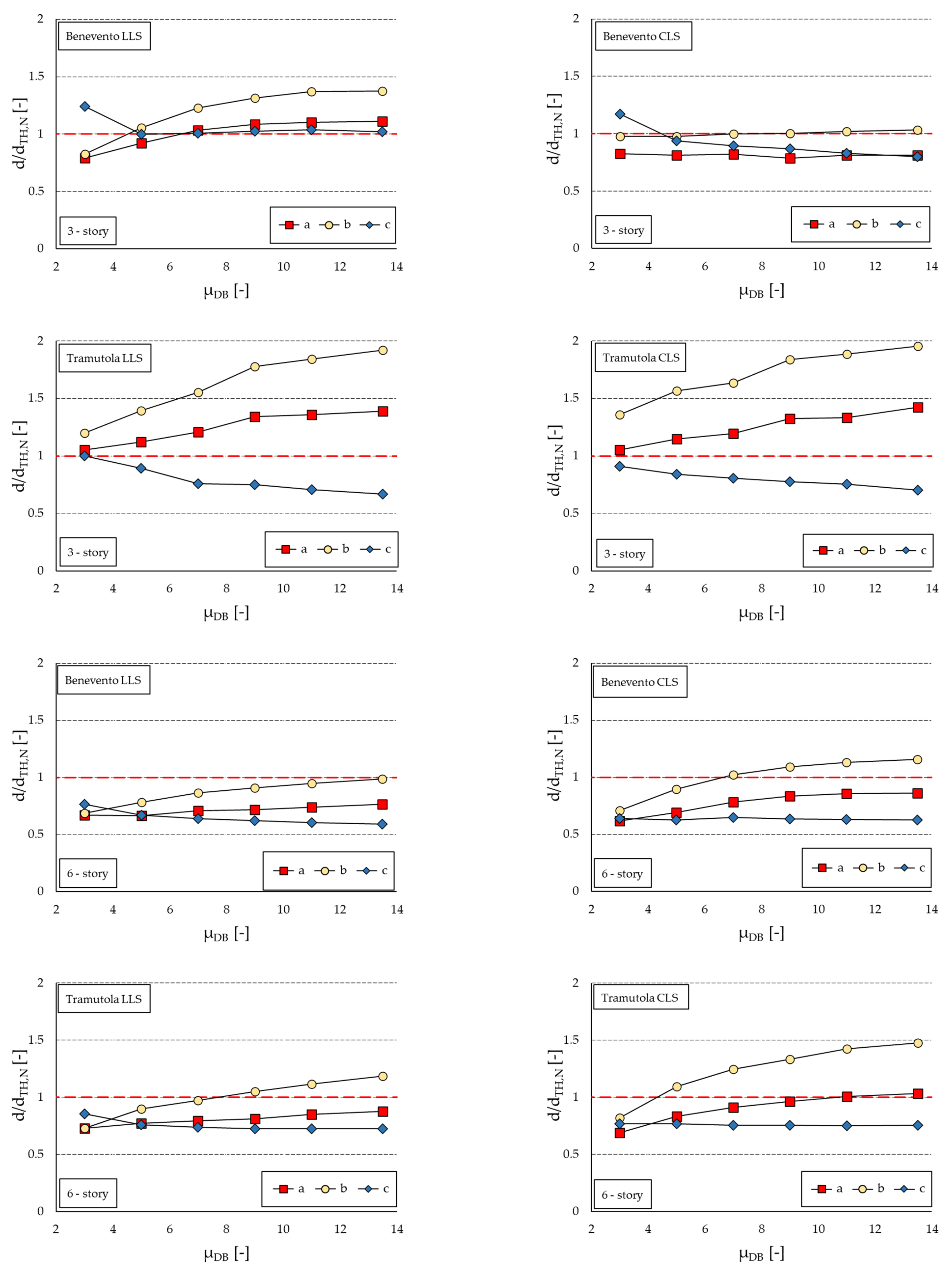
• NLSAs provided accurate estimates of forces for both buildings (maximum deviation +15% in the study), and the accuracy was virtually unaffected by the ductility of the dampers.
• NLSAs are not accurate when the structural performance is evaluated referring to displacements and deformations, e.g., maximum displacements between adjacent buildings or inter-story drifts. Only for low values (μ_DB = 3) and in some cases even medium–low values (μ_DB = 5) of ductility of the dissipative bracing system the estimates provided by NLSAs are fair, while the accuracy deteriorates as the damping capacity of the bracing systems increases. These estimates are always on the conservative side, but there is a potential concern of ending up with a design that is overly conservative.
• Focusing on the outcomes in terms of maximum displacements at the top floor, the study is unable to provide conclusive results, as deviations from the benchmark range from −30% to +200% depending on the building type, seismic scenario, and characteristics of the dissipative bracing system. However, as previously highlighted, the general trend shows that the accuracy of results deteriorates as μ_DB increases. Moreover, in the six-story building, NLSAs with ${\eta }_{IBC}=\max (0.55;\sqrt{10/(5+{\xi }_{eq})})$ underestimate the displacement for low μ_DBs (≤5) and overestimate it for high μ_DBs.
• NLTHA,N generally underestimate the demand values in terms of forces and displacements, often by up to 30%. This underestimation occasionally shows a modest reduction with increasing μ_DBs. In some cases, e.g., for μ_DB = 3, there is even an overestimation of the maximum displacement and maximum inter-story drift. It is important to emphasize that in this study, the results of NLTHA,N are referred to as benchmark. However, both NLTHA,N and NLTHA,A are considered equivalent according to the IBC [30].

The study has some limitations, and its findings should not be considered as general until confirmed by further data. Firstly, the study focused only on two RC frames representative of low- to medium-rise structures with regular floor in plans and elevations; therefore, these results are representative of these categories of buildings. However, it is important to emphasize that in Italy, a significant percentage of existing structures consists of low- to medium-rise buildings, such as residential and industrial structures, school buildings, etc. [63], which therefore are covered by the case studies. In particular, almost 70% of the existing residential buildings located in high- and medium-seismicity zones are characterized by a number of stories between one and four [63]. As a second limitation, the study only considered two design scenarios, represented by two design spectra. From the point of view of earthquake engineering, it is evident that the structural dynamic response is significantly influenced also by the dynamic characteristics of the earthquake [64,65]. Therefore, the results of the study need to be confirmed by further analyses considering different sites characterized by diverse topographies and soil conditions to generate a wider set of seismic scenarios. Nonetheless, it is believed that the trends highlighted in the study are of a general nature and therefore can be a valid starting point for a discussion on the reliability of the non-linear analysis methods proposed by the code.

7. Conclusions

This paper aims at assessing the accuracy of NLSAs for analyses of RC buildings retrofitted with hysteretic dampers by means of a parametric study conducted on two regular buildings of either three or six stories. As a matter of fact, no dedicated guidance exists either in the Italian Building Code or in the European code for practitioners who must tackle the design of damping systems for enhancing the seismic performance of buildings, including any instruction on the type of analyses to be performed. The study intends to delve deeper into this gap by providing a first insight into the topic. To this end, engineering demand parameters such as maximum horizontal displacement on the top of the building, maximum inter-story drift ratio, and maximum base shear are calculated and compared to the values predicted by NLTHAs with natural accelerograms. Eventually, the study is extended to NLTHAs using artificial accelerograms.

The main results of the study are summarized in the next points:

• When referring to the calculation of the total base shear forces, NLSAs can provide acceptable results at significantly lower computational cost compared to NLTHAs. Therefore, they can be suitable when the effectiveness of the retrofit design is evaluated comparing internal actions with capacities; the accuracy of the analyses seems to be not substantially affected by the mechanical characteristics of dissipative braces;
• NLSAs provide fair predictions of inter-story drift only for dampers with low or moderate–low ductility (e.g., μ_DB ≤ 5); the accuracy quickly deteriorates as μ_DB increases, and the error can be higher than 100% when μ_DB ≥ 10. Even in case, in derogation to the code, a damping reduction factor η < 0.55 is considered, the deviation can be unacceptable, leading to an extremely overconservative design;
• The study was unconclusive regarding the accuracy of NLSAs in predicting absolute displacements, even if it suggests that the analyses underestimate the displacement for small μ_DBs and overestimate for high μ_DBs;
• Results of NLTHAs are significantly affected by the set of accelerograms used, either artificial or natural, with absolute deviations on the order of up to 30%; the consistency between the analyses depends on the characteristics of the building and of the examined seismic scenario.

Though the results are restricted to two regular RC buildings and two seismic scenarios, the study has the merit, according to the authors’ opinion, of highlighting some limitations of non-linear static analyses for RC buildings retrofitted with hysteretic dampers, pointing out the conditions where a fair accuracy can be expected and when not.

It is therefore hoped that the next code revision will introduce practical recommendations for carrying out seismic analyzes of structures retrofitted with dissipative bracing, specifying the limits of applicability of the various methods. Furthermore, the code should also clarify the methods for performing non-linear dynamic analyses, recommending the accelerograms to be used. As shown in the study, sets of artificial and natural accelerograms, considered equivalent at a regulatory level, can produce significantly different results.