Continuous Eddy Simulation (CES) of Transonic Shock-Induced Flow Separation
Abstract
1. Introduction
- O1.
- Performance features: demonstration that CES methods are characterized by a simulation performance that is better than the performance of RANS and usually applied hybrid RANS-LES (in particular DES and WMLES methods) and at least as good as the performance of WRLES.
- O2.
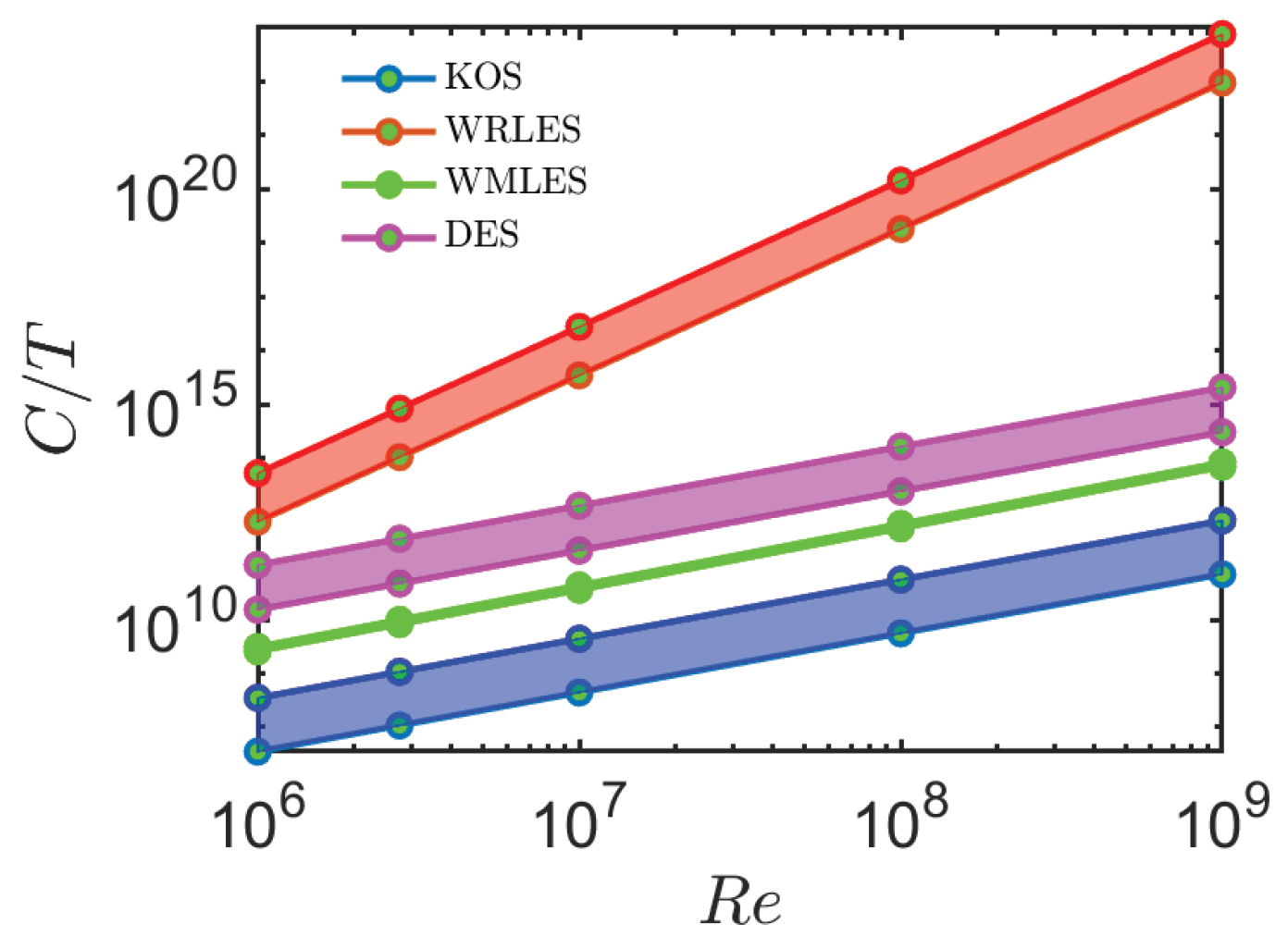
- Cost features: demonstration that the computational cost of CES is significantly below the cost of hybrid RANS-LES (DES and WMLES methods) and WRLES.
- O3.
- Functionality features: Demonstration that CES is independent of significant functionality requirements of hybrid RANS-LES and WRLES (choice of sufficiently fine grids, appropriate mesh distributions, specific simulation settings for a flow considered, validation data needed to determine simulation settings).
2. Modeling and Computational Approach
2.1. Modeling Approach
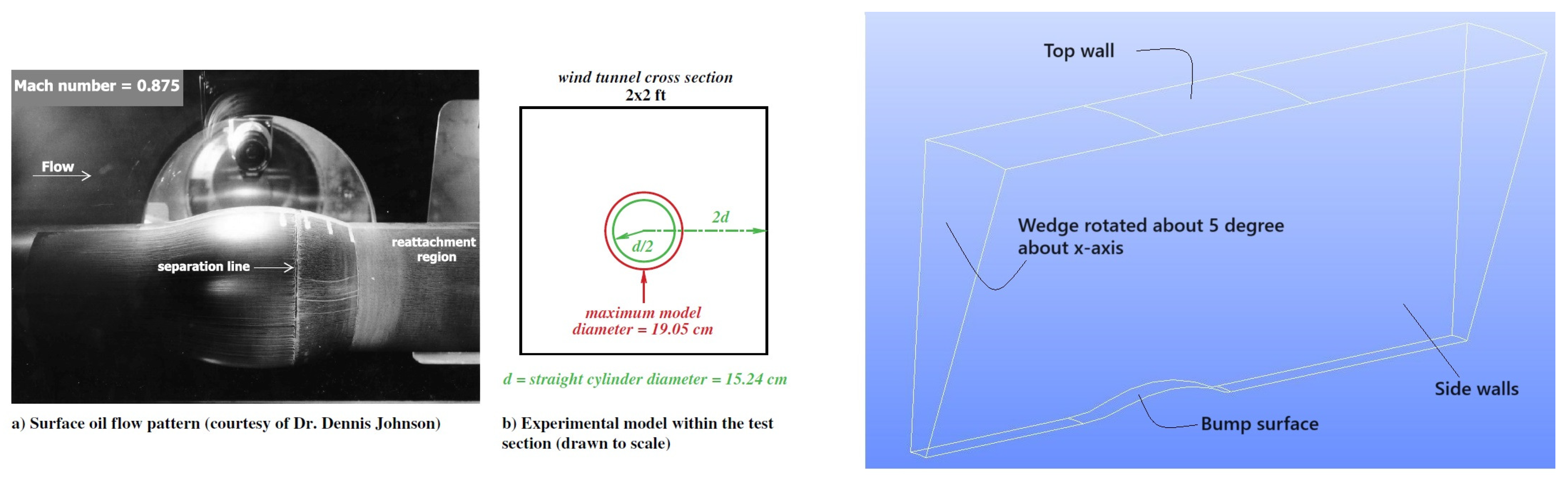
2.2. Flow Considered
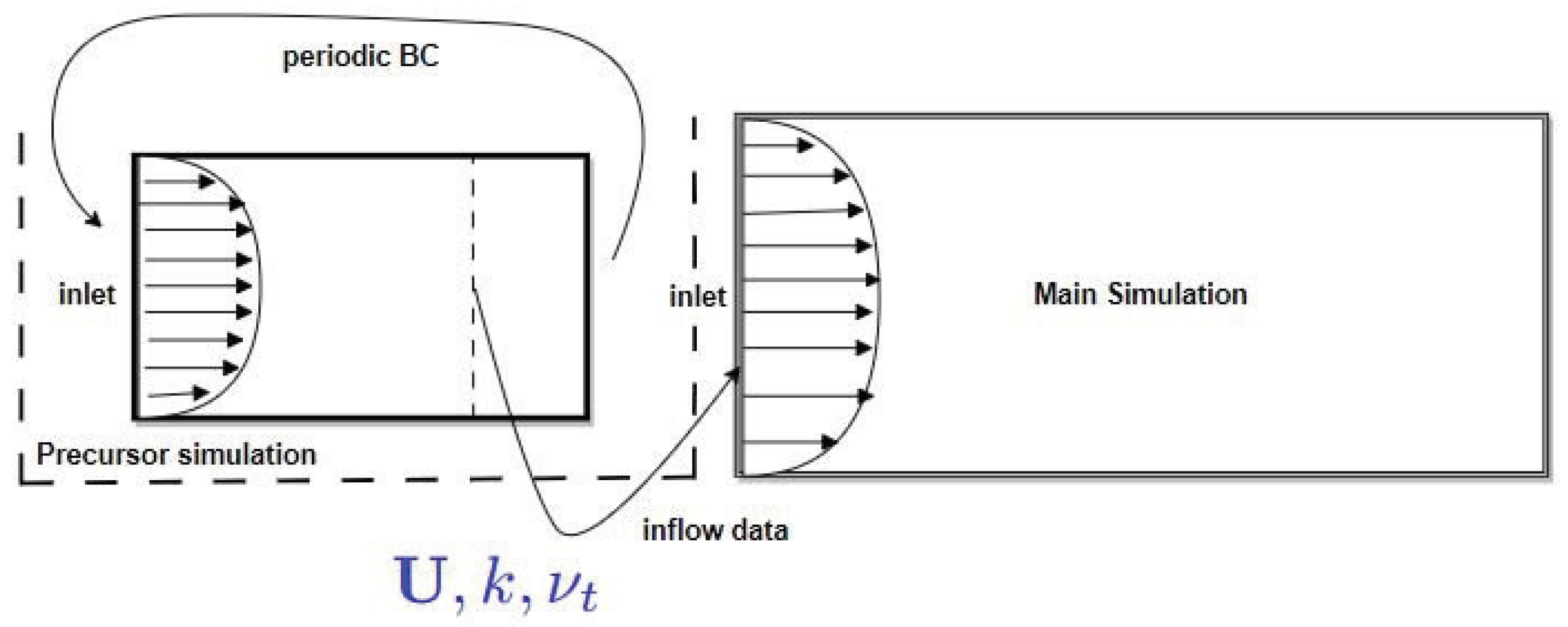
2.3. Computational Approach
3. CES-KOS Resolution Features
3.1. Resolution Features
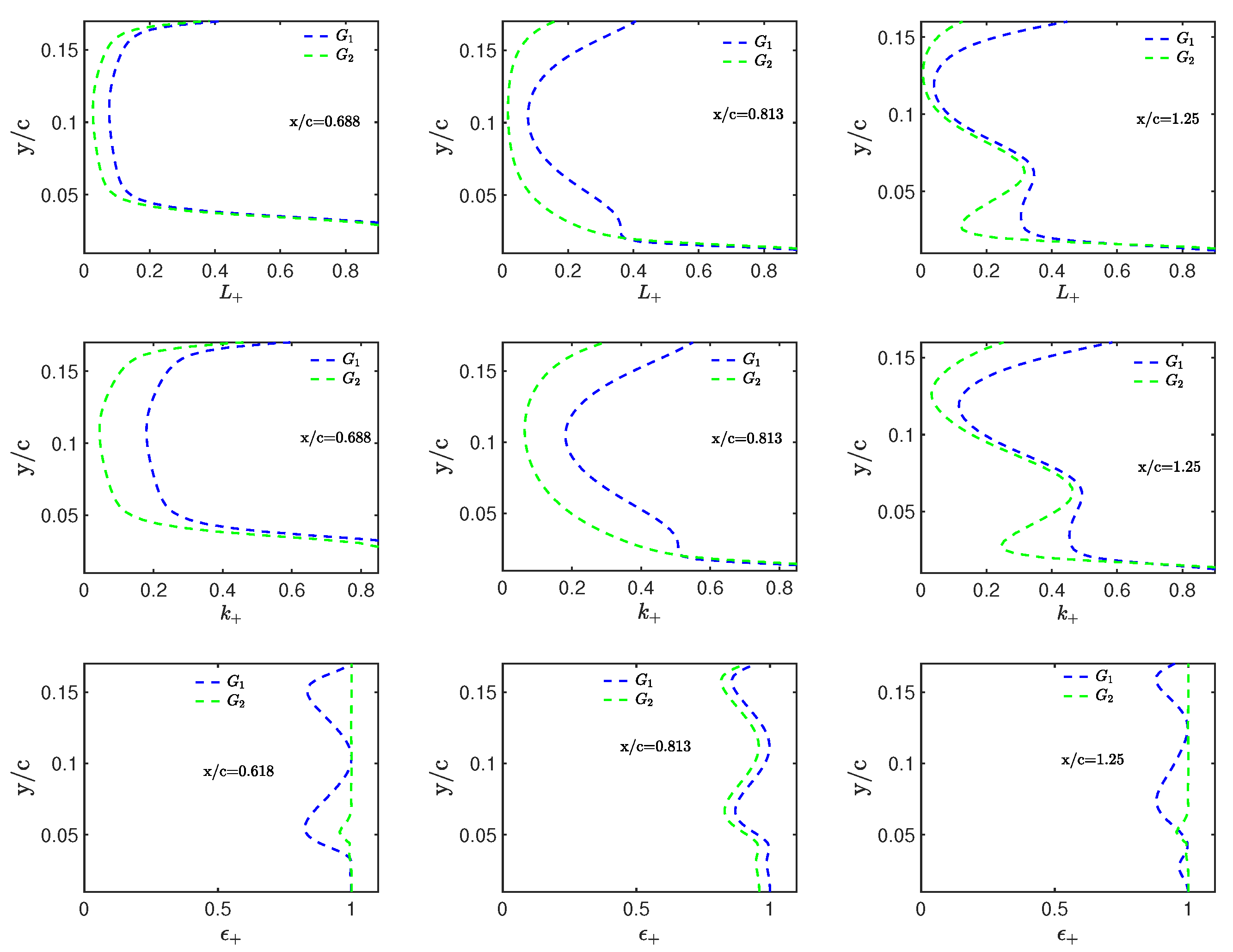
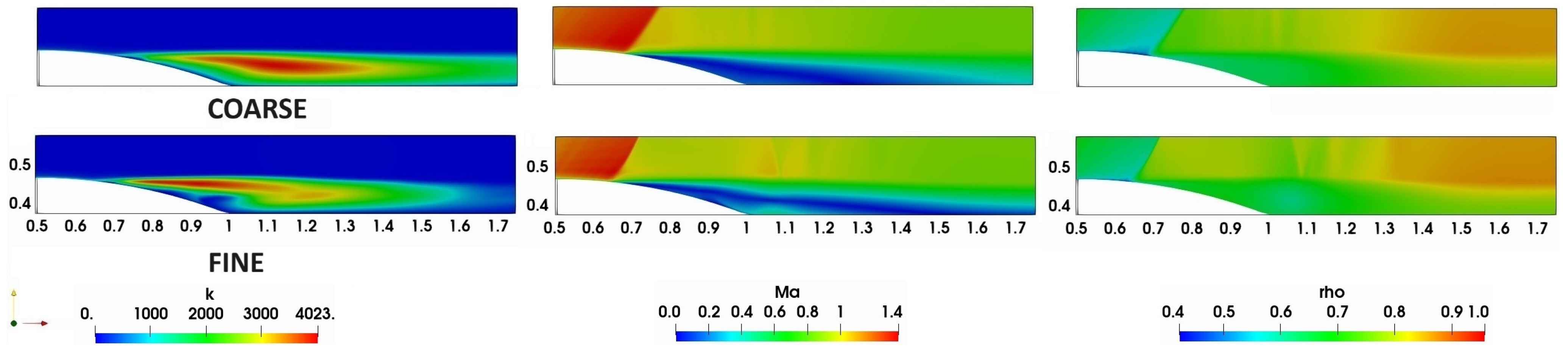
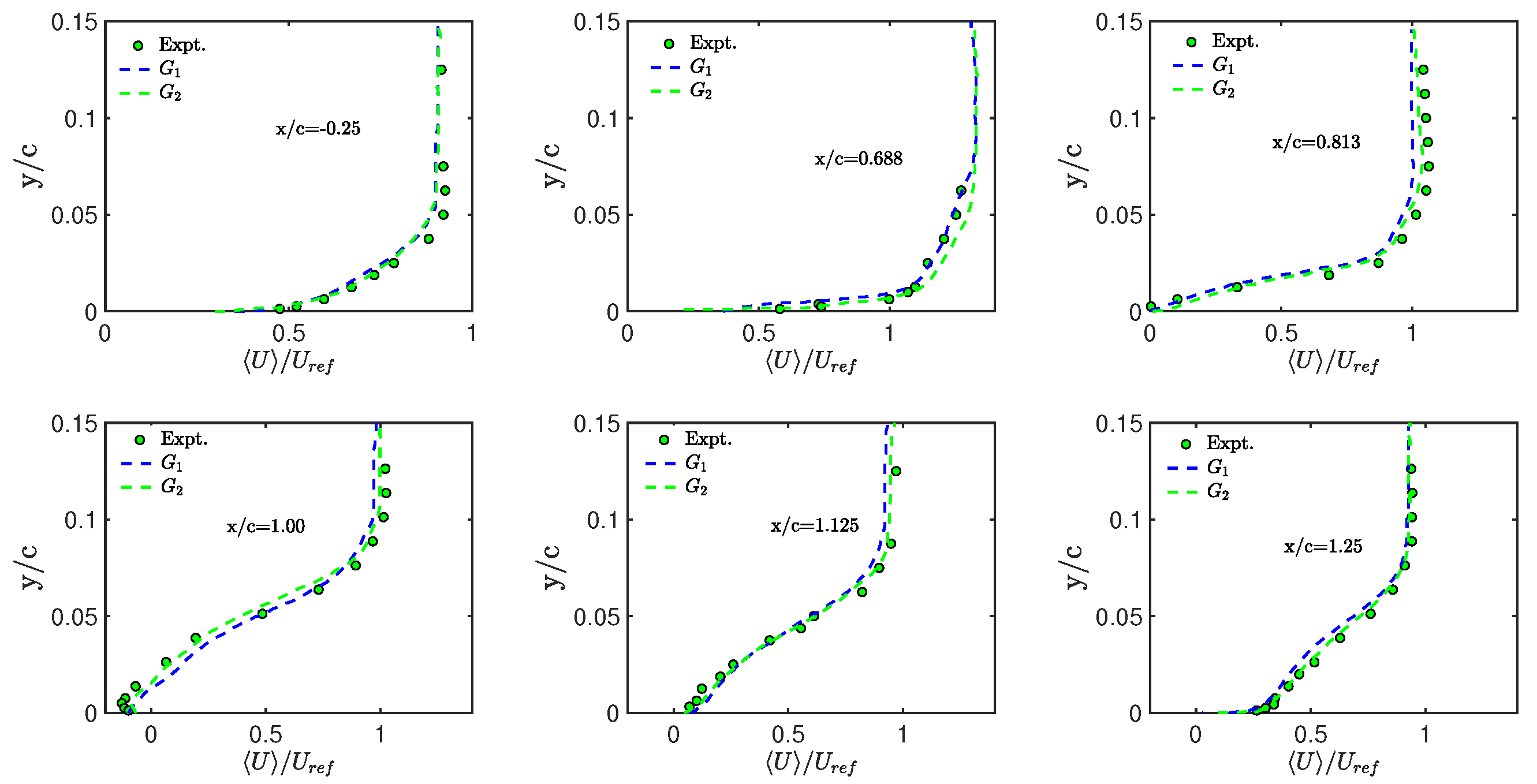
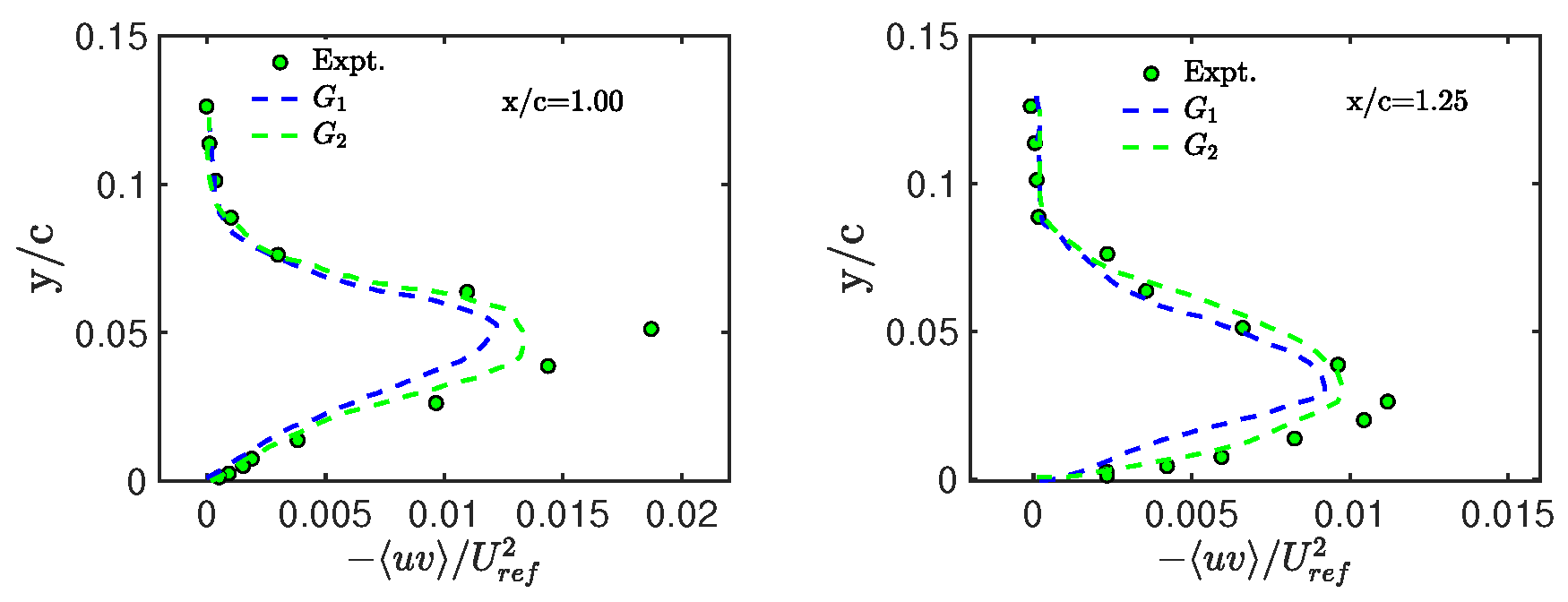
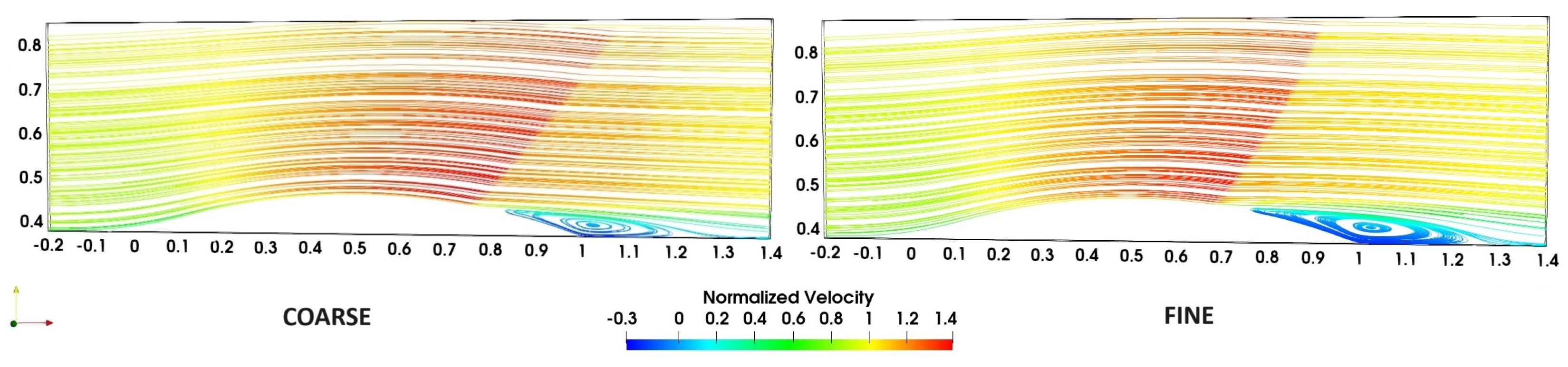
3.2. Flow Simulations: Grid Effects
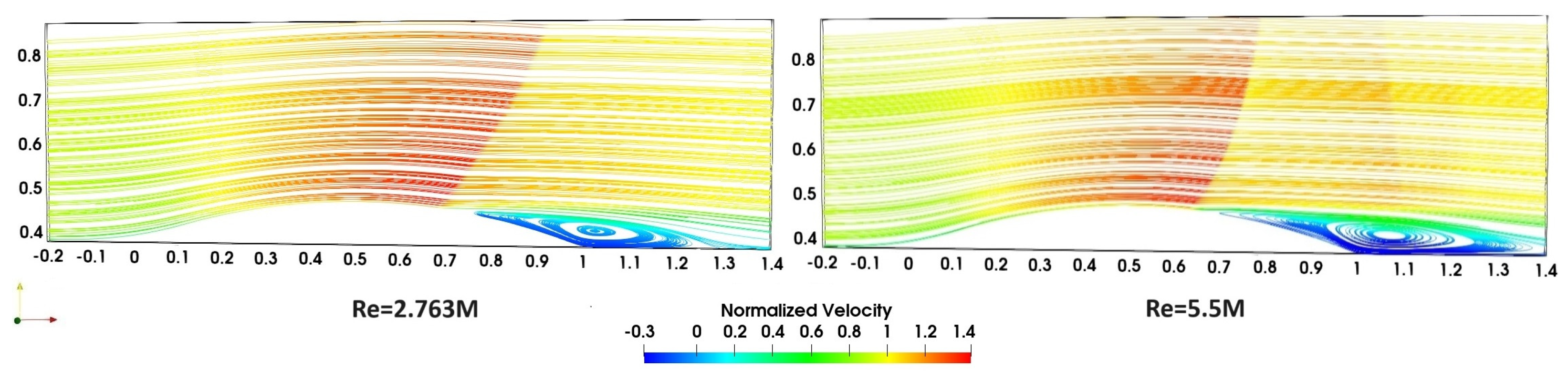
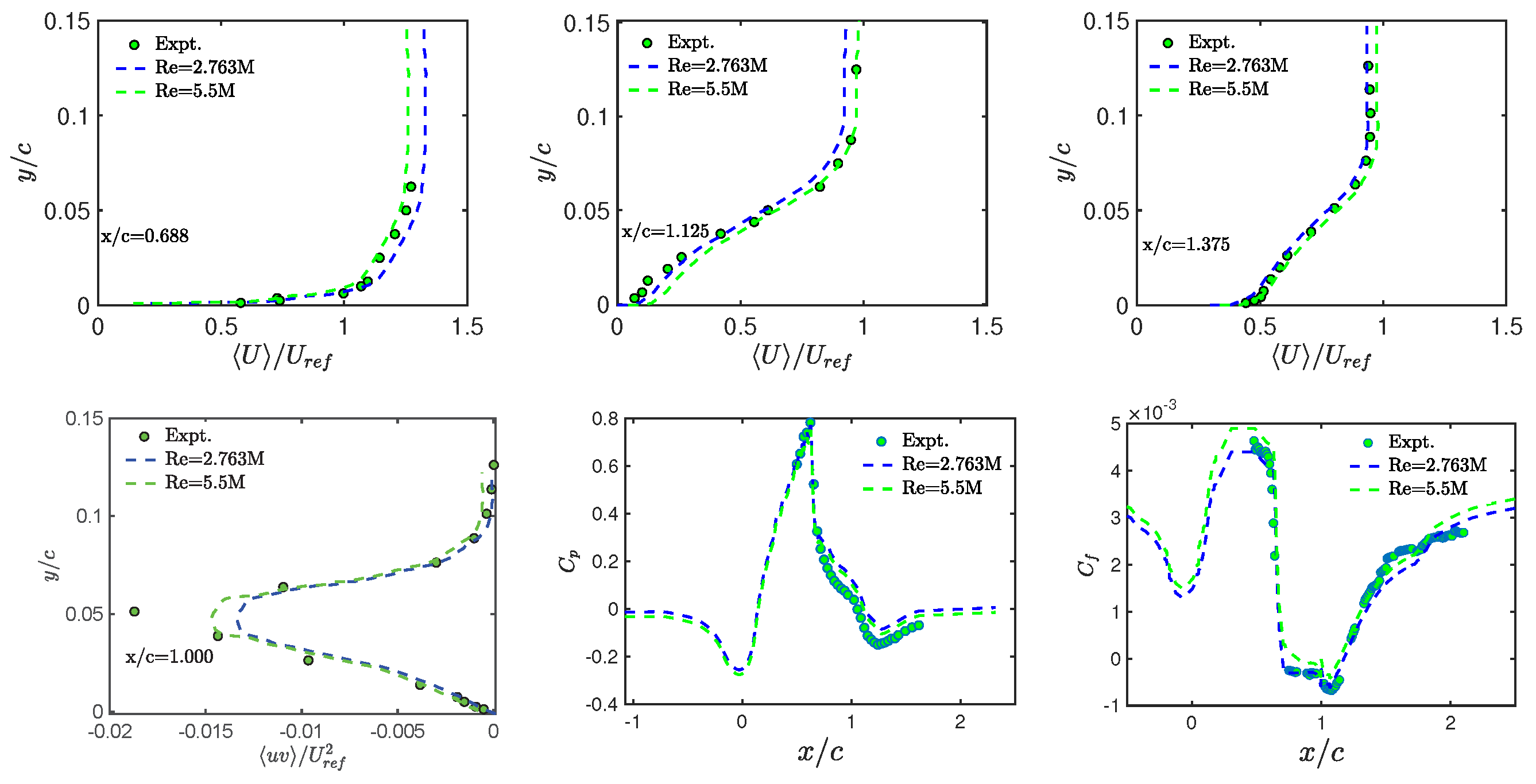
3.3. Flow Simulations: Reynolds Number Effects
4. CES-KOS vs. RANS, DES, WMLES, and WRLES
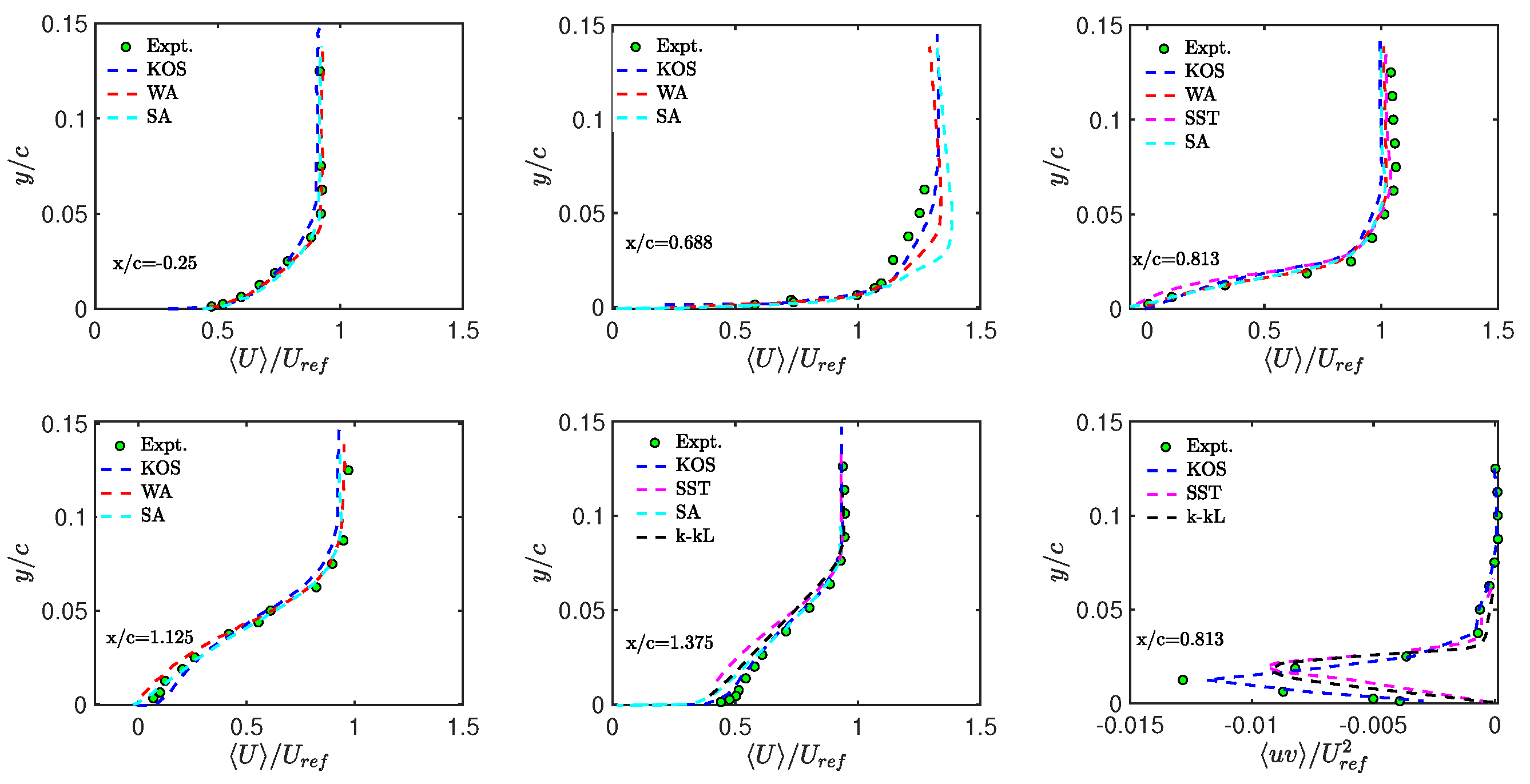
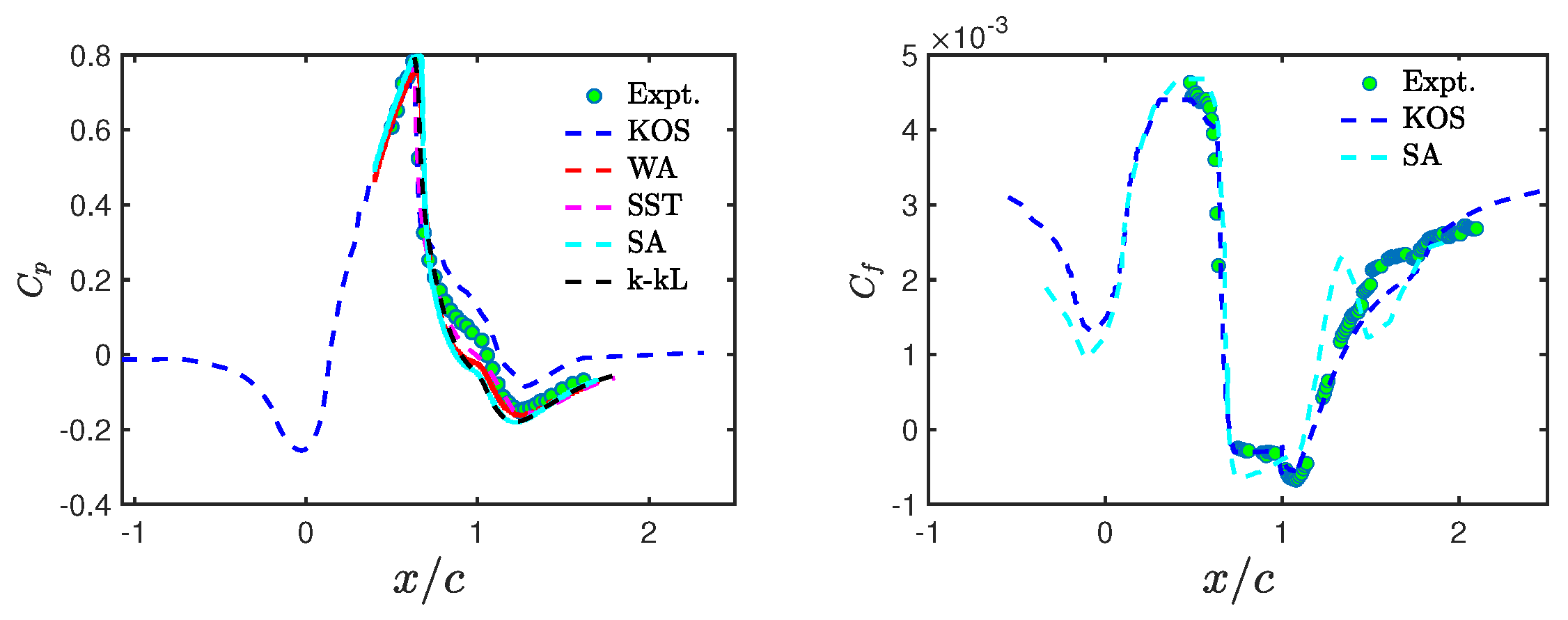
4.1. CES-KOS vs. RANS
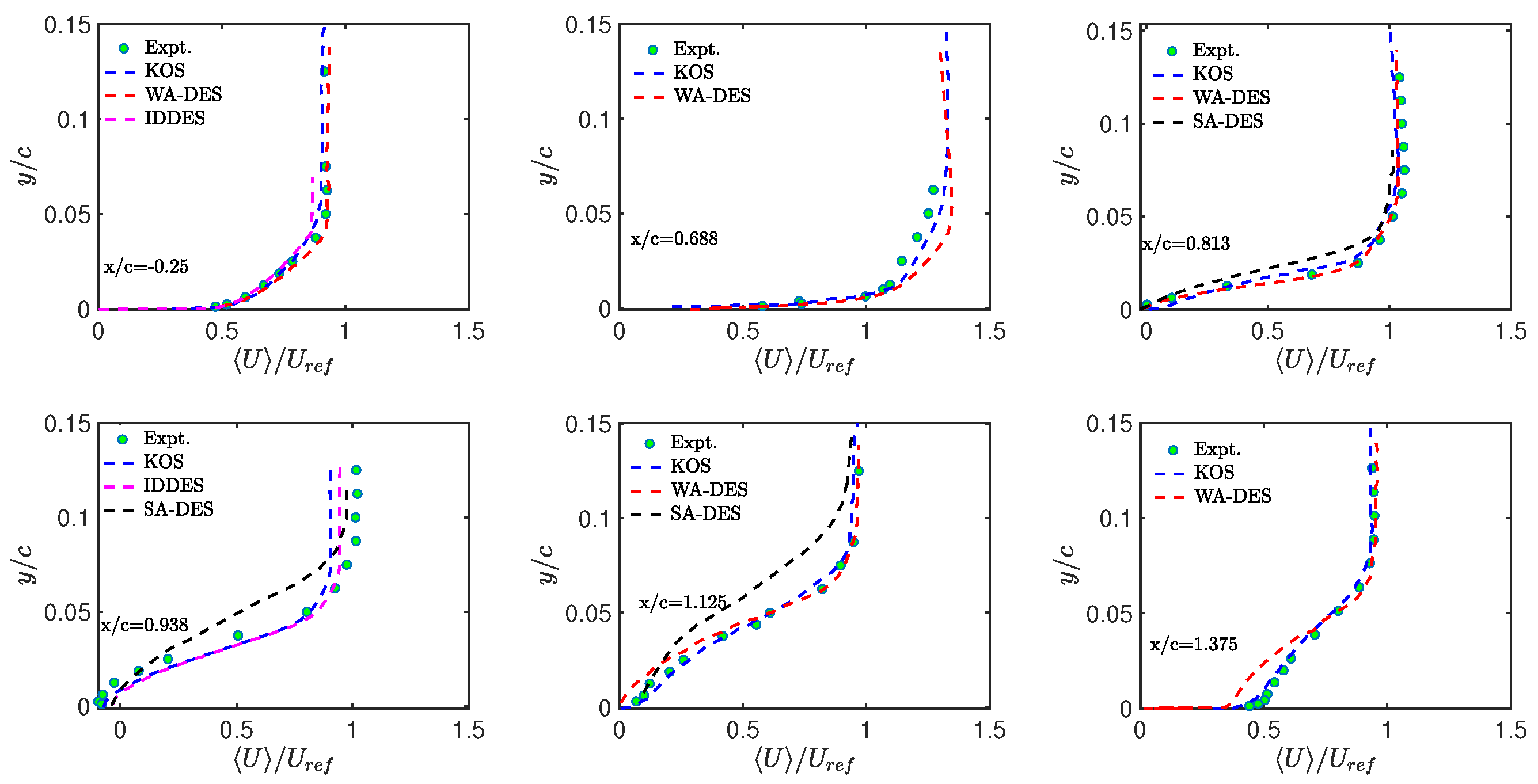
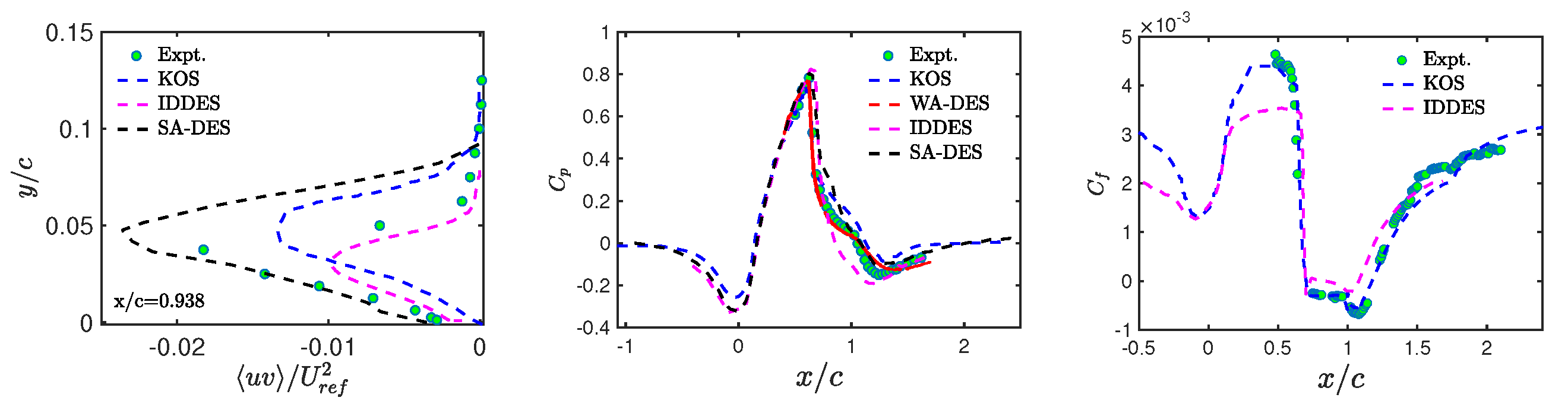
4.2. CES-KOS vs. DES
4.3. CES-KOS vs. WMLES and WRLES
4.4. Cost Estimates
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Runchal, A. (Ed.) 50 Years of CFD in Engineering Sciences; Springer Nature: Singapore, 2020. [Google Scholar]
- Pope, S.B. Turbulent Flows; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Sagaut, P. Large Eddy Simulation for Incompressible Flows: An Introduction; Springer: Berlin, Germany, 2002. [Google Scholar]
- Lesieur, M.; Metais, O.; Comte, P. Large-Eddy Simulations of Turbulence; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Piomelli, U. Large-eddy simulation: Achievements and challenges. Prog. Aerosp. Sci. 1999, 35, 335–362. [Google Scholar] [CrossRef]
- Meneveau, C.; Katz, J. Scale-invariance and turbulence models for large-eddy simulation. Annu. Rev. Fluid Mech. 2000, 32, 1–32. [Google Scholar] [CrossRef]
- Heinz, S. A review of hybrid RANS-LES methods for turbulent flows: Concepts and applications. Prog. Aerosp. Sci. 2020, 114, 100597. [Google Scholar] [CrossRef]
- Speziale, C. Turbulence modeling for time-dependent RANS and VLES: A review. AIAA J. 1998, 36, 173–184. [Google Scholar] [CrossRef]
- Germano, M. Properties of the hybrid RANS/LES filter. Theor. Comput. Fluid Dyn. 2004, 17, 225–231. [Google Scholar] [CrossRef]
- Hanjalić, K. Will RANS survive LES?: A view of perspectives. ASME J. Fluids Eng. 2005, 127, 831–839. [Google Scholar] [CrossRef]
- Breuer, A.; Jaffrezic, B.; Arora, K. Hybrid LES-RANS techniques Reynolds-averaged based on a one-equation near-wall model. Theoretical. Comput. Fluid Dyn. 2008, 22, 157–187. [Google Scholar] [CrossRef]
- Fröhlich, J.; Terzi, D.V. Hybrid LES/RANS methods for the simulation of turbulent flows. Prog. Aerosp. Sci. 2008, 44, 349–377. [Google Scholar] [CrossRef]
- Mockett, C.; Fuchs, M.; Thiele, F. Progress in DES for wall-modelled LES of complex internal flows. Comput. Fluids 2012, 65, 44–55. [Google Scholar] [CrossRef]
- Chaouat, B. The state of the art of hybrid RANS/LES modeling for the simulation of turbulent flows. Flow Turbul. Combust. 2017, 99, 279–327. [Google Scholar] [CrossRef]
- Menter, F.; Hüppe, A.; Matyushenko, A.; Kolmogorov, D. An overview of hybrid RANS–LES models developed for industrial CFD. Appl. Sci. 2021, 11, 2459. [Google Scholar] [CrossRef]
- Spalart, P. Detached-Eddy Simulation. Annu. Rev. Fluid Mech. 2009, 41, 181–202. [Google Scholar] [CrossRef]
- Shur, M.L.; Spalart, P.R.; Strelets, M.K.; Travin, A. A hybrid RANS-LES approach with delayed-DES and wall-modelled LES capabilities. Int. J. Heat Fluid Flow 2008, 29, 1638–1649. [Google Scholar] [CrossRef]
- Spalart, P.R.; Deck, S.; Shur, M.L.; Squires, K.D.; Strelets, M.K.; Travin, A. A new version of detached-eddy simulation, resistant to ambiguous grid densities. Theor. Comput. Fluid Dyn. 2006, 20, 181–195. [Google Scholar] [CrossRef]
- Menter, F.R.; Kuntz, M.; Langtry, R. Ten years of industrial experience with SST turbulence model. Turb. Heat Mass Transf. 2003, 4, 625–632. [Google Scholar]
- Bose, S.T.; Park, G. Wall-modeled large eddy simulation for complex turbulent flow. Annu. Rev. Fluid Mech. 2018, 50, 535–561. [Google Scholar] [CrossRef] [PubMed]
- Larsson, J.; Kawai, S.; Bodart, J.; Bermejo-Moreno, I. Large eddy simulation with modeled wall-stress: Recent progress and future directions. Mech. Eng. Rev. 2016, 3, 15-00418. [Google Scholar] [CrossRef]
- Iyer, P.S.; Malik, M.R. Wall-modeled large eddy simulation of flow over a wallmounted hump. In Proceedings of the AIAA Aerospace Sciences Meeting, AIAA SciTech Forum, Washington, DC, USA, 13–17 June 2016; pp. 1–22. [Google Scholar]
- Wyngaard, J.C. Toward numerical modeling in the “Terra Incognita”. J. Atmos. Sci. 2004, 61, 1816–1826. [Google Scholar] [CrossRef]
- Juliano, T.W.; Kosović, B.; Jiménez, P.A.; Eghdami, M.; Haupt, S.E.; Martilli, A. “Gray Zone” simulations using a three-dimensional planetary boundary layer parameterization in the Weather Research and Forecasting Model. Mon. Weather Rev. 2022, 150, 1585–1619. [Google Scholar] [CrossRef]
- Fagbade, A.; Heinz, S. Continuous eddy simulation vs. resolution-imposing simulation methods for turbulent flows. Fluids 2024, 9, 22. [Google Scholar] [CrossRef]
- Heinz, S. A mathematical solution to the Computational Fluid Dynamics (CFD) dilemma. Mathematics 2023, 11, 3199. [Google Scholar] [CrossRef]
- Heinz, S. Minimal error partially resolving simulation methods for turbulent flows: A dynamic machine learning approach. Phys. Fluids 2022, 34, 051705. [Google Scholar] [CrossRef]
- Heinz, S. From two-equation turbulence models to minimal error resolving simulation methods for complex turbulent flows. Fluids 2022, 7, 368. [Google Scholar] [CrossRef]
- Heinz, S. Remarks on energy partitioning control in the PITM hybrid RANS/LES method for the simulation of turbulent flows. Flow Turb. Combust. 2022, 108, 927–933. [Google Scholar] [CrossRef]
- Heinz, S. The continuous eddy simulation capability of velocity and scalar probability density function equations for turbulent flows. Phys. Fluids 2021, 33, 025107. [Google Scholar] [CrossRef]
- Heinz, S.; Mokhtarpoor, R.; Stoellinger, M.K. Theory-based Reynolds-Averaged Navier-Stokes equations with large eddy simulation capability for separated turbulent flow simulations. Phys. Fluids 2020, 32, 065102. [Google Scholar] [CrossRef]
- Heinz, S. The large eddy simulation capability of Reynolds-averaged Navier-Stokes equations: Analytical results. Phys. Fluids 2019, 31, 021702. [Google Scholar] [CrossRef]
- Bachalo, W.D.; Johnson, D.A. Transonic, turbulent boundary-layer separation generated on an axisymmetric flow model. AIAA J. 1986, 24, 437–443. [Google Scholar] [CrossRef]
- Spalart, P.R.; Belyaev, K.V.; Garbaruk, A.V.; Shur, M.L.; Strelets, M.K.; Travin, A.K. Large-eddy and direct numerical simulations of the Bachalo-Johnson flow with shock-induced separation. Flow Turbul. Combust. 2017, 99, 865–885. [Google Scholar] [CrossRef]
- Pope, S.B. Ten questions concerning the large-eddy simulation of turbulent flows. New J. Phys. 2004, 6, 35. [Google Scholar] [CrossRef]
- Heinz, S. Comment on “A dynamic nonlinear subgrid-scale stress model” [Phys. Fluid 17, 035109 (2005)]. Phys. Fluids 2005, 17, 099101. [Google Scholar] [CrossRef]
- Bredberg, J.; Peng, S.; Davidson, L. An improved k-ω turbulence model applied to recirculating flows. Int. J. Heat Fluid Flow 2002, 23, 731–743. [Google Scholar] [CrossRef]
- Bredberg, J. On Two-Equation Eddy-Viscosity Models; Department of Thermo and Fluid Dynamics, Chalmers University of Technology: Göteborg, Sweden, 2001. [Google Scholar]
- Wilcox, D. Turbulence Modeling for CFD, 2nd ed.; DCW Industries: La Canada, CA, USA, 1998. [Google Scholar]
- Mokhtarpoor, R.; Heinz, S.; Stoellinger, m. Dynamics unified RANS-LES simulations of high Reynolds number separated flows. Phys. Fluids 2016, 28, 095101. [Google Scholar] [CrossRef]
- Ren, X.; Su, H.; Yu, H.H.; Yan, Z. Wall-modeled large eddy simulation and detached eddy simulation of wall-mounted separated flow via OpenFOAM. Aerospace 2022, 9, 759. [Google Scholar] [CrossRef]
- Uzun, A.; Malik, M.R. Wall-resolved large-eddy simulations of transonic shock-induced flow separation. AIAA J. 2019, 57, 1955–1971. [Google Scholar] [CrossRef]
- Elkhoury, M. On eddy viscosity transport models with elliptic relaxation. J. Turbul. 2017, 18, 240–259. [Google Scholar] [CrossRef]
- Lynch, K.P.; Lance, B.; Lee, G.S.; Naughton, J.W.; Miller, N.E.; Barone, M.F.; Beresh, S.J.; Spillers, R.; Soehnel, M. A CFD validation challenge for transonic, shock-induced separated flow: Experimental characterization. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020; pp. 1–19. [Google Scholar]
- Openfoam Documentation. Technical Report. 2009. Available online: www.openfoam.org (accessed on 1 January 2020).
- Elnahhas, A.; Agrawal, R.; Moin, P. Wall-modeled large-eddy simulation of the Sandia axisymmetric transonic bump. Cent. Turbul. Res. Annu. Res. Briefs 2022, 31–42. [Google Scholar]
- Mor-Yossef, Y. AUFSR+: Low Mach number enhancement of the AUFSR scheme. Comput. Fluids 2016, 136, 301–311. [Google Scholar] [CrossRef]
- Gad-el Hak, M.; Bandyopadhyay, P.R. Reynolds number effects in wall-bounded turbulent flows. Appl. Mech. Rev. 1994, 47, 307–365. [Google Scholar] [CrossRef]
- Örlü, R.; Schlatter, P. On the fluctuating wall-shear stress in zero pressure-gradient turbulent boundary layer flows. Phys. Fluids 2011, 23, 021704. [Google Scholar] [CrossRef]
- Han, X.; Wray, T.; Agarwal, R.K. Application of a new DES model based on Wray-Agarwal turbulence model for simulation of wall-bounded flows with separation. In Proceedings of the 47th AIAA Fluid Dynamics Conference, Denver, CO, USA, 5–9 June 2017; pp. 1–23. [Google Scholar]
- Abdol-Hamild, K. Development of kL-based linear, nonlinear, and full Reynolds stress turbulence models, In Proceedings of the AIAA SciTech Forum 2019, San Diego, CA, USA, 7–11 January 2019.
- Wray, T.J.; Agarwal, R.K. A new low Reynolds number one equation turbulence model based on a k-ω closure. AIAA J. 2015, 53, 2216–2227. [Google Scholar] [CrossRef]
- Egorov, Y.; Menter, F.; Lechner, R.; Cokljat, D. The scale-adaptive simulation method for unsteady turbulent flow predictions. Part 2: Application to complex flows. Flow Turbul. Combust. 2010, 85, 139–165. [Google Scholar] [CrossRef]
- Abdol-Hamid, K.S. Assessments of k-kl turbulence model based on Menter’s modification to Rotta’s two-equation model. Int. J. Aerosp. Eng. 2015, 2015, 987682. [Google Scholar] [CrossRef]
- Abdol-Hamid, K.S.; Carlson, J.; Rumsey, C.L. Verification and Validation of the k-kL Turbulence Model in FUN3D and CFL3D Codes. In Proceedings of the 46th AIAA Fluid Dynamics Conference, Washington, DC, USA, 13–17 June 2016. [Google Scholar]
- Drikakis, D.; Durst, F. Investigation of flux formulae in transonic shock wave: Turbulent boundary layer interaction. Int. J. Numer. Methods Fluids 1994, 18, 385–413. [Google Scholar] [CrossRef]
- Sahu, J.; Danberg, J. Navier–Stokes computations of transonic flows with a two-equation turbulence model. AIAA J. 1986, 24, 1744–1751. [Google Scholar] [CrossRef]
- Yang, X.I.A.; Griffin, K.P. Grid-point and time-step requirements for direct numerical simulation and large-eddy simulation. Phys. Fluids 2021, 33, 015108. [Google Scholar] [CrossRef]
- Lei, D.; Yang, H.; Zheng, Y.; Gao, Q.; Jin, X. A modified shielding and rapid transition DDES model for separated flows. Entropy 2023, 25, 613. [Google Scholar] [CrossRef]
- Uzun, A.; Malik, M.R. High-fidelity simulation of turbulent flow past Gaussian bump. AIAA J. 2022, 60, 2130–2149. [Google Scholar] [CrossRef]






| Run | Grid | Min. Wall Spacing | |||
|---|---|---|---|---|---|
| Coarse | 1.08 M | 0.00001 | 1.00 | ||
| Fine | 5.4 M | 0.000001 | 0.85 | ||
| Reynolds numbers | Mach number | Char. length | Spatial domain | ||
| = (2.763 M, 5.5 M) | 0.875 | c = 0.2032 m | 7.63 D × 3.62 D × 5° |
| Fluc. | |||
|---|---|---|---|
| u | |||
| v |
| Cases | Re | Separation Location | Reattachment Location | Bubble Length | Error in Bubble Length Prediction |
|---|---|---|---|---|---|
| Expt. [33] | 2.763 M | - | |||
| 2.763 M | 0.8338 | 1.1479 | 0.3141 | 21.5 | |
| 2.763 M | 0.703 | 1.1188 | 0.4158 | 3.95 | |
| 5.5 M | 0.7105 | 1.1652 | 0.4547 | - |
| Cases | Grid Points | Separation Location | Reattachment Location | Bubble Length | Error in Bubble Length Prediction |
|---|---|---|---|---|---|
| Expt. [33] | - | - | |||
| CES-KOS | 5.4 M | 0.703 | 1.1188 | 0.4158 | 3.95 |
| SA [16,50,52] | - | 0.688 | 1.1600 | 0.472 | 18 |
| SST-k- [51,53] | 0.21 M | 0.665 | 1.1600 | 0.495 | 23.7 |
| k-kL [51,54,55] | 0.21 M | 0.669 | 1.1200 | 0.450 | 12.75 |
| WA [16,50,52] | - | 0.817 | 1.1230 | 0.306 | −23.5 |
| Cases | Grid Points | Separation Location | Reattachment Location | Bubble Length | Error in Bubble Length Prediction |
|---|---|---|---|---|---|
| Expt. [33] | - | - | |||
| CES-KOS | 5.4M | 0.703 | 1.1188 | 0.4158 | 3.95 |
| IDDES [34] | 1.6B | 0.7 | 1.0800 | 0.3800 | −5.00 |
| WA-DES [16,50,52] | - | 0.696 | 1.1660 | 0.4700 | 17.50 |
| Cases | Grid Points | Separation Location | Reattachment Location | Bubble Length | Error in Bubble Length Prediction |
|---|---|---|---|---|---|
| Expt. [33] | - | - | |||
| CES-KOS | 5.4M | 0.703 | 1.1188 | 0.4158 | 3.95 |
| WRLES [42] | 24B | 0.69(0.68) | 1.17(1.16) | 0.48 | 20 |
| WMLES [34] | 24.09M | 0.7 | 1.17 | 0.47 | 17.5 |
| Factors | CES-KOS | DES [34] | WMLES [41] | WRLES [42] | ||||
|---|---|---|---|---|---|---|---|---|
| Coarse | Fine | Coarse | Fine | Coarse | Fine | Coarse | Fine | |
| 1.08 M | 5.4 M | 470 M | 1.6 B | 20.74 M | 24.90 M | 3 B | 24 B | |
| - | ||||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fagbade, A.; Heinz, S. Continuous Eddy Simulation (CES) of Transonic Shock-Induced Flow Separation. Appl. Sci. 2024, 14, 2705. https://doi.org/10.3390/app14072705
Fagbade A, Heinz S. Continuous Eddy Simulation (CES) of Transonic Shock-Induced Flow Separation. Applied Sciences. 2024; 14(7):2705. https://doi.org/10.3390/app14072705
Chicago/Turabian StyleFagbade, Adeyemi, and Stefan Heinz. 2024. "Continuous Eddy Simulation (CES) of Transonic Shock-Induced Flow Separation" Applied Sciences 14, no. 7: 2705. https://doi.org/10.3390/app14072705
APA StyleFagbade, A., & Heinz, S. (2024). Continuous Eddy Simulation (CES) of Transonic Shock-Induced Flow Separation. Applied Sciences, 14(7), 2705. https://doi.org/10.3390/app14072705






