1. Introduction
Nowadays, filling materials of high quality are becoming rare in the infrastructure engineering construction process. With a sustainable concept and solution, more types of soils are considered as filling materials. Some soils that were previously not allowed to be used as road construction materials now can be utilized after testing and evaluation, which achieve waste resource recycling and utilization.
Compaction performance is a vital property to determine whether a kind of soil can be used as a filling for roads or other engineering. The density of soils can be increased by increasing the contact area between particles and decreasing the distance between particles when subjected to an external force [
1,
2]. In geotechnical engineering, the compaction can affect the stability, deformation characteristics, and bearing capacity of soil [
3,
4]. By controlling the compaction state of soil, the strength and stability of soil can be improved, and deformation can be reduced, which ensures the safety and reliability of geotechnical engineering. Therefore, in engineering construction, it is crucial to control the compaction of soil reasonably.
Evaluating the compaction of soils can usually be accomplished by determining the maximum dry density (MDD) and optimum moisture content (OMC) [
5]. The standard and modified Proctor test is the most commonly used compaction test for determining OMC and MDD. In the Proctor compaction test, the dry density of the soil when it reaches the tightest state under a certain number of strikes is MDD, while the moisture content of the soil at the same state is OMC. These parameters are important for construction facilities such as highways, bridges, and houses. For example, Oluremi et al. [
6] used OMC and MDD to evaluate the compaction characteristics of cured lead-contaminated red soil; Rahman et al. [
7] used OMC and MDD to study the engineering properties of roadbed soils; and Chen et al. [
8] investigated the microstructure and hydraulic properties of roadbed soils using OMC and MDD.
The accurate prediction of OMC and MDD can improve the design accuracy, construction quality, and economic efficiency of geotechnical engineering. The Proctor compaction test can be used to predict OMC and MDD [
9], but it is a time-consuming and labor-intensive method that requires multiple tests to plot compaction curves [
10]. Although this method can provide reasonable predictions in many cases, it may be subject to a certain amount of error because it is limited by experimental conditions and sample size. Regression analysis is a statistical method for calculating soil compaction parameters and can be used to predict soil compaction parameters [
11,
12,
13,
14,
15]. However, this method can only make preliminary predictions of soil MDD and OMC and has a large error [
16,
17,
18,
19,
20]. Multiple linear regression allows the creation of empirical equations to predict the OMC and MDD of soils [
21,
22]. Empirical equations may affect the reliability of prediction due to the presence of multiple factors, and empirical equations can only reflect linear soil behavior, not complex nonlinear soil behavior. Therefore, this requires researchers to develop more advanced methods to predict OMC and MDD.
In recent years, with the increasing development of artificial intelligence technology, some researchers have utilized this technology to predict the compaction parameters of soils, which have been proved to have good performance and advantages. Saikia et al. [
23] established a prediction model for the compaction characteristics of fine-grained soil through logistic regression analysis. Hasnat et al. [
24] applied Support Vector Machine (SVM) to develop a model for predicting the compaction parameters of soil. Zhu et al. [
25] used the Support Vector Machine (SVM), Additive Regression Support Vector Machine (AD-SVM), and Imperialist Competitive Algorithm Support Vector Machine (ICA-SVM) to predict the compaction parameters of lateritic soils, and the comparison showed that the ICA-SVM algorithm outperformed the other two algorithms. Sinha et al. [
16] used Artificial Neural Network (ANN) to develop a predictive model for compaction parameters and permeability of soils. Khuntia et al. [
12] used Artificial Neural Network (ANN), Least Squares Support Vector Machine (LS-SVM), and Multiple Adaptive Regression Spline Curve (MARS) to develop a prediction model for the compaction parameters of sandy soils, and the MARS model was more accurate. Othman [
26] constructed a prediction model for aggregate base materials by ANN trained with different numbers of hidden layers, different numbers of hidden layer neurons, and three activation functions. The results showed that the hyperbolic tangent function (Tanh) is the most effective activation function and the performance of the ANN deteriorates with an increase in the number of hidden layers or the number of neurons per hidden layer. Jalal et al. [
27] used Gene Expression Programming (GEP) and Multiple Gene Expression Programming (MEP) to develop a prediction model for the compaction parameters of expansive soils. In addition, the researchers conducted feature importance analysis, which showed that liquid limit (LL), plastic limit (PL), and sand content (S) affect OMC and MDD predictions [
12,
28].
Machine learning (ML) is an important branch of artificial intelligence. In this paper, ML is used to predict OMC and MDD. Compared to traditional methods, ML saves a lot of time and labor cost through the process of data processing, model training, and model testing, and it can achieve more accurate results. Compared to multivariate linear regression, ML can handle large, nonlinear data and is able to continuously learn and improve as it receives new data to adapt to the needs of engineering and the evolution of the data. For a trained machine learning model, it has the adaptability and generalization ability to handle various types of data and tasks, and it still performs well in the face of never-before-seen data. These advantages make machine learning an important tool and technique in various fields. However, there are fewer studies using machine learning (especially Random Forest and Extreme Gradient Boosting Tree) to predict MDD and OMC. Therefore, further research on prediction models for MDD and OMC based on machine learning is necessary.
Firstly, this paper builds MDD and OMC prediction models based on 168 sets of soil sample data collected by using four machine learning algorithms, namely Support Vector Machine (SVM), Random Forest (RF), Extreme Gradient Boosting Tree (XGBoost), and Artificial Neural Network (ANN). Secondly, in order to improve the performance and generalization ability of the models, hyperparameter tuning and K-fold cross-validation are carried out in this paper. Then, the best models among the four algorithms are compared to obtain the most effective and accurate final model for predicting OMC and MDD by evaluating the metrics. Finally, feature importance analysis is used to investigate the impact of each feature on OMC and MDD to improve the interpretability of the overall model.
2. Materials and Methods
In this paper, the soils are from a particular region of the country and the data are obtained from standard physical and compaction tests. When certain types of soils are lacking, the database can be supplemented and secondary development of the model can be performed at a relatively small computational cost. The ultimate goal is to form a large database covering multiple regions in multiple countries to train a large predictive model that can be used directly. As the first step of the goal, the main objective of this paper is to evaluate the feasibility of machine learning in predicting soil compaction parameters and to compare the advantages and disadvantages of different models. In terms of generalization performance, a large database is being collected and models are being trained.
2.1. Soil Database
In the research, 168 sets of soil sample data were collected. In the Gunaydin [
17] literature, nine different soil types were gathered from the small dams constructed in the vicinity of Nigde in Turkey, which were high-plasticity inorganic clay (CH), medium-plasticity inorganic clay (CI), low-plasticity inorganic clay (CL), clayey gravel (GC), silty gravel (GM), high-compressibility inorganic silt (MH), medium-plasticity inorganic silt (MI), low-plasticity inorganic silt (ML), sandy clay (SC), and 126 sets of data were obtained through the Proctor compaction test. In the study by Nagaraj et al. [
29], different natural soil types are collected from different geologic locations in India, including high-plasticity inorganic clay (CH), medium-plasticity inorganic clay (CI), low-plasticity inorganic clay (CL), high-compressibility inorganic silt (MH), medium-plasticity inorganic silt (MI), low-plasticity inorganic silt (ML), sandy clay (SC), ML-CL, sandy silt (SM), and MI-CI, and 42 sets of data were obtained through the Proctor compaction test.
In this database, there are six features, which are fine content (content of particle size less than 0.075 mm, clay and silt, FC), sand content (S), specific gravity (SG), liquid limit (LL), and plastic limit (PL).
Table 1 shows that the soil samples in this database have a fine content of 13–98%, a sand content of 2–80%, a specific gravity of 2.58–2.85, a liquid limit of 23.1–115%, a plastic limit of 13.68–45.3%, an OMC of 7.6–36.8%, and an MDD of 12.6–20.51 kN/m
3. Then, in order to evaluate the generalization ability of the model, 134 (80%) and 34 (20%) sets of soil sample data were randomly selected as training and test sets from the soil database. The training set is used for the training of the model and the test set is distinguished from the training set for testing and validating the performance of the model.
Randomized division is a data division method commonly used in machine learning. It can reduce assessment bias, improve model generalization, and ensure objectivity, accuracy, and reliability in model assessment.
2.2. Statistical Analysis of Database
Pearson’s correlation coefficient is a common method to measure the degree of linear correlation between parameters. In machine learning, Pearson’s correlation coefficient can discover the linear relationship between features by calculating the correlation coefficient between different features, and by avoiding redundant feature information input into the model. In addition, Pearson’s correlation coefficient, by calculating the correlation coefficient between each feature and the target variable, allows for the selection of features that are highly correlated with the target variable for constructing machine learning models. This helps us to reduce the feature dimension and improve the explanatory ability and generalization performance of the model.
Figure 1 illustrates the distribution of the parameter densities and the Pearson correlation coefficients between the parameters, with the Pearson correlation coefficients denoted by r. The
r within ±0.81 to ±1.0, ±0.61 to ±0.80, ±0.41 to ±0.60, ±0.21 to ±0.40, and ±0.0 to ±0.20 represents very strong, strong, moderate, weak, and irrelevant, respectively.
As shown in
Figure 1, FC has a strong correlation with S (−0.7189) and MDD (−0.6151), and a moderate correlation with LL (0.4899) and OMC (0.5703). S has medium correlation with LL (−0.4442), MDD (0.4414), and OMC (−0.3997). There was no complex covariance between FC and LL, PL, OMC, and MDD. Therefore, FC, S, LL, and PL can be used as input characteristics to predict OMC and MDD.
SGl is largely independent of the other parameters. This shows that SG, as an input feature, contributes to a very small extent to predicting OMC and MDD. In addition, LL was strongly correlated with PL (0.7966), OMC (0.7990), and MDD (−0.7520). PL has a very strong correlation with OMC (0.8497) and MDD (−0.7901) and a weak correlation with FC (0.3869) and S (−0.2880). The results indicate that LL is multicollinear with PI and OMC.
2.3. Machine Learning Algorithms
2.3.1. Support Vector Machines
SVM is a classic model for the binary classification of data, which is based on the principle of distinguishing data into two classes in an optimal way through hyperplanes [
30]. SVM has good performance and advantages for small- and medium-sized data samples, nonlinear, and high-dimensional problems and can be used to handle regression and classification tasks [
31]. As shown in
Figure 2, the SVM hyperplane equation expression is
where
is the weight vector and
b is the offset.
The marginal hyperplane spacing between the two sides of the hyperplane is
, which is required to maximize the spacing:
where
is the input variable and
is the output indicator.
The maximum interval problem is then converted to a simpler dyadic problem using the Lagrange optimization method, which can be used to find the unique optimal solutions
and
. The Lagrange optimization function is
where
is the Lagrange multiplier and
.
The optimal solution is brought in to obtain the separation decision function
where
is the kernel function.
SVM built-in kernel function expressions are as follows:
Gaussian kernel function:
2.3.2. Artificial Neural Network
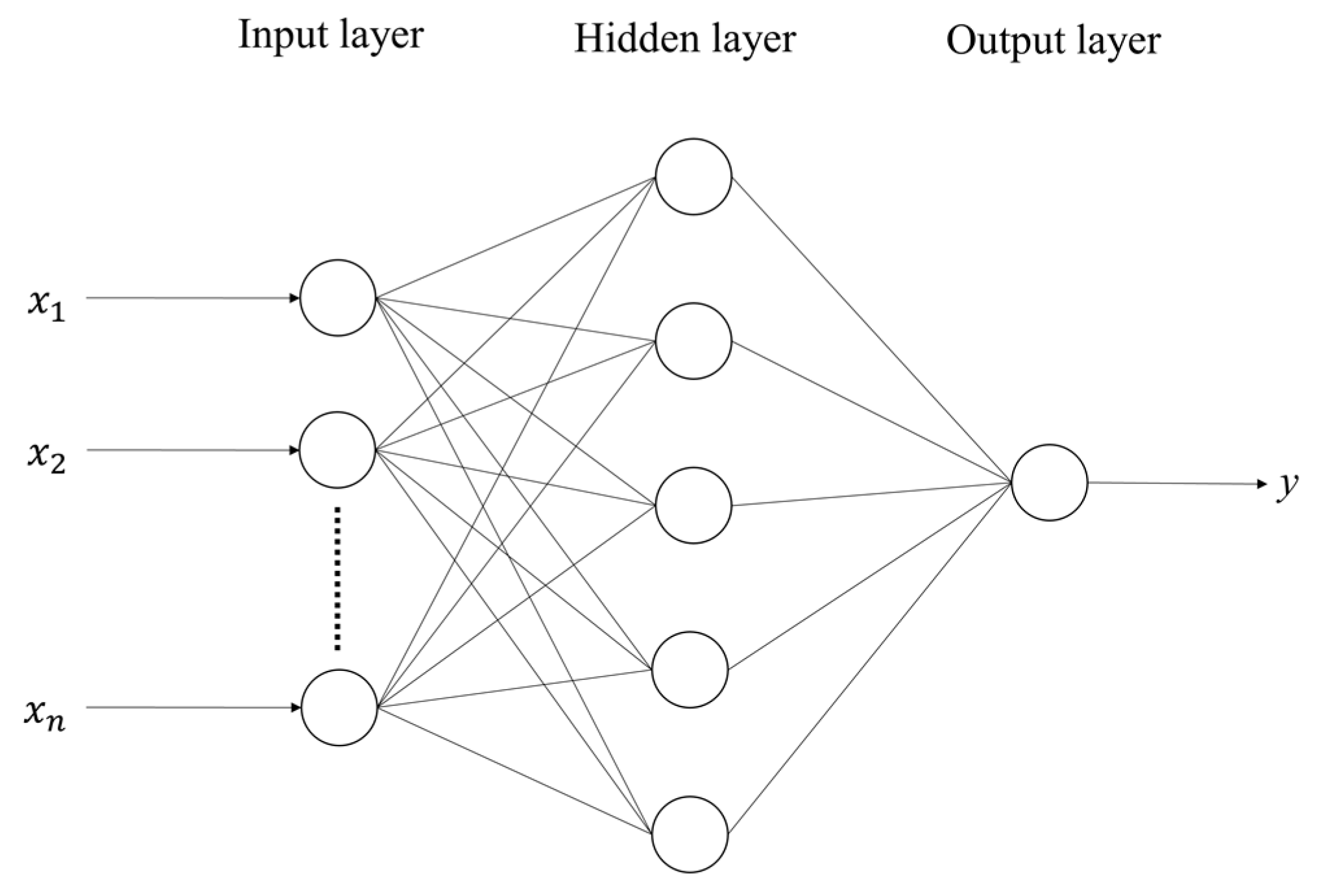
ANN is an information processing model that resembles the structure and function of neurons in the brain and consists of a large number of neurons built on top of each other [
32]. As shown in
Figure 3, ANN is composed of the input layer, hidden layer, and output layer. The role of the input layer is to accept the input data and pass the data into the hidden layer; the role of the hidden layer is to access the data of the input layer and then train to build the model. The role of the output layer is to access the data of the hidden layer, and then calculate the final output value [
33]. The role of the output layer is to access the data of the hidden layer and then calculate the final output value.
ANN has many advantages, such as dealing with complex nonlinear data, utilizing parallel distributed training, adaptively adjusting the weights and parameters of the network, and learning deeper features. However, ANN also has many problems. For instance, it is easy to fall into the local optimum. In addition, too many hyperparameters lead to difficulty in tuning, and it is quite sensitive to noise and outliers. Therefore, before choosing an ANN model, it is crucial to consider its advantages and disadvantages and weigh them according to the needs of the problem.
BP (Back Propagation) neural network is one of the most used neural network models in engineering prediction [
34]. The BP algorithm is used to backpropagate the error between the output value of the forward propagation and the actual value, and it continuously adjusts the weights and thresholds through multiple iterations and gradient descent methods to minimize the error.
2.3.3. Random Forest
RF belongs to the bagging algorithm in ensemble learning, and its basic unit is the decision tree. As shown in
Figure 4, RF utilizes multiple decision trees for prediction or classification, and the final result is the average or voting result of all decision trees. In constructing each decision tree, RF employs two randomization methods: bagging and random feature selection. Random feature selection is to randomly select a subset of features in the feature set for tree node partitioning, which can reduce the correlation between decision trees and further improve the performance of the model [
35].
The general steps of RF are as follows:
- (1)
Bag a certain amount of data from the original database as a data subset. Then, randomly select a feature subset from the original feature set.
- (2)
Build a decision tree for the data and feature subsets. At each tree node, select the optimal features from the feature subset for splitting.
- (3)
Repeat steps (1) and (2) to construct multiple decision trees. Each decision tree is constructed from a different subset of data and a subset of features.
- (4)
For classification problems, the results of all decision trees are voted to obtain the final classification result. For regression problems, the results of all decision trees are averaged to obtain the final value.
RF is considered as an ensemble algorithm with the advantages of high accuracy, resistance to overfitting, parallelized training, flexibility, and ease of use. Therefore, RF is widely used in various areas to solve classification and prediction problems [
36].
2.3.4. Extreme Gradient Boosting
XGBoost is improved from the Gradient Boosting Decision Tree (GBDT) and belongs to the boosting algorithm in ensemble learning. As shown in
Figure 5, the boosting algorithm is used to integrate many weak classifiers together to form a strong classifier, and its core idea is to correct the error of the previous model each time a new tree model is trained, so as to improve the overall performance of the model [
37].
XGBoost is an additive model consisting of k tree models. The tree model to be trained in the
tth iteration is
, and then there is
where
is the prediction result of sample
i after the
tth iteration,
is the prediction result of the first
t − 1 tree, and
is the model of the
tth tree.
The loss function can be represented by the predicted value
and the true value
:
where
n is the number of samples.
The objective function is composed of the loss function L of the model and the canonical term, and so the objective function is
where
is the canonical term.
Bringing Equation (7) into the objective function, the objective function is transformed into
The second-order Taylor expansion formula is
Definition:
A second-order Taylor expansion of the loss function gives the objective function as
On the one hand, XGBoost improves the overfitting resistance and generalization ability of the models by adding regular terms to the loss function. On the other hand, the introduction of second-order Taylor expansion makes the model more accurate and efficient in the training and optimization process. The advantages of XGBoost include a more accurate approximation of the loss function, faster convergence of the model, more stable training of the model, more optimized splitting strategy, and a better handling of nonlinear data, etc. [
38,
39,
40]. In addition, XGBoost supports parallel processing to increase the speed of model training and provides feature significance to study the impact of features on model results. XGBoost has become one of the most respected algorithms today due to its excellence in most aspects. The risk of overfitting can be reduced by limiting the depth of the tree or setting the minimum number of samples for leaf nodes, which can prevent the model from generating overly complex trees.
2.4. Model Performance Evaluation Metrics
Prediction models in machine learning are generally evaluated with evaluation metrics such as Root Mean Square Error (RMSE) and coefficient of determination (
R2). In the extremely perfect model, RMSE is equal to 0. When RMSE is smaller, the model is more accurate, and, on the contrary, it is worse. The range of
R2 is from 0 to 1, and the closer its value is to 1, the better the model fits the data. The mathematical expressions are as follows:
where
n is the number of samples,
is the true value,
is the predicted value, and
is the mean value.
3. Results
3.1. Support Vector Machines
Since there are different kernel functions built into the SVM, the linear kernel and Gaussian kernel function are adopted for the prediction of OMC and MDD to study the effect of different kernel functions on the SVM. The prediction results of OMC and MDD by linear kernel and Gaussian kernel function models are shown in
Table 2.
From
Table 2 and
Figure 6, it can be seen that the Gaussian kernel function model outperforms the linear kernel in predicting OMC, with RMSE = 1.6308% and
R2 = 0.8847. Similarly, the Gaussian kernel function model outperforms the linear kernel in predicting MDD, with RMSE = 0.5039 kN/m
3 and
R2 = 0.8831. Therefore, in the prediction of compaction parameters by the SVM, the performance using the Gaussian kernel function is superior.
It can be observed from the results and previous research that when the data present a complex nonlinear structure, a Gaussian kernel can be used to obtain a good model performance, while a linear kernel can be chosen when the data are linearly differentiable.
3.2. Artificial Neural Network
BP neural network is used to build OMC and MDD prediction models. ANN is a customized network model, since, on the one hand, the higher number of hidden layers in ANN is beneficial to the network to solve complex nonlinear problems, but too many hidden layers may lead to the overfitting of the model. On the other hand, a higher number of neurons is beneficial to increase the expressive ability and learning ability of the network. However, an unreasonable number of neurons may also lead to overfitting or underfitting. Therefore, it is important to determine the appropriate number of hidden layers and neurons. According to existing research, ANNs with one hidden layer have been able to meet most of the requirements [
41,
42,
43,
44,
45]. Therefore, in this paper, an ANN with one hidden layer is used to study the effect of the number of neurons on the prediction model, and the results are shown in
Table 3.
As shown in
Figure 7, in the OMC prediction model, when the number of neurons increases, the RMSE of the training set tends to decrease and then increase, and then decrease and then increase again. And the test set tends to decrease and then increase. Therefore, a neuron number of 7 is the best OMC prediction model. In the MDD prediction model, both the training set and the test set tend to decrease and then increase. Therefore, a neuron number of 7 is the best MDD prediction model. From
Table 3 and
Figure 8, in the best OMC model, RMSE = 1.6302% and
R2 = 0.8848. In the best MDD model, RMSE = 0.5727 kN/m
3 and
R2 = 0.8490.
3.3. Random Forest
In the construction of the prediction model with the RF algorithm, maximum tree depth, the minimum number of samples required to split a node, minimum samples required to be at a leaf node, and the number of trees in the forest have a large impact on the RF model. In this paper, the above four hyperparameters are tuned, and the rest of the hyperparameters are adopted as the default values. In the tuning process, the Bayesian optimization method is applied.
As shown in
Table 4 and
Figure 9, in the best prediction model for OMC, RMSE = 1.3605% and
R2 = 0.9198. In the best prediction model for MDD, RMSE = 0.5664 kN/m
3 and
R2= 0.8523. Through the results, it is shown that RF has an excellent performance in predicting OMC, with an
R2 of more than 0.90, while for MDD, although the
R2 reaches about 0.85, there is still a gap of about 6% in comparison with OMC.
3.4. Extreme Gradient Boosting
XGBoost is proven to be an ensemble algorithm that has excellent performance. However, more hyperparameters need to be tuned, such as the number of trees in the forest, maximum tree depth, regularization parameter and learning rate, etc. Similar to Random Forests, Bayesian optimization is employed for tuning. Compared with the grid search and other tuning methods, Bayesian optimization can find the global optimal solution with high efficiency [
38].
As shown in
Table 5 and
Figure 10, in the best prediction model, RMSE = 1.3290% and
R2 = 0.9234 for OMC, and RMSE = 0.4447 kN/m
3 and
R2 = 0.9089 for MDD. The results show that XGBoost has a good performance in predicting both OMC and MDD, and its
R2 can reach above 0.90.
XGBoost has superior model performance and generalization ability whether it deals with classification problems or prediction problems. As a result, XGBoost has become one of the preferred algorithms for problem-solving in the field of machine learning. However, XGBoost has many built-in hyperparameters and still needs to be carefully tuned for the problem to be solved to obtain the best model performance.
3.5. Feature Importance Analysis
Feature importance analysis is a key step in machine learning, which can help us to assess the degree of contribution of each feature to the prediction results and to understand the decision-making way of the model. And it can also help us to identify the reasons for model performance degradation through the importance of each feature and to find the potential problems in the model and optimize and improve it accordingly. Therefore, feature importance analysis plays a very important role in model evaluation, understanding, and optimization.
RF feature importance is derived by calculating the importance of each feature in all decision trees. XGBoost feature importance is derived from how often each feature is used as a split feature in all decision trees. Although both feature importance is judged by different criteria, they are integrated algorithms with stability and robustness. Therefore, RF and XGBoost are chosen for feature importance analysis in this paper.
As can be seen from
Figure 11, in RF feature importance, the feature that affects OMC the most is PL with an impact factor of 0.598, followed by LL with 0.294, and the lesser impacts are FC, Sand, and SG. In XGBoost feature importance, the feature that affects OMC the most is LL with an impact factor of 0.476, followed by PL with 0.297, and the lesser impacts are FC, Sand, and SG. In summary, the two features that affect OMC the most are PL and LL, which is consistent with geotechnical engineering experience.
As can be seen from
Figure 12, in RF feature importance, the two features that affect the MDD the most are LL and PL, whose influencing factors are 0.403 and 0.391, respectively, and the lesser influences are FC, SG, and Sand. In the feature importance analysis of XGBoost, the feature that affects the MDD the most is PL, with an influence factor of 0.466, followed by LL with 0.25, and the lesser influences of FC, Sand, and SG. Similarly, the two features that affect the MDD the most are PL and LL.
The above findings coincide with those found in the literature [
12,
28]. Feature importance analysis is meaningful in engineering to guide feature selection, interpret model predictions, identify data anomalies, guide decision making, etc., thus improving the efficiency, performance, and credibility of engineering.
4. Discussion
In this paper, different prediction models are trained for different machine learning algorithms, different kernel functions, and different numbers of neurons, and all models are evaluated for model performance by 5-fold cross validation to obtain the best performing prediction model. The k-fold cross-validation is a commonly used method for model evaluation, in which the database is first divided into k subsets, then each subset is made a test set once, and the remaining k-1 subsets are used as the training set. Finally, the results of multiple evaluations are averaged, thus eliminating the effect of unbalanced database partitioning. The results of the best prediction models in SVM, RF, XGBoost, and ANN are shown in
Table 6.
As shown in
Figure 13, XGBoost has excellent performance in predicting both OMC and MDD, with its
R2 reaching above 0.90, and RF also has good performance in predicting OMC (RMSE = 1.3605,
R2 = 0.9198), which suggests that the ensemble algorithm possesses superior model performance and generalization ability. However, RF performs poorly in predicting MDD, which may be attributed to the failure to optimize the best combination of hyperparameters. SVM has moderate performance in predicting both OMC and MDD, which is attributed to the fact that the core idea and fundamentals of SVM have not been changed, and it is still considered as a single machine learning algorithm. For ANN, whether it is predicting OMC or MDD, it shows the worst model performance. On the one hand, it may be related to the sample size being too small. On the other hand, it is not paired with an optimization algorithm to optimize the global optimal solution. The optimization algorithm is a kind of algorithm with global optimization performance, generality, and it is suitable for parallel processing. Optimization algorithms can theoretically find the optimal solution or near-optimal solution in a certain time. Commonly used optimization algorithms are Genetic Algorithm (GA), Simulated Annealing (SA), Particle Swarm Optimization (PSO), Ant Colony Algorithm (ACA), and so on.
Figure 14 and
Figure 15 show the actual and predicted values of OMC and MDD for the test set in XGBoost, respectively. From the figures, it can be seen that the overlap between the real and predicted values is very high when the model has excellent performance. Even though some of the data are poorly predicted, the error with the true values is around 4%, which is an acceptable range. This shows that machine learning algorithms can be applied to predict OMC and MDD with great efficiency and advantage.
5. Conclusions
The prediction of compaction parameters of soil based on machine algorithms is a promising option; however, this method requires knowledge of the characteristic parameters of the soil. In this paper, OMC and MDD prediction models of machine learning algorithms such as SVM, ANN, RF, and XGBoost are developed and compared based on collected soil sample data. Some beneficial conclusions can be drawn.
- (1)
When dealing with large and complex data, SVM based on Gaussian kernel function can predict OMC and MDD better than SVM based on linear kernel function.
- (2)
In ANN modeling, the model performance varies greatly for different neurons. When the hidden layer is certain, the number of neurons has a great impact on predicting OMC and MDD.
- (3)
Comparing the four machine learning algorithms, XGBoost is the best model for predicting OMC and MDD, while RF has good performance in predicting OMC. This shows that the ensemble algorithm has better model performance and generalization ability than the other algorithms.
- (4)
Regarding outcomes, ANN is less successful in predicting both OMC and MDD. This suggests that ANN requires large high-quality databases paired with optimized algorithms to achieve higher model performance.
- (5)
Finally, the feature importance output was analyzed by RF and XGBoost. The results show that PL and LL are the two features that affect the performance of the model the most, which is in line with reality.
According to this research, it is proved that machine learning, especially ensemble learning, can be applied for the compaction parameter prediction of soil-filling materials. With this method, the amount of laboratory work can be significantly reduced and the efficiency optimization significantly improved, which is meaningful for soil resource utilization in engineering construction.