Influence of Non-Uniform Rail Loads on the Rotation of Railway Sleepers
Abstract
:1. Introduction
Basic Assumptions
- A linear, two-layer track model in the vertical plane was analysed;
- The load of both rails q1 and q2 for any moment in time t and x coordinate can be presented as a sum of two elements: average load qav (symmetric) and antisymmetric Δq, i.e., (Figure 1):
- The rails are modelled as Euler–Bernoulli beams and sleepers as stiffblocks, and fastening systems and a sleeper bed are treated as viscoelastic bonds (Figure 2)
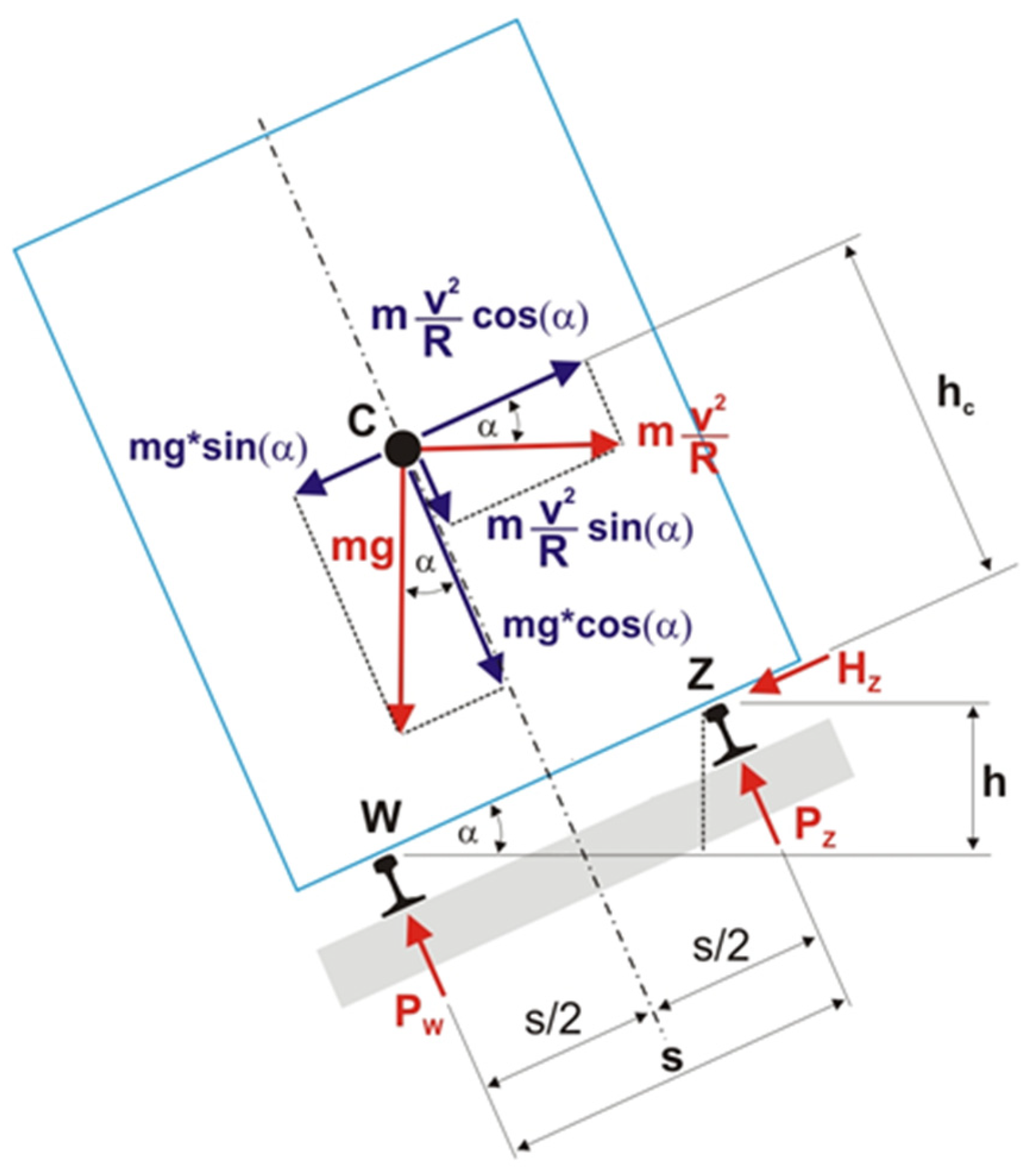
- The assumption is that the distribution of the sleeper mass along its axis is symmetric in relation to the centre of mass, and its rotations in relation to the centre of mass are small, i.e., the vertical displacement of the sleeper under the rail can be presented as a product of the rotation angle α and the distance between the cross-section directly under the rail from the sleeper’s centre of mass b (Figure 1).
2. Movement Equations and Their Solutions
2.1. Solution for Time-Invariable Forces
- For the symmetric load:
- For the antisymmetric load:
- yrΔ—the rail displacement with an antisymmetric load (opposite signs for both rails) [m];
- Ip—the moment of inertia for individual sleepers (Ip = Is/ls, where Is—the moment of inertia of a sleeper [kgm2], and ls—the sleeper axis spacing along the track [m]);
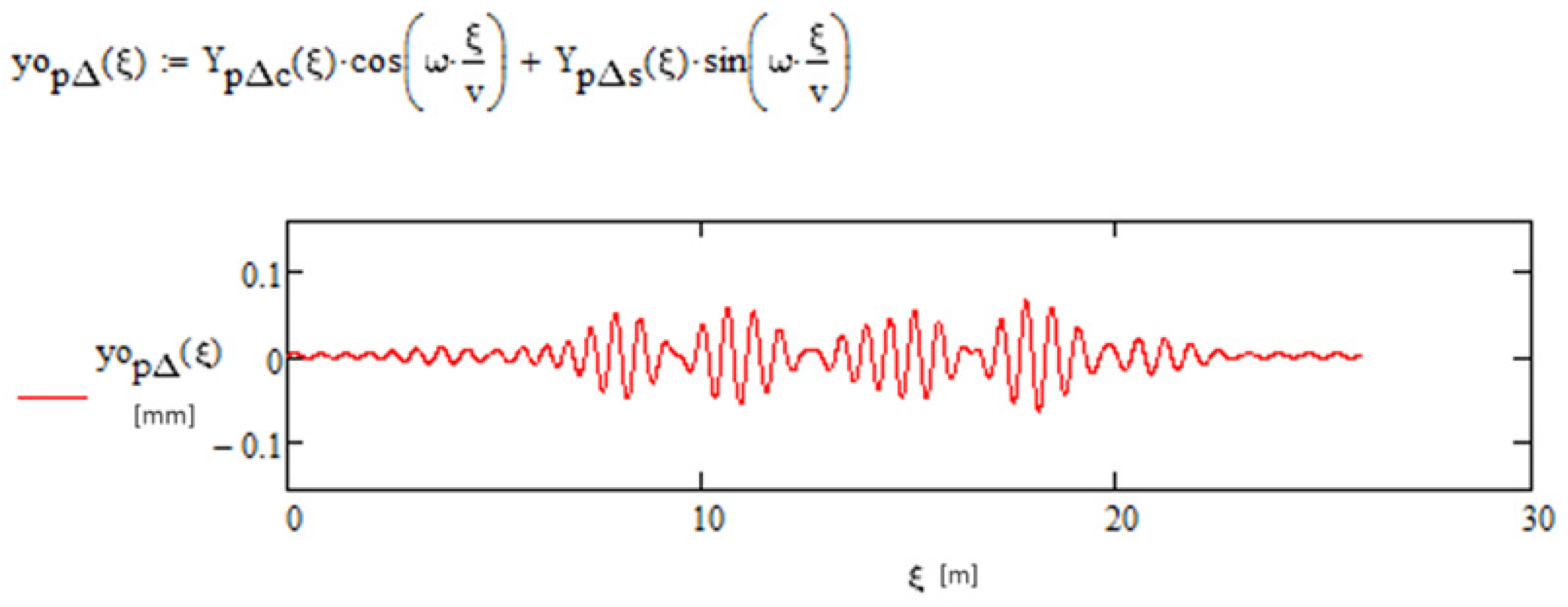
2.2. Solution for Oscillating Forces
2.3. Solution for Track Response as a Two-Layer Structure
- For the given functions of rails loads q1 and q2, determine the symmetric qav and antisymmetric Δq components of the load according to Formula (1).
- Isolate from every form of the load a time-invariable component and a time-variable component, i.e.,
- 3.
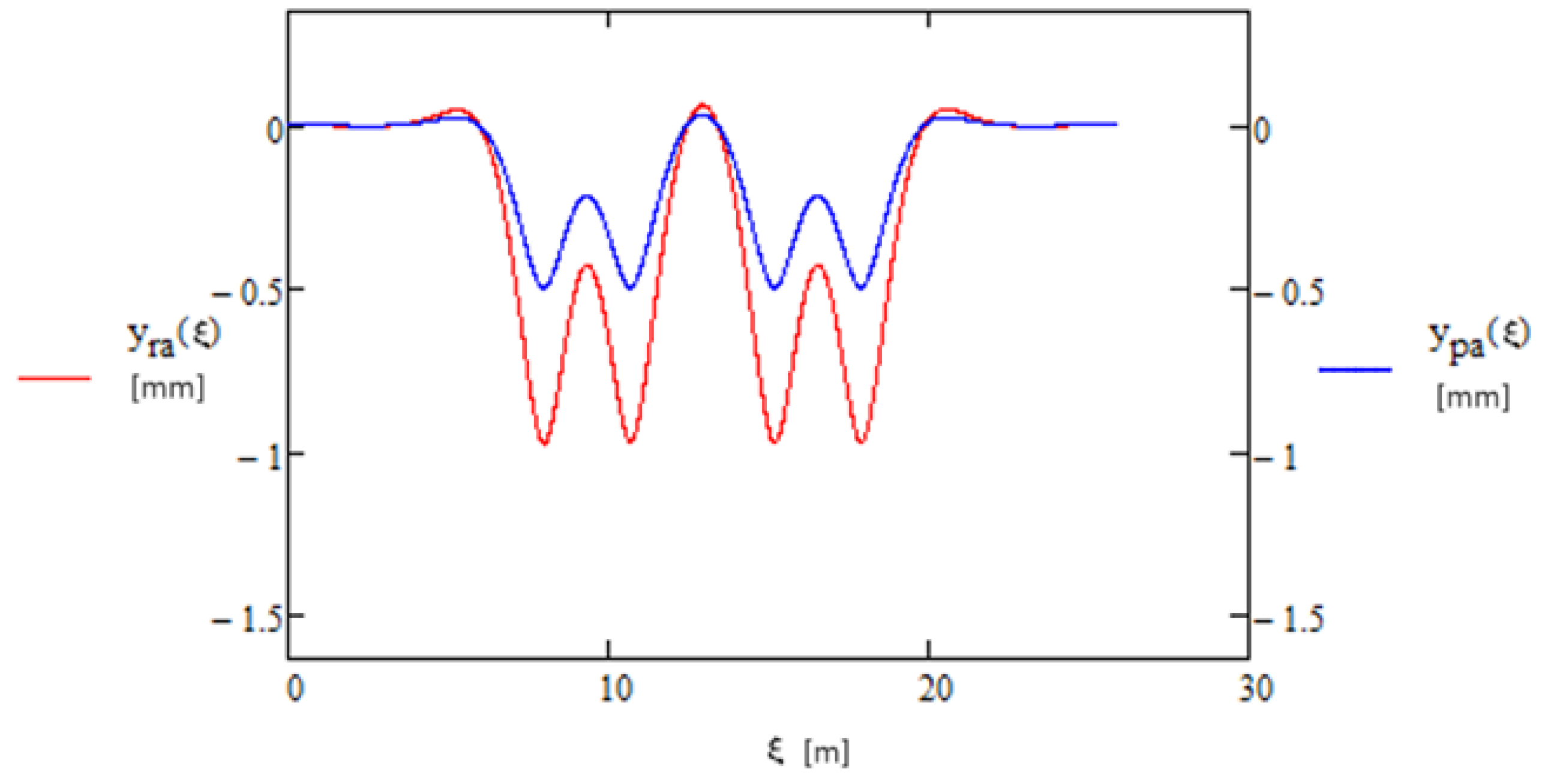
- Using symbol yr1 for the rail displacement for which the quasi-static load (time-invariable) is greater than for the other rail, which will be designated as yr2, respectively, the sleeper displacement under both rails, yp1 and yp2, determine them, using Formulas (8)–(15):
- 4.
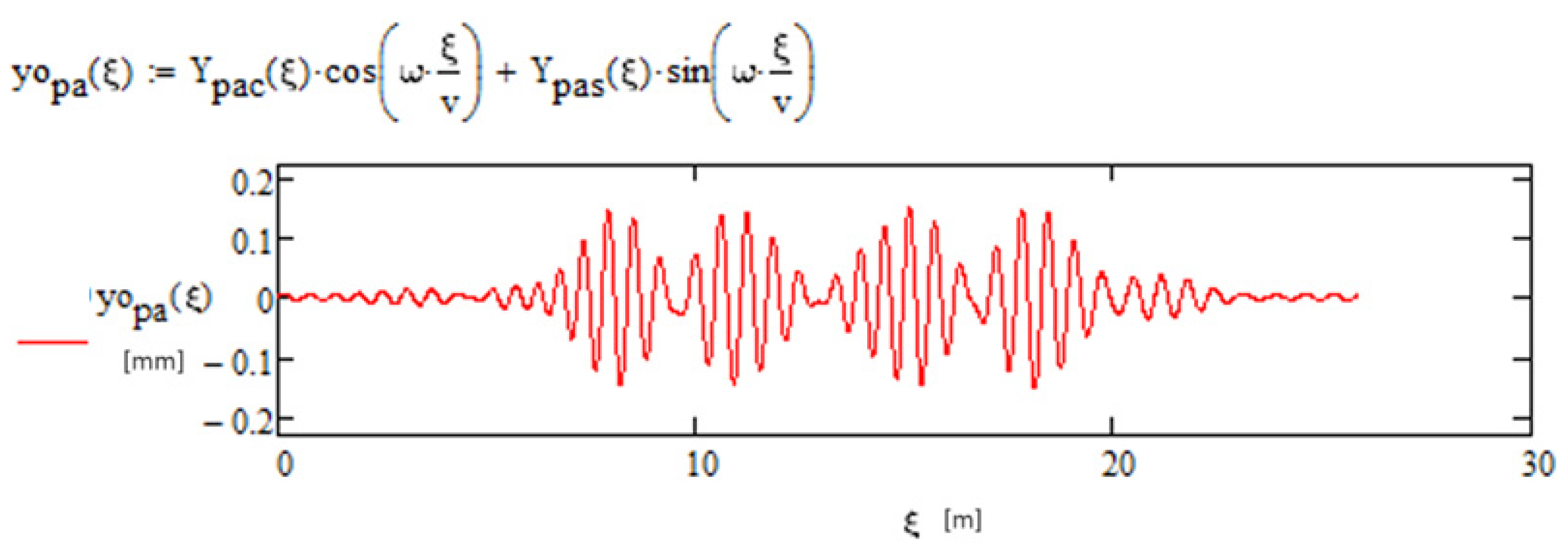
- Using Formulas (17)–(24), determine the rail displacement and sleeper displacement for the time-variable load qo (oscillating with a given frequency ω):
- 5.
- If a variable load is polyharmonic (more than one frequency ω), the calculations expressed with Formula (27) should be repeated as many times for as many harmonic components of time-variable force there are.
- 6.
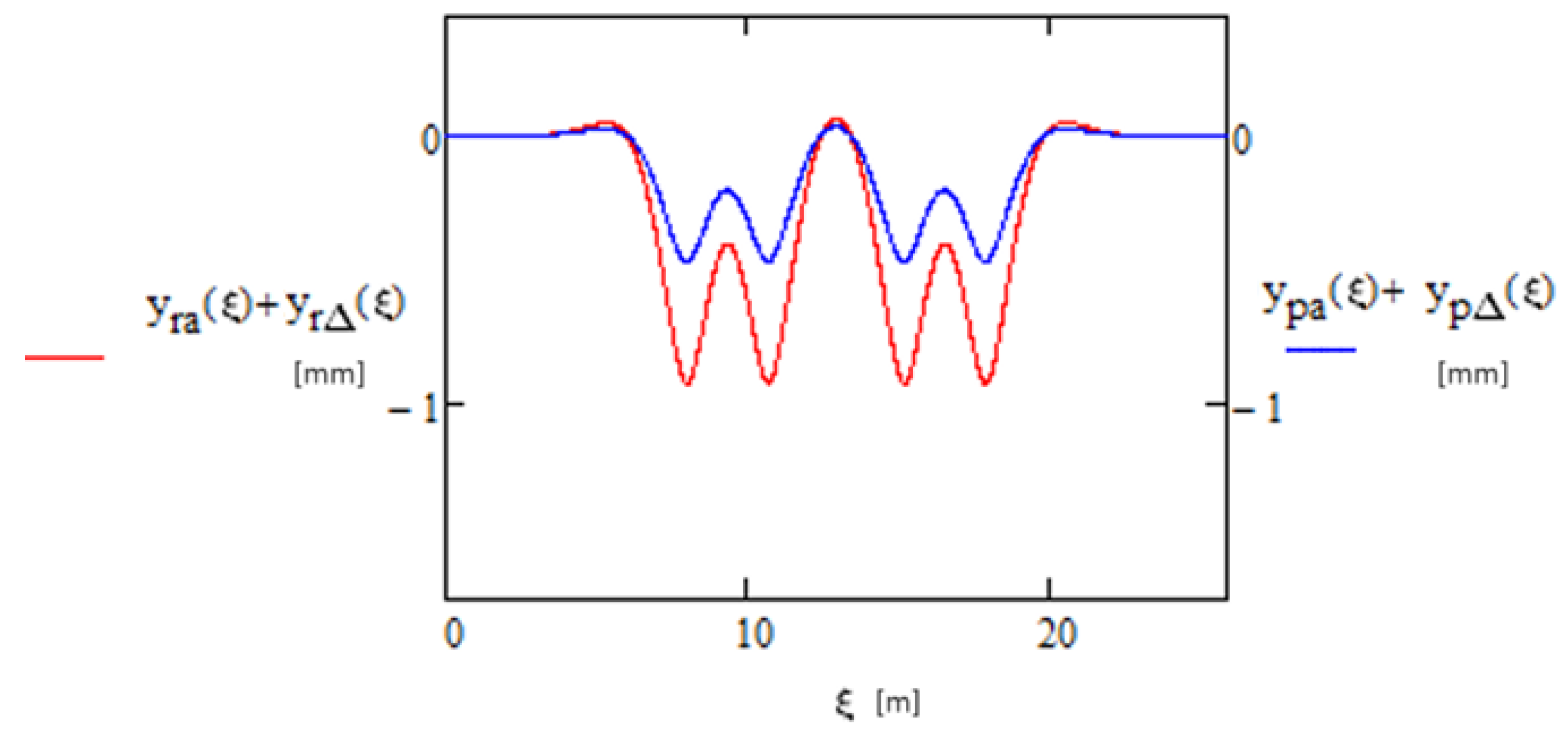
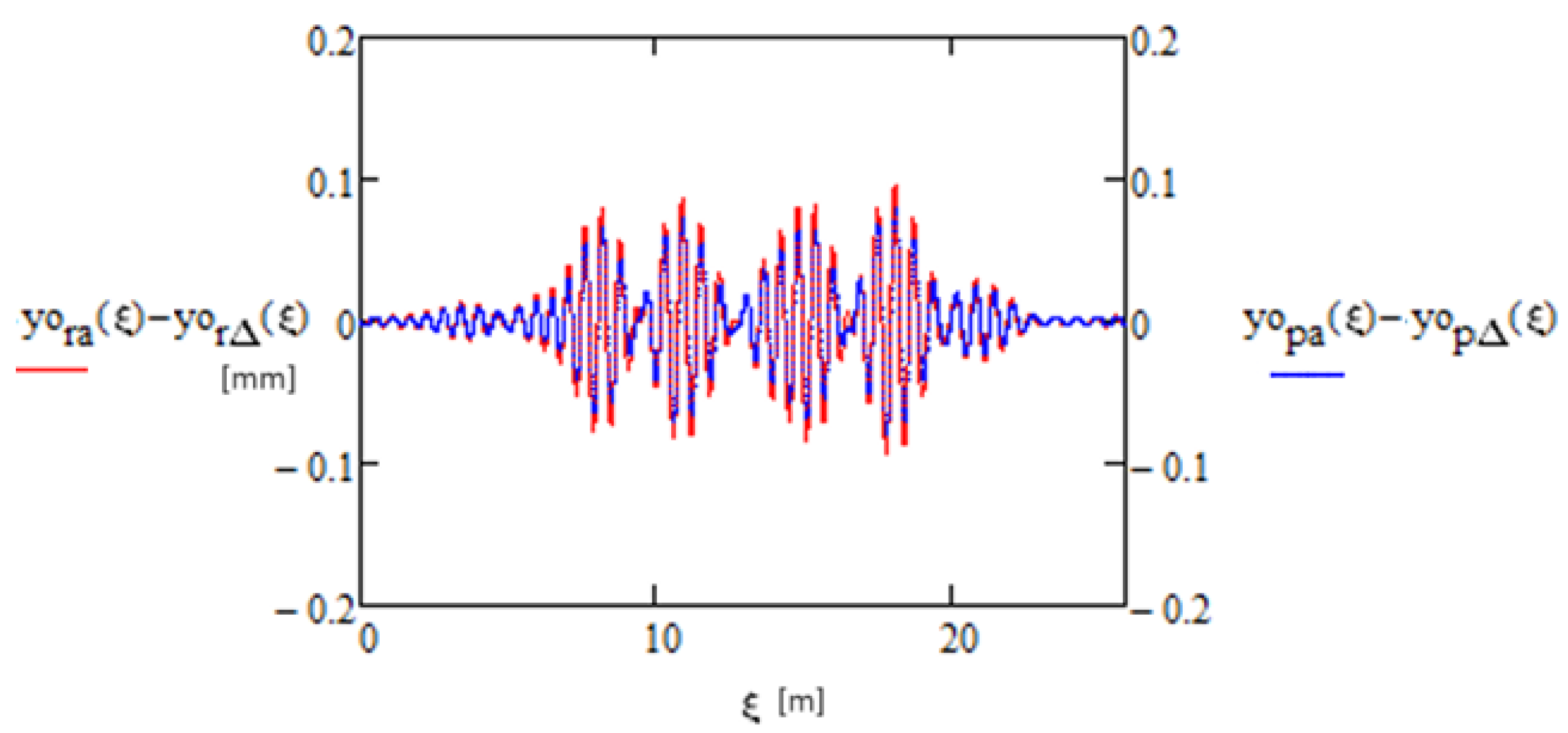
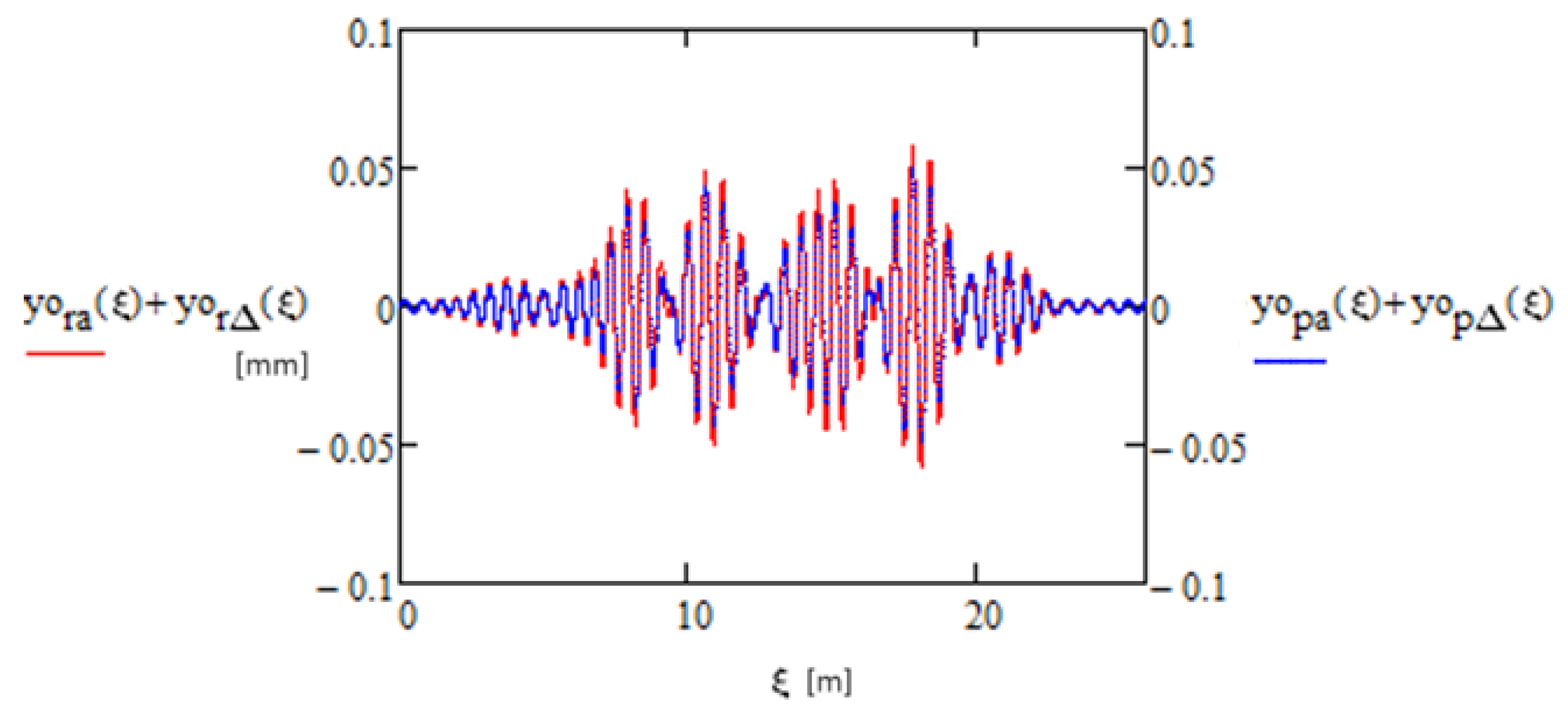
- The total rail displacements and total sleeper displacements are a sum of these displacements resulting from the constant load (Formula (27)) and variable load (Formula (26)), whereas—in the case of a polyharmonic load, where there are m harmonic components—Formula (28) should be applied m times, and the results should be added.
3. Calculation Examples
3.1. Introductory Notes
3.2. Adopted Parameters
- A 60 E1 rail, as the Euler–Bernoulli beam: E = 2.1 × 108 N/m2, I = 3055 × 10−8 m4, mr = 60 kg.
- PS94 concrete sleepers, as stiffblocks: A = 0.68/2 m2, mp = 267 kg/m.
- An elastic fastening system with elastic-dampening parameters (rail–sleeper bonds): kr = 9.1 × 107 N/m, cr = 3950 Ns/m.
- The foundation under the sleepers with elastic-dampening parameters (sleeper–foundation bonds): kp = 8.8 × 107 N/m2, cp = 49,000 Ns/m2.
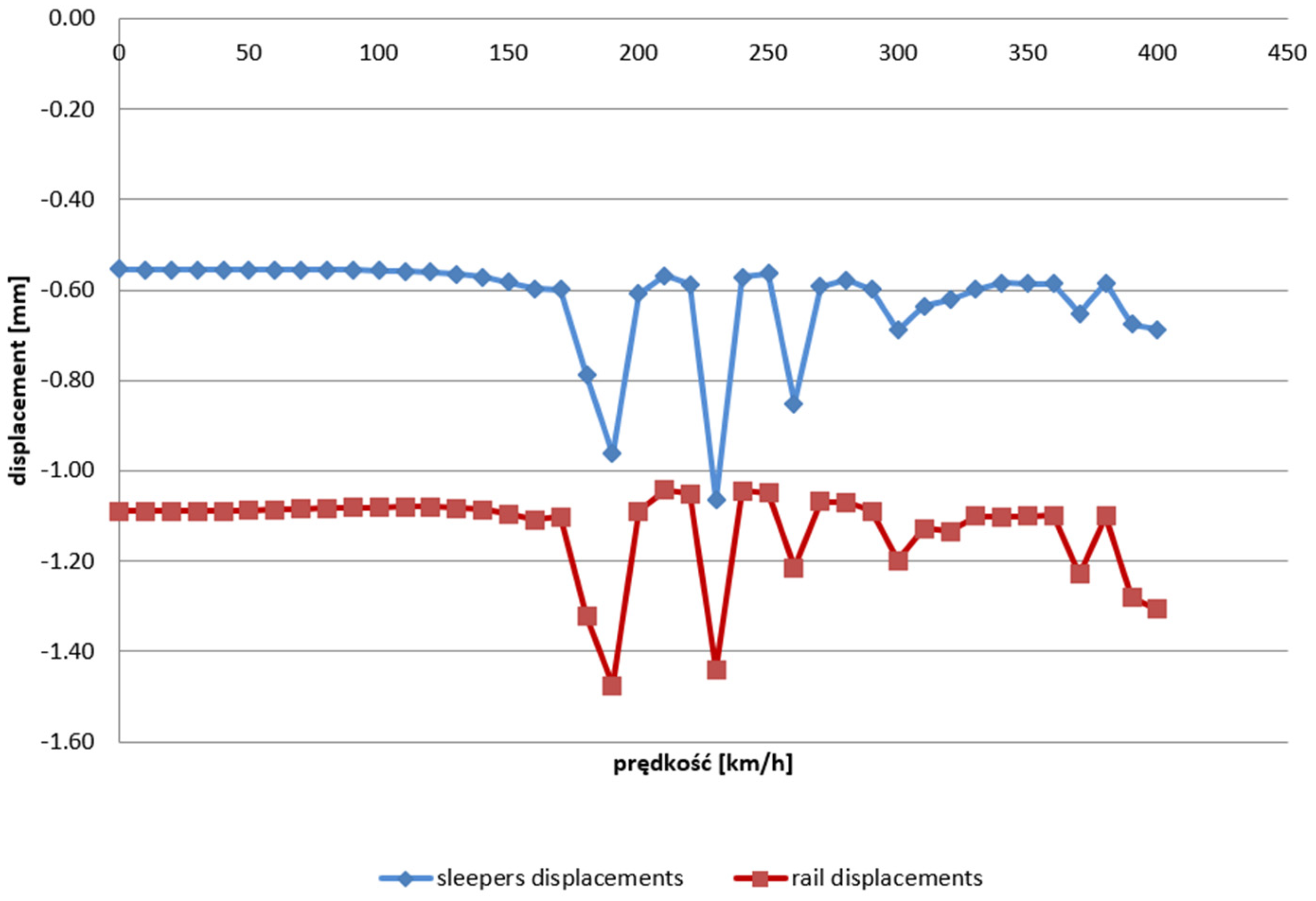
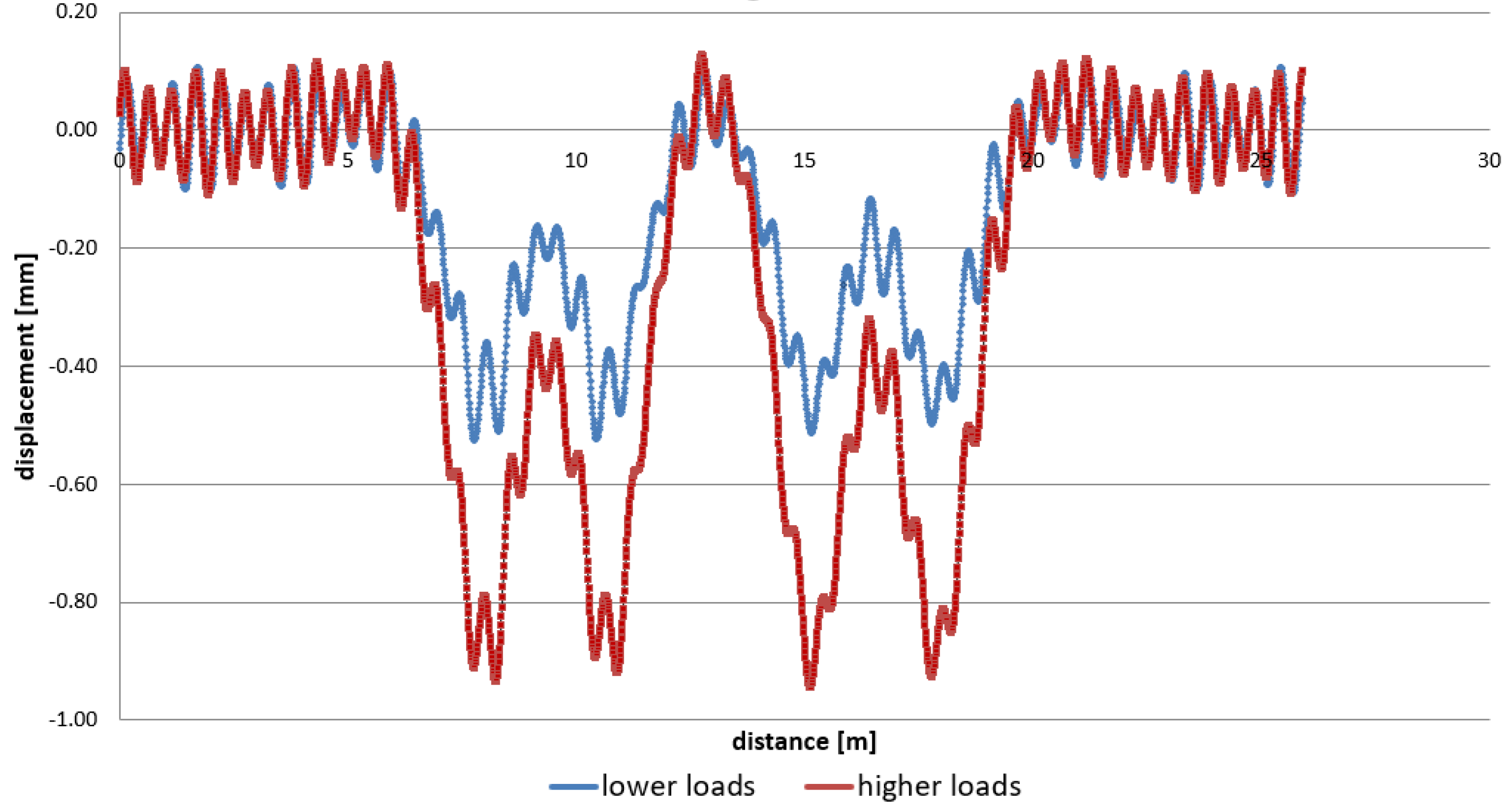
- A variable parameter of the train speed v (force system) was adopted, which was changing from 0 km/h to 400 km/h, leading to a change in the wheel loads on the internal and external rails (higher and lower loads) with the given constant curve radius R = 5580 m, cant hp = 100 mm, and wheel load on the axis Q = 160 kN. The values of the forces influencing the internal track Pw (with lower load) and the external track Pz (with higher load) were calculated with Formula (29), and they are, respectively, Pw = 64.1 kN and Pz = 94.4 kN. Examples of the calculations for the rails and sleepers for the speed v = 170 km/h are presented in the following chapters.
3.3. Example of Determining Rail and Sleeper Displacements with Time-Invariable Load
3.4. Example of Determining Rail and Sleeper Displacements with Time-Variable Load
4. Analysis of the Influence of Variable Parameters
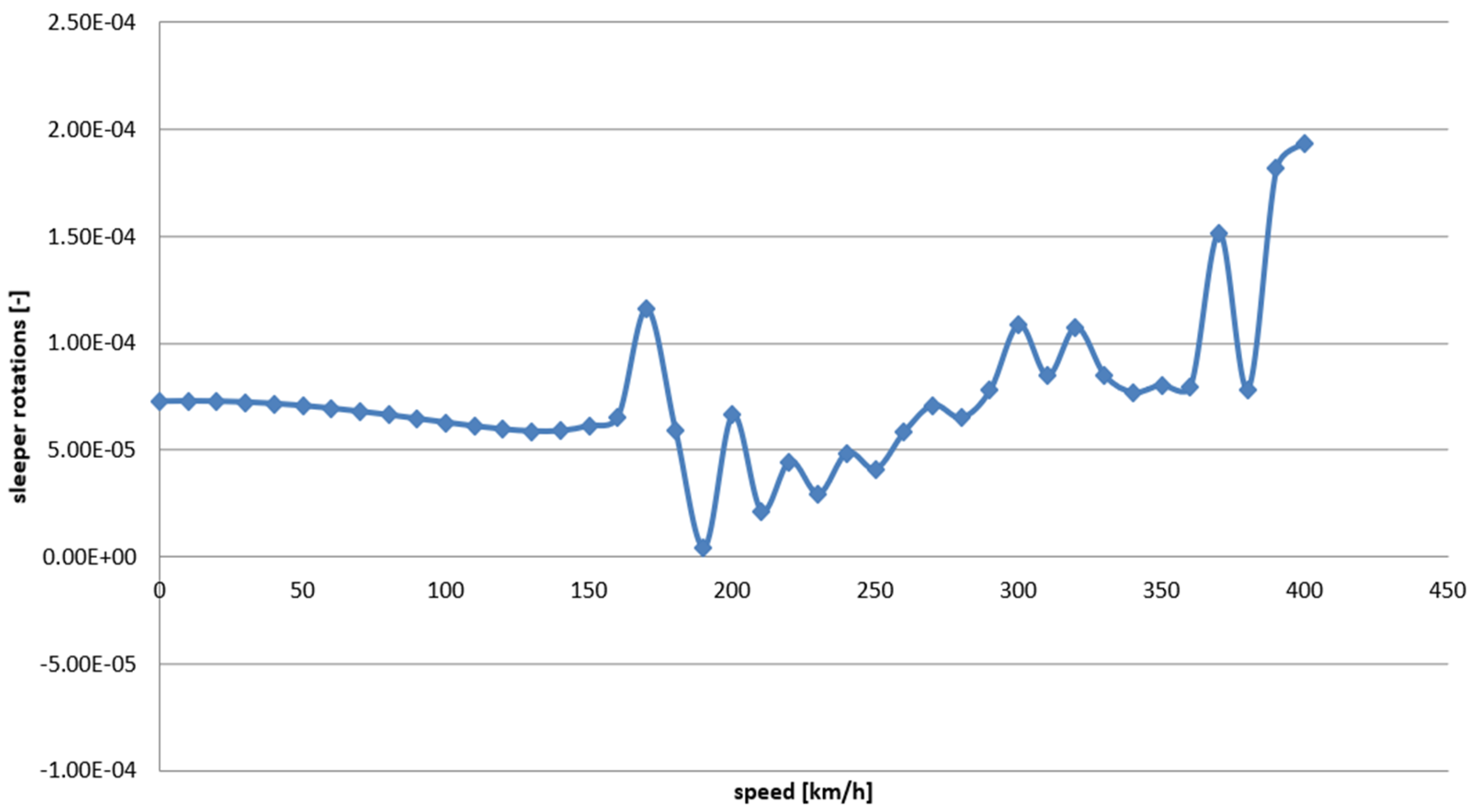
4.1. Speed
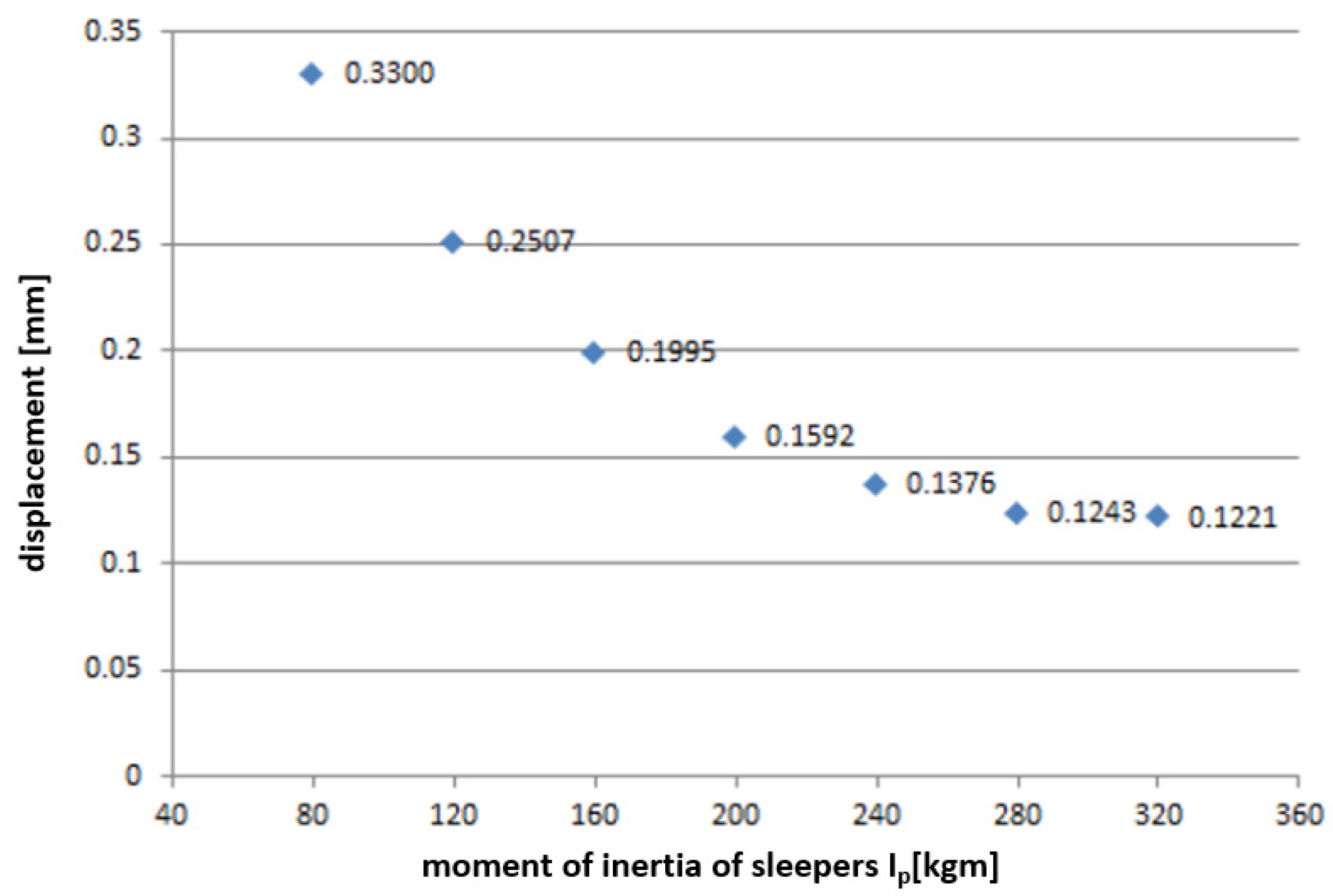
4.2. Influence of Sleeper’s Moment of Inertia
5. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sysyn, M.; Nabochenko, O.; Kovalchuk, V. Experimental investigation of the dynamic behavior of railway track with sleeper voids. Railw. Eng. Sci. 2020, 28, 290–304. [Google Scholar] [CrossRef]
- Sysyn, M.; Przybyłowicz, M.; Nabochenko, O.; Kou, L. Identification of Sleeper Support Conditions Using Mechanical Model Supported Data-Driven Approach. Sensors 2021, 21, 3609. [Google Scholar] [CrossRef] [PubMed]
- Timoshenko, S. Method of analysis of static and dynamic stresses in rail. In Proceedings of the 2nd International Congress on Applied Mechanics, Zurich, Switzerland, 12–17 September 1926; pp. 407–418. [Google Scholar]
- Basiewicz, T. Nawierzchnia Kolejowa na Podkładach Betonowych; WKiŁ: Warsaw, Poland, 1969. [Google Scholar]
- Czyczuła, W. Analiza Wpływu Drgań Nawierzchni Kolejowej na Deformacje Podsypki. Ph.D. Thesis, Politechnika Krakowska im. Tadusza Kościuszki, Krakow, Poland, 1984. [Google Scholar]
- Czyczula, W.; Kozioł, P.; Blaszkiewicz, D. On the equivalence between static and dynamic railway track response and on the Euler-Bernoulli and Timoshenko beams analogy. Shock. Vib. 2017, 2017, 2701715. [Google Scholar] [CrossRef]
- Fryba, L. Vibration of Solids and Structures under Moving Loads; Noordhoff: Groningen, The Netherlands, 1972. [Google Scholar]
- Koziol, P. Nonlinear response of railway track subjected to a moving train. In Proceedings of the ICEDYN 2015 International Conference on Structural Engineering Dynamics, Lagos, Algarve, Portugal, 22–24 June 2015; Maia, N.M.M., Neves, M.M., Sampaio, R.P.C., Eds.; paper K03. Instituto de Engenharia Mecânica: Lisabon, Portugal; Porto, Portugal, 2015; ISBN 978-989-96276-9-7. [Google Scholar]
- Bogacz, R. Dynamics of continuous systems subjected to traveling loads. Appl. Mech. Mater. 2009, 9, 509–516. [Google Scholar] [CrossRef]
- Kargarnovin, M.H.; Younesian, D.; Thompson, D.J.; Jones, C.J.C. Response of beams on nonlinear viscoelastic foundations to harmonic moving loads. Comput. Struct. 2005, 83, 1865–1877. [Google Scholar] [CrossRef]
- Czyczula, W.; Koziol, P.; Kudla, D.; Lisowski, S. Analytical evaluation of track response in vertical direction due to moving load. J. Vib. Control. 2017, 23, 2989–3006. [Google Scholar] [CrossRef]
- Sołkowski, J. The Transition Effect in Rail Tracks; Monografia 435; Politechnika Krakowska im. Tadeusza Kościuszki: Krakow, Poland, 2013. [Google Scholar]
- Koziol, P.; Neves, M.M. Multilayered infinite medium subject to a moving load: Dynamic response and optimization using coiflet expansion. Shock. Vib. 2012, 19, 1009–1018. [Google Scholar] [CrossRef]
- Zhai, W.; Xia, H.; Cai, C.; Gao, M.; Li, X.; Guo, X.; Zhang, N.; Wang, K. High-speed train-track-bridge dynamic interactions—Part I: Theoretical model and numerical simulation. Int. J. Rail Transp. 2013, 1, 3–24. [Google Scholar] [CrossRef]
- Zhai, W.; Xia, H.; Cai, C.; Gao, M.; Li, X.; Guo, X.; Zhang, N.; Wang, K. High-speed train-track-bridge dynamic interactions—Part II: Experimental validation and engineering application. Int. J. Rail Transp. 2013, 1, 25–41. [Google Scholar] [CrossRef]
- Bogacz, R.; Krzyżyński, T. O Belce Bernoulliego-Eulera Spoczywającej na Lepkosprężystym Podłożu Poddanej Działaniu Ruchomego Oscylacyjnego Obciążenia; Raport 38; Prace IPPT-PAN: Warsaw, Poland, 1986. [Google Scholar]
- Ferrara, R.; Leonardi, G.; Jourdan, F. A Two-Dimansional Numerical Model to Analyse the Critical Velocity of High Speed Infrastructure. In Proceedings of the XIV-th International Conference on Civil, Structural and Environmental Engineering Computing, Cagliari, Sardinia, Italy, 3–6 September 2013. [Google Scholar]
- Kerr, A.D. The continuously supported rail subjected to axial force and moving load. Int. J. Mech. Sci. 1972, 14, 71–78. [Google Scholar] [CrossRef]
- Koziol, P.; Mares, C. Wavelet approach for vibration analysis of fast moving load on a viscoelastic medium. Shock. Vib. 2010, 17, 461–472. [Google Scholar] [CrossRef]
- Hryniewicz, Z.; Koziol, P. Wavelet approach for analysis of dynamic response of Timoshenko beam on random foundation. In Proceedings of the ICSV16, The Sixteenth International Congress on Sound and Vibration, Krakow, Poland, 5–9 July 2009; Pawelczyk, M., Bismor, D., Eds.; Paper 421. International Institute of Acoustics and Vibration (IIAV): Woodbridge, ON, Canada, 2009. ISBN 978-83-60716-71-7. [Google Scholar]
- Auersch, L. Excitation of ground vibration due to the passage of trains over a track with trackbed irregularities and a varying support stiffness. Veh. Syst. Dyn. 2015, 53, 1–29. [Google Scholar] [CrossRef]
- Czyczula, W.; Tatara, T. Badania drgań Elementów Nawierzchni, Podłoża oraz Propagacji Drgań i Hałasu w Otoczeniu Drogi Kolejowej Przy Przejeździe Pociągu EMU-250 (Pendolino); Raport Politechniki Krakowskiej; Politechniki Krakowskiej: Krakow, Poland, 2014. [Google Scholar]








Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Czyczuła, W.; Błaszkiewicz-Juszczęć, D. Influence of Non-Uniform Rail Loads on the Rotation of Railway Sleepers. Appl. Sci. 2024, 14, 2746. https://doi.org/10.3390/app14072746
Czyczuła W, Błaszkiewicz-Juszczęć D. Influence of Non-Uniform Rail Loads on the Rotation of Railway Sleepers. Applied Sciences. 2024; 14(7):2746. https://doi.org/10.3390/app14072746
Chicago/Turabian StyleCzyczuła, Włodzimierz, and Dorota Błaszkiewicz-Juszczęć. 2024. "Influence of Non-Uniform Rail Loads on the Rotation of Railway Sleepers" Applied Sciences 14, no. 7: 2746. https://doi.org/10.3390/app14072746
APA StyleCzyczuła, W., & Błaszkiewicz-Juszczęć, D. (2024). Influence of Non-Uniform Rail Loads on the Rotation of Railway Sleepers. Applied Sciences, 14(7), 2746. https://doi.org/10.3390/app14072746




