A Single-Phase Lightweight Double-Leaf Multi-Stage Acoustic Black Hole Model of Metamaterial
Abstract
:1. Introduction
2. Materials and Methods
2.1. Structural Model
2.2. Calculation of the Complex Energy Band
3. Calculation Results and Discussion
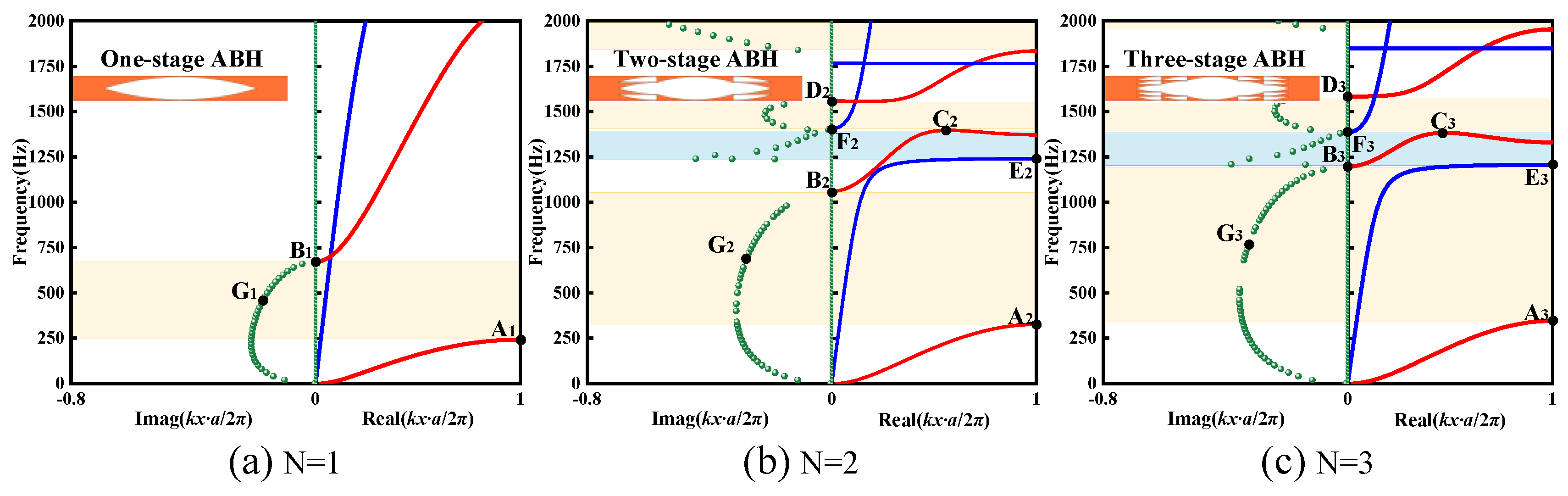
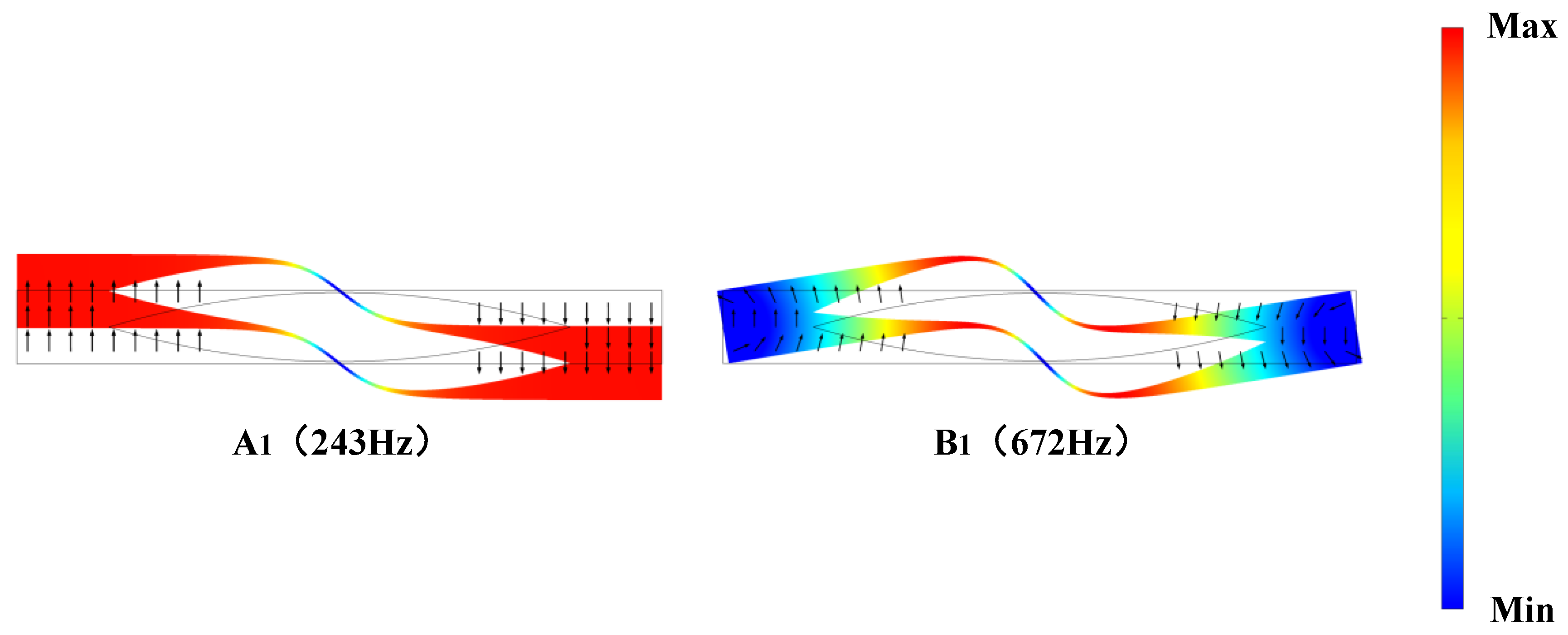
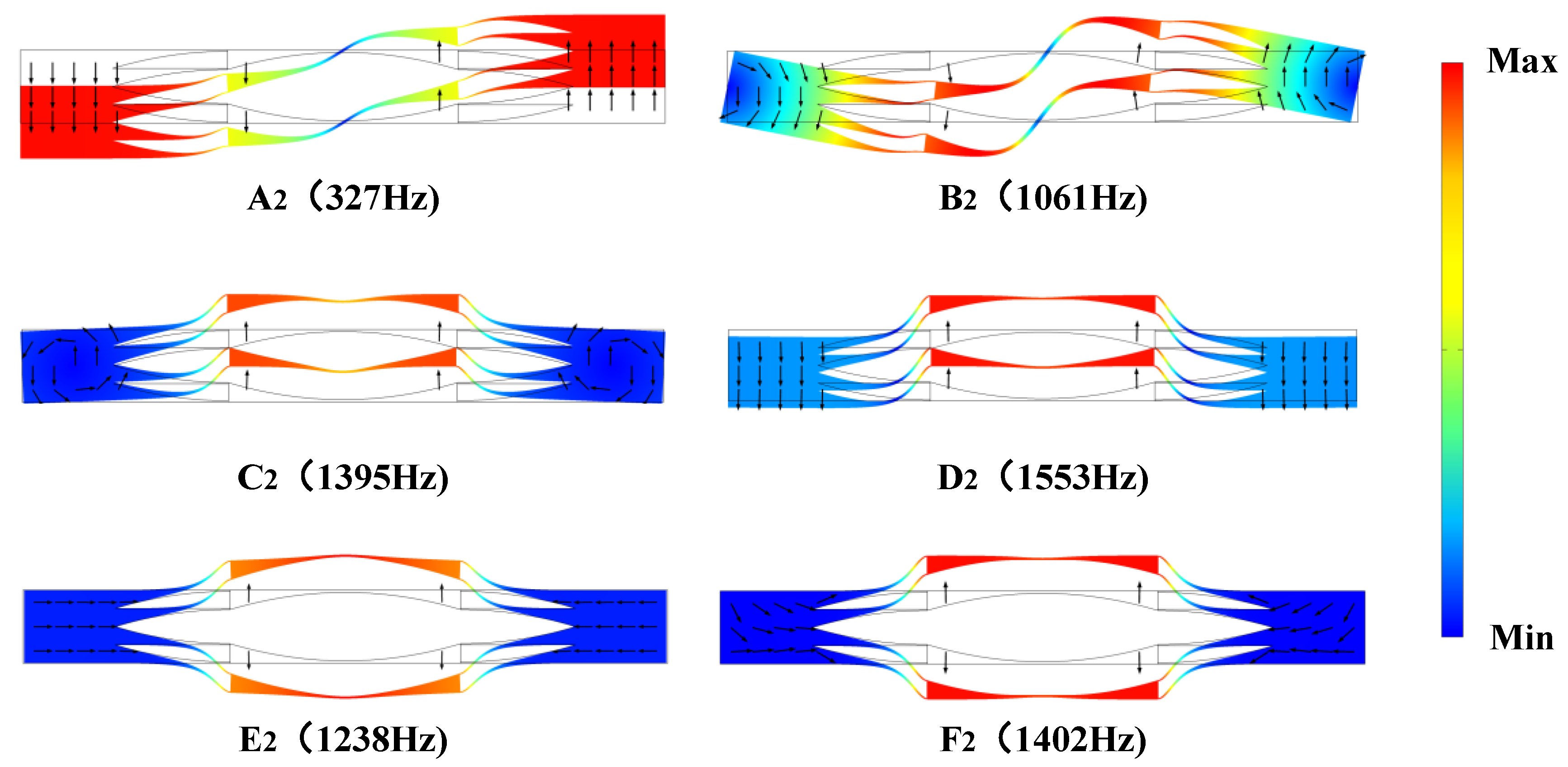
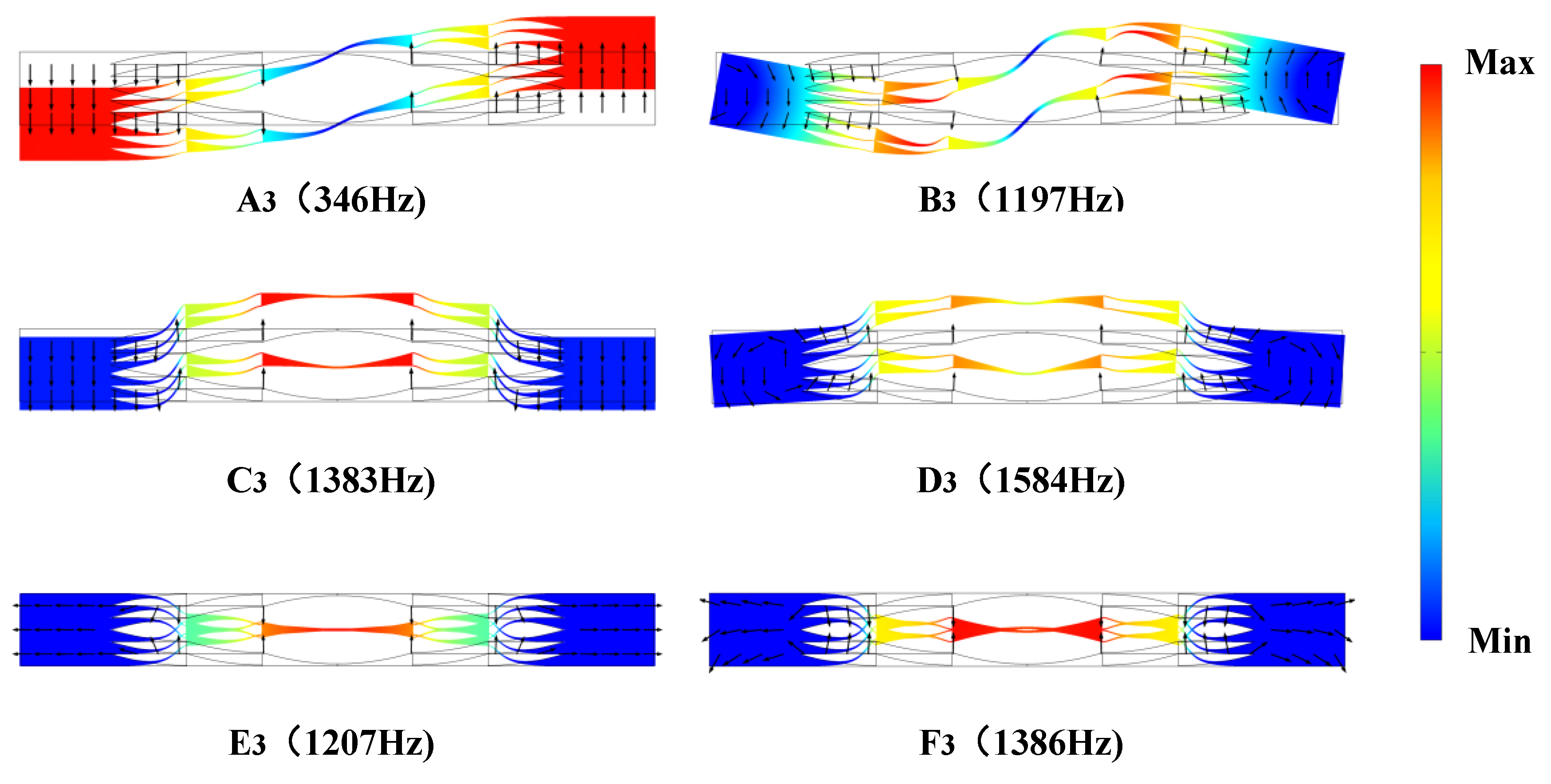
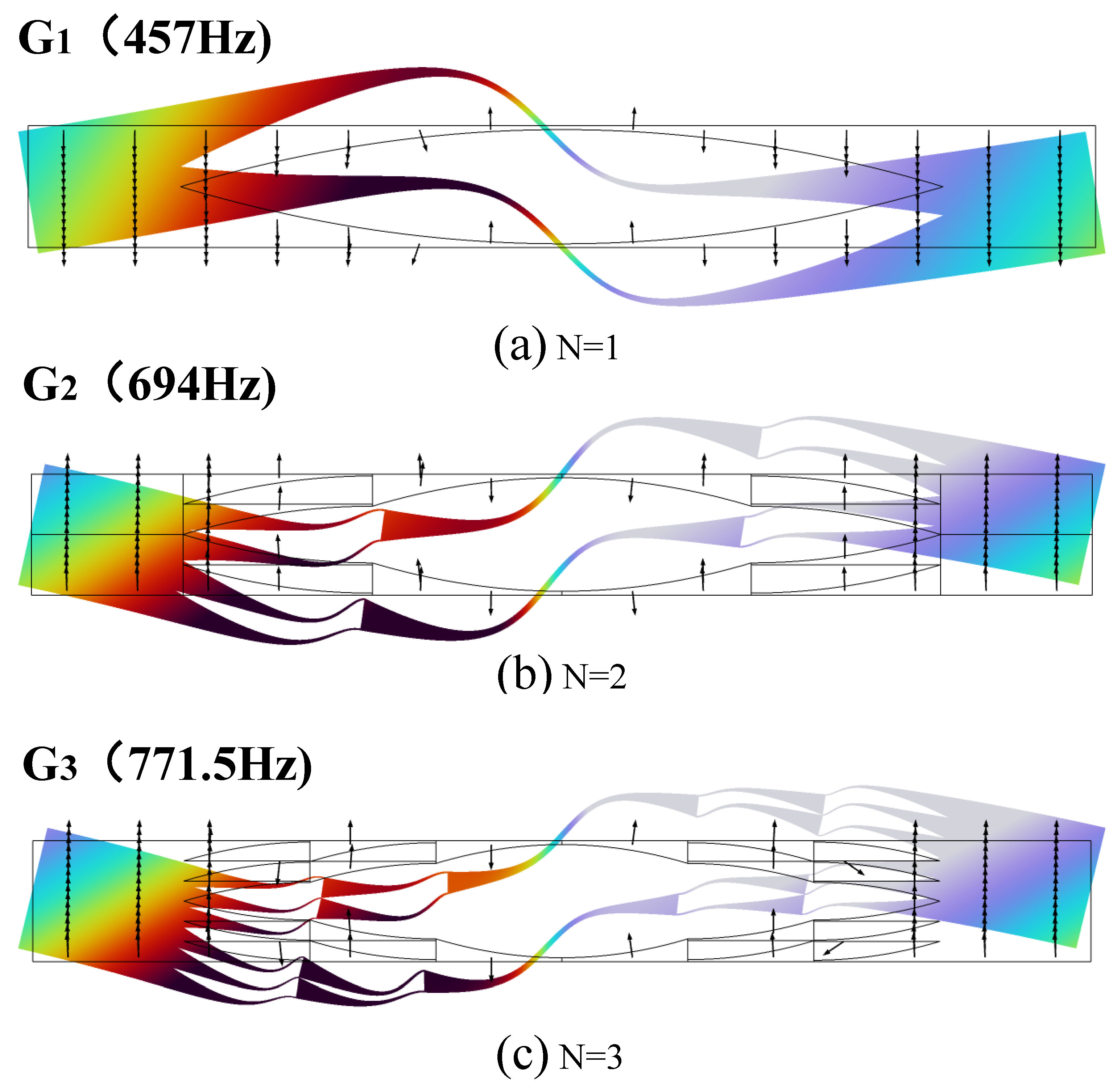
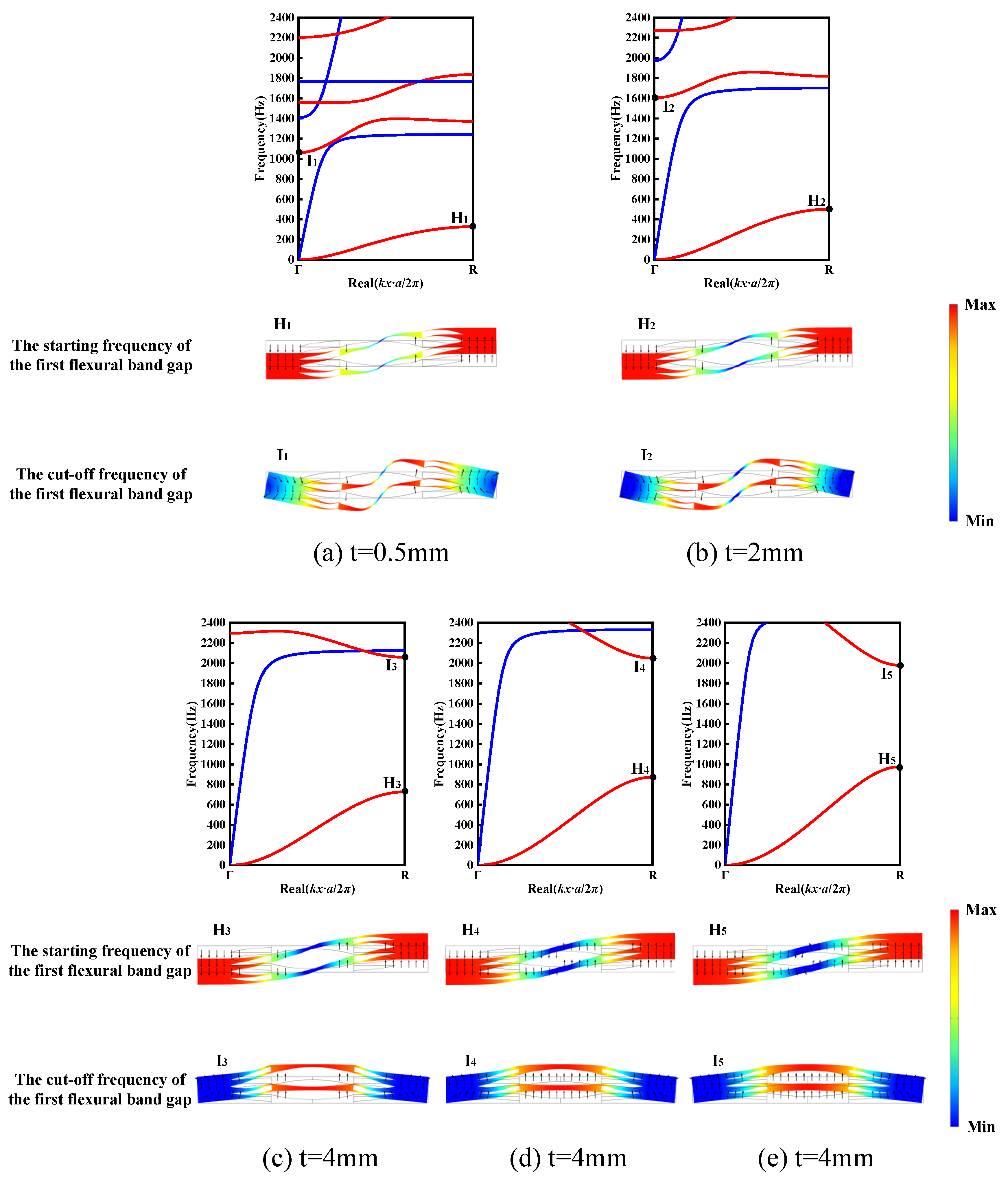
3.1. Complex Energy Band Structure and Vibration Modes
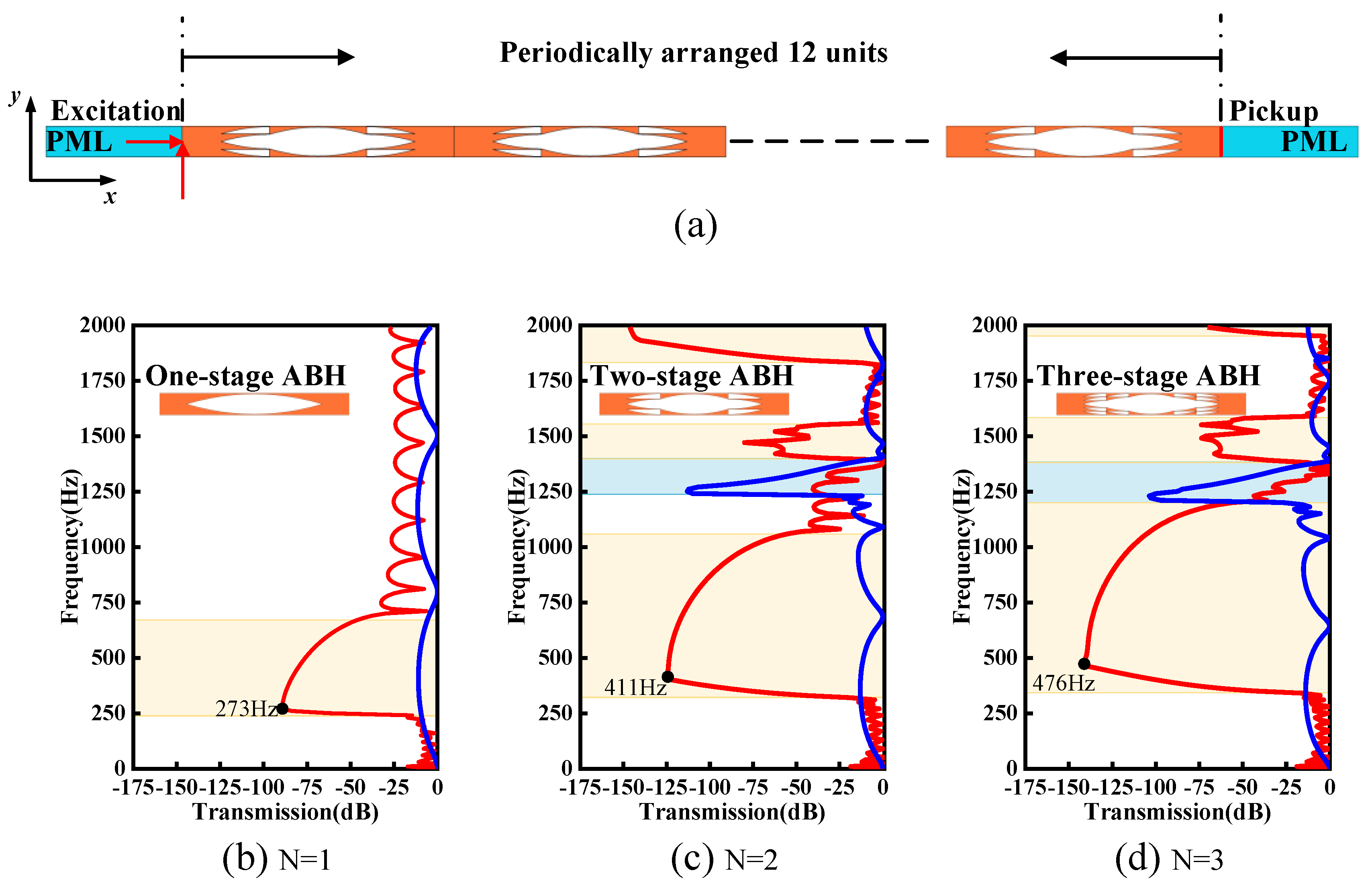
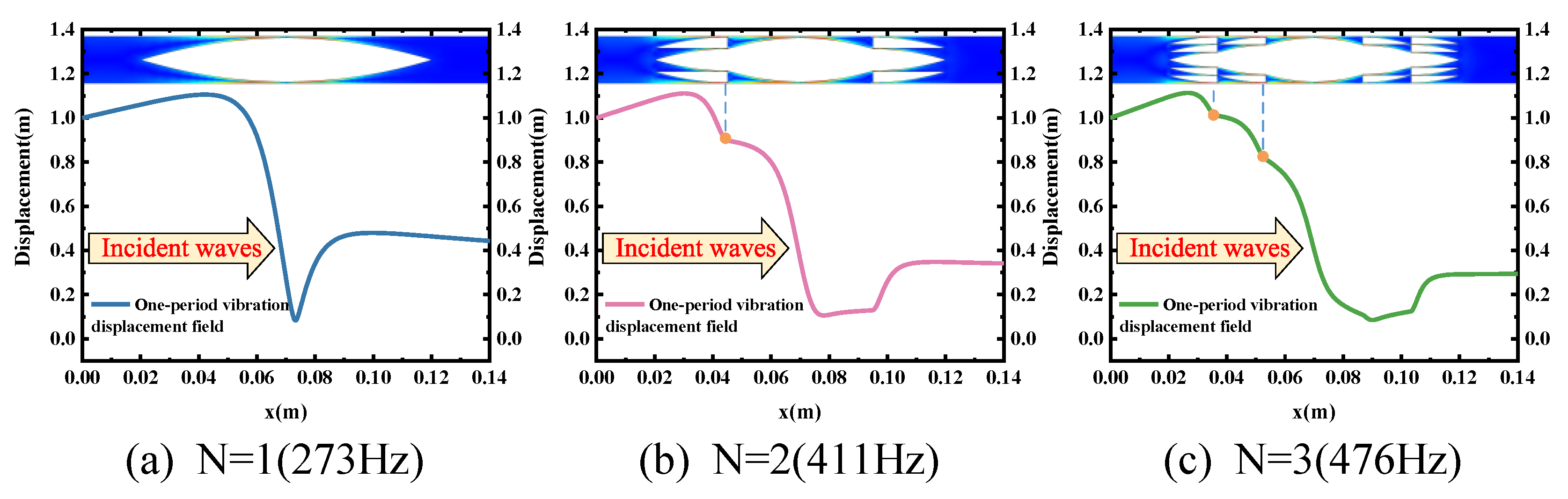
3.2. Vibration Transmission and Vibration Displacement Field
4. Discussion of Geometric Parameter on Complex Band Structure
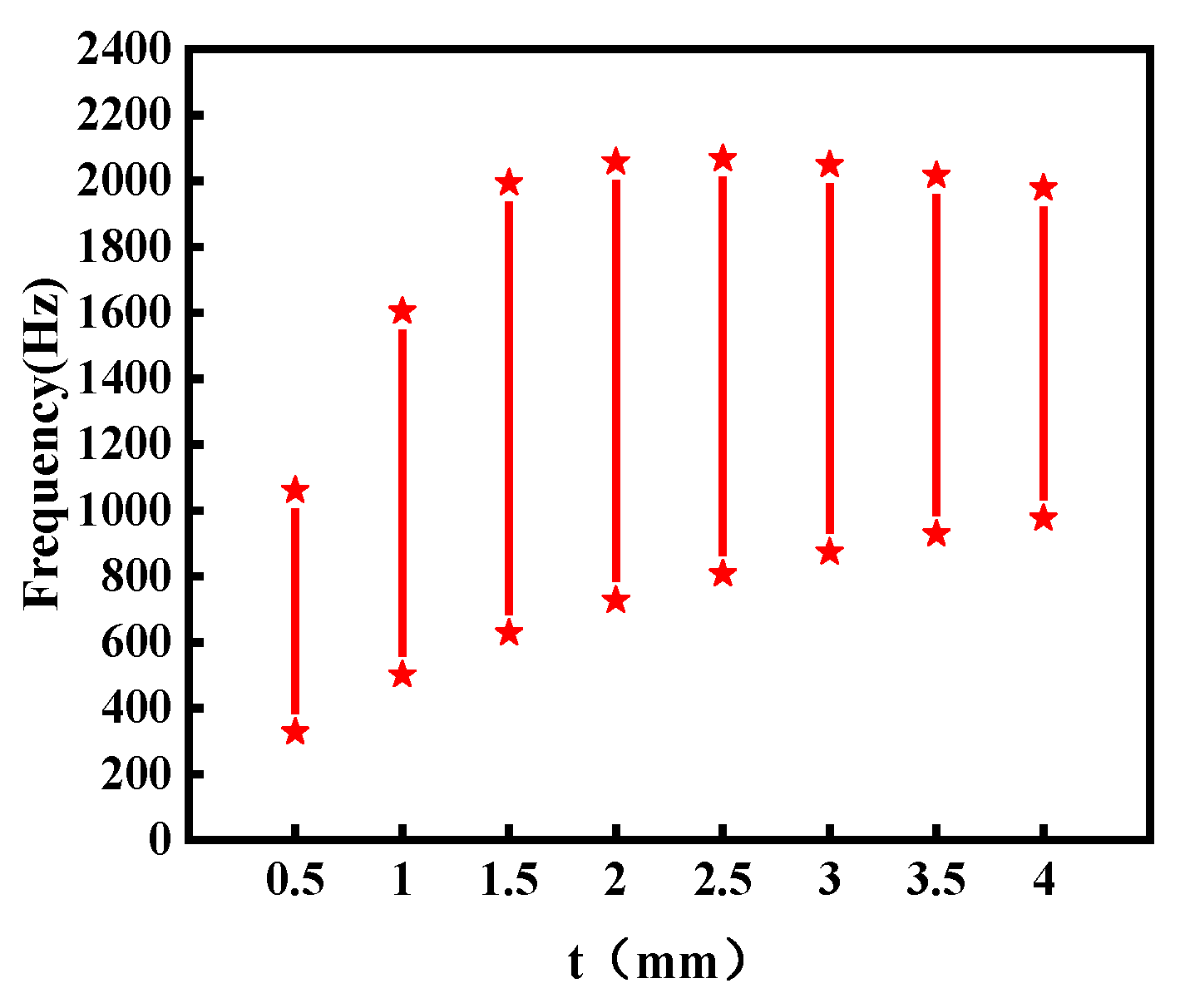
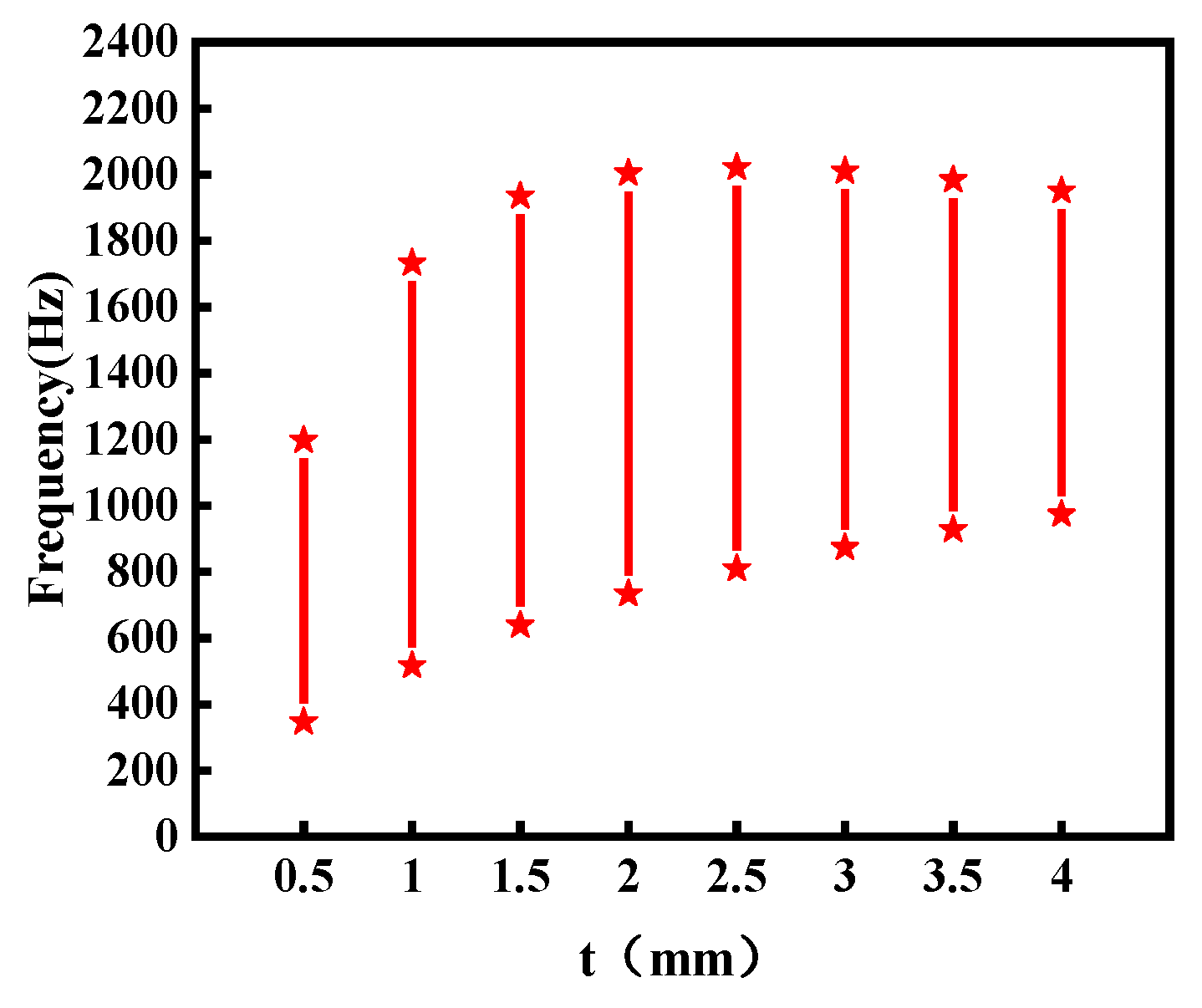
4.1. Effect of Truncated Thickness t on Band Gap
4.2. Effect of Power Exponent on Bandgap
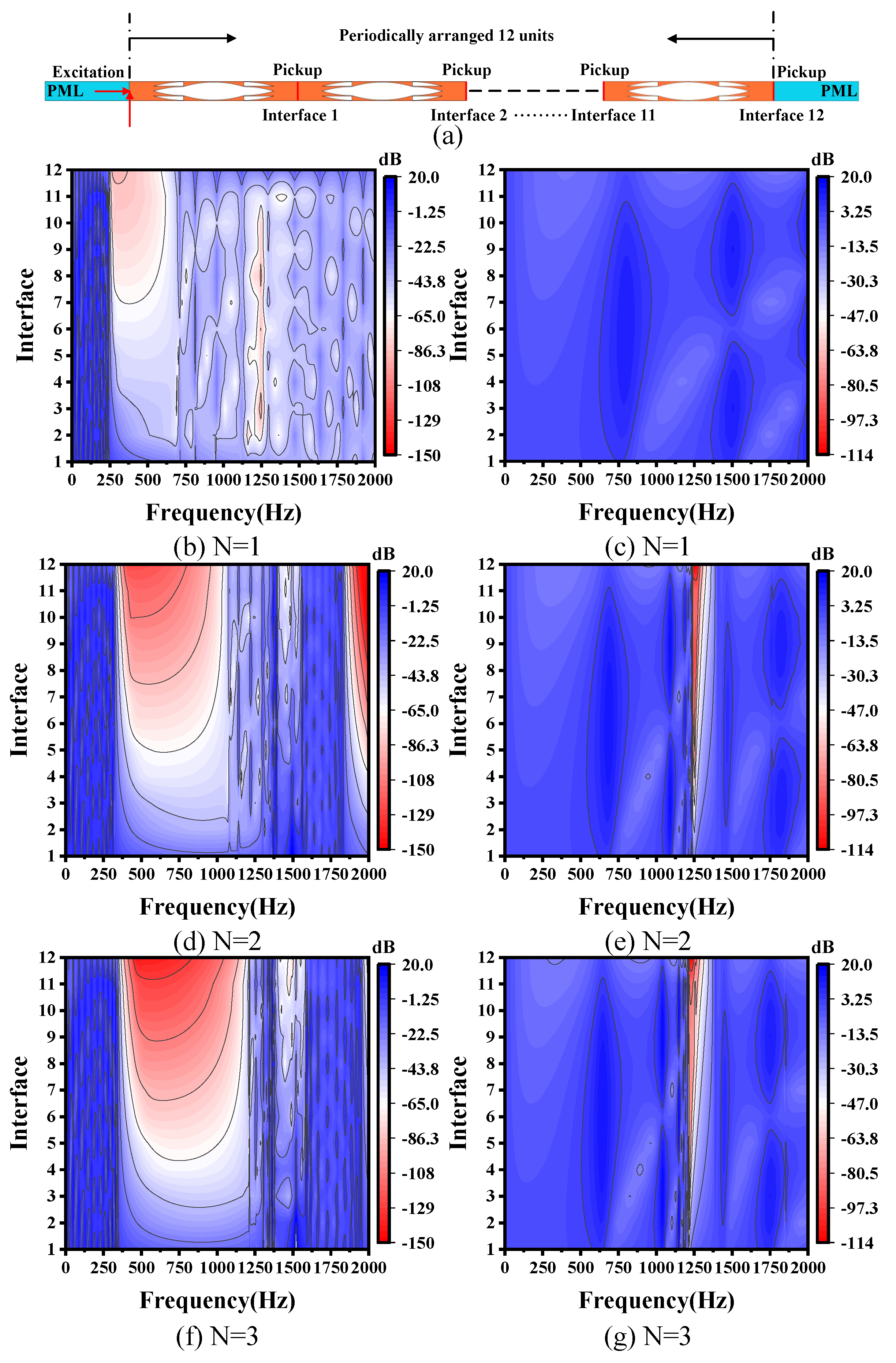
5. Interface Frequency Response
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yu, X.L.; Zhou, J. Mechanical metamaterials: Architected materials and unexplored properties. Mater. China 2019, 38, 14–21. [Google Scholar]
- Fang, X.; Wen, J.; Cheng, L.; Yu, D.; Zhang, H.; Gumbsch, P. Programmable gear-based mechanical metamaterials. Nat. Mater. 2022, 21, 869–876. [Google Scholar] [CrossRef] [PubMed]
- Yuan, M.; Cao, Z.; Luo, J.; Pang, Z. Helix structure for low frequency acoustic energy harvesting. Rev. Sci. Instrum. 2018, 89, 055002. [Google Scholar] [CrossRef]
- Li, L.; Su, K.; Liu, H.; Yang, Q.; Li, L.; Xie, M. Elastic metasurface for flexural wave refraction based on acoustic black hole. J. Appl. Phys. 2023, 133, 105103. [Google Scholar] [CrossRef]
- Yin, J.F.; Cai, L.; Fang, X.; Xiao, Y.; Yang, H.B.; Zhang, H.J.; Zhong, J.; Zhao, H.G.; Yu, D.L.; Wen, J.H. Review on research progress of mechanical metamaterials and their applications in vibration and noise control. Adv. Mech. 2022, 52, 508–586. [Google Scholar]
- Mironov, M. Propagation of a flexural wave in a plate whose thickness decreases smoothly to zero in a finite interval. Sov. Phys. Acoust. 1988, 34, 318–319. [Google Scholar]
- Krylov, V.; Tilman, F. Acoustic ‘black holes’ for flexural waves as effective vibration dampers. J. Sound Vib. 2003, 274, 605–619. [Google Scholar] [CrossRef]
- O’Boy, D.J.; Bowyer, E.P.; Krylov, V.V. Point mobility of a cylindrical plate incorporating a tapered hole of power-law profile. J. Acoust. Soc. Am. 2011, 129, 3475–3482. [Google Scholar] [CrossRef] [PubMed]
- Krylov, V.V. On the velocities of localized vibration modes in immersed solid wedges. J. Acoust. Soc. Am. 1998, 103, 767–770. [Google Scholar] [CrossRef]
- Krylov, V.V. New type of vibration dampers utilising the effect of acoustic ‘black holes’. Acta Acust. United Acust. 2004, 90, 830–837. [Google Scholar]
- O’Boy, D.J.; Krylov, V.V.; Kralovic, V. Damping of flexural vibrations in rectangular plates using the acoustic black hole effect. J. Sound Vib. 2010, 329, 4672–4688. [Google Scholar] [CrossRef]
- Zhao, L.; Semperlotti, F. Embedded acoustic black holes for semi-passive broadband vibration attenuation in thin-walled structures. J. Sound Vib. 2017, 388, 42–52. [Google Scholar] [CrossRef]
- Tang, L.; Cheng, L. Broadband locally resonant band gaps in periodic beam structures with embedded acoustic black holes. J. Appl. Phys. 2017, 121, 194901. [Google Scholar] [CrossRef]
- Tang, L.; Cheng, L. Ultrawide band gaps in beams with double-leaf acoustic black hole indentations. J. Acoust. Soc. Am. 2017, 142, 2802–2807. [Google Scholar] [CrossRef] [PubMed]
- Gao, N.; Wei, Z.; Zhang, R.; Hou, H. Low-frequency elastic wave attenuation in a composite acoustic black hole beam. Appl. Acoust. 2019, 154, 68–76. [Google Scholar] [CrossRef]
- Lyu, X.; Ding, Q.; Yang, T. Merging phononic crystals and acoustic black holes. Appl. Math. Mech. 2020, 41, 279–288. [Google Scholar] [CrossRef]
- Deng, J.; Guasch, O.; Maxit, L.; Gao, N. A metamaterial consisting of an acoustic black hole plate with local resonators for broadband vibration reduction. J. Sound Vib. 2022, 526, 116803. [Google Scholar] [CrossRef]
- Ji, H.; Han, B.; Cheng, L.; Inman, D.J.; Qiu, J. Frequency attenuation band with low vibration transmission in a finite-size plate strip embedded with 2D acoustic black holes. Mech. Syst. Signal Process. 2022, 163, 108149. [Google Scholar] [CrossRef]
- Sheng, H.; He, M.X.; Ding, Q. Vibration suppression by mistuning acoustic black hole dynamic vibration absorbers. J. Sound Vib. 2023, 542, 117370. [Google Scholar] [CrossRef]
- Sheng, H.; He, M.X.; Lyu, X.F.; Ding, Q. Ultra-low frequency broadband gap optimization of 1D periodic structure with dual power-law acoustic black holes. J. Intell. Mater. Syst. Struct. 2022, 33, 532–546. [Google Scholar] [CrossRef]
- He, C.; Lim, K.M.; Zhang, F. A novel periodic beam with multilayer acoustic black holes for deep sub-wavelength vibration attenuation. Acta Mech. 2023, 234, 2585–2598. [Google Scholar] [CrossRef]
- Huang, H.H.; Sun, C.T.; Huang, G.L. On the negative effective mass density in acoustic metamaterials. Int. J. Eng. Sci. 2009, 47, 610–617. [Google Scholar] [CrossRef]
- Huang, G.L.; Sun, C.T. Band Gaps in a Multiresonator Acoustic Metamaterial. J. Vib. Acoust. 2010, 031003. [Google Scholar] [CrossRef]
- Song, G.Y.; Cheng, Q.; Huang, B.; Dong, H.Y.; Cui, T.J. Broadband fractal acoustic metamaterials for low-frequency sound attenuation. Appl. Phys. Lett. 2016, 109, 131901. [Google Scholar] [CrossRef]
- Li, L.; Lv, R.; Cai, A.; Xie, M.; Chen, Y.; Huang, G. Low-frequency vibration suppression of a multi-layered elastic metamaterial shaft with discretized scatters. J. Phys. D Appl. Phys. 2018, 52, 055105. [Google Scholar] [CrossRef]
- Gorshkov, V.; Sareh, P.; Navadeh, N.; Tereshchuk, V.; Fallah, A.S. Multi-resonator metamaterials as multi-band metastructures. Mater. Des. 2021, 202, 109522. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, Z.; Mei, J.; Liu, Y. Acoustic band gaps for a two-dimensional periodic array of solid cylinders in viscous liquid. J. Phys. Condens. Matter 2003, 15, 8207. [Google Scholar] [CrossRef]
- Oudich, M.; Badreddine Assouar, M. Complex band structures and evanescent Bloch waves in two-dimensional finite phononic plate. J. Appl. Phys. 2012, 112, 104509. [Google Scholar] [CrossRef]
- Laude, V.; Achaoui, Y.; Benchabane, S.; Khelif, A. Evanescent Bloch waves and the complex band structure of phononic crystals. Phys. Rev. B 2009, 80, 092301. [Google Scholar] [CrossRef]
- Bavencoffe, M.; Morvan, B.; Izbicki, J.L.; Hladky-Hennion, A.C. Characterization of evanescent ultrasonic waves in a band gap of a 1D phononic crystal. In Proceedings of the 2009 IEEE International Ultrasonics Symposium, Rome, Italy, 20–23 September 2009; pp. 1024–1027. [Google Scholar]
- Achaoui, Y.; Khelif, A.; Benchabane, S.; Robert, L.; Laude, V. Experimental observation of locally-resonant and Bragg band gaps for surface guided waves in a phononic crystal of pillars. Phys. Rev. B 2011, 83, 104201. [Google Scholar] [CrossRef]
- Zhou, X.Z.; Wang, Y.S.; Zhang, C. Effects of material parameters on elastic band gaps of two-dimensional solid phononic crystals. J. Appl. Phys. 2009, 106, 014903. [Google Scholar] [CrossRef]
- Yan, Z.Z.; Wang, Y.S. Wavelet-based method for calculating elastic band gaps of two-dimensional phononic crystals. Phys. Rev. B 2006, 74, 224303. [Google Scholar] [CrossRef]
- Veres, I.A.; Berer, T.; Matsuda, O. Complex band structures of two dimensional phononic crystals: Analysis by the finite element method. J. Appl. Phys. 2013, 114, 083519. [Google Scholar] [CrossRef]
- Fang, X.; Wen, J.; Bonello, B.; Yin, J.; Yu, D. Ultra-low and ultra-broad-band nonlinear acoustic metamaterials. Nat. Commun. 2017, 8, 1288. [Google Scholar] [CrossRef] [PubMed]
- Ho, K.M.; Cheng, C.K.; Yang, Z.; Zhang, X.X.; Sheng, P. Broadband locally resonant sonic shields. Appl. Phys. Lett. 2003, 83, 5566–5568. [Google Scholar] [CrossRef]
- Xiao, Y.; Mace, B.R.; Wen, J.; Wen, X. Formation and coupling of band gaps in a locally resonant elastic system comprising a string with attached resonators. Phys. Lett. A 2011, 375, 1485–1491. [Google Scholar] [CrossRef]
- Yu, D.; Liu, Y.; Wang, G.; Cai, L.; Qiu, J. Low frequency torsional vibration gaps in the shaft with locally resonant structures. Phys. Lett. A 2006, 348, 410–415. [Google Scholar] [CrossRef]
- Robillard, J.F.; Bucay, J.; Deymier, P.A.; Shelke, A.; Muralidharan, K.; Merheb, B.; Vasseur, J.O.; Sukhovich, A.; Page, J.H. Resolution limit of a phononic crystal superlens. Phys. Rev. B 2011, 83, 224301. [Google Scholar] [CrossRef]
- Wang, Y.F.; Wang, Y.S.; Laude, V. Wave propagation in two-dimensional viscoelastic metamaterials. Phys. Rev. B 2015, 92, 104110. [Google Scholar] [CrossRef]
- Wen, J.H.; Cai, L.; Yu, D.L.; Xiao, Y.; Zhao, H.G.; Yin, J.F.; Yang, H.B. Fundamental Theories and Applications of Acoustic Metamaterials; Science Press: Beijing, China, 2018. [Google Scholar]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, L.; Jiang, S.; Bai, J.; Su, K.; Hu, H.; Zhang, L. A Single-Phase Lightweight Double-Leaf Multi-Stage Acoustic Black Hole Model of Metamaterial. Appl. Sci. 2024, 14, 2875. https://doi.org/10.3390/app14072875
Li L, Jiang S, Bai J, Su K, Hu H, Zhang L. A Single-Phase Lightweight Double-Leaf Multi-Stage Acoustic Black Hole Model of Metamaterial. Applied Sciences. 2024; 14(7):2875. https://doi.org/10.3390/app14072875
Chicago/Turabian StyleLi, Lixia, Shanhe Jiang, Jin Bai, Kun Su, Haiteng Hu, and Lei Zhang. 2024. "A Single-Phase Lightweight Double-Leaf Multi-Stage Acoustic Black Hole Model of Metamaterial" Applied Sciences 14, no. 7: 2875. https://doi.org/10.3390/app14072875
APA StyleLi, L., Jiang, S., Bai, J., Su, K., Hu, H., & Zhang, L. (2024). A Single-Phase Lightweight Double-Leaf Multi-Stage Acoustic Black Hole Model of Metamaterial. Applied Sciences, 14(7), 2875. https://doi.org/10.3390/app14072875






